Diff-SySC: An Approach Using Diffusion Models for Semi-Supervised Image Classification

Diff-SySC: 一种基于扩散模型 (Diffusion Models) 的半监督图像分类方法

Abstract:

摘要：

Diffusion models have revolutionized the field of generative machine learning due to their effectiveness in capturing complex, multimodal data distributions. Semi-supervised learning represents a technique that allows the extraction of information from a large corpus of unlabeled data, assuming that a small subset of labeled data is provided. While many generative methods have been previously used in semi-supervised learning tasks, only few approaches have integrated diffusion models in such a context. In this work, we are adapting state-of-the-art generative diffusion models to the problem of semi-supervised image classification. We propose Diff-SySC, a new semi-supervised, pseudo-labeling pipeline which uses a diffusion model to learn the conditional probability distribution characterizing the label generation process. Experimental evaluations highlight the robustness of Diff-SySC when evaluated on image classification benchmarks and show that it outperforms related work approaches on CIFAR-10 and STL-10, while achieving competitive performance on CIFAR-100. Overall, our proposed method outperforms the related work in $90.74%$ of the cases.

扩散模型 (Diffusion models) 因其在捕捉复杂多模态数据分布方面的卓越表现，彻底改变了生成式机器学习领域。半监督学习作为一种技术，能够在提供少量标注数据的前提下，从大量无标注数据中提取信息。虽然此前已有多种生成式方法应用于半监督学习任务，但将扩散模型整合到该场景的研究却寥寥无几。本研究将最先进的生成式扩散模型适配至半监督图像分类问题，提出Diff-SySC——一种新型半监督伪标签生成框架，该框架利用扩散模型学习标签生成过程的条件概率分布。实验评估表明，Diff-SySC在图像分类基准测试中展现出强大鲁棒性：在CIFAR-10和STL-10数据集上超越现有方法，在CIFAR-100上达到具有竞争力的性能。总体而言，我们提出的方法在$90.74%$的案例中优于相关研究。

1 INTRODUCTION

1 引言

Semi-supervised learning (SSL) represents a machine learning (ML) paradigm wherein a model leverages both labeled and unlabeled data to achieve enhanced predictive performance. Traditional supervised learning relies solely on labeled data for training, thus requiring a labour-intensive and costly annotation process. In contrast, SSL reduces the labeling effort by utilizing abundant unlabeled data alongside a smaller set of labeled samples. The labeled subset provides explicit guidance for the model, allowing it to learn from known examples. The unlabeled data is used to enhance the model’s understanding of the broader data distribution and to improve generalization. SSL is particularly valuable in scenarios where obtaining annotations is resource-intensive or impractical, as it maximizes the utility of available labeled data while harnessing the vast, often readily accessible, unlabeled data for achieving enhanced performance (Yang et al., 2023).

半监督学习 (SSL) 是一种机器学习范式，模型通过同时利用标注和未标注数据来提升预测性能。传统监督学习仅依赖标注数据进行训练，需要耗费大量人力成本的标注流程。相比之下，SSL通过结合少量标注样本与大量未标注数据，显著降低了标注需求。标注数据子集为模型提供明确指导，使其能从已知样本中学习；未标注数据则用于增强模型对整体数据分布的理解，从而提升泛化能力。在标注获取成本高昂或不可行的场景中，SSL展现出独特价值——它既能最大化有限标注数据的效用，又能利用海量易获取的未标注数据来提升模型表现 (Yang et al., 2023)。

Generative learning comprises a set of methods which focus on modeling and understanding the underlying statistical structure of a given dataset. Diffusion models represent a class of generative models that simulate the diffusion process of particles through a system, capturing the dynamics of how data spreads or evolves over time (Dhariwal and Nichol, 2021). While generative models such as Generative Adversarial Networks (GANs) or Variation al Autoencoders (VAEs) have been extensively explored in the past for designing semi-supervised learning procedures (Yang et al., 2023), only few studies have employed diffusion models for this task (You et al., 2023; Gong et al., 2023). These approaches use diffusion models as generative processes for images, by sampling new instances to be added to the training set.

生成式学习 (Generative learning) 包含一系列专注于建模和理解给定数据集底层统计结构的方法。扩散模型 (Diffusion models) 是一类通过模拟粒子在系统中的扩散过程来捕捉数据随时间传播或演化动态的生成模型 (Dhariwal and Nichol, 2021)。虽然过去已有大量研究探索使用生成对抗网络 (GANs) 或变分自编码器 (VAEs) 等生成模型来设计半监督学习流程 (Yang et al., 2023)，但仅有少数研究采用扩散模型完成该任务 (You et al., 2023; Gong et al., 2023)。这些方法将扩散模型作为图像的生成过程，通过采样新实例来扩充训练集。

This paper introduces Diff-SySC, a new approach based on diffusion models for semi-supervised image classification. Our approach uses a diffusion model for label generation. Our goal is to train a model to learn the distribution $p(\bar{y}\vert x)$ , where $x$ denotes the input image, $y$ represents the corresponding target label of $x$ and $\bar{y}$ describes an aggregated label obtained using the neighbors of $y$ . We design a self-training semi-supervised procedure using the trained diffusion model to progressively generate pseudo-labels for the unlabeled data. To the best of our knowledge, our proposal of directly using diffusion to model the labeled data distribution in a semi-supervised fashion is the first of its kind. To summarize, the main contributions of the paper are the following: (1) integration of diffusion models for label generation in semi- supervised learning; and (2) design of an iterative pseudo-labeling pipeline that is robust to noisy labels. To achieve the proposed goals, our work aims to answer two research questions: RQ1. How can diffusion models be used for designing a semi-supervised image classification approach? and RQ2. How robust is the semi-supervised diffusion-based method when evaluated on literature established image classification benchmarks and how does its performance compare to related work?

本文介绍了Diff-SySC，一种基于扩散模型 (diffusion model) 的半监督图像分类新方法。我们的方法使用扩散模型进行标签生成，目标是训练模型学习分布 $p(\bar{y}\vert x)$ ，其中 $x$ 表示输入图像， $y$ 代表 $x$ 对应的目标标签， $\bar{y}$ 描述通过 $y$ 的邻域标签聚合得到的标签。我们设计了一个自训练半监督流程，利用训练好的扩散模型逐步为未标注数据生成伪标签。据我们所知，这是首次提出直接以半监督方式使用扩散模型对标注数据分布进行建模的工作。主要贡献包括：(1) 将扩散模型集成到半监督学习的标签生成过程中；(2) 设计了抗噪声标签的迭代式伪标签生成流程。为实现目标，本研究旨在回答两个研究问题：RQ1. 如何利用扩散模型设计半监督图像分类方法？RQ2. 基于扩散的半监督方法在经典图像分类基准测试中的鲁棒性如何？其性能与相关工作相比有何优劣？

The rest of the paper is organized as follows. Section 2 briefly presents the main literature advance- ments in the approached fields. The methodology employed for designing and validating our Diff-SySC model is introduced in Section 3. Section 4 presents the experimental analysis, while a discussion of the results is conducted in Section 5. Section 6 concludes the paper and indicates directions for future work.

本文的其余部分结构如下。第2节简要介绍了相关领域的主要文献进展。第3节阐述了设计和验证Diff-SySC模型所采用的方法论。第4节展示了实验分析，而第5节对结果进行了讨论。第6节总结了全文并指出了未来工作的方向。

2 BACKGROUND

2 背景

2.1 Semi-Supervised Image Classification

2.1 半监督图像分类

In their survey, (Yang et al., 2023) divide the SSL approaches in several classes of methods: generative methods, consistency regular iz ation methods, graphbased methods, pseudo-labeling methods and hybrid methods. The first category comprises different methodologies using generative models with the goal of improving the performance of semi-supervised class if i ers. These strategies include the use of GANs and VAEs for pre-training, the integration of unsupervised training objectives and generative architectural components in supervised class if i ers (Spring e nberg, 2016) or the generation of additional training samples by class conditioning. Recently, diffusion models have been incorporated into semi-supervised training pipelines. (You et al., 2023) employed a diffusion model for augmenting the training set of a semisupervised classifier, by generating new images for multiple labels. The approach was able to outperform strong baselines on the ImageNet dataset, achieving an accuracy of $59%$ using one label per class and $74.4%$ when using five labels per class.

(Yang et al., 2023) 在其综述中将SSL (半监督学习) 方法划分为以下几类：生成式方法、一致性正则化方法、基于图的方法、伪标签方法以及混合方法。第一类方法涵盖多种利用生成模型提升半监督分类器性能的技术，包括使用GAN (生成对抗网络) 和VAE (变分自编码器) 进行预训练、在监督分类器中整合无监督训练目标与生成架构组件 (Springenberg, 2016) ，或通过类别条件生成额外训练样本。近期，扩散模型也被引入半监督训练流程。(You et al., 2023) 采用扩散模型为多标签生成新图像以扩充半监督分类器的训练集，该方法在ImageNet数据集上以每类1个标注达到59%准确率、每类5个标注达到74.4%准确率的性能超越基线模型。

The majority of the SSL methods employing consistency regular iz ation (Zhang and Qi, 2020) follow the Teacher-Student structure that involves training a Teacher model using the labeled data, and then using this model to train a Student model using the unlabeled data. Some approaches opted for using the same network as both Teacher and Student models. One such example is the Π-Model (Sajjadi et al., 2016), which applies a consistency regularize r on the predictions obtained by the network using two different augmentations of the same image. The Mean Teacher (Tarvainen and Valpola, 2017) method computes an exponential moving average (EMA) of the network’s parameters to build a teacher model. The Mean Teacher approach was evaluated on the CIFAR, SVHN and ImageNet datasets and it significantly improved the state-of-the-art results on ImageNet with $10%$ labels by reaching an error rate of $9.11%$ . The pseudo-labeling based SSL methods produce artificial labels for the unlabeled data and use them in the following training stages. There are many variations of this semi-supervised pipeline, with methods such as Pseudo-label, Noisy Student (Yang et al., 2023), Meta Pseudo Labels (MPL) (Pham et al., 2021) or SimCLRv2 (Chen et al., 2020).

大多数采用一致性正则化 (Zhang and Qi, 2020) 的SSL方法遵循教师-学生结构，即先使用标注数据训练教师模型，再利用该模型通过未标注数据训练学生模型。部分方法选择使用相同网络同时作为教师和学生模型，例如Π-Model (Sajjadi et al., 2016) 会对同一图像两种不同增强版本生成的预测施加一致性正则器。Mean Teacher (Tarvainen and Valpola, 2017) 方法则通过计算网络参数的指数移动平均 (EMA) 来构建教师模型。该方法在CIFAR、SVHN和ImageNet数据集上进行了评估，在使用 $10%$ 标注数据的ImageNet任务中将错误率降至 $9.11%$ ，显著提升了当时的最高水平。基于伪标签的SSL方法会为未标注数据生成人工标签，并将其用于后续训练阶段。这类半监督流程存在多种变体，包括Pseudo-label、Noisy Student (Yang et al., 2023)、Meta Pseudo Labels (MPL) (Pham et al., 2021) 和SimCLRv2 (Chen et al., 2020) 等方法。

Hybrid methods incorporate multiple complementary techniques in order to achieve improved performance. MixMatch (Berthelot et al., 2019) is an example of such an approach which produces pseudolabels by averaging and sharpening the predictions for multiple augmentations of a sample. MixMatch was able to consistently outperform baselines such as the Π-model, Pseudo-labeling and Mean Teacher on CIFAR-10 and SVHN. FixMatch (Sohn et al., 2020) builds on the intuition given by other hybrid methods, but proposes a simplified and more effective training procedure. FixMatch generates pseudo-labels for unlabeled data by passing weakly augmented images through the classification network. The generated pseudo-labels are used during training as targets for strong augmentations of the images. FixMatch was evaluated on the CIFAR, SVHN, STL-10 and ImageNet datasets and it was able to outperform more complex baselines such as MixMatch, Pseudolabeling, Mean Teacher and the Π-Model. CRMatch (Fan et al., 2023) extended FixMatch by adding a feature loss and a rotation prediction training objective. CRMatch was able to consistently outperform other approaches on multiple datasets. (Zheng et al., 2022) proposed the concept of SSL based on similarity matching (SimMatch). In SimMatch, the key component is the integration of consistency regularization at both semantic and instance levels. SimMatch achieved state-of-the-art performance on the CIFAR and ImageNet benchmarks. SimMatchV2 (Zheng et al., 2023) introduced multiple consistency regularization terms, by defining a graph in which sample images and their augmentations represent nodes and edges are weighted by the similarities between nodes.

混合方法通过结合多种互补技术来提升性能表现。MixMatch (Berthelot et al., 2019) 是该类方法的代表，它通过对样本多次增强的预测结果进行平均化和锐化操作来生成伪标签。在CIFAR-10和SVHN数据集上，MixMatch持续超越了Π-model、伪标签和均值教师等基线方法。FixMatch (Sohn et al., 2020) 基于其他混合方法的思路，提出了一种更简洁高效的训练流程：首先对弱增强图像通过分类网络生成伪标签，随后将这些伪标签作为强增强图像的目标进行训练。该方法在CIFAR、SVHN、STL-10和ImageNet数据集上的表现优于MixMatch、伪标签、均值教师及Π-Model等复杂基线。CRMatch (Fan et al., 2023) 通过引入特征损失和旋转预测训练目标对FixMatch进行扩展，在多个数据集上实现了持续领先。(Zheng et al., 2022) 提出基于相似度匹配的自监督学习框架SimMatch，其核心在于语义级和实例级一致性正则化的协同整合，该方法在CIFAR和ImageNet基准测试中达到最先进水平。SimMatchV2 (Zheng et al., 2023) 通过构建以样本图像及其增强版本为节点、节点相似度为边权重的图结构，引入了多重一致性正则化项。

2.2 Diffusion Models for Classification

2.2 用于分类的扩散模型 (Diffusion Models)

Denoising Diffusion Probabilistic Models (DDPM) (Dhariwal and Nichol, 2021) are generative models which learn to sample new data points by defining an iterative denoising procedure. DDPMs consist of forward and backward diffusion processes. The forward process progressively adds Gaussian noise to a data sample $x_{0}$ until it becomes indistinguishable from an isotropic normal distribution. In the backward process, a neural network is trained to approximate the conditional probabilities needed for sampling the original image $x_{0}$ from the corrupted version $x_{T}$ .

去噪扩散概率模型 (Denoising Diffusion Probabilistic Models, DDPM) (Dhariwal and Nichol, 2021) 是一种通过学习迭代去噪过程来生成新数据点的生成模型。DDPM包含前向扩散和反向扩散两个过程。前向过程逐步向数据样本 $x_{0}$ 添加高斯噪声，直至其与各向同性正态分布无法区分。在反向过程中，训练神经网络来近似从损坏版本 $x_{T}$ 采样原始图像 $x_{0}$ 所需的条件概率。

The Classification and Regression Diffusion (CARD) framework introduced by (Han et al., 2022) extended generative diffusion models to classification and regression tasks. The proposed approach first trains a classifier network $f_{\Phi}$ in a supervised manner on the available dataset $\mathcal{D}$ to approximate the expected value of the output $y$ given the input $x$ . Afterwards, a diffusion model is trained, by iterative ly corrupting the ground truth label values $y_{0}$ . The forward diffusion process outputs $y_{T}$ , which is characterized by a normal conditional probability distribution centered around the classifier prediction $f_{\Phi}(x)$ . During the backward diffusion process, the CARD model learns to reconstruct the original $y_{0}$ label value.

(Han et al., 2022)提出的分类回归扩散(CARD)框架将生成式扩散模型扩展至分类和回归任务。该方法首先在可用数据集$\mathcal{D}$上以监督方式训练分类器网络$f_{\Phi}$，用于近似给定输入$x$时输出$y$的期望值。随后通过迭代破坏真实标签值$y_{0}$来训练扩散模型。前向扩散过程输出的$y_{T}$服从以分类器预测值$f_{\Phi}(x)$为中心的条件正态分布。在反向扩散过程中，CARD模型学习重建原始标签值$y_{0}$。

(Chen et al., 2023) used the innovations brought by CARD to introduce a new generative perspective on the task of learning with noisy labels. In their framework, Label-Retrieval-Augmented Diffusion (LRA-Diffusion), the labeling of a sample is viewed as a stochastic process. Intuitively, LRADiffusion aims to recreate through a diffusion pro- cess the true, clean label of a sample starting from a noisy one. Due to the fact that the clean labels are not available, the model uses annotations refined by aggregation over the nearest neighbors. In order to identify the neighbors of a data point, LRA-Diffusion computes distances in the embedding space learned by an unsupervised feature extractor $f_{p}$ . The labels of the neighbors of a data point are used to construct an aggregated label, ${\bar{y}}$ , which is corrupted throughout the forward diffusion process. To reconstruct ${\bar{y}}$ , the backward diffusion process makes use of representations learned by $f_{p}$ . By augmenting the training process with labels retrieved from the neighborhood of the learned representations, the architecture becomes highly resistant to noisy labels.

(Chen et al., 2023) 利用 CARD 的创新性成果，为带噪声标签学习任务提出了全新的生成视角。在其框架 Label-Retrieval-Augmented Diffusion (LRA-Diffusion) 中，样本标注被视为随机过程。直观上，LRA-Diffusion 旨在通过扩散过程从含噪标签重建样本的真实干净标签。由于无法获取干净标签，该模型采用最近邻聚合精修的标注结果。为识别数据点的邻域样本，LRA-Diffusion 通过无监督特征提取器 $f_{p}$ 学习嵌入空间的距离度量。数据点邻域标签用于构建聚合标签 ${\bar{y}}$ ，该标签在前向扩散过程中持续被破坏。为重建 ${\bar{y}}$ ，反向扩散过程利用 $f_{p}$ 学习到的表征。通过用学习表征邻域检索的标签增强训练过程，该架构展现出极强的噪声标签鲁棒性。

3 METHODOLOGY

3 方法论

For answering research question RQ1, this section introduces the methodology employed in developing and validating our Diff-SySC approach.

为回答研究问题RQ1，本节介绍开发和验证Diff-SySC方法所采用的方法论。

Let us consider the input space $\mathbb{X}$ and a set of given classes/labels $C={c_{1},c_{2},\ldots,c_{k}}$ (the output space). Assuming that each input instance belongs to a class, we are given a single-label classification task formalized as a function $f:\mathbb{X}\to C$ . In this formalization, $f(x)$ represents the class assigned to an object $x\in\mathbb{X}$ . In ML, the classification task should be formalized as searching for an approximation of $f$ by minimizing a loss (error) function $\mathcal{L}$ defined on the input space. We further consider the SSL setting, in which we have a dataset $X\subset\mathbb{X}$ consisting of a small number of labeled samples $(X^{\ell})$ and a larger number of unlabeled ones $(X^{u})$ such that $X=X^{\bar{\ell}}\cup X^{u}$ and $X^{\ell}\cap X^{u}=\emptyset$ . For each instance $x\in X^{\ell}$ its label is known and is denoted as $y^{x}\in C$ . Let us denote by $Y^{\ell}={y^{x}|x\in X^{\ell}}$ the set of available labels for the instances from $X^{\ell}$ .

让我们考虑输入空间 $\mathbb{X}$ 和一组给定的类别/标签 $C={c_{1},c_{2},\ldots,c_{k}}$ (输出空间)。假设每个输入实例属于一个类别，我们将单标签分类任务形式化为函数 $f:\mathbb{X}\to C$。在这种形式化中，$f(x)$ 表示分配给对象 $x\in\mathbb{X}$ 的类别。在机器学习中，分类任务应形式化为通过最小化定义在输入空间上的损失(误差)函数 $\mathcal{L}$ 来寻找 $f$ 的近似。我们进一步考虑半监督学习(SSL)设置，其中我们有一个数据集 $X\subset\mathbb{X}$，由少量标记样本 $(X^{\ell})$ 和大量未标记样本 $(X^{u})$ 组成，满足 $X=X^{\bar{\ell}}\cup X^{u}$ 且 $X^{\ell}\cap X^{u}=\emptyset$。对于每个实例 $x\in X^{\ell}$，其标签已知并表示为 $y^{x}\in C$。我们用 $Y^{\ell}={y^{x}|x\in X^{\ell}}$ 表示来自 $X^{\ell}$ 的实例可用标签集合。

3.1 Overview of Diff-SySC

3.1 Diff-SySC 概述

We introduce the Diff-SySC approach that integrates a LRA-Diffusion model into a semi-supervised pipeline. Figure 1 provides a high-level overview of Diff-SySC, highlighting the motivation behind our proposal. On the left and right sides, we show a represent ation of the feature extractor embedding space. As with any semi-supervised context, we rely on several assumptions. The clustering assumption implies that the data samples sharing the same labels tend to form clusters in a lower-dimensionality manifold. The continuity assumption implies that close data samples have a strong likelihood of sharing the same label. The low-density assumption indicates that decision boundary planes do not intersect with highdensity regions (Yang et al., 2023).

我们介绍了Diff-SySC方法，该方法将LRA-Diffusion模型集成到半监督流程中。图1: 提供了Diff-SySC的高级概览，突出了我们提案背后的动机。在左右两侧，我们展示了特征提取器嵌入空间的表示。与任何半监督场景一样，我们依赖于几个假设。聚类假设意味着共享相同标签的数据样本倾向于在低维流形中形成聚类。连续性假设意味着相近的数据样本有很大可能共享相同标签。低密度假设表明决策边界平面不会与高密度区域相交 (Yang et al., 2023)。

The center of Figure 1 presents the training process of the diffusion model. We train a LRA- Diffusion model through the methodology proposed in (Chen et al., 2023). The feature embeddings of the input sample $x.$ obtained using a pre-trained CLIP (Radford et al., 2021) model, are used as conditioning information in the backward diffusion pro- cess. Diff-SySC is an iterative procedure that initially trains a LRA-Diffusion model $\mathcal{D}_{0}$ on the available labeled data $\left\langle X^{\ell},Y^{\ell}\right\rangle$ . Subsequently, the trained model is used to generate pseudo-annotations for the unlabeled dataset $X^{u}$ , which are added to $\left\langle X^{\ell},Y^{\ell}\right\rangle$ . The training stage of the Diff-SySC approach is described in Algorithm 1. Thus, for each iteration $i.$ , a

图 1 的中心展示了扩散模型 (diffusion model) 的训练过程。我们通过 (Chen et al., 2023) 提出的方法训练了一个 LRA-Diffusion 模型。使用预训练 CLIP (Radford et al., 2021) 模型获取输入样本 $x.$ 的特征嵌入 (feature embeddings)，作为反向扩散过程的条件信息。Diff-SySC 是一个迭代过程，首先在可用标注数据 $\left\langle X^{\ell},Y^{\ell}\right\rangle$ 上训练初始 LRA-Diffusion 模型 $\mathcal{D}_{0}$，随后使用训练好的模型为未标注数据集 $X^{u}$ 生成伪标注 (pseudo-annotations)，并将其加入 $\left\langle X^{\ell},Y^{\ell}\right\rangle$。Diff-SySC 方法的训练阶段如算法 1 所述。因此，对于每次迭代 $i.$，一个

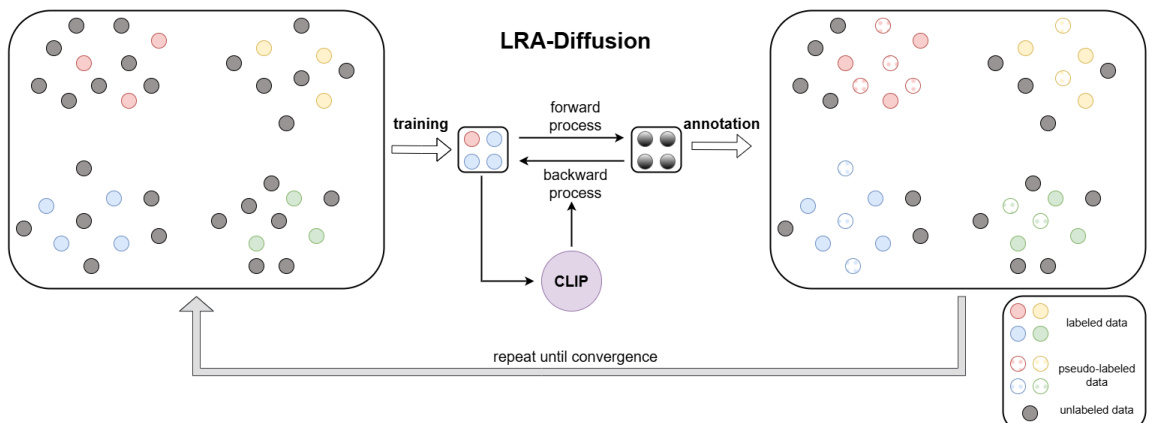
Figure 1: General overview of Diff-SySC. A LRA-Diffusion model is trained on the labeled dataset. The confident pseudolabels generated at the end of one iteration are added to the labeled set and the training is repeated until convergence.

图 1: Diff-SySC 总体框架。LRA-Diffusion 模型在标注数据集上进行训练。每次迭代结束时生成的高置信度伪标签会被加入标注集，该训练过程重复直至收敛。

LRA-Diffusion $\mathcal{D}_{i}$ is trained on the current labeled dataset $\left\langle X^{\ell},Y^{\ell}\right\rangle$ .

LRA-Diffusion $\mathcal{D}_{i}$ 在当前标注数据集 $\left\langle X^{\ell},Y^{\ell}\right\rangle$ 上进行训练。

Once the training of the model is finished, at the end of an iteration, the predictions of the model are calibrated using temperature scaling (Guo et al., 2017). This technique is employed in order to achieve a better reflection of the likelihood that the predicted classes are correct, by granting a more accurate quantification of the model’s confidence in its predictions. The optimal temperature parameter $\uptau$ is found using the validation dataset $\left<X^{\nu},Y^{\nu}\right>$ . More specifically, a range of temperature values is considered and the value which minimizes the Expected Calibration Error (Guo et al., 2017) on the validation set is selected. Using the trained model $\mathcal{D}_{i}$ and the temperature $\uptau$ , the confident pseudo-labels dataset $\langle X^{p},Y^{p}\rangle$ is constructed via annotation. The selection of confident predictions aids in limiting the amount of noisy labels introduced by the usage of pseudo-labels. Concurrently, the demonstrated robustness of LRA-Diffusion to noisy labels represents another strategy for reducing the impact of incorrect pseudo-labels.

模型训练完成后，在每次迭代结束时，使用温度缩放 (temperature scaling) (Guo et al., 2017) 对模型的预测结果进行校准。该技术通过更精确地量化模型对其预测结果的置信度，从而更好地反映预测类别的正确可能性。最优温度参数 $\uptau$ 通过验证数据集 $\left<X^{\nu},Y^{\nu}\right>$ 确定。具体而言，会考虑一系列温度值，并选择在验证集上使预期校准误差 (Expected Calibration Error) (Guo et al., 2017) 最小化的值。利用训练好的模型 $\mathcal{D}_{i}$ 和温度 $\uptau$，通过标注构建高置信度伪标签数据集 $\langle X^{p},Y^{p}\rangle$。选择高置信度预测有助于限制伪标签使用引入的噪声标签数量。同时，LRA-Diffusion 对噪声标签的鲁棒性也代表了另一种降低错误伪标签影响的策略。

The annotation process is further described in Algorithm 2. For each unlabeled data sample, the model’s label prediction and its confidence in the pseudo-label are computed. If the model’s confidence is larger than the threshold $\upgamma,$ the pseudo-label is stored in the annotated dataset.

标注过程在算法2中进一步描述。对于每个未标记的数据样本，计算模型的标签预测及其对伪标签的置信度。如果模型的置信度大于阈值 $\upgamma,$ 则将伪标签存储在标注数据集中。

The predicted class and its confidence are obtained as follows. For any input image $x.$ , we sample from the model’s learned distribution $p(\bar{y}\vert x)$ . The obtained logits ${z}=(z_{1},...,z_{k})$ are further divided by the temperature $\uptau$ . The scaled logits $z_{i}/\uptau$ are given as input to a Softmax function $\upsigma$ , where $\mathbf{\sigma}_{i}(z/\tau)=$ $\frac{\exp(z_{i}/\uptau)}{\sum_{j=1}^{k}\exp(z_{j}/\uptau)}$ , in order to obtain the calibrated class probabilities of the model for input $x$ . Thus, the predicted confidence for sample $x$ is the maximum entry in the vector $\upsigma(z/\uptau)$ , while the predicted label $y^{x}$ is the

预测类别及其置信度获取方式如下。对于任意输入图像$x.$，我们从模型学习到的分布$p(\bar{y}\vert x)$中采样。获得的logits${z}=(z_{1},...,z_{k})$需进一步除以温度参数$\uptau$。缩放后的logits$z_{i}/\uptau$作为Softmax函数$\upsigma$的输入，其中$\mathbf{\sigma}_{i}(z/\tau)=$$\frac{\exp(z_{i}/\uptau)}{\sum_{j=1}^{k}\exp(z_{j}/\uptau)}$，从而得到模型对输入$x$的校准类别概率。因此，样本$x$的预测置信度是向量$\upsigma(z/\uptau)$中的最大值，而预测标签$y^{x}$则是

Algorithm 1: Diff-SySC Training.

算法 1: Diff-SySC 训练

算法 2: Diff-SySC 标注
函数标注(D, X", ): XP←0; YP←0
for x in X" do
y ← predict_label(D, , x)
if conf > then conf ← predict_confidence(D, , x)
XP ← XP U {x}; YP ← YP U {y}
end
return (XP, YP)

index in the array corresponding to this maximum value.

数组中对应此最大值的索引。

The augmented labeled set, obtained after the annotation procedure, is further used to train a new LRA-Diffusion model $\mathcal{D}_{i},i\geq1$ from scratch. The process is repeated until any of the following convergence criteria are met: (1) all unlabeled samples have been annotated $(X^{u}=\varnothing)$ ); (2) there are no new confident predictions $(X^{p}=\varnothing)$ ); (3) a pre-defined maximum number of iterations $m$ has been reached. After the training iterations have been completed, the obtained models are evaluated on the validation set and the best performing model is selected. This model is afterwards evaluated on the test set.

经过标注流程增强的标记集，将被进一步用于从头训练新的LRA-Diffusion模型$\mathcal{D}_{i},i\geq1$。该过程会重复进行，直到满足以下任一收敛条件：(1) 所有未标记样本均已完成标注$(X^{u}=\varnothing)$；(2) 不再产生新的高置信度预测$(X^{p}=\varnothing)$；(3) 达到预设的最大迭代次数$m$。训练迭代完成后，所有模型将在验证集上进行评估，并选择性能最优的模型。最终该模型会在测试集上进行评估。

3.2 Performance Evaluation

3.2 性能评估

The performance of Diff-SySC is evaluated on image classification datasets with various proportions of labeled data. We randomly sample a fixed number of data points from each class to form the labeled dataset $\left\langle{{{\cal X}^{\ell}},{\cal Y}^{\ell}}\right\rangle$ . The validation dataset $\left<X^{\nu},Y^{\nu}\right>$ is built using $10%$ of the data, while all the remaining data samples are used to form the unlabeled subset $X^{u}$ . The performance of the trained model $\mathcal{D}{b e s t}$ is evaluated on a fixed test set. For each dataset and labeled set ratio, the training is repeated three times, using three different random seeds and corresponding data splits. The performance of the models is measured using the Error Rate, a standard evaluation metric used for semi-supervised image classification. It is defined as the proportion of incorrect predictions given by the model: $\begin{array}{r}{E r r=100\cdot\frac{n_{i n c o r r e c t}}{n_{t o t a l}}}\end{array}$ . The mean and standard deviation of the obtained error rate values are reported.

Diff-SySC的性能在具有不同比例标注数据的图像分类数据集上进行了评估。我们从每个类别中随机抽取固定数量的数据点构成标注数据集$\left\langle{{{\cal X}^{\ell}},{\cal Y}^{\ell}}\right\rangle$。验证数据集$\left<X^{\nu},Y^{\nu}\right>$使用$10%$的数据构建，其余所有数据样本则构成未标注子集$X^{u}$。训练好的模型$\mathcal{D}{b e s t}$在固定测试集上进行性能评估。针对每个数据集和标注集比例，使用三个不同的随机种子及对应数据划分重复训练三次。模型性能采用错误率（Error Rate）衡量，这是半监督图像分类的标准评估指标，定义为模型错误预测的比例：$\begin{array}{r}{E r r=100\cdot\frac{n_{i n c o r r e c t}}{n_{t o t a l}}}\end{array}$。最终报告所得错误率值的均值与标准差。

4 EXPERIMENTAL SETUP

4 实验设置

4.1 Datasets

4.1 数据集

Diff-SySC was evaluated on three semi-supervised image classification benchmarks. Table 1 summarizes the characteristics of the datasets: the number of available samples, the number of classes and the number of labeled samples used in our experiments.

Diff-SySC 在三个半监督图像分类基准上进行了评估。表 1: 总结了数据集的特性: 可用样本数量、类别数量以及实验中使用的标注样本数量。

Table 1: Summary of publicly available image datasets used for the training and evaluation of Diff-SySC.

表 1: 用于 Diff-SySC 训练和评估的公开图像数据集汇总

数据集	样本数量	类别数量	标注数据样本数量
CIFAR-10	60000	10	250/4000
CIFAR-100	60000	100	2500/10000
STL-10	113000	10	250/1000

CIFAR-10 and CIFAR-100 (Krizhevsky, 2009) represent balanced datasets of images of resolution 32 $\times32$ containing real world objects and animals