Set Distribution Networks: a Generative Model for Sets of Images
集合分布网络:一种面向图像集合的生成模型
Shuangfei Zhai, Walter Talbott, Miguel Angel Bautista, Carlos Guestrin, Josh M. Susskind Apple Inc. {szhai,wtalbott,m bautista martin,guestrin,jsusskind}@apple.com
双飞翟、Walter Talbott、Miguel Angel Bautista、Carlos Guestrin、Josh M. Susskind
Apple Inc.
{szhai, wtalbott, mbautistamartin, guestrin, jsusskind}@apple.com
Abstract
摘要
Images with shared characteristics naturally form sets. For example, in a face verification benchmark, images of the same identity form sets. For generative models, the standard way of dealing with sets is to represent each as a one hot vector, and learn a conditional generative model $p(\mathbf{x}|\mathbf{y})$ . This representation assumes that the number of sets is limited and known, such that the distribution over sets reduces to a simple multi no mi al distribution. In contrast, we study a more generic problem where the number of sets is large and unknown. We introduce Set Distribution Networks (SDNs), a novel framework that learns to autoencode and freely generate sets. We achieve this by jointly learning a set encoder, set disc rim in at or, set generator, and set prior. We show that SDNs are able to reconstruct image sets that preserve salient attributes of the inputs in our benchmark datasets, and are also able to generate novel objects/identities. We examine the sets generated by SDN with a pre-trained 3D reconstruction network and a face verification network, respectively, as a novel way to evaluate the quality of generated sets of images.
具有共同特征的图像自然形成集合。例如,在人脸验证基准中,同一身份的图像构成集合。对于生成模型,处理集合的标准方法是将其表示为独热向量,并学习条件生成模型 $p(\mathbf{x}|\mathbf{y})$。这种表示假设集合数量有限且已知,使得集合分布简化为简单的多项分布。相比之下,我们研究了一个更通用的问题:集合数量庞大且未知。我们提出了集合分布网络(Set Distribution Networks,SDN),这是一个能够学习自动编码和自由生成集合的新框架。通过联合学习集合编码器、集合判别器、集合生成器和集合先验,我们实现了这一目标。实验表明,SDN能够重建保留基准数据集中输入图像关键属性的集合,并能生成新物体/身份。我们分别使用预训练的3D重建网络和人脸验证网络来检验SDN生成的集合,以此作为评估生成图像集质量的新方法。
1 Introduction
1 引言
Generative modeling of natural images has seen great advances in recent years. State of the art models such as GANs [3], EBMs [9] and VAEs [19] can generate single images with high perceptual quality. In many applications, however, images often come in sets with shared characteristics. For example, a set might be constructed from images that belong to the same semantic category, or those that share the same attribute. When the number of sets is limited and known, one is able to easily extend a generative model to its conditional version by representing the set information as a one hot vector [15, 17]. We refer to these models as class conditional generative models (CCGMs). CCGMs are fundamentally limited by the pre-defined enumeration of all possible sets in their encoding, which prevents recognizing or generating sets that are not specifically encoded from the training distribution. Also, the number of parameters needed for a CCGM grows linearly w.r.t the number of sets (classes) during training, which limits its s cal ability.
近年来,自然图像的生成建模取得了巨大进展。诸如GANs [3]、EBMs [9]和VAEs [19]等最先进的模型能够生成具有高感知质量的单张图像。然而在许多应用中,图像往往以具有共享特征的集合形式出现。例如,一个集合可能由属于同一语义类别的图像组成,或具有相同属性的图像构成。当集合数量有限且已知时,通过将集合信息表示为独热向量(one hot vector) [15, 17],可以轻松将生成模型扩展为条件版本。我们将这些模型称为类别条件生成模型(CCGMs)。CCGMs从根本上受限于其编码中预定义的所有可能集合的枚举,这阻碍了识别或生成未在训练分布中明确编码的集合。此外,CCGM训练期间所需的参数数量与集合(类别)数量呈线性增长,这限制了其可扩展性。
In this paper, we study the problem of generative modeling of sets of images with a generic approach. We propose Set Distribution Networks (SDNs), a probabilistic model that is capable of learning to stochastic ally reconstruct a given set and generate novel sets at the same time. Stochastic reconstruction of a set means that the individual images in the input set will not be reproduced exactly, but the generated images will share set-defining attributes with the input images. We achieve this by jointly training a set encoder, a set disc rim in at or, a set generator, and a set prior. We train an SDN by following the MLE objective, which results in an adversarial game where the encoder, disc rim in at or and prior are trained against the generator.
本文研究了一种通用的图像集合生成建模问题。我们提出了集合分布网络 (Set Distribution Networks, SDNs) —— 一种能够随机重建给定集合并同时生成新集合的概率模型。集合的随机重建意味着输入集合中的单个图像不会被精确复制,但生成的图像将与输入图像共享集合定义属性。我们通过联合训练集合编码器、集合判别器、集合生成器和集合先验来实现这一目标。SDN的训练遵循最大似然估计 (MLE) 目标,由此形成编码器、判别器和先验共同对抗生成器的对抗博弈框架。
We evaluate SDNs on two benchmarks: 1. ShapeNet [5], which consists of objects in various viewpoints; 2. VGGFace2 [4], which consists of various faces of human identities. We show that the same SDN architecture can be successfully trained on the two datasets, and can learn to both reconstruct an unseen set, and generate a novel set. We measure the quality of the set generative model by examining the generated samples with a pre-trained 3D reconstruction network, and face verification network, respectively, and show that SDNs learn to generate faithful and coherent sets.
我们在两个基准上评估SDN:1. ShapeNet [5],包含不同视角的物体;2. VGGFace2 [4],包含人类身份的各种面部。实验表明,相同的SDN架构能成功在这两个数据集上训练,并学会重建未见集合与生成新集合。通过分别使用预训练的3D重建网络和人脸验证网络检测生成样本,我们验证了SDN能生成忠实且连贯的集合,以此衡量集合生成模型的质量。
2 Methodology
2 方法论
2.1 Set Distribution Networks
2.1 集合分布网络
We denote an image set of size $n$ as $\mathbf{X}\in{\mathcal{X}}$ , with $\mathbf{X}={\mathbf{x}_ {i}}_ {i=1\dots n}$ , $\mathbf{x}_ {i}\in R^{d}$ , and we are interested in learning a probabilistic model $p_ {\boldsymbol{\theta}}(\mathbf{X})$ . To do so, we propose a novel encoder-decoder styled model, dubbed Set Distribution Networks (SDNs), that takes the form:
我们称大小为$n$的图像集为$\mathbf{X}\in{\mathcal{X}}$,其中$\mathbf{X}={\mathbf{x}_ {i}}_ {i=1\dots n}$,$\mathbf{x}_ {i}\in R^{d}$。我们关注于学习一个概率模型$p_ {\boldsymbol{\theta}}(\mathbf{X})$。为此,我们提出了一种新颖的编码器-解码器风格模型,称为集合分布网络(Set Distribution Networks,SDNs),其形式如下:
$$
p_ {\theta}(\mathbf{X})=p_ {\theta}(z(\mathbf{X};\theta))p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta)).
$$
$$
p_ {\theta}(\mathbf{X})=p_ {\theta}(z(\mathbf{X};\theta))p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta)).
$$
Here $z:\mathcal{X}\rightarrow\mathcal{Z}$ is a deterministic function that maps a set $\mathbf{X}$ to an element $\mathbf{z}$ in a discrete space Z. $p_ {\theta}(\cdot)$ is a prior distribution, with the support given by $s u p p(z)={z(\mathbf{X};\theta):\mathbf{X}\in\mathcal{X}}$ which is a subset of $\mathcal{Z}$ . $p_ {\theta}(\mathbf{X}|z(\mathbf{X}))$ is a conditional distribution which is defined as :
这里 $z:\mathcal{X}\rightarrow\mathcal{Z}$ 是一个确定性函数,将集合 $\mathbf{X}$ 映射到离散空间 Z 中的元素 $\mathbf{z}$。$p_ {\theta}(\cdot)$ 是先验分布,其支撑集由 $supp(z)={z(\mathbf{X};\theta):\mathbf{X}\in\mathcal{X}}$ 给出,这是 $\mathcal{Z}$ 的一个子集。$p_ {\theta}(\mathbf{X}|z(\mathbf{X}))$ 是一个条件分布,定义为:
$$
p_ {\theta}(\mathbf{X}|\mathbf{z})=\frac{I(z(\mathbf{X})=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)}}{\int_ {\mathbf{X^{\prime}}\in\mathcal{X}}I(z(\mathbf{X^{\prime}})=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X^{\prime}}}E(\mathbf{x},\mathbf{z};\theta)}d\mathbf{X^{\prime}}}.
$$
$$
p_ {\theta}(\mathbf{X}|\mathbf{z})=\frac{I(z(\mathbf{X})=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)}}{\int_ {\mathbf{X^{\prime}}\in\mathcal{X}}I(z(\mathbf{X^{\prime}})=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X^{\prime}}}E(\mathbf{x},\mathbf{z};\theta)}d\mathbf{X^{\prime}}}.
$$
Here $I(\cdot)$ is the indicator function. The conditional probability takes the form of an energy based model (EBM), where density is only assigned to sets $\mathbf{X}^{\prime}$ that are mapped to the same $\mathbf{z}$ .
这里 $I(\cdot)$ 是指示函数。条件概率采用基于能量的模型 (energy based model, EBM) 的形式,其中密度仅分配给映射到相同 $\mathbf{z}$ 的集合 $\mathbf{X}^{\prime}$。
We first show that Equation 1 indeed defines a valid distribution of $\mathbf{X}$ . To see this, we have:
我们首先证明式1确实定义了$\mathbf{X}$的有效分布。为此,我们有:
$$
\begin{array}{l}{{\displaystyle\int_ {{\bf X}\in\mathcal{X}}p_ {\theta}({\bf X})d{\bf X}=\int_ {{\bf X}\in\mathcal{X}}p_ {\theta}(z({\bf X};\theta))p_ {\theta}({\bf X}|z({\bf X}))d{\bf X}=\displaystyle\sum_ {\bf z\sim s u p p(z)}\int_ {{\bf X}\in\mathcal{X}_ {\bf z}}p_ {\theta}({\bf z})p_ {\theta}({\bf X}|{\bf z})d{\bf X}}}\ {{\displaystyle\qquad=\sum_ {\bf z\in\it s u p p(z)}p_ {\theta}({\bf z})\int_ {{\bf X}\in\mathcal{X}_ {\bf z}}p_ {\theta}({\bf X}|{\bf z})d{\bf X}=\sum_ {\bf z\in s u p p(z)}p_ {\theta}({\bf z})=1},}\end{array}
$$
$$
\begin{array}{l}{{\displaystyle\int_ {{\bf X}\in\mathcal{X}}p_ {\theta}({\bf X})d{\bf X}=\int_ {{\bf X}\in\mathcal{X}}p_ {\theta}(z({\bf X};\theta))p_ {\theta}({\bf X}|z({\bf X}))d{\bf X}=\displaystyle\sum_ {\bf z\sim s u p p(z)}\int_ {{\bf X}\in\mathcal{X}_ {\bf z}}p_ {\theta}({\bf z})p_ {\theta}({\bf X}|{\bf z})d{\bf X}}}\ {{\displaystyle\qquad=\sum_ {\bf z\in\it s u p p(z)}p_ {\theta}({\bf z})\int_ {{\bf X}\in\mathcal{X}_ {\bf z}}p_ {\theta}({\bf X}|{\bf z})d{\bf X}=\sum_ {\bf z\in s u p p(z)}p_ {\theta}({\bf z})=1},}\end{array}
$$
where $\mathcal{X}_ {z} \triangleq { X \mid z(X; \theta) = z, X \in \mathcal{X} }$. Here we first partition the integration by grouping $\mathbf{X}$ that share the same $\mathbf{z}$ , then move $p_ {\boldsymbol{\theta}}(\mathbf{z})$ out of the integral as it’s a constant within the partition, and lastly recognize that the integration evaluates to 1 according to the definition of Equation 2.
其中 $\mathcal{X}_ {z} \triangleq { X \mid z(X; \theta) = z, X \in \mathcal{X} }$ 。这里我们首先通过将共享相同 $\mathbf{z}$ 的 $\mathbf{X}$ 分组来划分积分,然后将 $p_ {\boldsymbol{\theta}}(\mathbf{z})$ 移出积分,因为它在分区内是常数,最后根据公式2的定义认识到积分结果为1。
Intuitively, the SDN is an encoder-decoder model with discrete latent variables, with $z(\cdot;\theta)$ being the encoder and $p_ {\theta}(\cdot|\cdot)$ being the probabilistic decoder. The encoder serves the role of partitioning the input space, while the decoder defines a normalized distribution over sets mapped to the same partition.
直观上,SDN是一种带有离散隐变量的编码器-解码器模型,其中$z(\cdot;\theta)$是编码器,$p_ {\theta}(\cdot|\cdot)$是概率解码器。编码器的作用是对输入空间进行划分,而解码器则定义了映射到同一分区的集合上的归一化分布。
2.2 Approximate Inference with Learned Prior and Generator
2.2 基于学习先验和生成器的近似推断
We apply MLE to estimate the parameters of $p_ {\boldsymbol{\theta}}(\mathbf{X})$ , where the negative log likelihood loss for an observed set $\mathbf{X}$ in the training split is:
我们采用最大似然估计(MLE)来估计 $p_ {\boldsymbol{\theta}}(\mathbf{X})$ 的参数,其中训练集观测数据 $\mathbf{X}$ 的负对数似然损失函数为:
$$
-\log p_ {\theta}(z(\mathbf{X};\theta))-\log p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta)),
$$
$$
-\log p_ {\theta}(z(\mathbf{X};\theta))-\log p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta)),
$$
which is decomposed into two parts, corresponding to the prior and decoder distribution respectively. We adopt a simple parameter iz ation of the prior distribution as: $\begin{array}{r}{p_ {\theta}(\mathbf{z})=\frac{\bar{p}_ {\theta}(\mathbf{z})}{\sum_ {\mathbf{z}\in s u p p(z),:\overline{{p}}_ {\theta}(\mathbf{z})}},\forall\mathbf{z}\in}\end{array}$ ; otherwise. Here is a normalized distribution over $\mathcal{Z}$ . Because $s u p p(z)$ is always a subset of $\mathcal{Z}$ , we have that $p_ {\theta}(\mathbf{z})\geq\bar{p}_ {\theta}(\mathbf{z}),\forall\mathbf{z}\in s u p p(z)$ . We then achieve an upper bound of $-\mathrm{log}p_ {\theta}(z(\mathbf{X};\theta))$ given by
其可分解为两部分,分别对应先验分布和解码器分布。我们采用如下先验分布的简单参数化形式:
$\begin{array}{r}{p_ {\theta}(\mathbf{z})=\frac{\bar{p}_ {\theta}(\mathbf{z})}{\sum_ {\mathbf{z}\in s u p p(z),:\overline{{p}}_ {\theta}(\mathbf{z})}},\forall\mathbf{z}\in}\end{array}$
否则。此处是$\mathcal{Z}$上的归一化分布。由于$s u p p(z)$始终是$\mathcal{Z}$的子集,故有$p_ {\theta}(\mathbf{z})\geq\bar{p}_ {\theta}(\mathbf{z}),\forall\mathbf{z}\in s u p p(z)$。由此我们得到$-\mathrm{log}p_ {\theta}(z(\mathbf{X};\theta))$的上界:
$$
\mathcal{L}_ {0}(\theta)\triangleq-\log\bar{p}_ {\theta}(z(\mathbf{X};\theta)),
$$
$$
\mathcal{L}_ {0}(\theta)\triangleq-\log\bar{p}_ {\theta}(z(\mathbf{X};\theta)),
$$
which gets rid of the need for the intractable $s u p p(z)$ . For - $-\mathrm{log}p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta))$ , we apply variation al inference with a learned generator, as in [6, 22, 24, 25], where we have:
这消除了对难以处理的 $supp(z)$ 的需求。对于 $-\mathrm{log}p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta))$ ,我们采用如[6, 22, 24, 25]中所述的基于学习生成器的变分推断方法,其中我们有:
$$
\begin{array}{r l}&{-\log p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta))=-\log\frac{I(z(\mathbf{X};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)}}{\int_ {\mathbf{X}^{\prime}\in\mathcal{X}}I(z(\mathbf{X}^{\prime};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\theta)}d\mathbf{X}^{\prime}}\bigg|_ {\mathbf{z}=z(\mathbf{X};\theta)}}\ &{=\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)+\log\int_ {\mathbf{X}^{\prime}\in\mathcal{X}}I(z(\mathbf{X}^{\prime};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\theta)}d\mathbf{X}^{\prime}\bigg|_ {\mathbf{z}=z(\mathbf{X};\theta)}}\ &{\geq\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)+\mathrm{E}_ {\mathbf{X}^{\prime}\sim p_ {\psi}(\mathbf{X}|\mathbf{z})}\log[I(z(\mathbf{X}^{\prime};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\theta)}]+H(p_ {\psi})\bigg|_ {\mathbf{z}=z(\mathbf{X};\theta)}}\end{array}
$$
$$
\begin{array}{r l}&{-\log p_ {\theta}(\mathbf{X}|z(\mathbf{X};\theta))=-\log\frac{I(z(\mathbf{X};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)}}{\int_ {\mathbf{X}^{\prime}\in\mathcal{X}}I(z(\mathbf{X}^{\prime};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\theta)}d\mathbf{X}^{\prime}}\bigg|_ {\mathbf{z}=z(\mathbf{X};\theta)}}\ &{=\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)+\log\int_ {\mathbf{X}^{\prime}\in\mathcal{X}}I(z(\mathbf{X}^{\prime};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\theta)}d\mathbf{X}^{\prime}\bigg|_ {\mathbf{z}=z(\mathbf{X};\theta)}}\ &{\geq\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}}E(\mathbf{x},\mathbf{z};\theta)+\mathrm{E}_ {\mathbf{X}^{\prime}\sim p_ {\psi}(\mathbf{X}|\mathbf{z})}\log[I(z(\mathbf{X}^{\prime};\theta)=\mathbf{z})e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\theta)}]+H(p_ {\psi})\bigg|_ {\mathbf{z}=z(\mathbf{X};\theta)}}\end{array}
$$
Here we have derived a lower bound of $-\mathrm{log}p_ {\boldsymbol{\theta}}(\mathbf{X}|\mathbf{z})^{1}$ by introducing a variation al distribution $p_ {\boldsymbol{\psi}}({\mathbf{X}}|{\mathbf{z}})$ , which we parameter ize in the form of a generator:
我们通过引入变分分布 $p_ {\boldsymbol{\psi}}({\mathbf{X}}|{\mathbf{z}})$ 推导出了 $-\mathrm{log}p_ {\boldsymbol{\theta}}(\mathbf{X}|\mathbf{z})^{1}$ 的下界,并将其参数化为生成器的形式:
$$
\int_ {\mathbf{X}\sim p_ {\psi}(\mathbf{X}|\mathbf{z})}f(\mathbf{X})d\mathbf{X}\triangleq\int_ {{\mathbf{z^{\prime}}_ {i}\sim p_ {\psi}(\mathbf{z^{\prime}})}_ {i=1,\dots n}}f({G(\mathbf{z},\mathbf{z}_ {\mathrm{i}}^{\prime};\psi)}_ {i=1,\dots n})d{\mathbf{z^{\prime}}_ {i}}_ {i=1,\dots n},\forall f.
$$
$$
\int_ {\mathbf{X}\sim p_ {\psi}(\mathbf{X}|\mathbf{z})}f(\mathbf{X})d\mathbf{X}\triangleq\int_ {{\mathbf{z^{\prime}}_ {i}\sim p_ {\psi}(\mathbf{z^{\prime}})}_ {i=1,\dots n}}f({G(\mathbf{z},\mathbf{z}_ {\mathrm{i}}^{\prime};\psi)}_ {i=1,\dots n})d{\mathbf{z^{\prime}}_ {i}}_ {i=1,\dots n},\forall f.
$$
Here $p_ {\boldsymbol{\psi}}(\mathbf{z}^{\prime})$ is a simple distribution (e.g., Isotropic Gaussian) over $\mathcal{Z}^{\prime}$ , and $G:\mathcal{Z}\times\mathcal{Z}^{\prime}\rightarrow R^{d}$ is a deterministic function (the generator) that maps a $(\mathbf{z},\mathbf{z}^{\prime})$ tuple to the image space. The lower bound $\mathcal{L}_ {1}(\theta,\psi)$ can be tightened by solving $\operatorname*{max}_ {\psi}\mathcal{L}_ {1}(\theta,\psi)$ [22].
这里 $p_ {\boldsymbol{\psi}}(\mathbf{z}^{\prime})$ 是 $\mathcal{Z}^{\prime}$ 上的简单分布(如各向同性高斯分布),而 $G:\mathcal{Z}\times\mathcal{Z}^{\prime}\rightarrow R^{d}$ 是一个确定性函数(生成器),它将 $(\mathbf{z},\mathbf{z}^{\prime})$ 元组映射到图像空间。通过求解 $\operatorname*{max}_ {\psi}\mathcal{L}_ {1}(\theta,\psi)$ [22],可以收紧下界 $\mathcal{L}_ {1}(\theta,\psi)$。
2.3 Model Architectures
2.3 模型架构
There are four interacting modules for SDNs: the prior $p_ {\boldsymbol{\theta}}(\mathbf{z})$ , the encoder $z(\mathbf{X};\theta)$ , the disc rim in at or (energy) $E(\mathbf{x},\mathbf{z};\theta)$ and the generator $G(\mathbf{z},\mathbf{z}^{\prime};\psi)$ . We now explain the architecture and design choice for each of them. See Figure 1 for an illustration.
SDN包含四个交互模块:先验分布 $p_ {\boldsymbol{\theta}}(\mathbf{z})$、编码器 $z(\mathbf{X};\theta)$、判别器(能量函数)$E(\mathbf{x},\mathbf{z};\theta)$ 和生成器 $G(\mathbf{z},\mathbf{z}^{\prime};\psi)$。下面将分别说明各模块的架构与设计选择,示意图见 图 1: 。
Prior. In all of our implementations, we adopt binary set codes, i.e., letting $\mathcal{Z}={-1,1}^{d_ {z}}$ . In theory, one can choose any prior distribution over discrete variables. We use a standard auto-regressive model MADE [10] with three fully connected layers, mainly for its simplicity and robustness.
先验。在我们的所有实现中,均采用二进制集合编码,即令 $\mathcal{Z}={-1,1}^{d_ {z}}$ 。理论上,可以选择离散变量上的任意先验分布。我们使用具有三个全连接层的标准自回归模型 MADE [10],主要因其简单性和鲁棒性。
Encoder. As a necessary condition, an encoder for a set needs to satisfy the permutation invariant property [21]. We opt to use a simple architecture design where we let $z(\mathbf{X};\theta)~=$ $\begin{array}{r}{b i n a r i z e(\frac{1}{n}\sum_ {i=1}^{\bar{n}}c(\mathbf{\bar{x}}_ {i};\theta))}\end{array}$ , where $c(\cdot;\theta)$ is a standard CNN image encoder. The outputs of the image codes are averaged across the set and then passed to a differentiable b inari z ation operator (with straight through gradient estimation) to produce the final set code.
编码器。作为必要条件,集合的编码器需要满足置换不变性 [21]。我们选择采用一种简单的架构设计,令 $z(\mathbf{X};\theta)~=$ $\begin{array}{r}{binarize(\frac{1}{n}\sum_ {i=1}^{\bar{n}}c(\mathbf{\bar{x}}_ {i};\theta))}\end{array}$ ,其中 $c(\cdot;\theta)$ 是标准的 CNN 图像编码器。图像编码的输出在集合中进行平均,然后通过可微分二值化算子(采用直通梯度估计)生成最终的集合编码。
Disc rim in at or. The disc rim in at or’s job is to assign low energy to observed images and high energy to generated images, given a set code $\mathbf{z}$ . We use an auto encoder based energy function implementation, similar to [25]. We have found that this choice is important as it enables effective learning in early stages of training. We reuse $c(\cdot;\theta)$ as the encoder, and separately learn a decoder $d(\mathbf{z},c(\mathbf{x}))$ , which takes the concatenation of the binary set code $\mathbf{z}$ and dense image code $c(\mathbf{x})$ as input, and outputs a “reconstruction" of $\mathbf{x}$ . We additionally learn a unary energy term of $\mathbf{x}$ with a small MLP $d_ {0}:R^{d_ {z}}\to R$ that takes $c(\mathbf{x})$ as input and outputs a scalar. This gives us the final output of the disc rim in at or as:
判别器。判别器的任务是在给定集合代码 $\mathbf{z}$ 的情况下,为观测图像分配低能量,为生成图像分配高能量。我们采用基于自编码器的能量函数实现方式,类似于[25]。我们发现这一选择至关重要,因为它能在训练初期实现有效学习。我们复用 $c(\cdot;\theta)$ 作为编码器,并独立学习一个解码器 $d(\mathbf{z},c(\mathbf{x}))$ ——该解码器以二进制集合代码 $\mathbf{z}$ 和稠密图像代码 $c(\mathbf{x})$ 的拼接作为输入,输出 $\mathbf{x}$ 的"重构"结果。此外,我们通过小型MLP网络 $d_ {0}:R^{d_ {z}}\to R$ 学习 $\mathbf{x}$ 的一元能量项,该网络以 $c(\mathbf{x})$ 为输入并输出标量值。最终判别器的输出表达式为:
$$
E(\mathbf{x},\mathbf{z};\theta)=|\mathbf{x}-d(\mathbf{z},c(\mathbf{x};\theta);\theta)|_ {2}^{2}+d_ {0}(c(\mathbf{x};\theta);\theta).
$$
$$
E(\mathbf{x},\mathbf{z};\theta)=|\mathbf{x}-d(\mathbf{z},c(\mathbf{x};\theta);\theta)|_ {2}^{2}+d_ {0}(c(\mathbf{x};\theta);\theta).
$$
Generator. The generator generates a set conditioned on a set code $\mathbf{z}$ by sampling $n$ random variables ${\mathbf{z}^{\prime}{}_ {i}\sim p_ {\psi}(\mathbf{z}^{\prime})}_ {i=1\dots n}$ , each of which is concatenated with $\mathbf{z}$ and generates an image independently.
生成器。生成器通过采样 $n$ 个随机变量 ${\mathbf{z}^{\prime}{}_ {i}\sim p_ {\psi}(\mathbf{z}^{\prime})}_ {i=1\dots n}$ 来生成以集合代码 $\mathbf{z}$ 为条件的一组数据,每个随机变量都与 $\mathbf{z}$ 拼接并独立生成一张图像。
2.4 Losses
2.4 损失函数
SDNs consist of two sets of parameters to be optimized, $\theta$ and $\psi$ , where $\theta$ denotes the combined parameters for the prior, encoder and disc rim in at or; and $\psi$ denotes those for the generator. During training, with $\theta$ fixed, we first optimize $\psi$ to tighten the lower bound by solving $\mathrm{inax}_ {\psi}\mathcal{L}_ {1}(\theta,\psi)$ . In order to make this practical, we make two simplifications. First, we do not explicitly include the entropy term $H(p_ {\psi})$ . This seems problematic at first glance as $H(p_ {\psi})$ plays the role of encouraging $p_ {\boldsymbol{\psi}}({\mathbf{X}}|{\mathbf{z}})$ to have high entropy which prevents the mode collapse problem. However, we have found that we can implicitly achieve high diversity of the generated samples with careful learning scheduling and architectural design choices as commonly used in GAN training, see Sec. 4.2 for more details. Also refer to [22] for more justification of this choice. Second, the indicator function $I(z(\mathbf{X}^{\prime})=\mathbf{z})$ which ensures that the generated sets are mapped to the same set code $\mathbf{z}$ is not differentiable. We thus choose to use a soft approximation: $I(z(\mathbf{X}^{\prime})=\mathbf{z})\approx e^{-|[z(\mathbf{X}^{\prime};\theta)\odot\mathbf{z}]_ {-}|_ {1}}$ , where $\odot$ is the element-wise product, $[\cdot]_ {-}$ is the operator that zeros out the positive elements, and $|\cdot|_ {1}$ is the $\ell_ {1}$ norm. Intuitively, this approximation equates the indicator function when $s i g n(z(\mathbf{X}^{\prime};\theta))=\mathbf{z}$ , and induces a value in $(0,1)$ otherwise. This leads us to the final form of the loss for the generator:
SDN包含两组待优化参数$\theta$和$\psi$,其中$\theta$表示先验、编码器和判别器的组合参数;$\psi$表示生成器的参数。训练时固定$\theta$,我们首先通过求解$\mathrm{inax}_ {\psi}\mathcal{L}_ {1}(\theta,\psi)$来优化$\psi$以收紧下界。为实现这一目标,我们做了两处简化:首先,未显式包含熵项$H(p_ {\psi})$。初看这可能存在问题,因为$H(p_ {\psi})$的作用是激励$p_ {\boldsymbol{\psi}}({\mathbf{X}}|{\mathbf{z}})$保持高熵值以避免模式坍塌。但实践发现,通过采用GAN训练中常用的精心设计的学习调度和架构选择,可以隐式实现生成样本的高多样性(详见第4.2节),该选择的合理性亦可参考文献[22]。其次,用于确保生成集合映射到相同集合编码$\mathbf{z}$的指示函数$I(z(\mathbf{X}^{\prime})=\mathbf{z})$不可微。因此我们采用软近似:$I(z(\mathbf{X}^{\prime})=\mathbf{z})\approx e^{-|[z(\mathbf{X}^{\prime};\theta)\odot\mathbf{z}]_ {-}|_ {1}}$,其中$\odot$表示逐元素乘积,$[\cdot]_ {-}$为置零正元素的算子,$|\cdot|_ {1}$是$\ell_ {1}$范数。直观上,当$sign(z(\mathbf{X}^{\prime};\theta))=\mathbf{z}$时该近似等价于指示函数,否则产生$(0,1)$区间的值。最终得到生成器的损失函数形式:
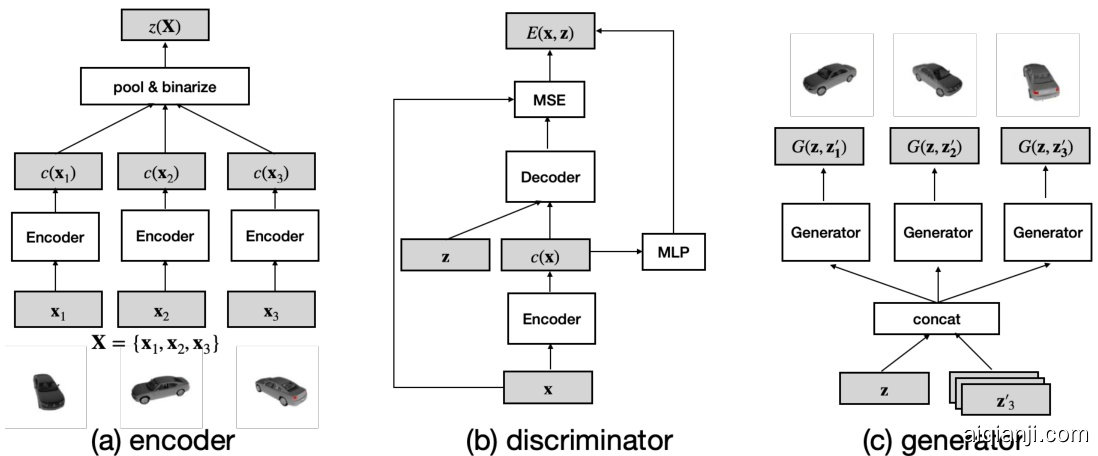
Figure 1: Model architectures of SDNs. SDNs consist of three modules: (a) a set encoder that maps a set of images into a discrete code, with a shared convolutional encoder encoding each image followed by average pooling and disc ret iz ation; (b) a conditional disc rim in at or (energy) for each image that takes the form of an auto encoder (similar to [25]); (c) a conditional generator that generates images conditioned on a set code $\mathbf{z}$ .
图 1: SDN的模型架构。SDN包含三个模块:(a) 集合编码器,将图像集合映射为离散代码,通过共享卷积编码器编码每张图像后执行平均池化和离散化;(b) 每个图像的条件判别器(能量函数),采用自编码器形式(类似[25]);(c) 基于集合代码$\mathbf{z}$生成图像的条件生成器。
$$
\begin{array}{r l}&{\mathcal{L}_ {\psi}=-\mathrm{E}_ {{\mathbf{z}^{\prime},\sim p_ {\psi}(\mathbf{z}^{\prime})}_ {i=1,\dots,n}}\log[e^{-|[\mathbf{z}(\mathbf{X}^{\prime};\boldsymbol{\theta})\odot\mathbf{z}]-|_ {1}}e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\boldsymbol{\theta})\big)}]\big|_ {\mathbf{X}^{\prime}={G(\mathbf{z},\mathbf{z}^{\prime};\boldsymbol{\psi})}_ {i=1,\dots,n}}}\ &{\qquad=\mathrm{E}_ {{\mathbf{z}^{\prime},\sim p_ {\psi}(\mathbf{z}^{\prime})}_ {i=1,\dots,n}}[|[\boldsymbol{z}(\mathbf{X}^{\prime};\boldsymbol{\theta})\odot\mathbf{z}]-|_ {1}+\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\boldsymbol{\theta})\big)\big|_ {\mathbf{X}^{\prime}={G(\mathbf{z},\mathbf{z}^{\prime};\boldsymbol{\psi})}_ {i=1,\dots,n}}.}\end{array}
$$
$$
\begin{array}{r l}&{\mathcal{L}_ {\psi}=-\mathrm{E}_ {{\mathbf{z}^{\prime},\sim p_ {\psi}(\mathbf{z}^{\prime})}_ {i=1,\dots,n}}\log[e^{-|[\mathbf{z}(\mathbf{X}^{\prime};\boldsymbol{\theta})\odot\mathbf{z}]-|_ {1}}e^{-\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\boldsymbol{\theta})\big)}]\big|_ {\mathbf{X}^{\prime}={G(\mathbf{z},\mathbf{z}^{\prime};\boldsymbol{\psi})}_ {i=1,\dots,n}}}\ &{\qquad=\mathrm{E}_ {{\mathbf{z}^{\prime},\sim p_ {\psi}(\mathbf{z}^{\prime})}_ {i=1,\dots,n}}[|[\boldsymbol{z}(\mathbf{X}^{\prime};\boldsymbol{\theta})\odot\mathbf{z}]-|_ {1}+\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}E(\mathbf{x},\mathbf{z};\boldsymbol{\theta})\big)\big|_ {\mathbf{X}^{\prime}={G(\mathbf{z},\mathbf{z}^{\prime};\boldsymbol{\psi})}_ {i=1,\dots,n}}.}\end{array}
$$
With $\psi$ fixed, we can optimize $\theta$ with a loss that combines $\mathcal{L}_ {0}(\theta)$ and $\mathcal{L}_ {1}(\theta,\psi)$ . As is common practice in GAN and deep EBM training [3, 9, 25], we apply a margin based loss on $E(\mathbf{x},\mathbf{z};\theta)$ . In particular, we have found that it’s beneficial to apply two separate margins on the two terms of $E$ , this leads to the loss function of $\theta$ update as:
固定 $\psi$ 后,我们可以通过结合 $\mathcal{L}_ {0}(\theta)$ 和 $\mathcal{L}_ {1}(\theta,\psi)$ 的损失函数来优化 $\theta$。遵循GAN和深度EBM训练的常见做法 [3, 9, 25],我们对 $E(\mathbf{x},\mathbf{z};\theta)$ 应用基于间隔的损失函数。具体而言,我们发现对 $E$ 的两项分别应用独立间隔能带来更好效果,因此 $\theta$ 更新的损失函数定义为:
$$
\begin{array}{r l}&{\mathcal{L}_ {\theta}=-\log\bar{p}_ {\theta}\big(\Omega\big(z\big(\mathbf{X};\theta\big)\big)\big)}\ &{\qquad+\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}}|\mathbf{x}-d\big(z\big(\mathbf{X};\theta\big),c(\mathbf{x};\theta);\theta\big)|_ {2}^{2}+\big[\gamma_ {0}+d_ {0}(\mathbf{x};\theta)\big]_ {+}}\ &{\qquad+\operatorname{E}_ {\mathbf{X}^{\prime}\sim p_ {\psi}(\mathbf{X}|z(\mathbf{X}))}\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}\big[\gamma_ {1}-|\mathbf{x}-d\big(z(\mathbf{X};\theta),c(\mathbf{x};\theta);\theta\big)|_ {2}^{2}\big]_ {+}+\big[\gamma_ {0}-d_ {0}(\mathbf{x};\theta)\big]_ {+}.}\end{array}
$$
$$
\begin{array}{r l}&{\mathcal{L}_ {\theta}=-\log\bar{p}_ {\theta}\big(\Omega\big(z\big(\mathbf{X};\theta\big)\big)\big)}\ &{\qquad+\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}}|\mathbf{x}-d\big(z\big(\mathbf{X};\theta\big),c(\mathbf{x};\theta);\theta\big)|_ {2}^{2}+\big[\gamma_ {0}+d_ {0}(\mathbf{x};\theta)\big]_ {+}}\ &{\qquad+\operatorname{E}_ {\mathbf{X}^{\prime}\sim p_ {\psi}(\mathbf{X}|z(\mathbf{X}))}\displaystyle\sum_ {\mathbf{x}\in\mathbf{X}^{\prime}}\big[\gamma_ {1}-|\mathbf{x}-d\big(z(\mathbf{X};\theta),c(\mathbf{x};\theta);\theta\big)|_ {2}^{2}\big]_ {+}+\big[\gamma_ {0}-d_ {0}(\mathbf{x};\theta)\big]_ {+}.}\end{array}
$$
Here $\Omega$ is the stop gradient operator, indicating that we do not pass gradient from the prior to the encoder. $[\cdot]_ {+}$ is the operator that zeros out the negative portions of the input. $\gamma_ {0},\gamma_ {1}\in R^{+}$ are two margin parameters.
这里 $\Omega$ 是停止梯度算子,表示我们不将梯度从先验传递到编码器。$[\cdot]_ {+}$ 是将输入负值部分置零的算子。$\gamma_ {0},\gamma_ {1}\in R^{+}$ 是两个边界参数。
3 Related Work
3 相关工作
Generative Modeling of sets. Generative modeling of sets is a challenging task. Hierarchical Bayes models have previously been widely applied to document modeling, which can be considered as a set of words, represented by the LDA model [2]. Recently, there has been a a body of work dedicated to point cloud generative modeling, where sets are composed of 3D points in Euclidean space [1, 13, 20]. However, image sets considered in our work contain much richer structure than 3D points. It is thus unclear how methods developed from the point cloud or document modeling lines of work generalize to more complex image data.
集合的生成式建模 (Generative Modeling)。集合的生成式建模是一项具有挑战性的任务。分层贝叶斯模型 (Hierarchical Bayes models) 此前已广泛应用于文档建模——文档可视为由LDA模型 [2] 表示的词集合。近期涌现了大量专注于点云生成建模的研究,这类集合由欧几里得空间中的3D点构成 [1, 13, 20]。然而,本文研究的图像集合比3D点具有更丰富的结构特征。因此,从点云或文档建模领域发展而来的方法如何泛化到更复杂的图像数据仍不明确。
Auto encoding GANs. SDNs are similar to a handful of existing works which involve an encoder, generator/decoder and a disc rim in at or [7, 8, 12]. Notably, BiGAN [7] trains a two channel discriminator that tries to separate the two joint distributions $p(\mathbf{z})p(\mathbf{x}|\mathbf{z})$ and $p(\mathbf{x})p(\mathbf{z}|\mathbf{x})$ . Aside from the set modeling aspect, in a BiGAN the encoder and decoder work jointly against the disc rim in at or, whereas in SDNs, the encoder and the disc rim in at or work jointly against the generator. Intuitively, SDNs encourage the encoder to learn disc rim i native representations by not allowing it to cooperate with the generator, which in turn improves the generator’s quality as well.
自编码生成对抗网络。SDN与少数现有工作类似,这些工作都包含编码器、生成器/解码器和判别器 [7, 8, 12]。值得注意的是,BiGAN [7] 训练了一个双通道判别器,试图区分两个联合分布 $p(\mathbf{z})p(\mathbf{x}|\mathbf{z})$ 和 $p(\mathbf{x})p(\mathbf{z}|\mathbf{x})$。除了集合建模方面,在BiGAN中编码器和解码器共同对抗判别器,而在SDN中,编码器和判别器共同对抗生成器。直观上,SDN通过禁止编码器与生成器合作,促使编码器学习判别性表征,这反过来也提高了生成器的质量。
Conditional GANs. A conditional GAN (cGAN) [15, 17] modifies the generator and disc rim in at or of a GAN to be conditional on class labels. SDNs can be considered a generalization of cGANs, as it learns the parametric set representation jointly with the generator and disc rim in at or.
条件GAN (Conditional GAN)。条件GAN (cGAN) [15, 17] 通过修改GAN的生成器和判别器,使其能够基于类别标签生成样本。SDN可视为cGAN的泛化形式,因为它能联合学习参数化集合表示与生成器及判别器。
VQ-VAEs. VQ-VAEs [18, 19] are related to SDNs in that they learn encoders that output discrete and deterministic codes. They also learn auto-regressive priors which greatly improves their capability of generative modeling. SDNs differ from VQ-VAEs in that they have a more sophisticated encoder and disc rim in at or, which are essential to cope with set structures.
VQ-VAEs。VQ-VAEs [18, 19] 与 SDNs 相关,因为它们学习的编码器输出离散且确定的代码。它们还学习自回归先验,这大大提高了生成建模的能力。SDNs 与 VQ-VAEs 的不同之处在于它们具有更复杂的编码器和判别器,这对于处理集合结构至关重要。
4 Experiments
4 实验
4.1 Datasets
4.1 数据集
The first dataset we use is ShapeNet [5], which consists of 3D objects with projected 2d views. We use a subset which contains 13 popular categories, namely airplane, bench, cabinet, car, chair, monitor, lamp, speaker, gun, couch, table, phone, ship. The training set consists of 32,837 unique objects and 788,088 images in total. The second dataset is VGGFace2 [4], which is a face dataset containing 9,131 subjects and 3.31M images.
我们使用的第一个数据集是ShapeNet [5],它包含带有投影2D视图的3D对象。我们采用包含13个常见类别的子集:飞机、长椅、橱柜、汽车、椅子、显示器、台灯、音箱、枪支、沙发、餐桌、电话和轮船。训练集共包含32,837个独立对象和788,088张图像。第二个数据集VGGFace2 [4]是人脸数据集,涵盖9,131个主体和331万张图像。
For both datasets, we randomly construct fixed-size sets of 8 elements for training. For ShapeNet, this is done by randomly selecting an object and 8 of its views; for VGGFace2, we similarly select one identity and 8 of her/his faces. A mini-batch is constructed by selecting $N$ objects/subjects, which amounts to $N\times8$ images in total. All images are scaled to a size of $128\times128$ .
对于这两个数据集,我们随机构建固定大小为8元素的集合用于训练。在ShapeNet中,通过随机选择一个物体及其8个视角实现;在VGGFace2中,则随机选取一个身份及其8张人脸图像。每个小批量(mini-batch)通过选择$N$个物体/主体构成,共计$N\times8$张图像。所有图像统一缩放至$128\times128$分辨率。
4.2 Implementation Details
4.2 实现细节
Our implementation resembles that of SAGAN [23] w.r.t. base architecture and learning scheduling. The encoder is identical to the disc rim in at or in SAGAN, namely a CNN enhanced with Spectral Normalization (SN) [16] and Self Attention (SA), except that the number of output units is changed to $d_ {z}$ instead of 1. The dimension of $\mathbf{z}$ is 2048 and 256 for ShapeNet and VGGFace2, respectively. The generator is also the same as that in SAGAN, which is a CNN with SN, Batch Norm [11] and
