Abstract

摘要

We present Meta Pseudo Labels, a semi-supervised learning method that achieves a new state-of-the-art top-1 accuracy of $90.2%$ on ImageNet, which is $1.6%$ better than the existing state-of-the-art [16]. Like Pseudo Labels, Meta Pseudo Labels has a teacher network to generate pseudo labels on unlabeled data to teach a student network. However, unlike Pseudo Labels where the teacher is fixed, the teacher in Meta Pseudo Labels is constantly adapted by the feedback of the student’s performance on the labeled dataset. As a result, the teacher generates better pseudo labels to teach the student.1

我们提出元伪标签 (Meta Pseudo Labels)，这是一种半监督学习方法，在 ImageNet 上实现了 90.2% 的最新 top-1 准确率，比现有最佳结果 [16] 高出 1.6%。与伪标签 (Pseudo Labels) 类似，元伪标签通过教师网络在未标记数据上生成伪标签来指导学生网络。然而，与固定教师的伪标签不同，元伪标签中的教师会根据学生在标记数据集上的表现反馈不断调整。因此，教师能生成更优质的伪标签来指导学生。1

1. Introduction

1. 引言

The methods of Pseudo Labels or self-training [57, 81, 55, 36] have been applied successfully to improve state-ofthe-art models in many computer vision tasks such as image classification (e.g., [79, 77]), object detection, and semantic segmentation (e.g., [89, 51]). Pseudo Labels methods work by having a pair of networks, one as a teacher and one as a student. The teacher generates pseudo labels on unlabeled images. These pseudo labeled images are then combined with labeled images to train the student. Thanks to the abundance of pseudo labeled data and the use of regular iz ation methods such as data augmentation, the student learns to become better than the teacher [77].

伪标签 (Pseudo Labels) 或自训练方法 [57, 81, 55, 36] 已成功应用于提升图像分类 (如 [79, 77])、目标检测和语义分割 (如 [89, 51]) 等计算机视觉任务中的前沿模型性能。该方法通过构建教师-学生双网络架构实现：教师网络为无标注图像生成伪标签，随后将这些伪标注图像与真实标注数据共同训练学生网络。得益于海量伪标注数据以及数据增强等正则化手段，学生网络的性能最终超越教师网络 [77]。

Despite the strong performance of Pseudo Labels methods, they have one main drawback: if the pseudo labels are inaccurate, the student will learn from inaccurate data. As a result, the student may not get significantly better than the teacher. This drawback is also known as the problem of confirmation bias in pseudo-labeling [2].

尽管伪标签 (Pseudo Labels) 方法表现出色，但它们存在一个主要缺点：如果伪标签不准确，学生模型将从错误数据中学习。这会导致学生模型的性能无法显著超越教师模型。该缺点也被称为伪标签中的确认偏误问题 [2]。

In this paper, we design a systematic mechanism for the teacher to correct the bias by observing how its pseudo labels would affect the student. Specifically, we propose Meta Pseudo Labels, which utilizes the feedback from the student to inform the teacher to generate better pseudo labels. In our implementation, the feedback signal is the performance of the student on the labeled dataset. This feedback signal is used as a reward to train the teacher throughout the course of the student’s learning. In summary, the teacher and student of Meta Pseudo Labels are trained in parallel: (1) the student learns from a minibatch of pseudo labeled data annotated by the teacher, and (2) the teacher learns from the reward signal of how well the student performs on a minibatch drawn from the labeled dataset.

本文设计了一种系统性机制，使教师模型能够通过观察伪标签对学生模型的影响来纠正偏差。具体而言，我们提出元伪标签 (Meta Pseudo Labels) 方法，利用学生模型的反馈信号指导教师模型生成更优质的伪标签。在实现中，该反馈信号表现为学生模型在标注数据集上的性能指标，该信号将作为奖励函数在整个学习过程中训练教师模型。总结来说，元伪标签框架中的教师模型与学生模型并行训练：(1) 学生模型从教师模型标注的伪标签小批量数据中学习；(2) 教师模型则根据学生模型在标注数据小批量样本上的表现获得奖励信号进行优化。

We experiment with Meta Pseudo Labels, using the ImageNet [56] dataset as labeled data and the JFT-300M dataset [26, 60] as unlabeled data. We train a pair of Efficient Net-L2 networks, one as a teacher and one as a student, using Meta Pseudo Labels. The resulting student network achieves the top-1 accuracy of $90.2%$ on the ImageNet ILSVRC 2012 validation set [56], which is $1.6%$ better than the previous record of $88.6%$ [16]. This student model also generalizes to the ImageNet-ReaL test set [6], as summarized in Table 1. Small scale semi-supervised learning experiments with standard ResNet models on CIFAR10-4K, SVHN-1K, and ImageNet $10%$ also show that Meta Pseudo Labels outperforms a range of other recently proposed methods such as FixMatch [58] and Unsupervised Data Augmentation [76].

我们采用元伪标签 (Meta Pseudo Labels) 方法进行实验，使用 ImageNet [56] 数据集作为标注数据，JFT-300M 数据集 [26, 60] 作为未标注数据。通过训练一对 Efficient Net-L2 网络（分别作为教师模型和学生模型），最终的学生网络在 ImageNet ILSVRC 2012 验证集 [56] 上实现了 90.2% 的 top-1 准确率，比之前 88.6% [16] 的纪录提升了 1.6%。如表 1 所示，该学生模型在 ImageNet-ReaL 测试集 [6] 上也表现出良好的泛化能力。此外，在 CIFAR10-4K、SVHN-1K 和 ImageNet 10% 数据集上使用标准 ResNet 模型进行的小规模半监督学习实验表明，元伪标签方法的性能优于 FixMatch [58] 和无监督数据增强 [76] 等近期提出的其他方法。

Table 1: Summary of our key results on ImageNet ILSVRC 2012 validation set [56] and the ImageNet-ReaL test set [6].

表 1: 我们在ImageNet ILSVRC 2012验证集[56]和ImageNet-ReaL测试集[6]上的关键结果总结。

数据集	ImageNet Top-1准确率	ImageNet-ReaL Precision@1
Previous SOTA [16, 14]	88.6	90.72
Ours	90.2	91.02

2. Meta Pseudo Labels

2. Meta Pseudo Labels

An overview of the contrast between Pseudo Labels and Meta Pseudo Labels is presented in Figure 1. The main difference is that in Meta Pseudo Labels, the teacher receives feedback of the student’s performance on a labeled dataset.

图1展示了伪标签（Pseudo Labels）与元伪标签（Meta Pseudo Labels）的对比概况。主要区别在于元伪标签中，教师模型会接收学生在标注数据集上表现的反馈。

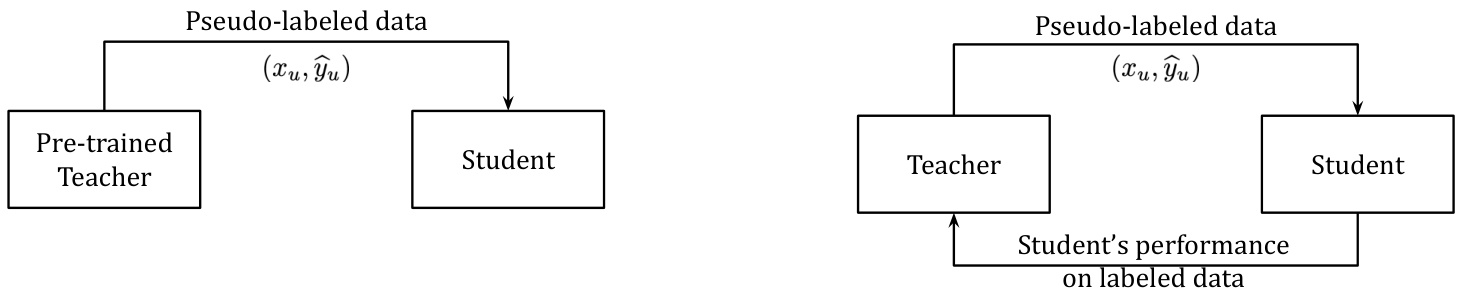
Figure 1: The difference between Pseudo Labels and Meta Pseudo Labels. Left: Pseudo Labels, where a fixed pre-trained teacher generates pseudo labels for the student to learn from. Right: Meta Pseudo Labels, where the teacher is trained along with the student. The student is trained based on the pseudo labels generated by the teacher (top arrow). The teacher is trained based on the performance of the student on labeled data (bottom arrow).

图 1: 伪标签 (Pseudo Labels) 与元伪标签 (Meta Pseudo Labels) 的区别。左图：伪标签，由固定的预训练教师模型生成伪标签供学生模型学习；右图：元伪标签，教师模型与学生模型协同训练。学生模型根据教师模型生成的伪标签进行训练 (上方箭头)，教师模型则根据学生模型在标注数据上的表现进行更新 (下方箭头)。

Notations. Let $T$ and $S$ respectively be the teacher network and the student network in Meta Pseudo Labels. Let their corresponding parameters be $\theta_{T}$ and $\theta_{S}$ . We use $(x_{l},y_{l})$ to refer to a batch of images and their corresponding labels, e.g., ImageNet training images and their labels, and use $x_{u}$ to refer to a batch of unlabeled images, e.g., images from the internet. We denote by $T(x_{u};\theta_{T})$ the soft predictions of the teacher network on the batch $x_{u}$ of unlabeled images and likewise for the student, e.g. $S(x_{l};\theta_{S})$ and $S(x_{u};\theta_{S})$ . We use $\mathrm{CE}(q,p)$ to denote the cross-entropy loss between two distributions $q$ and $p$ ; if $q$ is a label then it is understood as a one-hot distribution; if $q$ and $p$ have multiple instances in them then $\mathrm{CE}(q,p)$ is understood as the average of all instances in the batch. For example, $\mathbf{CE}\left(y_{l},S(x_{l};\theta_{S})\right)$ is the canonical cross-entropy loss in supervised learning.

符号说明。设 $T$ 和 $S$ 分别为元伪标签 (Meta Pseudo Labels) 中的教师网络和学生网络，其对应参数分别为 $\theta_{T}$ 和 $\theta_{S}$。我们用 $(x_{l},y_{l})$ 表示一批图像及其对应标签（例如 ImageNet 训练图像及标签），用 $x_{u}$ 表示一批未标注图像（例如来自互联网的图像）。$T(x_{u};\theta_{T})$ 表示教师网络对未标注图像批 $x_{u}$ 的软预测，同理 $S(x_{l};\theta_{S})$ 和 $S(x_{u};\theta_{S})$ 为学生网络的预测。$\mathrm{CE}(q,p)$ 表示两个分布 $q$ 和 $p$ 之间的交叉熵损失：若 $q$ 为标签则视为独热分布；若 $q$ 和 $p$ 包含多个实例，则 $\mathrm{CE}(q,p)$ 表示批次中所有实例的平均值。例如 $\mathbf{CE}\left(y_{l},S(x_{l};\theta_{S})\right)$ 即为监督学习中的标准交叉熵损失。

Pseudo Labels as an optimization problem. To introduce Meta Pseudo Labels, let’s first review Pseudo Labels. Specifically, Pseudo Labels (PL) trains the student model to minimize the cross-entropy loss on unlabeled data:

伪标签作为优化问题。在介绍元伪标签之前，我们先回顾伪标签方法。具体而言，伪标签(PL)通过让学生模型最小化未标注数据的交叉熵损失进行训练：

$$
\theta_{S}^{\mathrm{PL}}=\underset{\theta_{S}}{\arg\operatorname*{min}}\underbrace{\mathbb{E}{x_{u}}\Big[\mathrm{CE}\big(T(x_{u};\theta_{T}),S(x_{u};\theta_{S})\big)\Big]}{:=\mathcal{L}{u}\big(\theta_{T},\theta_{S}\big)}
$$

$$
\theta_{S}^{\mathrm{PL}}=\underset{\theta_{S}}{\arg\operatorname*{min}}\underbrace{\mathbb{E}{x_{u}}\Big[\mathrm{CE}\big(T(x_{u};\theta_{T}),S(x_{u};\theta_{S})\big)\Big]}{:=\mathcal{L}{u}\big(\theta_{T},\theta_{S}\big)}
$$

where the pseudo target $T(x_{u};\theta_{T})$ is produced by a well pre-trained teacher model with fixed parameter $\theta_{T}$ . Given a good teacher, the hope of Pseudo Labels is that the obtained $\theta_{S}^{\mathrm{PL}}$ would ultimately achieve a low loss on labeled data, i.e. $\begin{array}{r}{\tilde{\mathbb{E}}{x_{l},y_{l}}\left[\mathbf{CE}\big(y_{l},S(x_{l};\theta_{S}^{\mathrm{PL}})\big)\right]:=\mathcal{L}{l}\big(\theta_{S}^{\mathrm{PL}}\big).}\end{array}$ .

其中伪目标 $T(x_{u};\theta_{T})$ 由参数固定为 $\theta_{T}$ 的预训练优良教师模型生成。给定优质教师模型时，伪标签方法的期望是最终获得的 $\theta_{S}^{\mathrm{PL}}$ 能在标注数据上实现较低损失，即 $\begin{array}{r}{\tilde{\mathbb{E}}{x_{l},y_{l}}\left[\mathbf{CE}\big(y_{l},S(x_{l};\theta_{S}^{\mathrm{PL}})\big)\right]:=\mathcal{L}{l}\big(\theta_{S}^{\mathrm{PL}}\big).}\end{array}$ 。

Under the framework of Pseudo Labels, notice that the optimal student parameter $\theta_{S}^{\mathrm{PL}}$ always depends on the teacher parameter $\theta_{T}$ via the pseudo targets $T(x_{u};\theta_{T})$ . To facilitate the discussion of Meta Pseudo Labels, we can explicitly express the dependency as $\theta_{S}^{\mathrm{PL}}(\theta_{T})$ . As an immediate observation, the ultimate student loss on labeled data $\mathcal{L}{l}\left(\theta_{S}^{\mathrm{PL}}(\theta_{T})\right)$ is also a “function” of $\theta_{T}$ . Therefore, we could further opti

在伪标签 (Pseudo Labels) 框架下，最优学生参数 $\theta_{S}^{\mathrm{PL}}$ 始终通过伪目标 $T(x_{u};\theta_{T})$ 依赖于教师参数 $\theta_{T}$。为了便于讨论元伪标签 (Meta Pseudo Labels)，我们可以显式地将这种依赖关系表示为 $\theta_{S}^{\mathrm{PL}}(\theta_{T})$。显而易见，标记数据上的最终学生损失 $\mathcal{L}{l}\left(\theta_{S}^{\mathrm{PL}}(\theta_{T})\right)$ 也是 $\theta_{T}$ 的“函数”。因此，我们可以进一步优化

mize $\mathcal{L}{l}$ with respect to $\theta_{T}$ :

最小化 $\mathcal{L}{l}$ 关于 $\theta_{T}$：

$$
\begin{array}{r l}{\underset{\theta_{T}}{\mathrm{min}}}&{\mathcal{L}{l}\left(\theta_{S}^{\mathrm{PL}}(\theta_{T})\right),}\ {\mathrm{where}}&{\theta_{S}^{\mathrm{PL}}(\theta_{T})=\underset{\theta_{S}}{\mathrm{argmin}}\mathcal{L}{u}\left(\theta_{T},\theta_{S}\right).}\end{array}
$$

$$
\begin{array}{r l}{\underset{\theta_{T}}{\mathrm{min}}}&{\mathcal{L}{l}\left(\theta_{S}^{\mathrm{PL}}(\theta_{T})\right),}\ {\mathrm{where}}&{\theta_{S}^{\mathrm{PL}}(\theta_{T})=\underset{\theta_{S}}{\mathrm{argmin}}\mathcal{L}{u}\left(\theta_{T},\theta_{S}\right).}\end{array}
$$

Intuitively, by optimizing the teacher’s parameter according to the performance of the student on labeled data, the pseudo labels can be adjusted accordingly to further improve student’s performance. As we are effectively trying to optimize the teacher on a meta level, we name our method Meta Pseudo Labels. However, the dependency of $\theta_{S}^{\mathrm{PL}}(\theta_{T})$ on $\theta_{T}$ is extremely complicated, as computing the gradient $\nabla_{\theta_{T}}\theta_{S}^{\mathrm{PL}}(\theta_{T})$ requires unrolling the entire student training process (i.e. $\mathrm{argmin}{\theta_{S}}$ ).

直观地说，通过根据学生在标注数据上的表现来优化教师的参数，可以相应调整伪标签以进一步提升学生性能。由于我们实际上是在元层级优化教师模型，因此将本方法命名为元伪标签 (Meta Pseudo Labels) 。然而 $\theta_{S}^{\mathrm{PL}}(\theta_{T})$ 对 $\theta_{T}$ 的依赖关系极其复杂，因为计算梯度 $\nabla_{\theta_{T}}\theta_{S}^{\mathrm{PL}}(\theta_{T})$ 需要展开整个学生训练过程 (即 $\mathrm{argmin}{\theta_{S}}$ ) 。

Practical approximation. To make Meta Pseudo Labels feasible, we borrow ideas from previous work in meta learning [40, 15] and approximate the multi-step $\mathrm{argmin}{\theta_{S}}$ with the one-step gradient update of $\theta_{S}$ :

实用近似方法。为使元伪标签 (Meta Pseudo Labels) 可行，我们借鉴元学习领域先前工作 [40, 15] 的思路，将多步优化 $\mathrm{argmin}{\theta_{S}}$ 近似为 $\theta_{S}$ 的单步梯度更新：

$$
\theta_{S}^{\mathrm{PL}}(\theta_{T})\approx\theta_{S}-\eta_{S}\cdot\nabla_{\theta_{S}}\mathcal{L}{u}\big(\theta_{T},\theta_{S}\big),
$$

$$
\theta_{S}^{\mathrm{PL}}(\theta_{T})\approx\theta_{S}-\eta_{S}\cdot\nabla_{\theta_{S}}\mathcal{L}{u}\big(\theta_{T},\theta_{S}\big),
$$

where $\eta_{S}$ is the learning rate. Plugging this approximation into the optimization problem in Equation 2 leads to the practical teacher objective in Meta Pseudo Labels:

其中 $\eta_{S}$ 是学习率。将此近似代入公式 2 的优化问题中，可得到 Meta Pseudo Labels 中的实际教师目标：

$$
\begin{array}{r l}{\underset{\theta_{T}}{\operatorname*{min}}}&{{}\mathcal{L}{l}\Big(\theta_{S}-\eta_{S}\cdot\nabla_{\theta_{S}}\mathcal{L}{u}\big(\theta_{T},\theta_{S}\big)\Big).}\end{array}
$$

$$
\begin{array}{r l}{\underset{\theta_{T}}{\operatorname*{min}}}&{{}\mathcal{L}{l}\Big(\theta_{S}-\eta_{S}\cdot\nabla_{\theta_{S}}\mathcal{L}{u}\big(\theta_{T},\theta_{S}\big)\Big).}\end{array}
$$

Note that, if soft pseudo labels are used, i.e. $T(x_{u};\theta_{T})$ is the full distribution predicted by teacher, the objective above is fully differentiable with respect to $\theta_{T}$ and we can perform standard back-propagation to get the gradient.2 However, in this work, we sample the hard pseudo labels from the teacher distribution to train the student. We use hard pseudo labels because they result in smaller computational graphs which are necessary for our large-scale experiments in Section 4. For smaller experiments where we can use either soft pseudo labels or hard pseudo labels, we do not find significant performance difference between them. A caveat of using hard pseudo labels is that we need to rely on a slightly modified version of REINFORCE to obtain the approximated gradient of $\mathcal{L}{l}$ in Equation 3 with respect to $\theta_{T}$ . We defer the detailed derivation to Appendix A.

需要注意的是，如果使用软伪标签（即 $T(x_{u};\theta_{T})$ 为教师模型预测的完整概率分布），上述目标函数对 $\theta_{T}$ 完全可微，我们可以通过标准反向传播来获取梯度。然而在本工作中，我们从教师分布中采样硬伪标签来训练学生模型。采用硬伪标签的原因是它们能生成更小的计算图，这对第4节的大规模实验至关重要。在可以使用软/硬伪标签的小规模实验中，我们发现两者性能差异不大。使用硬伪标签的注意事项是：我们需要依赖改进版REINFORCE算法来近似计算式3中 $\mathcal{L}{l}$ 对 $\theta_{T}$ 的梯度，详细推导见附录A。

On the other hand, the student’s training still relies on the objective in Equation 1, except that the teacher parameter is not fixed anymore. Instead, $\theta_{T}$ is constantly changing due to the teacher’s optimization. More interestingly, the student’s parameter update can be reused in the one-step approximation of the teacher’s objective, which naturally gives rise to an alternating optimization procedure between the student update and the teacher update:

另一方面，学生的训练仍依赖于公式1中的目标函数，只是教师参数不再固定。相反，由于教师的优化过程，$\theta_{T}$ 会持续变化。更有趣的是，学生参数的更新可复用于教师目标函数的单步近似计算，这自然形成了学生更新与教师更新交替进行的优化流程：

• Student: draw a batch of unlabeled data $x_{u}$ , then sample $T(x_{u};\theta_{T})$ from teacher’s prediction, and optimize objective 1 with SGD: $\theta_{S}^{\prime}=\theta_{S}-\eta_{S}\nabla_{\theta_{S}}\mathcal{L}{u}(\theta_{T},\theta_{S})$ , • Teacher: draw a batch of labeled data $(x_{l},y_{l})$ , and “reuse” the student’s update to optimize objective 3 with SGD: $\theta_{T}^{\prime}=\theta_{T}-\eta_{T}\bar{\nabla}{\theta_{T}}\mathcal{L}{l}\left(\begin{array}{l}{\bar{\theta_{S}}-\nabla_{\theta_{S}}\bar{\mathcal{L}{u}}\left(\theta_{T},\theta_{S}\right)}\end{array}\right)$ . $=\theta_{S}^{\prime}$ reused fro{mz student’s upd}ate

• 学生：抽取一批无标签数据 $x_{u}$，从教师预测中采样 $T(x_{u};\theta_{T})$，并通过SGD优化目标1：$\theta_{S}^{\prime}=\theta_{S}-\eta_{S}\nabla_{\theta_{S}}\mathcal{L}{u}(\theta_{T},\theta_{S})$
• 教师：抽取一批带标签数据 $(x_{l},y_{l})$，并“复用”学生的更新，通过SGD优化目标3：$\theta_{T}^{\prime}=\theta_{T}-\eta_{T}\bar{\nabla}{\theta_{T}}\mathcal{L}{l}\left(\begin{array}{l}{\bar{\theta_{S}}-\nabla_{\theta_{S}}\bar{\mathcal{L}{u}}\left(\theta_{T},\theta_{S}\right)}\end{array}\right)$。$=\theta_{S}^{\prime}$ 复用自学生更新

Teacher’s auxiliary losses. We empirically observe that Meta Pseudo Labels works well on its own. Moreover, it works even better if the teacher is jointly trained with other auxiliary objectives. Therefore, in our implementation, we augment the teacher’s training with a supervised learning objective and a semi-supervised learning objective. For the supervised objective, we train the teacher on labeled data. For the semi-supervised objective, we additionally train the teacher on unlabeled data using the UDA objective [76]. For the full pseudo code of Meta Pseudo Labels when it is combined with supervised and UDA objectives for the teacher, please see Appendix B, Algorithm 1.

教师辅助损失。我们通过实验观察到，元伪标签 (Meta Pseudo Labels) 方法本身表现良好。若教师模型同时结合其他辅助目标进行联合训练，效果会进一步提升。因此，在实现中我们为教师模型增加了监督学习目标和半监督学习目标：监督目标使用标注数据训练教师模型；半监督目标则基于未标注数据采用UDA目标 [76] 进行额外训练。完整伪代码（结合监督目标和UDA目标的教师模型训练流程）详见附录B算法1。

Finally, as the student in Meta Pseudo Labels only learns from unlabeled data with pseudo labels generated by the teacher, we can take a student model that has converged after training with Meta Pseudo Labels and finetune it on labeled data to improve its accuracy. Details of the student’s finetuning are reported in our experiments.

最后，由于Meta Pseudo Labels中的学生模型仅通过教师生成的伪标签从无标注数据中学习，我们可以选取一个在Meta Pseudo Labels训练后已收敛的学生模型，并在有标注数据上对其进行微调以提升准确率。实验部分将详述学生模型的微调细节。

Next, we will present the experimental results of Meta Pseudo Labels, and organize them as follows:

接下来，我们将展示元伪标签 (Meta Pseudo Labels) 的实验结果，并按以下方式组织：

• Section 3 presents small scale experiments where we compare Meta Pseudo Labels against other state-of-the-art semi-supervised learning methods on widely used benchmarks. • Section 4 presents large scale experiments of Meta Pseudo Labels where we push the limits of ImageNet accuracy.

• 第3节展示了小规模实验，我们在广泛使用的基准测试中将元伪标签 (Meta Pseudo Labels) 与其他最先进的半监督学习方法进行了比较。
• 第4节展示了元伪标签的大规模实验，我们在ImageNet准确率上突破了极限。

3. Small Scale Experiments

3. 小规模实验

In this section, we present our empirical studies of Meta Pseudo Labels at small scales. We first study the role of feedback in Meta Pseudo Labels on the simple TwoMoon dataset [7]. This study visually illustrates Meta Pseudo Labels’ behaviors and benefits. We then compare Meta Pseudo Labels against state-of-the-art semi-supervised learning methods on standard benchmarks such as CIFAR-10-4K, SVHN-1K, and ImageNet $10%$ . We conclude the section with experiments on the standard ResNet-50 architecture with the full ImageNet dataset.

在本节中，我们展示了小规模下元伪标签 (Meta Pseudo Labels) 的实证研究。首先在简单的双月数据集 (TwoMoon) [7] 上探究反馈机制在元伪标签中的作用，通过可视化方式阐明其行为模式和优势。随后在 CIFAR-10-4K、SVHN-1K 和 ImageNet $10%$ 等标准基准测试中，将元伪标签与当前最先进的半监督学习方法进行对比。最后通过完整 ImageNet 数据集上的标准 ResNet-50 架构实验作为本节总结。

3.1. TwoMoon Experiment

3.1. TwoMoon 实验

To understand the role of feedback in Meta Pseudo Labels, we conduct an experiment on the simple and classic TwoMoon dataset [7]. The 2D nature of the TwoMoon dataset allows us to visualize how Meta Pseudo Labels behaves compared to Supervised Learning and Pseudo Labels.

为了理解反馈在元伪标签 (Meta Pseudo Labels) 中的作用，我们在简单而经典的双月数据集 (TwoMoon dataset) [7] 上进行了实验。双月数据集的二维特性使我们能够直观地比较元伪标签与监督学习和伪标签的行为差异。

Dataset. For this experiment, we generate our own version of the TwoMoon dataset. In our version, there are 2,000 examples forming two clusters each with 1,000 examples. Only 6 examples are labeled, 3 examples for each cluster, while the remaining examples are unlabeled. Semi-supervised learning algorithms are asked to use these 6 labeled examples and the clustering assumption to separate the two clusters into correct classes.

数据集。在本实验中，我们生成了自制的双月形数据集版本。该版本包含2,000个样本，形成两个各含1,000个样本的簇群。其中仅有6个样本被标注（每个簇群3个），其余样本均为未标注数据。半监督学习算法需利用这6个标注样本和聚类假设，将两个簇群正确划分至对应类别。

Training details. Our model architecture is a feed-forward fully-connected neural network with two hidden layers, each has 8 units. The sigmoid non-linearity is used at each layer. In Meta Pseudo Labels, both the teacher and the student share this architecture but have independent weights. All networks are trained with SGD using a constant learning rate of 0.1. The networks’ weights are initialized with the uniform distribution between -0.1 and 0.1. We do not apply any regular iz ation.

训练细节。我们的模型架构是一个具有两个隐藏层的前馈全连接神经网络，每层包含8个单元。每层均采用sigmoid非线性激活函数。在元伪标签( Meta Pseudo Labels )方法中，教师模型和学生模型共享该架构但拥有独立权重。所有网络均使用学习率为0.1的SGD(随机梯度下降)进行训练，网络权重采用-0.1至0.1之间的均匀分布初始化，未施加任何正则化措施。

Results. We randomly generate the TwoMoon dataset for a few times and repeat the three methods: Supervised Learning, Pseudo Labels, and Meta Pseudo Labels. We observe that Meta Pseudo Labels has a much higher success rate of finding the correct classifier than Supervised Learning and Pseudo Labels. Figure 2 presents a typical outcome of our experiment, where the red and green regions correspond to the class if i ers’ decisions. As can be seen from the figure, Supervised Learning finds a bad classifier which classifies the labeled instances correctly but fails to take advantage of the clustering assumption to separate the two “moons”. Pseudo Labels uses the bad classifier from Supervised Learning and hence receives incorrect pseudo labels on the unlabeled data. As a result, Pseudo Labels finds a classifier that mis classifies half of the data, including a few labeled instances. Meta Pseudo Labels, on the other hand, uses the feedback from the student model’s loss on the labeled instances to adjust the teacher to generate better pseudo labels. As a result, Meta Pseudo Labels finds a good classifier for this dataset. In other words, Meta Pseudo Labels can address the problem of confirmation bias [2] of Pseudo Labels in this experiment.

结果。我们多次随机生成TwoMoon数据集，并重复三种方法：监督学习(Supervised Learning)、伪标签(Pseudo Labels)和元伪标签(Meta Pseudo Labels)。实验表明，元伪标签找到正确分类器的成功率显著高于监督学习和伪标签。图2展示了典型实验结果，其中红色和绿色区域分别对应分类器的决策结果。如图所示，监督学习找到的分类器虽然能正确分类标注样本，但未能利用聚类假设分离两个"月牙"分布。伪标签方法沿用监督学习的错误分类器，导致未标注数据获得错误伪标签，最终得到的分类器对半数数据（包括部分标注样本）产生误判。相比之下，元伪标签通过学生模型在标注样本上的损失反馈来调整教师模型，从而生成更优质的伪标签，最终为该数据集找到理想分类器。这表明元伪标签能有效解决本实验中伪标签方法存在的确认偏误(confirmation bias)问题[2]。

Figure 2: An illustration of the importance of feedback in Meta Pseudo Labels (right). In this example, Meta Pseudo Labels works better than Supervised Learning (left) and Pseudo Labels (middle) on the simple TwoMoon dataset. More details are in Section 3.1.

图 2: 展示反馈在元伪标签(Meta Pseudo Labels)中的重要性(右图)。在这个简单的TwoMoon数据集示例中，元伪标签方法表现优于监督学习(左图)和伪标签方法(中图)。更多细节见第3.1节。

3.2. CIFAR-10-4K, SVHN-1K, and ImageNet $10%$ Experiments

3.2. CIFAR-10-4K、SVHN-1K 和 ImageNet $10%$ 实验

Datasets. We consider three standard benchmarks: CIFAR-10-4K, SVHN-1K, and ImageNet $10%$ , which have been widely used in the literature to fairly benchmark semisupervised learning algorithms. These benchmarks were created by keeping a small fraction of the training set as labeled data while using the rest as unlabeled data. For CIFAR-10 [34], 4,000 labeled examples are kept as labeled data while 41,000 examples are used as unlabeled data. The test set for CIFAR-10 is standard and consists of 10,000 examples. For SVHN [46], 1,000 examples are used as labeled data whereas about 603,000 examples are used as unlabeled data. The test set for SVHN is also standard, and has 26,032 examples. Finally, for ImageNet [56], 128,000 examples are used as labeled data which is approximately $10%$ of the whole ImageNet training set while the rest of 1.28 million examples are used as unlabeled data. The test set for ImageNet is the standard ILSVRC 2012 version that has 50,000 examples. We use the image resolution of 32x32 for CIFAR-10 and SVHN, and $224\mathrm{x}224$ for ImageNet.

数据集。我们采用三个标准基准：CIFAR-10-4K、SVHN-1K和ImageNet $10%$ ，这些基准在文献中被广泛用于公平比较半监督学习算法。这些基准通过保留训练集的一小部分作为标注数据，其余部分作为未标注数据构建而成。对于CIFAR-10 [34]，保留4,000个标注样本作为标注数据，41,000个样本作为未标注数据。CIFAR-10的标准测试集包含10,000个样本。对于SVHN [46]，使用1,000个样本作为标注数据，约603,000个样本作为未标注数据。SVHN的标准测试集包含26,032个样本。最后对于ImageNet [56]，使用128,000个样本作为标注数据（约占整个ImageNet训练集的 $10%$ ），其余128万样本作为未标注数据。ImageNet测试集采用标准ILSVRC 2012版本，包含50,000个样本。CIFAR-10和SVHN使用32x32图像分辨率，ImageNet使用 $224\mathrm{x}224$ 分辨率。

Training details. In our experiments, our teacher and our student share the same architecture but have independent weights. For CIFAR-10-4K and SVHN-1K, we use a WideResNet-28-2 [84] which has 1.45 million parameters. For ImageNet, we use a ResNet-50 [24] which has 25.5 million parameters. These architectures are also commonly used by previous works in this area. During the Meta Pseudo Labels training phase where we train both the teacher and the student, we use the default hyper-parameters from previous work for all our models, except for a few modifications in Rand Augment [13] which we detail in Appendix C.2. All hyper-parameters are reported in Appendix C.4. After training both the teacher and student with Meta Pseudo Labels, we finetune the student on the labeled dataset. For this finetuning phase, we use SGD with a fixed learning rate of $10^{-5}$ and a batch size of 512, running for 2,000 steps for ImageNet $10%$ and 1,000 steps for CIFAR-10 and SVHN. Since the amount of labeled examples is limited for all three datasets, we do not use any heldout validation set. Instead, we return the model at the final checkpoint.

训练细节。在我们的实验中，教师模型和学生模型共享相同架构但具有独立权重。对于CIFAR-10-4K和SVHN-1K数据集，我们使用包含145万个参数的WideResNet-28-2 [84]。对于ImageNet数据集，我们采用包含2550万个参数的ResNet-50 [24]。这些架构也是该领域先前工作中常用的选择。在同时训练教师模型和学生模型的元伪标签（Meta Pseudo Labels）阶段，除Rand Augment [13]的若干调整（详见附录C.2）外，所有模型均沿用先前工作的默认超参数。完整超参数配置见附录C.4。完成元伪标签联合训练后，我们在标注数据集上对学生模型进行微调：使用固定学习率$10^{-5}$的SGD优化器，批大小为512，ImageNet $10%$数据集微调2000步，CIFAR-10和SVHN数据集微调1000步。由于三个数据集的标注样本量有限，我们未设置保留验证集，而是直接返回最终检查点的模型。

Baselines. To ensure a fair comparison, we only compare Meta Pseudo Labels against methods that use the same architectures and do not compare against methods that use larger architectures such as Larger-WideResNet-28-2 and PyramidNet+ShakeDrop for CIFAR-10 and SVHN [5, 4, 72, 76], or ResNet $50\times{2,3,4}$ , ResNet-101, ResNet-152, etc. for ImageNet $10%$ [25, 23, 10, 8, 9]. We also do not compare Meta Pseudo Labels with training procedures that include self-distillation or distillation from a larger teacher [8, 9]. We enforce these restrictions on our baselines since it is known that larger architectures and distillation can improve any method, possibly including Meta Pseudo Labels.

基线方法。为确保公平比较，我们仅将元伪标签 (Meta Pseudo Labels) 与使用相同架构的方法进行对比，而不与采用更大架构的方法（例如 CIFAR-10 和 SVHN 任务中的 Larger-WideResNet-28-2 和 PyramidNet+ShakeDrop [5, 4, 72, 76]，或 ImageNet 10% 任务中的 ResNet $50\times{2,3,4}$、ResNet-101、ResNet-152 等 [25, 23, 10, 8, 9]）进行比较。我们也不将元伪标签与包含自蒸馏或从更大教师模型蒸馏的训练流程 [8, 9] 进行对比。对基线方法施加这些限制是因为已知更大的架构和蒸馏技术可以提升任何方法的性能，其中可能包括元伪标签。

We directly compare Meta Pseudo Labels against two baselines: Supervised Learning with full dataset and Unsupervised Data Augmentation (UDA [76]). Supervised Learning with full dataset represents the headroom because it unfairly makes use of all labeled data (e.g., for CIFAR10, it uses all 50,000 labeled examples). We also compare against UDA because our implementation of Meta Pseudo Labels uses UDA in training the teacher. Both of these baselines use the same experimental protocols and hence ensure a fair comparison. We follow [48]’s train/eval/test splitting, and we use the same amount of resources to tune hyperparameters for our baselines as well as for Meta Pseudo Labels. More details are in Appendix C.

我们直接将元伪标签 (Meta Pseudo Labels) 与两个基线方法进行对比：全数据集监督学习 (Supervised Learning with full dataset) 和无监督数据增强 (Unsupervised Data Augmentation, UDA [76])。全数据集监督学习代表性能上限，因为它不公平地使用了所有标注数据（例如对于 CIFAR10 使用了全部 50,000 个标注样本）。选择 UDA 作为基线是因为我们在实现元伪标签时使用了 UDA 来训练教师模型。这两个基线都采用相同的实验协议以确保公平对比。我们遵循 [48] 的训练/验证/测试划分方式，并为基线方法和元伪标签分配相同的超参数调优资源。更多细节见附录 C。

Additional baselines. In addition to these two baselines, we also include a range of other semi-supervised baselines in two categories: Label Propagation and Self-Supervised. Since these methods do not share the same controlled environment, the comparison to them is not direct, and should be contextual i zed as suggested by [48]. More controlled experiments comparing Meta Pseudo Labels to other baselines

其他基线方法。除了这两个基线外，我们还包含了两类半监督基线方法：标签传播 (Label Propagation) 和自监督 (Self-Supervised)。由于这些方法未在相同受控环境下测试，与其对比并非直接性比较，应按照 [48] 的建议进行情境化解读。更多将元伪标签 (Meta Pseudo Labels) 与其他基线方法对比的受控实验

Table 2: Image classification accuracy on CIFAR-10-4K, SVHN-1K, and ImageNet $10%$ . Higher is better. For CIFAR-10-4K and SVHN1K, we report mean $\pm$ std over 10 runs, while for ImageNet $10%$ , we report Top-1/Top-5 accuracy of a single run. For fair comparison, we only include results that share the same model architecture: WideResNet-28-2 for CIFAR-10-4K and SVHN-1K, and ResNet-50 for ImageNet $10%$ . ∗ indicates our implementation which uses the same experimental protocols. Except for UDA, results in the first two blocks are from representative important papers, and hence do not share the same controlled environment with ours.

表 2: CIFAR-10-4K、SVHN-1K 和 ImageNet 10% 上的图像分类准确率。数值越高越好。对于 CIFAR-10-4K 和 SVHN-1K，我们报告了 10 次运行的平均值 ± 标准差，而对于 ImageNet 10%，我们报告了单次运行的 Top-1/Top-5 准确率。为了公平比较，我们仅包含使用相同模型架构的结果：CIFAR-10-4K 和 SVHN-1K 使用 WideResNet-28-2，ImageNet 10% 使用 ResNet-50。∗ 表示我们使用相同实验协议的实现。除 UDA 外，前两个模块的结果来自代表性重要论文，因此与我们的受控环境不同。

	方法	CIFAR-10-4K (平均值 ± 标准差)	SVHN-1K (平均值 ± 标准差)	ImageNet-10% Top-1	Top-5
标签传播方法	Temporal Ensemble [35]	83.63 ± 0.63	92.81 ± 0.27
	Mean Teacher [64]	84.13 ± 0.28	94.35 ± 0.47
	VAT + EntMin [44]	86.87 ± 0.39	94.65 ± 0.19		83.39
	LGA + VAT [30]	87.94 ± 0.19	93.42 ± 0.36
	ICT [71]	92.71 ± 0.02	96.11 ± 0.04
	MixMatch [5]	93.76 ± 0.06	96.73 ± 0.31
	ReMixMatch [4]	94.86 ± 0.04	97.17 ± 0.30
	EnAET [72]	94.65	97.08
	FixMatch [58]	95.74 ± 0.05	97.72 ± 0.38	71.5	89.1
	UDA* [76]	94.53 ± 0.18	97.11 ± 0.17	68.07	88.19
自监督方法	SimCLR [8, 9]			71.7	90.4
	MOC0v2 [10]			71.1
	PCL [38]			-	85.6
	PIRL [43]				84.9
	BYOL [21]			68.8	89.0
	MetaPseudoLabels	96.11 ± 0.07	98.01 ± 0.07	73.89	91.38
	全数据集监督学习*	94.92 ± 0.17	97.41 ± 0.16	76.89	93.27

are presented in Appendix D.

详见附录D。

Results. Table 2 presents our results with Meta Pseudo Labels in comparison with other methods. The results show that under strictly fair comparisons (as argued by [48]), Meta Pseudo Labels significantly improves over UDA. Inte rest ingly, on CIFAR-10-4K, Meta Pseudo Labels even exceeds the headroom supervised learning on full dataset. On ImageNet $10%$ , Meta Pseudo Labels outperforms the UDA teacher by more than $5%$ in top-1 accuracy, going from $68.07%$ to $73.89%$ . For ImageNet, such relative improvement is very significant.

结果。表 2 展示了 Meta Pseudo Labels 与其他方法的对比结果。实验表明，在严格公平的对比条件下 (如 [48] 所述)，Meta Pseudo Labels 显著优于 UDA。值得注意的是，在 CIFAR-10-4K 数据集上，Meta Pseudo Labels 甚至超越了全量数据监督学习的性能上限。在 ImageNet $10%$ 数据集上，Meta Pseudo Labels 的 top-1 准确率比 UDA 教师模型高出 $5%$ 以上，从 $68.07%$ 提升至 $73.89%$。对于 ImageNet 数据集而言，这种相对提升具有重大意义。

Comparing to existing state-of-the-art methods. Compared to results reported from past papers, Meta Pseudo Labels has achieved the best accuracies among the same model architectures on all the three datasets: CIFAR-10- 4K, SVHN-1K, and ImageNet $10%$ . On CIFAR-10-4K and SVHN-1K, Meta Pseudo Labels leads to almost $10%$ relative error reduction compared to the highest reported baselines [58]. On ImageNet $10%$ , Meta Pseudo Labels outperforms SimCLR [8, 9] by $2.19%$ top-1 accuracy.

与现有最先进方法相比。相较于以往论文报告的结果，Meta Pseudo Labels 在 CIFAR-10-4K、SVHN-1K 和 ImageNet $10%$ 三个数据集上均实现了同模型架构下的最高准确率。在 CIFAR-10-4K 和 SVHN-1K 上，Meta Pseudo Labels 相较最高基线 [58] 实现了近 $10%$ 的相对错误率降低。在 ImageNet $10%$ 上，Meta Pseudo Labels 的 top-1 准确率比 SimCLR [8, 9] 高出 $2.19%$。

While better results on these datasets exist, to our knowledge, such results are all obtained with larger models, stronger regular iz ation techniques, or extra distillation procedures. For example, the best reported accuracy on CIFAR10-4K is $97.3%$ [76] but this accuracy is achieved with a PyramidNet which has $17\mathbf{x}$ more parameters than our WideResNet-28-2 and uses the complex ShakeDrop regu lari z ation [80]. On the other hand, the best reported top-1 accuracy for ImageNet $10%$ is $80.9%$ , achieved by SimCLRv2 [9] using a self-distillation training phase and a ResNet $152\times3$ which has $32\mathbf{x}$ more parameters than our ResNet-50. Such enhancements on architectures, regularization, and distillation can also be applied to Meta Pseudo Labels to further improve our results.

虽然这些数据集上存在更好的结果，但据我们所知，这些结果都是通过更大的模型、更强的正则化技术或额外