Input Perturbation Reduces Exposure Bias in Diffusion Models
输入扰动降低扩散模型的曝光偏差
Abstract
摘要
Denoising Diffusion Probabilistic Models have shown an impressive generation quality although their long sampling chain leads to high computational costs. In this paper, we observe that a long sampling chain also leads to an error accumulation phenomenon, which is similar to the exposure bias problem in auto regressive text generation. Specifically, we note that there is a discrepancy between training and testing, since the former is conditioned on the ground truth samples, while the latter is conditioned on the previously generated results. To alleviate this problem, we propose a very simple but effective training regu lari z ation, consisting in perturbing the ground truth samples to simulate the inference time prediction errors. We empirically show that, without affecting the recall and precision, the proposed input perturbation leads to a significant improvement in the sample quality while reducing both the training and the inference times. For instance, on CelebA $64\times64$ , we achieve a new state-of-theart FID score of 1.27, while saving $37.5%$ of the training time. The code is available at https: //github.com/forever208/DDPM-IP.
去噪扩散概率模型 (Denoising Diffusion Probabilistic Models) 虽然因其长采样链导致高计算成本,但仍展现出卓越的生成质量。本文发现,长采样链还会引发误差累积现象,这与自回归文本生成中的曝光偏差问题类似。具体而言,我们注意到训练与测试之间存在差异:前者以真实样本为条件,而后者则依赖于先前生成的结果。为缓解此问题,我们提出了一种简单但有效的训练正则化方法,即通过扰动真实样本来模拟推理阶段的预测误差。实验表明,在不影响召回率和精确度的前提下,所提出的输入扰动能显著提升样本质量,同时减少训练和推理时间。例如在CelebA $64\times64$ 数据集上,我们以1.27的FID分数刷新了当前最佳纪录,并节省了 $37.5%$ 的训练时间。代码已开源:https://github.com/forever208/DDPM-IP。
1. Introduction
1. 引言
Denoising Diffusion Probabilistic Models (DDPMs) (SohlDickstein et al., 2015; Ho et al., 2020) are a new generative paradigm which is attracting a growing interest due to its very high-quality sample generation capabilities (Dhariwal & Nichol, 2021; Nichol et al., 2022; Ramesh et al., 2022). Differently from most existing generative methods which synthesize a new sample in a single step, DDPMs resemble the Langevin dynamics (Welling & Teh, 2011) and the generation process is based on a sequence of denoising steps, in which a synthetic sample is created starting from pure noise and auto regressive ly reducing the noise component. In more detail, during training, a real sample $\pmb{x}{0}$ is progressively destroyed in $T$ steps adding Gaussian noise (forward process). The sequence ${ x}{0},...,{ x}{t},...,{\pmb x}{T}$ so obtained, is used to train a deep denoising auto encoder $(\mu(\cdot))$ to invert the forward process: $\hat{\mathbf{\pmbx}}{t-1}=\mu(\mathbf{\pmbx}{t},t)$ . At inference time, the generation process is auto regressive because it depends on the previously generated samples: $\hat{\mathbf{x}}{t-1}=\mu(\hat{\mathbf{x}}_{t},t)$ (Sec. 3).
去噪扩散概率模型 (Denoising Diffusion Probabilistic Models, DDPMs) (SohlDickstein et al., 2015; Ho et al., 2020) 是一种新兴的生成范式,因其卓越的样本生成质量而受到越来越多的关注 (Dhariwal & Nichol, 2021; Nichol et al., 2022; Ramesh et al., 2022)。与大多数现有单步生成样本的方法不同,DDPMs 类似于朗之万动力学 (Welling & Teh, 2011),其生成过程基于一系列去噪步骤:从纯噪声出发,通过自回归方式逐步降低噪声分量来合成样本。具体而言,在训练阶段,真实样本 $\pmb{x}{0}$ 会通过 $T$ 步逐步叠加高斯噪声被破坏 (前向过程)。由此得到的序列 ${\pmb x}{0},...,{ x}{t},...,{ x}{T}$ 用于训练深度去噪自编码器 $(\mu(\cdot))$ 以逆转前向过程:$\hat{\mathbf{\pmbx}}{t-1}=\mu(\mathbf{\pmbx}{t},t)$。在推理阶段,生成过程具有自回归特性,因为它依赖于前一步生成的样本:$\hat{\mathbf{x}}{t-1}=\mu(\hat{\mathbf{x}}_{t},t)$ (第3节)。
Despite the large success of DDPMs in different generative fields (Sec. 2), one of the main drawbacks of these models is their very long computational time, which depends on the large number of steps $T$ required at both the training and the inference stage. As recently emphasised in (Xiao et al., 2022), the fundamental reason why $T$ needs to be large is that each denoising step is assumed to be Gaussian, and this assumption holds only for small step sizes. Conversely, with larger step sizes, the prediction network $(\mu(\cdot))$ needs to solve a harder problem and it becomes progressively less accurate (Xiao et al., 2022). However, in this paper, we observe that there is a second phenomenon, related to the sampling chain, but partially in contrast with the first, which is the accumulation of these errors over the $T$ inference sampling steps. This is basically due to the discrepancy between the training and the inference stage, in which the latter generates a sequence of samples based on the results of the previous steps, hence possibly accumulating errors. In fact, at training time, $\mu(\cdot)$ is trained with a ground truth pair $({\pmb x}{t},{\pmb x}{t-1})$ and, given $\pmb{x}{t}$ , it learns to reconstruct $\pmb{x}{t-1}$ $(\mu(\pmb{x}{t},t))$ . However, at inference time, $\mu(\cdot)$ has no access to the “real” $\pmb{x}{t}$ , and its prediction depends on the previously generated $\hat{\pmb x}{t}$ $(\mu(\hat{\pmb x}{t},t))$ . This input mismatch between $\mu(\pmb{x}{t},t)$ , used during training, and $\mu(\hat{\mathbf{\boldsymbol{x}}}_{t},t)$ , used during testing, is similar to the exposure bias problem (Ranzato et al., 2016; Schmidt, 2019) shared by other auto regressive generative methods. For example, Rennie et al. (2017) argue that training a network to maximize the likelihood of the next ground-truth word given the previous ground-truth word (called “Teacher-Forcing” (Bengio et al., 2015)) results in error accumulation at inference time, since the model has never been exposed to its own predictions.
尽管 DDPM (Denoising Diffusion Probabilistic Models) 在不同生成领域取得了巨大成功 (第 2 节),这些模型的主要缺点之一是其计算时间非常长,这取决于训练和推理阶段所需的大量步骤 $T$。正如 (Xiao et al., 2022) 最近强调的那样,$T$ 需要很大的根本原因是假设每个去噪步骤都是高斯的,而这种假设仅适用于小步长。相反,对于较大的步长,预测网络 $(\mu(\cdot))$ 需要解决一个更难的问题,并且其准确性会逐渐降低 (Xiao et al., 2022)。然而,在本文中,我们观察到存在第二种现象,与采样链相关,但与第一种现象部分相反,即这些误差在 $T$ 个推理采样步骤中的累积。这基本上是由于训练和推理阶段之间的差异,后者基于前一步骤的结果生成一系列样本,因此可能累积误差。事实上,在训练时,$\mu(\cdot)$ 使用真实值对 $({\pmb x}{t},{\pmb x}{t-1})$ 进行训练,给定 $\pmb{x}{t}$,它学习重建 $\pmb{x}{t-1}$ $(\mu(\pmb{x}{t},t))$。然而,在推理时,$\mu(\cdot)$ 无法访问“真实”的 $\pmb{x}{t}$,其预测依赖于先前生成的 $\hat{\pmb x}{t}$ $(\mu(\hat{\pmb x}{t},t))$。这种训练时使用的 $\mu(\pmb{x}{t},t)$ 和测试时使用的 $\mu(\hat{\mathbf{\boldsymbol{x}}}_{t},t)$ 之间的输入不匹配,类似于其他自回归生成方法共有的曝光偏差问题 (Ranzato et al., 2016; Schmidt, 2019)。例如,Rennie et al. (2017) 认为,训练网络以最大化给定先前真实词的下一个真实词的可能性(称为“教师强制”(Bengio et al., 2015))会导致推理时的误差累积,因为模型从未接触过自己的预测。
In this paper, we first empirically analyze this accumulation error phenomenon. For instance, we show that a standard DDPM (Dhariwal & Nichol, 2021), trained with $T$ steps, can generate better results using a number of inference steps $T^{\prime}<T$ (Sec. 6.2). A similar phenomenon was also observed by Nichol & Dhariwal (2021), but the authors did not provide an explanation for that. We believe that the reason for this apparently contrasting result is that while, on the one hand, longer chains can better satisfy the Gaussian assumption in the reverse diffusion process, on the other hand, they lead to a larger accumulation of errors.
本文首先对这一误差累积现象进行了实证分析。例如,我们发现标准DDPM (Dhariwal & Nichol, 2021) 在使用$T$步训练时,通过$T^{\prime}<T$步推理即可生成更优结果(第6.2节)。Nichol & Dhariwal (2021) 也观察到类似现象,但未给出合理解释。我们认为这种看似矛盾的结果源于:更长的马尔可夫链虽能更好地满足反向扩散过程的高斯假设,但同时会导致更大的误差累积。
Second, in order to alleviate the exposure bias problem, we propose a surprisingly simple yet very effective method, which consists in explicitly modelling the prediction error during training. Specifically, at training time, we perturb $\pmb{x}{t}$ and we feed $\mu(\cdot)$ with a noisy version of $\pmb{x}{t}$ , this way simulating the training-inference discrepancy, and forcing the learned network to take into account possible inferencetime prediction errors. Note that our perturbation is different from the content-destroying forward process, because the new noise is not used in the ground truth prediction target (Sec. 5.2). The proposed method is a training regular iz ation which forces the network to smooth its prediction function: to solve the proposed task, two spatially close points $\pmb{x}{1}$ and $\pmb{x}{2}$ should lead to similar predictions $\mu(\pmb{x}{1},t)$ and $\mu(\pmb{x}_{2},t)$ This regular iz ation approach is similar to Mixup (Zhang et al., 2018) and the Vicinal Risk Minimization (VRM) principle (Chapelle et al., 2000), where a neighborhood around each sample in the training data is defined and then used to perturb that sample keeping fixed its target class label.
其次,为缓解曝光偏差问题,我们提出了一种简单却极为有效的方法:在训练期间显式建模预测误差。具体而言,在训练时对$\pmb{x}{t}$施加扰动,将带噪版本的$\pmb{x}{t}$输入$\mu(\cdot)$,从而模拟训练与推理的差异,迫使学习网络考虑推理阶段可能出现的预测误差。需注意我们的扰动不同于破坏性前向过程,因为新增噪声不会用于真实预测目标(见第5.2节)。该方法作为训练正则化手段,能促使网络平滑其预测函数:对于空间邻近点$\pmb{x}{1}$和$\pmb{x}{2}$,应产生相似预测$\mu(\pmb{x}{1},t)$与$\mu(\pmb{x}_{2},t)$。此正则化思路类似于Mixup (Zhang et al., 2018) 和邻域风险最小化(VRM)准则 (Chapelle et al., 2000),二者通过定义训练样本邻域来扰动样本,同时保持其目标类别标签不变。
Third, we propose alternative solutions to the exposure bias problem for diffusion models, in which, rather than using input perturbation, we obtain a smoother prediction function $\mu(\cdot)$ by explicitly encouraging $\mu(\cdot)$ to be Lipschitz continuous (Sec. 5.4). The rationale behind this is that a Lipschitz continuous function $\mu(\cdot)$ generates small prediction differences between neighbouring points in its domain, leading to a DDPM which is more robust to the inference-time errors.
第三,我们针对扩散模型的曝光偏差问题提出了替代解决方案。不同于输入扰动方法,我们通过显式鼓励预测函数 $\mu(\cdot)$ 满足Lipschitz连续性(见第5.4节),从而获得更平滑的预测函数 $\mu(\cdot)$ 。其原理在于:Lipschitz连续函数 $\mu(\cdot)$ 会在其定义域内相邻点之间产生较小的预测差异,这使得DDPM对推理阶段的误差具有更强鲁棒性。
Finally, we empirically analyse all the proposed solutions and we show that, despite being all effective for improving the final generation quality, input perturbation is both more efficient and more effective than the explicit minimization of the Lipschitz constant in DDPMs (Sec. 6.1). Moreover, directly perturbing the network input at training time has no additional training overhead and this solution is very easy to be reproduced and plugged into existing DDPM frameworks: it can be obtained with just two lines of code without any change in the network architecture or the loss function. We call our method Denoising Diffusion Probabilistic Models with Input Perturbation (DDPM-IP) and we show that it can significantly improve the generation quality of state-of-theart DDPMs (Dhariwal & Nichol, 2021; Song et al., 2021a) and speed up the inference-time sampling. For instance, on the CIFAR10 (Krizhevsky et al., 2009), the ImageNet $32\times32$ (Chrabaszcz et al., 2017), the LSUN $64\times64$ (Yu et al., 2015) and the FFHQ $128\times128$ (Karras et al., 2019) datasets, DDPM-IP, with only 80 sampling steps, generates lower FID scores than the state-of-the-art ADM (Dhariwal & Nichol, 2021) with 1,000 steps, corresponding to a more than $12.5\times$ sampling acceleration.
最后,我们通过实证分析所有提出的解决方案,并证明尽管这些方法都能有效提升最终生成质量,但在DDPM中,输入扰动(input perturbation)比显式最小化Lipschitz常数更高效且更有效(见第6.1节)。此外,在训练时直接扰动网络输入不会产生额外训练开销,该方案极易复现并嵌入现有DDPM框架:仅需两行代码即可实现,无需改变网络架构或损失函数。我们将该方法命名为带输入扰动的去噪扩散概率模型(DDPM-IP),并证明它能显著提升前沿DDPM模型(Dhariwal & Nichol, 2021; Song et al., 2021a)的生成质量,同时加速推理阶段采样。例如在CIFAR10(Krizhevsky et al., 2009)、ImageNet $32\times32$(Chrabaszcz et al., 2017)、LSUN $64\times64$(Yu et al., 2015)和FFHQ $128\times128$(Karras et al., 2019)数据集上,仅用80次采样步数的DDPM-IP生成的FID分数,优于采用1,000步的前沿ADM模型(Dhariwal & Nichol, 2021),相当于实现超过 $12.5\times$ 的采样加速。
In summary, our contributions are:
总之,我们的贡献包括:
• We show that there is an exposure bias problem in DDPMs which has not been investigated so far. • To alleviate this problem, we propose different regularization methods whose common goal is to smooth the prediction function, and we specifically suggest input perturbation (DDPM-IP) as the best and the simplest of such solutions. • Using common benchmarks, we show that DDPM-IP can significantly improve the generation quality and drastically speed up both training and inference.
• 我们证明了DDPM中存在一个尚未被研究的曝光偏差问题。
• 为缓解该问题,我们提出了多种正则化方法,其共同目标是平滑预测函数,并特别推荐输入扰动 (DDPM-IP) 作为最优且最简单的解决方案。
• 通过常见基准测试,我们表明DDPM-IP能显著提升生成质量,并大幅加速训练和推理过程。
2. Related Work
2. 相关工作
Diffusion models were introduced by Sohl-Dickstein et al. (2015) and later improved in (Song & Ermon, 2019; Ho et al., 2020; Song et al., 2021b; Nichol & Dhariwal, 2021). More recently, Dhariwal & Nichol (2021) have shown that DDPMs can yield higher-quality images than Generative Adversarial Networks (GANs) (Goodfellow et al., 2014; Brock et al., 2018). Similarly to GANs, the generation process in DDPMs can be both unconditional and conditioned. For instance, GLIDE (Nichol et al., 2022) learns to generate images according to an input textual sentence. Differently from GLIDE, where the diffusion model is defined on the image space, DALL E-2 (Ramesh et al. (2022)) uses a DDPM to learn a prior distribution on the CLIP (Radford et al., 2021) space. Text-to-image generation is explored also in Stable Diffusion (Rombach et al., 2021) and Imagen (Saharia et al., 2022). Apart from images, DDPMs can also be used with categorical distributions (Hoogeboom et al., 2021; Gu et al., 2021), in an audio domain (Mittal et al., 2021; Chen et al., 2021), in time series forecasting (Rasul et al., 2021) and in other generative tasks (Yang et al., 2022; Croitoru et al., 2022). Differently from previous work, our goal is not to propose an application-specific prediction network, but rather to investigate the training-testing discrepancy of the DDPMs and propose a solution which can be used in different application fields and jointly with different denoising architectures.
扩散模型由 Sohl-Dickstein 等人 (2015) 提出,随后在 (Song & Ermon, 2019; Ho 等人, 2020; Song 等人, 2021b; Nichol & Dhariwal, 2021) 的研究中得到改进。最近,Dhariwal & Nichol (2021) 证明 DDPM 能生成比生成对抗网络 (GANs) (Goodfellow 等人, 2014; Brock 等人, 2018) 更高质量的图像。与 GANs 类似,DDPM 的生成过程可以是无条件或条件式的。例如,GLIDE (Nichol 等人, 2022) 通过学习根据输入文本生成图像。不同于 GLIDE 在图像空间定义扩散模型,DALL·E 2 (Ramesh 等人, 2022) 使用 DDPM 学习 CLIP (Radford 等人, 2021) 空间中的先验分布。Stable Diffusion (Rombach 等人, 2021) 和 Imagen (Saharia 等人, 2022) 也探索了文本到图像生成。除图像外,DDPM 还可用于类别分布 (Hoogeboom 等人, 2021; Gu 等人, 2021)、音频领域 (Mittal 等人, 2021; Chen 等人, 2021)、时间序列预测 (Rasul 等人, 2021) 及其他生成任务 (Yang 等人, 2022; Croitoru 等人, 2022)。与之前工作不同,我们的目标不是提出特定应用的预测网络,而是研究 DDPM 的训练-测试差异,并提出一种可跨不同应用领域且兼容多种去噪架构的解决方案。
Accelerating the DDPM training or reducing the number of sampling steps $T$ (Sec. 1) have been thoroughly investigated due to their practical implications. For instance, Song et al. (2021a) propose Denoising Diffusion Implicit Models (DDIMs), based on a non-Markovian diffusion process, which can use a number of inference sampling steps smaller than those used at training time, without retraining the network. Salimans & Ho (2022) propose to distil the prediction network into new networks which progressively reduce the number of sampling steps. However, the disadvantage is the need of training multiple networks. Rombach et al. (2021) speed up sampling by splitting the process into a compression stage and a generation stage, and applying the DDPM on the compressed (latent) space. Hoogeboom et al. (2022) present an order-agnostic DDPM, inspired by XLNet (Yang et al., 2019), in which the sequence $\pmb{x}{0},...,\pmb{x}_{T}$ is randomly permuted at training time, leading to a partially parallel i zed sampling process. Chen et al. (2021) found that, instead of conditioning the prediction network $(\mu(\cdot))$ on a discrete diffusion step $t$ , it is beneficial to condition $\mu(\cdot)$ on a continuous noise level. Similarly, Kong & Ping (2021) introduce continuous diffusion steps, resulting in a unified framework for fast sampling. In order to use larger size sampling steps and a non-Gaussian reverse process (Sec. 1) Xiao et al. (2022) include an adversarial loss in DDPMs and propose Denoising Diffusion GANs. Karras et al. (2022) suggest using Heun’s second-order deterministic sampling method, leading to high quality results and fast sampling. Xu et al. (2022) accelerate the generation process of continuous normalizing flow using a Poisson flow generative model. Our approach is orthogonal to these previous works, and it can potentially be used jointly with most of them.
加速DDPM训练或减少采样步骤数$T$(第1节)因其实际意义已被深入研究。例如,Song等人(2021a)提出了基于非马尔可夫扩散过程的去噪扩散隐式模型(DDIM),可在不重新训练网络的情况下使用比训练时更少的推理采样步骤。Salimans & Ho(2022)提出将预测网络蒸馏到逐步减少采样步骤数的新网络中,但缺点是需要训练多个网络。Rombach等人(2021)通过将过程分为压缩阶段和生成阶段,并在压缩(潜在)空间上应用DDPM来加速采样。Hoogeboom等人(2022)受XLNet(Yang等人,2019)启发提出顺序无关的DDPM,在训练时随机排列序列$\pmb{x}{0},...,\pmb{x}_{T}$,实现部分并行化采样过程。Chen等人(2021)发现,相较于基于离散扩散步$t$调节预测网络$(\mu(\cdot))$,基于连续噪声水平调节$\mu(\cdot)$更有优势。类似地,Kong & Ping(2021)引入连续扩散步,建立了快速采样的统一框架。为使用更大步长和非高斯逆向过程(第1节),Xiao等人(2022)在DDPM中加入对抗损失并提出去噪扩散GAN。Karras等人(2022)建议采用Heun二阶确定性采样方法,实现高质量结果和快速采样。Xu等人(2022)利用泊松流生成模型加速连续归一化流的生成过程。我们的方法与这些先前工作正交,且有望与其中大多数方法联合使用。
3. Background
3. 背景
Without loss of generality, we assume an image domain and we focus on DDPMs which define a diffusion process on the input space. Following (Nichol & Dhariwal, 2021; Dhariwal & Nichol, 2021), we assume that each pixel value is linearly scaled into $[-1,1]$ . Given a sample $\pmb{x}{0}$ from the data distribution $q(\pmb{x}{0})$ and a prefixed noise schedule $(\beta_{1},...,\beta_{T})$ , a DDPM defines the forward process as a Markov chain which starts from a real image ${\pmb x}{0}\sim q({\pmb x}_{0})$ and iterative ly adds Gaussian noise for $T$ diffusion steps:
在不失一般性的情况下,我们假设一个图像域,并专注于在输入空间上定义扩散过程的DDPMs。遵循 (Nichol & Dhariwal, 2021; Dhariwal & Nichol, 2021) 的方法,我们假设每个像素值被线性缩放到 $[-1,1]$。给定来自数据分布 $q(\pmb{x}{0})$ 的样本 $\pmb{x}{0}$ 和预定义的噪声调度 $(\beta_{1},...,\beta_{T})$,DDPM将前向过程定义为一个马尔可夫链,该链从真实图像 ${\pmb x}{0}\sim q({\pmb x}_{0})$ 开始,并迭代地添加高斯噪声进行 $T$ 步扩散:
$$
q(\pmb{x}{t}|\pmb{x}{t-1})=\mathcal{N}(\pmb{x}{t};\sqrt{1-\beta_{t}}\pmb{x}{t-1},\beta_{t}\pmb{I}),
$$
$$
q(\pmb{x}{t}|\pmb{x}{t-1})=\mathcal{N}(\pmb{x}{t};\sqrt{1-\beta_{t}}\pmb{x}{t-1},\beta_{t}\pmb{I}),
$$
$$
q(\pmb{x}{1:T}|\pmb{x}{0})=\prod_{t=1}^{T}q(\pmb{x}{t}|\pmb{x}_{t-1}),
$$
$$
q(\pmb{x}{1:T}|\pmb{x}{0})=\prod_{t=1}^{T}q(\pmb{x}{t}|\pmb{x}_{t-1}),
$$
until obtaining a completely noisy image $\pmb{x}_{T}\sim\mathcal{N}(\mathbf{0},I)$ . On the other hand, the reverse process is defined by transition probabilities parameterized by $\pmb\theta$ :
直到获得完全噪声图像 $\pmb{x}_{T}\sim\mathcal{N}(\mathbf{0},I)$ 。另一方面,反向过程由参数化转移概率 $\pmb\theta$ 定义:
$$
p_{\pmb\theta}(\pmb x_{t-1}|\pmb x_{t})=\mathcal N(\pmb x_{t-1};\mu_{\pmb\theta}(\pmb x_{t},t),\sigma_{t}\pmb I),
$$
$$
p_{\pmb\theta}(\pmb x_{t-1}|\pmb x_{t})=\mathcal N(\pmb x_{t-1};\mu_{\pmb\theta}(\pmb x_{t},t),\sigma_{t}\pmb I),
$$
where σt = 1βt withat =I=a anda =1-β Given $\mathbf{\boldsymbol{\mathbf{\mathit{x}}}}{0},\mathbf{\boldsymbol{\mathbf{\mathit{x}}}}_{t}$ can be obtained (H o et al., 2020) by:
给定 $\mathbf{\boldsymbol{\mathbf{\mathit{x}}}}{0},\mathbf{\boldsymbol{\mathbf{\mathit{x}}}}_{t}$ 可通过以下方式获得 (Ho et al., 2020) :
其中 σt = 1βt ,at = I = a 且 a = 1 - β
$$
\begin{array}{r}{\pmb{x}{t}=\sqrt{\bar{\alpha}{t}}\pmb{x}{0}+\sqrt{1-\bar{\alpha}_{t}}\pmb{\epsilon},}\end{array}
$$
$$
\begin{array}{r}{\pmb{x}{t}=\sqrt{\bar{\alpha}{t}}\pmb{x}{0}+\sqrt{1-\bar{\alpha}_{t}}\pmb{\epsilon},}\end{array}
$$
where $\epsilon$ is a noise vector $(\epsilon\sim\mathcal{N}(\mathbf{0},I))$ . Instead of predicting the mean of the forward process posterior (i.e., $\hat{\pmb x}{t-1}=\mu_{\pmb\theta}(\pmb x_{t},t))$ , Ho et al. (2020) propose to use a network $\epsilon_{\pmb{\theta}}(\cdot)$ which predicts the noise vector (e). Using $\epsilon_{\pmb{\theta}}(\cdot)$ and a simple $L_{2}$ loss function, the training objective becomes:
其中 $\epsilon$ 是噪声向量 $(\epsilon\sim\mathcal{N}(\mathbf{0},I))$。Ho 等人 (2020) [20] 提出使用网络 $\epsilon_{\pmb{\theta}}(\cdot)$ 来预测噪声向量 (e),而非直接预测前向过程后验的均值 (即 $\hat{\pmb x}{t-1}=\mu{\pmb\theta}(\pmb x_{t},t))$。通过采用 $\epsilon_{\pmb{\theta}}(\cdot)$ 和简单的 $L_{2}$ 损失函数,训练目标可表示为:
$$
\begin{array}{r}{L(\pmb\theta)=\mathbb{E}{\pmb x_{0}\sim q(\pmb x_{0}),\pmb\epsilon\sim\mathcal{N}(\pmb0,I),t\sim\mathbb{U}({1,...,T})}[||\pmb\epsilon-\pmb\epsilon_{\theta}(\pmb x_{t},t)||^{2}].}\end{array}
$$
$$
\begin{array}{r}{L(\pmb\theta)=\mathbb{E}{\pmb x_{0}\sim q(\pmb x_{0}),\pmb\epsilon\sim\mathcal{N}(\pmb0,I),t\sim\mathbb{U}({1,...,T})}[||\pmb\epsilon-\pmb\epsilon_{\theta}(\pmb x_{t},t)||^{2}].}\end{array}
$$
Note that, in Eq. 5, $\pmb{x}{t}$ and $\epsilon$ are ground-truth terms, while $\epsilon_{\pmb{\theta}}(\pmb{x}_{t},t)$ is the network prediction. Using Eq. 5, the training and the sampling algorithms are described in Alg. 1-2, respectively.
注意,在公式5中,$\pmb{x}{t}$ 和 $\epsilon$ 是真实值项,而 $\epsilon_{\pmb{\theta}}(\pmb{x}_{t},t)$ 是网络预测值。使用公式5,训练和采样算法分别在算法1-2中描述。
Algorithm 1 DDPM Standard Training
算法 1 DDPM 标准训练
Algorithm 2 DDPM Standard Sampling
算法 2 DDPM 标准采样
4. Exposure Bias Problem in Diffusion Models
4. 扩散模型中的曝光偏差问题
Comparing line 4 of Alg. 1 with line 4 of Alg. 2, we note that the inputs of the prediction network $\epsilon_{\theta}(\cdot)$ are different between the training and the inference phase. Concretely, at training time, standard DDPMs use $\epsilon_{\pmb{\theta}}(\pmb{x}{t},t)$ , where $\pmb{x}{t}$ is a ground truth sample (Eq. 4). In contrast, at inference time, they use $\pmb{\epsilon}{\pmb{\theta}}(\hat{\pmb{x}}{t},t))$ , where $\hat{\pmb x}{t}$ is computed based on the output of $\epsilon_{\theta}(\cdot)$ at the previous sampling step ${\mathbf{t}+1}$ . As mentioned in Sec. 1, this leads to a training-inference discrepancy, which is similar to the exposure bias problem observed, e.g., in text generation models, in which the training generation is conditioned on a ground-truth sentence, while the testing generation is conditioned on the previously generated words (Ranzato et al., 2016; Schmidt, 2019; Ren- nie et al., 2017; Bengio et al., 2015). In order to quantify the error accumulation with respect to the number of inference sampling steps, we use a simple experiment in which we start from a (randomly selected) real image $\pmb{x}{0}$ , we compute $\pmb{x}_{t}$ using Eq. 4, and then apply the reverse process (Alg. 2)
对比算法1第4行与算法2第4行,我们注意到预测网络$\epsilon_{\theta}(\cdot)$的输入在训练阶段和推理阶段存在差异。具体而言,训练时标准DDPM采用$\epsilon_{\pmb{\theta}}(\pmb{x}{t},t)$(其中$\pmb{x}{t}$是真实样本,见公式4),而推理时则使用$\pmb{\epsilon}{\pmb{\theta}}(\hat{\pmb{x}}{t},t))$(其中$\hat{\pmb x}{t}$基于前一步采样${\mathbf{t}+1}$时$\epsilon_{\theta}(\cdot)$的输出计算)。如第1节所述,这会导致训练-推理差异,类似于文本生成模型中观察到的曝光偏差问题(Ranzato等人,2016;Schmidt,2019;Rennie等人,2017;Bengio等人,2015)——训练时生成基于真实语句,而测试时生成基于先前生成的词语。为量化推理采样步数导致的误差累积,我们设计了一个简单实验:从(随机选择的)真实图像$\pmb{x}{0}$出发,通过公式4计算$\pmb{x}_{t}$,再执行逆向过程(算法2)。
starting from $\pmb{x}{t}$ instead of a random ${\pmb x}{T}$ . This way, when $t$ is small enough, the network should be able to “recover” the path to $\pmb{x}{0}$ (the denoising task is easier). We quantify the total error accumulated in $t$ reverse diffusion steps by comparing the difference between the ground truth distribution $q(\pmb{x}{0})$ and the predicted distribution $q(\hat{\pmb x}_{0})$ using the FID scores in Tab. 1. The experiment was done using ADM (Dhariwal & Nichol, 2021) (trained with $T=1,000;$ ) and ImageNet $32\times32$ , and we compute the FID scores using $50\mathrm{k\Omega}$ samples. Tab. 1 (first row) shows that the longer the reverse process, the higher the FID scores, indicating the existence of an error accumulation which is larger with larger values of $t$ . In Appendix 5, we repeat this experiment using deterministic sampling, which quantifies the error accumulation removing the randomness from the sampling process.
从 $\pmb{x}{t}$ 而非随机 ${\pmb x}{T}$ 开始反向扩散。当 $t$ 足够小时,网络应能"恢复"到 $\pmb{x}{0}$ 的路径(去噪任务更简单)。我们通过比较真实分布 $q(\pmb{x}{0})$ 与预测分布 $q(\hat{\pmb x}_{0})$ 的差异,使用表1中的FID分数量化 $t$ 步反向扩散累积的总误差。实验采用ADM (Dhariwal & Nichol, 2021) (训练时 $T=1,000;$ )和ImageNet $32\times32$ 数据集,使用 $50\mathrm{k\Omega}$ 样本计算FID分数。表1(首行)显示反向过程越长,FID分数越高,表明误差累积现象存在且 $t$ 值越大误差越大。附录5中我们使用确定性采样重复该实验,通过消除采样过程的随机性来量化误差累积。
Table 1. An empirical estimate of the exposure bias on ImageNet $32\times32$ .
表 1: ImageNet $32\times32$ 上曝光偏差的经验估计
| 模型 | 反向扩散步数 | ||||
|---|---|---|---|---|---|
| 100 | 300 | 500 | 700 | 1,000 | |
| ADM | 0.983 | 1.808 | 2.587 | 3.105 | 3.544 |
| ADM-IP (ours) | 0.972 | 1.594 | 2.198 | 2.539 | 2.742 |
Finally, in Tab. 3 we will report the FID scores of ADM on different datasets, which show that most of the best results are obtained in the range from 100 to 300 sampling steps, despite all the models have been trained with 1,000 diffusion steps. These results confirm previous similar observations (Nichol & Dhariwal, 2021), and we believe that the reason for this apparently counter intuitive phenomenon, in which fewer sampling steps lead to a better generation quality, is due to the exposure bias problem. Indeed, while more sampling steps correspond to a reverse process which can be more easily approximated with a Gaussian distribution (Sec. 1), longer sampling trajectories produce a larger accumulation of the prediction errors. Hence, the range [100, 300] leads to a better generation quality because it presumably trades off these two opposing aspects.
最后,在表 3 中我们将报告 ADM 在不同数据集上的 FID 分数,这些结果表明尽管所有模型都经过 1,000 次扩散步训练,但最佳结果大多出现在 100 至 300 采样步范围内。这些结果验证了先前类似的观察 (Nichol & Dhariwal, 2021) ,我们认为这种看似反直觉的现象(即更少采样步反而获得更优生成质量)源于曝光偏差问题。实际上,虽然更多采样步对应的高斯分布近似更容易实现反向过程(第 1 节),但更长的采样轨迹会导致预测误差的更大累积。因此,[100, 300] 区间能实现更优生成质量,可能是由于平衡了这两个对立因素。
5. Method
5. 方法
5.1. Regular iz ation with Input Perturbation
5.1. 基于输入扰动的正则化
The solution we propose to alleviate the exposure bias problem is very simple: we explicitly model the prediction error using a Gaussian input perturbation at training time. More specifically, we assume that the error of the prediction network in the reverse process at time $t+1$ is normally distributed with respect to the ground-truth input $\pmb{x}{t}$ (see Sec. 5.3). This is simulated using a second, dedicated random noise vector ${\pmb\xi}\sim\mathcal{N}({\bf0},{\pmb I})$ , using which, we create a perturbed version $({\pmb y}{t})$ of $\pmb{x}_{t}$ :
我们提出的缓解曝光偏差问题的解决方案非常简单:在训练时使用高斯输入扰动显式建模预测误差。具体而言,我们假设反向过程中时间步$t+1$的预测网络误差相对于真实输入$\pmb{x}{t}$服从正态分布(见第5.3节)。这通过第二个专用随机噪声向量${\pmb\xi}\sim\mathcal{N}({\bf0},{\pmb I})$进行模拟,并由此生成$\pmb{x}{t}$的扰动版本$({\pmb y}_{t})$:
$$
\begin{array}{r}{\pmb{y}{t}=\sqrt{\bar{\alpha}{t}}\pmb{x}{0}+\sqrt{1-\bar{\alpha}{t}}(\pmb{\epsilon}+\gamma_{t}\pmb{\xi}).}\end{array}
$$
$$
\begin{array}{r}{\pmb{y}{t}=\sqrt{\bar{\alpha}{t}}\pmb{x}{0}+\sqrt{1-\bar{\alpha}{t}}(\pmb{\epsilon}+\gamma_{t}\pmb{\xi}).}\end{array}
$$
For simplicity, we use a uniform noise schedule for $\xi$ by setting $\gamma_{0}=...=\gamma_{T}=\gamma $ . In fact, although selecting the best noise schedule $(\beta_{1},...,\beta_{T})$ in DDPMs is usually very important to get high-quality results (Ho et al., 2020; Chen et al., 2021), it is nevertheless an expensive hyper parameter tuning operation (Chen et al., 2021). Therefore, to avoid adding a second noise schedule $(\gamma_{0},...,\gamma_{T})$ to the training procedure, we opted for a simpler (although most likely suboptimal) solution, in which $\gamma_{t}$ does not vary depending on $t$ (more details in Sec. 5.3). In Alg. 3 we show the proposed training algorithm, in which $\pmb{x}_{t}$ is replaced by $\pmb{y}_{t}$ . In contrast, at inference time, we use Alg. 2 without any change.
为简化操作,我们对$\xi$采用统一的噪声调度,设$\gamma_{0}=...=\gamma_{T}=\gamma$。事实上,尽管在DDPM中选择最优噪声调度$(\beta_{1},...,\beta_{T})$对获得高质量结果通常至关重要(Ho et al., 2020; Chen et al., 2021),但这仍是一项昂贵的超参数调优操作(Chen et al., 2021)。因此,为避免在训练过程中引入第二个噪声调度$(\gamma_{0},...,\gamma_{T})$,我们选择了更简单(尽管很可能非最优)的方案,即$\gamma_{t}$不随$t$变化(详见第5.3节)。算法3展示了改进后的训练算法,其中$\pmb{x}{t}$被替换为$\pmb{y}_{t}$。而在推理阶段,我们直接使用未经修改的算法2。
Algorithm 3 DDPM-IP: Training with input perturbation
算法 3 DDPM-IP: 带输入扰动的训练
| 1: 重复 |
| 2: o ~ q(xo), t ~ U({1, ., T}) |
| 3: ∈ ~ N(0, 1), ≤ ~ N(0, I) |
| 4: 使用公式 6 计算 yt |
| 5: 对 Velle - eo(yt, t)I|2 执行梯度下降步骤 |
| 6: 直到收敛 |
5.2. Discussion
5.2. 讨论
In this section, we analyze the difference between Alg. 3 and Alg. 1. Specifically, in line 5 of Alg. 3, we use $\pmb{y}{t}$ as the input of the prediction network $\epsilon_{\theta}(\cdot)$ but we keep using $\epsilon$ as the regression target. In other words, the new noise term $(\pmb{\xi})$ we introduce is used asymmetrically, because it is applied to the input but not to the prediction target (e). For this reason, Alg. 3 is not equivalent to choose a different value of $\epsilon$ in Alg. 1, where e is instead used symmetrically both in the forward process (Eq. 4) and as the target of the prediction network (line 4 of Alg. 1).
在本节中,我们分析算法3与算法1的区别。具体而言,在算法3的第5行中,我们使用$\pmb{y}{t}$作为预测网络$\epsilon_{\theta}(\cdot)$的输入,但继续将$\epsilon$作为回归目标。换句话说,我们引入的新噪声项$(\pmb{\xi})$被非对称地使用,因为它被应用于输入但未应用于预测目标(e)。因此,算法3并不等同于在算法1中选择不同的$\epsilon$值,在算法1中e在前向过程(公式4)和预测网络目标(算法1第4行)中被对称使用。
This difference is schematically illustrated in Fig. 1, where, for both Alg. 1 (i.e., DDPM) and Alg. 3 (DDPM-IP), we show the corresponding pairs of input and target vectors of the prediction network (respectively, $(\pmb{x}{t},\pmb{\epsilon})$ and $\left(\pmb{y}{t},\pmb{\epsilon}\right),$ ). In the same figure, we also show a second version of Alg. 1 (called DDPM $y$ ), where we use the standard training protocol (Alg. 1) but change the noise variance in order to adhere to the same distribution generating $\pmb{y}{t}$ . In fact, it can be easy shown that ${\pmb y}_{t}$ in Alg. 3 is generated using the following distribution (see Appendix A.2 for a proof):
图 1: 以示意图形式展示了这种差异。对于算法 1 (即 DDPM) 和算法 3 (DDPM-IP),我们分别展示了预测网络的输入向量与目标向量对 ( $(\pmb{x}{t},\pmb{\epsilon})$ 和 $\left(\pmb{y}{t},\pmb{\epsilon}\right),$ )。在同一图中,我们还展示了算法 1 的第二个版本 (称为 DDPM $y$ ),该版本采用标准训练协议 (算法 1) 但调整了噪声方差以符合生成 $\pmb{y}{t}$ 的相同分布。实际上可以证明,算法 3 中的 ${\pmb y}_{t}$ 是通过以下分布生成的 (证明见附录 A.2):
$$
q({\pmb y}{t}|{\pmb x}{0})=\mathcal{N}({\pmb y}{t};\sqrt{\bar{\alpha}{t}}{\pmb x}{0},(1-\bar{\alpha}_{t})(1+\gamma^{2}){\pmb I}).
$$
$$
q({\pmb y}{t}|{\pmb x}{0})=\mathcal{N}({\pmb y}{t};\sqrt{\bar{\alpha}{t}}{\pmb x}{0},(1-\bar{\alpha}_{t})(1+\gamma^{2}){\pmb I}).
$$
Hence, we can obtain the same input noise distribution of Alg. 3 in Alg. 1 using $\epsilon^{\prime}\sim\mathcal{N}(0,I)$ and:
因此,我们可以使用 $\epsilon^{\prime}\sim\mathcal{N}(0,I)$ 并通过以下方式在算法 1 中获得与算法 3 相同的输入噪声分布:
$$
\begin{array}{r}{{\pmb y}{t}=\sqrt{\bar{\alpha}{t}}{\pmb x}{0}+\sqrt{1-\bar{\alpha}_{t}}\sqrt{1+\gamma^{2}}{\pmb\epsilon}^{\prime}.}\end{array}
$$
$$
\begin{array}{r}{{\pmb y}{t}=\sqrt{\bar{\alpha}{t}}{\pmb x}{0}+\sqrt{1-\bar{\alpha}_{t}}\sqrt{1+\gamma^{2}}{\pmb\epsilon}^{\prime}.}\end{array}
$$
We call DDPM $\cdot y$ the version of Alg. 1 with this new noise distribution. DDPM $y$ is obtained from Alg. 1 using Eq. 8 in line 3 and replacing $\pmb{x}{t}$ with $\pmb{y}{t}$ and $\epsilon$ with $\epsilon^{\prime}$ in line 4. However, note that, for a given $\pmb{y}{t}$ , if $\pmb{\xi}\neq\mathbf{0}$ , then $\epsilon\neq\epsilon^{\prime}$ (see Fig. 1), thus, DDPM-IP and DDPM $y$ share the same input to $\epsilon_{\pmb{\theta}}(\cdot)$ , but they use different targets. In Appendix A.3, we empirically show that DDPM $_y$ is even worse than the standard DDPM.
我们将采用新噪声分布的算法1版本称为DDPM $\cdot y$。DDPM $y$ 是通过在算法1第3行使用公式8,并在第4行将 $\pmb{x}{t}$ 替换为 $\pmb{y}{t}$、$\epsilon$ 替换为 $\epsilon^{\prime}$ 得到的。但需注意,对于给定的 $\pmb{y}{t}$,若 $\pmb{\xi}\neq\mathbf{0}$,则 $\epsilon\neq\epsilon^{\prime}$(见图1)。因此,DDPM-IP与DDPM $y$ 虽然共享 $\epsilon_{\pmb{\theta}}(\cdot)$ 的相同输入,但使用了不同目标。附录A.3通过实验表明,DDPM $_y$ 的表现甚至逊于标准DDPM。
Intuitively, the proposed training protocol, DDPM-IP, decouples the noise vector $\epsilon^{\prime}$ actually generating $\pmb{y}{t}$ from the ground truth target vector $\epsilon$ which is asked to be predicted by $\epsilon_{\theta}(\cdot)$ . In order to solve this problem, $\epsilon_{\theta}(\cdot)$ needs to smooth its prediction function, reducing the difference between $\epsilon_{\pmb{\theta}}(\pmb{x}{t},t)$ and $\epsilon_{\pmb{\theta}}({\pmb y}_{t},t)$ , and this leads to a training regular iz ation which is similar to VRM (Sec. 1).
直观上,所提出的训练协议 DDPM-IP 将实际生成 $\pmb{y}{t}$ 的噪声向量 $\epsilon^{\prime}$ 与需要由 $\epsilon_{\theta}(\cdot)$ 预测的真实目标向量 $\epsilon$ 解耦。为解决这一问题,$\epsilon_{\theta}(\cdot)$ 需要平滑其预测函数,减小 $\epsilon_{\pmb{\theta}}(\pmb{x}{t},t)$ 与 $\epsilon_{\pmb{\theta}}({\pmb y}_{t},t)$ 之间的差异,这会产生类似于 VRM (第 1 节) 的训练正则化效果。
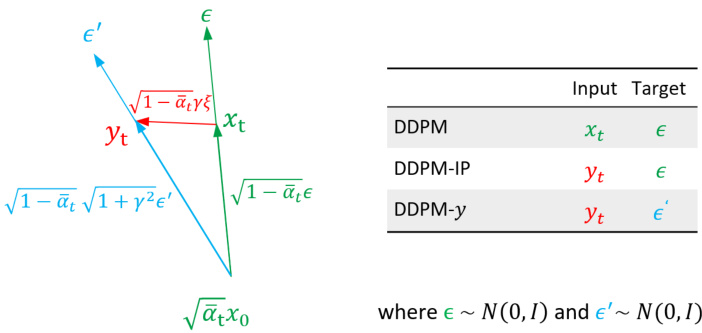
Figure 1. The inputs and the prediction targets are different in vanilla DDPM, DDPM-IP and DDPM- $\cdot y$ .
图 1: 原始 DDPM、DDPM-IP 和 DDPM-$\cdot y$ 的输入与预测目标存在差异。
5.3. Estimating the Prediction Error
5.3. 预测误差估计
In this section, we analyze the actual prediction error of $\epsilon_{\theta}(\cdot)$ and we use this analysis to choose the value of $\gamma$ in Eq. 6. Analogously to Sec. 4, we use ADM, trained using the standard algorithm Alg. 1 and two datasets: CIFAR10 and ImageNet $32\times32$ . At testing time, for a given $t$ and $\hat{\pmb{\epsilon}}=\pmb{\epsilon}{\pmb{\theta}}(\hat{\pmb{x}}{t},t)$ , we replace e with e in Eq. 4 and we compute the predicted $\hat{\pmb x}{0}$ . Finally, the prediction error at time $t$ is $\pmb{e}{t}=\hat{\pmb x}{0}-\pmb x_{0}$ . Note that using $\hat{\pmb x}{0}$ and $\pmb{x}{0}$ to estimate the error instead of comparing $\hat{\pmb x}{t}$ and $\pmb{x}{t}$ , has the advantage that the former is independent of scaling factors $(\sqrt{1-\bar{\alpha}{t}})$ and, thus, it makes the statistical analysis easier. Using different values of $t$ , uniformly selected in ${1,...,T}$ , we empirically verified that, for a given $t$ , $e_{t}$ is normally distributed: $e_{t}\sim$ $\mathcal{N}(\mathbf{0},\nu_{t}^{2}I)$ , with standard deviation $\nu_{t}$ (see Appendix A.5).
在本节中,我们分析 $\epsilon_{\theta}(\cdot)$ 的实际预测误差,并利用该分析为公式6中的 $\gamma$ 取值。与第4节类似,我们采用标准算法Alg. 1训练的ADM模型,在CIFAR10和ImageNet $32\times32$ 两个数据集上进行测试。给定时间步 $t$ 和噪声估计 $\hat{\pmb{\epsilon}}=\pmb{\epsilon}{\pmb{\theta}}(\hat{\pmb{x}}{t},t)$ 时,我们将公式4中的e替换为e来计算预测值 $\hat{\pmb x}{0}$ 。最终,时间步 $t$ 的预测误差为 $\pmb{e}{t}=\hat{\pmb x}{0}-\pmb x_{0}$ 。需要注意的是,相比直接比较 $\hat{\pmb x}{t}$ 和 $\pmb{x}{t}$ ,采用 $\hat{\pmb x}{0}$ 与 $\pmb{x}{0}$ 计算误差的优势在于前者不受缩放因子 $(\sqrt{1-\bar{\alpha}{t}})$ 影响,从而简化统计分析。通过在 ${1,...,T}$ 中均匀选取不同 $t$ 值进行实验验证,我们发现对于给定 $t$ ,误差 $e_{t}$ 服从正态分布: $e_{t}\sim$ $\mathcal{N}(\mathbf{0},\nu_{t}^{2}I)$ ,其标准差为 $\nu_{t}$ (详见附录A.5)。
In Fig. 2 we plot the value of $\nu_{t}$ with respect to $t$ . The two curves corresponding to the two datasets are surprisingly close to each other. In principle, we could use this empirical analysis and set $\gamma_{t}=\nu_{t}$ in Eq. 6. In this way, when we perturb the input to $\epsilon_{\theta}(\cdot)$ , we empirically imitate its actual prediction error which is the base of the exposure bias problem. However, this choice would require a two-step training: first, using Alg. 1 to train the base model and empirically estimate $\nu_{t}$ for different $t$ . Then, using Alg. 3 with the estimated $\gamma_{t}$ schedule to retrain the model from scratch. To avoid this and make the whole procedure as simple as possible, we simply use a constant value $\gamma$ , independe
