TOWARDS ACCURATE STATE ESTIMATION: KALMAN FILTER INCORPORATING MOTION DYNAMICS FOR 3D MULTI-OBJECT TRACKING

迈向精确状态估计：融合运动动力学的卡尔曼滤波在3D多目标跟踪中的应用

ABSTRACT

摘要

This work addresses the critical lack of precision in state estimation in the Kalman filter for 3D multi-object tracking (MOT) and the ongoing challenge of selecting the appropriate motion model. Existing literature commonly relies on constant motion models for estimating the states of objects, neglecting the complex motion dynamics unique to each object. Consequently, trajectory division and imprecise object localization arise, especially under occlusion conditions. The core of these challenges lies in the limitations of the current Kalman filter formulation, which fails to account for the variability of motion dynamics as objects navigate their environments. This work introduces a novel formulation of the Kalman filter that incorporates motion dynamics, allowing the motion model to adaptively adjust according to changes in the object’s movement. The proposed Kalman filter substantially improves state estimation, localization, and trajectory prediction compared to the traditional Kalman filter. This is reflected in tracking performance that surpasses recent benchmarks on the KITTI and Waymo Open Datasets, with margins of $0.56%$ and $0.81%$ in higher order tracking accuracy (HOTA) and multi-object tracking accuracy (MOTA), respectively. Furthermore, the proposed Kalman filter consistently outperforms the baseline across various detectors. Additionally, it shows an enhanced capability in managing long occlusions compared to the baseline Kalman filter, achieving margins of $1.22%$ in higher order tracking accuracy (HOTA) and $1.55%$ in multi-object tracking accuracy (MOTA) on the KITTI dataset. The formulation’s efficiency is evident, with an additional processing time of only approximately $0.078~\mathrm{ms}$ per frame, ensuring its applicability in real-time applications.

本研究针对3D多目标跟踪(MOT)中卡尔曼滤波器的状态估计精度不足及运动模型选择难题展开。现有方法普遍采用恒定运动模型进行目标状态估计，忽略了各物体独特的复杂运动特性，导致轨迹断裂和定位失准问题（尤其在遮挡情况下）。这些问题的核心在于当前卡尔曼滤波器框架无法适应物体运动动态变化。我们提出了一种融合运动动态的新型卡尔曼滤波器框架，使运动模型能根据目标运动变化自适应调整。相比传统卡尔曼滤波器，新方法显著提升了状态估计、定位和轨迹预测性能，在KITTI和Waymo开放数据集上的跟踪指标分别实现$0.56%$（高阶跟踪精度HOTA）和$0.81%$（多目标跟踪精度MOTA）的提升。该框架在不同检测器上均稳定优于基线模型，且在长时遮挡处理方面表现突出——在KITTI数据集上HOTA和MOTA指标分别提升$1.22%$和$1.55%$。算法效率优势明显，每帧仅增加约$0.078~\mathrm{ms}$处理时长，完全满足实时性要求。

1 Introduction

1 引言

3D multi-object tracking (MOT) is a vital module for autonomous vehicles (AVs) that provides critical information about their surroundings, allowing them to navigate safely without collision. The MOT methods are either algorithm-based (classical) or learning-based approaches; however, classical methods are commonly used due to their substantially lower latency and comparable performance to learning-based approaches. These approaches follow the tracking-by-detection paradigm in which an independent detector is employed to locate objects in a 3D point cloud, followed by a separate tracking algorithm.

3D多目标跟踪(MOT)是自动驾驶车辆(AV)的关键模块，可提供周围环境的关键信息，使其能够安全导航而不会发生碰撞。MOT方法分为基于算法(经典)和基于学习两类；然而经典方法因其显著更低的延迟和与基于学习方法相当的性能而被广泛使用。这些方法遵循检测跟踪范式，即先使用独立检测器定位3D点云中的物体，再执行独立的跟踪算法。

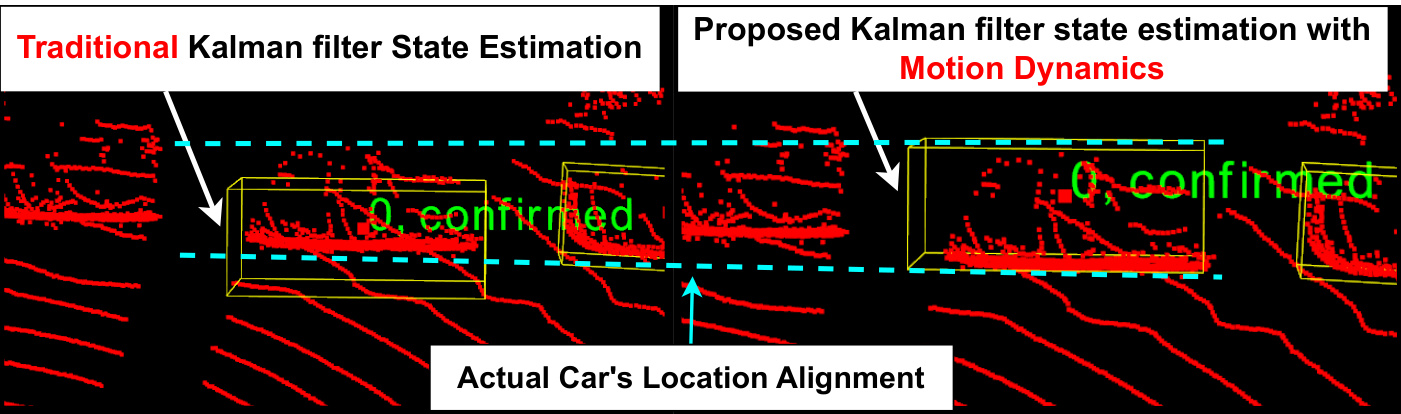
Figure 1: State estimation (yellow bounding box) of an off-scene car drifts away from the actual car location (disconnected lines) with the traditional Kalman filter. Meanwhile, the proposed Kalman filter with motion dynamics shows robust localization for the car.

图 1: 传统卡尔曼滤波器对场外车辆的状态估计(黄色边界框)会偏离实际车辆位置(断开的线条)。而采用运动动力学的改进卡尔曼滤波器则能实现稳健的车辆定位。

Given an object’s current location (measurement), classical methods use Bayesian filters, such as the Kalman Filter (KF), to estimate the object’s next position (state) with uncertainty, a process known as state prediction. The estimation of the object’s state is refined when a new measurement arrives, which is called a state update. In the literature of MOT methods, state prediction estimates the next state of an object based on a constant motion model, such as a constantvelocity or constant-acceleration model. The main limitation of these models is that they do not always reflect the motion status of the objects (motion dynamics). For instance, the state estimation of a car with no change in velocity while employing a constant velocity model has a better state estimation than the constant acceleration or jerk model (3rd derivative of motion equation), as presented in Figure 2 case A. On the other hand, when the car accelerates, as shown in Figure 2 case B, the constant jerk model has the lowest state estimation error for the car. Similarly, the constant acceleration model outperforms in state estimation when the car exhibits a change in velocity with slight to no change in acceleration, as shown in Figure 2 case C.

给定物体的当前位置(测量值)，经典方法使用贝叶斯滤波器(如卡尔曼滤波器(KF))来估计物体的下一个位置(状态)及其不确定性，这一过程称为状态预测。当新的测量值到达时，会优化对物体状态的估计，这称为状态更新。在多目标跟踪(MOT)方法的文献中，状态预测基于恒定运动模型(如匀速或匀加速模型)来估计物体的下一个状态。这些模型的主要局限性在于它们并不总能反映物体的运动状态(运动动力学)。例如，如图2案例A所示，当汽车速度不变时，采用匀速模型的状态估计优于匀加速或加加速度模型(运动方程的三阶导数)。另一方面，如图2案例B所示，当汽车加速时，加加速度模型的状态估计误差最小。类似地，如图2案例C所示，当汽车速度变化而加速度几乎不变时，匀加速模型在状态估计中表现更优。

This behavior has been repeatedly observed in multiple scenarios, indicating that the precision of state estimation from a motion model depends on its alignment with the object’s current motion dynamics. The state estimation precision reduces as the motion dynamics do not match the employed motion model, eventually injecting noise into the state estimation process in the KF that impacts object localization, particularly occluded and off-scene objects, as demonstrated in Figure 1. This work proposes a novel formulation of the KF that accounts for objects’ motion dynamics and adaptively adjusts a dynamic motion model based on observed changes. The proposed solution shows precise state estimation localization (Figure 1) and less trajectory deviation for occluded and off-scene objects over the traditional KF, outperforming recent KITTI and Waymo Open Dataset (WOD) benchmarks.

这一现象在多个场景中被反复观察到，表明运动模型的状态估计精度取决于其与物体当前运动动态的匹配程度。当运动动态与所采用的运动模型不匹配时，状态估计精度会降低，最终在卡尔曼滤波 (KF) 的状态估计过程中引入噪声，从而影响物体定位，特别是被遮挡和离开场景的物体，如图 1 所示。本研究提出了一种新颖的卡尔曼滤波公式，该公式考虑了物体的运动动态，并根据观测到的变化自适应调整动态运动模型。所提出的解决方案在状态估计定位上表现出更高的精度 (图 1)，并且相较于传统卡尔曼滤波，对于被遮挡和离开场景的物体具有更小的轨迹偏差，其性能超越了近期 KITTI 和 Waymo 开放数据集 (WOD) 的基准。

The contribution of this work can be summarized as follows:

本工作的贡献可概括如下：

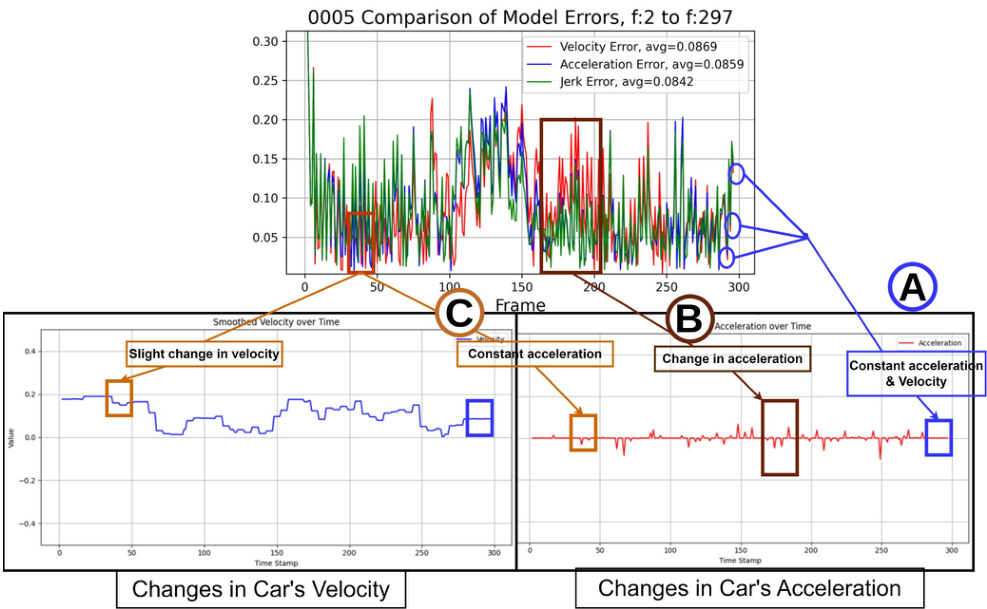
Figure 2: The graph demonstrates the performance fluctuation in state estimation for three motion models: constant velocity (Red), constant acceleration (Blue), and constant jerk (Green). The top graph compares the Euclidean distance error in state estimation obtained by the three models of the 0005 stream in the KITTI [2] dataset. The second row shows graphs of the car’s motion dynamics, change in velocity (Blue), and change in acceleration (Red).

图 2: 该图展示了三种运动模型在状态估计中的性能波动：匀速(红色)、匀加速(蓝色)和匀加加速(绿色)。顶部图表对比了KITTI数据集[2]中0005数据流通过三种模型获得的状态估计欧氏距离误差。第二行显示了车辆运动动力学图表，包括速度变化(蓝色)和加速度变化(红色)。

3. As the opposite of the attempts in the literature, multiple motion models simultaneously, this work maintains the singularity of the assigned motion model that adaptively adjusted as per the captured motion dynamics, resulting in low latency with an average additional computational cost of $0.078\mathrm{ms}$ per frame (Table 4), making it efficient for real-time applications.
4. 与文献中尝试同时使用多个运动模型的做法相反，本研究保持所分配运动模型的单一性，并根据捕获的运动动态进行自适应调整，从而实现了低延迟，平均每帧额外计算成本仅为 $0.078\mathrm{ms}$ (表4)，使其适用于实时应用。

2 Related Work

2 相关工作

The KF is widely used in MOT literature [3–11], particularly for methods that follow tracking-by-detection paradigms. It predicts the state of tracked objects that nearly resample their actual location and motion states. An imprecise state prediction of an object can lead to failure in the association stage, where the object’s recent position is associated with the closest state prediction. Hence, motion model selection for state prediction in the KF becomes critical in the MOT literature, as it significantly affects tracking performance. The literature shows conflicting preferences for the proper motion model, which has consistently improved state prediction localization. Some methods [7, 8, 10–15] favor the constant velocity model, claiming its out performance over other motion models. At the same time, other methods [5, 6, 9] utilize the acceleration motion model, as the constant velocity motion model is too simplistic to handle maneuvering in tracking.

KF（卡尔曼滤波器）在MOT（多目标跟踪）文献[3-11]中被广泛使用，尤其适用于遵循检测跟踪范式的方法。它能预测被跟踪对象的状态，这些状态几乎复现了目标的实际位置和运动状态。若物体状态预测不准确，会导致关联阶段失败——该阶段需要将物体当前位置与最接近的状态预测相关联。因此，KF中用于状态预测的运动模型选择成为MOT文献中的关键因素，因为它显著影响跟踪性能。

文献显示对于最佳运动模型存在分歧观点，这些模型持续改进了状态预测的定位精度。部分方法[7,8,10-15]倾向于恒定速度模型，声称其性能优于其他运动模型；而另一些方法[5,6,9]则采用加速运动模型，认为恒定速度模型过于简单，无法处理跟踪中的机动动作。

For varied reasons, the velocity motion model in the KF is the most commonly used in MOT literature [7, 8, 10–15]. Some MOT methods [7, 10, 13, 14] employ a constant velocity model over others due to its simplicity that facilitates the integration into various frameworks in addition to its lower computational cost, which makes it an efficient choice for real-time systems. Another study [3] has shown that, in some cases, the constant velocity model outperforms higher-degree motion models. Similarly, Na et al. [4] have observed that the constant velocity model is more robust when the target acceleration is slight or unpredictable, especially in noisy environments.

由于多种原因，卡尔曼滤波器(KF)中的匀速运动模型是多目标跟踪(MOT)文献中最常用的方法[7, 8, 10–15]。部分MOT方法[7, 10, 13, 14]采用匀速模型而非其他模型，因其简单性便于集成到各类框架中，且计算成本较低，使其成为实时系统的高效选择。另一项研究[3]表明，在某些情况下，匀速模型表现优于高阶运动模型。类似地，Na等人[4]发现当目标加速度较小或不可预测时（尤其在噪声环境中），匀速模型具有更强的鲁棒性。

On the other hand, some recent MOT methods [5, 6, 9] adopt a constant acceleration motion model instead of a constant velocity. Part of the recent MOT methods [6, 9] claim that the constant velocity model is trivial and cannot predict precise positions for objects when they face dramatic velocity changes. Wu et al. [6] state that the prediction error accumulates from employing a constant velocity model, which increases exponentially as objects temporarily disappear due to occlusion. In the context of AVs, Reich et al. [9] underline that the maneuvering of a target object depends not only on the target motion but also on the ego motion of the AV. Even though some objects, like parked cars, seem to have no motion, an accelerated AV observes them as objects in motion equal to its motion, which still requires a constant acceleration motion model to handle the ego-motion maneuvering. Despite the maneuvering concerns for objects of MOT methods replacing constant velocity with an acceleration model for state prediction,

另一方面，部分近期多目标跟踪(MOT)方法[5,6,9]采用恒定加速度运动模型替代恒定速度模型。其中[6,9]指出恒定速度模型过于简单，在目标速度剧烈变化时无法准确预测位置。Wu等人[6]表明恒定速度模型会导致预测误差累积，当目标因遮挡暂时消失时误差呈指数级增长。针对自动驾驶车辆(AVs)场景，Reich等人[9]强调目标机动性不仅取决于目标运动，还需考虑AV自身运动。即使如停放车辆等看似静止的物体，加速中的AV也会将其视为与自身运动状态相同的运动物体，仍需恒定加速度模型来处理自车运动机动。尽管这些MOT方法关注机动性问题并采用加速度模型进行状态预测以替代恒定速度模型，

Nagy et al. [5] reveal that the tracking performance for occluded objects for MOT methods using constant acceleration can also miss recovering the objects after occlusion due to memory size constraints. The main issue with using a single motion model, either constant velocity or acceleration, is that the performance of state estimation degrades whenever the target’s motion dynamics do not match the assigned motion model, because the current KF formulation neglects motion dynamics.

Nagy等人[5]指出，由于内存大小限制，使用恒定加速度的MOT方法对遮挡物体的跟踪性能也可能在遮挡后无法恢复物体。使用单一运动模型（无论是恒定速度还是恒定加速度）的主要问题是，每当目标的运动动态与分配的运动模型不匹配时，状态估计的性能就会下降，因为当前的KF公式忽略了运动动态。

Further studies [3, 4] show that the motion model’s performance for tracking a target depends on the maneuvers demonstrated by the target. Na et al. [3] conduct experiments that show the constant velocity model is sufficient for non-maneuvering situations, while the constant acceleration model outperforms in maneuvering scenarios. Recent research [4, 16] attempts to tackle this issue by employing an interactive multi-model KF that uses multiple motion models simultaneously, with model selection based on an initial predefined probability for each model. Despite the improvement shown in state estimation, operating multiple motion models simultaneously is highly computationally expensive, particularly in multi-object tracking, where calculations for each model are performed for all targets, in addition to the difficulty of handling sudden motion changes.

进一步的研究 [3, 4] 表明，运动模型在目标跟踪中的性能取决于目标所展示的机动行为。Na 等人 [3] 进行的实验显示，恒速模型足以应对非机动场景，而恒加速模型在机动场景中表现更优。近期研究 [4, 16] 尝试通过采用交互式多模型卡尔曼滤波器 (KF) 来解决这一问题，该滤波器同时使用多个运动模型，并根据每个模型的初始预设概率进行模型选择。尽管在状态估计方面有所改进，但同时运行多个运动模型的计算成本极高，尤其是在多目标跟踪中，除了难以处理突然的运动变化外，还需为所有目标执行每个模型的计算。

Our investigation of the problem shows that the state estimation performance depends on the target’s motion dynamics. Figure 2 shows the state estimation performance of three motion models: velocity, acceleration, and jerk, of a car with many maneuvers. The performance of the jerk model peaks when the car is driving at mixed accelerations. Meanwhile, the acceleration model takes over as the car accelerates consistently. Lastly, the velocity motion model outperforms other models when the car’s velocity is consistent. This scenario shows the importance of considering the target motion dynamics for precise state estimation.

我们对问题的研究表明，状态估计性能取决于目标的运动动态。图 2 展示了进行多机动动作的汽车在三种运动模型（匀速、匀加速和加加速度）下的状态估计表现。当车辆处于混合加速度状态时，加加速度模型的表现达到峰值；当车辆持续加速时，匀加速模型则占据优势；而当车速保持稳定时，匀速运动模型的表现优于其他模型。这一场景揭示了考虑目标运动动态对实现精确状态估计的重要性。

This work addresses the limitation mentioned earlier by proposing a dynamic motion model with a novel formulation of the KF that accounts for the target motion dynamics and adaptively integrates them into the dynamic motion model, eliminating the need to operate multiple motion models while maintaining computational efficiency.

本工作针对前述局限性提出了一种动态运动模型，通过创新性地构建卡尔曼滤波器 (KF) 来捕捉目标运动动态特征，并将其自适应地整合到动态运动模型中，从而在保持计算效率的同时无需运行多个运动模型。

3 Methodology

3 方法论

This work addresses the limitations of current motion models and the neglect of object motion dynamics in the standard KF formulation by introducing a novel formulation of the KF state update and state prediction that considers the motion dynamics of objects in state estimation. Figure 3 shows a high-level overview of the pipeline of the proposed formulation of the KF incorporating object motion dynamics. Given an object observed at time $t-1$ , the object has three primary parameters: state estimation $\hat{x}{t-1|t-1}$ at time $t-1$ updated according to a measurement taken at time $t-1$ , the state estimation uncertainty covariance $P_{t-1|t-1}$ at time $t-1$ , and weighted motion dynamics $\hat{w}_{t-1|t-1}$ of the object at time $t-1$ updated based on a measurement taken at time $t-1$ .

本研究通过提出一种考虑物体运动动态的卡尔曼滤波(KF)状态更新与状态预测新公式，解决了当前运动模型的局限性以及标准KF公式中对物体运动动态的忽视问题。图3展示了融合物体运动动态的KF公式流程概览。给定在时间$t-1$观测到的物体，该物体具有三个主要参数：根据$t-1$时刻测量值更新的状态估计$\hat{x}{t-1|t-1}$，$t-1$时刻的状态估计不确定协方差$P_{t-1|t-1}$，以及基于$t-1$时刻测量值更新的物体加权运动动态$\hat{w}_{t-1|t-1}$。

At the prediction step, covered in Section 3.1, the model estimates the next state estimation $\hat{x}{t\mid t-1}$ of the object at time $t$ of measurement $t-1$ through the state-transition model $F_{t}$ . As shown in the estimated position state diagram in Figure 3, the state-transition model $F_{t}$ maps the state $\hat{x}{t-1|t-1}$ , highlighted by red dot-eclipse, to $\hat{x}{t\mid t-1}$ , marked by red eclipse; however, this transition is weighted by the estimated weights of object dynamics $\hat{w}{t-1}$ that adjusts the state according to the object motions, marked by blue eclipse. Thus, the obtained $\hat{x}{t\mid t-1}$ is the estimated state at time $t$ considering the latest dynamics observed at time $t-1$ . The state estimation uncertainty covariance will increase as the model becomes uncertain about the new estimate, obtaining an updated covariance $\hat{P}_{t|t-1}$ .

在预测步骤（见第3.1节）中，模型通过状态转移模型 $F_{t}$ 根据 $t-1$ 时刻的测量值估算 $t$ 时刻物体的下一状态估计 $\hat{x}{t\mid t-1}$。如图3的估计位置状态图所示，状态转移模型 $F_{t}$ 将红色点椭圆标记的状态 $\hat{x}{t-1|t-1}$ 映射到红色椭圆标记的 $\hat{x}{t\mid t-1}$；但该转移过程受蓝色椭圆标记的物体动态估计权重 $\hat{w}{t-1}$ 调节，该权重会根据物体运动调整状态。因此，所得 $\hat{x}{t\mid t-1}$ 是结合 $t-1$ 时刻最新动态观测的 $t$ 时刻估计状态。随着模型对新估计值的不确定性增加，状态估计不确定协方差将增大，从而获得更新的协方差 $\hat{P}_{t|t-1}$。

When a new measurement arrives $y_{t}$ at the following time frame $t$ , the estimated state $\hat{x}{t\mid t-1}$ will be compared and updated according to the new measurement at time $t$ of the object state to obtain a refined state estimation $\hat{x}{t\mid t}$ . Accordingly, the object dynamics are also updated as per the new measurement, which requires eliminating any noise impact on the measurement localization of the object, as discussed in Section 3.2. The noise mitigation term $D_{t}$ , introduced in [1], eliminates the localization noise from the employed detector.

当新测量值 $y_{t}$ 在下一时间帧 $t$ 到达时，预估状态 $\hat{x}{t\mid t-1}$ 将根据目标在 $t$ 时刻的新测量值进行比对和更新，从而得到优化后的状态估计 $\hat{x}{t\mid t}$。相应地，目标动态也会根据新测量值进行更新，这需要消除测量定位中噪声对目标的影响，如第3.2节所述。文献[1]引入的噪声抑制项 $D_{t}$ 可消除所用检测器的定位噪声。

Next, a Gaussian distribution of motion dynamics of the object observed through a time window called the ”Smoothing window”, discussed in Section 3.4, is formed for each motion dynamic term in the motion model used in the prediction step. In this case, we use a motion model consisting of the position’s first three derivatives (Jerk motion model). Thus, the three Gaussian distribution dynamics shown in the updated motion dynamics graph in Figure 3 represent the change in position (first derivative), change in velocity (second derivative), and change in acceleration

接下来，通过一个称为"平滑窗口"(Smoothing window)的时间窗口(详见第3.4节)观测到的物体运动动态，会为预测步骤中使用的运动模型中的每个动态项形成一个高斯分布。在本研究中，我们采用了包含位置前三阶导数(Jerk运动模型)的运动模型。因此，图3更新后的运动动态图中显示的三个高斯分布动态分别代表：位置变化(一阶导数)、速度变化(二阶导数)和加速度变化。

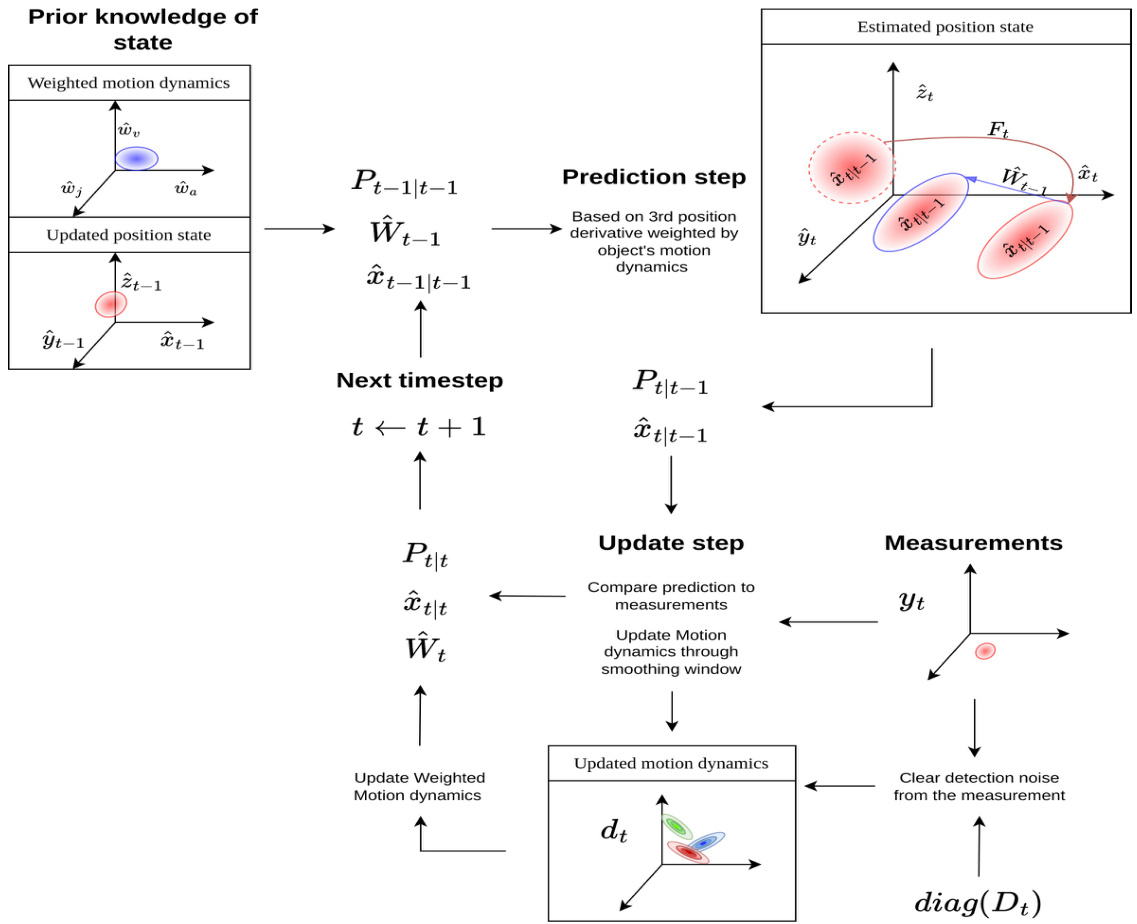
Figure 3: The diagram shows an overview of the proposed Kalman filter incorporating motion dynamics. The flow begins with the prior knowledge of an object’s states at time $t-1$ . The information includes state uncertainty $P_{t-1|t-1}$ , weighted motion dynamics of the object $\hat{W}{t-1}$ , and object’s state $\hat{x}{t-1|t-1}$ . This information is used to predict the next state estimation of the object, considering its captured motion dynamics, and adjust the estimated state accordingly. This results in the next state estimation $\hat{x}{t\mid t-1}$ and an updated uncertainty $P_{t|t-1}$ . With a new measurement, the object’s spatial state will be updated to obtain $\hat{x}{t\mid t}$ , and new motion dynamics will be captured through the Gaussian distribution of changes observed in motion dynamics parameters (Position, velocity, and acceleration). The obtained updated motion dynamics $d_{t}$ from the Gaussian distribution is weighted to form an updated weighted motion dynamics $\hat{W}_{t}$ . The flow will be repeated in the next time step $t+1$ .

图 3: 该图展示了融合运动动力学的卡尔曼滤波器 (Kalman filter) 整体流程。流程始于物体在时间 $t-1$ 的状态先验知识，包括状态不确定性 $P_{t-1|t-1}$ 、加权运动动力学 $\hat{W}{t-1}$ 以及物体状态 $\hat{x}{t-1|t-1}$ 。这些信息用于预测物体下一状态估计值，同时考虑其捕获的运动动力学并相应调整估计状态，最终得到下一状态估计 $\hat{x}{t\mid t-1}$ 和更新后的不确定性 $P_{t|t-1}$ 。当获得新测量值时，物体空间状态将更新为 $\hat{x}{t\mid t}$ ，并通过运动动力学参数 (位置、速度、加速度) 变化的高斯分布捕获新运动动力学。从高斯分布中获取的更新后运动动力学 $d_{t}$ 经过加权形成更新后的加权运动动力学 $\hat{W}_{t}$ 。该流程将在下一时间步 $t+1$ 重复执行。

(third derivative).

(三阶导数).

The motion dynamics of the object $d_{t}$ at time $t$ will be adjusted according to the obtained Gaussian distributions of the object’s motion dynamics. Then, the weighted motion dynamics $\hat{w}{t}$ will be updated based on the new observed motion dynamics $d_{t}$ based on measurement $y_{t}$ at time $t$ . Finally, the state estimation uncertainty covariance $\hat{P}{t|t-1}$ decreases as new information about the object’s state is observed, in the form of measurement $y_{t}$ , to obtain an updated covariance $\hat{P}_{t|t}$ . Lastly, the procedures will be repeated at each time stamp.

物体在时间 $t$ 的运动动态 $d_{t}$ 将根据获得的运动动态高斯分布进行调整。随后，基于时间 $t$ 的测量值 $y_{t}$ 观测到的新运动动态 $d_{t}$ ，加权运动动态 $\hat{w}{t}$ 将被更新。最后，随着以测量值 $y_{t}$ 形式观测到物体状态的新信息，状态估计不确定协方差 $\hat{P}{t|t-1}$ 会减小，从而得到更新后的协方差 $\hat{P}_{t|t}$ 。上述步骤将在每个时间戳重复执行。

3.1 Motion Dynamics in State Prediction

3.1 状态预测中的运动动力学

The subsequent estimated state should consider the objects’ motion dynamics at the prediction step. In this work, we use the third derivative of the motion equation (Jerk motion equation), which consists of the object’s position, velocity, acceleration, and changes in acceleration (Jerk), as shown in Equation 1.

随后的估计状态应考虑物体在预测步骤中的运动动力学。在本研究中，我们采用运动方程的三阶导数（Jerk运动方程），该方程包含物体的位置、速度、加速度及加速度变化率（Jerk），如公式1所示。

$$
x(t)=x_{t}+v_{t}t+{\frac{1}{2}}a_{t}t^{2}+{\frac{1}{6}}j_{t}t^{3}
$$

$$
x(t)=x_{t}+v_{t}t+{\frac{1}{2}}a_{t}t^{2}+{\frac{1}{6}}j_{t}t^{3}
$$

The main problem of using Equation 1 as a motion model for state prediction in the KF is the assumption of observing the object’s motion state velocity $v_{t}$ , acceleration $a_{t}$ , and jerk $j_{t}$ as the absolute motion state of the object. However, this assumption is not valid as the motion state of the object is influenced by the process noise and measurement

将方程1作为卡尔曼滤波器(KF)中状态预测的运动模型的主要问题在于：其假设观测到的物体运动状态速度$v_{t}$、加速度$a_{t}$和加加速度$j_{t}$代表物体的绝对运动状态。然而这一假设并不成立，因为物体的运动状态会受到过程噪声和测量噪声的影响。

noise from the update state in the KF. For instance, if a stationary object is observed, its motion state in the KF will still have values for $v_{t},a_{t}$ , and $j_{t}$ , leading to a slight deviation of the predicted bounding box. This deviation in prediction accumulates, particularly for occluded objects.

卡尔曼滤波器 (KF) 更新状态中的噪声。例如，当观测到静止物体时，其在 KF 中的运动状态仍会包含 $v_{t},a_{t}$ 和 $j_{t}$ 的数值，导致预测边界框出现轻微偏差。这种预测偏差会不断累积，尤其对于被遮挡物体更为明显。

To tackle this issue while maintaining the singularity of the motion model, Equation 1 is weighted by the weighted motion dynamics of the target object $\hat{w}_{t}$ as shown in Equation 2.

为解决这一问题，同时保持运动模型的单一性，如式2所示，将式1乘以目标物体的加权运动动力学 $\hat{w}_{t}$。

$$
x(t)=x_{0}+(\hat{w_{v}}.v_{t})t+\frac{1}{2}(\hat{w_{a}}.a_{t})t^{2}+\frac{1}{6}(\hat{w_{j}}.j_{t})t^{3}
$$

$$
x(t)=x_{0}+(\hat{w_{v}}.v_{t})t+\frac{1}{2}(\hat{w_{a}}.a_{t})t^{2}+\frac{1}{6}(\hat{w_{j}}.j_{t})t^{3}
$$

$\hat{w_{v}},\hat{w_{a}}$ , and $\hat{w}{j}$ represent the amount of change in the object motion to the motion parameters. For instance, $\hat{w_{v}}=$ $\hat{w_{a}}=\hat{w_{j}}=0$ when the observed object is in a stationary state (no motion). In motion, the weight value will change up to the extent of the changes observed in position, velocity, and acceleration, and the motion model will be adjusted to match the object’s observed motion dynamics. These motion dynamics can be used to formulate the matrix $\hat{W}_{t}$ , representing the target object’s recent dynamics at time $t$ .

$\hat{w_{v}}$、$\hat{w_{a}}$ 和 $\hat{w_{j}}$ 表示物体运动对运动参数的变化量。例如，当观测对象处于静止状态(无运动)时，$\hat{w_{v}} = \hat{w_{a}} = \hat{w_{j}} = 0$。在运动过程中，权重值会根据观测到的位置、速度和加速度变化程度进行调整，运动模型也将被修正以匹配物体的观测运动动态。这些运动动态可用于构建矩阵 $\hat{W}_{t}$，该矩阵表示目标物体在时间 $t$ 的最新动态。

$$
\hat{W_{t}}=\left[\begin{array}{c c c c}{1}&{0}&{0}&{0}\ {0}&{\hat{w_{v}}}&{0}&{0}\ {0}&{0}&{\hat{w_{a}}}&{0}\ {0}&{0}&{0}&{\hat{w_{j}}}\end{array}\right]
$$

$$
\hat{W_{t}}=\left[\begin{array}{c c c c}{1}&{0}&{0}&{0}\ {0}&{\hat{w_{v}}}&{0}&{0}\ {0}&{0}&{\hat{w_{a}}}&{0}\ {0}&{0}&{0}&{\hat{w_{j}}}\end{array}\right]
$$

Accordingly, the next state prediction of the KF can be presented as follows:

因此，KF (Kalman Filter) 的下一状态预测可表示如下:

$$
\hat{\mathbf{x}}{\mathbf{t}|\mathbf{t}-\mathbf{1}}=\mathbf{F}{\mathbf{t}}\hat{\mathbf{W}}{\mathbf{t}-\mathbf{1}}\hat{\mathbf{x}}_{\mathbf{t}-\mathbf{1}|\mathbf{t}-\mathbf{1}}
$$

$$
\hat{\mathbf{x}}{\mathbf{t}|\mathbf{t}-\mathbf{1}}=\mathbf{F}{\mathbf{t}}\hat{\mathbf{W}}{\mathbf{t}-\mathbf{1}}\hat{\mathbf{x}}_{\mathbf{t}-\mathbf{1}|\mathbf{t}-\mathbf{1}}
$$

Where $F_{t}\hat{W}{t-1}$ maps the current state $\hat{x}{t-1|t-1}$ to the next state $\hat{x}_{t\mid t-1}$ based on measurement $t-1$ by considering the objects motion dynamics observed at time $t-1$ .

其中 $F_{t}\hat{W}{t-1}$ 将当前状态 $\hat{x}{t-1|t-1}$ 映射到下一状态 $\hat{x}_{t\mid t-1}$ ，这是基于时间 $t-1$ 的测量值，并考虑了在时间 $t-1$ 观测到的物体运动动力学。

3.2 Localization Term Selection for Motion Dynamics

3.2 运动动力学的定位术语选择

Acquiring data that perceives the motion dynamics of objects is a critical part of this work. Neglecting the motion dynamics can lead to dramatic drift in the estimated state of the objects. The motion dynamics of an object can be perceived across consecutive measurements of its states. As shown in Equation 5, acquiring and perceiving the amount of change in position and velocity requires at least three successive position states of the object, assuming $z$ is the object’s actual position.

获取能够感知物体运动动态的数据是这项工作的关键部分。忽略运动动态会导致物体估计状态出现显著漂移。通过连续测量物体状态可以感知其运动动态。如公式5所示，假设$z$为物体实际位置，获取并感知位置和速度的变化量至少需要该物体三个连续的位置状态。

$$
\begin{array}{r l}&{\mathrm{Velocity:}\quad\Delta z_{t}=z_{t}-z_{t-1},}\ &{\sigma_{\Delta z_{t}}\propto\mathrm{accelerationfluctuations},}\ &{\mathrm{Acceleration:}\quad\Delta^{2}z_{t}=\Delta z_{t}-\Delta z_{t-1},}\ &{\sigma_{\Delta^{2}z_{t}}\propto\mathrm{jerkfuctuations}.}\end{array}
$$

$$
\begin{array}{r l}&{\text{速度:}\quad\Delta z_{t}=z_{t}-z_{t-1},}\ &{\sigma_{\Delta z_{t}}\propto\text{加速度波动},}\ &{\text{加速度:}\quad\Delta^{2}z_{t}=\Delta z_{t}-\Delta z_{t-1},}\ &{\sigma_{\Delta^{2}z_{t}}\propto\text{加加速度波动}.}\end{array}
$$

Equation 5 computes the amount of change required to provide an estimation of the motion dynamics for the jerk motion model, as discussed in Section 3.3; however, an accurate measurement of the objects’ position $z_{t}$ is needed to obtain it. Since the actual position of the objects is unavailable, $z_{t}$ can be replaced by three potential terms representing the objects’ position state. The first option is the measurement from the employed detector, $\mathbf{z_{t}}$ , at time $t$ . The second option is the updated state estimation $\mathbf{x_{t|t}}$ of measurement $t$ at time $t$ . The third option is to use detection measurement $\mathbf{z_{t}}$ (from the first option) and use the noise mitigation detection $\mathbf{D_{t}}$ proposed in [1] to remove any noise coming from the detector (Post measurement).

方程5计算了为急动运动模型提供运动动态估计所需的变化量，如第3.3节所述；然而，需要准确测量物体位置$z_{t}$才能获得该值。由于物体的实际位置不可用，$z_{t}$可以用表示物体位置状态的三个潜在项替代。第一个选项是所采用检测器在时间$t$的测量值$\mathbf{z_{t}}$。第二个选项是时间$t$对测量$t$的更新状态估计$\mathbf{x_{t|t}}$。第三个选项是使用检测测量值$\mathbf{z_{t}}$（来自第一个选项），并采用[1]中提出的噪声抑制检测$\mathbf{D_{t}}$来消除检测器产生的任何噪声（后测量）。

To determine which term better represents the objects’ actual location, an experiment is conducted on the KITTI [2] dataset across multiple streams, evaluating the localization performance of each term to the objects’ actual locations from the ground truth. At each timestamp, each term is computed for all objects, and the localization error is calculated using Euclidean distance to the actual location of these objects.

为确定哪个术语能更准确地表示物体的实际位置，我们在KITTI [2] 数据集上进行了多组流数据的实验，评估各术语相对于地面真实值中物体实际位置的定位性能。在每个时间戳，计算所有物体的各术语值，并通过与物体实际位置的欧氏距离来计算定位误差。

Figure 4 shows a graphical representation of the Euclidean distance error between the localization obtained from each term discussed earlier and the actual localization of two cars from the ground truth localization. The post-measurement term shows the closest capture of the car’s localization to the ground truth, achieving the lowest mean square error and standard deviation, which matches the observations in work [1].

图 4 展示了从先前讨论的每个定位项获得的定位与两辆车的真实定位之间的欧氏距离误差的图形表示。测量后项显示出对车辆定位最接近真实值的捕捉，实现了最低的均方误差和标准差，这与文献 [1] 中的观察结果一致。

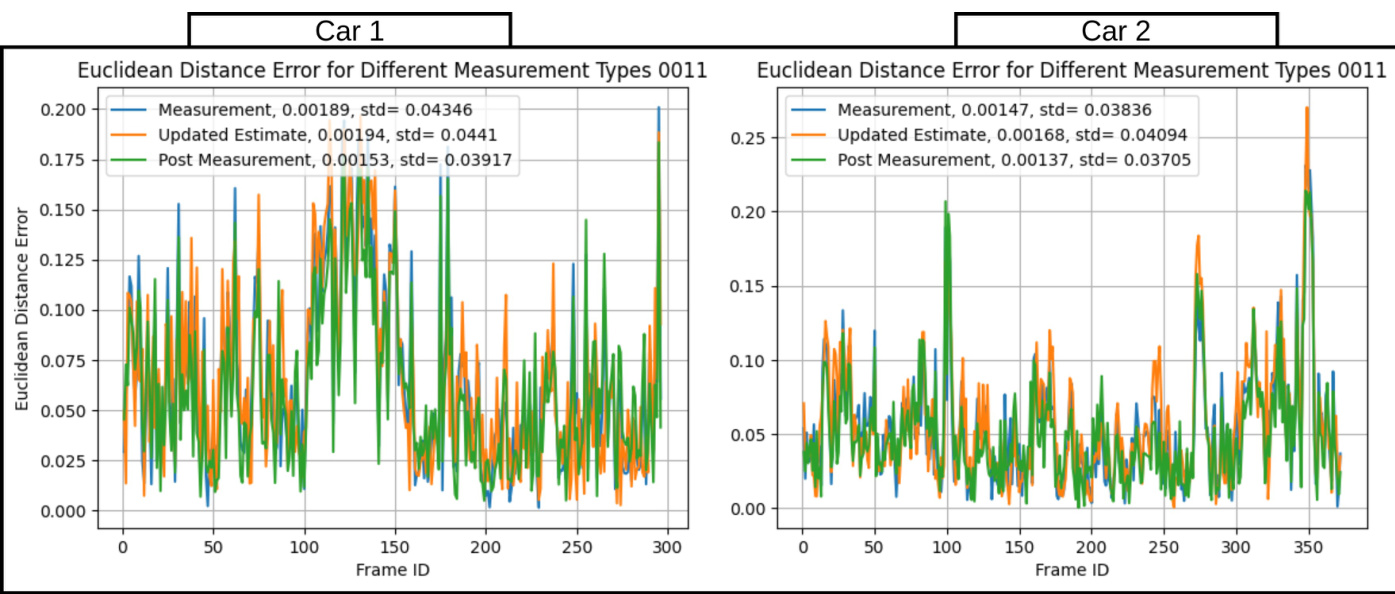
Figure 4: The graph shows the Euclidean distance error comparison between the localization measurements obtained from the employed detector (Blue-line), the updated state estimation of the object’s location (Orange-line), and the measurement from the detector with cleared noise by the proposed term $D_{t}$ (Green-line). The experiment is conducted in two cars over more than 300 consecutive frames. The numerical values in the legend present the mean square error and standard deviation, respectively.

图 4: 该图展示了采用检测器获得的定位测量值(蓝线)、物体位置的更新状态估计(橙线)以及通过提出的 $D_{t}$ 项消除噪声后的检测器测量值(绿线)之间的欧氏距离误差对比。实验在两辆车上进行了超过300帧的连续测试。图例中的数值分别表示均方误差和标准差。

To this end, the post-measurement (third) term is used to determine the recent position of objects. The term is computed by eliminating the localization noise from the detector $D_{t}$ , as presented in [1], from the measurement $z_{t}$ and obtaining the post-measurement localization $\hat{z}_{t}$ .

为此，后测量（第三）项用于确定物体的最近位置。该项通过从检测器 $D_{t}$ 中消除定位噪声（如文献[1]所述），从测量值 $z_{t}$ 中计算得出，并获取后测量定位 $\hat{z}_{t}$。

$$
\hat{\bf z_{t}}={\bf z_{t}}-\left({\bf H}{\bf K_{t}}\right)\mathrm{diag}({\bf D_{t}})
$$

$$
\hat{\bf z_{t}}={\bf z_{t}}-\left({\bf H}{\bf K_{t}}\right)\mathrm{diag}({\bf D_{t}})
$$

As shown in Equation 6, Kalman gain $\mathbf{K_{t}}$ is incorporated into the noise residual, $\mathrm{diag(\mathbf{D}{t})}$ , to include the model uncertainty while clearing the noise from the measurement. Since $\mathbf{K_{t}}$ is in the estimation space, $\mathbf{H}$ maps it to the measurement space. Finally, the obtained refinement noise is removed from the measurement.

如式6所示，卡尔曼增益 $\mathbf{K_{t}}$ 被纳入噪声残差 $\mathrm{diag(\mathbf{D}{t})}$ 中，在消除测量噪声的同时引入模型不确定性。由于 $\mathbf{K_{t}}$ 位于估计空间，$\mathbf{H}$ 将其映射至测量空间。最终从测量值中移除了所得到的修正噪声。

3.3 Temporal Evolution in Motion Dynamics Estimation

3.3 运动动力学估计中的时间演化

As shown in Equation 5, three consecutive observations of an object’s position are used to quantify the fluctuation in an object’s velocity and acceleration motion dynamics. Nevertheless, a single quant if i cation is insufficient to conclude an object’s motion dynamics since external noise could impact the measurement $z_{t}$ . A distribution of multiple quant if i cations can provide a more accurate estimation of an object’s motion dynamics. The distribution of consecutive quant if i cations of motion dynamics parameters (position $z_{t}$ , velocity $\Delta z_{t}$ , and acceleration $\Delta^{2}z_{t}$ ) of an object, obtained from Equation 5, resamples a 2D Gaussian distributions in $\mathbf{X}$ and y directions, as shown in Figure 3 (Updated motion dynamics). The distribution of each motion dynamics parameter shapes a Gaussian distribution around its potential value.

如公式5所示，通过物体位置的连续三次观测来量化其速度和加速度运动动态的波动。然而，单次量化不足以确定物体的运动动态，因为外部噪声可能影响测量值$z_{t}$。多次量化的分布能更准确地估计物体运动动态。根据公式5获得的物体运动动态参数（位置$z_{t}$、速度$\Delta z_{t}$和加速度$\Delta^{2}z_{t}$）连续量化分布，在$\mathbf{X}$和y方向上重采样为二维高斯分布，如图3(更新后的运动动态)所示。每个运动动态参数的分布在其潜在值周围形成高斯分布。

To obtain an estimation of an object’s motion dynamics, consider a single motion parameter: fluctuation in velocity $\sigma_{\Delta z_{t}}$ . Assume a car drives at a constant velocity. The amount of change in position (traveling distance) value $\Delta z_{t\leftarrow s}$ from time $s$ to time $t$ will remain constant, which refers to the mean of the distribution $\Delta\bar{z}$ . In this case, the deviation of the data $\sigma_{\Delta z_{t\leftarrow s}}$ from the mean will be approximately zero. On the other hand, if the car starts to drive at a variable velocity, the amount of change in position will change over time. In this case, the deviation of the data from the mean increases as the variation in velocity increases. Thus, the standard deviation $\sigma_{\Delta z_{t\leftarrow s}}$ approximates the fluctuation in the velocity motion dynamics of the object from time $s$ to time $t$ . Given the consecutive readings and the gradual behavior of objects’ motion, the formulation will shape a Gaussian distribution.

为估算物体的运动动态，考虑单一运动参数：速度波动 $\sigma_{\Delta z_{t}}$。假设汽车以恒定速度行驶，从时刻 $s$ 到时刻 $t$ 的位置变化量（行驶距离）$\Delta z_{t\leftarrow s}$ 将保持恒定，即分布均值 $\Delta\bar{z}$。此时数据与均值的偏差 $\sigma_{\Delta z_{t\leftarrow s}}$ 近似为零。反之，若汽车以变速行驶，位置变化量将随时间改变，此时数据与均值的偏差会随速度变化幅度增大而增加。因此标准差 $\sigma_{\Delta z_{t\leftarrow s}}$ 可近似表征物体从时刻 $s$ 到时刻 $t$ 的速度运动动态波动。鉴于连续读数与物体运动的渐进特性，该公式将形成高斯分布。

In other words, the standard deviation $\sigma_{\Delta z_{t\leftarrow s}}$ increases when the car accelerates, resulting in varying travel distance changes over time. This increased variance in traveling distance widens the Gaussian distribution, thereby enlarging $\sigma_{\Delta z_{t\leftarrow s}}$ . Hence, $\sigma_{\Delta z_{t\leftarrow s}}$ reflects not only changes in velocity but also quantifies fluctuations in acceleration. Generalizing this relationship to motion dynamics parameters (velocity $\Delta z$ , acceleration $\Delta^{2}z$ ), the motion dynamics for observations from time $s$ to $t$ (with $k=t-s+1$ total observations) are estimated as:

换句话说，标准差 $\sigma_{\Delta z_{t\leftarrow s}}$ 会随着车辆加速而增大，导致行驶距离随时间变化。这种行驶距离方差的增大会拓宽高斯分布，从而扩大 $\sigma_{\Delta z_{t\leftarrow s}}$ 。因此，$\sigma_{\Delta z_{t\leftarrow s}}$ 不仅反映速度变化，还能量化加速度波动。将这一关系推广到运动动力学参数（速度 $\Delta z$、加速度 $\Delta^{2}z$），从时间 $s$ 到 $t$ 的观测数据（共 $k=t-s+1$ 次观测）的运动动力学估计为：

$$
\begin{array}{l}{\displaystyle\sigma(\Delta\theta_{t\leftarrow s})=\sqrt{\frac{1}{\displaystyle k-1}\sum_{i=1}^{k}\left(\Delta\theta_{i}-\overline{{\Delta\theta}}\right)^{2}},}\ {\displaystyle\mathrm{where}\Delta\theta\in{\Delta z,\Delta^{2}z},}\ {\displaystyle\overline{{\Delta\theta}}=\frac{1}{\displaystyle k}\sum_{i=1}^{k}\Delta\theta_{i}.}\end{array}
$$

$$
\begin{array}{l}{\displaystyle\sigma(\Delta\theta_{t\leftarrow s})=\sqrt{\frac{1}{\displaystyle k-1}\sum_{i=1}^{k}\left(\Delta\theta_{i}-\overline{{\Delta\theta}}\right)^{2}},}\ {\displaystyle\mathrm{where}\Delta\theta\in{\Delta z,\Delta^{2}z},}\ {\displaystyle\overline{{\Delta\theta}}=\frac{1}{\displaystyle k}\sum_{i=1}^{k}\Delta\theta_{i}.}\end{array}
$$

Here, $\Delta\theta_{t\leftarrow s}$ represents the finite differences of velocity $(\Delta z)$ or acceleration $({\mit\Delta}^{2}z)$ over the time window $t\leftarrow s$ , and $\overline{{\Delta\theta}}$ denotes their sample mean. The standard deviation $\sigma(\Delta\theta_{t\leftarrow s})$ quantifies fluctuations in the corresponding motion parameter.

这里，$\Delta\theta_{t\leftarrow s}$ 表示速度 $(\Delta z)$ 或加速度 $({\mit\Delta}^{2}z)$ 在时间窗口 $t\leftarrow s$ 内的有限差分，$\overline{{\Delta\theta}}$ 表示它们的样本均值。标准差 $\sigma(\Delta\theta_{t\leftarrow s})$ 量化了相应运动参数的波动。

The motion dynamics estimation vector $d_{t}$ is then derived as:

运动动态估计向量 $d_{t}$ 的计算公式为:

$$
d_{t}=\left[\begin{array}{c}{{1}}\ {{\sigma(z_{t\leftarrow s})}}\ {{\sigma(\Delta z_{t\leftarrow s})}}\ {{\sigma(\Delta^{2}z_{t\leftarrow s})}}\end{array}\right],
$$

$$
d_{t}=\left[\begin{array}{c}{{1}}\ {{\sigma(z_{t\leftarrow s})}}\ {{\sigma(\Delta z_{t\leftarrow s})}}\ {{\sigma(\Delta^{2}z_{t\leftarrow s})}}\end{array}\right],
$$

matri

矩阵

$$
\begin{array}{r l}{\sigma(z_{t\leftarrow s})}&{{}{\mathrm{captures position fluctuations,}}}\ {\sigma(\Delta z_{t\leftarrow s})}&{{}{\mathrm{corresponds to velocity~fluctuations,}}}\ {\sigma(\Delta^{2}z_{t\leftarrow s})}&{{}{\mathrm{reflects acceleration fluctuations.}}}\end{array}
$$

$$
\begin{array}{r l}{\sigma(z_{t\leftarrow s})}&{{}{\mathrm{captures position fluctuations,}}}\ {\sigma(\Delta z_{t\leftarrow s})}&{{}{\mathrm{corresponds to velocity~fluctuations,}}}\ {\sigma(\Delta^{2}z_{t\leftarrow s})}&{{}{\mathrm{reflects acceleration fluctuations.}}}\end{array}
$$

3.4 Motion Dynamics Transition and Smoothing Window

3.4 运动动力学过渡与平滑窗口

As demonstrated in Equation 7, the estimation of motion dynamics can be obtained from the distribution of $\sigma(\Delta\theta_{t\leftarrow s})$ across $k$ consecutive measurements. The determination of $k$ , called transition window size, should be carefully selected as it controls when the model alternates from one motion dynamic state to another.

如公式7所示，运动动态的估计可以通过连续k次测量中$\sigma(\Delta\theta_{t\leftarrow s})$的分布获得。其中k值（称为过渡窗口大小）的确定需要谨慎选择，因为它控制着模型从一个运动动态状态切换到另一个状态的时机。

For a better understanding of the motion dynamic transition and its influence on the state estimation, Figure 5 shows a use case of a car that accelerates and then decelerates. The car starts to accelerate at frame 140 to 160, as shown in the second graph when the change in distance shifts. The error in state estimation of the constant acceleration and jerk models decreases as expected, while increasing for the constant velocity model. From frame 160 to 168, there is a transition in the motion dynamics as the car starts to decelerate. At the transition state, the constant velocity yields the lowest error as the change in velocity approaches 0. This transition state is essential to consider while selecting the size of the transition window $k$ . The large window size can cause the failure to capture changes in motion dynamics that occur quickly, as shown in the transition state of Figure 5. On the other hand, a window that is too small can cause quick motion state transitions, which also impact the stability of the estimated state.

为了更好地理解运动动态转变及其对状态估计的影响，图5展示了一辆汽车加速后减速的用例。如第二张图表所示，当距离变化发生偏移时，车辆在140至160帧期间开始加速。恒定加速度和加加速度模型的状态估计误差如预期般下降，而恒定速度模型的误差则增大。在160至168帧期间，随着车辆开始减速，运动动态发生转变。在过渡状态下，由于速度变化趋近于0，恒定速度模型的误差最小。选择过渡窗口大小$k$时必须重点考虑这种过渡状态。如图5的过渡状态所示，过大的窗口尺寸可能导致无法快速捕捉运动动态的变化。另一方面，过小的窗口会引起运动状态快速切换，同样会影响估计状态的稳定性。

The transition window size $k$ determines how many observations are needed to gather adequate information about the object’s motion dynamics. The window size controls the motion dynamics weights, as presented in Equation 3, which adjusts the state estimation based on the observed motion dynamics. Figure 6 shows how different transition window sizes impact the motion dynamics weights presented in Equation 3.

过渡窗口大小 $k$ 决定了需要多少观测值才能收集足够的物体运动动态信息。如公式3所示，窗口大小控制着运动动态权重，该权重会根据观测到的运动动态调整状态估计。图6展示了不同过渡窗口大小如何影响公式3中的运动动态权重。

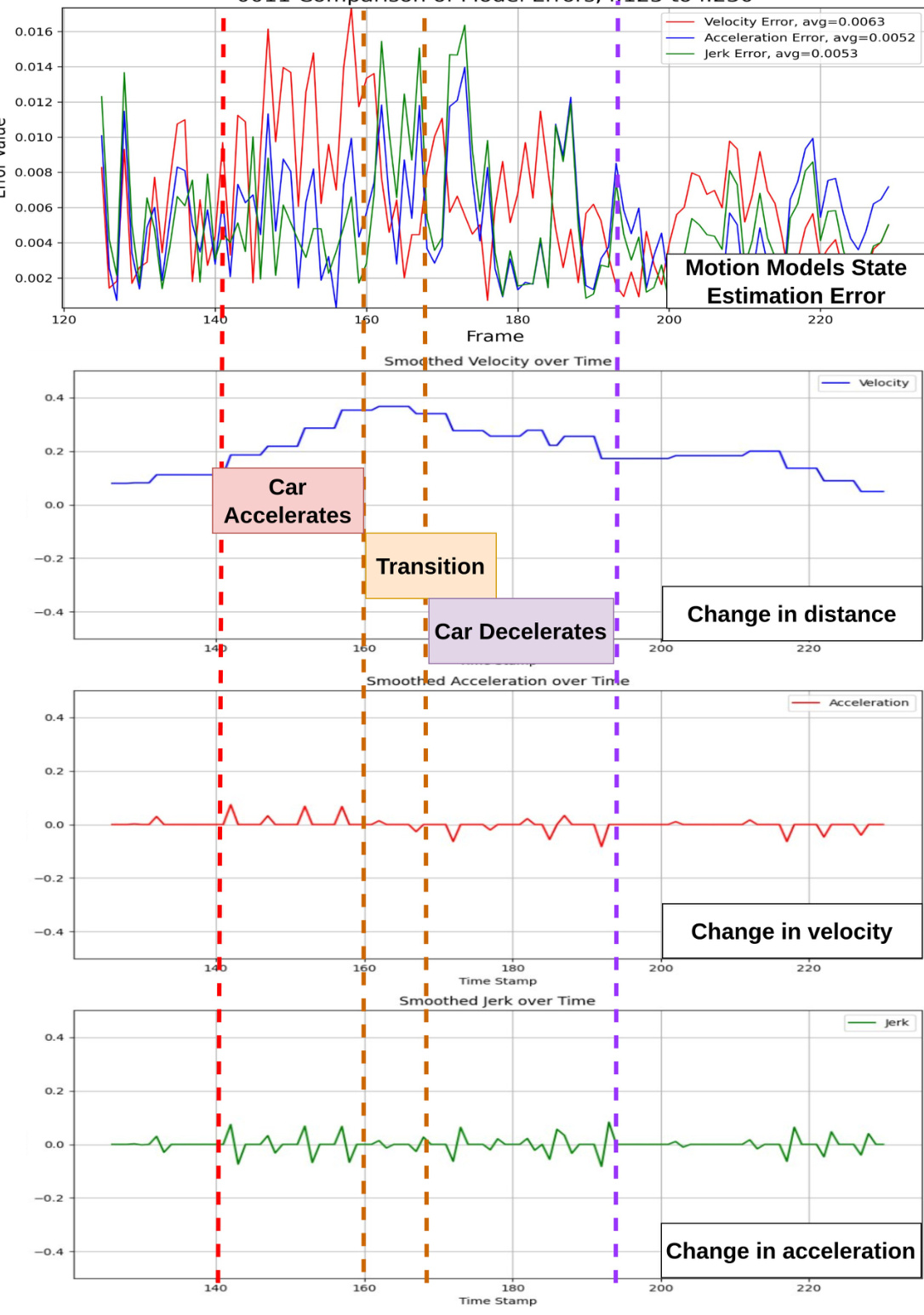
0011 Comparison of Model Errors,f:125tof:230 Figure 5: The graphs show a car’s motion dynamics, which accelerates and decelerates for a particular time stamp. The first graph shows the Euclidean distance error of state estimation from three different motion models: constant velocity (Red), constant acceleration (Blue), and constant Jerk (Green). The second graph shows the corresponding change in traveling distances from the ground truth, presenting the car motion dynamics for velocity. Meanwhile, the third graph shows the car’s velocity change compared to the ground truth, illustrating the motion dynamics for acceleration. The last graph shows the change in car acceleration from the ground truth, illustrating the motion dynamics for jerk. The graph highlights three transition states in the motion dynamics of the car: Acceleration (Red dot-line), transition from acceleration to deceleration (Orange dot-line), and deceleration (Violet dot-line).

图 5: 图表展示了车辆在特定时间戳下的加减速运动动态。第一幅图呈现了三种不同运动模型的状态估计欧氏距离误差：匀速(红色)、匀加速(蓝色)和匀加加速度(绿色)。第二幅图显示了与真实轨迹相比的行进距离变化，反映车辆速度维度的运动动态。第三幅图展示了车辆速度相对于真实值的变化，体现加速度维度的运动动态。最后一幅图呈现车辆加速度与真实值的偏差，展示加加速度维度的运动动态。图中特别标注了车辆运动动态的三个过渡状态：加速阶段(红色虚线)、加速转减速过渡阶段(橙色虚线)和减速阶段(紫色虚线)。

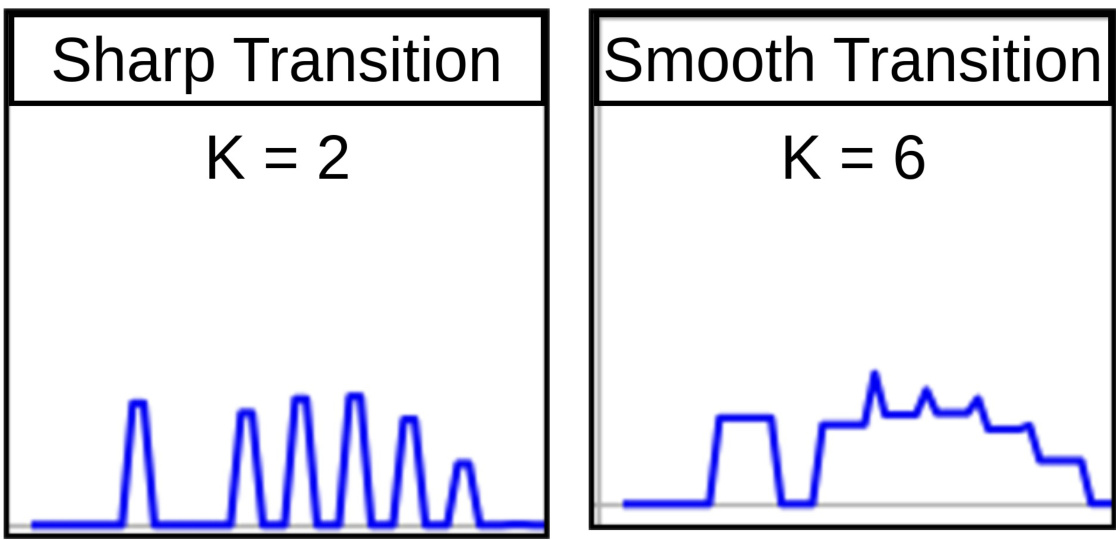
Figure 6: The graphs show the impact of the smoothing window of sizes 2 and 6 on the motion dynamics weight that responds to transitions between motion models. With a small smoothing window, the transition between models becomes sharp, causing an immediate switch; on the other hand, a larger window size shows smoother transitions.

图 6: 图表展示了大小为2和6的平滑窗口对响应运动模型间转换的运动动态权重的影响。较小的平滑窗口会使模型间转换变得尖锐，导致立即切换；而较大的窗口则呈现更平滑的过渡。

4 Weighted Motion Dynamics Evolution for State Update

4 状态更新的加权运动动态演化

The obtained motion dynamics vector $d_{t}$ cannot be used directly as weights into the motion parameters in Equation 2 because the standard deviation values can be between $[0,\infty[$ , they must be normalized to be in the range $[0,1]$ . For instance, constant velocity motion model can obtained from Equation 2 when $\hat{w}{a}=\hat{w}{j}=0$ . Meanwhile, the constant acceleration model can be obtained when $\hat{w}{j}=0$ . Hence, the primary purpose of the weights is to alternate between the three derivative models. Thus, the amount of change the model needs to alternate from one motion model to another must be determined, which will be used to normalize $d_{t}$ . This amount of change is called the motion dynamics factor donated by $\ell_{t}$ , which should be fine-tuned for all three derivatives. Assuming a one-dimensional space, the motion dynamic factor will be:

获得的运动动态向量 $d_{t}$ 不能直接作为方程2中运动参数的权重，因为标准差值可能介于 $[0,\infty[$ 之间，必须将其归一化到 $[0,1]$ 范围内。例如，当 $\hat{w}{a}=\hat{w}{j}=0$ 时，可从方程2得到匀速运动模型；而当 $\hat{w}{j}=0$ 时，则可得到匀加速运动模型。因此，权重的主要作用是在三个导数模型之间切换。需要确定模型从一个运动模型切换到另一个运动模型所需的变化量，该变化量将用于归一化 $d_{t}$。这个变化量称为运动动态因子，记作 $\ell_{t}$，应对所有三个导数进行微调。假设为一维空间，运动动态因子为：

$$
\ell_{t}=[1\quad\ell_{v}\quad\ell_{a}\quad\ell_{j}]
$$

$$
\ell_{t}=[1\quad\ell_{v}\quad\ell_{a}\quad\ell_{j}]
$$

Accordingly, the weighted motion dynamics are obtained as:

因此，加权运动动力学可表示为：

$$
\begin{array}{r l}&{\hat{w}{v}=\operatorname*{min}\left(\frac{\sigma\left(z_{t\rightarrow k}\right)}{\ell_{v}},1\right),}\ &{\hat{w}{a}=\operatorname*{min}\left(\frac{\sigma\left(\Delta z_{t\rightarrow k}\right)}{\ell_{a}},1\right),}\ &{\hat{w}{j}=\operatorname*{min}\left(\frac{\sigma\left(\Delta^{2}z_{t\rightarrow k}\right)}{\ell_{j}},1\right).}\end{array}
$$

$$
\begin{array}{r l}&{\hat{w}{v}=\operatorname*{min}\left(\frac{\sigma\left(z_{t\rightarrow k}\right)}{\ell_{v}},1\right),}\ &{\hat{w}{a}=\operatorname*{min}\left(\frac{\sigma\left(\Delta z_{t\rightarrow k}\right)}{\ell_{a}},1\right),}\ &{\hat{w}{j}=\operatorname*{min}\left(\frac{\sigma\left(\Delta^{2}z_{t\rightarrow k}\right)}{\ell_{j}},1\right).}\end{array}
$$

The normalization procedure can be formalized algebraically as matrix operations, as shown in Equation 10.

归一化过程可以用矩阵运算形式化表示，如式 10 所示。

$$
\begin{array}{l}{{\displaystyle{d_{t_{\mathrm{norm}}}=d_{t}\circ\ell_{t}^{-1}},}}\ {{\displaystyle{\hat{\pmb w}{t}=\frac{1}{2}\left({\bf1}{n}+d_{t_{\mathrm{norm}}}-|{\bf1}{n}-d_{t_{\mathrm{norm}}}|\right).}}}\end{array}
$$

$$
\begin{array}{l}{{\displaystyle{d_{t_{\mathrm{norm}}}=d_{t}\circ\ell_{t}^{-1}},}}\ {{\displaystyle{\hat{\pmb w}{t}=\frac{1}{2}\left({\bf1}{n}+d_{t_{\mathrm{norm}}}-|{\bf1}{n}-d_{t_{\mathrm{norm}}}|\right).}}}\end{array}
$$

By Equation 10, the weights are updated by the current evolution in the motion dynamics of objects.

根据公式10，权重通过物体运动动态的当前演变进行更新。

5 Results and Discussion

5 结果与讨论

This work proposes a formulation of the KF that accounts for the motion dynamics of tracked objects. For adequate evaluation of the proposed formulation, the tracking framework proposed in the state-of-the-art work [1] is used, and the traditional KF is replaced with the proposed KF formulation in this work. The evaluation procedures consist of quantitative evaluation, qualitative evaluation, run-time performance, and an ablation study about challenging scenarios in tracking. The quantitative (Section 5.2.1) and qualitative assessments (Section 5.2.2) show the tracking performance and enhanced localization of state estimation compared to recent benchmarks on KITTI [2] and the WOD [17]. The performance evaluation is extended in Section 5.2.3 to include a run-time comparison of the traditional KF and the proposed KF, quantifying the difference in computational cost. Lastly, an ablation study is conducted, Section 5.3, to evaluate the tracking performance of simulated occlusion scenarios that asses the proposed KF with motion dynamics performance of tracking occluded objects compared to the traditional KF.

本研究提出了一种考虑被追踪目标运动动态的卡尔曼滤波器 (KF) 公式。为充分评估该公式性能，我们采用前沿研究[1]提出的追踪框架，并将其传统KF替换为本研究提出的KF公式。评估流程包含定量分析（第5.2.1节）、定性评估（第5.2.2节）、运行时性能对比以及针对追踪挑战场景的消融实验。定量与定性评估表明，相较于KITTI[2]和WOD[17]的最新基准测试，该方案在追踪性能和状态估计定位精度方面均有提升。第5.2.3节进一步扩展性能评估，通过对比传统KF与提出KF的运行时表现，量化计算成本差异。最后在第5.3节开展消融研究，通过模拟遮挡场景评估所提KF在运动动态建模方面的优势，与传统KF相比显著提升了被遮挡目标的追踪性能。

5.1 Environment Setup

5.1 环境设置

This experiment uses an AMD Ryzen 6900HX processor with $32\mathrm{GB}$ of RAM (Single CPU); no GPU is involved. The KF formulation is implemented from scratch using the Eigen3 library in $\mathrm{C}{+}{+}17$ . Additionally, OpenCV 4.6 and PCL 1.14 libraries are used for visualization. All performance evaluations in this work are done using the official evaluation tools from KITTI [2] and WOD [17].

本实验采用 AMD Ryzen 6900HX 处理器，配备 $32\mathrm{GB}$ 内存（单 CPU），未使用 GPU。KF (Kalman Filter) 算法通过 Eigen3 库在 $\mathrm{C}{+}{+}17$ 中从头实现，同时使用 OpenCV 4.6 和 PCL 1.14 库进行可视化。所有性能评估均基于 KITTI [2] 和 WOD [17] 的官方评测工具完成。

5.2 Comparison with Benchmarks

5.2 与基准测试对比

5.2.1 Quantitative Evaluation

5.2.1 定量评估

This section consists of three parts of this work’s quantitative evaluation of the proposed KF. The first Part (B.I) evaluates the overall tracking performance of the proposed KF embedded in RobMOT [1] work with recent benchmarks, including RobMOT [1] with a baseline KF. Next, the performance generalization of the proposed work is discussed in Part (B.II), which assesses its performance using various detectors compared to the baseline KF. Lastly, the tracking performance in challenging conditions, such as tracking distant targets, is e