Domain Specific Question Answering Over Knowledge Graphs Using Logical Programming and Large Language Models
基于逻辑编程与大语言模型的知识图谱领域问答
Abstract
摘要
Answering questions over domain-specific graphs requires a tailored approach due to the limited number of relations and the specific nature of the domain. Our approach integrates classic logical programming languages into large language models (LLMs), enabling the utilization of logical reasoning capabilities to tackle the KGQA task. By representing the questions as Prolog queries, which are readable and near close to natural language in representation, we facilitate the generation of programmatically derived answers. To validate the effectiveness of our approach, we evaluate it using a well-known benchmark dataset, MetaQA. Our experimental results demonstrate that our method achieves accurate identification of correct answer entities for all test questions, even when trained on a small fraction of annotated data. Overall, our work presents a promising approach to addressing question answering over domain-specific graphs, offering an explainable and robust solution by incorporating logical programming languages.
针对特定领域图谱的问答需要定制化方法,因其关系数量有限且领域特性鲜明。我们将经典逻辑编程语言 (Prolog) 与大语言模型 (LLM) 相结合,利用逻辑推理能力解决知识图谱问答 (KGQA) 任务。通过将问题转换为可读性强且接近自然语言表达的 Prolog 查询,我们实现了程序化推导答案的生成。为验证方法有效性,我们在 MetaQA 基准数据集上进行评估。实验结果表明,即使仅使用少量标注数据训练,我们的方法也能准确识别所有测试问题的正确答案实体。总体而言,这项工作通过融合逻辑编程语言,为特定领域图谱问答提供了兼具可解释性和鲁棒性的解决方案。
1 Introduction
1 引言
Question Answering over Knowledge Graphs (KGQA) poses significant challenges in the field of Natural Language Processing (NLP). As structured knowledge graphs capturing rich semantic information become prevalent, there is a pressing need for intelligent systems that can reason effectively and provide accurate answers to intricate questions within specific domains. The primary focus of KGQA is to bridge the gap between human language and structured knowledge representations. When presented with a question in natural language, KGQA systems aim to traverse the knowledge graph consisting of entities and their relationships, extracting relevant information to generate precise answers. This task demands not only language comprehension but also the ability to perform logical reasoning across the edges of the graph to derive meaningful insights. Although large language models (LLMs) powered by deep learning have shown remarkable capabilities in natural language understanding and generation, they may not be specifically trained on a particular knowledge source or possess a deep understanding of domain-specific facts. However, LLMs can serve as a valuable tool to represent questions within a domain, extracting query or question meanings. Leveraging logical programming approaches, these representations can be processed to handle reasoning and knowledge representation. One notable advantage of this approach is that it empowers users of the system to manage knowledge dynamically. They can modify, delete, or add new entries into the knowledge graph without requiring changes to the system itself. By integrating logical programming techniques with LLMs, KGQA systems gain the flexibility to adapt to evolving knowledge requirements while maintaining their functionality.
知识图谱问答(KGQA)在自然语言处理(NLP)领域提出了重大挑战。随着捕获丰富语义信息的结构化知识图谱日益普及,对能在特定领域内有效推理并准确回答复杂问题的智能系统需求迫切。KGQA的核心目标是弥合人类语言与结构化知识表示之间的鸿沟。当面对自然语言提问时,KGQA系统旨在遍历由实体及其关系构成的知识图谱,提取相关信息以生成精确答案。该任务不仅需要语言理解能力,还需具备跨图谱边界的逻辑推理能力以获得有意义的洞察。尽管基于深度学习的大语言模型(LLM)在自然语言理解与生成方面展现出卓越能力,它们可能未针对特定知识源进行专门训练,或缺乏对领域特定事实的深入理解。然而,LLM可作为重要工具来表示领域内的问题,提取查询或问题的含义。通过结合逻辑编程方法,这些表示可被处理以应对推理和知识表示。该方法的显著优势在于使系统用户能动态管理知识——他们可修改、删除或向知识图谱添加新条目,而无需更改系统本身。通过将逻辑编程技术与LLM相结合,KGQA系统获得了适应不断演进的知识需求的同时保持功能的灵活性。
In this paper, we address the challenges of domain-specific KGQA by combining the strengths of large language models and logical programming. We propose an approach that utilizes LLMs to represent questions within a specific domain, extracting their meanings, while employing logical programming techniques for reasoning and knowledge representation. Our objective is to demonstrate how this integration enables robust and adaptable KGQA systems that can navigate domain-specific knowledge graphs and provide accurate answers to complex questions. To evaluate the effectiveness of our proposed approach, we conduct experiments using the MetaQA dataset (Zhang et al., 2018), a widely adopted benchmark in KGQA research. By comparing our method against state-of-the-art approaches, we demonstrate its capability to accurately identify the correct answer entities for a range of questions. Notably, our experiments show promising results even when our model is trained on only a small fraction of the available training data, indicating its efficiency and generalization ability.
本文通过结合大语言模型和逻辑编程的优势,解决了特定领域知识图谱问答(KGQA)的挑战。我们提出了一种方法,利用大语言模型在特定领域内表示问题并提取其含义,同时采用逻辑编程技术进行推理和知识表示。我们的目标是展示这种整合如何实现稳健且适应性强的KGQA系统,能够导航特定领域的知识图谱并为复杂问题提供准确答案。
为评估所提方法的有效性,我们使用KGQA研究中广泛采用的基准数据集MetaQA (Zhang et al., 2018)进行实验。通过与最先进方法的对比,我们证明了该方法能够准确识别各类问题的正确答案实体。值得注意的是,实验结果表明即使仅使用少量可用训练数据进行训练,我们的模型仍能取得良好效果,显示出其高效性和泛化能力。
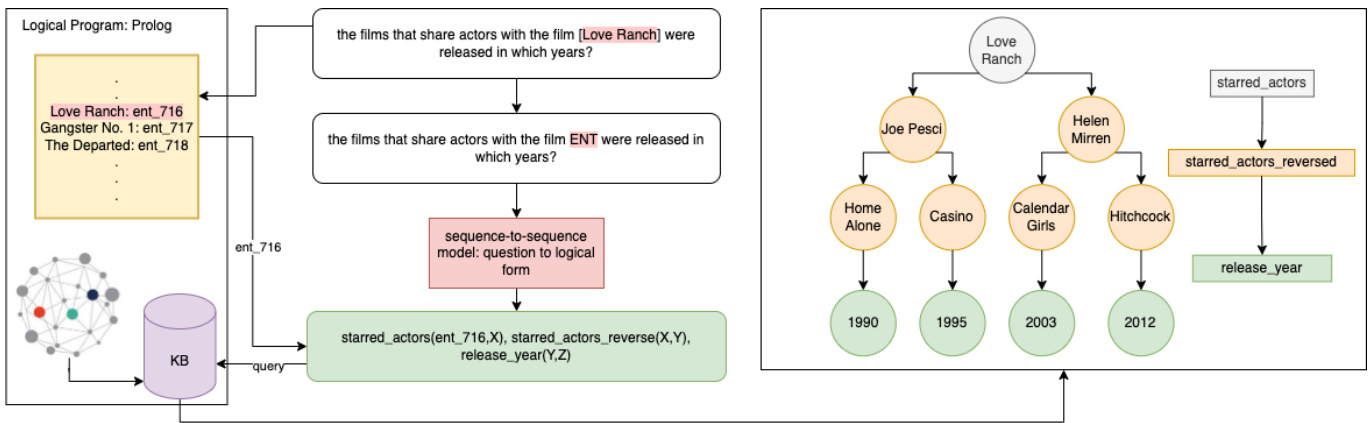
Figure 1: The complete inference pipeline of our proposed method. Note that the inference tree on the right side is a subset of the answer drawn here to clarify the schema of the model’s output.
图 1: 我们提出方法的完整推理流程。请注意右侧的推理树是此处绘制答案的子集,用以阐明模型输出的结构。
The contributions of this paper are two-fold:
本文的贡献包括两个方面:
2 Related Work
2 相关工作
A variety of approaches have been taken to address the problem of multi-hop question answering. A number of prior works have used graph embedding models to encode entities and relations in a knowledge graph and then score the triples in a KG and construct a scoring function so that the score for a correct triple is higher than the score of an incorrect one (Nickel et al., 2011; Yang et al., 2014a; Balazevic et al., 2019; Dettmers et al., 2017; Vashishth et al., 2019). Others have approached the problem by constructing a function that maps the question embedding along with an embedding of the graph or a subgraph around the question entity to the answer entity’s embedding in knowledge graph (Sun et al., 2018; Saxena et al., 2020; Sun et al., 2019; He et al., 2021). Still others adapt a slightly different method, training a teacher model to learn intermediate signals and a student model to answer the questions (He et al., 2021). There also has been efforts by (Xie et al., 2022) that pushed the performance of these models on 2 and 3 hop splits to the limits. They propose a sequential reasoning self-attention mechanism which is guided by a GRU-inspired Flow Control (GFC) and their work is inspired by (Shi et al., 2021). Finally, most relevant to our work, (Yang et al., 2014b) and (Yang et al., 2015) try to learn the logical form of the natural language questions by building a semantic embedding space. However, our work differs from theirs in that we use LLMs to represent the question in logical form instead of manually building a semantic mapping space. The present work is thus the first to use large language models to represent questions in logical form and equip LLMs with logical programming tools to answer questions.
为解决多跳问答问题,研究者们采取了多种方法。部分先前工作使用图嵌入模型对知识图谱中的实体和关系进行编码,然后对知识图谱中的三元组进行评分,并构建评分函数,使得正确三元组的分数高于错误三元组 (Nickel et al., 2011; Yang et al., 2014a; Balazevic et al., 2019; Dettmers et al., 2017; Vashishth et al., 2019)。另一些研究则通过构建函数,将问题嵌入与问题实体周围的图或子图嵌入映射到知识图谱中答案实体的嵌入 (Sun et al., 2018; Saxena et al., 2020; Sun et al., 2019; He et al., 2021)。还有研究采用稍不同的方法,训练教师模型学习中间信号,学生模型回答问题 (He et al., 2021)。(Xie et al., 2022) 的工作将这些模型在2跳和3跳任务上的性能推向极限,他们提出了一种由GRU启发的流控制 (GFC) 引导的序列推理自注意力机制,其工作灵感来自 (Shi et al., 2021)。与本文最相关的是 (Yang et al., 2014b) 和 (Yang et al., 2015),他们尝试通过构建语义嵌入空间来学习自然语言问题的逻辑形式。然而,我们的工作与他们的不同之处在于,我们使用大语言模型以逻辑形式表示问题,而非手动构建语义映射空间。因此,本研究首次利用大语言模型以逻辑形式表示问题,并为其配备逻辑编程工具来回答问题。
3 Dataset
3 数据集
The MetaQA dataset is a widely used benchmark dataset for question answering over knowledge graphs (KGQA). The MetaQA dataset consists of questions that require reasoning over a given knowledge graph. The knowledge graph represents a structured database of 134,741 facts and 9 relations, providing a rich source of information for answering domain specific questions. Appendix A describes the dataset in detail.
MetaQA数据集是知识图谱问答(KGQA)领域广泛使用的基准数据集。该数据集包含需要基于给定知识图谱进行推理的问题。该知识图谱由134,741条事实数据和9种关系构成的结构化数据库组成,为回答领域特定问题提供了丰富的信息来源。附录A详细描述了该数据集。
4 Approach
4 方法
4.1 Question to Logical Form
4.1 问题到逻辑形式
To facilitate the translation of questions into their corresponding logical forms, we begin by developing a question comprehension module. To accomplish this task, we harness the power of encoderdecoder transformer models, known for their exceptional potential in sequence to sequence transformation ability (Vaswani et al., 2017). To collect the dataset necessary for fine-tuning a sequence-tosequence transformer model, we leverage the multihop path information provided by the MetaQA dataset. We will go over the implementation details of annotating each question with a prolog query using it’s intermediate steps in appendix B. From the total pool of 329,282 multi-hop training examples in MetaQA, we randomly sample and annotate subsets consisting of 100, 250, 500, and 1000 samples with each subset consisting of equal number of examples from each of the 1, 2 and 3 hop samples. These subsets are respectively labeled as s100, $s250$ , $s500$ and $s I O O O$ . To transform the question into an intermediate query representation, we employ a T5-small sequence-to-sequence transformer model (Raffel et al., 2019). This model effectively learns to generate accurate representations of the questions, serving as a bridge between natural language input and logical query output. For the training process, we fine-tune the model using each of the annotated training sets, iterating through 5000 training steps. The best-performing model is selected based on the exact match score obtained from the development dataset.To optimize the model’s performance, we utilize the AdamW optimizer with an initial learning rate of 5e-5. Additionally, a linear learning rate scheduler is employed. The training is conducted using a batch size of 8, making efficient use of a single A100 GPU for computational acceleration.
为了将问题翻译成对应的逻辑形式,我们首先开发了一个问题理解模块。为此,我们利用了编码器-解码器Transformer模型的强大能力,该模型在序列到序列转换任务中展现出卓越潜力 (Vaswani et al., 2017)。为了收集微调序列到序列Transformer模型所需的数据集,我们利用MetaQA数据集提供的多跳路径信息。关于使用中间步骤为每个问题标注Prolog查询的实现细节,我们将在附录B中详细说明。从MetaQA的329,282个多跳训练样本中,我们随机抽取并标注了包含100、250、500和1000个样本的子集,每个子集包含等量的1跳、2跳和3跳样本。这些子集分别标记为s100、$s250$、$s500$和$sIOOO$。为了将问题转换为中间查询表示,我们采用了T5-small序列到序列Transformer模型 (Raffel et al., 2019)。该模型能有效学习生成问题的准确表示,作为自然语言输入和逻辑查询输出之间的桥梁。在训练过程中,我们使用每个标注训练集对模型进行微调,迭代5000个训练步骤,并根据开发数据集上的精确匹配分数选择表现最佳的模型。为了优化模型性能,我们采用AdamW优化器,初始学习率为5e-5,并配合线性学习率调度器。训练使用批量大小为8,高效利用单个A100 GPU进行加速计算。
4.2 Question Answering
4.2 问答系统
The question answering process in our proposed model is illustrated in Figure 1. To begin, we transform each triple in the knowledge base of the MetaQA dataset into a first-order logic predicate. For instance, given the triple (Innocence | written_by | Hilary Brougher), we construct the corresponding predicate written_by(Innocence, Hilary Brougher).
我们提出的模型中的问答过程如图 1 所示。首先,我们将 MetaQA 数据集知识库中的每个三元组转化为一阶逻辑谓词。例如,给定三元组 (Innocence | written_by | Hilary Brougher),我们构建相应的谓词 written_by(Innocence, Hilary Brougher)。
When processing a specific question, we generate its logical form using the transformer model. The logical form provides a structured representation of the question’s meaning. Subsequently, we replace the ENT token in the logical form with the corresponding entity ID from the knowledge graph. This substitution results in the final Prolog query. Finally, we execute the Prolog query, which involves querying the knowledge graph. By executing the query, we retrieve both the answers to the question and the logical path that connects the question entity to the answer entities. This path provides valuable insights into the reasoning process and the information flow within the knowledge graph.
在处理特定问题时,我们使用Transformer模型生成其逻辑形式。逻辑形式提供了问题含义的结构化表示。随后,我们将逻辑形式中的ENT Token替换为知识图谱中相应的实体ID。这种替换会生成最终的Prolog查询。最后,我们执行Prolog查询,这涉及查询知识图谱。通过执行查询,我们既能获取问题的答案,也能获得连接问题实体与答案实体的逻辑路径。该路径为推理过程及知识图谱内的信息流提供了有价值的洞察。
5 Experiments and Results
5 实验与结果
MetaQA questions mostly come with multiple answers. Prior methods have used hit $@1$ as a metric to measure the performance of their model. This means that they measure if the highest ranked entity given by their model exists in the answer set. Our approach produces the exact solution path inside the knowledge graph and consequently it outputs all of the answers to the question instead of producing a score distribution over graph entities (as depicted in Figure 1). For the sake of comparison, we also measure the hit $@1$ metric for our model over multi hop test datasets. In other words, we randomly pick one of the answer entities and assume it is the rank 1 answer of the model and consequently we calculate the hit $@1$ score. Table 1 compares our method with prior work.
MetaQA问题通常带有多个答案。先前的方法使用命中$@1$作为衡量模型性能的指标,即检测模型给出的最高排名实体是否存在于答案集合中。我们的方法在知识图谱内生成精确的求解路径,因此能输出问题的所有答案,而非在图实体上生成分数分布(如图1所示)。为了便于比较,我们同样在多跳测试数据集上测量了模型的命中$@1$指标,即随机选取一个答案实体作为模型的排名第一答案来计算命中$@1$分数。表1将我们的方法与先前工作进行了对比。
In order to get robust results we repeat the process of sampling training data and annotating it 5 times and each time we sampled 100, 250, 500 and 1000 samples. The sampling process was straightforward; each time we sample randomly and equally from each of the 1-hop, 2-hop and 3- hop training datasets. We also annotated 3000 samples from the validation and test set of the MetaQA dataset. Figure 2 shows the variance of performance on each of these datasets. Since the variance was high on the test set with 100 samples we only reported s250, s500 and s1000 in table 1. According to these results the 3-hop test set’s representation is the easiest to learn since it doesn’t come with many variations of natural language to describe. On the other hand the 2-hop dataset is the hardest to learn. However, all of these samples are collected randomly. But with a manual and careful sample collection, we can see that even 500 samples are enough to learn the whole dynamics of this dataset and learn to represent questions in logical form. We conclude that our model is capable of correctly answering all questions in the test dataset with only 1000 annotated examples.
为了获得稳健的结果,我们重复了5次训练数据采样和标注过程,每次分别采样100、250、500和1000个样本。采样过程简单直接:每次从1跳、2跳和3跳训练数据集中随机等量抽取。我们还标注了MetaQA数据集中验证集和测试集的3000个样本。图2展示了各数据集上的性能方差。由于100样本测试集的方差较高,表1中仅报告了s250、s500和s1000的结果。
