Hyper spectral MAE: The Hyper spectral Imagery Classification Model using Fourier-Encoded Dual-Branch Masked Auto encoder

高光谱MAE：基于傅里叶编码双分支掩码自编码器的高光谱图像分类模型

Abstract—Hyper spectral imagery provides rich spectral detail but poses unique challenges due to its high dimensionality in both spatial and spectral domains. Therefore, we propose Hyper spectral MAE, a transformer-based foundation model for hyper spectral data featuring a dual-masking strategy that randomly occludes $50%$ of the spatial patches and $50%$ of the spectral bands during pre-training. This forces the model to learn meaningful representations by reconstructing missing information across both dimensions. A positional embedding with spectral wavelength based on learnable harmonic Fourier components is introduced to encode the identity of each spectral band, ensuring that the model is sensitive to spectral order and spacing. The reconstruction objective employs a composite loss combining mean-squared error (MSE) and spectral angle mapper (SAM) to balance pixel-level accuracy and spectral-shape fidelity.

摘要—高光谱图像提供了丰富的光谱细节，但由于其在空间和光谱维度上的高复杂性，也带来了独特的挑战。为此，我们提出了高光谱MAE (Hyper spectral MAE)，这是一种基于Transformer的高光谱数据基础模型，其特点是在预训练过程中采用双重掩码策略，随机遮挡50%的空间块和50%的光谱波段。这迫使模型通过重建两个维度上缺失的信息来学习有意义的表征。我们引入了一种基于可学习谐波傅里叶分量的光谱波长位置嵌入，以编码每个光谱波段的身份，确保模型对光谱顺序和间距敏感。重建目标采用了均方误差(MSE)和光谱角制图(SAM)相结合的复合损失，以平衡像素级精度和光谱形状保真度。

The resulting model is of foundation scale $\left(\approx\bf{0.18~B}\right.$ parameters, 768-dimensional embeddings), indicating a high-capacity architecture suitable for transfer learning. We evaluated Hyper spectral MAE on two large-scale hyper spectral corpora—NASA EO-1 Hyperion (1,600 scenes, about 300 billion pixel spectra) and DLR EnMAP Level-0 (1,300 scenes, about 300 billion pixel spectra)—and fine-tuned it for land-cover classification on the Indian Pines benchmark. Transfer-learning results on Indian Pines demonstrate state-of-the-art performance, confirming that our masked pre-training yields robust spectral–spatial representations. The proposed approach highlights how dual masking and spectral embeddings can advance hyperspectral image reconstruction.

最终得到的模型具有基础规模（约 0.18 B 参数，768 维嵌入），表明其适合迁移学习的高容量架构。我们在两个大规模高光谱数据集——NASA EO-1 Hyperion（1,600 个场景，约 3000 亿像素光谱）和 DLR EnMAP Level-0（1,300 个场景，约 3000 亿像素光谱）上评估了 Hyper spectral MAE，并在 Indian Pines 基准测试上对其进行了土地覆盖分类的微调。Indian Pines 的迁移学习结果展示了最先进的性能，证实了我们的掩码预训练能够产生稳健的光谱-空间表征。所提出的方法凸显了双重掩码和光谱嵌入如何推动高光谱图像重建的进步。

• Dual-Masking Strategy: We simultaneously mask spatial patches and spectral bands, forcing the model to capture cross-dimensional dependencies [4]. • Fourier-Based Spectral Encoding: Spectral wavelength embeddings are introduced via harmonic Fourier components, encouraging the model to learn spectral locality and periodicity [5]. • Spectral–Spatial Reconstruction Loss: A composite loss combining mean-squared error (MSE) and spectral angle mapper (SAM) [6] ensures both numerical accuracy and high-fidelity spectral profiles [7]. Foundation-Scale Model: Our transformer architecture scales to hundreds of millions of parameters, setting a new size benchmark for hyper spectral foundation models.

• 双重掩码策略：同时掩码空间区块和光谱波段，迫使模型捕捉跨维度依赖性 [4]。
• 基于傅里叶的光谱编码：通过谐波傅里叶分量引入光谱波长嵌入，促使模型学习光谱局部性与周期性 [5]。
• 光谱-空间重建损失：结合均方误差 (MSE) 和光谱角制图 (SAM) [6] 的复合损失函数，确保数值精度与高保真光谱特征 [7]。
• 基础规模模型：我们的Transformer架构可扩展至数亿参数，为高光谱基础模型设定了新的规模基准。

A. Masked Auto encoders (MAE)

A. 掩码自编码器 (Masked Autoencoders, MAE)

B. Organization

B. 组织架构

The remainder of the paper is organized as follows. Section II reviews related work on masked auto encoders and hyper spectral representation learning. Section III details the proposed model and training methodology. Section IV describes the experimental setup and datasets. Section V presents empirical results, and Section VI concludes the paper.

本文的剩余部分结构如下。第 II 节回顾了掩码自编码器 (masked auto encoders) 和高光谱表示学习的相关工作。第 III 节详细介绍了所提出的模型和训练方法。第 IV 节描述了实验设置和数据集。第 V 节展示了实证结果，第 VI 节对全文进行了总结。

II. RELATED WORK

II. 相关工作

I. INTRODUCTION

I. 引言

H dYrPedEsR SofP Eco Cn TtiR gAu oL u ism sapgeecst r(aHl SbIas)n dcsa pptuerr e pdioxzele,n se ntoa bhliunng- fine-grained material discrimination in fields such as remote sensing, agriculture, and mineral exploration. However, this wealth of spectral information leads to high dimensionality and large data volume, making representation learning for HSIs challenging [1], [2].

高光谱图像 (HSI) 能够捕获连续光谱信息，在遥感、农业和矿产勘探等领域实现细粒度物质判别。然而，丰富的光谱信息导致高维度和海量数据，使得高光谱图像的表征学习极具挑战性 [1] [2]。

Self-supervised foundation models—especially masked autoencoders (MAE)—have recently shown promise in learning robust representations from unlabeled data in computer vision [3]. In the hyper spectral domain, such models offer the potential to exploit rich spectral–spatial redundancies, yet existing work remains limited to small-scale tasks. Therefore, we propose Hyper spectral MAE, a dedicated masked-modeling framework that scales MAE principles to foundation-model size for hyper spectral imagery.

自监督基础模型——尤其是掩码自编码器 (MAE) ——近期在计算机视觉领域展现了从未标注数据中学习鲁棒表征的潜力 [3]。在高光谱领域，此类模型有望利用丰富的光谱-空间冗余特性，但现有研究仍局限于小规模任务。为此，我们提出高光谱MAE框架，将MAE原理扩展至高光谱图像的基础模型规模。

A. Motivation and Contributions

A. 动机与贡献

Our main contributions are:

我们的主要贡献是:

* Corresponding author. Email: ds.kim@gnewsoft.com

• 通讯作者。邮箱：ds.kim@gnewsoft.com

Masked image modeling has gained popularity after the success of Vision MAE by He et al. [3], which showed that reconstructing masked patches is an effective pretext task for learning image representations. The original MAE applies random masking to input image patches and uses a ViT [8] encoder to encode visible patches and a lightweight decoder to reconstruct the missing patches. This approach has been extended to various domains.

掩码图像建模 (Masked Image Modeling) 在何恺明等人提出的Vision MAE [3] 取得成功后广受欢迎，该研究证明重建掩码图像块是学习图像表征的有效预训练任务。原始MAE对输入图像块进行随机掩码，使用ViT [8] 编码器处理可见图像块，并通过轻量级解码器重建缺失块。该方法已被扩展至多个领域。

In hyper spectral imaging, a straightforward application is to mask spatial patches of the HSI cube and reconstruct them. Zhuang et al. [9] applied an MAE-like augmentation network for target detection in HSI, using a 1-D positional encoding for spectra because 2-D positional encoding was deemed unsuitable for spectral data. Similarly, Lin et al. [10] introduced SS-MAE, a spatial–spectral masked auto encoder with two branches: one masks and reconstructs random spatial patches, while the other masks and reconstructs random spectral bands. Their results confirm that incorporating spectral masking in addition to spatial masking leads to better feature learning. Our dual-masking strategy is inspired by this idea, but we integrate both aspects within a single unified architecture and additionally introduce cross-branch interactions.

在高光谱成像中，一种直接的应用是对HSI立方体的空间块进行掩膜并重建。Zhuang等人[9]采用类似MAE的增强网络进行HSI目标检测，由于二维位置编码被认为不适合光谱数据，因此对光谱使用了一维位置编码。类似地，Lin等人[10]提出了SS-MAE，这是一种具有双分支的空间-光谱掩膜自编码器：一个分支对随机空间块进行掩膜和重建，另一个分支对随机光谱波段进行掩膜和重建。他们的结果证实，在空间掩膜基础上加入光谱掩膜能带来更好的特征学习。我们的双掩膜策略受此启发，但我们在单一统一架构中整合了这两个方面，并额外引入了跨分支交互。

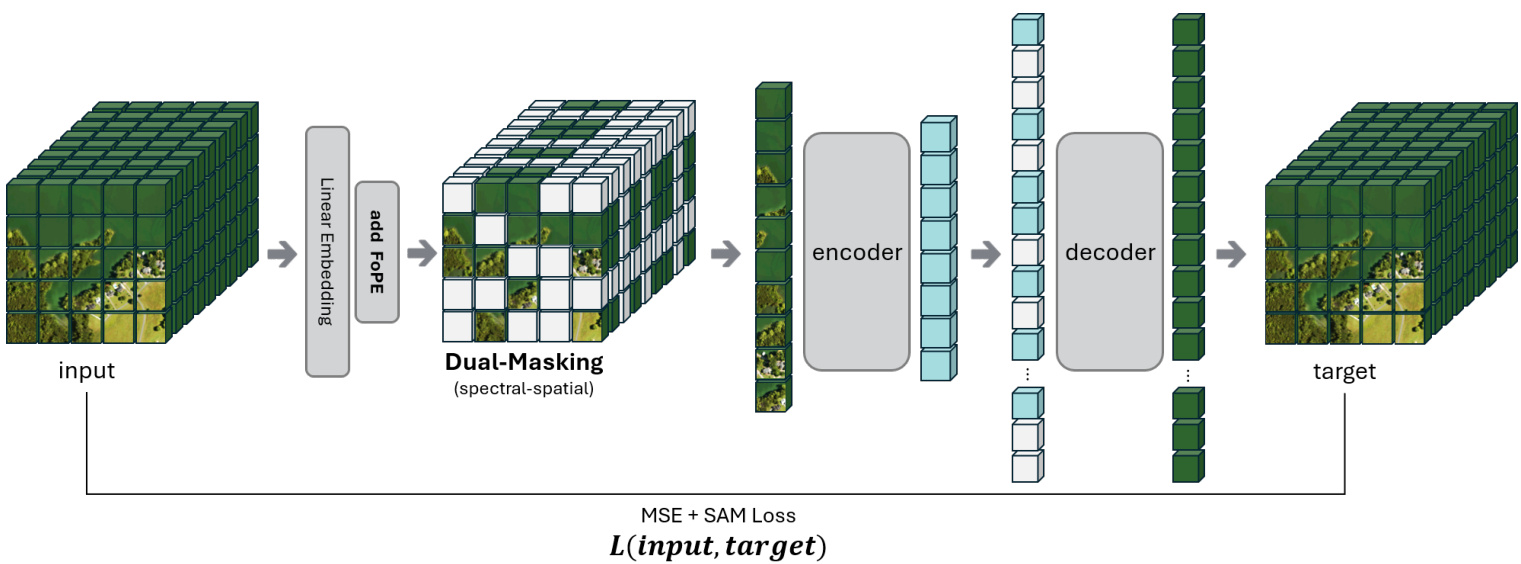
Fig. 1. Hyper spectral MAE overall pipeline.

图 1: 高光谱MAE整体流程。

B. Transformers for HSI

B. 高光谱成像的Transformer

Vision Transformers (ViT) [8] have been applied to hyper spectral images in recent studies. A naïve approach treats each hyper spectral patch (with all bands) as a token sequence and applies ViT for classification. While ViTs can model long-range spatial relationships, early attempts often ignored the explicit spectral structure. For example, some works reduced HSI to RGB (three bands) to apply pretrained ViTs, losing most spectral information. Others processed each pixel’s spectrum with a spectral transformer, treating each pixel’s spectral vector as a sequence of tokens.

视觉Transformer (ViT) [8] 近年来被应用于高光谱图像研究。一种简单的方法是将每个高光谱图像块(包含所有波段)视为一个token序列，并应用ViT进行分类。虽然ViT能够建模长距离空间关系，但早期尝试往往忽略了显式的光谱结构。例如，部分研究将高光谱图像降维至RGB(三个波段)以应用预训练ViT，导致大部分光谱信息丢失。另一些研究则使用光谱Transformer处理每个像素的光谱，将每个像素的光谱向量视为token序列。

Sche i ben re if et al. [11] proposed a Spectral Transformer that attends to bands for each pixel, significantly improving accuracy by leveraging full spectral information. They further introduced a factorized Spatial–Spectral Transformer (SST), which applies self-attention sequentially along spatial and spectral dimensions to handle the large token count in HSI. Factorizing attention in this way proved efficient and boosted performance. Our dual-branch transformer shares a similar motivation of decoupling spectral and spatial attention, but instead of sequential factorization, we employ parallel branches with cross-attention fusion to jointly learn spectral–spatial features.

Sche i ben re if等[11]提出了一种关注每个像素波段的Spectral Transformer (光谱Transformer)，通过利用完整光谱信息显著提高了准确性。他们进一步引入了分解式空间-光谱Transformer (SST)，沿空间和光谱维度顺序应用自注意力机制来处理HSI中的大量Token。这种注意力分解方式被证明是高效的，并提升了性能。我们的双分支Transformer具有类似的光谱与空间注意力解耦动机，但不同于顺序分解，我们采用具有交叉注意力融合的并行分支来联合学习光谱-空间特征。

C. HSI-Specific Networks

C. 高光谱成像专用网络

Recently, various specialized networks have been designed explicitly for hyper spectral image (HSI) classification tasks. Traditionally, methods such as 3-D convolutional neural networks (3-D CNNs) and hybrid spectral-spatial CNNs have been widely adopted due to their ability to directly extract spatial-spectral features from HSI cubes via volumetric convolutions.

近年来，针对高光谱图像(HSI)分类任务已设计出多种专用网络。传统方法如三维卷积神经网络(3-D CNNs)和混合光谱-空间CNN因其能通过立体卷积直接从HSI立方体中提取空间-光谱特征而被广泛采用。

Emerging advancements have focused on incorporating transformer architectures into HSI-specific contexts to leverage self-attention mechanisms for improved representation learning. For example, Zhu et al. [1] developed Spectral MAE, a spectral-focused masked auto encoder explicitly designed for reconstructing spectral bands from partially masked inputs. Spectral MAE employs a specialized positional encoding tailored to spectral data, achieving superior reconstruction quality for various band combinations.

新兴进展主要集中在将Transformer架构融入高光谱成像(HSI)特定场景，利用自注意力机制提升表征学习效果。例如Zhu等学者[1]提出了Spectral MAE，这是一种专为从部分掩码输入重建光谱波段而设计的谱向掩码自编码器。该模型采用针对光谱数据特制的定位编码方案，在不同波段组合下都能实现卓越的重建质量。

Similarly, Wang et al. [4] introduced HSI-MAE, which utilizes separate spatial and spectral encoders with fusion layers. HSI-MAE explicitly learns spatial context and spectral correlation via two encoder branches, somewhat similar to our dual-branch design.

同样地，Wang等人[4]提出的HSI-MAE采用了带有融合层的独立空间与光谱编码器。该模型通过双编码器分支显式学习空间上下文与光谱相关性，这与我们的双分支设计有一定相似性。

Our work, Hyper spectral MAE goes further by introducing learnable Fourier-based positional features and a cross-attention-based embedding mechanism with MSE $^+$ SAM Loss function.

我们的工作 Hyper spectral MAE 更进一步，引入了基于可学习傅里叶的位置特征和采用 MSE $^+$ SAM 损失函数的跨注意力嵌入机制。

In summary, whereas previous works have addressed spectral–spatial feature learning in parts (e.g., 1-D positional embeddings or dual-branch encoders), our work combines and extends these ideas in a unified framework with foundation model scale. We next describe the components of HyperspectralMAE in detail.

总之，以往的研究仅部分解决了光谱-空间特征学习问题（例如一维位置嵌入或双分支编码器），而我们的工作将这些思想结合并扩展到一个具有基础模型规模的统一框架中。接下来我们将详细阐述HyperspectralMAE的各个组件。

III. METHODOLOGY

III. 方法论

We begin by outlining the encoder–decoder Transformer architecture of Hyper spectral MAE, which employs specialized embedding modules and dual masking operations. The encoder receives a partially masked hyper spectral image and produces latent representations, while the decoder reconstructs the full HSI from these latents. During pre-training, a fraction of the input is masked both spatially and spectrally, forcing the encoder to infer missing information from the unmasked context along both dimensions. To this end, several key modules are introduced and detailed below.

我们首先概述Hyper spectral MAE的编码器-解码器Transformer架构，该架构采用专用嵌入模块和双重掩码操作。编码器接收部分掩码的高光谱图像并生成潜在表征，而解码器则从这些潜在表征中重建完整HSI。在预训练期间，输入数据会在空间和光谱维度上进行部分掩码，迫使编码器从两个维度的未掩码上下文中推断缺失信息。为此，我们引入并详细说明以下关键模块：

A. Overview of Hyper spectral MAE Architecture

A. 高光谱 MAE 架构概述

Figure 1 shows Hyper spectral MAE’s overall pipeline. Let some of X RH×W ×B,

图 1: 展示了高光谱MAE的整体流程。设X RH×W ×B的部分数据，

$$
\mathbf{X}={x_{i,j,b}\in\mathbb{R}\mid i=1,\ldots,H;j=1,\ldots,W;b=1,\ldots,B}
$$

$$
\mathbf{X}={x_{i,j,b}\in\mathbb{R}\mid i=1,\ldots,H;j=1,\ldots,W;b=1,\ldots,B}
$$

be an input hyper spectral image with spatial height $H$ , width $W$ , and $B$ spectral bands. We partition X into non-overlapping spatial-spectral patches: each spatial patch covers a $9\times9$ pixel window and each spectral patch spans a block of 8 consecutive bands. Formally, for spatial indices $p=1,\ldots,\lfloor H/9\rfloor$ and $q=$ $1,\dots,\lfloor W/9\rfloor$ , and spectral-group index $k=1,\ldots,\lfloor B/8\rfloor$ , a patch is defined as

设输入高光谱图像的空间高度为 $H$，宽度为 $W$，具有 $B$ 个光谱波段。我们将 X 划分为不重叠的空谱联合块：每个空间块覆盖 $9\times9$ 像素窗口，每个光谱块跨越连续的8个波段。形式上，对于空间索引 $p=1,\ldots,\lfloor H/9\rfloor$ 和 $q=1,\dots,\lfloor W/9\rfloor$，以及光谱组索引 $k=1,\ldots,\lfloor B/8\rfloor$，每个块定义为

as HSI-MAE [4] did. This yields tokens that represent local spatial–spectral regions. Each token is augmented with learned positional encodings—2-D spatial encodings (as in ViT) and our proposed spectral wavelength encodings for the band-group index. The encoder, a ViT-like Transformer, operates on visible unmasked tokens to produce latent features; a lightweight decoder then combines these latents with learned mask tokens to reconstruct the original hyper spectral image.

如HSI-MAE [4]所做的那样。这会生成代表局部空间-光谱区域的token。每个token都通过学习的定位编码进行增强——包括二维空间编码（与ViT相同）和我们提出的针对波段组索引的光谱波长编码。编码器采用类似ViT的Transformer架构，对可见的未遮蔽token进行处理以生成潜在特征；随后一个轻量级解码器将这些潜在特征与学习的遮蔽token相结合，重建原始高光谱图像。

B. Dual Spatial–Spectral Masking

B. 双重空间-光谱掩蔽

Inspired by HSI-MAE [4], For spatial masking, we randomly sample $50%$ of spatial grid coordinates $(p,q)$ and mask all tokens whose spatial index equals any of the selected $(p,q)$ pairs-i.e., every spectral-group slice at those positions is hidden. and for spectral masking from the remaining tokens after spatial masking, we randomly sample $50%$ of spectralgroup indices $k$ (equivalently, band groups $b$ ) and mask every token whose spectral index belongs to this set, regardless of its spatial location.

受HSI-MAE [4]启发，在空间掩码方面，我们随机采样50%的空间网格坐标$(p,q)$，并掩码所有空间索引等于任一选定$(p,q)$对的token（即这些位置上的每个光谱组切片都被隐藏）。对于光谱掩码，在空间掩码后的剩余token中，我们随机采样50%的光谱组索引$k$（等效于波段组$b$），并掩码所有光谱索引属于该集合的token，无论其空间位置如何。

C. Spectral Wavelength Positional Encoding

C. 光谱波长位置编码

In Hyper spectral MAE, we introduce a spectral wavelength positional embedding to capture global spectral dependencies. For each spectral patch $k$ (eight consecutive bands) we first compute its representative wavelength as the arithmetic mean of the centre-wavelengths of those bands:

在高光谱MAE中，我们引入了光谱波长位置嵌入（spectral wavelength positional embedding）来捕获全局光谱依赖性。对于每个光谱块$k$（八个连续波段），我们首先计算其代表波长作为这些波段中心波长的算术平均值：

$$
\lambda_{k}=\frac{1}{8}\sum_{m=1}^{8}\lambda_{b_{k}^{(m)}},
$$

$$
\lambda_{k}=\frac{1}{8}\sum_{m=1}^{8}\lambda_{b_{k}^{(m)}},
$$

Can be corresponding angulaer frequency is

对应角频率为

$$
\omega_{k}={\frac{2\pi}{\lambda_{k}}}.
$$

$$
\omega_{k}={\frac{2\pi}{\lambda_{k}}}.
$$

Where original [12] positional encoding(PE) is

原始[12]位置编码(PE)是

$$
\begin{array}{r l r}&{}&{\mathrm{PE}(\mathrm{pos},2i)=\mathrm{sin}\left(\frac{\mathrm{pos}}{10000^{2i/d_{\mathrm{model}}}}\right),}\ &{}&{\mathrm{PE}(\mathrm{pos},2i+1)=\mathrm{cos}\left(\frac{\mathrm{pos}}{10000^{2i/d_{\mathrm{model}}}}\right),}\end{array}
$$

$$
\begin{array}{r l r}&{}&{\mathrm{PE}(\mathrm{pos},2i)=\mathrm{sin}\left(\frac{\mathrm{pos}}{10000^{2i/d_{\mathrm{model}}}}\right),}\ &{}&{\mathrm{PE}(\mathrm{pos},2i+1)=\mathrm{cos}\left(\frac{\mathrm{pos}}{10000^{2i/d_{\mathrm{model}}}}\right),}\end{array}
$$

where $i$ indexes the dimension and $d_{m o d e l}$ is the embedding dimention. We can analogously define a multi-frequency spectral encoding that injects the wavelength $\lambda_{k}$ at multiple scales. Let $d_{s p e c}$ be our desired embedding dimension. For $i=0,1,\ldots,\frac{d_{\mathrm{spec}}}{2}-1$ , we define:

其中 $i$ 表示维度索引，$d_{model}$ 为嵌入维度。我们可以类似地定义一个多频光谱编码，将波长 $\lambda_{k}$ 以多尺度形式注入。设 $d_{spec}$ 为目标嵌入维度，对于 $i=0,1,\ldots,\frac{d_{\mathrm{spec}}}{2}-1$，定义如下：

$$
\begin{array}{r l r}&{}&{\mathrm{SpecEnc}\left(\lambda_{k},2i\right)=\mathrm{sin}\left(\frac{\omega_{k}}{10000^{\frac{2i}{d_{\mathrm{spec}}}}}\right),}\ &{}&{\mathrm{SpecEnc}\left(\lambda_{k},2i+1\right)=\mathrm{cos}\left(\frac{\omega_{k}}{10000^{\frac{2i}{d_{\mathrm{pec}}}}}\right),}\end{array}
$$

$$
\begin{array}{r l r}&{}&{\mathrm{SpecEnc}\left(\lambda_{k},2i\right)=\mathrm{sin}\left(\frac{\omega_{k}}{10000^{\frac{2i}{d_{\mathrm{spec}}}}}\right),}\ &{}&{\mathrm{SpecEnc}\left(\lambda_{k},2i+1\right)=\mathrm{cos}\left(\frac{\omega_{k}}{10000^{\frac{2i}{d_{\mathrm{pec}}}}}\right),}\end{array}
$$

Hence, the spectral embedding vector for band $\mathbf{b}$ is

因此，波段 $\mathbf{b}$ 的光谱嵌入向量为

$$
\begin{array}{r}{\mathbf{v}{\mathrm{spec}}(\lambda_{k})=\left[\sin\left(\frac{\omega_{k}}{10000^{0}}\right),\cos\left(\frac{\omega_{k}}{10000^{0}}\right),\right.\qquad}\ {\left.\sin\left(\frac{\omega_{k}}{10000^{2/d_{\mathrm{spec}}}}\right),\cos\left(\frac{\omega_{k}}{10000^{2/d_{\mathrm{spec}}}}\right),\dots\right].}\end{array}
$$

$$
\begin{array}{r}{\mathbf{v}{\mathrm{spec}}(\lambda_{k})=\left[\sin\left(\frac{\omega_{k}}{10000^{0}}\right),\cos\left(\frac{\omega_{k}}{10000^{0}}\right),\right.\qquad}\ {\left.\sin\left(\frac{\omega_{k}}{10000^{2/d_{\mathrm{spec}}}}\right),\cos\left(\frac{\omega_{k}}{10000^{2/d_{\mathrm{spec}}}}\right),\dots\right].}\end{array}
$$

cycling over all $i$ .

遍历所有 $i$。

$D$ . Training Objective: MSE with SAM

$D$。训练目标：带SAM的均方误差 (MSE)

Let some of Y RH×W ×B,

令部分 Y RH×W ×B,

$$
\mathbf{Y}={y_{i,j,b}\in\mathbb{R}\mid1\leq i\leq H,1\leq j\leq W,1\leq b\leq B}
$$

$$
\mathbf{Y}={y_{i,j,b}\in\mathbb{R}\mid1\leq i\leq H,1\leq j\leq W,1\leq b\leq B}
$$

denote the ground-truth hyper spectral data cube, where $H$ and $W$ are the spatial dimensions and $B$ is the number of spectral bands.

表示真实的高光谱数据立方体，其中$H$和$W$为空间维度，$B$为光谱波段数。

The network produces a reconstruction

网络生成重建结果

$$
\hat{\mathbf{Y}}={\hat{y}_{i,j,b}}\in\mathbb{R}^{H\times W\times B