Deep Outdoor Illumination Estimation

深度户外光照估计

Abstract

摘要

We present a CNN-based technique to estimate highdynamic range outdoor illumination from a single low dynamic range image. To train the CNN, we leverage a large dataset of outdoor panoramas. We fit a low-dimensional physically-based outdoor illumination model to the skies in these panoramas giving us a compact set of parameters (including sun position, atmospheric conditions, and camera parameters). We extract limited field-of-view images from the panoramas, and train a CNN with this large set of input image–output lighting parameter pairs. Given a test image, this network can be used to infer illumination parameters that can, in turn, be used to reconstruct an outdoor illumination environment map. We demonstrate that our approach allows the recovery of plausible illumination conditions and enables photo realistic virtual object insertion from a single image. An extensive evaluation on both the panorama dataset and captured HDR environment maps shows that our technique significantly outperforms previous solutions to this problem.

我们提出了一种基于CNN（卷积神经网络）的技术，用于从单张低动态范围图像中估算高动态范围的户外光照。为了训练CNN，我们利用了一个大型户外全景图数据集。通过将低维物理基础的户外光照模型拟合到这些全景图的天空部分，我们得到了一组紧凑的参数（包括太阳位置、大气条件和相机参数）。我们从全景图中提取有限视场的图像，并利用大量输入图像-输出光照参数对来训练CNN。给定测试图像时，该网络可用于推断光照参数，进而重建户外光照环境贴图。我们证明，该方法能够恢复合理的光照条件，并实现从单张图像中进行照片级真实感的虚拟物体插入。对全景图数据集和捕获的HDR环境贴图进行的广泛评估表明，我们的技术显著优于该问题的先前解决方案。

1. Introduction

1. 引言

Illumination plays a critical role in deciding the appearance of a scene, and recovering scene illumination is important for a number of tasks ranging from scene understanding to reconstruction and editing. However, the process of image formation conflates illumination with scene geometry and material properties in complex ways and inverting this process is an extremely ill-posed problem. This is especially true in outdoor scenes, where we have little to no control over the capture process.

光照在决定场景外观方面起着关键作用，恢复场景光照对于从场景理解到重建和编辑的众多任务都至关重要。然而，图像形成过程以复杂的方式将光照与场景几何和材质属性混为一谈，逆转这一过程是一个极度不适定问题。这在户外场景中尤为明显，因为我们对拍摄过程几乎无法控制。

Previous approaches to this problem have relied on extracting cues such as shadows and shading [26] and combining them with (reasonably good) estimates of scene geometry to recover illumination. However, both these tasks are challenging and existing attempts often result in poor performance on real-world images. Alternatively, techniques for intrinsic images can estimate low-frequency illumination but rely on hand-tuned priors on geometry and ma- terial properties [3, 29] that may not generalize to largescale scenes. In this work, we seek a single image outdoor illumination inference technique that generalizes to a wide range of scenes and does not make strong assumptions about scene properties.

先前解决这一问题的方法依赖于提取阴影和明暗等线索 [26]，并将其与场景几何的（相对较好的）估计相结合来恢复光照。然而，这两项任务都具有挑战性，现有尝试在真实世界图像上往往表现不佳。此外，本征图像技术虽能估计低频光照，但依赖于对几何和材质属性的手动调整先验 [3, 29]，这些先验可能无法泛化到大规模场景。本文中，我们探索一种适用于广泛场景的单张图像户外光照推断技术，且不对场景属性做强假设。

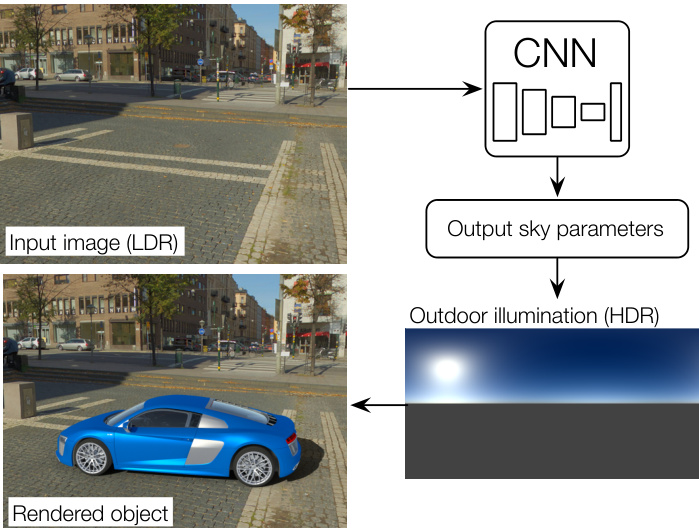
Figure 1. We present an approach for predicting full HDR lighting conditions from a single LDR outdoor image. Our prediction can readily be used to insert a virtual object into the image. Our key idea is to train a CNN using input-output pairs of LDR images and HDR illumination parameters that are automatically extracted from a large database of $360^{\circ}$ panoramas.

图 1: 我们提出了一种从单张低动态范围 (LDR) 户外图像预测完整高动态范围 (HDR) 光照条件的方法。我们的预测结果可直接用于将虚拟物体插入图像。核心思路是通过从大型 $360^{\circ}$ 全景图数据库自动提取的 LDR-HDR 光照参数对来训练卷积神经网络 (CNN)。

To this end, our goal is to train a CNN to directly regress a single input low dynamic range image to its corresponding high dynamic range (HDR) outdoor lighting conditions. Given the success of deep networks at related tasks like intrinsic images [42] and reflectance map estimation [34], our hope is that an appropriately designed CNN can learn this relationship. However, training such a CNN requires a very large dataset of outdoor images with their corresponding HDR lighting conditions. Unfortunately, such a dataset currently does not exist, and, because capturing light probes requires significant time and effort, acquiring it is prohibitive.

为此，我们的目标是训练一个CNN（卷积神经网络），将单个输入的低动态范围 (LDR) 图像直接回归到对应的高动态范围 (HDR) 户外光照条件。鉴于深度网络在本征图像 [42] 和反射率图估计 [34] 等相关任务中的成功表现，我们希望一个设计得当的CNN能够学习这种关系。然而，训练这样的CNN需要一个包含大量户外图像及其对应HDR光照条件的庞大数据集。遗憾的是，目前这样的数据集并不存在，而且由于采集光照探针需要大量时间和精力，获取这样的数据集几乎不可行。

Our insight is to exploit a large dataset of outdoor panoramas [40], and extract photos with limited field of view from them. We can thus use pairs of photos and panoramas to train the neural network. However, this approach is bound to fail since: 1) the panoramas have low dynamic range and therefore do not provide an accurate estimate of outdoor lighting; and 2) even if notable attempts have been made [41], recovering full spherical panoramas from a single photo is both improbable and unnecessary for a number of tasks (e.g., many of the high-frequency details in the panoramas are not required when rendering Lambertian objects into the scene).

我们的思路是利用户外全景图的大规模数据集[40]，从中提取有限视野的照片。这样就能用照片和全景图配对来训练神经网络。但这种方法注定会失败，因为：1) 全景图动态范围低，无法准确估计户外光照；2) 尽管已有显著尝试[41]，但从单张照片恢复完整球面全景既不可能，也对许多任务没有必要（例如，在场景中渲染朗伯物体时，通常不需要全景图中的高频细节）。

Instead, we use a physically-based sky model—the Hošek-Wilkie model [16, 17]—and fit its parameters to the visible sky regions in the input panorama. This has two advantages: first, it allows us to recover physically accurate, high dynamic range information from the panoramas (even in saturated regions). Second, it compresses the panorama to a compact set of physically meaningful and representative parameters that can be efficiently learned by a CNN. At test time, we recover these parameters—including sun position, atmospheric turbidity, and geometric and radiometric camera calibration—from an input image and use them to construct an HDR sky environment map.

相反，我们采用基于物理的天空模型——Hošek-Wilkie模型[16, 17]——并将其参数拟合到输入全景图的可见天空区域。这种方法具有双重优势：首先，它能从全景图中还原物理精确的高动态范围信息（即使在过曝区域）；其次，它将全景图压缩为一组紧凑且具有物理意义的代表性参数，这些参数可被CNN高效学习。在测试阶段，我们从输入图像中恢复这些参数（包括太阳位置、大气浑浊度、几何与辐射相机校准），并利用它们构建HDR天空环境贴图。

To our knowledge, we are the first to address the complete scope of estimating a full HDR lighting representation—which can readily be used for image-based lighting [7]—from a single outdoor image (fig. 1). Previous techniques have typically addressed only aspects of this problem, e.g., Lalonde et al. [26] recover the position of the sun but need to observe sky pixels in order to recover the atmospheric conditions. Similarly, [30] uses a neural network to estimate the sun azimuth to perform localization in roadside environments. Karsch et al. [19] estimate full environment map lighting, but their panorama transfer technique may yield illumination conditions arbitrarily far away from the real ones. In contrast, our technique can recover an accurate, full HDR sky environment map from an arbitrary input image. We show through extensive evaluation that our estimates of the lighting conditions are significantly better than previous techniques and that they can be used “as is” to photo realistically relight and render 3D models into images.

据我们所知，我们是首个通过单张户外图像（图1）完整估算HDR光照表示（可直接用于基于图像的照明[7]）的研究。先前技术通常仅解决该问题的部分环节，例如Lalonde等人[26]能恢复太阳位置，但需观测天空像素来推算大气条件；类似地，[30]通过神经网络估算太阳方位角以进行路边环境定位。Karsch等人[19]虽能估算完整环境贴图光照，但其全景迁移技术可能导致光照条件与实际情况存在显著偏差。相比之下，我们的技术能从任意输入图像中还原精确的完整HDR天空环境贴图。大量评估表明，我们对光照条件的估算显著优于现有技术，且能直接用于照片级真实感的3D模型重光照与图像合成。

2. Related work

2. 相关工作

Outdoor illumination models Perez et al. [31] proposed an all-weather sky luminance distribution model. This model was a generalization of the CIE standard sky model and is parameterized by five coefficients that can be varied to generate a wide range of skies. Preetham [32] proposed a simplified version of the Perez model that explains the five coefficients using a single unified atmospheric turbidity parameter. Lalonde and Matthews [27] combined the Preetham sky model with a novel empirical sun model.

户外光照模型
Perez等人[31]提出了一个全天气天空亮度分布模型。该模型是CIE标准天空模型的泛化版本，通过五个可调节系数参数化，能生成多种天空状态。Preetham[32]提出了Perez模型的简化版本，使用统一的大气浑浊度参数来解释这五个系数。Lalonde和Matthews[27]将Preetham天空模型与一个新颖的经验太阳模型相结合。

Hošek and Wilkie proposed a sky luminance model [16] and solar radiance function [17].

Hošek 和 Wilkie 提出了天空亮度模型 [16] 和太阳辐射函数 [17]。

Outdoor lighting estimation Lalonde et al. [26] combine multiple cues, including shadows, shading of vertical surfaces, and sky appearance to predict the direction and visibility of the sun. This is combined with an estimation of sky illumination (represented by the Perez model [31]) from sky pixels [28]. Similar to this work, we use a physically-based model for outdoor illumination. However, instead of designing hand-crafted features to estimate illumination, we train a CNN to directly learn the highly complex mapping between image pixels and illumination parameters.

户外光照估计 Lalonde等人 [26] 结合了多种线索（包括阴影、垂直表面的明暗变化和天空外观）来预测太阳的方向和可见度。该方法与通过天空像素估算天空光照（采用Perez模型 [31] 表示）的技术 [28] 相结合。与这项工作类似，我们采用基于物理模型的户外光照模拟。但不同于手工设计特征来估算光照，我们训练了一个CNN（卷积神经网络）直接学习图像像素与光照参数之间高度复杂的映射关系。

Other techniques for single image illumination estimation rely on known geometry and/or strong priors on scene reflectance, geometry and illumination [3, 4, 29]. These priors typically do not generalize to large-scale outdoor scenes. Karsch et al. [19] retrieve panoramas (from the SUN360 panorama dataset [40]) with features similar to the input image, and refine the retrieved panoramas to compute the illumination. However, the matching metric is based on image content which may not be directly linked with illumination.

单幅图像光照估计的其他技术依赖于已知的几何结构和/或场景反射率、几何结构及光照的强先验 [3, 4, 29]。这些先验通常无法泛化到大规模户外场景。Karsch等人 [19] 从SUN360全景数据集 [40] 中检索与输入图像特征相似的全景图，并通过优化检索到的全景图来计算光照。然而，其匹配度量基于图像内容，可能与光照无直接关联。

Another class of techniques simplify the problem by estimating illumination from image collections. Multi-view image collections have been used to reconstruct geometry, which is used to recover outdoor illumination [14, 27, 35, 8], sun direction [39], or place and time of capture [15]. Appearance changes have also been used to recover colorimetric variations of outdoor sun-sky illumination [37].

另一类技术通过从图像集合中估计光照来简化问题。多视角图像集合已被用于重建几何结构，进而恢复室外光照 [14, 27, 35, 8]、太阳方向 [39] 或拍摄地点和时间 [15]。外观变化也被用于恢复室外日光-天空光照的色度变化 [37]。

Inverse graphics/vision problems in deep learning Following the remarkable success of deep learning-based methods on high-level recognition problems, these approaches are now being increasingly used to solve inverse graphics problems [24]. In the context of understanding scene appearance, previous work has leveraged deep learning to estimate depth and surface normals [9, 2], recog- nize materials [5], decompose intrinsic images [42], recover reflectance maps [34], and estimate, in a setup similar to physics-based techniques [29], lighting from objects of specular materials [11]. We believe ours is the first attempt at using deep learning for full HDR outdoor lighting estimation from a single image.

深度学习中的逆向图形/视觉问题
随着基于深度学习的方法在高级识别问题上取得显著成功，这些方法现在正越来越多地用于解决逆向图形问题 [24]。在理解场景外观的背景下，先前的研究利用深度学习来估计深度和表面法线 [9, 2]、识别材质 [5]、分解本征图像 [42]、恢复反射率图 [34]，并在类似于基于物理技术的设置 [29] 中，从镜面材质物体估计光照 [11]。我们相信，这是首次尝试使用深度学习从单张图像中完整估计高动态范围 (HDR) 户外光照。

3. Overview

3. 概述

We aim to train a CNN to predict illumination conditions from a single outdoor image. We use full spherical, $360^{\circ}$ panoramas, as they capture scene appearance while also providing a direct view of the sun and sky, which are the most important sources of light outdoors. Unfortunately, there exists no database containing true high dynamic range outdoor panoramas, and we must resort to using the saturated, low dynamic range panoramas in the

我们致力于训练一个CNN（卷积神经网络）从单张户外图像预测光照条件。我们采用完整的球形$360^{\circ}$全景图，因为它们能捕捉场景外观，同时直接呈现太阳和天空——这是户外最重要的光源。然而，目前尚无包含真实高动态范围（HDR）户外全景图的数据库，我们只能使用现有饱和的低动态范围全景图。

Figure 2. Impact of sky turbidity $t$ on rendered objects. The top row shows environment maps (in latitude-longitude format), and the bottom row shows corresponding renders of a bunny model on a ground plane for varying values for the turbidity $t$ , ranging from low (left) to high (right). Images have been tonemapped with $\gamma=2.2$ for display.

图 2: 天空浑浊度 $t$ 对渲染物体的影响。顶行展示环境贴图(采用经纬度格式)，底行展示对应不同浑浊度 $t$ 值的平面兔子模型渲染效果，浑浊度从左至右依次递增。所有图像均经过 $\gamma=2.2$ 色调映射处理以便显示。

SUN360 dataset [40]. To overcome this limitation, and to provide a small set of meaningful parameters to learn to the CNN, we first fit a physically-based sky model to the panoramas (sec. 4). Then, we design and train a CNN that given an input image sampled from the panorama, outputs the fit illumination parameters (sec. 5), and thoroughly evaluate its performance in sec. 6.

SUN360数据集 [40]。为了克服这一限制，并为CNN提供一组可学习的有意义参数，我们首先将基于物理的天空模型拟合到全景图中（第4节）。接着，我们设计并训练了一个CNN，该网络在输入从全景图中采样的图像后，能输出拟合的照明参数（第5节），并在第6节全面评估其性能。

Throughout this paper, and following [40], will use the term photo to refer to a standard limited-field-of-view image as taken with a normal camera, and the term panorama to denote a 360-degree full-view panoramic image.

本文遵循[40]的术语规范，将使用"照片(photo)"指代普通相机拍摄的标准有限视野图像，用"全景图(panorama)"表示360度全视角全景图像。

4. Dataset preparation

4. 数据集准备

In this section, we detail the steps taken to augment the SUN360 dataset [40] with HDR data via the use of the Hošek-Wilkie sky model, and simultaneously extract lighting parameters that can be learned by the network. We first briefly describe the sky model parameter iz ation, followed by the optimization strategy used to recover its parameters from a LDR panorama.

在本节中，我们详细介绍了通过使用Hošek-Wilkie天空模型为SUN360数据集[40]增强HDR数据，并同时提取可由网络学习的照明参数的步骤。首先简要描述天空模型的参数化，然后介绍用于从LDR全景图中恢复其参数的优化策略。

4.1. Sky lighting model

4.1. 天空光照模型

We employ the model proposed by Hošek and Wilkie [16], which has been shown [21] to more accurately represent skylight than the popular Preetham model [32]. The model has also been extended to include a solar radiance function [17], which we also exploit.

我们采用Hošek和Wilkie [16]提出的模型，该模型已被证明[21]能比流行的Preetham模型[32]更准确地表现天光。该模型还扩展了包含太阳辐射函数[17]，我们也利用了这一点。

In its simplest form, the Hošek-Wilkie (HW) model expresses the spectral radiance $L_{\lambda}$ of a lighting direction along the sky hemisphere ${\mathbf l}\in\Omega_{\mathrm{sky}}$ as a function of several parameters:

Hošek-Wilkie (HW) 模型的最简形式将沿天空半球 ${\mathbf l}\in\Omega_{\mathrm{sky}}$ 方向的光谱辐射亮度 $L_{\lambda}$ 表达为多个参数的函数:

$$
L_{\lambda}(1)=f_{\mathrm{HW}}(1,\lambda,t,\sigma_{g},1_{s}),
$$

$$
L_{\lambda}(1)=f_{\mathrm{HW}}(1,\lambda,t,\sigma_{g},1_{s}),
$$

where $\lambda$ is the wavelength, $t$ the atmospheric turbidity (a measure of the amount of aerosols in the air), $\sigma_{g}$ the ground albedo, and ${\bf l}{s}$ the sun position. Here, we fix $\sigma{g}~=~0.3$ (approximate average albedo of the Earth [12]).

其中 $\lambda$ 为波长，$t$ 为大气浑浊度(衡量空气中气溶胶含量的指标)，$\sigma_{g}$ 为地面反照率，${\bf l}{s}$ 为太阳位置。此处我们固定 $\sigma{g}~=~0.3$(地球近似平均反照率 [12])。

From this spectral model, we obtain RGB values by rendering it at a discrete set wavelengths spanning the $360-$ $700\mathrm{nm}$ spectrum, convert to CIE XYZ via the CIE standard observer color matching functions, and finally convert again from XYZ to CIE RGB [16]. Referring to this conversion process as $f_{\mathrm{RGB}}(\cdot)$ , we express the RGB color $C_{\mathrm{RGB}}(1)$ of a sky direction l as the following expression:

根据该光谱模型，我们通过在$360-$ $700\mathrm{nm}$光谱范围内离散波长点进行渲染获得RGB值，通过CIE标准观察者配色函数转换为CIE XYZ，最终再次从XYZ转换为CIE RGB [16]。将该转换过程记为$f_{\mathrm{RGB}}(\cdot)$，天空方向l的RGB颜色$C_{\mathrm{RGB}}(1)$可表示为以下表达式：

$$
C_{\mathrm{RGB}}(1)=\omega f_{\mathrm{RGB}}(1,t,1_{s}).
$$

$$
C_{\mathrm{RGB}}(1)=\omega f_{\mathrm{RGB}}(1,t,1_{s}).
$$

In this equation, $\omega$ is a scale factor applied to all three color channels, which aims at estimating the (arbitrary and varying) exposure for each panorama. To generate a sky environment map from this model, we simply discretize the sky hemisphere $\Omega_{\mathrm{sky}}$ into several directions (in this paper, we use the latitude-longitude format [33]), and render the RGB values with (2). Pixels which fall within $0.25^{\circ}$ of the sun position ${\bf l}_{s}$ are rendered with the HW sun model [17] instead (converted to RGB as explained above).

在此方程中，$\omega$ 是应用于所有三个颜色通道的比例因子，旨在估计每个全景图的（任意且变化的）曝光。为了从该模型生成天空环境贴图，我们简单地将天空半球 $\Omega_{\mathrm{sky}}$ 离散化为若干方向（本文采用经纬度格式 [33]），并用 (2) 式渲染 RGB 值。对于落在太阳位置 ${\bf l}_{s}$ 周围 $0.25^{\circ}$ 范围内的像素，则改用 HW 太阳模型 [17] 进行渲染（并按上述方法转换为 RGB）。

Thus, we are left with three important parameters: the sun position ${\bf l}_{s}$ , which indicate where the main directional light source is located in the sky, the exposure $\omega$ , and the turbidity $t$ . The turbidity is of paramount importance as it controls the relative sun color (and intensity) with respect to that of the sky. As illustrated in fig. 2, a low turbidity indicates a clear sky with a very bright sun, and a high turbidity represents a sky closer that is closer to overcast situations, where the sun is much dimmer.

因此，我们剩下三个重要参数：太阳位置 ${\bf l}_{s}$ （指示主要定向光源在天空中的位置）、曝光量 $\omega$ 以及浊度 $t$ 。浊度最为关键，因为它控制着太阳颜色（及强度）与天空颜色的相对关系。如图 2 所示，低浊度代表晴朗天空下太阳非常明亮，而高浊度则意味着天空更接近阴天状态，此时太阳明显更暗。

4.2. Optimization procedure

4.2. 优化流程

We now describe how the sky model parameters are estimated from a panorama in the SUN360 dataset. This procedure is carefully crafted to be robust to the extremely varied set of conditions encountered in the dataset which severely violates the linear relationship between sky radiance and pixel values such as: unknown camera response function and white-balance, manual post-processing by photographers and stitching artifacts.

我们现在描述如何从SUN360数据集的 panoramas (全景图) 中估算天空模型参数。这一流程经过精心设计，能够稳健应对数据集中各种极端条件——这些条件严重破坏了天空辐射与像素值之间的线性关系，例如：未知的相机响应函数和白平衡、摄影师手动后期处理以及拼接伪影。

Given a panorama $P$ in latitude-longitude format and a set of pixels indices $p\in S$ corresponding to sky pixels in $P$ , we wish to obtain the sun position ${\bf l}_{s}$ , exposure $\omega$ and sky turbidity $t$ by minimizing the visible sky reconstruction error in a least-squares sense:

给定一张经纬度格式的全景图 $P$ 及其对应的天空像素索引集合 $p\in S$，我们希望通过最小二乘法最小化可见天空重建误差，从而获取太阳位置 ${\bf l}_{s}$、曝光度 $\omega$ 和天空浊度 $t$：

$$
\begin{array}{r l}&{\mathbf{l}{s}^{},\omega^{},t^{}=\underset{\mathbf{l}{s},\omega,t}{\arg\operatorname*{min}}\displaystyle\sum_{p\in\Omega_{s}}\left(P(p)^{\gamma}-\omega f_{\mathrm{RGB}}(\mathbf{l}{p},t,\mathbf{l}_{s})\right)^{2}}\ &{\qquad\mathrm{s.t.}\quad t\in[1,10],}\end{array}
$$

$$
\begin{array}{r l}&{\mathbf{l}{s}^{},\omega^{},t^{}=\underset{\mathbf{l}{s},\omega,t}{\arg\operatorname*{min}}\displaystyle\sum_{p\in\Omega_{s}}\left(P(p)^{\gamma}-\omega f_{\mathrm{RGB}}(\mathbf{l}{p},t,\mathbf{l}_{s})\right)^{2}}\ &{\qquad\mathrm{s.t.}\quad t\in[1,10],}\end{array}
$$

where $f_{\mathrm{RGB}}(\cdot)$ is defined in (2) and ${\bf l}{p}$ is the light direction corresponding to pixel $p\in\Omega_{s}$ (according to the latitudelongitude mapping). Here, we model the inverse response function of the camera with a simple gamma curve $(\gamma:=$ 2.2). Optimizing for gamma was found to be unstable and keeping it fixed yielded much more robust results.

其中 $f_{\mathrm{RGB}}(\cdot)$ 在公式 (2) 中定义，${\bf l}{p}$ 表示像素 $p\in\Omega_{s}$ 对应的光照方向 (根据经纬度映射确定)。此处我们采用简单的伽马曲线 $(\gamma:=2.2)$ 来模拟相机的逆响应函数。实验发现优化伽马值会导致不稳定，而将其固定能获得更稳健的结果。

Figure 3. The proposed CNN architecture. After a series of 7 convolutional layers, a fully-connected layer segues to two heads: one for regressing the sun position, and another one for the sky and camera parameters. The ELU activation function [6] is used on all layers except the outputs.

图 3: 提出的CNN架构。经过7个卷积层后，全连接层分流为两个头部：一个用于回归太阳位置，另一个用于天空和相机参数。除输出层外，所有层均使用ELU激活函数 [6]。

层	步长	分辨率
输入		320×240
conv7-64	2	160×120
conv5-128	2	80×60
conv3-256	2	40×30
conv3-256	1	40×30
conv3-256	2	20×15
conv3-256	1	20×15
conv3-256	2	10×8
FC-2048
FC-160		FC-5
LogSoftMax		Linear
输出: 太阳位置分布s		输出: 天空和相机参数q

We solve (3) in a 2-step procedure. First, the sun position ${\bf l}_{s}$ is estimated by finding the largest connected component of the sky above a threshold (98th percentile), and by computing its centroid. The sun position is fixed at this value, as it was determined that optimizing for its position at the next stage too often made the algorithm converge to undesirable local minima.

我们采用两步法求解(3)。首先，通过寻找高于阈值(第98百分位数)的天空最大连通区域并计算其质心，估算太阳位置${\bf l}_{s}$。该太阳位置在此阶段固定，因为经验证实在后续阶段优化其位置常导致算法收敛至不理想的局部极小值。

Second, the turbidity $t$ is initialized to ${1,2,3,...,10}$ and (3) is optimized using the Trust Region Reflective algorithm (a variant of the Levenberg-Marquardt algorithm which supports bounds) for each of these starting points. The parameters resulting in the lowest error are kept as the final result. During the optimization loop, for the current value of $t,\omega^{*}$ is obtained through the closed-form solution

其次，将浊度 $t$ 初始化为 ${1,2,3,...,10}$，并针对每个起始点使用信赖域反射算法（Levenberg-Marquardt算法的变体，支持边界约束）优化式(3)。保留误差最小的参数作为最终结果。在优化循环中，对于当前 $t$ 值，$\omega^{*}$ 通过闭式解获得。

$$
\omega^{*}=\frac{\sum_{p\in\cal{S}}P(p)f_{\mathrm{RGB}}(\boldsymbol{1}{p},t,\boldsymbol{1}{s})}{\sum_{p\in\cal{S}}f_{\mathrm{RGB}}(\boldsymbol{1}{p},t,\boldsymbol{1}_{s})^{2}}.
$$

$$
\omega^{*}=\frac{\sum_{p\in\cal{S}}P(p)f_{\mathrm{RGB}}(\boldsymbol{1}{p},t,\boldsymbol{1}{s})}{\sum_{p\in\cal{S}}f_{\mathrm{RGB}}(\boldsymbol{1}{p},t,\boldsymbol{1}_{s})^{2}}.
$$

Finally, the sky mask $s$ is obtained with the sky segmentation method of [38], followed by a CRF refinement [23].

最后，通过[38]的天空分割方法获得天空掩膜$s$，随后进行CRF（条件随机场）精修[23]。

4.3. Validation of the optimization procedure

4.3. 优化流程的验证

While our fitting procedure minimizes reconstruction errors w.r.t. the panorama pixel intensities, the radiometrically un calibrated nature of this data means that these fits may not accurately represent the true lighting conditions. We validate the procedure in two ways. First, the sun position estimation algorithm is evaluated on 543 panoramic sky images from the Laval HDR sky database [25, 27], which contains ground truth sun position, and which we tonemapped and converted to JPG to simulate the conditions in SUN360.

虽然我们的拟合程序最小化了与全景图像素强度相关的重建误差，但这些数据的辐射度未校准特性意味着这些拟合可能无法准确反映真实光照条件。我们通过两种方式验证该程序：首先，在包含真实太阳位置数据的Laval HDR天空数据库[25,27]的543张全景天空图像上评估太阳位置估计算法（这些图像经过色调映射并转换为JPG格式以模拟SUN360的环境）。

The median sun position estimation error of this algorithm is $4.59^{\circ}$ (25th prct. $=1.96^{\circ}$ , 75th prct. $=8.42^{\circ}.$ ). Second, we ask a user to label 1,236 images from the SUN360 dataset, by indicating whether the estimated sky parameters agree with the scene visible in the panorama. To do so, we render a bunny model on a ground plane, and light it with the sky synthesized by the physical model. We then ask the user to indicate whether the bunny is lit similarly to the other elements present in the scene. In all, $65.6%$ of the images were deemed to be a successful fit, which is testament to the challenging imaging conditions present in the dataset.

该算法的太阳位置估计误差中位数为 $4.59^{\circ}$ (25百分位数 $=1.96^{\circ}$，75百分位数 $=8.42^{\circ}$)。其次，我们邀请用户对SUN360数据集中的1,236张图像进行标注，判断估计的天空参数是否与全景图中可见的场景相符。具体方法是：在地平面上渲染兔子模型，并通过物理模型合成的天空光照进行照明，然后让用户判断兔子是否与场景中其他元素的照明效果一致。总体而言，$65.6%$ 的图像被判定为成功匹配，这证明了数据集中存在极具挑战性的成像条件。

5. Learning to predict outdoor lighting

5. 学习预测室外光照

5.1. Dataset organization

5.1. 数据集组织

To train the CNN, we first apply the optimization procedure from sec. 4.2 to 38,814 high resolution outdoor panoramas in the SUN360 [40] database. We then extract 7 photos from each panorama using a standard pinhole camera model and randomly sampling its parameters: its elevation with respect to the horizon in $[-20^{\circ},20^{\circ}]$ , azimuth in $[-180^{\circ},180^{\circ}]$ , and vertical field of view in $[35^{\circ},68^{\circ}]$ . The resulting photos are bilinearly interpolated from the panorama to a resolution $320\times240$ , and used directly to train the CNN described in the next section. This results in a dataset of 271,698 pairs of photos and their corresponding lighting parameters, which is split into (261,288 $\langle1,751/8,659\rangle$ subsets for (train / validation / test). These splits were computed on the panoramas to ensure that photos taken from the same panorama do not end up in training and test. Example panoramas and corresponding photos are shown in fig. 6.

为训练CNN，我们首先对SUN360 [40]数据库中的38,814张高分辨率户外全景图应用第4.2节的优化流程。随后采用标准针孔相机模型从每张全景图中提取7张照片，并随机采样以下参数：相对于地平线的仰角 $[-20^{\circ},20^{\circ}]$ 、方位角 $[-180^{\circ},180^{\circ}]$ 、垂直视场角 $[35^{\circ},68^{\circ}]$ 。通过双线性插值将生成的照片分辨率调整为 $320\times240$ ，直接用于训练下一节描述的CNN。最终获得包含271,698组照片及其对应光照参数的数据集，划分为 (261,288 / 1,751 / 8,659) 子集用于 (训练/验证/测试) 。划分基于全景图层级，确保同一全景图生成的照片不会同时出现在训练集和测试集。示例全景图及对应照片如图6所示。

5.2. CNN architecture

5.2. CNN架构

We adopt a standard feed-forward convolutional neural network to learn the relationship between the input image $I$ and the lighting parameters. As shown in fig. 3, its architecture is composed of 7 convolutional layers, followed by a fully-connected layer. It then splits into two separate heads: one for estimating the sun position (left in fig. 3), and one for the sky and camera parameters (right in fig. 3).

我们采用标准的前馈卷积神经网络来学习输入图像 $I$ 与光照参数之间的关系。如图 3 所示，其架构由 7 个卷积层组成，后接一个全连接层。随后网络分成两个独立的分支：一个用于估计太阳位置（图 3 左侧），另一个用于估计天空和相机参数（图 3 右侧）。

The sun position head outputs a probability distribution over the likely sun positions s by disc ret i zing the sky hemisphere into 160 bins (5 for elevation, 32 for azimuth), and outputs a value for each of these bins. This was also done in [26]. As opposed to regressing the sun position directly, this has the advantage of indicating other regions believed to be likely sun positions in the prediction, as illustrated in fig. 6 below. The parameters head directly regresses a 4- vector of parameters q: 2 for the sky $(\omega,t)$ , and 2 for the camera (elevation and field of view). The ELU activation function [6] and batch normalization [18] are used at the output of every layer.

太阳位置头部通过将天空半球离散化为160个区间（5个仰角区间，32个方位角区间），输出可能太阳位置s的概率分布，并为每个区间输出一个值。这一方法同样在[26]中采用。与直接回归太阳位置相比，其优势在于能显示预测中被认为可能作为太阳位置的其他区域，如图6所示。参数头部直接回归一个4维向量q：其中2个参数对应天空$(\omega,t)$，2个参数对应相机（仰角和视场角）。每层输出均使用ELU激活函数[6]和批量归一化[18]。

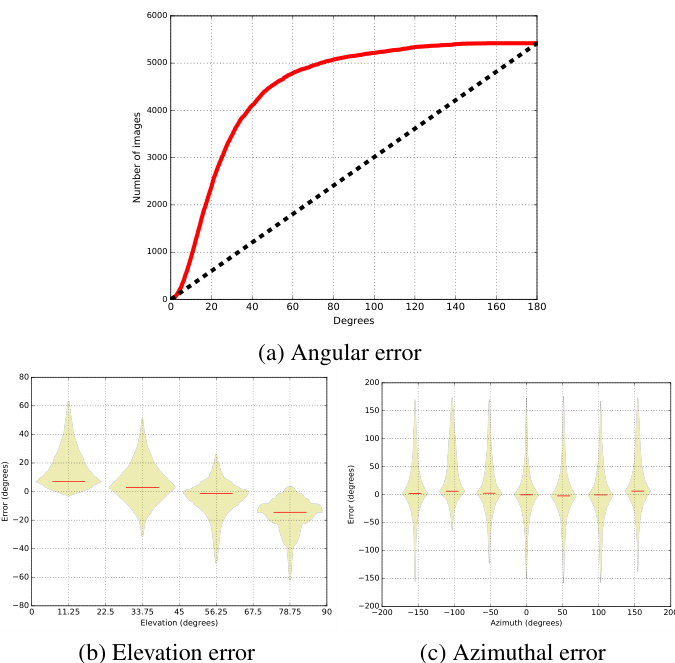
Figure 4. Quantitative evaluation of sun position estimation on all 8659 images in the SUN360 test set. (a) The cumulative distribution function of the angular error on the sun position. The esti- mation error as function of the sun elevation (b) and (c) azimuth relative to the camera ( $0^{\circ}$ means the sun is in front of the camera). The last two figures are displayed as “box-percentile plots” [10], where the envelope of each bin represents the percentile and the median is shown as a red bar.

图 4: SUN360测试集中8659张图像的太阳位置估计定量评估。(a) 太阳位置角度误差的累积分布函数。(b) 和 (c) 分别显示估计误差随太阳高度角及相对于相机的方位角( $0^{\circ}$ 表示太阳位于相机正前方)的变化关系。后两图采用"箱形百分位图"[10]展示，其中每个区间的包络线代表百分位，中位数以红色条形显示。

5.3. Training details

5.3. 训练细节

We define the loss to be optimized as the sum of two losses, one for each head:

我们将待优化的损失定义为两个损失之和，每个损失对应一个头部：

$$
\begin{array}{r}{\mathcal{L}(\mathbf{s}^{},\mathbf{q}^{},\mathbf{s},\mathbf{q})=\mathcal{L}(\mathbf{s}^{},\mathbf{s})+\beta\mathcal{L}(\mathbf{q}^{*},\mathbf{q}),}\end{array}
$$

$$
\begin{array}{r}{\mathcal{L}(\mathbf{s}^{},\mathbf{q}^{},\mathbf{s},\mathbf{q})=\mathcal{L}(\mathbf{s}^{},\mathbf{s})+\beta\mathcal{L}(\mathbf{q}^{*},\mathbf{q}),}\end{array}
$$

where $\beta=160$ to compensate for the number of bins in s. The target sun position $\mathbf{s}^{*}$ is computed for each bin $\mathbf{s}_{j}$ as

其中 $\beta=160$ 用于补偿 s 中的 bin 数量。每个 bin $\mathbf{s}_{j}$ 的目标太阳位置 $\mathbf{s}^{*}$ 计算为

$$
\mathbf{s}{j}^{}=\exp(\kappa\mathbf{l}{s}^{*\top}\mathbf{l}_{j}),
$$

$$
\mathbf{s}{j}^{}=\exp(\kappa\mathbf{l}{s}^{*\top}\mathbf{l}_{j}),
$$

and normalized so that $\textstyle\sum_{j}\mathbf{s}{j}^{}=1$ . The equation in (6) represents a von Mises-F isher distribution [1] centered about the ground truth sun position ${\bf l}_{s}$ . Since the network must predict a confident value around