Augmented Auto encoders: Implicit 3D Orientation Learning for 6D Object Detection

增强型自动编码器：面向6D物体检测的隐式3D姿态学习

Abstract We propose a real-time RGB-based pipeline for object detection and 6D pose estimation. Our novel 3D orientation estimation is based on a variant of the Denoising Auto encoder that is trained on simulated views of a 3D model using Domain Random iz ation.

摘要 我们提出了一种基于RGB的实时目标检测与6D姿态估计流程。其中创新的3D朝向估计算法基于改进版降噪自编码器(Denoising Autoencoder)，该模型通过域随机化(Domain Randomization)技术在3D模型仿真视图上进行训练。

This so-called Augmented Auto encoder has several advantages over existing methods: It does not require real, pose-annotated training data, generalizes to various test sensors and inherently handles object and view symmetries. Instead of learning an explicit mapping from input images to object poses, it provides an implicit representation of object orientations defined by samples in a latent space. Our pipeline achieves stateof-the-art performance on the T-LESS dataset both in the RGB and RGB-D domain. We also evaluate on the LineMOD dataset where we can compete with other synthetically trained approaches.

这种所谓的增强型自动编码器 (Augmented Autoencoder) 相比现有方法具有多项优势：无需真实带有姿态标注的训练数据、可泛化至多种测试传感器、并能天然处理物体与视角对称性问题。该方法并非学习从输入图像到物体姿态的显式映射，而是通过潜在空间中的样本来提供物体朝向的隐式表征。我们的流水线在T-LESS数据集上实现了RGB和RGB-D领域的最先进性能。在LineMOD数据集上的评估结果表明，该方法可与其他基于合成数据训练的方法相媲美。

We further increase performance by correcting 3D orientation estimates to account for perspective errors when the object deviates from the image center and show extended results. Our code is available here 1

我们通过校正3D方向估计来进一步提升性能，以解决物体偏离图像中心时的透视误差问题，并展示了扩展结果。代码可在此处获取1

Keywords 6D Object Detection Pose Estimation Domain Random iz ation Auto encoder Synthetic Data · Symmetries

关键词 6D物体检测 位姿估计 域随机化 自编码器 合成数据 · 对称性

1 Introduction

1 引言

One of the most important components of modern computer vision systems for applications such as mobile robotic manipulation and augmented reality is a reliable and fast 6D object detection module. Although, there are very encouraging recent results from Xiang Wohlhart and Lepetit (2015); Vidal et al. (2018); Hinter s to is ser et al. (2016); Tremblay et al. (2018), a general, easily applicable, robust and fast solution is not available, yet. The reasons for this are manifold. First and foremost, current solutions are often not robust enough against typical challenges such as object occlusions, different kinds of background clutter, and dynamic changes of the environment. Second, existing methods often require certain object properties such as enough textural surface structure or an asymmetric shape to avoid confusions. And finally, current systems are not efficient in terms of run-time and in the amount and type of annotated training data they require.

现代计算机视觉系统在移动机器人操作和增强现实等应用中最关键的组件之一，是可靠且快速的6D物体检测模块。尽管Xiang Wohlhart和Lepetit (2015)、Vidal等人 (2018)、Hinterstoiser等人 (2016)、Tremblay等人 (2018)的研究取得了非常鼓舞人心的成果，但目前仍缺乏一种通用、易用、鲁棒且快速的解决方案。其原因有多方面：首先，现有方案通常对物体遮挡、各类背景干扰以及环境动态变化等典型挑战的鲁棒性不足；其次，现有方法往往要求物体具备特定属性，例如足够的纹理表面结构或非对称形状以避免误判；最后，当前系统在运行效率以及所需标注训练数据的数量与类型方面仍不够高效。

Therefore, we propose a novel approach that directly addresses these issues. Concretely, our method operates on single RGB images, which significantly increases the usability as no depth information is required. We note though that depth maps may be incorporated optionally to refine the estimation. As a first step, we build upon state-of-the-art 2D Object Detectors of (Liu et al. (2016); Lin et al. (2018)) which provide object bounding boxes and identifiers. On the resulting scene crops, we employ our novel 3D orientation estimation algorithm, which is based on a previously trained deep network architecture. While deep networks are also used in existing approaches, our approach differs in that we do not explicitly learn from 3D pose annotations during training. Instead, we implicitly learn representa- tions from rendered 3D model views. This is accomplished by training a generalized version of the Denoising Auto encoder from Vincent et al. (2010), that we call ’Augmented Auto encoder $(A A E)^{\mathstrut}$ , using a novel Domain Random iz ation strategy. Our approach has several advantages: First, since the training is independent from concrete representations of object orientations within $S O(3)$ (e.g. qua tern ions), we can handle ambiguous poses caused by symmetric views because we avoid one-to-many mappings from images to orientations. Second, we learn representations that specifically encode 3D orientations while achieving robustness against occlusion, cluttered backgrounds and generalizing to different environments and test sensors. Finally, the AAE does not require any real pose-annotated training data. Instead, it is trained to encode 3D model views in a self-supervised way, overcoming the need of a large pose-annotated dataset. A schematic overview of the approach based on S under meyer et al. (2018) is shown in Fig 1.

因此，我们提出了一种直接解决这些问题的新方法。具体而言，我们的方法基于单张RGB图像运行，这显著提高了实用性，因为不需要深度信息。不过我们注意到，可以可选地结合深度图来优化估计。首先，我们基于最先进的2D目标检测器（Liu等人（2016）；Lin等人（2018））构建，这些检测器提供目标边界框和标识符。在生成的场景裁剪上，我们采用了新颖的3D方向估计算法，该算法基于先前训练的深度网络架构。虽然现有方法也使用深度网络，但我们的方法不同之处在于，在训练期间我们不显式地从3D姿态标注中学习。相反，我们通过渲染的3D模型视图隐式学习表示。这是通过训练Vincent等人（2010）的去噪自动编码器的广义版本实现的，我们称之为“增强自动编码器 $(A A E)^{\mathstrut}$”，并采用了一种新颖的域随机化策略。我们的方法有几个优点：首先，由于训练独立于 $S O(3)$ 内对象方向的具体表示（例如四元数），我们可以处理由对称视图引起的模糊姿态，因为我们避免了从图像到方向的一对多映射。其次，我们学习的表示专门编码3D方向，同时实现了对遮挡、杂乱背景的鲁棒性，并能泛化到不同环境和测试传感器。最后，AAE不需要任何真实的姿态标注训练数据。相反，它以自监督的方式训练编码3D模型视图，克服了对大规模姿态标注数据集的需求。基于Sundermeyer等人（2018）的方法示意图如图1所示。

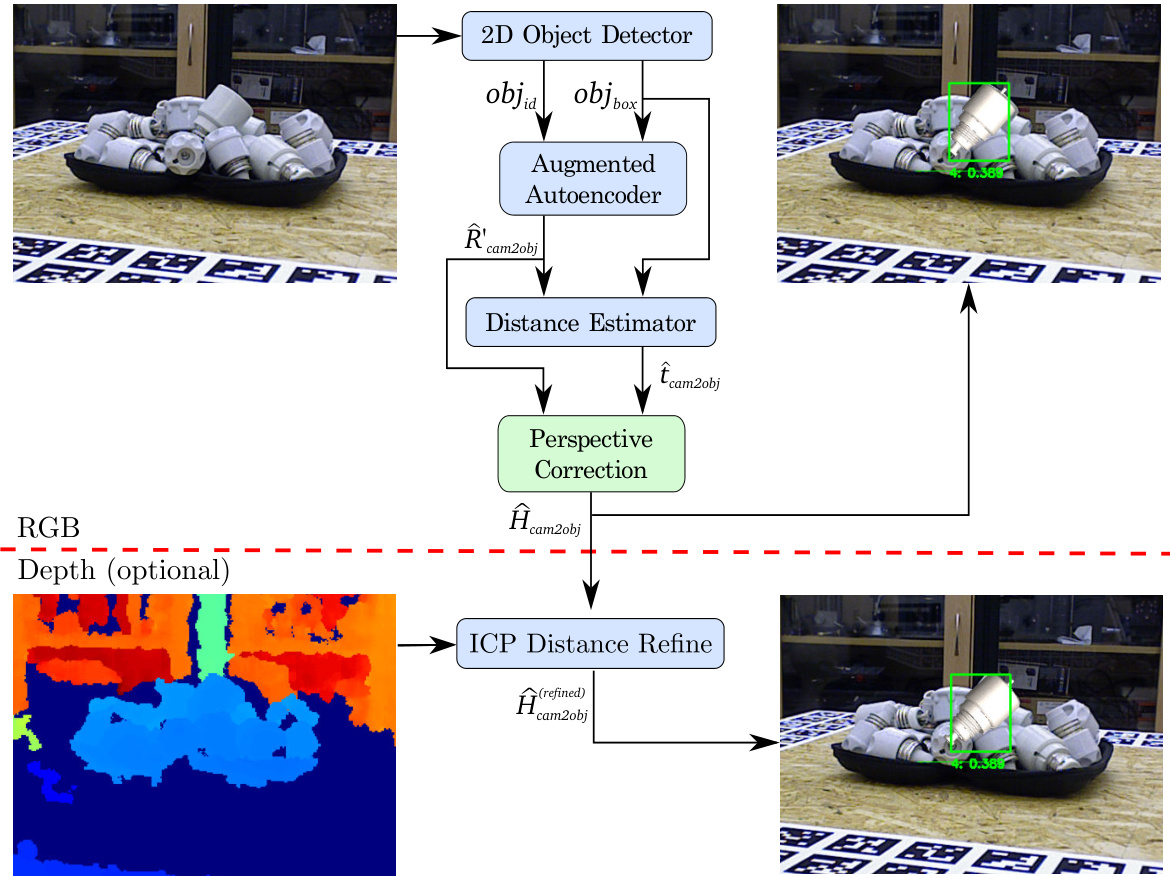
Fig. 1: Our full 6D Object Detection pipeline: after detecting an object (2D Object Detector), the object is quadratically cropped and forwarded into the proposed Augmented Auto encoder. In the next step, the bounding box scale ratio at the estimated 3D orientation $\hat{R}{o b j2c a m}^{\prime}$ is used to compute the 3D translation $\hat{t}{o b j2c a m}$ . The resulting euclidean transformation $\hat{H}^{\prime}{}{o b j2c a m}\in\mathcal{R}^{4x4}$ already shows promising results as presented in S under meyer et al. (2018), however it still lacks of accuracy given a translation in the image plane towards the borders. Therefore, the pipeline is extended by the Perspective Correction block which addresses this problem and results in more accurate 6D pose estimates $\hat{H}{o b j2c a m}$ for objects which are not located in the image center. Additionally, given (dbeoptttho dma).ta, the result can be further refined $(\hat{H}_{o b j2c a m}^{(r e f i n e d)})$ by applying an Iterative Closest Point post-processing

图 1: 我们的完整6D物体检测流程：在检测到物体（2D物体检测器）后，物体被方形裁剪并输入到提出的增强自编码器中。下一步，在估计的3D朝向$\hat{R}{obj2cam}^{\prime}$下使用边界框缩放比例来计算3D平移$\hat{t}{obj2cam}$。得到的欧几里得变换$\hat{H}^{\prime}{}{obj2cam}\in\mathcal{R}^{4x4}$已显示出如S under meyer等人(2018)所展示的良好结果，但对于图像平面中向边缘平移的情况仍缺乏精度。因此，流程通过透视校正模块进行扩展，解决了这一问题，并为不在图像中心的物体提供了更精确的6D姿态估计$\hat{H}{obj2cam}$。此外，给定(dbeoptttho dma)数据，结果可以通过应用迭代最近点后处理进一步细化$(\hat{H}_{obj2cam}^{(refined)})$。

2 Related Work

2 相关工作

Depth-based methods (e.g. using Point Pair Features (PPF) from Vidal et al. (2018); H inters to is ser et al. (2016)) have shown robust pose estimation performance on multiple datasets, winning the SIXD challenge (Hodan, 2017; Hodan et al., 2018). However, they usually rely on the computationally expensive evaluation of many pose hypotheses and do not take into account any high level features. Furthermore, existing depth sensors are often more sensitive to sunlight or specular object surfaces than RGB cameras.

基于深度的方法（例如使用Vidal等人(2018)提出的点对特征(PPF)或Hinterstoisser等人(2016)的技术）已在多个数据集上展现出稳健的姿态估计性能，并赢得了SIXD挑战赛(Hodan, 2017; Hodan et al., 2018)。然而，这些方法通常依赖于计算成本高昂的多姿态假设评估，且未考虑任何高级特征。此外，现有深度传感器对阳光或物体镜面反射的敏感度往往高于RGB相机。

Convolutional Neural Networks (CNNs) have revolutionized 2D object detection from RGB images (Ren et al., 2015; Liu et al., 2016; Lin et al., 2018). But, in comparison to 2D bounding box annotation, the effort of labeling real images with full 6D object poses is magnitudes higher, requires expert knowledge and a complex setup (Hodan et al., 2017).

卷积神经网络 (CNN) 彻底改变了基于RGB图像的2D目标检测 (Ren et al., 2015; Liu et al., 2016; Lin et al., 2018) 。但与2D边界框标注相比，为真实图像标注完整的6D物体姿态所需工作量高出数个数量级，既需要专业知识又依赖复杂配置 (Hodan et al., 2017) 。

Nevertheless, the majority of learning-based pose estimation methods, namely Tekin et al. (2017); Wohlhart and Lepetit (2015); Brachmann et al. (2016); Rad and Lepetit (2017); Xiang et al. (2017), use real labeled images that you only obtain within pose-annotated datasets

然而，大多数基于学习的姿态估计方法，如Tekin等人(2017)、Wohlhart和Lepetit(2015)、Brachmann等人(2016)、Rad和Lepetit(2017)、Xiang等人(2017)，都使用只能在带姿态标注数据集中获取的真实标注图像

In consequence, Kehl et al. (2017); Wohlhart and Lepetit (2015); Tremblay et al. (2018); Zakharov et al. (2019) have proposed to train on synthetic images rendered from a 3D model, yielding a great data source with pose labels free of charge. However, naive training on synthetic data does not typically generalize to real test images. Therefore, a main challenge is to bridge the domain gap that separates simulated views from real camera recordings.

因此，Kehl等人 (2017) 、Wohlhart和Lepetit (2015) 、Tremblay等人 (2018) 以及Zakharov等人 (2019) 提出通过从3D模型渲染合成图像进行训练，从而免费获得大量带有姿态标签的数据源。然而，直接在合成数据上进行训练通常无法泛化到真实的测试图像。因此，主要挑战在于弥合模拟视图与真实相机记录之间的领域差距。

2.1 Simulation to Reality Transfer

2.1 从仿真到现实的迁移

There exist three major strategies to generalize from synthetic to real data:

从合成数据泛化到真实数据存在三大主要策略：

2.1.1 Photo-Realistic Rendering

2.1.1 照片级真实感渲染

The works of Movshovitz-Attias et al. (2016); Su et al. (2015); Mitash et al. (2017); Richter et al. (2016) have shown that photo-realistic renderings of object views and backgrounds can in some cases benefit the generalization performance for tasks like object detection and viewpoint estimation. It is especially suitable in simple environments and performs well if jointly trained with a relatively small amount of real annotated images. However, photo-realistic modeling is often imperfect and requires much effort. Recently, Hodan et al. (2019) have shown promising results for 2D Object Detection trained on physically-based renderings.

Movshovitz-Attias等人 (2016)、Su等人 (2015)、Mitash等人 (2017) 和Richter等人 (2016) 的研究表明，在某些情况下，物体视角和背景的逼真渲染可以提升目标检测和视角估计等任务的泛化性能。这种方法尤其适用于简单环境，并且与少量真实标注图像联合训练时表现良好。然而，逼真建模通常不够完美且需要大量精力。最近，Hodan等人 (2019) 展示了基于物理渲染训练的2D目标检测取得了有前景的结果。

2.1.2 Domain Adaptation

2.1.2 领域自适应 (Domain Adaptation)

Domain Adaptation (DA) (Csurka, 2017) refers to leveraging training data from a source domain to a target domain of which a small portion of labeled data (supervised DA) or unlabeled data (unsupervised DA) is available. Generative Adversarial Networks (GANs) have been deployed for unsupervised DA by generating realistic from synthetic images to train class if i ers (Shri vast ava et al., 2017), 3D pose estimators (Bousmalis et al., 2017b) and grasping algorithms (Bousmalis et al., 2017a). While constituting a promising approach, GANs often yield fragile training results. Supervised DA can lower the need for real annotated data, but does not abstain from it.

领域自适应 (DA) (Csurka, 2017) 是指利用源域的训练数据来适应目标域，其中目标域有少量标注数据 (监督式DA) 或未标注数据 (无监督DA) 可用。生成对抗网络 (GAN) 已被用于无监督DA，通过从合成图像生成逼真图像来训练分类器 (Shrivastava et al., 2017)、3D姿态估计器 (Bousmalis et al., 2017b) 和抓取算法 (Bousmalis et al., 2017a)。虽然这是一种有前景的方法，但GAN通常会产生不稳定的训练结果。监督式DA可以减少对真实标注数据的需求，但并不能完全避免使用真实数据。

2.1.3 Domain Random iz ation

2.1.3 领域随机化 (Domain Randomization)

Domain Random iz ation (DR) builds upon the hypothesis that by training a model on rendered views in a variety of semi-realistic settings (augmented with random lighting conditions, backgrounds, saturation, etc.), it will also generalize to real images. Tobin et al. (2017) demonstrated the potential of the DR paradigm for 3D shape detection using CNNs. H inters to is ser et al. (2017) showed that by training only the head network of FasterRCNN of Ren et al. (2015) with randomized synthetic views of a textured 3D model, it also generalizes well to real images. It must be noted, that their rendering is almost photo-realistic as the textured 3D models have very high quality. Kehl et al. (2017) pioneered an end-to-end CNN, called ’SSD6D’, for 6D object detection that uses a moderate DR strategy to utilize synthetic training data. The authors render views of textured 3D object reconstructions at random poses on top of MS COCO background images (Lin et al., 2014) while varying brightness and contrast. This lets the network generalize to real images and enables 6D detection at 10Hz. Like us, for accurate distance estimation they rely on Iterative Closest Point (ICP) post-processing using depth data. In contrast, we do not treat 3D orientation estimation as a classification task.

域随机化 (Domain Randomization, DR) 基于这样一个假设：通过在多种半真实设置（辅以随机光照条件、背景、饱和度等）的渲染视图上训练模型，模型也能泛化到真实图像。Tobin等人 (2017) 展示了DR范式在CNN三维形状检测中的潜力。Hinterstoisser等人 (2017) 表明，仅使用纹理化3D模型的随机合成视图训练Ren等人 (2015) FasterRCNN的头部网络，也能很好地泛化到真实图像。值得注意的是，他们的渲染近乎照片级真实，因为纹理化3D模型质量极高。Kehl等人 (2017) 率先提出名为"SSD6D"的端到端CNN，用于6D物体检测，采用适度DR策略利用合成训练数据。作者在MS COCO背景图像 (Lin等人, 2014) 上随机姿态渲染纹理化3D物体重建视图，同时改变亮度和对比度。这使得网络能泛化到真实图像，并以10Hz频率实现6D检测。与我们类似，为精确估计距离，他们依赖使用深度数据的迭代最近点 (Iterative Closest Point, ICP) 后处理。不同的是，我们并未将3D方向估计视为分类任务。

2.2 Training Pose Estimation with SO(3) targets

2.2 使用SO(3)目标训练姿态估计

We describe the difficulties of training with fixed SO(3) parameter iz at ions which will motivate the learning of view-based representations.

我们描述了使用固定SO(3)参数化进行训练的困难，这将促使学习基于视角的表征。

2.2.1 Regression

2.2.1 回归

Since rotations live in a continuous space, it seems natural to directly regress a fixed SO(3) parameter iz at ions like qua tern ions. However, representational constraints and pose ambiguities can introduce convergence issues as investigated by Saxena et al. (2009). In practice, direct regression approaches for full 3D object orientation estimation have not been very successful (Mahendran et al., 2017). Instead Tremblay et al. (2018); Tekin et al. (2017); Rad and Lepetit (2017) regress local 2D3D correspondences and then apply a Perspective-nPoint (PnP) algorithm to obtain the 6D pose. However, these approaches can also not deal with pose ambiguities without additional measures (see Sec. 2.2.3).

由于旋转存在于连续空间中，直接回归固定的SO(3)参数化方法（如四元数）看似自然。但正如Saxena等人(2009)所研究的，表征约束和位姿歧义性会导致收敛问题。实践中，直接回归方法在完整3D物体朝向估计任务中表现不佳 (Mahendran等人, 2017)。因此Tremblay等人(2018)、Tekin等人(2017)以及Rad和Lepetit(2017)转而回归局部2D-3D对应关系，再通过Perspective-nPoint(PnP)算法获取6D位姿。不过若不采取额外措施，这些方法同样无法处理位姿歧义性问题（参见2.2.3节）。

2.2.2 Classification

2.2.2 分类

Classification of 3D object orientations requires a disc ret iz ation of SO(3). Even rather coarse intervals of $\sim5^{o}$ lead to over 50.000 possible classes. Since each class appears only sparsely in the training data, this hinders convergence. In SSD6D (Kehl et al., 2017) the 3D orientation is learned by separately classifying a discretized viewpoint and in-plane rotation, thus reducing the complexity to $\mathcal{O}(n^{2})$ . However, for non-canonical views, e.g. if an object is seen from above, a change of viewpoint can be nearly equivalent to a change of inplane rotation which yields ambiguous class combinations. In general, the relation between different orientations is ignored when performing one-hot classification.

对3D物体朝向的分类需要对SO(3)进行离散化。即使采用较粗的$\sim5^{o}$间隔，也会产生超过50,000个可能的类别。由于每个类别在训练数据中仅稀疏出现，这会阻碍模型收敛。SSD6D (Kehl et al., 2017)通过分别对离散化视角和平面内旋转进行分类来学习3D朝向，从而将复杂度降低至$\mathcal{O}(n^{2})$。然而，对于非规范视角（例如从上方观察物体时），视角变化可能与平面内旋转变化几乎等效，从而导致类别组合的歧义性。一般而言，在进行独热分类时会忽略不同朝向之间的关联性。

2.2.3 Symmetries

2.2.3 对称性

Symmetries are a severe issue when relying on fixed represent at ions of 3D orientations since they cause pose ambiguities (Fig. 2). If not manually addressed, identical training images can have different orientation labels assigned which can significantly disturb the learning process. In order to cope with ambiguous objects, most approaches in literature are manually adapted (Wohlhart and Lepetit, 2015; H inters to is ser et al., 2012a; Kehl et al., 2017; Rad and Lepetit, 2017). The strategies reach from ignoring one axis of rotation (Wohlhart and Lepetit, 2015; H inters to is ser et al., 2012a) over adapt- ing the disc ret iz ation according to the object (Kehl et al., 2017) to the training of an extra CNN to predict symmetries (Rad and Lepetit, 2017). These depict tedious, manual ways to filter out object symmetries (Fig. 2a) in advance, but treating ambiguities due to self-occlusions (Fig. 2b) and occlusions (Fig. 2c) are harder to address.

对称性是依赖固定三维方向表示时面临的严重问题，因为它们会导致姿态歧义（图 2）。若未手动处理，相同的训练图像可能被分配不同方向标签，这将严重干扰学习过程。针对模糊物体，现有文献大多采用人工适配方案 (Wohlhart and Lepetit, 2015; Hinterstoisser et al., 2012a; Kehl et al., 2017; Rad and Lepetit, 2017)。具体策略包括：忽略某旋转轴 (Wohlhart and Lepetit, 2015; Hinterstoisser et al., 2012a)、根据物体调整离散化方案 (Kehl et al., 2017)，或训练专用CNN预测对称性 (Rad and Lepetit, 2017)。这些方法虽能预先过滤物体对称性（图 2a），但难以处理自遮挡（图 2b）和遮挡（图 2c）导致的歧义问题。

Symmetries do not only affect regression and classification methods, but any learning-based algorithm that discriminates object views solely by fixed SO(3) representations.

对称性不仅影响回归和分类方法，还会影响任何仅通过固定SO(3)表示来区分物体视图的基于学习的算法。

2.3 Learning Representations of 3D orientations

2.3 三维方向的学习表示

We can also learn indirect pose representations that relate object views in a low-dimensional space. The descriptor learning can either be self-supervised by the object views themselves or still rely on fixed SO(3) represent at ions.

我们还可以学习间接的姿态表示，将物体视角关联到低维空间中。描述符学习可以通过物体视角本身进行自监督，或者仍然依赖于固定的SO(3)表示。

2.3.1 Descriptor Learning

2.3.1 描述符学习

Wohlhart and Lepetit (2015) introduced a CNN-based descriptor learning approach using a triplet loss that minimizes/maximizes the Euclidean distance between similar/dissimilar object orientations. In addition, the distance between different objects is maximized. Although mixing in synthetic data, the training also relies on pose-annotated sensor data. The approach is not immune against symmetries since the descriptor is built using explicit 3D orientations. Thus, the loss can be dominated by symmetric object views that appear the same but have opposite orientations which can produce incorrect average pose predictions.

Wohlhart和Lepetit (2015) 提出了一种基于CNN的描述符学习方法，该方法使用三元组损失来最小化/最大化相似/不相似物体方向之间的欧氏距离。此外，不同物体之间的距离也被最大化。尽管混合了合成数据，训练仍依赖于带有姿态标注的传感器数据。由于描述符是使用显式的3D方向构建的，该方法无法避免对称性问题。因此，损失可能由对称物体视角主导，这些视角看起来相同但方向相反，可能导致错误的平均姿态预测。

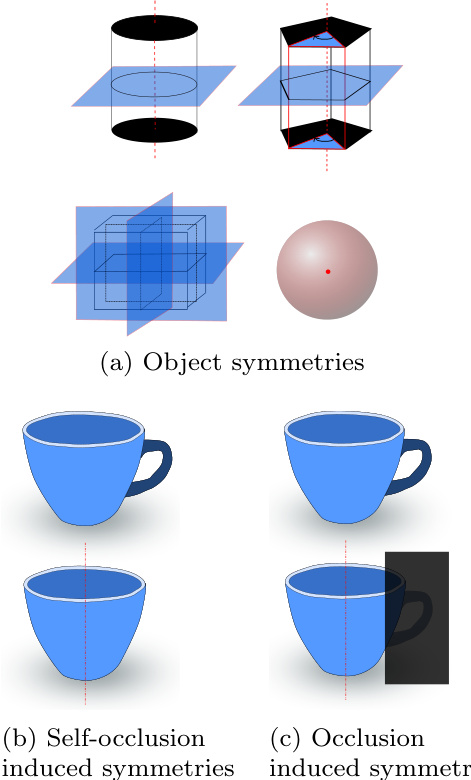
Fig. 2: Causes of pose ambiguities

图 2: 姿态模糊性成因

Balntas et al. (2017) extended this work by enforcing proportionality between descriptor and pose distances. They acknowledge the problem of object symmetries by weighting the pose distance loss with the depth difference of the object at the considered poses. This heuristic increases the accuracy on symmetric objects with respect to Wohlhart and Lepetit (2015).

Balntas等人(2017)通过强制描述符距离与位姿距离成比例扩展了这项工作。他们通过用物体在考虑位姿下的深度差异加权位姿距离损失，承认了物体对称性问题。这种启发式方法相较于Wohlhart和Lepetit(2015)提高了对称物体的准确率。

Our work is also based on learning descriptors, but in contrast we train our Augmented Auto encoders (AAEs) such that the learning process itself is independent of any fixed SO(3) representation. The loss is solely based on the appearance of the reconstructed object views and thus symmetrical ambiguities are inherently regarded. Thus, unlike Balntas et al. (2017); Wohlhart and Lepetit (2015) we abstain from the use of real labeled data during training and instead train completely self-supervised. This means that assigning 3D orientations to the descriptors only happens after the training.

我们的工作同样基于学习描述符，但不同的是，我们训练增强自编码器 (AAE) 时，使学习过程本身独立于任何固定的 SO(3) 表示。损失函数仅基于重建物体视图的外观，因此对称性模糊问题被自然纳入考量。因此，与 Balntas 等人 (2017) 和 Wohlhart 与 Lepetit (2015) 不同，我们在训练过程中避免使用真实标注数据，而是完全采用自监督训练。这意味着描述符的 3D 方向分配仅在训练完成后进行。

Kehl et al. (2016) train an Auto encoder architecture on random RGB-D scene patches from the LineMOD dataset H inters to is ser et al. (2011). At test time, descriptors from scene and object patches are compared to find the 6D pose. Since the approach requires the evaluation of a lot of patches, it takes about 670ms per prediction. Furthermore, using local patches means to ignore holistic relations between object features which is crucial if few texture exists. Instead we train on holistic object views and explicitly learn domain invariance.

Kehl等人 (2016) 在LineMOD数据集 [Hinterstoisser等人 (2011)] 的随机RGB-D场景块上训练了一个自动编码器 (Auto encoder) 架构。测试时，通过比较场景和物体块的描述符来寻找6D位姿。由于该方法需要评估大量图像块，每个预测耗时约670毫秒。此外，使用局部块意味着忽略了物体特征间的整体关联性——这在纹理稀少时尤为关键。与之相反，我们在完整物体视图上进行训练，并显式学习域不变性。

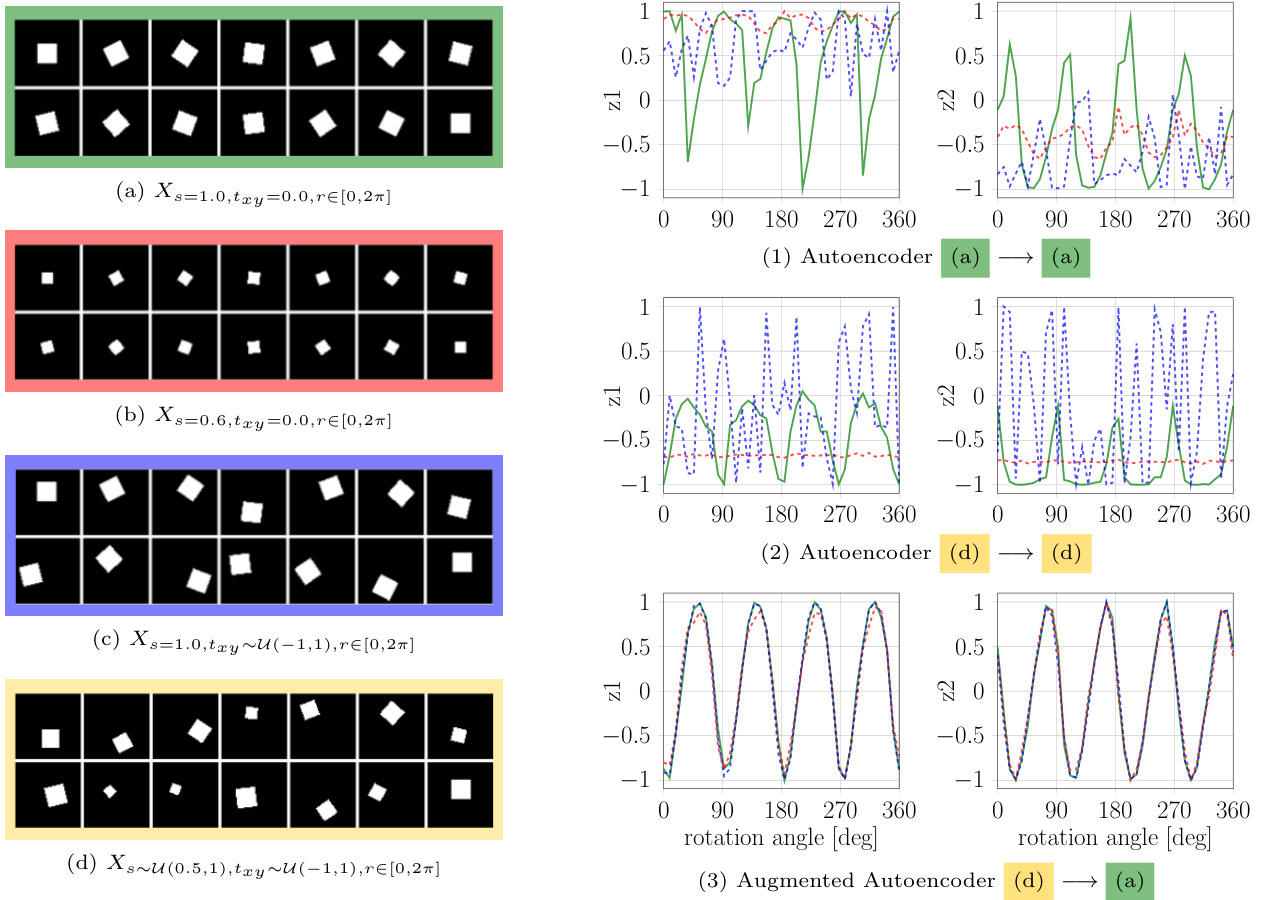
Fig. 3: Experiment on the dsprites dataset of Matthey et al. (2017). Left: $64\mathrm{x64}$ squares from four distributions (a,b,c and d) distinguished by scale (s) and translation $({t_{x y}})$ that are used for training and testing. Right: Normalized latent dimensions $z_{1}$ and $z_{2}$ for all rotations ( $r$ ) of the distribution (a), (b) or (c) after training ordinary Auto encoders (AEs) (1),(2) and an AAE (3) to reconstruct squares of the same orientation.

图 3: Matthey等人(2017)在dsprites数据集上的实验。左: 用于训练和测试的四个分布(a,b,c和d)的$64\mathrm{x64}$正方形，通过尺度(s)和平移$({t_{x y}})$区分。右: 训练普通自编码器(AEs)(1),(2)和AAE(3)重建相同方向正方形后，分布(a)、(b)或(c)所有旋转($r$)的归一化潜在维度$z_{1}$和$z_{2}$。

3 Method

3 方法

In the following, we mainly focus on the novel 3D orientation estimation technique based on the AAE.

以下我们主要介绍基于AAE的新型3D方向估计技术。

3.1 Auto encoders

3.1 自编码器

The original AE, introduced by Rumelhart et al. (1985), is a dimensionality reduction technique for high dimensional data such as images, audio or depth. It consists of an Encoder $\phi$ and a Decoder $\psi$ , both arbitrary learnable function ap proxima tors which are usually neural networks. The training objective is to reconstruct the input $x\in\mathcal{R}^{\mathcal{D}}$ after passing through a low-dimensional bottleneck, referred to as the latent representation $z\in\mathcal{R}^{n}$ with $n<<\mathcal{D}$ :

由Rumelhart等人(1985)提出的原始自编码器(AE)是一种针对图像、音频或深度等高维数据的降维技术。它由编码器$\phi$和解码器$\psi$组成，两者都是任意可学习的函数逼近器，通常为神经网络。训练目标是通过一个低维瓶颈(称为潜在表示$z\in\mathcal{R}^{n}$，其中$n<<\mathcal{D}$)后重构输入$x\in\mathcal{R}^{\mathcal{D}}$:

$$
\hat{x}=(\varPsi\circ\varPhi)(x)=\varPsi(z)
$$

$$
\hat{x}=(\varPsi\circ\varPhi)(x)=\varPsi(z)
$$

The per-sample loss is simply a sum over the pixel-wise L2 distance

每个样本的损失仅是逐像素L2距离之和

$$
\ell_{2}=\sum_{i\in\cal D}\parallel x_{i}-\hat{x}{i}\parallel_{2}
$$

$$
\ell_{2}=\sum_{i\in\cal D}\parallel x_{i}-\hat{x}{i}\parallel_{2}
$$

The resulting latent space can, for example, be used for unsupervised clustering.

生成的潜在空间可用于无监督聚类等任务。

Denoising Auto encoders introduced by Vincent et al. (2010) have a modified training procedure. Here, artificial random noise is applied to the input images $x\in\mathcal{R}^{\mathcal{D}}$ while the reconstruction target stays clean. The trained model can be used to reconstruct denoised test images. But how is the latent representation affected?

Vincent等人(2010)提出的降噪自编码器采用了改进的训练方法。该方法在输入图像$x\in\mathcal{R}^{\mathcal{D}}$上施加人工随机噪声，同时保持重构目标为干净图像。训练后的模型可用于重构降噪后的测试图像。但潜在表征会受到什么影响呢？

Hypothesis 1: The Denoising AE produces latent representations which are invariant to noise because it facilitates the reconstruction of de-noised images.

假设1：去噪自编码器 (Denoising AE) 生成的潜在表征对噪声具有不变性，因为它促进了去噪图像的重建。

We will demonstrate that this training strategy actually enforces invariance not only against noise but against a variety of different input augmentations. Finally, it allows us to bridge the domain gap between simulated and real data.

我们将证明这种训练策略不仅能强制模型对噪声保持不变性，还能应对多种不同的输入增强。最终，它使我们能够弥合仿真数据与真实数据之间的领域差距。

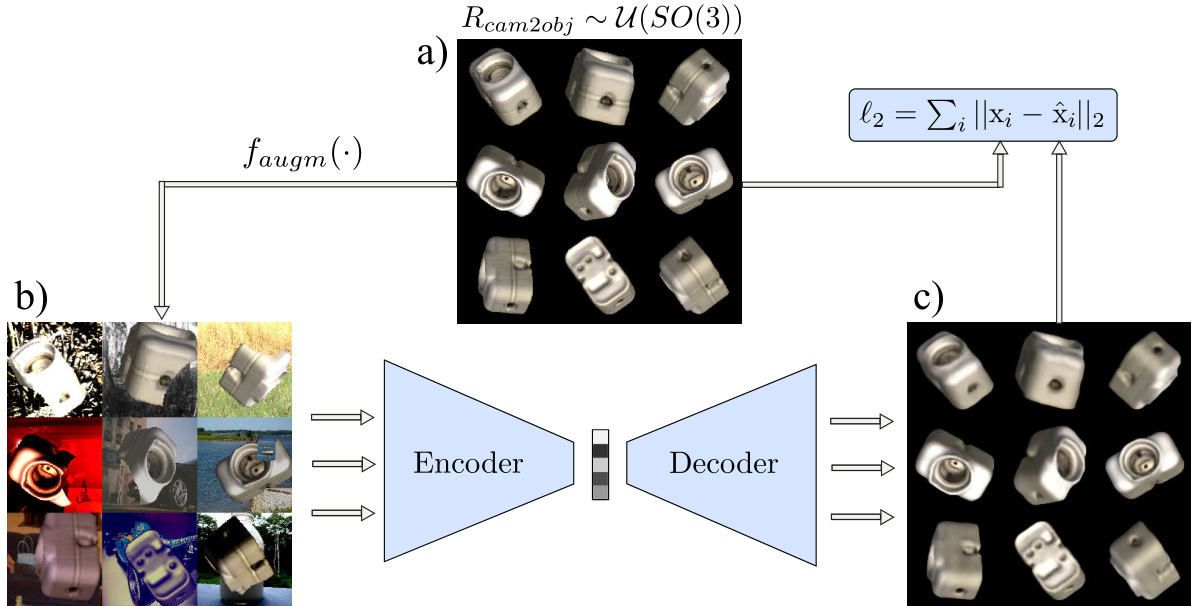
Fig. 4: Training process for the AAE; a) reconstruction target batch $\pmb{x}$ of uniformly sampled SO(3) object views; b) geometric and color augmented input; c) reconstruction $\hat{\pmb{x}}$ after 40000 iterations

图 4: AAE训练过程；a) 均匀采样SO(3)物体视角的重建目标批次$\pmb{x}$；b) 几何与颜色增强的输入；c) 40000次迭代后的重建结果$\hat{\pmb{x}}$

3.2 Augmented Auto encoder

3.2 增强型自动编码器

The motivation behind the AAE is to control what the latent representation encodes and which properties are ignored. We apply random augmentations $f_{a u g m}(.)$ to the input images $x\in\mathcal{R}^{\mathcal{D}}$ against which the encoding should become invariant. The reconstruction target remains eq. (2) but eq. (1) becomes

AAE的动机在于控制潜在表征编码的内容以及忽略哪些属性。我们对输入图像$x\in\mathcal{R}^{\mathcal{D}}$应用随机增强$f_{a u g m}(.)$，编码应对此保持不变。重建目标仍为式(2)，但式(1)变为

$$
\hat{x}=(\varPsi\circ\varPhi\circ f_{a u g m})(x)=(\varPsi\circ\varPhi)(x^{\prime})=\varPsi(z^{\prime})
$$

$$
\hat{x}=(\varPsi\circ\varPhi\circ f_{a u g m})(x)=(\varPsi\circ\varPhi)(x^{\prime})=\varPsi(z^{\prime})
$$

To make evident that Hypothesis $\mathbf{1}$ holds for geometric transformations, we learn latent representations of binary images depicting a 2D square at different scales, in-plane translations and rotations. Our goal is to encode only the in-plane rotations $r\in[0,2\pi]$ in a two dimensional latent space $z\in\mathcal{R}^{2}$ independent of scale or translation. Fig. 3 depicts the results after training a CNN-based AE architecture similar to the model in Fig. 5. It can be observed that the AEs trained on reconstructing squares at fixed scale and translation (1) or random scale and translation (2) do not clearly encode rotation alone, but are also sensitive to other latent factors. Instead, the encoding of the AAE (3) becomes invariant to translation and scale such that all squares with coinciding orientation are mapped to the same code. Furthermore, the latent representation is much smoother and the latent dimensions imitate a shifted sine and cosine function with frequency f = 24π respectively. The reason is that the square has two perpendicular axes of symmetry, i.e. after rotating $\frac{\pi}{2}$ the square appears the same. This property of representing the orientation based on the appearance of an object rather than on a fixed para me tri z ation is valuable to avoid ambiguities due to symmetries when teaching 3D object orientations.

为验证假设 $\mathbf{1}$ 在几何变换中的适用性，我们学习了描绘不同尺度、平面内平移和旋转的二维正方形二值图像的潜在表征。目标是在二维潜在空间 $z\in\mathcal{R}^{2}$ 中仅编码与尺度或平移无关的平面内旋转 $r\in[0,2\pi]$。图3展示了采用类似图5模型的CNN自编码器(AE)架构的训练结果。可观察到：在固定尺度和平移(1)或随机尺度和平移(2)条件下训练的自编码器未能清晰独立编码旋转，还受其他潜在因素影响；而对抗自编码器(AAE)(3)的编码对平移和尺度具有不变性，使得所有同方向正方形映射至相同编码。此外，潜在表征更平滑，其维度分别模拟频率f=24π的平移正弦和余弦函数——这是由于正方形具有两条垂直对称轴（旋转$\frac{\pi}{2}$后视觉不变）。这种基于物体外观而非固定参数化来表征方向的特征，对于避免三维物体方向教学中对称性导致的歧义具有重要价值。

3.3 Learning 3D Orientation from Synthetic Object Views

3.3 从合成物体视图中学习3D方向

Our toy problem showed that we can explicitly learn representations of object in-plane rotations using a geometric augmentation technique. Applying the same geometric input augmentations we can encode the whole SO(3) space of views from a 3D object model (CAD or 3D reconstruction) while being robust against inaccurate object detections. However, the encoder would still be unable to relate image crops from real RGB sensors because (1) the 3D model and the real object differ, (2) simulated and real lighting conditions differ, (3) the network can’t distinguish the object from background clutter and foreground occlusions. Instead of trying to imitate every detail of specific real sensor recordings in simulation we propose a Domain Randomization (DR) technique within the AAE framework to make the encodings invariant to insignificant environment and sensor variations. The goal is that the trained encoder treats the differences to real camera images as just another irrelevant variation. Therefore, while keeping reconstruction targets clean, we randomly apply ad- ditional augmentations to the input training views: (1)

我们的玩具问题表明，可以通过几何增强技术显式学习物体平面内旋转的表征。应用相同的几何输入增强方法，我们能从3D物体模型（CAD或三维重建）中编码完整的SO(3)视角空间，同时对不精确的物体检测保持鲁棒性。然而，编码器仍无法关联真实RGB传感器获取的图像区域，原因在于：(1) 3D模型与真实物体存在差异，(2) 模拟与真实光照条件不同，(3) 网络无法将目标物体与背景杂波及前景遮挡区分开来。我们未尝试在仿真中复现真实传感器记录的每个细节，而是在AAE框架内提出域随机化（DR）技术，使编码对环境与传感器无关变化保持恒定。其目标是让训练后的编码器将真实相机图像的差异视作另一种无关变异。因此，在保持重建目标纯净的同时，我们对输入训练视图随机施加以下增强：(1)

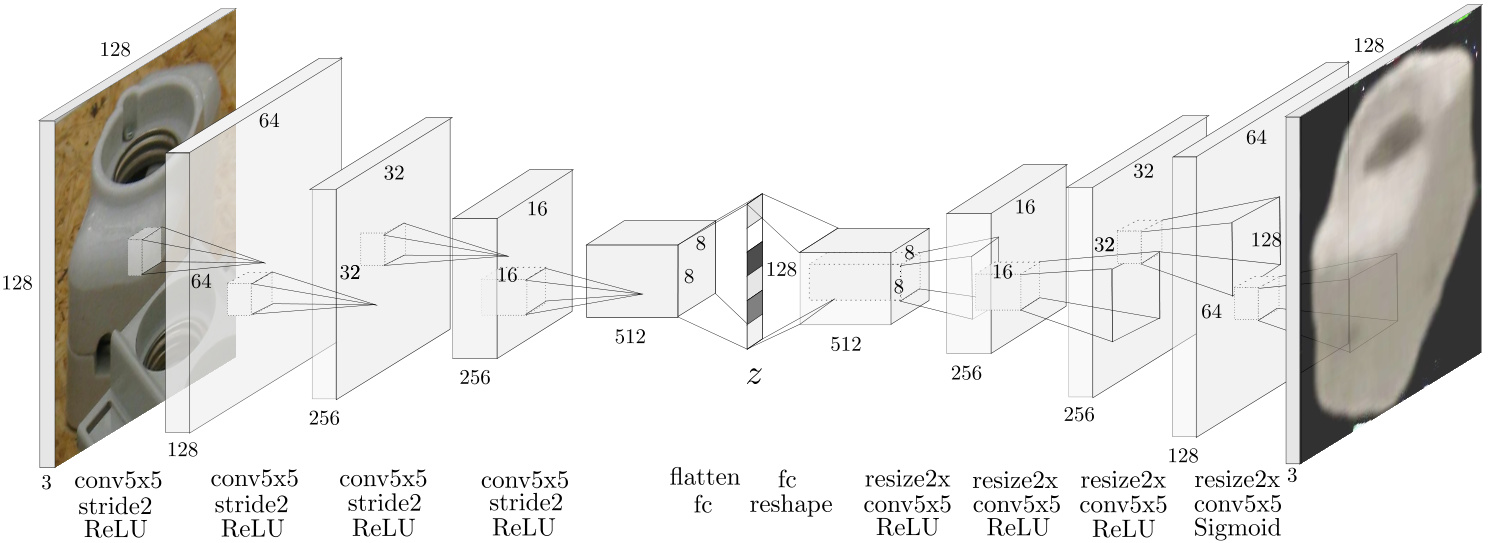
Fig. 5: Auto encoder CNN architecture with occluded test input, ”resize2x” depicts nearest-neighbor upsampling

图 5: 带有遮挡测试输入的自动编码器CNN架构 (Auto encoder CNN architecture with occluded test input)，"resize2x"表示最近邻上采样 (nearest-neighbor upsampling)

Table 1: Augmentation Parameters of AAE; Scale and translation is in relation to image shape and occlusion is in proportion of the object mask

表 1: AAE (Adversarial Autoencoder) 增强参数；缩放和平移相对于图像形状，遮挡相对于物体掩模比例

	50%概率 (每通道30%)	轻度 (随机位置) &几何变换
加法	U(-0.1,0.1)	环境光 0.4
对比度	U(0.4,2.3)	漫反射 U(0.7,0.9)
乘法	U(0.6,1.4)	镜面反射 U(0.2,0.4)
反相高斯模糊	0～U(0.0,1.2)	缩放 U(0.8,1.2) 平移 U(-0.15,0.15)

Fig. 6: AAE decoder reconstruction of LineMOD (left) and T-LESS (right) scene crops

图 6: LineMOD (左) 和 T-LESS (右) 场景裁剪的 AAE 解码器重建结果

3.4 Network Architecture and Training Details

3.4 网络架构与训练细节

The convolutional Auto encoder architecture that is used in our experiments is depicted in Fig. 5. We use a boots trapped pixel-wise L2 loss, first introduced by Wu et al. (2016). Only the pixels with the largest reconstruction errors contribute to the loss. Thereby, finer details are reconstructed and the training does not converge to local minima like reconstructing black images for all views. In our experiments, we choose a bootstrap factor of $k=4$ per image, meaning that $\textstyle{\frac{1}{4}}$ of all pixels contribute to the loss. Using OpenGL, we render 20000 views of each object uniformly at random 3D orientations and constant distance along the camera axis (700mm). The resulting images are quadratically cropped using the longer side of the bounding box and resized (nearest neighbor) to $128\times128\times3$ as shown in Fig. 4. All geometric and color input augmentations besides the rendering with random lighting are applied online during training at uniform random strength, parameters are found in Tab. 1. We use the Adam (Kingma and Ba, 2014) optimizer with a learning rate of $2\times10^{-4}$ , Xavier initialization (Glorot and Bengio, 2010), a batch size = 64 and 40000 iterations which takes $\sim4$ hours on a single Nvidia Geforce GTX 1080.

实验中采用的卷积自编码器 (Auto encoder) 架构如图 5 所示。我们使用了 Wu 等人 (2016) 首次提出的基于 bootstrap 的逐像素 L2 损失函数，仅重建误差最大的像素会参与损失计算。这种方法能重建更精细的细节，并避免训练陷入局部最优解（例如对所有视角都重建出黑色图像）。实验中，我们为每幅图像设置 bootstrap 因子 $k=4$，这意味着所有像素中 $\textstyle{\frac{1}{4}}$ 的像素会参与损失计算。

使用 OpenGL 渲染时，我们为每个物体在 700mm 固定相机距离下随机生成 20000 个均匀分布的 3D 视角，如图 4 所示，所得图像以包围盒长边为基准进行方形裁剪，并通过最近邻插值调整为 $128\times128\times3$ 分辨率。除随机光照渲染外，所有几何与色彩输入增强均在训练时以均匀随机强度在线应用，具体参数见表 1。优化器采用 Adam (Kingma and Ba, 2014)，学习率设为 $2\times10^{-4}$，使用 Xavier 初始化 (Glorot and Bengio, 2010)，批量大小为 64，迭代 40000 次，在单块 Nvidia Geforce GTX 1080 上耗时约 $\sim4$ 小时。

rendering with random light positions and randomized diffuse and specular reflection (simple Phong model (Phong,3.5 Codebook Creation and Test Procedure

3.5 码本创建与测试流程

1975. in OpenGL), (2) inserting random background images from the Pascal VOC dataset (Everingham et al., 2012), (3) varying image contrast, brightness, Gaussian blur and color distortions, (4) applying occlusions using random object masks or black squares. Fig. 4 depicts an exemplary training process for synthetic views of object 5 from T-LESS (Hodan et al., 2017).
1976. 在 OpenGL 中), (2) 从 Pascal VOC 数据集 (Everingham et al., 2012) 插入随机背景图像, (3) 改变图像对比度、亮度、高斯模糊和色彩失真, (4) 使用随机物体掩码或黑色方块进行遮挡。图 4 展示了 T-LESS (Hodan et al., 2017) 中物体 5 的合成视图训练过程示例。

After training, the AAE is able to extract a 3D object from real scene crops of many different camera sensors (Fig. 6). The clarity and orientation of the decoder reconstruction is an indicator of the encoding quality. To determine 3D object orientations from test scene crops we create a codebook (Fig. 7 (top)):

训练完成后，AAE能够从多种不同相机传感器的真实场景截图中提取3D物体（图6）。解码器重建的清晰度和方向性是编码质量的指标。为从测试场景截图中确定3D物体朝向，我们创建了一个码本（图7（上））：

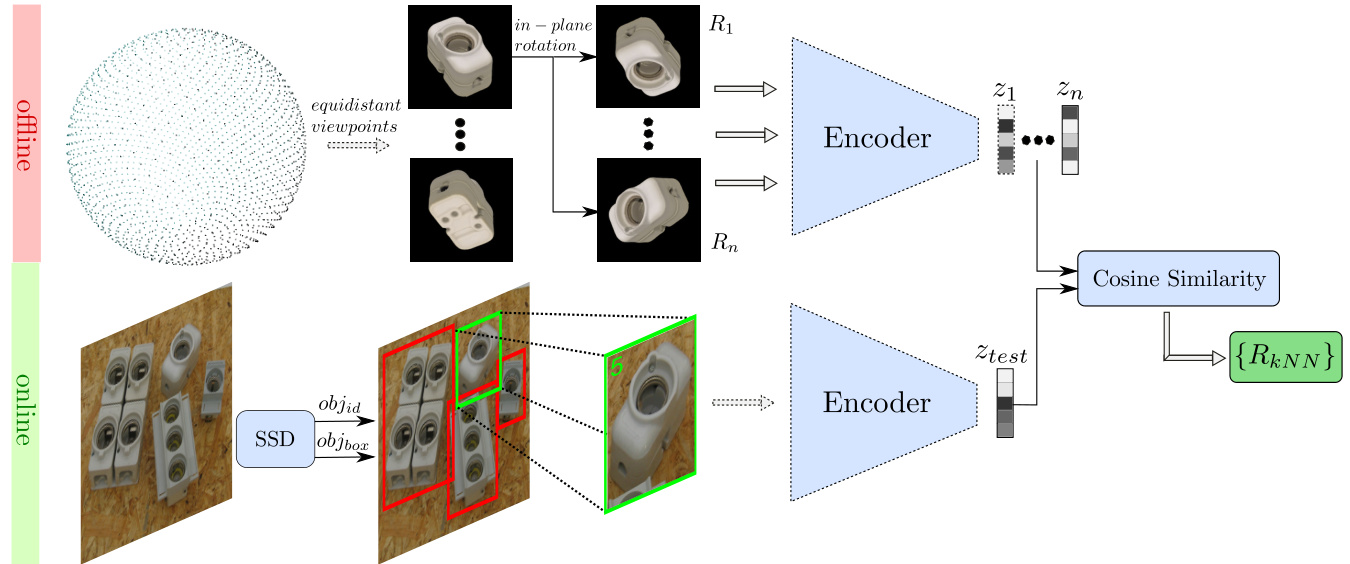
Fig. 7: Top: creating a codebook from the encodings of discrete synthetic object views; bottom: object detection and 3D orientation estimation using the nearest neighbor(s) with highest cosine similarity from the codebook

图 7: 上: 从离散合成物体视图的编码创建码本; 下: 使用码本中余弦相似度最高的最近邻进行物体检测和3D朝向估计

At test time, the considered object(s) are first detected in an RGB scene. The image is quadratically cropped using the longer side of the bounding box multiplied with a padding factor of 1.2 and resized to match the encoder input size. The padding accounts for imprecise bounding boxes. After encoding we compute the cosine similarity between the test code $z_{t e s t}\in\mathcal{R}^{128}$ and all codes $z_{i}\in\mathcal{R}^{128}$ from the codebook:

测试时，首先在RGB场景中检测目标物体。图像以边界框长边乘以1.2的填充因子进行方形裁剪，并调整尺寸以匹配编码器输入大小。该填充用于补偿边界框的不精确性。编码后，我们计算测试编码$z_{test}\in\mathcal{R}^{128}$与码本中所有编码$z_{i}\in\mathcal{R}^{128}$的余弦相似度：

$$
c o s_{i}=\frac{\pmb{z}{i}\pmb{z}{t e s t}}{|\pmb{z}{i}||\pmb{z}_{t e s t}|}
$$

$$
c o s_{i}=\frac{\pmb{z}{i}\pmb{z}{t e s t}}{|\pmb{z}{i}||\pmb{z}_{t e s t}|}
$$

The highest similarities are determined in a k-NearestNeighbor (kNN) search and the corresponding rotation matrices ${R_{k N N}}$ from the codebook are returned as estimates of the 3D object orientation. For the quantitative evaluation we use $k=1$ , however the next neighbors can yield valuable information on ambiguous views and could for example be used in particle filter based tracking. We use cosine similarity because (1) it can be very efficiently computed on a single GPU even for large codebooks. In our experiments we have 2562 equidistant viewpoints $\times~36$ in-plane rotation $=92232$ total entries. (2) We observed that, presumably due to the circular nature of rotations, scaling a latent test code does not change the object orientation of the decoder reconstruction (Fig. 8).

通过k近邻(kNN)搜索确定最高相似度，并从码本中返回相应的旋转矩阵${R_{k N N}}$作为3D物体朝向的估计值。定量评估时我们采用$k=1$，但邻近样本能为模糊视角提供有价值信息，例如可用于基于粒子滤波的追踪。选用余弦相似度的原因是：(1) 即使处理大型码本(实验中采用2562个等距视点$\times~36$个平面内旋转$=92232$个总条目)，单块GPU也能高效计算；(2) 我们观察到，可能由于旋转的循环特性，缩放潜在测试编码不会改变解码器重建的物体朝向(图8)。

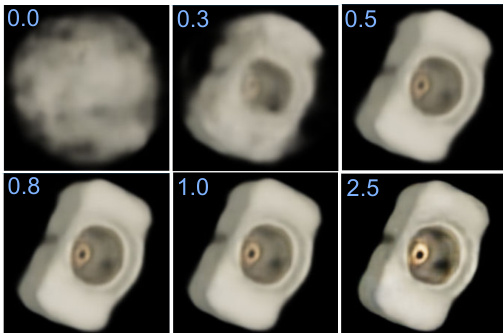
Fig. 8: AAE decoder reconstruction of a test code $z_{t e s t}\in\mathcal{R}^{128}$ scaled by a factor $s\in[0,2.5]$

图 8: 测试代码 $z_{test}\in\mathcal{R}^{128}$ 的 AAE (Adversarial Autoencoder) 解码器重建结果，缩放因子为 $s\in[0,2.5]$

Table 2: Augmentation Parameters for Object Detectors, top five are applied in random order; bottom part describes phong lighting from random light positions

表 2: 目标检测器的增强参数，前五项按随机顺序应用；底部描述随机光源位置的冯氏光照

	概率 (每项)	SIXDtrain	渲染的3D模型
加法	0.5 (0.15)	U(-0.08,0.08)	U(-0.1,0.1)
对比度归一化	0.5 (0.15)	U(0.5,2.2)	U(0.5,2.2)
乘法	0.5 (0.25)	U(0.6,1.4)	U(0.5,1.5)
高斯模糊	0.2	0~U(0.5,1.0)	= 0.4
高斯噪声	0.1 (0.1)	0= 0.04
环境光	1.0		0.4
漫反射	1.0		u(0.7,0.9)
镜面反射	1.0		U(0.2,0.4)

3.6 Extending to 6D Object Detection

3.6 扩展到6D物体检测

3.6.1 Training the 2D Object Detector.

3.6.1 训练2D物体检测器

We finetune the 2D Object Detectors using the object views on black background which are provided in the training datasets of LineMOD and T-LESS. In LineMOD we additionally render domain randomized views of the provided 3D models and freeze the backbone like in Hinter s to is ser et al. (2017). Multiple object views are sequentially copied into an empty scene at random translation, scale and in-plane rotation. Bounding box annotations are adapted accordingly. If an object view is more than 40% occluded, we re-sample it. Then, as for the AAE, the black background is replaced with Pascal VOC images. The random iz ation schemes and parameters can be found in Table 2. In T-LESS we train SSD (Liu et al., 2016) with VGG16 backbone and RetinaNet (Lin et al., 2018) with ResNet50 backbone which is slower but more accurate, on LineMOD we only train RetinaNet. For T-LESS we generate 60000 training samples from the provided training dataset and for LineMOD we generate 60000 samples from the training dataset plus 60000 samples from 3D model renderings with randomized lighting conditions (see Table 2). The RetinaNet achieves 0.73mAP@0.5IoU onT-LESS and 0.62mAP@0.5IoU on LineMOD. On Occluded LineMOD, the detectors trained on the simplistic renderings failed to achieve good detection performance. However, recent work of Hodan et al. (2019) quantitatively investigated the training of 2D detectors on synthetic data and they reached decent detection performance on Occluded LineMOD by fine-tuning FasterRCNN on photo-realistic synthetic images showing the feasibility of a purely synthetic pipeline.

我们使用LineMOD和T-LESS训练数据集中提供的黑色背景物体视图对2D目标检测器进行微调。在LineMOD中，我们还额外渲染了所提供3D模型的域随机化视图，并像Hinterstoisser等人(2017)那样冻结骨干网络。多个物体视图以随机平移、缩放和平面内旋转的方式依次复制到空场景中，边界框标注也相应调整。若物体视图被遮挡超过40%，则重新采样。随后与AAE方法类似，将黑色背景替换为Pascal VOC图像。随机化方案和参数详见表2。

在T-LESS数据集上，我们训练了基于VGG16骨干网络的SSD(Liu等人,2016)和基于ResNet50骨干网络(速度较慢但精度更高)的RetinaNet(Lin等人,2018)，而在LineMOD上仅训练RetinaNet。对于T-LESS，我们从提供的训练数据集中生成60000个训练样本；对于LineMOD，则从训练数据集生成60000个样本，外加60000个采用随机光照条件渲染的3D模型样本(见表2)。RetinaNet在T-LESS上达到0.73mAP@0.5IoU，在LineMOD上达到0.62mAP@0.5IoU。

在Occluded LineMOD数据集上，基于简单渲染训练的检测器未能取得良好性能。但Hodan等人(2019)的最新研究定量分析了合成数据训练2D检测器的方法，他们通过在逼真合成图像上微调FasterRCNN，在Occluded LineMOD上取得了不错的检测性能，证明了纯合成管道的可行性。

3.6.2 Projective Distance Estimation

3.6.2 投影距离估计

We estimate the full 3D translation $t_{r e a l}$ from came