MixMatch: A Holistic Approach to Semi-Supervised Learning
MixMatch:半监督学习的整体方法
Abstract
摘要
Semi-supervised learning has proven to be a powerful paradigm for leveraging unlabeled data to mitigate the reliance on large labeled datasets. In this work, we unify the current dominant approaches for semi-supervised learning to produce a new algorithm, MixMatch, that guesses low-entropy labels for data-augmented unlabeled examples and mixes labeled and unlabeled data using MixUp. MixMatch obtains state-of-the-art results by a large margin across many datasets and labeled data amounts. For example, on CIFAR-10 with 250 labels, we reduce error rate by a factor of 4 (from $38%$ to $11%$ ) and by a factor of 2 on STL-10. We also demonstrate how MixMatch can help achieve a dramatically better accuracy-privacy trade-off for differential privacy. Finally, we perform an ablation study to tease apart which components of MixMatch are most important for its success. We release all code used in our experiments.1
半监督学习已被证明是利用未标记数据减轻对大型标记数据集依赖的强大范式。在本研究中,我们统一了当前主流的半监督学习方法,提出了一种新算法MixMatch:该算法通过数据增强为未标记样本预测低熵标签,并利用MixUp混合标记与未标记数据。MixMatch在多个数据集和不同标记数据量上均以显著优势取得最先进成果。例如在仅含250个标记的CIFAR-10数据集上,我们将错误率降低了4倍(从$38%$降至$11%$),在STL-10上降低2倍。我们还展示了MixMatch如何显著提升差分隐私的精度-隐私权衡效果。最后通过消融实验解析了MixMatch各组件对其成功的关键贡献。我们公开了实验中的所有代码。[20]
1 Introduction
1 引言
Much of the recent success in training large, deep neural networks is thanks in part to the existence of large labeled datasets. Yet, collecting labeled data is expensive for many learning tasks because it necessarily involves expert knowledge. This is perhaps best illustrated by medical tasks where measurements call for expensive machinery and labels are the fruit of a time-consuming analysis that draws from multiple human experts. Furthermore, data labels may contain private information. In comparison, in many tasks it is much easier or cheaper to obtain unlabeled data.
近期在训练大型深度神经网络方面取得的成功,很大程度上得益于大规模标注数据集的存在。然而,对于许多学习任务而言,收集标注数据成本高昂,因为这必然涉及专业知识。医疗任务最能体现这一点:测量需要昂贵设备,而标注则是多位专家耗时分析的结果。此外,数据标注可能包含隐私信息。相比之下,许多任务中获取未标注数据要容易或廉价得多。
Semi-supervised learning [6] (SSL) seeks to largely alleviate the need for labeled data by allowing a model to leverage unlabeled data. Many recent approaches for semi-supervised learning add a loss term which is computed on unlabeled data and encourages the model to generalize better to unseen data. In much recent work, this loss term falls into one of three classes (discussed further in Section 2): entropy minimization [18, 28]—which encourages the model to output confident predictions on unlabeled data; consistency regular iz ation—which encourages the model to produce the same output distribution when its inputs are perturbed; and generic regular iz ation—which encourages the model to generalize well and avoid over fitting the training data.
半监督学习 [6] (SSL) 旨在通过让模型利用未标注数据来大幅减少对标注数据的需求。近期许多半监督学习方法都添加了一个基于未标注数据计算的损失项,以促使模型更好地泛化到未见数据。在近期工作中,这类损失项主要分为三类 (详见第2节讨论) : 熵最小化 [18, 28] —— 促使模型对未标注数据输出置信度更高的预测;一致性正则化 —— 促使模型在输入受到扰动时保持相同的输出分布;以及通用正则化 —— 促使模型实现良好泛化并避免对训练数据的过拟合。
In this paper, we introduce MixMatch, an SSL algorithm which introduces a single loss that gracefully unifies these dominant approaches to semi-supervised learning. Unlike previous methods, MixMatch targets all the properties at once which we find leads to the following benefits:
本文提出MixMatch算法,这是一种半监督学习(SSL)算法,通过单一损失函数优雅地统一了当前主流的半监督学习方法。与先前方法不同,MixMatch能同时实现所有目标属性,我们研究发现这带来了以下优势:

Figure 1: Diagram of the label guessing process used in MixMatch. Stochastic data augmentation is applied to an unlabeled image $K$ times, and each augmented image is fed through the classifier. Then, the average of these $K$ predictions is “sharpened” by adjusting the distribution’s temperature. See algorithm 1 for a full description.
图 1: MixMatch中使用的标签猜测过程示意图。对未标记图像应用随机数据增强 $K$ 次,每次增强后的图像通过分类器处理。然后,通过调整分布温度对这些 $K$ 次预测的平均值进行"锐化"。完整描述参见算法1。
• Experimentally, we show that MixMatch obtains state-of-the-art results on all standard image benchmarks (section 4.2), and reducing the error rate on CIFAR-10 by a factor of 4; • We further show in an ablation study that MixMatch is greater than the sum of its parts; • We demonstrate in section 4.3 that MixMatch is useful for differential ly private learning, enabling students in the PATE framework [36] to obtain new state-of-the-art results that simultaneously strengthen both privacy guarantees and accuracy.
• 实验表明,MixMatch 在所有标准图像基准测试( section 4.2)中都取得了最先进的结果,并将 CIFAR-10 的错误率降低了 4 倍;
• 我们在消融研究中进一步表明,MixMatch 的效果优于其各部分的总和;
• 我们在 section 4.3 中证明,MixMatch 对差分隐私学习非常有用,使 PATE 框架 [36] 中的学生能够同时增强隐私保证和准确性,从而获得新的最先进结果。
In short, MixMatch introduces a unified loss term for unlabeled data that seamlessly reduces entropy while maintaining consistency and remaining compatible with traditional regular iz ation techniques.
简而言之,MixMatch为无标签数据引入了一个统一的损失项,该损失项在保持一致性并与传统正则化技术兼容的同时,还能无缝降低熵值。
2 Related Work
2 相关工作
To set the stage for MixMatch, we first introduce existing methods for SSL. We focus mainly on those which are currently state-of-the-art and that MixMatch builds on; there is a wide literature on SSL techniques that we do not discuss here (e.g., “trans duct ive” models [14, 22, 21], graph-based methods [49, 4, 29], generative modeling [3, 27, 41, 9, 17, 23, 38, 34, 42], etc.). More comprehensive overviews are provided in [49, 6]. In the following, we will refer to a generic model $\mathrm{p}_{\mathrm{model}}(y\mid x;\theta)$ which produces a distribution over class labels $y$ for an input $x$ with parameters $\theta$ .
为介绍MixMatch方法,我们首先回顾现有的半监督学习(SSL)技术。本文主要关注当前最先进且MixMatch所基于的方法,其他SSL技术(如转导模型[14, 22, 21]、基于图的方法[49, 4, 29]、生成式建模[3, 27, 41, 9, 17, 23, 38, 34, 42]等)不在讨论范围内。更全面的综述可参考[49, 6]。下文将使用通用模型$\mathrm{p}_{\mathrm{model}}(y\mid x;\theta)$表示参数为$\theta$的模型对输入$x$输出类别标签$y$的概率分布。
2.1 Consistency Regular iz ation
2.1 一致性正则化 (Consistency Regularization)
A common regular iz ation technique in supervised learning is data augmentation, which applies input transformations assumed to leave class semantics unaffected. For example, in image classification, it is common to elastically deform or add noise to an input image, which can dramatically change the pixel content of an image without altering its label [7, 43, 10]. Roughly speaking, this can artificially expand the size of a training set by generating a near-infinite stream of new, modified data. Consistency regular iz ation applies data augmentation to semi-supervised learning by leveraging the idea that a classifier should output the same class distribution for an unlabeled example even after it has been augmented. More formally, consistency regular iz ation enforces that an unlabeled example $x$ should be classified the same as ${\mathrm{Augment}}(x)$ , an augmentation of itself.
监督学习中一种常见的正则化技术是数据增强(data augmentation),该方法通过应用输入变换来保持类别语义不受影响。例如在图像分类任务中,通常会采用弹性变形或添加噪声等方式处理输入图像,这些操作能在不改变图像标签的前提下显著改变其像素内容[7,43,10]。从本质上说,这种方法能通过生成近乎无限的新增修改数据,人为地扩大训练集规模。一致性正则化(consistency regularization)将数据增强应用于半监督学习,其核心思想是分类器应对未标注样本及其增强版本输出相同的类别分布。更形式化地说,一致性正则化要求未标注样本$x$应与自身增强版本${\mathrm{Augment}}(x)$获得相同的分类结果。
In the simplest case, for unlabeled points $x$ , prior work [25, 40] adds the loss term
对于未标注点$x$的最简单情况,先前工作[25, 40]添加了损失项
$$
|{\mathrm{p}}{\mathrm{model}}(y\mid{\mathrm{Augment}}(x);\theta)-{\mathrm{p}}{\mathrm{model}}(y\mid{\mathrm{Augment}}(x);\theta)|_{2}^{2}.
$$
$$
|{\mathrm{p}}{\mathrm{model}}(y\mid{\mathrm{Augment}}(x);\theta)-{\mathrm{p}}{\mathrm{model}}(y\mid{\mathrm{Augment}}(x);\theta)|_{2}^{2}.
$$
Note that ${\mathrm{Augment}}(x)$ is a stochastic transformation, so the two terms in eq. (1) are not identical. “Mean Teacher” [44] replaces one of the terms in eq. (1) with the output of the model using an exponential moving average of model parameter values. This provides a more stable target and was found empirically to significantly improve results. A drawback to these approaches is that they use domain-specific data augmentation strategies. “Virtual Adversarial Training” [31] (VAT) addresses this by instead computing an additive perturbation to apply to the input which maximally changes the output class distribution. MixMatch utilizes a form of consistency regular iz ation through the use of standard data augmentation for images (random horizontal flips and crops).
请注意 ${\mathrm{Augment}}(x)$ 是一种随机变换,因此等式 (1) 中的两项并不相同。"Mean Teacher" [44] 将等式 (1) 中的一项替换为使用模型参数指数移动平均值的模型输出。这提供了更稳定的目标,并根据经验发现能显著改善结果。这些方法的缺点在于它们使用了特定领域的数据增强策略。"Virtual Adversarial Training" [31] (VAT) 通过计算一个使输出类别分布变化最大的加性扰动来解决这个问题。MixMatch 通过对图像使用标准数据增强 (随机水平翻转和裁剪) 来实现一种形式的正则化一致性。
2.2 Entropy Minimization
2.2 熵最小化
A common underlying assumption in many semi-supervised learning methods is that the classifier’s decision boundary should not pass through high-density regions of the marginal data distribution.
许多半监督学习方法的共同潜在假设是,分类器的决策边界不应穿过边缘数据分布的高密度区域。
One way to enforce this is to require that the classifier output low-entropy predictions on unlabeled data. This is done explicitly in [18] with a loss term which minimizes the entropy of $\operatorname{p}_{\mathrm{model}}(y\mid x;\theta)$ for unlabeled data $x$ . This form of entropy minimization was combined with VAT in [31] to obtain stronger results. “Pseudo-Label” [28] does entropy minimization implicitly by constructing hard (1-hot) labels from high-confidence predictions on unlabeled data and using these as training targets in a standard cross-entropy loss. MixMatch also implicitly achieves entropy minimization through the use of a “sharpening” function on the target distribution for unlabeled data, described in section 3.2.
一种强制执行方法是要求分类器对未标记数据输出低熵预测。[18]中明确采用了一种损失项来实现这一点,该损失项最小化未标记数据$x$的$\operatorname{p}_{\mathrm{model}}(y\mid x;\theta)$熵。这种形式的熵最小化与[31]中的虚拟对抗训练(VAT)结合,获得了更强的结果。"Pseudo-Label"[28]通过从高置信度未标记数据预测中构建硬(one-hot)标签,并在标准交叉熵损失中将其用作训练目标,从而隐式实现了熵最小化。MixMatch也通过3.2节描述的未标记数据目标分布"锐化"函数隐式实现了熵最小化。
2.3 Traditional Regular iz ation
2.3 传统正则化
Regular iz ation refers to the general approach of imposing a constraint on a model to make it harder to memorize the training data and therefore hopefully make it generalize better to unseen data [19]. We use weight decay which penalizes the $L_{2}$ norm of the model parameters [30, 46]. We also use MixUp [47] in MixMatch to encourage convex behavior “between” examples. We utilize MixUp as both as a regularize r (applied to labeled datapoints) and a semi-supervised learning method (applied to unlabeled datapoints). MixUp has been previously applied to semi-supervised learning; in particular, the concurrent work of [45] uses a subset of the methodology used in MixMatch. We clarify the differences in our ablation study (section 4.2.3).
正则化 (regularization) 是指通过对模型施加约束使其更难记住训练数据,从而有望提升对未见数据的泛化能力的通用方法 [19]。我们采用权重衰减 (weight decay) 来惩罚模型参数的 $L_{2}$ 范数 [30, 46]。在 MixMatch 中我们还使用 MixUp [47] 来促进样本"之间"的凸行为。我们将 MixUp 同时作为正则化器 (应用于标注数据点) 和半监督学习方法 (应用于未标注数据点) 使用。MixUp 此前已被应用于半监督学习,特别是同期研究 [45] 采用了 MixMatch 方法中的部分技术。我们将在消融研究 (章节 4.2.3) 中阐明这些差异。
3 MixMatch
3 MixMatch
In this section, we introduce MixMatch, our proposed semi-supervised learning method. MixMatch is a “holistic” approach which incorporates ideas and components from the dominant paradigms for SSL discussed in section 2. Given a batch $\mathcal{X}$ of labeled examples with one-hot targets (representing one of $L$ possible labels) and an equally-sized batch $\mathcal{U}$ of unlabeled examples, MixMatch produces a processed batch of augmented labeled examples $\mathcal{X}^{\prime}$ and a batch of augmented unlabeled examples with “guessed” labels $\mathcal{U}^{\prime},\mathcal{U}^{\prime}$ and $\mathcal{X}^{\prime}$ are then used in computing separate labeled and unlabeled loss terms. More formally, the combined loss $\mathcal{L}$ for semi-supervised learning is defined as
在本节中,我们将介绍提出的半监督学习方法MixMatch。MixMatch是一种"整体性"方法,融合了第2节讨论的主流半监督学习(SSL)范式的思想和组件。给定一个带独热目标(表示L个可能标签之一)的标记样本批次$\mathcal{X}$和同等大小的未标记样本批次$\mathcal{U}$,MixMatch会生成增强后的标记样本批次$\mathcal{X}^{\prime}$和带有"猜测"标签的增强未标记样本批次$\mathcal{U}^{\prime}$。随后$\mathcal{U}^{\prime}$和$\mathcal{X}^{\prime}$将分别用于计算标记和未标记的损失项。更正式地说,半监督学习的组合损失$\mathcal{L}$定义为
$$
\begin{array}{r l}&{\mathcal{X}^{\prime},\mathcal{U}^{\prime}=\displaystyle\mathrm{MixMatch}(\mathcal{X},\mathcal{U},T,K,\alpha)}\ &{\quad\mathcal{L}_{\mathcal{X}}=\displaystyle\frac{1}{|\mathcal{X}^{\prime}|}\sum_{\boldsymbol{x},\boldsymbol{p}\in\mathcal{X}^{\prime}}\mathrm{H}(\boldsymbol{p},\mathrm{p}_{\mathrm{model}}(\boldsymbol{y}\mid\boldsymbol{x};\boldsymbol{\theta}))}\ &{\quad\mathcal{L}_{\mathcal{U}}=\displaystyle\frac{1}{L|\mathcal{U}^{\prime}|}\sum_{\boldsymbol{u},\boldsymbol{q}\in\mathcal{U}^{\prime}}|\boldsymbol{q}-\mathrm{p}_{\mathrm{model}}(\boldsymbol{y}\mid\boldsymbol{u};\boldsymbol{\theta})|_{2}^{2}}\ &{\quad\textit{\textbf{c}},\quad\textit{\textbf{\textit{\textbf{\textit{\textbf{\imath}}}}}},\quad\alpha}\end{array}
$$
$$
\begin{array}{r l}&{\mathcal{X}^{\prime},\mathcal{U}^{\prime}=\displaystyle\mathrm{MixMatch}(\mathcal{X},\mathcal{U},T,K,\alpha)}\ &{\quad\mathcal{L}_{\mathcal{X}}=\displaystyle\frac{1}{|\mathcal{X}^{\prime}|}\sum_{\boldsymbol{x},\boldsymbol{p}\in\mathcal{X}^{\prime}}\mathrm{H}(\boldsymbol{p},\mathrm{p}_{\mathrm{model}}(\boldsymbol{y}\mid\boldsymbol{x};\boldsymbol{\theta}))}\ &{\quad\mathcal{L}_{\mathcal{U}}=\displaystyle\frac{1}{L|\mathcal{U}^{\prime}|}\sum_{\boldsymbol{u},\boldsymbol{q}\in\mathcal{U}^{\prime}}|\boldsymbol{q}-\mathrm{p}_{\mathrm{model}}(\boldsymbol{y}\mid\boldsymbol{u};\boldsymbol{\theta})|_{2}^{2}}\ &{\quad\textit{\textbf{c}},\quad\textit{\textbf{\textit{\textbf{\textit{\textbf{\imath}}}}}},\quad\alpha}\end{array}
$$
$$
\mathcal{L}=\mathcal{L}{\mathcal{X}}+\lambda_{\mathcal{U}}\mathcal{L}_{\mathcal{U}}
$$
$$
\mathcal{L}=\mathcal{L}{\mathcal{X}}+\lambda_{\mathcal{U}}\mathcal{L}_{\mathcal{U}}
$$
where $\mathrm{H}(p,q)$ is the cross-entropy between distributions $p$ and $q$ , and $T,K,\alpha$ , and $\lambda_{\mathcal{U}}$ are hyperparameters described below. The full MixMatch algorithm is provided in algorithm 1, and a diagram of the label guessing process is shown in fig. 1. Next, we describe each part of MixMatch.
其中 $\mathrm{H}(p,q)$ 表示分布 $p$ 和 $q$ 之间的交叉熵,$T,K,\alpha$ 以及 $\lambda_{\mathcal{U}}$ 是下文将描述的超参数。完整的 MixMatch 算法如算法 1 所示,标签猜测过程的示意图见图 1。接下来我们将介绍 MixMatch 的各个部分。
3.1 Data Augmentation
3.1 数据增强
As is typical in many SSL methods, we use data augmentation both on labeled and unlabeled data. For each $x_{b}$ in the batch of labeled data $\mathcal{X}$ , we generate a transformed version $\hat{x}{b}=\mathrm{Augment}(x_{b})$ (algorithm 1, line 3). For each $u_{b}$ in the batch of unlabeled data $\mathcal{U}$ , we generate $K$ augmentations ${{\hat{u}}{b,k}}=\mathrm{Augment}({u_{b}}),k\in(1,\ldots,K)$ (algorithm 1, line 5). We use these individual augmentations to generate a “guessed label” $q_{b}$ for each $u_{b}$ , through a process we describe in the following subsection.
与许多SSL方法类似,我们对标注数据和未标注数据都进行了数据增强。对于标注数据批次$\mathcal{X}$中的每个$x_{b}$,生成变换版本$\hat{x}{b}=\mathrm{Augment}(x_{b})$(算法1第3行)。对于未标注数据批次$\mathcal{U}$中的每个$u_{b}$,生成$K$个增强版本${{\hat{u}}{b,k}}=\mathrm{Augment}({u_{b}}),k\in(1,\ldots,K)$(算法1第5行)。我们通过这些独立增强样本为每个$u_{b}$生成"猜测标签"$q_{b}$,具体过程将在下个小节说明。
3.2 Label Guessing
3.2 标签猜测
For each unlabeled example in $\mathcal{U}$ , MixMatch produces a “guess” for the example’s label using the model’s predictions. This guess is later used in the unsupervised loss term. To do so, we compute the average of the model’s predicted class distributions across all the $K$ augmentations of $u_{b}$ by
对于 $\mathcal{U}$ 中的每个未标注样本,MixMatch 利用模型预测为该样本生成一个"猜测"标签。这一猜测后续将用于无监督损失项。具体实现时,我们通过计算模型对 $u_{b}$ 所有 $K$ 次增强版本的预测类别分布平均值来实现。
$$
\bar{q}{b}=\frac{1}{K}\sum_{k=1}^{K}\operatorname{p}{\operatorname{model}}(y\mid\hat{u}_{b,k};\theta)
$$
$$
\bar{q}{b}=\frac{1}{K}\sum_{k=1}^{K}\operatorname{p}{\operatorname{model}}(y\mid\hat{u}_{b,k};\theta)
$$
in algorithm 1, line 7. Using data augmentation to obtain an artificial target for an unlabeled example is common in consistency regular iz ation methods [25, 40, 44].
在算法1第7行中,使用数据增强为未标注样本生成人工目标是一致性正则化方法中的常见做法 [25, 40, 44]。
Algorithm 1 MixMatch takes a batch of labeled data $\mathcal{X}$ and a batch of unlabeled data $\mathcal{U}$ and produces a collection $\mathcal{X}^{\prime}$ (resp. $\mathcal{U}^{\prime}$ ) of processed labeled examples (resp. unlabeled with guessed labels).
算法 1 MixMatch 接收一批带标签数据 $\mathcal{X}$ 和一批无标签数据 $\mathcal{U}$ ,生成处理后的带标签样本集合 $\mathcal{X}^{\prime}$ (对应地,无标签样本的猜测标签集合 $\mathcal{U}^{\prime}$ )。
Sharpening. In generating a label guess, we perform one additional step inspired by the success of entropy minimization in semi-supervised learning (discussed in section 2.2). Given the average prediction over augmentations $\bar{q}_{b}$ , we apply a sharpening function to reduce the entropy of the label distribution. In practice, for the sharpening function, we use the common approach of adjusting the “temperature” of this categorical distribution [16], which is defined as the operation
锐化。在生成标签猜测时,我们额外增加了一个步骤,其灵感来自于半监督学习中熵最小化的成功(在第2.2节中讨论)。给定数据增强的平均预测 $\bar{q}_{b}$ ,我们应用锐化函数来降低标签分布的熵。实际上,对于锐化函数,我们采用了调整分类分布"温度"的常见方法 [16],其定义为操作
$$
{\mathrm{Sharpen}}(p,T){i}:=p_{i}^{\frac{1}{T}}{\Bigg/}\sum_{j=1}^{L}p_{j}^{\frac{1}{T}}
$$
$$
{\mathrm{Sharpen}}(p,T){i}:=p_{i}^{\frac{1}{T}}{\Bigg/}\sum_{j=1}^{L}p_{j}^{\frac{1}{T}}
$$
where $p$ is some input categorical distribution (specifically in MixMatch, $p$ is the average class prediction over augmentations $\bar{q}{b}$ , as shown in algorithm 1, line 8) and $T$ is a hyper parameter. As $T\rightarrow0$ , the output of ${\mathrm{Sharpen}}(p,T)$ will approach a Dirac (“one-hot”) distribution. Since we will later use $q_{b}=\mathrm{Sharpen}(\bar{q}{b},T)$ as a target for the model’s prediction for an augmentation of $u_{b}$ , lowering the temperature encourages the model to produce lower-entropy predictions.
其中 $p$ 是某个输入分类分布 (在 MixMatch 中特指增强预测的平均类别概率 $\bar{q}{b}$,如算法 1 第 8 行所示),$T$ 是超参数。当 $T\rightarrow0$ 时,${\mathrm{Sharpen}}(p,T)$ 的输出将趋近狄拉克 ("独热") 分布。由于后续我们将使用 $q_{b}=\mathrm{Sharpen}(\bar{q}{b},T)$ 作为模型对 $u_{b}$ 增强样本的预测目标,降低温度参数会促使模型产生更低熵的预测结果。
3.3 MixUp
3.3 MixUp
We use MixUp for semi-supervised learning, and unlike past work for SSL we mix both labeled examples and unlabeled examples with label guesses (generated as described in section 3.2). To be compatible with our separate loss terms, we define a slightly modified version of MixUp. For a pair of two examples with their corresponding labels probabilities $(x_{1},p_{1}),(x_{2},p_{2})$ we compute $(x^{\prime},p^{\prime})$ by
我们在半监督学习中使用MixUp方法,与以往SSL (Semi-Supervised Learning) 工作不同,我们会混合带标签样本和带有标签猜测(生成方式如第3.2节所述)的无标签样本。为了兼容我们独立的损失项,我们定义了一个略微修改版的MixUp。对于一对样本及其对应的标签概率 $(x_{1},p_{1}),(x_{2},p_{2})$,我们通过计算得到 $(x^{\prime},p^{\prime})$
$$
\begin{array}{l}{{\lambda\sim\mathrm{Beta}(\alpha,\alpha)}}\ {{\lambda^{\prime}=\operatorname*{max}(\lambda,1-\lambda)}}\ {{x^{\prime}=\lambda^{\prime}x_{1}+(1-\lambda^{\prime})x_{2}}}\ {{p^{\prime}=\lambda^{\prime}p_{1}+(1-\lambda^{\prime})p_{2}}}\end{array}
$$
$$
\begin{array}{l}{{\lambda\sim\mathrm{Beta}(\alpha,\alpha)}}\ {{\lambda^{\prime}=\operatorname*{max}(\lambda,1-\lambda)}}\ {{x^{\prime}=\lambda^{\prime}x_{1}+(1-\lambda^{\prime})x_{2}}}\ {{p^{\prime}=\lambda^{\prime}p_{1}+(1-\lambda^{\prime})p_{2}}}\end{array}
$$
where $\alpha$ is a hyper parameter. Vanilla MixUp omits eq. (9) (i.e. it sets $\lambda^{\prime}=\lambda$ ). Given that labeled and unlabeled examples are concatenated in the same batch, we need to preserve the order of the batch to compute individual loss components appropriately. This is achieved by eq. (9) which ensures that $x^{\prime}$ is closer to $x_{1}$ than to $x_{2}$ . To apply MixUp, we first collect all augmented labeled examples with their labels and all unlabeled examples with their guessed labels into
其中$\alpha$是一个超参数。原始MixUp忽略了公式(9)(即设$\lambda^{\prime}=\lambda$)。由于标注样本和无标注样本在同一个批次中被拼接,我们需要保持批次顺序以正确计算各损失分量。公式(9)通过确保$x^{\prime}$更接近$x_{1}$而非$x_{2}$来实现这一点。应用MixUp时,我们首先将所有增强的标注样本及其标签、所有无标注样本及其猜测标签收集到
$$
\begin{array}{r l}&{\hat{\mathcal{X}}=\left((\hat{x}{b},p_{b});b\in(1,\ldots,B)\right)}\ &{\hat{\mathcal{U}}=\left((\hat{u}{b,k},q_{b});b\in(1,\ldots,B),k\in(1,\ldots,K)\right)}\end{array}
$$
$$
\begin{array}{r l}&{\hat{\mathcal{X}}=\left((\hat{x}{b},p_{b});b\in(1,\ldots,B)\right)}\ &{\hat{\mathcal{U}}=\left((\hat{u}{b,k},q_{b});b\in(1,\ldots,B),k\in(1,\ldots,K)\right)}\end{array}
$$
(algorithm 1, lines 10–11). Then, we combine these collections and shuffle the result to form $\mathcal{W}$ which will serve as a data source for MixUp (algorithm 1, line 12). For each the $i^{t h}$ example-label pair in $\hat{\mathcal X}$ , we compute $\mathrm{MixUp}(\hat{\mathcal{X}}{i},\mathcal{W}{i})$ and add the result to the collection $\mathcal{X}^{\prime}$ (algorithm 1, line 13). We compute $\mathcal{U}{i}^{\prime}=\mathrm{MixUp}(\hat{\mathcal{U}}{i},\mathcal{W}_{i+|\hat{\mathcal{X}}|})$ for $i\in(1,\dots,|\hat{\mathcal{U}}|)$ , intentionally using the remainder of $\mathcal{W}$ that was not used in the construction of $\mathcal{X}^{\prime}$ (algorithm 1, line 14). To summarize, MixMatch transforms $\mathcal{X}$ into $\mathcal{X}^{\prime}$ , a collection of labeled examples which have had data augmentation and MixUp (potentially mixed with an unlabeled example) applied. Similarly, $\mathcal{U}$ is transformed into $\mathcal{U}^{\prime}$ , a collection of multiple augmentations of each unlabeled example with corresponding label guesses.
(算法1,第10-11行)。接着,我们将这些集合合并并打乱顺序,形成作为MixUp数据源的$\mathcal{W}$(算法1,第12行)。对于$\hat{\mathcal X}$中的每个第$i^{t h}$个样本-标签对,我们计算$\mathrm{MixUp}(\hat{\mathcal{X}}{i},\mathcal{W}{i})$并将结果加入集合$\mathcal{X}^{\prime}$(算法1,第13行)。同时,针对$i\in(1,\dots,|\hat{\mathcal{U}}|)$,我们计算$\mathcal{U}{i}^{\prime}=\mathrm{MixUp}(\hat{\mathcal{U}}{i},\mathcal{W}_{i+|\hat{\mathcal{X}}|})$,这里特意使用$\mathcal{W}$中未被用于构建$\mathcal{X}^{\prime}$的剩余部分(算法1,第14行)。总结来说,MixMatch将$\mathcal{X}$转换为$\mathcal{X}^{\prime}$——一个经过数据增强和MixUp(可能与无标签样本混合)处理的带标签样本集合;类似地,$\mathcal{U}$被转换为$\mathcal{U}^{\prime}$——每个无标签样本经多次增强并带有对应预测标签的集合。
3.4 Loss Function
3.4 损失函数
Given our processed batches $\mathcal{X}^{\prime}$ and $\mathcal{U}^{\prime}$ , we use the standard semi-supervised loss shown in eqs. (3) to (5). Equation (5) combines the typical cross-entropy loss between labels and model predictions from $\mathcal{X}^{\prime}$ with the squared $L_{2}$ loss on predictions and guessed labels from $\mathcal{U}^{\prime}$ . We use this $L_{2}$ loss in eq. (4) (the multiclass Brier score [5]) because, unlike the cross-entropy, it is bounded and less sensitive to incorrect predictions. For this reason, it is often used as the unlabeled data loss in SSL [25, 44] as well as a measure of predictive uncertainty [26]. We do not propagate gradients through computing the guessed labels, as is standard [25, 44, 31, 35]
给定处理后的批次 $\mathcal{X}^{\prime}$ 和 $\mathcal{U}^{\prime}$,我们使用公式 (3) 至 (5) 所示的标准半监督损失函数。公式 (5) 将 $\mathcal{X}^{\prime}$ 中标签与模型预测的常规交叉熵损失,与 $\mathcal{U}^{\prime}$ 中预测值和猜测标签的平方 $L_{2}$ 损失相结合。我们在公式 (4) 中使用这种 $L_{2}$ 损失(多分类 Brier 分数 [5]),因为与交叉熵不同,它是有界的且对错误预测的敏感性较低。因此,它常被用作半监督学习 (SSL) 中的无标签数据损失 [25, 44],以及预测不确定性的度量 [26]。按照惯例 [25, 44, 31, 35],我们不会通过计算猜测标签来传播梯度。
3.5 Hyper parameters
3.5 超参数
Since MixMatch combines multiple mechanisms for leveraging unlabeled data, it introduces various hyper parameters – specifically, the sharpening temperature $T$ , number of unlabeled augmentations $K$ , $\alpha$ parameter for Beta in MixUp, and the unsupervised loss weight $\lambda_{\mathcal{U}}$ . In practice, semi-supervised learning methods with many hyper parameters can be problematic because cross-validation is difficult with small validation sets [35, 39, 35]. However, we find in practice that most of MixMatch’s hyper parameters can be fixed and do not need to be tuned on a per-experiment or per-dataset basis. Specifically, for all experiments we set $T=0.5$ and $K=2$ . Further, we only change $\alpha$ and $\lambda_{\mathcal{U}}$ on a per-dataset basis; we found that $\alpha=0.75$ and $\lambda_{\mathcal{U}}=100$ are good starting points for tuning. In all experiments, we linearly ramp up $\lambda_{\mathcal{U}}$ to its maximum value over the first 16,000 steps of training as is common practice [44].
由于MixMatch结合了多种利用未标记数据的机制,它引入了多个超参数——具体包括锐化温度 $T$ 、未标记数据增强次数 $K$ 、MixUp中Beta分布的 $\alpha$ 参数,以及无监督损失权重 $\lambda_{\mathcal{U}}$ 。实践中,具有大量超参数的半监督学习方法可能存在问题,因为在小规模验证集上难以进行交叉验证[35, 39, 35]。但我们发现MixMatch的大部分超参数可固定使用,无需针对每个实验或数据集单独调整。具体而言,所有实验中我们设定 $T=0.5$ 和 $K=2$ 。此外,仅根据数据集调整 $\alpha$ 和 $\lambda_{\mathcal{U}}$ ——我们发现 $\alpha=0.75$ 和 $\lambda_{\mathcal{U}}=100$ 是良好的调优起点。按照常规做法[44],所有实验均在训练前16,000步线性提升 $\lambda_{\mathcal{U}}$ 至最大值。
4 Experiments
4 实验
We test the effectiveness of MixMatch on standard SSL benchmarks (section 4.2). Our ablation study teases apart the contribution of each of MixMatch’s components (section 4.2.3). As an additional application, we consider privacy-preserving learning in section 4.3.
我们在标准半监督学习基准测试中验证了MixMatch的有效性(见4.2节)。消融实验解析了MixMatch各组件的作用(见4.2.3节)。作为延伸应用,我们在4.3节探讨了隐私保护学习场景。
4.1 Implementation details
4.1 实现细节
Unless otherwise noted, in all experiments we use the “Wide ResNet-28” model from [35]. Our implementation of the model and training procedure closely matches that of [35] (including using 5000 examples to select the hyper parameters), except for the following differences: First, instead of decaying the learning rate, we evaluate models using an exponential moving average of their parameters with a decay rate of 0.999. Second, we apply a weight decay of 0.0004 at each update for the Wide ResNet-28 model. Finally, we checkpoint every $2^{16}$ training samples and report the median error rate of the last 20 checkpoints. This simplifies the analysis at a potential cost to accuracy by, for example, averaging checkpoints [2] or choosing the checkpoint with the lowest validation error.
除非另有说明,所有实验中我们均使用[35]提出的"Wide ResNet-28"模型。我们的模型实现与训练流程基本遵循[35]的方案(包括使用5000个样本选择超参数),仅存在以下差异:首先,我们不再衰减学习率,而是采用衰减率为0.999的参数指数移动平均值来评估模型;其次,Wide ResNet-28模型每次更新时应用0.0004的权重衰减;最后,每训练$2^{16}$个样本保存一次检查点,并报告最后20个检查点的错误率中位数。这种做法简化了分析流程,但可能牺牲部分准确性,例如未采用检查点平均[2]或选择验证误差最低的检查点等优化手段。
4.2 Semi-Supervised Learning
4.2 半监督学习
First, we evaluate the effectiveness of MixMatch on four standard benchmark datasets: CIFAR-10 and CIFAR-100 [24], SVHN [32], and STL-10 [8]. Standard practice for evaluating semi-supervised learning on the first three datasets is to treat most of the dataset as unlabeled and use a small portion as labeled data. STL-10 is a dataset specifically designed for SSL, with 5,000 labeled images and 100,000 unlabeled images which are drawn from a slightly different distribution than the labeled data.
首先,我们在四个标准基准数据集上评估MixMatch的效果:CIFAR-10和CIFAR-100 [24]、SVHN [32]以及STL-10 [8]。前三个数据集评估半监督学习的标准做法是将大部分数据视为未标记,仅使用一小部分作为标记数据。STL-10是专为SSL设计的数据集,包含5,000张标记图像和100,000张未标记图像,这些未标记图像与标记数据的分布略有不同。
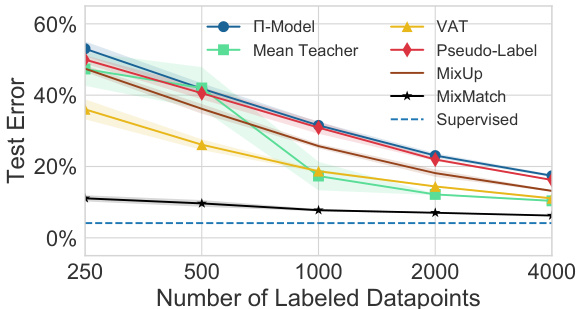
Figure 2: Error rate comparison of MixMatch to baseline methods on CIFAR-10 for a varying number of labels. Exact numbers are provided in table 5 (appendix). “Supervised” refers to training with all 50000 training examples and no unlabeled data. With 250 labels MixMatch reaches an error rate comparable to next-best method’s performance with 4000 labels.
图 2: CIFAR-10数据集上MixMatch与基线方法在不同标签数量下的错误率对比。具体数值见表5(附录)。"Supervised"表示使用全部50000个训练样本且不使用未标注数据进行训练。当仅使用250个标签时,MixMatch达到的错误率与次优方法使用4000个标签时的性能相当。
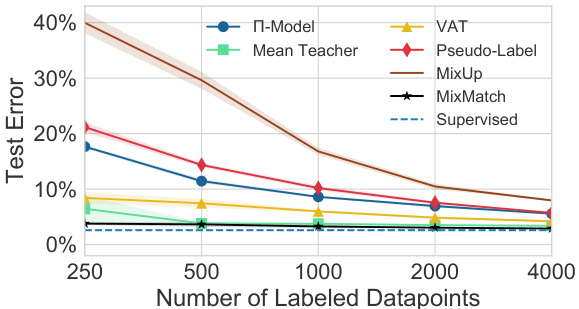
Figure 3: Error rate comparison of MixMatch to baseline methods on SVHN for a varying number of labels. Exact numbers are provided in table 6 (appendix). “Supervised” refers to train-ing with all 73257 training examples and no unlabeled data. With 250 examples MixMatch nearly reaches the accuracy of supervised training for this model.
图 3: MixMatch与基线方法在SVHN数据集上随标签数量变化的错误率对比。具体数值见表6(附录)。"Supervised"表示使用全部73257个训练样本且无未标注数据的训练结果。当使用250个样本时,MixMatch几乎达到了该模型在监督训练下的准确率。
4.2.1 Baseline Methods
4.2.1 基线方法
As baselines, we consider the four methods considered in [35] (Π-Model [25, 40], Mean Teacher [44], Virtual Adversarial Training [31], and Pseudo-Label [28]) which are described in section 2. We also use MixUp [47] on its own as a baseline. MixUp is designed as a regularize r for supervised learning, so we modify it for SSL by applying it both to augmented labeled examples and augmented unlabeled examples with their corresponding predictions. In accordance with standard usage of MixUp, we use a cross-entropy loss between the MixUp-generated guess label and the model’s prediction. As advocated by [35], we re implemented each of these methods in the same codebase and applied them to the same model (described in section 4.1) to ensure a fair comparison. We re-tuned the hyper parameters for each baseline method, which generally resulted in a marginal accuracy improvement compared to those in [35], thereby providing a more competitive experimental setting for testing out MixMatch.
作为基线方法,我们采用[35]中涉及的四种方法(Π-Model [25, 40]、Mean Teacher [44]、Virtual Adversarial Training [31]和Pseudo-Label [28]),这些方法在第2节已有描述。同时,我们将MixUp [47]单独作为基线使用。MixUp原本是监督学习中的正则化方法,我们通过将其同时应用于增强后的标注样本和带有预测结果的未标注样本,使其适用于半监督学习(SSL)。按照MixUp的标准用法,我们在混合生成的猜测标签与模型预测之间采用交叉熵损失。如[35]所建议,我们在同一代码库中重新实现了每种方法,并将其应用于同一模型(见第4.1节描述)以确保公平比较。我们为每个基线方法重新调整了超参数,相比[35]的结果普遍获得了小幅精度提升,从而为测试MixMatch提供了更具竞争力的实验环境。
4.2.2 Results
4.2.2 结果
CIFAR-10 For CIFAR-10, we evaluate the accuracy of each method with a varying number of label
