Deep Ensembles: A Loss Landscape Perspective

Deep Ensembles: 从损失函数视角解读

Stanislav Fort∗ Google Research sfort1@stanford.edu

Stanislav Fort∗ Google Research sfort1@stanford.edu

Balaji Lakshmi narayan an† DeepMind balajiln@google.com

Balaji Lakshmi narayan an† DeepMind balajiln@google.com

Abstract

摘要

Deep ensembles have been empirically shown to be a promising approach for improving accuracy, uncertainty and out-of-distribution robustness of deep learning models. While deep ensembles were theoretically motivated by the bootstrap, non-bootstrap ensembles trained with just random initialization also perform well in practice, which suggests that there could be other explanations for why deep ensembles work well. Bayesian neural networks, which learn distributions over the parameters of the network, are theoretically well-motivated by Bayesian principles, but do not perform as well as deep ensembles in practice, particularly under dataset shift. One possible explanation for this gap between theory and practice is that popular scalable variation al Bayesian methods tend to focus on a single mode, whereas deep ensembles tend to explore diverse modes in function space. We investigate this hypothesis by building on recent work on understanding the loss landscape of neural networks and adding our own exploration to measure the similarity of functions in the space of predictions. Our results show that random initialization s explore entirely different modes, while functions along an optimization trajectory or sampled from the subspace thereof cluster within a single mode predictions-wise, while often deviating significantly in the weight space. Developing the concept of the diversity–accuracy plane, we show that the de correlation power of random initialization s is unmatched by popular subspace sampling methods. Finally, we evaluate the relative effects of ensembling, subspace based methods and ensembles of subspace based methods, and the experimental results validate our hypothesis.

深度集成方法已被实证证明是一种提升深度学习模型准确性、不确定性和分布外鲁棒性的有效途径。虽然深度集成的理论依据源于自助法(bootstrap)，但仅通过随机初始化的非自助法集成在实践中同样表现优异，这表明深度集成效果卓越可能存在其他解释。贝叶斯神经网络通过贝叶斯原理学习网络参数分布，具有扎实的理论基础，但在实际应用中（尤其是数据集偏移时）表现不及深度集成。理论与实践的差距可能源于：主流可扩展变分贝叶斯方法往往聚焦单一模态，而深度集成倾向于探索函数空间中的多样化模态。我们基于近期神经网络损失景观的研究成果，通过预测空间中函数相似度的测量验证该假设。实验表明：随机初始化能探索完全不同的模态，而优化轨迹上的函数或其子空间采样在预测层面聚集于单一模态，权重空间却常存在显著差异。通过构建"多样性-准确性平面"概念，我们发现随机初始化的解相关能力远超主流子空间采样方法。最后评估了集成方法、基于子空间的方法及其集成组合的相对效果，实验结果支持了我们的假设。

1 Introduction

1 引言

Consider a typical classification problem, where $\pmb{x}_ {n}\in\mathbb{R}^{D}$ denotes the $D$ -dimensional features and $y_ {n}\in[1,\ldots,K]$ denotes the class label. Assume we have a parametric model $p(\boldsymbol{y}|\boldsymbol{x},\boldsymbol{\theta})$ for the conditional distribution where $\pmb{\theta}$ denotes weights and biases of a neural network, and $p(\pmb\theta)$ is a prior distribution over parameters. The Bayesian posterior over parameters is given by $\begin{array}{r}{p(\pmb{\theta}|{\pmb{x}_ {n},y_ {n}}_ {n=1}^{N})\propto p(\pmb{\theta})\prod_ {n=1}^{N}p(y_ {n}|\pmb{x}_ {n},\pmb{\theta}).}\end{array}$ .

考虑一个典型的分类问题，其中 $\pmb{x}_ {n}\in\mathbb{R}^{D}$ 表示 $D$ 维特征，$y_ {n}\in[1,\ldots,K]$ 表示类别标签。假设我们有一个参数化模型 $p(\boldsymbol{y}|\boldsymbol{x},\boldsymbol{\theta})$ 用于条件分布，其中 $\pmb{\theta}$ 表示神经网络的权重和偏置，$p(\pmb\theta)$ 是参数的先验分布。参数的贝叶斯后验分布由 $\begin{array}{r}{p(\pmb{\theta}|{\pmb{x}_ {n},y_ {n}}_ {n=1}^{N})\propto p(\pmb{\theta})\prod_ {n=1}^{N}p(y_ {n}|\pmb{x}_ {n},\pmb{\theta}).}\end{array}$ 给出。

Computing the exact posterior distribution over $\pmb{\theta}$ is computationally expensive (if not impossible) when $p(y_ {n}|\pmb{x}_ {n},\pmb{\theta})$ is a deep neural network (NN). A variety of approximations have been developed for Bayesian neural networks, including Laplace approximation [MacKay, 1992], Markov chain Monte Carlo methods [Neal, 1996, Welling and Teh, 2011, Spring e nberg et al., 2016], variation al Bayesian methods [Graves, 2011, Blundell et al., 2015, Louizos and Welling, 2017, Wen et al., 2018] and Monte-Carlo dropout [Gal and Ghahramani, 2016, Srivastava et al., 2014]. While computing the posterior is challenging, it is usually easy to perform maximum-a-posteriori (MAP) estimation, which corresponds to a mode of the posterior. The MAP solution can be written as the minimizer of the following loss:

计算 $\pmb{\theta}$ 的精确后验分布在 $p(y_ {n}|\pmb{x}_ {n},\pmb{\theta})$ 为深度神经网络 (NN) 时计算成本高昂（甚至不可能）。针对贝叶斯神经网络已发展出多种近似方法，包括拉普拉斯近似 [MacKay, 1992]、马尔可夫链蒙特卡洛方法 [Neal, 1996, Welling and Teh, 2011, Springenberg et al., 2016]、变分贝叶斯方法 [Graves, 2011, Blundell et al., 2015, Louizos and Welling, 2017, Wen et al., 2018] 以及蒙特卡洛 dropout [Gal and Ghahramani, 2016, Srivastava et al., 2014]。虽然计算后验具有挑战性，但执行最大后验 (MAP) 估计通常较为容易，这对应于后验的众数。MAP 解可表示为以下损失函数的最小化：

$$
\begin{array}{l}{{\mathrm{wing~loss:}}}\ {{\hat{\theta}_ {\mathrm{MAP}}=\underset{\theta}{\operatorname{argmin}}L(\theta,{x_ {n},y_ {n}}_ {n=1}^{N})=\underset{\theta}{\operatorname{argmin}}-\log p(\theta)-\displaystyle\sum_ {n=1}^{N}\log p(y_ {n}|x_ {n},\theta).}}\end{array}
$$

$$
\begin{array}{l}{{\mathrm{wing~loss:}}}\ {{\hat{\theta}_ {\mathrm{MAP}}=\underset{\theta}{\operatorname{argmin}}L(\theta,{x_ {n},y_ {n}}_ {n=1}^{N})=\underset{\theta}{\operatorname{argmin}}-\log p(\theta)-\displaystyle\sum_ {n=1}^{N}\log p(y_ {n}|x_ {n},\theta).}}\end{array}
$$

The MAP solution is computationally efficient, but only gives a point estimate and not a distribution over parameters. Deep ensembles, proposed by Lakshmi narayan an et al. [2017], train an ensemble of neural networks by initializing at $M$ different values and repeating the minimization multiple times which could lead to $M$ different solutions, if the loss is non-convex. Lakshmi narayan an et al. [2017] found adversarial training provides additional benefits in some of their experiments, but we will ignore adversarial training and focus only on ensembles with random initialization.

MAP (Maximum A Posteriori) 解在计算上是高效的，但仅给出点估计而非参数分布。Lakshmi narayan an 等人 [2017] 提出的深度集成 (deep ensembles) 方法通过以 $M$ 个不同的初始值初始化并多次重复最小化过程来训练神经网络集成，若损失函数非凸则可能得到 $M$ 个不同解。Lakshmi narayan an 等人 [2017] 发现对抗训练 (adversarial training) 在其部分实验中能带来额外收益，但我们将忽略对抗训练，仅关注随机初始化的集成方法。

Given finite training data, many parameter values could equally well explain the observations, and capturing these diverse solutions is crucial for quantifying epistemic uncertainty [Kendall and Gal, 2017]. Bayesian neural networks learn a distribution over weights, and a good posterior approximation should be able to learn multi-modal posterior distributions in theory. Deep ensembles were inspired by the bootstrap [Breiman, 1996], which has useful theoretical properties. However, it has been empirically observed by Lakshmi narayan an et al. [2017], Lee et al. [2015] that training individual networks with just random initialization is sufficient in practice and using the bootstrap can even hurt performance (e.g. for small ensemble sizes). Furthermore, Ovadia et al. [2019] and Gustafsson et al. [2019] independently benchmarked existing methods for uncertainty quant if i cation on a variety of datasets and architectures, and observed that ensembles tend to outperform approximate Bayesian neural networks in terms of both accuracy and uncertainty, particularly under dataset shift.

在有限的训练数据下，许多参数值都能同样好地解释观测结果，而捕捉这些多样化的解对于量化认知不确定性至关重要 [Kendall and Gal, 2017]。贝叶斯神经网络学习权重的分布，理论上一个好的后验近似应该能够学习多模态后验分布。深度集成方法受到自助法 (bootstrap) [Breiman, 1996] 的启发，该方法具有有益的理论特性。然而，Lakshminarayanan 等人 [2017] 和 Lee 等人 [2015] 通过实验观察到，在实践中仅通过随机初始化训练单个网络就足够了，使用自助法甚至可能损害性能（例如对于小规模集成）。此外，Ovadia 等人 [2019] 和 Gustafsson 等人 [2019] 分别对各种数据集和架构上的不确定性量化现有方法进行了基准测试，发现集成方法在准确性和不确定性方面往往优于近似贝叶斯神经网络，尤其是在数据集偏移的情况下。

These empirical observations raise an important question: Why do deep ensembles trained with just random initialization work so well in practice? One possible hypothesis is that ensembles tend to sample from different modes3 in function space, whereas variational Bayesian methods (which minimize $D_ {\mathrm{KL}}(q(\pmb{\theta})|\dot{p}(\pmb{\theta}|{\pmb{x}_ {n},y_ {n}}_ {n=1}^{N}))$ ) might fail to explore multiple modes even though they are effective at capturing uncertainty within a single mode. See Figure 1 for a cartoon illustration. Note that while the MAP solution is a local optimum for the training loss,it may not necessarily be a local optimum for the validation loss.

这些实证观察引发了一个重要问题：为什么仅通过随机初始化训练的深度集成 (deep ensembles) 在实践中表现如此出色？一种可能的假设是，集成倾向于从函数空间中的不同模式 (modes) 采样，而变分贝叶斯方法（最小化 $D_ {\mathrm{KL}}(q(\pmb{\theta})|\dot{p}(\pmb{\theta}|{\pmb{x}_ {n},y_ {n}}_ {n=1}^{N}))$）可能无法探索多个模式，尽管它们在单个模式内有效捕捉不确定性。参见图 1 的示意图。需要注意的是，虽然 MAP (最大后验概率) 解是训练损失的局部最优解，但它不一定是验证损失的局部最优解。

Figure 1: Cartoon illustration of the hypothesis. $x$ -axis indicates parameter values and $y$ -axis plots the negative loss $-L(\pmb{\theta},{x_ {n},y_ {n}}_ {n=1}^{N})$ on train and validation data.

图 1: 假设的卡通示意图。$x$轴表示参数值，$y$轴绘制训练和验证数据上的负损失$-L(\pmb{\theta},{x_ {n},y_ {n}}_ {n=1}^{N})$。

Recent work on understanding loss landscapes [Garipov et al., 2018, Draxler et al., 2018, Fort and J as tr zeb ski, 2019] allows us to investigate this hypothesis. Note that prior work on loss landscapes has focused on mode-connectivity and low-loss tunnels, but has not explicitly focused on how diverse the functions from different modes are. The experiments in these papers (as well as other papers on deep ensembles) provide indirect evidence for this hypothesis, either through downstream metrics (e.g. accuracy and calibration) or by visualizing the performance along the low-loss tunnel. We complement these works by explicitly measuring function space diversity within training trajectories and subspaces thereof (dropout, diagonal Gaussian, low-rank Gaussian and random subspaces) and across different randomly initialized trajectories across multiple datasets, architectures, and dataset shift. Our findings show that the functions sampled along a single training trajectory or subspace thereof tend to be very similar in predictions (while potential far away in the weight space), whereas functions sampled from different randomly initialized trajectories tend to be very diverse.

近期关于理解损失景观的研究 [Garipov et al., 2018, Draxler et al., 2018, Fort and Jastrzebski, 2019] 使我们能够验证这一假设。需要注意的是，先前关于损失景观的工作主要集中在模式连通性和低损失通道上，但并未明确关注不同模式间函数的多样性。这些论文中的实验（以及其他关于深度集成学习的论文）通过下游指标（如准确率和校准度）或可视化低损失通道上的性能，间接支持了这一假设。我们通过明确测量训练轨迹及其子空间（如dropout、对角高斯、低秩高斯和随机子空间）内的函数空间多样性，以及跨多个数据集、架构和数据集偏移的不同随机初始化轨迹间的多样性，对这些工作进行了补充。研究结果表明，沿单一训练轨迹或其子空间采样的函数在预测上往往非常相似（尽管在权重空间中可能相距甚远），而从不同随机初始化轨迹采样的函数则表现出高度多样性。

2 Background

2 背景

The loss landscape of neural networks (also called the objective landscape) – the space of weights and biases that the network navigates during training – is a high dimensional function and therefore could potentially be very complicated. However, many empirical results show surprisingly simple properties of the loss surface. Goodfellow and Vinyals [2014] observed that the loss along a linear path from an initialization to the corresponding optimum is monotonically decreasing, encountering no significant obstacles along the way. Li et al. [2018] demonstrated that constraining optimization to a random, low-dimensional hyperplane in the weight space leads to results comparable to full-space optimization, provided that the dimension exceeds a modest threshold. This was geometrically understood and extended by Fort and Scherlis [2019].

神经网络损失面(又称目标面)是网络在训练过程中探索的权重和偏置空间，作为一种高维函数，其形态可能极为复杂。然而大量实证研究揭示了损失面出人意料的简单特性。Goodfellow和Vinyals[2014]发现，从初始点到最优解的线性路径上损失值单调递减，全程未遇显著障碍。Li等[2018]证明，只要维度超过适度阈值，将优化约束在权重空间的随机低维超平面上，就能获得与全空间优化相当的结果。Fort和Scherlis[2019]对此现象进行了几何学阐释与拓展。

Garipov et al. [2018], Draxler et al. [2018] demonstrate that while a linear path between two independent optima hits a high loss area in the middle, there in fact exist continuous, low-loss paths connecting any pair of optima (or at least any pair empirically studied so far). These observations are unified into a single phenom eno logical model in [Fort and J as tr zeb ski, 2019]. While low-loss tunnels create functions with near-identical low values of loss along the path, the experiments of Fort and J as tr zeb ski [2019], Garipov et al. [2018] provide preliminary evidence that these functions tend to be very different in function space, changing significantly in the middle of the tunnel, see Appendix A for a review and additional empirical evidence that complements their results.

Garipov等人[2018]和Draxler等人[2018]的研究表明，虽然两个独立最优解之间的线性路径会在中间遇到高损失区域，但实际上存在连续的低损失路径连接任意一对最优解（或至少迄今为止实证研究过的任意一对）。这些观察结果在[Fort和Jastrzebski, 2019]中被统一为一个单一的现象学模型。虽然低损失隧道创建了沿路径损失值近乎相同的函数，但Fort和Jastrzebski[2019]、Garipov等人[2018]的实验提供了初步证据，表明这些函数在函数空间中往往差异很大，在隧道中间发生显著变化，详见附录A的综述及补充其实证结果的其他经验证据。

3 Experimental setup

3 实验设置

We explored the CIFAR-10 [Krizhevsky, 2009], CIFAR-100 [Krizhevsky, 2009], and ImageNet [Deng et al., 2009] datasets. We train convolutional neural networks on the CIFAR-10 dataset, which contains 50K training examples from 10 classes. To verify that our findings translate across architectures, we use the following 3 architectures on CIFAR-10:

我们探索了 CIFAR-10 [Krizhevsky, 2009]、CIFAR-100 [Krizhevsky, 2009] 和 ImageNet [Deng et al., 2009] 数据集。我们在 CIFAR-10 数据集上训练卷积神经网络，该数据集包含来自 10 个类别的 50K 训练样本。为了验证我们的发现适用于不同架构，我们在 CIFAR-10 上使用了以下 3 种架构：

We use the Adam optimizer [Kingma and Ba, 2015] for training and to make sure the effects we observe are general, we validate that our results hold for vanilla stochastic gradient descent (SGD) as well (not shown due to space limitations). We use batch size 128 and dropout 0.1 for training SmallCNN and MediumCNN. We used 40 epochs of training for each. To generate weight space and prediction space similarity results, we use a constant learning rate of $1.6\times10^{-3}$ and halfing it every 10 epochs, unless specified otherwise. We do not use any data augmentation with those two architectures. For ResNet20v1, we use the data augmentation and learning rate schedule used in Keras examples.4 The overall trends are consistent across all architectures, datasets, and other hyper parameter and non-linearity choices we explored.

我们使用 Adam 优化器 [Kingma and Ba, 2015] 进行训练，并确保观察到的效果具有普适性。我们还验证了结果在普通随机梯度下降 (SGD) 上也成立（由于篇幅限制未展示）。训练 SmallCNN 和 MediumCNN 时，批大小设为 128，dropout 率为 0.1，各训练 40 轮。生成权重空间和预测空间相似性结果时，除非另有说明，我们使用恒定学习率 $1.6\times10^{-3}$，并每 10 轮减半。这两个架构未使用任何数据增强。对于 ResNet20v1，我们采用 Keras 示例中的数据增强和学习率调度策略。所有架构、数据集及其他超参数和非线性选择中，整体趋势保持一致。

To test if our observations generalize to other datasets, we also ran certain experiments on more complex datasets such as CIFAR-100 [Krizhevsky, 2009] which contains 50K examples belonging to 100 classes and ImageNet [Deng et al., 2009], which contains roughly 1M examples belonging to 1000 classes. CIFAR-100 is trained using the same ResNet20v1 as above with Adam optimizer, batch size 128 and total epochs of 200. The learning rate starts from $10^{-3}$ and decays to $(1\dot{0}^{-4},5\times$ $10^{-5}$ , $10^{-5}$ , $5\times10^{-7})$ at epochs (100, 130, 160, 190). ImageNet is trained with ResNet50v2 [He et al., 2016b] and momentum optimizer (0.9 momentum), with batch size 256 and 160 epochs. The learning rate starts from 0.15 and decays to (0.015, 0.0015) at epochs (80, 120).

为了验证我们的观察结果是否适用于其他数据集，我们还在更复杂的数据集上进行了部分实验，例如包含100个类别共5万张图片的CIFAR-100 [Krizhevsky, 2009] 以及包含1000个类别约100万张图片的ImageNet [Deng et al., 2009]。CIFAR-100采用与之前相同的ResNet20v1架构进行训练，使用Adam优化器，批大小为128，总训练轮数为200。初始学习率为$10^{-3}$，并在第(100, 130, 160, 190)轮时分别衰减至$(1\dot{0}^{-4},5\times$$10^{-5}$, $10^{-5}$, $5\times10^{-7})$。ImageNet则采用ResNet50v2 [He et al., 2016b] 和动量优化器（动量系数0.9）进行训练，批大小为256，总训练轮数为160。初始学习率为0.15，并在第(80, 120)轮时分别衰减至(0.015, 0.0015)。

In addition to evaluating on regular test data, we also evaluate the performance of the methods on corrupted versions of the dataset using the CIFAR-10-C and ImageNet-C benchmarks [Hendrycks and Dietterich, 2019] which contain corrupted versions of original images with 19 corruption types (15 for ImageNet-C) and varying intensity values (1-5), and was used by Ovadia et al. [2019] to measure calibration of the uncertainty estimates under dataset shift. Following Ovadia et al. [2019], we measure accuracy as well as Brier score [Brier, 1950] (lower values indicate better uncertainty estimates). We use the SVHN dataset [Netzer et al., 2011] to evaluate how different methods trained on CIFAR-10 dataset react to out-of-distribution (OOD) inputs.

除了在常规测试数据上进行评估外，我们还使用CIFAR-10-C和ImageNet-C基准[Hendrycks and Dietterich, 2019]评估了各方法在数据损坏版本上的性能。这些基准包含原始图像的19种损坏类型(ImageNet-C为15种)和不同强度值(1-5)的损坏版本，Ovadia等人[2019]曾用其衡量数据集偏移下不确定性估计的校准程度。遵循Ovadia等人[2019]的方法，我们同时测量了准确率和Brier分数Brier, 1950。我们使用SVHN数据集[Netzer et al., 2011]来评估基于CIFAR-10数据集训练的不同方法对分布外(OOD)输入的反应。

4 Visualizing Function Space Similarity

4 可视化函数空间相似性

4.1 Similarity of Functions Within and Across Randomly Initialized Trajectories

4.1 随机初始化轨迹内及轨迹间的函数相似性

First, we compute the similarity between different checkpoints along a single trajectory. In Figure 2(a), we plot the cosine similarity in weight space, defined as $\begin{array}{r}{c o s(\pmb{\theta}_ {1},\pmb{\theta}_ {2})=\frac{\pmb{\theta}_ {1}^{\top}\pmb{\theta}_ {2}}{||\pmb{\theta}_ {1}||||\pmb{\theta}_ {2}||}}\end{array}$ . In Figure 2(b), we plot the disagreement in function space, defined as the fraction of points the checkpoints disagree on, that is, N1 nN=1[ $\begin{array}{r}{\frac{1}{N}\sum_ {n=1}^{N}[f(\pmb{x}_ {n};\pmb{\theta}_ {1})\neq f(\pmb{x}_ {n};\pmb{\theta}_ {2})]}\end{array}$ , where $f({\pmb x};{\pmb\theta})$ denotes the class label predicted by the network for input $_ {x}$ . We observe that the checkpoints along a trajectory are largely similar both in the weight space and the function space. Next, we evaluate how diverse the final solutions from different random initialization s are. The functions from different initialization are different, as demonstrated by the similarity plots in Figure 3. Comparing this with Figures 2(a) and 2(b), we see that functions within a single trajectory exhibit higher similarity and functions across different trajectories exhibit much lower similarity.

首先，我们计算单个轨迹上不同检查点之间的相似度。在图2(a)中，我们绘制了权重空间的余弦相似度，定义为$\begin{array}{r}{c o s(\pmb{\theta}_ {1},\pmb{\theta}_ {2})=\frac{\pmb{\theta}_ {1}^{\top}\pmb{\theta}_ {2}}{||\pmb{\theta}_ {1}||||\pmb{\theta}_ {2}||}}\end{array}$。在图2(b)中，我们绘制了函数空间的分歧度，定义为检查点预测不一致的数据点比例，即$\begin{array}{r}{\frac{1}{N}\sum_ {n=1}^{N}[f(\pmb{x}_ {n};\pmb{\theta}_ {1})\neq f(\pmb{x}_ {n};\pmb{\theta}_ {2})]}\end{array}$，其中$f({\pmb x};{\pmb\theta})$表示网络对输入$x$预测的类别标签。我们观察到，同一轨迹上的检查点在权重空间和函数空间都具有高度相似性。接着，我们评估不同随机初始化的最终解之间的差异程度。如图3的相似度曲线所示，不同初始化的函数存在明显差异。与图2(a)和图2(b)对比可见，同一轨迹内的函数表现出更高相似性，而不同轨迹间的函数相似性显著降低。

Figure 2: Results using SmallCNN on CIFAR-10. Left plot: Cosine similarity between checkpoints to measure weight space alignment along optimization trajectory. Middle plot: The fraction of labels on which the predictions from different checkpoints disagree. Right plot: t-SNE plot of predictions from checkpoints corresponding to 3 different randomly initialized trajectories (in different colors).

图 2: 在CIFAR-10数据集上使用SmallCNN的结果。左图: 检查点之间的余弦相似度，用于衡量优化轨迹上的权重空间对齐程度。中图: 不同检查点预测结果不一致的标签比例。右图: 对应3条不同随机初始化轨迹(不同颜色)的检查点预测结果的t-SNE可视化。

Next, we take the predictions from different checkpoints along the individual training trajectories from multiple initialization s and compute a t-SNE plot [Maaten and Hinton, 2008] to visualize their similarity in function space. More precisely, for each checkpoint we take the softmax output for a set of examples, flatten the vector and use it to represent the model’s predictions. The t-SNE algorithm is then used to reduce it to a 2D point in the t-SNE plot. Figure 2(c) shows that the functions explored by different trajectories (denoted by circles with different colors) are far away, while functions explored within a single trajectory (circles with the same color) tend to be much more similar.

接下来，我们选取多个初始化路径中不同训练阶段的检查点预测结果，计算t-SNE图 [Maaten and Hinton, 2008] 以可视化它们在函数空间的相似性。具体而言，对每个检查点提取一组样本的softmax输出，将向量展平后作为模型预测的表征，再通过t-SNE算法降维为二维坐标点。图2(c)显示：不同训练路径探索的函数（不同颜色圆圈表示）彼此远离，而同一路径内探索的函数（同色圆圈）则表现出更高相似性。

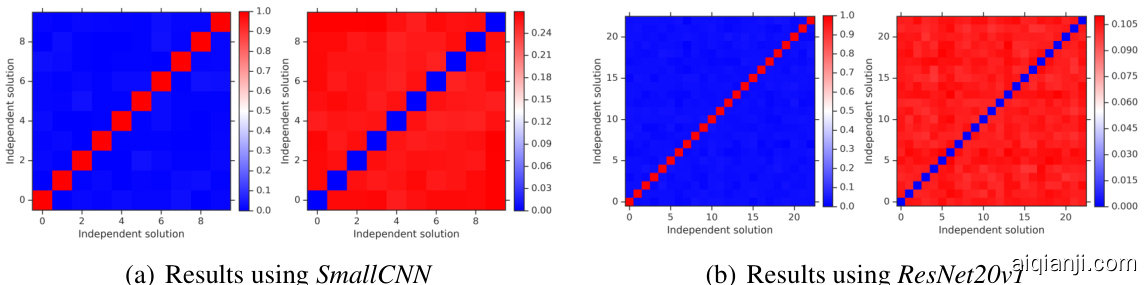
Figure 3: Results on CIFAR-10 using two different architectures. For each of these architectures, the left subplot shows the cosine similarity between different solutions in weight space, and the right subplot shows the fraction of labels on which the predictions from different solutions disagree. In general, the weight vectors from two different initialization s are essentially orthogonal, while their predictions are approximately as dissimilar as any other pair.

图 3: 在CIFAR-10数据集上使用两种不同架构的结果。对于每种架构，左子图显示权重空间中不同解之间的余弦相似度，右子图展示不同解预测结果出现分歧的标签比例。总体而言，两种不同初始化的权重向量基本正交，而它们的预测差异程度与任意其他配对近似。

4.2 Similarity of Functions Within Subspace from Each Trajectory and Across Trajectories

4.2 子空间内各轨迹间及跨轨迹的函数相似性

In addition to the checkpoints along a trajectory, we also construct subspaces based on each individual trajectory. Scalable variation al Bayesian methods typically approximate the distribution of weights along the training trajectory, hence visualizing the diversity of functions between the subspaces helps understand the difference between Bayesian neural networks and ensembles. We use a representative set of four subspace sampling methods: Monte Carlo dropout, a diagonal Gaussian approximation, a low-rank covariance matrix Gaussian approximation and a random subspace approximation. Unlike dropout and Gaussian approximations which assume a parametric form for the variation al posterior, the random subspace method explores all high-quality solutions within the subspace and hence could be thought of as a non-parametric variation al approximation to the posterior. Due to space constraints, we do not consider Markov Chain Monte Carlo (MCMC) methods in this work; Zhang et al. [2020] show that popular stochastic gradient MCMC (SGMCMC) methods may not explore multiple modes and propose cyclic SGMCMC. We compare diversity of random initialization and cyclic SGMCMC in Appendix C. In the descriptions of the methods, let $\theta_ {\mathrm{0}}$ be the optimized weight-space solution (the weights and biases of our trained neural net) around which we will construct the subspace.

除了轨迹上的检查点外，我们还基于每条独立轨迹构建子空间。可扩展的变分贝叶斯方法通常沿训练轨迹近似权重的分布，因此可视化子空间之间的函数多样性有助于理解贝叶斯神经网络与集成方法之间的差异。我们采用四种代表性的子空间采样方法：蒙特卡洛dropout、对角高斯近似、低秩协方差矩阵高斯近似和随机子空间近似。与假设变分后验具有参数形式的dropout和高斯近似不同，随机子空间方法探索子空间内所有高质量解，因此可视为后验的非参数变分近似。由于篇幅限制，本文未考虑马尔可夫链蒙特卡洛(MCMC)方法；Zhang等人[2020]表明流行的随机梯度MCMC(SGMCMC)方法可能无法探索多模态，并提出循环SGMCMC。我们在附录C中比较了随机初始化和循环SGMCMC的多样性。在方法描述中，设$\theta_ {\mathrm{0}}$为优化后的权重空间解(训练神经网络的权重和偏置)，我们将围绕该解构建子空间。

• Random subspace sampling: We start at an optimized solution $\pmb{\theta}_ {0}$ and choose a random direction $_ {v}$ in the weight space. We step in that direction by choosing different values of $t$ and looking at predictions at configurations $\mathbf{\nabla}\theta_ {0}+t\mathbf{v}$ . We repeat this for many random directions $_ {v}$ . • Dropout subspace: We start at an optimized solution $\pmb{\theta}_ {0}$ apply dropout with a randomly chosen $p_ {\mathrm{keep}}$ , evaluate predictions at $\mathrm{dropout}_ {p_ {\mathrm{keep}}}(\pmb{\theta}_ {0})$ and repeat this many times with different $p_ {\mathrm{keep}}$ . • Diagonal Gaussian subspace: We start at an optimized solution $\theta_ {\mathrm{0}}$ and look at the most recent iterations of training proceeding it. For each trainable parameter $\theta_ {i}$ , we calculate the mean $\mu_ {i}$ and standard deviation $\sigma_ {i}$ independently for each parameter, which corresponds to a diagonal covariance matrix. This is similar to SWAG-diagonal [Maddox et al., 2019]. To sample solutions from the subspace, we repeatedly draw samples where each parameter independently as $\theta_ {i}\sim\mathcal N(\mu_ {i},\sigma_ {i})$ . • Low-rank Gaussian subspace: We follow the same procedure as the diagonal Gaussian subspace above to compute the mean $\mu_ {i}$ for each trainable parameter. For the covariance, we use a rank $k$ approximation, by calculating the top $k$ principal components of the recent weight vectors ${\pmb{v}_ {i}\in\mathbb{R}^{\mathrm{params}}}_ {k}$ . We sample from a $k$ -dimensional normal distribution and obtain the weight configurations as $\begin{array}{r}{\pmb{\theta}\sim\pmb{\mu}+\sum_ {i}\mathcal{N}(0^{k},1^{k})\pmb{v}_ {i}}\end{array}$ . Throughout the text, we use the terms low-rank and PCA Gaussian interchange ably.

• 随机子空间采样：从优化解 $\pmb{\theta}_ {0}$ 出发，在权重空间中随机选取方向 $_ {v}$。通过选择不同的 $t$ 值，观察配置 $\mathbf{\nabla}\theta_ {0}+t\mathbf{v}$ 处的预测结果。对多个随机方向 $_ {v}$ 重复此过程。
• Dropout子空间：从优化解 $\pmb{\theta}_ {0}$ 出发，应用随机选择的 $p_ {\mathrm{keep}}$ 进行dropout，在 $\mathrm{dropout}_ {p_ {\mathrm{keep}}}(\pmb{\theta}_ {0})$ 处评估预测，并针对不同 $p_ {\mathrm{keep}}$ 多次重复。
• 对角高斯子空间：从优化解 $\theta_ {\mathrm{0}}$ 出发，考察其最近的训练迭代历史。对每个可训练参数 $\theta_ {i}$，独立计算均值 $\mu_ {i}$ 和标准差 $\sigma_ {i}$（对应对角协方差矩阵），类似SWAG-diagonal [Maddox et al., 2019]。通过独立采样 $\theta_ {i}\sim\mathcal N(\mu_ {i},\sigma_ {i})$ 从子空间中获取解。
• 低秩高斯子空间：沿用上述对角高斯子空间方法计算各参数的均值 $\mu_ {i}$。协方差采用秩$k$近似，通过计算近期权重向量 ${\pmb{v}_ {i}\in\mathbb{R}^{\mathrm{params}}}_ {k}$ 的top $k$主成分。从$k$维正态分布采样，获得权重配置 $\begin{array}{r}{\pmb{\theta}\sim\pmb{\mu}+\sum_ {i}\mathcal{N}(0^{k},1^{k})\pmb{v}_ {i}}\end{array}$。文中"低秩"与"PCA高斯"可互换使用。

Figure 4: Results using SmallCNN on CIFAR-10: t-SNE plots of validation set predictions for each trajectory along with four different subspace generation methods (showed by squares), in addition to 3 independently initialized and trained runs (different colors). As visible in the plot, the subspacesampled functions stay in the prediction-space neighborhood of the run around which they were constructed, demonstrating that truly different functions are not sampled.

图 4: 在CIFAR-10上使用SmallCNN的结果：验证集预测的t-SNE图，展示了每条轨迹以及四种不同的子空间生成方法（用方块表示），此外还有3个独立初始化和训练的运行（不同颜色）。从图中可以看出，子空间采样的函数始终围绕其构建的运行保持在预测空间邻域内，这表明并未采样到真正不同的函数。

Figure 4 shows that functions sampled from a subspace (denoted by colored squares) corresponding to a particular initialization, are much more similar to each other. While some subspaces are more diverse, they still do not overlap with functions from another randomly initialized trajectory.

图 4: 从对应特定初始化的子空间(以彩色方块表示)采样的函数彼此间相似度更高。虽然某些子空间更具多样性，但它们仍不会与另一随机初始化轨迹产生的函数重叠。

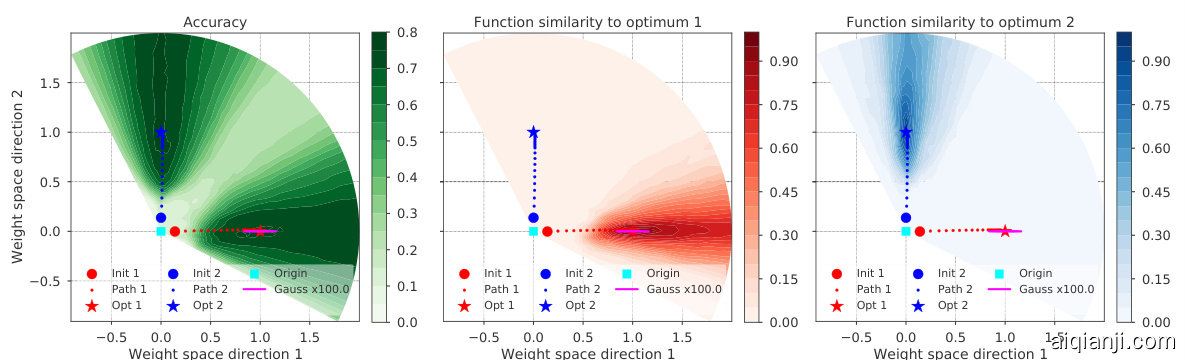
Figure 5: Results using MediumCNN on CIFAR-10: Radial loss landscape cut between the origin and two independent optima. Left plot shows accuracy of models along the paths of the two independent trajectories, and the middle and right plots show function space similarity to the two optima.

图 5: 在CIFAR-10上使用MediumCNN的结果：原点与两个独立最优解之间的径向损失景观切片。左图显示两个独立轨迹路径上模型的准确率，中间和右图显示与两个最优解在函数空间的相似性。

As additional evidence, Figure 5 provides a two-dimensional visualization of the radial landscape along the directions of two different optima. The 2D sections of the weight space visualized are defined by the origin (all weights are 0) and two independently initialized and trained optima. The weights of the two trajectories (shown in red and blue) are initialized using standard techniques and they increase radially with training due to their softmax cross-entropy loss. The left subplot shows that different randomly initialized trajectories eventually achieve similar accuracy. We also sample from a Gaussian subspace along trajectory 1 (shown in pink). The middle and the right subplots show function space similarity (defined as the fraction of points on which they agree on the class prediction) of the parameters along the path to optima 1 and 2. Solutions along each trajectory (and Gaussian subspace) are much more similar to their respective optima, which is consistent with the cosine similarity and t-SNE plots.

作为补充证据，图5展示了沿两个不同最优方向径向景观的二维可视化。所展示的权重空间二维截面由原点（所有权重为0）和两个独立初始化训练的最优点定义。两条轨迹（红色与蓝色所示）的权重采用标准技术初始化，并因其softmax交叉熵损失而在训练过程中径向增长。左子图显示不同随机初始化轨迹最终达到相近的准确率。我们还沿轨迹1（粉色所示）在高斯子空间中进行采样。中间与右侧子图展示了参数在通往最优1和2路径上的函数空间相似性（定义为类别预测一致点的比例）。每条轨迹（及高斯子空间）上的解与其对应最优解的相似度显著更高，这与余弦相似度和t-SNE图的结果一致。

4.3 Diversity versus Accuracy plots

4.3 多样性 vs 准确率曲线图

To illustrate the difference in another fashion, we sample functions from a single subspace and plot accuracy versus diversity, as measured by disagreement between predictions from the baseline solution. From a bias-variance trade-off perspective, we require a procedure to produce functions that are accurate (which leads to low bias by aggregation) as well as de-correlated (which leads to lower variance by aggregation). Hence, the diversity vs accuracy plot allows us to visualize the trade-off that can be achieved by subspace sampling methods versus deep ensembles.

为了以另一种方式说明差异，我们从单一子空间中采样函数，并绘制准确性与多样性之间的关系图，其中多样性通过基线解决方案预测之间的分歧来衡量。从偏差-方差权衡的角度来看，我们需要一种方法生成既准确（通过聚合降低偏差）又去相关（通过聚合降低方差）的函数。因此，多样性-准确性关系图使我们能够直观比较子空间采样方法与深度集成方法所能实现的权衡效果。

The diversity score quantifies the difference of two functions (a base solution and a sampled one), by measuring fraction of datapoints on which their predictions differ. We chose this approach due to its simplicity; we also computed the KL-divergence and other distances between the output probability distributions, leading to equivalent conclusions. Let $d_ {\mathrm{diff}}$ denote the fraction of predictions on which the two functions differ. It is 0 when the two functions make identical class predictions, and 1 when they differ on every single example. To account for the fact that the lower the accuracy of a function, the higher its potential $d_ {\mathrm{diff}}$ due to the possibility of the wrong answers being random and uncorrelated between the two functions, we normalize this by $(1-a)$ , where $a$ is the accuracy of the sampled solution. We also derive idealized lower and upper limits of these curves (showed in dashed lines) by perturbing the reference solution’s predictions (lower limit) and completely random predictions at a given accuracy (upper limit), see Appendix D for a discussion.

多样性分数通过衡量两个函数（一个基础解和一个采样解）预测结果不同的数据点比例，来量化它们之间的差异。我们选择这种方法是因为其简单性；同时我们还计算了输出概率分布之间的KL散度和其他距离，得出了等效的结论。设$d_ {\mathrm{diff}}$表示两个函数预测结果不同的比例。当两个函数做出完全相同的类别预测时为0，当它们在所有样本上都不同时为1。考虑到函数准确率越低，由于错误答案可能在两个函数间随机且不相关，其潜在的$d_ {\mathrm{diff}}$会越高，我们通过$(1-a)$对其进行归一化，其中$a$是采样解的准确率。我们还通过扰动参考解的预测（下限）和在给定准确率下完全随机的预测（上限），推导出这些曲线的理想化上下限（以虚线显示），具体讨论见附录D。

Figure 6: Diversity versus accuracy plots for 3 models trained on CIFAR-10: SmallCNN, MediumCNN and a ResNet20v1. Independently initialized and optimized solutions (red stars) achieve better diversity vs accuracy trade-off than the four different subspace sampling methods.

图 6: CIFAR-10数据集上训练的3个模型( SmallCNN、MediumCNN和ResNet20v1 )的多样性-准确率关系图。独立初始化和优化的解决方案(红星)比四种不同的子空间采样方法实现了更好的多样性-准确率权衡。

Figure 6 shows the results on CIFAR-10. Comparing these subspace points (colored dots) to the baseline optima (green star) and the optima from different random initialization s (denoted by red stars), we observe that random initialization s are much more effective at sampling diverse and accurate solutions, than subspace based methods constructed out of a single trajectory. The results are consistent across different architectures and datasets. Figure 7 shows results on CIFAR-100 and ImageNet. We observe that solutions obtained by subspace sampling methods have a worse trade off between accuracy and prediction diversity, compared to independently initialized and trained optima. Interestingly, the separation between the subspace sampling methods and independent optima in the diversity–accuracy plane gets more pronounced the more difficult the problem and the more powerful the network.

图6展示了CIFAR-10上的实验结果。将这些子空间采样点(彩色圆点)与基线最优解(绿色星标)及不同随机初始化得到的最优解(红色星标)对比时，我们发现随机初始化在获取多样且精确解方面，远比基于单条轨迹构建的子空间方法更有效。该结论在不同架构和数据集上保持一致性。图7呈现了CIFAR-100和ImageNet的实验结果。我们观察到，相较于独立初始化训练得到的最优解，子空间采样方法获得的解在准确率与预测多样性之间呈现更差的权衡关系。值得注意的是，随着任务难度提升和网络能力增强，子空间采样方法与独立最优解在多样性-准确率平面上的分离现象会愈发显著。

(a) ResNet20v1 trained on CIFAR-100. (b) ResNet50v2 trained on ImageNet. igure 7: Diversity vs. accuracy plots for ResNet20v1 on CIFAR-100, and ResNet50v2 on ImageNe

(a) 在CIFAR-100上训练的ResNet20v1。(b) 在ImageNet上训练的ResNet50v2。
图7: ResNet20v1在CIFAR-100上及ResNet50v2在ImageNet上的多样性与准确率关系图

5 Evaluating the Relative Effects of Ensembling versus Subspace Methods

5 评估集成方法与子空间方法的相对效果

Our hypothesis in Figure 1 and the empirical observations in the previous section suggest that subspace-based methods and ensembling should provide complementary benefits in terms of uncertainty and accuracy. Since our goal is not to propose a new method, but to carefully test this hypothesis, we evaluate the performance of the following four variants for controlled comparison:

图 1 中的假设及前文实证观察表明，基于子空间的方法和集成技术应在不确定性与准确性方面形成互补优势。由于我们的目标并非提出新方法，而是严谨验证该假设，因此通过以下四种变体进行对照实验评估：

To maintain the accuracy of random samples at a reasonable level for fair comparison, we reject the sample if validation accuracy is below 0.65. For the CIFAR-10 experiment, we use a rank-4 approximation of the random samples using PCA. Note that diagonal Gaussian, low-rank Gaussian and random subspace sampling methods to approximate each mode of the posterior leads to an increase in the number of parameters required for each mode. However, using just the mean weights for each mode would not cause such an increase. Izmailov et al. [2018] proposed stochastic weight averaging (SWA) for better generalization. One could also compute an (exponential moving) average of the weights along the trajectory, inspired by Polyak-Ruppert averaging in convex optimization, (see also [Mandt et al., 2017] for a Bayesian view on iterate averaging). As weight averaging (WA) has been already studied by Izmailov et al. [2018], we do not discuss it in detail. Our goal is to test if WA finds a better point estimate within each mode (see cartoon illustration in Figure 1) and provides complementary benefits to ensembling over random initial