HyperML: A Boosting Metric Learning Approach in Hyperbolic Space for Recommend er Systems

HyperML: 推荐系统中双曲空间的度量学习增强方法

ABSTRACT

摘要

This paper investigates the notion of learning user and item represent at ions in non-Euclidean space. Specifically, we study the connection between metric learning in hyperbolic space and collaborative filtering by exploring Möbius gyrovector spaces where the formalism of the spaces could be utilized to generalize the most common Euclidean vector operations. Overall, this work aims to bridge the gap between Euclidean and hyperbolic geometry in recommend er systems through metric learning approach. We propose HyperML (Hyperbolic Metric Learning), a conceptually simple but highly effective model for boosting the performance. Via a series of extensive experiments, we show that our proposed HyperML not only outperforms their Euclidean counterparts, but also achieves state-of-the-art performance on multiple benchmark datasets, demonstrating the effectiveness of personalized recommendation in hyperbolic geometry.

本文研究了在非欧几里得空间中学习用户和物品表示的概念。具体而言，我们通过探索Möbius陀螺向量空间，研究了双曲空间中的度量学习与协同过滤之间的联系，该空间的形式体系可用于推广最常见的欧几里得向量运算。总体而言，这项工作旨在通过度量学习方法弥合推荐系统中欧几里得几何与双曲几何之间的差距。我们提出了HyperML（双曲度量学习），这是一个概念简单但非常有效的性能提升模型。通过一系列广泛的实验，我们表明所提出的HyperML不仅优于欧几里得对应方法，还在多个基准数据集上实现了最先进的性能，证明了双曲几何中个性化推荐的有效性。

CCS CONCEPTS

KEYWORDS

关键词

Recommend er Systems; Collaborative Filtering; Hyperbolic Neural Networks

推荐系统；协同过滤；双曲神经网络

ACM Reference Format:

ACM 参考文献格式:

Lucas Vinh Tran, Yi Tay, Shuai Zhang, Gao Cong, and Xiaoli Li. 2020. HyperML: A Boosting Metric Learning Approach in Hyperbolic Space for Recommend er Systems. In The Thirteenth ACM International Conference on Web Search and Data Mining (WSDM’20), February 3–7, 2020, Houston, TX,

Lucas Vinh Tran、Yi Tay、Shuai Zhang、Gao Cong 和 Xiaoli Li。2020. HyperML：双曲空间中用于推荐系统的度量学习增强方法。见：第十三届 ACM 国际网络搜索与数据挖掘会议 (WSDM'20)，2020 年 2 月 3-7 日，美国德克萨斯州休斯顿。

USA. ACM, New York, NY, USA, 9 pages. https://doi.org/10.1145/3336191. 3371850

美国。ACM，纽约，纽约州，美国，9页。https://doi.org/10.1145/3336191.3371850

1 INTRODUCTION

1 引言

A diverse plethora of machine learning models solves the personalized ranking problem in recommend er systems via building matching functions [17, 26, 30, 31]. Across the literature, a variety of matching functions have been traditionally adopted, such as inner product [31], metric learning [19, 33] and/or neural networks [16, 17]. Among those approaches, metric learning models (e.g., Collaborative Metric Learning (CML) [19] and Latent Relational Metric Learning (LRML) [33]) are primarily focused on designing distance functions over objects (i.e., between users and items), demonstrating reasonable empirical success for collaborative ranking with implicit feedback. Nevertheless, those matching functions only covered the scope of Euclidean space.

多种多样的机器学习模型通过构建匹配函数来解决推荐系统中的个性化排序问题[17,26,30,31]。纵观现有文献，传统上采用了多种匹配函数，例如内积[31]、度量学习[19,33]和/或神经网络[16,17]。在这些方法中，度量学习模型（如协同度量学习(Collaborative Metric Learning, CML)[19]和潜在关系度量学习(Latent Relational Metric Learning, LRML)[33]）主要专注于设计对象（即用户与物品之间）的距离函数，在隐式反馈的协同排序中展现了合理的实证效果。然而，这些匹配函数仅覆盖了欧几里得空间的范围。

For the first time, our work explores the notion of learning useritem representations in terms of metric learning in hyperbolic space, in which hyperbolic representation learning has recently demonstrated great potential across a diverse range of applications such as learning entity hierarchies [27] and/or natural language processing [8, 34]. Due to the exponentially expansion property of hyperbolic space, we discovered that metric learning with the pull-push mechanism in hyperbolic space could boost the performance significantly: moving a point to a certain distance will require a much smaller force in hyperbolic space than in Euclidean space. To this end, in order to perform metric learning in hyperbolic space, we employ Möbius gyrovector spaces to generally formalize most common Euclidean operations such as addition, multiplication, exponential map and logarithmic map [11, 38].

我们的工作首次探索了在双曲空间中通过度量学习来学习用户-物品表示的概念，其中双曲表示学习最近在多种应用中展现出巨大潜力，例如学习实体层次结构 [27] 和/或自然语言处理 [8, 34]。由于双曲空间的指数扩展特性，我们发现利用双曲空间中的推拉机制进行度量学习可以显著提升性能：在双曲空间中移动一个点到特定距离所需的力远小于欧几里得空间。为此，为了在双曲空间中进行度量学习，我们采用Möbius陀螺向量空间来形式化大多数常见的欧几里得操作，例如加法、乘法、指数映射和对数映射 [11, 38]。

Moreover, the ultimate goal when embedding a space into another is to preserve distances and more complex relationships. Thus, our work also introduces the definition of distortion to maintain good representations in hyperbolic space both locally and globally, while controlling the performance through the multi-task learning framework. This reinforces the key idea of modeling user-item pairs in hyperbolic space, while maintaining the simplicity and effectiveness of the metric learning paradigm.

此外，将空间嵌入另一空间的终极目标是保持距离及更复杂的关系。因此，我们的工作还引入了失真(distortion)的定义，以在双曲空间中同时保持局部和全局的良好表征，并通过多任务学习框架控制性能。这强化了在双曲空间中建模用户-物品对的核心思想，同时保持了度量学习范式的简洁性与有效性。

We show that a conceptually simple hyperbolic adaptation in terms of metric learning is capable of not only achieving very competitive results, but also outperforming recent advanced Euclidean metric learning models on multiple personalized ranking benchmarks.

我们证明，在度量学习方面采用概念简单的双曲适应方法，不仅能够取得极具竞争力的结果，还在多个个性化排序基准上超越了近期先进的欧几里得度量学习模型。

Our Contributions. The key contributions of our work are summarized as follows:

我们的贡献。我们工作的主要贡献总结如下：

2 HYPERBOLIC METRIC LEARNING

2 双曲度量学习

This section provides the overall background and outlines the formulation of our proposed model. The key motivation behind our proposed model is to embed the two user-item pairs into hyperbolic space, creating the gradients of pulling the distance between the positive user-item pair close and pushing the negative user-item pair away.

本节概述了整体背景并阐述了我们提出模型的构建思路。该模型的核心动机是将用户-物品对嵌入双曲空间，通过梯度变化拉近正样本用户-物品对的距离，同时推离负样本用户-物品对。

Figure 1 depicts our overall proposed HyperML model. The figures illustrate our two approaches: 1) optimizing the embeddings within the unit ball and 2) transferring the points to the tangent space via the exponential and logarithmic maps for optimization. In the experiments, we also compare the mentioned variants of HyperML where both approaches achieve competitive results compared to Euclidean metric learning models.

图1展示了我们提出的HyperML模型整体架构。图中说明了我们的两种方法：1) 在单位球内优化嵌入向量，2) 通过指数和对数映射将点转换到切空间进行优化。在实验中，我们还比较了HyperML的不同变体，这两种方法相比欧几里得度量学习模型都取得了具有竞争力的结果。

2.1 Hyperbolic Geometry & Poincaré Embeddings

2.1 双曲几何与庞加莱嵌入

The hyperbolic space $\mathbb{D}$ is uniquely defined as a complete and simply connected Riemannian manifold with constant negative curvature [24]. In fact, there are three types of the Riemannian manifolds of constant curvature, which are Euclidean geometry (constant vanishing sectional curvature), spherical geometry (constant positive sectional curvature) and hyperbolic geometry (constant negative sectional curvature). In this paper, we focus on Euclidean space and hyperbolic space due to the key difference in their space expansion. Indeed, hyperbolic spaces expand faster (exponentially) than Euclidean spaces (polynomial ly). Specifically, for instance, in the two-dimensional hyperbolic space $\mathbb{D}_{\epsilon}^{2}$ of constant curvature

双曲空间 $\mathbb{D}$ 被唯一定义为具有恒定负曲率的完备单连通黎曼流形 [24]。实际上，存在三种类型的恒定曲率黎曼流形，分别是欧几里得几何（恒定零截面曲率）、球面几何（恒定正截面曲率）和双曲几何（恒定负截面曲率）。本文重点关注欧几里得空间和双曲空间，因为它们在空间扩展方面存在关键差异。事实上，双曲空间的扩展速度（指数级）快于欧几里得空间（多项式级）。具体而言，例如在恒定曲率的二维双曲空间 $\mathbb{D}_{\epsilon}^{2}$ 中

$K=-\epsilon^{2}<0$ , $\epsilon>0$ with the hyperbolic radius of $r$ , we have:

$K=-\epsilon^{2}<0$，$\epsilon>0$，双曲半径为$r$，则有：

in which $L(r)$ is the length of the circle and $A(r)$ is the area of the disk. Hence, both equations illustrate the exponentially expansion of the hyperbolic space $\mathbb{H}_{\epsilon}^{2}$ with respect to the radius $r$ .

其中 $L(r)$ 是圆的周长，$A(r)$ 是圆盘的面积。因此，这两个方程都说明了双曲空间 $\mathbb{H}_{\epsilon}^{2}$ 相对于半径 $r$ 的指数级扩张。

Although hyperbolic space cannot be iso metrically embedded into Euclidean space, there exists multiple models of hyperbolic geometry that can be formulated as a subset of Euclidean space and are very insightful to work with, depending on different tasks. In this work, we prefer the Poincaré ball model due to its con formality (i.e., angles are preserved between hyperbolic and Euclidean space) and convenient parameter iz ation [27].

虽然双曲空间无法等距嵌入欧几里得空间，但根据不同的任务需求，存在多种双曲几何模型可以表述为欧几里得空间的子集，且具有很高的实用价值。本文基于Poincaré圆盘模型的共形性 (即双曲空间与欧几里得空间的角度保持不变) 和便捷的参数化特性 [27]，优先采用该模型。

The Poincaré ball model is the Riemannian manifold $\begin{array}{r l}{\mathcal{P}^{n}}&{{}=}\end{array}$ $(\mathbb{D}^{n},g_{\mathcal{P}})$ , in which $\mathbb{D}^{n}={{\bf x}\in\mathbb{R}^{n}:|{\bf x}|<1}$ is the open $n$ - dimensional unit ball that is equipped with the metric:

Poincaré 球模型是黎曼流形 $\begin{array}{r l}{\mathcal{P}^{n}}&{{}=}\end{array}$ $(\mathbb{D}^{n},g_{\mathcal{P}})$，其中 $\mathbb{D}^{n}={{\bf x}\in\mathbb{R}^{n}:|{\bf x}|<1}$ 是开放的 $n$ 维单位球，其度量为：

where $\mathbf{x}\in\mathbb{D}^{n};\parallel\cdot\parallel$ denotes the Euclidean norm; and $g_{e}$ is the Euclidean metric tensor with components ${\mathbf{I}}_{n}$ of $\mathbb{R}^{n}$ .

其中 $\mathbf{x}\in\mathbb{D}^{n};\parallel\cdot\parallel$ 表示欧几里得范数；$g_{e}$ 是欧几里得度量张量，其分量为 $\mathbb{R}^{n}$ 的 ${\mathbf{I}}_{n}$。

The induced distance between two points on $\mathbb{D}^{n}$ is given by:

$\mathbb{D}^{n}$ 上两点间的诱导距离由下式给出：

In fact, if we adopt the hyperbolic distance function as a matching function to model the relationships between users and items, the hyperbolic distance $d_{\mathbb{D}}(\mathbf{u},\mathbf{v})$ between user $u$ and item $\boldsymbol{v}$ could be calculated based on Eqn. (4).

事实上，如果我们采用双曲距离函数作为匹配函数来建模用户与物品的关系，用户 $u$ 与物品 $\boldsymbol{v}$ 之间的双曲距离 $d_{\mathbb{D}}(\mathbf{u},\mathbf{v})$ 可通过公式(4)计算得出。

On a side note, let $\mathbf{v}{j}$ and $\mathbf{v}{k}$ represent the items user $i$ liked and did not like with $d_{\mathbb{D}}(\mathbf{u}{i},\mathbf{v}{j})$ and $d_{\mathbb{D}}(\mathbf{u}{i},\mathbf{v}{k})$ are their distances to the user i on hyperbolic space, respectively. Our goal is to pull $\mathbf{v}{j}$ close to $\mathbf{u}{i}$ while pushing $\mathbf{v}{k}$ away from $\mathbf{u}{i}$ . If we consider the triplet as a tree with two children $\mathbf{v}{j},\mathbf{v}{k}$ of parent $\mathbf{u}{i}$ and place $\mathbf{u}{i}$ relatively close to the origin, the graph distance of $\mathbf{v}{j}$ and $\mathbf{v}{k}$ is obviously calculated as $d(\mathbf{v}{j},\mathbf{v}{k})=d(\mathbf{u}{i},\mathbf{v}{j})+d(\mathbf{u}{i},\mathbf{v}{k}),$ , or we will obtain the ratio $\begin{array}{r}{\frac{d(\mathbf{v}{j},\mathbf{v}{k})}{d(\mathbf{u}{i},\mathbf{v}{j})+d(\mathbf{u}{i},\mathbf{v}{k})}=1.}\end{array}$ $d_{\mathbb{E}}(\mathbf{v}{j},\mathbf{v}{k})$ . If we embed the triplet in Euclidean space, the ratio dE(ui,vj()+dE( )ui,vk ) is constant, which seems not to capture the mentioned graph-like structure. However, in hyperbolic space, the rat io dD(ui,vj()+jdDk( )ui,vk ) approaches 1 as the edges are long enough, which makes the distances nearly preserved [32].

顺便提一下，设 $\mathbf{v}{j}$ 和 $\mathbf{v}{k}$ 分别表示用户 $i$ 喜欢和不喜欢的物品，其中 $d_{\mathbb{D}}(\mathbf{u}{i},\mathbf{v}{j})$ 和 $d_{\mathbb{D}}(\mathbf{u}{i},\mathbf{v}{k})$ 是它们在双曲空间中与用户 $i$ 的距离。我们的目标是将 $\mathbf{v}{j}$ 拉近 $\mathbf{u}{i}$，同时将 $\mathbf{v}{k}$ 推离 $\mathbf{u}{i}$。如果我们将这个三元组视为一棵树，其中 $\mathbf{v}{j},\mathbf{v}{k}$ 是父节点 $\mathbf{u}{i}$ 的两个子节点，并将 $\mathbf{u}{i}$ 放置在相对靠近原点的位置，那么 $\mathbf{v}{j}$ 和 $\mathbf{v}{k}$ 的图距离显然可以计算为 $d(\mathbf{v}{j},\mathbf{v}{k})=d(\mathbf{u}{i},\mathbf{v}{j})+d(\mathbf{u}{i},\mathbf{v}{k}),$，或者我们会得到比值 $\begin{array}{r}{\frac{d(\mathbf{v}{j},\mathbf{v}{k})}{d(\mathbf{u}{i},\mathbf{v}{j})+d(\mathbf{u}{i},\mathbf{v}{k})}=1.}\end{array}$ $d_{\mathbb{E}}(\mathbf{v}{j},\mathbf{v}{k})$。如果我们将这个三元组嵌入欧几里得空间，比值 dE(ui,vj()+dE( )ui,vk ) 是恒定的，这似乎无法捕捉到上述的图状结构。然而，在双曲空间中，当边足够长时，比值 dD(ui,vj()+jdDk( )ui,vk ) 趋近于 1，这使得距离几乎得以保留 [32]。

Thus, it is worth mentioning our key idea is that for a given triplet, we aim to embed the root (the user) arbitrarily close to the origin and space the children (positive and negative items) around a sphere centered at the parent. Notably, the distances between points grows exponentially as the norm of the vectors approaches 1. Geometrically, if we place the root node of a tree at the origin of $\mathbb{D}^{n}$ , the children nodes spread out exponentially with their distances to the root towards the boundary of the ball due to the above mentioned property.

因此，值得强调的是，我们的核心思想是：对于给定的三元组，目标是将根节点（用户）嵌入到尽可能接近原点的位置，并将子节点（正负样本项）均匀分布在以父节点为中心的球面上。值得注意的是，当向量范数趋近于1时，点间距会呈指数级增长。从几何角度看，若将树的根节点置于$\mathbb{D}^{n}$空间原点，由于上述特性，子节点会随着与根节点距离的增大而呈指数级扩散，直至接近球体边界。

2.2 Gyrovector spaces

2.2 陀螺向量空间

In this section, we make use of Möbius gyrovector spaces operations [11] to generally design the distance of user-item pairs for further extension.

在本节中，我们利用Möbius陀螺向量空间运算[11]来通用地设计用户-物品对的距离，以便进一步扩展。

Specifically, for $c\geq0$ , we denote $\mathbb{D}_{c}^{n}=\left{x\in\mathbb{R}^{n}:c|x|^{2}<1\right}$ , which is considered as the open ball of radius $\textstyle{\frac{1}{\sqrt{c}}}$ . Note that if $c=0$ , we get $\mathbb{D}_{c}^{n}=\mathbb{R}^{n}$ ; and if $c=1$ , we retrieve the usual unit ball as $\mathbb{D}_{c}^{n}=\mathbb{D}^{n}$ .

具体地，对于 $c\geq0$ ，我们记 $\mathbb{D}_{c}^{n}=\left{x\in\mathbb{R}^{n}:c|x|^{2}<1\right}$ ，将其视为半径为 $\textstyle{\frac{1}{\sqrt{c}}}$ 的开球。注意当 $c=0$ 时，得到 $\mathbb{D}_{c}^{n}=\mathbb{R}^{n}$ ；当 $c=1$ 时，则恢复通常的单位球 $\mathbb{D}_{c}^{n}=\mathbb{D}^{n}$ 。

Some widely used Möbius operations of gyrovector spaces are introduced as follows:

以下介绍几种陀螺向量空间中广泛使用的莫比乌斯(Möbius)运算:

Möbius addition: The Möbius addition of $x$ and $y$ in $\mathbb{D}_{c}^{n}$ is defined:

莫比乌斯加法：$\mathbb{D}_{c}^{n}$ 中 $x$ 和 $y$ 的莫比乌斯加法定义为：

Möbius scalar multiplication: For $c>0$ , the Möbius scalar multiplication of $x\in\mathbb{D}_{c}^{n}\setminus{\mathbf{0}}$ with $r\in\mathbb{R}$ is defined:

莫比乌斯标量乘法：对于 $c>0$，定义 $x\in\mathbb{D}_{c}^{n}\setminus{\mathbf{0}}$ 与 $r\in\mathbb{R}$ 的莫比乌斯标量乘法为：

and $r\otimes_{c}\mathbf{0}=\mathbf{0}$ . Note that when $c\to0$ , we recover the Euclidean addition and scalar multiplication. The Möbius subtraction can also be obtained as $x\ominus_{c}y=x\oplus_{c}(-y)$ .

且 $r\otimes_{c}\mathbf{0}=\mathbf{0}$。注意当 $c\to0$ 时，我们恢复了欧几里得加法和标量乘法。莫比乌斯减法也可表示为 $x\ominus_{c}y=x\oplus_{c}(-y)$。

Möbius exponential and logarithmic maps: For any $x\in\mathbb{D}_{c}^{n}$ , the Möbius exponential map and logarithmic map, given $\mathbf{\Lambda}\Rightarrow\neq{\textbf{0}}$ and $y\ne x$ , are defined:

Möbius指数和对数映射：对于任意$x\in\mathbb{D}_{c}^{n}$，给定$\mathbf{\Lambda}\Rightarrow\neq{\textbf{0}}$和$y\ne x$，Möbius指数映射和对数映射定义为：

where λcx = 1 c x 2 is the conformal factor of $(\mathbb{D}_{c}^{n},g^{c})$ in which $g^{c}$ is the generalized hyperbolic metric tensor. We also recover the Euclidean exponential map and logarithmic map as $c\to0$ . Readers can refer to [11, 38] for the detailed introduction to Gyrovector spaces.

其中 λcx = 1 c x 2 是 $(\mathbb{D}_{c}^{n},g^{c})$ 的共形因子，其中 $g^{c}$ 是广义双曲度量张量。当 $c\to0$ 时，我们还能还原欧几里得指数映射和对数映射。读者可以参考 [11, 38] 了解陀螺向量空间的详细介绍。

We then obtain the generalized distance in Gyrovector spaces:

然后我们得到陀螺向量空间中的广义距离：

When $c\to0$ , we recover the Euclidean distance since we have $\begin{array}{r}{\operatorname*{lim}{c\rightarrow0}d{c}(x,y)=2|x-y|}\end{array}$ . When $c=1$ , we retrieve the Eqn. (4). In other words, hyperbolic space resembles Euclidean as it gets closer to the origin, which motivates us to design our loss function in the multi-task learning framework.

当 $c\to0$ 时，由于 $\begin{array}{r}{\operatorname*{lim}{c\rightarrow0}d{c}(x,y)=2|x-y|}\end{array}$ ，我们恢复了欧几里得距离。当 $c=1$ 时，我们得到式 (4) 。换句话说，双曲空间在接近原点时与欧几里得空间相似，这促使我们在多任务学习框架中设计损失函数。

2.3 Model Formulation

2.3 模型构建

Our proposed model takes a user (denoted as $\mathbf{u}{i}$ ), a positive (observed) item (denoted as $\mathbf{v}{j}$ ) and a negative (unobserved) item (denoted as $\mathbf{v}_{k}$ ) as an input. Each user and item is represented as a one-hot vector which map onto a dense low-dimensional vector by indexing onto an user/item embedding matrix. We learn these vectors with the generalized distance:

我们提出的模型以用户 (表示为 $\mathbf{u}{i}$ ) 、正样本 (已观测) 项目 (表示为 $\mathbf{v}{j}$ ) 和负样本 (未观测) 项目 (表示为 $\mathbf{v}_{k}$ ) 作为输入。每个用户和项目都表示为一个独热向量 (one-hot vector) ，通过索引用户/项目嵌入矩阵映射到密集的低维向量。我们使用广义距离学习这些向量:

in which an item $j$ that user $i$ liked (positive) is expected to be closer to the user than the ones he did not like (negative).

其中用户 $i$ 喜欢的物品 $j$ (正样本) 应比不喜欢的物品 (负样本) 更接近该用户。

In fact, we would like to learn the user-item joint metric to encode the observed positive feedback. Specifically, the learned metric pulls the positive pairs closer and pushes the other pairs further apart.

事实上，我们希望学习用户-物品联合度量(metric)来编码观察到的正向反馈。具体而言，习得的度量会使正样本对彼此靠近，而使其他样本对相互远离。

Notably, this process will also cluster the users who like the same items together, and the items that are liked by the same users together, due to the triangle inequalities. Similar to [19], for a given user, the nearest neighborhood items are: 1) the items liked by this user previously, and 2) the items liked by other users with similar interests to this user. In other words, we are also able to indirectly observe the relationships between user-user pairs and item-item pairs through the pull-push mechanism of metric learning.

值得注意的是，由于三角不等式的作用，这一过程还会将喜欢相同物品的用户聚集在一起，并将被相同用户喜欢的物品聚集在一起。与[19]类似，对于给定用户，其最近邻物品包括：1) 该用户此前喜欢的物品，以及2) 与该用户兴趣相似的其他用户喜欢的物品。换句话说，我们还能通过度量学习的拉推机制间接观察用户-用户对和物品-物品对之间的关系。

Pull-and-Push Optimization. To formulate such constraint, we define our pull-and-push loss function as:

推拉优化 (Pull-and-Push Optimization) 。为了构建这种约束，我们将推拉损失函数定义为：

where $j$ is an item user $i$ liked and $k$ is the one he did not like; $\mathbb{S}$ contains all the observed implicit feedback, i.e. positive item-user pairs; $[z]_{+}=\operatorname*{max}(0,z)$ is the standard hinge loss; and $m>0$ is the safety margin size. Notably, our loss function does not adopt the ranking loss weight compared to [19].

其中 $j$ 是用户 $i$ 喜欢的物品，$k$ 是他不喜欢的物品；$\mathbb{S}$ 包含所有观察到的隐式反馈，即正物品-用户对；$[z]_{+}=\operatorname*{max}(0,z)$ 是标准的合页损失 (hinge loss)；$m>0$ 是安全边际大小。值得注意的是，与[19]相比，我们的损失函数没有采用排序损失权重。

Distortion Optimization. The ultimate goal when embedding a space into another is to preserve distances while maintaining complex structures/relationships [32]. Thus, it becomes a challenge when embedding user-item pairs to hyperbolic space with the needs of preserving good structure quality for metric learning. To this end, we consider the two factors of good representations namely local and global factor. Locally, the children items must be spread out on the sphere around the parent user as described, with pull and push forces created by the gradients. Globally, the learned triplets should be separated reasonably from each other. While pull-andpush optimization satisfies the local requirement, we define the distortion optimization function to meet the global requirement as:

失真优化 (Distortion Optimization) 。将一个空间嵌入另一个空间的终极目标是在保持复杂结构/关系的同时保留距离 [32]。因此，在将用户-物品对嵌入双曲空间时，如何保持良好结构质量以支持度量学习就成为一个挑战。为此，我们考虑良好表征的两个因素：局部因素和全局因素。局部上，子物品必须如所述围绕父用户分布在球面上，并通过梯度产生吸引力和排斥力。全局上，学习到的三元组之间应当合理分离。虽然推拉优化 (pull-and-push optimization) 满足局部要求，但我们定义失真优化函数来满足全局要求如下：

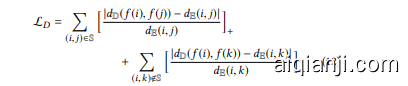
where $|\cdot|$ defines the absolute value; and $f(\cdot)$ is a mapping function $f:\mathbb{E}\rightarrow\mathbb{D}$ from Euclidean space $\mathbb{E}$ to hyperbolic space $\mathbb{D}$ . In this paper, we take $f(\cdot)$ as an identity function.

其中 $|\cdot|$ 定义绝对值；$f(\cdot)$ 是一个映射函数 $f:\mathbb{E}\rightarrow\mathbb{D}$，从欧几里得空间 $\mathbb{E}$ 到双曲空间 $\mathbb{D}$。在本文中，我们将 $f(\cdot)$ 视为恒等函数。

We aim to preserve the distances by minimizing $\mathcal{L}_{D}$ for the global factor. Ideally, the lower the distortion, the better the preservation.

我们旨在通过最小化全局因子 $\mathcal{L}_{D}$ 来保持距离。理想情况下，失真越低，保持效果越好。

Multi-Task Learning. We then integrate the pull-and-push part (i.e., $\mathcal{L}{P})$ and the distortion part (i.e., $\mathcal{L}{D})$ into an end-to-end fashion through a multi-task learning framework. The objective function is defined as:

多任务学习。随后，我们将拉推部分（即 $\mathcal{L}{P}$）和失真部分（即 $\mathcal{L}{D}$）通过多任务学习框架整合为端到端形式。目标函数定义为：

where $\Theta$ is the total parameter space, including all embeddings and variables of the networks; and $\gamma$ is the multi-task learning weight.

其中 $\Theta$ 是总参数空间，包含所有嵌入向量和网络变量；$\gamma$ 是多任务学习权重。

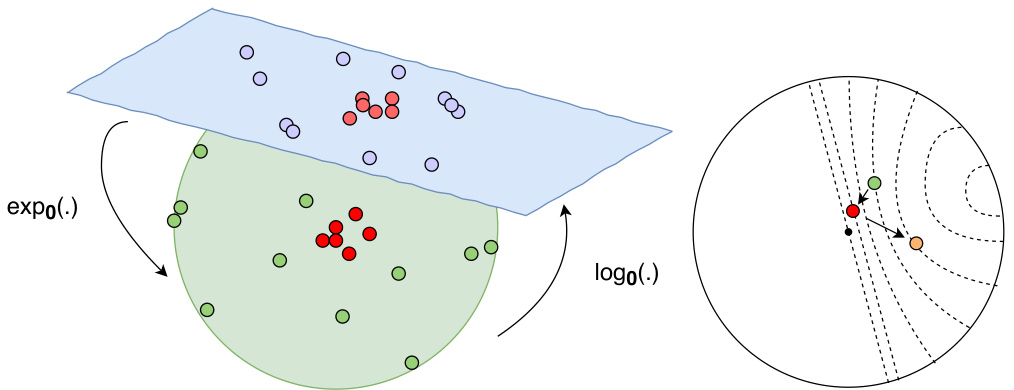
Figure 1: Illustration of our proposed HyperML. The left figure with the greenish ball represents the hyperbolic unit ball and the pale blue parallelogram illustrates its tangent space; red and vermeil circles represent user embeddings; green and purple circles represent item embeddings. The right figure illustrates an example of a triplet embedding of user (red circle), positive item (green circle) and negative item (orange circle), in which it demonstrates a small tree of one root and two children which is embedded into hyperbolic space with the exponentially expansion property (Best viewed in color).

图 1: 我们提出的 HyperML 示意图。左侧带有绿色球的图表示双曲单位球，淡蓝色平行四边形表示其切空间；红色和朱红色圆圈表示用户嵌入；绿色和紫色圆圈表示物品嵌入。右侧图展示了一个用户（红色圆圈）、正样本物品（绿色圆圈）和负样本物品（橙色圆圈）的三元组嵌入示例，其中演示了一个具有指数扩展特性的双曲空间中的单根双子树结构（建议彩色查看）。

Table 1: Statistics of all datasets used in our experimental evaluation

数据集	交互次数	用户数	物品数	密度(%)
Movie20M	16M	53K	27K	1.15
Movie1M	1M	6K	4K	4.52
Goodbooks	6M	53K	10K	1.14
Yelp	1M	22K	18K	0.26
Meetup	248K	47K	17K	0.03
Clothing	358K	39K	23K	0.04
Sports&Outdoors	368K	36K	18K	0.06
CellPhones	250K	28K	10K	0.09
Toys&Games	206K	19K	12K	0.09
Automotive	26K	3K	2K	0.49

表 1: 实验评估所用全部数据集统计信息

There is an unavoidable trade-off between the precision (learned from the pull-push mechanism) and the distortion as similar to [32]. Thus, jointly training $\mathcal{L}{P}$ and $\mathcal{L}{D}$ can help to boost the model performance while providing good representations. Indeed, we examine the performance of HyperML with and without the distortion by varying different multi-task learning weight $\gamma$ in our experiment in Section 3.

在精度（通过推拉机制学习得到）和失真之间存在着不可避免的权衡，这与[32]类似。因此，联合训练 $\mathcal{L}{P}$ 和 $\mathcal{L}{D}$ 可以在提供良好表征的同时提升模型性能。实际上，我们在第3节的实验中通过调整多任务学习权重 $\gamma$ 来考察HyperML在有失真和无失真情况下的性能表现。

Gradient Conversion. The parameters of our model are learned by projected Riemannian stochastic gradient descent (RSGD) [27] with the form:

梯度转换。我们的模型参数通过投影黎曼随机梯度下降 (RSGD) [27] 进行学习，其形式为：

where $\Re_{\theta_{t}}$ denotes a retraction onto $\mathbb{D}$ at $\theta$ and $\eta_{t}$ is the learning rate at time $t$ .

其中 $\Re_{\theta_{t}}$ 表示在 $\theta$ 处对 $\mathbb{D}$ 的回缩 (retraction)，$\eta_{t}$ 是时间 $t$ 的学习率。

The Riemannian gradient $\nabla_{R}$ is then calculated from the Euclidean gradient by rescaling $\nabla_{E}$ with the inverse of the Poincaré ball metric tensor as $\begin{array}{r}{\nabla_{R}=\frac{(1-|\theta_{t}|^{2})^{2}}{4}\nabla_{E}}\end{array}$ , in which this scaling factor depends on the Euclidean distance of the point at time $t$ from the origin [27, 34]. Notably, one could also exploit full RSGD for optimization to perform the updates instead of using first-order approximation to the exponential map [1, 2, 10, 41].

黎曼梯度 $\nabla_{R}$ 通过将欧几里得梯度 $\nabla_{E}$ 与庞加莱球度量张量的逆进行缩放计算得出，即 $\begin{array}{r}{\nabla_{R}=\frac{(1-|\theta_{t}|^{2})^{2}}{4}\nabla_{E}}\end{array}$ ，其中该缩放因子取决于时间 $t$ 时该点与原点之间的欧几里得距离 [27, 34]。值得注意的是，也可以利用完整RSGD进行优化来执行更新，而非使用指数映射的一阶近似 [1, 2, 10, 41]。

3 EXPERIMENTS

3 实验

Datasets. To evaluate our experiments, we use a wide spectrum of datasets with diverse domains and densities. The statistics of the datasets are reported in Table 1.

数据集。为了评估实验效果，我们采用了涵盖多个领域和数据密度的多样化数据集。各数据集的统计信息详见表 1:

Evaluation Protocol and Metrics. We experiment on the one-class collaborative filtering setup. We adopt nDCG@10 (normalized discounted cumulative gain) and HR $@10$ (Hit Ratio) evaluation metrics, which are well-established ranking metrics for recommendation task. Following [17, 33], we randomly select 100 negative samples which the user have not interacted with and rank the ground truth amongst these negative samples. For all datasets, the last item the user has interacted with is withheld as the test set while the penultimate serves as the validation set. During training, we report the test scores of the model based on the best validation scores. All models are evaluated on the validation set at every 50 epochs.

评估协议与指标。我们在单类协同过滤设置下进行实验，采用nDCG@10（归一化折损累积增益）和HR@10（命中率）这两种推荐任务中成熟的排序指标。参照[17, 33]的方法，我们随机选取100个用户未交互的负样本，并将真实项与这些负样本进行排序。所有数据集中，用户最后交互的项作为测试集，倒数第二项作为验证集。训练过程中，我们根据最佳验证分数报告模型的测试分数。所有模型每50个epoch在验证集上评估一次。

3.1 Experimental Setup

3.1 实验设置

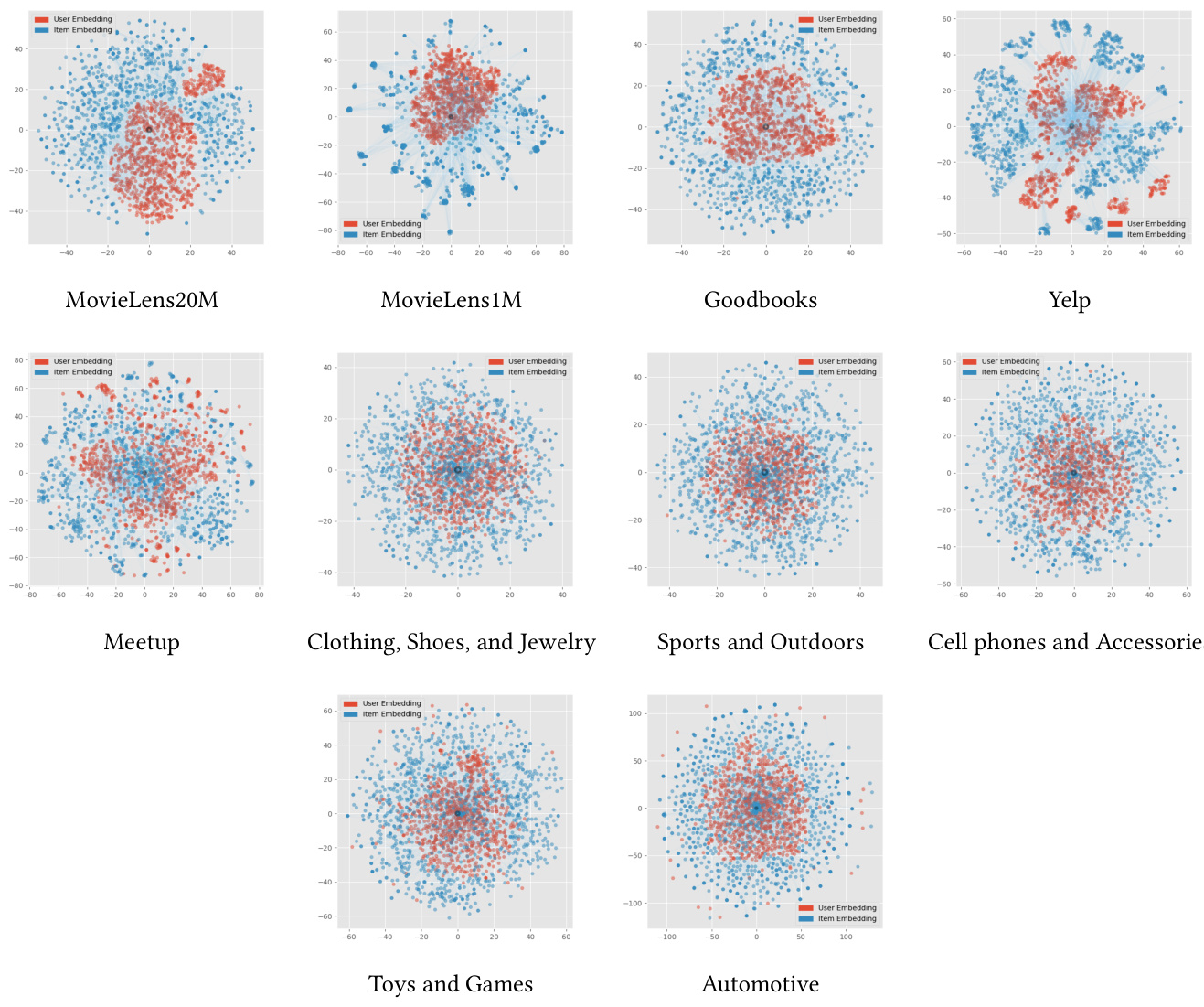
Figure 2: Two-dimensional hyperbolic embedding of ten benchmark datasets in the Poincaré disk using t-SNE. The images illustrate the embedding of user and item pairs after the convergence (Best viewed in color).

图 2: 采用 t-SNE 在庞加莱圆盘中对十个基准数据集进行二维双曲嵌入的可视化。图像展示了用户和物品对在收敛后的嵌入情况 (建议彩色查看)。

Compared Baselines. In our experiments, we compare with five well-established and competitive baselines which in turn employ different matching functions: inner product (MF-BPR), neural networks (MLP, NCF) and metric learning (CML, LRML).

对比基线。在我们的实验中，我们与五种成熟且具有竞争力的基线进行比较，这些基线分别采用不同的匹配函数：内积 (MF-BPR)、神经网络 (MLP, NCF) 和度量学习 (CML, LRML)。

• Matrix Factorization with Bayesian Personalized Ranking (MF-BPR) [31] is the standard and strong collaborative filtering (CF) baseline for recommend er systems. It models the user-item representation using the inner product and explores the triplet objective to rank items. • Multi-layered Perceptron (MLP) is a feed forward neural network that applies multiple layers of nonlinear i ties to capture the relationship between users and items. We select the best number of MLP layers from ${3,4,5}$ . • Neural Collaborative Filtering (NCF) [17] is a neural network based method for collaborative filtering which models nonlinear user-item interaction. The key idea of NCF is to fuse the last hidden representation of MF and MLP into a joint model. Following [17], we use a three layered MLP with a pyramid structure.

• 基于贝叶斯个性化排序的矩阵分解 (Matrix Factorization with Bayesian Personalized Ranking, MF-BPR) [31] 是推荐系统中标准且强大的协同过滤 (Collaborative Filtering, CF) 基线方法。它通过内积建模用户-物品表征，并利用三元组目标函数对物品进行排序。
• 多层感知机 (Multi-layered Perceptron, MLP) 是一种前馈神经网络，通过多层非线性变换捕捉用户与物品间的关系。我们从 ${3,4,5}$ 中选择最佳MLP层数。
• 神经协同过滤 (Neural Collaborative Filtering, NCF) [17] 是一种基于神经网络的协同过滤方法，用于建模非线性用户-物品交互。NCF的核心思想是将MF和MLP的最终隐藏表征融合为联合模型。参照[17]，我们采用具有金字塔结构的三层MLP。

• Collaborative Metric Learning (CML) [19] is a strong metric learning baseline that learns user-item similarity using the Euclidean distance. CML can be considered a key ablative baseline in our experiments, signifying the difference between Hyperbolic and Euclidean metric spaces. • Latent Relational Metric Learning (LRML) [33] is also a strong metric learning baseline that learns adaptive relation vectors between user and item interactions to find a single optimal translation vector between each user-item pair.

• 协同度量学习 (Collaborative Metric Learning, CML) [19] 是一种基于欧氏距离学习用户-物品相似性的强力度量学习基线方法。该模型可作为我们实验中关键消融基线，用于验证双曲度量空间与欧氏度量空间的差异。
• 潜在关系度量学习 (Latent Relational Metric Learning, LRML) [33] 是另一种强力度量学习基线，该方法通过自适应学习用户与物品交互间的关系向量，为每对用户-物品组合寻找单一最优平移向量。

Implementation Details. We implement all models in Tensorflow. All models are trained with the Adam [21] or AdaGrad [9] optimizer with learning rates from $\left{0.01,0.001,0.0001,0.00001\right}$ . The embedding size $d$ of all models is tuned amongst ${32,64,128}$ and the batch size $B$ is tuned amongst ${128,256,512}$ . The multi-task learning weight $\gamma$ is empirically chosen from ${0,0.1,0.25,0.5,0.75}$ , $1.0}$ . For models that optimize the hinge loss, the margin $\lambda$ is selected from ${0.1,0.2,0.5}$ . For NCF, we use a pre-trained model as reported in [17] to achieve its best performance. All the embeddings and parameters are randomly initialized using the random uniform initialize r $\mathcal{U}(-\alpha,\alpha)$ . For non-metric learning baselines, we set $\alpha=0.01$ . For metric learning models, we empirically set $\alpha=(\frac{3\beta^{2}}{2d})^{\frac{1}{3}}$ ,a illn twheh iechm bweed dcihnogoss eo $\beta=0.01$ .r iTch lee ar rena is no gn ims otdhealts wtoe be initialized arbitrarily close to the origin of the balls5 for a fair comparison. For most datasets and baselines, we empirically set the embedding size of 64 and the batch size is 512. We also empirically set the dropout rate $\rho=0.5$ to prevent over fitting. For each dataset, the optimal parameters are established by repeating each experiment for $N$ runs and assessing the average results. We have used $N=5$ for our experiment.

实现细节。我们使用Tensorflow实现所有模型。所有模型均采用Adam [21]或AdaGrad [9]优化器进行训练，学习率从$\left{0.01,0.001,0.0001,0.00001\right}$中选择。所有模型的嵌入维度$d$在${32,64,128}$范围内调优，批量大小$B$在${128,256,512}$范围内调优。多任务学习权重$\gamma$从${0,0.1,0.25,0.5,0.75}$和$1.0}$中根据经验选择。对于优化合页损失的模型，边界值$\lambda$从${0.1,0.2,0.5}$中选择。对于NCF，我们使用[17]中报告的预训练模型以达到其最佳性能。所有嵌入和参数均采用均匀分布初始化器$\mathcal{U}(-\alpha,\alpha)$进行随机初始化。对于非度量学习基线，我们设置$\alpha=0.01$。对于度量学习模型，我们根据经验设置$\alpha=(