Leveraging the Feature Distribution in Transfer-based Few-Shot Learning

基于迁移的少样本学习中特征分布的利用

Abstract

摘要

Few-shot classification is a challenging problem due to the uncertainty caused by using few labelled samples. In the past few years, many methods have been proposed to solve few-shot classification, among which transferbased methods have proved to achieve the best performance. Following this vein, in this paper we propose a novel transfer-based method that builds on two successive steps: 1) preprocessing the feature vectors so that they become closer to Gaussian-like distributions, and 2) leveraging this preprocessing using an optimal-transport inspired algo- rithm (in the case of trans duct ive settings). Using standardized vision benchmarks, we prove the ability of the proposed methodology to achieve state-of-the-art accuracy with various datasets, backbone architectures and few-shot settings. The code can be found at https://github.com/yhu01/PT-MAP.

少样本分类是一个具有挑战性的问题，因为使用少量标注样本会带来不确定性。在过去几年中，许多方法被提出来解决少样本分类问题，其中基于迁移学习的方法已被证明能够取得最佳性能。沿着这一思路，本文提出了一种新颖的基于迁移学习的方法，该方法建立在两个连续的步骤上：1) 对特征向量进行预处理，使其更接近高斯分布；2) 在转导设置的情况下，利用这种预处理，采用一种受最优传输启发的算法。通过标准化的视觉基准测试，我们证明了所提出的方法能够在各种数据集、骨干架构和少样本设置下实现最先进的准确率。代码可以在 https://github.com/yhu01/PT-MAP 找到。

more parameters than the dataset contains. This is why in the past few years, few-shot learning (i.e. the problem of learning with few labelled examples) has become a trending research subject in the field. In more details, there are two settings that authors often consider: a) “inductive few-shot”, where only a few labelled samples are available during training and prediction is performed on each test input independently, and b) “trans duct ive few-shot”, where prediction is performed on a batch of (non-labelled) test inputs, allowing to take into account their joint distribution.

数据集包含的参数更多。这就是为什么在过去几年中，少样本学习（即用少量标注样本进行学习的问题）已成为该领域的一个热门研究课题。更详细地说，作者通常考虑两种设置：a) “归纳少样本”，在训练期间只有少量标注样本可用，并且对每个测试输入独立进行预测；b) “转导少样本”，对一批（未标注的）测试输入进行预测，允许考虑它们的联合分布。

Many works in the domain are built based on a “learning to learn” guidance, where the pipeline is to train an optimizer [8, 23, 30] with different tasks of limited data so that the model is able to learn generic experience for novel tasks. Namely, the model learns a set of initialization parameters that are in an advantageous position for the model to adapt to a new (small) dataset. Recently, the trend evolved towards using well-thoughtout transfer architectures (called backbones) [31, 6] trained one time on the same training data, but seen as a unique large dataset.

该领域的许多工作都是基于“学会学习”的指导原则构建的，其流程是通过训练一个优化器 [8, 23, 30] 来处理不同任务的有限数据，从而使模型能够学习到适用于新任务的通用经验。也就是说，模型学习到一组初始化参数，这些参数使模型在适应新的（小型）数据集时处于有利位置。最近，趋势演变为使用精心设计的迁移架构（称为骨干网络）[31, 6]，这些架构在相同的训练数据上进行一次训练，但被视为一个独特的大型数据集。

1 Introduction

1 引言

Thanks to their outstanding performance, Deep Learning methods are widely considered for vision tasks such as object classification or detection. To reach top performance, these systems are typically trained using very large labelled datasets that are representative enough of the inputs to be processed afterwards.

得益于其出色的性能，深度学习方法在视觉任务（如物体分类或检测）中被广泛采用。为了达到最佳性能，这些系统通常使用非常大的标注数据集进行训练，这些数据集足以代表之后要处理的输入。

However, in many applications, it is costly to acquire or to annotate data, resulting in the impossibility to create such large labelled datasets. In this context, it is challenging to optimize Deep Learning architectures considering the fact they typically are made of way

然而，在许多应用中，获取或标注数据的成本很高，导致无法创建如此大规模的标注数据集。在这种情况下，考虑到深度学习架构通常由大量参数组成，优化这些架构具有挑战性。

A main problem of using feature vectors extracted using a backbone architecture is that their distribution is likely to be complex, as the problem the backbone has been optimized for most of the time differs from the considered task. As such, methods that rely on strong assumptions about the data distributions are likely to fail in leveraging the quality of features. In this paper, we tackle the problem of transfer-based fewshot learning with a twofold strategy: 1) preprocessing the data extracted from the backbone so that it fits a particular distribution (i.e. Gaussian-like) and 2) leveraging this specific distribution thanks to a well-thought proposed algorithm based on maximum a posteriori and optimal transport (only in the case of trans duct ive few-shot). Using standardized benchmarks in the field, we demonstrate the ability of the proposed method to obtain state-of-the-art accuracy, for various problems and backbone architectures in some inductive settings and most trans duct ive ones.

使用通过骨干架构提取的特征向量的一个主要问题是，它们的分布可能非常复杂，因为骨干网络大多数时候优化的任务与当前考虑的任务不同。因此，依赖于对数据分布强假设的方法可能无法充分利用特征的质量。在本文中，我们通过双重策略来解决基于迁移的少样本学习问题：1) 对从骨干网络中提取的数据进行预处理，使其符合特定的分布（例如高斯分布）；2) 利用这种特定分布，通过基于最大后验概率和最优传输（仅在转导式少样本情况下）的精心设计的算法来提升性能。通过使用该领域的标准化基准测试，我们展示了所提出方法在各种问题和骨干架构下，在某些归纳式设置和大多数转导式设置中，能够达到最先进的准确率。

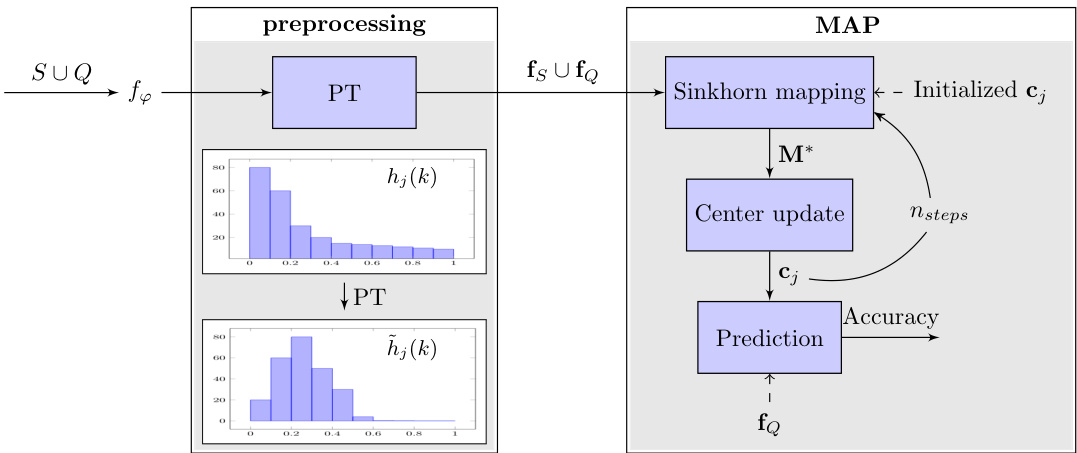
Figure 1: Illustration of the proposed method. First we extract feature vectors of all the inputs in $\mathbf{D}{n o v e l}$and preprocess them to obtain$\mathbf{f}{S}\cup\mathbf{f}{Q}$. Note that the Power transform (PT) has the effect of mapping a skewed feature distribution into a gaussian-like distribution ($h{j}(k)$denotes the histogram of feature$k$in class$j$). In MAP, we perform Sinkhorn mapping with class center$\mathbf{c}{j}$initialized on fS to obtain the class allocation matrix$\mathbf{M}^{*}$for$\mathbf{f}{Q}$, and we update the class centers for the next iteration. After$\boldsymbol{n_{s t e p s}}$we evaluate the accuracy on$\mathbf{f}_{Q}$ .

图 1: 所提出方法的示意图。首先，我们提取 $\mathbf{D}{n o v e l}$中所有输入的特征向量，并对它们进行预处理以获得$\mathbf{f}{S}\cup\mathbf{f}{Q}$。注意，幂变换 (PT) 的效果是将偏斜的特征分布映射为类似高斯分布（$h{j}(k)$表示类$j$中特征$k$的直方图）。在 MAP 中，我们在 fS 上初始化的类中心$\mathbf{c}{j}$上执行 Sinkhorn 映射，以获得$\mathbf{f}{Q}$的类分配矩阵$\mathbf{M}^{*}$，并为下一次迭代更新类中心。在$\boldsymbol{n_{s t e p s}}$之后，我们评估$\mathbf{f}_{Q}$ 上的准确率。

2 Related work

2 相关工作

A large volume of works in few-shot classification is based on meta learning [30] methods, where the training data is transformed into few-shot learning episodes to better fit in the context of few examples. In this branch, optimization based methods [30, 8, 23] train a well-initialized optimizer so that it quickly adapts to unseen classes with a few epochs of training. Other works [41, 4] utilize data augmentation techniques to artificially increase the size of the training datasets.

少样本分类领域的大量工作基于元学习 (meta learning) [30] 方法，其中训练数据被转换为少样本学习任务，以更好地适应少量样本的场景。在这一分支中，基于优化的方法 [30, 8, 23] 训练一个良好初始化的优化器，使其能够通过少量训练周期快速适应未见过的类别。其他工作 [41, 4] 则利用数据增强技术，人为增加训练数据集的规模。

In the past few years, there have been a growing interest in transfer-based methods. The main idea consists in training feature extractors able to efficiently segregate novel classes it never saw before. For example, in [3] the authors train the backbone with a distance-based classifier [22] that takes into account the inter-class distance. In [21], the authors utilize self-supervised learning techniques [2] to co-train an extra rotation classifier for the output features, improving the accuracy in few-shot settings. Many approaches are built on top of a feature extractor. For instance, in [38] the authors implement a nearest class mean classifier to associate an input with a class whose centroid is the closest in terms of the $\ell_{2}$ distance. In [18] an iterative approach is used to adjust the class centers. In [13] the authors build a graph neural neural network to gather the feature information from similar samples. Transferbased techniques typically reach the best performance on standardized benchmarks.

过去几年，基于迁移的方法引起了越来越多的关注。其主要思想是训练特征提取器，使其能够有效分离从未见过的新类别。例如，在 [3] 中，作者使用基于距离的分类器 [22] 训练骨干网络，该分类器考虑了类间距离。在 [21] 中，作者利用自监督学习技术 [2] 共同训练一个额外的旋转分类器来处理输出特征，从而提高了少样本设置中的准确性。许多方法都是基于特征提取器构建的。例如，在 [38] 中，作者实现了一个最近类均值分类器，将输入与在 $\ell_{2}$ 距离上最接近的类中心相关联。在 [18] 中，使用迭代方法来调整类中心。在 [13] 中，作者构建了一个图神经网络，以从相似样本中收集特征信息。基于迁移的技术通常在标准化基准测试中达到最佳性能。

Although many works involve feature extraction, few have explored the features in terms of their distribution [11]. Often, assumptions are made that the features in a class align to a certain distribution, even though these assumptions are rarely experimentally discussed. In our work, we analyze the impact of the features distributions and how they can be transformed for better processing and accuracy. We also introduce a new algorithm to improve the quality of the association between input features and corresponding classes in typical few-shot settings.

虽然许多工作涉及特征提取，但很少有研究从特征分布的角度进行探讨 [11]。通常，人们会假设某一类别的特征符合某种分布，尽管这些假设很少通过实验进行讨论。在我们的工作中，我们分析了特征分布的影响，以及如何通过转换特征来提高处理效率和准确性。我们还引入了一种新算法，以在典型的少样本设置中改善输入特征与对应类别之间的关联质量。

Contributions. Let us highlight the main contributions of this work. (1) We propose to preprocess the raw extracted features in order to make them more aligned with Gaussian assumptions. Namely we introduce transforms of the features so that they become less skewed. (2) We use a wasser stein-based method to better align the distribution of features with that of the considered classes. (3) We show that the proposed method can bring large increase in accuracy with a variety of feature extractors and datasets, leading to state-of-the-art results in the considered benchmarks.

贡献。让我们重点介绍这项工作的主要贡献。(1) 我们提出对原始提取的特征进行预处理，以使它们更符合高斯假设。具体来说，我们引入了特征的变换，以减少它们的偏斜。(2) 我们使用基于Wasserstein距离的方法，以更好地将特征的分布与所考虑的类别的分布对齐。(3) 我们展示了所提出的方法可以在多种特征提取器和数据集上带来显著的准确率提升，从而在所考虑的基准测试中取得了最先进的结果。

3 Methodology

3 方法论

In this section we introduce the problem settings. We discuss the training of the feature extractors, the preprocessing steps that we apply on the trained features and the final classification algorithm. A summary of our proposed method is depicted in Figure 1.

在本节中，我们介绍了问题设置。我们讨论了特征提取器的训练、对训练特征进行的预处理步骤以及最终的分类算法。我们提出的方法总结如图1所示。

3.1 Problem statement

3.1 问题陈述

We consider a typical few-shot learning problem. We are given a base dataset $\mathbf{D}{b a s e}$and a novel dataset$\mathbf{D}{n o v e l}$such that$\mathbf{D}{b a s e}\cap\mathbf{D}{n o v e l}=\emptyset$.$\mathbf{D}{b a s e}$contains a large number of labelled examples from$K$different classes.$\mathbf{D}{n o v e l}$, also referred to as a task in other works, contains a small number of labelled examples (support set$S$), along with some unlabelled ones (query set$Q$), all from$w$new classes. Our goal is to predict the class of the unlabelled examples in the query set. The following parameters are of particular importance to define such a few-shot problem: the number of classes in the novel dataset$w$(called$w$-way), the number of labelled samples per class$s$(called$s$-shot) and the number of unlabelled samples per class$q$. So the novel dataset contains a total of$w(s+q)$samples,$w s$of them being labelled, and$w q$of them being those to classify. In the case of inductive few-shot, the prediction is performed independently on each one of the$w q$samples. In the case of trans duct ive few-shot [20, 18], the prediction is performed considering all$w q$samples together. In the latter case, most works exploit the information that there are exactly$q$ samples in each class. We discuss this point in the experiments.

我们考虑一个典型的少样本学习问题。给定一个基础数据集 $\mathbf{D}{base}$和一个新数据集$\mathbf{D}{novel}$，且$\mathbf{D}{base}\cap\mathbf{D}{novel}=\emptyset$。$\mathbf{D}{base}$包含来自$K$个不同类别的大量标注样本。$\mathbf{D}{novel}$（在其他工作中也称为任务）包含少量标注样本（支持集$S$）以及一些未标注样本（查询集$Q$），所有这些样本都来自$w$个新类别。我们的目标是预测查询集中未标注样本的类别。以下参数对于定义这样的少样本问题尤为重要：新数据集中的类别数$w$（称为$w$-way），每个类别的标注样本数$s$（称为$s$-shot），以及每个类别的未标注样本数$q$。因此，新数据集总共包含$w(s+q)$个样本，其中$ws$个是标注的，$wq$个是需要分类的。在归纳少样本的情况下，预测是独立地对每个$wq$样本进行的。在转导少样本的情况下 [20, 18]，预测是考虑所有$wq$样本一起进行的。在后一种情况下，大多数工作利用了每个类别中恰好有$q$ 个样本的信息。我们在实验中讨论了这一点。

3.2 Feature extraction

3.2 特征提取

The first step is to train a neural network backbone model using only the base dataset. In this work we consider multiple backbones, with various training procedures. Once the considered backbone is trained, we obtain robust embeddings that should generalize well to novel classes. We denote by $f_{\varphi}$ the backbone function, obtained by extracting the output of the penultimate layer from the considered architecture, with $\varphi$ being the trained architecture parameters. Note that importantly, in all backbone architectures used in the experiments of this work, the penultimate layers are obtained by applying a ReLU function, so that all feature components coming out of $f_{\varphi}$ are non negative.

第一步是仅使用基础数据集训练一个神经网络骨干模型。在本工作中，我们考虑了多个骨干模型，并采用了不同的训练方法。一旦所考虑的骨干模型训练完成，我们就能获得鲁棒的嵌入，这些嵌入应该能够很好地泛化到新类别。我们用 $f_{\varphi}$ 表示骨干函数，该函数通过从所考虑的架构中提取倒数第二层的输出获得，其中 $\varphi$ 是训练好的架构参数。需要注意的是，在本工作的所有实验中使用的骨干架构中，倒数第二层是通过应用 ReLU 函数获得的，因此从 $f_{\varphi}$ 输出的所有特征分量都是非负的。

3.3 Feature preprocessing

3.3 特征预处理

As mentioned in Section 2, many works hypothesize, explicitly or not, that the features from the same class are aligned with a specific distribution (often Gaussianlike). But this aspect is rarely experimentally verified. In fact, it is very likely that features obtained using the backbone architecture are not Gaussian. Indeed, usually the features are obtained after applying a relu function, and exhibit a positive distribution mostly concentrated around 0 (see details in the next section).

如第2节所述，许多工作明确或隐含地假设来自同一类别的特征与特定分布（通常是类高斯分布）对齐。但这一方面很少经过实验验证。事实上，使用骨干架构获得的特征很可能不是高斯分布。实际上，通常特征是在应用ReLU函数后获得的，并且呈现出主要集中在0附近的正分布（详见下一节）。

Multiple works in the domain [38, 18] discuss the different statistical methods (e.g. normalization) to better fit the features into a model. Although these methods may have provable assets for some distributions, they could worsen the process if applied to an unexpected input distribution. This is why we propose to preprocess the obtained feature vectors so that they better align with typical distribution assumptions in the field. Namely, we use a power transform as follows.

该领域中的多项研究 [38, 18] 讨论了不同的统计方法（例如归一化），以更好地将特征拟合到模型中。尽管这些方法可能对某些分布具有可证明的优势，但如果应用于意外的输入分布，可能会使过程恶化。这就是为什么我们建议对获得的特征向量进行预处理，以便它们更好地与该领域的典型分布假设对齐。具体而言，我们使用如下的幂变换。

Power transform (PT). Denote $\textbf{v}=\mathbf{\nabla}f_{\varphi}(\mathbf{x})\in\mathbf{\sigma}$ $(\mathbb{R}^{+})^{d},\mathbf{x}\in\mathbf{D}{n o v e l}$as the obtained features on$\mathbf{D}{n o v e l}$ We hereby perform a power transformation method, which is similar to Tukey’s Transformation Ladder [32], on the features. We then follow a unit variance projection, the formula is given by:

幂变换 (PT)。设 $\textbf{v}=\mathbf{\nabla}f_{\varphi}(\mathbf{x})\in\mathbf{\sigma}$ $(\mathbb{R}^{+})^{d},\mathbf{x}\in\mathbf{D}{n o v e l}$为在$\mathbf{D}{n o v e l}$ 上获得的特征。我们在此对特征进行一种类似于 Tukey 变换阶梯 [32] 的幂变换方法。随后，我们进行单位方差投影，公式如下：

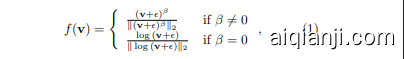
where $\epsilon=1e{-6}$ is used to make sure that ${\mathbf{v}}\boldsymbol{+}\epsilon$ is strictly positive and $\beta$ is a hyper-parameter. The rationales of the preprocessing above are: (1) Power transforms have the functionality of reducing the skew of a distribution, adjusted by $\beta$ , (2) Unit variance projection scales the features to the same area so that large variance features do not predominate the others. This preprocessing step is often able to map data from any distribution to a close-to-Gaussian distribution. We will analyse this ability and the effect of power transform in more details in Section 4.

其中 $\epsilon=1e{-6}$ 用于确保 ${\mathbf{v}}\boldsymbol{+}\epsilon$ 严格为正，$\beta$ 是一个超参数。上述预处理的原理是：(1) 幂变换具有减少分布偏斜的功能，通过 $\beta$ 进行调整，(2) 单位方差投影将特征缩放到相同的区域，使得大方差特征不会主导其他特征。此预处理步骤通常能够将任何分布的数据映射到接近高斯分布。我们将在第4节中更详细地分析这种能力以及幂变换的效果。

Note that $\beta=1$ leads to almost no effect. More generally, the skew of the obtained distribution changes when $\beta$ varies. For instance, if a raw distribution is rightskewed, decreasing $\beta$ phases out the right skew, and phases into a left-skewed distribution when $\beta$ becomes negative. After experiments, we found that $\beta=0.5$ gives the most consistent results for our considered experiments. More details based on our considered experiments are available in Section 4.

注意到当 $\beta=1$ 时，几乎没有任何效果。更一般地，当 $\beta$ 变化时，所获得分布的偏斜度也会发生变化。例如，如果原始分布是右偏的，减小 $\beta$ 会逐渐消除右偏，并在 $\beta$ 变为负值时逐渐转变为左偏分布。经过实验，我们发现 $\beta=0.5$ 在我们所考虑的实验中给出了最一致的结果。更多基于我们实验的细节见第4节。

This first step of feature preprocessing can be performed in both inductive and trans duct ive settings.

特征预处理的第一步可以在归纳和传导两种设置下进行。

3.4 MAP

3.4 MAP

Let us assume that the pre processed feature distribution for each class is Gaussian or Gaussian-like. As such, a well-positioned class center is crucial to a good prediction. In this section we discuss how to best estimate the class centers when the number of samples is very limited and classes are only partially labelled. In more details, we propose an Expectation–Maximization [7]- like algorithm that will iterative ly find the Maximum A Posteriori (MAP) estimates of the class centers.

假设每个类别的预处理特征分布是高斯或类高斯的。因此，一个良好定位的类别中心对于良好的预测至关重要。在本节中，我们讨论了在样本数量非常有限且类别仅部分标记的情况下，如何最好地估计类别中心。更详细地说，我们提出了一种类似于期望最大化 (Expectation–Maximization) [7] 的算法，该算法将迭代地找到类别中心的最大后验 (Maximum A Posteriori, MAP) 估计。

We firstly show that estimating these centers through MAP is similar to the minimization of Wasser stein distance. Then, an iterative procedure based on a Wasser stein distance estimation, using the sinkhorn algorithm [5, 33, 14], is designed to estimate the optimal transport from the initial distribution of the feature vectors to one that would correspond to the draw of samples from Gaussian distributions.

我们首先展示了通过最大后验概率 (MAP) 估计这些中心与最小化 Wasserstein 距离的相似性。然后，设计了一种基于 Wasserstein 距离估计的迭代过程，使用 sinkhorn 算法 [5, 33, 14]，以估计从特征向量的初始分布到与从高斯分布中抽取样本相对应的分布的最优传输。

Note that in this step we consider what is called the “trans duct ive” setting in many other few shot learning works [20, 18, 19, 13, 17, 9, 16, 10, 39], where we exploit unlabelled samples during the procedure as well as priors about their relative proportions.

请注意，在这一步中，我们考虑了许多其他少样本学习工作中所谓的“转导式”设置 [20, 18, 19, 13, 17, 9, 16, 10, 39]，其中我们在过程中利用了未标记的样本以及它们相对比例的先验信息。

In the following, we denote by $\mathbf{f}{S}$the set of feature vectors corresponding to labelled inputs and by fQ the set of feature vectors corresponding to unlabelled inputs. For a feature vector$\mathbf{f}\in\mathbf{f}{S}\cup\mathbf{f}{Q}$, we denote by$\ell(\mathbf{f})$the corresponding label. We use$0<i\leq w q$to denote the index of an unlabelled sample, so that$\mathbf{f}{Q}=(\mathbf{f}{i}){i}$, and we denote$\mathbf{c}_{j},0<j\leq w$the estimated center for feature vectors corresponding to class$j$ .

在下文中，我们用 $\mathbf{f}{S}$表示标记输入对应的特征向量集合，用$\mathbf{f}{Q}$表示未标记输入对应的特征向量集合。对于特征向量$\mathbf{f}\in\mathbf{f}{S}\cup\mathbf{f}{Q}$，我们用$\ell(\mathbf{f})$表示其对应的标签。我们使用$0<i\leq w q$表示未标记样本的索引，因此$\mathbf{f}{Q}=(\mathbf{f}{i}){i}$，并用$\mathbf{c}{j},0<j\leq w$表示类别$j$ 对应的特征向量的估计中心。

Our algorithm consists in several steps in which we estimate class centers from a soft allocation matrix $\mathbf{M}^{*}$ , then we update the allocation matrix based on the newly found class centers and iterate the process. In the following paragraphs, we detail these steps.

我们的算法由几个步骤组成，在这些步骤中，我们从软分配矩阵 $\mathbf{M}^{*}$ 中估计类中心，然后根据新找到的类中心更新分配矩阵，并迭代该过程。在接下来的段落中，我们将详细描述这些步骤。

Sinkhorn mapping. Considering using MAP estimation for the class centers, and assuming a Gaussian distribution for each class, we typically aim at solving:

Sinkhorn映射。考虑使用最大后验概率估计（MAP estimation）来估计类别中心，并假设每个类别服从高斯分布，我们通常旨在解决：

where $\mathit{c}$ represents the set of admissible labelling sets. Let us point out that the last term corresponds exactly to the Wasser stein distance used in the Optimal Transport problem formulation [5].

其中 $\mathit{c}$ 表示可接受的标签集集合。我们指出，最后一项正好对应于最优传输问题公式中使用的 Wasserstein 距离 [5]。

Therefore, in this step we find the class mapping matrix that minimizes the Wasser stein distance. Inspired by the Sinkhorn algorithm [35, 5], we define the mapping matrix $\mathbf{M}^{*}$ as follows:

因此，在这一步中，我们寻找最小化 Wasserstein 距离的类别映射矩阵。受 Sinkhorn 算法 [35, 5] 的启发，我们将映射矩阵 $\mathbf{M}^{*}$ 定义如下：

where $\mathbb{U}(\mathbf{p},\mathbf{q})\in\mathbb{R}_{+}^{w q\times w}$ is a set of positive matrices for which the rows sum to $\mathbf{p}$ and the columns sum to $\mathbf{q}$ . Formally, $\mathbb{U}(\mathbf{p},\mathbf{q})$ can be written as:

其中 $\mathbb{U}(\mathbf{p},\mathbf{q})\in\mathbb{R}_{+}^{w q\times w}$ 是一组正矩阵，其行和为 $\mathbf{p}$，列和为 $\mathbf{q}$。形式上，$\mathbb{U}(\mathbf{p},\mathbf{q})$ 可以写成：

$\mathbf{p}$ denotes the distribution of the amount that each unlabelled example uses for class allocation, and $\mathbf{q}$ denotes the distribution of the amount of unlabelled examples allocated to each class. Therefore, $\mathbb{U}(\mathbf{p},\mathbf{q})$ contains all the possible ways of allocating examples to classes. The cost function $\mathbf{L}\in\mathbb{R}^{w q\times w}$ in Equation (3) consists of the euclidean distances between unlabelled examples and class centers, hence $\mathbf{L}_{i j}$ denotes the euclidean distance between example $i$ and class center $j$ . Here we assume a soft class mapping, meaning that each example can be “sliced” into different classes.

$\mathbf{p}$ 表示每个未标记样本用于类别分配的量的分布，$\mathbf{q}$ 表示分配给每个类别的未标记样本的量的分布。因此，$\mathbb{U}(\mathbf{p},\mathbf{q})$ 包含了所有将样本分配到类别的可能方式。公式 (3) 中的成本函数 $\mathbf{L}\in\mathbb{R}^{w q\times w}$ 由未标记样本与类别中心之间的欧几里得距离组成，因此 $\mathbf{L}_{i j}$ 表示样本 $i$ 与类别中心 $j$ 之间的欧几里得距离。这里我们假设一个软类别映射，意味着每个样本可以被“切片”到不同的类别中。

The second term on the right of Equation (3) denotes the entropy of M: $\begin{array}{r}{H(\mathbf{M})=-\sum_{i j}\mathbf{M}{i j}\log\mathbf{M}{i j}}\end{array}$, regu- larized by a hyper-parameter$\lambda$. Increasing$\lambda$would force the entropy to become smaller, so that the mapping is less homogeneous. This term also makes the objective function strictly convex [5, 29] and thus a practical and effective computation. From lemma 2 in [5], the result of this Sinkhorn mapping has the typical form$\mathbf{M}^{*}=\mathrm{diag}(\mathbf{u})\cdot\exp(-\mathbf{L}/\lambda)\cdot\mathrm{diag}(\mathbf{v})$ .

方程 (3) 右边的第二项表示 M 的熵：$\begin{array}{r}{H(\mathbf{M})=-\sum_{i j}\mathbf{M}{i j}\log\mathbf{M}{i j}}\end{array}$，通过超参数$\lambda$进行正则化。增加$\lambda$会使熵变小，从而使映射更加不均匀。这一项还使目标函数严格凸 [5, 29]，从而实现了实用且有效的计算。根据 [5] 中的引理 2，这种 Sinkhorn 映射的结果具有典型形式$\mathbf{M}^{*}=\mathrm{diag}(\mathbf{u})\cdot\exp(-\mathbf{L}/\lambda)\cdot\mathrm{diag}(\mathbf{v})$。

Iterative center estimation. In this step, our aim is to estimate class centers. As shown in Algorithm 1, we initialize $\mathbf{c}{j}$as the average of labelled samples belonging to class$j$. Then$\mathbf{c}{j}$is iterative ly re-estimated. At each iteration, we compute a mapping matrix M$^*$on the unlabelled examples using the sinkhorn mapping. Along with labelled examples, we re-estimate$\mathbf{c}{j}$(temporarily denoted$\pmb{\mu}{j}$) by weighted-averaging the features with their allocated portions for class$j$ :

迭代中心估计。在这一步中，我们的目标是估计类别中心。如算法 1 所示，我们将 $\mathbf{c}{j}$初始化为属于类别$j$的标记样本的平均值。然后，$\mathbf{c}{j}$被迭代地重新估计。在每次迭代中，我们使用 sinkhorn 映射在未标记样本上计算映射矩阵 M$^*$。结合标记样本，我们通过加权平均特征及其分配给类别$j$的部分来重新估计$\mathbf{c}{j}$（暂时表示为$\pmb{\mu}{j}$）：

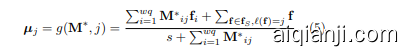
This formula corresponds to the minimization of Equation (3). Note that labelled examples do not participate in the mapping process. Since their labels are known, we instead set allocations for their belonging classes to be 1 and to the others to be $0$ . Therefore, labelled examples have the largest possible weight when re-estimating the class centers.

该公式对应于方程 (3) 的最小化。需要注意的是，已标注的样本不参与映射过程。由于它们的标签已知，我们将其所属类别的分配设置为 1，其他类别设置为 $0$。因此，在重新估计类别中心时，已标注的样本具有最大的权重。

Proportioned center update. In order to avoid taking risky harsh decisions in early iterations of the algorithm, we propose to proportionate the update of class centers using an inertia parameter. In more details, we update the center with a learning rate $0<$ $\alpha\leq1$ . When $\alpha$ is close to $0$ , the update becomes very slow, whereas $\alpha=1$ corresponds to directly allocating the newly found class centers:

比例中心更新。为了避免在算法的早期迭代中做出风险较大的激进决策，我们提出使用惯性参数来按比例更新类别中心。具体来说，我们以学习率 $0<$ $\alpha\leq1$ 更新中心。当 $\alpha$ 接近 $0$ 时，更新变得非常缓慢，而 $\alpha=1$ 则对应于直接分配新找到的类别中心：

Final decision. After a fixed number of steps nsteps, the rows of $\mathbf{M}^{*}$ are interpreted as probabilities to belong to each class. The maximal value corresponds to the decision of the algorithm.

最终决策。经过固定步骤数 nsteps 后，$\mathbf{M}^{*}$ 的行被解释为属于每个类别的概率。最大值对应算法的决策。

A summary of our proposed algorithm is presented in Algorithm 1. In Table 1 we summarize the main parameters and hyper parameters of the considered problem and proposed solution. The code is available at XXX.

我们提出的算法总结见算法 1。在表 1 中，我们总结了所考虑问题和提出解决方案的主要参数和超参数。代码可在 XXX 获取。

4 Experiments

4 实验

4.1 Datasets

4.1 数据集

We evaluate the performance of the proposed method using standardized few-shot classification datasets: mini Image Net [36], tiered Image Net [24], CUB [37] and

我们使用标准化的少样本分类数据集评估所提出方法的性能：mini ImageNet [36]、tiered ImageNet [24]、CUB [37] 和

算法 1: 提出的算法

参数 :w, s, q, 入, Q, Nsteps

f

重复 nsteps 次: Lij = |f - cll², V, j M* = Sinkhorn(L, p = lwq, q = qlw, ^)

CIFAR-FS [1]. The mini Image Net dataset contains 100 classes randomly chosen from ILSVRC- 2012 [25] and 600 images of size $84\times84$ pixels per class. It is split into 64 base classes, 16 validation classes and 20 novel classes. The tiered Image Net dataset is another subset of ImageNet, it consists of 34 high-level categories with 608 classes in total. These categories are split into 20 meta-training super classes, 6 meta-validation superclasses and 8 meta-test super classes, which corresponds to 351 base classes, 97 validation classes and 160 novel classes respectively. The CUB dataset contains 200 classes and has 11,788 images of size $84\times84$ pixels in total. Following [13], it is split into 100 base classes, 50 validation classes and 50 novel classes. The CIFARFS dataset has 100 classes, each class contains 600 images of size $32\times32$ pixels. The splits of this dataset are the same as those in mini Image Net.

CIFAR-FS [1]。mini Image Net 数据集包含从 ILSVRC-2012 [25] 中随机选择的 100 个类别，每个类别有 600 张大小为 $84\times84$ 像素的图像。它被分为 64 个基础类别、16 个验证类别和 20 个新类别。tiered Image Net 数据集是 ImageNet 的另一个子集，它包含 34 个高级类别，总共有 608 个类别。这些类别被分为 20 个元训练超类、6 个元验证超类和 8 个元测试超类，分别对应 351 个基础类别、97 个验证类别和 160 个新类别。CUB 数据集包含 200 个类别，总共有 11,788 张大小为 $84\times84$ 像素的图像。根据 [13]，它被分为 100 个基础类别、50 个验证类别和 50 个新类别。CIFARFS 数据集有 100 个类别，每个类别包含 600 张大小为 $32\times32$ 像素的图像。该数据集的划分与 mini Image Net 相同。

4.2 Implementation details

4.2 实现细节

In order to stress the genericity of our proposed method with regards to the chosen backbone architecture and training strategy, we perform experiments using WRN [40], ResNet18 and ResNet12 [12], along with some other pretrained backbones (e.g. DenseNet [15]). For each dataset we train the feature extractor with base classes, tune the hyper parameters with validation classes and test the performance using novel classes. Therefore, for each test run, $w$ classes are drawn uniformly at random among novel classes. Among these $w$ classes, $s$ labelled examples and $q$ unlabelled examples per class are uniformly drawn at random to form $\mathbf{D}_{n o v e l}$ . The WRN and ResNet are trained following [21]. In the inductive setting, we use our proposed Power Transform followed by a basic Nearest Class Mean (NCM) classifier. In the transductive setting, the MAP or an alternative is applied after PT. In order to better segregate between feature vectors of corresponding classes for each task, we implement the “trans-mean-sub” [18] before MAP where we separately subtract inputs by the means of labelled and unlabelled examples, followed by a unit hyper sphere projection. All our experiments are performed using $w=5,q=15$ , $s=1$ or 5. We run 10,000 random draws to obtain mean accuracy score and indicate confidence scores (95%) when relevant. The tuned hyperparameters for mini Image Net are $\beta=0.5,\lambda=10,\alpha=0.4$ and $n_{s t e p s}=30$ for $s=1$ ; $\beta=0.5,\lambda=10,\alpha=0.2$ and $n_{s t e p s}=20$ for $s=5$ . Hyper parameters for other datasets are detailed in the experiments below.

为了强调我们提出的方法在选择骨干架构和训练策略方面的通用性，我们使用 WRN [40]、ResNet18 和 ResNet12 [12] 以及其他一些预训练骨干（例如 DenseNet [15]）进行实验。对于每个数据集，我们使用基础类训练特征提取器，使用验证类调整超参数，并使用新类测试性能。因此，对于每次测试运行，从新类中均匀随机抽取 $w$ 个类。在这些 $w$ 个类中，每个类均匀随机抽取 $s$ 个标记样本和 $q$ 个未标记样本，形成 $\mathbf{D}_{n o v e l}$。WRN 和 ResNet 的训练遵循 [21]。在归纳设置中，我们使用提出的 Power Transform，然后使用基本的最近类均值 (NCM) 分类器。在转导设置中，PT 后应用 MAP 或替代方法。为了更好地分离每个任务中对应类的特征向量，我们在 MAP 之前实现“trans-mean-sub” [18]，其中我们分别减去标记和未标记样本的均值，然后进行单位超球投影。所有实验均使用 $w=5,q=15$，$s=1$ 或 5 进行。我们运行 10,000 次随机抽取以获得平均准确率分数，并在相关时指示置信分数 (95%)。mini Image Net 的超参数调整为 $s=1$ 时 $\beta=0.5,\lambda=10,\alpha=0.4$ 和 $n_{s t e p s}=30$；$s=5$ 时 $\beta=0.5,\lambda=10,\alpha=0.2$ 和 $n_{s t e p s}=20$。其他数据集的超参数在以下实验中详细说明。

4.3 Comparison with state-of-the-art methods

4.3 与最先进方法的比较

In the first experiment, we conduct our proposed method on different benchmarks and compare the performance with other state-of-the-art solutions. The results are presented in Table 2, we observe that our method with WRN as backbone reaches the state-ofthe-art performance for most cases in both inductive and trans duct ive settings on all the benchmarks. In Table 3 we also implement our proposed method on tiered Image Net based on a pre-trained Dense Net 121 backbone following the procedure described in [38]. From these exper