GLocal-K: Global and Local Kernels for Recommend er Systems
GLocal-K: 推荐系统中的全局与局部核函数
ABSTRACT
摘要
Recommend er systems typically operate on high-dimensional sparse user-item matrices. Matrix completion is a very challenging task to predict one’s interest based on millions of other users having each seen a small subset of thousands of items. We propose a GlobalLocal Kernel-based matrix completion framework, named GLocalK, that aims to generalise and represent a high-dimensional sparse user-item matrix entry into a low dimensional space with a small number of important features. Our GLocal-K can be divided into two major stages. First, we pre-train an auto encoder with the local kernelised weight matrix, which transforms the data from one space into the feature space by using a 2d-RBF kernel. Then, the pre-trained auto encoder is fine-tuned with the rating matrix, produced by a convolution-based global kernel, which captures the characteristics of each item. We apply our GLocal-K model under the extreme low-resource setting, which includes only a user-item rating matrix, with no side information. Our model outperforms the state-of-the-art baselines on three collaborative filtering benchmarks: ML-100K, ML-1M, and Douban.
推荐系统通常基于高维稀疏的用户-物品矩阵运行。矩阵补全是一项极具挑战性的任务,它需要根据数百万用户(每个用户仅接触过数千物品中的一小部分)来预测个体兴趣。我们提出了一个基于全局-局部核的矩阵补全框架GLocalK,旨在将高维稀疏用户-物品矩阵条目泛化并表示为具有少量重要特征的低维空间。
GLocal-K可分为两个主要阶段:
- 首先,我们使用局部核化权重矩阵预训练自动编码器,通过2d-RBF核将数据从原始空间转换到特征空间。
- 随后,用基于卷积的全局核生成的评分矩阵对预训练好的自动编码器进行微调,该全局核能捕捉每个物品的特征。
我们在极低资源设置下应用GLocal-K模型,该设置仅包含用户-物品评分矩阵,无任何辅助信息。我们的模型在三个协同过滤基准测试(ML-100K、ML-1M和豆瓣)上均优于当前最先进的基线方法。
CCS CONCEPTS
CCS概念
• Information systems $\rightarrow$ Recommend er systems; $\bullet$ Theory of computation $\rightarrow$ Kernel methods.
• 信息系统 $\rightarrow$ 推荐系统
• 计算理论 $\rightarrow$ 核方法
KEYWORDS
关键词
Recommend er Systems, Matrix Completion, Kernel Methods
推荐系统、矩阵补全、核方法
ACM Reference Format:
ACM参考文献格式:
Soyeon Caren Han, Taejun Lim, Siqu Long, Bernd Burgs taller, and Josiah Poon. 2021. GLocal-K: Global and Local Kernels for Recommend er Systems. In Proceedings of the 30th ACM Int’l Conf. on Information and Knowledge
Soyeon Caren Han、Taejun Lim、Siqu Long、Bernd Burgstaller 和 Josiah Poon。2021。GLocal-K: 推荐系统中的全局与局部核函数。见《第30届ACM国际信息与知识管理会议论文集》
∗Co-first authors †Corresponding author
∗共同第一作者 †通讯作者
Management (CIKM ’21), November 1–5, 2021, Virtual Event, Australia. ACM, New York, NY, USA, 5 pages. https://doi.org/10.1145/3459637.3482112
知识管理与信息管理国际会议 (CIKM '21),2021年11月1-5日,澳大利亚线上会议。ACM,美国纽约,5页。https://doi.org/10.1145/3459637.3482112
1 INTRODUCTION
1 引言
Collaborative filtering-based recommend er systems focus on making a prediction about the interests of a user by collecting preferences from large number of other users. Matrix completion[2] is one of the most common formulation, where rows and columns of a matrix represent users and items, respectively. The prediction of users’ ratings in items corresponds to the completion of the missing entries in a high-dimensional user-item rating matrix. In practice, the matrix used for collaborative filtering is extremely sparse since it has ratings for only a limited number of user-item pairs.
基于协同过滤的推荐系统通过收集大量其他用户的偏好来预测用户的兴趣。矩阵补全[2]是最常见的表述方式之一,其中矩阵的行和列分别代表用户和物品。对用户物品评分的预测对应于高维用户-物品评分矩阵中缺失项的补全。实际上,用于协同过滤的矩阵极其稀疏,因为它仅包含有限数量用户-物品对的评分。
Traditional recommend er systems focus on general ising sparsely observed matrix entries to a low dimensional feature space by using an auto encoder(AE)[11]. AEs would help the system better understand users and items by learning the non-linear user-item relationship efficiently, and encoding complex abstractions into data representations. I-AutoRec[8] designed an item-based AE, which takes high-dimensional matrix entries, projects them into a lowdimensional latent hidden space, and then reconstructs the entries in the output space to predict missing ratings. SparseFC[6] employs an AE whose weight matrices were sparsified using finite support kernels. Inspired by this, GC-MC[1] proposed a graph-based AE framework for matrix completion, which produces latent features of user and item nodes through a form of message passing on the bipartite interaction graph. These latent user and item representations are used to reconstruct the rating links via a bilinear decoder. Such link prediction with a bipartite graph extends the model with structural and external side information. Recent studies [7, 9, 10] focused on utilising side information, such as opinion information or attributes of users. However, in most real-world settings (e.g., platforms and websites), there is no (or insufficient) side information available about users.
传统推荐系统主要通过自编码器 (AE) [11] 将稀疏观测的矩阵条目泛化到低维特征空间。自编码器能高效学习用户与物品间的非线性关系,并将复杂抽象特征编码为数据表示,从而帮助系统更好地理解用户和物品。I-AutoRec[8] 设计了基于物品的自编码器,该模型将高维矩阵条目投射到低维潜在隐空间,随后在输出空间重构条目以预测缺失评分。SparseFC[6] 采用了一种权重矩阵通过有限支撑核稀疏化的自编码器。受此启发,GC-MC[1] 提出了基于图的自编码器框架用于矩阵补全,该框架通过在二分交互图上进行消息传递来生成用户节点和物品节点的潜在特征。这些潜在的用户和物品表示通过双线性解码器重构评分链接。这种基于二分图的链接预测模型通过结构和外部辅助信息得到扩展。近期研究 [7,9,10] 侧重于利用辅助信息(如用户意见信息或属性),但在大多数现实场景(例如平台和网站)中,用户相关辅助信息往往缺失(或不足)。
Instead of considering side information, we focus on improving the feature extraction performance for a high-dimensional useritem rating matrix into a low-dimensional latent feature space. In this research, we apply two types of kernels that have strong ability in feature extraction. The first kernel, named “local kernel”, is known to give optimal separating surfaces by its ability to perform the data transformation from high-dimensional space, and widely used with support vector machines(SVMs). The second kernel, named “global kernel” is from convolutional neural network(CNN) architectures. The more kernel with deeper depth, the higher their feature extraction ability. Integrating these two kernels to have best of both worlds successfully extract the low-dimensional feature space.
我们不考虑辅助信息,而是专注于提升从高维用户-物品评分矩阵到低维潜在特征空间的特征提取性能。本研究采用两种具有强大特征提取能力的内核。第一种名为"局部核 (local kernel)"的内核,因其能将数据从高维空间转换并形成最优分离面的能力而闻名,常与支持向量机 (SVM) 结合使用。第二种名为"全局核 (global kernel)"的内核源自卷积神经网络 (CNN) 架构。内核深度越深,其特征提取能力越强。通过整合这两种内核的优势,我们成功提取出低维特征空间。
With this in mind, we propose a Global-Local Kernel-based matrix completion framework, called GLocal-K, which includes two stages: 1) pre-training the auto-encoder using a local kernelised weight matrix, and 2) fine-tuning with the global kernel-based rating matrix. Note that our evaluation is under an extreme setting where no side information is available, like most real-world cases. The main research contributions are summarised as follows: (1) We introduce a global and local kernel-based auto encoder model, which mainly pays attention to extract the latent features of users and items. (2) We propose a new way to integrate pre-training and fine-tuning tasks for the recommend er system. (3) Without using any extra information, our GLocal-K achieves the smallest RMSEs on three widely-used benchmarks, even beating models augmented by side information.
基于此,我们提出了一种全局-局部核矩阵补全框架GLocal-K,包含两个阶段:(1) 使用局部核化权重矩阵预训练自编码器,(2) 基于全局核评分矩阵进行微调。需注意,我们的评估是在极端无辅助信息场景下进行的(符合多数现实情况)。主要研究贡献如下:(1) 提出全局与局部核化自编码模型,重点提取用户和项目的潜在特征;(2) 创新性地整合推荐系统的预训练与微调任务;(3) 在不使用辅助信息的情况下,GLocal-K在三个常用基准测试中实现了最低RMSE,甚至优于使用辅助信息的增强模型。
2 GLOCAL-K
2 GLOCAL-K
Figure 1 depicts the architecture of our proposed GLocal-K model, which applies two types of kernels in two stages respectively: pretraining (with the local kernelised weight matrix) and fine-tuning (with the global-kernel based matrix)1. Note that we pre-train our model to make dense connections denser and sparse connections sparser using a finite support kernel, and fine-tune with the rating matrix. This matrix is produced from a convolution kernel by reducing the data dimension and producing a less redundant but small number of important feature sets. In this research, we mainly focus on a matrix completion task, which is conducted on a rating matrix $\boldsymbol{R}\in\mathbb{R}^{m\times n}$ with $m$ items and $n$ users. Each item $i\in I={1,2,...,m}$ is represented by a vector $r_{i}=(R_{i1},R_{i2},...,R_{i n})\in\mathbb{R}^{n}$ .
图1: 展示了我们提出的GLocal-K模型架构,该模型在两个阶段分别应用两种核函数:预训练阶段(使用局部核化权重矩阵)和微调阶段(基于全局核的矩阵)。需要注意的是,我们通过有限支撑核进行预训练,使密集连接更密集、稀疏连接更稀疏,并利用评分矩阵进行微调。该矩阵通过卷积核降维生成,能够产生冗余较少但数量精简的重要特征集。本研究主要聚焦于矩阵补全任务,该任务在评分矩阵$\boldsymbol{R}\in\mathbb{R}^{m\times n}$上进行,其中包含$m$个物品和$n$个用户。每个物品$i\in I={1,2,...,m}$由向量$r_{i}=(R_{i1},R_{i2},...,R_{i n})\in\mathbb{R}^{n}$表示。
2.1 Pre-training with Local Kernel
2.1 基于局部核的预训练
Auto-Encoder Pre-training
Auto-Encoder (自编码器) 预训练
We first deploy and train an item-based AE, inspired by [8], which takes each item vector $r_{i}$ as input, and outputs the reconstructed vector $r_{i}^{\prime}$ to predict the missing ratings. The model is represented as follows:
我们首先部署并训练了一个基于物品的自编码器 (Autoencoder, AE),其灵感来源于 [8]。该模型以每个物品向量 $r_{i}$ 作为输入,输出重构向量 $r_{i}^{\prime}$ 以预测缺失评分。模型表示如下:

where $W^{(e)}\in\mathbb{R}^{h\times m}$ and $W^{(d)}\in\mathbb{R}^{m\times h}$ are weight matrices, $b\in\mathbb{R}^{h}$ and $b^{\prime}\in\mathbb{R}^{m}$ are bias vectors, and $f(\cdot)$ and $g(\cdot)$ are non-linear activa- tion functions. The AE deploys an auto-associative neural network with a single $h$ -dimensional hidden layer. In order to emphasise the dense and sparse connection, we re parameter is e weight matrices in the AE with a radial-basis-function(RBF) kernel, which is known as Kernel Trick[3].
其中 $W^{(e)}\in\mathbb{R}^{h\times m}$ 和 $W^{(d)}\in\mathbb{R}^{m\times h}$ 是权重矩阵,$b\in\mathbb{R}^{h}$ 和 $b^{\prime}\in\mathbb{R}^{m}$ 是偏置向量,$f(\cdot)$ 和 $g(\cdot)$ 是非线性激活函数。该自编码器(AE)部署了具有单一 $h$ 维隐藏层的自关联神经网络。为了突出密集和稀疏连接特性,我们通过径向基函数(RBF)核重新参数化了AE中的权重矩阵,该方法被称为核技巧[3]。
Local Kernelised Weight Matrix
局部核化权重矩阵
The weight matrices $W^{(e)}$ and $W^{(d)}$ in Eq. (1) are re parameter is ed by a 2d-RBF kernel, named local kernelised weight matrix. The RBF kernel can be defined as follows:
式(1)中的权重矩阵$W^{(e)}$和$W^{(d)}$通过名为局部核化权重矩阵的2d-RBF核进行重新参数化。该RBF核定义如下:

where $K(\cdot)$ is a RBF kernel function, which computes the similarity between two sets of vectors $U$ , 𝑉 . Here, $u_{i}\in U$ and $v_{j}\in V$ . The kernel function can represent the output as a kernel matrix $\pmb{L K}$ (see Figure 1), in which each element maps to 1 for identical vectors and approaches 0 for very distant vectors between $u_{i}$ and $v_{j}$ . Then, we compute a local kernelised weight matrix as follows:
其中 $K(\cdot)$ 是一个RBF核函数,用于计算两组向量 $U$ 和 $V$ 之间的相似度。这里 $u_{i}\in U$ 且 $v_{j}\in V$。该核函数可将输出表示为核矩阵 $\pmb{L K}$ (见图1),其中每个元素在 $u_{i}$ 和 $v_{j}$ 为相同向量时映射为1,在两者相距甚远时趋近于0。接着,我们按如下方式计算局部核化权重矩阵:

where $W^{\prime}$ is computed by the Hadamard-product of weight and kernel matrices to obtain a sparsified weight matrix. The distance between each vector of $U$ and $V$ determines the connection of neurons in neural networks, and the degree of sparsity is dynamically varied as vectors are being changed at each step of training. As a result, applying the kernel trick to weight matrices enables regularising weight matrices and learning general is able representations.
其中 $W^{\prime}$ 通过权重矩阵与核矩阵的哈达玛积计算得到稀疏化权重矩阵。$U$ 和 $V$ 各向量间的距离决定了神经网络中神经元的连接方式,稀疏度会随着训练过程中向量的动态变化而调整。因此,对权重矩阵应用核技巧能够实现权重矩阵的正则化,并学习通用的可表征特征。
2.2 Fine-tuning with Global Kernel
2.2 全局核微调
Global kernel-based Rating Matrix
基于全局核的评分矩阵
We fine-tune the pre-trained auto encoder with the rating matrix, produced by the global convolutional kernel. Prior to fine-tuning, we firstly describe how the global kernel is constructed and applied to build the global kernel-based rating matrix. The entire construction procedure can be defined as follows:
我们使用由全局卷积核生成的评分矩阵对预训练的自编码器进行微调。在微调之前,首先描述如何构建全局核并应用于构建基于全局核的评分矩阵。整个构建过程可定义如下:

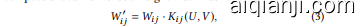
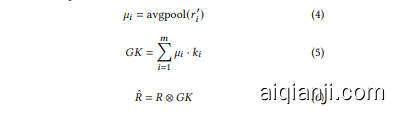
As shown in Figure 1, the decoder output of the pre-trained model is the matrix that includes initial predicted ratings in the missing entries, and passed to pooling. With item-based average pooling, we summarise each item information in the rating matrix. Eq. (4) shows the reconstructed item vector $\hat{r}{i}$ from the decoder output matrix $R^{\prime}$ is passed to pooling, and interpreted as item-based sum maris ation. Let $M={\mu{1},\mu_{2},...,\mu_{m}}\in\mathbb{R}^{m}$ be the pooling result, which plays a role as the weights of multiple kernels $K={k_{1},k_{2},...,k_{m}}\in\mathbb{R}^{m\times t^{2}}$ In Eq. (5), these kernels are aggregated by using an inner product. The result can be dynamically determined by different weights and different rating matrices so that it can be regarded as the ratingdependent mechanism. Then, the aggregated kernel $G K\in\mathbb{R}^{t\times t}$ is used as a global convolution kernel. We apply a global kernel-based convolution operation to the user-item rating matrix for global kernel-based feature extraction. In Eq. (6), $\hat{R}$ is the global kernelbased rating matrix, which is used as input for fine-tuning, and $\otimes$ denotes a convolution operation.
如图1所示,预训练模型的解码器输出是包含缺失条目初始预测评分的矩阵,该矩阵被传递至池化层。通过基于物品的平均池化,我们对评分矩阵中的每个物品信息进行汇总。公式(4)展示了从解码器输出矩阵$R^{\prime}$重构的物品向量$\hat{r}{i}$经池化处理后,可解释为基于物品的摘要表示。设$M={\mu{1},\mu_{2},...,\mu_{m}}\in\mathbb{R}^{m}$为池化结果,其作为多核$K={k_{1},k_{2},...,k_{m}}\in\mathbb{R}^{m\times t^{2}}$的权重参与计算。在公式(5)中,这些核函数通过内积进行聚合,其结果可根据不同权重和不同评分矩阵动态确定,因此可视为评分依赖机制。最终,聚合核$G K\in\mathbb{R}^{t\times t}$被用作全局卷积核,我们对用户-物品评分矩阵实施基于全局核的卷积操作以实现特征提取。公式(6)中,$\hat{R}$表示经全局核处理的评分矩阵,将作为微调阶段的输入,其中$\otimes$表示卷积运算。
Auto-Encoder Fine-tuning
自编码器微调
We then explore how the fine-tuning process works. The global kernel-based rating matrix 𝑅 is used as input for fine-tuning. It takes weights of a pre-trained AE model and makes an adjustment of the model based on the global kernel-based rating matrix, as depicted in Figure 1. The reconstructed result from the fine-tuned AE corresponds to the final predicted ratings for matrix completion in recommend er system.
我们随后探究微调过程的工作原理。基于全局核的评分矩阵𝑅被用作微调的输入。该过程采用预训练自编码器(AE)模型的权重,并根据基于全局核的评分矩阵对模型进行调整,如图1所示。经微调后的自编码器重建结果对应于推荐系统中矩阵补全的最终预测评分。
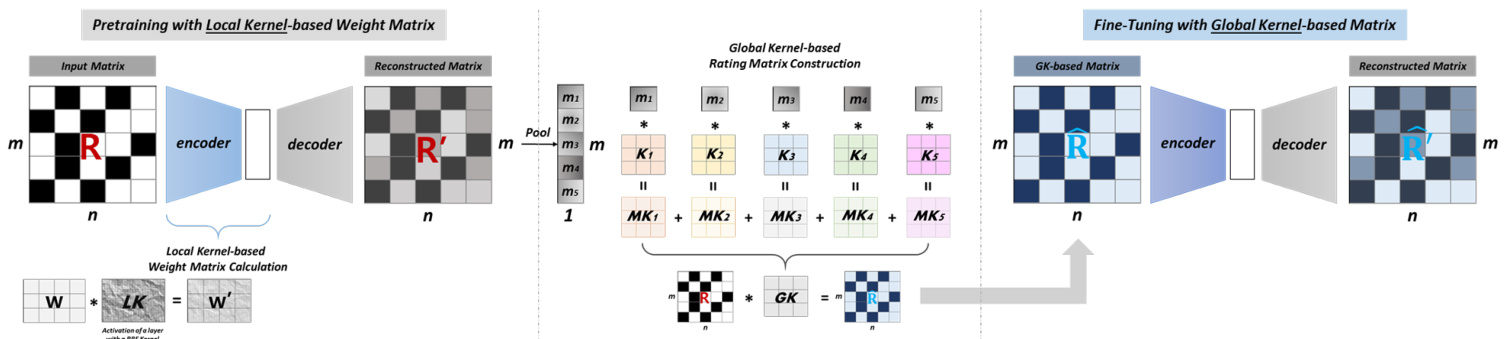
Figure 1: The GLocal-K architecture for matrix completion. (1) We pre-train the AE with the local kernelised weight matrix. (2) Then, fine-tune the trained AE with the global kernel-based matrix. The fine-tuned AE produces the matrix completion result.
图 1: 用于矩阵补全的GLocal-K架构。(1) 我们使用局部核化权重矩阵预训练AE。(2) 然后,用基于全局核的矩阵对训练好的AE进行微调。微调后的AE产生矩阵补全结果。
3 EXPERIMENTS
3 实验
3.1 Datasets
3.1 数据集
We conduct experiments on three widely used matrix completion benchmark datasets: MovieLens-100K (ML-100K), MovieLens-1M (ML-1M) and Douban (density $0.0630~/0.0447/~0.0152)$ . These datasets comprise of $(100\mathrm{k}/\mathrm{1}\mathrm{m}/\mathrm{1}36\mathrm{k})$ ratings of $\left(1,682/3,706$ $/3,000)$ movies by $(943/6,040/~3,000)$ users on a scale of $r\in$ ${1,2,3,4,5}$ . For ML-100K, we use the canonical u1.base/u1.test train/test split. For ML-1M, we randomly split into 90:10 train/test sets. For Douban, we use the pre processed subsets and splits provided by Monti et al. [5].
我们在三个广泛使用的矩阵补全基准数据集上进行了实验:MovieLens-100K (ML-100K)、MovieLens-1M (ML-1M) 和 Douban (密度 $0.0630~/0.0447/~0.0152)$。这些数据集包含 $(100\mathrm{k}/\mathrm{1}\mathrm{m}/\mathrm{1}36\mathrm{k})$ 条评分,涉及 $\left(1,682/3,706$ $/3,000)$ 部电影和 $(943/6,040/~3,000)$ 位用户,评分范围为 $r\in$ ${1,2,3,4,5}$。对于 ML-100K,我们使用标准的 u1.base/u1.test 训练/测试划分。对于 ML-1M,我们随机划分为 90:10 的训练/测试集。对于 Douban,我们使用 Monti 等人 [5] 提供的预处理子集和划分。
3.2 Baselines
3.2 基线方法
We compare the RMSE with the eleven recommendation baselines: (1) LLORMA[4] is a matrix factorization model using local low rank sub-matrices factorization. (2) I-AutoRec[8] is a autoencoder based model considering only the user or item embeddings in the encoder. (3) CF-NADE[13] replaces the role of the restricted Boltzmann machine (RBM) with the neural auto-regressive distribution estimator (NADE) for rating reconstruction. (4) GC-MC[1] is a graph-based AE framework that applies GNN on the bipartite interaction graph for rating link reconstruction. We consider GCMC with side information as (5) GC-MC $^+$ Extra. (6) GraphRec[7] is a matrix factorization utilizing graph-based features from the bipartite interaction graph. We consider GraphRec with side information as (7) GraphRec $^+$ Extra. (8) GRAEM[9] formulates a probabilistic generative model and uses expectation maximization to extend graph-regular is ed alternating least squares based on additional side information (SI) graphs. (9) SparseFC[6] is a neural network in which weight matrices are re parameter is ed in terms of low-dimensional vectors, interacting through finite support kernel functions. This is technically equivalent to the local kernel of GLocal-K. (10) IGMC[12] is similar to GCMC but applies a graphlevel GNN to the enclosing one-hot subgraph and maps a subgraph to the rating
