Towards Robust and Smooth 3D Multi-Person Pose Estimation from Monocular Videos in the Wild

面向野外单目视频的鲁棒平滑3D多人姿态估计

Abstract

摘要

3D pose estimation is an invaluable task in computer vision with various practical applications. Especially, $3D$ pose estimation for multi-person from a monocular video (3DMPPE) is particularly challenging and is still largely uncharted, far from applying to in-the-wild scenarios yet. We pose three unresolved issues with the existing methods: lack of robustness on unseen views during training, vulnerability to occlusion, and severe jittering in the output. As a remedy, we propose POTR-3D, the first realization of a sequence-to-sequence 2D-to-3D lifting model for 3DMPPE, powered by a novel geometry-aware data augmentation strategy, capable of generating unbounded data with a variety of views while caring about the ground plane and occlusions. Through extensive experiments, we verify that the proposed model and data augmentation robustly generalizes to diverse unseen views, robustly recovers the poses against heavy occlusions, and reliably generates more natural and smoother outputs. The effectiveness of our approach is verified not only by achieving the state-of-theart performance on public benchmarks, but also by qualitative results on more challenging in-the-wild videos. Demo videos are available at https://www.youtube.com/@potr3d.

3D姿态估计是计算机视觉中一项极具价值的任务，拥有多种实际应用。特别是基于单目视频的多人物3D姿态估计（3DMPPE）尤为困难，目前仍存在大量未探索领域，远未达到应用于真实场景的水平。我们指出现有方法的三个未解决问题：训练时对未见视角缺乏鲁棒性、易受遮挡影响以及输出存在严重抖动。为此，我们提出POTR-3D——首个面向3DMPPE的序列到序列2D转3D提升模型，采用创新的几何感知数据增强策略，能够生成无限视角数据并兼顾地平面约束与遮挡处理。通过大量实验验证，该模型与数据增强方案能稳健泛化至多样未见视角，有效恢复重度遮挡下的姿态，并生成更自然平滑的输出。我们的方法不仅在公开基准测试中达到最先进性能，更通过更具挑战性的真实场景视频定性结果验证了其有效性。演示视频详见https://www.youtube.com/@potr3d。

1. Introduction

1. 引言

3D pose estimation aims to reproduce the 3D coordinates of a person appearing in an untrimmed 2D video. It has been extensively studied in literature with many real-world applications, e.g., sports [3], healthcare [38], games [17], movies [1], and video compression [36]. Instead of fully rendering 3D voxels, we narrow down the scope of our discussion to reconstructing a handful number of body keypoints (e.g., neck, knees, or ankles), which concisely represent dynamics of human motions in the real world.

3D姿态估计旨在从未经剪辑的2D视频中还原人物的三维坐标。该技术已在文献中被广泛研究，并拥有众多实际应用场景，例如体育[3]、医疗保健[38]、游戏[17]、电影[1]和视频压缩[36]。与完全渲染3D体素不同，我们将讨论范围限定为重建少量身体关键点（如颈部、膝盖或脚踝），这些关键点能简洁表征现实世界中人体运动的动态特征。

Depending on the number of subjects, 3D pose estimation is categorized into 3D Single-Person Pose Estimation (3DSPPE) and 3D Multi-Person Pose Estimation (3DMPPE). In this paper, we mainly tackle 3DMPPE, reproducing the 3D coordinates of body keypoints for everyone appearing in a video. Unlike 3DSPPE that has been extensively studied and already being used for many applications, 3DMPPE is still largely uncharted whose models are hardly applicable to in-the-wild scenarios yet. For this reason, we pose 3 unresolved issues with previous models.

根据目标人数，3D姿态估计可分为3D单人姿态估计(3DSPPE)和3D多人姿态估计(3DMPPE)。本文主要研究3DMPPE任务，旨在为视频中出现的每个人重建身体关键点的3D坐标。与已被广泛研究并投入实际应用的3DSPPE不同，3DMPPE仍存在大量未知领域，现有模型难以适用于真实场景。为此，我们提出了当前模型尚未解决的三个问题。

First, existing models are not robustly applicable to unseen views (e.g. unusual camera angle or distance). Trained on a limited amount of data, most existing models perform well only on test examples captured under similar views, significantly under performing when applied to unseen views. Unfortunately, however, most 3D datasets provide a limited number of views (e.g., 4 for Human 3.6M [12] or 14 for MPI-INF-3DHP [24]), recorded under limited conditions like the subjects’ clothing or lighting due to the high cost of motion capturing (MoCap) equipment [8]. This practical restriction hinders learning a universally applicable model, failing to robustly generalize to in-the-wild videos.

首先，现有模型无法稳健地应用于未见过的视角（如非常规相机角度或距离）。由于训练数据量有限，大多数现有模型仅在相似视角下拍摄的测试样本上表现良好，而在处理未见视角时性能显著下降。然而，大多数3D数据集仅提供有限数量的视角（例如Human 3.6M [12]为4个视角，MPI-INF-3DHP [24]为14个视角），且受限于动作捕捉（MoCap）设备的高成本 [8]，这些数据通常在有限条件下（如受试者服装或光照）采集。这种实际限制阻碍了学习具有普适性的模型，导致无法稳健地泛化到真实场景视频中。

Second, occlusion is another long-standing challenge that most existing models still suffer from. Due to the invisible occluded keypoints, there is unavoidable ambiguity since there are multiple plausible answers for them. Occlusion becomes a lot more severe when a person totally blocks another from the camera, making the model output inconsistent estimation throughout the frames.

其次，遮挡是大多数现有模型仍面临的另一长期挑战。由于被遮挡的关键点不可见，存在不可避免的模糊性，因为这些关键点可能存在多个合理答案。当一个人完全遮挡另一个人时，遮挡问题会变得更加严重，导致模型在整个帧序列中输出不一致的估计结果。

Third, the existing methods often produce a sequence of 3D poses with severe jittering. This is an undesirable byproduct of the models, not present in the training data.

第三，现有方法通常会产生严重抖动的3D姿态序列。这是模型训练数据中不存在的不良副产品。

In this paper, we propose a 3DMPPE model, called POTR-3D, that works robustly and smoothly on in-the-wild videos with severe occlusion cases. Our model is powered by a novel data augmentation strategy, which generates training examples by combining and adjusting existing single-person data, to avoid actual data collection that requires high cost. For this augmentation, we decouple the core motion from pixel-level details, as creating a realistic 3D video at the voxel level is not a trivial task. Thereby, we adopt the 2D-to-3D lifting approach, which first detects the 2D body keypoints using an off-the-shelf model and trains a model to lift them into the 3D space. Benefiting from a more robust and general iz able 2D pose estimator, 2D-to-3D lifting approaches have been successfully applied to 3DSPPE [29, 41]. Observing that we only need the body keypoints, not the pixel-level details, of the subjects for training, we can easily generate an unlimited number of 2D-3D pairs using given camera parameters under various conditions, e.g., containing arbitrary number of subjects under various views. Translating and rotating the subjects as well as the ground plane itself, our augmentation strategy makes our model operate robustly on diverse views.

本文提出了一种名为POTR-3D的3DMPPE模型，该模型能在存在严重遮挡的野外视频中稳健流畅地运行。我们的模型采用了一种新颖的数据增强策略，通过组合调整现有人体单目数据生成训练样本，避免了高成本的实际数据采集。为此，我们将核心动作从像素级细节中解耦，因为在体素级别创建逼真的3D视频并非易事。因此，我们采用2D转3D的提升方法：先使用现成模型检测2D人体关键点，再训练模型将其提升至3D空间。得益于更鲁棒且泛化能力更强的2D姿态估计器，2D转3D方法已成功应用于3DSPPE [29,41]。考虑到训练仅需人体关键点而非像素级细节，我们可轻松利用给定相机参数生成无限量的2D-3D数据对（例如包含任意视角下多主体的场景）。通过对主体及地平面进行平移旋转，我们的增强策略使模型能在多样化视角下稳健运行。

To alleviate the occlusion problem, we take a couple of remedies. The main reason that existing models suffer from occlusion is that they process a single frame at a time (frame 2 frame). Following a previous work, MixSTE [41], which effectively process multiple frames at once (seq2seq) for 3DSPPE, our POTR-3D adopts a similar Transformerbased 2D-to-3D structure, naturally extending it to multiperson. Lifting the assumption that there is always a single person in the video, POTR-3D tracks multiple people at the same time, equipped with an additional self-attention across multiple people appearing in the same frame. We infer the depth and relative poses in a unified paradigm, helpful for a comprehensive understanding of the scene. To the best of our knowledge, POTR-3D is the first seq2seq 2D-to-3D lifting method for 3DMPPE. Alongside, we carefully design the augmentation method to reflect occlusion among people with a simple but novel volumetric model. We generate training examples with heavy occlusion, where expected outputs of off-the-shelf models are realistically mimicked, and thus the model is expected to learn from these noisy examples how to confidently pick useful information out of confusing situations.

为缓解遮挡问题，我们采取了若干改进措施。现有模型受限于遮挡的主要原因是其逐帧处理方式（frame2frame）。受MixSTE[41]（一种通过序列到序列（seq2seq）方式高效处理多帧的3DSPPE方法）启发，我们的POTR-3D采用类似的基于Transformer的2D转3D结构，并将其自然扩展至多人场景。通过摒弃视频中仅存在单人的假设，POTR-3D可同步追踪多人，并新增对同帧多人的自注意力机制。我们在统一范式下推断深度与相对姿态，这有助于全面理解场景。据我们所知，POTR-3D是首个面向3DMPPE的seq2seq式2D转3D提升方法。同时，我们精心设计数据增强方法，通过简洁而新颖的体积模型来模拟人际遮挡。通过生成包含严重遮挡的训练样本（其中模拟了现有模型的预期输出），使模型能从这些含噪样本中学习如何从混乱场景中准确提取有效信息。

The seq2seq approach also helps the model to reduce jittering, allowing the model to learn temporal dynamics by observing multiple frames at the same time. In addition, we propose an additional loss based on MPJVE, which has been introduced to measure temporal consistency [29], to further smoothen the prediction across the frames.

seq2seq方法还有助于减少模型的抖动，使其能够通过同时观察多帧来学习时间动态。此外，我们提出了一种基于MPJVE的额外损失函数（该指标用于衡量时间一致性[29]），以进一步平滑跨帧的预测结果。

In summary, we propose POTR-3D, the first realization of a seq2seq 2D-to-3D lifting model for 3DMPPE, and devise a simple but effective data augmentation strategy, allowing us to generate an unlimited number of occlusionaware augmented data with diverse views. Putting them together, our overall methodology effectively tackles the aforementioned three challenges in 3DMPPE and adapts well to in-the-wild videos. Specifically,

总之，我们提出了POTR-3D，这是首个用于3DMPPE的seq2seq二维到三维提升模型实现，并设计了一种简单但有效的数据增强策略，使我们能够生成具有多样化视角的无限数量遮挡感知增强数据。综合来看，我们的整体方法有效解决了3DMPPE中上述三个挑战，并很好地适应了野外视频。具体来说，

• Our method produces a more natural and smoother sequence of motion compared to existing methods.

• 与现有方法相比，我们的方法能生成更自然、更流畅的运动序列。

Trained on our augmented data, POTR-3D outperforms existing methods both quantitatively on several representative benchmarks and qualitatively on in-the-wild videos.

在我们增强数据上训练的POTR-3D在多个代表性基准测试的定量评估和真实场景视频的定性分析中均优于现有方法。

2. Related Work

2. 相关工作

3D Human pose estimation has been studied on singleview (monocular) or on multi-view images. Seeing the scene only from one direction through a monocular camera, the single-view pose estimation is inherently challenging to reproduce the original 3D landscape. Multi-view systems [16, 10, 11, 15, 13, 30, 9, 4, 40] are developed to ease this problem. In this paper, we focus on the monocular 3D human pose estimation, as we are particularly interested in in-the-wild videos captured without special setups.

3D人体姿态估计已在单视角（单目）或多视角图像上得到研究。通过单目相机仅从一个方向观察场景，单视角姿态估计本质上难以还原原始的3D场景。为缓解这一问题，多视角系统[16, 10, 11, 15, 13, 30, 9, 4, 40]被开发出来。本文聚焦于单目3D人体姿态估计，因为我们特别关注无需特殊配置拍摄的野外视频。

3D Single-Person Pose Estimation (3DSPPE). There are two directions tackling this task. The first type directly constructs 3D pose from a given 2D image or video endto-end at pixel-level [28, 33]. Another direction, the 2D-to3D lifting, treats only a few human body keypoints instead of pixel-level details, leveraging off-the-shelf 2D pose estimator trained on larger data. Video Pose 3 D [29] performs sequence-based 2D-to-3D lifting for 3DSPPE using dilated convolution. Some recent works [43, 22, 7] apply Graph Neural Networks [19] to 2D-to-3D lifting. PoseFormer [45] utilizes a Transformer for 3DSPPE to capture the spatiotemporal dependency, referring to a sequence of 2D singleperson pose from multiple frames at once to estimate the pose of the central frame (seq2frame). It achieves competent performance, but redundant computation is known as a drawback since large amount of sequences overlaps to infer 3D poses for all frames. MixSTE [41] further extends it to reconstruct for all frames at once, better modeling sequence coherence and enhancing efficiency.

3D单人姿态估计 (3DSPPE)。该任务有两个研究方向。第一种方法直接从给定的2D图像或视频端到端地在像素级别构建3D姿态 [28, 33]。另一种方向是2D到3D提升，仅处理少量人体关键点而非像素级细节，利用在更大数据上训练的现成2D姿态估计器。Video Pose 3D [29] 使用扩张卷积进行基于序列的2D到3D提升以实现3DSPPE。近期一些工作 [43, 22, 7] 将图神经网络 [19] 应用于2D到3D提升。PoseFormer [45] 采用Transformer进行3DSPPE以捕捉时空依赖性，通过一次性参考多帧的2D单人姿态序列来估计中心帧的姿态 (seq2frame)。该方法取得了优异性能，但由于推断所有帧3D姿态时需要处理大量重叠序列，冗余计算被认为是其缺点。MixSTE [41] 进一步扩展该方法，实现一次性重构所有帧，更好地建模序列连贯性并提升效率。

3D Multi-Person Pose Estimation (3DMPPE). Lifting the assumption that only a single person exists in the entire video, 3DMPPE gets far more challenging. In addition to the relative 3D position of body keypoints for each individual, depth of all persons in the scene also should be predicted in 3DMPPE, as geometric relationship between them does matter. Also, each individual needs to be identified across frames.

3D多人姿态估计(3DMPPE)。与假设整个视频中仅存在单人的传统方法不同，3DMPPE面临更大挑战。除了需要预测每个个体的身体关键点相对3D位置外，该方法还需推断场景中所有人的深度信息，因为人物间的几何关系至关重要。此外，还需实现跨帧的人物身份关联。

Similarly to the 3DSPPE, 3D poses may be constructed end-to-end. Moon et al. [26] directly estimates each individual’s depth assuming a typical size of 3D bounding box. However, this approach fails when the pose of a subject significantly varies. BEV [34] explicitly estimates a bird’seye-view to better model the inherent 3D geometry. It also infers the height of each individual by age estimation.

与3DSPPE类似，3D姿态也可以端到端构建。Moon等人[26]通过假设一个典型3D边界框尺寸直接估计每个人的深度，但当主体姿态变化较大时该方法会失效。BEV[34]通过显式估计鸟瞰视角来更好地建模固有3D几何关系，同时结合年龄推断来推算每个人的身高。

2D-to-3D lifting is also actively proposed. Ugrinovic et al. [35] considers the common ground plane, where appearing people are standing on, to help depth disambiguation.

2D到3D提升技术也备受关注。Ugrinovic等人[35]考虑了人物站立所在的共同地面平面，以辅助深度消歧。

They firstly estimate 2D pose and SMPL [23] parameters of each person, and lift them to 3D with the ground plane constraint and re projection consistency. Virtual Pose [31] extracts 2D representation from heat maps of keypoints and lifts them to 3D, trained on a synthetic paired dataset of 2D representation and 3D pose.

他们首先估计每个人的2D姿态和SMPL [23]参数，然后通过地平面约束和重投影一致性将其提升至3D。Virtual Pose [31]从关键点热图中提取2D表征，并在合成的2D表征与3D姿态配对数据集上训练，将其提升至3D。

However, all aforementioned methods are frame 2 frame approaches, vulnerable to occlusion, which is the main challenge in 3DMPPE. Multiple frames may be considered simultaneously to resolve occlusion, but end-to-end approaches are limited to enlarge the receptive field due to heavy computation (e.g., 3D convolution). 2D-to-3D lifting approach is potentially suitable, but no previous work has tried to combine temporal modeling with it, to the best of our knowledge. Here, Each subject should be reidentified, as most off-the-shelf 2D pose estimator operates in frame 2 frame manner. By using an additional offthe-shelf 2D pose tracking model with some adaptation and geometry-aware data augmentation, we tackle the challenges in 3DMPPE with a seq2seq approach.

然而，上述所有方法都是逐帧处理方案，易受遮挡影响，而遮挡正是3D多人姿态估计(3DMPPE)的主要挑战。虽然可通过同时考虑多帧来解决遮挡问题，但端到端方法因计算量过大(如3D卷积)难以扩大感受野。2D到3D提升方法具有潜在适用性，但据我们所知，此前未有研究尝试将其与时序建模相结合。由于现成的2D姿态估计器多为逐帧操作，每个目标都需要重新识别。我们通过采用经过适配的现成2D姿态跟踪模型和几何感知数据增强，以序列到序列(seq2seq)方法应对3DMPPE的挑战。

Data Augmentation for 3D Pose Estimation. Since 3D pose annotation is expensive to collect, limited training data is another critical challenge that overfits a model. For this, several data augmentation methods have been proposed.

3D姿态估计的数据增强。由于3D姿态标注的采集成本高昂，有限的训练数据是导致模型过拟合的另一关键挑战。为此，研究者们提出了多种数据增强方法。

The 2D-to-3D lifting approach allows unbounded data augmentation of 2D-3D pose pairs by decoupling the 3D pose estimation problem into 2D pose estimation and 2Dto-3D lifting. Most 2D-to-3D lifting methods apply horizontal flipping [29, 45, 41, 31]. PoseAug [8] suggests adaptive differentiable data augmentation for 3DSPPE which adjusts bone angle, bone length, and body orientation.

2D到3D的提升方法通过将3D姿态估计问题解耦为2D姿态估计和2D到3D提升，实现了2D-3D姿态对的无限制数据增强。大多数2D到3D提升方法采用水平翻转 [29, 45, 41, 31]。PoseAug [8] 提出了一种针对3DSPPE的自适应可微分数据增强方法，可调整骨骼角度、骨骼长度和身体朝向。

Data augmentation for 3DMPPE gets more complicated, since geometric relationship (e.g. distance) among individuals should be additionally considered. Virtual Pose [31] proposes random translation and rotation of each person, and trains the lifting model solely with the augmented data. This work shares the motivation with ours, but it does not care about the augmentation of the ground plane or camera view, and it does not simulate occlusion cases. Our augmentation method, on the other hand, explicitly considers the ground plane to make the result feasible and to help disambiguation of depth [35]. Also, we further propose to augment the ground plane itself for robustness on various views. In addition, we specially treat occluded keypoints to simulate actual occlusion cases.

3DMPPE的数据增强更为复杂，因为需要额外考虑个体间的几何关系（如距离）。Virtual Pose [31] 提出对每个人进行随机平移和旋转，并仅使用增强数据训练提升模型。该研究与我们的动机一致，但未考虑地平面或相机视角的增强，也未模拟遮挡情况。相比之下，我们的增强方法显式考虑地平面以确保结果可行，并辅助深度消歧 [35]。此外，我们进一步提出增强地平面本身以提高多视角鲁棒性。同时，我们专门处理被遮挡关键点以模拟真实遮挡场景。

Depth Estimation on a Monocular Image. It is in nature an ill-posed problem to estimate the depth from a monocular input, since the size of an object is coupled with it. For instance, if an object gets $2\times$ larger and moves away from the camera by $2\times$ distance, the object will still look the same in the projected 2D image. Thus, an additional clue is needed to estimate the distance, e.g., typical size of well-known objects like a person. Assuming all people in the scene roughly have a similar height, one can estimate a plausible depth. Some previous works, e.g., BEV [34], try to disambiguate heights of people by inferring age. We admit that such an attempt may somehow beneficial, but in this paper, we do not explicitly infer the size of people. The model might implicitly learn how to estimate depth of a person with a usual height observed in the training data. This might result in a sub-optimal result in some complicated cases, e.g., a scene with both adults and children. We leave this disambiguation as an interesting future work to concentrate more on aforementioned issues.

单目图像的深度估计。从单目输入估计深度本质上是一个不适定问题，因为物体的大小与其深度相互耦合。例如，如果一个物体的尺寸变为原来的2倍，同时与相机的距离也增加2倍，该物体在投影的2D图像中看起来仍然相同。因此，需要额外的线索来估计距离，例如已知物体（如人）的典型尺寸。假设场景中所有人的身高大致相似，就可以估计出合理的深度。先前的一些工作（如BEV [34]）试图通过推断年龄来消除人身高的歧义。我们承认这种尝试可能有一定帮助，但在本文中，我们并不显式推断人的尺寸。模型可能会隐式学习如何根据训练数据中观察到的常见身高来估计人的深度。这在某些复杂场景（例如同时存在成人和儿童的场景）中可能导致次优结果。我们将这种歧义消除作为未来有趣的研究方向，以便更专注于上述问题。

3. Preliminaries

3. 预备知识

Problem Formulation. In the 3D Multi-person Pose Estimation (3DMPPE) problem, the input consists of a video $\mathbf{V}=[\mathbf{v}{1},...,\mathbf{v}{T}]$ of $T$ frames, where each frame is $\mathbf{v}_{t}\in\mathbb{R}^{H\times W\times3}$ and (up to) $N$ persons may appear in the video. The task is locating a predefined set of $K$ human body keypoints (e.g., neck, ankles, or knees; see Fig. 4 for an example) in the 3D space for all persons appearing in the video in every frame. The body keypoints in the 2D image space are denoted by $\mathbf{X}\in\mathbb{R}^{T\times N\times\bar{K}\times2}$ , and the output Y RT ×N×K×3 s pecifies the 3D coordinates of each body keypoint for all $N$ people across $T$ frames. We follow the common assumption that the camera is static.

问题定义。在三维多人姿态估计 (3DMPPE) 任务中，输入为一个包含 $T$ 帧的视频 $\mathbf{V}=[\mathbf{v}{1},...,\mathbf{v}{T}]$ ，其中每帧图像为 $\mathbf{v}_{t}\in\mathbb{R}^{H\times W\times3}$ ，且视频中可能出现 (最多) $N$ 个人物。该任务的目标是在三维空间中定位视频每帧所有人物预定义的 $K$ 个身体关键点 (例如颈部、脚踝或膝盖；示例见图 4) 。二维图像空间中的身体关键点记为 $\mathbf{X}\in\mathbb{R}^{T\times N\times\bar{K}\times2}$ ，输出 $\mathbf{Y}\in\mathbb{R}^{T\times N\times K\times3}$ 则指定了所有 $N$ 个人物在 $T$ 帧中每个身体关键点的三维坐标。我们遵循相机静止的通用假设。

Notations. For convenience, we define a common notation for 2D and 3D points throughout the paper. Let us denote a 2D point $\mathbf{X}{t,i,k}\in\mathbb{R}^{2}$ as $(u,v)$ , where $u\in$ ${0,...,H{-1}}$ and $v\in{0,...,W{-1}}$ is the vertical and horizontal coordinate in the image, respectively. Similarly, we denote a 3D point within the camera coordinate $\mathbf{Y}_{t,i,k}\in\mathbb{R}^{3}$ as $(x,y,z)$ , where $x$ and $y$ are the coordinates through the two directions parallel to the projected 2D image, and $z$ is the depth from the camera.

符号说明。为方便起见，我们在全文中为2D和3D点定义了统一符号。用$\mathbf{X}{t,i,k}\in\mathbb{R}^{2}$表示2D点$(u,v)$，其中$u\in{0,...,H{-1}}$和$v\in{0,...,W{-1}}$分别表示图像的垂直和水平坐标。类似地，用$\mathbf{Y}_{t,i,k}\in\mathbb{R}^{3}$表示相机坐标系中的3D点$(x,y,z)$，其中$x$和$y$为平行于投影2D图像的两个方向坐标，$z$表示相机深度。

Data Preprocessing. We adjust the input in two ways, following common practice. First, we specially treat a keypoint called a root joint (typically pelvis, the body center; denoted by $\mathbf{Y}{t,i,1}\in\mathbb{R}^{3},$ for a person $i$ at frame $t$ . The ground truth for this point is given by $(u,v,z)$ , where $(u,v)$ is the true 2D coordinate of the root joint and $z$ is its depth. For root joints, the model estimates $(\hat{u},\hat{v},\hat{z})$ , the absolute values for $(u,v,z)$ . (Note that $\hat{u}\approx u$ and $\hat{v}\approx v$ but they are still estimated to compensate for imperfect 2D pose estimation by the off-the-shelf model.) Other regular joints, $\mathbf{Y}{t,i,k}\in\mathbb{R}^{3}$ for $k=2,...,K$ , are represented as the relative difference from the corresponding root joint, $\mathbf{Y}_{t,i,1}$ .

数据预处理。我们按照常规做法对输入进行两种调整。首先，我们特殊处理一个称为根关节的关键点（通常是骨盆，即身体中心；对于第t帧中的第i个人，用$\mathbf{Y}{t,i,1}\in\mathbb{R}^{3}$表示）。该点的真实值由$(u,v,z)$给出，其中$(u,v)$是根关节的真实2D坐标，$z$是其深度。对于根关节，模型估计$(\hat{u},\hat{v},\hat{z})$，即$(u,v,z)$的绝对值。（注意$\hat{u}\approx u$且$\hat{v}\approx v$，但仍需估计以补偿现成模型在2D姿态估计中的不完美性。）其他常规关节$\mathbf{Y}{t,i,k}\in\mathbb{R}^{3}$（$k=2,...,K$）则表示为与对应根关节$\mathbf{Y}_{t,i,1}$的相对差值。

Second, we normalize the ground truth depth of the root joints by the camera focal length.1 When a 2D pose is mapped to the 3D space, the depth of each 2D keypoint towards the direction of projection needs to be estimated. Since the estimated depth would be proportional to the camera focal length used at training, we normalize the ground truth depth $z$ by the focal length, following common practice. That is, we use $\bar{z}=z/f$ , where $f$ is the camera focal length. In this way, our model operates independently of the camera focal length.

其次，我们通过相机焦距对根关节的真实深度进行归一化处理。当将2D姿态映射到3D空间时，需要估计每个2D关键点在投影方向上的深度。由于估计的深度与训练时使用的相机焦距成正比，我们按照常规做法，用焦距对真实深度$z$进行归一化处理。即使用$\bar{z}=z/f$，其中$f$为相机焦距。通过这种方式，我们的模型能够独立于相机焦距运行。

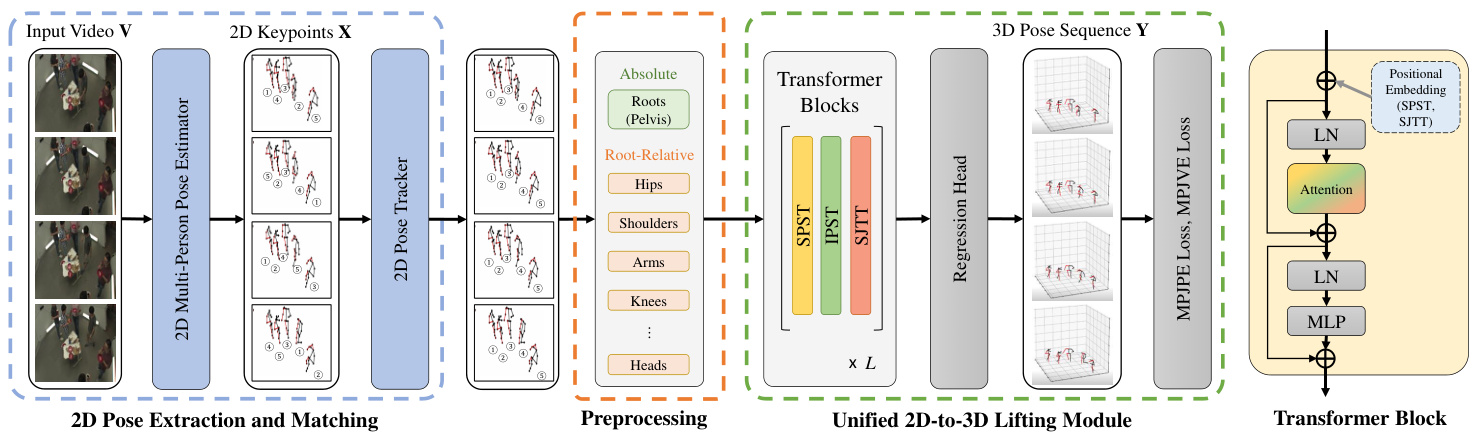
Figure 1. Overview of the POTR-3D. The input video is converted to 2D keypoints, followed by 2D-to-3D lifting, composed of stacked three types of Transformers (SPST, IPST, SJTT).

图 1: POTR-3D 概述。输入视频被转换为 2D 关键点，随后通过由三种堆叠式 Transformer (SPST、IPST、SJTT) 组成的 2D 转 3D 提升模块进行处理。

4. The POTR-3D Model

4. POTR-3D 模型

The overall model workflow is depicted in Fig. 1. First, the input frames $\mathbf{V}$ are converted to a sequence of 2D keypoints by an off-the-shelf model (Sec. 4.1). Then, they are lifted into the 3D space (Sec. 4.2).

整体模型工作流程如图 1 所示。首先，输入帧 $\mathbf{V}$ 通过现成模型转换为一系列 2D 关键点 (见第 4.1 节)。随后，这些关键点被提升至 3D 空间 (见第 4.2 节)。

4.1. 2D Pose Extraction and Matching

4.1. 2D姿态提取与匹配

Given an input video $\textbf{V}\in\mathbb{R}^{T\times H\times W\times3}$ , we first extract the 2D coordinates $\mathbf{X}\in\mathbb{R}^{T\times N\times K\times2}$ of the (up to) $N$ persons appearing in the video, where $T$ is the number of frames, and $K$ is the number of body keypoints, determined by the dataset. Since we treat multiple people in the video, each individual should be re-identified across all frames. That is, the second index of $\mathbf{X}$ and $\mathbf{Y}$ must be consistent for each individual across all frames. Any off-theshelf 2D multi-person pose estimator and a tracking model can be adopted for each, and we use HRNet [32] and ByteTrack [42], respectively. Note that these steps need to be done only at testing, since we train our model on augmented videos, where the 2D coordinates can be computed from the ground truth 3D poses and camera parameters (see Sec. 5).

给定输入视频 $\textbf{V}\in\mathbb{R}^{T\times H\times W\times3}$，我们首先提取视频中（最多）$N$ 个人的二维坐标 $\mathbf{X}\in\mathbb{R}^{T\times N\times K\times2}$，其中 $T$ 为帧数，$K$ 为身体关键点数量（由数据集决定）。由于需要处理视频中的多个人物，每个个体应在所有帧中被重新识别。也就是说，$\mathbf{X}$ 和 $\mathbf{Y}$ 的第二个索引必须对所有帧中的每个个体保持一致。可采用任意现成的二维多人姿态估计器和跟踪模型，我们分别使用 HRNet [32] 和 ByteTrack [42]。请注意，这些步骤仅在测试时需要执行，因为我们在增强视频上训练模型，其中二维坐标可直接从真实三维姿态和相机参数计算得出（参见第5节）。

4.2. Unified 2D-to-3D Lifting Module

4.2. 统一的2D到3D提升模块

From the input $\mathbf{X}$ , this module lifts it to the 3D coordinates, $\textbf{Y}\in\mathbb{R}^{T\times N\times K\times3}$ . To effectively comprehend the spatio-temporal geometric context, we adapt encoder of [41]. The coordinates of each 2D keypoints $\mathbf{X}_{t,i,k}$ at a specific frame $t~\in~{1,...,T}$ for a specific person $i\in{1,...,N}$ and body keypoint $k\in{1,...,K}$ , is linearly mapped to a $D$ -dimensional token embedding. Thus, the input is now converted to a sequence of $T\times N\times K$ tokens in $\mathbb{R}^{D}$ , and let us denote these tokens as ${\bf Z}^{(0)}\in\mathbb{R}^{T\times N\times K\times D}$ . Here, in contrast to most existing methods [26, 34, 31], which separately process the root and regular joints, we treat them with a single unified model. This unified model is not just simpler, but also enables more comprehensive estimation of depth and pose by allowing attention across them.

从输入 $\mathbf{X}$ 出发，该模块将其提升为3D坐标 $\textbf{Y}\in\mathbb{R}^{T\times N\times K\times3}$。为了有效理解时空几何上下文，我们采用了[41]的编码器。对于特定帧 $t~\in~{1,...,T}$ 中特定人物 $i\in{1,...,N}$ 的每个2D关键点 $\mathbf{X}_{t,i,k}$ 及身体关键点 $k\in{1,...,K}$ 的坐标，我们通过线性映射将其转换为 $D$ 维token嵌入。因此，输入现在被转换为 $\mathbb{R}^{D}$ 中的 $T\times N\times K$ 个token序列，记为 ${\bf Z}^{(0)}\in\mathbb{R}^{T\times N\times K\times D}$。与大多数现有方法[26, 34, 31]单独处理根关节和常规关节不同，我们采用单一统一模型进行处理。这种统一模型不仅更简单，还能通过跨关节注意力机制实现更全面的深度和姿态估计。

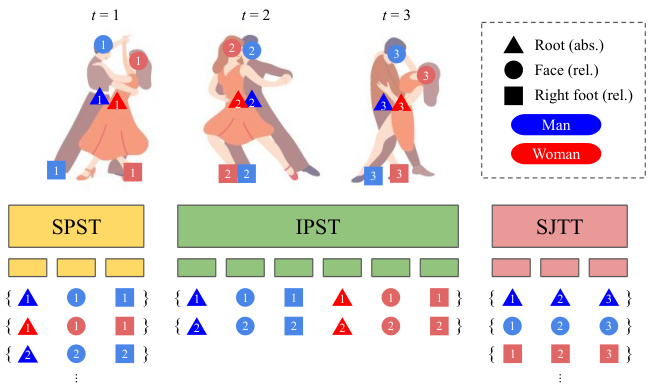
Figure 2. Illustration of 2D-to-3D Lifting Transformers.

图 2: 二维到三维提升变换器 (2D-to-3D Lifting Transformers) 示意图。

They are fed into the repeated 3 types of Transformers, where each of them is designed to model a specific relationship between different body keypoints. This factorization is also beneficial to reduce the quadratic computation cost of the attention mechanism. In addition to the two Transformers in [41], SPST for modeling spatial and SJTT for temporal relationships, we propose an additional Transformer (IPST) designed to learn inter-person relationships among all body keypoints. The role of each Transformer is illustrated in Fig. 2 and detailed below. The input Z(ℓ−1) RT ×N×K×D at each layer ℓ goes through SPST, IPST, and SJTT to contextual ize within the sequence, and outputs the same sized tensor Z(ℓ) RT ×N×K×D.

它们被输入到重复的3种Transformer中，每种Transformer都设计用于建模不同身体关键点之间的特定关系。这种分解也有助于降低注意力机制的二次计算成本。除了[41]中的两种Transformer（用于建模空间关系的SPST和用于时间关系的SJTT），我们还提出了一种额外的Transformer（IPST），旨在学习所有身体关键点之间的人际关系。每种Transformer的作用如图2所示，并在下文详细说明。每一层ℓ的输入Z(ℓ−1) RT ×N×K×D会依次通过SPST、IPST和SJTT在序列中进行上下文建模，并输出相同尺寸的张量Z(ℓ) RT ×N×K×D。

Single Person Spatial Transformer (SPST). Located at the first stage of each layer $\ell$ , SPST learns spatial correlation of each person’s joints in each frame. From the input $\mathcal{X}\in~\mathbb{R}^{T\times N\times K\times D}$ , SPST takes $K$ tokens of size $D$ corresponding to $\mathcal{X}{t,i}\in\mathbb{R}^{K\times D}$ for $t\in{1,...,T}$ and $i\in{1,...,N}$ , separately at a time. In other words, SPST takes $K$ different body keypoints belonging to a same person i at a specific frame t. The output Y ∈ RT ×N×K×D has the same shape, where each token $y_{t,i,k}$ is a transformed one by contextual i zing across other tokens belonging to the same person.

单人空间变换器 (SPST)。位于每一层 $\ell$ 的第一阶段，SPST学习每个人在每帧中关节的空间相关性。从输入 $\mathcal{X}\in~\mathbb{R}^{T\times N\times K\times D}$ 中，SPST每次单独处理对应于 $\mathcal{X}{t,i}\in\mathbb{R}^{K\times D}$ 的 $K$ 个大小为 $D$ 的Token，其中 $t\in{1,...,T}$ 且 $i\in{1,...,N}$。换句话说，SPST处理特定帧t中属于同一人i的 $K$ 个不同身体关键点。输出Y ∈ RT ×N×K×D具有相同的形状，其中每个Token $y_{t,i,k}$ 是通过对属于同一人的其他Token进行上下文转换得到的。

Inter-Person Spatial Transformer (IPST). After SPST, IPST learns correlation among multiple individuals in the same frame. Through this, the model learns spatial interpersonal relationship in the scene. IPST is newly designed to extend the previous 3DSPPE model to 3DMPPE. More formally, IPST takes $N\times K$ tokens of size $D$ as input at a time; that is, given the input $\boldsymbol{\mathcal{X}}\in\mathbb{R}^{T\times N\times K\times D}$ , all $N\times K$ tokens in the frame $\mathcal{X}{t}\in\mathbb{R}^{N\times K\times D}$ are fed into IPST, contextulize from each other, and are transformed to the output tokens $\mathcal{V}_{t}$ . This process is separately performed for each frame at $t=1,...,T$ . After IPST, each token is knowledgeable about other people in the same scene.

人际空间Transformer (IPST)。在SPST之后，IPST学习同一帧中多个个体之间的相关性。通过这种方式，模型学习场景中的人际空间关系。IPST是全新设计的，旨在将之前的3DSPPE模型扩展到3DMPPE。更正式地说，IPST一次接收大小为$D$的$N\times K$个token作为输入；即给定输入$\boldsymbol{\mathcal{X}}\in\mathbb{R}^{T\times N\times K\times D}$时，将帧$\mathcal{X}{t}\in\mathbb{R}^{N\times K\times D}$中的所有$N\times K$个token输入IPST，彼此进行上下文关联，并转换为输出token $\mathcal{V}_{t}$。这一过程在$t=1,...,T$的每一帧中分别执行。经过IPST后，每个token都能感知同一场景中的其他人。

This is a novel part of our method to deal with multiple individuals. Different from the TDBU-Net [5], which uses a disc rim in at or to validate relationship between subjects at the final stage, IPST progressively enhances its contextual understanding on inter-personal relationship by iterative attentions.

这是我们方法中处理多人的新颖部分。与TDBU-Net [5]在最后阶段使用判别器来验证主体间关系不同，IPST通过迭代注意力逐步增强其对人际关系的上下文理解。

Single Joint Temporal Transformer (SJTT). From the input $\bar{\mathcal{X}}\in\mathbb{R}^{T\times N\times K\times D}$ , we create $N\times K$ input se- quences of length $T$ , corresponding to $\mathcal{X}{\cdot,i,k}\in\mathbb{R}^{T\times D}$ for $i~=~1,...,N$ and $k=1,...,K$ . Each sequence is fed into SJTT, temporally contextual i zing each token in the sequence, and the transformed output tokens $\mathcal{V}_{\cdot,i,k}$ are returned. Completing all $N\times K$ sequences, the transformed sequence $\mathcal{Y}\in\mathbb{R}^{\bar{T}\times N\times K\times D}$ is output as the result of the $\ell$ -th layer of our 2D-to-3D lifting module, $\mathbf{Z}^{(\ell)}$ .

单关节时序Transformer (SJTT)。从输入$\bar{\mathcal{X}}\in\mathbb{R}^{T\times N\times K\times D}$中，我们创建$N\times K$个长度为$T$的输入序列，对应于$\mathcal{X}{\cdot,i,k}\in\mathbb{R}^{T\times D}$，其中$i~=~1,...,N$且$k=1,...,K$。每个序列被输入到SJTT中，对序列中的每个token进行时序上下文处理，并返回转换后的输出token$\mathcal{V}_{\cdot,i,k}$。完成所有$N\times K$个序列处理后，转换后的序列$\mathcal{Y}\in\mathbb{R}^{\bar{T}\times N\times K\times D}$作为我们2D到3D提升模块第$\ell$层的结果$\mathbf{Z}^{(\ell)}$输出。

These 3 blocks constitute a single layer of our 2D-to3D lifting module, and multiple such layers are stacked. A learnable positional encoding is added to each token at the first layer $\ell=1$ ) of SPST and SJTT. No positional encoding is added for IPST, since there is no natural ordering between multiple individuals in a video.

这3个模块构成了我们2D到3D提升模块的一个层级，多个这样的层级会被堆叠起来。在SPST和SJTT的第一层( $\ell=1$ )，每个Token都会添加一个可学习的位置编码。而对于IPST则不会添加位置编码，因为视频中多个个体之间不存在自然的顺序关系。

Regression Head. After repeating $L$ layers of ${{\mathrm{SPST}},$ , IPST, $\mathrm{SJTT}}$ , we get the output tokens for all body keypoints, ${\bf Z}^{(L)}\in\mathbb{R}^{T\times N\times K\times D}$ . This is fed into a regression head, composed of a multilayer perceptron (MLP). It maps each body keypoint embedding in $\mathbf{Z}^{(\bar{L})}$ to the corresponding 3D coordinates, Y E RTxNxKx3.

回归头 (Regression Head)。经过重复 $L$ 层 ${{\mathrm{SPST}},$ IPST, $\mathrm{SJTT}}$ 后，我们得到所有身体关键点的输出 token ${\bf Z}^{(L)}\in\mathbb{R}^{T\times N\times K\times D}$。这些 token 被输入到一个由多层感知机 (MLP) 构成的回归头中。该回归头将 $\mathbf{Z}^{(\bar{L})}$ 中的每个身体关键点嵌入映射到对应的 3D 坐标 Y E RTxNxKx3。

4.3. Training Objectives

4.3. 训练目标

Given the predicted $\hat{\mathbf{Y}}\in\mathbb{R}^{T\times N\times K\times3}$ and ground truth $\mathbf{Y}\in\mathbb{R}^{T\times N\times\mathbf{\bar{K}}\times3}$ , we minimize the following two losses.

给定预测的 $\hat{\mathbf{Y}}\in\mathbb{R}^{T\times N\times K\times3}$ 和真实值 $\mathbf{Y}\in\mathbb{R}^{T\times N\times\mathbf{\bar{K}}\times3}$ ，我们最小化以下两个损失函数。

Mean per Joint Position Error (MPJPE) Loss is the mean $L_{2}$ distance between the prediction and the target:

平均每关节位置误差 (MPJPE) 损失是预测值与目标值之间的平均 $L_{2}$ 距离：

$$
\mathcal{L}{\mathrm{MPJPE}}=\frac{1}{T N K}\sum_{t=1}^{T}\sum_{i=1}^{N}\sum_{k=1}^{K}|\hat{{\mathbf{Y}}}{t,i,k}-{\mathbf{Y}}{t,i,k}|_{2}.
$$

$$
\mathcal{L}{\mathrm{MPJPE}}=\frac{1}{T N K}\sum_{t=1}^{T}\sum_{i=1}^{N}\sum_{k=1}^{K}|\hat{{\mathbf{Y}}}{t,i,k}-{\mathbf{Y}}{t,i,k}|_{2}.
$$

Mean per Joint Velocity Error (MPJVE) Loss [41] is the mean $L_{2}$ distance between the first derivatives of the prediction and the target with regards to time, measuring smoothness of the predicted sequence:

平均每关节速度误差 (MPJVE) 损失 [41] 是预测序列与目标序列关于时间的一阶导数之间的平均 $L_{2}$ 距离，用于衡量预测序列的平滑度：

$$
\mathcal{L}{\mathrm{MPJVE}}=\frac{1}{T N K}\sum_{t=1}^{T}\sum_{i=1}^{N}\sum_{k=1}^{K}\left|\frac{\partial\hat{\mathbf{Y}}{t,i,k}}{\partial t}-\frac{\partial\mathbf{Y}{t,i,k}}{\partial t}\right|_{2}.
$$

$$
\mathcal{L}{\mathrm{MPJVE}}=\frac{1}{T N K}\sum_{t=1}^{T}\sum_{i=1}^{N}\sum_{k=1}^{K}\left|\frac{\partial\hat{\mathbf{Y}}{t,i,k}}{\partial t}-\frac{\partial\mathbf{Y}{t,i,k}}{\partial t}\right|_{2}.
$$

The overall loss $\mathcal{L}$ is a weighted sum of the two losses; that is, $\mathcal{L}=\mathcal{L}{\mathrm{MPJPE}}+\lambda\cdot\mathcal{L}_{\mathrm{MPJVE}}$ , where $\lambda$ controls the relative importance between them. Optionally, different weights can be applied to the root joints and others.

整体损失 $\mathcal{L}$ 是两个损失的加权和，即 $\mathcal{L}=\mathcal{L}{\mathrm{MPJPE}}+\lambda\cdot\mathcal{L}_{\mathrm{MPJVE}}$，其中 $\lambda$ 控制两者之间的相对重要性。可选地，可以为根关节和其他关节应用不同的权重。

4.4. Inference and S cal ability

4.4. 推理与可扩展性

To perform inference on a long video, we first track every subject throughout the whole frames, then the tracked 2D keypoints are lifted to 3D at the regularly-split clip level. The final result is obtained by concatenating the clip-level lifting. In this way, our approach is scalable for a long video without extremely growing computational cost.

对长视频进行推理时，我们首先在全帧范围内追踪每个主体，随后将追踪到的2D关键点以固定分段为单元提升至3D空间。最终结果通过拼接各片段级别的三维重建获得。该方法可扩展应用于长视频处理，且计算成本不会呈指数级增长。

5. Geometry-Aware Data Augmentation

5. 几何感知数据增强 (Geometry-Aware Data Augmentation)

Being free from the pixel-level details, we can freely augment the training data as proposed below, making POTR-3D robust on diverse inputs, resolving the data scarcity issue for this task.

由于不受像素级细节的限制，我们可以自由地按照以下方式增强训练数据，使POTR-3D能够适应多样化的输入，从而解决该任务中数据稀缺的问题。

Specifically, we take $N$ samples $\mathbf{Y}^{(i)}\in\mathbb{R}^{T\times K\times3}$ captured by a fixed camera from a single-person dataset, where $i=1,...,N$ . We simply overlay them onto a single tensor $\textbf{Y}\in\mathbb{R}^{T\times N\times K\times3}$ , and project it to the 2D space by applying the perspective camera model, producing $\textbf{X}\in$ $\mathbb{R}^{T\times N\times K\times2}$ . A point $(x,y,z)$ in the 3D space is mapped to $(u,v)$ by

具体来说，我们从单人数据集中选取由固定摄像头捕获的$N$个样本$\mathbf{Y}^{(i)}\in\mathbb{R}^{T\times K\times3}$（其中$i=1,...,N$），将其简单叠加为单个张量$\textbf{Y}\in\mathbb{R}^{T\times N\times K\times3}$，并通过透视相机模型投影至二维空间，生成$\textbf{X}\in\mathbb{R}^{T\times N\times K\times2}$。三维空间中的点$(x,y,z)$通过下式映射为$(u,v)$：

$$
{\Bigg[}{\boldsymbol{u}}{\Bigg]}\approx{\left[\begin{array}{l l l}{f_{u}}&{0}&{c_{u}}\ {0}&{f_{v}}&{c_{v}}\ {0}&{0}&{1}\end{array}\right]}{\left[\begin{array}{l}{x}\ {y}\ {z}\end{array}\right]}~,
$$

$$
{\Bigg[}{\boldsymbol{u}}{\Bigg]}\approx{\left[\begin{array}{l l l}{f_{u}}&{0}&{c_{u}}\ {0}&{f_{v}}&{c_{v}}\ {0}&{0}&{1}\end{array}\right]}{\left[\begin{array}{l}{x}\ {y}\ {z}\end{array}\right]}~,
$$

where $f_{u},f_{v}$ are the focal lengths, and $c_{u},c_{v}$ are the prin- cipal point in the 2D image coordinates. This $(\mathbf{X},\mathbf{Y})$ is an augmented 3DMPPE training example, and repeating this with different samples will infinitely generate new ones.

其中 $f_{u},f_{v}$ 为焦距，$c_{u},c_