CAUSALITY COMPENSATED ATTENTION FOR CONTEXTUAL BIASED VISUAL RECOGNITION
基于因果补偿注意力的上下文偏置视觉识别
ABSTRACT
摘要
Visual attention does not always capture the essential object representation desired for robust predictions. Attention modules tend to underline not only the target object but also the common co-occurring context that the module thinks helpful in the training. The problem is rooted in the confounding effect of the context leading to incorrect causalities between objects and predictions, which is further exacerbated by visual attention. In this paper, to learn causal object features robust for contextual bias, we propose a novel attention module named Interventional Dual Attention (IDA) for visual recognition. Specifically, IDA adopts two attention layers with multiple sampling intervention, which compensates the attention against the confounder context. Note that our method is model-agnostic and thus can be implemented on various backbones. Extensive experiments show our model obtains significant improvements in classification and detection with lower computation. In particular, we achieve the state-of-the-art results in multi-label classification on MS-COCO and PASCAL-VOC.
视觉注意力并不总能捕获到鲁棒预测所需的关键物体表征。注意力模块不仅会突出目标物体,还会强调模块认为对训练有帮助的常见共现上下文。该问题源于上下文混杂效应导致物体与预测间错误因果关联,而视觉注意力进一步放大了这种效应。本文提出一种名为干预双重注意力 (Interventional Dual Attention, IDA) 的新颖注意力模块,用于学习对上下文偏置具有鲁棒性的因果物体特征。具体而言,IDA采用双重注意力层配合多重采样干预机制,通过补偿注意力来对抗混杂上下文。我们的方法具有模型无关性,可适配多种骨干网络。大量实验表明,该模型以更低计算量在分类和检测任务中取得显著提升,尤其在MS-COCO和PASCAL-VOC多标签分类任务中实现了最先进性能。
1 INTRODUCTION
1 引言
The last several years have witnessed the huge success of attention mechanisms in computer vision. The key insight behind different attention mechanisms (Wang et al., 2018; Hu et al., 2018; Woo et al., 2018; Chen et al., 2017; Zhu & Wu, 2021; Dosovitskiy et al., 2020; Liu et al., 2021) is the same, i.e., emphasizing key facts in inputs, while different aspects of information such as feature map and token query are considered. The impressive performances of these works show that attention is proficient in fitting training data and exploiting valuable features.
近年来,注意力机制在计算机视觉领域取得了巨大成功。各类注意力机制 (Wang et al., 2018; Hu et al., 2018; Woo et al., 2018; Chen et al., 2017; Zhu & Wu, 2021; Dosovitskiy et al., 2020; Liu et al., 2021) 的核心思想一致,即强调输入中的关键要素,同时兼顾特征图和token查询等不同维度的信息。这些工作的卓越性能表明,注意力机制擅长拟合训练数据并挖掘有价值的特征。
However, whether the information deemed valuable by attention is always helpful in real application scenarios? In Fig.1(a), the Spatial Class-Aware Attention (SCA) considers the context dining table as the cause of spoon, which helps the model make correct predictions even if the stressed region is wrong, but it fails in cases where the object is absent in the familiar context. Fig.1(b) illustrates the problem in a quantitative view: we calculate the mIOU between the attention map (or the activation map for baseline) and the ground-truth mask. As is shown in the figure, although the model with attention gains some improvement measured by common evaluation metrics, the mIOU does not see progress, which means attention does not capture the more accurate regions of targets than the baseline. Moreover, Fig.1(c) illustrates the attention mechanism more easily attends to the wrong context regions when the training samples are insufficient. All above evidence reveals that attention mechanisms may not always improve the performance of the model by accessing meaningful factors and could be harmful, especially in the case of out-of-distribution scenarios.
然而,注意力机制认定的有价值信息在实际应用场景中是否总是有益的?图1(a)中,空间类别感知注意力(SCA)将餐桌背景视为勺子的关联因素,这使得模型即使关注区域错误也能做出正确预测,但当目标物体未出现在熟悉场景时就会失效。图1(b)通过量化视角展示了问题本质:我们计算了注意力图(或基线模型的激活图)与真实掩膜之间的mIOU。如图所示,尽管注意力模型在常规评估指标上有所提升,但mIOU并未进步,这意味着注意力机制并未比基线模型捕捉到更精确的目标区域。此外,图1(c)表明当训练样本不足时,注意力机制更容易关注错误的上下文区域。上述证据共同揭示了注意力机制未必总能通过获取有效因素来提升模型性能,在分布外场景中甚至可能产生负面影响。
Fortunately, the causality provides us with a theoretical perspective for this problem (Pearl et al., 2000; Neuberg, 2003). The familiar context of an object is a confounder (Yue et al., 2020; Zhang et al., 2020; Wang et al., 2020) confusing the causality between the object and its prediction. Even though the scene of the dining table is not the root cause for the spoon, the model is fooled into setting up a spurious correlation between them. On the other hand, the problem is tricky because context is naturally biased in the real world, and common datasets annotated by experts (e.g., MSCOCO (Lin et al., 2014)) also suffer from severe contextual bias. As is well known, networks equipped with attention can learn better representations of the datasets. However, the contextual bias in datasets can be also exacerbated when using the attention mechanism.
幸运的是,因果关系为我们提供了解决该问题的理论视角 (Pearl et al., 2000; Neuberg, 2003)。物体所处的熟悉环境是一个混淆因子 (Yue et al., 2020; Zhang et al., 2020; Wang et al., 2020),它干扰了物体与其预测结果之间的因果关系。尽管餐桌场景并非勺子的根本成因,模型仍会错误地建立二者之间的伪相关性。另一方面,该问题具有复杂性,因为现实世界中的环境本身就存在固有偏差,专家标注的常见数据集 (如MSCOCO (Lin et al., 2014)) 也存在严重的环境偏置问题。众所周知,配备注意力机制的神经网络能学习到更好的数据集表征。然而在使用注意力机制时,数据集中的环境偏置也可能被进一步放大。
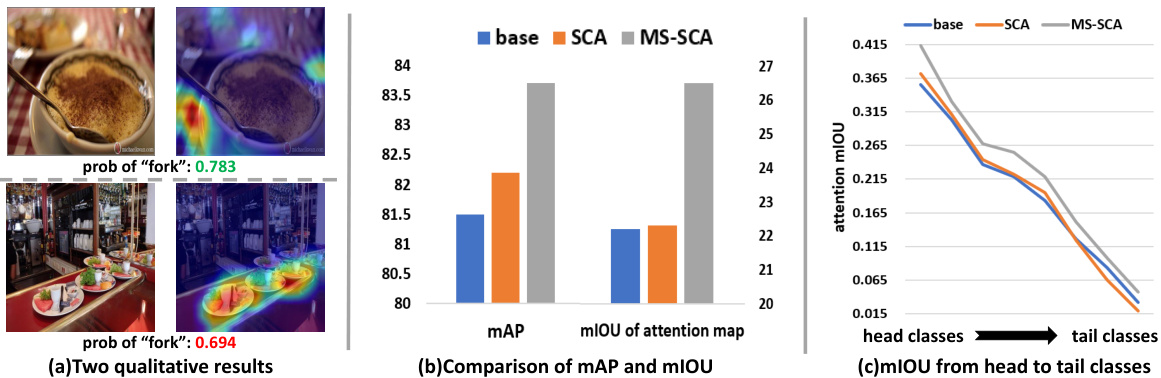
Figure 1: (a) The attention maps of two examples in MS-COCO (Lin et al., 2014) using ResNet $.01+\mathrm{SCA}$ (our baseline attention). (b) The mAP and attention map mIOU of ResNet101 baseline, SCA, and the MS-SCA (our de-confounded model). (c) Attention map mIOU of the three models from head classes to tail classes.
图 1: (a) 使用 ResNet $0.1+\mathrm{SCA}$ (我们的基线注意力) 在 MS-COCO (Lin et al., 2014) 中两个示例的注意力图。(b) ResNet101 基线、SCA 和 MS-SCA (我们的去混杂模型) 的 mAP 和注意力图 mIOU。(c) 从头部类别到尾部类别,三种模型的注意力图 mIOU。
To tackle the con founders in visual tasks, a common method is the causal intervention (Pearl et al., 2000; Neuberg, 2003). The interventions in most existing methods (Wang et al., 2021; Yang et al., 2021b; Yue et al., 2020; Zhang et al., 2020) share a maturity pipeline: defining the causality among given elements, implementing the con founders and ultimately implementing the backdoor adjustment (Pearl, 2014). Most of these methods, however, are difficult to implement on attention mechanism and migrate among different tasks. In this paper, we prove that a simple weighted multisampling operation on attention can be viewed as the intervention for the attention and confounding context. Based on that, we develop a novel causal attention module: Interventional Dual Attention (IDA). We first employ spatial class-aware attention (SCA) to extract the class-specific information in different positions of the feature map. Then, a multiple-sampling operation with Dot-Product Attention (DPA) re-weighting is implemented upon the SCA, which is essentially the causal intervention and builds a more robust attention map insensitive to the contextual bias. To receive a better trade-off between the performance and computation, we have two versions of IDA: the light one (pure two layers of attention) achieves huge improvements with limited parameter increment; the heavy one (the DPA is extended as a transformer) obtains the state-of-the-arts results with lower computation compared with the popular transformer-based models on the multi-label classification task. Furthermore, improvements in both classification and detection demonstrate the potential of our method to be applied in general visual tasks.
为解决视觉任务中的混杂因素,一种常见方法是因果干预 (Pearl et al., 2000; Neuberg, 2003)。现有大多数方法 (Wang et al., 2021; Yang et al., 2021b; Yue et al., 2020; Zhang et al., 2020) 的干预流程具有共性:先定义给定元素间的因果关系,再实施混杂因素控制,最终执行后门调整 (Pearl, 2014)。然而这些方法大多难以在注意力机制上实现,也难以跨任务迁移。本文证明,对注意力进行简单的加权多重采样操作可视为对注意力与混杂上下文的干预。基于此,我们开发了新型因果注意力模块:干预式双重注意力 (IDA)。首先采用空间类别感知注意力 (SCA) 提取特征图不同位置的类别特定信息,随后在SCA基础上实施带点积注意力 (DPA) 重加权的多重采样操作——该操作本质上是因果干预,能构建对上下文偏置不敏感的鲁棒注意力图。为平衡性能与计算开销,我们设计了两种IDA版本:轻量版 (纯双层注意力结构) 以有限参数增长实现显著性能提升;重量版 (将DPA扩展为Transformer结构) 在多标签分类任务中,相比主流基于Transformer的模型能以更低计算量取得最优结果。分类与检测任务的双重提升表明该方法在通用视觉任务中的应用潜力。
Our main contributions can be summarized as follows:
我们的主要贡献可概括如下:
2 RELATED WORK
2 相关工作
Attention Mechanism. Attention mechanism (Itti et al., 1998; Rensink, 2000; Corbetta & Shulman, 2002) aims at imitating the perception system of humans, which adopts sequence signals and selects to focus on salient parts. Hence, no matter in what forms, attention is expected to bias the weight towards the most informative parts of an input signal, and the signal can be varied from a sequence, feature map, or token queries in different tasks.
注意力机制 (Attention Mechanism)。注意力机制 (Itti et al., 1998; Rensink, 2000; Corbetta & Shulman, 2002) 旨在模仿人类的感知系统,通过处理序列信号并选择关注显著部分。因此,无论以何种形式实现,注意力机制都会将权重偏向输入信号中最具信息量的部分,而该信号在不同任务中可能表现为序列、特征图或token查询等形式。
Over the past several years, attention mechanism has won huge success in a wide range of tasks in computer vision. At the early stage, most of the works apply the attention to sequence-based models and tasks (Bluche, 2016; Stollenga et al., 2014). Then, here comes the age of attention is all your need (Vaswani et al., 2017), and many classic attention structures in computer vision arise such as SENET (Hu et al., 2018), Non-local (Wang et al., 2018) and CBAM (Woo et al., 2018). Finally is the popularity of self-attention (Do sov it ski y et al., 2020; Liu et al., 2021; Yuan et al., 2021) in these years, and it can be concluded as the operation among the query, key and value, which even totally replaces the CNN in pure visual tasks. However, as mentioned above, the usage of attention is usually not explicitly supervised. Consequently, the weight of attention is easily biased towards the bias in the dataset.
过去几年,注意力机制在计算机视觉的广泛任务中取得了巨大成功。早期大多数工作将注意力应用于基于序列的模型和任务 (Bluche, 2016; Stollenga et al., 2014)。随后进入《Attention Is All You Need》(Vaswani et al., 2017) 时代,涌现出SENET (Hu et al., 2018)、Non-local (Wang et al., 2018) 和CBAM (Woo et al., 2018) 等经典视觉注意力结构。近年来则是自注意力 (Dosovitskiy et al., 2020; Liu et al., 2021; Yuan et al., 2021) 的盛行,其本质可归结为查询(query)、键(key) 和值(value) 之间的运算,甚至在纯视觉任务中完全取代了CNN。但如前所述,注意力的使用通常缺乏显式监督,导致注意力权重容易偏向数据集中的偏差。
Causalities in Computer Vision. Causality is one of the most important research areas in machine learning including causal discovery (Yehezkel Rohekar et al., 2021; $\mathrm{Ng}$ et al., 2021), causal structure learning (Kivva et al., 2021; Akbari et al., 2021) and causal inference (Zhang et al., 2021; Kaddour et al., 2021). Recent years have also witnessed growing applications of causalities in visual tasks such as long-tail classification (Tang et al., 2020; Zhu et al., 2022), few/zero-shot learning (Yue et al., 2020; 2021), and Visual Question Answering (Chen et al., 2020; Niu et al., 2021; Yang et al., 2021a). Significantly, many of these works are about conquering the contextual bias in their tasks. Yue et al. (2020) considered pre-training information as the culprit for the bias and debiased by implementing the backdoor adjustment. Niu et al. (2021) clarified the “good” and “bad” language context and eliminated the bias by pursuing counter factual total causal effect.
计算机视觉中的因果关系。因果关系是机器学习中最重要的研究领域之一,包括因果发现 (Yehezkel Rohekar et al., 2021; $\mathrm{Ng}$ et al., 2021)、因果结构学习 (Kivva et al., 2021; Akbari et al., 2021) 和因果推断 (Zhang et al., 2021; Kaddour et al., 2021)。近年来,因果关系在视觉任务中的应用也日益增多,例如长尾分类 (Tang et al., 2020; Zhu et al., 2022)、少样本/零样本学习 (Yue et al., 2020; 2021) 和视觉问答 (Chen et al., 2020; Niu et al., 2021; Yang et al., 2021a)。值得注意的是,这些研究大多致力于克服任务中的上下文偏差。Yue et al. (2020) 将预训练信息视为偏差的根源,并通过实施后门调整来消除偏差。Niu et al. (2021) 区分了“好”与“坏”的语言上下文,并通过追求反事实总因果效应来消除偏差。
Most similar to our work, Yang et al. (2021b) and Wang et al. (2021) also visited the issue of attention aggravating the bias. Yang dealt with the confounding effect in vision-language tasks, and Wang resolved to build a more robust attention in OOD settings. However, our IDA is inherently different, especially with Wang et al. (2021) in two respects: 1) Different methods: we steer by the implementation of the confounder and other components when approximating the intervention, while Wang et al. (2021) focusing on the partition and annotation of each confounder explicitly. 2) Different applications: Wang et al. (2021) was aimed at OOD settings, which is a direct task for contextual debiasing, but lacks flexibility due to the requirement of pre-defining or clustering each context. In contrast, our model does not have as many limitations, and thus has the potential to be applied in more areas. Furthermore, Wang et al. (2021) has two defects: being evaluated in limited foregrounds and backgrounds (only animals in $I0$ contexts in NICO) and performing poorly when there are multiple objects. The two points are particularly attended to in our method because our model works well in full large-scale datasets of multi-label classification and detection.
与我们工作最为相似的是,Yang等人 (2021b) 和Wang等人 (2021) 也研究了注意力加剧偏差的问题。Yang处理了视觉语言任务中的混杂效应,而Wang致力于在OOD (Out-of-Distribution) 设置中构建更稳健的注意力机制。然而,我们的IDA (Intervention-based Debiased Attention) 在本质上有所不同,特别是与Wang等人 (2021) 在两个方面存在差异:1) 方法不同:我们在近似干预时通过混杂因子和其他组件的实现来引导,而Wang等人 (2021) 则明确关注每个混杂因子的划分和标注。2) 应用场景不同:Wang等人 (2021) 针对OOD设置,这是上下文去偏的直接任务,但由于需要预定义或聚类每个上下文而缺乏灵活性。相比之下,我们的模型没有那么多限制,因此有潜力应用于更多领域。此外,Wang等人 (2021) 存在两个缺陷:在有限的前景和背景中进行评估 (仅在NICO数据集的 $I0$ 上下文中使用动物) ,以及在存在多个对象时表现不佳。这两点在我们的方法中得到了特别关注,因为我们的模型在多标签分类和检测的大规模数据集中表现良好。
3 PRELIMINARIES: CAUSALITIES IN CONTEXTUAL BIAS
3 基础概念:上下文偏见中的因果关系
In this section, we first demonstrate a causal view of contextual bias in visual recognition. As is conveyed in Fig.2(a), we set up a simple Structural Causal Model (SCM), which clarifies the causality among the context $(C)$ , image content $(X)$ and the prediction $(Y)$ . In SCM, each link denotes causalities between two entities, e.g., $X\rightarrow Y$ means effect $Y$ is generated from $X$ . Although the appearance of SCM describing the contextual bias may be different in different tasks (Yue et al., 2020; Zhang et al., 2020; Yang et al., 2021b; Wang et al., 2021), their essence is depicted in Fig.2(a): an extra element $(C)$ respectively points to a pair of the cause $(X)$ and effect $(Y)$ where we want to build a mapping. Next, we will explore the rationale behind the SCM in detail.
在本节中,我们首先展示视觉识别中上下文偏见的因果视角。如图2(a)所示,我们建立了一个简单的结构因果模型(SCM),阐明了上下文$(C)$、图像内容$(X)$和预测结果$(Y)$之间的因果关系。在SCM中,每条连线表示两个实体间的因果关系,例如$X\rightarrow Y$表示效应$Y$由$X$产生。尽管描述上下文偏见的SCM表现形式可能因任务而异[20][21][22][23],但其本质如图2(a)所示:一个额外元素$(C)$分别指向我们希望建立映射关系的成因$(X)$和效应$(Y)$。接下来,我们将详细探讨该SCM背后的原理。
$X\rightarrow Y$ denotes the predictions depend on the content in images, which is the desired causal effect: to learn a network mapping an image to its prediction. The prediction is unbiased if the target in $X$ is the only causal relation between $X$ and $Y$ . $C\rightarrow X$ means the context prior determines how an image is constructed by the contents. For example, if all spoons in a dataset appear on the dining table, the dining table may be regarded as a necessary context when picturing the image of spoon. $C\rightarrow Y$ exists because the contextual information has a considerable impact on the prediction, i.e., the object itself and its context both affect the recognition of it. $X\leftarrow C\rightarrow Y$ together gives rise to a confounding effect: the network will be fooled into building a spurious causal relation e.g., dining table is taken as the cause for the prediction of spoon. Fig.2(b) further illustrates the role of attention. The attention module can not identify the confounding effect, but focus on intensifying the causal effect $X\rightarrow Y$ even if this causal link is wrong, causing the deterioration of context bias.
$X\rightarrow Y$ 表示预测依赖于图像中的内容,这是期望的因果效应:学习一个将图像映射到其预测的网络。如果 $X$ 中的目标是 $X$ 和 $Y$ 之间唯一的因果关系,则预测是无偏的。 $C\rightarrow X$ 表示上下文先验决定了图像如何由内容构建。例如,如果数据集中所有勺子都出现在餐桌上,餐桌可能被视为拍摄勺子图像时的必要背景。 $C\rightarrow Y$ 存在是因为上下文信息对预测有显著影响,即物体本身及其背景都会影响其识别。 $X\leftarrow C\rightarrow Y$ 共同产生了混杂效应:网络会被误导建立虚假的因果关系,例如将餐桌视为预测勺子的原因。图 2(b) 进一步说明了注意力的作用。注意力模块无法识别混杂效应,而是专注于强化因果效应 $X\rightarrow Y$,即使这种因果关系是错误的,从而导致上下文偏差的恶化。

Figure 2: (a) The proposed causal graph for the causalities in contextual bias. (b) Two concrete causal examples. (c) The schematic diagram of causal intervention.
图 2: (a) 针对上下文偏差因果性提出的因果图。(b) 两个具体因果实例。(c) 因果干预示意图。
The sole way to eliminate the confounder is by causal intervention. The operation preserves the unavoidable context prediction $C\rightarrow Y$ and cuts off the bad link that an object relies on certain context. Common approaches to realizing intervention include RCT, frontdoor adjustment and backdoor adjustment (Pearl, 2014), while backdoor adjustment is the most frequently used in computer vision:
消除混杂因子的唯一方法是进行因果干预。该操作保留了不可避免的上下文预测 $C\rightarrow Y$ ,同时切断了物体依赖特定上下文的不良关联。实现干预的常用方法包括随机对照试验 (RCT) 、前门调整和后门调整 (Pearl, 2014) ,其中后门调整在计算机视觉领域应用最为广泛:
$$
\mathrm{P}(Y|\mathrm{do}(X))=\sum_{c}\mathrm{P}(Y|X,C=c)\mathrm{P}(C=c),
$$
$$
\mathrm{P}(Y|\mathrm{do}(X))=\sum_{c}\mathrm{P}(Y|X,C=c)\mathrm{P}(C=c),
$$
where the do-operation denotes the causal intervention cutting off the edge $C\rightarrow X$ as illustrated in Fig.2(c). Free from the interference of confounding path, the network can always learn the unbiased causality between $X$ and $Y$ . Here, $X$ can be extended as attention features. Consequently, the reinforcement from the attention mechanism can lead to a better prediction.
其中do操作表示因果干预切断边 $C\rightarrow X$ ,如图2(c)所示。摆脱混杂路径的干扰后,网络总能学习到 $X$ 和 $Y$ 之间的无偏因果关系。此处 $X$ 可扩展为注意力特征。因此,注意力机制的强化能带来更好的预测效果。
4 METHODOLOGY
4 方法论
In this section, we present a novel framework that strengthens the robustness of attention on contextual bias. The overview of our model is illustrated in Fig.3. We first introduce our baseline attention: Spatial Class-Aware Attention (SCA), which can obtain class-specific representations but need guidance (Section 4.1). Then, to guarantee the attention module emphasizes the proper causality, we deduce and migrate the backdoor adjustment for the attention, where the intervention is approximated as the multiple sampling with re-weighting upon SCA (Section 4.2). Finally, we present the concrete implementation in our method, i.e., implementing three versions of multiple sampling on SCA (MS-SCA) and implementing the re-weighting as Dot-Product Attention (DPA) or the transformer (Section 4.3).
在本节中,我们提出了一种增强上下文偏置注意力鲁棒性的新框架。模型概览如图3所示。首先介绍基线注意力机制:空间类感知注意力 (SCA) ,它能获取类特定表征但需要引导 (第4.1节) 。接着,为确保注意力模块聚焦正确的因果关系,我们推导并迁移了注意力的后门调整方法,通过SCA的多重采样与重加权来近似干预 (第4.2节) 。最后展示具体实现方案:在SCA上实现三重采样变体 (MS-SCA) ,并将重加权实现为点积注意力 (DPA) 或Transformer (第4.3节) 。
4.1 CLASS-AWARE LAYER
4.1 类别感知层
The target of our Spatial Class-Aware Attention (SCA) is to bias the spatial representations toward where the objects are the most likely to show up for each category. Given an image, we can obtain its feature map $\mathbf{X}\in\mathbb{R}^{H\times W\times D}$ from either a CNN-based or a transformer-based backbone, where $D,H,W$ denotes the channel dimension, height, and width. Our purpose is to turn $\mathbf{X}$ into a categoryaware representations $\mathbf{E}={\mathbf{e}{k}}{k=1}^{K}\in\mathbb{R}^{K\times D}$ , where $K$ is the number of the classes. For each specific class $k$ , its representation $\mathbf{e}_{k}$ is computed from the weighted average of the spatial feature in $\mathbf{X}$ . Then, the feature for each category can be reformed according to its unique spatial information:
我们的空间类别感知注意力 (Spatial Class-Aware Attention, SCA) 的目标是让空间表征偏向于每个类别最可能出现物体的区域。给定一张图像,我们可以从基于 CNN 或基于 Transformer 的主干网络中获取其特征图 $\mathbf{X}\in\mathbb{R}^{H\times W\times D}$ ,其中 $D,H,W$ 分别表示通道维度、高度和宽度。我们的目的是将 $\mathbf{X}$ 转换为类别感知表征 $\mathbf{E}={\mathbf{e}{k}}{k=1}^{K}\in\mathbb{R}^{K\times D}$ ,其中 $K$ 是类别数量。对于每个特定类别 $k$ ,其表征 $\mathbf{e}_{k}$ 是通过对 $\mathbf{X}$ 中的空间特征进行加权平均计算得到的。这样,每个类别的特征可以根据其独特的空间信息进行重构:
$$
\mathbf{e}{k}=\sum_{i=1}^{H}\sum_{j=1}^{W}\operatorname{P}(Y=k|X=x_{i,j})x_{i,j},
$$
$$
\mathbf{e}{k}=\sum_{i=1}^{H}\sum_{j=1}^{W}\operatorname{P}(Y=k|X=x_{i,j})x_{i,j},
$$
where $\mathrm{P}(Y=k|X=x_{i,j})$ is obtained by feeding $x_{i,j}$ into a linear classifier $\mathrm{f^{clf}}\left(.\right)$ followed with a softmax $(.)$ regular iz ation.
其中 $\mathrm{P}(Y=k|X=x_{i,j})$ 是通过将 $x_{i,j}$ 输入线性分类器 $\mathrm{f^{clf}}\left(.\right)$ 再经过 softmax $(.)$ 归一化得到的。
We adopt SCA as our baseline attention for two reasons: 1) SCA is useful for multi-object tasks. 2) SCA is easier to be affected by contextual bias (Zhu et al., 2017a; Ye et al., 2020; Zhao et al., 2021). Quite a few works adopt similar class-specific representations, due to the insight and interpret ability that they empower the models to capture object-aware features in different areas of different images, which is significant for multi-instance tasks. However, pure SCA works badly because it needs guidance to capture causal locations. SCA is designed to underline crucial positions for each class, while the “crucial position” could be the familiar background due to the bias in the dataset. To tackle this problem, other works mainly employ complicated structures (e.g., GCN or Transformer) to further process the representations. By contrast, we argue that a simple intervention (Sec.4.2) is enough to inspire the potentiality of class-aware attention. In the appendix A.4, we show our framework also gains improvement on other classic attention structures.
我们采用SCA作为基线注意力机制的原因有二:1) SCA适用于多目标任务;2) SCA更容易受到上下文偏差的影响 (Zhu et al., 2017a; Ye et al., 2020; Zhao et al., 2021)。许多工作采用类似的类别特定表示方法,因为它们能赋予模型捕捉不同图像区域中物体感知特征的能力,这对多实例任务至关重要。然而纯SCA效果不佳,因为它需要引导才能捕捉因果位置。SCA的设计初衷是突出每个类别的关键位置,但由于数据集偏差,这些"关键位置"可能是熟悉的背景。为解决这个问题,其他工作主要采用复杂结构(如GCN或Transformer)进一步处理表示。相比之下,我们认为简单干预(第4.2节)就足以激发类别感知注意力的潜力。附录A.4显示我们的框架在其他经典注意力结构上也能获得改进。
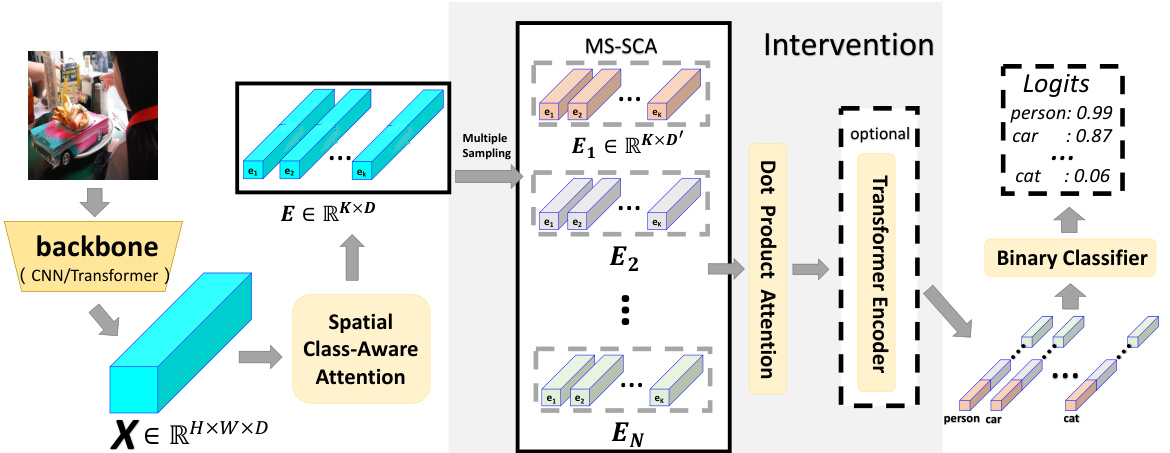
Figure 3: Overview of our proposed model. $X$ could be either image feature from visual backbone or ROI feature from detection backbone. The model is composed of the baseline attention (SCA), the multiple sampling on SCA (MS-SCA), and the second attention layer (DPA or transformer).
图 3: 我们提出的模型概览。$X$ 可以是视觉主干网络提取的图像特征,也可以是检测主干网络提取的 ROI 特征。该模型由基线注意力 (SCA)、SCA 多重采样 (MS-SCA) 和第二注意力层 (DPA 或 Transformer) 组成。
4.2 CAUSAL INTERVENTION
4.2 因果干预
$\operatorname{P}(Y|\mathrm{do}(X=x))$ calculates the probability of $Y$ when all $X$ turns to $x$ , which is infeasible. Thereby, backdoor adjustment indeed uses realistic statistics (without $d o$ ) to attain the effect equivalent to do-operation. However, it is still challenging that we are required to stratify and sample every possible $c$ for rigorous backdoor adjustment in Eq. 1. In practice, it’s difficult to quant if i cat every possible context, and consequently the $\mathrm{P}(C=c)$ is not explicitly observable.
$\operatorname{P}(Y|\mathrm{do}(X=x))$ 计算当所有 $X$ 变为 $x$ 时 $Y$ 的概率,这是不可行的。因此,后门调整 (backdoor adjustment) 实际上使用现实统计量(不含 $do$ 运算)来达到与干预操作等效的效果。然而,挑战在于我们需要对每个可能的 $c$ 进行分层采样才能严格满足公式 1 的后门调整要求。实践中很难量化所有可能的上下文 (context) ,因此 $\mathrm{P}(C=c)$ 无法显式观测到。
Thanks to the perspective of Inverse Probability Weighting (IPW) (Pearl, 2009), which further reforms the adjustment and simplifies the implementation, we can approximate the sampling on $c$ via the sampling on the observed data, i.e., $(k,x)$ . Firstly, we rewrite Eq. 1 to get the equivalent formula:
得益于逆概率加权 (Inverse Probability Weighting, IPW) (Pearl, 2009) 的视角,它进一步改进了调整方法并简化了实现,我们可以通过观测数据 $(k,x)$ 上的采样来近似 $c$ 上的采样。首先,我们将公式 1 重写为等价形式:
$$
\begin{array}{l}{{\displaystyle\mathrm{P}(Y=k|\mathrm{d}\mathrm{o}(X=x))=\sum_{c}\frac{\mathrm{P}(Y=k,X=x|C=c)\mathrm{P}(C=c)}{\mathrm{P}(X=x|C=c)}.}}\ {{\displaystyle=\sum_{c}\frac{\mathrm{P}(Y=k,X=x,C=c)}{\mathrm{P}(X=x|C=c)},}}\end{array}
$$
$$
\begin{array}{l}{{\displaystyle\mathrm{P}(Y=k|\mathrm{d}\mathrm{o}(X=x))=\sum_{c}\frac{\mathrm{P}(Y=k,X=x|C=c)\mathrm{P}(C=c)}{\mathrm{P}(X=x|C=c)}.}}\ {{\displaystyle=\sum_{c}\frac{\mathrm{P}(Y=k,X=x,C=c)}{\mathrm{P}(X=x|C=c)},}}\end{array}
$$
where $1/\mathrm{P}(X=x|C=c)$ is the so-called inverse weight. Although it’s hard to sample $c$ , in Eq. 4, there is only one $(k,x)$ given one $c$ , thereby, the number of $c$ that Eq. 4 would encounter equals the number of samples $(k,x)$ we observe. As a result, the observed $\mathrm{P}(Y,X,C)$ can be used to approximate $\operatorname{P}(Y=k|\mathrm{do}(X=x))$ , i.e., the essence of IPW lies in “assign the Inverse Weight $1/\bar{\mathrm{P}(X=x|C=c)}$ to every observed $\mathrm{P}(Y,X,C)$ , and act as though they were drawn from the post-intervention $\operatorname{P}(Y=k|\mathrm{do}(X=x))^{,}$ (Pearl, 2009). Hence, Eq. 4 can be further approximated as:
其中 $1/\mathrm{P}(X=x|C=c)$ 是所谓的逆概率权重。尽管难以对 $c$ 进行采样,但在公式4中,给定一个 $c$ 时仅存在一个 $(k,x)$ ,因此公式4会遇到的 $c$ 数量等于我们观察到的样本 $(k,x)$ 数量。于是,观测到的 $\mathrm{P}(Y,X,C)$ 可用于近似 $\operatorname{P}(Y=k|\mathrm{do}(X=x))$ ,即IPW的核心思想在于"为每个观测到的 $\mathrm{P}(Y,X,C)$ 分配逆权重 $1/\bar{\mathrm{P}(X=x|C=c)}$ ,并视作它们来自干预后的 $\operatorname{P}(Y=k|\mathrm{do}(X=x))^{,}$" (Pearl, 2009)。因此,公式4可进一步近似为:
$$
\operatorname{P}\left(Y=k|\operatorname{do}(X=x)\right)\approx\sum_{n=1}^{N}{\frac{\operatorname{P}(Y=k,X=x^{n},C=c)}{\operatorname{P}(X=x^{n}|C=c)}},
$$
$$
\operatorname{P}\left(Y=k|\operatorname{do}(X=x)\right)\approx\sum_{n=1}^{N}{\frac{\operatorname{P}(Y=k,X=x^{n},C=c)}{\operatorname{P}(X=x^{n}|C=c)}},
$$
which transforms the summation of $\mathrm{^C}$ into the sampling of X, and $\mathbf{N}$ is sampling times. Here, $C$ in the numerator can be omitted following the common practice of IPW. Then, we model terms in the summation as the sigmoid activated classification probability of the class-aware attention features :
将 $\mathrm{^C}$ 的求和转化为对 X 的采样,其中 $\mathbf{N}$ 为采样次数。根据逆概率加权 (IPW) 的常规做法,分子中的 $C$ 可省略。随后,我们将求和项建模为类别感知注意力特征经 sigmoid 激活后的分类概率:
$$
\mathrm{P}(Y=k|\mathrm{do}(X=x))=\sum_{n=1}^{N}{\frac{\mathrm{P}(Y=k|X=x^{n})\mathrm{P}(X=x^{n})}{\mathrm{P}(X=x^{n}|C=c)}}=\sum_{n=1}^{N}{\frac{\mathrm{Sigmoid}(w_{k}e_{k}^{n})\mathrm{P}(e_{k}^{n})}{\mathrm{P}(X=e_{k}^{n}|C=c)}}
$$
$$
\mathrm{P}(Y=k|\mathrm{do}(X=x))=\sum_{n=1}^{N}{\frac{\mathrm{P}(Y=k|X=x^{n})\mathrm{P}(X=x^{n})}{\mathrm{P}(X=x^{n}|C=c)}}=\sum_{n=1}^{N}{\frac{\mathrm{Sigmoid}(w_{k}e_{k}^{n})\mathrm{P}(e_{k}^{n})}{\mathrm{P}(X=e_{k}^{n}|C=c)}}
$$
where $w_{k}$ is the classifier weight for class $\mathrm{k\Omega}$ and $e_{k}$ is the feature of class $\mathrm{k\Omega}$ in Sec. 4.1. Meanwhile, the denominator, $i.e.$ , the inverse weight, can be the Propensity Score (Austin, 2011) in the classification model following Rubin’s theory, where the normalization effect is divided into the treated
其中 $w_{k}$ 是类别 $\mathrm{k\Omega}$ 的分类器权重,$e_{k}$ 是第4.1节中类别 $\mathrm{k\Omega}$ 的特征。同时,分母(即逆权重)可以是分类模型中遵循Rubin理论的倾向得分 (Propensity Score) (Austin, 2011),其中归一化效应被划分为处理组
class-specific group $(|w_{k}|{2}\cdot|e_{k}^{n}|{2})$ and untreated class-agnostic group $(\gamma\cdot|e_{k}^{n}|{2})$ . Moreover, the confounder (context) in our model is countable, thereby the sampled $e_{k}^{n}$ is finite and we simplify the $|e_{k}^{n}|_{2}$ as 1. Finally, we compute the ultimate intervention effect by assembling them as follows:
特定类别组 $(|w_{k}|{2}\cdot|e_{k}^{n}|{2})$ 和未处理的类别无关组 $(\gamma\cdot|e_{k}^{n}|{2})$ 。此外,我们模型中的混杂因素(上下文)是可数的,因此采样的 $e_{k}^{n}$ 是有限的,并将 $|e_{k}^{n}|_{2}$ 简化为1。最终,我们通过如下方式组合计算最终的干预效果:
$$
\operatorname{P}(Y=k|\mathrm{d}\boldsymbol{0}(X=x))=\sum_{n=1}^{N}{\frac{\mathrm{Sigmoid}(w_{k}e_{k}^{n})}{|w_{k}|{2}+\gamma}}\mathrm{P}(e_{k}^{n}),
$$
$$
\operatorname{P}(Y=k|\mathrm{d}\boldsymbol{0}(X=x))=\sum_{n=1}^{N}{\frac{\mathrm{Sigmoid}(w_{k}e_{k}^{n})}{|w_{k}|{2}+\gamma}}\mathrm{P}(e_{k}^{n}),
$$
where the implementations of $e^{n}$ and $\mathrm{P}(e_{k}^{n})$ are unfolded in the next section. In Sec.5.3, we will show that the SCA with multiple sampling intervention makes up a $\mathrm{{}^{\cdot\leftarrow}1+1>2^{\prime\prime}}$ effect.
其中 $e^{n}$ 和 $\mathrm{P}(e_{k}^{n})$ 的具体实现将在下一节展开。在5.3节中,我们将证明采用多重采样干预的SCA能产生 $\mathrm{{}^{\cdot\leftarrow}1+1>2^{\prime\prime}}$ 效应。
4.3 SAMPLING AND RE-WEIGHTING LAYER
4.3 采样与重加权层
In Eq. 7, the multiple sampling on $e_{k}$ is crucial to the intervention on the attention. Next, given a fixed feature dimension and sampling dimension (e.g., 2048 and 512), we describe several versions of multiple sampling on SCA (MS-SCA): 1) Random sampling: complete randomness is of no mean and unfriendly to back propagation, hence, we assign random starting points and random intervals for each sample, and the interval for a single sample is fixed. 2) Multi-head (Vaswani et al., 2017): we equally divide the channel into $\mathbf{N}$ groups and take each group as a sample. 3) Channel-shuffle: considering the success of Pixel Shuffle (Shi et al., 2016; Liu et al., 2021), the shuffle on the channel may also be meaningful. In fact, the multi-head operation is a Channel-shuffle with interval 1. Moreover, channel-shuffle can boost the sampling times with different assigned intervals. Interestingly, we will show by experiments that our model is not sensitive to these choices, indicating that the generic multi-sampling behavior is the main reason for the observed improvements.
在公式7中,对 $e_{k}$ 的多重采样是注意力干预的关键。接下来,在给定固定特征维度和采样维度(例如2048和512)的情况下,我们描述了SCA (MS-SCA) 多重采样的几种实现方式:
- 随机采样:完全随机性缺乏意义且不利于反向传播,因此我们为每个样本分配随机起始点和随机间隔,单个样本的间隔保持固定。
- 多头机制 (Vaswani et al., 2017) :将通道均匀划分为 $\mathbf{N}$ 组,每组视为一个样本。
- 通道混洗:受Pixel Shuffle (Shi et al., 2016; Liu et al., 2021) 成功的启发,通道混洗可能同样有效。实际上,多头操作是间隔为1的通道混洗特例。此外,通道混洗可通过不同间隔设置提升采样次数。有趣的是,实验将表明我们的模型对这些选择并不敏感,说明通用的多重采样行为才是性能提升的主因。
Finally is the implementation of $\mathrm{P}(e_{k}^{n})$ . The simplest way is to assign $\mathrm{P}(e_{k}^{n})$ as $1/N$ , which assumes a uniform prior of each sample. However, the status of each sample is unequal. Different positions in channel-wise dimension attend to different objects (Zhu et al., 2017b), hence, to achieve better class-aware features, it is necessary to bias the weight into the more crucial samples rather than the average. Another alternative is to introduce the learnable re-weight parameters, nonetheless, the learning capacity is limited and it is hard to scale up the model.
最后是实现 $\mathrm{P}(e_{k}^{n})$ 的方法。最简单的方式是将 $\mathrm{P}(e_{k}^{n})$ 设为 $1/N$ ,即假设每个样本具有均匀先验。然而,每个样本的状态并不平等。通道维度上的不同位置关注不同对象 (Zhu et al., 2017b) ,因此为了获得更好的类感知特征,需要将权重偏向更关键的样本而非平均分配。另一种方案是引入可学习的重加权参数,但其学习能力有限且难以扩展模型规模。
In consequence, we adopt another attention to operate the re-weighting. After the multiple sampling, we get sample-specific class-aware feature $\mathbf{E}\in\mathbb{R}^{B\times N\times K\times D^{\prime}}$ , where $B$ denotes the batch size and $D^{\prime}$ is sampling dimension. Then, we resize $\mathbf{E}$ into the sequence $\mathbf{E}^{s}\in\mathbb{R}^{N\times(B*K)\times D^{\prime}}$ . Now, we can implement the scaled Dot-Product Attention (Vaswani et al., 2017) (DPA) to re-weight among different samples, for each class-aware representation:
因此,我们采用另一种注意力机制进行重新加权。经过多次采样后,我们得到样本特定的类感知特征 $\mathbf{E}\in\mathbb{R}^{B\times N\times K\times D^{\prime}}$ ,其中 $B$ 表示批次大小, $D^{\prime}$ 为采样维度。随后,我们将 $\mathbf{E}$ 调整为序列形式 $\mathbf{E}^{s}\in\mathbb{R}^{N\times(B*K)\times D^{\prime}}$ 。此时,我们可以对每个类感知表征实施缩放点积注意力 (Vaswani et al., 2017) (DPA) 来实现样本间的重新加权:
$$
\mathbf{E^{\delta^{\prime}}}=\operatorname{softmax}(\frac{(W_{q}\mathbf{E}^{s})(W_{k}\mathbf{E}^{s})^{T}}{\sqrt{D^{\prime}}})(W_{v}\mathbf{E}^{s}),
$$
$$
\mathbf{E^{\delta^{\prime}}}=\operatorname{softmax}(\frac{(W_{q}\mathbf{E}^{s})(W_{k}\mathbf{E}^{s})^{T}}{\sqrt{D^{\prime}}})(W_{v}\mathbf{E}^{s}),
$$
where $W_{q},W_{k},W_{v}$ are the linear projection mapping the sequence into a common subspace for similarity measure. Thus far, we have explained our lightweight version of IDA. Our method increases almost no parameter except the shared KQV projection, and it outperforms all other models with comparable computation. Furthermore, to scale up the model, Eq. 8 can be naturally extended as the transformer, providing opportunities to trade-off between computation and performance:
其中 $W_{q},W_{k},W_{v}$ 是将序列线性投影到公共子空间以进行相似度度量的矩阵。至此,我们已阐述了轻量级IDA (Iterative Deepening Attention) 的实现方案。该方法除共享的KQV (Key-Query-Value) 投影外几乎不增加参数,在计算量相当的情况下性能优于所有其他模型。此外,为扩展模型规模,公式8可自然扩展为Transformer架构,从而在计算量与性能之间实现灵活权衡:
$$
\mathbf{E}^{s+1}=\operatorname*{max}(0,\mathbf{E}^{s^{\prime}}W_{1}+b_{1})W_{2}+b_{2}.
$$
$$
\mathbf{E}^{s+1}=\operatorname*{max}(0,\mathbf{E}^{s^{\prime}}W_{1}+b_{1})W_{2}+b_{2}.
$$
Eq. 8 and Eq. 9 can continue iterating to build a stronger class-specific representation, which becomes our heavyweight version of IDA. Finally, the class-aware representations are fed into a binary classifier followed by a sigmoid activation, and the average logit of all samples is taken as the final logit for that class, where the classifier shares the same learnable weight with $\mathrm{f^{clf}}\left(.\right)$ in $\mathrm{Sec4.1}$ .
式8和式9可以继续迭代以构建更强的类特定表示,这成为我们的重量级IDA版本。最后,类感知表示被输入到一个二元分类器中,后接一个sigmoid激活函数,所有样本的平均logit作为该类的最终logit,其中分类器与$\mathrm{Sec4.1}$中的$\mathrm{f^{clf}}\left(.\right)$共享相同的可学习权重。
5 EXPERIMENTS
5 实验
In this section, we conduct extensive experiments to demonstrate the superiority of the proposed method. We first introduce the general settings. Then, we present our quantitative results of multilabel classification and detection on three widely used datasets: MS-COCO (Lin et al., 2014), VOC2007, and VOC2012 (Everingham et al., 2010). Finally, we perform various ablation studies and analyses to show the effectiveness of different components in our model.
在本节中,我们通过大量实验验证所提方法的优越性。首先介绍通用实验设置,随后在三个广泛使用的数据集(MS-COCO (Lin et al., 2014)、VOC2007和VOC2012 (Everingham et al., 2010))上展示多标签分类与检测的量化结果。最后通过消融实验与分析,验证模型中各组成部分的有效性。
Table 1: Comparison of mAP $(%)$ on the MS-COCO in multi-label classification. L and H mean the light version and the heavy version respectively, and WH denotes the resolution.
表 1: MS-COCO 多标签分类任务中 mAP (%) 的对比。L 和 H 分别表示轻量版和重量版,WH 表示分辨率。
| 方法 | 分辨率 | mAP | All | All | Top3 | Top3 |
|---|---|---|---|---|---|---|
| CF1 | OF1 | CF1 | OF1 | |||
| ResNet-101 (He et al., 2016) | 448 * 448 | 81.5 | 76.3 | 80.0 | 73.5 | 76.0 |
| ML-GCN (Chen et al., 2019c) | 448 * 448 | 83.0 | 78.0 | 80.3 | 74.2 | 76.3 |
| MS-CMA (You et al., 2020) | 448 * 448 | 83.8 | 78.4 | 81.0 | 74.9 | 77.1 |
| CSRA (Zhu & Wu, 2021) | 448 * 448 | 83.5 | 77.9 | 80.3 | 74.4 | 76.5 |
| IDA-R101(L) | 448 * 448 | 84.3 | 78.5 | 81.1 | 73.6 | 77.3 |
| IDA-R101(H) | 448 * 448 | 84.8 | 78.7 | 80.9 | 73.9 | 77.4 |
| SSGRL (Chen et al., 2019b) | 576 * 576 | 83.8 | 76.8 | 79.7 | 72.7 | 76.2 |
| C-Trans (Lanchantin et al., 2021) | 576 * 576 | 85.1 | 79.9 | 81.7 | 76.0 | 77.6 |
| ADD-GCN (Ye et al., 2020) | 576 * 576 | 85.2 | 80.1 | 82.0 | 75.8 | 77.9 |
| CCD (Liu et al., 2022) | 576 * 576 | 85.3 | 80.2 | 82.1 | 76.0 | 77.9 |
| TDRG (Zhao et al., 2021) | 576 * 576 | 86.0 | 80.4 | 82.4 | 76.2 | 78.1 |
| IDA-R101(L) | 576 * 576 | 85.5 | 79.8 | 82.3 | 75.2 | 78.1 |
| IDA-R101(H) | 576 * 576 | 86.3 | 80.4 | 82.5 | 76.4 | 78.2 |
| Swin-Base (Liu et al., 2021) | 384 * 384 | 88.4 | 82.2 | 84.0 | 77.2 | 79.9 |
| Swin-Large (Liu et al., 2021) | 384 * 384 | 89.3 | 83.6 | 85.6 | 78.1 | 80.8 |
| MA-SwinB(H) | 384 * 384 | 89.3 | 83.7 | 85.1 | 78.0 | 80.4 |
| IMA-SwinL(H) | 384 * 384 | 90.3 | 84.7 | 85.9 | 79.0 | 81.1 |
Table 2: Comparison of between our method and the baseline on the MS-COCO and VOC07 in object detection.
表 2: 我们的方法与基线在目标检测任务中 MS-COCO 和 VOC07 数据集上 的对比
| 方法 | 检测器 | MS-COCO mAP@.5 mAP@.75 | VOC07 mAP@.5 |
|---|---|---|---|
| 基线 | Faster-RCNN-ROIAlign-R50 | 58.1 | 40.5 |
| IDA (L) | Faster-RCNN-ROIAlign-R50 | 59.3 | 42.0 |
| IDA (L) | RetinaNet-R50 | 52.5 | 36.6 |
| 基线 IDA (L) | RetinaNet-R50 | 55.8 | 38.6 |
| 基线 IDA (L) | DeTR-DC5-R101 | 64.7 | 47.7 |
| 基线 IDA (L) | DeTR-DC5-R101 | 65.7 | 49.2 |
5.1 EXPERIMENTS SETTINGS
5.1 实验设置
Implementation details. Unless otherwise stated, we use ResNet101 (He et al., 2016) pre-trained on ImageNet 1k (Deng et al., 2009) as our backbone. For the multiple-sampling module, we adopt channel-shuffle with start point $=0$ , intervals $=1$ & 2, and sampling dimension $=512$ (1/4 of the full dimension), and thus we have $=8$ . $\gamma$ is set as 1/32. For the heavy version of IDA, we only have 2 layers of transformer and do not implement the multi-head operation on dot-product attention. There is no extra data preprocessing besides the standard data augmentation (Ridnik et al., 2021; Chen et al., 2019c). The multi-label classification model and the detection model are both optimized by the Binary Cross Entropy Loss with sigmoid. We choose Adam as our optimizer with weight decay of $1e-4$ and $(\beta_{1},\bar{\beta_{2}})=(0.9,0.9\bar{9}99)$ . The learning rate is $1e-4$ for the batch size of 128 with a 1-cycle policy. All our codes were implemented in Pytorch (Paszke et al., 2017).
实现细节。除非另有说明,我们使用在ImageNet 1k (Deng et al., 2009) 上预训练的ResNet101 (He et al., 2016) 作为主干网络。对于多重采样模块,我们采用通道混洗(channel-shuffle),起始点 $=0$,间隔 $=1$ 和 2,采样维度 $=512$ (全维度的1/4),因此得到 $=8$。$\gamma$ 设为1/32。在IDA的重度版本中,我们仅使用2层Transformer且未在点积注意力中实现多头操作。除标准数据增强(Ridnik et al., 2021; Chen et al., 2019c)外,未进行额外数据预处理。多标签分类模型和检测模型均采用带sigmoid的二值交叉熵损失进行优化。我们选择Adam作为优化器,权重衰减为 $1e-4$,$(\beta_{1},\bar{\beta_{2}})=(0.9,0.9\bar{9}99)$。学习率设为 $1e-4$,批量大小为128,采用1-cycle策略。所有代码均基于Pytorch (Paszke et al., 2017)实现。
Evaluation metrics. For multi-label classification, we adopt the mean average precision (mAP) as our main evaluation metric, and overall/per-class F1-measure (OF1/CF1) as supplements. Separate precision and recall are not employed because they are easily affected by the hyper-parameter. For detection, we employ the $\operatorname*{mAP}@.5$ , mAP $\ @.7$ 5 and mAP $@$ [.5, .95] for MS-COCO, and $\operatorname*{mAP}@.5$ for Pascal VOC. In Sec. 5.3, we also evaluate our method on contextual bias benchmarks. The result of classification on Pascal VOC can be found in Appendix A.1.
评估指标。对于多标签分类任务,我们采用平均精度均值 (mAP) 作为主要评估指标,并以整体/各类别 F1 值 (OF1/CF1) 作为补充指标。未单独采用精确率和召回率,因为它们容易受超参数影响。在检测任务中,我们对 MS-COCO 数据集使用 $\operatorname*{mAP}@.5$、mAP $\ @.7$ 5 和 mAP $@$ [.5, .95] 指标,对 Pascal VOC 数据集使用 $\operatorname*{mAP}@.5$ 指标。在 5.3 节中,我们还针对上下文偏置基准测试评估了本方法。Pascal VOC 上的分类结果详见附录 A.1。
5.2 QUANTITATIVE RESULTS.
5.2 定量结果
Multi-label classification on MS-COCO. MS-COCO (Lin et al., 2014) is the most popular benchmark for object detection, segmentation and caption, and has also become widely used in multi-label recognition recently. It contains 122,218 images and covers 80 categories with 2.9 for each image on average. Considering the result of multi-label classification is highly related to the resolution and backbone, we perform experiments with different backbones and different resolutions to make the result more persuasive.
MS-COCO上的多标签分类。MS-COCO (Lin et al., 2014) 是最流行的目标检测、分割和描述基准数据集,近年来也广泛应用于多标签识别领域。该数据集包含122,218张图像,涵盖80个类别,平均每张图像包含2.9个标签。考虑到多标签分类结果与图像分辨率和主干网络(backbone)高度相关,我们采用不同主干网络和分辨率进行实验以使结果更具说服力。
As is demonstrated in Table 1, for CNN backbone, we adopt ResNet101 pre-trained on ImageNet 1k with the resolutions of $448\times448$ and $576\times576$ . The results of lightweight and heavyweight versions are both present for fair comparisons. The first block shows that our light model has an obvious advantage over other methods with comparable computation (e.g., CSRA (Zhu & Wu, 2021)). For heavyweight models, other models universally adopt 3 or more layers of transformer or GNN (e.g., ADDGCN (Ye et al., 2020), C-Trans (Lanchantin et al., 2021) and TDRG (Zhao et al., 2021)), while ours only has two layers but outperforms all of them, confirming the trade-off between computation and performance in our method is more efficient. For transformer backbone, we use the recently popular Swin-Transformer (Liu et al., 2021) pre-trained on ImageNet $22\mathrm{k\Omega}$ . The results in the last block convey our improvement. Based on such a strong backbone, it is very difficult to advance the performance, but our method still brings about considerable progress. In Appendix A.2, we further present
