ADVERSARIAL DISTORTION LEARNING FOR MEDICAL IMAGE DENOISING
医学图像去噪的对抗性失真学习
ABSTRACT
摘要
We present a novel adversarial distortion learning (ADL) for denoising both two- and threedimensional (2D/3D) biomedical image data. The proposed ADL methodology deploys two inter connected auto-encoders, a denoiser and a disc rim in at or. The primary function of the denoiser is to effectively eliminate noise from the input data, while the disc rim in at or plays a crucial role in assessing and comparing the denoised image against its noise-free counterpart. This iterative process is perpetuated until the disc rim in at or attains the inability to differentiate between the denoised data and the corresponding reference image. The foundational elements of both the denoiser and the disc rim in at or are founded upon the proposed Efficient-UNet. The Efficient-UNet encompasses a novel multiscale architecture, effectively utilizing residual blocks and introducing a novel pyramidal approach in the backbone to facilitate the efficient extraction of texture and the reuse of feature maps. By virtue of this innovative architectural design, the model ensures the coherence of the denoised data concerning both its local and global attributes. Traditional adversarial learning methods often fall short in preserving crucial textural, global, and local data representations. Our proposed Efficient-UNet is equipped with two novel loss functions to conserve the inherent textural information and contrast during the training phase to overcome this limitation. We generalized the proposed ADL to any biomedical data. The 2D version of our network was trained on natural images and tested on biomedical datasets featuring entirely distinct distributions from natural images, so re-training is unnecessary. Experiments on magnetic resonance images (MRI), der matos copy, electron microscopy, and X-ray datasets show that the proposed method achieved state-of-the-art denoising each benchmark. Our implementation and pre-trained models are available at https://github.com/mogvision/ADL.
我们提出了一种新颖的对抗性失真学习(ADL)方法,用于对二维和三维(2D/3D)生物医学图像数据进行去噪。该ADL方法部署了两个相互连接的自动编码器:去噪器和判别器。去噪器的主要功能是有效消除输入数据中的噪声,而判别器则负责评估并比较去噪图像与无噪声参考图像。这个迭代过程将持续进行,直到判别器无法区分去噪数据与对应的参考图像为止。去噪器和判别器的基础架构均基于我们提出的Efficient-UNet。Efficient-UNet采用了一种新颖的多尺度架构,有效利用残差块,并在主干网络中引入了一种新的金字塔式方法,以促进纹理特征的高效提取和特征图的重用。通过这种创新的架构设计,该模型确保了去噪数据在局部和全局属性上的一致性。传统对抗学习方法往往难以保留关键的纹理、全局和局部数据表征。我们提出的Efficient-UNet配备了两个新颖的损失函数,在训练阶段保留固有纹理信息和对比度以克服这一局限。我们将所提出的ADL方法推广到任何生物医学数据。网络的2D版本在自然图像上训练,并在与自然图像分布完全不同的生物医学数据集上测试,因此无需重新训练。在磁共振成像(MRI)、皮肤镜、电子显微镜和X射线数据集上的实验表明,该方法在每个基准测试中都达到了最先进的去噪性能。我们的实现和预训练模型可在https://github.com/mogvision/ADL获取。
1 Introduction
1 引言
Image denoising aims to recover latent noise-free two/three-dimensional (2D/3D) image data x from its noisy counterpart ${\bf y}={\bf x}+{\bf n}$ , where n denotes noise that is independent of x. The denoising problem is an ill-posed inverse problem as no unique solution exists. Denoising is an essential preprocessing step in many medical imaging applications. A vast number of methods have been proposed over the past decades [1, 2, 3, 4], and recently, methods based on deep neural networks (DNNs) attract more attention due to their good performance [5, 6, 7, 8, 9].
图像去噪旨在从其含噪版本 ${\bf y}={\bf x}+{\bf n}$ 中恢复潜在的无噪二维/三维(2D/3D)图像数据x,其中n表示与x独立的噪声。由于不存在唯一解,去噪问题是一个不适定的逆问题。去噪是许多医学影像应用中的关键预处理步骤。过去几十年已提出大量方法[1, 2, 3, 4],近年来基于深度神经网络(DNNs)的方法因其优异性能受到更多关注[5, 6, 7, 8, 9]。
For additive noise, it is possible to estimate denoised visual datax using the Bayesian approach, where the posterior $P_{x|y}(\mathbf{x}|\mathbf{y})$ is a combination of the data likelihood $P_{y|x}(\mathbf{y}|\mathbf{x})$ and a prior model $P_{x}(\mathbf{x})$ , i.e.:
对于加性噪声,可以采用贝叶斯方法估计去噪后的视觉数据x,其中后验概率 $P_{x|y}(\mathbf{x}|\mathbf{y})$ 由数据似然 $P_{y|x}(\mathbf{y}|\mathbf{x})$ 和先验模型 $P_{x}(\mathbf{x})$ 共同决定,即:
$$
\hat{\mathbf{x}}=\underset{\mathbf{x}}{\mathrm{argmax}}P_{x|y}(\mathbf{x}|\mathbf{y})=\underset{\mathbf{x}}{\mathrm{argmax}}\log P_{y|x}(\mathbf{y}|\mathbf{x})+\log P_{\mathbf{x}}(\mathbf{x}).
$$
$$
\hat{\mathbf{x}}=\underset{\mathbf{x}}{\mathrm{argmax}}P_{x|y}(\mathbf{x}|\mathbf{y})=\underset{\mathbf{x}}{\mathrm{argmax}}\log P_{y|x}(\mathbf{y}|\mathbf{x})+\log P_{\mathbf{x}}(\mathbf{x}).
$$
The denoising problem Eq. 1 can also be expressed as an optimization of a data term penalized by one or more regular iz ation terms as follows:
去噪问题式(1)也可表示为数据项与一个或多个正则化项的优化问题:
$$
\begin{array}{r}{\hat{\mathbf{x}}=\underset{\mathbf{x}}{\operatorname{argmin}}~\left|\mathbf{y}-\mathbf{x}\right|_{p}^{p}+\lambda\mathcal{R}(\mathbf{x}),}\end{array}
$$
$$
\begin{array}{r}{\hat{\mathbf{x}}=\underset{\mathbf{x}}{\operatorname{argmin}}~\left|\mathbf{y}-\mathbf{x}\right|_{p}^{p}+\lambda\mathcal{R}(\mathbf{x}),}\end{array}
$$
where $\left\Vert.\right\Vert_{p}$ denotes the $\ell p$ -norm, $1\le p\le2$ . $\mathcal{R}$ poses penalty terms on the unknown latent $\mathbf{x}$ which is associated with the prior term $P_{x}(\mathbf{x})$ defined in Eq. 1. $\lambda$ is a Lagrangian parameter, which can be determined manually or automatically [10]. In general, the denoising methods can be divided into model- and learning-based categories. The model-based approach solves Eq. 2 using one or several regular iz ation terms [11, 12, 13, 14]. In the learning-based approach, a model can learn features with supervision [15, 16] or it may learn the features simultaneously during image reconstruction [17].
其中 $\left\Vert.\right\Vert_{p}$ 表示 $\ell p$ 范数,$1\le p\le2$。$\mathcal{R}$ 对未知潜在变量 $\mathbf{x}$ 施加惩罚项,该变量与式1中定义的先验项 $P_{x}(\mathbf{x})$ 相关联。$\lambda$ 是拉格朗日参数,可通过手动或自动方式确定 [10]。一般来说,去噪方法可分为基于模型和基于学习的两类。基于模型的方法通过一个或多个正则化项求解式2 [11, 12, 13, 14]。基于学习的方法中,模型可通过监督方式学习特征 [15, 16],或在图像重建过程中同步学习特征 [17]。
Recently, the deep learning-based approaches [5, 7, 18, 19, 20, 21, 22, 23, 24] have reached excellent performance in denoising biomedical images by training DNNs on paired or unpaired images of target clean and noisy data. Despite the success of the existing denoising techniques, images denoised by such methods still suffer from poor preservation of texture and contrast. Other limitations of the current techniques are requiring prior knowledge of noise and the lack of general iz ability to various types of biomedical image data.
近年来,基于深度学习的方法[5,7,18,19,20,21,22,23,24]通过在目标干净与噪声图像的成对或非成对数据上训练深度神经网络(DNN),在生物医学图像去噪领域取得了优异性能。尽管现有去噪技术已取得成功,但这类方法处理的图像仍存在纹理和对比度保留不足的问题。当前技术的其他局限还包括需要噪声先验知识,以及缺乏对各类生物医学图像数据的泛化能力。
In this study, we introduce an innovative adversarial distortion learning-based (ADL) method that does not require prior knowledge about the image noise. ADL is a supervised feature learning method comprising a denoiser and a disc rim in at or that mutually optimizes each other to find high-quality denoised contents. The denoiser and the disc rim in at or are built upon a novel network called Efficient-UNet. Efficient-UNet has a light architecture with a pyramidal residual blocks backbone that enforces the higher-level features align with each other hierarchically. A remarkable feature of our approach is that it can denoise any 2D/3D biomedical image data without re-training. The light architecture of the proposed method allows a fast evaluation of test data, considerably reducing the computational time of the conventional model-based approaches. The key contributions of this study are as follows:
本研究提出了一种创新的基于对抗性失真学习(ADL)的方法,该方法无需预先了解图像噪声信息。ADL是一种监督式特征学习方法,由去噪器和判别器组成,二者通过相互优化来寻找高质量的去噪内容。去噪器和判别器均基于名为Efficient-UNet的新型网络构建。Efficient-UNet采用轻量级架构,其核心是金字塔残差块结构,可确保高层特征在层级间保持对齐。我们方法的一个显著特点是无需重新训练即可处理任何2D/3D生物医学图像数据。所提方法的轻量架构能够快速评估测试数据,大幅减少了传统基于模型方法的计算时间。本研究的主要贡献如下:
• We provide both 2D and 3D networks of our method for denoising any type of 2D/3D biomedical image data. The experimental outcomes demonstrate that the proposed ADL outperforms existing methods, attaining state-of-the-art results across all benchmarks. Moreover, ADL effectively addresses issues related to over fitting, ensures general iz ability to diverse biomedical data types, and mitigates computational burdens.
• 我们提供了适用于任何类型2D/3D生物医学图像数据去噪的二维和三维网络方案。实验结果表明,所提出的ADL方法优于现有技术,在所有基准测试中均达到最先进水平。此外,ADL能有效解决过拟合问题、确保对不同生物医学数据类型的泛化能力,并显著降低计算负担。
2 Related Work
2 相关工作
Medical image denoising approaches can be grouped into two subcategories: model-based and learning-based methods. In the model-based approach, the optimization of Eq.1 solely based on the likelihood term is typically ill-posed. To address this issue and stabilize the denoised outputs, one or more regular iz ation terms are incorporated alongside the data fidelity term. As a result, a diverse range of model-based techniques has been developed, encompassing total variation (TV) regularize rs[11, 14, 26] and non-local self-similarity regularize rs [12, 13, 27, 28], among others. TV-based regular iz ation terms can successfully recover piecewise constant images but cause several artifacts to complex images with rich edges and textures. Since images tend to contain repetitive edge and textural information, a combination of non-local self-similarity [12, 13, 27] with the sparse representation [16] and low-rank approximation [29] lead to significant improvements over their local counterparts. Despite the acceptable performance of the model-based methods in image denoising, there are still several drawbacks with these techniques. Requiring a specific model for a single denoising task, lack of general iz ability to various types of data, or the need for manually or semi-automatically tuning parameters are the challenges that are still required to be addressed. Moreover, the non-local self-similarity-based methods iterative ly optimize Eq. 2 resulting in slow convergence.
医学图像去噪方法可分为两大类:基于模型的方法和基于学习的方法。在基于模型的方法中,仅依靠似然项对公式1进行优化通常是不适定的。为解决这一问题并稳定去噪输出,通常会在数据保真项之外加入一个或多个正则化项。因此衍生出了多种基于模型的技术,包括全变分(TV)正则化器[11,14,26]和非局部自相似性正则化器[12,13,27,28]等。基于TV的正则化项能有效恢复分段恒定图像,但会对具有丰富边缘和纹理的复杂图像产生伪影。由于图像往往包含重复的边缘和纹理信息,将非局部自相似性[12,13,27]与稀疏表示[16]及低秩近似[29]相结合,相比局部方法取得了显著改进。尽管基于模型的方法在图像去噪中表现尚可,但仍存在若干缺陷:单一去噪任务需要特定模型、缺乏对不同类型数据的泛化能力、需要手动或半自动调整参数等问题仍需解决。此外,基于非局部自相似性的方法需要迭代优化公式2,导致收敛速度缓慢。
Learning-based methods aim to learn a model’s parameters with available training data. Sparsity-based techniques are well-studied learning approaches, which represent local image structures with a few elemental structures, so-called atoms from an off-the-shelf transformation matrix-like Wavelets [30] or a learned dictionary [31, 17]. Deep neural networks (DNNs) have been widely used for the enhancement of biomedical images, ranging from magnetic resonance imaging (MRI) [23, 32], computed tomography (CT) [6, 33], X-ray [5], to electron microscopy (EM) [34, 22]. The learning process of DNNs can be categorized into supervised [18, 7, 19] or unsupervised [20, 21, 22] approaches. Supervised learning DNNs consider clean and noisy image pairs for training where the noisy counterparts are obtained by adding synthesized noise to the target clean ones. To address the challenge of insufficient clean data for training, unsupervised methods [20, 35, 22] have been developed that estimate the map of noise from unpaired images, leveraging the supervision of clean targets. Unsupervised techniques often explore the noise map by generative adversarial networks (GANs) [36] and its variants like conditional GAN [37] or CycleGAN [20]. Typically, the supervised DNNs have shown superior performance over the unsupervised and conventional model-based approaches. Despite the great success of DNNs in denoising biomedical images, denoised images still suffer from poor textural information. Although several works [19, 7, 38, 39, 40] show less tendency toward over fitting and being data-driven, their performance is still highly dependent on the training samples. Since clean biomedical images for training are not available or available only in very limited quantities, this aspect of the current DNN techniques limits their general iz ability to different sorts of biomedical images.
基于学习的方法旨在利用现有训练数据学习模型参数。稀疏性技术是经过充分研究的学习方法,它通过少量基本结构(即现成变换矩阵如小波[30]或学习字典[31, 17]中的原子)来表示局部图像结构。深度神经网络(DNNs)已广泛应用于生物医学图像增强领域,涵盖磁共振成像(MRI)[23, 32]、计算机断层扫描(CT)[6, 33]、X射线[5]和电子显微镜(EM)[34, 22]。DNNs的学习过程可分为监督式[18, 7, 19]或无监督式[20, 21, 22]方法。监督学习DNNs使用干净与噪声图像对进行训练,其中噪声图像是通过向目标干净图像添加合成噪声获得。为解决训练清洁数据不足的挑战,无监督方法[20, 35, 22]通过从未配对图像中估计噪声映射,利用清洁目标的监督进行训练。无监督技术通常通过生成对抗网络(GANs)[36]及其变体(如条件GAN[37]或CycleGAN[20])探索噪声映射。通常,监督式DNNs展现出优于无监督和传统基于模型方法的性能。尽管DNNs在生物医学图像去噪方面取得巨大成功,去噪图像仍存在纹理信息保留不足的问题。虽然部分研究[19, 7, 38, 39, 40]显示出较低过拟合倾向和数据驱动特性,但其性能仍高度依赖训练样本。由于可用于训练的清洁生物医学图像稀缺或数量极其有限,当前DNN技术的这一特点限制了其对不同种类生物医学图像的泛化能力。
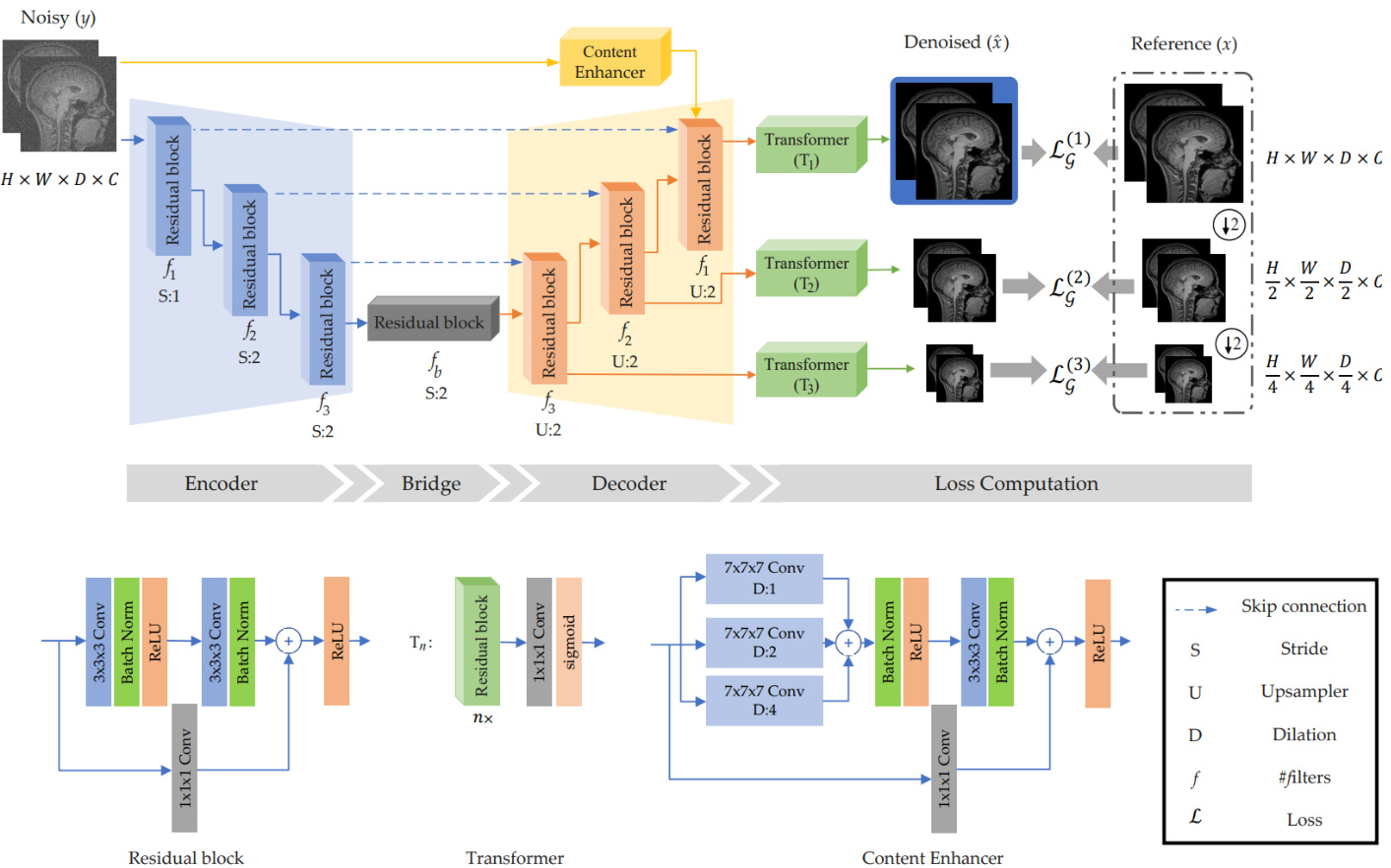
Figure 1: Framework of the Efficient-UNet for denoiser with the training steps. Efficient-UNet is composed of the encoder, decoder, and Content Enhancer blocks. The output of the decoder at every scale is mapped into the image domain by a Transformer block. We then enforce consistency between the outputs of the decoder and their counterparts $x$ . Low-level features further contribute to the denoised image by the Content Enhancer block. When the noise level is low, the filters of this block are activated, improving the convergence with no need for high-level features.
图 1: 带训练步骤的Efficient-UNet去噪框架。该网络由编码器、解码器和内容增强器模块组成。每个尺度下解码器的输出通过Transformer模块映射到图像域,随后强制保持解码器输出与对应真实值$x$之间的一致性。低级特征通过内容增强器模块进一步优化去噪效果。当噪声水平较低时,该模块的滤波器会被激活,无需依赖高级特征即可提升收敛性。
3 Proposed Method
3 研究方法
The core concept behind ADL is that image representations should exhibit resilience against noise and distortion. ADL comprises a denoiser and a disc rim in at or, each employing a similar architecture referred to as Efficient-UNet1. ADL is trained by minimizing competing multiscale objectives between the denoiser and the disc rim in at or. During training, we enforce the networks on keeping the edges, histogram, and pyramidal information of the reference/ground-truth data. The proposed loss functions are detailed in Section 3.2.
ADL的核心概念在于图像表征应具备对噪声和失真的鲁棒性。该框架由去噪器(denoiser)和判别器(discriminator)组成,两者均采用称为Efficient-UNet1的相似架构。通过最小化去噪器与判别器之间的多尺度对抗目标来完成训练,期间强制网络保持参考数据/真实数据的边缘、直方图和金字塔信息。具体损失函数详见3.2节。
3.1 Efficient-UNet
3.1 Efficient-UNet
Given a noise-free 3D (or 2D) visual data with $C$ channels represented as $\mathbf{x}\in\mathbb{R}^{H\times W\times D\times C}$ (or $\mathbf{x}\in\mathbb{R}^{H\times W\times C}$ for 2D). Let $\mathbf{y}\in\mathbb{R}^{H\times W\times D\times C}$ represent the observed visual data, which is generated by introducing white Gaussian noise 1There are slight differences in the architecture of the denoiser’s Efficient-UNet and the disc rim in at or’s, detailed in Section 3.1.
给定一个无噪声的3D(或2D)视觉数据,其具有 $C$ 个通道,表示为 $\mathbf{x}\in\mathbb{R}^{H\times W\times D\times C}$(对于2D数据则为 $\mathbf{x}\in\mathbb{R}^{H\times W\times C}$)。令 $\mathbf{y}\in\mathbb{R}^{H\times W\times D\times C}$ 表示观测到的视觉数据,该数据通过引入高斯白噪声生成。去噪器的高效UNet (Efficient-UNet) 架构与判别器存在细微差异,详见第3.1节。
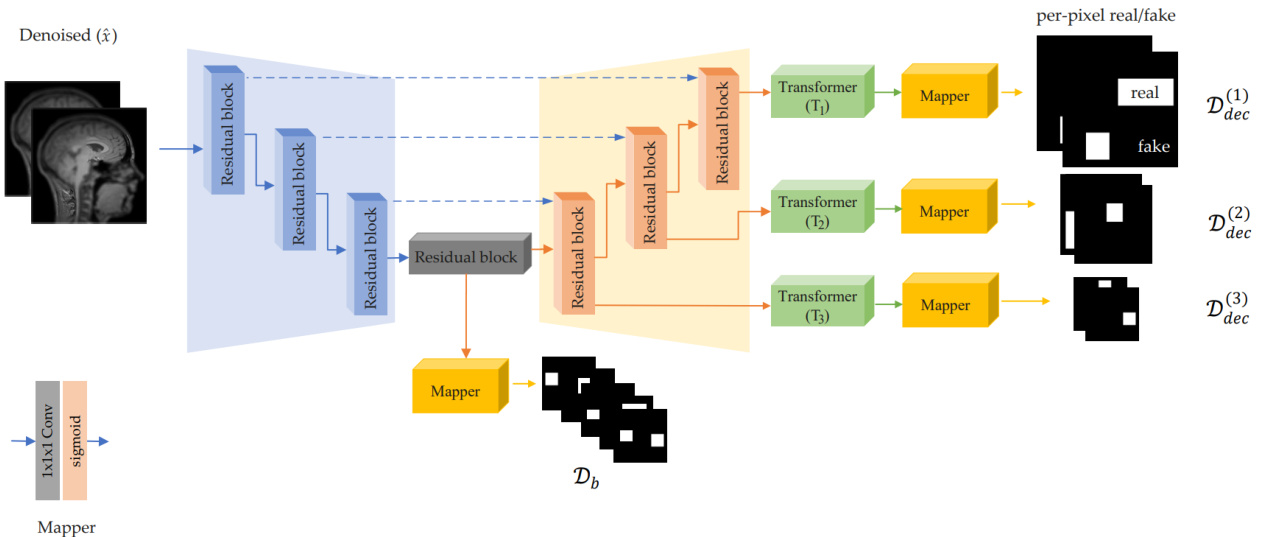
Figure 2: Framework of the proposed Efficient-UNet for disc rim in at or with the training steps.
图 2: 所提出的Efficient-UNet判别器框架及训练步骤
(WGN) with a standard deviation, denoted $\sigma$ , to the noise-free latent image x. x serves as a reference throughout the training process, and the noise level $(\sigma)$ remains unspecified. The objective is to reconstruct y from $\mathbf{x}$ . The architecture employed for training the denoiser is illustrated in Figure 1, which relies on the Efficient-UNet framework. Efficient-UNet is composed of several components, including an encoder, a bridge, a decoder, a content enhancer, and transformers. Likewise, the architecture of Efficient-UNet for the disc rim in at or is depicted in Figure 2. The encoder unit is comprised of three consecutive residual blocks with strides one and two (denoted by $S$ in Figure 1) that extract the features from the observed data. The number of filters in the encoder layers is doubled after each down sampling operation (i.e., $S=2$ ). Several studies [41, 18, 7] have shown the effectiveness of residual blocks in deep learning. We use the residual blocks in our auto-encoder structure for denoiser prior modeling. To have large activation maps, we delay the down sampling of the first layer, whose stride is 1. The extracted features by the encoder are then passed through a bridge with $f_{b}$ filters followed by the decoder unit that estimates the denoised input data $\hat{\bf x}$ in the feature domain. The features of each decoder layer are mapped into the image domain by the transformer unit $T_{n}$ where $n$ is the index of the corresponding layer. The transformer unit is a set of $n$ residual blocks followed by a $1\times1\times1$ convolution and a sigmoid activation layer. The number of filters in the transformer layers is halved $n$ times2 and the filter size of $1\times1\times1$ convolution layer is equal to $C$ , which is the number of input channels. Throughout this study, the kernel size and dilation of the convolutional layers are 3 and 1, respectively, unless otherwise noted.
规则:
- 输出中文翻译部分的时候,只保留翻译的标题,不要有任何其他的多余内容,不要重复,不要解释。
- 不要输出与英文内容无关的内容。
- 翻译时要保留原始段落格式,以及保留术语,例如 FLAC,JPEG 等。保留公司缩写,例如 Microsoft, Amazon, OpenAI 等。
- 人名不翻译
- 同时要保留引用的论文,例如 [20] 这样的引用。
- 对于 Figure 和 Table,翻译的同时保留原有格式,例如:“Figure 1: ”翻译为“图 1: ”,“Table 1: ”翻译为:“表 1: ”。
- 全角括号换成半角括号,并在左括号前面加半角空格,右括号后面加半角空格。
- 在翻译专业术语时,第一次出现时要在括号里面写上英文原文,例如:“生成式 AI (Generative AI)”,之后就可以只写中文了。
- 以下是常见的 AI 相关术语词汇对应表(English -> 中文):
- Transformer -> Transformer
- Token -> Token
- LLM/Large Language Model -> 大语言模型
- Zero-shot -> 零样本
- Few-shot -> 少样本
- AI Agent -> AI智能体
- AGI -> 通用人工智能
- Python -> Python语言
策略:
分三步进行翻译工作:
- 不翻译无法识别的特殊字符和公式,原样返回
- 将HTML表格格式转换成Markdown表格格式
- 根据英文内容翻译成符合中文表达习惯的内容,不要遗漏任何信息
最终只返回Markdown格式的翻译结果,不要回复无关内容。
现在请按照上面的要求开始翻译以下内容为简体中文:(WGN) with a standard deviation, denoted $\sigma$ , to the noise-free latent image x. x serves as a reference throughout the training process, and the noise level $(\sigma)$ remains unspecified. The objective is to reconstruct y from $\mathbf{x}$ . The architecture employed for training the denoiser is illustrated in Figure 1, which relies on the Efficient-UNet framework. Efficient-UNet is composed of several components, including an encoder, a bridge, a decoder, a content enhancer, and transformers. Likewise, the architecture of Efficient-UNet for the disc rim in at or is depicted in Figure 2. The encoder unit is comprised of three consecutive residual blocks with strides one and two (denoted by $S$ in Figure 1) that extract the features from the observed data. The number of filters in the encoder layers is doubled after each down sampling operation (i.e., $S=2$ ). Several studies [41, 18, 7] have shown the effectiveness of residual blocks in deep learning. We use the residual blocks in our auto-encoder structure for denoiser prior modeling. To have large activation maps, we delay the down sampling of the first layer, whose stride is 1. The extracted features by the encoder are then passed through a bridge with $f_{b}$ filters followed by the decoder unit that estimates the denoised input data $\hat{\bf x}$ in the feature domain. The features of each decoder layer are mapped into the image domain by the transformer unit $T_{n}$ where $n$ is the index of the corresponding layer. The transformer unit is a set of $n$ residual blocks followed by a $1\times1\times1$ convolution and a sigmoid activation layer. The number of filters in the transformer layers is halved $n$ times2 and the filter size of $1\times1\times1$ convolution layer is equal to $C$ , which is the number of input channels. Throughout this study, the kernel size and dilation of the convolutional layers are 3 and 1, respectively, unless otherwise noted.
Thus far, the only difference between the Efficient-UNet of the denoiser and that of the disc rim in at or is the filter size of convolution layers, i.e., . It is set as ${96,128,160,192}$ for the denoiser and ${48,64,80,96}$ for the disc rim in at or. The disc rim in at or network needs a lower number of learning parameters compared to the denoiser. This is primarily because the disc rim in at or functions as a classifier, responsible for computing the loss by distinguishing between noise-free and noisy, thereby determining if an instance is classified as noise-free or noisy. Since the disc rim in at or is a classifier, the output of each transformer is mapped into a binary mask by a mapper shown in Figure 2. The mapping layer comprises convolution layers with a filter size of 1 followed by a sigmoid activation layer to map the input to a binary mask. The denoiser also includes an additional component, a content enhancer. This specific unit is strategically designed to retain sparse information, such as edges and textures, which may be minimally affected or remain unaffected by noise. As shown in Figure 1, the content enhancer is a residual block, wherein the first layer extracts features by three different dilation values. Several studies [42, 25] have shown that the structural information, which is mainly edges and textures, exists at different scales. So we consider three convolutions of strides 1, 2, and 4 to extract such features from the input noisy data directly. In the absence of noise, this unit has more activated layers. The content enhancer layer is concatenated by the last layer of the decoder before feeding $T_{1}$ . The denoised data $\hat{\bf x}$ is the output of layer $T_{1}$ , shown by a blue rectangle in Figure 1. It is also worth mentioning that the bias parameter in the proposed Efficient-UNet is deactivated since bias-free networks increase the linearity property by canceling the bias parameter3 [43]. Moreover, when the magnitude of the bias is much larger than that of filters, the model’s general iz ability is limited, so less prone to over fitting [9].
目前,去噪器中的Efficient-UNet与判别器 (discriminator) 的唯一区别在于卷积层的滤波器大小。去噪器的滤波器大小设置为 ${96,128,160,192}$,而判别器的设置为 ${48,64,80,96}$。与去噪器相比,判别器网络需要更少的学习参数。这主要是因为判别器作为分类器,负责通过区分无噪声和有噪声来计算损失,从而判断实例是否被分类为无噪声或有噪声。由于判别器是分类器,每个Transformer的输出会通过图2所示的映射器转换为二值掩码。映射层由滤波器大小为1的卷积层和sigmoid激活层组成,用于将输入映射为二值掩码。
去噪器还包含一个额外的组件——内容增强器 (content enhancer)。该单元专门设计用于保留稀疏信息(如边缘和纹理),这些信息可能受噪声影响较小或完全不受影响。如图1所示,内容增强器是一个残差块,其中第一层通过三种不同的膨胀值提取特征。多项研究[42, 25]表明,主要包含边缘和纹理的结构信息存在于不同尺度中。因此,我们采用步长为1、2和4的三种卷积直接从输入噪声数据中提取这些特征。在无噪声情况下,该单元的激活层更多。内容增强器层与解码器的最后一层拼接后输入 $T_{1}$。去噪后的数据 $\hat{\bf x}$ 是 $T_{1}$ 层的输出,如图1中的蓝色矩形所示。
值得一提的是,所提出的Efficient-UNet中的偏置参数被禁用,因为无偏置网络通过取消偏置参数提高了线性特性[43]。此外,当偏置的幅值远大于滤波器时,模型的泛化能力会受到限制,因此更不容易过拟合[9]。
3.2 Multiscale loss framework
3.2 多尺度损失框架
ADL consists of two auto-encoders: a denoiser $\mathcal{G}$ and a disc rim in at or $\mathcal{D}$ . In a general setting, the parameters of adversarial networks are optimized by minimizing a two-player game in an alternating manner [36]:
ADL由两个自编码器组成:去噪器$\mathcal{G}$和判别器$\mathcal{D}$。在一般设定中,对抗网络的参数通过交替最小化双玩家博弈进行优化[36]:
$$
\begin{array}{r l}{\mathcal{L}{\mathcal{D}}=-\mathbb{E}{\mathbf{x}}{\log\mathcal{D}(\mathbf{x})}-\mathbb{E}{\mathbf{y}}{\log\left(1-\mathcal{D}(\mathcal{G}(\mathbf{y}))\right)},}\ {\mathcal{L}{\mathcal{G}}=-\mathbb{E}_{\mathbf{y}}{\log\mathcal{D}(\mathcal{G}(\mathbf{y}))}.}\end{array}
$$
Denoiser $\mathcal{G}$ aims to estimate a clean image while disc rim in at or $\mathcal{D}$ distinguishes between reference $\mathbf{x}$ and denoised $\mathcal{G}(\mathbf{y})$ instances. Eq. (3) does not maintain textural, global, and local data representation. To this end, we propose novel multiscale loss functions for both the denoiser and the disc rim in at or to replace the ones in Eq 3. We minimize the loss of denoiser from coarse to fine resolution for enforcing the participation of the decoder’s features in the resultant high-resolution denoised image. Likewise, we enforce the disc rim in at or network to discriminate the target and the denoised images from bottom to top. Moving from coarse resolution towards fine one enhances structural features at the corresponding resolution, resulting in rich edge and textural information in the denoised data.
去噪器 $\mathcal{G}$ 旨在估计干净图像,而判别器 $\mathcal{D}$ 则区分参考图像 $\mathbf{x}$ 与去噪结果 $\mathcal{G}(\mathbf{y})$。公式(3) 未能保持纹理、全局和局部数据表征。为此,我们提出了新颖的多尺度损失函数,同时替代去噪器和判别器在公式3中的原有函数。我们通过从粗分辨率到细分辨率最小化去噪器损失,以强制解码器特征参与生成高分辨率去噪图像。同样地,我们要求判别器网络从底层到顶层区分目标图像与去噪图像。从粗分辨率向细分辨率推进能增强对应分辨率下的结构特征,从而使去噪数据包含丰富的边缘和纹理信息。
3.2.1 Denoiser’s loss function
3.2.1 降噪器的损失函数
We define the loss function of the denoiser as a combination of an $\ell_{1}$ loss (denoted by $\mathcal{L}{\ell_{1}}$ ), a novel pyramidal textural loss $\mathcal{L}{p y r}$ , and a novel histogram loss $\mathcal{L}{H i s t}$ that are weighted by $\lambda_{\ell_{1}},\lambda_{p}$ , and $\lambda_{\mathcal{H}}$ , respectively
我们将去噪器的损失函数定义为 $\ell_{1}$ 损失 (记为 $\mathcal{L}{\ell_{1}}$ )、新型金字塔纹理损失 $\mathcal{L}{p y r}$ 和新型直方图损失 $\mathcal{L}{H i s t}$ 的加权组合,其权重分别为 $\lambda_{\ell_{1}}$、$\lambda_{p}$ 和 $\lambda_{\mathcal{H}}$
− $\mathcal{L}{\ell_{1}}$ : The data fidelity is an $\ell_{1}$ -norm between the denoised and reference instances. Compared to the $\ell_{2}$ -norm, the $\ell_{1}$ -norm is more robust against outliers.
- $\mathcal{L}{\ell_{1}}$ : 数据保真度是去噪实例与参考实例之间的 $\ell_{1}$ 范数。与 $\ell_{2}$ 范数相比,$\ell_{1}$ 范数对异常值更具鲁棒性。
$\mathcal{L}{\mathrm{pyr}}$ : The pyramidal textural loss aims at preserving edges and textures in to-be-denoised images. Unlike the conventional edge-preserving regular iz ation terms such as TV and its variants [44, 45] that compute the differential of given noisy images, our goal is to measure the textural difference between to-be-denoised images and their corresponding reference only. Traditional TVs use first-, second-, or higher-order-based derivative operators to filter noisy images. The main drawback of such operators is to boost the pixels with high-level noise so that it may bias the loss towards dominant values. For this reason, the images denoised by TV-like regular is ation terms are often accompanied by smoothness in both textural and non-textural regions. To cope with this problem, we introduce a pyramidal loss function using ATW [25]. ATW is a stationary Wavelet transform that decomposes an image into several levels by a cubic spline filter and then subtracts any two successive layers to obtain fine images with edges and textures. The low-pass filters in ATW alleviate the side effects of noise, enabling us to include texture information of input images in the loss function. Figure 3 briefs ATW. In short, it decomposes an input image into $J$ levels by a cubic spline finite impulse response denoted by $h^{(1)}$ . Unlike the non-stationary multiscale transforms that downscale the images and then apply a filter, ATW upscales the kernel by inserting ${}^{\cdot}2^{j-1}-1^{}$ ’ zeros between each pair of adjacent elements in $h^{(1)}$ , where $j$ denotes the $j$ -th decomposition level. Fine images with texture and edges are derived via subtraction of any two successive filtered images. Further details can be found in [25, 42]. In Eq. $4^{\cdot}\Delta_{j}$ .’ denotes the textural image at the $j$ -th level derived by ATW. $J$ is a positive integer that denotes the number of decomposition levels. Typically, four decomposition levels $\acute{J}=4$ ) have been able to extract the majority of edges and textures laid in a wide range of sigma values [42].
$\mathcal{L}{\mathrm{pyr}}$:金字塔纹理损失旨在保留待去噪图像中的边缘和纹理。与传统基于TV及其变体[44,45]的边缘保留正则化方法不同(这些方法通过计算给定噪声图像的微分实现),我们的目标是仅衡量待去噪图像与其对应参考图像之间的纹理差异。传统TV方法使用一阶、二阶或更高阶微分算子来过滤噪声图像,这类算子的主要缺陷是会放大高噪声像素,导致损失函数偏向主导值。因此,TV类正则项去噪后的图像常在纹理和非纹理区域均出现过度平滑。为解决该问题,我们采用ATW[25]构建金字塔损失函数。ATW是一种平稳小波变换,通过三次样条滤波器将图像分解为多个层级,再通过相邻层差分提取包含边缘纹理的精细图像。ATW中的低通滤波器可缓解噪声干扰,从而在损失函数中有效融入输入图像的纹理信息。图3展示了ATW原理:通过三次样条有限脉冲响应滤波器$h^{(1)}$将输入图像分解为$J$个层级。与非平稳多尺度变换(先降采样再滤波)不同,ATW通过在$h^{(1)}$相邻元素间插入${}^{\cdot}2^{j-1}-1^{}$个零来实现核函数上采样,其中$j$表示第$j$级分解层。纹理边缘的精细图像通过相邻滤波图像的差分获得,详见[25,42]。公式$4^{\cdot}\Delta_{j}$中$\Delta_j$表示ATW第$j$级分解得到的纹理图像,$J$为分解层数正整数。实验表明四层分解$\acute{J}=4$即可提取宽范围sigma值下的大部分边缘纹理[42]。
− $\mathcal{L}_{\mathcal{H}\mathbf{ist}}$ : The histogram loss assures that the histograms of $\mathcal{G}(\mathbf{y})$ and $\mathbf{x}$ are close to each other. This term maintains the global structure of $\mathcal{G}(\mathbf{y})$ with respect to $\mathbf{x}$ since the added edges and texture information (by ATW) may change the overall histogram of the denoised instance. To compute this loss, we first compute the histogram of both $\mathcal{G}(\mathbf{y})$ and $\mathbf{x}$ denoted by $\mathcal{H}$ . We then use a strictly increasing function that computes the loss between $\mathcal{H}\left[\mathcal{G}(\mathbf{y})\right]$ and $\mathcal{H}$ [x]. To this end, we use $\mathrm{logcosh}(p)=\log(\cosh(p))$ that is approximately equal to $\frac{p^{2}}{2}$ for small $p$ and to $\log(p)-\log(2)$ for large $p^{4}$ . Note that we use the histogram loss for preserving the global structure between the denoised image and its reference, and this is different from other histogram-based works like [46, 47]. In [46], a gradient histogram is used for texture preservation, and Delbracio et al. [47] proposed a DNN-based histogram as a fidelity term.
- $\mathcal{L}_{\mathcal{H}\mathbf{ist}}$:直方图损失确保$\mathcal{G}(\mathbf{y})$和$\mathbf{x}$的直方图彼此接近。该损失项通过保持$\mathcal{G}(\mathbf{y})$相对于$\mathbf{x}$的全局结构,因为ATW添加的边缘和纹理信息可能改变去噪实例的整体直方图。计算该损失时,首先计算$\mathcal{G}(\mathbf{y})$和$\mathbf{x}$的直方图$\mathcal{H}$,随后采用严格递增函数计算$\mathcal{H}\left[\mathcal{G}(\mathbf{y})\right]$与$\mathcal{H}$[x]之间的损失。此处使用$\mathrm{logcosh}(p)=\log(\cosh(p))$函数——当$p$较小时近似于$\frac{p^{2}}{2}$,当$p^{4}$较大时近似于$\log(p)-\log(2)$。需注意,该直方图损失用于保持去噪图像与参考图像间的全局结构,这与[46, 47]等基于直方图的研究不同:[46]利用梯度直方图保持纹理,而Delbracio等[47]提出基于DNN的直方图作为保真项。
In Efficient-UNet, features at fine-resolution maps are reconstructed from their coarser ones (Figure 1). Thus, an inefficiency in coarser spatial scales (or, equivalently, higher-level feature maps) may yield poor resultant feature maps. To cope with this problem, we propose a pyramidal version of the loss function defined in Eq. 4 that maintains the consistency between $\mathcal{G}(\mathbf{y})$ and its counterpart $\mathbf{x}$ at each spatial scale. To compute the proposed multiscale loss, we generalize the transformer unit, introduced in Section 3.1, to lower spatial scales (here, two scales $T_{2}$ and $T_{3}$ ) and then get the corresponding denoised image data. We compute the loss function presented in Eq. 4 at every scale and finally take an average of the losses to yield the denoiser loss:
在Efficient-UNet中,精细分辨率特征图是从其更粗糙的对应部分重建的(图1)。因此,在更粗糙的空间尺度(或等效地,更高层次的特征图)上的低效可能会导致生成的特征图质量较差。为了解决这个问题,我们提出了一个金字塔版本的损失函数(如公式4所定义),该函数在每个空间尺度上保持$\mathcal{G}(\mathbf{y})$与其对应$\mathbf{x}$之间的一致性。为了计算所提出的多尺度损失,我们将第3.1节中介绍的transformer单元推广到更低的空间尺度(这里指两个尺度$T_{2}$和$T_{3}$),然后获得相应的去噪图像数据。我们在每个尺度上计算公式4中给出的损失函数,最后取这些损失的平均值来得到去噪器的损失:
$$
\mathcal{L}{\mathcal{G}}=\sum_{s=1}^{3}\left(\lambda_{\ell_{1}}\mathcal{L}{\ell_{1}}^{(s)}+\lambda_{e}\mathcal{L}{e d g e}^{(s)}+\lambda_{\mathcal{H}}\mathcal{L}_{\mathcal{H}i s t}^{(s)}\right),
$$
$$
\mathcal{L}{\mathcal{G}}=\sum_{s=1}^{3}\left(\lambda_{\ell_{1}}\mathcal{L}{\ell_{1}}^{(s)}+\lambda_{e}\mathcal{L}{e d g e}^{(s)}+\lambda_{\mathcal{H}}\mathcal{L}_{\mathcal{H}i s t}^{(s)}\right),
$$
where superscript $s$ denotes the scale of the data pyramid. The total number of scales is set to 3 in this study.
其中上标 $s$ 表示数据金字塔的尺度。本研究中的尺度总数设为3。
3.2.2 Disc rim in at or’s loss function
3.2.2 判别器损失函数
Most disc rim in at or s are based on an encoder that determines whether the input instance is fake or real. Schonfeld et al.[48] have shown that using an U-Net structure for a disc rim in at or could increase the generator’s performance (here, the denoiser). Borrowed a similar concept from [48], we propose the following loss function for the disc rim in at or (see Figure 2):
大多数判别器基于一个编码器来判断输入实例是伪造的还是真实的。Schonfeld等人[48]证明,采用U-Net结构作为判别器可以提升生成器(此处指去噪器)的性能。借鉴[48]的类似思路,我们为判别器提出以下损失函数(见图2):
$$
\mathcal{L}{\mathcal{D}}=\mathcal{L}{\mathcal{D}{b}}+\sum_{s=1}^{3}\mathcal{L}{\mathcal{D}_{d e c}}^{(s)},
$$
$$
\mathcal{L}{\mathcal{D}}=\mathcal{L}{\mathcal{D}{b}}+\sum_{s=1}^{3}\mathcal{L}{\mathcal{D}_{d e c}}^{(s)},
$$
where $\mathcal{L}{\mathcal{D}_{b}}$ is the bridge loss defined as
其中 $\mathcal{L}{\mathcal{D}_{b}}$ 是定义为的桥接损失
Here, subscripts ${m,n,d}$ denote disc rim in at or decision at pixel $(m,n,d)$ .
这里,下标 ${m,n,d}$ 表示像素 $(m,n,d)$ 处的判别器决策。
3.3 Training details
3.3 训练细节
We implemented ADL for both 2D and 3D image data. To show the general iz ability of the denoiser, we trained the 2D model on ImageNet [49], whose data distribution is different from that of biomedical images. The training and the validation sets contain 1,281,168 and 50,000 natural images of size $224\times224$ , respectively. The denoiser model was trained on color and gray-scale images separately. We augmented the data by rotation, $\theta\in{90^{\circ},180^{\circ},270^{\circ}}$ , and flips. We added zero-mean WGN to input images with $\sigma$ randomly selected in the interval [0,55]. The noisy images were not clipped into the interval [0,255], ensuring that the added noise distribution was still WGN. The 3D model was trained on the IXI Dataset5, containing approximately 570 8-bit T1, T2, and PD-weighted MR images acquired at three different hospitals in London: Hammersmith Hospital using a Philips 3T system, Guy’s Hospital using a Philips $1.5\mathrm{T}$ system, and Institute of Psychiatry using a GE 1.5T system. The size of MRI volumes is $256\times256\times n$ , where $n\in[28,150]$ . We randomly cropped the volumes into sub-volumes of $128\times128\times48$ to facilitate the training. we added zero-mean white Gaussian $(\sigma\in[0,55])$ , Rician $(\sigma\in[0,25]$ and $\nu\in[0,15],$ ), and Rayleigh $\prime\sigma\in[0,25],$ ) noise to input MRI volumes. Likewise, in the 2D training, the values of the parameters in the above-mentioned intervals were randomly selected. We used the Adam algorithm [50] as an optimizer with the Reduce LR on Plateau scheduler6. The optimization started with a learning rate of $10^{-4}$ and was reduced (by the Reduce LR on Plateau scheduler) until the PSNR of validation stopped improving. The weights in Eq. 7, i.e. ${\lambda_{\ell_{1}},\lambda_{e},\lambda_{\mathcal{H}}}$ , were set to 1.
我们针对2D和3D图像数据均实现了ADL (Adaptive Denoising Layer)。为验证去噪器的泛化能力,2D模型在ImageNet [49]数据集上训练,该数据分布与生物医学图像不同。训练集和验证集分别包含1,281,168张和50,000张尺寸为$224\times224$的自然图像。去噪模型分别针对彩色和灰度图像进行训练。数据增强采用旋转($\theta\in{90^{\circ},180^{\circ},270^{\circ}}$)和翻转操作。输入图像添加了$\sigma$值在[0,55]区间随机选取的零均值高斯白噪声(WGN),且未将含噪图像截断至[0,255]范围以保证噪声分布仍符合WGN特性。
3D模型在IXI Dataset5上训练,该数据集包含约570幅8位T1、T2和PD加权MR图像,采集自伦敦三家医院:Hammersmith Hospital使用Philips 3T系统,Guy’s Hospital使用Philips $1.5\mathrm{T}$系统,Institute of Psychiatry使用GE 1.5T系统。MRI体数据尺寸为$256\times256\times n$ ($n\in[28,150]$),训练时随机裁剪为$128\times128\times48$的子体积。输入MRI体数据添加了:零均值高斯噪声($\sigma\in[0,55]$)、Rician噪声($\sigma\in[0,25]$且$\nu\in[0,15]$)以及Rayleigh噪声($\sigma\in[0,25]$),参数值均在对应区间随机选取。
采用Adam算法[50]作为优化器,配合Reduce LR on Plateau调度器。初始学习率为$10^{-4}$,当验证集PSNR停止提升时自动降低学习率。公式7中的权重参数${\lambda_{\ell_{1}},\lambda_{e},\lambda_{\mathcal{H}}}$均设为1。
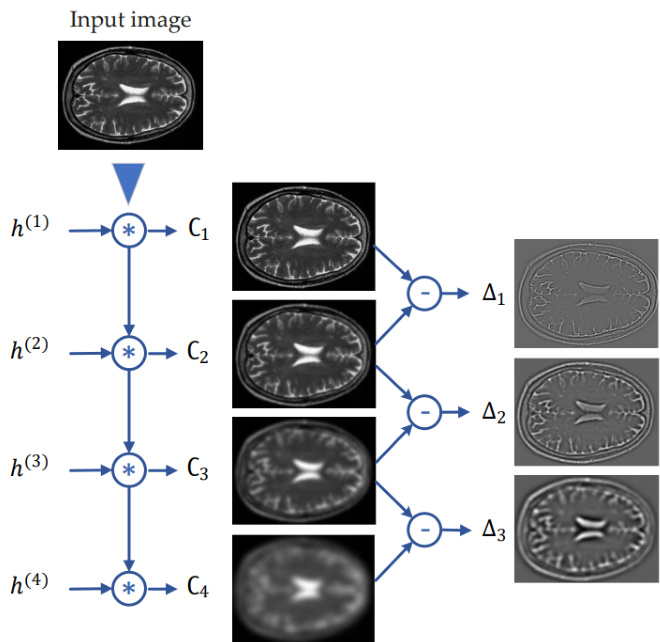
Figure 3: ATW decomposition for image data. Since the 2D kernel $h$ is separable, the ATW decomposition for 3D image data is obtained by convolving three 1D cubic kernels in the $\mathbf{X}$ , y, and $\mathbf{Z}$ directions. ATW is comprised of inherently low-pass filters that attenuate the side effects of noise.
图 3: 图像数据的 ATW 分解。由于二维核 $h$ 是可分离的,因此通过对 $\mathbf{X}$、y 和 $\mathbf{Z}$ 方向上的三个一维立方核进行卷积,即可获得三维图像数据的 ATW 分解。ATW 由固有的低通滤波器组成,可抑制噪声的副作用。
Reproducibility: The reference implementation of ADL is based on TensorFlow. All the experiments were conducted on 4 A-100 GPUs. The implementation and pre-trained models are available at https://github.com/mogvision/ADL. We also pro
