HYPER NETWORK-BASED ADAPTIVE IMAGE RESTORATION
基于超网络的自适应图像恢复
ABSTRACT
摘要
Adaptive image restoration models can restore images with different degradation levels at inference time without the need to retrain the model. We present an approach that is highly accurate and allows a significant reduction in the number of parameters. In contrast to existing methods, our approach can restore images using a single fixed-size model, regardless of the number of degradation levels. On popular datasets, our approach yields state-of-the-art results in terms of size and accuracy for a variety of image restoration tasks, including denoising, deJPEG, and super-resolution.
自适应图像修复模型能够在推理时无需重新训练即可修复不同退化程度的图像。我们提出了一种高精度且能大幅减少参数数量的方法。与现有方法不同,我们的方案仅需使用单一固定尺寸模型,即可处理任意数量的退化程度。在多个主流数据集上,该方法在去噪、去JPEG伪影和超分辨率等多种图像修复任务中,均实现了模型尺寸与精度的最先进水平。
Index Terms— Image Denoising, DeJPEG, super-resolution
索引术语— 图像去噪 (Image Denoising)、DeJPEG、超分辨率 (super-resolution)
1. INTRODUCTION
1. 引言
The common approach in deep learning for image restoration tasks is to train the model in a supervised manner, optimizing the model for only a single degradation level. The exact degradation level of the degraded image is not known a priori, and treating all degradation levels the same lowers restoration quality. Recently, adaptive image restoration methods have gained popularity as an alternative. They enable image- and user-specific adaptation for all degradation levels with a single model without the need for retraining or deploying multiple models. At runtime, the user can adjust the restoration effect in order to generate a variety of output images and select one according to his preferences.
深度学习在图像修复任务中的常见方法是采用监督方式训练模型,仅针对单一退化级别进行优化。由于退化图像的确切退化程度事先未知,对所有退化级别采用相同处理方式会降低修复质量。近年来,自适应图像修复方法作为替代方案受到关注。这类方法通过单一模型即可实现针对所有退化级别的图像与用户自适应性调整,无需重新训练或部署多个模型。在运行时,用户可通过调节修复效果生成多种输出图像,并根据个人偏好进行选择。
Various approaches have been presented for adaptive models. State-of-the-art approaches [1, 2, 3, 4] reduce the needed number of parameters with respect to multiple independent models by training the network to restore two degradation levels that span the desired range and interpolate the weights for any other degradation level within the range. However, to support a wide range of levels it is necessary to use several models or significantly increase the size of the basic model [5].
针对自适应模型已提出多种方法。当前最先进的方法[1, 2, 3, 4]通过训练网络恢复两个涵盖目标范围的退化级别,并对该范围内任意其他退化级别的权重进行插值,从而减少相对于多个独立模型所需的参数量。然而,要支持大范围退化级别,仍需使用多个模型或大幅增加基础模型规模[5]。
In this work, we present an approach that allows a standard single restoration model to achieve very high accuracy across a wide range of degradation levels without having to add any extra parameters. We introduce a hyper network that learns to generate the filter weights of an image restoration network conditionally based on the required restoration level given as an input parameter. As part of the training process, our hyper network is optimized with multiple main networks to simultaneously restore images with a variety of degradation levels. Based on the input degradation level, our hypernetwork generates a single network with the most accurate filter weights at runtime.
在本工作中,我们提出了一种方法,使标准单一恢复模型无需增加额外参数即可在多种退化级别上实现极高精度。我们引入了一个超网络(hyper network),该网络能根据输入的修复级别参数,有条件地生成图像修复网络的滤波器权重。训练过程中,我们的超网络与多个主网络协同优化,可同时处理不同退化程度的图像修复任务。基于输入退化级别,该超网络能在运行时生成具有最精准滤波器权重的单一网络。
Contribution. Our architecture can restore images of different degrees of degradation with $26%-56%$ of the parameters and higher accuracy than existing adaptive image restoration methods.
贡献。我们的架构能以现有自适应图像修复方法26%-56%的参数量,恢复不同程度的退化图像,且准确率更高。
2. PRIOR WORK
2. 已有研究
Recently, there has been a growing interest in constructing networks that can be continuously tuned at inference time. These can broadly be categorized into two categories, models which allow tuning different objectives at inference time and models which allow different restoration levels of the same objective, where our approach falls into the latter category. The typical approach is to train two related networks on different objectives and apply interpolation between their weights. The networks can be either the same or with additional tuning blocks. Dynamic-Net [3] adds specialized blocks directly after the convolution layers, which are optimized during the training for the additional objective. CFSNet [4] used branches, each based on a different objective. AdaFM [1] added modulation filters after each convolution layer. DNI [2] train the same network architecture on different objective and interpolates all the parameters. Son [6] extended the approach of [1] with an FTN module allowing better non-linear interpolation. [7] generates kernels for the super-resolution task. They employ an off-the-shelf SR network [8] as a backbone which is $\times10$ bigger than our network, and their proposed solution is applicable only to the super-resolution task. [9] proposed solving the image restoration task as a multi-task problem. Their network, however, is specialized for restoring only a limited number of degradation levels, each of which must be trained individually. In our approach, the model is trained on a small set of degradation levels and can continuously restore any other level inside and even outside this range.
近来,构建可在推理阶段连续调节的网络架构日益受到关注。这类方法主要分为两类:支持推理时调整不同目标任务的模型,以及支持同一目标任务多级复原的模型(我们的方法属于后者)。典型做法是在不同目标任务上训练两个关联网络后对其权重进行插值,这些网络可采用相同结构或附加调节模块。Dynamic-Net [3] 直接在卷积层后添加专用于新目标的优化模块;CFSNet [4] 采用基于不同目标的分支结构;AdaFM [1] 为每层卷积添加调制滤波器;DNI [2] 对同一架构进行多目标训练后插值全部参数;Son [6] 通过FTN模块扩展了[1]的方法以实现更优非线性插值。[7] 为超分任务生成专用卷积核,其采用现成超分网络[8]作为主干(规模达我们网络的10倍),且方案仅适用于超分任务。[9] 将图像复原视为多任务问题,但其网络仅能复原有限且需单独训练的退化等级。我们的方法只需在少量退化等级上训练,即可连续复原该范围内外任意等级的图像。
Learning to learn, or meta learner, uses meta networks to generate weights for the main network for various tasks [10].
学会学习 (meta learner) 利用元网络为不同任务的主网络生成权重 [10]。
Hyper network, introduced in [11], uses a small network with a reduced number of parameters to generate the weights for a larger target network. It often uses weight sharing across layers, while providing accurate results. [12] presented an image restoration hyper network with a single main network. In our approach, we employ a hyper network to generate the weights of kernels in multiple target networks simultaneously.
超网络 (Hyper network) 在文献[11]中被提出,它使用参数较少的小型网络为更大的目标网络生成权重。该方法通常采用跨层权重共享机制,同时保持结果准确性。[12]提出了一种基于单一主网络的图像复原超网络。在我们的方法中,我们采用超网络同时为多个目标网络中的核生成权重。
3. METHOD
3. 方法
3.1. Formulation
3.1. 公式化
Our model consists of a hyper network $h$ and main restoration networks $n_{i}$ . The weights of our hyper network, $\theta^{h}$ , are learned during the training process and fixed during inference time. The input to hyper network $h$ is a degradation level $c_{i}\in\mathbb{R}$ and the output is $\theta^{n_{i}}$ , the kernels’ weights for the main restoration networks $n_{i}$ , $\theta^{n_{i}}=h(c_{i};\theta^{h})$ . The input for each main network $n_{i}$ is a degraded image $\mathbf{I}^{c_{i}}\in\mathbb{R}^{3\times H\times W}$ with a degradation level $c_{i},H,W$ are the height and width of the image and the output is the restored image with the same dimensions, $n_{i}(\mathbf{I}^{c_{i}};\theta^{n_{i}})$ . The goal is to learn $\theta^{h}$ from $\mathbf{I}^{c_{i}},c_{i}$ so that $h$ can generate the optimal weights for the corresponding restoration network $\theta^{n_{i}}$ in order to restore the degraded image. The optimization problem associated with our model is formulated as:
我们的模型由一个超网络 $h$ 和主修复网络 $n_{i}$ 组成。超网络的权重 $\theta^{h}$ 在训练过程中学习并在推理时固定。超网络 $h$ 的输入是退化级别 $c_{i}\in\mathbb{R}$,输出是主修复网络 $n_{i}$ 的核权重 $\theta^{n_{i}}$,即 $\theta^{n_{i}}=h(c_{i};\theta^{h})$。每个主网络 $n_{i}$ 的输入是退化图像 $\mathbf{I}^{c_{i}}\in\mathbb{R}^{3\times H\times W}$,其中 $c_{i},H,W$ 分别表示图像的退化级别、高度和宽度,输出是相同维度的修复图像 $n_{i}(\mathbf{I}^{c_{i}};\theta^{n_{i}})$。目标是从 $\mathbf{I}^{c_{i}},c_{i}$ 中学习 $\theta^{h}$,使得 $h$ 能为对应的修复网络生成最优权重 $\theta^{n_{i}}$ 以修复退化图像。该模型的优化问题表述为:
$$
\underset{\theta^{h}}{\arg\operatorname*{min}}\sum_{i=1}^{k}\mathbb{E}{\mathbf{I}^{c_{i}},\mathbf{I}}\big[\mathcal{L}\big(n_{i}(\mathbf{I}^{c_{i}};h(c_{i};\theta^{h})),\mathbf{I}\big)\big]
$$
$$
\underset{\theta^{h}}{\arg\operatorname*{min}}\sum_{i=1}^{k}\mathbb{E}{\mathbf{I}^{c_{i}},\mathbf{I}}\big[\mathcal{L}\big(n_{i}(\mathbf{I}^{c_{i}};h(c_{i};\theta^{h})),\mathbf{I}\big)\big]
$$
where $k$ is the number of main networks, $\mathcal{L}:\mathbb{R}^{3\times H\times W}\times$ $\mathbb{R}^{3\times H\times W}\to\mathbb{R}_{+}\cup{0}$ is our restoration loss for each main network. We train our hyper network, $h$ , by simultaneously generating the weights for all the $k$ main networks (and degradation levels), and optimizing them together. We demonstrate that this enables our hyper network to generate optimal weights for all other degradation levels within the continuous range that are not included in the $k$ levels.
其中 $k$ 是主干网络数量,$\mathcal{L}:\mathbb{R}^{3\times H\times W}\times$ $\mathbb{R}^{3\times H\times W}\to\mathbb{R}_{+}\cup{0}$ 是每个主干网络的修复损失函数。我们通过同时为所有 $k$ 个主干网络(及退化等级)生成权重并联合优化的方式训练超网络 $h$ 。实验表明,该方法能使超网络为连续范围内未包含在 $k$ 个等级中的其他退化等级生成最优权重。
3.2. The Network
3.2. 网络
Para me tri z ation of Main Network. The hyper network $h$ consists of $l$ meta blocks, where $l$ is the number of kernels in the main network’s residual blocks. Each meta block is a fully connected layer constructed out of weights and biases, $\mathbf{\bar{w}}^{j},\mathbf{b}^{j}\in\mathbb{R}^{(\dot{C}{o u t}\times\boldsymbol{C}{i n}\times\boldsymbol{K}\times\boldsymbol{K})\times1}$ , where $C_{i n}$ and $C_{o u t}$ are the number of input and output channels, respectively, and $K\times K$ is the kernel’s size. The $j^{t h}$ kernel of main network $n_{i}$ is $\mathbf{k}{i}^{j}$ , of the same dimensions as the meta block. The parameters of the hyper network and each main network are $\mathbf{\bar{\theta}}^{h}={(\mathbf{w}^{j},\mathbf{b}^{j})}{j=1}^{l}$ , $\theta^{n_{i}}={(\mathbf{k}{i}^{j},}_{j=1}^{l}$ .
主网络的参数化。超网络 $h$ 由 $l$ 个元块组成,其中 $l$ 是主网络残差块中核的数量。每个元块是由权重和偏置构建的全连接层,$\mathbf{\bar{w}}^{j},\mathbf{b}^{j}\in\mathbb{R}^{(\dot{C}{o u t}\times\boldsymbol{C}{i n}\times\boldsymbol{K}\times\boldsymbol{K})\times1}$,其中 $C_{i n}$ 和 $C_{o u t}$ 分别是输入和输出通道数,$K\times K$ 是核的大小。主网络 $n_{i}$ 的第 $j^{t h}$ 个核是 $\mathbf{k}{i}^{j}$,其维度与元块相同。超网络和每个主网络的参数分别为 $\mathbf{\bar{\theta}}^{h}={(\mathbf{w}^{j},\mathbf{b}^{j})}{j=1}^{l}$,$\theta^{n_{i}}={(\mathbf{k}{i}^{j},}_{j=1}^{l}$。
We parameter ize the kernels of the main network as a linear combination of our hyper network’s weights and biases with the degradation level as a scaling parameter. Thus, our hyper network $h$ generates the weights of the $j^{t h}$ kernel of main network $n_{i}$ for degradation level $c_{i}$ by:
我们将主网络的内核参数化,作为超网络权重和偏置的线性组合,其中退化水平作为缩放参数。因此,我们的超网络 $h$ 为退化水平 $c_{i}$ 生成主网络 $n_{i}$ 的第 $j^{t h}$ 个内核权重的方式为:
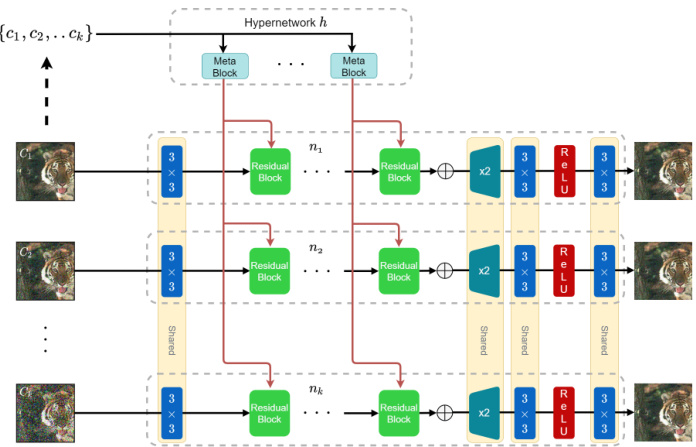
Fig. 1: The training framework. $k$ main networks are generated by the hyper network using the same kernels. Each is fed with a corresponding degraded image, and the losses are summed and back-propagated to the shared and hypernetwork weights. At runtime, a single main network is generated based on a single input parameter.
图 1: 训练框架。通过超网络使用相同内核生成 $k$ 个主网络。每个主网络输入对应的退化图像,损失求和后反向传播至共享权重和超网络权重。运行时根据单一输入参数生成单个主网络。
$$
\mathbf{k}{i}^{j}=c_{i}\mathbf{w}^{j}+\mathbf{b}^{j}.
$$
$$
\mathbf{k}{i}^{j}=c_{i}\mathbf{w}^{j}+\mathbf{b}^{j}.
$$
This allows a highly efficient representation as we only need to store the weights and biases of the hyper network in order to generate the corresponding kernels for each possible restoration network given the degradation level. We demonstrate that, despite the compact representation, our model is highly accurate. Note that, unlike hyper networks [11], our method assigns each meta block to generate weights for a specific main network layer with one common input scalar. Due to the bias term, the output convolutional kernels are not identical throughout the various main networks up to the input scalar.
这使得我们可以实现高效的表示,因为只需存储超网络 (hyper network) 的权重和偏置,就能根据退化级别为每个可能的复原网络生成相应卷积核。我们证明,尽管采用紧凑表示,该模型仍具有高精度。需注意,与超网络 [11] 不同,我们的方法为每个元块分配生成特定主网络层的权重,且共享同一个输入标量。由于偏置项的存在,不同主网络的输出卷积核不会仅因输入标量不同而完全相同。
Training. During training, the hyper network generates multiple main networks, each main network $n_{i}$ is optimized to restore a degraded image with a corresponding degradation level $c_{i}$ . The number of main networks $(k)$ is fixed dur- ing the training process. The main network is a standard image restoration network [13]. It consists of a down sampling layer using convolution with a stride of 2, 16 residual [14] blocks and upsampling layers using pixel shuffle [15] and a skip-connection over the residual blocks. The weights of each main network are the weights of the residual block’s kernels generated by the hyper network (Fig. 1, green background) and the weights of the head and tail of the network which are shared among all the main networks (Fig. 1, yellow background).
训练。在训练过程中,超网络会生成多个主网络,每个主网络 $n_{i}$ 都被优化用于恢复具有相应退化水平 $c_{i}$ 的退化图像。主网络的数量 $(k)$ 在训练过程中是固定的。主网络是一个标准的图像恢复网络 [13],它由一个步长为2的卷积下采样层、16个残差块 [14]、使用像素洗牌 [15] 的上采样层以及跨越残差块的跳跃连接组成。每个主网络的权重由超网络生成的残差块卷积核权重(图1,绿色背景)和所有主网络共享的网络头尾权重(图1,黄色背景)构成。
Each image in the training set $\mathcal{D}={\mathbf{I_{1}},\mathbf{I_{2}},\ldots,\mathbf{I_{n}}}$ is degraded with $k$ degradation levels ${c_{1},c_{2},\ldots,c_{k}}$ and fed into the corresponding main network ${n_{1},n_{2},\dots,n_{k}}$ . Each main network is generated according to the degradation level $c_{i}$ and meta blocks. Our goal is to optimize the overall restoration accuracy under the different degradation levels. Therefore, no degradation level is privileged and our total loss is the unweighted sum of individual $\mathcal{L}_{1}$ losses. Since the aforementioned weight generation operations are completely diffe rent i able, the parameters in our hyper network $h$ are optimized simultaneously following the chain rule. The $L1$ loss is used throughout all the experiments. The training process is illustrated in Fig. 1.
训练集 $\mathcal{D}={\mathbf{I_{1}},\mathbf{I_{2}},\ldots,\mathbf{I_{n}}}$ 中的每张图像均通过 $k$ 个退化等级 ${c_{1},c_{2},\ldots,c_{k}}$ 进行退化处理,并输入对应的主干网络 ${n_{1},n_{2},\dots,n_{k}}$。每个主干网络根据退化等级 $c_{i}$ 和元模块生成。我们的目标是在不同退化等级下优化整体复原精度,因此所有退化等级具有同等重要性,总损失函数为各 $\mathcal{L}_{1}$ 损失的未加权求和。由于前述权重生成操作完全可微分,超网络 $h$ 中的参数通过链式法则同步优化。所有实验均采用 $L1$ 损失函数。训练过程如图 1 所示。
Table 1: Results for DeJPEG artifacts removal task.
表 1: DeJPEG伪影去除任务结果
| Baseline Ours | PSNR | |||||
|---|---|---|---|---|---|---|
| 10 28.82 28.81 |
