Full-scale Representation Guided Network for Retinal Vessel Segmentation

全尺度表征引导的视网膜血管分割网络

Abstract

摘要

The U-Net architecture and its variants have remained state-of-the-art (SOTA) for retinal vessel segmentation over the past decade. In this study, we introduce a Full Scale Guided Network (FSG-Net), where the feature representation network with modernized convolution blocks extracts full-scale information and the guided convolution block refines that information. Attention-guided filter is introduced to the guided convolution block under the interpretation that the filter behaves like the unsharp mask filter. Passing full-scale information to the attention block allows for the generation of improved attention maps, which are then passed to the attention-guided filter, resulting in performance enhancement of the segmentation network. The structure preceding the guided convolution block can be replaced by any U-Net variant, which enhances the scalability of the proposed approach. For a fair comparison, we re-implemented recent studies available in public repositories to evaluate their s cal ability and re prod uci bility. Our experiments also show that the proposed network demonstrates competitive results compared to current SOTA models on various public datasets. Ablation studies demonstrate that the proposed model is competitive with much smaller parameter sizes. Lastly, by applying the proposed model to facial wrinkle segmentation, we confirmed the potential for s cal ability to similar tasks in other domains. Our code is available on https://github. com/ZombaSY/FSG-Net-pytorch.

U-Net架构及其变体在过去十年中一直是视网膜血管分割领域的最先进(SOTA)技术。本研究提出全尺度引导网络(FSG-Net)，其中采用现代化卷积块的特征表示网络提取全尺度信息，引导卷积块则对这些信息进行精炼。在引导卷积块中引入注意力引导滤波器，其原理是该滤波器的行为类似于非锐化掩模滤波器。将全尺度信息传递至注意力块可以生成改进的注意力图，这些注意力图随后被传递至注意力引导滤波器，从而提升分割网络的性能。引导卷积块之前的结构可替换为任何U-Net变体，这增强了所提方法的可扩展性。为公平比较，我们重新实现了公开代码库中的近期研究，以评估其可扩展性和可复现性。实验表明，与当前SOTA模型相比，所提网络在多个公开数据集上展现出具有竞争力的结果。消融研究证明，所提模型在参数量显著减小的情况下仍具竞争力。最后，通过将所提模型应用于面部皱纹分割，我们验证了其向其他领域类似任务扩展的潜力。代码已开源：https://github.com/ZombaSY/FSG-Net-pytorch。

1. Introduction

1. 引言

Convolutional neural networks (CNNs) have seen significant improvements in performance and optimization since the 2010s. The introduction of hardware acceleration using GPUs, ReLU activation function, and residual block [11, 1] has enabled smooth back-propagation in deep neural network architectures. Research in this field has focused on finding a balance between computational efficiency, parameter size, code s cal ability, and fidelity. Depthwise separable convolution [5] and squeeze-and-excitation [12] have been particularly influential in this regard. The inverted residual block [19] achieved higher fidelity with optimized computational efficiency and a smaller parameter size compared to ResNet.

卷积神经网络(CNN)自2010年代以来在性能和优化方面取得了显著进步。通过引入GPU硬件加速、ReLU激活函数和残差块[11,1]，深度神经网络架构实现了平滑的反向传播。该领域的研究重点在于计算效率、参数量、代码可扩展性和保真度之间的平衡。深度可分离卷积[5]和压缩激励模块[12]在这方面产生了特别重要的影响。与ResNet相比，倒残差块[19]以优化的计算效率和更小的参数量实现了更高的保真度。

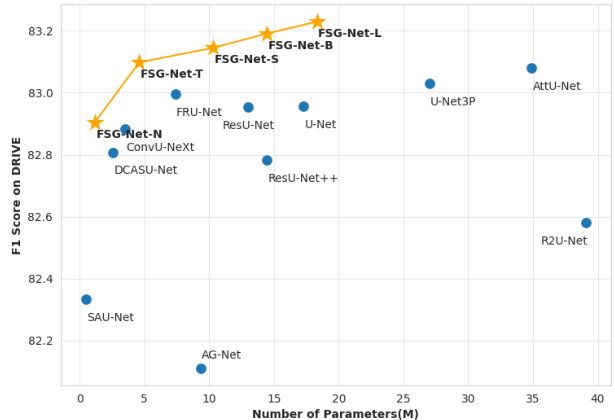
Figure 1. F1 scores of compared networks on the DRIVE dataset, measured against the validation dataset comprising zero-padded images of resolution $608\times608$ . Among the considered architectures, FSG-Net-T achieved a superior F1 score compared to competitive models while maintaining a reduced parameter size relative to its counterparts. Additionally, the FSG-Net-L achieved the highest F1 scores while possessing a median parameter size.

图 1: 在DRIVE数据集上各对比网络的F1分数，评测基于由分辨率$608\times608$的零填充图像组成的验证集。在考虑的架构中，FSG-Net-T在保持较小参数量级的同时，获得了优于竞争模型的F1分数。此外，FSG-Net-L以中等参数量级取得了最高的F1分数。

In the evolutionary history of CNNs, a noteworthy highlight is the dominance of U-Net [18] and its variants [14, 21, 20, 28, 13, 8, 22] as SOTA models in the field of medical image segmentation, especially for retinal vessel segmentation tasks on well-known datasets such as DRIVE, STARE, CHASE_DB1, and HRF. On the contrary, for clinical segmentation tasks on the CVC-clinic and Kvasir-SEG datasets, vision transformer models are employed [23, 2, 3, 9]. The primary distinction between retinal vessels and other clinical datasets lies in the level of feature intricacy required. Vision transform models exhibit some limitations in overcoming their constrained inductive bias. Meanwhile, our experiments underscore the ongoing relevance and effectiveness of attention mechanisms in addressing such challenges.

在CNN的发展历程中，一个值得关注的亮点是U-Net [18]及其变体[14, 21, 20, 28, 13, 8, 22]作为医学图像分割领域的SOTA模型占据主导地位，尤其是在DRIVE、STARE、CHASE_DB1和HRF等知名数据集上的视网膜血管分割任务中。相反，对于CVC-clinic和Kvasir-SEG数据集上的临床分割任务，则采用了视觉Transformer模型[23, 2, 3, 9]。视网膜血管与其他临床数据集的主要区别在于所需特征的复杂程度。视觉Transformer模型在克服其有限的归纳偏置方面表现出一些局限性。同时，我们的实验强调了注意力机制在应对此类挑战时持续的相关性和有效性。

In this study, we aimed to propose a U-Net-based segmentation network that reflects the thin and elongated structural characteristics of retinal vessels, starting with the lower layers and gradually working our way up to the upper layers. Furthermore, based on the understanding that the guided filter [10] can function as a type of edge sharpening filter, the guided filter is located at the decoder after features from the encoder are merged so that full scale features can be used as input to the guided filters at each stage. Our network architecture improves both performance and computational efficiency simultaneously as shown in Figure 1. To ensure a fair comparison of the robustness of competing models, the training environment was maintained consistently.

在本研究中，我们旨在提出一种基于U-Net的分割网络，该网络从底层开始逐步向上层延伸，以反映视网膜血管细长结构的特性。此外，基于引导滤波器 [10] 可作为边缘锐化滤波器使用的认知，我们将引导滤波器置于解码器中编码器特征合并之后，从而使全尺度特征能够作为各阶段引导滤波器的输入。如图1所示，我们的网络架构同时提升了性能和计算效率。为确保公平比较各竞争模型的鲁棒性，训练环境始终保持一致。

The main contributions of this paper are summarized as follows: Firstly, enhancement of feature extraction through the proposal of a novel and efficient convolutional block. Secondly, proposing guided convolution blocks in the decoder, demonstrating performance enhancement as a result and enabling integration with various U-Net segmentation models. Thirdly, a comparison of various SOTA algorithms under a fixed experimental environment.

本文的主要贡献总结如下：首先，通过提出一种新颖高效的卷积块 (convolutional block) 来增强特征提取能力。其次，在解码器中引入引导卷积块 (guided convolution block)，验证了其性能提升效果，并实现了与各类U-Net分割模型的兼容性。第三，在固定实验环境下对比了多种SOTA算法。

2. Method

2. 方法

2.1. Motivation

2.1. 动机

The guided filter was first introduced in [10] for image processing under the assumption that the guidance image and the filtered output have a locally linear relationship. The guided filter is formulated as:

导向滤波最初在[10]中提出，用于图像处理，其假设引导图像与滤波输出具有局部线性关系。导向滤波的公式为：

$$
\hat{I}{i}=a_{k}I_{i}+b_{k},\quad\forall i\in{w}_{k},
$$

$$
\hat{I}{i}=a_{k}I_{i}+b_{k},\quad\forall i\in{w}_{k},
$$

where $a,b$ are linear coefficients, and $w$ is a local window. Here, we show why the guided filter can improve edgelike blood vessel segmentation performance. If we consider overlapping windows, the $i\cdot$ -th pixel has several $a_{k}$ and $b_{k}$ values depending on the window size. Thus, the guided filter output of $I_{i}$ can be averaged as follows:

其中 $a,b$ 是线性系数，$w$ 是局部窗口。这里我们说明引导滤波器为何能提升类边缘血管分割性能。若考虑重叠窗口，第 $i$ 个像素会因窗口尺寸不同而拥有多个 $a_{k}$ 和 $b_{k}$ 值。因此，$I_{i}$ 的引导滤波器输出可按下式求取平均值：

$$
{\hat{I}}{i}={\frac{1}{|w|}}\sum_{k\in w_{i}}\left(a_{k}I_{i}+b_{k}\right),\quad\forall i\in w_{k}.
$$

$$
{\hat{I}}{i}={\frac{1}{|w|}}\sum_{k\in w_{i}}\left(a_{k}I_{i}+b_{k}\right),\quad\forall i\in w_{k}.
$$

Now, (2) can be rewritten to have a more intuitive form. In the original paper of the guided filter [10], $b_{k}$ is computed as:

现在，(2) 可以改写为更直观的形式。在引导滤波的原始论文 [10] 中，$b_{k}$ 的计算方式为：

$$
\begin{array}{r}{b_{k}=\bar{p}{k}-a_{k}\bar{I}_{k},}\end{array}
$$

$$
\begin{array}{r}{b_{k}=\bar{p}{k}-a_{k}\bar{I}_{k},}\end{array}
$$

where $\bar{(\cdot)}{k}$ means average in $w_{k}$ . Then, by putting Eq. (3) into Eq. (2), we have the following formulation:

其中 $\bar{(\cdot)}{k}$ 表示在 $w_{k}$ 上的平均值。然后，将方程(3)代入方程(2)，得到以下表达式：

$$
\hat{I}{i}=\bar{a}{i}(I_{i}-\bar{I}{i})+\tilde{p}_{i},
$$

$$
\hat{I}{i}=\bar{a}{i}(I_{i}-\bar{I}{i})+\tilde{p}_{i},
$$

where $(\tilde{\cdot}){k}$ denotes the average of the average, meaning $\begin{array}{r}{\tilde{p}{i}=\frac{1}{|w|}\sum_{k\in w_{i}}\bar{p}{k}}\end{array}$ . The unsharp mask filtering is defined as $\hat{I}=\alpha\left(I-L(I)\right)+I,$ , where $L(\cdot)$ is a low-pass filter such as the Gaussian filter. Eq. (4) looks like unsharping mask filter, where sharpening mask $\left({{I}{i}}-{{\bar{I}}_{i}}\right)$ from the guidance image is added to the averaged target image. The filter strength is controlled by $\alpha$ .

其中 $(\tilde{\cdot}){k}$ 表示平均值的平均，即 $\begin{array}{r}{\tilde{p}{i}=\frac{1}{|w|}\sum_{k\in w_{i}}\bar{p}{k}}\end{array}$。非锐化掩模滤波定义为 $\hat{I}=\alpha\left(I-L(I)\right)+I,$ ，其中 $L(\cdot)$ 是低通滤波器（如高斯滤波器）。式(4)类似于非锐化掩模滤波器，其将引导图像的锐化掩模 $\left({{I}{i}}-{{\bar{I}}_{i}}\right)$ 叠加到平均后的目标图像上。滤波强度由 $\alpha$ 控制。

In their pioneering work [26], Zhang et al. adopted the guided filter in the segmentation network and suggested incorporating the attention map $M$ into the minimization problem to estimate $a$ and $b$ :

在开创性研究[26]中，Zhang等人将引导滤波器应用于分割网络，并提出将注意力图$M$纳入最小化问题来估计$a$和$b$：

$$
E(a_{k},b_{k})=\sum_{i\in w_{k}}\left(M_{i}^{2}\left(a_{k}I_{d i}+b_{k}-g_{i}\right)^{2}+\mu a_{k}^{2}\right).
$$

$$
E(a_{k},b_{k})=\sum_{i\in w_{k}}\left(M_{i}^{2}\left(a_{k}I_{d i}+b_{k}-g_{i}\right)^{2}+\mu a_{k}^{2}\right).
$$

In Eq. (5), the $I_{d i}$ is the down sampled input feature from encoding parts, and the $g_{i}$ is the gating signal from upward path at the decoding parts. Eq. (5) implies that an improved attention map can lead to better solutions. In the following, we are going to propose a method that can generate an improved attention map with full-scale information.

在式(5)中，$I_{di}$是来自编码部分的下采样输入特征，$g_{i}$是解码部分上采样路径的门控信号。式(5)表明改进的注意力图可以带来更好的解决方案。接下来，我们将提出一种能够生成具有全尺度信息的改进注意力图的方法。

2.2. Network architecture

2.2. 网络架构

As can be seen in Figure 2, the proposed network basically follows the U-Net architecture but has an additional guided convolution block after the feature representation network, unlike usual U-Net based structures. Contrary to the standard U-Net consisting of five stages, we have opted for four stages in FSG-Net based on the assumption that a wider receptive field is less critical for retinal vessel segmentation.

如图 2 所示，该网络基本遵循 U-Net 架构，但与常见的基于 U-Net 的结构不同，它在特征表示网络后增加了一个引导卷积块。不同于标准 U-Net 的五阶段设计，我们基于"视网膜血管分割对宽感受野需求较低"的假设，在 FSG-Net 中采用了四阶段结构。

As described in the left part of FSG-Net, which is called the feature representation network, the input layer of the down-convolution is concatenated with a separate convolution from the other layers. These preserved features are then connected to the up-convolution layer. The deep bottleneck structure of the convolution block, indicated by the thick arrows, delivers a more enhanced feature representation. In the feature representation network, the key area to note is the feature merging section, indicated by the red dashed box. In this feature merging process, features from three paths—the current, upper, and lower stages—are concatenated and passed through a newly designed convolution block before being forwarded to the subsequent stages. This approach allows the integration and transmission of information across all scales.

如FSG-Net左侧部分所示，该模块称为特征表示网络 (feature representation network) ，其下采样卷积层的输入层与其他层的独立卷积相拼接。这些保留的特征随后连接到上采样卷积层。由粗箭头标示的卷积块深度瓶颈结构能提供更强大的特征表示能力。在特征表示网络中，需重点关注红色虚线框标注的特征融合区域。该融合过程将当前阶段、上层阶段和下层阶段的三路特征拼接后，通过新设计的卷积块处理，再传递至后续阶段。这种方法实现了跨所有尺度的信息整合与传递。

In the right part of the model, namely the guided convolution block, compressed features reflecting full scale information are given as the current stage input to the guided residual module (GRM). Up-stage input from the higher stage is given as another input for guided filtering. After GRM, predictions are derived through convolution and activation. For training, a combination of the dice loss and

在模型的右侧部分，即引导卷积块中，反映全尺度信息的压缩特征作为当前阶段输入被提供给引导残差模块(GRM)。来自更高阶段的上游输入作为引导滤波的另一个输入。经过GRM处理后，通过卷积和激活操作得到预测结果。训练时采用dice损失与...

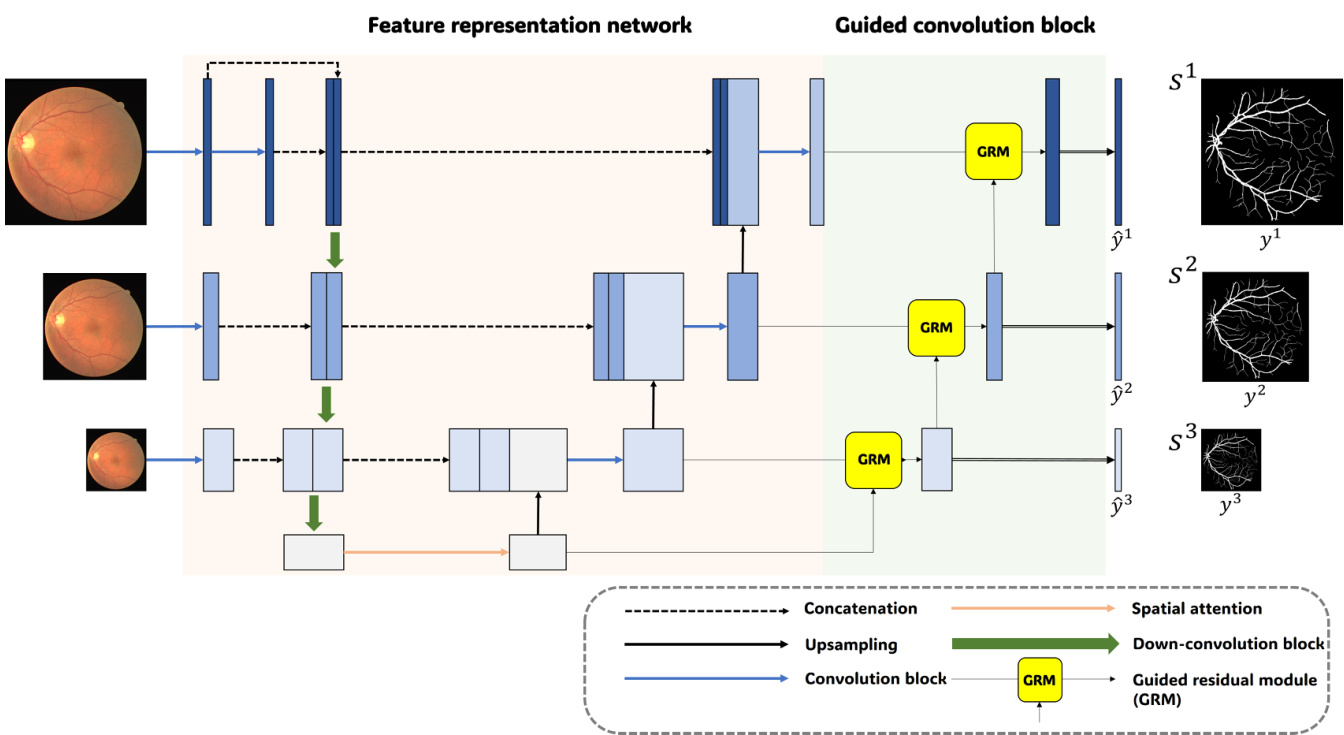
Figure 2. Network architecture of the proposed FSG-Net.

图 2: 提出的FSG-Net网络架构。

BCE loss was employed to improve segmentation performance of the edge-like structures [7]:

采用BCE损失函数提升边缘状结构的分割性能 [7]:

$$
L_{\mathrm{DS}}=\sum_{d=1}^{D}\sum_{i=0}^{S^{d}}\left(y_{i}\log\hat{y}{i}^{d}+(1-y_{i})\log(1-\hat{y}_{i}^{d})\right),
$$

$$
L_{\mathrm{DS}}=\sum_{d=1}^{D}\sum_{i=0}^{S^{d}}\left(y_{i}\log\hat{y}{i}^{d}+(1-y_{i})\log(1-\hat{y}_{i}^{d})\right),
$$

$$
L_{D i c e}=1-\sum_{d=1}^{D}\sum_{i=1}^{S^{d}}\frac{2\left(y_{i}\cdot\hat{y}{i}^{(d)}\right)}{y_{i}+\hat{y}_{i}^{(d)}+\epsilon},
$$

$$
L_{D i c e}=1-\sum_{d=1}^{D}\sum_{i=1}^{S^{d}}\frac{2\left(y_{i}\cdot\hat{y}{i}^{(d)}\right)}{y_{i}+\hat{y}_{i}^{(d)}+\epsilon},
$$

$$
L_{t o t a l}=L_{D S}+L_{D i c e},
$$

$$
L_{t o t a l}=L_{D S}+L_{D i c e},
$$

where $S$ denotes the indices and $\scriptstyle L_{D i c e}$ for Dice loss over pixels. For deep-supervision, $D$ represents the number of layers, the prediction at layer $d$ , and weights for each layer, respectively.

其中 $S$ 表示索引，$\scriptstyle L_{D i c e}$ 为像素级的Dice损失。对于深度监督，$D$ 分别表示层数、第 $d$ 层的预测结果以及各层的权重。

Lastly, we can consider the s cal ability of the proposed architecture. The feature representation network can be replaced by other U-Net variants, enabling integration with the guided convolution block. For instance, we can consider integrating with FR-UNet [15], which proposes alternative methods for utilizing full-scale information.

最后，我们可以考虑所提出架构的可扩展性。特征表示网络可替换为其他U-Net变体，从而与引导卷积块集成。例如，可以考虑与FR-UNet [15] 集成，该研究提出了利用全尺度信息的替代方法。

2.3. Modernized convolution block

2.3. 现代化卷积块

The standard U-Net has a fundamental structure comprising skip connections and double convolution blocks. Recent studies have shown that incorporating different CNN structures can significantly improve the performance of the original model [16, 9]. Inspired by the ConvNeXt [16], we have designed a convolutional block suitable for retinal vessel segmentation.

标准U-Net的基础结构包含跳跃连接和双重卷积块。近期研究表明，融入不同的CNN结构能显著提升原始模型性能 [16, 9]。受ConvNeXt [16] 启发，我们设计了一个适用于视网膜血管分割的卷积块。

Figure 3(a) and (b) represent the depthwise residual block and inverted residual block, respectively. Figure 3(c) shows the proposed convolution block. The structure of the block is an extension of the latest advancements in convolutional block development, characterized by features such as $1\times1$ convolution, inverted bottleneck, and depth-wise convolution. Like other modernized convolution blocks, the proposed block employs a convolution with kernel size 2 and stride 2 in the first stage. By incorporating spatial and dimensional changes within the first block, we enable the design of a deep bottleneck stage in the down-convolution structure. This approach not only increases the information on the feature but also separates it from the bottleneck, allowing for more detailed feature representation. Furthermore, to maintain linearity, we utilize unique ReLU activa- tion between each inverted residual block. For regularization purposes, we employ a learnable gamma parameter and apply a drop block before joining the identity block.

图 3(a) 和 (b) 分别展示了深度残差块 (depthwise residual block) 和倒残差块 (inverted residual block)。图 3(c) 展示了提出的卷积块结构。该模块是对卷积块开发最新进展的扩展，具有 $1\times1$ 卷积、倒置瓶颈 (inverted bottleneck) 和深度卷积 (depth-wise convolution) 等特征。与其他现代化卷积块类似，该模块在第一阶段采用了核大小为2、步长为2的卷积操作。通过在首个模块内融入空间和维度变化，我们实现了下采样卷积结构中深度瓶颈阶段的设计。这种方法不仅增加了特征信息量，还将其与瓶颈区分开，从而实现更精细的特征表示。此外，为保持线性特性，我们在每个倒残差块之间采用了独特的ReLU激活函数。出于正则化目的，我们使用了可学习的gamma参数，并在连接恒等块前应用了drop block技术。

2.4. Guided convolution block

2.4. 引导卷积块

As shown in Figure 2, the guided convolution block consists of GRM to refine the input from the feature representation network and a convolution to output the prediction map. Figure 4 shows the overall process of GRM. The purpose of GRM is to refine the feature from the feature represent ation network at the same stage. In GRM, both the features at the current stage and at the higher stage are used to generate an attention map, and then the attention map is multiplied with the current feature to generate the output, which is described in the right part of Figure 4. Here we can expect an improved attention map $M$ can be estimated to solve Eq. (5) because the input feature from the feature representation network has full scale information. To further enhance the feature refinement, a residual block is introduced after the attention-guided filtering, as shown in the left part of Figure 4. By passing the features through the residual block, a stable map is generated for both the deep supervision and subsequent layers. Moreover, we incorporate a $1\times1$ convolution to preserve the semantic information present in the feature maps.

如图 2 所示，引导卷积块由 GRM (Guided Refinement Module) 和用于输出预测图的卷积层组成。图 4 展示了 GRM 的整体流程。GRM 的作用是对同阶段特征表示网络输出的特征进行细化。在 GRM 中，当前阶段和高阶特征共同生成注意力图，随后该注意力图与当前特征相乘产生输出 (如图 4 右侧所示)。由于来自特征表示网络的输入特征包含完整尺度信息，我们可以预期通过改进的注意力图 $M$ 来求解公式 (5)。为进一步增强特征细化能力，在注意力引导滤波后引入了残差块 (如图 4 左侧所示)。特征经过残差块处理后，会生成同时适用于深度监督和后续层的稳定特征图。此外，我们还采用 $1\times1$ 卷积来保留特征图中的语义信息。

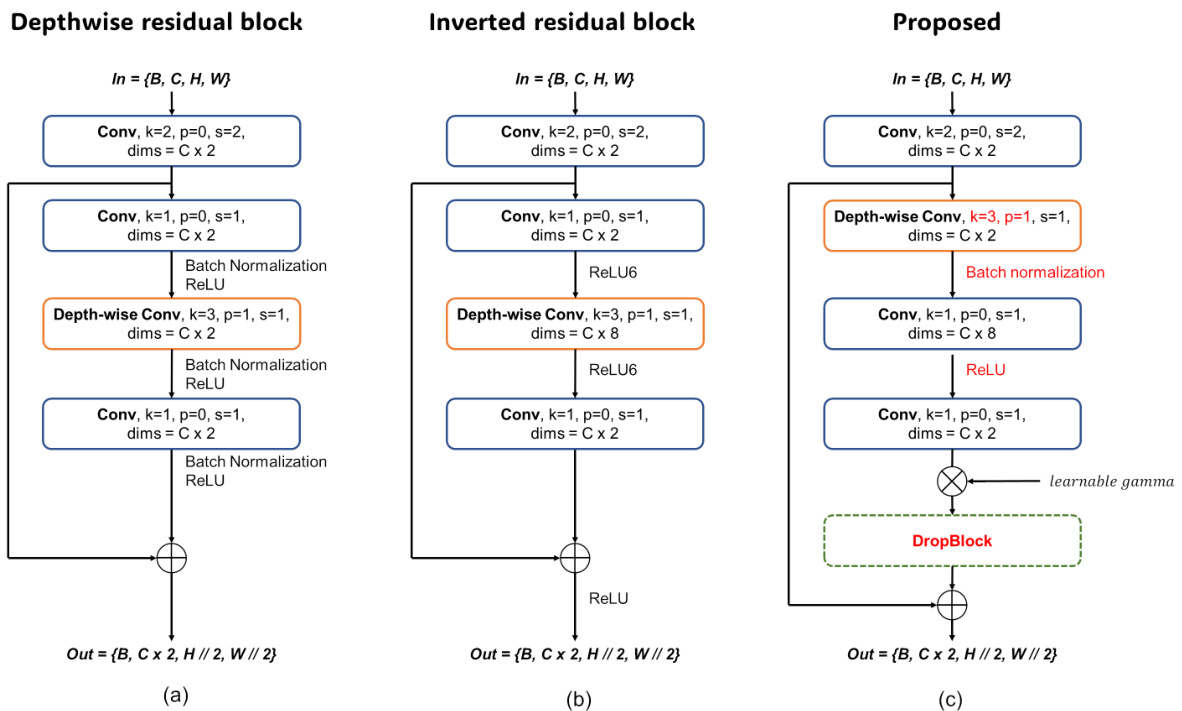
Figure 3. The evolutionary structure from (a): Depthwise residual block, (b): Inverted residual block to (c): The proposed convolutio block.

图 3: 从 (a) 深度残差块, (b) 逆残差块到 (c) 所提出的卷积块的演进结构。

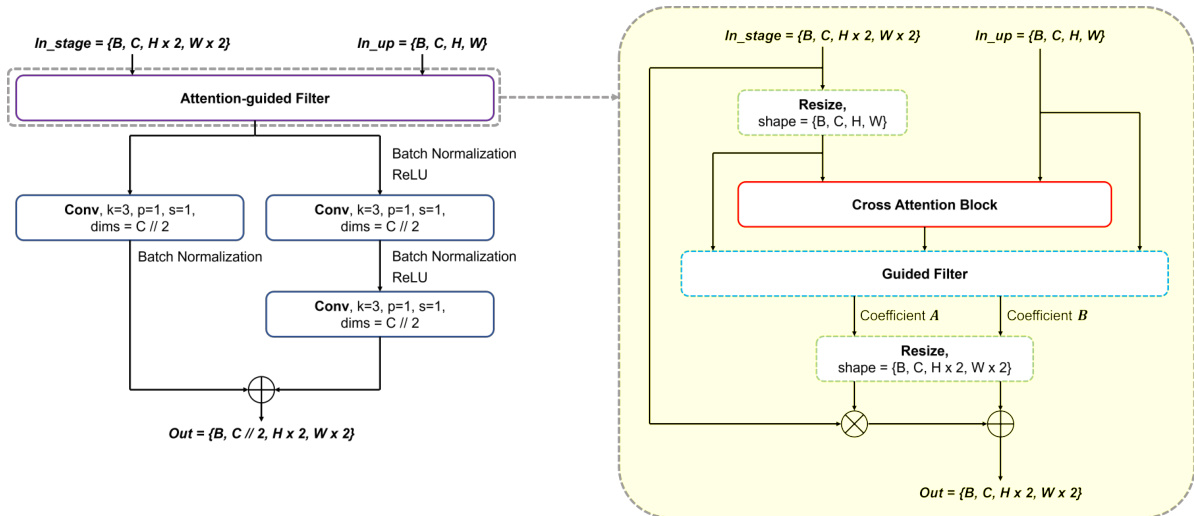
Figure 4. Detailed structure of guided residual module (GRM)

图 4: 引导残差模块 (GRM) 的详细结构

3. Experiments

3. 实验

3.1. Training Techniques

3.1. 训练技术

In retinal vessel segmentation, the performance of studies is often determined by subtle gaps. We believe that these subtle gaps are highly influenced by the choice of hyperparameters and training/inference environment. To address this imbalance, we fixed all hyper parameters for training and inference. We empirically found that Rand Augment [6] with a specific scale did not work well on medical datasets; therefore, we customized it to better suit our datasets. Training techniques include blur, color jitter, horizontal flip, perspective transformation, resize, crop, and CutMix [25].

在视网膜血管分割任务中，研究性能往往由细微差距决定。我们认为这些细微差距很大程度上受超参数选择及训练/推理环境影响。为解决这种不平衡性，我们固定了所有训练和推理阶段的超参数。通过实验发现，特定尺度的Rand Augment [6]在医学数据集上表现不佳，因此我们对其进行了定制化调整以更好地适配我们的数据集。训练技术包括模糊处理、色彩抖动、水平翻转、透视变换、尺寸调整、裁剪以及CutMix [25]。

Table 1. Train settings and hyper-parameters.

表 1: 训练设置与超参数。

超参数	值
基础学习率 (base lr)	1e-3
学习率调度器 (lr scheduler)	余弦退火 (Cosine annealing)
学习率调度器预热轮数 (lr scheduler warm-up epochs)	20
学习率调度器周期轮数 (lrscheduler cycleepochs)	100
学习率调度器最小学习率 (lrscheduleretamin)	1e-5
早停轮数 (earlystopepochs)	400
早停指标 (earlystopmetric)	F1分数 (F1 score)
优化器 (optimizer)	AdamW
优化器动量 (optimizermomentum)	β1,β2=0.9,0.999
权重衰减 (weightdecay)	0.05
损失函数 (criterion)	Dice +BCE
二值化阈值 (binary threshold)	0.5
批量大小 (batch size)	4
随机裁剪 (random crop)	288
随机模糊 (random blur)	概率=0.8
随机抖动 (random jitter)	概率=0.8
随机水平翻转 (random horizontalflip)	概率=0.5
随机透视变换 (random perspective)	概率=0.3
随机缩放 (randomrandomresize)	概率=0.8
CutMix	n=1, 概率=0.8

3.2. Implementation Details

3.2. 实现细节

Our experimental environment comprises an Intel Xeon Gold 5220 processor, a Tesla V100-SXM2-32GB GPU, Pytorch 1.13.1, and CUDA version 11.7. The inference time for FSG-Net-L was approximately $600m s$ for an input size of (608, 608) using a GPU-synchronized flow. To address as much variability as possible, we re-implemented comparison studies and integrated them into a single environment. To ensure experimental fairness, certain hyper parameters, including the framework, loss function, metric, data augmentation, and random seed, were fixed to measure the robustness of the model. Our training settings followed the hyper parameters in Table 1, used for segmentation tasks in ADE20K multiscale learning in ConvNeXt [16].

我们的实验环境包括Intel Xeon Gold 5220处理器、Tesla V100-SXM2-32GB GPU、Pytorch 1.13.1和CUDA 11.7版本。在使用GPU同步流程处理(608, 608)输入尺寸时，FSG-Net-L的推理时间约为$600m s$。为了尽可能覆盖各种变量，我们重新实现了对比研究并将其整合到统一环境中。为确保实验公平性，固定了包括框架、损失函数、评估指标、数据增强和随机种子在内的超参数，以测量模型鲁棒性。训练设置遵循表1中用于ConvNeXt [16]在ADE20K多尺度学习分割任务的超参数。

表1:

To evaluate the compared models under the same conditions, we prioritized the search for an optimized model in our training settings. For example, the learning rate can affect the gradient updating and training time, depending on the model’s parameter size and depth. Training for a predetermined number of epochs can result in diverging weights for heavy models and, conversely, for light models. Therefore, we chose the optimized model using an early stop based on cycles in the learning rate scheduler. To select the optimized model during the training step, we used the highest F1 score [27], with an early stop of 400 epochs. To balance exploitation and exploration in the learning parameters, we stack the batch to have more than two sets of minibatches in one epoch with a learning rate scheduler. The detailed hyper-parameters are described in Table 1. With these experimental settings, the performance of the pure UNet dramatically increased and even surpassed that of some recent studies, as shown in Table 2.

为了在相同条件下评估对比模型，我们优先在训练设置中寻找优化模型。例如，学习率会影响梯度更新和训练时间，具体取决于模型的参数量和深度。对于重型模型，固定训练轮数可能导致权重发散，而轻型模型则相反。因此，我们基于学习率调度器的周期采用早停机制来选择优化模型。在训练阶段，我们使用最高F1分数[27]作为选择标准，并设置400轮早停阈值。为平衡学习参数的利用与探索，我们采用批次堆叠技术使每轮训练包含超过两组小批次，并配合学习率调度器。详细超参数如 表 1 所示。实验表明，通过这些设置，纯UNet性能显著提升，甚至超越部分近期研究成果，如 表 2 所示。

3.3. Datasets

3.3. 数据集

The DRIVE dataset comprised 40 retinal images with a resolution of $565\times584$ pixels, captured as part of a retinopathy screening study in the Netherlands. The STARE dataset comprises 20 retinal fundus images with a resolution of $700\times605$ pixels, and the CHASE_DB1 dataset includes 28 retinal images from schoolchildren with a resolution of $999\times960$ pixels. Both the STARE and CHASE_DB1 datasets were manually annotated by two independent experts. We used the annotation of the first expert, named "Hoover A." in STARE and "1stHO" in CHASE_DB1, for our analysis. The HRF dataset comprises 45 images, equally divided into a 1:1:1 ratio of healthy patients, diabetic ret in o paths, and glaucoma to us patients, with a high resolution of $3504\times2336$ pixels. To measure the performance of the models, it is necessary to divide the data into training and validation sets. As the retinal vessel segmentation dataset was relatively limited, we split the data into a 1:1 ratio of the training and validation sets. The DRIVE dataset was officially divided into training and validation set