U-Net: Convolutional Networks for Biomedical Image Segmentation

U-Net: 用于生物医学图像分割的卷积网络

Abstract. There is large consent that successful training of deep networks requires many thousand annotated training samples. In this paper, we present a network and training strategy that relies on the strong use of data augmentation to use the available annotated samples more efficiently. The architecture consists of a contracting path to capture context and a symmetric expanding path that enables precise localization. We show that such a network can be trained end-to-end from very few images and outperforms the prior best method (a sliding-window convolutional network) on the ISBI challenge for segmentation of neuronal structures in electron microscopic stacks. Using the same network trained on transmitted light microscopy images (phase contrast and DIC) we won the ISBI cell tracking challenge 2015 in these categories by a large margin. Moreover, the network is fast. Segmentation of a $512\mathrm{x512}$ image takes less than a second on a recent GPU. The full implementation (based on Caffe) and the trained networks are available at http://lmb.informatik.uni-freiburg.de/people/ronneber/u-net.

摘要。人们普遍认为，深度网络的训练成功需要成千上万的标注训练样本。本文提出了一种网络及训练策略，通过充分利用数据增强技术来更高效地利用现有标注样本。该架构包含捕捉上下文的收缩路径和实现精确定位的对称扩展路径。我们证明，这种网络可以从极少量图像端到端训练，并在ISBI电子显微镜堆栈神经元结构分割挑战中超越了先前最佳方法（滑动窗口卷积网络）。使用相同网络在透射光学显微镜图像（相差干涉和DIC）上训练后，我们以显著优势赢得了2015年ISBI细胞追踪挑战赛相应类别。此外，该网络速度极快，在现代GPU上分割$512\mathrm{x512}$图像仅需不到一秒。完整实现（基于Caffe）及训练好的网络详见http://lmb.informatik.uni-freiburg.de/people/ronneber/u-net。

1 Introduction

1 引言

In the last two years, deep convolutional networks have outperformed the state of the art in many visual recognition tasks, e.g. [7,3]. While convolutional networks have already existed for a long time [8], their success was limited due to the size of the available training sets and the size of the considered networks. The breakthrough by Krizhevsky et al. [7] was due to supervised training of a large network with 8 layers and millions of parameters on the ImageNet dataset with 1 million training images. Since then, even larger and deeper networks have been trained [12].

近两年，深度卷积网络在许多视觉识别任务中超越了现有最佳技术 [7,3]。尽管卷积网络早已存在 [8]，但由于可用训练集的规模和所考虑网络的规模限制，其成功一直有限。Krizhevsky等人 [7] 的突破在于使用包含100万张训练图像的ImageNet数据集，对有800万参数、8层的大型网络进行了监督训练。此后，更大更深的网络相继被训练出来 [12]。

The typical use of convolutional networks is on classification tasks, where the output to an image is a single class label. However, in many visual tasks, especially in biomedical image processing, the desired output should include localization, i.e., a class label is supposed to be assigned to each pixel. Moreover, thousands of training images are usually beyond reach in biomedical tasks. Hence, Ciresan et al. [1] trained a network in a sliding-window setup to predict the class label of each pixel by providing a local region (patch) around that pixel as input. First, this network can localize. Secondly, the training data in terms of patches is much larger than the number of training images. The resulting network won the EM segmentation challenge at ISBI 2012 by a large margin.

卷积网络的典型应用是分类任务，即对图像输出单个类别标签。然而，在许多视觉任务中，尤其是生物医学图像处理领域，期望的输出应包含定位信息，也就是需要为每个像素分配类别标签。此外，生物医学任务通常难以获取数千张训练图像。为此，Ciresan等人[1]采用滑动窗口方法训练网络，通过输入目标像素周围的局部区域（图像块）来预测每个像素的类别标签。这种设计首先实现了定位功能，其次以图像块为单位的训练数据量远大于原始图像数量。该网络以显著优势赢得了2012年ISBI大会的EM分割挑战赛。

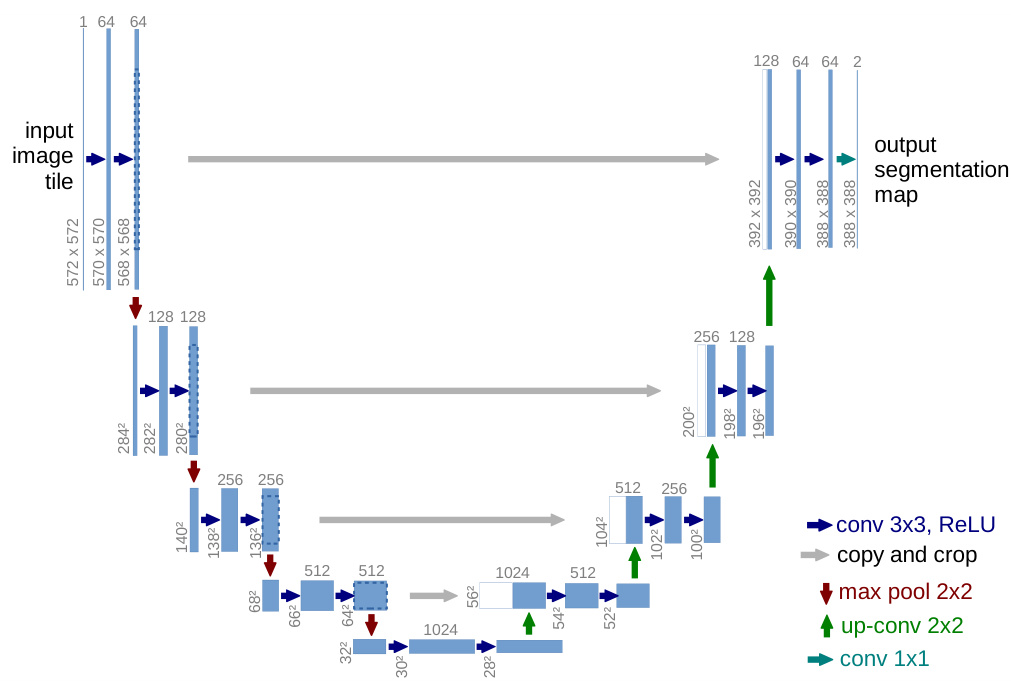
Fig. 1. U-net architecture (example for $32\mathrm{x32}$ pixels in the lowest resolution). Each blue box corresponds to a multi-channel feature map. The number of channels is denoted on top of the box. The x-y-size is provided at the lower left edge of the box. White boxes represent copied feature maps. The arrows denote the different operations.

图 1: U-net架构 (最低分辨率为 $32\mathrm{x32}$ 像素的示例)。每个蓝色框对应一个多通道特征图，通道数标注在框体上方，x-y尺寸标注在框体左下角。白色框表示复制的特征图，箭头表示不同的操作。

Obviously, the strategy in Ciresan et al. [1] has two drawbacks. First, it is quite slow because the network must be run separately for each patch, and there is a lot of redundancy due to overlapping patches. Secondly, there is a trade-off between localization accuracy and the use of context. Larger patches require more max-pooling layers that reduce the localization accuracy, while small patches allow the network to see only little context. More recent approaches [11,4] proposed a classifier output that takes into account the features from multiple layers. Good localization and the use of context are possible at the same time.

显然，Ciresan等人[1]提出的策略存在两个缺点。首先，由于需要对每个图像块单独运行网络且重叠块导致大量冗余计算，该方法速度较慢。其次，定位精度与上下文利用之间存在矛盾：较大的图像块需要更多最大池化层（max-pooling layers）从而降低定位精度，而较小图像块又限制了网络感知上下文的能力。最新研究[11,4]提出通过融合多层特征的分类器输出方案，实现了定位精度与上下文利用的同步优化。

In this paper, we build upon a more elegant architecture, the so-called “fully convolutional network” [9]. We modify and extend this architecture such that it works with very few training images and yields more precise segmentation s; see Figure 1. The main idea in [9] is to supplement a usual contracting network by successive layers, where pooling operators are replaced by upsampling operators. Hence, these layers increase the resolution of the output. In order to localize, high resolution features from the contracting path are combined with the upsampled output. A successive convolution layer can then learn to assemble a more precise output based on this information.

在本文中，我们基于一种更优雅的架构——所谓的"全卷积网络 (fully convolutional network)" [9]进行构建。我们对该架构进行修改和扩展，使其能够在极少量训练图像下工作，并产生更精确的分割结果（参见图1）。文献[9]的核心思想是通过连续层来补充常规的收缩网络，其中池化算子被上采样算子取代。因此，这些层提高了输出的分辨率。为了实现定位，收缩路径中的高分辨率特征与上采样输出相结合。随后，连续的卷积层可以基于这些信息学习组装出更精确的输出。

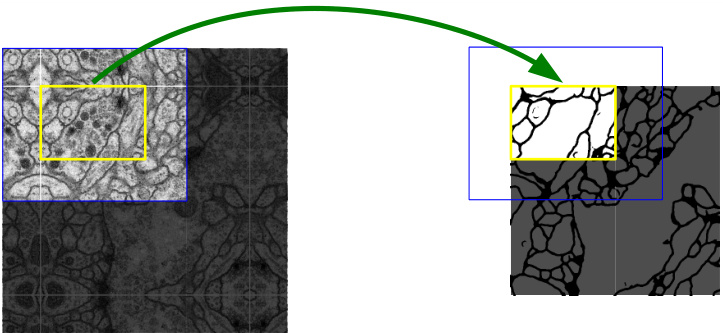
Fig. 2. Overlap-tile strategy for seamless segmentation of arbitrary large images (here segmentation of neuronal structures in EM stacks). Prediction of the segmentation in the yellow area, requires image data within the blue area as input. Missing input data is extrapolated by mirroring

图 2: 用于任意大图像无缝分割的重叠平铺策略 (此处为EM堆栈中神经元结构的分割)。黄色区域的分割预测需要蓝色区域内的图像数据作为输入。缺失的输入数据通过镜像进行外推

One important modification in our architecture is that in the upsampling part we have also a large number of feature channels, which allow the network to propagate context information to higher resolution layers. As a consequence, the expansive path is more or less symmetric to the contracting path, and yields a u-shaped architecture. The network does not have any fully connected layers and only uses the valid part of each convolution, i.e., the segmentation map only contains the pixels, for which the full context is available in the input image. This strategy allows the seamless segmentation of arbitrarily large images by an overlap-tile strategy (see Figure 2). To predict the pixels in the border region of the image, the missing context is extrapolated by mirroring the input image. This tiling strategy is important to apply the network to large images, since otherwise the resolution would be limited by the GPU memory.

我们架构中的一个重要改进是在上采样部分也设置了大量特征通道，这使得网络能将上下文信息传递到更高分辨率的层级。因此，扩展路径与收缩路径基本对称，从而形成了U型架构。该网络不含任何全连接层，仅使用每个卷积的有效部分，即分割图仅包含输入图像中具备完整上下文的像素。这种策略通过重叠切片技术（见图2）实现了任意尺寸图像的无缝分割。为预测图像边缘区域的像素，缺失的上下文通过镜像输入图像进行外推。这种切片策略对处理大尺寸图像至关重要，否则分辨率将受限于GPU显存容量。

As for our tasks there is very little training data available, we use excessive data augmentation by applying elastic deformations to the available training images. This allows the network to learn invariance to such deformations, without the need to see these transformations in the annotated image corpus. This is particularly important in biomedical segmentation, since deformation used to be the most common variation in tissue and realistic deformations can be simulated efficiently. The value of data augmentation for learning invariance has been shown in Do sov it ski y et al. [2] in the scope of unsupervised feature learning.

由于我们的任务可用的训练数据非常少，我们通过对现有训练图像施加弹性变形来进行过度的数据增强。这使得网络能够学习对此类变形的不变性，而无需在标注图像库中看到这些变换。这在生物医学分割中尤为重要，因为变形曾是组织中最常见的变化，且可以高效模拟真实的变形。数据增强对学习不变性的价值已在Dosovitskiy等人[2]的无监督特征学习研究中得到证实。

Another challenge in many cell segmentation tasks is the separation of touching objects of the same class; see Figure 3. To this end, we propose the use of a weighted loss, where the separating background labels between touching cells obtain a large weight in the loss function.

许多细胞分割任务中的另一个挑战是分离同一类别中相互接触的物体；见图3。为此，我们提出使用加权损失函数，其中相互接触细胞之间的分隔背景标签在损失函数中获得较大权重。

The resulting network is applicable to various biomedical segmentation problems. In this paper, we show results on the segmentation of neuronal structures in EM stacks (an ongoing competition started at ISBI 2012), where we outperformed the network of Ciresan et al. [1]. Furthermore, we show results for cell segmentation in light microscopy images from the ISBI cell tracking challenge 2015. Here we won with a large margin on the two most challenging 2D transmitted light datasets.

生成的网络适用于多种生物医学分割问题。本文展示了在EM堆栈中神经元结构分割的结果(始于ISBI 2012的持续竞赛)，我们的表现优于Ciresan等人的网络[1]。此外，我们还展示了2015年ISBI细胞追踪挑战赛中光镜图像细胞分割的结果，在两个最具挑战性的2D透射光数据集上以显著优势获胜。

2 Network Architecture

2 网络架构

The network architecture is illustrated in Figure 1. It consists of a contracting path (left side) and an expansive path (right side). The contracting path follows the typical architecture of a convolutional network. It consists of the repeated application of two 3x3 convolutions (unpadded convolutions), each followed by a rectified linear unit (ReLU) and a 2x2 max pooling operation with stride 2 for down sampling. At each down sampling step we double the number of feature channels. Every step in the expansive path consists of an upsampling of the feature map followed by a 2x2 convolution (“up-convolution”) that halves the number of feature channels, a concatenation with the correspondingly cropped feature map from the contracting path, and two 3x3 convolutions, each followed by a ReLU. The cropping is necessary due to the loss of border pixels in every convolution. At the final layer a 1x1 convolution is used to map each 64- component feature vector to the desired number of classes. In total the network has 23 convolutional layers.

网络架构如图 1 所示。它由收缩路径 (left side) 和扩展路径 (right side) 组成。收缩路径遵循卷积网络的典型架构，包含重复应用的两个 3x3 卷积 (unpadded convolutions)，每个卷积后接一个线性修正单元 (ReLU) 和步长为 2 的 2x2 最大池化操作进行下采样。每次下采样时我们将特征通道数量翻倍。扩展路径中的每个步骤包含对特征图进行上采样，接着是一个 2x2 卷积 ("up-convolution") 将特征通道数减半，与收缩路径中相应裁剪的特征图进行拼接，以及两个 3x3 卷积，每个卷积后接一个 ReLU。由于每次卷积会丢失边缘像素，裁剪是必要的操作。在最后一层使用 1x1 卷积将 64 维特征向量映射到目标类别数。该网络共包含 23 个卷积层。

To allow a seamless tiling of the output segmentation map (see Figure 2), it is important to select the input tile size such that all 2x2 max-pooling operations are applied to a layer with an even x- and y-size.

为了实现输出分割图的无缝平铺 (参见图 2)，必须选择适当的输入图块尺寸，确保所有2x2最大池化操作都在x和y维度为偶数的层上执行。

3 Training

3 训练

The input images and their corresponding segmentation maps are used to train the network with the stochastic gradient descent implementation of Caffe [6]. Due to the unpadded convolutions, the output image is smaller than the input by a constant border width. To minimize the overhead and make maximum use of the GPU memory, we favor large input tiles over a large batch size and hence reduce the batch to a single image. Accordingly we use a high momentum (0.99) such that a large number of the previously seen training samples determine the update in the current optimization step.

输入图像及其对应的分割图用于训练网络，采用Caffe [6] 的随机梯度下降实现。由于未填充卷积操作，输出图像会比输入图像小一个固定的边界宽度。为降低开销并最大化利用GPU内存，我们优先选择大尺寸输入图块而非大批次量，因此将批次大小缩减为单张图像。相应地，我们采用高动量值 (0.99) ，使得当前优化步骤的更新由大量先前见过的训练样本决定。

The energy function is computed by a pixel-wise soft-max over the final feature map combined with the cross entropy loss function. The soft-max is defined as $\begin{array}{r}{p_{k}(\mathbf{x})=\exp(a_{k}(\mathbf{x}))/\left(\sum_{k^{\prime}=1}^{K}\exp(a_{k^{\prime}}(\mathbf{x}))\right)}\end{array}$ where $a_{k}(\mathbf{x})$ denotes the activation in feature channel $k$ at the pixel position $\mathbf{x}\in\varOmega$ with $\varOmega\subset\mathbb{Z}^{2}$ . $K$ is the number of classes and $p_{k}(\mathbf{x})$ is the approximated maximum-function. I.e. $p_{k}(\mathbf{x})\approx1$ for the $k$ that has the maximum activation $a_{k}(\mathbf x)$ and $p_{k}(\mathbf{x})\approx0$ for all other $k$ . The cross entropy then penalizes at each position the deviation of $p_{\ell(\mathbf{x})}(\mathbf{x})$ from 1 using

能量函数通过结合交叉熵损失函数对最终特征图进行逐像素soft-max计算得到。soft-max定义为 $\begin{array}{r}{p_{k}(\mathbf{x})=\exp(a_{k}(\mathbf{x}))/\left(\sum_{k^{\prime}=1}^{K}\exp(a_{k^{\prime}}(\mathbf{x}))\right)}\end{array}$ ，其中 $a_{k}(\mathbf{x})$ 表示在像素位置 $\mathbf{x}\in\varOmega$ ( $\varOmega\subset\mathbb{Z}^{2}$ ) 处特征通道 $k$ 的激活值。 $K$ 是类别总数， $p_{k}(\mathbf{x})$ 为近似最大值函数。即当 $k$ 对应的激活值 $a_{k}(\mathbf x)$ 最大时 $p_{k}(\mathbf{x})\approx1$ ，其余情况 $p_{k}(\mathbf{x})\approx0$ 。交叉熵通过以下方式惩罚每个位置上 $p_{\ell(\mathbf{x})}(\mathbf{x})$ 与1的偏差：

$$
E=\sum_{\mathbf{x}\in\Omega}w(\mathbf{x})\log(p_{\ell(\mathbf{x})}(\mathbf{x}))
$$

$$
E=\sum_{\mathbf{x}\in\Omega}w(\mathbf{x})\log(p_{\ell(\mathbf{x})}(\mathbf{x}))
$$

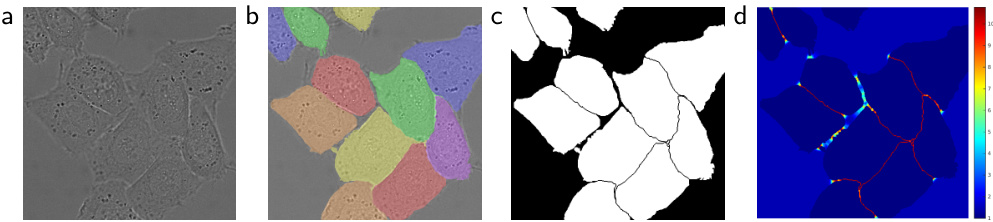
Fig. 3. HeLa cells on glass recorded with DIC (differential interference contrast) microscopy. (a) raw image. (b) overlay with ground truth segmentation. Different colors indicate different instances of the HeLa cells. (c) generated segmentation mask (white: foreground, black: background). (d) map with a pixel-wise loss weight to force the network to learn the border pixels.

图 3: 使用DIC (微分干涉差) 显微镜记录的玻璃上的HeLa细胞。(a) 原始图像。(b) 与真实分割叠加的效果图。不同颜色表示不同的HeLa细胞实例。(c) 生成的分割掩码 (白色: 前景, 黑色: 背景)。(d) 带有逐像素损失权重的映射图, 用于强制网络学习边界像素。

where $\ell:\varOmega\to{1,\dots,K}$ is the true label of each pixel and $w:\varOmega\to\mathbb{R}$ i