On Mixup Training: Improved Calibration and Predictive Uncertainty for Deep Neural Networks

关于Mixup训练：提升深度神经网络的校准性和预测不确定性

Abstract

摘要

Mixup [40] is a recently proposed method for training deep neural networks where additional samples are generated during training by convexly combining random pairs of images and their associated labels. While simple to implement, it has been shown to be a surprisingly effective method of data augmentation for image classification: DNNs trained with mixup show noticeable gains in classification performance on a number of image classification benchmarks. In this work, we discuss a hitherto untouched aspect of mixup training – the calibration and predictive uncertainty of models trained with mixup. We find that DNNs trained with mixup are significantly better calibrated – i.e., the predicted softmax scores are much better indicators of the actual likelihood of a correct prediction – than DNNs trained in the regular fashion. We conduct experiments on a number of image classification architectures and datasets – including large-scale datasets like ImageNet – and find this to be the case. Additionally, we find that merely mixing features does not result in the same calibration benefit and that the label smoothing in mixup training plays a significant role in improving calibration. Finally, we also observe that mixup-trained DNNs are less prone to over-confident predictions on out-of-distribution and random-noise data. We conclude that the typical over confidence seen in neural networks, even on in-distribution data is likely a consequence of training with hard labels, suggesting that mixup be employed for classification tasks where predictive uncertainty is a significant concern.

Mixup [40] 是近期提出的一种深度神经网络训练方法，通过在训练过程中对随机图像对及其关联标签进行凸组合来生成额外样本。尽管实现简单，该方法已被证明在图像分类数据增强中效果显著：采用mixup训练的深度神经网络在多项图像分类基准测试中展现出明显的性能提升。本文探讨了mixup训练中一个尚未被研究的维度——模型校准性与预测不确定性。我们发现，相比常规训练方式，mixup训练的深度神经网络具有显著更优的校准性（即预测softmax分数能更准确反映实际正确预测概率）。我们在多种图像分类架构和数据集（包括ImageNet等大规模数据集）上进行了实验验证。此外，研究发现仅混合特征无法带来相同的校准优势，而mixup训练中的标签平滑对改善校准性起关键作用。最后，我们还观察到mixup训练的深度神经网络对分布外数据和随机噪声数据的过自信预测倾向更低。我们得出结论：神经网络中常见的过度自信现象（即使在分布内数据上）很可能是硬标签训练导致的，建议在预测不确定性至关重要的分类任务中采用mixup方法。

1 Introduction: Over confidence and Uncertainty in Deep Learning

1 引言：深度学习中的过度自信与不确定性

Machine learning algorithms are replacing or expected to increasingly replace humans in decisionmaking pipelines. With the deployment of AI-based systems in high risk fields such as medical diagnosis [26], autonomous vehicle control [21] and the legal sector [1], the major challenges of the upcoming era are thus going to be in issues of uncertainty and trust-worthiness of a classifier. With deep neural networks having established supremacy in many pattern recognition tasks, it is the predictive uncertainty of these types of class if i ers that will be of increasing importance. The DNN must not only be accurate, but also indicate when it is likely to get the wrong answer. This allows the decision-making to be routed as needed to a human or another more accurate, but possibly more expensive, classifier, with the assumption being that the additional cost incurred is greatly surpassed by the consequences of a wrong prediction.

机器学习算法正在取代或预计将越来越多地取代人类在决策流程中的角色。随着基于AI的系统在医疗诊断[26]、自动驾驶控制[21]和法律领域[1]等高风险领域的部署，即将到来的时代主要挑战将集中在分类器的不确定性和可信度问题上。深度神经网络已在许多模式识别任务中确立主导地位，因此这类分类器的预测不确定性将愈发重要。DNN不仅需要保持高准确率，还必须能够指出何时可能给出错误答案。这使得决策可以根据需要转交给人类或其他更准确（但可能成本更高）的分类器，前提是错误预测带来的后果远超额外增加的成本。

For this reason, quantifying the predictive uncertainty for deep neural networks has seen increased attention in recent years [6, 19, 7, 20, 16, 31]. One of the first works to examine the issue of calibration for modern neural networks was [9]; noting that in a well-calibrated classifier, predictive scores should be indicative of the actual likelihood of correctness, the authors in [9] show significant empirical evidence that modern deep neural networks are poorly calibrated, with depth, weight decay and batch normalization all influencing calibration. Modern architectures, it turns out, are prone to over confidence, meaning accuracy is likely to be lower than what is indicated by the predictive score. The top row in Figure 1 illustrates this phenomena: shown are a series of joint density plots of the average winning score and accuracy of a VGG-16 [32] network over the CIFAR-100 [18] validation set, plotted at different epochs. Both the confidence (captured by the winning score) as well as accuracy start out low and gradually increase as the network learns. However, what is interesting – and concerning – is that the confidence always leads accuracy in the later stages of training; accuracy saturates while confidence continues to increase resulting in a very sharply peaked distribution of winning scores and an overconfident model.

因此，近年来量化深度神经网络的预测不确定性受到越来越多的关注[6, 19, 7, 20, 16, 31]。最早研究现代神经网络校准问题的成果之一是[9]；作者指出，在一个良好校准的分类器中，预测分数应当反映实际正确概率，并通过大量实证表明现代深度神经网络存在严重校准不足问题，其中网络深度、权重衰减和批量归一化都会影响校准效果。事实证明，现代架构容易产生过度自信现象，即实际准确率往往低于预测分数所显示的数值。图1顶行展示了这一现象：图中呈现了VGG-16[32]网络在CIFAR-100[18]验证集上平均获胜分数与准确率在不同训练周期下的联合密度图。随着网络学习，置信度（由获胜分数体现）和准确率都从较低水平逐步提升。但值得注意的是（也令人担忧），在训练后期阶段置信度总是领先于准确率；当准确率达到饱和时，置信度仍持续上升，导致获胜分数呈现尖锐峰值分布，最终形成过度自信的模型。

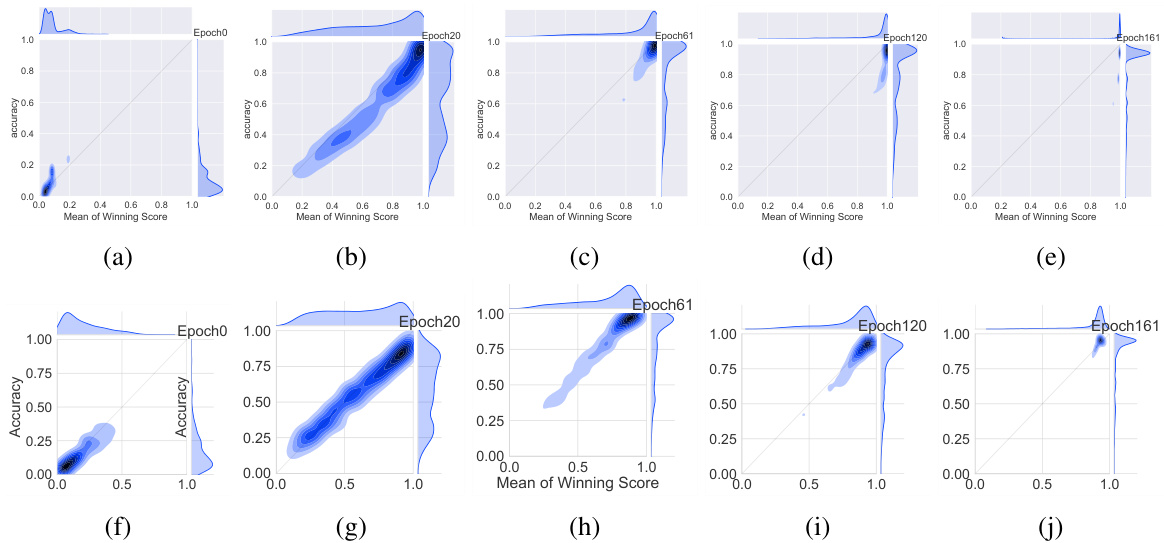
Figure 1: Joint density plots of accuracy vs confidence (captured by the mean of the winning softmax score) on the CIFAR-100 validation set at different training epochs for the VGG-16 deep neural network. Top Row: In regular training, the DNN moves from under-confidence, at the beginning of training, to over confidence at the end. A well-calibrated classifier would have most of the density lying on the $x=y$ gray line. Bottom Row: Training with mixup on the same architecture and dataset. At corresponding epochs, the network is much better calibrated.

图 1: VGG-16深度神经网络在CIFAR-100验证集上不同训练周期时准确率与置信度(通过获胜softmax分数的均值捕获)的联合密度图。上排: 常规训练中，DNN从训练初期的欠置信状态逐渐过渡到训练结束时的过置信状态。理想校准的分类器应使大部分密度分布在$x=y$灰色线上。下排: 同一架构和数据集上使用mixup训练的结果。在对应训练周期，网络显示出更好的校准性。

While tempering over confidence in neural networks using alternatives to the final softmax layer has been studied before [25], here we investigate the effect of entropy of the training labels on calibration. Most modern DNNs, when trained for classification in a supervised learning setting, are trained using one-hot encoded labels that have all the probability mass in one class; the training labels are thus zero-entropy signals that admit no uncertainty about the input. The DNN is thus, in some sense, trained to become overconfident. Hence a worthwhile line of exploration is whether principled approaches to label smoothing can somehow temper over confidence. Label smoothing and related work has been explored before [33, 30]. In this work, we carry out an exploration along these lines by investigating the effect of the recently proposed mixup [40] method of training deep neural networks. In mixup, additional synthetic samples are generated during training by convexly combining random pairs of images and, importantly, their labels as well. While simple to implement, it has shown to be a surprisingly effective method of data augmentation: DNNs trained with mixup show noticeable gains in classification performance on a number of image classification benchmarks. However neither the original work nor any subsequent extensions to mixup [36, 10, 23] have explored the effect of mixup on predictive uncertainty and DNN calibration; this is precisely what we address in this paper.

虽然此前已有研究探讨通过替代最终softmax层来调节神经网络过度自信的问题[25]，但本文重点研究了训练标签熵值对模型校准的影响。在监督学习的分类任务中，大多数现代深度神经网络(DNN)使用独热编码标签进行训练，这类标签将所有概率质量集中于单一类别，因此训练标签是零熵信号，不包含任何输入不确定性。从某种意义上说，这导致DNN被训练得过于自信。因此值得探索的是：基于原则的标签平滑方法能否有效抑制这种过度自信。标签平滑及相关工作已有先例研究[33, 30]。本文通过研究近期提出的mixup[40]深度神经网络训练方法，沿着这一方向展开探索。mixup通过在训练期间对随机图像对及其标签进行凸组合来生成合成样本，这种简单实现的方法被证明是异常有效的数据增强技术：采用mixup训练的DNN在多项图像分类基准测试中均显示出显著性能提升。然而无论是原始研究还是后续mixup扩展工作[36, 10, 23]，都未探讨mixup对预测不确定性和DNN校准的影响，这正是本文要解决的核心问题。

Our findings are as follows: mixup trained DNNs are significantly better calibrated – i.e the predicted softmax scores are much better indicators of the actual likelihood of a correct prediction – than DNNs trained without mixup (see Figure 1 bottom row for an example). We also observe that merely mixing features does not result in the same calibration benefit and that the label smoothing in mixup training plays a significant role in improving calibration. Further, we also observe that mixup-trained DNNs are less prone to over-confident predictions on out-of-distribution and random-noise data. We note here that in this work we do not consider the calibration and uncertainty over adversarial ly perturbed inputs; we leave that for future exploration.

我们的发现如下：使用 mixup 训练的深度神经网络 (DNN) 比未使用 mixup 训练的模型具有显著更好的校准性——即预测的 softmax 分数能更准确地反映正确预测的实际可能性 (示例见图 1 底行)。我们还观察到，仅混合特征不会带来相同的校准优势，而 mixup 训练中的标签平滑对改善校准性起到了重要作用。此外，mixup 训练的 DNN 对分布外数据和随机噪声数据的预测也表现出更低的过度自信倾向。需要说明的是，本研究未考虑对抗性扰动输入下的校准性和不确定性，该方向留待未来探索。

The rest of the paper is organized as follows: Section 2 provides a brief overview of the mixup training process; Section 3 discusses calibration metrics, experimental setup and mixup’s calibration benefits for image data with additional results on natural language data described in Section 4; in Section 5, we explore in more detail the effect of mixup-based label smoothing on calibration, and further discuss the effect of training time on calibration in Section 6; in Section 7 we show additional evidence for the benefit of mixup training on predictive uncertainty when dealing with out-of-distribution data. Further discussions and conclusions are in Section 8.

本文其余部分的结构安排如下：第2节简要概述混合训练(mixup)过程；第3节讨论校准指标、实验设置及mixup对图像数据的校准优势，第4节补充说明其在自然语言数据上的实验结果；第5节深入探讨基于mixup的标签平滑对校准的影响；第6节进一步分析训练时长对校准的作用；第7节展示mixup训练在处理分布外数据时对预测不确定性的改善证据。第8节包含进一步讨论与结论。

2 An Overview of Mixup Training

2 Mixup训练概述

Mixup training [40] is based on the principle of Vicinal Risk Minimization 3: the classifier is trained not only on the training data, but also in the vicinity of each training sample. The vicinal points are generated according to the following simple rule introduced in [40]:

Mixup训练 [40] 基于邻域风险最小化 3 原则：分类器不仅要在训练数据上训练，还要在每个训练样本的邻域内进行训练。邻域点根据 [40] 中提出的以下简单规则生成：

where $x_{i}$ and $x_{j}$ are two randomly sampled input points, and $y_{i}$ and $y_{j}$ are their associated one-hot encoded labels. This has the effect of the empirical Dirac delta distribution

其中 $x_{i}$ 和 $x_{j}$ 是两个随机采样的输入点，$y_{i}$ 和 $y_{j}$ 是它们关联的独热编码标签。这会产生经验狄拉克δ分布的效果。

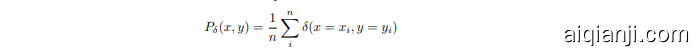
centered at $(x_{i},y_{i})$ being replaced with the empirical vicinal distribution

以 $(x_{i},y_{i})$ 为中心的经验邻域分布替换

where $\nu$ is a vicinity distribution that gives the probability of finding the virtual feature-target pair $(\Tilde{x},\Tilde{y})$ in the vicinity of the original pair $(x_{i},y_{i})$ . The vicinal samples $(\Tilde{x},\Tilde{y})$ are generated as above, and during training minimization is performed on the empirical vicinal risk using the vicinal dataset Dy := {(,gi)}1:

其中 $\nu$ 是一个邻域分布，表示在原始特征-目标对 $(x_{i},y_{i})$ 附近找到虚拟特征-目标对 $(\Tilde{x},\Tilde{y})$ 的概率。邻域样本 $(\Tilde{x},\Tilde{y})$ 按上述方式生成，训练时在邻域数据集 Dy := {(,gi)}1: 上对经验邻域风险进行最小化。

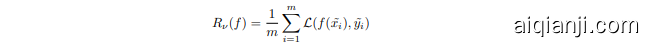
where $L$ is the standard cross-entropy loss, but calculated on the soft-labels $\tilde{y_{i}}$ instead of hard labels. Training this way not only augments the feature set $\tilde{X}$ , but the induced set of soft-labels also encourages the strength of the classification regions to vary linearly betweens samples. The experiments in [40] and related work in [15, 36, 10] show noticeable performance gains in various image classification tasks. The linear interpol at or $\lambda\in[0,1]$ that determines the mixing ratio is drawn from a symmetric Beta distribution, $B e t a(\alpha,\alpha)$ at each training iteration, where $\alpha$ is the hyperparameter that controls the strength of the interpolation between pairs of images and the associated smoothing of the training labels. $\alpha=0$ recovers the base case corresponding to zero-entropy training labels (one-hot encodings, in which case the resulting image is either just $x_{i}$ or $x_{j}$ ), while a high value of $\alpha$ ends up in always averaging the inputs and labels. The authors in [40] remark that relatively smaller values of $\alpha\in[0.1,0.4]$ gave the best performing results for classification, while high values of $\alpha$ resulted in significant under-fitting. In this work, we also look at the effect of $\alpha$ on calibration performance.

其中 $L$ 是标准交叉熵损失，但基于软标签 $\tilde{y_{i}}$ 而非硬标签计算。这种训练方式不仅扩充了特征集 $\tilde{X}$，其诱导的软标签集还能促使分类区域的强度在样本间线性变化。[40]中的实验及[15,36,10]的相关研究表明，该方法在多种图像分类任务中均取得显著性能提升。线性插值系数 $\lambda\in[0,1]$ 控制混合比例，每次训练迭代时从对称Beta分布 $Beta(\alpha,\alpha)$ 中采样，其中 $\alpha$ 是控制图像对间插值强度及训练标签平滑程度的超参数。当 $\alpha=0$ 时对应零熵训练标签的基准情况（独热编码，此时生成图像仅为 $x_{i}$ 或 $x_{j}$），而高 $\alpha$ 值会导致始终对输入和标签取平均。[40]作者指出，相对较小的 $\alpha\in[0.1,0.4]$ 在分类任务中表现最佳，而高 $\alpha$ 值会导致严重欠拟合。本文还研究了 $\alpha$ 对校准性能的影响。

3 Experiments

3 实验

We perform numerous experiments to analyze the effect of mixup training on the calibration of the resulting trained class if i ers on both image and natural language data. We experiment with various deep architectures and standard datasets, including large-scale training with ImageNet. In all the experiments in this paper, we only apply mixup to pairs of images as done in [40]. The mixup functionality was implemented using the mixup authors’ code available at [39].

我们进行了大量实验，以分析混合训练 (mixup training) 对图像和自然语言数据上最终训练分类器校准效果的影响。我们采用多种深度架构和标准数据集进行实验，包括使用ImageNet进行大规模训练。本文所有实验中，我们仅如[40]所述对图像对应用混合方法。混合功能通过[39]提供的原作者代码实现。

3.1Setup

3.1 设置

For the small-scale image experiments, we use the following datasets in our experiments: STL-10 [4], CIFAR-10 and CIFAR-100 [18] and Fashion-MNIST [37]. For STL-10, we use the VGG-16 [32] network. CIFAR-10 and CIFAR-100 experiments were carried out on VGG-16 as well as ResNet34 [12] models. For Fashion-MNIST, we used a ResNet-18 [12] model. For all experiments, we use batch normalization, weight decay of $5\times10^{-4}$ and trained the network using SGD with Nesterov momentum, training for 200 epochs with an initial learning rate of 0.1 halved at 2 at 60,120 and 160 epochs. Unless otherwise noted, calibration results are reported for the best performing epoch on the validation set.

在小规模图像实验中，我们使用了以下数据集：STL-10 [4]、CIFAR-10、CIFAR-100 [18] 和 Fashion-MNIST [37]。对于 STL-10，我们采用 VGG-16 [32] 网络。CIFAR-10 和 CIFAR-100 实验在 VGG-16 及 ResNet34 [12] 模型上进行。Fashion-MNIST 实验使用了 ResNet-18 [12] 模型。所有实验均采用批归一化 (batch normalization)、权重衰减系数为 $5\times10^{-4}$，并使用带动量的 SGD (Nesterov momentum) 进行训练，共训练 200 个周期 (epoch)，初始学习率为 0.1 并在第 60、120 和 160 周期时减半。除非特别说明，校准结果均基于验证集上表现最佳的周期进行报告。

3.2 Calibration Metrics

3.2 校准指标

We measure the calibration of the network as follows (and as described in [9]): predictions are grouped into $M$ interval bins of equal size. Let $B_{m}$ be the set of samples whose prediction scores (the winning softmax score) fall into bin $m$ . The accuracy and confidence of $B_{m}$ are defined as

我们按照以下方式(以及[9]中所述)测量网络的校准度：将预测结果分成$M$个等宽区间。设$B_{m}$为预测得分(即最大softmax得分)落在第$m$个区间的样本集合。$B_{m}$的准确率和置信度定义为

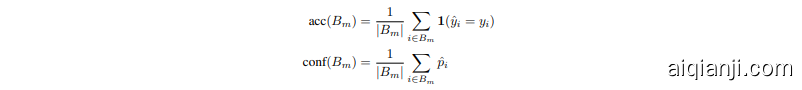
where $\hat{p}_{i}$ is the confidence (winning score) of sample $i$ . The Expected Calibration Error (ECE) is then defined as:

其中 $\hat{p}_{i}$ 是样本 $i$ 的置信度(获胜分数)。预期校准误差(ECE)定义为:

In high-risk applications, confident but wrong predictions can be especially harmful; thus we also define an additional calibration metric – the Over confidence Error (OE) – as follows

在高风险应用中，自信但错误的预测可能尤其有害；因此我们还定义了一个额外的校准指标——过度自信误差 (Over confidence Error, OE)，如下所示

3.3 Comparison Methods

3.3 对比方法

Since mixup produces smoothed labels over mixtures of inputs, we compare the calibration performance of mixup to two other label smoothing techniques:

由于 mixup 会在输入混合上生成平滑标签，我们将其校准性能与另外两种标签平滑技术进行比较：

• ϵ−label smoothing described in [33], where the one-hot encoded training signal is smoothed by distributing an $\epsilon$ mass over the other (i.e., non ground-truth) classes, and • entropy-regularized loss (ERL) described in [30] that discourages the neural network from being over-confident by penalizing low-entropy distributions.

• [33] 中描述的 ϵ-标签平滑 (ϵ-label smoothing)，其中通过将 $\epsilon$ 质量分布到其他（即非真实标签）类别来平滑 one-hot 编码的训练信号，
• [30] 中描述的熵正则化损失 (entropy-regularized loss, ERL)，通过惩罚低熵分布来抑制神经网络的过度自信。

Our baseline comparison (no mixup) is regular training where no label smoothing or mixing of features is applied. We also note that in this section we do not compare against the temperature scaling method described in [9], which is a post-training calibration method and will generally produce well-calibrated scores. Here we would like to see the effect of label smoothing while training; experiments with temperature scaling are reported in Section 7.

我们的基线对比(无混合)是常规训练，不应用标签平滑或特征混合。我们还需指出，本节未与[9]中描述的温度缩放方法进行比较，这是一种训练后校准方法，通常能生成校准良好的分数。此处我们想观察训练过程中标签平滑的效果；温度缩放实验将在第7节报告。

3.4 Results

3.4 结果

Results on the various datasets and architectures are shown in Figure 2. While the performance gains in validation accuracy are generally consistent with the results reported in [40], here we focus on the effect of mixup on network calibration. The top row shows a calibration scatter plot for STL-10 and CIFAR-100, highlighting the effect of mixup training. In a well calibrated model, where the confidence matches the accuracy most of the points will be on $x=y$ line. We see that in the base case, both for STL-10 and CIFAR-100, most of the points tend to lie in the overconfident region. The mixup case is much better calibrated, noticeably in the high-confidence regions. The bar plots in the middle row provide results for accuracy and calibration for various combinations of datasets and architectures against comparison methods. We report the calibration error for the best performing model (in terms of validation accuracy). For label smoothing, an $\epsilon\in[0.05,0.1]$ performed best while for ERL, the best-performing confidence penalty hyper-parameter was 0.1. The trends in the comparison are clear: label smoothing either via $\epsilon$ -smoothing, ERL or mixup generally provides a calibration advantage and tempers over confidence, with the latter generally performing the best in comparison to other methods. We also show the effect on ECE as we vary the hyper parameter $\alpha$ of the mixing parameter distribution. For very low values of $\alpha$ , the behavior is similar to the base case (as expected), but ECE also noticeably worsens for higher values of $\alpha$ due to the model being under-confident. Indeed, mixup models can be under-confident if $\alpha$ is large which is related to manifold intrusion [10]: for large $\alpha$ , a mixed-up sample is more likely to lie away from the original manifold and thus be affected by manifold intrusion, where a mixed sample collides with a real sample on the data manifold, but is given a soft label that is different from the label of the real example. Over confidence alone decreases monotonically as we increase $\alpha$ as shown in Figure 2i. We also show the accuracy of mixup models at various levels of calibration determined by $\alpha$ . As can be seen, a well-tuned $\alpha$ can result in a better-calibrated model with very little loss in performance. Our classification results here are consistent with those reported in [40] where the best performing $\alpha$ was in the [0.1, .0.4] range.

不同数据集和架构下的结果如图2所示。虽然验证准确率的提升效果与[40]报告的结果基本一致，但本文主要关注mixup对网络校准的影响。首行展示了STL-10和CIFAR-100的校准散点图，突出mixup训练的效果。在理想校准模型中，当置信度匹配准确率时，多数数据点应落在$x=y$直线上。可见在基准情况下（STL-10和CIFAR-100），多数数据点倾向于位于过度自信区域。而经过mixup处理的模型校准效果显著改善，尤其在高置信度区域表现突出。

中间行的柱状图展示了不同数据集与架构组合下，各对比方法在准确率和校准指标上的表现。我们报告了最佳验证准确率模型对应的校准误差。标签平滑(Label Smoothing)方法中，$\epsilon\in[0.05,0.1]$区间表现最优；而ERL方法的最佳置信惩罚超参数为0.1。对比趋势清晰可见：无论是通过$\epsilon$-平滑、ERL还是mixup实现的标签平滑，普遍具有校准优势并能抑制过度自信，其中mixup方法相较其他方法表现最佳。

我们还展示了混合参数分布超参数$\alpha$对ECE指标的影响规律。当$\alpha$取值极低时，其表现与基准情况相似（符合预期），但随着$\alpha$增大，由于模型变得信心不足，ECE指标明显恶化。实际上，当$\alpha$过大时，mixup模型可能出现信心不足现象，这与流形入侵(manifold intrusion)[10]有关：$\alpha$值越大，混合样本越可能偏离原始数据流形，从而受到流形入侵影响——即混合样本与真实样本在数据流形上发生碰撞，却被赋予不同于真实样本的软标签。如图2i所示，随着$\alpha$增大，过度自信现象呈现单调递减趋势。

我们还统计了mixup模型在不同$\alpha$值校准水平下的准确率。结果表明，经过适当调参的$\alpha$可以在几乎不影响性能的前提下实现更优的校准效果。本文分类结果与[40]的研究结论一致，其中最佳$\alpha$值位于[0.1,0.4]区间。

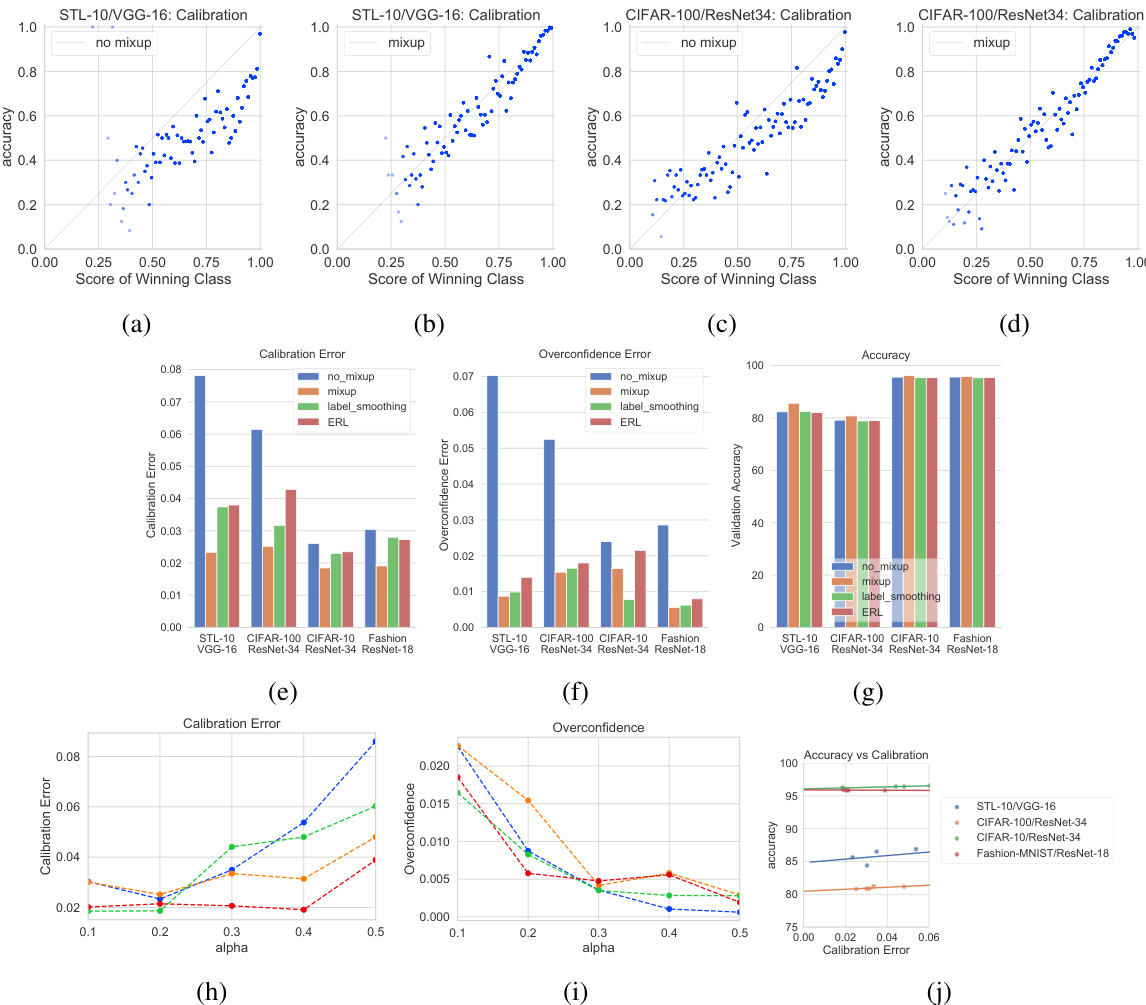
Figure 2: Calibration results for mixup and baseline (no mixup) on various image datasets and architectures. Top Row: Scatter plots for accuracy and confidence for STL-10(a,b) and CIFAR100(c,d). The mixup case is much better calibrated with the points lying closer to the $x=y$ line, while in the baseline, points tend to lie in the overconfident region. Middle Row: Mixup versus comparison methods where label smoothing is the $\epsilon$ -label smoothing method and ERL is the entropy regularized loss. Bottom Row: Expected calibration error (e) and over confidence error (f) on various architectures. Experiments suggest best ECE is achieved for $\alpha$ in the [0.2,0.4] (h), while over confidence error decreases monotonically with $\alpha$ due to under-fitting (i). Accuracy behavior for differently calibrated models is shown in (j).

图 2: 在不同图像数据集和架构上mixup与基线(无mixup)的校准结果。首行: STL-10(a,b)和CIFAR100(c,d)的准确率与置信度散点图。mixup案例的校准效果更好，点更接近$x=y$线，而基线中的点倾向于位于过度自信区域。中行: mixup与对比方法(标签平滑为$\epsilon$-标签平滑方法，ERL为熵正则化损失)的比较。末行: 不同架构上的预期校准误差(e)和过度自信误差(f)。实验表明，当$\alpha$在[0.2,0.4]区间时能获得最佳ECE(h)，而由于欠拟合(i)，过度自信误差随$\alpha$单调递减。不同校准模型的准确率表现如(j)所示。

3.4.1 Large-scale Experiments on ImageNet

3.4.1 ImageNet上的大规模实验

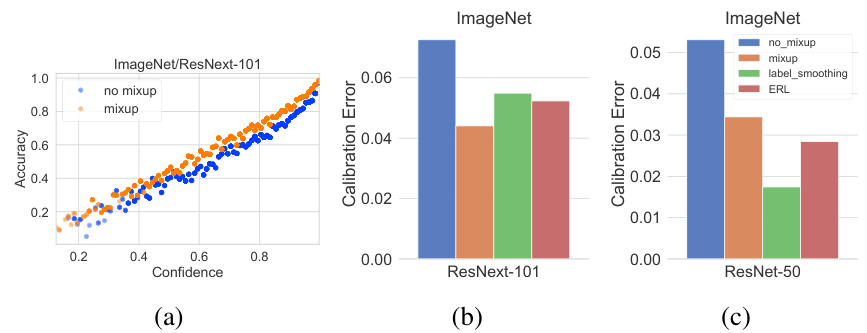
Figure 3: Calibration on ImageNet for ResNet architectures

图 3: ImageNet 上 ResNet 架构的校准情况

Here we report the results of calibration metrics resulting from mixup training on the 1000-class version of the ImageNet [5] data comprising of over 1.2 million images. One of the advantages of mixup and its implementation is that it adds very little overhead to the training time, and thus can be easily applied to large scale datasets like ImageNet. We perform distributed parallel training using the synchronous version of stochastic gradient descent. We use the learning-rate schedule described in [8] on a 32-GPU cluster and train till $93%$ accuracy is reached over the top-5 predictions. We test on two modern state-of-the-art arch ic ture s: ResNet-50 [12] and ResNext-101 (32x4d) [38]. The results are shown in Figure 3. The scatter-plot showing calibration for ResNext-101 architecture suggests that mixup training provides noticeable benefits even in the large-data scenario, where the models should be less prone to over-fitting the one-hot labels. On the deeper ResNext-101, mixup provides better calibration than the label smoothing models, though this same effect was not visible for the ResNet-50 model. However, both calibration error and over confidence show noticeable improvements using label smoothing over the baseline. The mixup model did however achieve a consistently higher classification performance of $\approx0.4$ percent over the other methods.

我们报告了在包含120多万张图像的1000类ImageNet [5]数据上采用mixup训练得到的校准指标结果。mixup方法及其实现的一个优势是几乎不会增加训练时间开销，因此能轻松应用于ImageNet等大规模数据集。我们使用同步随机梯度下降进行分布式并行训练，在32-GPU集群上采用[8]所述的学习率调度策略，训练至top-5预测准确率达到93%。测试选用两种现代最先进架构：ResNet-50 [12]和ResNext-101 (32x4d) [38]，结果如图3所示。ResNext-101架构的散点图显示，即使在大数据场景下（模型应不易过拟合one-hot标签），mixup训练仍能带来显著优势。在更深的ResNext-101上，mixup比标签平滑模型具有更好的校准效果，但这一现象未出现在ResNet-50模型中。不过与基线相比，标签平滑方法在校准误差和过度自信指标上均有明显改善。值得注意的是，mixup模型始终比其他方法获得约0.4%的分类性能提升。

4 Experiments on Natural Language Data

4 自然语言数据实验

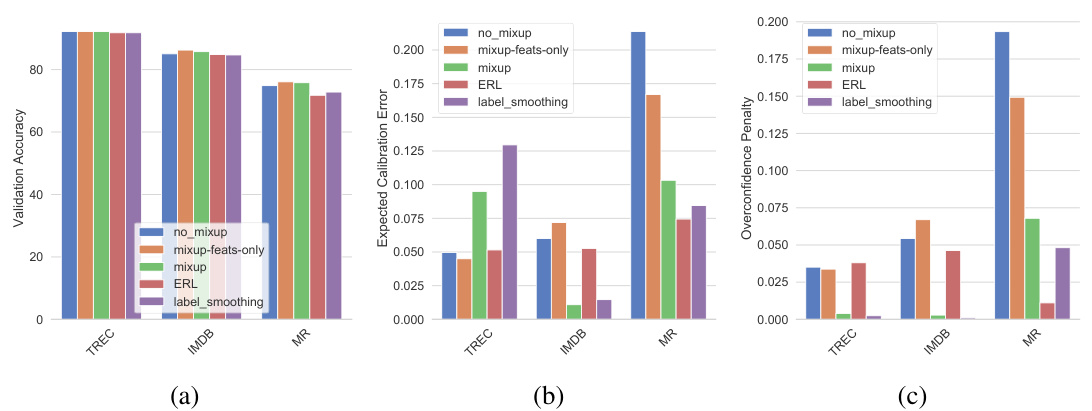
Figure 4: Accuracy, calibration and over confidence on various NLP datasets

图 4: 不同NLP数据集上的准确率、校准性和过度自信程度

While mixup was originally suggested as a method to mostly improve performance on image classification tasks, here we explore the effect of mixup training in the natural language processing (NLP) domain. A straight-forward mixing of inputs (as in pixel-mixing in images) will generally produce nonsense input since the semantics are unclear. To avoid this, we modify the mixup strategy to perform mixup on the embeddings layer rather than directly on the input documents. We note that this approach is similar to the recent work described in [11] that utilizes mixup for improving sentence classification which is among the few works, besides ours, studying the effects of mixup in the NLP domain. For our experiments, we employ mixup on NLP data for text classification using the MR [28], TREC [22] and IMDB [24] datasets.We train a CNN for sentence classification (Sentence-level CNN) [17], where we initialize all the words with pre-trained GloVe [29] embeddings, which are modified while training on each dataset. For the remaining parameters, we use the values suggested in [17]. We refrain from training the most recent NLP models [14, 2, 41] since our aim here is not to show state-of-art classification performance on these datasets, but to study the effect on calibration. We show these results in Figure 4 where it is evident that mixup provides noticeable gains for all datasets, both in terms of calibration and over confidence. We leave further exploration of principled strategies for mixup for NLP as future work.

虽然mixup最初是作为主要提升图像分类任务性能的方法提出的，但本文探讨了其在自然语言处理(NLP)领域应用的效果。直接对输入进行混合（如图像中的像素混合）通常会产生语义不明的无效输入。为避免这一问题，我们改进mixup策略，在嵌入层而非原始文档上实施混合。值得注意的是，该方法与[11]中利用mixup改进句子分类的研究思路相似——除了我们的工作外，这是少数探索mixup在NLP领域影响的文献之一。

实验中，我们采用MR [28]、TREC [22]和IMDB [24]数据集，在文本分类任务上应用mixup策略。我们训练了一个句子级CNN模型[17]，所有单词均使用预训练的GloVe [29]嵌入进行初始化，并在各数据集训练过程中动态调整。其余参数设置遵循[17]的建议。由于本研究目标并非展示当前最优分类性能，而是探究校准效果，因此未采用最新NLP模型[14, 2, 41]进行训练。

图4结果显示：mixup在所有数据集上都显著提升了校准效果并降低了过度自信现象。关于NLP领域mixup原理性策略的深入探索将作为未来研究方向。

5 Effect of Soft Labels on Calibration

5 软标签对校准的影响

So far we have seen that mixup consistently leads to better calibrated networks compared to the base case, in addition to improving classification performance as has been observed in a number of works [36, 10, 23]. This behavior is not surprising given that mixup is a form of data augmentation: in mixup training, due to random sampling of both images as well as the mixing parameter $\lambda$ , the probability that the learner sees the same image twice is small. This has a strong regularizing effect in terms of preventing memorization and over-fitting, even for high-capacity neural networks. Indeed, unlike regular training, the training loss in the mixup case is always significantly higher than the base case as observed by the mixup authors [40]. Because of the significant amount of data augmentation resulting from the random combination in mixup, from the perspective of statistical learning theory, the improved calibration of a mixup classifier can be viewed as the classifier learning the true posteriors $P(Y|X)$ in the infinite data limit [35]. However this leads to the following question: if the improved calibration is essentially an effect of data augmentation, does simply combining the images without combining the labels provide the same calibration benefit?

截至目前，我们已观察到与基准情况相比，mixup不仅能提升分类性能（如多项研究[36, 10, 23]所述），还能持续改善网络校准度。考虑到mixup是一种数据增强形式，这一现象并不令人意外：在mixup训练中，由于图像和混合参数$\lambda$的随机采样，学习器两次看到相同图像的概率极低。即使对于高容量神经网络，这种机制也能通过防止记忆和过拟合产生强大的正则化效果。事实上，mixup作者[40]指出，与常规训练不同，mixup场景下的训练损失始终显著高于基准情况。从统计学习理论视角看，mixup中随机组合带来的大量数据增强，使得改进后的mixup分类器校准度可视为分类器在无限数据极限下学习真实后验概率$P(Y|X)$的结果[35]。但由此引出一个问题：若改进校准本质是数据增强的效果，那么仅组合图像而不组合标签是否也能带来相同的校准优势？

We perform a series of experiments on various image datasets and architectures to explore this question. Results from the earlier sections show that existing label smoothing techniques that increase the entropy of the training signal do provide better calibration without exploiting any data augmentation effects and thus we expect to see this effect in the mixup case as well. In the latter case, the entropies of the training labels are determined by the $\alpha$ parameter of the $B e t a(\alpha,\alpha)$ distribution from which the mixing parameter is sampled. The distribution of training entropies for a few cases of $\alpha$ are shown in Figure 5. The base-case is equivalent to $\alpha=0$ (not shown) where the entropy distribution is a point-mass at 0.

我们在多个图像数据集和架构上进行了一系列实验来探讨这个问题。前文结果表明，现有通过增加训练信号熵值的标签平滑技术确实能提供更好的校准效果，且无需利用任何数据增强效应，因此我们预期在mixup情况下也能观察到类似效果。在后一种情况中，训练标签的熵值由采样混合参数时使用的$B e t a(\alpha,\alpha)$分布的$\alpha$参数决定。图5展示了不同$\alpha$值对应的训练熵值分布情况。基线情况相当于$\alpha=0$（未显示），此时熵值分布为0处的点质量分布。

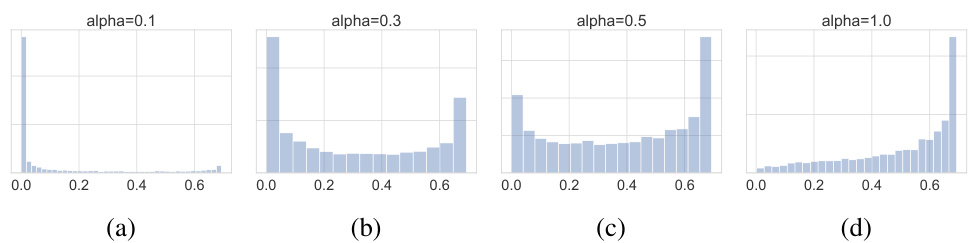
Figure 5: Entropy distribution of training labels as a function of the $\alpha$ parameter of the $B e t a(\alpha,\alpha)$ distribution from which the mixing parameter is sampled.

图 5: 训练标签的熵分布随 $B e t a(\alpha,\alpha)$ 分布参数 $\alpha$ 变化的函数关系，其中混合参数采样自该分布。

To tease out the effect of full mixup versus only mixing features, we convexly combine images as before, but the resulting image assumes the hard label of the nearer class; this provides data augmentation without the label smoothing effect. Results on a number of benchmarks and architectures are shown in Figure 6. The results are clear: merely mixing features does not provide the calibration benefit seen in the full-mixup case suggesting that the point-mass distributions in hard-coded labels are contributing factors to over confidence. As in label smoothing and entropy regular iz ation, having (or enforcing via a loss penalty) a non-zero mass in more than one class prevents the largest pre-softmax logit from becoming much larger than the others tempering over confidence and leading to improved calibration.

为了区分完全混合(mixup)与仅混合特征的效果，我们像之前那样对图像进行凸组合，但生成的图像采用较近类别的硬标签；这种方法实现了数据增强，同时避免了标签平滑效应。多个基准测试和架构的结果如图6所示。结果很明确：仅混合特征并不能带来完全混合情况下的校准优势，这表明硬编码标签中的点质量分布是导致过度自信的因素之一。与标签平滑和熵正则化类似，在多个类别中拥有(或通过损失惩罚强制实施)非零质量，可以防止最大的softmax前logit值远大于其他值，从而抑制过度自信并改善校准效果。

In addition to feature and label mixing, a recent extension to mixup [36] also proposes convexly combining the representations in the hidden layer of the network; we report the calibration effects of this approach in the supplementary material.

除了特征和标签混合外，mixup [36] 的最新扩展还提出了在网络隐藏层中对表示进行凸组合的方法；我们在补充材料中报告了该方法的校准效果。

![](https://miner.umaxing.com/miner/v2/analysis/pdf_img?as_attachment=False&user_id=931&pdf=bc9ff44bdcecdc35580c01b3062714