Exploring the Limit of Outcome Reward for Learning Mathematical Reasoning

探索结果奖励在数学推理学习中的极限

1Shanghai AI Laboratory 2Shanghai Jiao Tong University 3MMLab, The Chinese University of Hong Kong 4HKGAI under InnoHK {lvchengqi,gao song yang,guyuzhe,zhang wen wei,chenkai}@pjlab.org.cn

1上海人工智能实验室 2上海交通大学 3香港中文大学MMLab 4InnoHK旗下HKGAI {lvchengqi,gao song yang,guyuzhe,zhang wen wei,chenkai}@pjlab.org.cn

Abstract

摘要

Reasoning abilities, especially those for solving complex math problems, are crucial components of general intelligence. Recent advances by proprietary companies, such as o-series models of OpenAI, have made remarkable progress on reasoning tasks. However, the complete technical details remain unrevealed, and the techniques that are believed certainly to be adopted are only reinforcement learning (RL) and the long chain of thoughts. This paper proposes a new RL framework, termed OREAL, to pursue the performance limit that can be achieved through Outcome REwArd-based reinforcement Learning for mathematical reasoning tasks, where only binary outcome rewards are easily accessible. We theoretically prove that behavior cloning on positive trajectories from best-of-N (BoN) sampling is sufficient to learn the KL-regularized optimal policy in binary feedback environments. This formulation further implies that the rewards of negative samples should be further reshaped to ensure the gradient consistency between positive and negative samples. To alleviate the long-existing difficulties brought by sparse rewards in RL, which are even exacerbated by the partial correctness of the long chain of thought for reasoning tasks, we further apply a token-level reward model to sample important tokens in reasoning trajectories for learning. With OREAL, for the first time, a 7B model can obtain 94.0 pass $@1$ accuracy on MATH-500 through RL, being on par with 32B models. OREAL-32B also surpasses previous 32B models trained by distillation with $95.0,\mathrm{pass}@1$ accuracy on MATH-500. Our investigation also indicates the importance of initial policy models and training queries for RL. Code, models, and data will be released to benefit future research .

推理能力，尤其是解决复杂数学问题的能力，是通用人工智能的关键组成部分。最近，像 OpenAI 的 o-series 模型这样的专有公司取得了显著的进展。然而，完整的技术细节仍未公开，而被认为肯定采用的技术只有强化学习 (RL) 和长链思维。本文提出了一种新的 RL 框架，称为 OREAL，旨在通过基于结果奖励的强化学习 (Outcome REwArd-based Reinforcement Learning) 来追求数学推理任务的性能极限，其中只有二元结果奖励是容易获得的。我们从理论上证明，在二元反馈环境中，通过对最佳 N 采样 (Best-of-N sampling) 的正向轨迹进行行为克隆，足以学习到 KL 正则化的最优策略。这一公式进一步表明，负样本的奖励应进一步重塑，以确保正负样本之间的梯度一致性。为了缓解 RL 中因稀疏奖励带来的长期困难（这一困难在长链思维的部分正确性下进一步加剧），我们进一步应用了 Token 级奖励模型来采样推理轨迹中的重要 Token 以进行学习。通过 OREAL，一个 7B 模型首次能够在 MATH-500 上通过 RL 获得 94.0 的 pass@1 准确率，与 32B 模型相当。OREAL-32B 也超越了之前通过蒸馏训练的 32B 模型，在 MATH-500 上达到了 95.0 的 pass@1 准确率。我们的研究还表明了初始策略模型和训练查询对 RL 的重要性。代码、模型和数据将被发布，以造福未来的研究。

1 Introduction

1 引言

Solving complex problems with reasoning capability forms one of the cornerstones of human cognition - a cognitive ability that artificial general intelligence must ultimately master [1, 2]. Among various problem domains, the mathematical problem emerges as a particularly compelling experimental paradigm for AI research [3–6], owing to its relatively well-defined structure and availability of precise binary correctness feedback based on the verifiable final answers.

解决复杂问题的推理能力构成了人类认知的基石之一——这也是通用人工智能最终必须掌握的认知能力 [1, 2]。在众多问题领域中，数学问题由于其相对清晰的结构和基于可验证最终答案的精确二元反馈，成为了AI研究中特别引人注目的实验范式 [3–6]。

Recent advances in large language models (LLMs) have achieved remarkable progress in mathematical reasoning by the chain-of-thought technics [7–9], in which the LLMs are elicited to produce a series of intermediate reasoning steps before providing the final answers to the problem. However, as most of the capable models (e.g., the o-series models by OpenAI [10]) are developed by proprietary companies, there is no clear pathway to develop state-of-the-art reasoning models. Some recent work shows that distillation [11, 12] is sufficient to obtain high performance given the accessibility to existing best or near best AI models, reinforcement learning (RL) is believed to be a more fundamental approach and has exhibited potential [13] to advance beyond the intelligence boundary of current AI models, using the most capable open-source foundation models (DeepSeek-V3-base [14], inter alia).

大语言模型 (LLMs) 的最新进展在数学推理方面取得了显著进步，这主要得益于思维链技术 [7–9]，该技术引导大语言模型在提供问题最终答案之前生成一系列中间推理步骤。然而，由于大多数高性能模型（例如 OpenAI 的 o 系列模型 [10]）是由专有公司开发的，因此没有明确的途径来开发最先进的推理模型。最近的一些研究表明，在能够访问现有最佳或接近最佳的 AI 模型的情况下，蒸馏 [11, 12] 足以获得高性能，但强化学习 (RL) 被认为是一种更根本的方法，并且在使用最强大的开源基础模型（如 DeepSeek-V3-base [14] 等）时，已经展现出超越当前 AI 模型智能边界的潜力 [13]。

Figure 1: Overall performance between OREAL-32B and some competitive baselines.

图 1: OREAL-32B 与一些竞争基线的整体性能对比。

However, fundamental challenges of sparse reward in RL persist and are even exacerbated in mathematical reasoning tasks that mainly rely on the chain of thought technics with LLMs [7]: the evaluation of intermediate reasoning steps is labor intensive [15] and its accurate automation approach is still under-explored, thus, the only reliable reward is based on the outcome (correctness of final answer), which is inherently binary and sparse when faced with more than 2000 tokens in the long reasoning trajectories [13, 16]. Existing approaches have attempted to estimate the advantages or values of reasoning steps by search [17, 18] or value function-based credit assignment [19, 20], yet, their performance remains unsatisfactory in comparison with the distilled models [13].

然而，RL（强化学习）中稀疏奖励的基本挑战依然存在，在主要依赖大语言模型的思维链技术的数学推理任务中甚至更加严重 [7]：对中间推理步骤的评估是劳动密集型的 [15]，其准确的自动化方法仍在探索中，因此，唯一可靠的奖励是基于结果（最终答案的正确性），这在面对超过2000个Token的长推理轨迹时本质上是二元且稀疏的 [13, 16]。现有方法尝试通过搜索 [17, 18] 或基于价值函数的信用分配 [19, 20] 来估计推理步骤的优势或价值，然而，与蒸馏模型相比，它们的表现仍然不尽如人意 [13]。

This paper aims to conquer the above challenges and proposes a simple framework, termed OREAL, to push the limit of Outcome REwArd-based reinforcement Learning for mathematical reasoning tasks. OREAL is grounded in the unique characteristics of mathematical reasoning tasks that binary outcome feedback creates an environment where all positive trajectories are equally valid. We first establish that behavior cloning on BoN-sampled positive trajectories is sufficient to achieve KL-regularized optimality, which emerges from the analysis that the positive trajectory from BoN sampling converges to a distribution independent of the sample number. For learning on negative samples, OREAL reveals the necessity of reward shaping to maintain consistent gradient estimation between sampling and target distributions. Such a mechanism compensates for BoN’s under-sampling of negative gradients, and enables difficulty-adaptive optimization over both successful and failed trajectories.

本文旨在克服上述挑战，并提出一个名为OREAL的简单框架，以突破基于结果奖励的强化学习在数学推理任务中的极限。OREAL基于数学推理任务的独特特性，即二元结果反馈创造了一个所有正轨迹都同样有效的环境。我们首先证明，在BoN采样的正轨迹上进行行为克隆足以实现KL正则化最优性，这是因为从BoN采样得到的正轨迹收敛到一个与样本数量无关的分布。对于负样本的学习，OREAL揭示了奖励塑形的必要性，以保持采样分布和目标分布之间一致的梯度估计。这种机制补偿了BoN对负梯度的欠采样，并实现了对成功和失败轨迹的难度自适应优化。

Another intrinsic property of mathematical reasoning tasks is the partial correctness in long reasoning chains, which further imposes the learning difficulty of sparse rewards when only a binary outcome reward is available at each iteration of RL training. Thus, OREAL adopts a lightweight credit assignment scheme through a token-level reward model trained using outcome rewards. This mechanism automatically estimates step-wise importance weights by decomposing trajectory advantages, enabling focused learning of critical reasoning steps or errors. The integration of these components yields a theoretically sound framework that effectively bridges the gap between sparse binary feedback and dense policy optimization requirements for mathematical reasoning tasks.

数学推理任务的另一个内在特性是长推理链中的部分正确性，这进一步增加了在每次 RL 训练迭代中只有二元结果奖励时稀疏奖励的学习难度。因此，OREAL 通过使用结果奖励训练的 Token 级奖励模型，采用了一种轻量级的信用分配方案。该机制通过分解轨迹优势自动估计逐步重要性权重，从而实现对关键推理步骤或错误的集中学习。这些组件的整合产生了一个理论上合理的框架，有效弥补了数学推理任务中稀疏二元反馈与密集策略优化需求之间的差距。

Extensive experimental results show that OREAL effectively improves the mathematical reasoning capability of LLMs. At the 7B parameter scale, to the best of our knowledge, OREAL-7B is the first to obtain the pass $@1$ accuracy on MATH-500 [21] to 91.0 using RL instead of distillation, which even exceeds QwQ-32B-Preview [22] and o1-mini [10]. OREAL also improves DeepSeekR1-Distilled-Qwen-7B from 92.8 to 94.0 pass $@1$ accuracy, being on par with the previous best 32B models. For the 32B model, OREAL-32B outperforms all previous models (Figure 1), both distilled and RL-based, obtaining new state-of-the-art results with 95.0 pass $@1$ accuracy on MATH-500.

广泛的实验结果表明，ORAL 有效提升了大语言模型的数学推理能力。在 7B 参数规模下，据我们所知，ORAL-7B 首次通过 RL 而非蒸馏方法在 MATH-500 [21] 上达到了 91.0 的 pass $@1$ 准确率，甚至超过了 QwQ-32B-Preview [22] 和 o1-mini [10]。ORAL 还将 DeepSeekR1-Distilled-Qwen-7B 的 pass $@1$ 准确率从 92.8 提升至 94.0，与之前最佳的 32B 模型持平。对于 32B 模型，ORAL-32B 超越了所有先前模型（图 1），无论是基于蒸馏还是 RL 的方法，在 MATH-500 上以 95.0 的 pass $@1$ 准确率取得了新的最先进成果。

2 Methods

2 方法

To obtain a deeper understanding of the challenges when applying reinforcement learning (RL) for solving math word problems, we first analyze the formulation of RL and the intrinsic properties of underlying binary feedback environments (§2.1), and establish a theoretical foundation for our optimization framework about how to learn from positive samples (§2.2) and failure trials (§2.3). To further conquer the learning ambiguity brought by outcome rewards to the partially correct long reasoning chains, we adopt a new strategy to estimate the importance of tokens for learning (§2.4).

为了更深入地理解在解决数学应用题时应用强化学习 (RL) 所面临的挑战，我们首先分析了 RL 的公式化表达以及底层二元反馈环境的固有特性 (§2.1)，并建立了关于如何从正样本 (§2.2) 和失败尝试 (§2.3) 中学习的优化框架的理论基础。为了进一步克服结果奖励对部分正确的长推理链带来的学习模糊性，我们采用了一种新策略来评估 token 对学习的重要性 (§2.4)。

2.1 Preliminary

2.1 初步准备

When adopting a large language model (LLM) for mathematic reasoning, the input to the LLM policy is a textual math problem that prompts the LLM to output a multi-step reasoning trajectory consisting of multiple tokens as actions. During RL training, common practices [6, 23] conduct sampling on the LLM to produce multiple reasoning trajectories, assign binary feedback (0/1 reward) based solely on the correctness of their final answer, and perform corresponding policy optimization using the sampled trajectories with reward.

在采用大语言模型 (LLM) 进行数学推理时，LLM 策略的输入是一个文本形式的数学问题，提示 LLM 输出由多个 Token 组成的多步推理轨迹作为动作。在 RL 训练期间，常见的做法 [6, 23] 对 LLM 进行采样以生成多个推理轨迹，仅根据其最终答案的正确性分配二元反馈 (0/1 奖励)，并使用带有奖励的采样轨迹执行相应的策略优化。

Policy Optimization. Consider a Markov Decision Process (MDP) defined by the tuple $(S,\mathcal{A},P,\bar{r},\gamma)$ , where $\boldsymbol{S}$ is a finite state space (e.g., contextual steps in mathematical reasoning), $\boldsymbol{\mathcal{A}}$ is the action space (i.e. the token space of LLMs), $P(s^{\prime}|s,a)$ specifies the state transition dynamics, $r:S\times A\to\mathbb{R}$ is the reward function, and $\gamma\in[0,1)$ denotes the discount factor.

策略优化。考虑一个由元组 $(S,\mathcal{A},P,\bar{r},\gamma)$ 定义的马尔可夫决策过程 (MDP)，其中 $\boldsymbol{S}$ 是有限状态空间（例如，数学推理中的上下文步骤），$\boldsymbol{\mathcal{A}}$ 是动作空间（即大语言模型的 Token 空间），$P(s^{\prime}|s,a)$ 指定了状态转移动态，$r:S\times A\to\mathbb{R}$ 是奖励函数，$\gamma\in[0,1)$ 表示折扣因子。

In this section, we focus on KL-regularized policy optimization, which maximizes the expected cumulative returns while regularizing the policy $\pi_{\theta}(\cdot|s)$ toward a reference policy $\pi_{0}(\cdot|s)$ . The objective function is formulated as:

在本节中，我们专注于 KL 正则化的策略优化，它最大化期望累计回报的同时，将策略 $\pi_{\theta}(\cdot|s)$ 正则化至参考策略 $\pi_{0}(\cdot|s)$。目标函数表示为：

with the state-action value function $\begin{array}{r}{Q^{\pi}(s,a)=\mathbb{E}{\pi}\left[\sum{k=0}^{\infty}\gamma^{k}r(s_{t+k},a_{t+k})\mid s_{t}=s,a_{t}=a\right]}\end{array}$ under vanilla policy $\pi$ . This objective admits a closed-form solution for optimal policy $\pi^{*}$ :

使用状态-动作值函数 $\begin{array}{r}{Q^{\pi}(s,a)=\mathbb{E}{\pi}\left[\sum{k=0}^{\infty}\gamma^{k}r(s_{t+k},a_{t+k})\mid s_{t}=s,a_{t}=a\right]}\end{array}$ 在普通策略 $\pi$ 下。该目标允许最优策略 $\pi^{*}$ 的闭式解：

where $Z(s)=\mathbb{E}{a\sim\pi{0}(\cdot|s)}\left[\exp\left(Q^{\pi}(s,a)/\alpha\right)\right]$ is the partition function that ensures normalization.

其中 $Z(s)=\mathbb{E}{a\sim\pi{0}(\cdot|s)}\left[\exp\left(Q^{\pi}(s,a)/\alpha\right)\right]$ 是确保归一化的配分函数。

Best-of-N $(\bf{B o N})$ Sampling. As a common and efficient strategy to sample multiple reasoning trajectories from LLMs, Best-of $.N$ sampling selects the trajectory with maximal reward among $n$ independent rollouts from $\pi_{0}$ to enhance policy performance. Formally, given candidate actions ${a^{(i)}}{i=1}^{n}\sim\pi{0}(\cdot|s)$ , the chosen action is $a^{},=,\arg\operatorname{max}_{a^{(i)}}$ $Q(s,a^{(i)})$ . This strategy effectively leverages the exploration-exploitation trade-off through parallel sampling [24, 25].

Best-of-N $({\bf B o N})$ 采样

Binary Feedback under Outcome Supervision. Though a reasoning trajectory usually contains multiple reasoning steps with thousands of tokens, there lacks an efficient approach to automatically label the correctness of each token or reasoning step in math reasoning tasks. Thus, a practical way is to parse the final answer from the reasoning trajectory [13, 26], evaluate its correctness based on rules or models, and then provide an outcome reward at the end of the trajectory as below:

结果监督下的二元反馈

which intrinsically treats the correct trajectory equally for learning. Moreover, the reward signal is severely sparse when compared to the thousands of tokens and does not provide any signal of progress or correctness for intermediate steps. The resulting reward distribution of trajectories is also different from that of the dense reward function constructed through preference pairs in traditional RL for large language models [27], which induces a more appropriate optimization framework for mathematical reasoning tasks, discussed in the next section.

这本质上将正确的轨迹视为同等重要的学习对象。此外，与数千个Token相比，奖励信号极其稀疏，并且无法为中间步骤提供任何进展或正确性的信号。生成的轨迹奖励分布也不同于通过偏好对构建的密集奖励函数，后者为大语言模型[27]的传统强化学习提供了更合适的数学推理任务优化框架，这将在下一节中讨论。

2.2 Learning from Positive Samples

2.2 从正样本中学习

Building upon the reward equivalence principle stated in Eq. 3, we first formalize a key probabilistic characteristic of BoN sampling:

基于公式 3 所述的奖励等价原则，我们首先形式化 BoN 采样的一个关键概率特征：

Lemma 2.1. Let $\pi(\theta,s)$ be a distribution over parameters $\theta$ and trajectory s, where each s is associated with a binary reward $R(s)\in{0,1}$ . Define $p\triangleq\mathbb{E}_{s\sim\pi(\theta,\cdot)}[R(s)=1]>0$ . Consider the BoN sampling: $n=n_{0}\to\infty$ and sample ${s_{1},s_{2},\ldots,s_{n}}$ i.i.d. from $\pi_{\theta}$ . BoN selects $s^{*}$ uniformly from the subset with R(si) = 1. We have that, The probability of selecting s∗is converge to π(θp,s), which is independent of $n$ .

引理 2.1. 设 $\pi(\theta,s)$ 为参数 $\theta$ 和轨迹 s 的分布，其中每个 s 与一个二元奖励 $R(s)\in{0,1}$ 相关联。定义 $p\triangleq\mathbb{E}_{s\sim\pi(\theta,\cdot)}[R(s)=1]>0$。考虑 BoN 采样：$n=n_{0}\to\infty$ 并从 $\pi_{\theta}$ 中独立同分布地采样 ${s_{1},s_{2},\ldots,s_{n}}$。BoN 从 R(si) = 1 的子集中均匀选择 $s^{*}$。我们有，选择 s∗ 的概率收敛于 $\pi(\theta p,s)$，且与 $n$ 无关。

The proof follows directly from the union law of BoN sampling $(\mathrm{BoN}{n+m}=\mathrm{BoN}{2}(\mathrm{BoN}{m},\mathrm{BoN}{n}))$ and the trivial distinguish ability of $0-1$ rewards. This result reveals that for problems with attainable positive responses, we are using a BoN generator with an arbitrary sampling budget to construct the positive training samples.

证明直接来源于BoN采样的联合律 $(\mathrm{BoN}{n+m}=\mathrm{BoN}{2}(\mathrm{BoN}{m},\mathrm{BoN}{n}))$ 以及 $0-1$ 奖励的平凡区分能力。这一结果表明，对于可获得积极响应的问题，我们使用具有任意采样预算的BoN生成器来构建积极的训练样本。

To quantify the distribution al divergence induced by BoN sampling, prior work [28–30] has analyzed the KL divergence between the BoN distribution $\pi_{\mathrm{BoN}}$ and the original policy $\pi$ . For continuous trajectory spaces $\boldsymbol{S}$ , the BoN distribution admits the explicit form:

为了量化由 BoN 采样引起的分布差异，先前的研究 [28–30] 已经分析了 BoN 分布 $\pi_{\mathrm{BoN}}$ 与原始策略 $\pi$ 之间的 KL 散度。对于连续轨迹空间 $\boldsymbol{S}$，BoN 分布具有以下显式形式：

where $P(s)$ denotes the cumulative distribution function (CDF) associated with $\pi(s)$ . The corresponding KL divergence is given by

其中 $P(s)$ 表示与 $\pi(s)$ 相关的累积分布函数 (CDF)。对应的 KL 散度由下式给出

The KL divergence expression possesses two crucial properties, as $n\to\infty$ , the $\mathrm{KL}(\pi_{\mathrm{BoN}}\parallel\pi)$ is strictly increasing in $n$ for $n\geq1$ , and converge to $\log n\to\infty$ , covering the entire positive real axis. This implies that for any prescribed KL divergence constraint $\epsilon,>,0$ , there exists a BoN parameter iz ation for approximating the optimal policy, and can be simply sampled with the minimal $\bar{n}(\epsilon)$ satisfying that

KL 散度表达式具有两个关键性质，当 $n\to\infty$ 时，$\mathrm{KL}(\pi_{\mathrm{BoN}}\parallel\pi)$ 在 $n\geq1$ 时严格递增，并收敛到 $\log n\to\infty$，覆盖整个正实数轴。这意味着对于任何给定的 KL 散度约束 $\epsilon,>,0$，存在一个 BoN 参数化来近似最优策略，并且可以通过满足 $\bar{n}(\epsilon)$ 的最小值进行简单采样。

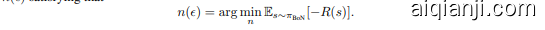
BoNBoN [31] empirically shows that BoN sampling achieves the optimal win rate under fixed KL constraint by exhaustive search over the positive support. Therefore, the behavior cloning on BoN-selected positive samples directly learns the analytic solution to Eq. 1. Intuitively, since every correct answer is preferred identically in the outcome-supervised sense, we only need to sample until we get a positive example, whose generating probability distribution will be the same as randomly picking from arbitrarily large numbers of samples.

BoNBoN [31] 通过实验表明，BoN采样通过对正样本支持集的穷举搜索，在固定的KL约束下实现了最优胜率。因此，在BoN选择的正样本上进行行为克隆，直接学习到了公式1的解析解。直观上，由于在结果监督的意义上每个正确答案都被同等偏好，我们只需要采样直到获得一个正样本，其生成的概率分布将等同于从任意大量样本中随机选取。

Based on the theoretical understanding established, we formulate the first component of the learning objective in OREAL by incorporating KL-constrained max-likelihood-objective over positive examples obtained through sampling:

基于已建立的理论理解，我们通过结合对通过采样获得的正例进行KL约束的最大似然目标，制定了OREAL中学习目标的第一个组成部分：

where $\mathcal{D}^{+}$ denotes the set of positive trajectories selected via BoN sampling from RL rollouts.

其中 $\mathcal{D}^{+}$ 表示通过从RL rollout中进行BoN采样选择的正向轨迹集合。

2.3 Learning from Negative Samples

2.3 从负样本中学习

As established in Section 2.2, direct behavioral cloning on positive responses can effectively recover the policy distribution. BOND [32] proposes estimating Jeffreys divergence [33] for the BoN strategy to train with both positive and negative samples, and demonstrates that signals from unsuccessful trajectories provide critical information about decision boundaries and failure modes.

正如第2.2节所述，直接对积极响应进行行为克隆可以有效恢复策略分布。BOND [32] 提出估计 BoN 策略的 Jeffreys 散度 [33]，以便同时使用正负样本进行训练，并证明了不成功轨迹中的信号提供了关于决策边界和失败模式的关键信息。

In this section, we will discuss the relationship between the BoN (Best-of-N) distribution and the optimization objective defined in Eq. 1, then elucidate the necessity of reward reshaping when training with negative samples. Notably, while Eq. 4 shares structural similarities with Eq. 2, its application to mathematical reasoning tasks with binary feedback requires reformulation. Specifically, the transformed BoN distribution can be expressed as

在本节中，我们将讨论 BoN（Best-of-N）分布与式 1 中定义的优化目标之间的关系，然后阐明在使用负样本进行训练时奖励重塑的必要性。值得注意的是，虽然式 4 与式 2 在结构上具有相似性，但在应用于具有二元反馈的数学推理任务时需要重新表述。具体而言，转换后的 BoN 分布可以表示为

which reveals fundamental differences between the BoN distribution and the original sampling distribution. Consider a scenario where two correct and two incorrect solutions are sampled, yielding an empirical accuracy of $50%$ . However, the probability of selecting negative samples under Bestof-4 becomes $(0.5)^{4},{}=6.25%$ , significantly lower than the original distribution. This discrepancy necessitates reward shaping to maintain consistency between our optimization target and the expected return under the BoN distribution.

这揭示了 BoN 分布与原始采样分布之间的根本差异。考虑一个场景，其中采样了两个正确和两个错误的解决方案，产生的经验准确率为 $50%$。然而，在 Bestof-4 下选择负样本的概率为 $(0.5)^{4},{}=6.25%$，显著低于原始分布。这种差异需要通过奖励调整来保持我们的优化目标与 BoN 分布下的预期回报之间的一致性。

Building on BoN-RLB’s [34] application of the log-likelihood trick for BoN-aware policy gradients, we analyze the reward shaping technic for negative samples to maintain gradient consistency with Section 2.2. With expectation return $p$ follow the definition in Lemma 2.1. The policy gradient under the BoN distribution can be derived as

基于 BoN-RLB [34] 应用对数似然技巧进行 BoN 感知的策略梯度，我们分析了负样本的奖励塑造技术，以保持与第 2.2 节的梯度一致性。期望回报 $p$ 遵循引理 2.1 中的定义。BoN 分布下的策略梯度可以推导为

where $I_{D_{+}}(s)$ and $I_{D_{-}}(s)$ denote indicator functions for positive and negative sample sets respectively. Notably, these indicators are independent of policy parameters $\theta$ . Given $\mathbb{E}{s\sim\pi{\mathrm{bon}}}[I_{D_{+}}(s)]=$ $1-{\dot{(}}1-p)^{n}$ , we derive the gradient components as

其中 $I_{D_{+}}(s)$ 和 $I_{D_{-}}(s)$ 分别表示正样本集和负样本集的指示函数。值得注意的是，这些指示函数与策略参数 $\theta$ 无关。给定 $\mathbb{E}{s\sim\pi{\mathrm{bon}}}[I_{D_{+}}(s)]=$ $1-{\dot{(}}1-p)^{n}$ ，我们推导出梯度分量为

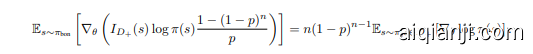
Similarly, we also have

同样地，我们也有

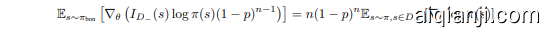
This derivation reveals that when assigning unit reward $(R(s)=1)$ ) to positive samples, gradient consistency requires reshaping negative sample rewards to $R^{\star}(s)\triangleq(1-p)R(s)$ . Based on this reward shaping, we can construct policy optimization both on positive and negative samples for optimal policy.

该推导揭示，当对正样本分配单位奖励 $(R(s)=1)$ 时，梯度一致性要求将负样本奖励重塑为 $R^{\star}(s)\triangleq(1-p)R(s)$ 。基于这种奖励重塑，我们可以在正样本和负样本上构建策略优化，以获得最优策略。

To obtain the parameter $1-p$ which can be linked to the Monte-Carlo (MC) advantage estimation, we can simply estimate that probability by calculating the expected accuracy on the sample space by counting a small number of responses. In this paper we apply a similar setting to RLOO [35], namely RRLOO(s) = R(s) −N1−1 s⋆̸=s R for unbiased mean reward and train with policy gradient. The second part of our OREAL objective is then formulated as below:

为了获得与蒙特卡罗（MC）优势估计相关的参数 $1-p$，我们可以通过计算样本空间上的期望准确率来简单估计该概率，只需统计少量响应即可。本文采用了与RLOO [35] 相似的设置，即RRLOO(s) = R(s) −N1−1 s⋆̸=s R，用于无偏均值奖励并使用策略梯度进行训练。我们OREAL目标的第二部分公式如下：

where $p=\mathbb{P}{\theta\sim\pi}[R(\theta)=1],,S{-}$ is the failed subset generated by policy model, and $F$ represents the preprocessing for advantage scores to serve as a generalized form, for example, $\begin{array}{r}{F(1-p)\triangleq}\end{array}$ $\frac{r_{i}-\bar{m}e a\bar{n}({r_{i}...r_{n}})}{s t d({r_{i}...r_{n}})}$ in the recent GRPO [6] algorithm, where $m e a n({r_{i}...r_{n}})\to p$ when $n\to\infty$ .

其中 $p=\mathbb{P}{\theta\sim\pi}[R(\theta)=1],,S{-}$ 是由策略模型生成的失败子集，$F$ 代表对优势分数进行预处理的广义形式，例如在最近的 GRPO [6] 算法中，$\begin{array}{r}{F(1-p)\triangleq}\end{array}$ $\frac{r_{i}-\bar{m}e a\bar{n}({r_{i}...r_{n}})}{s t d({r_{i}...r_{n}})}$，其中当 $n\to\infty$ 时，$m e a n({r_{i}...r_{n}})\to p$。

2.4 Dealing with Long Reasoning Chains

2.4 处理长推理链

In the previous discussion, we introduced the adaptation of binary reward training in response space. However, since the outcome supervision only provides feedback at the sequence level, this modeling essentially reduces to a contextual bandit without internal reward modeling within the

在之前的讨论中，我们介绍了在响应空间中适应二元奖励训练的方法。然而，由于结果监督仅在序列级别提供反馈，这种建模本质上简化为一种情境赌博机，而没有在内部进行奖励建模。

MDP. A common counterexample is PPO, which utilizes a separate critic model to estimate the value function. However, such a solution appears to be expensive and complex, which has induced numerous explorations on how to stabilize the PPO training.

MDP。一个常见的反例是 PPO，它使用一个独立的 critic 模型来估计价值函数。然而，这种解决方案显得昂贵且复杂，这引发了许多关于如何稳定 PPO 训练的探索。

Things become slightly different in mathematical reasoning, where the model can spontaneously revise omissions in intermediate steps to obtain the correct final answer. Therefore, outcome supervision is preferred, and the value function is more meant to be a simple credit assignment to determine how much the process step contributes to the outcome reward. With efficiency and performance trade-off considerations, we choose to use some low-cost alternatives for sequence-level re weighting.

在数学推理中，情况略有不同，模型可以自发修正中间步骤中的遗漏，从而获得正确的最终答案。因此，结果监督更受青睐，而价值函数更倾向于作为一种简单的信用分配机制，用于确定过程步骤对结果奖励的贡献程度。考虑到效率和性能的权衡，我们选择使用一些低成本替代方案进行序列级别的重新加权。

Taking into account the deterministic dynamics in mathematical reasoning $(s_{t+1}=f(s_{t},a_{t}))$ , the state-action function $Q^{\pi}(s_{<t},\pi(s_{t}))$ simplifies to the cumulative discounted reward of policy $\pi$ :

考虑到数学推理中的确定性动态 $(s_{t+1}=f(s_{t},a_{t}))$，状态-动作函数 $Q^{\pi}(s_{<t},\pi(s_{t}))$ 简化为策略 $\pi$ 的累积折现奖励：

Since intermediate rewards are not provided in mathematical reasoning tasks, we define an advantage function based solely on outcome feedback:

由于数学推理任务中不提供中间奖励，我们仅根据结果反馈定义了一个优势函数：

This formulation treats $A(s_{\leq t})$ as a token-wise credit assignment mechanism, estimating each token’s contribution toward the final outcome.

该公式将 $A(s_{\leq t})$ 视为一种 token 级别的信用分配机制，用于估计每个 token 对最终结果的贡献。

For a pair of responses $y_{1}$ and $y_{2}$ to the same query, their initial values coincide $V_{0}^{1}=V_{0}^{2}$ . The win rate between them then satisfies:

对于同一查询的一对响应 $y_{1}$ 和 $y_{2}$，它们的初始值重合 $V_{0}^{1}=V_{0}^{2}$。它们之间的胜率满足：

Equation 9 indicates that for any function family $A={A(s_{\leq t})}$ , a cumulative reward function through sequence aggregation can be constructed to model rewards:

公式9表明，对于任何函数族 $A={A(s_{\leq t})}$，都可以通过序列聚合构建一个累积奖励函数来建模奖励：

which is trainable via preference pairs ${(y_{w},y_{l})}$ by fitting the outcome feedback. The learned $A(s_{\leq t})$ serves as a weighting function for credit assignment, which is used to reweight the original training loss, emphasizing critical reasoning steps or errors. An analogous implementations is $r2Q^{*}$ [36, 37] by defining A = logππre(f(yyii)), PRIME [20] then apply this formulation to improve performance of RLOO. In our work, following the practice from [38], we directly train a token-level reward function $w(s_{\leq t})$ satisfying

其通过偏好对 ${(y_{w},y_{l})}$ 进行训练，以拟合结果反馈。学习到的 $A(s_{\leq t})$ 作为信用分配的权重函数，用于重新加权原始训练损失，强调关键推理步骤或错误。类似的实现是 $r2Q^{*}$ [36, 37]，通过定义 A = logππre(f(yyii))，PRIME [20] 随后应用此公式来提升 RLOO 的性能。在我们的工作中，遵循 [38] 的做法，直接训练一个满足以下条件的 token 级奖励函数 $w(s_{\leq t})$

without constraining KL-divergence to reference model in reward model training. These sequential rewards can serve as a proxy for the contribution of thinking steps to the result accuracy. Assuming a pair of prefix-consistent correct and incorrect samples, due to the causal inference nature of the token-level reward model, the preference optimization for these samples will only function on the steps that have different contents, which induces higher credits on the core reasoning step that affects the final result. We further discuss the training details of this model and analyze the visualization of its token-wise scoring effects later in Section 3.2 and Appendix A.

在奖励模型训练中不限制 KL 散度到参考模型。这些顺序奖励可以作为思考步骤对结果准确性贡献的代理。假设一对前缀一致的正确和错误样本，由于 Token 级奖励模型的因果推理性质，这些样本的偏好优化仅在不同的步骤上起作用，这会在影响最终结果的核心推理步骤上诱导更高的信用。我们将在第 3.2 节和附录 A 中进一步讨论该模型的训练细节，并分析其 Token 级评分效果的可视化。

In practice, we decompose the output weight $w(s)$ for positive and negative samples and clip on the positive axis to prevent reversing the direction of the optimized gradient, denoted as $\omega^{+}$ and $\omega^{-}$ :

在实践中，我们将正负样本的输出权重 $w(s)$ 分解，并在正轴上进行裁剪，以防止优化梯度的方向反转，分别表示为 $\omega^{+}$ 和 $\omega^{-}$：

Giving input query $d$ , the overall loss is as follows:

给定输入查询 $d$，总体损失如下：

where $\eta$ represents the balancing weights for positive and negative losses.

其中 $\eta$ 表示正负损失的平衡权重。

3 Implementation

3 实现

3.1 Policy Initialization

3.1 策略初始化

We utilize Qwen2.5-7B and Qwen2.5-32B [39] as the base model. Initially, we fine-tune the base models using long chain-of-thought data obtained through rejection sampling [23]. This rejection sampling fine-tuned (RFT) [23] models then serve as the initialization for the policy model in our RL framework. We also explore to use of DeepSeek-R1-Distill-Qwen-7B [13] as the initial policy model and perform OREAL on it and discuss the influence of different initial policy models in Section 4.4. The training data for the RFT models consists of in-house datasets supported by Open Data Lab [40] and open-source datasets including Numina [41] and the training set of MATH [21].

我们使用 Qwen2.5-7B 和 Qwen2.5-32B [39] 作为基础模型。首先，我们通过拒绝采样 (rejection sampling) [23] 获得的长链思维数据对基础模型进行微调。这些经过拒绝采样微调 (RFT) [23] 的模型随后作为我们强化学习框架中策略模型的初始化。我们还探索使用 DeepSeek-R1-Distill-Qwen-7B [13] 作为初始策略模型，并在其上进行 OREAL 训练，并在第 4.4 节中讨论了不同初始策略模型的影响。RFT 模型的训练数据包括由 Open Data Lab [40] 支持的内部数据集以及开源数据集，如 Numina [41] 和 MATH 的训练集 [21]。

3.2 Reinforcement Learning

3.2 强化学习

Data Preparation. During the on-policy RL process, we utilize questions from Numina, MATH training sets, and historical AMC/AIME (without AIME2024) competitions. For each question, we independently sample 16 trajectories from the RFT models. The correctness of each trajectory is then averaged to estimate the correctness rate of each query. To increase the difficulty of training queries, only questions with correctness rates between 0 and 0.8 are retained for further training.

数据准备。在策略强化学习过程中，我们利用来自Numina、MATH训练集以及历史AMC/AIME（不包括AIME2024）竞赛的问题。对于每个问题，我们从RFT模型中独立采样16条轨迹。然后，对每条轨迹的正确性进行平均，以估计每个查询的正确率。为了增加训练查询的难度，仅保留正确率在0到0.8之间的问题用于进一步训练。

Outcome Reward Signal. We employ the Qwen2.5-72B-Instruct [39] as a generative verifier, in conjunction with a rule-based verifier, to evaluate the correctness of the model’s outputs and provide binary rewards. This combination enhances the robustness of correctness assessment, mitigating issues related to the false negative of the rule-based verifier.

结果奖励信号。我们采用 Qwen2.5-72B-Instruct [39] 作为生成式验证器，结合基于规则的验证器，来评估模型输出的正确性并提供二元奖励。这种组合增强了正确性评估的鲁棒性，缓解了基于规则的验证器假阴性问题。

Training Token-level Reward Model. For the token-level reward model, we directly use the binary outcome rewards provided by the verifier and optimize using the cross-entropy loss:

训练Token级奖励模型
对于Token级奖励模型，我们直接使用验证器提供的二元结果奖励，并通过交叉熵损失进行优化：

where $s$ represents the sampled trajectory, $r\in{0,1}$ is the binary outcome reward from the verifier, and $\begin{array}{r}{p(s),=,\sigma(\frac{1}{T}\sum_{t}^{T}w(s_{t}))}\end{array}$ denotes the predicted probability of correctness by the token-level reward model $w$ .

其中 $s$ 表示采样的轨迹，$r\in{0,1}$ 是来自验证器的二元结果奖励，而 $\begin{array}{r}{p(s),=,\sigma(\frac{1}{T}\sum_{t}^{T}w(s_{t}))}\end{array}$ 表示由 Token 级别的奖励模型 $w$ 预测的正确概率。

To further analyze the behavior of the token-level reward model, we visualize its output distribution $w(s_{t})$ during the on-policy RL training process (see Appendix A). In this training paradigm, $w!\left(s_{t}\right)$ assigns token-wise importance scores across the chain-of-thought reasoning process, capturing each token’s contribution to the final correctness of the generated response. Consequently, this allows us to leverage $w!\left(s_{t}\right)$ for importance sampling during the optimization process, enabling a more principled selection of informative tokens.

为了进一步分析Token级别奖励模型的行为，我们可视化了其在策略RL训练过程中的输出分布 $w(s_{t})$（见附录A）。在这一训练范式中，$w!\left(s_{t}\right)$ 在思维链推理过程中为每个Token分配重要性分数，捕捉每个Token对生成响应最终正确性的贡献。因此，这使得我们能够在优化过程中利用 $w!\left(s_{t}\right)$ 进行重要性采样，从而实现更有原则地选择信息丰富的Token。

Training Algorithm. The loss function for the policy model follows the formulation described in Section 2. The complete RL training procedure is described in Algorithm 1.

训练算法。策略模型的损失函数遵循第2节中描述的公式。完整的强化学习训练过程在算法1中描述。

Hyper parameters. The policy model is initialized from the RFT model. Similarly, the token-level reward model is also initialized with the same weights, but its output layer is replaced with a linear

超参数。策略模型从RFT模型初始化。同样，Token级别的奖励模型也使用相同的权重进行初始化，但其输出层被替换为线性层。

layer that produces a one-dimensional scalar. The weights of this layer are initialized to zero to ensure unbiased importance sampling weight at the start of training.

生成一维标量的层。该层的权重初始化为零，以确保训练开始时的重要性采样权重无偏。

During training iterations, each batch consists of 64 questions, with 16 rollouts per question. The max length of each rollout trajectory is set to 16384 tokens. Then the correctness of each response is averaged to calculate the pass rate, and questions with an overall pass rate of 0 or 1 are discarded. For the remaining trajectories, we retain only one correct response and one incorrect response per question, ensuring a balanced distribution of positive and negative samples for token-level reward model training.

在训练迭代过程中，每个批次包含64个问题，每个问题有16次rollout。每次rollout轨迹的最大长度设置为16384个token。然后，计算每个回答的正确性并取平均值以计算通过率，整体通过率为0或1的问题将被丢弃。对于剩余的轨迹，我们每个问题只保留一个正确回答和一个错误回答，以确保在token级奖励模型训练中正负样本的均衡分布。

For optimization, the policy model is trained with a learning rate of $5e!-!7$ , while the token-level reward model is trained with a learning rate of $2e{-6}$ . The latter undergoes a 10-step warm-up phase before training begins. Both models employ a cosine annealing learning rate schedule, decaying to $1/5$ of the initial learning rate over time. We optimize both models using the AdamW optimizer. The total number of training steps is 80, with evaluation conducted every 10 steps. The KL coefficient $\beta$ is set to 0.01. We select the best-performing model determined by evaluation metrics.

在优化过程中，策略模型的学习率设置为 $5e!-!7$，而 Token 级别的奖励模型的学习率设置为 $2e{-6}$。后者在训练开始前会经历 10 步的预热阶段。两个模型均采用余弦退火学习率调度，学习率随时间衰减至初始学习率的 $1/5$。我们使用 AdamW 优化器对两个模型进行优化。总训练步数为 80 步，每 10 步进行一次评估。KL 系数 $\beta$ 设置为 0.01。我们根据评估指标选择表现最好的模型。

3.3 Skill-based Enhancement

3.3 基于技能的增强

During the RL training procedure, we observe that the model consistently struggles with certain types of questions, particularly those involving specific knowledge and skill areas, such as trigonometric constant transformations, probability statistics, series transformations, etc. We believe this is caused by the insufficient learning of the base model on these concepts in the Pre-training or RFT stages.

在 RL 训练过程中，我们观察到模型始终在某些类型的问题上表现不佳，特别是那些涉及特定知识和技能领域的问题，例如三角函数常数变换、概率统计、级数变换等。我们认为这是由于基础模型在预训练或 RFT 阶段对这些概念的学习不足所导致的。

To address this problem, we implement a skill-based enhancement approach, using the MATH dataset to reduce the high cost of skill annotation. Specifically, we annotate each question in the training set with its corresponding core skill. For questions that the model repeatedly fails to answer correctly during the RL phase, we perform data augmentation by including similar questions from the training set that share the same skill. These augmented questions are then added to the training data during the RFT stage to help the model better internalize these skills.

为了解决这个问题，我们实施了一种基于技能的增强方法，使用MATH数据集来降低技能标注的高成本。具体来说，我们对训练集中的每个问题标注其对应的核心技能。对于在强化学习阶段模型反复无法正确回答的问题，我们通过从训练集中包含相同技能的类似问题来进行数据增强。这些增强的问题随后被添加到RFT（强化微调）阶段的训练数据中，以帮助模型更好地内化这些技能。

4 Experiment

4 实验

4.1 Evaluation Setup

4.1 评估设置

Baseline. We conduct evaluations against several baselines, including GPT-4o-0513 [42], ClaudeSonnet-3.5-1022 [43], OpenAI-o1-mini, OpenAI-o1-preview [10], Qwen2.5-Instrust-7B, Qwen2.5- Math-Instrust-7B, Qwen2.5-Instrust-32B [39], QwQ-32B-Preview [22], DeepSeek-R1-Distill-Qwen7B, DeepSeek-R1-Distill-Qwen-32B [13], SimpleRL [44], PRIME [20], rStarMath [45]. For part of the baseline, we directly use the results from their report, which we mark with *.

基线。我们进行了多项基线评估，包括 GPT-4o-0513 [42]、ClaudeSonnet-3.5-1022 [43]、OpenAI-o1-mini、OpenAI-o1-preview [10]、Qwen2.5-Instrust-7B、Qwen2.5-Math-Instrust-7B、Qwen2.5-Instrust-32B [39]、QwQ-32B-Preview [22]、DeepSeek-R1-Distill-Qwen7B、DeepSeek-R1-Distill-Qwen-32B [13]、SimpleRL [44]、PRIME [20]、rStarMath [45]。对于部分基线，我们直接使用了他们报告中的结果，并用 * 标记。

Table 1: Overall evaluation results for OREAL and each baseline. “OREAL-DSR1-Distill-Qwen-7B” denotes the DeepSeek-R1-Distill-Qwen7B trained by OREAL. “AIME2025-I”, “LiveMath” and “Olympiad” represent “AIME 2025 Part1”, “Live Math Bench”, and “Olympiad Bench”, respectively. For models at the parameter scale of 7B and 32B, we use Bold and Underlined to represent the best and second best performance, respectively. For part of the baseline, we directly use the results from their report, marked with *.

表 1: OREAL 与各基线的整体评估结果。“OREAL-DSR1-Distill-Qwen-7B”表示由 OREAL 训练的 DeepSeek-R1-Distill-Qwen7B。“AIME2025-I”、“LiveMath”和“Olympiad”分别代表“AIME 2025 Part1”、“Live Math Bench”和“Olympiad Bench”。对于参数规模为 7B 和 32B 的模型，我们使用加粗和下划线分别表示最佳和次佳性能。对于部分基线，我们直接使用其报告中的结果，并标记为*。

Benchmark. We use some well-established mathematical datasets for evaluation, including MATH500 [21], AIME2024 [46], AIME2025 (Part1) [46], LiveMathBench [47], and OlympiadBench [48].

基准测试。我们使用一些成熟的数学数据集进行评估，包括 MATH500 [21]、AIME2024 [46]、AIME2025 (Part1) [46]、LiveMathBench [47] 和 OlympiadBench [48]。

Metrics. We use pass $@1$ as the metric for evaluation under the zero-shot chain-of-thought setting and use greedy decoding for each sample to assess correctness using Open Compass [49].

指标。我们使用 pass $@1$ 作为零样本思维链设置下的评估指标，并对每个样本使用贪婪解码，通过 Open Compass [49] 评估正确性。

4.2 Overall Results

4.2 总体结果

Tabel 1 shows the results of the comprehensive evaluation, highlighting the performance of our proposed models across different parameter scales. Notably, at the 7B scale, OREAL-7B achieves a remarkable pass $@1$ accuracy of 91.0 on the MATH-500 and 59.9 on Olympiad Bench. To the best of our knowledge, this is the first time a model of this size has reached such a high level of accuracy using RL instead of distillation. This performance not only establishes a new milestone for RL-based meth