High-Order Structure Based Middle-Feature Learning for Visible-Infrared Person Re-Identification

基于高阶结构的中层特征学习在可见光-红外行人重识别中的应用

Abstract

摘要

Visible-infrared person re-identification (VI-ReID) aims to retrieve images of the same persons captured by visible (VIS) and infrared (IR) cameras. Existing VI-ReID methods ignore high-order structure information of features while being relatively difficult to learn a reasonable common feature space due to the large modality discrepancy between VIS and IR images. To address the above problems, we propose a novel high-order structure based middle-feature learning network (HOS-Net) for effective VI-ReID. Specifically, we first leverage a short- and long-range feature extraction (SLE) module to effectively exploit both short-range and long-range features. Then, we propose a high-order structure learning (HSL) module to successfully model the high-order relationship across different local features of each person image based on a whitened hypergraph network. This greatly alleviates model collapse and enhances feature representations. Finally, we develop a common feature space learning (CFL) module to learn a disc rim i native and reasonable common feature space based on middle features generated by aligning features from different modalities and ranges. In particular, a modality-range identity-center contrastive (MRIC) loss is proposed to reduce the distances between the VIS, IR, and middle features, smoothing the training process. Extensive experiments on the SYSU-MM01, RegDB, and LLCM datasets show that our HOS-Net achieves superior state-ofthe-art performance. Our code is available at https://github. com/J aula u coen g/HOS-Net.

可见光-红外行人重识别(VI-ReID)旨在检索由可见光(VIS)和红外(IR)摄像头捕获的同一行人图像。现有VI-ReID方法忽略了特征的高阶结构信息，同时由于VIS和IR图像之间存在较大模态差异，较难学习到合理的共同特征空间。针对上述问题，我们提出了一种基于高阶结构的中间特征学习网络(HOS-Net)。具体而言，我们首先利用短长程特征提取(SLE)模块有效获取短程和长程特征。接着提出高阶结构学习(HSL)模块，基于白化超图网络成功建模每张行人图像不同局部特征间的高阶关系，极大缓解了模型坍塌问题并增强了特征表示能力。最后开发了共同特征空间学习(CFL)模块，通过对齐不同模态和范围的特征生成中间特征，进而学习判别性强且合理的共同特征空间。特别提出模态-范围身份中心对比(MRIC)损失函数，缩小VIS、IR与中间特征之间的距离，使训练过程更加平滑。在SYSU-MM01、RegDB和LLCM数据集上的大量实验表明，我们的HOS-Net取得了最先进的性能。代码已开源在https://github.com/Julaucong/HOS-Net。

Introduction

引言

Over the past few years, person re-identification (ReID) has attracted increasing attention due to its significant importance in surveillance and security applications. A large number of single-modality person ReID methods have been proposed based on visible (VIS) cameras. However, these methods may fail under low-light conditions. Unlike VIS cameras, infrared (IR) cameras are less affected by illumination changes. Recently, visible-infrared person re-identification (VI-ReID), which leverages both VIS and IR cameras, has been developed to match cross-modality person images, mitigating the limitations of single-modality person ReID.

近年来，行人重识别(ReID)因其在监控安防应用中的重要意义而受到越来越多的关注。基于可见光(VIS)摄像头的单模态行人ReID方法已被大量提出。然而，这些方法在低光照条件下可能失效。与可见光摄像头不同，红外(IR)摄像头受光照变化的影响较小。近期，可见光-红外行人重识别(VI-ReID)通过联合使用VIS和IR摄像头来匹配跨模态行人图像，从而缓解单模态行人ReID的局限性。

A major challenge of VI-ReID is the large modality discrepancy between VIS and IR images. To reduce the modality discrepancy, existing VI-ReID methods can be divided into image-level and feature-level methods. The image-level methods (Dai et al. 2018; Wang et al. 2020; Wei et al. 2022), generate middle-modality or new modality images based on generative adversarial networks (GAN). However, the GANbased methods easily suffer from the problems of color inconsistency or loss of image details. Hence, the generated images may not be reliable for subsequent classification.

可见光-红外跨模态行人重识别(VI-ReID)的主要挑战在于可见光(VIS)与红外(IR)图像间存在显著模态差异。为减小模态差异，现有方法可分为图像级和特征级两类。图像级方法(Dai et al. 2018; Wang et al. 2020; Wei et al. 2022)基于生成对抗网络(GAN)生成中间模态或新模态图像，但这类方法易出现色彩失真或图像细节丢失问题，导致生成图像可能不适用于后续分类任务。

The feature-level methods (Ye et al. 2021b; Lu, Zou, and Zhang 2023; Zhang et al. 2022) follow a two-step learning pipeline (i.e., they first extract features for VIS and IR images, and then map these features into a common feature space). Generally, these methods have two issues. On the one hand, they often ignore high-order structure information of features (i.e., the different levels of dependence across local features), which can be important for matching crossmodality images. On the other hand, they usually directly minimize the distances between VIS and IR features in the common feature space. However, such a manner increases the difficulty of learning a reasonable common feature space due to the large modality discrepancy.

特征级方法 (Ye et al. 2021b; Lu, Zou, and Zhang 2023; Zhang et al. 2022) 遵循两步学习流程 (即先提取可见光-红外(VIS-IR)图像特征，再将特征映射到公共特征空间)。这类方法通常存在两个问题：一方面，它们往往忽略特征的高阶结构信息 (即局部特征间不同层级的依赖关系)，而这些信息对跨模态图像匹配至关重要；另一方面，它们通常直接在公共特征空间中最小化VIS与IR特征的距离。然而，由于模态差异较大，这种方式会增加学习合理公共特征空间的难度。

To address the above issues, in this paper, we propose a novel high-order structure based middle-feature learning network (HOS-Net), which consists of a backbone, a shortand long-range feature extraction (SLE) module, a highorder structure learning (HSL) module, and a common feature space learning (CFL) module, for VI-ReID. The key novelty of our method lies in the novel formulation of exploiting high-order structure information and middle features to learn a disc rim i native and reasonable common feature space, greatly alleviating the modality discrepancy.

为了解决上述问题，本文提出了一种基于高阶结构的中层特征学习网络(HOS-Net)，该网络由主干网络、短长期特征提取(SLE)模块、高阶结构学习(HSL)模块和公共特征空间学习(CFL)模块组成，用于VI-ReID。我们方法的关键创新在于利用高阶结构信息和中层特征来学习一个判别性强且合理的公共特征空间，从而显著缓解模态差异。

Specifically, given a VIS-IR image pair, the SLE module (consisting of a convolutional branch and a Transformer branch) extracts short-range and long-range features. Then, the HSL module models the dependence on short-range and long-range features based on a whitened hypergraph. Finally, the CFL module learns a common feature space by generating and leveraging middle features. In the CFL module, instead of directly adding or concatenating features from different modalities and ranges, we leverage graph attention to properly align these features, obtaining middle features. Based on it, a modality-range identity-center contrastive (MRIC) loss is developed to reduce the distances between the VIS, IR, and middle features, smoothing the process of learning the common feature space.

具体来说，给定一个可见光-红外(VIS-IR)图像对，短长程特征提取(SLE)模块(由卷积分支和Transformer分支组成)会提取短程和长程特征。随后，基于白化超图的异质短长程(HSL)模块会建模对短程和长程特征的依赖关系。最后，通过生成并利用中间特征，共融特征学习(CFL)模块学习到一个共同特征空间。在CFL模块中，我们没有直接相加或拼接来自不同模态和范围的特征，而是利用图注意力机制来适当对齐这些特征，从而获得中间特征。基于此，我们开发了模态-范围身份中心对比(MRIC)损失函数，以减小可见光、红外和中间特征之间的距离，从而平滑共同特征空间的学习过程。

The contributions of our work are twofold:

我们工作的贡献有两方面：

• First, we introduce an HSL module to learn high-order structure information of both short-range and long-range features. Such an innovative way effectively models high-order relationship across different local features of a person image without suffering from model collapse, greatly enhancing feature representations. • Second, we design a CFL module to learn a discriminative and reasonable common feature space by taking advantage of middle features. In particular, a novel MRIC loss is developed to minimize the distances between VIS, IR, and middle features. This is beneficial for the extraction of disc rim i native modality-irrelevant ReID features.

• 首先，我们引入HSL模块来学习短程和长程特征的高阶结构信息。这种创新方法有效建模了行人图像不同局部特征间的高阶关系，避免了模型坍塌，显著增强了特征表示能力。
• 其次，我们设计了CFL模块，通过利用中间特征来学习具有判别力的合理公共特征空间。特别地，开发了新型MRIC损失函数来最小化可见光(VIS)、红外(IR)与中间特征之间的距离，这有利于提取判别性的模态无关ReID特征。

Extensive experiments on the SYSU-MM01, RegDB, and LLCM datasets demonstrate that our proposed HOS-Net obtains excellent performance in comparison with several state-of-the-art VI-ReID methods.

在SYSU-MM01、RegDB和LLCM数据集上的大量实验表明，与多种先进的可见光-红外行人重识别(VI-ReID)方法相比，我们提出的HOS-Net取得了优异的性能。

Related Work

相关工作

Single-Modality Person Re-Identification (ReID). A variety of single-modality person ReID methods have been developed and achieved promising performance in the cases of occlusion, cloth-changing, and pose changes. Yan et al. (Yan et al. 2021) propose an occlusion-based data augmentation strategy and a bounded exponential distance loss for oc- cluded person ReID. Jin et al. (Jin et al. 2022) introduce an additional gait recognition task to learn cloth-agnostic features. Note that these methods are based on VIS cameras and thus they perform poorly in low-light conditions.

单模态行人重识别(ReID)。针对遮挡、换装和姿态变化等情况，研究者们开发了多种单模态行人重识别方法并取得了良好性能。Yan等人(Yan et al. 2021)提出了一种基于遮挡的数据增强策略和有界指数距离损失函数来处理遮挡情况下的行人重识别。Jin等人(Jin et al. 2022)则通过引入额外的步态识别任务来学习与服装无关的特征。需要注意的是，这些方法都基于可见光(VIS)摄像头，因此在低光照条件下表现不佳。

Visible-Infrared Person Re-Identification (VI-ReID). The image-level methods (Dai et al. 2018; Wang et al. 2020; Wei et al. 2022) often reduce the modality discrepancy by generating middle-modality images or new modality images. Wei et al. (Wei et al. 2022) propose a bidirectional image translation subnetwork to generate middle-modality images from VIS and IR modalities. Li et al. (Li et al. 2020) and Zhang et al. (Zhang et al. 2021) introduce light-weight middle-modality image generators to mitigate the modality discrepancy. Instead of generating middle-modality images, we align the features from different modalities and ranges with graph attention, generating reliable middle features. Moreover, we design an MRIC loss to optimize the distances between VIS, IR, and middle features, benefiting the extraction of disc rim i native ReID features.

可见光-红外行人重识别 (VI-ReID)。图像级方法 (Dai et al. 2018; Wang et al. 2020; Wei et al. 2022) 通常通过生成中间模态图像或新模态图像来减少模态差异。Wei等人 (Wei et al. 2022) 提出双向图像转换子网络，从可见光(VIS)和红外(IR)模态生成中间模态图像。Li等人 (Li et al. 2020) 和 Zhang等人 (Zhang et al. 2021) 引入轻量级中间模态图像生成器以缓解模态差异。不同于生成中间模态图像，我们通过图注意力对齐来自不同模态和范围的特征，生成可靠的中间特征。此外，我们设计了MRIC损失函数来优化可见光、红外和中间特征之间的距离，有助于提取具有判别力的重识别特征。

The feature-level methods map the features of different modalities into a common feature space to reduce the modality discrepancy. A few methods (Ye et al. 2021b; Yang, Chen, and Ye 2023; Lu, Zou, and Zhang 2023) leverage CNN or ViT as the backbone to extract features. Some methods (Chen et al. 2022a; Wan et al. 2023) adopt off-the-shelf key point extractors to generate key point labels of person images and learn modality-irrelevant features. But the key point extractor may introduce noisy labels, deteriorating the disc rim inability of final ReID features. Many VI-ReID methods (Liu, Tan, and Zhou 2020; Huang et al. 2022, 2023)

特征级方法将不同模态的特征映射到共同的特征空间以减少模态差异。部分方法 (Ye et al. 2021b; Yang, Chen and Ye 2023; Lu, Zou and Zhang 2023) 采用CNN或ViT作为骨干网络提取特征。另有方法 (Chen et al. 2022a; Wan et al. 2023) 使用现成的关键点提取器生成行人图像关键点标签，学习模态无关特征。但关键点提取器可能引入噪声标签，降低最终ReID特征的判别能力。许多VI-ReID方法 (Liu, Tan and Zhou 2020; Huang et al. 2022, 2023)

employ the contrastive-based loss, which directly minimizes the distances between VIS and IR features, to obtain a common feature space. However, it is not a trivial task to learn a reasonable common feature space due to the large modality discrepancy between modalities.

采用基于对比的损失函数，直接最小化可见光(VIS)与红外(IR)特征间的距离，以获得共同特征空间。然而，由于模态间存在较大差异，学习合理的共同特征空间并非易事。

Our method belongs to feature-level methods. However, conventional feature-level methods mainly consider firstorder structure information of features (i.e., the pairwise relation across features). Moreover, they directly reduce the distances between VIS and IR features. Different from these methods, our method not only captures high-order structure information of features but also generates middle features, greatly facilitating our model to learn an effective common feature space.

我们的方法属于特征级方法。然而，传统的特征级方法主要考虑特征的一阶结构信息（即特征间的成对关系）。此外，它们直接减小可见光（VIS）与红外（IR）特征之间的距离。与这些方法不同，我们的方法不仅捕捉特征的高阶结构信息，还生成中间特征，极大地促进了模型学习有效的共同特征空间。

Graph Neural Networks in Person Re-Identification. Graph neural network (GNN) is a class of neural networks that is designed to operate on graph-structured data. Li et al. (Li et al. 2021) propose a pose and similarity basedGNN to reduce the problem of pose misalignment for singlemodality person ReID. Wan et al. (Wan et al. 2023) develop a geometry guided dual-alignment strategy to align VIS and IR features, improving the consistency of multi-modality node representations. Different from pairwise connections in the vanilla graph models, Feng et al. (Feng et al. 2019) propose a hypergraph neural network (HGNN) to encode highorder feature correlations in a hypergraph structure. Lu et al. (Lu et al. 2023) model high-order spatio-temporal correlations based on HGNN (which relies on high-quality skeleton labels) for video person ReID.

图神经网络在行人重识别中的应用。图神经网络 (GNN) 是一类专为处理图结构数据而设计的神经网络。Li 等人 (Li et al. 2021) 提出了一种基于姿态和相似性的 GNN 方法，以缓解单模态行人重识别中的姿态错位问题。Wan 等人 (Wan et al. 2023) 开发了几何引导的双对齐策略来对齐可见光 (VIS) 和红外 (IR) 特征，从而提升多模态节点表征的一致性。与传统图模型中的成对连接不同，Feng 等人 (Feng et al. 2019) 提出超图神经网络 (HGNN) 来编码超图结构中的高阶特征关联。Lu 等人 (Lu et al. 2023) 基于 HGNN (该方法依赖高质量骨骼标注) 对视频行人重识别中的高阶时空关联进行建模。

However, the above HGNN-based methods may easily suffer from the model collapse problem (i.e., high-order correlations collapse to a single correlation) since a hyperedge can connect an arbitrary number of nodes. Unlike the above methods, we leverage the whitening operation, which plays the role of “scattering” on the nodes of the hypergraph, to significantly alleviate model collapse.

然而，上述基于HGNN的方法容易因超边可连接任意数量节点而遭遇模型坍塌问题（即高阶相关性坍缩为单一相关性）。与这些方法不同，我们利用白化操作对超图节点进行"散射"式处理，从而显著缓解模型坍塌。

Proposed Method

提出的方法

Overview

概述

The overview of our proposed HOS-Net is given in Figure 1. HOS-Net consists of a backbone, an SLE module, an HSL module, and a CFL module. In this paper, we adopt a two-stream AGW (Ye et al. 2021b) as the backbone. Given a VIS-IR image pair with the same identity, we first pass it through the backbone to obtain paired VIS-IR features. Then, these features are fed into the SLE module to learn short-range and long-range features for each modality. Next, the HSL module exploits high-order structure information of short-range and long-range features based on a whitened hypergraph network. Finally, the CFL module learns a discri mi native common feature space based on middle features that are obtained by aligning VIS and IR features through graph attention. In the CFL module, we develop an MRIC loss to reduce the distances between the VIS, IR, and middle features, greatly smoothing the process of learning the common feature space.

图 1: 展示了我们提出的HOS-Net整体架构。HOS-Net由主干网络、SLE模块、HSL模块和CFL模块组成。本文采用双流AGW (Ye et al. 2021b)作为主干网络。给定同一身份的红外-可见光图像对，首先通过主干网络提取成对的可见光-红外特征。随后，这些特征被输入SLE模块，学习每种模态的短程和长程特征。接着，HSL模块基于白化超图网络利用短程和长程特征的高阶结构信息。最后，CFL模块通过学习中间特征构建判别性公共特征空间，这些中间特征通过图注意力机制对齐可见光和红外特征获得。在CFL模块中，我们设计了MRIC损失函数来缩小可见光、红外及中间特征之间的距离，显著平滑了公共特征空间的学习过程。

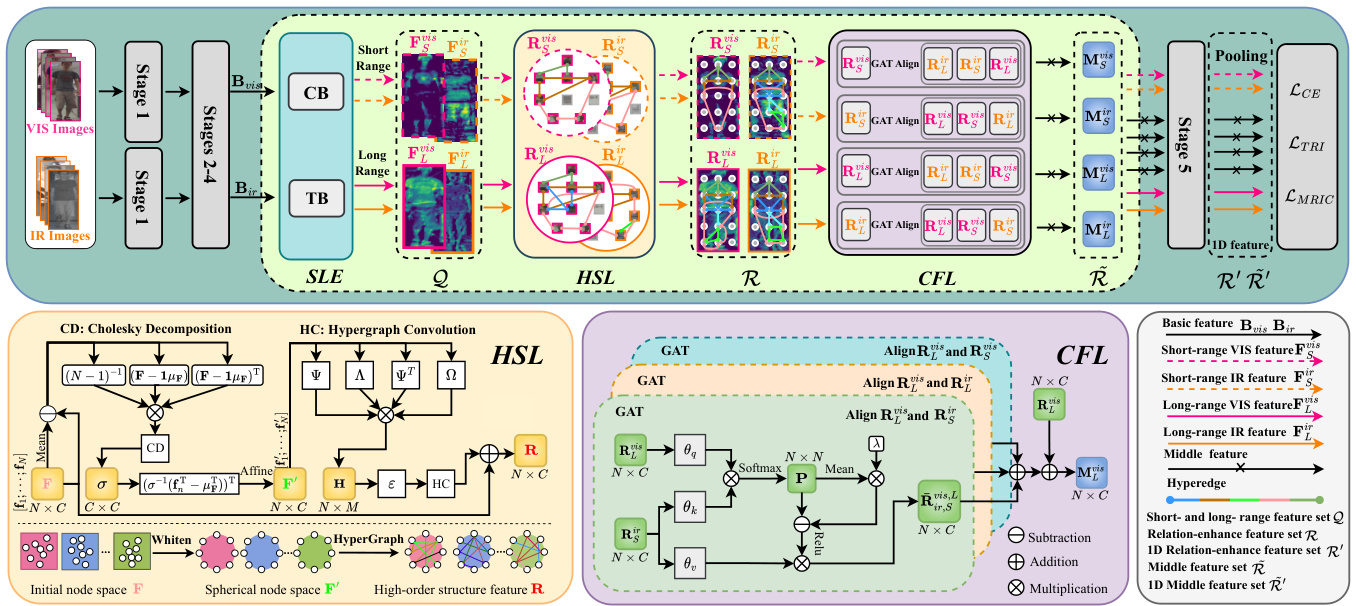
Figure 1: Overview of the proposed HOS-Net, including a backbone, a short- and long-range feature extraction (SLE) module, a high-order structure learning (HSL) module, and a common feature space learning (CFL) module. The HOS-Net is jointly optimized by $\mathcal{L}{C E}$ , $\mathcal{L}{T R I}$ , and $\mathcal{L}_{M R I C}$ .

图 1: 提出的HOS-Net概述，包括一个主干网络、短程和长程特征提取(SLE)模块、高阶结构学习(HSL)模块以及公共特征空间学习(CFL)模块。HOS-Net通过$\mathcal{L}{CE}$、$\mathcal{L}{TRI}$和$\mathcal{L}_{MRIC}$联合优化。

Short- and Long-Range Feature Extraction (SLE) Module

短程与长程特征提取 (SLE) 模块

Conventional VI-ReID methods (Ye et al. 2021b; Yang, Chen, and Ye 2023) often leverage CNN or ViT for feature extraction. CNN excels at capturing short-range features, while ViT is good at obtaining long-range features (Zhang, Hu, and Wang 2022; Chen et al. 2022b). In this paper, we adopt an SLE module to exploit short-range and long-range features by taking advantage of both CNN and ViT. The SLE module contains a convolutional branch (CB) and a Transformer branch (TB). CB contains 3 convolutional blocks and TB contains 2 Transformer blocks with 4 heads. Assume that we have a VIS-IR image pair ${\mathbf{I}^{v i s},\mathbf{I}^{i r}}$ with the same identity. We denote the VIS and IR features obtained from the backbone as ${\bf B}^{v i s}$ and $\mathbf{B}^{i r}$ , respectively.

传统VI-ReID方法 (Ye et al. 2021b; Yang, Chen和Ye 2023) 通常利用CNN或ViT进行特征提取。CNN擅长捕捉短程特征，而ViT善于获取长程特征 (Zhang, Hu和Wang 2022; Chen et al. 2022b)。本文采用SLE模块，通过结合CNN和ViT的优势来利用短程和长程特征。SLE模块包含一个卷积分支(CB)和一个Transformer分支(TB)。CB包含3个卷积块，TB包含2个具有4个头的Transformer块。假设我们有一个具有相同身份的VIS-IR图像对${\mathbf{I}^{v i s},\mathbf{I}^{i r}}$。我们将从主干网络获得的VIS和IR特征分别表示为${\bf B}^{v i s}$和$\mathbf{B}^{i r}$。

Then, ${\bf B}^{v i s}$ and $\mathbf{B}^{i r}$ are fed into the SLE module to obtain short-range and long-range features for each modality, i.e.,

然后，${\bf B}^{v i s}$ 和 $\mathbf{B}^{i r}$ 被输入到 SLE 模块中，以获取每种模态的短程和长程特征，即

$$
\begin{array}{r l}&{{\bf F}{S}^{v i s}=\mathrm{CB}({\bf B}^{v i s}),\quad{\bf F}{L}^{v i s}=\mathrm{TB}({\bf B}^{v i s}),}\ &{{\bf F}{S}^{i r}=\mathrm{CB}({\bf B}^{i r}),\quad{\bf F}_{L}^{i r}=\mathrm{TB}({\bf B}^{i r}),}\end{array}
$$

$$
\begin{array}{r l}&{{\bf F}{S}^{v i s}=\mathrm{CB}({\bf B}^{v i s}),\quad{\bf F}{L}^{v i s}=\mathrm{TB}({\bf B}^{v i s}),}\ &{{\bf F}{S}^{i r}=\mathrm{CB}({\bf B}^{i r}),\quad{\bf F}_{L}^{i r}=\mathrm{TB}({\bf B}^{i r}),}\end{array}
$$

where $\mathrm{CB}(\cdot)$ and $\mathrm{TB}(\cdot)$ represent the convolutional branch and the Transformer branch, respectively; $\mathbf{F}{S}^{v i s}\in\mathbb{R}^{H\times W\times C}$ and $\mathbf{F}{S}^{i r}~ \in~\mathbb{R}^{H\times W\times C}$ denote the short-range features for the VIS and IR images, respectively; $\mathbf{F}{L}^{v i s}\in\mathbb{R}^{H\times W\times C}$ and $\mathbf{F}{L}^{i r}\in\mathbb{R}^{H\times W\times C}$ denote the long-range features for the VIS and IR images, respectively; $H,W$ , and $C$ denote the height, width, and channel number of the feature, respectively. Thus, for a VIS-IR image pair, we can obtain the feature set $\mathcal{Q}={{\bf F}{L}^{v i s},{\bf F}{S}^{v i s},{\bf F}{L}^{i\bar{r}},\bar{\bf F}_{S}^{i r}}$ , which is used as the input of the HSL module.

其中 $\mathrm{CB}(\cdot)$ 和 $\mathrm{TB}(\cdot)$ 分别表示卷积分支和 Transformer 分支；$\mathbf{F}{S}^{v i s}\in\mathbb{R}^{H\times W\times C}$ 和 $\mathbf{F}{S}^{i r}\in~\mathbb{R}^{H\times W\times C}$ 分别表示可见光(VIS)和红外(IR)图像的短程特征；$\mathbf{F}{L}^{v i s}\in\mathbb{R}^{H\times W\times C}$ 和 $\mathbf{F}{L}^{i r}\in\mathbb{R}^{H\times W\times C}$ 分别表示可见光和红外图像的长程特征；$H,W$ 和 $C$ 分别表示特征的高度、宽度和通道数。因此，对于可见光-红外图像对，我们可以获得特征集 $\mathcal{Q}={{\bf F}{L}^{v i s},{\bf F}{S}^{v i s},{\bf F}{L}^{i\bar{r}},\bar{\bf F}_{S}^{i r}}$，该集合将作为 HSL 模块的输入。

High-Order Structure Learning (HSL) Module

高阶结构学习 (HSL) 模块

The features extracted from the SLE module only encode pixel-wise and region-wise dependencies in the person images. However, the high-order structure information, which indicates different levels of relation in the features (e.g., head, torso, upper arm, and lower arm belongs to the upper part of the body while head, torso, arm, and leg belong to the whole body), is not well exploited. Therefore, inspired by HGNN (Feng et al. 2019), we introduce the HSL module to capture high-order correlations across different local features, enhancing feature representations. Note that the conventional HGNN tends to suffer from the problem of model collapse. To alleviate this problem, we take advantage of the whitening operation and apply it to the hypergraph network, as shown in Figure 1.

从SLE模块提取的特征仅编码了人物图像中像素级和区域级的依赖关系。然而，高阶结构信息（例如头部、躯干、上臂和下臂属于身体上半部分，而头部、躯干、手臂和腿属于整个身体）所表示的特征间多层次关系尚未得到充分利用。因此，受HGNN (Feng et al. 2019) 启发，我们引入HSL模块来捕捉不同局部特征间的高阶相关性，从而增强特征表示。需要注意的是，传统HGNN容易陷入模型坍塌问题。为缓解该问题，我们利用白化操作并将其应用于超图网络，如图 1 所示。

Different from pairwise connections in the vanilla graph models, a hypergraph can connect an arbitrary number of nodes to exploit high-order structure information. We construct a whitened hypergraph for each feature in $\mathcal{Q}$ . The hypergraph is defined as $\bar{\mathcal{G}}~=(\mathcal{V},\mathcal{E},\mathbf{W})$ , where $\nu=$ ${v_{1},\cdots,v_{N}}$ denotes the node set, $\mathcal{E}={e_{1},\cdots,e_{M}}$ denotes the hyperedge set, and W represents the weight matrix of the hyperedge set. Here, $N=H W$ and $M$ are the numbers of nodes and hyperedges, respectively. In this paper, we consider each $1\times1\times C$ grid of each feature in $\mathcal{Q}$ as a node. We represent the $n$ -th node by $\mathbf{f}{n}\in\mathbb{R}^{1\times C}$ and thus all nodes are represented by $\mathbf{F}=[\mathbf{f}{1};\cdot\cdot\cdot;\mathbf{f}_{N}]\in\mathbb{R}^{N\times C}$ .

与传统图模型中的成对连接不同，超图 (hypergraph) 可以连接任意数量的节点以利用高阶结构信息。我们为 $\mathcal{Q}$ 中的每个特征构建一个白化超图，该超图定义为 $\bar{\mathcal{G}} =~(\mathcal{V},\mathcal{E},\mathbf{W})$ ，其中 $\nu=$ ${v_{1},\cdots,v_{N}}$ 表示节点集， $\mathcal{E}={e_{1},\cdots,e_{M}}$ 表示超边集，W 表示超边集的权重矩阵。这里 $N=H W$ 和 $M$ 分别是节点和超边的数量。在本文中，我们将 $\mathcal{Q}$ 中每个特征的 $1\times1\times C$ 网格视为一个节点，并用 $\mathbf{f}{n}\in\mathbb{R}^{1\times C}$ 表示第 $n$ 个节点，因此所有节点可表示为 $\mathbf{F}=[\mathbf{f}{1};\cdot\cdot\cdot;\mathbf{f}_{N}]\in\mathbb{R}^{N\times C}$ 。

The traditional hypergraph network allows for unrestricted connections among nodes to capture high-order structure information. Hence, it easily suffers from model collapse (i.e., the nodes connected by different hyperedges are the same) during hypergraph learning. To mitigate this problem, we introduce a whitening operation to project the nodes into a spherical distribution. In fact, the whitening operation plays the role of “scattering” on the nodes, thereby avoiding the collapse of diverse high-order connections to a single connection. This enables us to explore various highorder relationships across these features effectively.

传统超图网络允许节点之间无限制连接以捕获高阶结构信息。因此，在超图学习过程中容易发生模型坍塌（即不同超边连接的节点完全相同）。为解决该问题，我们引入白化操作将节点投影至球面分布。实际上，白化操作对节点起到"分散"作用，从而避免多样高阶连接坍缩为单一连接，使我们能有效探索这些特征间的各类高阶关系。

The whitened node $\mathbf{f}_{n}^{\prime}$ can be obtained as

白化节点 $\mathbf{f}_{n}^{\prime}$ 可通过以下方式获得

$$
\mathbf{f}{n}^{\prime}=\gamma_{n}\big(\sigma^{-1}(\mathbf{f}{n}^{\mathrm{T}}-\mu_{\mathbf{F}}^{\mathrm{T}})\big)^{\mathrm{T}}+\beta_{n,}
$$

$$
\mathbf{f}{n}^{\prime}=\gamma_{n}\big(\sigma^{-1}(\mathbf{f}{n}^{\mathrm{T}}-\mu_{\mathbf{F}}^{\mathrm{T}})\big)^{\mathrm{T}}+\beta_{n,}
$$

where $\sigma_{\mathrm{ \scriptsize~\in~\mathbb{R}^{C\times C} }}$ denotes the lower triangular matrix, which is obtained by the Cholesky decomposition $\sigma\sigma^{\mathrm{{T}}}=$ N1 1 (F − 1µF)T(F − 1µF); µF ∈ R1×C denotes the mean vector of $\mathbf{F}$ ; $\mathbf{1} \in~\mathbb{R}^{N\times1}$ is a column vector of all ones; $\gamma_{n} \in~\mathbb{R}^{1\times1}$ and $\beta_{n} \in~\mathbb{R}^{1\times C}$ are the affine parameters learned from the network. In this way, all the whitened nodes can be represented by $\mathbf{F}^{\prime}=[\mathbf{f}{1}^{\prime};\cdot\cdot\cdot;\mathbf{\dot{f}}_{N}^{\prime}]\in\mathbb{R}^{N\times C}$ .

其中 $\sigma_{\mathrm{ \scriptsize~\in~\mathbb{R}^{C\times C} }}$ 表示通过Cholesky分解 $\sigma\sigma^{\mathrm{{T}}}=$ N1 1 (F − 1µF)T(F − 1µF) 得到的下三角矩阵；$\mu_F \in \mathbb{R}^{1\times C}$ 表示 $\mathbf{F}$ 的均值向量；$\mathbf{1} \in~\mathbb{R}^{N\times1}$ 是全1列向量；$\gamma_{n} \in\mathbb{R}^{1\times1}$ 和 $\beta_{n} \in~\mathbb{R}^{1\times C}$ 是从网络中学到的仿射参数。这样，所有白化节点可以表示为 $\mathbf{F}^{\prime}=[\mathbf{f}{1}^{\prime};\cdot\cdot\cdot;\mathbf{\dot{f}}_{N}^{\prime}]\in\mathbb{R}^{N\times C}$。

Similar to (Higham and de Kergorlay 2022), we use crosscorrelation to learn the incidence matrix $\mathbf{H}\in\mathbb{R}^{N\times M}$ , i.e.,

类似于 (Higham 和 de Kergorlay 2022)，我们使用互相关学习关联矩阵 $\mathbf{H}\in\mathbb{R}^{N\times M}$，即

$$
\mathbf{H}=\varepsilon(\Psi(\mathbf{F}^{\prime})\Lambda(\mathbf{F}^{\prime})\Psi(\mathbf{F}^{\prime})^{\mathrm{T}}\boldsymbol{\Omega}(\mathbf{F}^{\prime})),
$$

$$
\mathbf{H}=\varepsilon(\Psi(\mathbf{F}^{\prime})\Lambda(\mathbf{F}^{\prime})\Psi(\mathbf{F}^{\prime})^{\mathrm{T}}\boldsymbol{\Omega}(\mathbf{F}^{\prime})),
$$

where $\Psi(\cdot)$ represents the linear transformation; $\Lambda(\cdot)$ and $\Omega(\cdot)$ are responsible for learning a distance metric by a diagonal operation and determining the contribution of the node to the corresponding hyperedges through the learnable parameters, respectively; $\varepsilon(\cdot)$ is the step function.

其中 $\Psi(\cdot)$ 表示线性变换；$\Lambda(\cdot)$ 和 $\Omega(\cdot)$ 分别负责通过对角操作学习距离度量，以及通过可学习参数确定节点对相应超边的贡献；$\varepsilon(\cdot)$ 是阶跃函数。

Based on the learned $\mathbf{H}$ , we adopt a hypergraph convolutional operation to aggregate high-order structure information and then enhance feature representations. The relation enhanced feature $\mathbf{R}\in\mathbb{R}^{N\times C}$ can be obtained as

基于学习到的$\mathbf{H}$，我们采用超图卷积操作来聚合高阶结构信息，进而增强特征表示。关系增强特征$\mathbf{R}\in\mathbb{R}^{N\times C}$可通过以下方式获得：

$$
\mathbf{R}=(\mathbf{I}-\mathbf{D}^{1/2}\mathbf{H}\mathbf{W}\mathbf{B}^{-1}\mathbf{H}^{\mathrm{T}}\mathbf{D}^{-1/2})\mathbf{F}^{\prime}\boldsymbol{\Theta}+\mathbf{F},
$$

$$
\mathbf{R}=(\mathbf{I}-\mathbf{D}^{1/2}\mathbf{H}\mathbf{W}\mathbf{B}^{-1}\mathbf{H}^{\mathrm{T}}\mathbf{D}^{-1/2})\mathbf{F}^{\prime}\boldsymbol{\Theta}+\mathbf{F},
$$

where $\mathbf{I}\in\mathbb{R}^{N\times N}$ is the identity matrix; $\mathbf{W_{\lambda}}\in\mathbb{R}^{M\times M}$ denotes the weight matrix; ${\bf D}\in\dot{\mathbb{R}}^{N\times N}$ and $\mathbf{B}\in\mathbb{R}^{M\times M}$ represent the node degree matrix and the hyperedge degree matrix obtained by the broadcast operation, respectively; Θ ∈ RC×C denotes the learnable parameters.

其中 $\mathbf{I}\in\mathbb{R}^{N\times N}$ 是单位矩阵；$\mathbf{W_{\lambda}}\in\mathbb{R}^{M\times M}$ 表示权重矩阵；${\bf D}\in\dot{\mathbb{R}}^{N\times N}$ 和 $\mathbf{B}\in\mathbb{R}^{M\times M}$ 分别表示通过广播操作获得的节点度矩阵和超边度矩阵；Θ ∈ RC×C 表示可学习参数。

Following the above process, we pass features in $\mathcal{Q}$ through the HSL module and obtain a relation-enhanced feature set $\mathcal{R}={{\bf R}{L}^{v i s},{\bf R}{S}^{v i s},{\bf R} {L}^{i r},{\bf R}_{S}^{i r}}$ , where each feature in $\mathcal{R}$ is obtained by Eq. (4).

按照上述流程，我们将特征集 $\mathcal{Q}$ 通过HSL模块处理，得到关系增强的特征集 $\mathcal{R}={{\bf R}{L}^{v i s},{\bf R}{S}^{v i s},{\bf R}{L}^{i r},{\bf R}_{S}^{i r}}$ ，其中 $\mathcal{R}$ 中的每个特征均由公式(4)计算获得。

Common Feature Space Learning (CFL) Module

通用特征空间学习 (CFL) 模块

Conventional feature-level VI-ReID methods usually learn a common feature space based on a contrastive-based loss, which directly minimizes the distances between VIS and IR features. However, such a manner cannot achieve a reasonable common feature space because of the large modality discrepancy. To address the above problem, it is desirable to learn the middle features from VIS and IR features, enabling us to obtain a reasonable common feature space.

传统的基于特征级别的可见光-红外行人重识别(VI-ReID)方法通常通过对比损失(contrastive-based loss)学习一个共同特征空间，直接最小化可见光(VIS)与红外(IR)特征之间的距离。然而，由于模态差异较大，这种方式难以获得合理的共同特征空间。为解决该问题，需要从可见光与红外特征中学习中间特征，从而构建合理的共同特征空间。

A straightforward way to obtain a middle feature is to add or concatenate the VIS or IR features from different ranges. However, the above way cannot generate reliable middle features due to feature misalignment and loss of semantic information. Therefore, we propose a CFL module, which aligns the features from different modalities and ranges by graph attention (GAT) (Guo et al. 2021) and generates reliable middle features, as shown in Figure 1.

获取中间特征的一种直接方法是对不同范围下的可见光(VIS)或红外(IR)特征进行相加或拼接。然而，由于特征错位和语义信息丢失，上述方法无法生成可靠的中间特征。因此，我们提出了CFL模块，该模块通过图注意力网络(GAT) (Guo et al. 2021) 对齐来自不同模态和范围的特征，并生成可靠的中间特征，如图 1 所示。

Specifically, we align each feature in $\mathcal{R}$ with the other three features in $\mathcal{R}$ and generate a middle feature, which involves the information from different modalities and ranges. We take the alignment between two features ${\bf R}{L}^{v i s}$ and $\mathbf{R}{S}^{i r}$ as an example. First, we establish the similarity between ${\bf R}{L}^{v i s}$ and $\mathbf{R}_{S}^{i r}$ by using the inner product and the softmax function. This process can be formulated as

具体来说，我们将 $\mathcal{R}$ 中的每个特征与其他三个特征对齐，并生成一个中间特征，该特征包含来自不同模态和范围的信息。以两个特征 ${\bf R}{L}^{v i s}$ 和 $\mathbf{R}{S}^{i r}$ 的对齐为例。首先，我们通过内积和 softmax 函数建立 ${\bf R}{L}^{v i s}$ 和 $\mathbf{R}_{S}^{i r}$ 之间的相似性。这一过程可以表述为

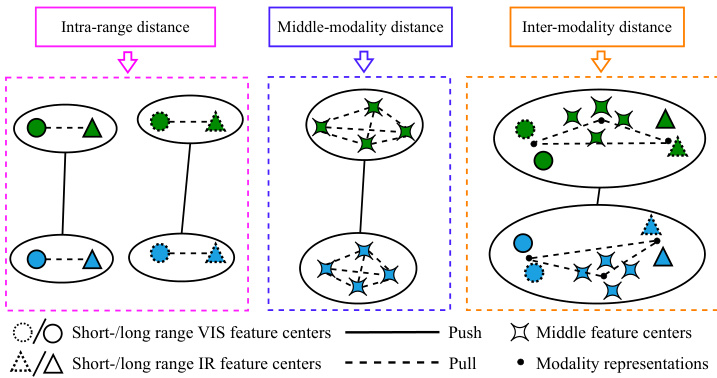
Figure 2: Illustration of the proposed MRIC loss. Different colors represent different identities.

图 2: 提出的MRIC损失示意图。不同颜色代表不同身份。

$$
\mathbf{P}=\mathrm{Softmax}((\theta_{q}\mathbf{R}{L}^{v i s})(\theta_{k}\mathbf{R}_{S}^{i r})^{\mathrm{T}}),
$$

$$
\mathbf{P}=\mathrm{Softmax}((\theta_{q}\mathbf{R}{L}^{v i s})(\theta_{k}\mathbf{R}_{S}^{i r})^{\mathrm{T}}),
$$

where $\theta_{q}$ and $\theta_{k}$ are linear transformations; $\mathbf{P}\in\mathbb{R}^{N\times N}$ denotes the similarity matrix; and $\operatorname{Softmax}(\cdot)$ denotes the softmax function.

其中 $\theta_{q}$ 和 $\theta_{k}$ 是线性变换；$\mathbf{P}\in\mathbb{R}^{N\times N}$ 表示相似度矩阵；$\operatorname{Softmax}(\cdot)$ 表示 softmax 函数。

Then, we adopt graph attention to perform alignment between ${\bf R}{L}^{v i s}$ and $\mathbf{R}{S}^{i r}$ according to the similarity matrix. Therefore, the aggregated node $\bar{\mathbf{R}}_{i r,S}^{v i s,L}\in\mathbb{R}^{N\times C}$ is

然后，我们采用图注意力机制根据相似度矩阵对 ${\bf R}{L}^{v i s}$ 和 $\mathbf{R}{S}^{i r}$ 进行对齐。因此，聚合节点 $\bar{\mathbf{R}}_{i r,S}^{v i s,L}\in\mathbb{R}^{N\times C}$ 为

$$
\begin{array}{r}{\bar{\mathbf{R}}{i r,S}^{v i s,L}=\mathrm{GAT}(\mathbf{R}{L}^{v i s},\mathbf{R}{S}^{i r})\quad\quad}\ {=\mathrm{ReLU}(\mathbf{P}-\lambda\mathrm{Mean}(\mathbf{P})\mathbf{11}^{\mathrm{T}})(\theta_{v}\mathbf{R}_{S}^{i r}),}\end{array}
$$

$$
\begin{array}{r}{\bar{\mathbf{R}}{i r,S}^{v i s,L}=\mathrm{GAT}(\mathbf{R}{L}^{v i s},\mathbf{R}{S}^{i r})\quad\quad}\ {=\mathrm{ReLU}(\mathbf{P}-\lambda\mathrm{Mean}(\mathbf{P})\mathbf{11}^{\mathrm{T}})(\theta_{v}\mathbf{R}_{S}^{i r}),}\end{array}
$$

where $\mathrm{GAT}(\cdot)$ denotes the graph attention operation; $\theta_{v}$ is the linear transformation; $\lambda$ is the balancing parameter that reduces nodes with low similarity; $\mathbf{11}^{\mathrm{T}}\in\mathbb{R}^{\ln^{\mathrm{\sum}}N^{\mathrm{\sum}}N}$ is a matrix of all ones; and $\mathrm{ReLU}(\cdot)$ and $\mathrm{Mean}(\cdot)$ represent the ReLU activation function and the mean operation, respectively.

其中 $\mathrm{GAT}(\cdot)$ 表示图注意力操作；$\theta_{v}$ 为线性变换；$\lambda$ 是降低低相似度节点影响的平衡参数；$\mathbf{11}^{\mathrm{T}}\in\mathbb{R}^{\ln^{\mathrm{\sum}}N^{\mathrm{\sum}}N}$ 为全1矩阵；$\mathrm{ReLU}(\cdot)$ 和 $\mathrm{Mean}(\cdot)$ 分别代表ReLU激活函数与均值运算。

Based on the above, a middle feature $\mathbf{M}{L}^{v i s}\in\mathbb{R}^{N\times C}$ is obtained by aligning ${\bf R}{L}^{v i s}$ with $\mathbf{R}{S}^{i r},\mathbf{R}{L}^{i r}$ , and ${\bf R}_{S}^{v i s}$ , that is,

基于上述方法，通过将 ${\bf R}{L}^{v i s}$ 与 $\mathbf{R}{S}^{i r}$、$\mathbf{R}{L}^{i r}$ 以及 ${\bf R}{S}^{v i s}$ 对齐，得到一个中间特征 $\mathbf{M}_{L}^{v i s}\in\mathbb{R}^{N\times C}$，即

$$
\begin{array}{r}{{\bf M}{L}^{v i s}=\mathrm{GAT}({\bf R}{L}^{v i s},{\bf R}{S}^{i r})+\mathrm{GAT}({\bf R}{L}^{v i s},{\bf R}{L}^{i r})+}\ {\mathrm{GAT}({\bf R}{L}^{v i s},{\bf R}{S}^{v i s})+{\bf R}_{L}^{v i s}.\qquad}\end{array}
$$

$$
\begin{array}{r}{{\bf M}{L}^{v i s}=\mathrm{GAT}({\bf R}{L}^{v i s},{\bf R}{S}^{i r})+\mathrm{GAT}({\bf R}{L}^{v i s},{\bf R}{L}^{i r})+}\ {\mathrm{GAT}({\bf R}{L}^{v i s},{\bf R}{S}^{v i s})+{\bf R}_{L}^{v i s}.\qquad}\end{array}
$$

To mitigate the intra-class difference and inter-class discrepancy, we propose the MRIC loss to improve feature representations and reduce the distances between the VIS, IR, and middle features. The MRIC loss consists of three items: an intra-range loss, a middle feature loss, and an intermodality loss based on the identity centers. The illustration of the MRIC loss is shown in Figure 2.

为缓解类内差异和类间差异，我们提出MRIC损失函数来改进特征表示并缩小可见光(VIS)、红外(IR)与中间特征之间的距离。MRIC损失包含三个组成部分：类内距离损失、中间特征损失以及基于身份中心的跨模态损失。该损失函数示意图如图2所示。

Technically, we first obtain identity centers, which are robust to pedestrian appearance changes, by the weighted average of the features of each person at one modality and a specific range. For instance, the center of the relation-enhanced features for the person with the identity $i$ at the VIS modality and long-range can be obtained as

技术上，我们首先通过单模态特定范围内各行人特征的加权平均，获得对行人外观变化具有鲁棒性的身份中心。例如，身份 $i$ 在可见光(VIS)模态和长距离下的关系增强特征中心可表示为

$$
\mathbf{c}{L,i}^{v i s}=\sum_{j=1}^{K}\frac{\exp({\sum_{k=1}^{K}\mathbf{r}{L,i,j}^{v i s}\mathbf{r}{L,i,k}^{v i s}}^{\mathrm{T}})}{\sum_{j=1}^{K}\exp({\sum_{k=1}^{K}\mathbf{r}{L,i,j}^{v i s}\mathbf{r}{L,i,k}^{v i s}}^{\mathrm{T}})}\mathbf{r}_{L,i,j}^{v i s},
$$

$$
\mathbf{c}{L,i}^{v i s}=\sum_{j=1}^{K}\frac{\exp({\sum_{k=1}^{K}\mathbf{r}{L,i,j}^{v i s}\mathbf{r}{L,i,k}^{v i s}}^{\mathrm{T}})}{\sum_{j=1}^{K}\exp({\sum_{k=1}^{K}\mathbf{r}{L,i,j}^{v i s}\mathbf{r}{L,i,k}^{v i s}}^{\mathrm{T}})}\mathbf{r}_{L,i,j}^{v i s},
$$

where $K$ is the number of VIS features of each person; $\mathbf{r}_{L,i,k}^{v i s}\in\mathbb{R}^{1\times C^{\prime}}$ denotes the $k$ -th 1D relation-enhanced longrange VIS feature defined in $\mathcal{R}^{\prime}$ with the identity $i$ .

其中 $K$ 表示每个人的 VIS (Visual Identity-Sensitive) 特征数量；$\mathbf{r}_{L,i,k}^{v i s}\in\mathbb{R}^{1\times C^{\prime}}$ 表示在 $\mathcal{R}^{\prime}$ 中定义的、身份标识为 $i$ 的第 $k$ 个一维关系增强长程 VIS 特征。

Accordingly, we can obtain the identity center sets $\mathcal{C}{L}^{v i s}$ $({\mathbf{c}{L,i}^{v i\check{s}}}{i=1}^{P})$ , $\mathcal{C}{S}^{v i s}$ $({\mathbf{c}{S,i}^{v i s}}{i=1}^{P})$ , $\mathcal{C}{L}^{i r}$ $({\mathbf{c}{L,i}^{i r}}{i=1}^{P})$ , $\mathcal{C}{S}^{i r}$ ${\mathbf{c}{S,i}^{i r}}{i=1}^{P})$ , $\tilde{\mathcal{C}}{L}^{v i s}$ $({\tilde{\mathbf{c}}{L,i}^{v i s}}{i=1}^{P})$ , $\tilde{\mathcal{C}}{S}^{v i s}$ $({\tilde{\mathbf{c}}{S,i}^{v i s}}{i=1}^{P})$ , $\tilde{\mathcal{C}}{L}^{i r}$ $({\tilde{\mathbf{c}}{L,i}^{i r}}{i=1,}^{P}),\tilde{\mathcal{C}}{S}^{i r}({\tilde{\mathbf{c}}{S,i}^{i r}}_{i=1}^{P}).$ , where $\mathcal{C}$ and $\tilde{\mathcal{C}}$ represent the center set for the enhanced features and the middle features at a specific range and modality, respectively; $P$ is the number of person identities in the training set.

因此，我们可以得到身份中心集 $\mathcal{C}{L}^{v i s}$ $({\mathbf{c}{L,i}^{v i\check{s}}}{i=1}^{P})$、$\mathcal{C}{S}^{v i s}$ $({\mathbf{c}{S,i}^{v i s}}{i=1}^{P})$、$\mathcal{C}{L}^{i r}$ $({\mathbf{c}{L,i}^{i r}}{i=1}^{P})$、$\mathcal{C}{S}^{i r}$ ${\mathbf{c}{S,i}^{i r}}{i=1}^{P})$、$\tilde{\mathcal{C}}{L}^{v i s}$ $({\tilde{\mathbf{c}}{L,i}^{v i s}}{i=1}^{P})$、$\tilde{\mathcal{C}}{S}^{v i s}$ $({\tilde{\mathbf{c}}{S,i}^{v i s}}{i=1}^{P})$、$\tilde{\mathcal{C}}{L}^{i r}$ $({\tilde{\mathbf{c}}{L,i}^{i r}}{i=1,}^{P})$、$\tilde{\mathcal{C}}{S}^{i r}({\tilde{\mathbf{c}}{S,i}^{i r}}_{i=1}^{P})$。其中，$\mathcal{C}$ 和 $\tilde{\mathcal{C}}$ 分别表示特定范围和模态下增强特征和中间特征的中心集；$P$ 为训练集中人员身份的数量。

The intra-range loss LSMLR IC is to reduce the distances between the same-r