Deep Constrained Least Squares for Blind Image Super-Resolution

基于深度约束最小二乘的盲图像超分辨率重建

Figure 1. Blind super-resolution of Img 28 from DIV2KRK [3], for scale factor 4. Based on the proposed deep constrained least squares (DCLS) de convolution, our method is effective in restoring sharp and clean edges, and outperforms previous state-of-the-art approaches such as KernelGAN $[3]+Z S S\mathrm{\textperthousand}$ [41], IKC [9], DAN [30, 31], AdaTarget [14], and KOALAnet [19].

图 1: 基于DIV2KRK [3]数据集中Img 28的盲超分辨率重建（放大因子4）。通过提出的深度约束最小二乘(DCLS)反卷积方法，我们的方案能有效恢复清晰锐利的边缘，其性能优于KernelGAN $[3]+Z S S\mathrm{\textperthousand}$ [41]、IKC [9]、DAN [30, 31]、AdaTarget [14]和KOALAnet [19]等现有最优方法。

Abstract

摘要

In this paper, we tackle the problem of blind image superresolution(SR) with a reformulated degradation model and two novel modules. Following the common practices of blind SR, our method proposes to improve both the kernel estimation as well as the kernel based high resolution image restoration. To be more specific, we first reformulate the degradation model such that the deblurring kernel estimation can be transferred into the low resolution space. On top of this, we introduce a dynamic deep linear filter module. Instead of learning a fixed kernel for all images, it can adaptively generate deblurring kernel weights conditional on the input and yields more robust kernel estimation. Subsequently, a deep constrained least square filtering module is applied to generate clean features based on the reformulation and estimated kernel. The deblurred feature and the low input image feature are then fed into a dual-path structured SR network and restore the final high resolution result. To evaluate our method, we further conduct evaluations on several benchmarks, including Gaussian8 and DIV2KRK. Our experiments demonstrate that the proposed method achieves better accuracy and visual improvements against state-of-the-art methods.

本文通过重新构建退化模型和引入两个新模块，解决了盲图像超分辨率(SR)问题。遵循盲SR的常规做法，我们的方法旨在改进核估计以及基于核的高分辨率图像恢复。具体而言，我们首先重构退化模型，使得去模糊核估计可以转换到低分辨率空间。在此基础上，我们提出了动态深度线性滤波模块，该模块能够根据输入自适应生成去模糊核权重，而非为所有图像学习固定核，从而获得更稳健的核估计。随后，应用深度约束最小二乘滤波模块，基于重构模型和估计核生成清晰特征。去模糊特征与低分辨率输入图像特征随后被送入双路径结构的SR网络，最终恢复出高分辨率结果。为评估方法性能，我们在Gaussian8和DIV2KRK等多个基准测试上进行了实验验证。结果表明，所提方法在精度和视觉效果上均优于当前最优方法。

1. Introduction

1. 引言

In this work, we study the problem of image superresolution,i.e., restoring high-resolution images from lowresolution inputs. Specially, we aim for single image superresolution (SISR), where only one observation is given which is a more practical setting and with a wide range of downstream applications [6, 8, 10, 17, 22, 26, 28, 48, 57, 59].

在本工作中，我们研究图像超分辨率问题，即从低分辨率输入恢复高分辨率图像。特别地，我们专注于单图像超分辨率 (SISR)，其中仅给定一个观测值，这是一种更实用的设置，并具有广泛的下游应用 [6, 8, 10, 17, 22, 26, 28, 48, 57, 59]。

Most existing works based on the classical SISR degradation model assuming that the input LR image $\mathbf{y}$ is a blurred and down-scaled HR image $\mathbf{x}$ with additional white Gaussian noise $\mathbf{n}$ , given by

大多数现有工作基于经典的SISR（单图像超分辨率）退化模型，假设输入的低分辨率(LR)图像$\mathbf{y}$是由高分辨率(HR)图像$\mathbf{x}$经过模糊和下采样后叠加高斯白噪声$\mathbf{n}$得到的，其表达式为

$$
\mathbf{y}=(\mathbf{x}*\mathbf{k}{h})_{\downarrow s}+\mathbf{n},
$$

$$
\mathbf{y}=(\mathbf{x}*\mathbf{k}{h})_{\downarrow s}+\mathbf{n},
$$

where $\mathbf{k}{h}$ is the blur kernel applied on $\mathbf{x},*$ denotes convolution operation and $\downarrow_{s}$ denotes down sampling with scale fac- tor $s$ . Previous blind SR approaches [9, 30] generally solve this problem with a two-stage framework: kernel estimation from LR image and kernel based HR image restoration.

其中 $\mathbf{k}{h}$ 是应用于 $\mathbf{x}$ 的模糊核，$*$ 表示卷积操作，$\downarrow_{s}$ 表示尺度因子为 $s$ 的下采样。以往的盲超分辨率方法 [9, 30] 通常采用两阶段框架解决该问题：从低分辨率图像估计核，以及基于核的高分辨率图像恢复。

We argue that although such a pipeline demonstrates reasonable performance for SR problem, there are two main drawbacks: First of all, it is difficult to accurately estimate blur kernels of HR space directly from LR images due to the ambiguity produced by under sampling step [38, 46]. And the mismatch between the estimated kernel and the real one will cause significant performance drop and even lead to unpleasant artifacts [3, 9, 13, 56]. Secondly, it is also challenging to find a suitable way to fully utilize the information of the estimated HR space kernel and LR space image. A common solution is to employ a kernel stretching strategy [9,30,56], where the principal components of the vectorized kernel are preserved and stretched into degradation maps with the same size as the LR input. These degradation maps then can be concatenated with the input image or its features to generate a clean HR image. However, the spatial relation of the kernel is destroyed by the process of vector i zing and PCA (Principal Component Analysis), which causes insufficient usage of the kernel. The subsequent reconstruction network requires a huge effort to harmonize the inconsistent information between LR features and HR-specific kernels, limiting its performance in super-resolving images.

我们认为，尽管这种流程在超分辨率(SR)问题上表现出合理性能，但仍存在两个主要缺陷：首先，由于欠采样步骤产生的模糊性[38,46]，直接从低分辨率(LR)图像准确估计高分辨率(HR)空间的模糊核十分困难。而估计核与真实核之间的不匹配会导致性能显著下降，甚至产生不理想的伪影[3,9,13,56]。其次，如何充分利用估计的HR空间核与LR空间图像的信息也颇具挑战性。常见解决方案是采用核拉伸策略[9,30,56]，该策略保留向量化核的主成分并将其拉伸为与LR输入尺寸相同的退化图。这些退化图随后可与输入图像或其特征拼接以生成清晰的HR图像。然而，向量化和PCA(主成分分析)过程破坏了核的空间关系，导致核信息利用不足。后续重建网络需要耗费大量精力协调LR特征与HR专属核之间的不一致信息，从而限制了其在图像超分辨率重建中的性能。

Towards this end, we present a modified learning strategy to tackle the blind SR problem, which can naturally avoid the above mentioned drawbacks. Specifically, we first reformulate the degradation model in a way such that the blur kernel estimation and image upsampling can be disentangled. In particular, as shown in Fig. 2, we derive a new kernel from the primitive kernel $\mathbf{k}_{h}$ and LR image. It transfers the kernel estimation into the LR space and the new kernel can be estimated without aliasing ambiguity. Based on the new degradation, we further introduce the dynamic deep linear kernel (DDLK) to provide more equivalent choices of possible optimal solutions for the kernel to accelerate training. Subsequently, a novel deep constrained least squares (DCLS) de convolution module is applied in the feature domain to obtain deblurred features. DCLS is robust to noise and can provide a theoretical and principled guidance to obtain clean images/features from blurred inputs. Moreover, it dosen’t require kernel stretching strategy and thus preserves the kernel’s spatial relation information. Then the deblurred features are fed into an upsampling module to restore the clean HR images. As illustrated in Fig. 1, the overall method has turned out to be surprisingly effective in recovering sharp and clean SR images.

为此，我们提出一种改进的学习策略来解决盲超分辨率问题，该方法能自然规避上述缺陷。具体而言，我们首先重构退化模型，使模糊核估计与图像上采样过程解耦。如图2所示，我们从原始核$\mathbf{k}_{h}$和低分辨率图像中推导出新核，将核估计转换至低分辨率空间，从而消除混叠歧义性。基于新退化模型，我们进一步引入动态深度线性核（DDLK），为核优化提供更多等效解选择以加速训练。随后，在特征域应用新型深度约束最小二乘（DCLS）反卷积模块获取去模糊特征。DCLS具有噪声鲁棒性，能为模糊输入到清晰图像/特征的转换提供理论化原则指导，且无需核拉伸策略，从而保留核的空间关系信息。最终将去模糊特征输入上采样模块重建高分辨率图像。如图1所示，该方法在恢复锐利清晰超分图像方面展现出显著效果。

The main contributions are summarized as follows:

主要贡献总结如下:

• We introduce a new practical degradation model derived from Eq. (1). Such degradation maintains consistency with the classical model and allows us reliably estimate blur kernel from low-resolution space. • We propose to use a dynamic deep linear kernel instead of a single layer kernel, which provides more equivalent choices of the optimal solution of the kernel, which is easier to learn.

• 我们基于公式(1) 推导出一种新的实用退化模型。该模型与经典模型保持一致性，并能可靠地从低分辨率空间估计模糊核。
• 我们提出使用动态深度线性核替代单层核，这为核的最优解提供了更多等效选择，从而更易于学习。

Figure 2. Kernel reformulation examples. The top row and middle row are the LR images and the corresponding primitive kernels. The bottom row is the reformulated kernels.

图 2: 核重构示例。顶行和中行分别是低分辨率 (LR) 图像及其对应的原始核。底行为重构后的核。

• We propose a novel de convolution module named DCLS that is applied on the features as channel-wise deblurring so that we can obtain a clean HR image. • Extensive experiments on various degradation kernels demonstrate that our method leads to state-of-the-art performance in blind SR problems.

• 我们提出了一种名为DCLS的新型反卷积模块，该模块在特征上进行通道级去模糊处理，从而获得清晰的高分辨率(HR)图像。
• 在各种退化核上的大量实验表明，我们的方法在盲超分辨率(SR)问题上实现了最先进的性能。

2. Related work

2. 相关工作

Non-blind SR Since pioneering work SRCNN [6] proposes to learn image SR with a three-layer convolution network, most subsequent works have focused on optimizing the network architectures [5, 10, 17, 18, 21, 28, 32, 40, 43, 55, 59, 61, 62] and loss functions [15, 22, 29, 47, 48, 52, 58]. These CNN-based methods have achieved impressive performance on SISR with a predefined single degradation setting (e.g., bicubic down sampling). However, they may suffer significant performance drops when the predefined degradation kernel is different from the real one.

非盲超分辨率 (Non-blind SR)
自开创性工作 SRCNN [6] 提出用三层卷积网络学习图像超分辨率以来，后续研究大多聚焦于优化网络架构 [5, 10, 17, 18, 21, 28, 32, 40, 43, 55, 59, 61, 62] 和损失函数 [15, 22, 29, 47, 48, 52, 58]。这些基于 CNN 的方法在预设单一退化设置 (如双三次下采样) 的单图像超分辨率 (SISR) 任务中表现出色。然而，当预设退化核与实际退化核不一致时，其性能会显著下降。

Some non-blind SR approaches address the multiple degradation problem by restoring HR images with given the corresponding kernels. Specifically, SRMD [56] is the first method that concatenates LR image with a stretched blur kernel as inputs to obtain a super-resolved image under different degradation s. Later, Zhang et al. [54, 57] incorporate advanced deblurring algorithms and extend the degradation to arbitrary blur kernels. UDVD [51] improves the performance by incorporating dynamic convolution. Hussein et al. [13] introduce a correction filter that transfers blurry LR images to match the bicubicly designed SR model. Besides, zero-shot methods [42, 51] have also been investigated in non-blind SR with multiple degradation s.

一些非盲超分辨率 (SR) 方法通过给定相应核函数来重建高分辨率 (HR) 图像，以解决多重退化问题。具体而言，SRMD [56] 是首个将低分辨率 (LR) 图像与拉伸模糊核拼接作为输入的方法，可在不同退化条件下获得超分辨率图像。随后，Zhang 等人 [54, 57] 结合先进去模糊算法，将退化扩展至任意模糊核。UDVD [51] 通过引入动态卷积提升性能。Hussein 等人 [13] 提出校正滤波器，将模糊 LR 图像转换以匹配双三次设计的 SR 模型。此外，零样本方法 [42, 51] 在多重退化的非盲 SR 领域也得到研究。

Blind SR Under the blind SR setting, HR image is recovered from the LR image degraded with unknown kernel [24, 25, 35]. Most approaches solve this problem with a two stage framework: kernel estimation and kernel-based HR image restoration. For the former, KernelGAN [3] estimates the degradation kernel by utilizing an internal generative adversarial network(GAN) on a single image, and applies that kernel to a non-blind SR approach such as ZSSR to get the SR result. Liang et al. [27] improve the kernel estimating performance by introducing a flow-based prior. Furthermore, Tao et al. [44] propose a spectrum-to-kernel network and demonstrate that estimating blur kernel in the frequency domain is more conducive than in spatial domain. For the latter, Gu et al. [9] propose to apply spatial feature transform (SFT) and iterative kernel correction (IKC) strategy for accurate kernel estimation and SR refinement. Luo et al. [30] develop an end-to-end training deep alternating network (DAN) by estimating reduced kernel and restoring HR image iterative ly. However, both IKC and DAN are time-consuming and computationally costly. The modified version of DAN [31] conducts a dual-path conditional block (DPCB) and supervises the estimator on the complete blur kernel to further improve the performance.

盲超分辨率 (Blind SR)
在盲超分辨率设置下，HR (高分辨率) 图像需从因未知退化核而劣化的LR (低分辨率) 图像中恢复[24, 25, 35]。多数方法通过两阶段框架解决该问题：退化核估计与基于核的HR图像重建。前者中，KernelGAN [3] 利用单幅图像的内部生成对抗网络(GAN)估计退化核，并将该核应用于ZSSR等非盲超分辨率方法以获取结果。Liang等[27] 通过引入基于流的先验提升核估计性能。Tao等[44] 提出频谱到核网络，证明在频域估计模糊核比空间域更具优势。后者中，Gu等[9] 提出采用空间特征变换(SFT)与迭代核校正(IKC)策略实现精确核估计与超分辨率优化。Luo等[30] 通过估计简化核并迭代恢复HR图像，开发了端到端训练的深度交替网络(DAN)。但IKC与DAN均存在耗时与计算成本高的问题。DAN的改进版本[31] 采用双路径条件块(DPCB)并对完整模糊核的估计器进行监督，以进一步提升性能。

3. Method

3. 方法

We now formally introduce our method which consists of three main components given a reformation of degradation: A dynamic deep linear kernel estimation module and a deep constrained least squares module for kernel estimation and LR space feature based deblur. A dual-path network is followed to generate the clean HR output. We will first derive the reformulation and then detail each module.

我们现在正式介绍由三个主要组件组成的退化重构方法：用于核估计和基于LR空间特征去模糊的动态深度线性核估计模块与深度约束最小二乘模块，随后通过双路径网络生成清晰的高分辨率输出。我们将首先推导重构公式，然后详述每个模块。

3.1. Degradation Model Reformulation

3.1. 退化模型重构

Ideally, the blur kernel to be estimated and its corresponding image should be in the same low-resolution space such that the degradation can be transformed to the deblurring problem followed by a SISR problem with bicubic degradation [56, 57]. Towards this end, we propose to reformulate Eq. (1) as

理想情况下，待估计的模糊核及其对应图像应处于同一低分辨率空间，从而将退化问题转化为去模糊问题，再处理为双三次退化的单图像超分辨率(SISR)问题[56, 57]。为此，我们将公式(1)重新表述为

$$
\begin{array}{r l}{\mathbf{y}=\mathcal{F}^{-1}\left(\mathcal{F}\left(\left(\mathbf{x}\mathbf{k}{h}\right){\downarrow_{s}}\right)\right)+\mathbf{n}}\ {\quad=\mathcal{F}^{-1}\left(\mathcal{F}\left(\mathbf{x}{\downarrow_{s}}\right)\frac{\mathcal{F}\left(\left(\mathbf{x}\mathbf{k}{h}\right){\downarrow_{s}}\right)}{\mathcal{F}\left(\mathbf{x}{\downarrow_{s}}\right)}\right)+\mathbf{n}}\ {\quad=\mathbf{x}{\downarrow_{s}}\mathcal{F}^{-1}\left(\frac{\mathcal{F}\left(\left(\mathbf{x}\mathbf{k}{h}\right){\downarrow_{s}}\right)}{\mathcal{F}\left(\mathbf{x}{\downarrow_{s}}\right)}\right)+\mathbf{n},}\end{array}
$$

where $\mathcal{F}$ denotes the Discrete Fourier Transform and ${\mathcal{F}}^{-1}$ denotes its inverse. Then let

其中 $\mathcal{F}$ 表示离散傅里叶变换 (Discrete Fourier Transform)，${\mathcal{F}}^{-1}$ 表示其逆变换。然后令

$$
\mathbf{k}{l}=\mathcal{F}^{-1}\left(\frac{\mathcal{F}\left(\left(\mathbf{x}*\mathbf{k}{h}\right){\downarrow s}\right)}{\mathcal{F}\left(\mathbf{x}{\downarrow_{s}}\right)}\right),
$$

we can obtain another form of degradation:

我们可以得到另一种形式的退化：

$$
\mathbf{y}=\mathbf{x}{\downarrow\ast}*\mathbf{k}_{l}+\mathbf{n}.
$$

$$
\mathbf{y}=\mathbf{x}{\downarrow\ast}*\mathbf{k}_{l}+\mathbf{n}.
$$

In the Eq. (6), $\mathbf{k}{l}$ is derived from the corresponding $\mathbf{k}{h}$ and applied on the down sampled HR image ${\bf x}{\downarrow{s}}$ . To ensure numerical stability, we rewrite Eq. (5) with a small regularization parameter $\epsilon$ :

在式 (6) 中，$\mathbf{k}{l}$ 由对应的 $\mathbf{k}{h}$ 推导得出，并应用于下采样的高分辨率图像 ${\bf x}{\downarrow_{s}}$。为确保数值稳定性，我们引入微小正则化参数 $\epsilon$ 重写式 (5)：

$$
\mathbf{k}{l}=\mathcal{F}^{-1}\left(\frac{\overline{{\mathcal{F}(\mathbf{x}{\downarrow_{s}})}}}{\overline{{\mathcal{F}(\mathbf{x}{\downarrow_{s}})}}\mathcal{F}(\mathbf{x}{\downarrow_{s}})+\epsilon}\mathcal{F}\left((\mathbf{x}*\mathbf{k}{h}){\downarrow_{s}}\right)\right),
$$

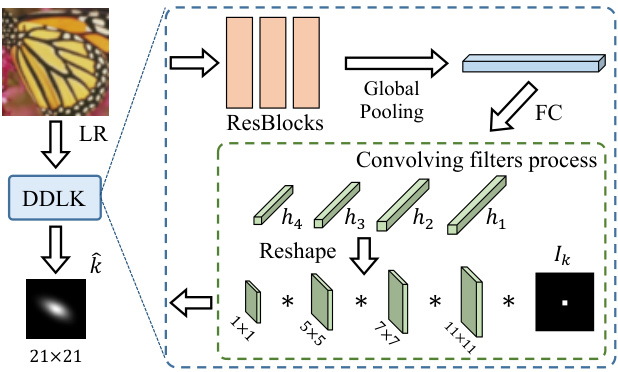
Figure 3. Architecture of the dynamic deep linear kernel.

图 3: 动态深度线性核架构。

where $\overline{{\mathcal{F}(\cdot)}}$ is the complex conjugate of $\mathcal{F}$ . Fig. 2 illustrates the results of reformulating kernels by Eq. (7). Based on the new degradation process, our goal is to estimate the blur kernel $\mathbf{k}_{l}$ and then restore HR image x.

其中 $\overline{{\mathcal{F}(\cdot)}}$ 是 $\mathcal{F}$ 的复共轭。图 2 展示了通过公式 (7) 重构核函数的结果。基于新的退化过程，我们的目标是估计模糊核 $\mathbf{k}_{l}$，然后恢复高分辨率图像 x。

3.2. Dynamic Deep Linear Kernel

3.2. 动态深度线性核

Following the reformation, we start our blind SR method from the kernel estimation. A straightforward solution is to adopt a regression network to estimate kernel $\hat{\mathbf{k}}$ by minimizing the L1 difference w.r.t the new ground-truth blur kernel $\mathbf{k}_{l}$ in Eq. (7). We argue such a single layer kernel (all weights of estimated kernel equal to the ground-truth kernel) estimation is in general difficult and unstable due to the highly non-convex of the blind SR problem [3], leading to kernel mismatch and performance drop [9, 30]. Instead, we propose an image-specific dynamic deep linear kernel (DDLK) which consists of a sequence of linear convolution layers without activation s. Theoretically, deep linear networks have infinitely equivalent global minimas [3, 16, 39], which allow us to find many different filter parameters to achieve the same correct solution. Moreover, since no nonlinearity is used in the network, we can analytically collapse a deep linear kernel as a single layer kernel.

在完成重构后，我们从核估计开始进行盲超分辨率方法。一个直接的解决方案是采用回归网络通过最小化与新真实模糊核$\mathbf{k}_{l}$的L1差异来估计核$\hat{\mathbf{k}}$（如式(7)所示）。我们认为，由于盲超分辨率问题的高度非凸性[3]，这种单层核（所有估计核的权重等于真实核）估计通常困难且不稳定，导致核不匹配和性能下降[9, 30]。相反，我们提出了一种图像特定的动态深度线性核（DDLK），它由一系列没有激活函数的线性卷积层组成。理论上，深度线性网络具有无限等效的全局最小值[3, 16, 39]，这使我们能够找到许多不同的滤波器参数来实现相同的正确解。此外，由于在网络中没有使用非线性，我们可以解析地将深度线性核折叠为单层核。

Fig. 3 depicts an example of estimating 4 layers dynamic deep linear kernel. The filters are set to $11\times11$ , $7\times7,5\times5$ and $1\times1$ , which make the receptive field to be $21\times21$ . We first generate the filters of each layer based on the LR image, and explicitly sequentially convolve all filters into a single narrow kernel with stride 1. Mathematically, let $\mathbf{h}_{i}$ represent the $i$ -th layer filter, we can get a single layer kernel following

图 3: 展示了一个估算4层动态深度线性核的示例。滤波器尺寸分别设置为 $11\times11$ 、 $7\times7$ 、 $5\times5$ 和 $1\times1$ ，这使得感受野达到 $21\times21$ 。我们首先基于低分辨率(LR)图像生成每层的滤波器，然后以步长1显式地顺序将所有滤波器卷积为单个窄核。用数学表达式表示，设 $\mathbf{h}_{i}$ 代表第 $i$ 层滤波器，可通过以下方式得到单层核：

$$
{\hat{\mathbf{k}}}=\mathbf{I_{k}}\mathbf{h_{1}}\mathbf{h_{2}}\cdot\cdot\cdot\mathbf{h}_{r}
$$

where $r$ is the number of linear layers, $\mathbf{I_{k}}$ is an identity kernel. As an empirically prior, we also constrain the kernel $\hat{\mathbf{k}}$ sum up to 1. The kernel estimation network can be optimized by minimizing the L1 loss between estimated kernel $\hat{\mathbf{k}}$ and new ground-truth blur kernel $\mathbf{k}_{l}$ from Eq. (7).

其中 $r$ 是线性层的数量，$\mathbf{I_{k}}$ 是单位核。根据经验先验，我们还约束核 $\hat{\mathbf{k}}$ 的和为1。通过最小化估计核 $\hat{\mathbf{k}}$ 与来自式(7)的新真实模糊核 $\mathbf{k}_{l}$ 之间的L1损失，可以优化核估计网络。

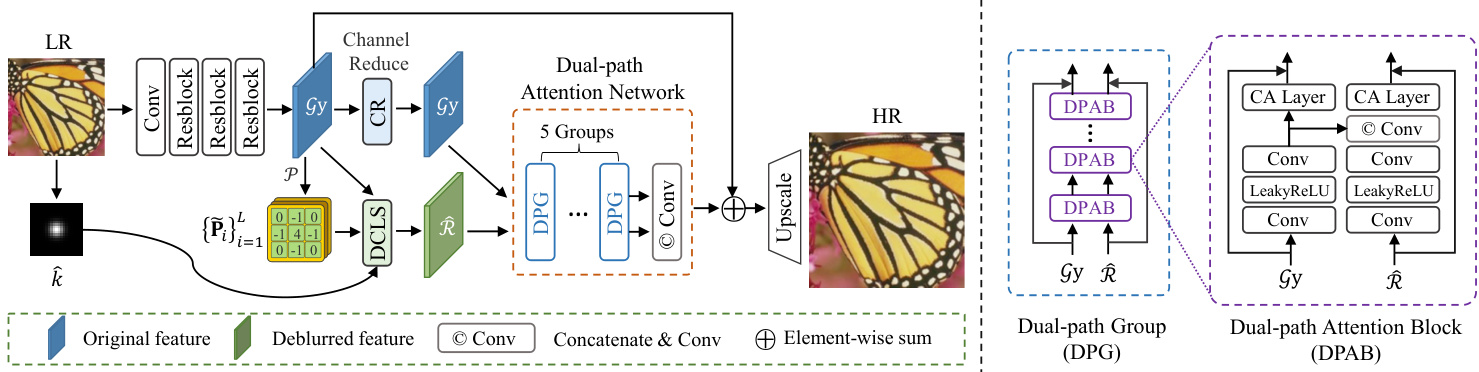
Figure 4. The overview architecture of the proposed method. Given an LR image y, we first estimate the degradation kernel $\hat{\mathbf{k}}$ , and involve it in the deep constrained least squares (DCLS) convolution in the feature domain. The deblurred features $\widehat{\mathcal{R}}$ are then concatenated with primitive features $\mathcal{G}\mathbf{y}$ to restore the clean HR image $\mathbf{x}$ through a dual-path attention network (DPAN).

图 4: 所提方法的整体架构。给定低分辨率(LR)图像y，我们首先估计退化核$\hat{\mathbf{k}}$，并将其应用于特征域中的深度约束最小二乘(DCLS)卷积。去模糊后的特征$\widehat{\mathcal{R}}$随后与原始特征$\mathcal{G}\mathbf{y}$拼接，通过双路径注意力网络(DPAN)恢复出清晰的高分辨率(HR)图像$\mathbf{x}$。

3.3. Deep Constrained Least Squares

3.3. 深度约束最小二乘法

Our goal is to restore HR image based on LR image and estimated kernel $\hat{\mathbf{k}}$ according to the new degradation model (Eq. (6)). Considering a group of feature extracting linear layers ${\mathcal{G}{i}}{i=1}^{L}$ provided to the LR image, we can rewrite Eq. (6) in the feature space, given by

我们的目标是根据新的退化模型（式(6)），基于LR图像和估计核 $\hat{\mathbf{k}}$ 恢复HR图像。考虑到为LR图像提供的一组特征提取线性层 ${\mathcal{G}{i}}{i=1}^{L}$，我们可以在特征空间中重写式(6)，得到

$$
\mathcal{G}{i}\mathbf{y}=\hat{\mathbf{k}}\mathcal{G}{i}\mathbf{x}{\downarrow_{s}}+\mathcal{G}_{i}\mathbf{n}.
$$

Let $\widehat{\mathcal{R}}{i}$ be the sought after deblurred feature corresponding to $\mathcal{G}{i}\mathbf{x}{\downarrow_{s}}$ . To solve Eq. (9), we minimize the following criterion function

设 $\widehat{\mathcal{R}}{i}$ 为与 $\mathcal{G}{i}\mathbf{x}{\downarrow_{s}}$ 对应的待求去模糊特征。为求解方程(9)，我们最小化以下准则函数

$$
\mathcal{C}=||\nabla\widehat{\mathcal{R}}{i}||^{2},s.t.||\mathcal{G}{i}\mathbf{y}-\widehat{\mathbf{k}}\widehat{\mathcal{R}}{i}||^{2}=||\mathcal{G}_{i}\mathbf{n}||^{2}
$$

where the $\nabla$ is a smooth filter which can be denoted by $\mathbf{P}$ . Then we introduce the Lagrange function, defined by

其中 $\nabla$ 是一个平滑滤波器，可以表示为 $\mathbf{P}$。接着我们引入拉格朗日函数，定义为

$$
\operatorname*{min}{\widehat{\mathcal{R}}{i}}\left[||\mathbf{P}\widehat{\mathcal{R}}{i}||^{2}+\lambda\left(||\mathcal{G}{i}\mathbf{y}-\widehat{\mathbf{k}}\widehat{\mathcal{R}}{i}||^{2}-||\mathcal{G}_{i}\mathbf{n}||^{2}\right)\right],
$$

where $\lambda$ is the Lagrange multiplier. Computing the derivative of Eq. (11) with respect to $\widehat{\mathcal{R}}_{i}$ and setting it to zero:

其中 $\lambda$ 为拉格朗日乘数。对式 (11) 关于 $\widehat{\mathcal{R}}_{i}$ 求导并令其为零：

$$
\left(\lambda\hat{\mathbf{k}}^{\mathsf{T}}\hat{\mathbf{k}}+\mathbf{P}^{\mathsf{T}}\mathbf{P}\right)\boldsymbol{\widehat{\mathcal{R}}}{i}-\lambda\hat{\mathbf{k}}^{\mathsf{T}}\boldsymbol{\mathcal{G}}_{i}\mathbf{y}=0.
$$

We can obtain the clear features as

我们可以获得清晰的特征

$$
{\widehat{\mathcal{R}}}{i}={\mathcal{H}}{\mathcal{G}}_{i}\mathbf{y}.
$$

where $\mathcal{H}_{i}$ denotes the deep constrained least squares deconvolution (DCLS) operator, given by

其中 $\mathcal{H}_{i}$ 表示深度约束最小二乘反卷积 (DCLS) 算子，由

$$
\mathcal{H}=\mathcal{F}^{-1}\left(\frac{\overline{{\mathcal{F}(\hat{\mathbf{k}})}}}{\overline{{\mathcal{F}(\hat{\mathbf{k}})}}\mathcal{F}(\hat{\mathbf{k}})+\frac{1}{\lambda}\overline{{\mathcal{F}(\mathbf{P})}}\mathcal{F}(\mathbf{P})}\right).
$$

$$
\mathcal{H}=\mathcal{F}^{-1}\left(\frac{\overline{{\mathcal{F}(\hat{\mathbf{k}})}}}{\overline{{\mathcal{F}(\hat{\mathbf{k}})}}\mathcal{F}(\hat{\mathbf{k}})+\frac{1}{\lambda}\overline{{\mathcal{F}(\mathbf{P})}}\mathcal{F}(\mathbf{P})}\right).
$$

Different from in the standard image space (e.g. RGB), smooth filter $\mathbf{P}$ and variable $\lambda$ in Eq. (14) might be inconsistent in the feature space. Alternatively, we predict a group

与标准图像空间(如RGB)不同,特征空间中的平滑滤波器$\mathbf{P}$和公式(14)中的变量$\lambda$可能存在不一致性。为此,我们预测了一组

of smooth filters with implicit Lagrange multiplier for different channels through a neural network $\mathcal{P}$ :

通过神经网络 $\mathcal{P}$ 为不同通道实现带有隐式拉格朗日乘子的平滑滤波器

$$
{\tilde{{\bf P}}{i}}{i=1}^{L}={{\mathcal P}(\mathcal{G}{i}{\bf y})}_{i=1}^{L}.
$$

Then the feature-specific operator $\mathcal{H}_{i}$ can be define by

然后特征特定算子 $\mathcal{H}_{i}$ 可以定义为

$$
\mathcal{H}{i}=\mathcal{F}^{-1}\left(\frac{\overline{{\mathcal{F}(\hat{\mathbf{k}})}}}{\overline{{\mathcal{F}(\hat{\mathbf{k}})}}\mathcal{F}(\hat{\mathbf{k}})+\overline{{\mathcal{F}(\tilde{\mathbf{P}}{i})}}\mathcal{F}(\tilde{\mathbf{P}}_{i})}\right).
$$

Now we can obtain the clear features by Eq. (13) and Eq. (16).

现在我们可以通过式(13)和式(16)获得清晰特征。

It is worth to note that a deep neural network (DNN) can be locally linear [7, 23, 36], thus we could apply DNN as $\mathcal{G}_{i}$ to extract useful features in Eq. (9). In addition, the consequent artifacts or errors can be compensated by the following dual-path attention module.

值得注意的是，深度神经网络 (DNN) 在局部可呈现线性特性 [7, 23, 36]，因此我们可以将 DNN 作为 $\mathcal{G}_{i}$ 应用于式 (9) 中以提取有效特征。此外，由此产生的伪影或误差可通过后续的双路径注意力模块进行补偿。

3.4. Dual-Path Attention Network

3.4. 双路径注意力网络

Unlike previous works [9, 31] in which the dual-path structures are only used to concatenate the stretched kernel with blurred features, we propose to utilize primitive blur features as additive path to compensate the artifacts and errors introduced by the estimated kernel, known as dual-path attention network (DPAN). DPAN is composed of several groups of dual-path attention blocks (DPAB), it receives both deblurred features $\widehat{\mathcal R}$ and primitive features $\mathcal{G}\mathbf{y}$ . The right of Fig. 4 illustrates tbhe architecture of DPAB.

与先前工作 [9, 31] 仅使用双路径结构将拉伸核与模糊特征拼接不同，我们提出利用原始模糊特征作为附加路径来补偿估计核引入的伪影和误差，称为双路径注意力网络 (DPAN)。DPAN 由多组双路径注意力块 (DPAB) 构成，同时接收去模糊特征 $\widehat{\mathcal R}$ 和原始特征 $\mathcal{G}\mathbf{y}$。图 4 右侧展示了 DPAB 的结构。

Since the additive path of processing $\mathcal{G}\mathbf{y}$ is independently updated and used to concatenate with R to provide primary information to refine the dec on vol ved fbeatures. We can reduce its channels to accelerate training and inference, as the channel reduction (CR) operation illustrated in left of Fig. 4. Moreover, on the dec on vol ved feature path, we apply the channel attention layer [60] after aggregating original features. In addition, we add a residual connection for each path on all groups and blocks. The pixel shuffle [11] is used as the upscale module. We can jointly optimize the SR network and kernel estimation network as follows:

由于处理 $\mathcal{G}\mathbf{y}$ 的加法路径是独立更新并与 R 拼接以提供主要信息来优化解卷积特征，我们可以通过通道缩减 (channel reduction, CR) 操作（如图 4 左侧所示）减少其通道数以加速训练和推理。此外，在解卷积特征路径上，我们在聚合原始特征后应用通道注意力层 [60]。同时，我们在所有组和块中的每条路径上添加了残差连接，并使用像素洗牌 (pixel shuffle) [11] 作为上采样模块。超分辨率网络与核估计网络的联合优化可表示为：

Table 1. Quantitative comparison on datasets with Gaussian8 kernels. The best two results are marked in red and blue colors, respective

表 1: 采用高斯核(Gaussian8)数据集的定量比较。最优的两个结果分别用红色和蓝色标出

方法	尺度	Set5 [4]	Set14 [53]	BSD100 [33]	Urban100 [12]	Manga109 [34]
		PSNR	SSIM	PSNR	SSIM	PSNR
Bicubic		28.82	0.8577	26.02	0.7634	25.92
CARN [2]	x2	30.99	0.8779	28.10	0.7879	26.78
Bicubic+ZSSR [41]	x2	31.08	0.8786	28.35	0.7933	27.92
Deblurring [37]+CARN [41]	x2	24.20	0.7496	21.12	0.6170	22.69
CARN [41]+Deblurring [37]	x2	31.27	0.8974	29.03	0.8267	28.72
IKC [9]	x2	37.19	0.9526	32.94	0.9024	31.51
DANv1 [30]	x2	37.34	0.9526	33.08	0.9041	31.76
DANv2 [31]	x2	37.60	0.9544	33.44	0.9094	32.00
DCLS(本文)	x2	37.63	0.9554	33.46	0.9103	32.04
Bicubic	x3	26.21	0.7766	24.01	0.6662	24.25
CARN [2]	x3	27.26	0.7855	25.06	0.6676	25.85
Bicubic+ZSSR [41]	x3	28.25	0.5226	26.15	0.6942	26.06
Deblurring [37]+CARN [41]	x3	19.05		17.61	0.4558	20.51
CARN [41]+Deblurring [37]	x3	30.31	0.8562	27.57	0.7531	27.14
IKC [9]	x3	33.06	0.9146	29.38	0.8233	28.53
DANv1 [30]	x3	34.04	0.9199	30.09	0.8287	28.94
DANv2 [31]	x3	34.12	0.9209	30.20	0.8309	29.03
DCLS(本文)	x3	34.21	0.9218	30.29	0.8329	29.07
Bicubic	x4	24.57	0.7108	22.79	0.6032	23.29
CARN [2]	x4	26.57	0.7420	24.62	0.6226	24.79
Bicubic+ZSSR [41]	x4	26.45	0.7279	24.78	0.6268	24.97
Deblurring [37]+CARN [41]	x4	18.10	0.4843	16.59	0.3994	18.46
CARN [41]+Deblurring [37]	x4	28.69	0.8092	26.40	0.6926	26.10
IKC [9]	x4	31.67	0.8829	28.31	0.7643	27.37
DANv1 [30]	x4	31.89	0.8864	28.42	0.7687	27.51
DANv2 [31]	x4	32.00	0.8885	28.50	0.7715	27.56
AdaTarget [14]	x4	31.58	0.8814	28.14	0.7626	27.43
DCLS(本文)	x4	32.12	0.8890	28.54	0.7728	27.60

Table 2. Quantitative comparison on various noisy datasets. The best one marks in red and the second best are in blue.

方法 x4	噪声水平	Set5 [4] PSNR	Set5 [4] SSIM	Set14 [53] PSNR	Set14 [53] SSIM	BSD100 [33] PSNR	BSD100 [33] SSIM	Urban100 [12] PSNR	Urban100 [12] SSIM	Manga109[34] PSNR	Manga109[34] SSIM
Bicubic+ZSSR[41]	15	23.32	0.4868	22.49	0.4256	22.61	0.3949	20.68	0.3966	22.04	0.4952
IKC [9]	15	26.89