Extract the Knowledge of Graph Neural Networks and Go Beyond it: An Effective Knowledge Distillation Framework

提取图神经网络的知识并超越它：一种有效的知识蒸馏框架

ABSTRACT

摘要

Semi-supervised learning on graphs is an important problem in the machine learning area. In recent years, state-of-the-art classification methods based on graph neural networks (GNNs) have shown their superiority over traditional ones such as label propagation. However, the sophisticated architectures of these neural models will lead to a complex prediction mechanism, which could not make full use of valuable prior knowledge lying in the data, e.g., structurally correlated nodes tend to have the same class. In this paper, we propose a framework based on knowledge distillation to address the above issues. Our framework extracts the knowledge of an arbitrary learned GNN model (teacher model), and injects it into a well-designed student model. The student model is built with two simple prediction mechanisms, i.e., label propagation and feature transformation, which naturally preserves structure-based and feature-based prior knowledge, respectively. In specific, we design the student model as a trainable combination of parameterized label propagation and feature transformation modules. As a result, the learned student can benefit from both prior knowledge and the knowledge in GNN teachers for more effective predictions. Moreover, the learned student model has a more interpret able prediction process than GNNs. We conduct experiments on five public benchmark datasets and employ seven GNN models including GCN, GAT, APPNP, SAGE, SGC, GCNII and GLP as the teacher models. Experimental results show that the learned student model can consistently outperform its corresponding teacher model by $1.4%\sim4.7%$ on average. Code and data are available at https://github.com/BUPT-GAMMA/CPF

图上半监督学习是机器学习领域的重要问题。近年来，基于图神经网络 (GNNs) 的最先进分类方法已展现出优于标签传播等传统方法的性能。然而，这些神经模型的复杂架构会导致预测机制难以充分利用数据中潜在的有价值先验知识（例如结构相关节点往往属于同一类别）。本文提出基于知识蒸馏的框架来解决上述问题。该框架从任意已训练的GNN模型（教师模型）中提取知识，并将其注入精心设计的学生模型。学生模型采用标签传播和特征变换两种简单预测机制，天然保留了基于结构和基于特征的先验知识。具体而言，我们将学生模型设计为参数化标签传播模块与特征变换模块的可训练组合，使其能同时受益于先验知识和GNN教师模型的知识，从而实现更有效的预测。此外，学生模型的预测过程比GNN更具可解释性。我们在五个公开基准数据集上进行实验，并采用GCN、GAT、APPNP、SAGE、SGC、GCNII和GLP等七种GNN作为教师模型。实验结果表明，学习得到的学生模型平均能持续超越对应教师模型1.4%~4.7%。代码和数据详见https://github.com/BUPT-GAMMA/CPF

CCS CONCEPTS

CCS概念

ACM Reference Format:

ACM参考文献格式:

Cheng Yang1,2, Jiawei ${\mathrm{Liu}}^{1}$ , Chuan $\mathrm{Shi^{1,2}}$ . 2020. Extract the Knowledge of Graph Neural Networks and Go Beyond it: An Effective Knowledge Distillation Framework. In Proceedings of the Web Conference 2021 (WWW ’21),

Cheng Yang1,2, Jiawei ${\mathrm{Liu}}^{1}$, Chuan $\mathrm{Shi^{1,2}}$。2020。提取图神经网络知识并超越：一种高效的知识蒸馏框架。见《2021年网络会议论文集》(WWW '21)。

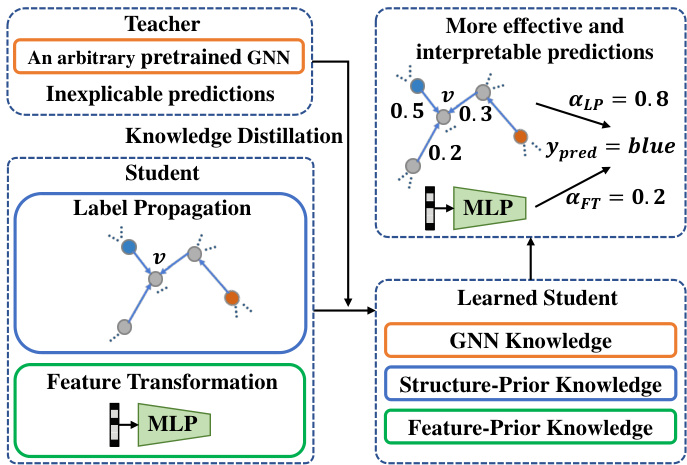
Figure 1: An overview of our knowledge distillation framework. The two simple prediction mechanisms of our student model ensure the full use of structure/feature-based prior knowledge. The knowledge in GNN teachers will be extracted and injected into the student during knowledge distillation. Thus the student can go beyond its corresponding teacher with more effective predictions.

图 1: 知识蒸馏框架概览。学生模型的两个简单预测机制确保充分利用基于结构/特征的先验知识。在知识蒸馏过程中，GNN教师模型中的知识将被提取并注入学生模型，从而使学生能够超越其对应的教师模型，实现更有效的预测。

April 19–23, 2021 ,Ljubljana, Slovenia. ACM, New York, NY, USA, 11 pages. https://doi.org/10.1145/3442381.3450068

2021年4月19–23日，斯洛文尼亚卢布尔雅那。ACM，美国纽约州纽约市，11页。https://doi.org/10.1145/3442381.3450068

1 INTRODUCTION

1 引言

Semi-supervised learning on graph-structured data aims at classifying every node in a network given the network structure and a subset of nodes labeled. As a fundamental task in graph analysis [3], the classification problem has a wide range of real-world applications such as user profiling [15], recommend er systems [28], text classification [1] and sociological studies [2]. Most of these applications have the homophily phenomenon [16], which assumes two linked nodes tend to have similar labels. With the homophily assumption, many traditional methods are developed to propagate labels by random walks [27, 39] or regularize the label differences between neighbors [9, 36].

图结构数据上的半监督学习旨在给定网络结构和部分已标注节点的条件下，对网络中每个节点进行分类。作为图分析中的基础任务[3]，该分类问题在用户画像[15]、推荐系统[28]、文本分类[1]和社会学研究[2]等现实场景中具有广泛应用。这些应用大多存在同质性现象(homophily)[16]，即假设相连的两个节点往往具有相似标签。基于同质性假设，传统方法主要通过随机游走[27,39]或邻居节点间标签差异正则化[9,36]来实现标签传播。

With the success of deep learning, methods based on graph neural networks (GNNs) [7, 11, 29] have demonstrated their effec ti ve ness in classifying node labels. Most GNN models adopt message passing strategy [6]: each node aggregates features from its neighborhood and then a layer-wise projection function with a non-linear activation will be applied to the aggregated information. In this way, GNNs can utilize both graph structure and node feature information in their models.

随着深度学习的成功，基于图神经网络 (GNNs) [7, 11, 29] 的方法在节点标签分类任务中展现了其有效性。大多数GNN模型采用消息传递策略 [6]：每个节点聚合其邻域特征，然后对聚合信息应用带有非线性激活的逐层投影函数。通过这种方式，GNNs能够在模型中同时利用图结构和节点特征信息。

However, the entanglement of graph topology, node features and projection matrices in GNNs leads to a complicated prediction mechanism and could not take full advantage of prior knowledge lying in the data. For example, the aforementioned homophily assumption adopted in label propagation methods represents structure-based prior, and has been shown to be underused [14, 30] in graph convolutional network (GCN) [11].

然而，图神经网络(GNN)中图拓扑、节点特征和投影矩阵的纠缠导致预测机制复杂化，无法充分利用数据中的先验知识。例如，标签传播方法采用的同质性假设代表基于结构的先验，但研究表明图卷积网络(GCN) [11] 未能充分利用这种先验 [14, 30]。

As an evidence, recent studies proposed to incorporate the label propagation mechanism into GCN by adding regular iz at ions [30] or manipulating graph filters [14, 24]. Their experimental results show that GCN can be improved by emphasizing such structure-based prior knowledge. Nevertheless, these methods have three major drawbacks: (1) The main bodies of their models are still GNNs and thus hard to fully utilize the prior knowledge; (2) They are single models rather than frameworks, and thus not compatible with other advanced GNN architectures; (3) They ignored another important prior knowledge, i.e., feature-based prior, which means that a node’s label is purely determined by its own features.

作为佐证，近期研究提出通过添加正则化项 [30] 或操纵图滤波器 [14, 24] 将标签传播机制融入GCN。实验结果表明，强调这类基于结构的先验知识可提升GCN性能。然而这些方法存在三个主要缺陷：(1) 模型主体仍为GNN架构，难以充分利用先验知识；(2) 属于单一模型而非框架，无法兼容其他先进GNN架构；(3) 忽略了另一重要先验知识——基于特征的先验性（即节点标签完全由其自身特征决定）。

To address these issues, we propose an effective knowledge distillation framework to inject the knowledge of an arbitrary learned GNN (teacher model) into a well-designed student model. The student model is built with two simple prediction mechanisms, i.e., label propagation and feature transformation, which naturally preserves structure-based and feature-based prior knowledge, respectively. In specific, we design the student model as a trainable combination of parameterized label propagation and feature-based 2-layer MLP (Multi-layer Perceptron). On the other hand, it has been recognized that the knowledge of a teacher model lies in its soft predictions [8]. By simulating the soft labels predicted by a teacher model, our student model is able to further make use of the knowledge in pretrained GNNs. Consequently, the learned student model has a more interpret able prediction process and can utilize both GNN and structure/feature-based priors. An overview of our framework is shown in Fig. 1.

为解决这些问题，我们提出了一种有效的知识蒸馏框架，将任意已训练GNN(教师模型)的知识注入精心设计的学生模型中。该学生模型采用两种简单预测机制构建：标签传播(label propagation)和特征变换(feature transformation)，分别天然保留了基于结构和基于特征的先验知识。具体而言，我们将学生模型设计为参数化标签传播与基于特征的双层MLP(多层感知机)的可训练组合。另一方面，已有研究指出教师模型的知识蕴含在其软预测中[8]。通过模拟教师模型预测的软标签，我们的学生模型能够进一步利用预训练GNN中的知识。最终，习得的学生模型具备更可解释的预测过程，并能同时利用GNN与结构/特征先验。图1展示了我们框架的概览。

We conduct experiments on five public benchmark datasets and employ several popular GNN models including GCN [11], GAT [29], SAGE [7], APPNP [12], SGC [32] and a recent deep GCN model GCNII [4] as teacher models. Experimental results show that a student model is able to outperform its corresponding teacher model by $1.4%\sim4.7%$ in terms of classification accuracy. It is worth noting that we also apply our framework on GLP [14] which unified GCN and label propagation by manipulating graph filters. As a result, we can still gain $1.5%\sim2.3%$ relative improvements, which demonstrates the potential compatibility of our framework. Furthermore, we investigate the interpret ability of our student model by probing the learned balance parameters between parameterized label propagation and feature transformation as well as the learned confidence score of each node in label propagation. To conclude, the improvements are consistent and significant with better interpret ability.

我们在五个公共基准数据集上进行实验，并采用多种流行的图神经网络 (GNN) 模型作为教师模型，包括 GCN [11]、GAT [29]、SAGE [7]、APPNP [12]、SGC [32] 以及近期提出的深度 GCN 模型 GCNII [4]。实验结果表明，学生模型在分类准确率上能超越对应教师模型 $1.4%\sim4.7%$。值得注意的是，我们还将该框架应用于通过操纵图滤波器统一 GCN 与标签传播的 GLP [14]，仍能获得 $1.5%\sim2.3%$ 的相对提升，这证明了我们框架的潜在兼容性。此外，我们通过探究参数化标签传播与特征变换之间的学习平衡参数，以及标签传播中每个节点的学习置信度分数，验证了学生模型的可解释性。总体而言，该框架在保持更好可解释性的同时，实现了稳定且显著的性能提升。

The contributions of this paper are summarized as follows:

本文的贡献总结如下:

• We propose an effective knowledge distillation framework to extract the knowledge of an arbitrary pretrained GNN model and inject it into a student model for more effective predictions.

• 我们提出了一种有效的知识蒸馏框架，用于提取任意预训练图神经网络 (GNN) 模型的知识，并将其注入学生模型以实现更有效的预测。

• We design the student model as a trainable combination of parameterized label propagation and feature-based 2-layer MLP.

• 我们将学生模型设计为可训练的参数化标签传播与基于特征的两层MLP组合。

Hence the student model has a more interpret able prediction process and naturally preserves the structure/feature-based priors. Consequently, the learned student model can utilize both GNN and prior knowledge.

因此，学生模型具备更可解释的预测过程，并能自然保留基于结构/特征的先验知识。这使得学习后的学生模型能同时利用图神经网络(GNN)和先验知识。

• Experimental results on five benchmark datasets with seven GNN teacher models demonstrate the effectiveness of our framework. Extensive studies by probing the learned weights in the student model also illustrate the potential interpret ability of our method.

• 在五个基准数据集上使用七种GNN教师模型的实验结果表明了我们框架的有效性。通过探究学生模型中学习到的权重进行的广泛研究，也展示了我们方法潜在的 interpret ability (可解释性)。

2 RELATED WORK

2 相关工作

This work is most relevant to graph neural network models and knowledge distillation methods.

本工作与图神经网络模型和知识蒸馏方法最为相关。

2.1 Graph Neural Networks

2.1 图神经网络 (Graph Neural Networks)

The concept of GNN was proposed [21] before 2010 and has become a rising topic since the emergence of GCN [11]. During the last five years, graph neural network models have achieved promising results in many research areas [33, 37]. Now we will briefly introduce some representative GNN methods in this section and employ them as our teacher models in the experiments.

GNN的概念在2010年之前就被提出[21]，并随着GCN[11]的出现成为一个新兴话题。过去五年间，图神经网络模型在许多研究领域取得了显著成果[33, 37]。本节将简要介绍几种代表性GNN方法，并将其作为实验中的教师模型。

As one of the most influential GNN models, Graph Convolutional Network (GCN) [11] targeted on semi-supervised learning on graph-structured data through layer-wise propagation of node features. GCN can be interpreted as a variant of convolutional neural networks that operates on graphs. Graph Attention Network (GAT) [29] further employed attention mechanism in the aggregation of neighbors’ features. SAGE [7] sampled and aggregated features from a node’s local neighborhood and is more spaceefficient. Approximate personalized propagation of neural predictions (APPNP) [12] studied the relationship between GCN and PageRank, and incorporated a propagation scheme derived from personalized PageRank into graph filters. Simple Graph Convolution (SGC) [32] simplified GCN by removing non-linear activations and collapsing weight matrices between layers. Graph Convolutional Network via Initial residual and Identity mapping (GCNII) [4] was a very recent deep GCN model which alleviates the over-smoothing problem.

作为最具影响力的图神经网络(GNN)模型之一，图卷积网络(GCN) [11] 通过节点特征的逐层传播，专注于图结构数据的半监督学习。GCN可被视为在图上运行的卷积神经网络变体。图注意力网络(GAT) [29] 进一步在邻居特征聚合中采用了注意力机制。SAGE [7] 通过采样和聚合节点局部邻域特征实现了更高的空间效率。神经预测近似个性化传播(APPNP) [12] 研究了GCN与PageRank的关系，并将源自个性化PageRank的传播方案融入图滤波器。简单图卷积(SGC) [32] 通过移除非线性激活函数和压缩层间权重矩阵简化了GCN。基于初始残差和恒等映射的图卷积网络(GCNII) [4] 是最新的深度GCN模型，有效缓解了过度平滑问题。

Recently, several works show that the performance of GNNs can be further improved by incorporating traditional prediction mechanisms, i.e., label propagation. For example, Generalized Label Propagation (GLP) [14] modified graph convolutional filters to generate smooth features with graph similarity encoded. UniMP [24] fused feature aggregation and label propagation by a shared messagepassing network. GCN-LPA [30] employed label propagation as regular iz ation to assist GCN for better performances. Note that the label propagation mechanism was built with simple structurebased prior knowledge. Their improvements indicate that such prior knowledge is not fully explored in GNNs. Nevertheless, these advanced models still suffer from several drawbacks as illustrated in the Introduction section.

最近，多项研究表明，通过结合传统预测机制（即标签传播）可以进一步提升图神经网络(GNN)的性能。例如，广义标签传播(GLP) [14] 通过修改图卷积滤波器来生成具有图相似性编码的平滑特征。UniMP [24] 通过共享的消息传递网络融合了特征聚合和标签传播。GCN-LPA [30] 将标签传播作为正则化手段来辅助GCN以获得更好的性能。需要注意的是，标签传播机制是基于简单的结构先验知识构建的。这些改进表明，此类先验知识在GNN中尚未得到充分探索。然而，如引言部分所述，这些先进模型仍存在若干缺陷。

2.2 Knowledge Distillation

2.2 知识蒸馏

Knowledge distillation [8] was proposed for model compression where a small light-weight student model is trained to mimic the soft predictions of a pretrained large teacher model. After the distillation, the knowledge in the teacher model will be transferred into the student model. In this way, the student model can reduce time and space complexities without losing prediction qualities. Knowledge distillation is widely used in the computer vision area, e.g., a deep convolutional neural network (CNN) will be compressed into a shallow one to accelerate the inference.

知识蒸馏 [8] 是一种模型压缩方法，通过训练一个轻量级的学生模型来模仿预训练大型教师模型的软预测结果。经过蒸馏后，教师模型中的知识将被迁移到学生模型中。这种方式使学生模型能在保持预测质量的同时降低时间和空间复杂度。知识蒸馏在计算机视觉领域应用广泛，例如将深度卷积神经网络 (CNN) 压缩为浅层网络以加速推理。

In fact, there are also a few studies combining knowledge distillation with GCN. However, their motivation and model architecture are quite different from ours. Yang et al. [34] which was proposed in the computer vision area, compressed a deep GCN with large feature maps into a shallow one with fewer parameters using a local structure preserving module. Reliable Data Distillation (RDD) [35] trained multiple GCN students with the same architecture and then ensembled them for better performance in a manner similar to BAN [5]. Graph Markov Neural Networks (GMNN) [19] can also be viewed as a knowledge distillation method where two GCNs with different reception sizes learn from each other. Note that both teacher and student models in these works are GCNs.

事实上，也有少数研究将知识蒸馏与GCN相结合。然而，它们的动机和模型架构与我们的工作存在显著差异。Yang等人[34]（源自计算机视觉领域）通过局部结构保留模块，将具有大型特征图的深度GCN压缩为参数更少的浅层网络。可靠数据蒸馏(RDD)[35]采用与BAN[5]类似的方式，训练多个同架构的GCN学生模型并进行集成以提升性能。图马尔可夫神经网络(GMNN)[19]也可视为一种知识蒸馏方法，其中两个具有不同感受野的GCN相互学习。值得注意的是，这些工作中的教师模型和学生模型均为GCN。

Compared with them, the goal of our framework is to extract the knowledge of GNNs and go beyond it. Our framework is very flexible and can be applied on an arbitrary GNN model besides GCN. We design a student model with simple prediction mechanisms and thus are able to benefit from both GNN and prior knowledge. As the output of our framework, the student model also has a more interpret able prediction process. In terms of training details, our framework is simpler and requires no ensembling or iterative distillations between teacher and student models for improving classification accuracies.

与它们相比，我们框架的目标是提取GNN (Graph Neural Network) 的知识并超越它。我们的框架非常灵活，可应用于除GCN (Graph Convolutional Network) 之外的任意GNN模型。我们设计了一个具有简单预测机制的学生模型，因此能够同时受益于GNN和先验知识。作为框架的输出，该学生模型还具有更易解释的预测过程。在训练细节方面，我们的框架更简单，无需通过师生模型集成或迭代蒸馏来提高分类准确率。

3 METHODOLOGY

3 方法论

In this section, we will start by formalizing the semi-supervised node classification problem and introducing the notations. Then we will present our knowledge distillation framework to extract the knowledge of GNNs. Afterwards, we will propose the architecture of our student model, which is a trainable combination of parameterized label propagation and feature-based 2-layer MLP. Finally, we will discuss the potential interpret ability of the student model and the computation complexity of our framework.

在本节中，我们将首先形式化半监督节点分类问题并介绍相关符号。随后提出用于提取图神经网络 (GNN) 知识的知识蒸馏框架。接着介绍学生模型的架构——该模型由参数化标签传播和基于特征的双层MLP (Multi-Layer Perceptron) 可训练组合构成。最后将探讨学生模型的潜在可解释性及本框架的计算复杂度。

3.1 Semi-supervised Node Classification

3.1 半监督节点分类

We begin by outlining the problem of node classification. Given a connected graph $G=(V,E)$ with a subset of nodes $V_{L}\subset V$ labeled, where $V$ is the vertex set and $E$ is the edge set, node classification targets on predicting the node labels for every node $v$ in unlabeled node set $V_{U}=V\setminus V_{L}$ . Each node $v\in V$ has label $y_{v}\in Y$ where $Y$ is the set of all possible labels. In addition, node features $X\in\mathbb{R}^{|V|\times d}$ are usually available in graph data and can be utilized for better classification accuracy. Each row $X_{v}\in\mathbb{R}^{d}$ of matrix $X$ denotes a $d$ -dimensional feature vector of node $v$ .

我们首先概述节点分类问题。给定一个连通图 $G=(V,E)$ ，其中部分节点 $V_{L}\subset V$ 已标注（ $V$ 为顶点集， $E$ 为边集），节点分类的目标是预测未标注节点集 $V_{U}=V\setminus V_{L}$ 中每个节点 $v$ 的标签。每个节点 $v\in V$ 的标签为 $y_{v}\in Y$ ，其中 $Y$ 是所有可能标签的集合。此外，图数据通常包含节点特征 $X\in\mathbb{R}^{|V|\times d}$ ，可用于提升分类准确率。矩阵 $X$ 的每一行 $X_{v}\in\mathbb{R}^{d}$ 表示节点 $v$ 的 $d$ 维特征向量。

3.2 The Knowledge Distillation Framework

3.2 知识蒸馏框架

Node classification approaches including GNNs can be summarized as a black box that outputs a classifier $f$ given graph structure $G$ labeled node set $V_{L}$ and node feature $X$ as inputs. The classifier $f$ will predict the probability $f(v,y)$ that unlabeled node $v\in V_{U}$ has label $y\in Y$ , where $\begin{array}{r}{\sum_{y^{\prime}\in Y}f(v,y^{\prime})=1}\end{array}$ . For labeled node $v$ , we set $f(v,y)=1$ if $v$ is annotated with label $y$ and $f(v,y^{\prime})=0$ for any other label $y^{\prime}$ . We use $f(v)\in\mathbb{R}^{|Y|}$ to denote the probability distribution over all labels for brevity.

包括GNN在内的节点分类方法可以概括为一个黑箱，它以图结构$G$、带标签的节点集$V_{L}$和节点特征$X$作为输入，输出分类器$f$。该分类器$f$将预测未标记节点$v\in V_{U}$具有标签$y\in Y$的概率$f(v,y)$，其中$\begin{array}{r}{\sum_{y^{\prime}\in Y}f(v,y^{\prime})=1}\end{array}$。对于带标签的节点$v$，如果$v$被标注为标签$y$，则设$f(v,y)=1$，对于其他任何标签$y^{\prime}$，设$f(v,y^{\prime})=0$。为简洁起见，我们用$f(v)\in\mathbb{R}^{|Y|}$表示所有标签上的概率分布。

In this paper, the teacher model employed in our framework can be an arbitrary GNN model such as GCN [11] or GAT [29]. We denote the pretrained classifier in a teacher model as $f_{G N N}$ On the other hand, we use 𝑓𝑆𝑇𝑈 ;Θ to denote the student model parameterized by $\Theta$ and $f_{S T U;\Theta}(v)\in\mathbb{R}^{|Y|}$ represents the predicted probability distribution of node $v$ by the student.

本文框架中采用的教师模型可以是任意图神经网络 (GNN) 模型，例如 GCN [11] 或 GAT [29]。我们将教师模型中的预训练分类器表示为 $f_{G N N}$，而学生模型则用 $f_{S T U;\Theta}$ 表示，其中 $\Theta$ 为参数，$f_{S T U;\Theta}(v)\in\mathbb{R}^{|Y|}$ 代表学生模型对节点 $v$ 的预测概率分布。

In knowledge distillation [8], the student model is trained to mimic the soft label predictions of a pretrained teacher model. As a result, the knowledge lying in the teacher model will be extracted and injected into the learned student. Therefore, the optimization objective which aligns the outputs between the student model and pretrained teacher model can be formulated as

在知识蒸馏 [8] 中，学生模型通过模仿预训练教师模型的软标签预测进行训练。因此，教师模型中的知识将被提取并注入到学习的学生模型中。于是，对齐学生模型与预训练教师模型输出的优化目标可表述为

$$
\operatorname*{min}{\Theta}\sum_{v\in V}d i s t a n c e(f_{G N N}(v),f_{S T U;\Theta}(v)),
$$

$$
\operatorname*{min}{\Theta}\sum_{v\in V}d i s t a n c e(f_{G N N}(v),f_{S T U;\Theta}(v)),
$$

where 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 $(\cdot,\cdot)$ measures the distance between two predicted probability distributions. Specifically, we use Euclidean distance in this work1.

其中 $distance$ $(\cdot,\cdot)$ 用于衡量两个预测概率分布之间的距离。具体而言，本研究采用欧氏距离1。

3.3 The Architecture of Student Model

3.3 学生模型架构

We hypothesize that a node’s label prediction follows two simple mechanisms: (1) label propagation from its neighboring nodes and (2) a transformation from its own features. Therefore, as shown in Fig. 2, we design our student model as a combination of these two mechanisms, i.e., a Parameterized Label Propagation (PLP) module and a Feature Transformation (FT) module, which can naturally preserve the structure/feature-based prior knowledge, respectively. After the distillation, the student will benefit from both GNN and prior knowledge with a more interpret able prediction mechanism.

我们假设节点的标签预测遵循两种简单机制：(1) 来自相邻节点的标签传播和(2) 自身特征的转换。因此，如图2所示，我们将学生模型设计为这两种机制的组合，即参数化标签传播(PLP)模块和特征转换(FT)模块，它们能分别自然地保留基于结构/特征的先验知识。蒸馏后，学生模型将通过更可解释的预测机制，同时受益于GNN和先验知识。

In this subsection, we will first briefly review the conventional label propagation algorithm. Then we will introduce our PLP and FT modules as well as their trainable combinations.

在本小节中，我们将首先简要回顾传统的标签传播算法 (label propagation algorithm) ，然后介绍我们的PLP和FT模块及其可训练组合。

3.3.1 Label Propagation. Label propagation (LP) [38] is a classical graph-based semi-supervised learning model. This model simply follows the assumption that nodes linked by an edge (or occupying the same manifold) are very likely to share the same label. Based on this hypothesis, labels will propagate from labeled nodes to unlabeled ones for predictions.

3.3.1 标签传播 (Label Propagation)。标签传播 (LP) [38] 是一种经典的基于图的半监督学习模型。该模型遵循一个简单假设：通过边连接的节点（或位于同一流形上的节点）很可能共享相同标签。基于这一假设，标签将从已标注节点传播到未标注节点以进行预测。

Formally, we use $f_{L P}$ to denote the final prediction of LP and $f_{L P}^{k}$ to denote the prediction of LP after $k$ iterations. In this work, we initialize the prediction of node 𝑣 as a one-hot label vector if $v$ is a labeled node. Otherwise, we will set a uniform label distribution for each unlabeled node $v$ , which indicates that the probabilities of all classes are the same at the beginning. The initialization can be formalized as:

形式上，我们用 $f_{L P}$ 表示 LP (Label Propagation) 的最终预测结果，用 $f_{L P}^{k}$ 表示 LP 经过 $k$ 次迭代后的预测结果。在本工作中，如果节点 𝑣 是已标注节点，我们将其预测初始化为一个独热 (one-hot) 标签向量；否则，我们会为每个未标注节点 𝑣 设置一个均匀的标签分布，这意味着所有类别的概率在初始时相同。

where $f_{L P}^{k}(v)$ is the predicted probability distribution of node $v$ at iteration $k$ . In the $k+1$ -th iteration, LP will update the label

其中 $f_{L P}^{k}(v)$ 表示节点 $v$ 在第 $k$ 次迭代时的预测概率分布。在第 $k+1$ 次迭代中，LP将更新标签

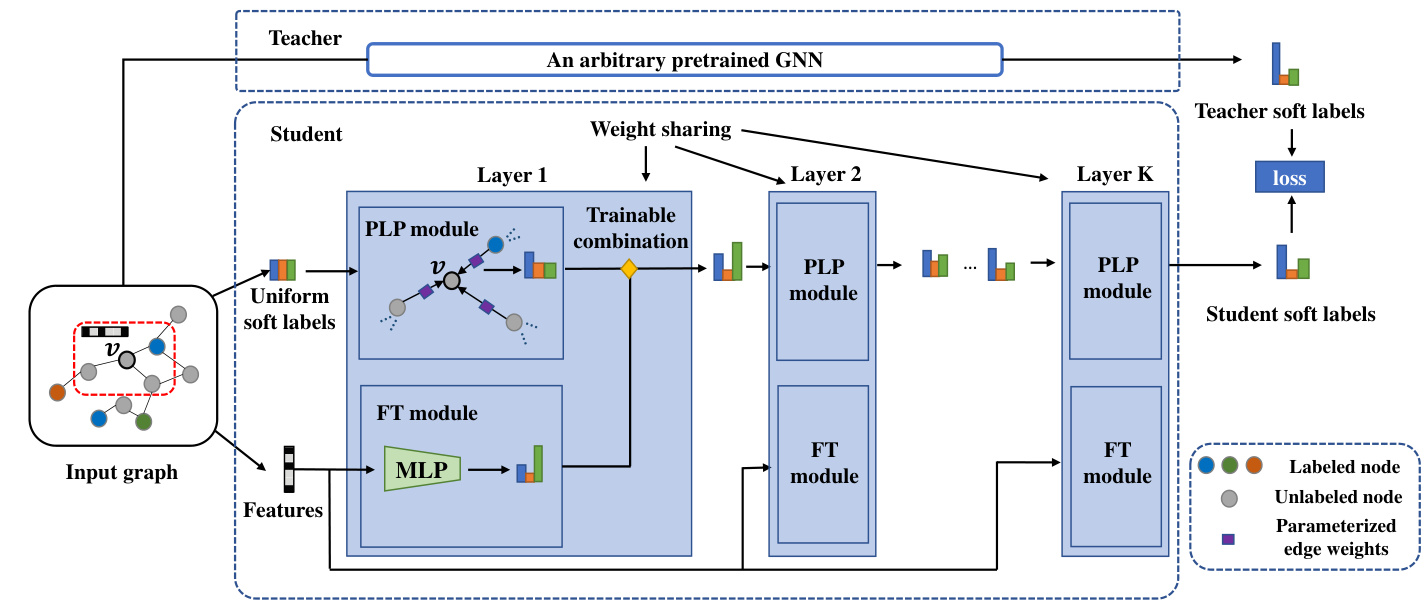
Figure 2: An illustration of the architecture of our proposed student model. Taking the center node 𝑣 as an example, the student model starts from node 𝑣’s raw features and a uniform label distribution as soft labels. Then at each layer, the soft label prediction of 𝑣 will be updated as a trainable combination of Parameterized Label Propagation (PLP) from 𝑣’s neighbors and Feature Transformation (FT) of 𝑣’s features. Finally, the distance between the soft label predictions of student and pretrained teacher will be minimized.

图 2: 我们提出的学生模型架构示意图。以中心节点𝑣为例，学生模型从节点𝑣的原始特征和均匀标签分布(作为软标签)开始。然后在每一层，𝑣的软标签预测将通过可训练的组合方式进行更新：包括来自𝑣邻居的参数化标签传播(PLP)和𝑣特征的特征转换(FT)。最终，学生模型与预训练教师模型的软标签预测之间的距离将被最小化。

predictions of each unlabeled node $v\in V_{U}$ as follows:

每个未标注节点 $v\in V_{U}$ 的预测结果如下：

$$
f_{L P}^{k+1}(v)=(1-\lambda)\frac{1}{\vert N_{v}\vert}\sum_{u\in N_{v}}{f_{L P}^{k}(u)}+\lambda f_{L P}^{k}(v),
$$

$$
f_{L P}^{k+1}(v)=(1-\lambda)\frac{1}{\vert N_{v}\vert}\sum_{u\in N_{v}}{f_{L P}^{k}(u)}+\lambda f_{L P}^{k}(v),
$$

where $N_{v}$ is the set of node $v$ ’s neighbors in the graph and $\lambda$ is a hyper-parameter controlling the smoothness of node updates.

其中 $N_{v}$ 是图中节点 $v$ 的邻居集合，$\lambda$ 是控制节点更新平滑度的超参数。

Note that LP has no parameters to be trained, and thus can not fit the output of a teacher model through end-to-end training. Therefore, we retrofit LP by introducing more parameters to increase its capacity.

需要注意的是，LP (Label Propagation) 没有可训练的参数，因此无法通过端到端训练来拟合教师模型的输出。为此，我们通过引入更多参数来改进LP，以提升其能力。

3.3.2 Parameterized Label Propagation Module. Now we will introduce our Parameterized Label Propagation (PLP) module by further parameter i zing edge weights in LP. As shown in Eq. 3, LP model treats all neighbors of a node equally during the propagation. However, we hypothesize that the importance of different neighbors to a node should be different, which determines the propagation intensities between nodes. To be more specific, we assume that the label predictions of some nodes are more “confident” than others: e.g., a node whose predicted label is similar to most of its neighbors. Such nodes will be more likely to propagate their labels to neighbors and keep themselves unchanged.

3.3.2 参数化标签传播模块
现在我们通过进一步参数化LP中的边权重来介绍参数化标签传播(PLP)模块。如公式3所示，LP模型在传播过程中平等对待节点的所有邻居。但我们假设不同邻居对节点的重要性应当不同，这决定了节点间的传播强度。具体而言，我们认为某些节点的标签预测比其他节点更"可信"：例如预测标签与大多数邻居相似的节点。这类节点更可能将标签传播给邻居并保持自身不变。

Formally, we will assign a confidence score $c_{v}\in\mathbb{R}$ to each node 𝑣. During the propagation, all node 𝑣’s neighbors and $v$ itself will compete to propagate their labels to 𝑣. Following the intuition that a larger confidence score will have a larger edge weight, we rewrite the prediction update function in Eq. 3 for $f_{P L P}$ as follows:

形式上，我们将为每个节点𝑣分配一个置信度分数$c_{v}\in\mathbb{R}$。在传播过程中，节点𝑣的所有邻居及其自身将竞争向𝑣传播标签。基于置信度分数越大则边权重越大的直觉，我们将式3中的预测更新函数$f_{PLP}$改写如下：

$$
f_{P L P}^{k+1}(v)=\sum_{u\in N_{v}\cup{v}}w_{u v}f_{P L P}^{k}(u),
$$

$$
f_{P L P}^{k+1}(v)=\sum_{u\in N_{v}\cup{v}}w_{u v}f_{P L P}^{k}(u),
$$

where $w_{u v}$ is the edge weight between node $u$ and $v$ computed by the following softmax function:

其中 $w_{u v}$ 是节点 $u$ 和 $v$ 之间的边权重，由以下 softmax 函数计算得出：

$$
w_{u v}=\frac{e x p(c_{u})}{\sum_{u^{\prime}\in N_{v}\cup{v}}e x p(c_{u^{\prime}})}.
$$

$$
w_{u v}=\frac{e x p(c_{u})}{\sum_{u^{\prime}\in N_{v}\cup{v}}e x p(c_{u^{\prime}})}.
$$

Similar to LP, $f_{P L P}^{0}(v)$ is initialized as Eq. 2 and $f_{P L P}^{k}(v)$ remains the one-hot ground truth label vector for every labeled node $v\in V_{L}$ during the propagation.

类似于 LP (Label Propagation)，$f_{P L P}^{0}(v)$ 初始化为公式 2，且在传播过程中，每个已标注节点 $v\in V_{L}$ 的 $f_{P L P}^{k}(v)$ 始终保持为独热编码的真实标签向量。

Note that we can further parameter ize confidence score $c_{v}$ for inductive setting as an optional choice:

我们可以进一步将置信度得分 $c_{v}$ 参数化为归纳设置的可选方案：

$$
\begin{array}{r}{c_{v}=z^{T}X_{v},}\end{array}
$$

$$
\begin{array}{r}{c_{v}=z^{T}X_{v},}\end{array}
$$

where $z\in\mathbb{R}^{d}$ is a learnable parameter that projects node $v$ ’s feature into the confidence score.

其中 $z\in\mathbb{R}^{d}$ 是一个可学习参数，用于将节点 $v$ 的特征映射为置信度分数。

3.3.3 Feature Transformation Module. Note that PLP module which propagates labels through edges emphasizes the structure-based prior knowledge. Thus we also introduce Feature Transformation (FT) module as a complementary prediction mechanism. The FT module predicts labels by only looking at the raw features of a node. Formally, denoting the prediction of FT module as $f_{F T}$ , we apply a 2-layer $\mathrm{MLP^{2}}$ followed by a softmax function to transform the features into soft label predictions:

3.3.3 特征转换模块。需要注意的是，通过边传播标签的PLP模块强调基于结构的先验知识。因此，我们还引入了特征转换 (Feature Transformation, FT) 模块作为补充预测机制。FT模块仅通过观察节点的原始特征来预测标签。形式上，将FT模块的预测表示为 $f_{F T}$，我们应用一个2层 $\mathrm{MLP^{2}}$ 后接softmax函数，将特征转换为软标签预测：

$$
f_{F T}(v)=s o f t m a x(M L P(X_{v})).
$$

$$
f_{F T}(v)=s o f t m a x(M L P(X_{v})).
$$

3.3.4 A Trainable Combination. Now we will combine the PLP and FT modules as the full model of our student. In detail, we will learn a trainable parameter $\alpha_{v}\in[0,1]$ for each node $v$ to balance the predictions between PLP and FT. In other words, the prediction from FT module will be incorporated into that from PLP at each propagation step. We name the full student model as Combination of Parameterized label propagation and Feature transformation (CPF) and thus the prediction update function for each unlabeled node $v\in V_{U}$ in Eq. 4 will be rewritten as

3.3.4 可训练组合。现在我们将PLP和FT模块组合为完整的学生模型。具体而言，我们将为每个节点$v$学习一个可训练参数$\alpha_{v}\in[0,1]$，以平衡PLP和FT之间的预测。换句话说，FT模块的预测将在每个传播步骤中融入PLP的预测。我们将完整的学生模型命名为参数化标签传播与特征变换的组合(CPF)，因此公式4中每个未标记节点$v\in V_{U}$的预测更新函数将被重写为

$$
f_{C P F}^{k+1}(v)=\alpha_{v}\sum_{u\in N_{v}\cup{v}}w_{u v}f_{C P F}^{k}(u)+(1-\alpha_{v})f_{F T}(v),
$$

$$
f_{C P F}^{k+1}(v)=\alpha_{v}\sum_{u\in N_{v}\cup{v}}w_{u v}f_{C P F}^{k}(u)+(1-\alpha_{v})f_{F T}(v),
$$

where edge weight $w_{u v}$ and initialization $f_{C P F}^{0}(v)$ are the same with PLP module. Whether parameter i zing confidence score $c_{v}$ as Eq. 6 or not will lead to inductive/trans duct ive variants CPF-ind/CPF-tra.

边权重 $w_{u v}$ 和初始化 $f_{C P F}^{0}(v)$ 与 PLP 模块相同。是否如式 6 所示参数化置信度分数 $c_{v}$ 将分别产生归纳式变体 CPF-ind 和传导式变体 CPF-tra。

3.4 The Overall Algorithm and Details

3.4 整体算法与细节

Assuming that our student model has a total of $K$ layers, the distillation objective in Eq. 1 can be detailed as:

假设我们的学生模型共有 $K$ 层，则公式 1 中的蒸馏目标可具体表示为：

$$
\operatorname*{min}{\Theta}\sum_{v\in V_{U}}|f_{G N N}(v)-f_{C P F;\Theta}^{K}(v)|_{2},
$$

where $|\cdot|{2}$ is the L2-norm and the parameter set $\Theta$ includes the balancing parameters between PLP and FT ${\alpha_{v},\forall v\in V}$ , confidence parameters in PLP module ${c_{v},\forall v\in V}$ (or parameter $z$ for induc- tive setting), and the parameters of MLP in FT module $\Theta_{M L P}$ . There is also an important hyper-parameter in the distillation framework: the number of propagation layers $K$ . Alg. 1 shows the pseudo code of the training process.

其中 $|\cdot|{2}$ 是 L2 范数，参数集 $\Theta$ 包括 PLP 和 FT 之间的平衡参数 ${\alpha_{v},\forall v\in V}$、PLP 模块中的置信参数 ${c_{v},\forall v\in V}$（或归纳设置中的参数 $z$），以及 FT 模块中 MLP 的参数 $\Theta_{M L P}$。蒸馏框架中还有一个重要的超参数：传播层数 $K$。算法 1 展示了训练过程的伪代码。

We implement our framework based on Deep Graph Library (DGL) [31] and Pytorch [18], and employ an Adam optimizer [10] for parameter training. Dropout [25] is also applied to alleviate over fitting.

我们基于深度图库 (DGL) [31] 和 Pytorch [18] 实现了框架，并采用 Adam 优化器 [10] 进行参数训练。同时应用 Dropout [25] 来缓解过拟合问题。

Algorithm 1 The proposed knowledge distillation framework.

算法 1: 提出的知识蒸馏框架

3.5 Discussions on Interpret ability and Complexity

3.5 可解释性与复杂性的讨论

In this subsection, we will discuss the interpret ability of the learned student model and the complexity of our algorithm.

在本小节中，我们将讨论所学学生模型的可解释性以及我们算法的复杂性。

After the knowledge distillation, our student model CPF will predict the label of a specific node $v$ as a weighted average between the predictions of label propagation and feature-based MLP. The balance parameter $\alpha_{v}$ indicates whether structure-based LP or feature-based MLP is more important for node 𝑣’s prediction. LP mechanism is almost transparent and we can easily find out node $v$ is influenced by which neighbor to what extent at each iteration. On the other hand, the understanding of feature-based MLP can be derived by existing works [20] or directly looking at the gradients of different features. Therefore, the learned student model has better interpret ability than GNN teachers.

经过知识蒸馏后，我们的学生模型CPF会将特定节点$v$的标签预测为标签传播和基于特征的MLP预测结果的加权平均值。平衡参数$\alpha_{v}$表示对于节点𝑣的预测而言，基于结构的LP还是基于特征的MLP更重要。LP机制几乎是透明的，我们可以轻松地发现节点$v$在每次迭代中受到哪些邻居的影响以及影响程度。另一方面，对基于特征的MLP的理解可以从现有研究[20]中得出，或者直接查看不同特征的梯度。因此，学习到的学生模型比GNN教师模型具有更好的可解释性。

The time complexity of each iteration (line 3 to 13 in Alg. 1) and the space complexity of our algorithm are both $O(|E|+d|V|)$ , which is linear to the scale of datasets. In fact, the operations can be easily implemented in matrix form and the training process can be finished in seconds on real-world benchmark datasets with a single GPU device. Therefore, our proposed knowledge distillation framework is very time/space-efficient.

每次迭代的时间复杂度（算法1中第3至13行）和我们算法的空间复杂度均为$O(|E|+d|V|)$，与数据集规模呈线性关系。实际上，这些操作可以轻松以矩阵形式实现，在单GPU设备上的实际基准数据集上训练过程可在数秒内完成。因此，我们提出的知识蒸馏框架具有极高的时间/空间效率。

4 EXPERIMENTS

4 实验

In this section, we will start by introducing the datasets and teacher models used in our experiments. Then we will detail the experimental settings of teacher models and student variants. Afterwards, we will present quantitative results on evaluating semi-su