Optimization of Graph Neural Networks with Natural Gradient Descent

基于自然梯度下降的图神经网络优化

Abstract

摘要

In this work, we propose to employ information-geometric tools to optimize a graph neural network architecture such as the graph convolutional networks. More specifically, we develop optimization algorithms for the graph-based semi-supervised learning by employing the natural gradient information in the optimization process. This allows us to efficiently exploit the geometry of the underlying statistical model or parameter space for optimization and inference. To the best of our knowledge, this is the first work that has utilized the natural gradient for the optimization of graph neural networks that can be extended to other semi-supervised problems. Efficient computations algorithms are developed and extensive numerical studies are conducted to demonstrate the superior performance of our algorithms over existing algorithms such as ADAM and SGD.

在本研究中，我们提出运用信息几何工具来优化图神经网络架构（如Graph Convolutional Networks）。具体而言，我们通过在优化过程中引入自然梯度信息，开发了基于图的半监督学习优化算法。这种方法能高效利用底层统计模型或参数空间的几何结构进行优化与推断。据我们所知，这是首个将自然梯度应用于图神经网络优化的研究，该框架可扩展至其他半监督学习问题。我们开发了高效的计算算法，并通过大量数值实验证明：相比ADAM、SGD等现有算法，新算法具有显著性能优势。

Index Terms

索引术语

Graph neural network, Fisher information, natural gradient descent, network data.

图神经网络 (Graph Neural Network)、费雪信息 (Fisher information)、自然梯度下降 (Natural Gradient Descent)、网络数据 (Network Data)

I. INTRODUCTION

I. 引言

In machine learning, the cost function is mostly evaluated using labeled samples that are not easy to collect. Semi-supervised learning tries to find a better model by using unlabeled samples. Most of the semi-supervised methods are based on a graph representation on (transformed) samples and labels [11]. For example, augmentation methods create a new graph in which original and augmented samples are connected. Graphs, as datasets with linked samples, have been the center of attention in semi-supervised learning. Graph Neural Network (GNN), initially proposed to capture graph representations in neural networks [20], have been used for semisupervised learning in a variety of problems like node classification, link predictions, and so on. The goal of each GNN layer is to transform features while considering the graph structure by aggregating information from connected or neighboring nodes. When there is only one graph, the goal of node classification becomes predicting node labels in a graph while only a portion of node labels are available (even though the model might have access to the features of all nodes). Inspired by the advance of convolutional neural networks [14] in computer vision [12], Graph Convolutional Network (GCN) [10] employs the spectra of graph Laplacian for filtering signals and the kernel can be approximated using Chebyshev polynomials or functions [24, 22]. GCN has become a standard and popular tool in the emerging field of geometric deep learning [2].

在机器学习中，成本函数主要通过难以收集的标注样本进行评估。半监督学习试图利用未标注样本来寻找更好的模型。大多数半监督方法基于(变换后)样本和标签的图表示[11]。例如，数据增强方法会创建一个新图，将原始样本与增强样本连接起来。作为具有关联样本的数据集，图一直是半监督学习的关注焦点。图神经网络(GNN)最初是为捕捉神经网络中的图表示而提出的[20]，现已被用于节点分类、链接预测等多种半监督学习问题。每个GNN层的目标是通过聚合相连或相邻节点的信息，在考虑图结构的同时转换特征。当仅存在单一图时，节点分类的目标就转变为在仅部分节点标签可用的情况下(尽管模型可能获取所有节点的特征)预测图中节点标签。受计算机视觉领域卷积神经网络(CNN)进展的启发[14][12]，图卷积网络(GCN)[10]利用图拉普拉斯谱进行信号滤波，其核函数可通过切比雪夫多项式或函数近似[24][22]。GCN已成为几何深度学习这一新兴领域的标准流行工具[2]。

From the optimization perspective, Stochastic Gradient Descent (SGD)-based methods that use an estimation of gradients have been popular choices due to their simplicity and efficiency. However, SGD-based algorithms may be slow in convergence and hard to tune on large datasets. Adding extra information about gradients, may help with the convergence but are not always possible or easy to obtain. For example, using second-order gradients like the Hessian matrix, resulting in the Newton method, is among the best choices which, however, are not easy to calculate especially in NNs. When the dataset is large or samples are redundant, NNs are trained using methods built on top of SGD like AdaGrad [4] or Adam [9]. Such methods use the gradients information from previous iterations or simply add more parameters like momentum to the SGD. Natural Gradient Descent (NGD) [1] provides an alternative based on the secondmoment of gradients. Using an estimation of the inverse of the Fisher information matrix (simply Fisher), NGD transforms gradients into so-called natural gradients that showed to be much faster compared to the SGD in many cases. The use of NGD allows efficient exploration of the geometry of the underlying parameter space in the optimization process. Also, Fisher information plays a pivotal role throughout statistical modeling [16]. In frequent is t statistics, Fisher information is used to construct hypothesis tests and confidence intervals by maximum likelihood estimators. In Bayesian statistics, it defines the Jeffreys’s prior, a default prior commonly used for estimation problems and nuisance parameters in a Bayesian hypothesis test. In minimum description length, Fisher information measures the model complexity and its role in model selection within the minimum description length framework like AIC and BIC. Under this interpretation, NGD is invariant to any smooth and invertible re parameter iz ation of the model, while SGD-based methods highly depend on the parameter iz ation. For models with a large number of parameters like DNN, Fisher is so huge that makes it almost impossible to evaluate natural gradients. Thus, for faster calculation it is preferred to use an approximation of Fisher like Kronecker-Factored Approximate Curvature (KFAC) [18] that are easier to store and inverse.

从优化角度来看，基于随机梯度下降 (Stochastic Gradient Descent, SGD) 的方法因其简单高效而广受欢迎。然而，基于SGD的算法在大数据集上可能收敛缓慢且难以调参。虽然增加梯度相关信息有助于提升收敛性，但这些信息往往难以获取。例如，使用二阶梯度（如Hessian矩阵）的牛顿法虽是最优选择之一，但在神经网络中尤其难以计算。针对大规模或冗余数据集，神经网络通常采用基于SGD改进的方法（如AdaGrad [4]或Adam [9]），这些方法利用历史梯度信息或通过添加动量等参数来增强SGD。自然梯度下降 (Natural Gradient Descent, NGD) [1] 则基于梯度二阶矩提供了另一种优化思路：通过估计费雪信息矩阵（简称Fisher）的逆矩阵，NGD将普通梯度转换为自然梯度，后者在多场景下展现出远超SGD的收敛速度。NGD能有效探索参数空间的几何特性，而Fisher信息在统计建模中具有核心地位 [16] —— 在频率统计中用于构建最大似然估计的假设检验与置信区间；在贝叶斯统计中定义Jeffreys先验（常用于估计问题与贝叶斯检验中的冗余参数）；在最小描述长度框架（如AIC和BIC）中衡量模型复杂度并参与模型选择。值得注意的是，NGD对模型任意光滑可逆的参数化变换具有不变性，而SGD类方法高度依赖参数化形式。对于深度神经网络等参数量庞大的模型，Fisher矩阵规模过大导致自然梯度计算不可行，因此通常采用便于存储求逆的近似方法（如Kronecker分解近似曲率 (KFAC) [18]）。

Both GNN and training NNs with NGD have been active areas of research in recent years but, to the best of our knowledge, this is the first attempt on using NGD in the semi-supervised learning. In this work, a new framework for optimizing GNNs is proposed that takes into account the unlabeled samples in the approximation of Fisher. Section II provides an overview of related topics such as semi-supervised learning, GNN, and NGD. The proposed algorithm is described in section III and a series of experiments are performed in section IV to evaluate the method’s efficiency and sensitivity to hyper-parameters. Finally, the work is concluded in section V.

近年来，图神经网络(GNN)和利用自然梯度下降(NGD)训练神经网络一直是活跃的研究领域，但据我们所知，这是首次尝试在半监督学习中使用NGD。本文提出了一个优化GNN的新框架，该框架在Fisher矩阵近似中考虑了未标记样本。第二节概述了相关主题，如半监督学习、GNN和NGD。第三节描述了所提出的算法，第四节通过一系列实验评估了该方法的效率和超参数敏感性。最后，第五节对工作进行了总结。

II. PROBLEM AND BACKGROUND

II. 问题与背景

In this section, first, the graph-based semi-supervised learning with a focus on least-squared regression and cross-entropy classification is defined. Required backgrounds on the optimization and neural networks are provided in the subsequent sections. A detailed description of the notation is summarized in the Table I.

本节首先定义了基于图的半监督学习，重点介绍最小二乘回归和交叉熵分类。后续章节将提供有关优化和神经网络的必要背景知识。表1总结了符号的详细说明。

A. Problem

A. 问题

Consider an information source $q(\mathbf{x})$ generating independent samples $\mathbf{x}{i}\in\mathbb{X}$ , the target distribution $q(\mathbf{y}|\mathbf{x})$ associating $\mathbf{y}{i} \in~\mathbb{Y}$ to each $\mathbf{x}_{i}$ , and the adjacency distribution $q(a|\mathbf{x},\mathbf{x}^{\prime})$ representing the link between two nodes given their covariates levels $\mathbf{x}$ and $\mathbf{x}^{\prime}$ . The problem of learning $q(\mathbf{y}|\mathbf{x})$ is to estimate some parameters $\pmb{\theta}$ that minimizes the cost function

考虑一个信息源 $q(\mathbf{x})$ 生成独立样本 $\mathbf{x}{i}\in\mathbb{X}$，目标分布 $q(\mathbf{y}|\mathbf{x})$ 将 $\mathbf{y}{i} \in~\mathbb{Y}$ 关联到每个 $\mathbf{x}_{i}$，以及邻接分布 $q(a|\mathbf{x},\mathbf{x}^{\prime})$ 表示给定协变量水平 $\mathbf{x}$ 和 $\mathbf{x}^{\prime}$ 时两个节点之间的链接。学习 $q(\mathbf{y}|\mathbf{x})$ 的问题在于估计某些参数 $\pmb{\theta}$ 以最小化成本函数

$$
r(\theta)=E_{\mathbf{x},\underline{{\mathbf{x}}}^{\prime}\sim q(\mathbf{x}),\underline{{a}}\sim q(a|\mathbf{x},\mathbf{x}^{\prime}),\mathbf{y}\sim q(\mathbf{y}|\mathbf{x})}[l(\mathbf{y},\mathbf{f}(\mathbf{x},\underline{{\mathbf{x}}}^{\prime},\underline{{a}};\theta))]
$$

where the loss function $l(\mathbf{y},\hat{\mathbf{y}})$ measures the prediction error between $\mathbf{y}$ and $\hat{\bf y}$ . Also, $\underline{{\mathbf{x}}}^{\prime}$ and $\underline{{\boldsymbol{a}}}$ show sequences of $\mathbf{x}^{\prime}$ and $a$ , respectively. As $q(\mathbf{x}),q(a|\mathbf{x},\mathbf{x}^{\prime})$ , and $q(\mathbf{y}|\mathbf{x})$ are usually unknown or unavailable, the cost $r(\pmb\theta)$ is estimated using samples from these distributions. Furthermore, it is often more expensive to sample from $q(\mathbf{y}|\mathbf{x})$ than $q(\mathbf{x})$ and $q(a|\mathbf{x},\mathbf{x}^{\prime})$ resulting in the different number of samples from each distribution being available.

其中损失函数 $l(\mathbf{y},\hat{\mathbf{y}})$ 用于衡量 $\mathbf{y}$ 与 $\hat{\bf y}$ 之间的预测误差。此外，$\underline{{\mathbf{x}}}^{\prime}$ 和 $\underline{{\boldsymbol{a}}}$ 分别表示 $\mathbf{x}^{\prime}$ 和 $a$ 的序列。由于 $q(\mathbf{x})$、$q(a|\mathbf{x},\mathbf{x}^{\prime})$ 和 $q(\mathbf{y}|\mathbf{x})$ 通常未知或不可得，因此需通过这些分布的样本来估计成本 $r(\pmb\theta)$。此外，从 $q(\mathbf{y}|\mathbf{x})$ 采样的成本通常高于 $q(\mathbf{x})$ 和 $q(a|\mathbf{x},\mathbf{x}^{\prime})$，这导致各分布可用的样本数量不同。

Let $X:=:X_{0}$ to be a $d_{0}\times n$ matrix of $n\geq1$ i.i.d $\mathbf{x}_{i}$ samples from $q(\mathbf{x})$ (equivalent to $X\sim q(X))$ . It is assumed that $n\times n$ adjacency matrix $A=[a_{i j}]$ is sampled from $q(a|\mathbf{x}_{i},\mathbf{x}_{j})$ for $i,j=1,\dots,n$ (equivalent to $A\sim q(A|X))$ . One can consider $(X,A)$ to be a graph of $n$ nodes in which the $i$ th column of $X$ shows the covariate at the node $i$ and $D=\mathrm{diag}(\textstyle\sum_{j}a_{i j})$ denotes the diagonal degree matrix. Also, denote $Y$ to be a $d_{m}\times\bar{n}$ matrix of $\bar{n}<n$ samples $\mathbf{y}_{i}$ from $q(\mathbf{y}|\mathbf{x}_{i})$ for $i=1,\dots,\bar{n}$ and $\mathbf{z}=[\mathbb{1}(i\in{1,\dots,\bar{n}})]_{i=1}^{n}$ to be the training mask vector. Note that 1(condition) is 1 if the condition is true and 0 otherwise. Thus, an empirical cost can be estimated by

设 $X:=:X_{0}$ 为一个 $d_{0}\times n$ 的矩阵，其中包含 $n\geq1$ 个来自 $q(\mathbf{x})$ 的独立同分布样本 $\mathbf{x}_{i}$ (等价于 $X\sim q(X))$。假设 $n\times n$ 的邻接矩阵 $A=[a_{i j}]$ 是从 $q(a|\mathbf{x}_{i},\mathbf{x}_{j})$ 中采样得到的，其中 $i,j=1,\dots,n$ (等价于 $A\sim q(A|X))$。可以将 $(X,A)$ 视为一个具有 $n$ 个节点的图，其中 $X$ 的第 $i$ 列表示节点 $i$ 的协变量，$D=\mathrm{diag}(\textstyle\sum_{j}a_{i j})$ 表示对角度矩阵。此外，定义 $Y$ 为一个 $d_{m}\times\bar{n}$ 的矩阵，其中包含 $\bar{n}<n$ 个来自 $q(\mathbf{y}|\mathbf{x}_{i})$ 的样本 $\mathbf{y}_{i}$，其中 $i=1,\dots,\bar{n}$，并定义 $\mathbf{z}=[\mathbb{1}(i\in{1,\dots,\bar{n}})]_{i=1}^{n}$ 为训练掩码向量。注意，1(condition) 在条件为真时为 1，否则为 0。因此，可以通过以下方式估计经验成本：

TABLE I NOTATION

表 I 符号说明

符号	描述
x, x, X	标量、向量、矩阵
∈, 入	正则化超参数
	学习率
A	邻接矩阵
XT	矩阵转置
I	单位矩阵
	x向量的序列
n	样本总数
n	已标注样本数
F	费舍尔信息矩阵
B	预处理矩阵
r(0)	参数0的代价
l(y,y)	y与y之间的损失
q(x)	源分布
q(y\|x)	目标分布
q(a\|x,x')	邻接分布
p(ylf(X, A;0))	预测分布
Φ()	逐元素非线性函数
Vef	标量f关于θ的梯度
Jef	向量f关于θ的雅可比矩阵
Hef	标量f关于θ的海森矩阵
	逐元素乘法运算

$$
\hat{r}(\pmb\theta)=\frac{1}{\bar{n}}\sum_{i=1}^{\bar{n}}l(\mathbf y_{i},\mathbf f(\mathbf x_{i},X,A;\pmb\theta)),
$$

where $\mathbf{f}\left(\mathbf{x}{i},X,A;\pmb\theta\right)$ shows the processed $\mathbf{x}{i}$ when having access to $n-1$ extra samples and links between them. Note that as $X$ contains $\mathbf{x}{i}$ (the $i$ th column), $\mathbf{f}\left(\mathbf{x}_{i},X,A;\pmb\theta\right)$ and $\mathbf{f}\left(X,A;\theta\right)$ are used interchangeably.

其中 $\mathbf{f}\left(\mathbf{x}{i},X,A;\pmb\theta\right)$ 表示在访问 $n-1$ 个额外样本及其间链接时对 $\mathbf{x}{i}$ 的处理结果。注意由于 $X$ 包含 $\mathbf{x}{i}$ (第 $i$ 列)，因此 $\mathbf{f}\left(\mathbf{x}_{i},X,A;\pmb\theta\right)$ 和 $\mathbf{f}\left(X,A;\theta\right)$ 可互换使用。

Assuming $p(\mathbf{y}|\mathbf{f}(X,A;\pmb\theta))=p_{\pmb\theta}(\mathbf{y}|X,A)$ to be an exponential family with natural parameters in $\mathbb{F}$ , the loss function becomes

假设 $p(\mathbf{y}|\mathbf{f}(X,A;\pmb\theta))=p_{\pmb\theta}(\mathbf{y}|X,A)$ 是指数族分布且自然参数属于 $\mathbb{F}$ ，则损失函数变为

$$
l(\mathbf{y},\mathbf{f}\left(X,A;\pmb{\theta}\right))=-\log p(\mathbf{y}|\mathbf{f}\left(X,A;\pmb{\theta}\right)).
$$

In the least-squared regression,

在最小二乘回归中，

$$
p(\mathbf{y}|\mathbf{f}(X,A;\pmb\theta))=\mathcal{N}(\mathbf{y}|\mathbf{f}(X,A;\pmb\theta),\sigma^{2})
$$

for fixed $\sigma^{2}$ and $\mathbb{F}=\mathbb{Y}=\mathbb{R}$ . In the cross-entropy classification to $c$ classes,

对于固定的 $\sigma^{2}$ 且 $\mathbb{F}=\mathbb{Y}=\mathbb{R}$ 情况。在分类到 $c$ 类的交叉熵中，

$$
p(y=k|\mathbf{f}(X,A;\pmb\theta))=\exp(\mathbf{f}_{k})/\sum_{j=1}^{c}\exp(\mathbf{f}_{j})
$$

for $\mathbb{F}=\mathbb{R}^{c}$ and $\mathbb{Y}={1,\ldots,c}$ .

对于 $\mathbb{F}=\mathbb{R}^{c}$ 和 $\mathbb{Y}={1,\ldots,c}$。

B. Parameter estimation

B. 参数估计

Having the first order approximation of $r(\pmb\theta)$ around a point $\pmb{\theta}_{0}$ ,

在点 $\pmb{\theta}_{0}$ 附近对 $r(\pmb\theta)$ 进行一阶近似，

$$
r(\pmb\theta)\approx r(\pmb\theta_{0})+\mathbf{g}{0}^{\top}(\pmb\theta-\pmb\theta_{0}),
$$

the gradient descent can be used to update parameter $\pmb{\theta}$ iterative ly:

梯度下降可用于迭代更新参数 $\pmb{\theta}$：

$$
\pmb{\theta}{t+1}=\pmb{\theta}{t}-\eta B\mathbf{g}_{0}
$$

where $\eta>0$ denotes the learning rate, ${\bf g}{0}={\bf g}(\pmb{\theta}{0})$ is the gradient at $\pmb{\theta}_{0}$ for

其中 $\eta>0$ 表示学习率，${\bf g}{0}={\bf g}(\pmb{\theta}{0})$ 是 $\pmb{\theta}_{0}$ 处的梯度。

$$
\mathbf{g}(\pmb\theta)=\frac{\partial r(\pmb\theta)}{\partial\pmb\theta}
$$

and $B$ shows a symmetric positive definite matrix called pre conditioner capturing the interplay between the elements of $\pmb{\theta}$ . In SGD, $B=I$ and ${\bf g}_{0}$ is approximated by:

且 $B$ 表示一个对称正定矩阵，称为预条件子 (pre conditioner)，用于捕捉 $\pmb{\theta}$ 各元素间的相互作用。在SGD中，$B=I$ 且 ${\bf g}_{0}$ 通过以下方式近似：

$$
\hat{\bf g}{0}=\frac{1}{\bar{n}}\sum_{i=1}^{\bar{n}}\frac{\partial l(y_{i},{\bf f}(X,A;\pmb\theta))}{\partial\pmb\theta}
$$

where $\bar{n}\geq1$ can be the mini-batch (a randomly drawn subset of the dataset) size.

其中 $\bar{n}\geq1$ 可以是小批量 (mini-batch) 大小（从数据集中随机抽取的子集）。

To take into the account the relation between $\pmb{\theta}$ elements, one can use the second order approximation of $r(\pmb\theta)$ :

考虑到 $\pmb{\theta}$ 元素之间的关系，可以使用 $r(\pmb\theta)$ 的二阶近似：

$$
\boldsymbol{r}(\pmb{\theta})\approx\boldsymbol{r}(\pmb{\theta}{0})+\mathbf{g}{0}^{\sf T}(\pmb{\theta}-\pmb{\theta}{0})+\frac{1}{2}(\pmb{\theta}-\pmb{\theta}{0})^{\sf T}H_{0}(\pmb{\theta}-\pmb{\theta}_{0}),
$$

where $H_{0}=H(\pmb\theta_{0})$ denotes the Hessian matrix at $\pmb{\theta}_{0}$ for

其中 $H_{0}=H(\pmb\theta_{0})$ 表示在 $\pmb{\theta}_{0}$ 处的Hessian矩阵。

$$
H(\pmb\theta)=\frac{\partial^{2}r(\pmb\theta)}{\partial\pmb\theta^{\top}\pmb\theta}.
$$

Thus, having the gradients of $r(\pmb\theta)$ around $\pmb{\theta}$ as:

因此，在 $\pmb{\theta}$ 附近得到 $r(\pmb\theta)$ 的梯度为：

$$
\begin{array}{r}{{\bf g}(\pmb{\theta})\approx{\bf g}{0}+H_{0}(\pmb{\theta}-\pmb{\theta}_{0}),}\end{array}
$$

the parameters can be updated using:

参数可通过以下方式更新：

$$
\pmb{\theta}{t+1}=(I-\eta B H_{0})\pmb{\theta}{t}-\eta B(\mathbf{g}{0}-H_{0}\pmb{\theta}_{0}).
$$

The convergence of Eq. 13 heavily depends on the selection of $\eta$ and the distribution of $I-\eta B H_{0}$ eigenvalues. Note that update rules Eqs. 7 and 13 coincides at $B=H_{0}^{-1}$ resulting the Newton’s method. As it is not always possible or desirable to obtain Hessian, several pre conditioners are suggested to adapt the information geometry of the parameter space.

式13的收敛性很大程度上取决于$\eta$的选择以及$I-\eta B H_{0}$特征值的分布。值得注意的是，当$B=H_{0}^{-1}$时，更新规则式7和式13会退化为牛顿法。由于获取Hessian矩阵并不总是可行或可取，研究者提出了若干预条件子(preconditioner)来适配参数空间的信息几何结构。

In NGD, the pre conditioner is defined to be the inverse of Fisher Information matrix:

在自然梯度下降(NGD)中，预条件子被定义为费舍尔信息矩阵的逆矩阵:

$$
\begin{array}{r l}{F(\pmb\theta):=E_{\mathbf x,\mathbf y\sim p(\mathbf x,\mathbf y;\theta)}[\nabla_{\pmb\theta}\nabla_{\pmb\theta}^{\mathsf{T}}]}\ {=E_{\mathbf x\sim q(\mathbf x),\mathbf y\sim p(\mathbf y|\mathbf x;\pmb\theta)}[\nabla_{\pmb\theta}\nabla_{\pmb\theta}^{\mathsf{T}}]}\end{array}
$$

where $p(\mathbf{x},\mathbf{y};\pmb\theta):=q(\mathbf{x})p(\mathbf{y}|\mathbf{x};\pmb\theta)$ and

其中 $p(\mathbf{x},\mathbf{y};\pmb\theta):=q(\mathbf{x})p(\mathbf{y}|\mathbf{x};\pmb\theta)$ 且

$$
\begin{array}{r}{\nabla_{\theta}:=-\nabla_{\theta}\log p(\mathbf{x},\mathbf{y};\theta).}\end{array}
$$

C. Neural Networks

C. 神经网络

A neural network is a mapping from the input space $\mathbb{X}$ to the output space $\mathbb{F}$ through a series of $m$ layers. Layer $k\in{1,\ldots,m}$ , projects $d_{k-1}$ -dimensional input $\mathbf{x}{k-1}$ to $d_{k}$ -dimensional output $\mathbf{x}_{k}$ and can be expressed as:

神经网络是通过一系列 $m$ 层将输入空间 $\mathbb{X}$ 映射到输出空间 $\mathbb{F}$ 的映射。第 $k\in{1,\ldots,m}$ 层将 $d_{k-1}$ 维输入 $\mathbf{x}{k-1}$ 投影为 $d_{k}$ 维输出 $\mathbf{x}_{k}$，可表示为：

$$
\mathbf{x}{k}=\phi_{k}(W_{k}\mathbf{x}_{k-1})
$$

D. Graph Neural Networks

D. 图神经网络

The Graph Neural Network (GNN) extends the NN mapping to the data represented in graph domains [20]. The basic idea is to use related samples when the adjacency information is available. In other words, the input to the $k$ ’th layer, $\mathbf{x}{k-1}$ is transformed into $\tilde{\mathbf{x}}{k-1}$ that take into the account unlabeled samples using the adjacency such that $p(\mathbf{x}{k-1},A)=p(\tilde{\mathbf{x}}_{k-1})$ . Therefore, for each node $i=1,\ldots,n$ , the Eq. 17 can be written by a local transition function (or a single message passing step) as:

图神经网络 (Graph Neural Network, GNN) 将神经网络映射扩展到图域表示的数据 [20]。其核心思想是在邻接信息可用时利用相关样本。换句话说，第 $k$ 层的输入 $\mathbf{x}{k-1}$ 会被转换为 $\tilde{\mathbf{x}}{k-1}$ ，该转换通过邻接矩阵考虑未标记样本，使得 $p(\mathbf{x}{k-1},A)=p(\tilde{\mathbf{x}}_{k-1})$ 。因此，对于每个节点 $i=1,\ldots,n$ ，方程 17 可通过局部转移函数（或单次消息传递步骤）表示为：

$$
\mathbf{x}{k,i}=\mathbf{f}{k}(\mathbf{x}{k-1,i},\underline{{\mathbf{x}}}{k-1,i},\underline{{\mathbf{x}}}{0,i},\underline{{\mathbf{x}}}{0,i};W_{k})
$$

where $\underline{{\mathbf{x}}}{k,i}$ denotes all the information coming from nodes connected to the $i$ th node at the $k$ th layer. The subscripts here are used to indicate both the layer and the node, i.e. $\mathbf{x}{k,i}$ means the state embedding of node $i$ in the layer $k$ . Also, the local transition Eq. 19, parameterized by $W_{k}$ , is shared by all nodes that includes the information of the graph structure, and $\mathbf{x}{0,i}=\mathbf{x}_{i}$ .

其中 $\underline{{\mathbf{x}}}{k,i}$ 表示第 $k$ 层中与第 $i$ 个节点相连的所有节点传入的信息。这里的下标同时用于表示层和节点，即 $\mathbf{x}{k,i}$ 代表第 $k$ 层中第 $i$ 个节点的状态嵌入。此外，由 $W_{k}$ 参数化的局部转移方程 (Eq. 19) 被所有包含图结构信息的节点共享，且 $\mathbf{x}{0,i}=\mathbf{x}_{i}$。

The Graph Convolutional Network (GCN) is a one of the GNN with the message passing operation as a linear approximation to spectral graph convolution, followed by a non-linear activation function as:

图卷积网络 (GCN) 是一种将消息传递操作作为谱图卷积线性近似的图神经网络 (GNN)，其后接非线性激活函数：

$$
\begin{array}{r l}&{\mathbf{x}{k,i}=\mathbf{f}{k}(\mathbf{x}{k-1,i},\underline{{\mathbf{x}}}{k-1,i};W_{k})}\ &{}\ &{X_{k}=\phi_{k}(W_{k}X_{k-1}\tilde{A})}\ &{}\ &{\qquad=\phi_{k}(W_{k}\tilde{X}_{k-1})}\end{array}
$$

where $\phi_{k}$ is a element-wise nonlinear activation function such as $\mathrm{RELU}(x)=\operatorname*{max}(x,0),\mid$ $W_{k}$ is a $d_{k}\times d_{k-1}$ parameter matrix that needs to be estimated. $\tilde{A}$ denotes the normalized adjacency matrix defined by:

其中 $\phi_{k}$ 是逐元素非线性激活函数，例如 $\mathrm{RELU}(x)=\operatorname*{max}(x,0),\mid$ $W_{k}$ 是需要估计的 $d_{k}\times d_{k-1}$ 参数矩阵。$\tilde{A}$ 表示由以下公式定义的归一化邻接矩阵：

$$
\tilde{A}=(D+I)^{-1/2}(A+I)(D+I)^{-1/2}
$$

to overcome the over fitting issue due to the small number of labeled samples $\bar{n}$ . In fact, a GCN layer is basically a NN (Eq. 17) where the input $\mathbf{x}{k-1}$ is initially updated into $\tilde{\mathbf{x}}{k-1}$ using a so-called re normalization trick such that $\begin{array}{r}{\tilde{\mathbf{x}}{k-1,i}=\sum_{j=1}^{n}\tilde{a}{i,j}\mathbf{x}{k-1,i}}\end{array}$ where $\tilde{A}=[\tilde{a}{i,j}]$ . Comparing Eq. 20 with the more general Eq. 19, the local transition function $\mathbf{f}{k}$ is defined as a linear combination followed by a nonlinear activation function. For classifying $\mathbf{x}$ into $c$ classes, having a $c$ -dimensional $\mathbf{x}{m}$ as the output of the last layer with a Softmax activation function, the loss between the label $\mathbf{y}$ and the prediction $\mathbf{x}_{m}$ becomes:

为克服因标记样本数量 $\bar{n}$ 过少导致的过拟合问题。实际上，GCN层本质上是一个神经网络（见公式17），其输入 $\mathbf{x}{k-1}$ 会通过所谓的重归一化技巧更新为 $\tilde{\mathbf{x}}{k-1}$，即 $\begin{array}{r}{\tilde{\mathbf{x}}{k-1,i}=\sum_{j=1}^{n}\tilde{a}{i,j}\mathbf{x}{k-1,i}}\end{array}$，其中 $\tilde{A}=[\tilde{a}{i,j}]$。将公式20与更通用的公式19进行比较，局部转移函数 $\mathbf{f}{k}$ 被定义为线性组合后接非线性激活函数。为了将 $\mathbf{x}$ 分类到 $c$ 个类别中，最后一层输出具有Softmax激活函数的 $c$ 维向量 $\mathbf{x}{m}$，标签 $\mathbf{y}$ 与预测 $\mathbf{x}_{m}$ 之间的损失函数为：

$$
l(\mathbf{y},\mathbf{x}{m})=-\sum_{j=1}^{c}\mathbb{1}(\mathbf{x}{m,j}=j)\log\mathbf{x}_{m,j}.
$$

III. METHOD

III. 方法

The basic idea of preconditioning is to capture the relation between the gradients of parameters $\nabla_{\theta}$ . This relation can be as complete as a matrix $B$ (for example, NGD) representing the pairwise relation between elements of $\nabla_{\theta}$ or as simple as a weighting vector (for example, Adam) with the same size as $\nabla_{\pmb{\theta}}$ resulting in a diagonal $B$ . Considering the flow of gradients $\nabla_{\pmb{\theta},t}$ over the training time as input features, the goal of preconditioning is to extract useful features that help with the updating rule. One can consider the pre conditioner to be the expected value of $B(\mathbf{x},\mathbf{y})=[b_{i j}]^{-1}$ for

预条件处理的基本思想是捕捉参数梯度 $\nabla_{\theta}$ 之间的关系。这种关系可以是一个完整的矩阵 $B$ (例如自然梯度下降法(NGD)) 表示 $\nabla_{\theta}$ 各元素间的成对关联，也可以简化为与 $\nabla_{\pmb{\theta}}$ 同维度的加权向量 (例如Adam)，此时 $B$ 为对角矩阵。将训练过程中梯度流 $\nabla_{\pmb{\theta},t}$ 视为输入特征时，预条件处理的目标是提取有助于更新规则的有效特征。可将预条件矩阵视为 $B(\mathbf{x},\mathbf{y})=[b_{i j}]^{-1}$ 的期望值。

$$
b_{i j}=b_{i,j}(\mathbf{x},\mathbf{y})=b(\nabla_{\theta i}||\nabla_{\theta j})^{1}.
$$

In methods with a diagonal pre conditioner like Adam, $B({\bf x},{\bf y})=\mathrm{diag}(\nabla_{\pmb\theta}\odot\nabla_{\pmb\theta})$ , the pairwise relation between gradients is neglected. Pre conditioners like Hessian inverse in Newton’s method with the form of $b_{i j}=\partial\nabla_{\pmb{\theta}_{i}}/\partial\theta_{j}$ are based on the second derivative that encodes the cost curvature in the parameter space. In NGD and similar methods, this curvature is approximated using the second moment of gradient $b_{i j}=\nabla_{\pmb{\theta}_{i}}\nabla_{\pmb{\theta}_{j}}$ , as an approximation of Hessian, in some empirical cases (see [13] for a detailed discussion).

在采用对角预条件器（如Adam）的方法中，$B({\bf x},{\bf y})=\mathrm{diag}(\nabla_{\pmb\theta}\odot\nabla_{\pmb\theta})$，梯度间的成对关系被忽略。而牛顿法等采用Hessian逆矩阵形式的预条件器 $b_{i j}=\partial\nabla_{\pmb{\theta}_{i}}/\partial\theta_{j}$ 基于二阶导数，编码了参数空间中的代价曲率。在自然梯度下降（NGD）及类似方法中，该曲率通过梯度的二阶矩 $b_{i j}=\nabla_{\pmb{\theta}_{i}}\nabla_{\pmb{\theta}_{j}}$ 作为Hessian矩阵的近似进行估计（具体讨论可参见[13]）。

In this section, a new preconditioning algorithm, motivated by natural gradient, is proposed for graph-based semi-supervised learning that improves the convergence of Adam and SGD with intuitive and insensitive hyper-parameters. The natural gradient is a concept from information geometry and stands for the steepest descent direction in the Riemannian manifold of probability distributions [1], where the distance in the distribution space is measured with a special Riemannian metric. This metric depends only on the properties of the distributions themselves and not their parameters, and in particular, it approximates the square root of the KL divergence within a small neighborhood [17]. Instead of measuring the distance between the parameters $\pmb{\theta}$ and $\pmb{\theta}^{\prime}$ , the cost is measured by the KL divergence between their distributions $p(\pmb\theta)$ and $p(\pmb\theta^{\prime})$ . Consequently, the steepest descent direction in the statistical manifold is the negative gradient preconditioned with the Fisher information matrix $F(\pmb\theta)$ . The validation cost on three different datasets is shown in Fig. 1 where preconditioning is applied to both Adam and SGD.

在本节中，受自然梯度启发，我们提出了一种新的预处理算法，用于基于图的半监督学习。该算法能改善Adam和SGD的收敛性，且具有直观且不敏感的超参数。自然梯度源于信息几何学，表示概率分布黎曼流形中最陡下降方向[1]，其中分布空间的距离由特殊黎曼度量衡量。该度量仅取决于分布本身特性而非参数，特别地，它能在小邻域内近似KL散度的平方根[17]。不同于测量参数$\pmb{\theta}$与$\pmb{\theta}^{\prime}$间的距离，其代价通过二者分布$p(\pmb\theta)$与$p(\pmb\theta^{\prime})$间的KL散度来衡量。因此，统计流形中最陡下降方向是经Fisher信息矩阵$F(\pmb\theta)$预处理的负梯度。图1展示了三个不同数据集上的验证成本，其中预处理同时应用于Adam和SGD。

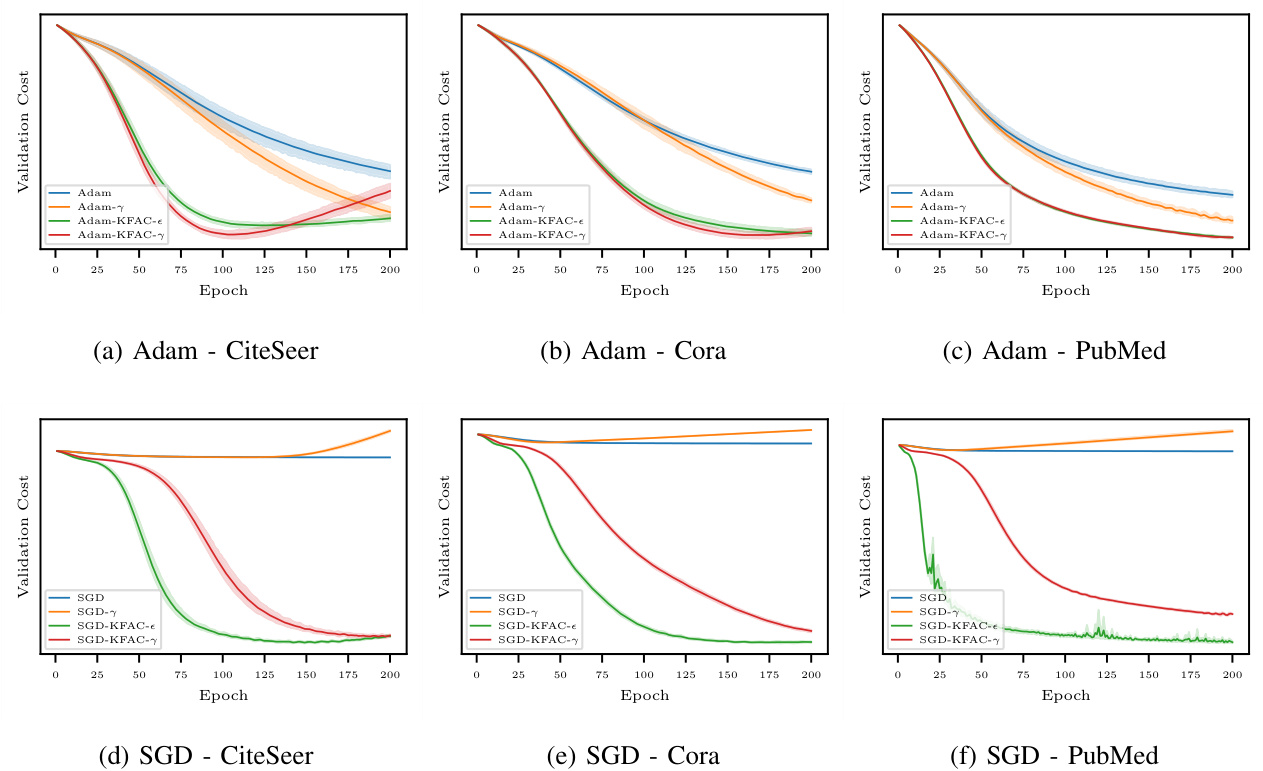
Fig. 1. The validation costs of four optimization methods on the second split of Citation datasets over 10 runs. A 2-layer GCN with a 64-dimensional hidden variable is used in all experiments. As shown in Fig. 1a, 1b, and 1c (upper row), the proposed Adam-KDAC methods (green and red curves) outperform vanilla Adam methods (blue and orange curves) on all three datasets. Also, Fig. 1d, 1e, and 1f (bottom row) reveal that the suggested SGD-KFAC methods (green and red curves) achieve a remarkably faster convergence than the vanilla SGD method (blue and orange curves) on all three datasets.

图 1: 四种优化方法在Citation数据集第二划分上10次运行的验证成本。所有实验均使用具有64维隐藏变量的2层GCN。如图1a、1b和1c(上行)所示，提出的Adam-KDAC方法(绿色和红色曲线)在所有三个数据集上均优于原始Adam方法(蓝色和橙色曲线)。此外，图1d、1e和1f(下行)表明，建议的SGD-KFAC方法(绿色和红色曲线)在所有三个数据集上比原始SGD方法(蓝色和橙色曲线)实现了显著更快的收敛。

As the original NGD (Eq. 14) is defined based on a prediction function with access only to a single sample, $p(\mathbf{y}|\mathbf{f}(\mathbf{x};\pmb\theta))$ , Fisher information matrix with the presence of the adjacency distribution becomes:

由于原始NGD (公式14) 是基于仅能访问单个样本的预测函数 $p(\mathbf{y}|\mathbf{f}(\mathbf{x};\pmb\theta))$ 定义的，存在邻接分布时的Fisher信息矩阵变为：

$$
\begin{array}{r l}&{F(\pmb\theta)=E_{\mathbf x,\underline{x}^{\prime},\underline{a},\mathbf y\sim p(\mathbf x,\underline{x}^{\prime},\underline{a},\mathbf y;\pmb\theta)}[\nabla_{\b\theta}\nabla_{\b\theta}^{\top}]}\ &{\qquad=E_{\mathbf x,\underline{x}^{\prime}\sim q(\mathbf x),\underline{a}\sim q({\boldsymbol a}|\mathbf x,\mathbf x^{\prime}),\mathbf y\sim p(\mathbf y|\mathbf x,\underline{x}^{\prime},\underline{a};\pmb\theta)}[\nabla_{\b\theta}\nabla_{\b\theta}^{\top}].}\end{array}
$$

With $n$ samples of $q(\mathbf{x})$ , i.e. $X$ and $n^{2}$ samples of $q(a|X)$ , i.e. $A$ , Fisher can be estimated as:

在获得 $q(\mathbf{x})$ 的 $n$ 个样本 $X$ 以及 $q(a|X)$ 的 $n^{2}$ 个样本 $A$ 后，Fisher 信息量可估计为：

$$
\begin{array}{r}{\hat{F}(\pmb{\theta})=E_{\mathbf{y}\sim p(\mathbf{y}|X,A;\pmb{\theta})}[\nabla_{\pmb{\theta}}\nabla_{\pmb{\theta}}^{\mathsf{T}}],}\end{array}
$$

where

其中

$$
\nabla_{\pmb{\theta}}=-\nabla_{\pmb{\theta}}\log p(X,A,\mathbf{y};\pmb{\theta}).
$$

In fact, to evaluate the expectation in Eq. 26, $q(X)$ and $q(A|X)$ are approximated with $\hat{q}(X)$ and $\hat{q}(A|X)$ using ${{\bf x}{i}}{i=1}^{n}$ and $A$ , respectively. However, there are only $\bar{n}$ samples from $\hat{q}(\mathbf{y}|\mathbf{x}{j})$ as an approximation of $q(\mathbf{y}|\mathbf{x}_{j})$ for the following replacement:

事实上，为了计算式26中的期望值，$q(X)$和$q(A|X)$分别通过${{\bf x}{i}}{i=1}^{n}$和$A$近似为$\hat{q}(X)$与$\hat{q}(A|X)$。但对于后续替换所需的$q(\mathbf{y}|\mathbf{x}{j})$，其近似分布$\hat{q}(\mathbf{y}|\mathbf{x}_{j})$仅能提供$\bar{n}$个样本。

$$
p(\mathbf{y}|X,A;\pmb{\theta})\approx\hat{q}(\mathbf{y}|\mathbf{x}_{i}).
$$

Therefore, an empirical Fisher can be obtained by

因此，可以通过经验获得Fisher信息矩阵

for

为了

$$
\hat{F}(\pmb\theta)=\frac{1}{\bar{n}}\sum_{i=1}^{\bar{n}}\nabla_{\pmb\theta,i}\nabla_{\pmb\theta,i}^{\mathsf{T}}=\sum_{i=1}^{\bar{n}}B_{i}(\pmb\theta)
$$

From the computation perspective, the matrix $B_{i}(\pmb\theta)$ can be very large, for example, in neural networks with multiple layers, the parameters could be huge, so it needs to be approximated too. In networks characterized with Eqs. 17 or 20, a simple solution would be ignoring the cross-layer terms so that $B_{i}(\pmb\theta)^{-1}$ and consequently $B_{i}(\pmb\theta)$ turns into a block-diagonal matrix:

从计算角度来看，矩阵$B_{i}(\pmb\theta)$可能非常大，例如在多层神经网络中参数量会极其庞大，因此也需要进行近似处理。对于式17或20描述的网络结构，一种简单解决方案是忽略跨层项，使$B_{i}(\pmb\theta)^{-1}$及对应的$B_{i}(\pmb\theta)$转化为块对角矩阵：

$$
B_{i}(\pmb\theta)=\mathrm{diag}(B_{1,i},\dots,B_{m,i})
$$

In KFAC, the diagonal block $B_{k,i}$ , corresponded to $k$ ’th layer with the dimension $d_{k}d_{k-1}\times d_{k}d_{k-1}$ , is approximated with the Kronecker product of the inverse of two smaller matrices $U_{k,i}$ and

[论文翻译]基于自然梯度下降的图神经网络优化

原文地址：https://arxiv.org/pdf/2008.09624v1