Bayesian Prompt Learning for Image-Language Model Generalization
贝叶斯提示学习用于图像-语言模型泛化
Abstract
摘要
Foundational image-language models have generated considerable interest due to their efficient adaptation to downstream tasks by prompt learning. Prompt learning treats part of the language model input as trainable while freezing the rest, and optimizes an Empirical Risk Minimization objective. However, Empirical Risk Minimization is known to suffer from distribution al shifts which hurt genera liz ability to prompts unseen during training. By leveraging the regular iz ation ability of Bayesian methods, we frame prompt learning from the Bayesian perspective and formulate it as a variation al inference problem. Our approach regularizes the prompt space, reduces over fitting to the seen prompts and improves the prompt generalization on unseen prompts. Our framework is implemented by modeling the input prompt space in a probabilistic manner, as an a priori distribution which makes our proposal compatible with prompt learning approaches that are unconditional or conditional on the image. We demonstrate empirically on 15 benchmarks that Bayesian prompt learning provides an appropriate coverage of the prompt space, prevents learning spurious features, and exploits transferable invariant features. This results in better generalization of unseen prompts, even across different datasets and domains.
基础图像-语言模型因其通过提示学习(prompt learning)高效适应下游任务而引发了广泛关注。提示学习将部分语言模型输入视为可训练参数,同时冻结其余部分,并优化经验风险最小化目标。然而,经验风险最小化已知存在分布偏移问题,这会损害模型对训练期间未见提示的泛化能力。通过利用贝叶斯方法的正则化能力,我们从贝叶斯角度构建提示学习框架,将其表述为变分推断问题。我们的方法规范了提示空间,减少对已见提示的过拟合,并提升对未见提示的泛化性能。
该框架通过概率化建模输入提示空间实现,将其视为先验分布,这使得我们的方案兼容无条件或图像条件型的提示学习方法。我们在15个基准测试中实证表明:贝叶斯提示学习能提供适当的提示空间覆盖,避免学习虚假特征,并利用可迁移的不变特征。这使得模型对未见提示(甚至跨数据集和跨领域)表现出更好的泛化能力。
Code available at: https://github.com/saic-fi/BayesianPrompt-Learning
代码地址:https://github.com/saic-fi/BayesianPrompt-Learning
1. Introduction
1. 引言
In the continuous quest for better pre-training strategies, models based on image and language supervision have set impressive milestones, with CLIP [38], ALIGN [22] and Flamingo [1] being leading examples. Contrastive ly trained image-language models consist of image and text encoders that align semantically-related concepts in a joint embedding space. Such models offer impressive zero-shot image classification by using the text encoder to generate classifier weights from arbitrarily newly defined category classes without relying on any visual data. In particular, the class name is used within a handcrafted prompt template and then tokenized and encoded into the shared embedding space to generate new classifier weights. Rather than manually defining prompts, both Lester et al. [28] and Zhou et al. [55] demonstrated prompts can instead be optimized in a data-driven manner through back propagation. However, as prompt learning typically has access to only a few training examples per prompt, over fitting to the seen prompts in lieu of the unseen prompts is common [55]. In this paper, we strive to mitigate the over fitting behavior of prompt learning so as to improve generalization for unseen prompts.
在持续探索更好的预训练策略过程中,基于图像和语言监督的模型已树立了令人印象深刻的里程碑,其中CLIP [38]、ALIGN [22]和Flamingo [1]是代表性成果。通过对比学习训练的图文模型由图像和文本编码器组成,能在联合嵌入空间中对齐语义相关的概念。这类模型通过文本编码器从任意新定义的类别中生成分类器权重,无需依赖任何视觉数据,从而实现了出色的零样本图像分类能力。具体而言,类别名称会被填入手工设计的提示模板,经过Token化编码至共享嵌入空间以生成新分类器权重。Lester等人[28]与Zhou等人[55]的研究表明,无需手动定义提示模板,而是可以通过反向传播以数据驱动的方式优化提示。然而,由于提示学习通常只能获取少量训练样本,模型往往会过度拟合已见提示而难以泛化到未见提示[55]。本文致力于缓解提示学习的过拟合问题,从而提升对未见提示的泛化能力。
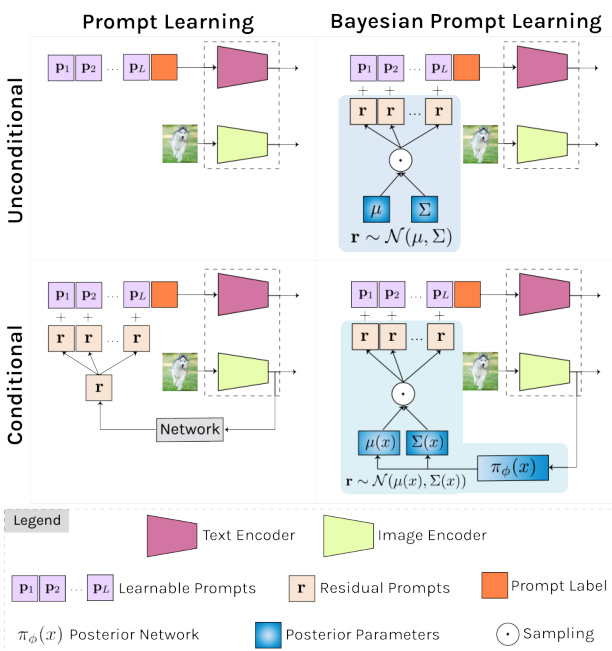
Figure 1: We present a Bayesian perspective on prompt learning by formulating it as a variation al inference problem (right column). Our framework models the prompt space as an a priori distribution which makes our proposal compatible with common prompt learning approaches that are unconditional (top) or conditional on the image (bottom).
图 1: 我们通过将提示学习 (prompt learning) 表述为变分推断问题 (右栏) 提出贝叶斯视角。该框架将提示空间建模为先验分布,使得我们的方案兼容无条件 (顶部) 或图像条件 (底部) 的常见提示学习方法。
Others before us have considered the generalization problem in prompt learning as well, e.g., [55, 54], be it they all seek to optimize a so-called Empirical Risk Minimization. It is, however, well known that Empirical Risk Minimization based models degrade drastically when training and testing distributions are different [37, 2]. To relax the i.i.d. assumption, Peters et al. [37] suggest exploiting the “invariance principle” for better generalization. Unfortunately, Invariant Risk Minimization methods for deep neural networks as of yet fail to deliver competitive results, as observed in [15, 31, 30]. To alleviate this limitation, Lin et al. [30] propose a Bayesian treatment of Invariant Risk Minimization that alleviates over fitting with deep models by defining a regular iz ation term over the posterior distribution of class if i ers, minimizing this term, and pushing the model’s backbone to learn invariant features. We take inspiration from this Bayesian Invariant Risk Minimization [30] and propose the first Bayesian prompt learning approach.
在我们之前,也有研究者考虑过提示学习中的泛化问题,例如[55, 54],但它们都试图优化所谓的经验风险最小化 (Empirical Risk Minimization)。然而众所周知,当训练和测试分布不同时,基于经验风险最小化的模型性能会急剧下降[37, 2]。为放宽独立同分布假设,Peters等人[37]提出利用"不变性原理"来提升泛化能力。但如[15, 31, 30]所述,目前针对深度神经网络的不变风险最小化方法尚未取得理想效果。为缓解这一局限,Lin等人[30]提出了不变风险最小化的贝叶斯处理方法,通过对分类器后验分布定义正则化项、最小化该正则项并推动模型主干学习不变特征,从而缓解深度模型的过拟合问题。我们受此贝叶斯不变风险最小化[30]的启发,提出了首个贝叶斯提示学习方法。
We make three contributions. First, we frame prompt learning from the Bayesian perspective and formulate it as a variation al inference problem (see Figure 1). This formulation provides several benefits. First, it naturally injects noise during prompt learning and induces a regular iz ation term that encourages the model to learn informative prompts, scattered in the prompt space, for each downstream task. As a direct result, we regularize the prompt space, reduce over fitting to seen prompts, and improve generalization on unseen prompts. Second, our framework models the input prompt space in a probabilistic manner, as an a priori distribution which makes our proposal compatible with prompt learning approaches that are unconditional [55] or conditional on the image [54]. Third, we empirically demonstrate on 15 benchmarks that Bayesian prompt learning provides an appropriate coverage of the prompt space, prevents learning spurious features, and exploits transferable invariant features, leading to a better generalization of unseen prompts, even across different datasets and domains.
我们做出三点贡献。首先,我们从贝叶斯视角构建提示学习框架,并将其表述为一个变分推断问题 (参见图1)。这种表述具有多重优势:其一,它自然地在提示学习过程中引入噪声,并产生一个正则化项,促使模型为每个下游任务学习信息丰富且分散在提示空间中的提示。直接效果是规范了提示空间,减少对已见提示的过拟合,提升对未见提示的泛化能力。其二,我们的框架以概率方式对输入提示空间建模,将其作为先验分布,这使得我们的方案兼容无条件[55]或图像条件[54]的提示学习方法。其三,我们在15个基准测试中实证表明,贝叶斯提示学习能恰当覆盖提示空间,避免学习虚假特征,并利用可迁移的不变特征,从而实现对未见提示的更好泛化,甚至跨越不同数据集和领域。
2. Related Work
2. 相关工作
Prompt learning in language. Prompt learning was originally proposed within natural language processing (NLP), by models such as GPT-3 [4]. Early methods constructed prompts by combining words in the language space such that the model would perform better on downstream evaluation [46, 24]. Li and Liang [29] prepend a set of learnable prompts to the different layers of a frozen model and optimize through back-propagation. In parallel, Lester et al. [28] demonstrate that with no intermediate layer pre- fixes or task-specific output layers, adding prefixes alone to the input of the frozen model is enough to compete with fine-tuning. Alternatively, [16] uses a Hyper Network to conditionally generate task-specific and layer-specific prompts pre-pended to the values and keys inside the selfattention layers of a frozen model. Inspired by progress from NLP, we propose a prompt learning method intended for image and language models.
语言中的提示学习。提示学习最初由GPT-3 [4]等模型在自然语言处理(NLP)领域提出。早期方法通过组合语言空间中的词汇构建提示,以提升模型在下游任务中的表现 [46, 24]。Li和Liang [29] 在冻结模型的不同层前添加可学习的提示序列,并通过反向传播进行优化。同时,Lester等人 [28] 证明无需中间层前缀或任务特定输出层,仅需在冻结模型输入前添加前缀即可与微调方法竞争。此外,[16] 采用超网络(Hyper Network)动态生成任务特定和层特定的提示,这些提示被添加到冻结模型自注意力层的键值对中。受NLP领域进展启发,我们提出了一种面向图像与语言模型的提示学习方法。
Prompt learning in image and language. Zhou et al. [55] propose Context Optimization (CoOp), a prompt learner for CLIP, which optimizes prompts in the continuous space through back-propagation. The work demonstrates the benefit of prompt learning over prompt engineering. While CoOp obtains good accuracy on prompts seen during training, it has difficulty generalizing to unseen prompts. It motivated Zhou et al. to introduce Conditional Context Optimization (CoCoOp) [54]. It generates instance-specific prompt residuals through a conditioning mechanism dependent on the image data, which generalizes better.ProGrad by Zhu et al. [56] also strives to bridge the generalization gap by matching the gradient of the prompt to the general knowledge of the CLIP model to prevent forgetting. Alternative directions consist of test-time prompt learning [47], where consistency across multiple views is the supervisory signal, and unsupervised prompt learning [21], where a pseudo-labeling strategy drives the prompt learning. More similar to ours is ProDA by Lu et al. [32], who propose an ensemble of a fixed number of hand-crafted prompts and model the distribution exclusively within the language embedding. Conversely, we prefer to model the input prompt space rather than relying on a fixed number of templates, as it provides us with a mechanism to cover the prompt space by sampling. Moreover, our approach is not limited to unconditional prompt learning from the language embedding, but like Zhou et al. [54], also allows for prompt learning conditioned on an image.
图像与语言中的提示学习。Zhou等人[55]提出了上下文优化(CoOp),一种针对CLIP的提示学习器,通过反向传播在连续空间中优化提示。该工作证明了提示学习相比提示工程的优势。虽然CoOp在训练期间见过的提示上获得了良好的准确性,但难以泛化到未见过的提示。这促使Zhou等人引入了条件上下文优化(CoCoOp)[54],它通过依赖于图像数据的条件机制生成实例特定的提示残差,具有更好的泛化能力。Zhu等人[56]提出的ProGrad也致力于通过将提示的梯度与CLIP模型的通用知识相匹配来弥合泛化差距,以防止遗忘。其他方向包括测试时提示学习47和无监督提示学习21。与我们的方法更相似的是Lu等人[32]提出的ProDA,他们对固定数量的手工提示进行集成,并仅在语言嵌入中建模分布。相反,我们更倾向于对输入提示空间进行建模而非依赖固定数量的模板,这为我们提供了通过采样覆盖提示空间的机制。此外,我们的方法不仅限于从语言嵌入进行无条件提示学习,还能像Zhou等人[54]那样支持以图像为条件的提示学习。
Prompt learning in vision and language. While beyond our current scope, it is worth noting that prompt learning has been applied to a wider range of vision problems and scenarios, which highlights its power and flexibility. Among them are important topics such as unsupervised domain adaptation [13], multi-label classification [49], video classification [25], object detection [9, 12] and pixel-level labelling [40]. Finally, prompt learning has also been applied to vision only models [23, 44] providing an efficient and flexible means to adapt pre-trained models.
视觉与语言中的提示学习。虽然超出了当前讨论范围,但值得注意的是,提示学习已被应用于更广泛的视觉问题和场景,这凸显了其强大性和灵活性。其中包括无监督域适应 [13]、多标签分类 [49]、视频分类 [25]、目标检测 [9,12] 和像素级标注 [40] 等重要课题。最后,提示学习也被应用于纯视觉模型 [23,44],为适应预训练模型提供了高效灵活的手段。
Variation al inference in computer vision. Variation al inference and, more specifically, variation al auto encoder variants have been extensively applied to computer vision tasks as diverse as image generation [39, 43, 42], action recognition [34], instance segmentation [20], few-shot learning [53, 45], domain generalization [10], and continual learning [7]. For example, Zhang et al. [53] focus on the reduction of noise vulnerability and estimation bias in few-shot learning through variation al inference. In the same vein, Du et al. [10] propose a variation al information bottleneck to better manage prediction uncertainty and unknown domains. Our proposed method also shares the advantages of variation al inference in avoiding over fitting in low-shot settings, improving generalization, and encourages the prompt space to be resilient against these challenges. To the best of our knowledge we are the first to introduce variation al inference in prompt learning.
计算机视觉中的变分推断。变分推断,尤其是变分自编码器 (variational autoencoder) 变体,已被广泛应用于各类计算机视觉任务,如图像生成 [39, 43, 42]、动作识别 [34]、实例分割 [20]、少样本学习 [53, 45]、领域泛化 [10] 以及持续学习 [7]。例如,Zhang 等人 [53] 通过变分推断减少少样本学习中的噪声敏感性和估计偏差。类似地,Du 等人 [10] 提出变分信息瓶颈以更好地处理预测不确定性和未知领域。我们提出的方法同样具备变分推断的优势,可避免低样本场景下的过拟合、提升泛化能力,并使提示空间能够抵御这些挑战。据我们所知,这是首次在提示学习中引入变分推断。
3. Method
3. 方法
3.1. Background
3.1. 背景
Contrastive Language-Image Pre training (CLIP) [38] consists of an image encoder $f(\mathbf{x})$ and text encoder $g(\mathbf{t})$ , each producing a $d$ -dimensional $X_{2}$ normalized) embedding from an arbitrary image $\mathbf{x}\in\mathbb{R}^{3\times H\times W}$ , and word embeddings $\textbf{t}\in\mathbb{R}^{L\times e}$ , with $L$ representing the text length and $e$ the embedding dimension1. Both encoders are trained together using a contrastive loss from a large-scale dataset composed of paired images and captions. Once trained, CLIP enables zero-shot $C$ -class image classification by generating each of the $c$ classifier weights $\mathbf{w}{c}$ as the $d$ -dimensional text encoding $g(\mathbf{t}{c})$ . Here $\mathbf{t}{c}$ results from adding the class-specific word embedding $\mathbf{e}{c}$ to a pre-defined prompt $\mathbf{p_{\lambda}}\in\bar{\mathbb{R}}^{L-1\times e}$ , i.e., $\mathbf{w}{c}{=}g(\mathbf{t}{c})$ with $\mathbf{t}{c}={\mathbf{p},\mathbf{e}{c}}$ . The prompt $\mathbf{p}$ is manually crafted to capture the semantic meaning of the downstream task, e.g., $\mathbf{t}_{c}\mathbf{=}^{\mathrm{\tiny~{\left[\Lambda\right]}~}}$ image of a ${\mathtt{c l a s s}}^{\gamma}$ . The probability of image $\mathbf{x}$ being classified as $y\in{1...C}$ is thus defined as $\begin{array}{r}{p(y|\mathbf{x})=\frac{e^{f(\mathbf{x})^{T}\mathbf{w}_{y}}}{\sum_{c}^{C}e^{f(\mathbf{x})^{T}\mathbf{w}_{c}}},}\end{array}$
对比语言-图像预训练 (CLIP) [38] 包含一个图像编码器 $f(\mathbf{x})$ 和文本编码器 $g(\mathbf{t})$ ,分别从任意图像 $\mathbf{x}\in\mathbb{R}^{3\times H\times W}$ 和词嵌入 $\textbf{t}\in\mathbb{R}^{L\times e}$ 生成 $d$ 维 $X_{2}$ 归一化嵌入,其中 $L$ 表示文本长度,$e$ 表示嵌入维度。两个编码器通过对比损失在大规模图文配对数据集上联合训练。训练完成后,CLIP 可通过将每个 $c$ 类分类器权重 $\mathbf{w}{c}$ 生成为 $d$ 维文本编码 $g(\mathbf{t}{c})$ 来实现零样本 $C$ 类图像分类。此处 $\mathbf{t}{c}$ 是将类别特定词嵌入 $\mathbf{e}{c}$ 添加到预定义提示 $\mathbf{p_{\lambda}}\in\bar{\mathbb{R}}^{L-1\times e}$ 的结果,即 $\mathbf{w}{c}{=}g(\mathbf{t}{c})$ 且 $\mathbf{t}{c}={\mathbf{p},\mathbf{e}{c}}$ 。提示 $\mathbf{p}$ 经人工设计以捕获下游任务的语义,例如 $\mathbf{t}_{c}\mathbf{=}^{\mathrm{\tiny~{\left[\Lambda\right]}~}}$ image of a ${\mathtt{c l a s s}}^{\gamma}$ 。图像 $\mathbf{x}$ 被分类为 $y\in{1...C}$ 的概率定义为 $\begin{array}{r}{p(y|\mathbf{x})=\frac{e^{f(\mathbf{x})^{T}\mathbf{w}_{y}}}{\sum_{c}^{C}e^{f(\mathbf{x})^{T}\mathbf{w}_{c}}。}\end{array}$
Context Optimization $\mathbf{\mu}(\mathbf{CoOp})$ [55] provides a learned alternative to manually defining prompts. CoOp learns a fixed prompt from a few annotated samples. The prompt is designed as a learnable embedding matrix $\textbf{p}\in\mathbb{R}^{L\times e}$ which is updated via back-propagating the classification error through the frozen CLIP model. Specifically, for a set of $N$ annotated meta-training samples ${{\bf x}{i},y{i}}_{i=1}^{N}$ , the prompt $\mathbf{p}$ is obtained by minimizing the cross-entropy loss, as:
上下文优化 (Context Optimization) $\mathbf{\mu}(\mathbf{CoOp})$ [55] 提供了一种学习替代方案来取代手动定义提示词。CoOp 通过少量标注样本学习固定提示模板,该提示被设计为可学习的嵌入矩阵 $\textbf{p}\in\mathbb{R}^{L\times e}$,通过将分类误差反向传播至冻结的 CLIP 模型中进行更新。具体而言,对于包含 $N$ 个标注元训练样本的集合 ${{\bf x}{i},y{i}}_{i=1}^{N}$,提示 $\mathbf{p}$ 通过最小化交叉熵损失获得,公式为:
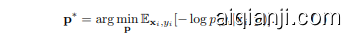
Note that this approach, while resembling that of common meta-learning approaches, can still be deployed in a zeroshot scenario provided that for new classes the classification weights will be given by the text encoder. Although this approach generalizes to new tasks with few training iterations, learning a fixed prompt is sensitive to domain shifts between the annotated samples and the unseen prompts.
需要注意的是,这种方法虽然类似于常见的元学习方法,但仍可部署在零样本场景中,前提是新类别的分类权重由文本编码器提供。尽管该方法通过少量训练迭代就能泛化到新任务,但学习固定提示词对标注样本与未见提示之间的领域偏移较为敏感。
Conditional Prompt Learning (CoCoOp) [54] attempts to overcome domain shifts by learning an instancespecific continuous prompt that is conditioned on the input image. To ease the training of a conditional prompt generator, CoCoOp defines each conditional token in a residual way, with a task-specific, learnable set of tokens p and a residual prompt that is conditioned on the input image. Assuming $\mathbf{p}$ to be composed of $L$ learnable tokens $\mathbf{p}{=}[\mathbf{p}{1},\mathbf{p}{2},\cdot\cdot\cdot\mathbf{\delta},\mathbf{p}_{L}]$ , the residual prompt $\mathbf{r}(\mathbf{x}){=}\pi_{\phi}(f(\mathbf{x}))\in\mathbb{R}^{e}$ is produced by a small neural network $\pi_{\phi}$ with as input the image features $f(\mathbf{x})$ . The new prompt is then computed as ${\bf p}({\bf x}){=}[{\bf p}_{1}+{\bf r}({\bf x}),{\bf p}_{2}+$ $\mathbf{r}(\mathbf{x}),\cdots,\mathbf{p}_{L}+\mathbf{r}(\mathbf{x})]$ . The training now comprises learning the task-specific prompt $\mathbf{p}$ and the parameters $\phi$ of the neural network $\pi_{\phi}$ . Defining the context-specific text embedding ${\bf t}_{c}({\bf x}){=}{{\bf p}({\bf x}),{\bf e}_{c}}$ , and $p(y\vert\mathbf{x})$ as :
条件提示学习 (CoCoOp) [54] 试图通过学习一个基于输入图像的条件化实例特定连续提示来克服领域偏移。为了简化条件提示生成器的训练,CoCoOp以残差方式定义每个条件token,包含一组任务特定的可学习token p和一个基于输入图像的残差提示。假设$\mathbf{p}$由$L$个可学习token组成$\mathbf{p}{=}[\mathbf{p}{1},\mathbf{p}{2},\cdot\cdot\cdot\mathbf{\delta},\mathbf{p}_{L}]$,残差提示$\mathbf{r}(\mathbf{x}){=}\pi_{\phi}(f(\mathbf{x}))\in\mathbb{R}^{e}$由一个小型神经网络$\pi_{\phi}$生成,其输入为图像特征$f(\mathbf{x})$。新提示通过${\bf p}({\bf x}){=}[{\bf p}_{1}+{\bf r}({\bf x}),{\bf p}_{2}+$$\mathbf{r}(\mathbf{x}),\cdots,\mathbf{p}_{L}+\mathbf{r}(\mathbf{x})]$计算得出。训练过程包括学习任务特定提示$\mathbf{p}$和神经网络$\pi_{\phi}$的参数$\phi$。定义上下文特定文本嵌入${\bf t}_{c}({\bf x}){=}{{\bf p}({\bf x}),{\bf e}_{c}}$,并将$p(y\vert\mathbf{x})$表示为:

the learning is formulated as:
学习被表述为:

While CoCoOp achieves good results in many downstream tasks, it is still prone to the domain shift problem, considering that $\pi_{\phi}$ provides a deterministic residual prompt from the domain-specific image features $f(\mathbf{x})$ .
尽管CoCoOp在许多下游任务中取得了良好效果,但由于$\pi_{\phi}$从领域特定图像特征$f(\mathbf{x})$中生成的是确定性残差提示,它仍然容易受到领域偏移问题的影响。
Prompt Distribution Learning (ProDA) [32] learns a distribution of prompts that generalize to a broader set of tasks. It learns a collection of prompts P={pk}kK=1 that subsequently generate an a posteriori distribution of the classifier weights for each of the target classes. For a given mini-batch of $K$ sampled prompts $\mathbf{p}{k}\mathrm{\sim}\mathbf{P}$ , the classifier weights $\mathbf{w}{c}$ are sampled from the posterior distribution $\mathbf{q}{=}\mathcal{N}(\mu_{\mathbf{w}_{1:C}},\Sigma_{\mathbf{w}_{1:C}})$ , with mean $\mu_{\mathbf{w}_{1:C}}$ and covariance $\Sigma_{{\bf w}_{1:C}}$ computed from the collection ${\mathbf{w}_{k,c}{=}g(\mathbf{t}_{k,c})}_{c=1:C,k=1:K}$ , with $\mathbf{t}_{k,c}~=~\left{\mathbf{p}_{k},\mathbf{e}_{c}\right}$ . The objective is formulated as:
提示分布学习 (Prompt Distribution Learning, ProDA) [32] 通过学习一组泛化性更强的提示分布来适应更广泛的任务。该方法学习一组提示集合 P={pk}kK=1,随后为每个目标类别生成分类器权重的后验分布。对于给定的包含 $K$ 个采样提示 $\mathbf{p}{k}\mathrm{\sim}\mathbf{P}$ 的小批量数据,分类器权重 $\mathbf{w}{c}$ 从后验分布 $\mathbf{q}{=}\mathcal{N}(\mu_{\mathbf{w}_{1:C}},\Sigma_{\mathbf{w}_{1:C}})$ 中采样得到,其均值 $\mu_{\mathbf{w}_{1:C}}$ 和协方差 $\Sigma_{{\bf w}_{1:C}}$ 由集合 ${\mathbf{w}_{k,c}{=}g(\mathbf{t}_{k,c})}_{c=1:C,k=1:K}$ 计算得出,其中 $\mathbf{t}_{k,c}~=~\left{\mathbf{p}_{k},\mathbf{e}_{c}\right}$。目标函数定义为:
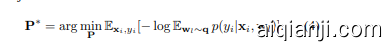
Computing $\mathbb{E}{\mathbf{w}{l}}p(y_{i}|\mathbf{x}{i},\mathbf{w}{l})]$ is intractable and an upper bound to Eq. 4 is derived. During inference, the classifier weights are set to those given by the predictive mean $\mathbf{w}{c}{=}\mu{\mathbf{w}_{1:C}}$ , computed across the set of learned prompts $\mathbf{P}$ .
计算 $\mathbb{E}{\mathbf{w}{l}}p(y_{i}|\mathbf{x}{i},\mathbf{w}{l})]$ 是不可行的,因此推导出式4的上界。在推理过程中,分类器权重设置为预测均值 $\mathbf{w}{c}{=}\mu{\mathbf{w}_{1:C}}$ ,该均值通过已学习的提示集 $\mathbf{P}$ 计算得出。
3.2. Conditional Bayesian Prompt Learning
3.2. 条件贝叶斯提示学习
We propose to model the input prompt space in a probabilistic manner, as an a priori, conditional distribution. We define a distribution $p_{\gamma}$ over the prompts $\mathbf{p}$ that is conditional on the image, i.e., ${\bf p}\sim p_{\gamma}({\bf x})$ . To this end, we as- sume that $\mathbf{p}$ can be split into a fixed set of prompts $\mathbf{p}_{i}$ and an conditional residual prompt $\mathbf{r}$ that act as a latent variable over p. The conditional prompt is then defined as:
我们提出以概率方式对输入提示空间进行建模,将其视为一个先验条件分布。我们定义了一个基于图像条件的提示分布 $p_{\gamma}$ ,即 ${\bf p}\sim p_{\gamma}({\bf x})$ 。为此,我们假设 $\mathbf{p}$ 可拆分为固定提示集 $\mathbf{p}_{i}$ 和作为潜在变量的条件残差提示 $\mathbf{r}$ ,此时条件提示定义为:

where $p_{\gamma}(\mathbf{x})$ refers to the real posterior distribution over $\mathbf{r}$ conditioned on the observed features $\mathbf{x}$ . Denoting the class
其中 $p_{\gamma}(\mathbf{x})$ 表示基于观测特征 $\mathbf{x}$ 条件下 $\mathbf{r}$ 的真实后验分布。设类别
specific input as $\mathbf{t}{c,\gamma}(\mathbf{x}){=}{\mathbf{p}{\gamma}(\mathbf{x}),\mathbf{e}_{c}}$ , the marginal likelihood $p(y\vert\mathbf{x})$ is:
特定输入为 $\mathbf{t}{c,\gamma}(\mathbf{x}){=}{\mathbf{p}{\gamma}(\mathbf{x}),\mathbf{e}_{c}}$ 时,边缘似然 $p(y\vert\mathbf{x})$ 为:

Solving Eq. 3 with the marginal likelihood from Eq. 6 is intractable, as it requires computing $p_{\gamma}(\mathbf{r}|\mathbf{x})p_{\gamma}(\mathbf{x})$ . Instead, we resort to deriving a lower bound by introducing a variational posterior distribution $\pi_{\phi}(\mathbf{x})$ from which the residual $\mathbf{r}_{\gamma}$ can be sampled. The variation al bound is defined as:
利用式6中的边缘似然来求解式3是不可行的,因为它需要计算 $p_{\gamma}(\mathbf{r}|\mathbf{x})p_{\gamma}(\mathbf{x})$ 。为此,我们转而通过引入变分后验分布 $\pi_{\phi}(\mathbf{x})$ 来推导下界,残差 $\mathbf{r}_{\gamma}$ 可从该分布中采样。变分下界定义为:

with $p(y|\mathbf{x},\mathbf{r}){\propto}e^{f(\mathbf{x})^{T}g(\mathbf{t}{c,\gamma}(\mathbf{x}))}$ , where the dependency on $\mathbf{r}$ comes through the definition of $\mathbf{t}{c,\gamma}$ . Following standard variation al optimization practices [26, 14], we define $\pi_{\phi}$ as a Gaussian distribution conditioned on the input image features $\mathbf{x}$ , as $\mathbf{r}(\mathbf{x}){\sim}\mathcal{N}(\mu(\mathbf{x}),\Sigma(\mathbf{x}))$ , with $\mu$ and $\Sigma$ parameterized by two linear layers followed by two linear heads on top to estimate the $\mu$ and $\Sigma$ of the residual distribution. The prior $p_{\gamma}(\mathbf{r})$ is defined as $\mathcal{N}(\mathbf{0},\mathbf{I})$ , and we use the reparameterization trick to generate Monte-Carlo samples from $\pi_{\phi}$ to maximize the right side of Eq. 7. The optimization of Eq. 7 comprises learning the prompt embeddings ${\mathbf{p}{i}}{i=1}^{L}$ as well as the parameters of the posterior network $\pi_{\phi}$ and the linear layers parameter i zing $\mu$ and $\Sigma$ . Note that this adds little complexity as it requires learning $\mathbf{p}$ and $\pi_{\phi}$ , given that $\mu$ and $\Sigma$ are defined as two linear layers on top of $\pi_{\phi}$ .
其中 $p(y|\mathbf{x},\mathbf{r}){\propto}e^{f(\mathbf{x})^{T}g(\mathbf{t}{c,\gamma}(\mathbf{x}))}$ ,$\mathbf{r}$ 的依赖性通过 $\mathbf{t}{c,\gamma}$ 的定义体现。遵循标准变分优化实践 [26, 14],我们将 $\pi_{\phi}$ 定义为以输入图像特征 $\mathbf{x}$ 为条件的高斯分布,即 $\mathbf{r}(\mathbf{x}){\sim}\mathcal{N}(\mu(\mathbf{x}),\Sigma(\mathbf{x}))$ ,其中 $\mu$ 和 $\Sigma$ 由两个线性层参数化,并通过顶部的两个线性头分别估计残差分布的 $\mu$ 和 $\Sigma$。先验 $p_{\gamma}(\mathbf{r})$ 定义为 $\mathcal{N}(\mathbf{0},\mathbf{I})$ ,并采用重参数化技巧从 $\pi_{\phi}$ 生成蒙特卡洛样本以最大化式7右侧。式7的优化包括学习提示嵌入 ${\mathbf{p}{i}}{i=1}^{L}$ 以及后验网络 $\pi_{\phi}$ 的参数,还有参数化 $\mu$ 和 $\Sigma$ 的线性层。需注意,由于 $\mu$ 和 $\Sigma$ 被定义为 $\pi_{\phi}$ 顶部的两个线性层,该方法仅需学习 $\mathbf{p}$ 和 $\pi_{\phi}$ ,复杂度增加有限。
Inference. At test time, $K$ residuals are sampled from the conditional distribution $\pi_{\phi}(\mathbf{x})$ , which are used to generate $K$ different prompts per class $\mathbf{p}{k}{=}[\mathbf{p}{1}\mathbf{\beta}+$ $\mathbf{r}{k},\mathbf{p}{2}+\mathbf{r}{k},\cdots,\mathbf{p}{L}+\mathbf{r}{k}]$ . Each prompt is prepended to the class-specific embedding to generate a series of $K$ separate classifier weights $\mathbf{w}{k,c}$ . We then compute $\begin{array}{r}{p(y=c|\mathbf x){=}(1/K)\sum_{k=1}^{K}p(y{=}c|\mathbf x,\mathbf w_{k,c})}\end{array}$ and select $\hat{c}{=}\arg\operatorname*{max}_{c}p(y{=}c|\mathbf{x})$ as the predicted class. It is worth noting that because the posterior distribution is generated by the text encoder, it is not expected that for $K\rightarrow\infty$ , $\begin{array}{r}{(1/K)\sum_{k}p(y=c\mid\mathbf{x},\mathbf{w}_{c,k})~\to~p(y=c|\mathbf{x},g({\mu(\mathbf{x}),\mathbf{e}_{c}})}\end{array}$ , meanin g that sampling at inference time remains relevant.
推理。在测试时,从条件分布 $\pi_{\phi}(\mathbf{x})$ 中采样 $K$ 个残差,用于为每个类别生成 $K$ 个不同的提示 $\mathbf{p}{k}{=}[\mathbf{p}{1}\mathbf{\beta}+$ $\mathbf{r}{k},\mathbf{p}{2}+\mathbf{r}{k},\cdots,\mathbf{p}{L}+\mathbf{r}{k}]$。每个提示被添加到类别特定的嵌入前,生成一系列 $K$ 个独立的分类器权重 $\mathbf{w}{k,c}$。然后计算 $\begin{array}{r}{p(y=c|\mathbf x){=}(1/K)\sum_{k=1}^{K}p(y{=}c|\mathbf x,\mathbf w_{k,c})}\end{array}$ 并选择 $\hat{c}{=}\arg\operatorname*{max}_{c}p(y{=}c|\mathbf{x})$ 作为预测类别。值得注意的是,由于后验分布由文本编码器生成,当 $K\rightarrow\infty$ 时,$\begin{array}{r}{(1/K)\sum_{k}p(y=c\mid\mathbf{x},\mathbf{w}_{c,k})~\to~p(y=c|\mathbf{x},g({\mu(\mathbf{x}),\mathbf{e}_{c}})}\end{array}$ 并不成立,这意味着推理时的采样仍然具有实际意义。
3.3. Unconditional Bayesian Prompt Learning
3.3. 无条件贝叶斯提示学习 (Unconditional Bayesian Prompt Learning)
Notably, our framework can also be reformulated as an unconditional case by simply removing the dependency of the input image from the latent distribution. In such a scenario, we keep a fixed set of prompt embeddings and learn a global latent distribution $p_{\gamma}$ over the residual prompts $\mathbf{r}$ , as $\mathbf{r}\sim\mathcal{N}(\boldsymbol{\mu},\boldsymbol{\Sigma})$ , where $\mu$ and $\Sigma$ are parameterized by two learnable vectors. To this end, we assume that $\mathbf{p}$ can be split into a fixed set of prompts $\mathbf{p}_{i}$ and a residual prompts $\mathbf{r}$ that act as a latent variable over $\mathbf{p}$ . For the unconditional case, the prompt is defined as:
值得注意的是,我们的框架也可以通过简单地从潜在分布中移除输入图像的依赖性,重新表述为无条件情况。在这种场景下,我们保留一组固定的提示嵌入 (prompt embeddings) ,并在残差提示 (residual prompts) $\mathbf{r}$ 上学习一个全局潜在分布 $p_{\gamma}$ ,即 $\mathbf{r}\sim\mathcal{N}(\boldsymbol{\mu},\boldsymbol{\Sigma})$ ,其中 $\mu$ 和 $\Sigma$ 由两个可学习向量参数化。为此,我们假设 $\mathbf{p}$ 可以拆分为一组固定的提示 $\mathbf{p}_{i}$ 和一个作为 $\mathbf{p}$ 潜在变量的残差提示 $\mathbf{r}$ 。对于无条件情况,提示定义为:
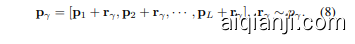
In this case, $p_{\gamma}$ is a general distribution learned during training with no dependency on the input sample x.
在这种情况下,$p_{\gamma}$ 是训练期间学习到的通用分布,不依赖于输入样本 x。
Having defined both unconditional Bayesian prompt learning and conditional Bayesian prompt learning we are now ready to evaluate their generalization ability.
在定义了无条件贝叶斯提示学习 (unconditional Bayesian prompt learning) 和有条件贝叶斯提示学习 (conditional Bayesian prompt learning) 后,我们现在可以评估它们的泛化能力了。
4. Experiments and Results 4.1. Experimental Setup
4. 实验与结果 4.1. 实验设置
Three tasks and fifteen datasets. We consider three tasks: unseen prompts generalization, cross-dataset prompts generalization, and cross-domain prompts generalization. For the first two tasks, we rely on the same 11 image recognition datasets as Zhou et al. [55, 54]. These include image classification (ImageNet [6] and Caltech101 [11]), fine-grained classification (OxfordPets [36], Stanford Cars [27], Flowers102 [35], Food101 [3] and FG VC Aircraft [33]), scene recognition (SUN397 [52]), action recognition (UCF101 [48]), texture classification (DTD [5]), and satellite imagery recognition (Eu- roSAT [17]). For cross-domain prompts generalization, we train on ImageNet and report on ImageNetV2 [41], ImageNet-Sketch [51], ImageNet-A [19], and ImageNetR [18].
三项任务和十五个数据集。我们考虑三项任务:未见提示泛化、跨数据集提示泛化和跨领域提示泛化。对于前两项任务,我们采用与Zhou等人[55, 54]相同的11个图像识别数据集,包括图像分类(ImageNet [6]和Caltech101 [11])、细粒度分类(OxfordPets [36]、Stanford Cars [27]、Flowers102 [35]、Food101 [3]和FG VC Aircraft [33])、场景识别(SUN397 [52])、动作识别(UCF101 [48])、纹理分类(DTD [5])以及卫星图像识别(EuroSAT [17])。对于跨领域提示泛化任务,我们在ImageNet上训练,并在ImageNetV2 [41]、ImageNet-Sketch [51]、ImageNet-A [19]和ImageNetR [18]上进行测试。
Evaluation metrics. For all three tasks we report average accuracy and standard deviation.
评估指标。针对所有三项任务,我们均报告平均准确率及标准差。
Implementation details. Our conditional variation al prompt learning contains three sub-networks: an image encoder $f(\mathbf{x})$ , a text encoder $g(\mathbf{t})$ , and a posterior network $\pi_{\phi}$ . The image encoder $f(\mathbf{x})$ is a ViT-B/16 [8] and the text encoder $g(\mathbf{t})$ a transformer [50], which are both initialized with CLIP’s pre-trained weights and kept frozen during training, as in [55, 54]. The posterior network $\pi_{\phi}$ consists of two linear layers followed by an ELU activation function as trunk and two linear heads on top to estimate the $\mu$ and $\Sigma$ of the residual distribution. For each task and dataset, we optimize the number of samples $K$ and epochs. Other hyper-parameters as well as the training pipeline in terms of few-shot task definitions are identical to [55, 54] (see Table 9 and 10 in the appendix).
实现细节。我们的条件变分提示学习包含三个子网络:图像编码器 $f(\mathbf{x})$、文本编码器 $g(\mathbf{t})$ 和后验网络 $\pi_{\phi}$。图像编码器 $f(\mathbf{x})$ 采用 ViT-B/16 [8] 架构,文本编码器 $g(\mathbf{t})$ 基于 Transformer [50] 架构,二者均使用 CLIP 预训练权重初始化并在训练期间保持冻结,如 [55, 54] 所述。后验网络 $\pi_{\phi}$ 由两个线性层和 ELU 激活函数构成主干,顶部通过两个线性头部分别估计残差分布的 $\mu$ 和 $\Sigma$。针对每个任务和数据集,我们优化样本数 $K$ 和训练周期数。其他超参数及少样本任务定义相关的训练流程均与 [55, 54] 保持一致(详见附录表 9 和表 10)。
4.2. Comparisons
4.2. 对比
We first compare against CoOp [55], CoCoOp [54], and ProDA [32] in terms of the generalization of learned prompts on unseen classes, datasets, or domains. For $\mathrm{CoOp}$ and $\mathrm{{CoCoOp}}$ , all results are adopted from [54], and we report results for ProDA using our re-implementation.
我们首先在未见过的类别、数据集或领域的提示泛化能力方面,与CoOp [55]、CoCoOp [54]和ProDA [32]进行对比。对于$\mathrm{CoOp}$和$\mathrm{CoCoOp}$,所有结果均引自[54],而ProDA的结果则基于我们的复现实现。
Task I: unseen prompts generalization We report the unseen prompts generalization of our method on 11 datasets for three different random seeds. Each dataset is divided into two disjoint subsets: seen classes and unseen classes. We train our method on the seen classes and evaluate it on the unseen classes. For a fair comparison, we follow [55, 54] in terms of dataset split and number of shots. From
任务 I: 未见提示泛化性
我们在11个数据集上针对三种不同随机种子报告了本方法的未见提示泛化性能。每个数据集被划分为两个互斥子集:已见类别和未见类别。我们在已见类别上训练方法,并在未见类别上评估其表现。为公平比较,我们遵循[55, 54]的数据集划分和样本数量设置。
Table 1: Task I: unseen prompts generalization comparison between conditional Bayesian prompt learning and alternatives. Our model provides better generalization on unseen prompts compared to CoOp, $\mathrm{{CoCoOp}}$ and ProDA.
表 1: 任务一:条件贝叶斯提示学习与其他方法在未见提示泛化能力上的对比。相比CoOp、$\mathrm{{CoCoOp}}$和ProDA,我们的模型在未见提示上展现出更好的泛化性能。
| CoOp [55] | CoCo0p [54] | ProDA [32] | Ours | |
|---|---|---|---|---|
| Caltech101 | 89.81 | 93.81 | 93.23 | 94.93±0.1 |
| DTD | 41.18 | 56.00 | 56.48 | 60.80±0.5 |
| EuroSAT | 54.74 | 60.04 | 66.00 | 75.30±0.7 |
| FGVCAircraft | 22.30 | 23.71 | 34.13 | 35.00±0.5 |
| Flowers102 | 59.67 | 71.75 | 68.68 | 70.40±1.8 |
| Food101 | 82.26 | 91.29 | 88.57 | 92.13±0.1 |
| ImageNet | 67.88 | 70.43 | 70.23 | 70.93±0.1 |
| OxfordPets | 95.29 | 97.69 | 97.83 | 98.00±0.1 |
| StanfordCars | 60.40 | 73.59 | 71.20 | 73.23±0.2 |
| SUN397 | 65.89 | 76.86 | 76.93 | 77.87±0.5 |
| UCF101 | 56.05 | 73.45 | 71.97 | 75.77±0.1 |
| Average | 63.22 | 71.69 | 72.30 | 74.94±0.2 |
Table 1, it can be seen that our best-performing method, conditional Bayesian prompt learning, outperforms $\mathrm{{CoOp}}$ and $\mathbf{CoCoOp}$ in terms of unseen prompts generalization by $11.72%$ and $3.25%$ , respectively. Our proposal also demonstrates minimal average variance across all datasets. This is achieved by regularizing the optimization by virtue of the variation al formulation. Moreover, our model also performs better than ProDA [32], its probabilistic counterpart, by $2.64%$ . This mainly happens because our proposed method learns the prompt distribution directly in the prompt space and allows us to sample more informative prompts for the downstream tasks.
表 1: 可以看出,我们表现最佳的条件贝叶斯提示学习 (conditional Bayesian prompt learning) 方法在未见提示泛化能力上分别以 11.72% 和 3.25% 的优势超越了 $\mathrm{CoOp}$ 和 $\mathbf{CoCoOp}$。我们的方案在所有数据集上也展现出最小的平均方差,这是通过变分公式对优化过程进行正则化实现的。此外,我们的模型性能还以 2.64% 的优势优于其概率对应方法 ProDA [32],这主要归因于我们提出的方法直接在提示空间中学习提示分布,从而能为下游任务采样信息量更丰富的提示。
Task II: cross-dataset prompts generalization For the next task, cross-dataset prompts generalization, the model is trained on a source dataset (ImageNet) and then assessed on 10 distinct target datasets. This experiment tries to determine how effectively our method generalizes beyond the scope of a single dataset. As reported in Table 2, our conditional Bayesian prompt learning outperforms $\mathrm{{CoOp}}$ and $\mathrm{CoCoOp}$ on the target dataset by $2.07%$ and $0.36%$ . This highlights that our method encourages the model to exploit transferable invariant features beneficial for datasets with a non-overlapping label space. Furthermore, our method improves accuracy for 7 out of 10 target datasets. Unlike CoCoOp, which performs better in ImageNet-like datasets such as Caltech101 and Stanford Cars, our Bayesian method exhibits improvement on dissimilar datasets (e.g., FGVCAircraft, DTD, and EuroSAT), demonstrating its capacity to capture the unique characteristics of each dataset.
任务二:跨数据集提示泛化
在跨数据集提示泛化任务中,模型先在源数据集(ImageNet)上训练,随后在10个不同的目标数据集上评估。该实验旨在验证我们的方法在单一数据集范围之外的泛化能力。如表2所示,我们的条件贝叶斯提示学习在目标数据集上分别以2.07%和0.36%的优势超过$\mathrm{CoOp}$与$\mathrm{CoCoOp}$。这表明我们的方法能促使模型利用可迁移的不变特征,这对具有非重叠标签空间的数据集尤为有益。此外,我们的方法在10个目标数据集中的7个上实现了精度提升。与CoCoOp在类ImageNet数据集(如Caltech101和Stanford Cars)表现更好不同,我们的贝叶斯方法在差异较大的数据集(如FGVCAircraft、DTD和EuroSAT)上展现出改进,证明其能捕捉不同数据集的独特特征。
Task III: cross-domain prompts generalization Lastly, we examine our conditional Bayesian prompt learning through the lens of distribution shift and robustness. We train our model on the source dataset ImageNet for three different random seeds, and assess it on ImageNetV2, ImageNet-Sketch, ImageNet-A, and ImageNet-R. Prior works such as CoOp [55] and CoCoOp [54] demonstrate empirically that learning a soft-prompt improves the model’s resilience against distribution shift and adversarial attack. Following their experiments, we are also interested in determining if treating prompts in a Bayesian manner maintains or improves performance. As reported in Table 2 compared with $\mathrm{{CoOp}}$ , our method improves the performance on ImageNet-Sketch, ImageNet-A, and ImageNetR by $1.21%$ , $1.62%$ , and $1.79%$ . Compared with $\mathrm{{CoCoOp}}$ , our proposed method consistently enhances the model accuracy on ImageNetV2, ImageNet-Sketch, ImageNet-A, and ImageNet-R by $0.16%$ , $0.45%$ , $0.7%$ , and $0.82%$ . This is because our proposed method prevents learning spurious features, e.g., high-frequency features, and instead learns invariant ones by virtue of the Bayesian formulation.
任务三:跨域提示泛化
最后,我们从分布偏移和鲁棒性的角度检验条件贝叶斯提示学习。我们在源数据集ImageNet上以三种不同的随机种子训练模型,并在ImageNetV2、ImageNet-Sketch、ImageNet-A和ImageNet-R上评估。先前工作如CoOp [55]和CoCoOp [54]通过实验证明,学习软提示能提升模型对分布偏移和对抗攻击的鲁棒性。基于这些实验,我们同样关注以贝叶斯方式处理提示是否能保持或提升性能。如表2所示,与$\mathrm{{CoOp}}$相比,我们的方法在ImageNet-Sketch、ImageNet-A和ImageNet-R上的性能分别提升了$1.21%$、$1.62%$和$1.79%$。与$\mathrm{{CoCoOp}}$相比,所提方法在ImageNetV2、ImageNet-Sketch、ImageNet-A和ImageNet-R上的模型准确率分别持续提高了$0.16%$、$0.45%$、$0.7%$和$0.82%$。这是因为所提方法通过贝叶斯公式避免了学习虚假特征(如高频特征),转而学习不变特征。
Table 2: Task II: cross-dataset prompts generalization. Our proposed model is evaluated on 11 datasets with different label spaces. As shown, conditional Bayesian prompt learning performs better than non-Bayesian alternatives on 7 out of 10 datasets. Task III: cross-domain prompts genera liz ation. Our model is evaluated on four datasets sharing the same label space as the training data. Our method outperforms alternatives on 3 out of 4 datasets.
表 2: 任务II: 跨数据集提示泛化。我们提出的模型在11个具有不同标签空间的数据集上进行评估。结果显示,条件贝叶斯提示学习在10个数据集中的7个上优于非贝叶斯方法。任务III: 跨领域提示泛化。我们的模型在与训练数据共享相同标签空间的四个数据集上进行评估。我们的方法在4个数据集中的3个上优于其他方法。
| CoOp [55] | CoCoOp [54] | Ours |
|---|---|---|
| 任务II: 跨数据集提示泛化 | ||
| Caltech101 93.70 | 94.43 | 93.67±0.2 |
| DTD 41.92 | 45.73 | 46.10±0.1 |
| EuroSAT 46.39 | 45.37 | 45.87±0.7 |
| FGVCAircraft 18.47 | 22.94 | 24.93±0.2 |
| Flowers102 68.71 | 70.20 | 70.90±0.1 |
| Food101 85.30 | 86.06 | 86.30±0.1 |
| OxfordPets 89.14 | 90.14 | 90.63±0.1 |
| StanfordCars 64.51 | 65.50 | 65.00±0.1 |
| SUN397 64.15 | 67.36 | 67.47±0.1 |
| UCF101 66.55 | 68.21 | 68.67±0.2 |
| Average 63.88 | 65.59 | 65.95±0.2 |
| 任务III: 跨领域提示泛化 | ||
| ImageNetV2 | 64.20 64.07 | 64.23±0.1 |
| ImageNet-Sketch | 47.99 48.75 | 49.20±0.0 |
| ImageNet-A 49.71 | 50.63 | 51.33±0.1 |
| ImageNet-R 75.21 | 76.18 | 77.00±0.1 |
| Average | 59.27 59.88 | 60.44±0.1 |
Table 3: In-domain performance. CoOp provides the best in-domain performance, but suffers from distribution shifts. Our proposal provides the best trade-off.
表 3: 领域内性能。CoOp 提供了最佳的领域内性能,但在分布偏移时表现不佳。我们的方案提供了最佳的权衡。
| CoOp [55] | CoCo0p [54] | ProDA [32] | Ours | |
|---|---|---|---|---|
| TaskI | 82.66 | 80.47 | 81.56 | 80.10±0.1 |
| Task II (III) | 71.51 | 71.02 | 70.70±0.2 |
In-domain performance Different from other prompt works, we focus on prompt generalization when we have distribution shift in the input space, the label space, or both.
域内性能
与其他提示工作不同,我们关注的是当输入空间、标签空间或两者同时存在分布偏移时提示的泛化能力。
Table 4: Effect of variation al formulation. Formulating prompt learning as variation al inference improves model generalization on unseen prompts compared to a non-Bayesian baseline [55], for both the unconditional and conditional setting.
表 4: 变分公式的效果。与非贝叶斯基线 [55] 相比,将提示学习 (prompt learning) 表述为变分推断 (variational inference) 能提升模型在未见提示上的泛化能力,该结论在无条件设定和条件设定下均成立。
| DTD | EuroSAT | FGVC | Flowers102 | UCF101 | |
|---|---|---|---|---|---|
| Baseline | 41.18 | 54.74 | 22.30 | 59.67 | 56.05 |
| Unconditional | 58.70 | 71.63 | 33.80 | 75.90 | 74.63 |
| Conditional | 60.80 | 75.30 | 35.00 | 70.40 | 75.77 |
Table 5: Benefit of the posterior distribution. The con- ditional posterior distribution $\mathcal{N}(\mu(\mathbf{x}),\Sigma(\mathbf{x}))$ outperforms the two distributions $\mathcal{U}(0,1)$ and $\mathcal{N}(0,\mathrm{I})$ by a large margin for all datasets, indicating that the conditional variant captures more informative knowledge regarding the underlying distribution of prompts in the prompt space.
表 5: 后验分布的优势。条件后验分布 $\mathcal{N}(\mu(\mathbf{x}),\Sigma(\mathbf{x}))$ 在所有数据集上均大幅优于 $\mathcal{U}(0,1)$ 和 $\mathcal{N}(0,\mathrm{I})$ 两种分布,表明条件变体能捕获提示空间中关于提示底层分布的更多信息知识。
| DTD | EuroSAT | FGVC | Flowers102 | UCF101 | |
|---|---|---|---|---|---|
| u(0,1) | 33.20 | 54.20 | 10.50 | 45.30 | 55.70 |
| N(0, 1) | 26.60 | 50.00 | 07.70 | 36.10 | 48.80 |
| N(μ(x),∑(x)) | 56.40 | 64.50 | 33.00 | 72.30 | 75.60 |
| N(μ(x),0) | 59.80 | 59.90 | 34.10 | 73.50 | 76.50 |
For reference, we provide the in-domain average performance in Table 3. As expected, our generalization ability comes with reduced over fitting on the in-domain setting, leading to $\mathrm{CoOp}$ exhibiting better in-domain per
