A bio-inspired bistable recurrent cell allows for long-lasting memory

一种受生物启发的双稳态循环单元可实现持久记忆

Nicolas Vecoven University of Liège nvecoven@uliege.be

Nicolas Vecoven 列日大学 nvecoven@uliege.be

Damien Ernst University of Liège

Damien Ernst 列日大学

Guillaume Drion University of Liège

Guillaume Drion University of Liège

Abstract

摘要

Recurrent neural networks (RNNs) provide state-of-the-art performances in a wide variety of tasks that require memory. These performances can often be achieved thanks to gated recurrent cells such as gated recurrent units (GRU) and long short-term memory (LSTM). Standard gated cells share a layer internal state to store information at the network level, and long term memory is shaped by network-wide recurrent connection weights. Biological neurons on the other hand are capable of holding information at the cellular level for an arbitrary long amount of time through a process called bi stability. Through bi stability, cells can stabilize to different stable states depending on their own past state and inputs, which permits the durable storing of past information in neuron state. In this work, we take inspiration from biological neuron bi stability to embed RNNs with long-lasting memory at the cellular level. This leads to the introduction of a new bistable biologically-inspired recurrent cell that is shown to strongly improves RNN performance on time-series which require very long memory, despite using only cellular connections (all recurrent connections are from neurons to themselves, i.e. a neuron state is not influenced by the state of other neurons). Furthermore, equipping this cell with recurrent neuro modulation permits to link them to standard GRU cells, taking a step towards the biological plausibility of GRU.

循环神经网络 (RNN) 在需要记忆能力的多种任务中提供了最先进的性能。这些性能通常可以通过门控循环单元 (GRU) 和长短期记忆 (LSTM) 等门控循环单元实现。标准的门控单元共享一个层内状态来存储网络级别的信息，而长期记忆则由网络范围内的循环连接权重塑造。另一方面，生物神经元能够通过一种称为双稳态 (bi stability) 的过程，在细胞水平上长时间保持信息。通过双稳态，细胞可以根据自身的过去状态和输入稳定到不同的稳定状态，从而允许在神经元状态中持久存储过去的信息。在这项工作中，我们从生物神经元双稳态中汲取灵感，在细胞水平上为 RNN 嵌入持久的记忆。这导致了一种新的双稳态生物启发循环单元的引入，该单元被证明可以显著提高 RNN 在需要极长记忆的时间序列上的性能，尽管仅使用细胞连接（所有循环连接都是从神经元到自身的，即神经元状态不受其他神经元状态的影响）。此外，为这种单元配备循环神经调制可以将其与标准 GRU 单元联系起来，朝着 GRU 的生物合理性迈出了一步。

1 Introduction

1 引言

Recurrent neural networks (RNNs) have been widely used in the past years, providing excellent performances on many problems requiring memory such as e.g. sequence to sequence modeling, speech recognition, and neural translation. These achievements are often the result of the development of the long short-term memory (LSTM [1]) and gated recurrent units (GRU [2]) recurrent cells, which allow RNNs to capture time-dependencies over long horizons. Despite all the work analyzing the performances of such cells [3], recurrent cells remain predominantly black-box models. There has been some advance in understanding the dynamical properties of RNNs as a whole from a non-linear control perspective ([4]), but little has been done in understanding the underlying system of recurrent cells themselves. Rather, they have been built for their robust mathematical properties when computing gradients with back-propagation through time (BPTT). Research on new recurrent cells is still ongoing and, building up on LSTM and GRU, recent works have proposed other types of gated units ([5], [6], [7]). In addition, an empirical search over hundreds of different gated architectures has been carried in [8].

循环神经网络 (RNN) 在过去几年中得到广泛应用，在需要记忆功能的诸多任务中表现出色，例如序列到序列建模、语音识别和神经翻译。这些成就往往源于长短期记忆网络 (LSTM [1]) 和门控循环单元 (GRU [2]) 等循环单元的创新发展，它们使RNN能够捕捉长程时间依赖性。尽管已有大量研究分析此类单元的性能 [3]，但循环单元本质上仍是黑箱模型。虽然从非线性控制角度对RNN整体动力学特性的理解取得了一定进展 [4]，但对循环单元内部系统机制的研究仍很有限。事实上，这些单元的设计初衷是为了在通过时间反向传播 (BPTT) 计算梯度时保持稳健的数学特性。基于LSTM和GRU的新型循环单元研究仍在持续，近期工作提出了其他类型的门控单元 ([5], [6], [7])。此外，文献 [8] 还对数百种不同门控架构进行了实证搜索。

In parallel, there has been an increased interest in assessing the biological plausibility of neural networks. There has not only been a lot of interest in spiking neural networks ([9, 10, 11]), but also in reconciling more traditional deep learning models with biological plausibility ([12, 13, 14]). RNNs are a promising avenue for the latter ([15]) as they are known to provide great performances from a deep learning point of view while theoretically allowing a discrete dynamical simulation of biological neurons.

与此同时，人们对评估神经网络的生物合理性产生了更多兴趣。不仅脉冲神经网络 ([9, 10, 11]) 备受关注，将传统深度学习模型与生物合理性相协调的研究 ([12, 13, 14]) 也日益增多。循环神经网络 (RNN) 是实现后者的重要途径 ([15])，因为从深度学习角度来看它们具有卓越性能，同时在理论上能对生物神经元进行离散动力学模拟。

RNNs combine simple cellular dynamics and a rich, highly recurrent network architecture. The recurrent network architecture enables the encoding of complex memory patterns in the connection weights. These memory patterns rely on global feedback interconnections of large neuronal populations. Such global feedback interconnections are difficult to tune, and can be a source of vanishing or exploding gradient during training, which is a major drawback of RNNs. In biological networks, a significant part of advanced computing is handled at the cellular level, mitigating the burden at the network level. Each neuron type can switch between several complex firing patterns, which include e.g. spiking, bursting, and bi stability. In particular, bi stability is the ability for a neuron to switch between two stable outputs depending on input history. It is a form of cellular memory ([16]).

RNN (Recurrent Neural Network) 通过结合简单的细胞动力学与丰富的高度循环网络架构，实现了对复杂记忆模式的编码。这种循环网络架构依赖大规模神经元群体的全局反馈连接来存储记忆模式。然而，全局反馈连接难以调节，可能导致训练过程中出现梯度消失或爆炸问题，这是RNN的主要缺陷。在生物神经网络中，高级计算的重要部分由细胞层面处理，从而减轻了网络层面的负担。每种神经元类型都能在多种复杂放电模式（如脉冲发放、簇状放电和双稳态）间切换。其中，双稳态指神经元根据输入历史在两个稳定输出状态间切换的能力，这是一种细胞层面的记忆形式 [16]。

In this work, we propose a new biologically motivated bistable recurrent cell (BRC), which embeds classical RNNs with local cellular memory rather than global network memory. More precisely, BRCs are built such that their hidden recurrent state does not directly influence other neurons (i.e. they are not re currently connected to other cells). To make cellular bi stability compatible with the RNNs feedback architecture, a BRC is constructed by taking a feedback control perspective on biological neuron excitability ([17]). This approach enables the design of biologically-inspired cellular dynamics by exploiting the RNNs structure rather than through the addition of complex mathematical functions.

在本工作中，我们提出了一种新的生物启发的双稳态循环单元(BRC)，它通过局部细胞记忆而非全局网络记忆来增强经典循环神经网络(RNN)。具体而言，BRC的设计使其隐藏循环状态不会直接影响其他神经元(即它们不与其他细胞建立循环连接)。为了使细胞双稳态特性与RNN反馈架构兼容，我们基于生物神经元兴奋性的反馈控制视角([17])构建了BRC。这种方法通过利用RNN自身结构(而非添加复杂数学函数)来实现生物启发的细胞动力学设计。

To test the capacities of cellular memory, the bistable cells are first connected in a feed forward manner, getting rid of the network memory coming from global recurrent connections. Despite having only cellular temporal connections, we show that BRCs provide good performances on standard benchmarks and surpass more standard ones such as LSTMs and GRUs on benchmarks with datasets composed of extremely sparse time-series. Secondly, we show that the proposed bio-inspired recurrent cell can be made more comparable to a standard GRU by using a special kind of recurrent neuro modulation. We call this neuro modulated bistable recurrent cell nBRC, standing for neuromodulated BRC. The comparison between nBRCs and GRUs provides food-for-thought and is a step towards reconciling traditional gated recurrent units and biological plausibility.

为测试细胞记忆能力，首先以前馈方式连接双稳态细胞( BRC )，消除全局循环连接带来的网络记忆。实验表明，尽管仅具备细胞级时序连接，BRC在标准基准测试中表现优异，且在极端稀疏时间序列数据集上超越LSTM、GRU等传统模型。其次，我们通过引入特殊类型的循环神经调控机制，使这种受生物启发的循环细胞( nBRC )性能更接近标准GRU。nBRC与GRU的对比研究发人深省，为调和传统门控循环单元与生物合理性迈出了重要一步。

2 Recurrent neural networks and gated recurrent units

2 循环神经网络与门控循环单元

RNNs have been widely used to tackle many problems having a temporal structure. In such problems, the relevant information can only be captured by processing observations obtained during multiple time-steps. More formally, a time-series can be defined as $\mathbf{X}=[\mathbf{x}_ {0},\dots,\mathbf{x}_ {T}]$ with $T\in\mathcal{N}_ {0}$ and $\mathbf{x}_ {i}\in\mathcal{R}^{n}$ . To capture time-dependencies, RNNs maintain a recurrent hidden state whose update depends on the previous hidden state and current observation of a time-series, making them dynamical systems and allowing them to handle arbitrarily long sequences of inputs. Mathematically, RNNs maintain a hidden state $\mathbf h_{t}=f(\mathbf h_{t-1},\mathbf x_{t};\theta)$ , where $\mathbf{h}_{0}$ is a constant and $\theta$ are the parameters of the network. In its most standard form, an RNN updates its state as follows:

RNN (Recurrent Neural Network) 已被广泛用于解决具有时间结构的诸多问题。在此类问题中，只有通过处理多个时间步长的观测数据才能捕获相关信息。更正式地说，时间序列可定义为 $\mathbf{X}=[\mathbf{x}_ {0},\dots,\mathbf{x}_ {T}]$，其中 $T\in\mathcal{N}_ {0}$ 且 $\mathbf{x}_ {i}\in\mathcal{R}^{n}$。为捕捉时间依赖性，RNN 会维护一个循环隐藏状态，其更新取决于前一个隐藏状态和当前时间序列的观测值，这使得它们成为动态系统，并能处理任意长度的输入序列。从数学上看，RNN 维护的隐藏状态为 $\mathbf h_{t}=f(\mathbf h_{t-1},\mathbf x_{t};\theta)$，其中 $\mathbf{h}_{0}$ 为常量，$\theta$ 是网络参数。其最标准的状态更新公式如下：

$$
\mathbf{h}_ {t}=g(U\mathbf{x}_ {t}+W\mathbf{h}_{t-1})
$$

$$
\mathbf{h}_ {t}=g(U\mathbf{x}_ {t}+W\mathbf{h}_{t-1})
$$

where $g$ is a standard activation function such as a sigmoid or a hyperbolic tangent. However, RNNs using Equation 1 as the update rule are known to be difficult to train on long sequences due to vanishing (or, more rarely, exploding) gradient problems. To alleviate this problem, more complex recurrent update rules have been proposed, such as LSTMs ([1]) and GRUs ([2]). These updates allow recurrent networks to be trained on much longer sequences by using gating principles. By way of illustration, the updates related to a gated recurrent unit are

其中 $g$ 是标准激活函数，例如 sigmoid 或双曲正切函数。然而，使用公式 1 作为更新规则的 RNN 由于梯度消失（或更罕见的梯度爆炸）问题，在长序列上训练较为困难。为了缓解这一问题，人们提出了更复杂的循环更新规则，例如 LSTM ([1]) 和 GRU ([2])。这些更新通过门控机制使循环网络能够在更长的序列上进行训练。举例来说，门控循环单元 (GRU) 的相关更新为

where $\mathbf{z}$ is the update gate (used to tune the update speed of the hidden state with respect to new inputs) and $\mathbf{r}$ is the reset gate (used to reset parts of the memory).

其中 $\mathbf{z}$ 是更新门(update gate) (用于调节隐藏状态对新输入的更新速度) ，$\mathbf{r}$ 是重置门(reset gate) (用于重置部分记忆单元)。

3 Neuronal bi stability: a feedback viewpoint

3 神经元双稳态：反馈视角

Biological neurons are intrinsically dynamical systems that can exhibit a wide variety of firing patterns. In this work, we focus on the control of bi stability, which corresponds to the coexistence of two stable states at the neuronal level. Bistable neurons can switch between their two stable states in response to transient inputs ([16, 18]), endowing them with a kind of never-fading cellular memory ([16]).

生物神经元本质上是动态系统，能够表现出多种放电模式。本研究聚焦于双稳态 (bi stability) 控制，即神经元层面两个稳定状态的共存现象。双稳态神经元可通过瞬态输入在两种稳定状态间切换 ([16, 18]) ，这种特性使其具备永不消退的细胞记忆功能 ([16]) 。

Complex neuron firing patterns are often modeled by systems of ordinary differential equations (ODEs). Translating ODEs into an artificial neural network algorithm often leads to mixed results due to increased complexity and the difference in modeling language. Another approach to model neuronal dynamics is to use a control systems viewpoint [17]. In this viewpoint, a neuron is modeled as a set of simple building blocks connected using a multiscale feedback, or recurrent, inter con nection pattern.

复杂神经元放电模式通常通过常微分方程(ODE)系统建模。将ODE转化为人工神经网络算法常因复杂度增加和建模语言差异导致效果参差不齐。另一种神经元动力学建模方法采用控制系统视角[17]，将神经元视为由多尺度反馈或循环互连模式连接的简单构件集合。

A neuronal feedback diagram focusing on one time-scale, which is sufficient for bi stability, is illustrated in Figure 1A. The block $1/(C s)$ accounts for membrane integration, $C$ being the membrane capacitance and $s$ the complex frequency. The outputs from pre synaptic neurons $V_{p r e}$ are combined at the input level to create a synaptic current $I_{s y n}$ . Neuron-intrinsic dynamics are modeled by the negative feedback interconnection of a nonlinear function $I_{i n t}=f(\dot{V_{p o s t}})$ , called the IV curve in neuro physiology, which outputs an intrinsic current $I_{i n t}$ that adds to $I_{s y n}$ to create the membrane current $I_{m}$ . The slope of $f(V_{p o s t})$ determines the feedback gain, a positive slope leading to negative feedback and a negative slope to positive feedback. $I_{m}$ is then integrated by the post synaptic neuron membrane to modify its output voltage $V_{p o s t}$ .

图1A展示了一个专注于单一时间尺度的神经元反馈示意图，该尺度足以实现双稳态。模块$1/(C s)$表示膜积分过程，其中$C$为膜电容，$s$为复频率。突触前神经元输出$V_{pre}$在输入端组合形成突触电流$I_{syn}$。神经元固有动力学通过非线性函数$I_{int}=f(\dot{V_{post}})$的负反馈连接建模（该函数在神经生理学中称为IV曲线），其输出的固有电流$I_{int}$与$I_{syn}$叠加形成膜电流$I_m$。函数$f(V_{post})$的斜率决定反馈增益：正斜率导致负反馈，负斜率导致正反馈。$I_m$随后被突触后神经元膜积分，从而改变其输出电压$V_{post}$。

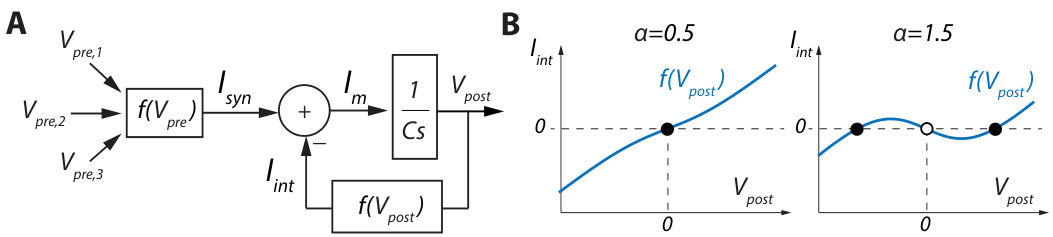
Figure 1: A. One timescale control diagram of a neuron. B. Plot of the function ${I_{i n t}=V_{p o s t}-}$ $\alpha\operatorname{tanh}(V_{p o s t})$ for two different values of $\alpha$ . Full dots correspond to stable states, empty dots to unstable states.

图 1: A. 神经元单时间尺度控制图。B. 函数 ${I_{i n t}=V_{p o s t}-}$ $\alpha\operatorname{tanh}(V_{p o s t})$ 在两种不同 $\alpha$ 值下的曲线图。实心圆点对应稳定状态，空心圆点对应不稳定状态。

The switch between mono stability and bi stability is achieved by shaping the nonlinear function ${\cal I}_ {i n t}=f(V_{p o s t})$ (Figure 1B). The neuron is monostable when $\bar{f}(V_{p o s t})$ is monotonic of positive slope (Figure 1B, left). Its only stable state corresponds to the voltage at which $I_{i n t}=0$ in the absence of synaptic inputs (full dot). The neuron switch to bi stability through the creation of a local region of negative slope in $f(V_{p o s t})$ (Figure 1B, left). Its two stable states correspond to the voltages at which $I_{i n t}=0$ with positive slope (full dots), separated by an unstable state where $I_{i n t}=0$ with negative slope (empty dot). The local region of negative slope corresponds to a local positive feedback where the membrane voltage is unstable.

单稳态和双稳态之间的切换是通过塑造非线性函数 ${\cal I}_ {i n t}=f(V_{p o s t})$ 实现的 (图 1B)。当 $\bar{f}(V_{p o s t})$ 具有正斜率的单调性时，神经元处于单稳态 (图 1B 左)。其唯一稳定状态对应于无突触输入时 $I_{i n t}=0$ 的电压值 (实心圆点)。通过在 $f(V_{p o s t})$ 中创建负斜率局部区域，神经元切换为双稳态 (图 1B 左)。其两个稳定状态对应于 $I_{i n t}=0$ 且斜率为正的电压值 (实心圆点)，中间被一个 $I_{i n t}=0$ 且斜率为负的不稳定状态隔开 (空心圆点)。负斜率局部区域对应膜电压不稳定的局部正反馈。

In biological neurons, a local positive feedback is provided by regenerative gating, such as sodium and calcium channel activation or potassium channel in activation ([18, 19]). The switch from mono stability to bi stability can therefore be controlled by tuning ion channel density. This property can be emulated in electrical circuits by combining trans conductance amplifiers to create the function

在生物神经元中，局部正反馈通过再生门控提供，例如钠和钙通道激活或钾通道失活 ([18, 19])。因此，通过调节离子通道密度可以控制从单稳态到双稳态的切换。这一特性可通过结合跨导放大器来创建功能电路进行模拟。

$$
I_{i n t}=V_{p o s t}-\alpha\operatorname{tanh}(V_{p o s t}),
$$

$$
I_{i n t}=V_{p o s t}-\alpha\operatorname{tanh}(V_{p o s t}),
$$

where the switch from mono stability to bi stability is controlled by a single parameter $\alpha$ ([20]). $\alpha$ models the effect of sodium or calcium channel activation, which tunes the local slope of the function, hence the local gain of the feedback loop (Figure 1B). For $\alpha\in]0,1]$ , which models a low sodium or calcium channel density, the function is monotonic, leading to mono stability (Figure 1B, left). For $\alpha\in]1,+\infty[$ , which models a high sodium or calcium channel density, a region of negative slope is created around $V_{p o s t}=0$ , and the neuron becomes bistable (Figure 1B, right). This bistability leads to never-fading memory, as in the absence of significant input perturbation the system will remain indefinitely in one of the two stable states depending on the input history.

其中从单稳态到双稳态的切换由单一参数 $\alpha$ 控制 ([20])。$\alpha$ 模拟了钠或钙通道激活的效果，调节了函数的局部斜率，从而调节反馈环路的局部增益 (图 1B)。对于 $\alpha\in]0,1]$ (模拟低钠或钙通道密度的情况)，函数是单调的，导致单稳态 (图 1B，左)。对于 $\alpha\in]1,+\infty[$ (模拟高钠或钙通道密度的情况)，在 $V_{post}=0$ 附近会产生一个负斜率区域，神经元变为双稳态 (图 1B，右)。这种双稳态会导致永不消逝的记忆，因为在没有显著输入扰动的情况下，系统会根据输入历史无限期地保持在两个稳定状态之一。

Neuronal bi stability can therefore be modeled by a simple feedback system whose dynamics is tuned by a single feedback parameter $\alpha$ . This parameter can switch between mono stability and bi stability by tuning the shape of the feedback function $f(V_{p o s t})$ , whereas neuron convergence dynamics is controlled by a single feed forward parameter $C$ . In biological neurons, both these parameters can be modified dynamically by other neurons via a mechanism called neuro modulation, providing a dynamic, controllable memory at the cellular level. The key challenge is to find an appropriate mathematical representation of this mechanism to be efficiently used in artificial neural networks, and, more particularly, in RNNs.

因此，神经元双稳态可以通过一个简单的反馈系统建模，其动力学由单一反馈参数 $\alpha$ 调节。该参数可通过调整反馈函数 $f(V_{post})$ 的形状在单稳态与双稳态之间切换，而神经元收敛动力学则由单一前馈参数 $C$ 控制。在生物神经元中，这两个参数均可通过神经调制机制被其他神经元动态修改，从而在细胞层面实现动态可控的记忆功能。关键挑战在于找到该机制的合适数学表征，以高效应用于人工神经网络，尤其是循环神经网络 (RNN) 中。

4 Cellular memory, bi stability and neuro modulation in RNNs

4 RNN中的细胞记忆、双稳态和神经调节

The bistable recurrent cell (BRC) To model controllable bi stability in RNNs, we start by drawing two main comparisons between the feedback structure Figure 1A and the GRU equations (Equation 2). First, we note that the reset gate $r$ has a role that is similar to the one played by the feedback gain $\alpha$ in Equation 3. In GRU equations, $r$ is the output of a sigmoid function, which implies $r\in]0,1[$ [. These possible values for $r$ correspond to negative feedback only, which does not allow for bi stability. The update gate $z$ , on the other hand, has a role similar to that of the membrane capacitance $C$ . Second, one can see through the matrix multiplications $W_{z}\mathbf{h}_ {t-1}$ , $W_{r}\mathbf{h}_ {t-1}$ and $W_{h}\mathbf{h}_ {t-1}$ that each cell uses the internal state of other neurons to compute its own state without going through synaptic connections. In biological neurons, the intrinsic dynamics defined by $I_{i n t}$ is constrained to only depend on its own state $V_{p o s t}$ , and the influence of other neurons comes only through the synaptic compartment $(I_{s y n})$ , or through neuro modulation.

双稳态循环单元 (BRC) 为在循环神经网络中建立可控双稳态模型，我们首先对反馈结构图1A和GRU方程(式2)进行两项主要比较。首先，我们发现重置门$r$的作用类似于式3中的反馈增益$\alpha$。在GRU方程中，$r$是sigmoid函数的输出，这意味着$r\in]0,1[$。$r$的这些可能取值仅对应负反馈，无法实现双稳态。而更新门$z$的作用则类似于膜电容$C$。其次，通过矩阵乘法$W_{z}\mathbf{h}_ {t-1}$、$W_{r}\mathbf{h}_ {t-1}$和$W_{h}\mathbf{h}_ {t-1}$可以看出，每个单元都使用其他神经元的内部状态来计算自身状态，而无需经过突触连接。在生物神经元中，由$I_{int}$定义的内在动力学仅依赖于其自身状态$V_{post}$，其他神经元的影响仅通过突触区$(I_{syn})$或神经调节实现。

To enforce this cellular feedback constraint in GRU equations and to endow them with bi stability, we propose to update $h_{t}$ as follows:

为了在GRU方程中实施这种细胞反馈约束并赋予其双稳态特性，我们提出按以下方式更新 $h_{t}$：

$$
\mathbf{h}_ {t}=\mathbf{c}_ {t}\odot\mathbf{h}_ {t-1}+\left(1-\mathbf{c}_ {t}\right)\odot\operatorname{tanh}(U\mathbf{x}_ {t}+\mathbf{a}_ {t}\odot\mathbf{h}_{t-1})
$$

$$
\mathbf{h}_ {t}=\mathbf{c}_ {t}\odot\mathbf{h}_ {t-1}+\left(1-\mathbf{c}_ {t}\right)\odot\operatorname{tanh}(U\mathbf{x}_ {t}+\mathbf{a}_ {t}\odot\mathbf{h}_{t-1})
$$

where $\mathbf{a}_ {t}=1+\operatorname{tanh}(U_{a}\mathbf{x}_ {t}+\mathbf{w}_ {a}\odot\mathbf{h}_ {t-1})$ and $\mathbf{c}_ {t}=\sigma(U_{c}\mathbf{x}_ {t}+\mathbf{w}_ {c}\odot\mathbf{h}_ {t-1})$ . $\mathbf{a}_ {t}$ corresponds to the feedback parameter $\alpha$ , with ${\mathbf a}_ {t}\in]0,2[$ [. $\mathbf{c}_{t}$ corresponds to the update gate in GRU and plays the role of the membrane capacitance $C$ , determining the convergence dynamics of the neuron. We call this updated cell the bistable recurrent cell (BRC).

其中 $\mathbf{a}_ {t}=1+\operatorname{tanh}(U_{a}\mathbf{x}_ {t}+\mathbf{w}_ {a}\odot\mathbf{h}_ {t-1})$ ，且 $\mathbf{c}_ {t}=\sigma(U_{c}\mathbf{x}_ {t}+\mathbf{w}_ {c}\odot\mathbf{h}_ {t-1})$ 。$\mathbf{a}_ {t}$ 对应反馈参数 $\alpha$ ，其中 ${\mathbf a}_ {t}\in]0,2[$ 。$\mathbf{c}_{t}$ 对应 GRU 中的更新门，并起到膜电容 $C$ 的作用，决定神经元的收敛动态特性。我们将这个更新后的单元称为双稳态循环单元 (BRC)。

The main differences between a BRC and a GRU are twofold. First, each neuron has its own internal state $\mathbf{h}_ {t}$ that is not directly affected by the internal state of the other neurons. Indeed, due to the four instances of $\mathbf{h}_ {t-1}$ coming from Hadamard products, the only temporal connections existing in layers of BRC are from neurons to themselves. This enforces the memory to be only cellular. Second, the feedback parameter $\mathbf{a}_{t}$ is allowed to take a value in the range $|0,2[$ rather than $]0,1[$ . This allows the cell to switch between mono stability $(a\leq1)$ and bi stability $\left(a>1\right)$ ) (Figure 2A,B). The proof of this switch is provided in Appendix A.

BRC与GRU的主要区别有两点。首先，每个神经元都有独立的内部状态$\mathbf{h}_ {t}$，不受其他神经元内部状态的直接影响。由于Hadamard积引入的四个$\mathbf{h}_ {t-1}$实例，BRC层中仅存在神经元自身的时序连接，这强制实现了细胞级记忆。其次，反馈参数$\mathbf{a}_{t}$的取值范围扩展为$|0,2[$而非$]0,1[$，使细胞能在单稳态$(a\leq1)$和双稳态$\left(a>1\right)$之间切换（图2A,B）。该切换机制的证明详见附录A。

It is important to note that the parameters $\mathbf{a}_ {t}$ and $\mathbf{c}_ {t}$ are dynamic. $\mathbf{a}_ {t}$ and $\mathbf{c}_{t}$ are neuro modulated by the previous layer, that is, their value depends on the output of other neurons. Tests were carried with a and c as parameters learned by stochastic gradient descent, which resulted in lack of represent at ional power, leading to the need for neuro modulation. This neuro modulation scheme was the most evident as it maintains the cellular memory constraint and leads to the most similar update rule with respect to standard recurrent cells (Equation 2). However, as will be discussed later, other neuro modulation schemes can be thought of.

需要注意的是，参数 $\mathbf{a}_ {t}$ 和 $\mathbf{c}_ {t}$ 是动态的。$\mathbf{a}_ {t}$ 和 $\mathbf{c}_{t}$ 受到上一层的神经调节 (neuro modulation) ，即它们的值取决于其他神经元的输出。实验曾尝试将a和c作为通过随机梯度下降 (stochastic gradient descent) 学习的参数，但会导致表征能力不足，从而需要引入神经调节。这种神经调节方案最为明显，因为它保持了细胞记忆约束，并产生了与标准循环单元最相似的更新规则 (Equation 2) 。不过，后文将讨论其他可能的神经调节方案。

Likewise, from a neuroscience perspective, $\mathbf{a}_ {t}$ could well be greater than 2. Limiting the range of $\mathbf{a}_ {t}$ to $|0,2[$ was made for numerical stability and for symmetry between the range of bistable and monostable neurons. We argue that this is not an issue as, for a value of $\mathbf{a}_{t}$ greater than 1.5, the dynamics of the neurons become very similar (as suggested in Figure 2A).

同样，从神经科学的角度来看，$\mathbf{a}_ {t}$ 完全可以大于2。将 $\mathbf{a}_ {t}$ 的范围限制在 $|0,2[$ 是为了数值稳定性以及双稳态和单稳态神经元范围之间的对称性。我们认为这不是问题，因为当 $\mathbf{a}_{t}$ 的值大于1.5时，神经元的动态行为变得非常相似（如图 2A 所示）。

Figure 2C shows the dynamics of a BRC with respect to $a_{t}$ and $c_{t}$ . For $a_{t}<1$ , the cell exhibits a classical monostable behavior, relaxing to the 0 stable state in the absence of inputs (blue curves in Figure 2C). On the other hand, a bistable behavior can be observed for $a_{t}>1$ : the cells can either stabilize on an upper stable state or a lower stable state depending on past inputs (red curves in Figure 2C). Since these upper and lower stable states do not correspond to an $h_{t}$ which is equal to 0, they can be associated with cellular memory that never fades over time. Furthermore, Figure 2 also illustrates that neuron convergence dynamics depend on the value of $c$ .

图 2C 展示了 BRC 相对于 $a_{t}$ 和 $c_{t}$ 的动态变化。当 $a_{t}<1$ 时，细胞表现出经典的单调稳定行为，在没有输入的情况下会弛豫到 0 稳定状态 (图 2C 中的蓝色曲线)。另一方面，当 $a_{t}>1$ 时可以观察到双稳态行为：细胞会根据过去的输入稳定在上稳定状态或下稳定状态 (图 2C 中的红色曲线)。由于这些上稳定状态和下稳定状态不对应于 $h_{t}$ 等于 0 的情况，因此它们可以与永不随时间消退的细胞记忆相关联。此外，图 2 还说明了神经元收敛动态取决于 $c$ 的值。

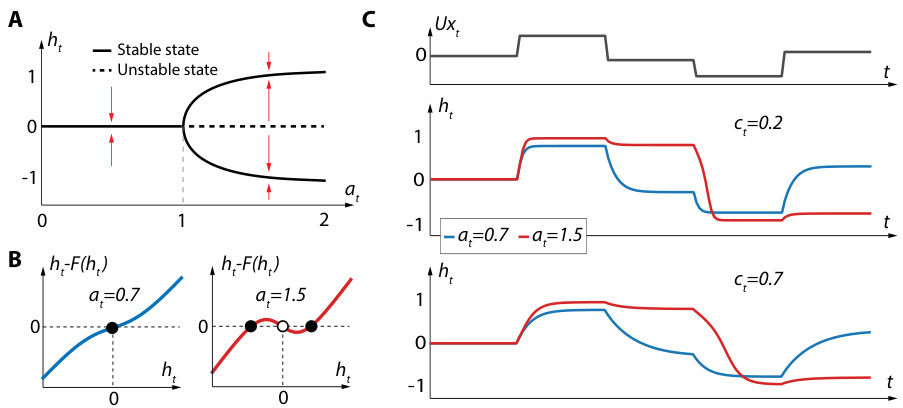
Figure 2: A. Bifurcation diagram of Equation 4 for $U\mathbf{x}_ {t}=0$ . B. Plots of the function $h_{t}-F(h_{t})$ for two values of $a_{t}$ , where $\bar{F(h_{t})}=c_{t}\bar{h}{t}+(1-c{t})\operatorname{tanh}(a_{t}h_{t})$ is the right hand side of Equation 4 with $x_{t}=0$ . Full dots correspond to stable states, empty dots to unstable states. C. Response of BRC to an input time-series for different values of $a_{t}$ and $c_{t}$ .

图 2: A. 当 $U\mathbf{x}_ {t}=0$ 时方程 4 的分岔图。B. 函数 $h_{t}-F(h_{t})$ 在两种 $a_{t}$ 值下的曲线图，其中 $\bar{F(h_{t})}=c_{t}\bar{h}{t}+(1-c{t})\operatorname{tanh}(a_{t}h_{t})$ 是方程 4 在 $x_{t}=0$ 时的右侧表达式。实心点表示稳定状态，空心点表示不稳定状态。C. BRC 在不同 $a_{t}$ 和 $c_{t}$ 值下对输入时间序列的响应。

The re currently neuro modulated bistable recurrent cell (nBRC) To further improve the performance of BRC, one can relax the cellular memory constraint. By creating a dependency of $a_{t}$ and $c_{t}$ on the output of other neurons of the layer, one can build a kind of recurrent layer-wise neuro modulation. We refer to this modified version of a BRC as an nBRC, standing for re currently neuro modulated BRC. The update rule for the nBRC is the same as for BRC, and follows Equation 4. The difference comes in the computation of $a_{t}$ and $c_{t}$ , which are neuro modulated as follows:

目前神经调制的双稳态循环单元 (nBRC)

为了进一步提升BRC的性能，可以放宽单元记忆约束。通过让$a_{t}$和$c_{t}$依赖于该层其他神经元的输出，可以构建一种循环层间神经调制机制。我们将这种改进版的BRC称为nBRC，意为"循环神经调制的BRC"。nBRC的更新规则与BRC相同，遵循公式4。差异体现在$a_{t}$和$c_{t}$的计算上，其神经调制方式如下：

The update rule of nBRCs being that of BRCs (Equation 4), bistable properties are maintained and hence the possibility of a cellular memory that does not fade over time. However, the new recurrent neuro modulation scheme adds a type of network memory on top of the cellular memory. This recurrent neuro modulation scheme brings the update rule even closer to standard GRU. This is highlighted when comparing Equation 2 and Equation 4 with parameters neuro modulated following Equation 5. We stress that, as opposed to GRUs, bi stability is still ensured through $a_{t}$ belonging to $|0,2[$ . A relaxed cellular memory constraint is also ensured, as each neuron past state $h_{t-1}$ only directly influences its own current state and not the state of other neurons of the layer (Hadamard product on the $\mathbf{h}_ {t}$ update in Equation 4). This is important for numerical stability as the introduction of a cellular positive feedback for bi stability leads to global instability if the update is computed using other neurons states directly (as it is done in the classical GRU update, see the matrix multiplication $W_{h}\mathbf{h}_{t-1}$ in Equation 2).

nBRC的更新规则与BRC相同（公式4），因此保留了双稳态特性，从而实现了不会随时间消退的细胞记忆。然而，新的循环神经调节机制在细胞记忆基础上新增了网络记忆功能。这种循环神经调节机制使更新规则更接近标准GRU结构，通过对比公式2与采用公式5进行神经调节的公式4即可看出这一特点。需要强调的是，与GRU不同，双稳态仍通过$a_{t}$属于$|0,2[$区间得以保证。同时实现了宽松的细胞记忆约束——每个神经元过去状态$h_{t-1}$仅直接影响自身当前状态，而不会直接影响同层其他神经元状态（见公式4中$\mathbf{h}_ {t}$更新的Hadamard积）。这对数值稳定性至关重要：若直接采用其他神经元状态进行计算（如经典GRU更新中的矩阵乘法$W_{h}\mathbf{h}_{t-1}$见公式2），为维持双稳态引入的细胞正反馈会导致全局不稳定性。

Finally, let us note that to be consistent with the biological model presented in Section 3, Equation 5 should be interpreted as a way to represent a neuro modulation mechanism of a neuron by those from its own layer and the layer that precedes. Hence, the possible analogy between gates $z$ and $r$ in GRUs and neuro modulation. In this respect, studying the introduction of new types of gates based on more biological plausible neuro modulation architectures would certainly be interesting.

最后，我们注意到，为了与第3节中提出的生物模型保持一致，方程5应被解释为一种表示神经元通过来自自身层和前一层神经元的神经调节机制的方式。因此，GRU中的门控 $z$ 和 $r$ 与神经调节之间可能存在类比。在这方面，研究基于更具生物学合理性的神经调节架构引入新型门控机制无疑会非常有趣。

5 Analysis of BRC and nBRC performance

5 BRC 和 nBRC 性能分析

To demonstrate the performances of BRCs and nBRCs with respect to standard GRUs and LSTMs, we tackle three problems. The first is a one-dimensional toy problem, the second is a twodimensional denoising problem and the third is the sequential MNIST problem. The supervised setting used is the same for all three benchmarks. The network is presented with a time-series and is asked to output a prediction (regression for the first two benchmarks and classification for the third) after having received the last element of the time-series $\mathbf{x}_{T}$ . We show that the introduction of bi stability in recurrent cells is especially useful for datasets in which only sparse time-series are available. In this section, we also take a look at the dynamics inside the BRC neurons in the context of the denoising benchmark and show that bi stability is heavily used by the neural network.

为了展示BRC和nBRC相对于标准GRU和LSTM的性能表现，我们研究了三个问题。第一个是一维玩具问题，第二个是二维去噪问题，第三个是顺序MNIST问题。这三个基准测试采用相同的监督设置：网络接收一个时间序列，并在接收到该序列的最后一个元素$\mathbf{x}_{T}$后输出预测结果（前两个基准测试为回归任务，第三个为分类任务）。我们证明，在循环单元中引入双稳态特性对于稀疏时间序列数据集特别有效。本节还通过去噪基准测试分析了BRC神经元内部的动态特性，表明神经网络充分运用了双稳态机制。

T	BRC	nBRC	GRU	LSTM
5	0.0157± 0.0124	0.0028± 0.0023	0.0019 ± 0.0011	0.0016± 0.0009
50	0.0142± 0.0081	0.0009 ± 0.0006	0.0004±0.0003	0.9919±0.0012
100	0.0046±0.0002	0.0006± 0.0001	0.0097± 0.006	1.0354± 0.0416
300	0.0013±0.0008	0.0007 ± 0.0002	0.6743± 0.4761	0.9989 ± 0.0170
600	0.1581±0.1574	0.0005±0.0001	0.9934±0.0182	0.9989±0.0162

T	BRC	nBRC	GRU	LSTM
5	0.0157±0.0124	0.0028±0.0023	0.0019±0.0011	0.0016±0.0009
50	0.0142±