Jukebox: A Generative Model for Music
Jukebox: 一种音乐生成模型
Prafulla Dhariwal * 1 Heewoo Jun * 1 Christine Payne * 1 Jong Wook Kim 1 Alec Radford 1 Ilya Sutskever 1
Prafulla Dhariwal * 1 Heewoo Jun * 1 Christine Payne * 1 Jong Wook Kim 1 Alec Radford 1 Ilya Sutskever 1
Abstract
摘要
We introduce Jukebox, a model that generates music with singing in the raw audio domain. We tackle the long context of raw audio using a multiscale VQ-VAE to compress it to discrete codes, and modeling those using auto regressive Transformers. We show that the combined model at scale can generate high-fidelity and diverse songs with coherence up to multiple minutes. We can condition on artist and genre to steer the musical and vocal style, and on unaligned lyrics to make the singing more controllable. We are releasing thousands of non cherry-picked samples, along with model weights and code.
我们推出Jukebox,这是一种在原始音频领域生成带人声音乐的模型。我们采用多尺度VQ-VAE(向量量化变分自编码器)压缩原始音频的长上下文为离散编码,并通过自回归Transformer进行建模。研究表明,这种规模化组合模型能生成保真度高且多样化的歌曲,其连贯性可达数分钟。该模型可通过艺术家和流派条件控制音乐与人声风格,并利用未对齐歌词增强演唱可控性。我们公开了数千个未经人工筛选的样本,同时开放模型权重和代码。
1. Introduction
1. 引言
Music is an integral part of human culture, existing from the earliest periods of human civilization and evolving into a wide diversity of forms. It evokes a unique human spirit in its creation, and the question of whether computers can ever capture this creative process has fascinated computer scientists for decades. We have had algorithms generating piano sheet music (Hiller Jr & Isaacson, 1957; Moorer, 1972; Hadjeres et al., 2017; Huang et al., 2017), digital vocoders generating a singer’s voice (Bonada & Serra, 2007; Saino et al., 2006; Blaauw & Bonada, 2017) and also synthesizers producing timbres for various musical instruments (Engel et al., 2017; 2019). Each captures a specific aspect of music generation: melody, composition, timbre, and the human voice singing. However, a single system to do it all remains elusive.
音乐是人类文化不可或缺的一部分,从人类文明早期就已存在,并演变成多种多样的形式。它在创作中唤起独特的人类精神,而计算机能否捕捉这种创作过程的问题几十年来一直吸引着计算机科学家。我们已经有了生成钢琴乐谱的算法 (Hiller Jr & Isaacson, 1957; Moorer, 1972; Hadjeres et al., 2017; Huang et al., 2017) 、生成人声的数字声码器 (Bonada & Serra, 2007; Saino et al., 2006; Blaauw & Bonada, 2017) ,以及为各种乐器生成音色的合成器 (Engel et al., 2017; 2019) 。每种技术都捕捉了音乐生成的特定方面:旋律、作曲、音色和人声演唱。然而,一个能完成所有这些任务的单一系统仍然难以实现。
The field of generative models has made tremendous progress in the last few years. One of the aims of generative modeling is to capture the salient aspects of the data and to generate new instances indistinguishable from the true data The hypothesis is that by learning to produce the data we can learn the best features of the data1. We are surrounded by highly complex distributions in the visual, audio, and text domain, and in recent years we have developed advances in text generation (Radford et al.), speech generation (Xie et al., 2017) and image generation (Brock et al., 2019; Razavi et al., 2019). The rate of progress in this field has been rapid, where only a few years ago we had algorithms producing blurry faces (Kingma & Welling, 2014; Goodfellow et al., 2014) but now we now can generate high-resolution faces indistinguishable from real ones (Zhang et al., 2019b).
生成式模型领域在过去几年取得了巨大进展。生成式建模的目标之一是捕捉数据的显著特征,并生成与真实数据无法区分的新实例。其核心假设是,通过学习生成数据,我们能够掌握数据的最佳特征[1]。我们被视觉、音频和文本领域中高度复杂的分布所包围,近年来在文本生成 (Radford et al.)、语音生成 (Xie et al., 2017) 和图像生成 (Brock et al., 2019; Razavi et al., 2019) 方面都取得了突破性进展。该领域的发展速度惊人:就在几年前,算法生成的还是模糊人脸 (Kingma & Welling, 2014; Goodfellow et al., 2014),而现在我们已经能够生成与真实人脸无法区分的高分辨率图像 (Zhang et al., 2019b)。
Generative models have been applied to the music generation task too. Earlier models generated music symbolically in the form of a pianoroll, which specifies the timing, pitch, velocity, and instrument of each note to be played. (Yang et al., 2017; Dong et al., 2018; Huang et al., 2019a; Payne, 2019; Roberts et al., 2018; Wu et al., 2019). The symbolic approach makes the modeling problem easier by working on the problem in the lower-dimensional space. However, it constrains the music that can be generated to being a specific sequence of notes and a fixed set of instruments to render with. In parallel, researchers have been pursuing the nonsymbolic approach, where they try to produce music directly as a piece of audio. This makes the problem more challenging, as the space of raw audio is extremely high dimensional with a high amount of information content to model. There has been some success, with models producing piano pieces either in the raw audio domain (Oord et al., 2016; Mehri et al., 2017; Yamamoto et al., 2020) or in the spec tr ogram domain (Vasquez & Lewis, 2019). The key bottleneck is that modeling the raw audio directly introduces extremely long-range dependencies, making it computationally challenging to learn the high-level semantics of music. A way to reduce the difficulty is to learn a lower-dimensional encoding of the audio with the goal of losing the less important information but retaining most of the musical information. This approach has demonstrated some success in generating short instrumental pieces restricted to a set of a few instruments (Oord et al., 2017; Dieleman et al., 2018).
生成式模型也被应用于音乐生成任务。早期模型以钢琴卷帘形式符号化生成音乐,通过指定每个音符的时序、音高、力度和演奏乐器来实现 (Yang et al., 2017; Dong et al., 2018; Huang et al., 2019a; Payne, 2019; Roberts et al., 2018; Wu et al., 2019)。符号化方法通过在低维空间处理问题简化了建模难度,但会限制生成音乐必须由特定音符序列和固定乐器组构成。与此同时,研究者们也在探索非符号化方法,试图直接生成音频形式的音乐片段。这使得问题更具挑战性,因为原始音频空间维度极高且需建模的信息量巨大。已有部分成功案例,包括在原始音频域生成钢琴曲目 (Oord et al., 2016; Mehri et al., 2017; Yamamoto et al., 2020) 或在频谱图域生成音乐 (Vasquez & Lewis, 2019)。关键瓶颈在于直接建模原始音频会引入超长程依赖关系,使得学习音乐高级语义面临巨大计算挑战。降低难度的方法之一是学习音频的低维编码,目标是舍弃次要信息而保留大部分音乐信息。该方法已在生成限定少数乐器的短篇器乐作品方面取得一定成功 (Oord et al., 2017; Dieleman et al., 2018)。
In this work, we show that we can use state-of-the-art deep generative models to produce a single system capable of generating diverse high-fidelity music in the raw audio domain, with long-range coherence spanning multiple minutes. Our approach uses a hierarchical VQ-VAE architecture (Razavi et al., 2019) to compress audio into a discrete space, with a loss function designed to retain the maximum amount of musical information, while doing so at increasing levels of compression. We use an auto regressive Sparse Transformer (Child et al., 2019; Vaswani et al., 2017) trained with maximum-likelihood estimation over this compressed space, and also train auto regressive upsamplers to recreate the lost information at each level of compression.
在本研究中,我们展示了如何利用最先进的深度生成模型构建单一系统,该系统能够在原始音频域生成多样化且高保真的音乐,并保持跨越数分钟的长期连贯性。我们的方法采用分层VQ-VAE架构 (Razavi et al., 2019) 将音频压缩至离散空间,其损失函数设计旨在保留最大程度的音乐信息,同时实现逐级增强的压缩效果。我们使用基于最大似然估计训练的自回归稀疏Transformer (Child et al., 2019; Vaswani et al., 2017) 处理该压缩空间,并训练自回归上采样器以重建每个压缩层级丢失的信息。
We show that our models can produce songs from highly diverse genres of music like rock, hip-hop, and jazz. They can capture melody, rhythm, long-range composition, and timbres for a wide variety of instruments, as well as the styles and voices of singers to be produced with the music. We can also generate novel completions of existing songs. Our approach allows the option to influence the generation process: by swapping the top prior with a conditional prior, we can condition on lyrics to tell the singer what to sing, or on midi to control the composition. We release our model weights and training and sampling code at https://github.com/openai/jukebox.
我们证明,该模型能生成摇滚、嘻哈、爵士等高度多样化的音乐风格作品,可捕捉旋律、节奏、长程乐曲结构及各类乐器的音色特征,还能同步生成与音乐匹配的歌手演唱风格和人声。此外,该模型能对现有歌曲进行创新性续写。我们的方法支持通过生成干预:将顶层先验替换为条件先验后,既可根据歌词生成对应演唱内容,也能通过MIDI控制乐曲编排。模型权重、训练及采样代码已发布于https://github.com/openai/jukebox。
2. Background
2. 背景
We consider music in the raw audio domain represented as a continuous waveform $\mathbf{x}\in[-1,1]^{T}$ , where the number of samples $T$ is the product of the audio duration and the sampling rate typically ranging from $16\mathrm{kHz}$ to $48\mathrm{kHz}$ . For music, CD quality audio, $44.1~\mathrm{kHz}$ samples stored in 16 bit precision, is typically enough to capture the range of frequencies perceptible to humans. As an example, a fourminute-long audio segment will have an input length of ${\sim}10$ million, where each position can have 16 bits of information. In comparison, a high-resolution RGB image with $1024\times$ 1024 pixels has an input length of ${\sim}3$ million, and each position has 24 bits of information. This makes learning a generative model for music extremely computationally demanding with increasingly longer durations; we have to capture a wide range of musical structures from timbre to global coherence while simultaneously modeling a large amount of diversity.
我们考虑将原始音频域中的音乐表示为连续波形 $\mathbf{x}\in[-1,1]^{T}$ ,其中样本数 $T$ 是音频时长与采样率 (通常为 $16\mathrm{kHz}$ 到 $48\mathrm{kHz}$) 的乘积。对于音乐而言,CD音质的音频 (以16位精度存储的 $44.1~\mathrm{kHz}$ 采样) 通常足以覆盖人类可感知的频率范围。例如,一段四分钟的音频片段输入长度约为1000万,其中每个位置可携带16位信息。相比之下,一张 $1024\times$ 1024像素的高分辨率RGB图像输入长度约为300万,每个位置包含24位信息。这使得学习音乐生成模型在时长增加时对计算资源的需求极高——我们不仅需要捕捉从音色到全局连贯性的广泛音乐结构,还需同时建模大量多样性。
2.1. VQ-VAE
2.1. VQ-VAE
To make this task feasible, we use the VQ-VAE (Oord et al., 2017; Dieleman et al., 2018; Razavi et al., 2019) to compress rVaQw -aVuAdiEo lteoa ar nlso twoe re-ndicomdeen saino nianlp supt asceeq. uAe nocnee $\mathbf{x}=\langle\mathbf{x}_ {t}\rangle_{t=1}^{T}$ using a sequence of discrete tokens $\mathbf{z}=\langle z_{s}\in[K]\rangle_{s=1}^{S}$ where $K$ denotes the vocabulary size and we call the ratio $T/S$ des $\mathbf{x}$ into a sequence of latent vectors $\mathbf{h}=\langle\mathbf{h}_ {s}\rangle_{s=1}^{S}$ $E(\mathbf{x})$ tao biottst l nee nae rce ks tt hvaetc tqoura $\mathbf{e}_ {z_{s}}$ efsr $\mathbf{h}_ {s}\mapsto\mathbf{e}_ {z_{s}}$ bboyo km $C={\mathbf{e}_ {k}}_ {k=1}^{K}$ $\mathbf{h}_{s}$ and a decoder that decodes the embedding vectors back to the input space. It is thus an auto-encoder with a disc ret iz ation bottleneck. The VQ-VAE is trained using the following objective:
为了使这一任务可行,我们使用VQ-VAE (Oord et al., 2017; Dieleman et al., 2018; Razavi et al., 2019) 将rVaQw -aVuAdiEo lteoa ar nlso twoe re-ndicomdeen saino nianlp supt asceeq. uA nocnee $\mathbf{x}=\langle\mathbf{x}_ {t}\rangle_{t=1}^{T}$ 压缩为离散token序列 $\mathbf{z}=\langle z_{s}\in[K]\rangle_{s=1}^{S}$ ,其中 $K$ 表示词汇表大小,我们将比率 $T/S$ 称为des $\mathbf{x}$ 转化为潜在向量序列 $\mathbf{h}=\langle\mathbf{h}_ {s}\rangle_{s=1}^{S}$ 。通过编码器 $E(\mathbf{x})$ tao biottst l nee nae rce ks tt hvaetc tqoura $\mathbf{e}_ {z_{s}}$ efsr $\mathbf{h}_ {s}\mapsto\mathbf{e}_ {z_{s}}$ bboyo km $C={\mathbf{e}_ {k}}_ {k=1}^{K}$ $\mathbf{h}_{s}$ 和解码器将嵌入向量解码回输入空间。因此,它是一个带有离散化瓶颈的自编码器。VQ-VAE使用以下目标进行训练:

where sg denotes the stop-gradient operation, which passes zero gradient during back propagation. The reconstruction loss $\mathcal{L}_ {\mathrm{recons}}$ penalizes for the distance between the input $\mathbf{x}$ and the reconstructed output $\widehat{\mathbf{x}}=D(\mathbf{e}_ {z})$ , and $\mathcal{L}_ {\mathrm{codebook}}$ penalizes the codebook for the d isbtance between the encodings $\mathbf{h}$ and their nearest neighbors $\mathbf{e}_ {z}$ from the codebook. To stabilize the encoder, we also add $\mathcal{L}_ {\mathrm{{commit}}}$ to prevent the encodings from fluctuating too much, where the weight $\beta$ controls the amount of contribution of this loss. To speed up training, the codebook loss $\mathcal{L}_{\mathrm{codebook}}$ instead uses EMA updates over the codebook variables. Razavi et al. (2019) extends this to a hierarchical model where they train a single encoder and decoder but break up the latent sequence $\mathbf{h}$ into a multi-level representation $[\mathbf{h}^{(\bar{1})},\cdot\cdot\cdot,\mathbf{h}^{(L)}]$ with decreasing sequence lengths, each learning its own codebook $C^{(l)}$ . They use non-auto regressive encoder-decoders and jointly train all levels with a simple mean-squared loss.
其中sg表示停止梯度操作,在反向传播过程中传递零梯度。重建损失$\mathcal{L}_ {\mathrm{recons}}$惩罚输入$\mathbf{x}$与重建输出$\widehat{\mathbf{x}}=D(\mathbf{e}_ {z})$之间的距离,而$\mathcal{L}_ {\mathrm{codebook}}$惩罚编码$\mathbf{h}$与其在码本中的最近邻$\mathbf{e}_ {z}$之间的距离。为了稳定编码器,我们还添加了$\mathcal{L}_ {\mathrm{{commit}}}$以防止编码波动过大,其中权重$\beta$控制该损失的贡献量。为加速训练,码本损失$\mathcal{L}_{\mathrm{codebook}}$改为对码本变量使用EMA更新。Razavi等人(2019)将其扩展为分层模型,训练单一编码器和解码器,但将潜在序列$\mathbf{h}$分解为多级表示$[\mathbf{h}^{(\bar{1})},\cdot\cdot\cdot,\mathbf{h}^{(L)}]$(序列长度递减),每级学习自己的码本$C^{(l)}$。他们采用非自回归编码器-解码器,并通过简单均方损失联合训练所有层级。
3. Music VQ-VAE
3. Music VQ-VAE
Inspired by the results from the hierarchical VQ-VAE model (Razavi et al., 2019) for images, we consider applying the same technique to model raw audio using three different levels of abstraction, as illustrated in Figure 1. At each level, we use residual networks consisting of WaveNet-style noncausal 1-D dilated convolutions, interleaved with downsampling and upsampling 1-D convolutions to match different hop lengths. A detailed description of the architecture is provided in Appendix B.1. We make a number of modifications to our VQ-VAE compared to the ones in (Oord et al., 2017; Razavi et al., 2019), as described in the following subsections.
受图像分层VQ-VAE模型(Razavi等人,2019)研究结果的启发,我们考虑将相同技术应用于原始音频建模,采用如图1所示的三个抽象层级。每个层级使用由WaveNet风格非因果一维扩张卷积构成的残差网络,并通过下采样和上采样一维卷积交错匹配不同跳跃长度。架构详细说明见附录B.1。相较于(Oord等人,2017;Razavi等人,2019)中的模型,我们对VQ-VAE进行了若干改进,具体如下文所述。
3.1. Random restarts for embeddings
3.1. 嵌入 (embeddings) 的随机重启
VQ-VAEs are known to suffer from codebook collapse, wherein all encodings get mapped to a single or few embedding vectors while the other embedding vectors in the codebook are not used, reducing the information capacity of the bottleneck. To prevent this, we use random restarts: when the mean usage of a codebook vector falls below a threshold, we randomly reset it to one of the encoder outputs from the current batch. This ensures all vectors in the codebook are being used and thus have a gradient to learn from, mitigating codebook collapse.
VQ-VAE 存在码本坍塌 (codebook collapse) 问题,即所有编码都被映射到单个或少数嵌入向量,而码本中的其他嵌入向量未被使用,从而降低了瓶颈层的信息容量。为防止这一问题,我们采用随机重启机制:当码本向量的平均使用率低于阈值时,将其随机重置为当前批次中的某个编码器输出。这确保码本中所有向量都能被使用并获取梯度更新,从而缓解码本坍塌。
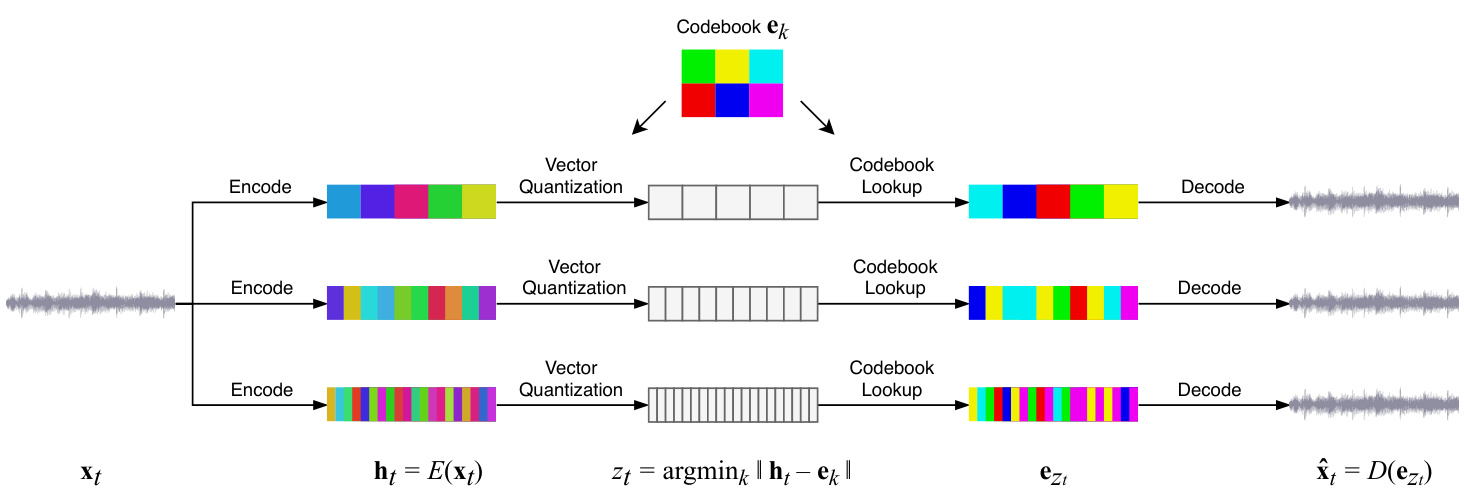
Figure 1. We first train three separate VQ-VAE models with different temporal resolutions. At each level, the input audio is segmented and encoded into latent vectors $\mathbf{h}_ {t}$ , which are then quantized to the closest codebook vectors $\mathbf{e}_ {z_{t}}$ . The code $z_{t}$ is a discrete representation of the audio that we later train our prior on. The decoder takes the sequence of codebook vectors and reconstructs the audio. The top level learns the highest degree of abstraction, since it is encoding longer audio per token while keeping the codebook size the same. Audio can be reconstructed using the codes at any one of the abstraction levels, where the least abstract bottom-level codes result in the highest-quality audio, as shown in Figure 4. For the detailed structure of each component, see Figure 7.
图 1: 我们首先训练三个具有不同时间分辨率的独立VQ-VAE模型。在每一层级,输入音频被分割并编码为潜在向量$\mathbf{h}_ {t}$,随后量化为最接近的码本向量$\mathbf{e}_ {z_{t}}$。代码$z_{t}$是音频的离散表示,后续将作为先验训练的基础。解码器接收码本向量序列并重建音频。顶层学习最高程度的抽象,因为它在保持码本大小不变的情况下,每个token编码更长的音频片段。如图4所示,使用任一抽象层级的代码均可重建音频,其中抽象程度最低的底层代码可生成最高质量的音频。各组件详细结构参见图7。
3.2. Separated Auto encoders
3.2. 分离式自编码器
When using the hierarchical VQ-VAE from (Razavi et al., 2019) for raw audio, we observed that the bottle necked top level is utilized very little and sometimes experiences a complete collapse, as the model decides to pass all information through the less bottle necked lower levels. To maximize the amount of information stored at each level, we simply train separate auto encoders with varying hop lengths. Discrete codes from each level can be treated as independent encodings of the input at different levels of compression.
在使用 (Razavi et al., 2019) 提出的分层VQ-VAE处理原始音频时,我们观察到瓶颈顶层利用率极低,有时甚至完全崩溃,因为模型选择将所有信息通过瓶颈较小的底层传递。为了最大化每层存储的信息量,我们直接训练具有不同跳跃长度的独立自编码器。每层的离散编码可视为输入在不同压缩层级下的独立表征。
3.3. Spectral Loss
3.3. 频谱损失 (Spectral Loss)
When using only the sample-level reconstruction loss, the model learns to reconstruct low frequencies only. To capture mid-to-high frequencies, we add a spectral loss which is defined as
当仅使用样本级重建损失时,模型仅学习重建低频信号。为捕捉中高频信号,我们增加了频谱损失,其定义为
$$
\mathcal{L}_ {\mathrm{spec}}=\Vert|\mathrm{STFT}(\mathbf{x})|-|\mathrm{STFT}(\widehat{\mathbf{x}})|\Vert_{2}
$$
$$
\mathcal{L}_ {\mathrm{spec}}=\Vert|\mathrm{STFT}(\mathbf{x})|-|\mathrm{STFT}(\widehat{\mathbf{x}})|\Vert_{2}
$$
It encourages the model to match the spectral components without paying attention to phase which is more difficult to learn. This is similar to the use of power loss (Oord et al., 2018) and spectral convergence (Arık et al., 2018b) when training parallel decoders for raw audio. One difference between the latter approach and ours is that we are no longer optimizing the spectral signal-to-noise ratio; dividing by the magnitude of the signal results in numerical instability for mostly silent inputs. To prevent the model from over fitting to a particular choice of the STFT parameters, we use the sum of the spectral losses $\mathcal{L}_{\mathrm{spec}}$ calculated over multiple STFT parameters that trade-off time and frequency resolutions (Yamamoto et al., 2020).
它鼓励模型匹配频谱成分而忽略更难学习的相位信息,这与训练原始音频并行解码器时使用的功率损失 (Oord et al., 2018) 和频谱收敛 (Arık et al., 2018b) 方法类似。后一种方法与我们的主要区别在于:我们不再优化频谱信噪比,因为对静默占主导的输入信号进行幅度除法会导致数值不稳定。为防止模型对特定STFT参数选择过拟合,我们采用多组STFT参数计算频谱损失 $\mathcal{L}_{\mathrm{spec}}$ 的总和 (Yamamoto et al., 2020) ,这些参数在时间分辨率和频率分辨率之间进行权衡。
4. Music Priors and Upsamplers
4. 音乐先验与上采样器
After training the VQ-VAE, we need to learn a prior $p(\mathbf{z})$ over the compressed space to generate samples. We break up the prior model as
训练完 VQ-VAE 后,我们需要在压缩空间上学习一个先验 $p(\mathbf{z})$ 来生成样本。我们将先验模型分解为
$$
\begin{array}{r l}&{p(\mathbf{z})=p(\mathbf{z}^{\mathrm{{top}}},\mathbf{z}^{\mathrm{{middle}}},\mathbf{z}^{\mathrm{{bottom}}})}\ &{\qquad=p(\mathbf{z}^{\mathrm{{top}}})p(\mathbf{z}^{\mathrm{{middle}}}|\mathbf{z}^{\mathrm{{top}}})p(\mathbf{z}^{\mathrm{{bottom}}}|\mathbf{z}^{\mathrm{{middle}}},\mathbf{z}^{\mathrm{{top}}})}\end{array}
$$
$$
\begin{array}{r l}&{p(\mathbf{z})=p(\mathbf{z}^{\mathrm{{top}}},\mathbf{z}^{\mathrm{{middle}}},\mathbf{z}^{\mathrm{{bottom}}})}\ &{\qquad=p(\mathbf{z}^{\mathrm{{top}}})p(\mathbf{z}^{\mathrm{{middle}}}|\mathbf{z}^{\mathrm{{top}}})p(\mathbf{z}^{\mathrm{{bottom}}}|\mathbf{z}^{\mathrm{{middle}}},\mathbf{z}^{\mathrm{{top}}})}\end{array}
$$
and train separate models for the top-level prior $p(\mathbf{z}^{\mathrm{top}})$ , and upsamplers $p(\mathbf{z}^{\mathrm{midle}}|\mathbf{z}^{\mathrm{top}})$ and $p\big(\mathbf{z}^{\mathrm{bottom}}\big|\mathbf{z}^{\mathrm{middle}},\mathbf{z}^{\mathrm{top}}\big)$ . Each of these is an auto regressive modeling problem in the discrete token space produced by the VQ-VAE. We use Transformers with sparse attention (Vaswani et al., 2017; Child et al., 2019) as they are currently the SOTA in auto regressive modeling. We propose a simplified version which we call the Scalable Transformer, that is easier to implement and scale (see Appendix A for details).
并为顶层先验 $p(\mathbf{z}^{\mathrm{top}})$ 、上采样器 $p(\mathbf{z}^{\mathrm{midle}}|\mathbf{z}^{\mathrm{top}})$ 以及 $p\big(\mathbf{z}^{\mathrm{bottom}}\big|\mathbf{z}^{\mathrm{middle}},\mathbf{z}^{\mathrm{top}}\big)$ 分别训练独立模型。这些均属于VQ-VAE生成的离散token空间中的自回归建模问题。我们采用带稀疏注意力机制的Transformer (Vaswani et al., 2017; Child et al., 2019) ,因其在自回归建模领域当前具有最先进(SOTA)性能。我们提出了一种简化版本,称为可扩展Transformer (Scalable Transformer) ,该架构更易于实现和扩展 (详见附录A)。
For the upsamplers, we need to provide the autoregressive Transformers with conditioning information from the codes of the upper levels. To do so, we use a deep residual WaveNet (Xie et al., 2017) followed by an upsampling strided convolution and a layer norm (Ba et al., 2016), and add the output as extra positional information to the embeddings of the current level. We condition the lower levels only on the chunk of upper level codes that correspond to the same segment of raw audio.
对于上采样器,我们需要向自回归Transformer提供来自上层编码的条件信息。为此,我们使用深度残差WaveNet (Xie et al., 2017) ,后接一个步进卷积上采样层和层归一化 (Ba et al., 2016) ,并将输出作为额外位置信息添加到当前层级的嵌入中。我们仅将下层条件约束在与原始音频相同片段对应的上层编码块上。
At each level, we use Transformers over the same context length of discrete codes, which correspond to increasing the raw audio length with larger hop lengths, and modeling longer temporal dependencies at the higher levels while keeping the same computational footprint for training each level. As our VQ-VAE is convolutional, we can use the same VQ-VAE to produce codes for arbitrary lengths of audio.
在每一层级,我们都在相同上下文长度的离散编码上使用Transformer,这对应于通过更大的跳跃长度增加原始音频长度,并在更高层级建模更长的时间依赖性,同时保持训练每个层级的计算量不变。由于我们的VQ-VAE是卷积结构,因此可以对任意长度的音频使用同一个VQ-VAE生成编码。
4.1. Artist, Genre, and Timing Conditioning
4.1. 艺术家、流派与时间条件控制
Our generative model can be made more controllable by providing additional conditioning signals while training. For our first models, we provide artist and genre labels for the songs. This has two advantages: first, it reduces the entropy of the audio prediction, so the model is able to achieve better quality in any particular style. Second, at generation time, we are able to steer the model to generate in a style of our choosing. Additionally, we attach a timing signal for each segment at training time. This signal includes the total duration of the piece, the start time of that particular sample and how much fraction of the song that has elapsed. This allows the model to learn audio patterns that depend on the overall structure, such as spoken or instrumental introductions and applause at the end of a piece.
通过在训练过程中提供额外的条件信号,我们可以使生成式模型更具可控性。对于我们的首批模型,我们为歌曲提供了艺术家和流派标签。这带来两个优势:首先,它降低了音频预测的熵值,使模型能在特定风格中实现更高质量的输出;其次,在生成阶段,我们可以引导模型按照选定的风格进行创作。此外,我们在训练时为每个片段附加了时序信号,该信号包含乐曲总时长、当前样本的起始时间以及歌曲已播放的比例。这使得模型能够学习依赖于整体结构的音频模式,例如口语或器乐前奏,以及曲末的掌声段落。
4.2. Lyrics Conditioning
4.2. 歌词条件化
While the conditioned models above are able to generate songs of diverse genres and artistic styles, singing voices generated by those models, while often sung in a compelling melody, are mostly composed of babbling, rarely producing recognizable English words. In order to be able to control the generative model with lyrics, we provide more context at training time by conditioning the model on the lyrics corresponding to each audio segment, allowing the model to produce singing si multan eos ly with the music.
虽然上述条件模型能够生成多种流派和艺术风格的歌曲,但这些模型生成的歌声虽然旋律动人,却大多由无意义的音节组成,很少能产生可识别的英文单词。为了让生成模型能够根据歌词进行控制,我们在训练时通过将每段音频对应的歌词作为条件输入,为模型提供更多上下文信息,使其能够同时生成与音乐同步的演唱内容。
Lyrics-to-singing (LTS) task: The conditioning signal only includes the text of the lyrics, without timing or vocalisation information. We thus have to model the temporal alignment of lyrics and singing, the artists voice and also the diversity of ways one can sing a phrase depending on the pitch, melody, rhythm and even genre of the song. The conditioning data isn’t precise as the lyrics data often contains textual references to repeated sections like “chorus” or mismatching portions of lyrics with the corresponding music. There is also no separation between lead vocals, accompanying vocals and the background music in target audio. This makes the Lyrics-to-singing (LTS) task significantly more challenging than the corresponding Text-to-speech (TTS) task.
歌词转歌唱 (LTS) 任务:条件信号仅包含歌词文本,不包含时间或发声信息。因此,我们必须对歌词与歌唱的时间对齐、歌手声音以及根据音高、旋律、节奏甚至歌曲流派等因素演唱一个乐句的多样性进行建模。由于歌词数据通常包含对重复部分(如"副歌")的文本引用,或歌词与相应音乐不匹配的部分,因此条件数据并不精确。目标音频中也没有主唱、伴唱和背景音乐的分离。这使得歌词转歌唱 (LTS) 任务比相应的文本转语音 (TTS) 任务更具挑战性。
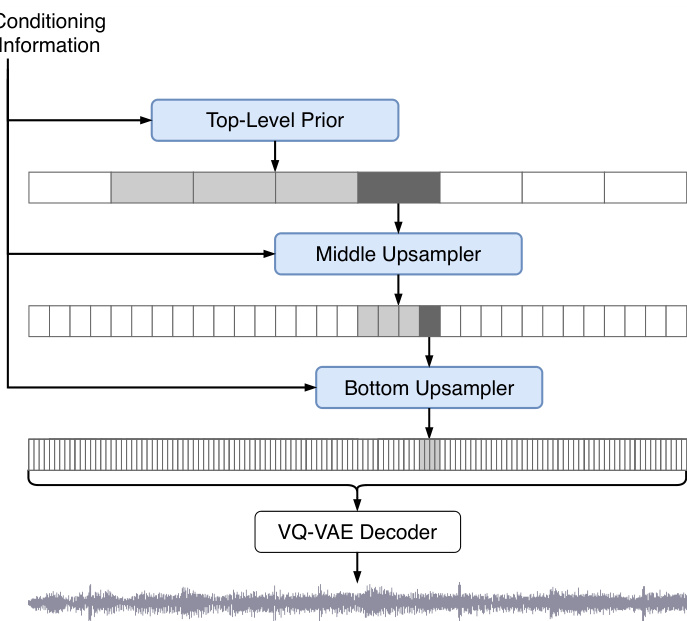
Providing lyrics for chunks of audio: Our dataset includes song-level lyrics, but to make the task easier we train on shorter $(24sec)$ chunks of audio. To provide the lyrics cor(a) Ancestral sampling: Priors for the VQ-VAE codes are trained using a cascade of Transformer models, shown in blue. Each model takes conditioning information such as genre, artist, timing, and lyrics, and the upsampler models are also conditioned on the codes from the upper levels. To generate music, the VQ-VAE codes are sampled from top to bottom using the conditioning information for control, after which the VQ-VAE decoder can convert the bottom-level codes to audio.
为音频片段提供歌词:我们的数据集包含歌曲级别的歌词,但为了简化任务,我们使用较短的$(24秒)$音频片段进行训练。为确保歌词与音频对齐,(a) 祖先采样:VQ-VAE编码的先验通过一系列Transformer模型(蓝色部分)进行训练。每个模型接收流派、艺术家、时间信息和歌词等条件输入,上采样模型还受到上层编码的条件约束。生成音乐时,VQ-VAE编码会自上而下地根据控制条件进行采样,随后VQ-VAE解码器可将底层编码转换为音频。

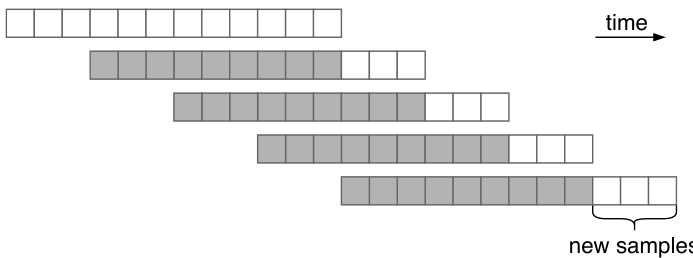

(b) Windowed sampling: To generate music longer than the model’s context length (12 in this figure), we repeatedly sample continuations at each level, using overlapping windows of previous codes as the context. The overlap amount is a hyper parameter, and the figure shows an example of $75%$ overlap with hop length 3.
(b) 窗口采样 (Windowed sampling): 为了生成超出模型上下文长度 (图中为12) 的音乐片段,我们在每个层级重复采样后续内容,使用重叠的先前编码片段作为上下文。重叠量是一个超参数,图中展示了重叠率为 $75%$ 、跳跃长度为3的示例。
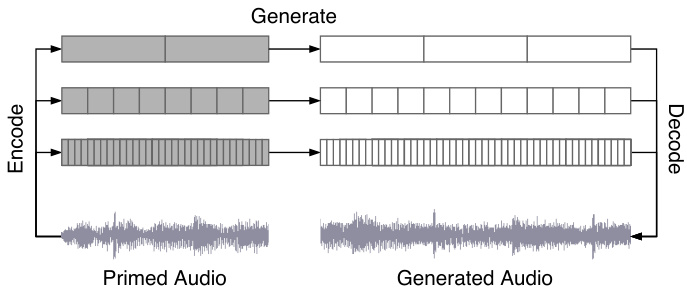
Figure 2. Sampling methods for generating music
图 2: 生成音乐的采样方法
(c) Primed sampling: The model can generate continuations of an existing audio signal by converting it into the VQ-VAE codes and sampling the subsequent codes in each level.
(c) Primed采样:模型可通过将现有音频信号转换为VQ-VAE编码并逐级采样后续编码,生成音频信号的延续部分。
responding to the audio during training, we began with a simple heuristics of aligning the characters of the lyrics to linearly span the duration of each song, and pass a fixed-side window of characters centered around the current segment during training. While this simple strategy of linear alignment worked surprisingly well, we found that it fails for certain genres such as hip-hop with fast lyrics. To address this, we use Spleeter (Hennequin et al., 2019) to extract vocals from each song and run NUS Auto Lyrics Align (Gupta et al., 2020) on the extracted vocals to obtain a word-level alignments of the lyrics, allowing us to more accurately provide the lyrics for a given chunk of audio. We choose a large enough window so that the actual lyrics have a high probability of being inside the window.
在训练过程中响应音频时,我们最初采用了一种简单的启发式方法:将歌词字符线性对齐至每首歌曲的时长范围,并在训练时传递一个以当前片段为中心、固定大小的字符窗口。虽然这种线性对齐策略效果出奇地好,但我们发现它对某些音乐类型(如歌词速度快的嘻哈音乐)会失效。为此,我们使用 Spleeter [Hennequin et al., 2019] 从每首歌中提取人声,并在提取的人声上运行 NUS Auto Lyrics Align [Gupta et al., 2020] 来获取歌词的词级对齐结果,从而能更准确地为给定音频片段提供歌词。我们选择了足够大的窗口,确保实际歌词有很高概率出现在窗口内。
Encoder-decoder model: We use an encoder-decoder style model to condition on the characters of the lyrics, with the encoder producing features from the lyrics which are attended to by the decoder which produces the top level music tokens. The lyrics encoder is a Transformer with an auto regressive modeling loss for lyrics, and its last level is used as features of the lyrics. In the music decoder, we interleave a few additional layers with encoder-decoder attention where the queries from the music tokens are only allowed to attend to keys and values from the lyrics tokens. These layers attend on the activation from the last layer of the lyrics encoder (see Figure 8c). In Figure 3, we see that the attention pattern learned by one of these layers corresponds to the alignment between the lyrics and the singing.
编码器-解码器模型:我们采用编码器-解码器架构的模型来处理歌词字符,编码器从歌词中提取特征,解码器则基于这些特征生成顶层的音乐Token。歌词编码器是一个带有自回归建模损失的Transformer,其最后一层的输出作为歌词特征。在音乐解码器中,我们穿插了几层额外的编码器-解码器注意力机制,其中来自音乐Token的查询仅允许关注歌词Token的键和值。这些注意力层作用于歌词编码器最后一层的激活(见图8c)。图3显示,其中一层学习到的注意力模式与歌词和演唱的对齐关系相对应。
4.3. Decoder Pre training
4.3. 解码器预训练
To reduce computation required to train the lyrics conditional model, we use a pretrained unconditional top-level prior as our decoder and introduce the lyrics encoder using model surgery (Berner et al., 2019). We initialize the output projection weights in the MLP and the attention layers of these residual blocks to zeros (Zhang et al., 2019a), so that the added layers perform the identity function at initialization. Thus, at initialization the model behaves identically as the pretrained decoder, but there is still a gradient with respect to the encoder state and parameters 2, allowing the model to learn to use the encoder.
为减少训练歌词条件模型所需的计算量,我们采用预训练的无条件顶层先验作为解码器,并通过模型手术 (Berner et al., 2019) 引入歌词编码器。我们将MLP中的输出投影权重及这些残差块注意力层的参数初始化为零 (Zhang et al., 2019a) ,从而使新增层在初始化时执行恒等函数。因此模型在初始化阶段表现与预训练解码器完全一致,但编码器状态和参数仍能获得梯度 2,使模型得以学习编码器的使用方式。
4.4. Sampling
4.4. 采样
After we have trained our VQ-VAE, upsamplers, and top level priors, we can then use them to sample novel songs.
在我们训练完VQ-VAE、上采样器和顶层先验后,就可以用它们来生成新歌曲了。
Ancestral sampling: We first generate the top level codes one token at a time by the usual ancestral sampling process (see Figure 2a): generating the first token, then passing all previously generated tokens into the model as inputs and outputting the next token conditioned on all previous tokens. We then run our conditioning wavenet on the top level codes to produce the conditioning information for the middle level and sample ancestral ly from it too, and do the same for the bottom level.
祖先采样 (ancestral sampling) : 我们首先通过常规的祖先采样过程逐token生成顶层代码 (参见图2a) : 生成第一个token后, 将所有已生成的token作为模型输入, 基于先前所有token输出下一个token。随后在顶层代码上运行条件WaveNet生成中层条件信息, 并同样进行祖先采样, 底层也采用相同处理流程。
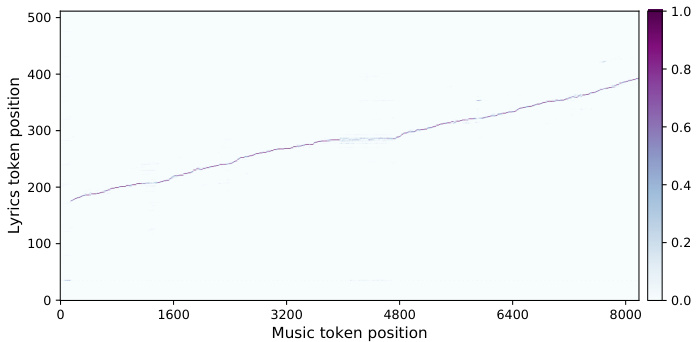
Figure 3. Lyrics-singing alignment learned by one of the encoderdecoder attention layers. The $_x$ -axis is the position of music queries, and the $y$ -axis is the position of lyric keys. The positions attended to by the decoder correspond to the characters being sung.
图 3: 由某个编码器-解码器注意力层学习到的歌词-演唱对齐关系。横轴 ($_x$ 轴) 表示音乐查询的位置,纵轴 ($y$ 轴) 表示歌词键的位置。解码器所关注的位置对应正在演唱的字符。
Windowed sampling: To sample segments longer than the context length, we use windowed sampling, where we move ahead our sampling window by half our context and continue sampling conditioned on this half context (See Figure 2b). We can trade off speed for quality by using a smaller hop length here.
窗口采样:为了采样超过上下文长度的片段,我们采用窗口采样方法,将采样窗口向前移动半个上下文长度,并基于这半个上下文继续采样(见图 2b)。通过使用较小的跳跃长度,可以在速度和质量之间进行权衡。
Primed sampling: Instead of sampling the entire token sequence from the model, we can also run a forward pass of the VQ-VAE to obtain the top, middle, and bottom level codes corresponding to a segment from an actual song, as shown in Figure 2c. We can use these as the initial tokens in our ancestral sampling process and continue sampling from these to produce novel completions of the song.
预采样 (Primed sampling):不同于从模型中采样整个token序列,我们还可以通过VQ-VAE的前向传递获取实际歌曲片段对应的高、中、底层编码 (如 图2c 所示)。这些编码可作为祖先采样过程的初始token,并继续从中采样以生成歌曲的新续写片段。
5. Experiments
5. 实验
5.1. Dataset
5.1. 数据集
We scraped a new dataset of 1.2 million songs (600k of which in English), paired with the lyrics and metadata from LyricWiki (LyricWiki). The metadata includes artist, album, genre, and year of the release, along with common moods or playlist keywords associated with each song. We train on 32 bit, $44.1\mathrm{kHz}$ raw audio and perform data augmentation by randomly downmixing the right and left channels to produce mono channel audio.
我们爬取了一个包含120万首歌曲的新数据集(其中60万首为英文歌曲),并与LyricWiki的歌词和元数据配对。元数据包括艺术家、专辑、流派、发行年份,以及每首歌关联的常见情绪或播放列表关键词。我们使用32位、44.1kHz原始音频进行训练,并通过随机下混左右声道生成单声道音频来实现数据增强。
5.2. Training Details
5.2. 训练细节
For the music VQ-VAE, we use 3 levels of bottlenecks compressing $44~\mathrm{kHz}$ audio in dimensionality by 8x, $32\mathbf{x}$ , and
对于音乐VQ-VAE,我们使用3层瓶颈结构,将44 kHz音频的维度分别压缩8倍、32倍和
$128\mathbf{X}$ respectively, with a codebook size of 2048 for each level. The VQ-VAE has 2 million parameters and is trained on 9-second audio clips on $256\mathrm{V100}$ for 3 days. We used exponential moving average to update the codebook following Razavi et al. (2019). For our prior and upsampler models, we use a context of 8192 tokens of VQ-VAE codes, which corresponds to approximately 24, 6, and 1.5 seconds of raw audio at the top, middle, and bottom level, respectively. The upsamplers have one billion parameters and are trained on $128~\mathrm{V100s}$ for 2 weeks, and the top-level prior has 5 billion parameters and is trained on $512\mathrm{V100s}$ for 4 weeks. We use Adam with learning rate 0.00015 and weight decay of 0.002. For lyrics conditioning, we reuse the prior and add a small encoder, after which we train the model on 512 V100s for 2 weeks. The detailed hyper parameters for our models and training are provided in Appendix B.3.
$128\mathbf{X}$,每个级别的码本大小为2048。VQ-VAE包含200万个参数,并在$256\mathrm{V100}$上对9秒音频片段进行了3天的训练。我们采用Razavi等人(2019)提出的指数移动平均方法更新码本。对于先验模型和上采样模型,我们使用8192个VQ-VAE编码token作为上下文,分别对应顶层、中层和底层约24秒、6秒和1.5秒的原始音频。上采样器具有10亿参数,在$128~\mathrm{V100s}$上训练了2周;顶层先验模型包含50亿参数,在$512\mathrm{V100s}$上训练了4周。我们使用学习率为0.00015、权重衰减为0.002的Adam优化器。对于歌词条件生成,我们复用先验模型并添加小型编码器,随后在512块V100上训练了2周。模型和训练的详细超参数见附录B.3。
5.3. Samples
5.3. 样本
We trained a sequence of models with increasing sample quality. Our first model was trained on the MAESTRO dataset using $22\mathrm{kHz}$ VQ-VAE codes and relatively small prior models. We observed that this could generate high fidelity classical music samples with piano and occasional violin. We then collected a larger and more diverse dataset of songs with genre and artist labels. The same model when trained on this new dataset was able to produce diverse samples other than classical music, and demonstrated musicality and coherence over more than a minute.
我们训练了一系列样本质量逐步提升的模型。首个模型基于MAESTRO数据集训练,使用22kHz VQ-VAE编码和相对较小的先验模型。实验发现该模型可生成带有钢琴和偶尔小提琴的高保真古典音乐样本。随后我们收集了更大规模、风格与艺术家标签更丰富的歌曲数据集。同一模型在新数据集上训练后,不仅能生成古典音乐外的多样化样本,还展现出超过一分钟的音乐性与连贯性。
Despite the novelty of being able to generate generally high fidelity and coherent songs, sample quality was still limited by a number of factors. First, the use of $22\mathrm{kHz}$ sampling rate along with small upsamplers introduced noise both in the upsampling and decoding steps, which we hear as grainy texture. We improved fidelity by using $44~\mathrm{{kHz}}$ VQ-VAE and 1B parameter upsamplers in all subsequent experiments at the expense of longer rendering time.
尽管能够生成总体上高保真且连贯的歌曲具有新颖性,但样本质量仍受多种因素限制。首先,使用22kHz采样率和小型上采样器在上采样和解码步骤中引入了噪声,表现为颗粒感音质。我们在后续所有实验中改用44kHz VQ-VAE和10亿参数上采样器以提高保真度,但代价是渲染时间延长。
Second, the 1B top-level prior was not big enough to produce singing and diverse musical timbres. We first explored increasing the model size to 5 billion parameters. Larger capacity allowed better modeling of the broader distribution of songs, resulting in samples with better musicality, longer coherence and initial singing. While there is an overall qualitative improvement, the unconditional model still struggled to sing recognizable words. Training a seq2seq model with lyric conditioning and limiting the dataset only to songs primarily in English made singing both intelligible and controllable.
其次,1B规模的顶层先验模型不足以生成歌唱和多样化的音乐音色。我们首先尝试将模型参数量提升至50亿。更大的容量能更好地建模更广泛的歌曲分布,从而生成音乐性更强、连贯性更久且带有初始歌唱的样本。虽然整体质量有所提升,但无条件模型仍难以唱出可识别的歌词。通过训练带有歌词条件的seq2seq模型,并将数据集限制为以英语为主的歌曲后,生成的歌声既清晰又可控。
The final model, which we call Jukebox, uses all these improvements. Because everyone experiences music differently, it is generally tricky and not very meaningful to evaluate samples by the mean opinion score or FID-like metrics. We manually evaluate coherence, musicality, diversity, and novelty of generated samples. The links to curated examples are embedded in text.
我们最终将模型命名为Jukebox,它融合了所有上述改进。由于每个人对音乐的体验各不相同,用平均意见分或类似FID的指标来评估样本通常既复杂又缺乏意义。我们通过人工方式评估生成样本的连贯性、音乐性、多样性和新颖性。精选示例的链接已嵌入文中。
Coherence: We find the samples stay very coherent musically through the context length of the top-level prior (approximate ly 24 seconds), and they maintain similar harmonies and textures as we slide the window to generate longer samples. However, because the top-level does not have the context of the entire song, we do not hear long term musical patterns, and we would never hear choruses or melodies that repeat.
连贯性:我们发现样本在顶级先验 (top-level prior) 的上下文长度(约24秒)内保持了极高的音乐连贯性,当滑动窗口生成更长样本时,它们仍能维持相似的和声与织体。但由于顶级模型不具备整首歌曲的上下文,我们听不到长期音乐模式,也永远不会出现重复的副歌或旋律。
The generations progress through beginnings of songs (for example applause or slow instrumental warm-ups), through sections that sound chorus-like, through instrumental interludes, and then fading or otherwise wrapping up at the end. The top-level prior always knows what fraction of the song is complete time-wise, so it is able to imitate appropriate beginnings, middles and ends.
生成的音乐片段会经历歌曲的各个阶段:开头(如掌声或缓慢的乐器前奏)、类似副歌的段落、乐器间奏,最终以淡出或其他方式收尾。顶层先验始终掌握歌曲时间进度的完成比例,因此能准确模仿恰当的开篇、中段与结尾。
Musicality: The samples frequently imitate familiar musical harmonies and the lyrics are usually set in ways that are very natural. Frequently the highest or longest notes of the melody match words that a human singer would choose to emphasize, and the lyrics are almost always rendered in ways that capture the prosody of the phrases. This is noticeable in hip hop generations, where the model reliably captures the rhythm of spoken text. We do find that the generated melodies are usually less interesting than human composed melodies. In particular, we do not hear the antecedent and consequent pattern familiar to many human melodies, and we rarely hear choruses that are melodically memorable.
音乐性:生成的样本经常模仿熟悉的音乐和声,歌词编排方式通常非常自然。旋律的最高音或最长音往往与人类歌手会选择强调的词语相匹配,歌词演绎几乎总能捕捉到短语的韵律。这在嘻哈音乐生成中尤为明显,模型能准确捕捉口语文本的节奏感。但我们发现生成的旋律通常不如人类创作的旋律有趣,特别是缺乏人类旋律中常见的前后呼应模式,且鲜少听到旋律上令人难忘的副歌段落。
Diversity: Likelihood training encourages covering of all modes, so we expect the model to produce diverse samples.
多样性:基于似然的训练鼓励覆盖所有模态,因此我们预期模型能生成多样化的样本。
– Re-renditions: We generate multiple samples conditioned on artist and lyrics combinations that exist in our training data. While occasionally drum and bass lines or melodic intervals echo the original versions, we find that none of the generated samples is noticeably similar to the original songs.
– 重新演绎:我们基于训练数据中存在的艺术家和歌词组合生成多个样本。虽然偶尔生成的鼓点、贝斯线或旋律音程会与原版产生呼应,但我们发现所有生成样本均未出现明显相似于原版歌曲的情况。
We also generate multiple songs conditioned on the same artist and lyrics as Sample 1 to obtain Samples 9–12. All five sound interesting in their own ways with different moods and melodies with Sample 10 playing a harmonic at 00:14 as part of a blues riff, showing that the model has learned a wide range of singing and playing styles.
我们还基于与样本1相同的艺术家和歌词生成了多首歌曲,得到样本9-12。这五首歌曲各具特色,呈现出不同的情绪和旋律:样本10在00:14处弹奏布鲁斯连复段时加入了和声音效,表明该模型已掌握了多样化的演唱及演奏风格。
– Completions: We prime the model with 12 seconds of existing songs and ask it to complete them in the same styles. When the priming samples include singing, the continuations are more likely to imitate the original tunes and rhythms. Songs primed with more generic or common intros tend to be more diverse. Even generated samples that are close to the originals early on deviate completely into new musical material after about 30 seconds.
– 补全:我们用12秒现有歌曲作为提示输入模型,要求其以相同风格完成创作。当提示样本包含人声演唱时,续写部分更倾向于模仿原曲旋律与节奏。使用较通用或常见前奏作为提示的歌曲,其续写结果往往更具多样性。即便早期生成片段与原曲高度接近,约30秒后也会完全偏离至全新音乐素材。
Re-renditions and completions are interesting and diverse, but overall, there is still room for improvement in music quality compared to the original songs.
重渲染和补全结果有趣且多样,但整体音乐质量与原曲相比仍有提升空间。
– Full tree: To understand diversity in a more systematic way, we generate multiple continuations from the same segment. We start with a one-minute sample and independently sample four times per one-minute extension. By the three minute mark, there are 16 completions. We can think of this branching tree as exploring different possibilities obtained by ancestral sampling. In the generated songs in the link, we hear diversity in singing and development even when the same initial segment is used. We note that this particular sample follows the lyrics more successfully than many. For certain genres like hip hop and rap, where linearly moving the window does not yield good lyrics alignment, the chance of obtaining plausible singing is lower.
- 完整树状结构:为了更系统地理解多样性,我们从同一片段生成多个延续版本。初始采用一分钟样本,每分钟扩展部分独立采样四次。到三分钟时会产生16个延续版本。这种分叉树结构可视为通过祖先采样探索不同可能性。在链接的生成歌曲中,即使使用相同初始片段,也能听到演唱风格和发展路径的多样性。需注意该样本比多数版本更成功地遵循了歌词。对于嘻哈和说唱等流派,线性移动窗口无法实现良好歌词对齐,因此获得合理演唱的概率较低。
Novelty: With the ability to condition on various styles, lyrics, and raw audio, we would like Jukebox to be a useful tool for both professional musicians and music enthusiasts alike. In this section, we are interested in exploring capabilities and applications of Jukebox.
创新性:Jukebox能够基于多种风格、歌词和原始音频进行条件生成,我们希望它成为专业音乐人和音乐爱好者的实用工具。本节将重点探索Jukebox的功能与应用场景。
– Novel styles: We generate songs in an unusual genre typically not associated with an artist. In general, we find that it is fairly difficult to generalize to a novel style of singing while using the same voice as the artist embedding overpowers other information. In Joe Bonamassa and Frank Sinatra samples, we hear a modest variation in instrumentation, energy, and ambience depending on the genre embedding. However, our attempts to mix country singer Alan Jackson with unusual genres like hip hop and punk did not seem to move the samples away from a country style in meaningful ways.
- 新颖风格:我们生成了与艺术家通常不相关的非典型流派歌曲。总体而言,我们发现当使用相同的艺术家音色嵌入时,推广到新颖的演唱风格相当困难,因为艺术家嵌入会压制其他信息。在Joe Bonamassa和Frank Sinatra的样本中,我们听到乐器编排、能量和氛围会根据流派嵌入产生适度变化。然而,当我们尝试将乡村歌手Alan Jackson与嘻哈和朋克等非典型流派混合时,样本并未以有意义的方式脱离乡村风格。
– Novel voices: We pick artists whose voices are reproduced reasonably well by the model, and interpolate their style embeddings to synthesize new voices. Some blending, for instance, between Frank Sinatra and Alan Jackson in Sample 4, still sounds similar to Frank Sinatra. In most cases, the model renders in a vaguely recognizable but distinct voice that preserves different vocal attributes. Samples 1 and 2 conditioned on the Céline Dion embeddings divided by two have slightly different timbre and tone but capture her unique vibrato.
- 新颖嗓音:我们选择那些模型能较好还原其声音特色的歌手,通过插值他们的风格嵌入来合成新嗓音。例如样本4中Frank Sinatra与Alan Jackson的混合音色仍接近前者。多数情况下,模型会生成一种隐约可辨但独具特色的声线,同时保留不同发声特征。基于Céline Dion嵌入向量减半处理的样本1和2,虽在音色与音调上略有差异,但完美捕捉了她标志性的颤音技巧。
We also experiment with changing the style embedding in the middle of a song to create a duet (Sample 7). This is another way of guiding generation during sampling. Continuing in another voice works best when the segment ends in an interlude; otherwise, the model blends voices in the middle of a word or a sentence.
我们还尝试在歌曲中途改变风格嵌入来创作二重唱(示例7)。这是在采样过程中引导生成的另一种方式。当段落以间奏结束时,切换另一种声音继续效果最佳;否则模型会在单词或句子中间混合声音。
– Novel lyrics: We ask Jukebox to sing poems and novel verses generated by GPT-2 (Radford et al.) to demonstrate that it can indeed sing new lyrics. While the training data consists of song lyrics with limited vocabulary and constrained structure, the model has learned to follow along most prompts and sing even new words that are reasonably pronounceable (including technical terms from the deep learning literature). To get the best results, however, we find that it is useful to spell out difficult words or acronyms as they are spoken. The generations are noticeably higher quality if the text matches the distribution of lyrics for the given artist, both in terms of length, and of rhyming or rhythmic qualities. For example, hip hop lyrics tend to be longer than most other genres, and the commonly emphasized syllables easily form clear rhythms.
– 新颖歌词:我们要求Jukebox演唱由GPT-2 (Radford et al.)生成的诗歌和小说段落,以证明它确实能演唱新歌词。虽然训练数据由词汇量有限且结构受限的歌曲歌词组成,但该模型已学会跟随大多数提示,甚至演唱合理可发音的新词(包括深度学习文献中的技术术语)。然而,为了获得最佳效果,我们发现拼读出难词或首字母缩略词的发音是有帮助的。如果文本在长度、押韵或节奏特性上与给定艺术家的歌词分布相匹配,生成质量会明显更高。例如,嘻哈歌词往往比其他大多数流派更长,且常强调的音节容易形成清晰的节奏。
– Novel riffs: Another useful application of Jukebox is the ability to record an incomplete idea and explore various continuations without ever needing to tabulate in symbolic representations, which would lose details of timbre and mood. We curate recordings of novel riffs by our in-house musicians and prime the model during sampling. Sample 6 starts with a musical style not widely used in Elton John’s songs. The model still carries out the tune and develops it further. Similarly, the beginning of Sample 1 is a progressive jazz piece with a $5/4$ polymeter, which has never been used in hip hop. Despite this novelty, the rhythm persists throughout the song and is incorporated naturally with rapping.
- 新颖即兴段落:Jukebox的另一实用功能是能录制不完整的音乐创意并探索多种发展可能,无需借助会丢失音色和情绪细节的符号化记谱。我们精选内部音乐人创作的新颖即兴段落录音,在采样阶段为模型提供引导。样本6以埃尔顿·约翰歌曲中罕见的音乐风格开场,模型仍能延续旋律并进一步发展。同样地,样本1开头是一段采用$5/4$复合节拍的先锋爵士乐段,这种节奏从未在嘻哈音乐中出现过。尽管存在这种创新性,该节奏始终贯穿全曲,并与说唱自然融合。
5.4. VQ-VAE Ablations
5.4. VQ-VAE消融实验
Table 1. Reconstruction fidelity degrades with higher compression. Restarting dead codes near random encoder outputs mitigates learning suboptimal codes.
| Level | Hop length | Spectral convergence (dB) | |
| Withoutrestart | Withrestart | ||
| Bottom | 8 | -21.1 | -23.0 |
| Middle | 32 | -12.4 | -12.4 |
| Top | 128 | -8.3 | -8.3 |
表 1: 重建保真度随压缩率提升而下降。在随机编码器输出附近重启失效码可缓解次优编码学习问题。
| 层级 | 跳跃长度 | 频谱收敛 (dB) 无重启 | 频谱收敛 (dB) 有重启 |
|---|---|---|---|
| 底层 | 8 | -21.1 | -23.0 |
| 中层 | 32 | -12.4 | -12.4 |
| 顶层 | 128 | -8.3 | -8.3 |
| Codebook size | Spectral convergence (dB) |
| 256 | -15.9 |
| 2048 | -23.0 |
| No quantization | -40.5 |
| 码本大小 | 频谱收敛性 (dB) |
|---|---|
| 256 | -15.9 |
| 2048 | -23.0 |
| 无量化 | -40.5 |
Table 2. Bottom-level VQ-VAE reconstruction results with different codebook sizes. Using larger codebooks helps reconstruction because it allows more information to be encoded at the bottleneck layers. Removing the bottleneck entirely yields almost perfect reconstruction.
表 2: 不同码本大小的底层 VQ-VAE 重建结果。使用更大的码本有助于重建,因为它允许在瓶颈层编码更多信息。完全移除瓶颈层几乎可以实现完美重建。
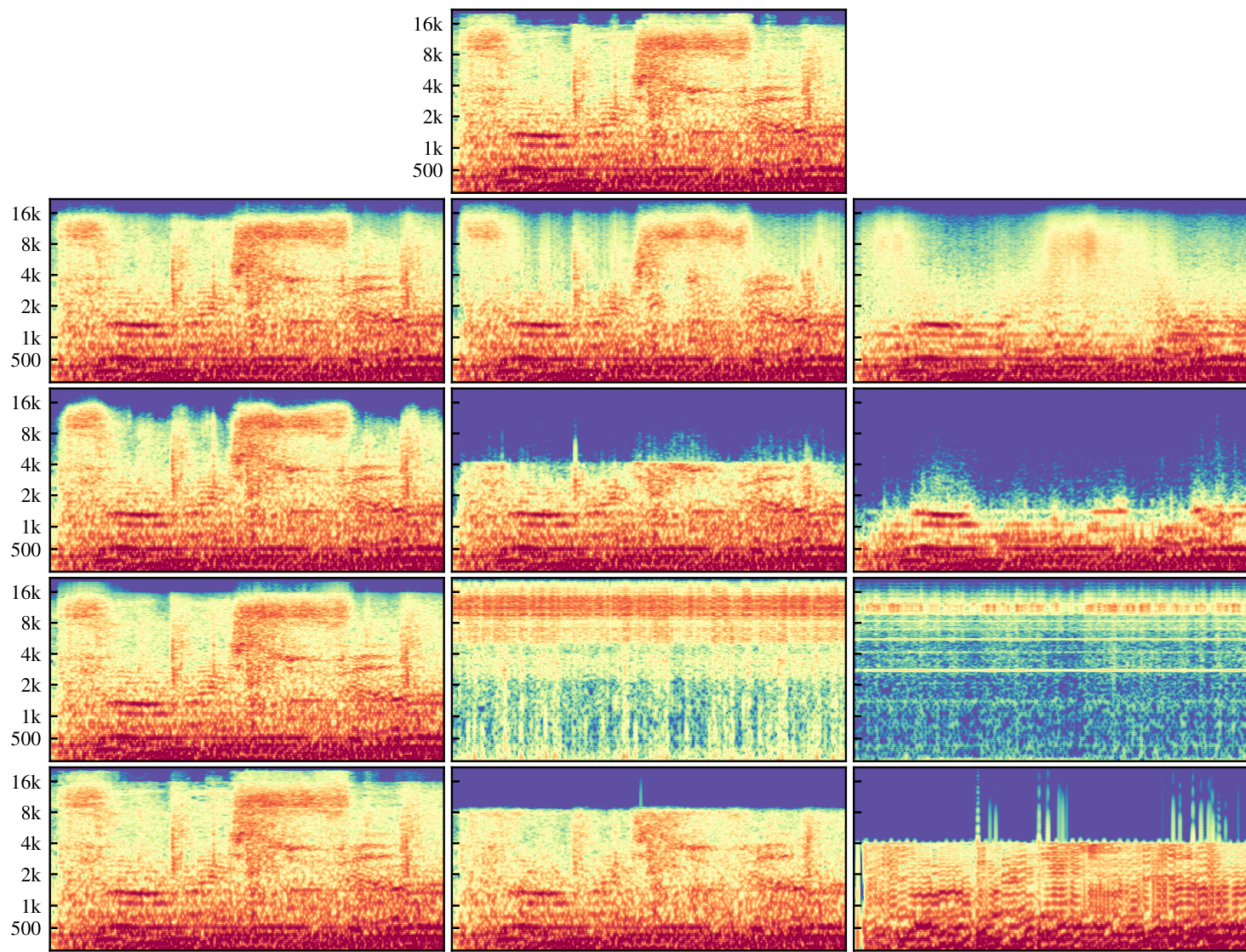
Figure 4. Comparison of reconstructions from different VQ-VAEs, $\mathbf{X}$ -axis is time and y-axis is frequency. The columns from left to right are bottom-, middle-, and top-level reconstructions at hop lengths 8, 32, and 128 respectively, visualized as Mel spec tro grams. The first row is the ground-truth, and the second row shows the spec tro grams of audio outputs from our VQ-VAE. In the third row, we remove the spectral loss, and see that the middle and top level lose high-frequency information. In the fourth row, we use a hierarchical VQ-VAE (Razavi et al., 2019) instead of separate auto-encoders (Figure 1), and we see the middle and top levels are not used for encoding pertinent information. Finally, the fifth row shows a baseline with the Opus codec that encodes audio at constant bitrates comparable to our VQ-VAE. It also fails to capture higher frequencies and adds noticeable artifacts at the highest level of compression.
图 4: 不同VQ-VAE重建效果对比。x轴为时间,y轴为频率。从左至右列分别为跃长8、32、128时的底层、中层、顶层重建结果,以梅尔频谱图形式呈现。第一行为真实频谱,第二行为本研究的VQ-VAE音频输出频谱。第三行去除频谱损失函数后,可见中高层丢失高频信息。第四行采用层级式VQ-VAE (Razavi et al., 2019) 替代独立自编码器 (图1),显示中高层未用于编码关键信息。第五行展示Opus编解码器基线方案(与本研究VQ-VAE比特率相当),同样无法捕捉高频成分并在最高压缩级别产生明显伪影。
Table 3. Top-level codes are generally difficult to train well without spectral loss or with a single hierarchical auto encoder. Resulting reconstructions may lose some to most of information.
| Ablation | Spectral convergence (dB) |
| None | -8.3 |
| Without spectralloss | -6.3 |
| With single autoencoder | 2.9 |
表 3: 在没有频谱损失或使用单一层次自编码器的情况下,顶层编码通常难以训练良好。重建结果可能会丢失部分甚至大部分信息。
| 消融项 | 频谱收敛性 (dB) |
|---|---|
| 无 | -8.3 |
| 无频谱损失 | -6.3 |
| 单一自编码器 | 2.9 |
We compare raw audio VQ-VAEs when trained with varying compression ratios, objectives, and architectures. As we use non auto regressive decoders with continuous representation for output, we report spectral convergence (Sturmel & Daudet, 2011), which measures the amount of spectral error relative to signal, as test error and proxy for reconstruction fidelity. We evaluate on 5000 held-out 3-second audio segments and report the average in decibels. All models in this section are trained with a batch size of 32, 3-second audio clips sampled at $44~\mathrm{{kHz}}$ . As before, we use hop lengths of 8, 32, and 128 for the bottom, middle and top level respectively.
我们比较了在不同压缩比、目标函数和架构下训练的原始音频VQ-VAE模型。由于我们使用具有连续表示的非自回归解码器进行输出,因此采用频谱收敛度(Sturmel & Daudet, 2011)作为测试误差和重建保真度的代理指标,该指标衡量相对于信号的频谱误差量。我们在5000段保留的3秒音频片段上进行评估,并以分贝为单位报告平均值。本节所有模型均以32的批次大小进行训练,音频片段为3秒时长,采样率为$44~\mathrm{{kHz}}$。与之前相同,底层、中层和顶层的跳跃长度分别设为8、32和128。
In Table 1, we see that increasing the hop size results in higher reconstruction error. Figure 4 indeed shows that a significant amount of information, especially higher frequencies, is missing at middle and top levels across all ablations we ran. This is expected as audio is compressed more with larger hop sizes. To mitigate codebook collapse, we restart dead codes near random encoder embeddings. In Figure 5, we see that this yields higher codebook usage even from early on in training. Models trained without random restarts can converge to the same test error and codebook usage but require more training steps. With poor initialization, these models sometimes end up with suboptimal codes hurting reconstruction fidelity.
在表1中,我们看到增加跳跃尺寸会导致更高的重建误差。图4确实表明,在我们运行的所有消融实验中,中高层缺失了大量信息(尤其是高频部分)。这是预期的,因为音频会随着跳跃尺寸增大而被压缩得更严重。为缓解码本崩溃问题,我们在随机编码器嵌入附近重启失效码字。图5显示,这种做法从训练早期就能获得更高的码本使用率。未采用随机重启训练的模型虽然最终能达到相同的测试误差和码本使用率,但需要更多训练步数。若初始化不佳,这些模型有时会陷入次优码字状态,损害重建保真度。
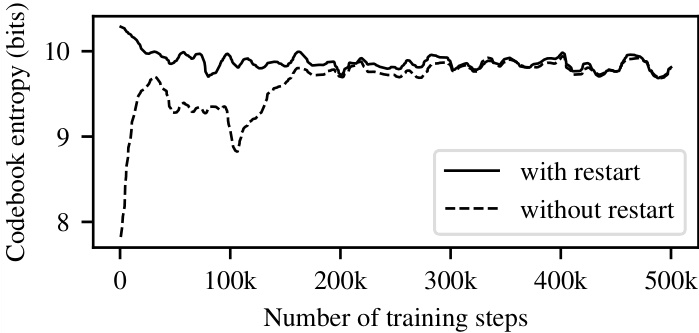
Figure 5. Entropy of codebook with 2048 codes, i.e 11 bits, over training. Reviving dead codes near random encoder outputs ensures good codebook utilization from the start of training.
图 5: 2048个码本(即11比特)在训练过程中的熵变化。通过在随机编码器输出附近激活闲置码本,确保训练初期就能实现良好的码本利用率。
Codebook size also matters, as it sets a limit on channel capacity through the bottleneck layers. In Table 2, we find that reconstruction error increases considerably when the codebook size is reduced from 2048 to 256. We also compare with a model that uses continuous representations without vector quantization. We can think of this model as using a vastly large codebook with all encoder embeddings. This achieves almost perfect reconstruction with negligible spectral error.
码本(codebook)大小同样重要,它通过瓶颈层限制了通道容量。在表2中我们发现,当码本大小从2048减少到256时,重构误差显著增加。我们还与使用连续表征(continuous representations)而非向量量化的模型进行了对比。可以将该模型视为使用了包含所有编码器嵌入向量的超大码本,其重构效果近乎完美,频谱误差可忽略不计。
When the model is trained with L2 loss only, reconstructions tend to sound muddy from missing high frequencies, and this problem is exacerbated as hop size is increased. In Figure 4, we see that top-level codes trained without spectral loss do not capture much information beyond $2\mathrm{kHz}$ , and obtain worse reconstructions (Table 3). However, we observe that while spectral loss helps encode more information, it also adds distortion artifacts which we hear as scratchy noise.
当模型仅使用L2损失进行训练时,重建音频往往会因缺失高频成分而显得沉闷,且随着跳跃尺寸增大该问题会加剧。图4显示,未经频谱损失训练的顶层编码在$2\mathrm{kHz}$以上几乎无法捕获信息,导致重建质量更差(表3)。但我们发现,虽然频谱损失有助于编码更多信息,但也会引入可感知为刺耳噪声的失真伪影。
Lastly, we train a raw audio hierarchical VQ-VAE (Razavi et al., 2019) and find that it is generally difficult to push information to higher levels. This model is trained twice as long as the previous models, but middle and top-level reconstructions as shown in Figure 4 are not capturing much. It is possible that higher level codes may have collapsed before bottom level starts to reconstruct the audio well. Making the bottom layers explicitly model residuals pushed more information to the top. But, we found separate auto encoders to be cleaner and more effective.
最后,我们训练了一个原始音频分层VQ-VAE (Razavi等人,2019) ,发现将信息推送到更高层级通常较为困难。该模型的训练时长是之前模型的两倍,但如图4所示,中层和顶层的重建效果捕捉到的信息很少。可能在底层开始良好重建音频之前,更高层级的编码已经崩溃。通过让底层显式建模残差,可以将更多信息推送到顶层。但我们发现独立的自动编码器方案更清晰且更有效。
6. Related Work
6. 相关工作
Generative modeling in deep learning: Generative models aim to learn the distribution of data by either explicitly by modeling the distribution or implicitly by constructing means to sample from it (Goodfellow, 2016). Modeling the inter dependency within high-dimensional data was traditionally considered extremely difficult, but starting with Deep Boltzmann Machines (Salak hut dino v & Hinton, 2009), various kinds of deep generative models have been introduced. Generative Adversarial Networks (GANs) (Goodfellow et al., 2014) use generator and disc rim in at or networks that contest each other to make the generated samples as indistinguishable as possible from the data, and they are renowned for their ability to generate high-quality pictures (Zhang et al., 2019b; Brock et al., 2019). Autoregres- sive generative models such as NADE (Uria et al., 2016), PixelCNN (Van den Oord et al., 2016), and Transformers (Vaswani et al., 2017) use the chain rule of probability to factorize the joint distribution of data into a product of simpler distributions, and flow-based models (Dinh et al., 2015; 2017; Rezende & Mohamed, 2015; Kingma & Dhariwal, 2018) learn a series of invertible transformations that maps the data distribution with a simpler one such as a Gaussian distribution. Auto regressive flows (Papa makarios et al., 2017; Kingma et al., 2016) combine the two ideas to achieve faster density estimation or data generation. Variational auto encoders (VAEs) (Rezende et al., 2014; Kingma & Welling, 2014) impose a Gaussian prior on the latent code in an encoder-decoder setup from which data can be sampled.
深度学习中的生成式建模:生成式模型旨在通过学习数据分布来生成新数据,其方法可分为显式建模分布或隐式构建采样机制 (Goodfellow, 2016)。传统上,高维数据内部依赖关系的建模被认为极其困难,但自深度玻尔兹曼机 (Salakhutdinov & Hinton, 2009) 起,各类深度生成模型相继涌现。生成对抗网络 (GANs) (Goodfellow et al., 2014) 通过生成器与判别器的对抗训练,使生成样本与真实数据难以区分,并以生成高质量图像的能力著称 (Zhang et al., 2019b; Brock et al., 2019)。自回归生成模型如 NADE (Uria et al., 2016)、PixelCNN (Van den Oord et al., 2016) 和 Transformer (Vaswani et al., 2017) 利用概率链式法则将联合分布分解为简单分布的乘积;基于流的模型 (Dinh et al., 2015; 2017; Rezende & Mohamed, 2015; Kingma & Dhariwal, 2018) 则学习一系列可逆变换,将数据分布映射到高斯分布等简单分布。自回归流 (Papamakarios et al., 2017; Kingma et al., 2016) 融合上述思想,实现了更高效的密度估计与数据生成。变分自编码器 (VAEs) (Rezende et al., 2014; Kingma & Welling, 2014) 在编码器-解码器框架中对隐变量施加高斯先验,从而支持数据采样。
Generative models for music: Generative modeling of symbolic music dates back to more than half a century, when Hiller Jr & Isaacson (1957) introduced the first computergenerated music based on Markov chains. There exists a variety of earlier approaches using rule-based systems (Moorer, 1972), chaos and self-similarity (Pressing, 1988), cellular automata (Beyls, 1989), con cate native synthesis (Jehan, 2005), and constraint programming (Anders & Miranda, 2011). More recent data-driven approaches include DeepBach (Hadjeres et al., 2017) and Coconet (Huang et al., 2017) which use Gibbs sampling to produce notes in the style of Bach chorals, MidiNet (Yang et al., 2017)
