Divide-and-Conquer Monte Carlo Tree Search For Goal-Directed Planning

分治蒙特卡洛树搜索在目标导向规划中的应用

Gia m battista Paras can do lo * 1 2 Lars Buesing * 3 Josh Merel 3 Leonard Has en clever 3 John Aslanides 3 Jessica B. Hamrick 3 Nicolas Heess 3 Alexander Neitz 1 Theophane Weber 3

Gia m battista Paras can do lo * 1 2 Lars Buesing * 3 Josh Merel 3 Leonard Has en clever 3 John Aslanides 3 Jessica B. Hamrick 3 Nicolas Heess 3 Alexander Neitz 1 Theophane Weber 3

Abstract

摘要

Standard planners for sequential decision making (including Monte Carlo planning, tree search, dynamic programming, etc.) are constrained by an implicit sequential planning assumption: The order in which a plan is constructed is the same in which it is executed. We consider alternatives to this assumption for the class of goal-directed Reinforcement Learning (RL) problems. Instead of an environment transition model, we assume an imperfect, goal-directed policy. This low-level policy can be improved by a plan, consisting of an appropriate sequence of sub-goals that guide it from the start to the goal state. We propose a planning algorithm, Divide-and-Conquer Monte Carlo Tree Search (DC-MCTS), for approximating the optimal plan by means of proposing intermediate sub-goals which hierarchically partition the initial tasks into simpler ones that are then solved independently and recursively. The algorithm critically makes use of a learned sub-goal proposal for finding appropriate partitions trees of new tasks based on prior experience. Different strategies for learning sub-goal proposals give rise to different planning strategies that strictly generalize sequential planning. We show that this algorithmic flexibility over planning order leads to improved results in navigation tasks in grid-worlds as well as in challenging continuous control environments.

顺序决策的标准规划器（包括蒙特卡洛规划、树搜索、动态规划等）受到隐式顺序规划假设的限制：构建计划的顺序与执行顺序相同。我们针对目标导向的强化学习（RL）问题类别，探讨了该假设的替代方案。我们假设存在一个不完美的目标导向策略，而非环境转移模型。该底层策略可通过包含适当子目标序列的计划进行改进，这些子目标能将其从初始状态引导至目标状态。我们提出了一种规划算法——分治蒙特卡洛树搜索（DC-MCTS），通过提出中间子目标来近似最优计划，这些子目标将初始任务分层划分为更简单的子任务，随后独立递归求解。该算法关键性地利用学习到的子目标提议，基于先验经验为新任务寻找合适的分割树。不同的子目标提议学习策略会产生严格泛化顺序规划的不同规划策略。我们证明，这种对规划顺序的算法灵活性在网格世界导航任务及具有挑战性的连续控制环境中均能提升结果。

1. Introduction

1. 引言

This is the first sentence of this paper, but it was not the first one we wrote. In fact, the entire introduction section was actually one of the last sections to be added to this manuscript. The discrepancy between the order of inception of ideas and the order of their presentation in this paper probably does not come as a surprise to the reader. Nonetheless, it serves as a point for reflection that is central to the rest of this work, and that can be summarized as “the order in which we construct a plan does not have to coincide with the order in which we execute it”.

这是本文的第一句话，但并非我们最初写下的内容。事实上，整个引言部分实际上是最后才添加到这篇论文中的。想法产生的顺序与它们在本文中呈现顺序之间的差异，对读者来说可能并不意外。尽管如此，这一点仍值得反思，它是本文后续工作的核心，可以总结为"我们制定计划的顺序不必与执行计划的顺序一致"。

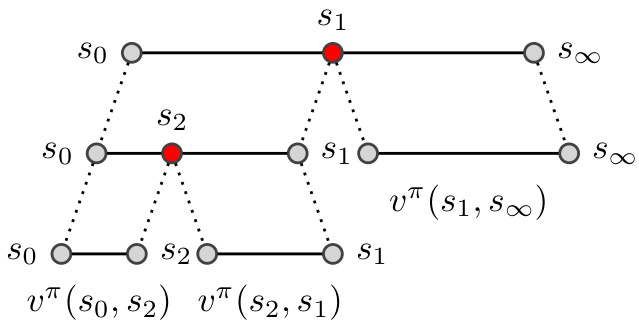
Figure 1. We propose a divide-and-conquer method to search for sub-goals (here $s_{1},s_{2})$ by hierarchical partitioning the task of guiding an agent from start state $s_{0}$ to goal state $s_{\infty}$ .

图 1: 我们提出一种分治法，通过分层划分从初始状态 $s_{0}$ 到目标状态 $s_{\infty}$ 的智能体引导任务，来搜索子目标 (此处为 $s_{1},s_{2}$)。

Most standard planners for sequential decision making problems—including Monte Carlo planning, Monte Carlo Tree Search (MCTS) and dynamic programming—have a baked-in sequential planning assumption (Browne et al., 2012; Bertsekas et al., 1995). These methods begin at either the initial or final state and then proceed to plan actions sequentially forward or backwards in time. However, this sequential approach faces two main challenges. (i) The transition model used for planning needs to be reliable over long horizons, which is often difficult to achieve when it has to be inferred from data. (ii) Credit assignment to each individual action is difficult: In a planning problem spanning a horizon of 100 steps, to assign credit to the first action, we have to compute the optimal cost-to-go for the remaining problem with a horizon of 99 steps, which is only slightly easier than solving the original problem.

大多数用于序列决策问题的标准规划器——包括蒙特卡洛规划、蒙特卡洛树搜索(MCTS)和动态规划——都内置了序列化规划假设 (Browne et al., 2012; Bertsekas et al., 1995)。这些方法从初始状态或最终状态出发，按时间顺序向前或向后逐步规划动作。但该序列化方法面临两大挑战：(i) 规划所用的转移模型需在长时域内保持可靠，当模型需从数据推断时往往难以实现；(ii) 单个动作的信用分配困难：在跨越100步的规划问题中，要为第一个动作分配信用，需计算剩余99步问题的最优成本，其难度仅略低于求解原问题。

To overcome these two fundamental challenges, we consider alternatives to the basic assumptions of sequential planners in this work. To this end, we focus on goal-directed decision making problems where an agent should reach a goal state from a start state. Instead of a transition and reward model of the environment, we assume a given goal-directed policy (the “low-level” policy) and the associated value oracle that returns the success probability of the low-level policy on any given task. In general, a low-level policy will not be not optimal, e.g. it might be too “myopic” to reliably reach goal states that are far away from its current state. We now seek to improve the low-level policy via a suitable sequence of subgoals that effectively guide it from the start to the final goal, thus maximizing the overall task success probability. This formulation of planning as finding good sub-goal sequences, makes learning of explicit environment models unnecessary, as they are replaced by low-level policies and their value functions.

为克服这两个根本性挑战，本研究重新审视序列规划器的基本假设。我们聚焦于目标导向型决策问题，即智能体需从初始状态抵达目标状态。不同于传统环境转移与奖励模型，我们采用给定目标导向策略（"底层"策略）及其关联的价值预言机——该预言机能返回底层策略在任何任务上的成功概率。由于底层策略通常并非最优（例如可能因"短视"而难以可靠到达远距离目标状态），我们通过构建合适的子目标序列来优化策略，从而有效引导其从起点抵达最终目标，实现整体任务成功概率最大化。这种将规划问题转化为子目标序列搜索的范式，消除了显式环境模型的学习需求，转而依赖底层策略及其价值函数实现决策。

The sub-goal planning problem can still be solved by a conventional sequential planner that begins by searching for the first sub-goal to reach from the start state, then planning the next sub-goal in sequence, and so on. Indeed, this is the approach taken in most hierarchical RL settings based on options or sub-goals (e.g. Dayan & Hinton, 1993; Sutton et al., 1999; Vezhnevets et al., 2017). However, the credit assignment problem mentioned above still persists, as assessing if the first sub-goal is useful still requires evaluating the success probability of the remaining plan. Instead, it could be substantially easier to reason about the utility of a sub-goal “in the middle” of the plan, as this breaks the long-horizon problem into two sub-problems with much shorter horizons: how to get to the sub-goal and how to get from there to the final goal. Based on this intuition, we propose the Divide-and-Conquer MCTS (DC-MCTS) planner that searches for sub-goals to split the original task into two independent sub-tasks of comparable complexity and then recursively solves these, thereby drastically facilitating credit assignment. To search the space of intermediate subgoals efficiently, DC-MCTS uses a heuristic for proposing promising sub-goals that is learned from previous search results and agent experience.

子目标规划问题仍可通过传统的顺序规划器解决，该规划器首先搜索从初始状态需达成的第一个子目标，随后依次规划后续子目标。事实上，这是大多数基于选项或子目标的层次强化学习（如 Dayan & Hinton, 1993; Sutton et al., 1999; Vezhnevets et al., 2017）采用的方法。然而，上述信用分配问题依然存在，因为评估首个子目标的有效性仍需考量剩余计划的成功概率。相比之下，分析计划"中间"子目标的效用可能更为简便——这将长视野问题拆解为两个视野更短的子问题：如何抵达该子目标，以及如何从该处到达最终目标。基于此直觉，我们提出分治蒙特卡洛树搜索（DC-MCTS）规划器，通过搜索子目标将原始任务分解为两个复杂度相当的独立子任务并递归求解，从而极大简化信用分配。为高效探索中间子目标空间，DC-MCTS采用启发式方法提出潜在子目标，该启发式通过先前的搜索结果和智能体经验学习获得。

The paper is structured as follows. In Section 2, we formulate planning in terms of sub-goals instead of primitive actions. In Section 3, as our main contribution, we propose the novel Divide-and-Conquer Monte Carlo Tree Search algorithm for this planning problem. In Section 5, we show that it outperforms sequential planners both on grid world and continuous control navigation tasks, demonstrating the utility of constructing plans in a flexible order that can be different from their execution order.

本文结构如下。第2节将规划问题表述为子目标而非原始动作。第3节作为主要贡献，针对该规划问题提出了新颖的分治蒙特卡洛树搜索算法。第5节通过网格世界和连续控制导航任务的实验表明，该算法性能优于顺序规划器，验证了以不同于执行顺序的灵活方式构建规划方案的实用性。

2. Improving Goal-Directed Policies with Planning

2. 通过规划改进目标导向策略

Let $s$ and $\mathcal{A}$ be finite sets of states and actions. We consider a multi-task setting, where for each episode the agent has to solve a new task consisting of a new Markov Decision Process (MDP) $\mathcal{M}$ over $s$ and $\mathcal{A}$ . Each $\mathcal{M}$ has a single start state $s_{0}$ and a special absorbing state $s_{\infty}$ , also termed the goal state. If the agent transitions into $s_{\infty}$ at any time it receives a reward of 1 and the episode terminates; otherwise the reward is 0. We assume that the agent observes the start and goal states $(s_{0},s_{\infty})$ at the beginning of each episode, as well as an encoding vector $c_{\mathcal{M}}\in\mathbb{R}^{d}$ . This vector provides the agent with additional information about the MDP $\mathcal{M}$ of the current episode and will be key to transfer learning across tasks in the multi-task setting. A stochastic, goal-directed policy $\pi$ is a mapping from $S\times S\times\mathbb{R}^{d}$ into distributions over $\mathcal{A}$ , where $\pi({a}|s,s_{\infty},c_{\mathcal{M}})$ denotes the probability of taking action $a$ in state $s$ in order to get to goal $s_{\infty}$ . For a fixed goal $s_{\infty}$ , we can interpret $\pi$ as a regular policy, here denoted as $\pi_{s_{\infty}}$ , mapping states to action probabilities. We denote the value of $\pi$ in state $s$ for goal $s_{\infty}$ as $v^{\pi}(s,s_{\infty}|c_{\mathcal{M}})$ ; we assume no discounting $\gamma=1$ . Under the above definition of the reward, the value is equal to the success probability of $\pi$ on the task, i.e. the absorption probability of the stochastic process starting in $s_{0}$ defined by running $\pi_{s_{\infty}}$ :

设 $s$ 和 $\mathcal{A}$ 为有限的状态集和动作集。我们考虑一个多任务场景，其中每个回合智能体需要解决一个新任务，该任务由在 $s$ 和 $\mathcal{A}$ 上定义的新马尔可夫决策过程 (MDP) $\mathcal{M}$ 组成。每个 $\mathcal{M}$ 有一个初始状态 $s_{0}$ 和一个特殊的吸收状态 $s_{\infty}$，也称为目标状态。如果智能体在任何时刻转移到 $s_{\infty}$，它将获得奖励 1 且回合终止；否则奖励为 0。我们假设智能体在每回合开始时观察初始和目标状态 $(s_{0},s_{\infty})$，以及一个编码向量 $c_{\mathcal{M}}\in\mathbb{R}^{d}$。该向量为智能体提供关于当前回合 MDP $\mathcal{M}$ 的额外信息，这将是多任务场景中跨任务迁移学习的关键。一个随机的、目标导向的策略 $\pi$ 是从 $S\times S\times\mathbb{R}^{d}$ 到 $\mathcal{A}$ 上概率分布的映射，其中 $\pi({a}|s,s_{\infty},c_{\mathcal{M}})$ 表示在状态 $s$ 中采取动作 $a$ 以达到目标 $s_{\infty}$ 的概率。对于一个固定的目标 $s_{\infty}$，我们可以将 $\pi$ 解释为一个常规策略，这里记为 $\pi_{s_{\infty}}$，它将状态映射到动作概率。我们将 $\pi$ 在状态 $s$ 对于目标 $s_{\infty}$ 的值记为 $v^{\pi}(s,s_{\infty}|c_{\mathcal{M}})$；我们假设无折扣 $\gamma=1$。在上述奖励定义下，该值等于 $\pi$ 在任务上的成功概率，即由运行 $\pi_{s_{\infty}}$ 定义的从 $s_{0}$ 开始的随机过程的吸收概率：

$$
v^{\pi}(s_{0},s_{\infty}|c_{\mathcal{M}})=P(s_{\infty}\in\tau_{s_{0}}^{\pi_{s_{\infty}}}|c_{\mathcal{M}}),
$$

$$
v^{\pi}(s_{0},s_{\infty}|c_{\mathcal{M}})=P(s_{\infty}\in\tau_{s_{0}}^{\pi_{s_{\infty}}}|c_{\mathcal{M}}),
$$

where τ sπ0s∞ is the trajectory generated by running πs from state $s_{0}$ 1. To keep the notation compact, we will omit the explicit dependence on $c_{\mathcal{M}}$ and abbreviate tasks with pairs of states in $s\times s$ .

其中τ sπ0s∞是从状态$s_{0}$开始执行πs生成的轨迹。为简化表示，我们将省略对$c_{\mathcal{M}}$的显式依赖，并用状态对$s\times s$来缩写任务。

2.1. Planning over Sub-Goal Sequences

2.1. 子目标序列规划

Assume a given goal-directed policy $\pi$ , which we also refer to as the low-level policy. If $\pi$ is not already the optimal policy, then we can potentially improve it by planning: If $\pi$ has a low probability of directly reaching $s_{\infty}$ from the initial state $s_{0}$ , i.e. $v^{\pi}(s_{0},s_{\infty})\approx0$ , we will try to find a plan consisting of a sequence of intermediate sub-goals such that they guide $\pi$ from the start $s_{0}$ to the goal state $s_{\infty}$ .

假设给定一个目标导向的策略 $\pi$ ，我们也称之为低级策略。如果 $\pi$ 还不是最优策略，那么我们可以通过规划来改进它：如果 $\pi$ 从初始状态 $s_{0}$ 直接到达 $s_{\infty}$ 的概率较低，即 $v^{\pi}(s_{0},s_{\infty})\approx0$ ，我们将尝试找到一个由一系列中间子目标组成的计划，以引导 $\pi$ 从起始状态 $s_{0}$ 到达目标状态 $s_{\infty}$ 。

Concretely, let $S^{ * }=\cup_{n=0}^{\infty}S^{n}$ be the set of sequences over $s$ , and let $|\sigma|$ be the length of a sequence $\sigma\in S^{ * }$ . We define for convenience $\bar{\mathcal{S}}:=\mathcal{S}\cup{\varnothing}$ , where $\mathcal{D}$ is them empty sequence representing no sub-goal. We refer to $\sigma$ as a plan for task $(s_{0},s_{\infty})$ if $\sigma_{1}=s_{0}$ and $\sigma_{|\sigma|}=s_{\infty}$ , i.e. if the first and last elements of $\sigma$ are equal to $s_{0}$ and $s_{\infty}$ , respectively. We denote the set of plans for this task as $s_{0}S^{*}s_{\infty}$ .

具体地，设 $S^{ * }=\cup_{n=0}^{\infty}S^{n}$ 为 $s$ 上的序列集合，$|\sigma|$ 表示序列 $\sigma\in S^{ * }$ 的长度。为方便起见，定义 $\bar{\mathcal{S}}:=\mathcal{S}\cup{\varnothing}$ ，其中 $\mathcal{D}$ 是表示无子目标的空序列。若序列 $\sigma$ 满足 $\sigma_{1}=s_{0}$ 且 $\sigma_{|\sigma|}=s_{\infty}$ （即首尾元素分别等于 $s_{0}$ 和 $s_{\infty}$ ），则称 $\sigma$ 为任务 $(s_{0},s_{\infty})$ 的规划。该任务的所有规划集合记为 $s_{0}S^{*}s_{\infty}$。

To execute a plan $\sigma$ , we construct a policy $\pi_{\sigma}$ by conditioning the low-level policy $\pi$ on each of the sub-goals in order: Starting with $n=1$ , we feed sub-goal $\sigma_{n+1}$ to $\pi$ , i.e. we run $\pi_{\sigma_{n+1}}$ ; if $\sigma_{n+1}$ is reached, we will execute $\pi_{\sigma_{n+2}}$ and so on. We now wish to do open-loop planning, i.e. find the plan with the highest success probability $P(s_{\infty}\in\tau_{s_{0}}^{\pi_{\sigma}})$ of reaching $s_{\infty}$ . However, this success probability depends on the transition kernels of the underlying MPDs, which might not be known. We can instead define planning as maximizing the following lower bound of the success probability, that can be expressed in terms of the low-level value $v^{\pi}$ .

要执行一个计划 $\sigma$，我们通过按顺序将低层策略 $\pi$ 条件化到每个子目标上来构建策略 $\pi_{\sigma}$：从 $n=1$ 开始，我们将子目标 $\sigma_{n+1}$ 输入给 $\pi$，即运行 $\pi_{\sigma_{n+1}}$；如果达到 $\sigma_{n+1}$，则继续执行 $\pi_{\sigma_{n+2}}$，依此类推。现在，我们希望进行开环规划 (open-loop planning)，即找到达到 $s_{\infty}$ 的成功概率 $P(s_{\infty}\in\tau_{s_{0}}^{\pi_{\sigma}})$ 最高的计划。然而，这一成功概率取决于底层 MPD 的转移核，而这些可能未知。于是，我们可以将规划定义为最大化以下成功概率的下界，该下界可以用低层价值 $v^{\pi}$ 表示。

Proposition 1 (Lower bound of success probability). The success probability $P(s_{\infty}\in\tau_{s_{0}}^{\pi_{\sigma}})\geq L(\sigma)$ of a plan $\sigma$ is bounded from below by $\begin{array}{r}{L(\sigma):=\prod_{i=1}^{|\sigma|-1}v^{\pi}(\sigma_{i},\sigma_{i+1}),}\end{array}$ i.e. the product of the success probab ilities of $\pi$ on the subtasks defined by $(\sigma_{i},\sigma_{i+1})$ .

命题1 (成功概率下界). 计划$\sigma$的成功概率$P(s_{\infty}\in\tau_{s_{0}}^{\pi_{\sigma}})\geq L(\sigma)$存在下界$\begin{array}{r}{L(\sigma):=\prod_{i=1}^{|\sigma|-1}v^{\pi}(\sigma_{i},\sigma_{i+1}),}\end{array}$, 即$\pi$在子任务$(\sigma_{i},\sigma_{i+1})$上成功概率的乘积。

The straight-forward proof is given in Appendix A.1. Intuitively, $L(\sigma)$ is a lower bound for the success of $\pi_{\sigma}$ , as it neglects the probability of “accidentally” (due to stochasticity of the policy or transitions) running into the goal $s_{\infty}$ before having executed the full plan. We summarize:

直观证明见附录A.1。从直观上看，$L(\sigma)$是$\pi_{\sigma}$成功概率的下界，因为它忽略了在完整执行计划前"意外"(由于策略或状态转移的随机性)抵达目标状态$s_{\infty}$的概率。我们总结如下：

Definition 1 (Open-Loop Goal-Directed Planning). Given a goal-directed policy $\pi$ and its corresponding value oracle $v^{\pi}$ , we define planning as optimizing $L(\sigma)$ over $\sigma\in$ $s_{0}S^{ * }s_{\infty}$ , i.e. the set of plans for task $(s_{0},s_{\infty})$ . We define the high-level (HL) value $v^{ * }(s_{0},s_{\infty}):=\operatorname*{max}_{\sigma}L(\sigma)$ as the maximum value of the planning objective.

定义 1 (开环目标导向规划) 。给定目标导向策略 $\pi$ 及其对应的价值预言机 $v^{\pi}$ ，我们将规划定义为在 $\sigma\in$ $s_{0}S^{ * }s_{\infty}$ (即任务 $(s_{0},s_{\infty})$ 的计划集合) 上优化 $L(\sigma)$ 。我们将高层 (HL) 价值 $v^{ * }(s_{0},s_{\infty}):=\operatorname*{max}_{\sigma}L(\sigma)$ 定义为规划目标的最大值。

Note the difference between the low-level value $v^{\pi}$ and the high-level $v^{ * }$ . $v^{\pi}(s,s^{\prime})$ is the probability of the agent directly reaching $s^{\prime}$ from $s$ following $\pi$ , whereas $v^{ * }(s,s^{\prime})$ the probability reaching $s^{\prime}$ from $s$ under the optimal plan, which likely includes intermediate sub-goals. In particular we have $v^{*}\geq v^{\pi}$ .

注意低层值 $v^{\pi}$ 和高层值 $v^{ * }$ 之间的区别。$v^{\pi}(s,s^{\prime})$ 是智能体遵循策略 $\pi$ 直接从 $s$ 到达 $s^{\prime}$ 的概率，而 $v^{ * }(s,s^{\prime})$ 是在最优计划下从 $s$ 到达 $s^{\prime}$ 的概率，其中可能包含中间子目标。特别地，我们有 $v^{*}\geq v^{\pi}$。

2.2. AND/OR Search Tree Representation

2.2. AND/OR 搜索树表示

In the following we cast the planning problem into a representation amenable to efficient search. To this end, we use the natural compositional it y of plans: We can concatenate, a plan $\sigma$ for the task $(s,s^{\prime})$ and a plan $\hat{\sigma}$ for the task $(s^{\prime},s^{\prime\prime})$ into a plan $\sigma\circ\hat{\sigma}$ for the task $(s,s^{\prime\prime})$ . Conversely, we can decompose any given plan $\sigma$ for task $(s_{0},s_{\infty})$ by splitting it at any sub-goal $s\in\sigma$ into $\sigma=\sigma^{l}\circ\sigma^{r}$ , where $\sigma^{l}$ is the “left” sub-plan for task $(s_{0},s)$ , and $\sigma^{r}$ is the “right” sub-plan for task $(s,s_{\infty})$ . For an illustration see Figure 1. Trivially, the planning objective and the optimal high-level value factorize wrt. to this decomposition:

以下我们将规划问题转化为适合高效搜索的表示形式。为此，我们利用规划的自然组合性：可以将任务$(s,s^{\prime})$的规划$\sigma$与任务$(s^{\prime},s^{\prime\prime})$的规划$\hat{\sigma}$拼接成任务$(s,s^{\prime\prime})$的规划$\sigma\circ\hat{\sigma}$。反之，对于任务$(s_{0},s_{\infty})$的任意给定规划$\sigma$，可通过在子目标$s\in\sigma$处将其拆分为$\sigma=\sigma^{l}\circ\sigma^{r}$，其中$\sigma^{l}$是任务$(s_{0},s)$的"左"子规划，$\sigma^{r}$是任务$(s,s_{\infty})$的"右"子规划。示意图见图1。显然，规划目标与最优高层价值函数均关于该分解具有可乘性：

$$
\begin{array}{l c l}{{{\cal L}(\sigma^{l}\circ\sigma^{r})}}&{{=}}&{{{\cal L}(\sigma^{l}){\cal L}(\sigma^{r})}}\ {{v^{ * }(s_{0},s_{\infty})}}&{{=}}&{{\displaystyle\operatorname*{max}_ {s\in\bar{S}}v^{ * }(s_{0},s)\cdot v^{*}(s,s_{\infty}).}}\end{array}
$$

$$
\begin{array}{l c l}{{{\cal L}(\sigma^{l}\circ\sigma^{r})}}&{{=}}&{{{\cal L}(\sigma^{l}){\cal L}(\sigma^{r})}}\ {{v^{ * }(s_{0},s_{\infty})}}&{{=}}&{{\displaystyle\operatorname*{max}_ {s\in\bar{S}}v^{ * }(s_{0},s)\cdot v^{*}(s,s_{\infty}).}}\end{array}
$$

This allows us to recursively reformulate planning as:

这使我们能够递归地将规划重新表述为：

$$
\underset{s\in\bar{\cal S}}{\arg\operatorname*{max}}\left(\arg\operatorname*{max}_ {\sigma_{l}\in s_{0}}L(\sigma^{l})\right)\cdot\left(\arg\operatorname*{max}_ {\sigma_{r}\in s{\cal S}^{\ast}s_{\infty}}L(\sigma^{r})\right).
$$

$$
\underset{s\in\bar{\cal S}}{\arg\operatorname*{max}}\left(\arg\operatorname*{max}_ {\sigma_{l}\in s_{0}}L(\sigma^{l})\right)\cdot\left(\arg\operatorname*{max}_ {\sigma_{r}\in s{\cal S}^{\ast}s_{\infty}}L(\sigma^{r})\right).
$$

The above equations are the Bellman equations and the Bellman optimality equations for the classical single pair shortest path problem in graphs, where the edge weights are given by $-\log v^{\pi}(s,s^{\prime})$ . We can represent this planning problem by an AND/OR search tree (Nilsson, N. J., 1980) consisting of alternating levels of OR and AND nodes. An OR node, also termed an action node, is labeled by a task $(s,s^{\prime\prime})\in\boldsymbol{\mathcal{S}}\times\boldsymbol{\mathcal{S}}$ ; the root of the search tree is an OR node labeled by the original task $(s_{0},s_{\infty})$ . A terminal OR node $(s,s^{\prime\prime})$ has a value $v^{\pi}(s,s^{\prime\prime})$ attached to it, which reflects the success probability of $\pi_{s^{\prime\prime}}$ for completing the sub-task $(s,s^{\prime\prime})$ . Each non-terminal OR node has $|S|+1$ AND nodes as children. Each of these is labeled by a triple $(s,s^{\prime},s^{\prime\prime})$ for $s^{\prime}\in\bar{S}$ , which correspond to inserting a sub-goal $s^{\prime}$ into the overall plan, or not inserting one in case of $s=\emptyset$ Every AND node $(s,s^{\prime},s^{\prime\prime})$ , which we will also refer to as a conjunction node, has two OR children, the “left” sub-task $(s,s^{\prime})$ and the “right” sub-task $(s^{\prime},s^{\prime\prime})$ .

上述方程是图中经典单对最短路径问题的贝尔曼方程和贝尔曼最优性方程，其中边权重由 $-\log v^{\pi}(s,s^{\prime})$ 给出。我们可以通过一个由交替的OR节点和AND节点层级组成的AND/OR搜索树 (Nilsson, N. J., 1980) 来表示这一规划问题。OR节点（也称为动作节点）由任务 $(s,s^{\prime\prime})\in\boldsymbol{\mathcal{S}}\times\boldsymbol{\mathcal{S}}$ 标记；搜索树的根节点是由原始任务 $(s_{0},s_{\infty})$ 标记的OR节点。终端OR节点 $(s,s^{\prime\prime})$ 附有一个值 $v^{\pi}(s,s^{\prime\prime})$ ，它反映了 $\pi_{s^{\prime\prime}}$ 完成子任务 $(s,s^{\prime\prime})$ 的成功概率。每个非终端OR节点有 $|S|+1$ 个AND子节点，每个子节点由三元组 $(s,s^{\prime},s^{\prime\prime})$ （其中 $s^{\prime}\in\bar{S}$ ）标记，对应于在整体计划中插入子目标 $s^{\prime}$ ，或在 $s=\emptyset$ 时不插入。每个AND节点 $(s,s^{\prime},s^{\prime\prime})$ （也称为合取节点）有两个OR子节点，即“左”子任务 $(s,s^{\prime})$ 和“右”子任务 $(s^{\prime},s^{\prime\prime})$ 。

In this representation, plans are induced by solution trees. A solution tree $\mathcal{T}_ {\sigma}$ is a sub-tree of the complete AND/OR search tree, with the properties that (i) the root $(s_{0},s_{\infty})\in$ $\mathcal{T}_ {\sigma}$ , (ii) each OR node in $\tau_{\sigma}$ has at most one child in $\mathcal{T}_ {\sigma}$ and (iii) each AND node in $\mathcal{T}_ {\sigma}$ as two children in $\mathcal{T}_ {\sigma}$ . The plan $\sigma$ and its objective $L(\sigma)$ can be computed from $\tau_{\sigma}$ by a depth-first traversal of $\tau_{\sigma}$ , see Figure 1. The correspondence of sub-trees to plans is many-to-one, as $\tau_{\sigma}$ , in addition to the plan itself, contains the order in which the plan was constructed. Figure 6 in the Appendix shows a example for a search and solution tree. Below we will discuss how to construct a favourable search order heuristic.

在此表示中，计划由解树推导得出。解树 $\mathcal{T}_ {\sigma}$ 是完整AND/OR搜索树的子树，具有以下特性：(i) 根节点 $(s_{0},s_{\infty})\in$ $\mathcal{T}_ {\sigma}$，(ii) $\tau_{\sigma}$ 中的每个OR节点在 $\mathcal{T}_ {\sigma}$ 中至多有一个子节点，(iii) $\mathcal{T}_ {\sigma}$ 中的每个AND节点在 $\mathcal{T}_ {\sigma}$ 中有两个子节点。计划 $\sigma$ 及其目标值 $L(\sigma)$ 可通过深度优先遍历 $\tau_{\sigma}$ 计算得出，如图1所示。子树与计划的对应关系是多对一的，因为 $\tau_{\sigma}$ 除了包含计划本身外，还包含计划的构建顺序。附录中的图6展示了搜索树与解树的示例。下文将讨论如何构建有利的搜索顺序启发式策略。

3. Best-First AND/OR Planning

3. 最佳优先与或规划

The planning problem from Definition 1 can be solved exactly by formulating it as shortest path problem from $s_{0}$ to $s_{\infty}$ on a fully connected graph with vertex set $s$ with non-negative edge weights given by $-\log v^{\pi}$ and applying a classical Single Source or All Pairs Shortest Path (SSSP / APSP) planner. This approach is appropriate if one wants to solve all goal-directed tasks in a single MDP. Here, we focus however on the multi-task setting described above, where the agent is given a new MDP wit a single task $(s_{0},s_{\infty})$ every episode. In this case, solving the ${\tt S S S P}/$ APSP problem is not feasible: Tabulating all graphs weights $-\log v^{\pi}(s,s^{\prime})$ would require $|\boldsymbol{S}|^{2}$ evaluations of $v^{\pi}(s,s^{\prime})$ for all pairs $(s,s^{\prime})$ . In practice, approximate evaluations of $v^{\pi}$ could be implemented by e.g. actually running the policy $\pi$ , or by calls to a powerful function approx im at or, both of which are often too costly to exhaustively evaluate for large state-spaces $s$ . Instead, we tailor an algorithm for approximate planning to the multi-task setting, which we call Divide-and-Conquer MCTS (DC-MCTS). To evaluate $v^{\pi}$ as sparsely as possible, DC-MCTS critically makes use of two learned search heuristics that transfer knowledge from previously encountered MDPs / tasks to new problem instance: (i) a distribution $p(s^{\prime}|s,s^{\prime\prime})$ , called the policy prior, for proposing promising intermediate sub-goals $s^{\prime}$ for a task $(s,s^{\prime\prime})$ ; and (ii) a learned approximation $v$ to the high-level value $v^{*}$ for bootstrap evaluation of partial plans. In the following we present DC-MCTS and discuss design choices and training for the two search heuristics.

根据定义1，规划问题可以通过将其表述为从$s_{0}$到$s_{\infty}$的最短路径问题来精确求解，该问题基于一个完全连通的图结构，其中顶点集为$s$，边权重由$-\log v^{\pi}$给出且非负，并应用经典的单源或全对最短路径（SSSP/APSP）规划器。这种方法适用于需要在一个MDP中解决所有目标导向任务的情况。然而，本文重点讨论上述多任务场景，其中智能体每回合会收到一个包含单一任务$(s_{0},s_{\infty})$的新MDP。此时，求解${\tt SSSP}/$APSP问题不可行：若对所有状态对$(s,s^{\prime})$制表$-\log v^{\pi}(s,s^{\prime})$，则需进行$|\boldsymbol{S}|^{2}$次$v^{\pi}(s,s^{\prime})$评估。实践中，可通过实际运行策略$\pi$或调用强大的函数逼近器来近似评估$v^{\pi}$，但对于大规模状态空间$s$，这两种方法往往因计算成本过高而难以穷举。为此，我们针对多任务场景定制了近似规划算法——分治蒙特卡洛树搜索（DC-MCTS）。为尽可能稀疏地评估$v^{\pi}$，DC-MCTS关键性地利用了两个从历史MDP/任务迁移知识的搜索启发式：(i) 策略先验分布$p(s^{\prime}|s,s^{\prime\prime})$，用于为任务$(s,s^{\prime\prime})$推荐潜在中间子目标$s^{\prime}$；(ii) 对高层价值$v^{*}$的学习近似$v$，用于部分规划的自举评估。下文将介绍DC-MCTS，并讨论两个搜索启发式的设计选择与训练过程。

Algorithm1 Divide-and-Conquer MCTSprocedures

Global low-level value oracle vm

Globalhigh-level value function v

Global policy prior p

Global search tree T

1: procedure TRAVERSE(OR node (s, s"))

2: if (s, s") T then

3: T← ExPAND(T,(s, s"))

4: return max(u"(s, s"),v(s, s")) bootstrap

5: end if

6: s'← SELECT(s, s") OR node

7: if s' = or max-depth reached then

8: G←u"(s, s"")

9: else > AND node

10: Gleft ← TRAVERSE(s, s')

11: Gright ← TRAVERSE(s', s")

12: // BACKUP

13: G← Gleft · Gright

14: end if

15: G← max(G,v"(s, s")) threshold the return

16: //UPDATE

17: V(s, s") < (V(s, s")N(s, s")+G)/(N(s, s")+1)

18: N(s, s") ← N(s,s") + 1

19: return G

20: end procedure

算法1 分治MCTS流程
全局低层价值评估器 vm
全局高层价值函数 v
全局策略先验 p
全局搜索树 T
1: 过程 TRAVERSE(或节点 (s, s"))
2: 如果 (s, s") 不在 T 中
3: T← 扩展(T,(s, s"))
4: 返回 max(u"(s, s"),v(s, s")) 自举值
5: 结束条件
6: s'← 选择(s, s") 或节点
7: 如果 s' = 空 或达到最大深度
8: G←u"(s, s"")
9: 否则 > 与节点
10: G左 ← 遍历(s, s')
11: G右 ← 遍历(s', s")
12: // 回传
13: G← G左 · G右
14: 结束条件
15: G← max(G,v"(s, s")) 阈值化返回值
16: //更新
17: V(s, s") ← (V(s, s")N(s, s")+G)/(N(s, s")+1)
18: N(s, s") ← N(s,s") + 1
19: 返回 G
20: 结束过程

3.1. Divide-and-Conquer Monte Carlo Tree Search

3.1. 分治蒙特卡洛树搜索

The input to the DC-MCTS planner is an MDP encoding $c_{\mathcal{M}}$ , a task $(s_{0},s_{\infty})$ as well as a planning budget, i.e. a maximum number $B\in\mathbb{N}$ of $v^{\pi}$ oracle evaluations. At each stage, DC-MCTS maintains a (partial) AND/OR search tree $\tau$ whose root is the OR node $(s_{0},s_{\infty})$ corresponding to the original task. Every OR node $(s,s^{\prime\prime})\in\mathcal{T}$ maintains an estimate $V(s,s^{\prime\prime})\approx v^{*}(s,s^{\prime\prime})$ of its high-level value. DC-MCTS searches for a plan by iterative ly constructing the search tree $\tau$ with TRAVERSE until the budget is exhausted, see Algorithm 1. During each traversal, if a leaf node of $\tau$ is reached, it is expanded, followed by a recursive bottom-up backup to update the value estimates $V$ of all OR nodes visited in this traversal. After this search phase, the currently best plan is extracted from $\tau$ by EXTRACTPLAN (essentially depth-first traversal, see Algorithm 2 in the Appendix). In the following we briefly describe the main methods of the search.

DC-MCTS规划器的输入是一个MDP编码$c_{\mathcal{M}}$、任务$(s_{0},s_{\infty})$以及规划预算(即$v^{\pi}$预言评估的最大次数$B\in\mathbb{N}$)。在每一阶段，DC-MCTS维护一个(部分)AND/OR搜索树$\tau$，其根节点是对应原始任务的OR节点$(s_{0},s_{\infty})$。每个OR节点$(s,s^{\prime\prime})\in\mathcal{T}$维护着其高层价值估计$V(s,s^{\prime\prime})\approx v^{*}(s,s^{\prime\prime})$。DC-MCTS通过迭代构建搜索树$\tau$(使用TRAVERSE算法)来寻找规划方案，直至预算耗尽(见算法1)。每次遍历期间，若到达$\tau$的叶节点，则对其进行扩展，随后通过递归自底向上回溯来更新本次遍历中访问的所有OR节点的价值估计$V$。搜索阶段结束后，通过EXTRACTPLAN(本质上是深度优先遍历，见附录算法2)从$\tau$中提取当前最优规划方案。下文将简要介绍搜索的主要方法。

TRAVERSE and SELECT $\tau$ is traversed from the root $(s_{0},s_{\infty})$ to find a promising node to expand. At an OR node $(s,s^{\prime\prime})$ , SELECT chooses one of its children $s^{\prime}\in\bar{S}$ to next traverse into, including $s=\emptyset$ for not inserting any further sub-goals into this branch. We implemented SELECT by the pUCT (Rosin, 2011) rule, which consists of picking the next node $s^{\prime}\in\bar{S}$ based on maximizing the following score:

遍历与选择
从根节点 $(s_{0},s_{\infty})$ 开始遍历 $\tau$ 以寻找有扩展潜力的节点。在OR节点 $(s,s^{\prime\prime})$ 处，SELECT会从其子节点 $s^{\prime}\in\bar{S}$ 中选择一个进行下一步遍历（包括 $s=\emptyset$ 表示不再向该分支插入子目标）。我们采用pUCT规则 (Rosin, 2011) 实现SELECT，其核心是通过最大化以下评分来选择下一个节点 $s^{\prime}\in\bar{S}$：

$$
V(s,s^{\prime})\cdot V(s^{\prime},s^{\prime\prime})+c\cdot p(s^{\prime}|s,s^{\prime\prime})\cdot\frac{\sqrt{N(s,s^{\prime\prime})}}{1+N(s,s^{\prime},s^{\prime\prime})},
$$

$$
V(s,s^{\prime})\cdot V(s^{\prime},s^{\prime\prime})+c\cdot p(s^{\prime}|s,s^{\prime\prime})\cdot\frac{\sqrt{N(s,s^{\prime\prime})}}{1+N(s,s^{\prime},s^{\prime\prime})},
$$

where $N(s,s^{\prime})$ , $N(s,s^{\prime},s^{\prime\prime})$ are the visit counts of the OR node $(s,s^{\prime})$ , AND node $(s,s^{\prime},s^{\prime\prime})$ respectively. The first term is the exploitation component, guiding the search to sub-goals that currently look promising, i.e. have high estimated value. The second term is the exploration term favoring nodes with low visit counts. Crucially, it is explicitly scaled by the policy prior $p(s^{\prime}|s,s^{\prime\prime})$ to guide exploration. At an AND node $(s,s^{\prime},s^{\prime\prime})$ , TRAVERSE traverses into both the left $(s,s^{\prime})$ and right child $(s^{\prime},s^{\prime\prime})$ .2 As the two subproblems are solved independently, computation from there on can be carried out in parallel. All nodes visited in a single traversal form a solution tree denoted here as $\tau_{\sigma}$ with plan $\sigma$ .

其中 $N(s,s^{\prime})$ 和 $N(s,s^{\prime},s^{\prime\prime})$ 分别是 OR 节点 $(s,s^{\prime})$ 和 AND 节点 $(s,s^{\prime},s^{\prime\prime})$ 的访问计数。第一项是开发(exploitation)部分，引导搜索到当前看起来有前景的子目标，即具有较高估计值的子目标。第二项是探索(exploration)部分，倾向于访问计数较低的节点。关键的是，它通过策略先验 $p(s^{\prime}|s,s^{\prime\prime})$ 显式缩放以引导探索。在 AND 节点 $(s,s^{\prime},s^{\prime\prime})$ 处，TRAVERSE 会同时遍历左子节点 $(s,s^{\prime})$ 和右子节点 $(s^{\prime},s^{\prime\prime})$。由于这两个子问题是独立求解的，后续计算可以并行进行。单次遍历中访问的所有节点形成一个解树，记为 $\tau_{\sigma}$，其对应计划为 $\sigma$。

EXPAND If a leaf OR node $(s,s^{\prime\prime})$ is reached during the traversal and its depth is smaller than a given maximum depth, it is expanded by evaluating the high- and low-level values $v(s,s^{\prime\prime})$ , $v^{\pi}(s,s^{\prime\prime})$ . The initial value of the node is defined as max of both values, as by definition $v^{*}\geq$ $v^{\pi}$ , i.e. further planning should only increase the success probability on a sub-task. We also evaluate the policy prior $p(s^{\prime}|s,s^{\prime\prime})$ for all $s^{\prime}$ , yielding the proposal distribution over sub-goals used in SELECT. Each node expansion costs one unit of budget $B$ .

EXPAND 如果在遍历过程中到达一个叶节点或节点 $(s,s^{\prime\prime})$ 且其深度小于给定的最大深度，则通过评估高层次和低层次值 $v(s,s^{\prime\prime})$ 、 $v^{\pi}(s,s^{\prime\prime})$ 来扩展该节点。节点的初始值定义为这两个值的最大值，因为根据定义 $v^{*}\geq$ $v^{\pi}$ ，即进一步的规划应仅增加子任务的成功概率。我们还会评估所有 $s^{\prime}$ 的策略先验 $p(s^{\prime}|s,s^{\prime\prime})$ ，生成用于SELECT的子目标提议分布。每次节点扩展消耗一个预算单位 $B$ 。

BACKUP and UPDATE We define the return $G_{\sigma}$ of the traversal tree $\tau_{\sigma}$ as follows. Let a refinement $\mathcal{T}_ {\sigma}^{+}$ of $\mathcal{T}_ {\sigma}$ be a solution tree such that ${\mathcal{T}}_ {\sigma}\subseteq{\mathcal{T}}_ {\sigma}^{+}$ , thus representing a plan $\sigma^{+}$ that has all sub-goals of $\sigma$ with additional inserted sub-goals. $G_{\sigma}$ is now defined as the value of the objective $L(\sigma^{+})$ of the optimal refinement of $\mathcal{T}_ {\sigma}$ , i.e. it reflects how well one could do on task $(s_{0},s_{\infty})$ by starting from the plan $\sigma$ and refining it. It can be computed by a simple back-up on the tree $\mathcal{T}_ {\sigma}$ that uses the bootstrap value $v\approx v^{ * }$ at the leafs. As $v^{\ast}(s_{0},s_{\infty})\geq G_{\sigma}\geq L(\sigma)$ and $G_{\sigma^{ * }}=v^{ * }(s_{0},s_{\infty})$ for the optimal plan $\sigma^{*}$ , we can use $G_{\sigma}$ to update the value estimate $V$ . Like in other MCTS variants, we employ a running average operation (line 17-18 in TRAVERSE).

备份与更新
我们将遍历树 $\tau_{\sigma}$ 的回报 $G_{\sigma}$ 定义如下。设 $\mathcal{T}_ {\sigma}$ 的一个细化 $\mathcal{T}_ {\sigma}^{+}$ 为满足 ${\mathcal{T}}_ {\sigma}\subseteq{\mathcal{T}}_ {\sigma}^{+}$ 的解树，表示一个包含 $\sigma$ 所有子目标并额外插入子目标的计划 $\sigma^{+}$。此时 $G_{\sigma}$ 定义为 $\mathcal{T}_ {\sigma}$ 最优细化的目标值 $L(\sigma^{+})$，即反映从计划 $\sigma$ 出发细化后能在任务 $(s_{0},s_{\infty})$ 上达到的最佳效果。它可通过在树 $\mathcal{T}_ {\sigma}$ 上执行简单备份计算得出，其中叶节点使用近似引导值 $v\approx v^{ * }$。由于对于最优计划 $\sigma^{ * }$ 有 $v^{\ast}(s_{0},s_{\infty})\geq G_{\sigma}\geq L(\sigma)$ 且 $G_{\sigma^{ * }}=v^{*}(s_{0},s_{\infty})$，我们可用 $G_{\sigma}$ 更新价值估计 $V$。与其他MCTS变体类似，我们采用滑动平均操作（TRAVERSE算法第17-18行）。

3.2. Designing and Training Search Heuristics

3.2. 设计和训练搜索启发式

Search results and experience from previous tasks can be used to improve DC-MCTS on new problem instances via adapting the search heuristics, i.e. the policy prior $p$ and the approximate value function $v$ , in the following way.

利用先前任务的搜索结果和经验，可通过以下方式调整搜索启发式策略（即策略先验 $p$ 和近似价值函数 $v$）来提升DC-MCTS在新问题实例上的表现。

Bootstrap Value Function We parametrize $v(s,s^{\prime}|c_{\mathcal{M}})\approx~v^{*}(s,s^{\prime}|c_{\mathcal{M}})$ as a neural network that takes as inputs the current task consisting of $(s,s^{\prime})$ and the MDP encoding $c_{\mathcal{M}}$ . A straight-forward approach to train $v$ is to regress it towards the non-parametric value estimates $V$ computed by DC-MCTS on previous problem instances. However, initial results indicated that this leads to $v$ being overly optimistic, an observation also made in (Kaelbling, 1993). We therefore used more conservative training targets, that are computed by backing the low-level values $v^{\pi}$ up the solution tree $\tau_{\sigma}$ of the plan $\sigma$ return by DC-MCTS. Details can be found in Appendix B.1.

Bootstrap值函数 我们将$v(s,s^{\prime}|c_{\mathcal{M}})\approx~v^{*}(s,s^{\prime}|c_{\mathcal{M}})$参数化为一个神经网络，其输入包括当前任务$(s,s^{\prime})$和MDP编码$c_{\mathcal{M}}$。训练$v$的直接方法是将其回归到DC-MCTS在先前问题实例上计算的非参数值估计$V$。然而，初步结果表明这会导致$v$过于乐观，这一现象在 (Kaelbling, 1993) 中也有提及。因此，我们采用了更保守的训练目标，这些目标通过将底层值$v^{\pi}$沿DC-MCTS返回的计划$\sigma$的解树$\tau_{\sigma}$反向传播计算得出。详情见附录B.1。

Policy Prior Best-first search guided by a policy prior $p$ can be understood as policy improvement of $p$ as described in (Silver et al., 2016). Therefore, a straight-forward way of training $p$ is to distill the search results back into into the policy prior, e.g. by behavioral cloning. When applying this to DC-MCTS in our setting, we found empirically that this yielded very slow improvement when starting from an untrained, uniform prior $p$ . This is due to plans with non-zero success probability $L>0$ being very sparse in $S^{ * }$ , equivalent to the sparse reward setting in regular MDPs. To address this issue, we propose to apply Hindsight Experience Replay (HER, (An dry ch owicz et al., 2017)): Instead of training $p$ exclusively on search results, we additionally execute plans $\sigma$ in the environment and collect the resulting trajectories, i.e. the sequence of visited states, $\tau_{s_{0}}^{\pi_{\sigma}}=(s_{0},s_{1},...,s_{T})$ HER then proceeds with hindsight relabeling, i.e. taking $\tau_{s_{0}}^{\pi_{\sigma}}$ as an approximately optimal plan for the “fictional” task $(s_{0},s_{T})$ that is likely different from the actual task $(s_{0},s_{\infty})$ In standard HER, these fictitious expert demonstrations are used for imitation learning of goal-directed policies, thereby circumventing the sparse reward problem. We can apply HER to train $p$ in our setting by extracting any ordered triplet $(s_{t_{1}},s_{t_{2}},s_{t_{3}})$ from $\tau_{s_{0}}^{\pi_{\sigma}}$ and use it as supervised learning targets for $p$ . This is a sensible procedure, as $p$ would then learn to predict optimal sub-goals $s_{t_{2}}^{ * }$ for sub-tasks $(s_{t_{1}}^{ * },s_{t_{3}}^{ * })$ under the assumption that the data was generated by an oracle producing optimal plans $\tau_{s_{0}}^{\pi_{\sigma}}=\sigma^{*}$ .

策略先验
由策略先验 $p$ 引导的最佳优先搜索可以理解为对 $p$ 的策略改进 (如 Silver 等人 2016 年所述)。因此，训练 $p$ 的直接方法是将搜索结果反蒸馏回策略先验，例如通过行为克隆。当在我们的设置中将此方法应用于 DC-MCTS 时，我们通过实验发现，从未经训练的均匀先验 $p$ 开始时，这种方法产生的改进非常缓慢。这是由于在 $S^{*}$ 中，具有非零成功概率 $L>0$ 的计划非常稀疏，相当于常规 MDP 中的稀疏奖励设置。

为了解决这个问题，我们提出应用后见之明经验回放 (Hindsight Experience Replay, HER) (Andrychowicz 等人, 2017)：除了在搜索结果上训练 $p$ 外，我们还在环境中执行计划 $\sigma$ 并收集生成的轨迹，即访问状态的序列 $\tau_{s_{0}}^{\pi_{\sigma}}=(s_{0},s_{1},...,s_{T})$。随后，HER 进行后见之明重标记，即将 $\tau_{s_{0}}^{\pi_{\sigma}}$ 视为“虚构”任务 $(s_{0},s_{T})$ 的近似最优计划，该任务可能与实际任务 $(s_{0},s_{\infty})$ 不同。

在标准 HER 中，这些虚构的专家演示用于目标导向策略的模仿学习，从而规避稀疏奖励问题。我们可以通过从 $\tau_{s_{0}}^{\pi_{\sigma}}$ 中提取任意有序三元组 $(s_{t_{1}},s_{t_{2}},s_{t_{3}})$ 并将其用作 $p$ 的监督学习目标，从而在我们的设置中应用 HER 来训练 $p$。这是一个合理的操作，因为 $p$ 随后会学习在假设数据是由生成最优计划 $\tau_{s_{0}}^{\pi_{\sigma}}=\sigma^{ * }$ 的预言机生成的情况下，预测子任务 $(s_{t_{1}}^{ * },s_{t_{3}}^{ * })$ 的最优子目标 $s_{t_{2}}^{*}$。

We have considerable freedom in choosing which triplets to extract from data and use as supervision, which we can characterize in the following way. Given a task $(s_{0},s_{\infty})$ , the policy prior $p$ defines a distribution over binary partition trees of the task via recursive application (until the terminal symbol $\boldsymbol{\mathcal{O}}$ closes a branch). A sample $\mathcal{T}_ {\sigma}$ from this distribution implies a plan $\sigma$ as described above; but furthermore it also contains the order in which the task was partitioned. Therefore, $p$ not only implies a distribution over plans, but also a search order: Trees with high probability under $p$ will be discovered earlier in the search with DC-MCTS. For generating training targets for supervised training of $p$ , we need to parse a given sequence $\tau_{s_{0}}^{\pi_{\sigma}}=(s_{0},s_{1},\ldots,s_{T})$ into a binary tree. Therefore, when applying HER we are free to chose any deterministic or probabilistic parser that generates a solution tree $\mathcal{T}_ {\tau_{s_{0}}^{\pi_{\sigma}}}$ from re-label HER data $\tau_{s_{0}}^{\pi_{\sigma}}$ . The particular choice of HER-parser will shape the search strategy defined by $p$ . Possible choices include:

在选择从数据中提取哪些三元组作为监督信号时，我们拥有相当大的自由度，这可以通过以下方式描述。给定任务$(s_{0},s_{\infty})$，策略先验$p$通过递归应用（直到终止符号$\boldsymbol{\mathcal{O}}$关闭分支）定义了任务二叉划分树的分布。从该分布中采样的$\mathcal{T}_ {\sigma}$不仅隐含了上述计划$\sigma$，还包含了任务被划分的顺序。因此，$p$不仅定义了计划的分布，还定义了搜索顺序：在DC-MCTS搜索中，高概率的树会优先被发现。为了生成用于监督训练$p$的目标，我们需要将给定序列$\tau_{s_{0}}^{\pi_{\sigma}}=(s_{0},s_{1},\ldots,s_{T})$解析为二叉树。因此，在应用HER时，我们可以自由选择任何确定性或概率性解析器，从重新标记的HER数据$\tau_{s_{0}}^{\pi_{\sigma}}$生成解树$\mathcal{T}_ {\tau_{s_{0}}^{\pi_{\sigma}}}$。HER解析器的具体选择将塑造由$p$定义的搜索策略。可能的选项包括：

4. Related Work

4. 相关工作

Goal-directed multi-task learning has been identified as an important special case of general RL and has been extensively studied. Universal value functions (Schaul et al., 2015) have been established as compact representation for this setting (Kulkarni et al., 2016; An dry ch owicz et al., 2017; Ghosh et al., 2018; Dhiman et al., 2018). This allows to use sub-goals as means for planning, as done in several works such as (Kaelbling & Lozano-Pérez, 2017; Gao et al., 2017; Savinov et al., 2018; Stein et al., 2018; Nasiriany et al., 2019), all of which rely on forward sequential planning. Gabor et al. (2019) use MCTS for traditional sequential planning based on heuristics, sub-goals and macro-actions. Zhang et al. (2018) apply traditional graph planners to find abstract sub-goal sequences. We extend this line of work by showing that the abstraction of sub-goals affords more general search strategies than sequential planning. Work concurrent to ours has independently investigated non-sequential sub-goals planning: Jurgenson et al. (2019) propose bottomup exhaustive planning; as discussed above this is infeasible in large state-spaces. We avoid exhaustive search by topdown search with learned heuristics. Nasiriany et al. (2019) propose gradient-based search jointly over a fixed number of sub-goals for continuous goal spaces. In contrast, DCMCTS is able to dynamically determine the complexity of

目标导向的多任务学习已被确认为通用强化学习(RL)的重要特例，并得到了广泛研究。通用价值函数(Schaul et al., 2015)已成为该场景下的紧凑表示方法(Kulkarni et al., 2016; Andrychowicz et al., 2017; Ghosh et al., 2018; Dhiman et al., 2018)。这使得子目标可作为规划手段，如(Kaelbling & Lozano-Pérez, 2017; Gao et al., 2017; Savinov et al., 2018; Stein et al., 2018; Nasiriany et al., 2019)等研究所示，这些工作均依赖前向序列规划。Gabor et al. (2019)基于启发式、子目标和宏动作，使用蒙特卡洛树搜索(MCTS)进行传统序列规划。Zhang et al. (2018)应用传统图规划器寻找抽象子目标序列。我们通过证明子目标抽象支持比序列规划更通用的搜索策略，拓展了该研究方向。与我们同期的工作也独立探索了非序列子目标规划：Jurgenson et al. (2019)提出自底向上的穷举式规划，如前所述，这在大状态空间不可行。我们通过采用带学习启发式的自顶向下搜索避免穷举。Nasiriany et al. (2019)针对连续目标空间提出基于梯度的固定数量子目标联合搜索。相比之下，DCMCTS能够动态确定...

Figure 2. Grid-world maze examples for wall density $d=0.75$ (top row) and $d=0.95$ (bottom row). (a) The distribution over sub-goals induced by the policy prior $p$ that guides the DC-MCTS planner. (b)-(d) Visualization of the solution tree found by DC-MCTS: (b) The first sub-goal, i.e. at depth 0 of the solution tree. It approximately splits the problem in half. (c) The sub-goals at depth 1. Note there are two of them. (d) The final plan with the depth of each sub-goal shown. See supplementary material for animations.

图 2: 墙体密度 $d=0.75$ (上行) 和 $d=0.95$ (下行) 的网格世界迷宫示例。(a) 由指导 DC-MCTS 规划器的策略先验 $p$ 诱导的子目标分布。(b)-(d) DC-MCTS 找到的解树可视化：(b) 第一个子目标，即解树深度为 0 的节点。它近似将问题对半分割。(c) 深度为 1 的子目标。注意存在两个子目标。(d) 显示各子目标深度的最终规划方案。动画请参阅补充材料。

the optimal plan.

最优方案。

The proposed DC-MCTS planner is a MCTS (Browne et al., 2012) variant, that is inspired by recent advances in best-first or guided search, such as AlphaZero (Silver et al., 2018). It can also be understood as a heuristic, guided version of the classic Floyd-Warshall algorithm. The latter iterates over all sub-goals and then, in an inner loop, over all paths to and from a given sub-goal, for exhaustively computing all shortest paths. In the special case of planar graphs, small sub-goal sets, also known as vertex separators, can be constructed that favourably partition the remaining graph, leading to linear time ASAP algorithms (Henzinger et al., 1997). The heuristic sub-goal proposer $p$ that guides DCMCTS can be loosely understood as a probabilistic version of a vertex separator. Nowak-Vila et al. (2016) also consider neural networks that mimic divide-and-conquer algorithms similar to the sub-goal proposals used here. However, while we do policy improvement for the proposals using search and HER, the networks in (Nowak-Vila et al., 2016) are purely trained by policy gradient methods.

提出的DC-MCTS规划器是MCTS (Browne等人，2012) 的变体，其灵感来源于最佳优先或引导搜索领域的最新进展，例如AlphaZero (Silver等人，2018) 。它也可以被理解为经典Floyd-Warshall算法的启发式引导版本。后者会遍历所有子目标，然后在内部循环中遍历与给定子目标相关的所有路径，以穷举计算所有最短路径。在平面图的特殊情况下，可以构建小子目标集（也称为顶点分隔符）来有利地分割剩余图，从而产生线性时间的ASAP算法 (Henzinger等人，1997) 。引导DCMCTS的启发式子目标提议器$p$可以粗略地理解为顶点分隔符的概率版本。Nowak-Vila等人 (2016) 也考虑了模仿分治算法的神经网络，类似于本文使用的子目标提议。然而，虽然我们使用搜索和HER对提议进行策略改进，但 (Nowak-Vila等人，2016) 中的网络仅通过策略梯度方法进行训练。

Decomposing tasks into sub-problems has been formalized as pseudo trees (Freuder & Quinn, 1985) and AND/OR graphs (Nilsson, N. J., 1980). The latter have been used especially in the context of optimization (Larrosa et al.,

将任务分解为子问题已被形式化为伪树 (Freuder & Quinn, 1985) 和与或图 (Nilsson, N. J., 1980)。后者尤其被用于优化问题的场景 (Larrosa et al.,

2002; Jégou & Terrioux, 2003; Dechter & Mateescu, 2004; Marinescu & Dechter, 2004). Our approach is related to work on using AND/OR trees for sub-goal ordering in the context of logic inference (Ledeniov & Markovitch, 1998). While DC-MCTS is closely related to the $A O^{ * }$ algorithm (Nilsson, N. J., 1980), which is the generalization of the heuristic $A^{ * }$ search to AND/OR search graphs, interesting differences exist: $A O^{*}$ assumes a fixed search heuristic, which is required to be lower bound on the cost-to-go. In contrast, we employ learned value functions and policy priors that are not required to be exact bounds. Relaxing this assumption, thereby violating the principle of “optimism in the face of uncertainty”, necessitates explicit exploration incentives in the SELECT method. Alternatives for searching AND/OR spaces include proof-number search, which has recently been successfully applied to chemical synthesis planning (Kishimoto et al., 2019).

2002; Jégou & Terrioux, 2003; Dechter & Mateescu, 2004; Marinescu & Dechter, 2004)。我们的方法与逻辑推理中子目标排序的AND/OR树应用研究相关(Ledeniov & Markovitch, 1998)。虽然DC-MCTS与$AO^{ * }$算法(Nilsson, N. J., 1980)——即启发式$A^{ * }$搜索在AND/OR搜索图上的泛化形式——存在紧密联系，但存在有趣的差异：$AO^{*}$假定固定的搜索启发函数需满足剩余代价下界要求，而我们采用的学习价值函数和策略先验无需严格满足边界条件。放宽该假设会违反"不确定性下的乐观原则"，因此需要在SELECT方法中显式引入探索激励。AND/OR空间搜索的替代方案包括证明数搜索，该方法近期已成功应用于化学合成规划(Kishimoto et al., 2019)。

5. Experiments

5. 实验

We evaluate the proposed DC-MCTS algorithm on navigation in grid-world mazes as well as on a challenging continuous control version of the same problem. In our experiments, we compared DC-MCTS to standard sequential MCTS (in sub-goal space) based on the fraction of “solved” mazes by executing their plans. The MCTS baseline was implemented by restricting the DC-MCTS algorithm to only expand the “right” sub-problem in line 11 of Algorithm 1; all remaining parameters and design choice were the same for both planners except where explicitly mentioned otherwise. Videos of results can be found at https://sites.google.com/view/dc-mcts/home.

我们在网格世界迷宫导航以及该问题的连续控制挑战版本上评估了提出的DC-MCTS算法。实验中，我们通过执行规划方案解决迷宫的比例，将DC-MCTS与基于子目标空间的标准顺序MCTS进行对比。MCTS基线实现方式是将DC-MCTS算法限制为仅扩展算法1第11行的"右侧"子问题；除非另有明确说明，两个规划器的其余参数和设计选择均保持一致。结果视频可在 https://sites.google.com/view/dc-mcts/home 查看。

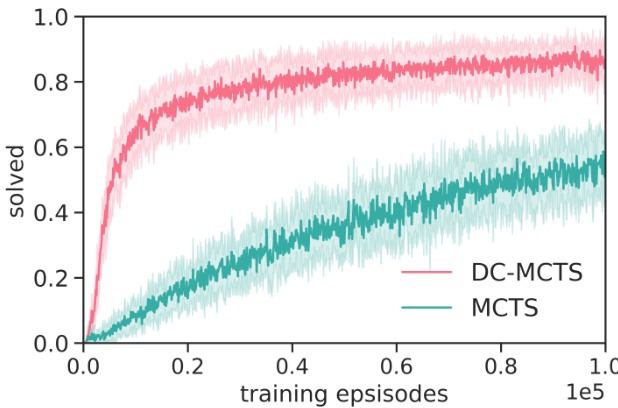
Figure 3. Performance of DC-MCTS and standard MCTS on gridworld maze navigation. Each episode corresponds to a new maze with wall density $d=0.75$ . Curves are averages and standard deviations over 20 different hyper parameters.

图 3: DC-MCTS与标准MCTS在网格世界迷宫导航中的性能对比。每个回合对应一个墙体密度 $d=0.75$ 的新迷宫。曲线为20组不同超参数下的平均值及标准差。

5.1. Grid-World Mazes

5.1. 网格世界迷宫

In this domain, each task consists of a new, procedurally generated maze on a $21\times21$ grid with start and goal locations $\left(s_{0},s_{\infty}\right)\in{1,\ldots,21}^{2}$ , see Figure 2. Task difficulty was controlled by the density of walls $d$ (under connected ness constraint), where the easiest setting $d=0.0$ corresponds to no walls and the most difficult one $d=1.0$ implies so-called perfect or singly-connected mazes. The task embedding $c_{\mathcal{M}}$ was given as the maze layout and $(s_{0},s_{\infty})$ encoded together as a feature map of $21\times21$ categorical variables with 4 categories each (empty, wall, start and goal location). The underlying MDPs have 5 primitive actions: up, down, left, right and NOOP. For sake of simplicity, we first tested our proposed approach by hard-coding a low-level policy $\pi^{0}$ as well as its value oracle $\boldsymbol{v}^{\pi^{0}}$ in the following way. If in state $s$ and conditioned on a goal $s^{\prime}$ , and if $s$ is adjacent to $s^{\prime}$ , $\pi_{s^{\prime}}^{0}$ successfully reaches $s^{\prime}$ with probability 1 in one step, i.e. $\begin{array}{r}{v^{\pi^{0}}(s,s^{\prime})=1}\end{array}$ ; otherwise $\begin{array}{r}{v^{\pi^{0}}(s,s^{\prime})=0}\end{array}$ . If $\pi_{s^{\prime}}^{0}$ is nevertheless executed, the agent moves to a random empty tile adjacent to $s$ . Therefore, $\pi^{0}$ is the “most myopic” goaldirected policy that can still navigate everywhere.

在该领域中，每个任务由程序化生成的 $21\times21$ 网格迷宫构成，包含起点和终点位置 $\left(s_{0},s_{\infty}\right)\in{1,\ldots,21}^{2}$ (见图2)。任务难度通过墙体密度 $d$ (在连通性约束下)控制，其中最简单设置 $d=0.0$ 对应无墙体，最困难设置 $d=1.0$ 对应所谓完美或单连通迷宫。任务嵌入 $c_{\mathcal{M}}$ 以迷宫布局和 $(s_{0},s_{\infty})$ 共同编码的形式给出，表示为 $21\times21$ 分类变量特征图，每个变量有4个类别(空地、墙体、起点和终点)。底层MDP包含5个基本动作：上、下、左、右和空操作(NOOP)。

为简化问题，我们首先通过硬编码低级策略 $\pi^{0}$ 及其值函数 $\boldsymbol{v}^{\pi^{0}}$ 来测试所提方法，具体实现如下：若在状态 $s$ 下以目标 $s^{\prime}$ 为条件，且 $s$ 与 $s^{\prime}$ 相邻时，策略 $\pi_{s^{\prime}}^{0}$ 能以概率1在一步内成功到达 $s^{\prime}$，即 $\begin{array}{r}{v^{\pi^{0}}(s,s^{\prime})=1}\end{array}$；否则 $\begin{array}{r}{v^{\pi^{0}}(s,s^{\prime})=0}\end{array}$。若仍执行 $\pi_{s^{\prime}}^{0}$，智能体会随机移动到与 $s$ 相邻的空地。因此，$\pi^{0}$ 是"最短视"但仍能全局导航的目标导向策略。

For each maze, MCTS and DC-MCTS were given a search budget of 200 calls to the low-level value oracle $\boldsymbol{v}^{\pi^{0}}$ . We implemented the search heuristics, i.e. policy prior $p$ and high-level value function $v$ , as convolutional neural networks which operate on input $c_{\mathcal{M}}$ ; details for the network architectures are given in Appendix B.3. With untrained networks, both planners were unable to solve the task $(<2%$ success probability), as shown in Figure 3. This illustrates that a search budget of 200 evaluations of $\boldsymbol{v}^{\pi^{0}}$ is insufficient for unguided planners to find a feasible path in most mazes. This is consistent with standard exhaustive SSSP / APSP graph planners requiring $21^{4}>10^{5}\gg200$ evaluations for optimal planning in the worst case on these tasks.

对于每个迷宫，MCTS和DC-MCTS的低级价值预言器$\boldsymbol{v}^{\pi^{0}}$的搜索预算设定为200次调用。我们将搜索启发式（即策略先验$p$和高级价值函数$v$）实现为卷积神经网络，其输入为$c_{\mathcal{M}}$；网络架构的详细信息见附录B.3。如图3所示，使用未经训练的网络时，两种规划器均无法完成任务（成功率<2%）。这表明，在大多数迷宫中，200次$\boldsymbol{v}^{\pi^{0}}$评估的搜索预算不足以让无引导的规划器找到可行路径。这与标准穷举SSSP/APSP图规划器在最坏情况下需要$21^{4}>10^{5}\gg200$次评估以实现最优规划的结果一致。

Next, we trained both search heuristics $v$ and $p$ as detailed in Section 3.2. In particular, the sub-goal proposal $p$ was also trained on hindsight-relabeled experience data, where for DC-MCTS we used the temporally balanced parser and for MCTS the corresponding left-first parser. Training of the heuristics greatly improved the performance of both planners. Figure 3 shows learning curves for mazes with wall density $d=0.75$ . DC-MCTS exhibits substantially improved performance compared to MCTS, and when compared at equal performance levels, DC-MCTS requires 5 to 10-times fewer training episodes than MCTS. The learned sub-goal proposal $p$ for DC-MCTS is visualized for two example tasks in Figure 2 (further examples are given in the Appendix in Figure 8). Probability mass concentrates on promising sub-goals that are far from both start and goal, approximately partitioning the task into equally hard subtasks.

接下来，我们按照第3.2节的详细说明训练了两种搜索启发式方法$v$和$p$。其中，子目标提议$p$的训练也使用了 hindsight-relabeled 经验数据：DC-MCTS采用时序平衡解析器，MCTS则使用对应的左优先解析器。启发式训练显著提升了两种规划器的性能。图3展示了墙体密度$d=0.75$迷宫的学习曲线。DC-MCTS相比MCTS展现出显著性能提升，在相同性能水平下，DC-MCTS所需的训练轮次比MCTS少5到10倍。图2展示