Concept Learning with Energy-Based Models

基于能量的模型的概念学习

Abstract

摘要

Many hallmarks of human intelligence, such as generalizing from limited experience, abstract reasoning and planning, analogical reasoning, creative problem solving, and capacity for language require the ability to consolidate experience into concepts, which act as basic building blocks of understanding and reasoning. We present a framework that defines a concept by an energy function over events in the environment, as well as an attention mask over entities participating in the event. Given few demonstration events, our method uses inference-time optimization procedure to generate events involving similar concepts or identify entities involved in the concept. We evaluate our framework on learning visual, quantitative, relational, temporal concepts from demonstration events in an unsupervised manner. Our approach is able to successfully generate and identify concepts in a few-shot setting and resulting learned concepts can be reused across environments. Example videos of our results are available at sites.google.com/site/energy concept models

人类智能的许多标志性特征，如从有限经验中泛化、抽象推理与规划、类比推理、创造性问题解决以及语言能力，都需要将经验整合为概念的能力，这些概念构成了理解和推理的基本构建模块。我们提出了一种框架，通过环境事件的能量函数 (energy function) 和参与事件的实体注意力掩码 (attention mask) 来定义概念。给定少量演示事件，我们的方法利用推理时优化程序生成涉及相似概念的事件，或识别参与概念的实体。我们在无监督环境下通过演示事件评估了该框架学习视觉、定量、关系和时序概念的能力。该方法能够在少样本 (few-shot) 设置中成功生成和识别概念，且所学概念可跨环境复用。结果示例视频详见 sites.google.com/site/energy concept models

1 Introduction

1 引言

Many hallmarks of human intelligence, such as generalizing from limited experience, abstract reasoning and planning, analogical reasoning, creative problem solving, and capacity for language and explanation are still lacking in the artificial intelligent agents. We, as others [25, 22, 21] believe what enables these abilities is the capacity to consolidate experience into concepts, which act as basic building blocks of understanding and reasoning.

人类智能的许多标志性特征，如从有限经验中泛化、抽象推理与规划、类比推理、创造性问题解决以及语言和解释能力，在AI智能体中仍然缺失。我们与其他人[25, 22, 21]一样认为，实现这些能力的关键在于将经验整合为概念的能力，这些概念是理解和推理的基本构建模块。

Examples of concepts include visual ("red" or "square"), spatial ("inside", "on top of"), temporal $({''s l o w'',~{''}a f t e r'})$ , social ("aggressive", "helpful") among many others [22]. These concepts can be either identified or generated - one can not only find a square in the scene, but also create a square, either physical or imaginary. Importantly, humans also have a largely unique ability to combine concepts composition ally ("red square") and recursively ("move inside moving square") - abilities reflected in the human language. This allows expressing an exponentially large number of concepts, and acquisition of new concepts in terms of others. We believe the operations of identification, generation, composition over concepts are the tools with which intelligent agents can understand and communicate existing experiences and reason about new ones.

概念的例子包括视觉的（"红色"或"方形"）、空间的（"内部"、"顶部"）、时间的（"缓慢"、"之后"）、社会的（"侵略性"、"乐于助人"）等众多类型 [22]。这些概念既可以被识别也可以被生成——人们不仅能在场景中发现一个方形，还能创造出一个方形，无论是实体的还是想象的。重要的是，人类还具备一种很大程度上独特的能力，能够以组合方式（"红色方形"）和递归方式（"移动中的方形内部移动"）结合概念——这些能力体现在人类语言中。这使得人类能够表达数量呈指数级增长的概念，并通过其他概念来获取新概念。我们认为，对概念进行识别、生成和组合的操作，是智能体理解和交流现有经验、并对新经验进行推理的工具。

Crucially, these operations must be performed on the fly throughout the agent’s execution, rather than merely being a static product of an offline training process. Execution-time optimization, as in recent work on meta-learning [6] plays a key role in this. We pose the problem of parsing experiences into an arrangement of concepts as well as the problems of identifying and generating concepts as optimization s performed during execution lifetime of the agent. The meta-level training is performed by taking into account such processes in the inner level.

关键在于，这些操作必须在智能体执行过程中实时完成，而不仅仅是离线训练过程的静态产物。执行时优化（如近期元学习研究[6]所示）在此起着关键作用。我们将经验解析为概念组合的问题，以及概念识别与生成的问题，都视为智能体执行生命周期内进行的优化过程。元层级训练通过考量这些内部层级的处理过程来实现。

Specifically, a concept in our work is defined by an energy function taking as input an event configuration (represented as trajectories of entities in the current work), as well as an attention mask over entities in the event. Zero-energy event and attention configurations imply that event entities selected by the attention mask satisfy the concept. Compositions of concepts can then be created by simply summing energies of constituent concepts. Given a particular event, optimization can be used to identify entities belonging to a concept by solving for attention mask that leads to zero-energy configuration. Similarly, an example of a concept can be generated by optimizing for a zero-energy event configuration. See Figure 1 for examples of these two processes.

具体而言，我们工作中的概念由一个能量函数定义，该函数以事件配置（在当前工作中表示为实体的轨迹）以及事件中实体的注意力掩码作为输入。零能量事件和注意力配置意味着被注意力掩码选择的事件实体满足该概念。通过简单叠加组成概念的能量函数，即可创建复合概念。给定特定事件时，可通过求解产生零能量配置的注意力掩码，来优化识别属于该概念的实体。类似地，通过优化零能量事件配置可生成概念的示例。这两个过程的示例见图1:

The energy function defines a family of concepts, from which a particular concept is selected with a specific concept code. Encoding of event and attention configurations can be achieved by executiontime optimization over concept codes. Once an event is encoded, the resulting concept code structure can be used to re-enact the event under different initial configurations (task of imitation learning), recognize similar events, or concisely communicate the nature of the event. We believe there is a strong link between concept codes and language, but leave it unexplored in this work.

能量函数定义了一系列概念族，通过特定概念代码从中选定具体概念。事件与注意力配置的编码可通过执行时对概念代码的优化实现。一旦事件被编码，生成的概念代码结构可用于在不同初始配置下重现该事件（模仿学习任务）、识别相似事件，或简洁传达事件本质。我们认为概念代码与语言存在深刻关联，但本文未对此展开探讨。

At the meta level, the energy function is the only entity that needs to be learned. This is different from generative model or inverse reinforcement learning approaches, which typically also learn an explicit generator/policy function, whereas we define it implicitly via optimization. Our advantage as that the learned energy function can be reused in other domains, for example using a robot platform to reenact concepts in the physical world. Such transfer is not possible with an explicit generation/policy function, as it is domain-specific.

在元层面上，能量函数 (energy function) 是唯一需要学习的实体。这与生成式模型 (generative model) 或逆强化学习方法不同——后者通常还需要学习显式的生成器/策略函数，而我们通过优化隐式定义该函数。我们的优势在于，学习到的能量函数可跨领域复用，例如使用机器人平台在物理世界中重现概念。这种迁移对于显式生成/策略函数是不可能的，因为后者具有领域特定性。

Figure 1: Examples of generation and identification processes for a "square" concept. a) Given initial state $\mathbf{x}^{0}$ and attention mask a, square consisting of entities in a is formed via optimization over $\mathbf{x}^{1}$ . b) Given states $\mathbf{x}$ , entities comprising a square are found by optimization over attention mask a.

图 1: "方形"概念的生成与识别过程示例。a) 给定初始状态 $\mathbf{x}^{0}$ 和注意力掩码 a，通过优化 $\mathbf{x}^{1}$ 形成由 a 中实体组成的方形。b) 给定状态 $\mathbf{x}$ ，通过优化注意力掩码 a 找到构成方形的实体。

2 Related Work

2 相关工作

We draw upon several areas for inspiration in our work, including energy-based models, concept learning, inverse reinforcement learning and meta-learning.

我们的工作从多个领域汲取灵感，包括基于能量的模型 (energy-based models) 、概念学习、逆强化学习和元学习。

Energy-based modelling approaches have a long history in machine learning, commonly used for density modeling [4, 16, 26, 9]. These approaches typically aim to learn a function that assigns low energy values to inputs in the data distribution and high energy values to other inputs. The resulting models can then be used to either discriminate whether or not a query input comes from the data distribution, or to generate new samples from the data distribution. One common choice for sampling procedure is Markov Chain Monte Carlo (MCMC), however it suffers from slow mixing and often requires many iterative steps to generate samples [26]. Another choice is to train a separate network to generate samples [18]. Generative Adversarial Networks [11] can be thought of as instances of this approach [7]. The key difficulty in training energy-based models lies in estimating their partition function, with many approaches relying on the sampling procedure to estimate it or further approximations [16]. Our approach avoids both the slow mixing of MCMC and the need to train a separate network. We use sampling procedure based on gradient of the energy (which mixes much faster than gradient-free MCMC), while training the energy function to have a gradient field that produces good samples.

基于能量的建模方法在机器学习领域有着悠久历史，常用于密度建模 [4, 16, 26, 9]。这类方法通常旨在学习一个函数，该函数为数据分布中的输入分配低能量值，而为其他输入分配高能量值。所得模型可用于判别查询输入是否来自数据分布，或从数据分布生成新样本。常见的采样方法是马尔可夫链蒙特卡洛 (MCMC)，但其混合速度慢且通常需要多次迭代才能生成样本 [26]。另一种方法是训练单独的网络生成样本 [18]，生成对抗网络 [11] 可视为该方法的实例 [7]。训练基于能量的模型主要难点在于估计其配分函数，许多方法依赖采样过程进行估计或采用近似计算 [16]。我们的方法既避免了 MCMC 的慢混合问题，也无需训练单独网络：采用基于能量梯度的采样方法（其混合速度远快于无梯度 MCMC），同时通过训练使能量函数的梯度场能产生优质样本。

The problem of learning and reasoning over concepts or other abstract representations has long been of interest in machine learning (see [21, 3] for review). Approaches based on Bayesian reasoning have notably been applied for numerical concepts [32]. A recent framework of [15] focuses on visual concepts such as color and shape, where concepts are defined in terms of distributions over latent variables produced by a variation al auto encoder. Instead of focusing solely on visual concepts from pixel input, our work explores learning of concepts that involve complex interaction of multiple entities.

学习和推理概念或其他抽象表示的问题长期以来在机器学习领域备受关注（综述见[21, 3]）。基于贝叶斯推理的方法尤其适用于数值概念[32]。近期[15]提出的框架专注于颜色和形状等视觉概念，这些概念被定义为变分自编码器生成的潜变量分布。与仅关注来自像素输入的视觉概念不同，我们的工作探索了涉及多实体复杂交互的概念学习。

Our method aims to learn concepts from demonstration events in the environment. A similar problem is tackled by inverse reinforcement learning (IRL) approaches, which aim to infer an underlying cost function that gives rise to demonstrated events. Our method’s concept energy functions are analogous to the cost or negative of value functions recovered by IRL approaches. Under this view, multiple concepts can easily be composed simply by summing their energy functions. Concepts are then enacted in our approach via energy minimization, mirroring the application a forward reinforcement learning step in IRL methods. Max entropy [36] is a common IRL formulation, and our method closely resembles recent instantiations of it [8, 5].

我们的方法旨在从环境中的示范事件中学习概念。类似的问题由逆强化学习 (IRL) 方法解决，其目标是推断出导致示范事件的潜在成本函数。我们方法中的概念能量函数类似于IRL方法恢复的成本函数或价值函数的负值。在这种视角下，多个概念可以简单地通过对其能量函数求和来组合。随后，我们的方法通过能量最小化来实施这些概念，这反映了IRL方法中前向强化学习步骤的应用。最大熵 [36] 是一种常见的IRL公式，我们的方法与它的最新实例 [8, 5] 非常相似。

Our method relies on performing inference-time optimization processes for concept generation and identification, as well as for determining which concepts are involved in an event. The training is performed by taking behavior of these inner optimization processes into account, similar to the meta-learning formulations of [6]. Relatedly, iterative processes have been explored in the context of control [30, 29, 34, 14, 28] and image generation [13].

我们的方法依赖于在推理时执行优化过程，用于概念生成和识别，以及确定哪些概念参与了某个事件。训练过程会考虑这些内部优化过程的行为，类似于[6]中提出的元学习框架。相关研究在控制[30, 29, 34, 14, 28]和图像生成[13]领域也探索了迭代过程的应用。

3 Energy-Based Concept Models

3 基于能量的概念模型

Concepts operate over events, which in this work is a trajectory of $T$ states $\mathbf{x}=\left[\mathbf{x}^{0},...,\mathbf{x}^{T}\right]$ . Each state contains a collection of $N$ entities $\mathbf{x}^{t}=[\mathbf{x}_ {0},...,\mathbf{x}_ {N}]$ and each entity $\mathbf{x}_{i}^{t}$ can contain information such as position and color of the entity. Considering entire trajectories and entities allows us to model temporal or relational concepts, unlike work that focuses on visual concepts [15]. Attention over entities in the event is specified by a mask $\mathbf{a}\in\mathbb{R}^{N}$ over each of the entities.

概念作用于事件上，在本研究中，事件是指由 $T$ 个状态 $\mathbf{x}=\left[\mathbf{x}^{0},...,\mathbf{x}^{T}\right]$ 组成的轨迹。每个状态包含 $N$ 个实体 $\mathbf{x}^{t}=[\mathbf{x}_ {0},...,\mathbf{x}_ {N}]$，每个实体 $\mathbf{x}_{i}^{t}$ 可以包含诸如位置和颜色等信息。与专注于视觉概念的研究[15]不同，考虑整个轨迹和实体使我们能够建模时间或关系概念。事件中实体的注意力由每个实体上的掩码 $\mathbf{a}\in\mathbb{R}^{N}$ 指定。

Existence of a particular concept is given by energy function $E(\mathbf{x},\mathbf{a},\mathbf{w})\in\mathbb{R}^{+}$ , where parameter vector w specifies a particular concept from a family. The interpretation of w is similar to that of a code in an auto encoder. $E(\mathbf{x},\mathbf{a},\mathbf{w})=0$ when state trajectory $\mathbf{x}$ under attention mask a over entities satisfies the concept w. Otherwise, $E(\mathbf{x},\mathbf{a},\mathbf{w})>0$ . The conditional probabilities of a particular event configuration belonging to a concept and a particular attention mask identifying a concept are given by the Boltzmann distributions:

特定概念的存在由能量函数 $E(\mathbf{x},\mathbf{a},\mathbf{w})\in\mathbb{R}^{+}$ 给出，其中参数向量 w 指定了该概念族中的某个具体概念。w 的解释类似于自编码器中的编码。当状态轨迹 $\mathbf{x}$ 在实体注意力掩码 a 下满足概念 w 时，$E(\mathbf{x},\mathbf{a},\mathbf{w})=0$；否则 $E(\mathbf{x},\mathbf{a},\mathbf{w})>0$。特定事件配置属于某概念的条件概率，以及特定注意力掩码识别某概念的条件概率，均由玻尔兹曼分布给出：

Given concept code $\mathbf{w}$ , the energy function can be used for both generation and identification of a concept implicitly via optimization (see Figure 1):

给定概念代码 $\mathbf{w}$，能量函数可通过优化隐式地用于概念的生成和识别（见图 1）：

$$
\mathbf{x}(\mathbf{a})=\underset{\mathbf{x}}{\operatorname{argmin}}E(\mathbf{x},\mathbf{a},\mathbf{w})\qquad\mathbf{a}(\mathbf{x})=\underset{\mathbf{a}}{\operatorname{argmin}}E(\mathbf{x},\mathbf{a},\mathbf{w})
$$

$$
\mathbf{x}(\mathbf{a})=\underset{\mathbf{x}}{\operatorname{argmin}}E(\mathbf{x},\mathbf{a},\mathbf{w})\qquad\mathbf{a}(\mathbf{x})=\underset{\mathbf{a}}{\operatorname{argmin}}E(\mathbf{x},\mathbf{a},\mathbf{w})
$$

Samples from distributions in (1) can be generated via stochastic gradient Langevin dynamics, effectively performing stochastic minimization in (2):

来自(1)中分布的样本可以通过随机梯度朗之万动力学生成，有效实现(2)中的随机最小化：

$$
\begin{array}{r l}&{\tilde{\mathbf{x}}\sim\pi_{x}\left(\mathbf{\sigma}\cdot|\mathbf{\sigma}\mathbf{a},\mathbf{w}\right)=\mathbf{x}^{K},\mathbf{x}^{k}=\mathbf{x}^{k-1}+\frac{\alpha}{2}\nabla_{\mathbf{x}}E(\mathbf{x},\mathbf{a},\mathbf{w})+\omega^{k}}\ &{\tilde{\mathbf{a}}\sim\pi_{a}\left(\mathbf{\sigma}\cdot|\mathbf{\sigma}\mathbf{x},\mathbf{w}\right)=\mathbf{a}^{K},\mathbf{a}^{k}=\mathbf{a}^{k-1}+\frac{\alpha}{2}\nabla_{\mathbf{a}}E(\mathbf{x},\mathbf{a},\mathbf{w})+\omega^{k},\omega^{k}\sim\mathcal{N}(0,\alpha)}\end{array}
$$

$$
\begin{array}{r l}&{\tilde{\mathbf{x}}\sim\pi_{x}\left(\mathbf{\sigma}\cdot|\mathbf{\sigma}\mathbf{a},\mathbf{w}\right)=\mathbf{x}^{K},\mathbf{x}^{k}=\mathbf{x}^{k-1}+\frac{\alpha}{2}\nabla_{\mathbf{x}}E(\mathbf{x},\mathbf{a},\mathbf{w})+\omega^{k}}\ &{\tilde{\mathbf{a}}\sim\pi_{a}\left(\mathbf{\sigma}\cdot|\mathbf{\sigma}\mathbf{x},\mathbf{w}\right)=\mathbf{a}^{K},\mathbf{a}^{k}=\mathbf{a}^{k-1}+\frac{\alpha}{2}\nabla_{\mathbf{a}}E(\mathbf{x},\mathbf{a},\mathbf{w})+\omega^{k},\omega^{k}\sim\mathcal{N}(0,\alpha)}\end{array}
$$

This stochastic optimization procedure is performed during execution time of the algorithm and is reminiscent of the Monte Carlo sampling procedures in prior work on energy-based models [16, 26, 9]. The procedure differs from approaches that use explicit generator functions [4, 20, 18] or explicit attention mechanisms, such as dot product attention [24].

该随机优化过程在算法执行时进行，让人联想到先前基于能量模型(energy-based models)研究中使用的蒙特卡洛采样方法[16, 26, 9]。此方法与使用显式生成函数[4, 20, 18]或显式注意力机制(如点积注意力[24])的方法不同。

It is shown in [35] that $\tilde{\bf x}$ and a will approach samples from posterior distributions $p$ as $K\mapsto\infty$ and $\alpha\mapsto0$ . However in practice it is only possible to execute the dynamics for a finite number of steps (we use $K=10$ in all our experiments). This truncated procedure results in samples drawn from a biased distribution, which we call $\pi$ and which may not be equal to $p$ . Similar issues of slow mixing are also present in prior work, which typically uses non-differentiable sampling procedures. In our case, the sampling procedure in equation (3) can be differentiated and can be trained to produce samples close to true distribution $p$ .

[35] 中指出，当 $K\mapsto\infty$ 和 $\alpha\mapsto0$ 时，$\tilde{\bf x}$ 和 a 会趋近于后验分布 $p$ 的样本。但在实际应用中，动力学过程只能执行有限步数（我们所有实验均采用 $K=10$）。这种截断过程会导致采样结果来自一个有偏分布，我们称之为 $\pi$，该分布可能与 $p$ 不相等。类似慢混合问题在先前工作中同样存在，那些研究通常采用不可微的采样过程。而本文的式 (3) 采样过程可微分，且可通过训练使样本接近真实分布 $p$。

There are many possible choices for the energy function as long as it is non-negative. The specific form we use in this work is based on relation network architecture [27] for its ability to easily capture interactions between pairs of entities

能量函数只要非负就有多种可能选择。本文采用的具体形式基于关系网络架构 [27]，因其能轻松捕捉实体对间的交互关系。

$$
E_{\theta}(\mathbf{x},\mathbf{a},\mathbf{w})=f_{\theta}(\sum_{t,i,j}\sigma(\mathbf{a}_ {i})\sigma(\mathbf{a}_ {j})\cdot g_{\theta}(\mathbf{x}_ {i}^{t},\mathbf{x}_{j}^{t},\mathbf{w}),\mathbf{w})^{2}
$$

$$
E_{\theta}(\mathbf{x},\mathbf{a},\mathbf{w})=f_{\theta}(\sum_{t,i,j}\sigma(\mathbf{a}_ {i})\sigma(\mathbf{a}_ {j})\cdot g_{\theta}(\mathbf{x}_ {i}^{t},\mathbf{x}_{j}^{t},\mathbf{w}),\mathbf{w})^{2}
$$

Where $f$ and $g$ are multi-layer neural networks that each take concept code as part of their input. $\sigma$ is the sigmoid function and is used to gate the entity pairs by their attention masks.

其中 $f$ 和 $g$ 是多层神经网络，它们都将概念代码作为输入的一部分。$\sigma$ 是 sigmoid 函数，用于通过注意力掩码对实体对进行门控。

4 Learning Concepts from Events

4 从事件中学习概念

To learn concepts from experience grounded in events, we pose a few-shot prediction task. Given a few demonstration examples $X^{\mathrm{{deino}}}$ containing tuples $(\mathbf{x},\mathbf{a})$ and initial state $\mathbf{x}^{0}$ for a new event in $X^{\mathrm{train}}$ , the task is to predict attention a and the future state trajectory $\mathbf{x}^{1:T}$ of the new event. The new event may contain a different configuration or number of entities, so it is not possible to directly transfer attention mask, for instance. To simplify notation, we consider prediction of only one future state $\mathbf{x}^{1}$ , although predicting more states is straightforward. The procedure is depicted in Figure 2.

为了从基于事件的经验中学习概念，我们提出了一个少样本预测任务。给定一些演示示例 $X^{\mathrm{{deino}}}$ ，其中包含元组 $(\mathbf{x},\mathbf{a})$ 和 $X^{\mathrm{train}}$ 中新事件的初始状态 $\mathbf{x}^{0}$ ，任务是预测新事件的注意力 a 和未来状态轨迹 $\mathbf{x}^{1:T}$ 。新事件可能包含不同的实体配置或数量，因此无法直接转移注意力掩码等。为简化表示，我们仅考虑预测一个未来状态 $\mathbf{x}^{1}$ ，尽管预测更多状态也很直接。该过程如图 2 所示。

Figure 2: Example of a few-shot prediction task we use to learn concept energy functions.

图 2: 用于学习概念能量函数(concept energy functions)的少样本预测任务示例。

We follow the maximum entropy inverse reinforcement learning formulation [36] and assume demonstrations are samples from the distributions given by the energy function $E$ . Given an inferred concept code w (details discussed below), finding energy function parameters $\theta$ is posed as as maximum likelihood estimation problem over future state and attention given initial state. The resulting loss for a particular dataset $X$ is

我们遵循最大熵逆强化学习框架 [36]，并假设演示样本来自由能量函数 $E$ 给出的分布。给定推断出的概念编码 w（具体讨论见下文），寻找能量函数参数 $\theta$ 被表述为基于初始状态对未来状态和注意力进行最大似然估计的问题。特定数据集 $X$ 的最终损失函数为

$$
\mathcal{L}_ {p}^{\mathrm{ML}}(X,\mathbf{w})=\mathbb{E}_ {(\mathbf{x},\mathbf{a})\sim X}\left[-\log p\left(\mathbf{x}^{1},\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}\right)\right]
$$

$$
\mathcal{L}_ {p}^{\mathrm{ML}}(X,\mathbf{w})=\mathbb{E}_ {(\mathbf{x},\mathbf{a})\sim X}\left[-\log p\left(\mathbf{x}^{1},\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}\right)\right]
$$

Where the joint probability can be decomposed in terms of probabilities in (1) as

联合概率可以按照(1)式中的概率分解为

$$
\log p\left(\mathbf{x}^{1},\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}\right)=\log p\left(\mathbf{x}^{1}\mid\mathbf{a},\mathbf{w}_ {x}\right)+\log p\left(\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}_ {a}\right),\quad\mathbf{w}=[\mathbf{w}_ {x},\mathbf{w}_{a}]
$$

$$
\log p\left(\mathbf{x}^{1},\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}\right)=\log p\left(\mathbf{x}^{1}\mid\mathbf{a},\mathbf{w}_ {x}\right)+\log p\left(\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}_ {a}\right),\quad\mathbf{w}=[\mathbf{w}_ {x},\mathbf{w}_{a}]
$$

We use two concept codes, $\mathbf{w}_ {x}$ and ${\bf w}_ {a}$ to specify the joint probability. The interpretation is that $\mathbf{w}_ {x}$ specifies the concept of the action that happens in the event (i.e. "be in center of") while ${\bf w}_{a}$ specifies the argument the action happens over (i.e. "square"). This is a concept structure or syntax that describes the event. The concept codes are interchangeable and same concept code can be used either as action or as an argument because the energy function defining the concept can either be used for generation or identification. This importantly allows concepts to be understood from their usage under multiple contexts.

我们使用两个概念编码 $\mathbf{w}_ {x}$ 和 ${\bf w}_ {a}$ 来指定联合概率。其含义是：$\mathbf{w}_ {x}$ 指定事件中发生的动作概念（例如"位于中心"），而 ${\bf w}_{a}$ 指定该动作作用的对象参数（例如"方形"）。这是一种描述事件的概念结构或语法。概念编码可互换使用，同一概念编码既可作为动作也可作为参数，因为定义该概念的能量函数既可用于生成也可用于识别。这一特性使得概念能够通过其在多种上下文中的使用方式被理解。

Conditioned on the two codes concatenated as $\mathbf{w}$ , the two log-likelihood terms in (6) can be approximated as (see Appendix for the derivation)

以拼接后的编码 $\mathbf{w}$ 为条件，(6) 式中的两个对数似然项可近似为 (推导过程见附录)

$$
\begin{array}{r l r l}&{\log p\left(\mathbf{x}^{1}\mid\mathbf{a},\mathbf{w}_ {x}\right)\approx-\left[E(\mathbf{x}^{1},\mathbf{a},\mathbf{w}_ {x})-E(\tilde{\mathbf{x}},\mathbf{a},\mathbf{w}_ {x})\right]_ {+}}&&{\tilde{\mathbf{x}}\sim\boldsymbol{\pi}_ {x}\left(\mathbf{\nabla}\cdot\mid\mathbf{a},\mathbf{w}_ {x}\right)}\ &{\log p\left(\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}_ {a}\right)\approx-\left[E(\mathbf{x}^{0},\mathbf{a},\mathbf{w}_ {a})-E(\mathbf{x}^{0},\tilde{\mathbf{a}},\mathbf{w}_ {a})\right]_ {+}}&&{\tilde{\mathbf{a}}\sim\boldsymbol{\pi}_ {a}\left(\mathbf{\nabla}\cdot\mid\mathbf{x}^{0},\mathbf{w}_{a}\right)}\end{array}
$$

$$
\begin{array}{r l r l}&{\log p\left(\mathbf{x}^{1}\mid\mathbf{a},\mathbf{w}_ {x}\right)\approx-\left[E(\mathbf{x}^{1},\mathbf{a},\mathbf{w}_ {x})-E(\tilde{\mathbf{x}},\mathbf{a},\mathbf{w}_ {x})\right]_ {+}}&&{\tilde{\mathbf{x}}\sim\boldsymbol{\pi}_ {x}\left(\mathbf{\nabla}\cdot\mid\mathbf{a},\mathbf{w}_ {x}\right)}\ &{\log p\left(\mathbf{a}\mid\mathbf{x}^{0},\mathbf{w}_ {a}\right)\approx-\left[E(\mathbf{x}^{0},\mathbf{a},\mathbf{w}_ {a})-E(\mathbf{x}^{0},\tilde{\mathbf{a}},\mathbf{w}_ {a})\right]_ {+}}&&{\tilde{\mathbf{a}}\sim\boldsymbol{\pi}_ {a}\left(\mathbf{\nabla}\cdot\mid\mathbf{x}^{0},\mathbf{w}_{a}\right)}\end{array}
$$

Where $[\cdot]_{+}=\log(1+\exp(\cdot))$ is the softplus operator. This form is similar to contrastive divergence [16] and structured SVM forms [2] and is a special case of guided cost learning formulation [8]. The approximation comes from sample-based estimates of the partition functions for $p(\mathbf{x})$ and $p(\mathbf{a})$ .

其中 $[\cdot]_{+}=\log(1+\exp(\cdot))$ 是softplus运算符。这种形式类似于对比散度 [16] 和结构化SVM形式 [2] ，并且是引导式成本学习公式 [8] 的特例。该近似来源于对 $p(\mathbf{x})$ 和 $p(\mathbf{a})$ 配分函数的样本估计。

The above equations make use of truncated and biased gradient-based sampling distributions $\pi_{x}$ and $\pi_{a}$ in (3) to estimate the respective partition functions. Following [8], the approximation error in these estimates is minimal when KL divergence between biased distribution $\pi$ and true distribution exp{-E} /Z is minimized:

上述方程利用(3)中截断且有偏的基于梯度的采样分布$\pi_{x}$和$\pi_{a}$来估计各自的配分函数。根据[8], 当有偏分布$\pi$与真实分布exp{-E} /Z之间的KL散度最小时, 这些估计的近似误差最小:

$$
\begin{array}{r l}&{\mathcal{L}_ {\boldsymbol{\pi}}^{\mathrm{KL}}(X,\mathbf{w})=\mathrm{KL}\left(\boldsymbol{\pi}_ {x}||\boldsymbol{p}_ {x}\right)+\mathrm{KL}\left(\boldsymbol{\pi}_ {a}||\boldsymbol{p}_ {a}\right)}\ &{\qquad=\mathbb{E}_ {(\mathbf{x},\mathbf{a})\sim X}\left[E(\tilde{\mathbf{x}},\mathbf{a},\mathbf{w}_ {x})+E(\mathbf{x}^{0},\tilde{\mathbf{a}},\mathbf{w}_ {a})\right]+\mathrm{H}\left[\boldsymbol{\pi}_ {x}\right]+\mathrm{H}\left[\boldsymbol{\pi}_ {a}\right]}\ &{\qquad\tilde{\mathbf{x}}\sim\boldsymbol{\pi}_ {x}\left(\mathbf{\nabla}\cdot|\mathbf{a},\mathbf{w}_ {x}\right),\tilde{\mathbf{a}}\sim\boldsymbol{\pi}_ {a}\left(\mathbf{\nabla}\cdot|\mathbf{x}^{0},\mathbf{w}_{a}\right)}\end{array}
$$

$$
\begin{array}{r l}&{\mathcal{L}_ {\boldsymbol{\pi}}^{\mathrm{KL}}(X,\mathbf{w})=\mathrm{KL}\left(\boldsymbol{\pi}_ {x}||\boldsymbol{p}_ {x}\right)+\mathrm{KL}\left(\boldsymbol{\pi}_ {a}||\boldsymbol{p}_ {a}\right)}\ &{\qquad=\mathbb{E}_ {(\mathbf{x},\mathbf{a})\sim X}\left[E(\tilde{\mathbf{x}},\mathbf{a},\mathbf{w}_ {x})+E(\mathbf{x}^{0},\tilde{\mathbf{a}},\mathbf{w}_ {a})\right]+\mathrm{H}\left[\boldsymbol{\pi}_ {x}\right]+\mathrm{H}\left[\boldsymbol{\pi}_ {a}\right]}\ &{\qquad\tilde{\mathbf{x}}\sim\boldsymbol{\pi}_ {x}\left(\mathbf{\nabla}\cdot|\mathbf{a},\mathbf{w}_ {x}\right),\tilde{\mathbf{a}}\sim\boldsymbol{\pi}_ {a}\left(\mathbf{\nabla}\cdot|\mathbf{x}^{0},\mathbf{w}_{a}\right)}\end{array}
$$

The above equation intuitively encourages sampling distributions $\pi$ to generate samples from lowenergy regions.

上述方程直观地鼓励采样分布 $\pi$ 从低能量区域生成样本。

Execution-Time Inference of Concepts Given a set of example events $X$ , the concept codes can be inferred at execution-time via finding codes w that minimize $\mathcal{L}^{\mathrm{ML}}$ and $\mathcal{L}^{\mathrm{KL}}$ . Similar to [12], in this work we only consider positive examples when adapting w and ignore the effect that changing w has on the sampling distribution $\pi$ . The result is simply minimizing the energy functions wrt w over the concept example events

执行时概念推断

给定一组示例事件$X$，可以通过找到最小化$\mathcal{L}^{\mathrm{ML}}$和$\mathcal{L}^{\mathrm{KL}}$的代码w，在执行时推断出概念代码。与[12]类似，在本工作中，我们仅在调整w时考虑正例，并忽略改变w对采样分布$\pi$的影响。结果就是简单地最小化关于w在概念示例事件上的能量函数。

$$
\mathbf{w}_ {\theta}^{*}(X)=\underset{\mathbf{w}}{\mathrm{argmin}}\mathbb{E}_ {(\mathbf{x},\mathbf{a})\sim X}\left[E_{\theta}(\mathbf{x}^{1},\mathbf{a},\mathbf{w}_ {x})+E_{\theta}(\mathbf{x}^{0},\mathbf{a},\mathbf{w}_{a})\right]
$$

$$
\mathbf{w}_ {\theta}^{*}(X)=\underset{\mathbf{w}}{\mathrm{argmin}}\mathbb{E}_ {(\mathbf{x},\mathbf{a})\sim X}\left[E_{\theta}(\mathbf{x}^{1},\mathbf{a},\mathbf{w}_ {x})+E_{\theta}(\mathbf{x}^{0},\mathbf{a},\mathbf{w}_{a})\right]
$$

This minimization is similar to execution-time parameter adaptation and the inner update of metalearning approaches [6]. We perform the optimization with stochastic gradient updates similar to equation (3). This approach again implicitly infers codes at execution time via meta-learning using only the energy model as opposed to incorporating additional explicit inference networks.

这种最小化过程类似于执行时参数适配和元学习方法中的内部更新[6]。我们采用与公式(3)类似的随机梯度更新进行优化。该方法再次通过仅使用能量模型(energy model)的元学习，在运行时隐式推断编码，而不是引入额外的显式推理网络。

Meta-Level Parameter Optimization We seek probability density functions $p$ that maximize the likelihood of training data $X$ via $\mathcal{L}_ {p}^{\mathrm{ML}}$ and simultaneously we seek sampling distributions $\pi$ that generate samples from $p$ via $\mathcal{L}_{\pi}^{\mathrm{KL}}$ . In inverse reinforcement learning setting of [8] and [10], these two objectives correspond to cost and policy function optimization are treated as separate alternating optimization problems because they operate over two different functions. However, in our case both $p$ and $\pi$ are implicitly a functions of the energy model and its parameters $\theta$ , a dependence which we denote as $p(\theta)$ and $\pi(\theta)$ . Consequently we can pose the problem as a single joint optimization

元级参数优化
我们寻求概率密度函数 $p$ ，通过 $\mathcal{L}_ {p}^{\mathrm{ML}}$ 最大化训练数据 $X$ 的似然性，同时寻求采样分布 $\pi$ ，通过 $\mathcal{L}_{\pi}^{\mathrm{KL}}$ 从 $p$ 生成样本。在 [8] 和 [10] 的逆强化学习设定中，这两个目标分别对应成本函数和策略函数优化，被视为独立的交替优化问题，因为它们作用于两个不同的函数。然而，在我们的场景中，$p$ 和 $\pi$ 隐式地依赖于能量模型及其参数 $\theta$ ，这种依赖关系我们表示为 $p(\theta)$ 和 $\pi(\theta)$ 。因此，我们可以将问题表述为单一联合优化。

$$
\operatorname*{min}_ {\theta}\mathcal{L}_ {p(\theta)}^{\mathrm{ML}}(X^{\mathrm{train}},\mathbf{w}_ {\theta}^{ * }(X^{\mathrm{demo}}))+\mathcal{L}_ {\pi(\theta)}^{\mathrm{KL}}(X^{\mathrm{train}},\mathbf{w}_{\theta}^{ * }(X^{\mathrm{demo}}))
$$

$$
\operatorname*{min}_ {\theta}\mathcal{L}_ {p(\theta)}^{\mathrm{ML}}(X^{\mathrm{train}},\mathbf{w}_ {\theta}^{ * }(X^{\mathrm{demo}}))+\mathcal{L}_ {\pi(\theta)}^{\mathrm{KL}}(X^{\mathrm{train}},\mathbf{w}_{\theta}^{ * }(X^{\mathrm{demo}}))
$$

We solve the above optimization problem via end-to-end back propagation, differentiation through gradient-based sampling procedures. See Figure 3 for an overview of our procedure and appendix for a detailed algorithm description.

我们通过端到端反向传播来解决上述优化问题，对基于梯度的采样过程进行微分。具体流程概览见图 3，详细算法描述见附录。

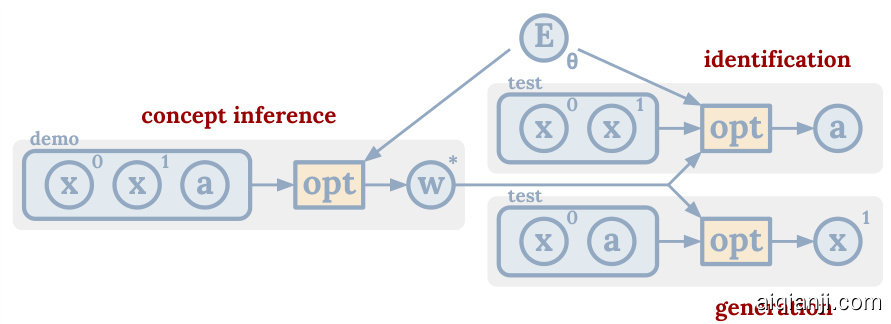
Figure 3: Execution-time inference in our method and the resulting optimization problems.

图 3: 我们方法中的执行时推理及由此产生的优化问题。

5 Experiments

5 实验

The main purpose of our experiments is to investigate 1) whether our single model is able to learn understanding of wide variety of concepts under multiple contexts, 2) the utility of iterative optimization-based inference processes, and 3) ability to reuse learned concepts on different environments and actuation platforms.

我们实验的主要目的是研究：1) 我们的单一模型是否能够在多种情境下学习理解广泛的概念；2) 基于迭代优化的推理过程的实用性；3) 在不同环境和驱动平台上重用已学习概念的能力。

5.1 Evaluation Environment and Tasks

5.1 评估环境与任务

We wish to evaluate understanding of concepts under multiple contexts - generation and identification. To the best of our knowledge we are not aware of any existing datasets or environments that simultaneously test both contexts for a wide range of concepts. For example, [17] tests understanding via question answering, while [15] focuses on visual concepts. Thus to evaluate our method, we introduce a new simulated environment and tasks which extend the work in [23]. The environment is a two-dimensional scene consisting of a varying collection of entities, each processing position, color, and shape properties. We wanted environment and tasks to be simple enough to facilitate ease of analysis, yet complex enough to lead to formation of a variety of concepts. In this work we focus on position-based environment representation, but a pixel-based representation and generation would be an exciting avenue for future work.

我们希望评估对多种情境下概念的理解——生成与识别。据我们所知，目前尚无同时测试广泛概念在这两种情境下的现有数据集或环境。例如，[17] 通过问答测试理解能力，而 [15] 则专注于视觉概念。因此，为评估我们的方法，我们引入了一个新的模拟环境和任务，扩展了 [23] 的工作。该环境是一个二维场景，包含各种实体，每个实体具有位置、颜色和形状属性。我们希望环境和任务足够简单以便于分析，同时又足够复杂以促成各种概念的形成。在这项工作中，我们专注于基于位置的环境表示，但基于像素的表示和生成将是未来研究的一个有趣方向。

The task in this environment is, given $N$ demonstration events that involve (we use $N=5$ ) that involve identical attention and state changes under different situations, perform analogous behavior under $N$ novel test situations (by attending to analogous entities and performing analogous state changes). Such behavior is not unique and these may be multiple possible solutions. Because our energy model architecture in section 3 processes all entities independently, the number of entities can vary between events. See Appendix for the description of events we consider in our dataset and sites.google.com/site/energy concept models for video results of our model learning on these events.

该环境中的任务是，给定 $N$ 个演示事件（我们使用 $N=5$），这些事件在不同情境下涉及相同的注意力与状态变化，然后在 $N$ 个新测试情境中执行类似行为（通过关注类似实体并执行类似状态变化）。此类行为并非唯一，可能存在多种解决方案。由于第3节中我们的能量模型架构独立处理所有实体，因此事件间的实体数量可以不同。关于数据集中所考虑事件的描述，请参阅附录；模型在这些事件上学习的视频结果，请访问 sites.google.com/site/energyconceptmodels。

5.2 Understanding Concepts in Multiple Contexts

5.2 理解多语境下的概念

An important property of our model is ability to learn from and apply it in both generation and identification contexts. We qualitatively observe that the model performs sensible behavior in both contexts. For example, we considered events with proximity relations "closest" and "farthest" and found model able to both attend to entities that are closest or furthest to another entity, and to move an entity to be closest or furthest to another entity as shown in figure 4. There are multiple admissible solutions which can be generated, as shown by the energy heatmap overlaid. We also wish to understand several other properties of this formulation, which we discuss below.

我们模型的一个重要特性是能够在生成和识别两种情境中学习并应用。通过定性观察，我们发现模型在这两种情境下都表现出合理的行为。例如，我们考察了具有"最近"和"最远"邻近关系的事件，发现模型既能关注到与另一实体最近或最远的实体，又能将某个实体移动到与另一实体最近或最远的位置，如图4所示。如叠加的能量热力图所示，可以生成多个可接受的解决方案。我们还希望理解该公式的其他几个特性，将在下文中讨论。

Figure 4: Outcomes of generation (left) and identification (right) for the concept of being farthest to cross-shaped entity. Path in left image is the optimization trajectory for the cross entity with the energy heatmap is overlaid.

图 4: