FMix: Enhancing Mixed Sample Data Augmentation
FMix: 提升混合样本数据增强效果
Abstract—Mixed Sample Data Augmentation (MSDA) has received increasing attention in recent years, with many successful variants such as MixUp and CutMix. By studying the mutual information between the function learned by a VAE on the original data and on the augmented data we show that MixUp distorts learned functions in a way that CutMix does not. We further demonstrate this by showing that MixUp acts as a form of adversarial training, increasing robustness to attacks such as Deep Fool and Uniform Noise which produce examples similar to those generated by MixUp. We argue that this distortion prevents models from learning about sample specific features in the data, aiding generalisation performance. In contrast, we suggest that CutMix works more like a traditional augmentation, improving performance by preventing mem or is ation without distorting the data distribution. However, we argue that an MSDA which builds on CutMix to include masks of arbitrary shape, rather than just square, could further prevent mem or is ation whilst preserving the data distribution in the same way. To this end, we propose FMix, an MSDA that uses random binary masks obtained by applying a threshold to low frequency images sampled from Fourier space. These random masks can take on a wide range of shapes and can be generated for use with one, two, and three dimensional data. FMix improves performance over MixUp and CutMix, without an increase in training time, for a number of models across a range of data sets and problem settings, obtaining a new single model state-of-the-art result on CIFAR-10 without external data. We show that FMix can outperform MixUp in sentiment classification tasks with one dimensional data, and provides an improvement over the baseline in three dimensional point cloud classification. Finally, we show that a consequence of the difference between interpolating MSDA such as MixUp and masking MSDA such as FMix is that the two can be combined to improve performance even further. Code for all experiments is provided at https://github.com/ecs-vlc/FMix.
摘要—混合样本数据增强(MSDA)近年来受到越来越多的关注,已涌现出MixUp和CutMix等成功变体。通过研究VAE在原始数据和增强数据上学习到的函数之间的互信息,我们发现MixUp会扭曲学习到的函数,而CutMix则不会。进一步研究表明,MixUp起到了一种对抗训练的作用,能提升模型对Deep Fool和均匀噪声等攻击的鲁棒性——这些攻击生成的样本与MixUp生成的样本类似。我们认为这种扭曲效应能防止模型学习数据中的样本特异性特征,从而提升泛化性能。相比之下,CutMix更像传统的数据增强方法,通过防止过拟合来提升性能,且不会扭曲数据分布。但我们指出,基于CutMix开发能生成任意形状(而非仅限于方形)掩模的MSDA方法,可以在保持数据分布的同时更好地防止过拟合。为此,我们提出FMix:这种MSDA方法通过对傅里叶空间采样的低频图像进行阈值处理来获取随机二值掩模。这些随机掩模可呈现多种形状,并能生成适用于一维、二维和三维数据的版本。在多个模型、数据集和问题场景中,FMix在保持训练时间不变的前提下,性能优于MixUp和CutMix,并在不使用外部数据的情况下取得了CIFAR-10数据集上新的单模型最优结果。我们证明FMix在一维数据的情感分类任务中能超越MixUp,并在三维点云分类任务中优于基线方法。最后研究表明,插值型MSDA(如MixUp)与掩模型MSDA(如FMix)的本质差异使得二者结合能获得更优性能。所有实验代码详见https://github.com/ecs-vlc/FMix。
I. INTRODUCTION
I. 引言
R EDaCtEa NATuLgYm, ean tap tli eot nh o(raM SofD aAp) phraovaec hbeese tno pr Moi px oe s de dS awmhipclhe obtain state-of-the-art results, particularly in classification tasks [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]. MSDA involves combining data samples according to some policy to create an augmented data set on which to train the model. The policies so far proposed can be broadly categorised as either combining samples with interpolation (e.g. MixUp) or masking (e.g. CutMix). Traditionally, augmentation is viewed through the framework of statistical learning as Vicinal Risk Minim is ation (VRM) [12, 13]. Given some notion of the vicinity of a data point, VRM trains with vicinal samples in addition to the data points themselves. This is the motivation for MixUp [2]; to provide a new notion of vicinity based on mixing data samples. In the classical theory, validity of this technique relies on the strong assumption that the vicinal distribution precisely matches the true distribution of the data. As a result, the classical goal of augmentation is to maximally increase the data space, without changing the data distribution. Clearly, for all but the most simple augmentation strategies, the data distribution is in some way distorted. Furthermore, there may be practical implications to correcting this, as is demonstrated in Touvron et al. [14]. In light of this, three important questions arise regarding MSDA: What is good measure of the similarity between the augmented and the original data? Why is MixUp so effective when the augmented data looks so different? If the data is distorted, what impact does this have on trained models?
规则:
- 输出中文翻译部分时仅保留翻译标题,不含冗余内容、重复或解释
- 不输出无关内容
- 保留原始段落格式及术语(如FLAC/JPEG)、公司缩写(如Microsoft/Amazon/OpenAI)
- 人名不译
- 保留文献引用标记(如[20])
- 图表翻译保留原格式("图1:"/"表1:")
- 全角括号转半角并添加间距(示例:(xxx) )
- 专业术语首现标注英文(如"生成式AI (Generative AI)"),后续直接使用中文
- AI术语对照:
- Transformer -> Transformer
- Token -> Token
- LLM -> 大语言模型
- Zero-shot -> 零样本
- Few-shot -> 少样本
- AI Agent -> AI智能体
- AGI -> 通用人工智能
- Python -> Python语言
策略:
- 特殊字符/公式原样保留
- HTML表格转Markdown格式
- 确保完整翻译且符合中文表达
(以下为符合要求的Markdown格式翻译结果)
混合样本数据增强 (MSDA) 方法通过特定策略组合数据样本创建增强数据集,在分类任务中取得了最先进成果 [1-11]。现有策略主要分为样本插值混合(如MixUp)和掩码混合(如CutMix)两类。传统增强框架基于统计学习中的邻域风险最小化 (VRM) [12,13],通过数据点及其邻域样本进行训练。MixUp [2] 的动机正是建立在这种基于样本混合的新邻域概念上。经典理论要求邻域分布必须严格匹配真实数据分布,因此传统增强目标是在不改变数据分布的前提下最大化扩展数据空间。然而除简单策略外,大多数增强都会以某种方式扭曲数据分布——Touvron等人 [14] 已证明修正这种扭曲的实际影响。由此引发三个关键问题:如何有效衡量增强数据与原始数据的相似性?为何MixUp在增强数据明显失真时仍高效?数据扭曲对训练模型有何影响?
To construct a good measure of similarity, we note that the data only need be ‘perceived’ similar by the model. As such, we measure the mutual information between representations learned from the real and augmented data, thus character ising how well learning from the augmented data simulates learning from the real data. This measure shows the data-level distortion of MixUp by demonstrating that learned representations are compressed in comparison to those learned from the unaugmented data. To address the efficacy of MixUp, we look to the information bottleneck theory of deep learning [15]. By the data processing inequality, summarised as ‘post-processing cannot increase information’, deep networks can only discard information about the input with depth whilst preserving information about the targets. Tishby and Zaslavsky [15] assert that more efficient generalisation is achieved when each layer maximises the information it has about the target and minimises the information it has about the previous layer. Consequently, we posit that the distortion and subsequent compression induced by MixUp promotes generalisation. Another way to view this is that compression prevents the network from learning about highly sample-specific features in the data. Regarding the impact on trained models, and again armed with the knowledge that MixUp distorts learned functions, we show that MixUp acts as a kind of adversarial training [16], promoting robustness to additive noise. This accords with the theoretical result of Perrault-Ar chamba ul t et al. [17] and the robustness results of Zhang et al. [2]. However, we further show that MSDA does not generally improve adversarial robustness when measured as a worst case accuracy following multiple attacks as suggested by Carlini et al. [18]. Ultimately, our adversarial robustness experiments show that the distortion in the data observed by our mutual information analysis corresponds to practical differences in learned function.
为了构建一个良好的相似性度量,我们注意到数据只需被模型"感知"为相似即可。因此,我们测量从真实数据和增强数据中学到的表征之间的互信息,从而刻画通过增强数据学习能在多大程度上模拟从真实数据中学习。该度量通过展示学习到的表征相比未增强数据存在压缩现象,揭示了MixUp在数据层面造成的失真。针对MixUp的有效性,我们参考深度学习的信息瓶颈理论[15]。根据数据处理不等式(可概括为"后处理无法增加信息"),深度网络只能在保留目标信息的同时,随着深度增加逐步丢弃输入信息。Tishby和Zaslavsky[15]主张,当每一层最大化其拥有的目标信息并最小化其拥有的前一层信息时,能实现更高效的泛化。因此,我们认为MixUp引发的失真和后续压缩有助于提升泛化能力。另一种理解是,压缩能防止网络学习数据中高度样本特定的特征。关于对训练模型的影响,结合MixUp会扭曲学习函数这一认知,我们证明MixUp可视为一种对抗训练[16],能提升对加性噪声的鲁棒性。这与Perrault-Ar chamba ul t等人[17]的理论结果及Zhang等人[2]的鲁棒性结论一致。但我们进一步表明,当按照Carlini等人[18]建议采用多重攻击下的最坏情况准确率衡量时,MSDA通常不会提升对抗鲁棒性。最终,我们的对抗鲁棒性实验表明,通过互信息分析观察到的数据失真与学习函数的实际差异存在对应关系。
In contrast to our findings regarding MixUp, our mutual information analysis shows that CutMix causes learned models to retain a good knowledge of the real data, which we argue derives from the fact that individual features extracted by a convolutional model generally only derive from one of the mixed data points. This is further shown by our adversarial robustness results, where CutMix is not found to promote robustness in the same way. We therefore suggest that CutMix limits the ability of the model to over-fit by dramatically increasing the number of observable data points without distorting the data distribution, in keeping with the original intent of VRM. However, by restricting to only masking a square region, CutMix imposes some unnecessary limitations. First, the number of possible masks could be much greater if more mask shapes could be used. Second, it is likely that there is still some distortion since all of the images used during training will involve a square edge. It should be possible to construct an MSDA which uses masking similar to CutMix whilst increasing the data space much more dramatically. Motivated by this, we introduce FMix, a masking MSDA that uses binary masks obtained by applying a threshold to low frequency images sampled randomly from Fourier space. Using our mutual information measure, we show that learning with FMix simulates learning from the real data even better than CutMix. We subsequently demonstrate performance of FMix for a range of models and tasks against a series of augmented baselines and other MSDA approaches. FMix obtains a new single model state-of-the-art performance on CIFAR-10 [19] without external data and improves the performance of several state-ofthe-art models (ResNet, SE-ResNeXt, DenseNet, WideResNet, PyramidNet, LSTM, and Bert) on a range of problems and modalities.
与我们在 MixUp 上的发现相反,互信息分析表明 CutMix 能使学习模型保留对真实数据的良好认知。我们认为这源于卷积模型提取的单个特征通常仅来自混合数据点之一。对抗鲁棒性结果进一步证明了这一点——CutMix 并未以相同方式提升鲁棒性。因此我们提出,CutMix 通过大幅增加可观测数据点数量(同时保持数据分布不变)来限制模型过拟合能力,这符合 VRM 的原始意图。
但仅限定方形掩码区域使 CutMix 存在不必要的限制:其一,若采用更多掩码形状,可能掩码数量会显著增加;其二,由于训练中所有图像都涉及方形边缘,仍可能存在某些失真。理论上可以构建一种类似 CutMix 掩码机制的 MSDA (混合样本数据增强) 方法,同时更大幅度扩展数据空间。
基于此,我们提出 FMix——通过傅里叶空间随机采样低频图像并阈值化获得二值掩码的 MSDA 方法。互信息测量显示,FMix 比 CutMix 更能模拟真实数据的学习过程。后续实验证明,在一系列模型、任务及增强基线对比中,FMix 均优于其他 MSDA 方法。FMix 在 CIFAR-10 [19] 上无需外部数据即达到新的单模型最优性能,并在多种任务和模态中提升了当前最优模型(ResNet、SE-ResNeXt、DenseNet、WideResNet、PyramidNet、LSTM 和 Bert)的表现。
In light of our experimental results, we go on to suggest that the compressing qualities of MixUp are most desirable when data is limited and learning from individual examples is easier. In contrast, masking MSDAs such as FMix are most valuable when data is abundant. We suggest that there is no reason to see the desirable properties of masking and interpolation as mutually exclusive. In light of these observations, we plot the performance of MixUp, FMix, a baseline, and a hybrid policy where we alternate between batches of MixUp and FMix, as the number of CIFAR-10 training examples is reduced. This experiment confirms our above suggestions and shows that the hybrid policy can outperform both MixUp and FMix.
根据实验结果,我们进一步提出:当数据有限且更容易从单个样本中学习时,MixUp的压缩特性最为理想;而当数据充足时,FMix等掩码型混合样本数据增强(MSDA)方法最具价值。我们认为,没有必要将掩码和插值的优势特性视为互斥关系。基于这些观察,我们绘制了MixUp、FMix、基线方法以及混合策略(在MixUp和FMix批次间交替使用)在CIFAR-10训练样本数量递减时的性能曲线。该实验验证了上述观点,并表明混合策略可以同时超越MixUp和FMix的表现。
II. RELATED WORK
II. 相关工作
In this section, we review the fundamentals of MSDA. Let $p_{X}(x)$ denote the input data distribution. In general, we can define MSDA for a given mixing function, $\operatorname*{mix}(X_{1},X_{2},\Lambda)$ , where $X_{1}$ and $X_{2}$ are independent random variables on the data domain and $\Lambda$ is the mixing coefficient. Synthetic minority over-sampling [1], a predecessor to modern MSDA approaches, can be seen as a special case of the above where $X_{1}$ and $X_{2}$ are dependent, jointly sampled as nearest neighbours in feature space. These synthetic samples are drawn only from the minority class to be used in conjunction with the original data, addressing the problem of imbalanced data. The mixing function is linear interpolation, $\operatorname*{mix}(x_{1},x_{2},\lambda)=$ $\lambda x_{1}+(1-\lambda)x_{2}$ , and $p_{\Lambda}=\mathcal{U}(0,1)$ . More recently, Zhang et al. [2], Tokozume et al. [3], and Inoue [5] concurrently proposed using this formulation (as MixUp, Between-Class (BC) learning, and sample pairing respectively) on the whole data set, although the choice of distribution for the mixing coefficients varies for each approach. Tokozume et al. [4] subsequently proposed $\mathrm{BC+}$ , which uses a normalised variant of the mixing function. We refer to these approaches as interpol at ive MSDA, where, following Zhang et al. [2], we use the symmetric Beta distribution, that is $p_{\Lambda}=\mathrm{Beta}(\alpha,\alpha)$ .
在本节中,我们回顾MSDA的基础知识。设$p_{X}(x)$表示输入数据分布。通常,我们可以为给定的混合函数$\operatorname*{mix}(X_{1},X_{2},\Lambda)$定义MSDA,其中$X_{1}$和$X_{2}$是数据域上的独立随机变量,$\Lambda$是混合系数。现代MSDA方法的前身——合成少数类过采样[1],可视为上述情况的一个特例,其中$X_{1}$和$X_{2}$是依赖的,在特征空间中作为最近邻联合采样。这些合成样本仅从少数类中抽取,与原始数据结合使用,以解决数据不平衡问题。混合函数为线性插值$\operatorname*{mix}(x_{1},x_{2},\lambda)=\lambda x_{1}+(1-\lambda)x_{2}$,且$p_{\Lambda}=\mathcal{U}(0,1)$。最近,Zhang等人[2]、Tokozume等人[3]和Inoue[5]分别提出了在整个数据集上使用该公式(分别称为MixUp、类间(BC)学习和样本配对),尽管每种方法对混合系数分布的选择各不相同。Tokozume等人[4]随后提出了$\mathrm{BC+}$,它使用了混合函数的归一化变体。我们将这些方法称为插值MSDA,其中遵循Zhang等人[2]的做法,使用对称Beta分布,即$p_{\Lambda}=\mathrm{Beta}(\alpha,\alpha)$。
Recent variants adopt a binary masking approach [6, 7, 8]. Let $M=\mathrm{mask}(\Lambda)$ be a random variable with $\mathrm{mask}(\lambda)\in$ ${0,1}^{n}$ and $\mu(\mathrm{mask}(\lambda))=\lambda$ , that is, generated masks are binary with average value equal to the mixing coefficient. The mask mixing function is $\operatorname*{mix}(\mathbf{x}{1},\mathbf{x}{2},\mathbf{m})=\mathbf{m}\odot\mathbf{x}{1}+$ $(1-\mathbf{m})\odot\mathbf{x}{2}$ , where $\odot$ denotes point-wise multiplication. A notable masking MSDA which motivates our approach is CutMix [6]. CutMix is designed for two dimensional data, with $\mathrm{mask}(\lambda)\in{0,1}^{w\times h}$ , and uses $\mathrm{mask}(\lambda){\it\Delta\phi}=$ ra $\mathrm{nd_rect}(w\sqrt{1-\lambda},h\sqrt{1-\lambda})$ , where rand rec $\mathrm{{;t}}(r_{w},r_{h})\in$ ${0,1}^{w\times h}$ yields a binary mask with a shaded rectangular region of size $r_{w}\times r_{h}$ at a uniform random coordinate. CutMix improves upon the performance of MixUp on a range of experiments.
最近的变体采用了二元掩码方法 [6, 7, 8]。设 $M=\mathrm{mask}(\Lambda)$ 为一个随机变量,其中 $\mathrm{mask}(\lambda)\in$ ${0,1}^{n}$ 且 $\mu(\mathrm{mask}(\lambda))=\lambda$,即生成的掩码是二元的,其平均值等于混合系数。掩码混合函数为 $\operatorname*{mix}(\mathbf{x}{1},\mathbf{x}{2},\mathbf{m})=\mathbf{m}\odot\mathbf{x}{1}+$ $(1-\mathbf{m})\odot\mathbf{x}{2}$,其中 $\odot$ 表示逐点乘法。CutMix [6] 是一个值得注意的掩码 MSDA,它启发了我们的方法。CutMix 专为二维数据设计,其中 $\mathrm{mask}(\lambda)\in{0,1}^{w\times h}$,并使用 $\mathrm{mask}(\lambda){\it\Delta\phi}=$ ra $\mathrm{nd_rect}(w\sqrt{1-\lambda},h\sqrt{1-\lambda})$,其中 rand rec $\mathrm{{;t}}(r_{w},r_{h})\in$ ${0,1}^{w\times h}$ 生成一个二元掩码,其阴影矩形区域大小为 $r_{w}\times r_{h}$,位于均匀随机坐标处。CutMix 在一系列实验中提升了 MixUp 的性能。
In all MSDA approaches the targets are mixed in some fashion, typically to reflect the mixing of the inputs. For the typical case of classification with a cross entropy loss (and for all of the experiments in this work), the objective function is simply the interpolation between the cross entropy against each of the ground truth targets. It could be suggested that by mixing the targets differently, one might obtain better results. However, there are key observations from prior art which give us cause to doubt this supposition; in particular, Liang et al. [20] performed a number of experiments on the importance of the mixing ratio of the labels in MixUp. They concluded that when the targets are not mixed in the same proportion as the inputs the model can be regular is ed to the point of under fitting. However, despite this conclusion their results show only a mild performance change even in the extreme event that targets are mixed randomly, independent of the inputs. For these reasons, we focus only on the development of a better input mixing function for the remainder of the paper.
在所有MSDA方法中,目标会以某种方式混合,通常是为了反映输入的混合情况。对于使用交叉熵损失进行分类的典型情况(以及本文中的所有实验),目标函数只是针对每个真实目标交叉熵的插值。有人可能会建议通过不同的方式混合目标来获得更好的结果。然而,先前研究的关键观察让我们对这一假设产生了怀疑;特别是,Liang等人[20]对MixUp中标签混合比例的重要性进行了大量实验。他们得出结论,当目标不以与输入相同的比例混合时,模型可能会被正则化到欠拟合的程度。然而,尽管得出了这一结论,他们的结果显示即使在目标与输入无关、随机混合的极端情况下,性能变化也很小。基于这些原因,在本文的剩余部分,我们仅专注于开发更好的输入混合函数。
Attempts to explain the success of MSDAs were not only made when they were introduced, but also through subsequent empirical and theoretical studies. In addition to their experimentation with the targets, Liang et al. [20] argue that linear interpolation of inputs limits the mem or is ation ability of the network. Gontijo-Lopes et al. [21] propose two measures to explain the impact of augmentation on generalisation when jointly optimised: affinity and diversity. While the former captures the shift in the data distribution as perceived by the baseline model, the latter measures the training loss when learning with augmented data. A more mathematical view on MSDA was adopted by Guo et al. [22], who argue that MixUp regular is es the model by constraining it outside the data manifold. They point out that this could lead to reducing the space of possible hypotheses, but could also lead to generated examples contradicting original ones, degrading quality. Upon Taylor-expanding the objective, Carratino et al.
试图解释多源数据增强(MSDA)成功的原因不仅在其被提出时就已开始,还贯穿于后续的实证与理论研究。除对目标数据的实验外,Liang等人[20]指出输入数据的线性插值会限制网络的记忆能力。Gontijo-Lopes等人[21]提出亲和度(affinity)与多样性(diversity)两项指标,用于解释联合优化时数据增强对泛化能力的影响:前者反映基线模型感知的数据分布偏移,后者衡量使用增强数据训练时的损失值。Guo等人[22]则从数学视角分析MSDA,认为MixUp通过将模型约束在数据流形之外实现正则化。他们指出这虽可能缩小假设空间,但也可能导致生成样本与原始数据矛盾而降低质量。Carratino等人通过对目标函数进行泰勒展开...
TABLE I: Mutual information between VAE latent spaces $(Z_{A})$ and the CIFAR-10 test set $(I(Z_{A};X))$ , and the CIFAR10 test set as reconstructed by a baseline VAE $(I(Z_{A};\hat{X}))$ for VAEs trained with a range of MSDAs. MixUp prevents the model from learning about specific features in the data. Uncertainty estimates are the standard deviation following 5 trials.
表 1: VAE潜在空间 $(Z_{A})$ 与CIFAR-10测试集 $(I(Z_{A};X))$ 之间的互信息,以及基线VAE重建的CIFAR10测试集 $(I(Z_{A};\hat{X}))$(使用多种MSDA方法训练的VAE)。MixUp会阻止模型学习数据中的特定特征。不确定性估计为5次试验后的标准差。
| I(ZA; X) | I(ZA;X) | MSE | |
|---|---|---|---|
| Baseline | 78.05±0.53 | 74.40±0.45 | 0.256±0.002 |
| MixUp | 70.38±0.90 | 68.58±1.12 | 0.288±0.003 |
| CutMix | 83.17±0.72 | 79.46±0.75 | 0.254±0.003 |
[23] motivate the success of MixUp by the co-action of four different regular is ation factors. A similar analysis is carried out in parallel by Zhang et al. [24].
[23] 将 MixUp 的成功归因于四种不同正则化因素的协同作用。Zhang 等人 [24] 也进行了类似的分析。
Following Zhang et al. [2], He et al. [25] take a statistical learning view of MSDA, basing their study on the observation that MSDA distorts the data distribution and thus does not perform VRM in the traditional sense. They subsequently propose separating features into ‘minor’ and ‘major’, where a feature is referred to as ‘minor’ if it is highly sample-specific. Augmentations that significantly affect the distribution are said to make the model predominantly learn from ‘major’ features. From an information theoretic perspective, ignoring these ‘minor’ features corresponds to increased compression of the input by the model. Although He et al. [25] noted the importance of character ising the effect of data augmentation from an information perspective, they did not explore any measures that do so. Instead, He et al. [25] analysed the variance in the learned representations. This is analogous to the entropy of the representation since entropy can be estimated via the pairwise distances between samples, with higher distances corresponding to both greater entropy and variance [26]. In proposing Manifold MixUp, Verma et al. [27] additionally suggest that MixUp works by increasing compression. The authors compute the singular values of the representations in early layers of trained networks, with smaller singular values again corresponding to lower entropy. A potential issue with these approaches is that the entropy of the representation is only an upper bound on the information that the representation has about the input.
遵循张等人[2]的研究思路,何等人[25]从统计学习视角分析多源域自适应(MSDA),基于MSDA会扭曲数据分布因而无法执行传统变分风险最小化(VRM)的观察。他们提出将特征划分为"次要"和"主要"两类——当某特征具有高度样本特异性时即被归为"次要特征"。那些显著影响数据分布的增强操作会使模型主要从"主要特征"中学习。从信息论角度看,忽略这些"次要特征"相当于模型对输入信息进行了更高程度的压缩。虽然何等人[25]指出从信息角度表征数据增强效果的重要性,但未深入探索相关度量方法,转而分析学习表征的方差。这与表征熵具有相似性,因为熵可以通过样本间成对距离来估算,距离越大对应熵和方差越高[26]。Verma等人在提出流形混合(Manifold MixUp)时[27]也指出MixUp通过增强压缩发挥作用,作者计算训练网络浅层表征的奇异值,较小奇异值同样对应较低熵。这些方法的潜在问题在于:表征熵仅是表征所含输入信息量的上限。
III. ANALYSIS
III. 分析
We now analyse both interpol at ive and masking MSDAs with a view to distinguishing their impact on learned representations and finding answers to the questions established in our introduction. We first desire a measure which captures the extent to which learning about the augmented data simulates learning about the original data. We propose training unsupervised models on real data and augmented data and then measuring the mutual information, the reduction in uncertainty about one variable given knowledge of another, between the representations they learn. To achieve this, we use Variation al Auto-Encoders (VAEs) [29], which provide a rich depiction of the salient or compressible information in the data [30]. Note that we do not expect these representations to directly relate to those of trained class if i ers. Our requirement is a probabilistic model of the data, for which a VAE is well suited.
我们现在分析插值和掩码两种多模态数据增强方法(MSDA),旨在区分它们对学习表示的影响,并回答引言中提出的问题。首先需要一种衡量标准,用于量化增强数据的学习能在多大程度上模拟原始数据的学习。我们提出在真实数据和增强数据上训练无监督模型,然后测量它们学习到的表示之间的互信息(即已知一个变量后对另一个变量不确定性的减少量)。为此,我们使用变分自编码器(VAE)[29],它能充分表征数据中的显著或可压缩信息[30]。需要注意的是,这些表示与训练分类器的表示不一定直接相关。我们需要的是一种数据概率模型,而VAE非常适合这一需求。
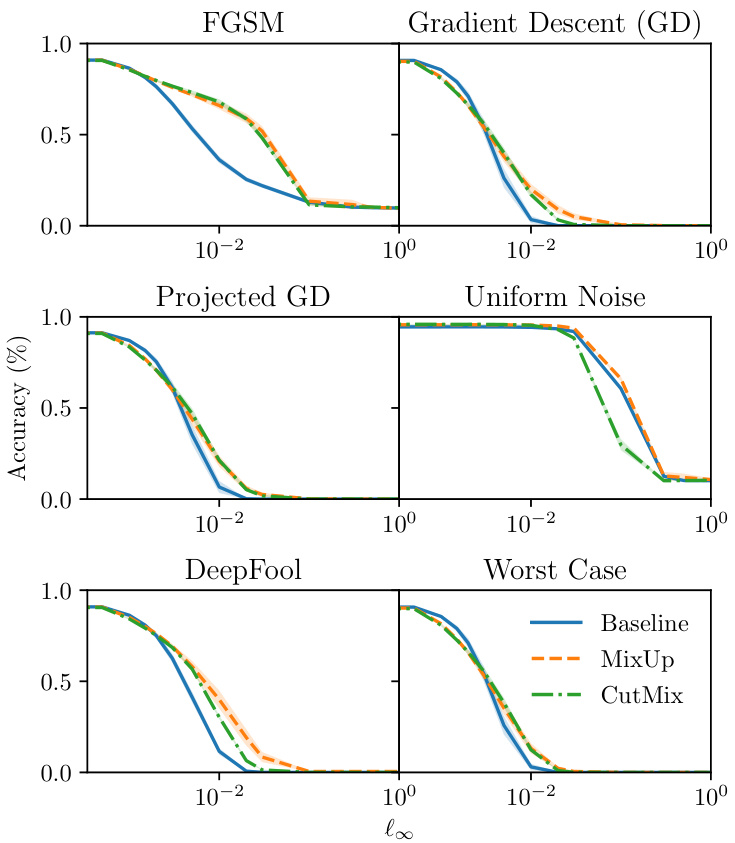
Fig. 1: Robustness of PreAct-ResNet18 models trained on CIFAR-10 with standard augmentations (Baseline) and the addition of MixUp and CutMix to the Fast Gradient Sign Method (FGSM), simple gradient descent, projected gradient descent, uniform noise, DeepFool [28], and the worst case performance after all attacks. MixUp improves robustness to adversarial examples with similar properties to images generated with MixUp (acting as adversarial training), but MSDA does not improve robustness in general. Shaded region indicates the standard deviation following 5 repeats.
图 1: 在CIFAR-10上训练的PreAct-ResNet18模型使用标准数据增强(基线)及加入MixUp和CutMix后,对快速梯度符号法(FGSM)、简单梯度下降、投影梯度下降、均匀噪声、DeepFool [28]以及所有攻击后最坏情况表现的鲁棒性。MixUp提升了对抗样本的鲁棒性(这些样本具有与MixUp生成图像相似的特性,起到对抗训练的作用),但混合样本数据增强(MSDA)总体上并未提高鲁棒性。阴影区域表示5次重复实验的标准差。
We wish to estimate the mutual information between the representation learned by a VAE from the original data set, $Z_{X}$ , and the representation learned from some augmented data set, $Z_{A}$ , written ${\cal I}\left(Z_{X};Z_{A}\right)=\mathbb{E}{Z_{X}}\left[D\left(p_{\left(Z_{A}\mid Z_{X}\right)}\mid\mid p_{Z_{A}}\right)\right]$ . This quantity acts as a good measure of the similarity between the augmented and the original data since it captures only the similarity between learnable or salient features. VAEs comprise an encoder, $p_{\left(Z\mid X\right)}$ , and a decoder, $p_{(X\mid Z)}$ . We impose a Normal prior on $Z$ , and train the model to maximise the Evidence Lower BOund (ELBO) objective
我们希望估计变分自编码器(VAE)从原始数据集学习到的表示 $Z_{X}$ 与从增强数据集学习到的表示 $Z_{A}$ 之间的互信息,记为 ${\cal I}\left(Z_{X};Z_{A}\right)=\mathbb{E}{Z_{X}}\left[D\left(p_{\left(Z_{A}\mid Z_{X}\right)}\mid\mid p_{Z_{A}}\right)\right]$。该量能有效衡量增强数据与原始数据之间的相似性,因为它仅捕捉可学习或显著特征之间的相似性。VAE包含编码器 $p_{\left(Z\mid X\right)}$ 和解码器 $p_{(X\mid Z)}$。我们对 $Z$ 施加正态先验,并通过最大化证据下界(ELBO)目标来训练模型。
$$
\begin{array}{r l}&{\mathcal{L}=\mathbb{E}{X}\left[\mathbb{E}{Z|X}\left[\mathrm{log}\big(p_{\left(X\mid Z\right)}\big)\right]\right.}\ &{\qquad\left.-D\big(p_{\left(Z|X\right)}\big|\big|\mathcal{N}\big(\mathbf{0},I\big)\big)\right].}\end{array}
$$
$$
\begin{array}{r l}&{\mathcal{L}=\mathbb{E}{X}\left[\mathbb{E}{Z|X}\left[\mathrm{log}\big(p_{\left(X\mid Z\right)}\big)\right]\right.}\ &{\qquad\left.-D\big(p_{\left(Z|X\right)}\big|\big|\mathcal{N}\big(\mathbf{0},I\big)\big)\right].}\end{array}
$$
Denoting the outputs of the decoder of the VAE trained on the augmentation as ${\bf\hat{X}}=d e c o d e(Z_{X})$ , and by the data processing inequality, we have $I(Z_{A};\hat{X})\leq I(Z_{A};Z_{X})$ with equality when the decoder retains all of the information in $Z$ . Now, we need only observe that we already have a model of $p_{(Z_{A}\mid X)}$ , the encoder trained on the augmented data. Estimating the marginal $p_{Z_{A}}$ presents a challenge as it is a Gaussian mixture. However, we can measure an alternative form of the mutual information that is equivalent up to an additive constant, and for which the divergence has a closed form solution, with
将经过增强训练的VAE解码器输出表示为 ${\bf\hat{X}}=d e c o d e(Z_{X})$ ,根据数据处理不等式可得 $I(Z_{A};\hat{X})\leq I(Z_{A};Z_{X})$ ,当解码器保留 $Z$ 中全部信息时取等号。此时只需注意到我们已拥有增强数据训练的编码器 $p_{(Z_{A}\mid X)}$ 模型。估计边缘分布 $p_{Z_{A}}$ 存在挑战,因其为高斯混合分布。不过我们可以测量另一种形式的互信息(该形式与原始互信息仅相差加性常数),其散度具有闭式解:
$$
\begin{array}{r l}{\mathbb{E}{\hat{X}}\big[D\big(p_{(Z_{A}|\hat{X})}\left\Vert p_{Z_{A}}\right)\big]=}&{}\ {\mathbb{E}{\hat{X}}\big[D\big(p_{(Z_{A}|\hat{X})}\left\Vert\mathcal{N}(\mathbf{0},I)\right)\big]}&{}\ {-D\big(p_{Z_{A}}\left\Vert\mathcal{N}(\mathbf{0},I)\right).}\end{array}
$$
$$
\begin{array}{r l}{\mathbb{E}{\hat{X}}\big[D\big(p_{(Z_{A}|\hat{X})}\left\Vert p_{Z_{A}}\right)\big]=}&{}\ {\mathbb{E}{\hat{X}}\big[D\big(p_{(Z_{A}|\hat{X})}\left\Vert\mathcal{N}(\mathbf{0},I)\right)\big]}&{}\ {-D\big(p_{Z_{A}}\left\Vert\mathcal{N}(\mathbf{0},I)\right).}\end{array}
$$
The above holds for any choice of distribution that does not depend on X. Conceptually, this states that we will always lose more information on average if we approximate $p_{\left(Z_{A}\mid\hat{X}\right)}$ with any constant distribution other than the marginal $p_{Z_{A}}$ . Additionally note that we implicitly minimise during training of the VAE [31]. In light of this fact, we can write $I(\bar{Z_{A}};\hat{X})\approx\mathbb{E}{\hat{X}}[D\big(p_{(Z_{A}|\hat{X})}\bar{|}\mathcal{N}(\mathbf{0},I)\big)]$ . We can now easily obtain a helpful upper bound of $I(Z_{A};Z_{X})$ such that it is bounded on both sides. Since $Z_{A}$ is just a function of $X$ , again by the data processing inequality, we have $I(Z_{A};X)\ge I(Z_{A};Z_{X})$ . This is easy to compute since it is just the relative entropy term from the ELBO objective.
上述结论适用于任何不依赖于X的分布选择。从概念上讲,这表明如果我们用任何非边缘分布$p_{Z_{A}}$的恒定分布来近似$p_{\left(Z_{A}\mid\hat{X}\right)}$,平均而言总会损失更多信息。此外需注意,在训练VAE时我们隐式地最小化了[31]。基于这一事实,可以表示为$I(\bar{Z_{A}};\hat{X})\approx\mathbb{E}{\hat{X}}[D\big(p_{(Z_{A}|\hat{X})}\bar{|}\mathcal{N}(\mathbf{0},I)\big)]$。现在我们可以轻松得到$I(Z_{A};Z_{X})$的一个有用上界,使其在两侧都有界。由于$Z_{A}$仅是$X$的函数,根据数据处理不等式可得$I(Z_{A};X)\ge I(Z_{A};Z_{X})$。这个值很容易计算,因为它就是ELBO目标函数中的相对熵项。
To summarise, we can compute our measure by first training two VAEs, one on the original data and one on the augmented data. We then generate reconstructions of data points in the original data with one VAE and encode them in the other. We now compute the expected value of the relative entropy between the encoded distribution and an estimate of the marginal to obtain an estimate of a lower bound of the mutual information between the representations. We then recompute this using real data points instead of reconstructions to obtain an upper bound. Table I gives these quantities for MixUp, CutMix, and a baseline. The results show that MixUp consistently reduces the amount of information that is learned about the original data. In contrast, CutMix manages to induce greater mutual information with the data than is obtained from just training on the un-augmented data. Crucially, the results present concrete evidence that interpol at ive MSDA differs fundamentally from masking MSDA in how it impacts learned representations.
总结来说,我们可以通过以下步骤计算该指标:首先训练两个VAE(变分自编码器),一个在原始数据上训练,另一个在增强数据上训练。接着用其中一个VAE生成原始数据点的重构样本,并用另一个VAE对其进行编码。此时,我们通过计算编码分布与边缘分布估计之间的相对熵期望值,来获得表示间互信息下界的估计。随后改用真实数据点(而非重构样本)重新计算该值,从而得到上界。表1展示了MixUp、CutMix和基线的这些量化结果。结果表明,MixUp持续降低了模型从原始数据中学习到的信息量;而CutMix则能诱导出比未增强数据训练更高的互信息。关键的是,这些结果为插值型多源数据增强(MSDA)与掩码型MSDA对学习表示的影响机制存在本质差异提供了具体证据。
Having shown this is true for VAEs, we now wish to understand whether the finding also holds for trained class if i ers. To this end, we analysed the decisions made by a classifier using Gradient-weighted Class Activation Maps (Grad-CAMs) [32]. Grad-CAM finds the regions in an image that contribute the most to the network’s prediction by taking the derivative of the model’s output with respect to the activation maps and weighting them according to their contribution. If MixUp prevents the network from learning about highly specific features in the data we would expect more of the early features to contribute to the network output. It would be difficult to ascertain qualitatively whether this is the case. Instead, we compute the average sum of Grad-CAM heatmaps over the CIFAR-10 test set for 5 repeats (independently trained PreActResNet18 models). We obtain the following scores: baseline - $146{\scriptstyle\pm5}$ , MixUp - $162{\scriptstyle\pm3}$ , CutMix - $131{\scriptstyle\pm6}$ . The result suggeststhat more of the early features contribute to the decisions made by MixUp trained models and that this result is consistent across independent runs.
在证明了VAE确实如此后,我们现在希望了解这一发现是否也适用于训练过的分类器。为此,我们使用梯度加权类激活图(Grad-CAMs)[32]分析了分类器的决策过程。Grad-CAM通过计算模型输出相对于激活图的导数,并根据其贡献进行加权,从而找出图像中对网络预测贡献最大的区域。如果MixUp阻止网络学习数据中高度特定的特征,我们预计会有更多早期特征对网络输出产生贡献。定性判断这种情况是否属实较为困难。因此,我们针对CIFAR-10测试集计算了5次独立训练的PreActResNet18模型的Grad-CAM热图平均总和,得到以下分数:基线 - $146{\scriptstyle\pm5}$,MixUp - $162{\scriptstyle\pm3}$,CutMix - $131{\scriptstyle\pm6}$。结果表明,MixUp训练的模型决策过程中有更多早期特征参与贡献,且该结果在不同独立运行中保持一致。
Having established that MixUp distorts learned functions, we now seek to answer the third question from our introduction by determining the impact of data distortion on trained class if i ers. Since it is our assessment that models trained with MixUp have an altered ‘perception’ of the data distribution, we suggest an analysis based on adversarial attacks, which involve perturbing images outside of the perceived data distribution to alter the given classification. We perform fast gradient sign method, standard gradient descent, projected gradient descent, additive uniform noise, and DeepFool [28] attacks over the whole CIFAR-10 test set on PreAct-ResNet18 models subject to $\ell_{\infty}$ constraints using the Foolbox library [33, 34]. The plots for the additive uniform noise and DeepFool attacks, given in Figure 1, show that MixUp provides an improvement over CutMix and the augmented baseline in this setting. This is because MixUp acts as a form of adversarial training [16], equipping the models with valid classifications for images of a similar nature to those generated by the additive noise and DeepFool attacks. In Figure 1, we additionally plot the worst case robustness following all attacks as suggested by Carlini et al. [18]. These results show that the adversarial training effect of MixUp is limited and does not correspond to a general increase in robustness. The key observation regarding these results is that there may be practical consequences to training with MixUp that are present but to a lesser degree when training with CutMix. There may be value to creating a new MSDA that goes even further than CutMix to minimise these practical consequences.
在确认MixUp会扭曲学习到的函数后,我们试图通过研究数据扭曲对训练分类器的影响来回答引言中的第三个问题。由于我们评估认为使用MixUp训练的模型对数据分布产生了"感知"上的改变,因此建议基于对抗攻击进行分析——这类攻击通过扰动感知分布之外的图像来改变既定分类。我们使用Foolbox库[33,34]对PreAct-ResNet18模型在整个CIFAR-10测试集上实施了快速梯度符号法、标准梯度下降、投影梯度下降、加性均匀噪声以及DeepFool[28]攻击,并施加$\ell_{\infty}$约束。图1所示的加性均匀噪声和DeepFool攻击曲线表明,在此设定下MixUp较CutMix和数据增强基线有所改进。这是因为MixUp作为一种对抗训练形式[16],使模型能对加性噪声和DeepFool攻击生成的同类图像进行有效分类。图1中我们还按照Carlini等人[18]的建议绘制了所有攻击后的最差鲁棒性曲线。这些结果表明MixUp的对抗训练效果有限,并未带来鲁棒性的普遍提升。关键发现在于:使用MixUp训练可能产生实际影响,而CutMix训练时这些影响程度较轻。开发比CutMix更进一步的新型混合样本数据增强(MSDA)方法来最小化这些实际影响可能具有价值。
IV. FMIX: IMPROVED MASKING
IV. FMIX: 改进的掩码策略
Our principle finding is that the masking MSDA approach works because it effectively preserves the data distribution in a way that interpol at ive MSDAs do not, particularly in the perceptual space of a Convolutional Neural Network (CNN). This derives from the fact that each convolutional neuron at a particular spatial position generally encodes information from only one of the inputs at a time. This could also be viewed as local consistency in the sense that elements that are close to each other in space typically derive from the same data point. To the detriment of CutMix, the number of possible examples is limited by only using square masks. In this section we propose FMix, a masking MSDA which maximises the number of possible masks whilst preserving local consistency. For local consistency, we require masks that are predominantly made up of a single shape or contiguous region. We might think of this as trying to minimise the number of times the binary mask transitions from $\mathbf{\nabla}^{\leftarrow}0^{\bullet}$ to $\mathbf{\hat{\Pi}}^{\epsilon}\mathbf{1}^{\epsilon}$ or vice-versa. For our approach, we begin by sampling a low frequency greyscale mask from Fourier space which can then be converted to binary with a threshold. We will first detail our approach for obtaining the low frequency image before discussing our approach for choosing the threshold. Let $Z$ denote a complex random variable with values on the domain $\mathcal{Z}=\mathbb{C}^{\bar{w}\times h}$ , with density $p_{\Re(Z)}=\mathcal{N}(\mathbf{0},I_{w\times h})$ and $p_{\Im(Z)}=\mathcal{N}(\mathbf{0},I_{w\times h})$ , where $\Re$ and $\mathfrak{I}$ return the real and imaginary parts of their input respectively. Let $\operatorname{freq}(w,h)[i,j]$ denote the magnitude of the sample frequency corresponding to the $i,j^{\prime}$ ’th bin of the $w\times h$ discrete Fourier transform. We can apply a low pass filter to $Z$ by decaying its high frequency components. Specifically, for a given decay power $\delta$ , we use
我们的核心发现是:掩码式混合样本数据增强(MSDA)方法之所以有效,是因为它能以插值式MSDA无法实现的方式保持数据分布特性,尤其在卷积神经网络(CNN)的感知空间中。这源于卷积神经元在特定空间位置通常每次仅编码单个输入信息的特性,也可理解为空间相邻元素往往源自同一数据点的局部一致性。CutMix的缺陷在于仅使用方形掩码限制了样本多样性。本节提出FMix——一种在保持局部一致性的同时最大化掩码可能性的掩码式MSDA方法。对于局部一致性,我们要求掩码主要由单一形状或连续区域构成,可视为最小化二值掩码在$\mathbf{\nabla}^{\leftarrow}0^{\bullet}$与$\mathbf{\hat{\Pi}}^{\epsilon}\mathbf{1}^{\epsilon}$间切换的次数。具体实现分为三步:首先从傅里叶空间采样低频灰度掩码,再通过阈值二值化。设$Z$为定义在$\mathcal{Z}=\mathbb{C}^{\bar{w}\times h}$上的复随机变量,其实部密度$p_{\Re(Z)}=\mathcal{N}(\mathbf{0},I_{w\times h})$,虚部密度$p_{\Im(Z)}=\mathcal{N}(\mathbf{0},I_{w\times h})$,其中$\Re$与$\mathfrak{I}$分别返回输入的实部和虚部。令$\operatorname{freq}(w,h)[i,j]$表示$w\times h$离散傅里叶变换第$i,j'$个频段对应的采样频率幅值。通过衰减高频分量可实现低通滤波:给定衰减功率$\delta$时,采用...

Fig. 2: Example masks and mixed images from CIFAR-10 for FMix with $\delta=3$ and $\lambda=0.5$ .
图 2: 使用 $\delta=3$ 和 $\lambda=0.5$ 参数时,CIFAR-10数据集上FMix生成的掩膜示例与混合图像。
$$
\mathrm{filter}({\bf z},\delta)[i,j]=\frac{{\bf z}[i,j]}{\mathrm{freq}(w,h)\left[i,j\right]^{\delta}}.
$$
$$
\mathrm{filter}({\bf z},\delta)[i,j]=\frac{{\bf z}[i,j]}{\mathrm{freq}(w,h)\left[i,j\right]^{\delta}}.
$$
Defining ${\mathcal{F}}^{-1}$ as the inverse discrete Fourier transform, we can obtain a grey-scale image with
定义 ${\mathcal{F}}^{-1}$ 为离散傅里叶逆变换,我们可以得到一个灰度图像
$$
G=\Re\big(\mathcal{F}^{-1}\big(\operatorname{filter}\big(Z,\delta\big)\big)\big)~.
$$
$$
G=\Re\big(\mathcal{F}^{-1}\big(\operatorname{filter}\big(Z,\delta\big)\big)\big)~.
$$
All that now remains is to convert the grey-scale image to a binary mask such that the mean value is some given $\lambda$ . Let $\mathrm{top}(n,{\bf x})$ return a set containing the top $n$ elements of the input $\mathbf{x}$ . Setting the top $\lambda w h$ elements of some grey-scale image $\mathbf{g}$ to have value $\mathbf{\hat{\Pi}}^{\epsilon}\mathbf{1}^{\epsilon}$ and all others to have value $\mathbf{\nabla}^{\leftarrow}0^{\cdot}$ we obtain a binary mask with mean $\lambda$ .
现在剩下的就是将灰度图像转换为二值掩码,使得平均值为某个给定的 $\lambda$。设 $\mathrm{top}(n,{\bf x})$ 返回一个包含输入 $\mathbf{x}$ 中前 $n$ 个元素的集合。将某个灰度图像 $\mathbf{g}$ 中前 $\lambda w h$ 个元素的值设为 $\mathbf{\hat{\Pi}}^{\epsilon}\mathbf{1}^{\epsilon}$,其余设为 $\mathbf{\nabla}^{\leftarrow}0^{\cdot}$,即可得到平均值为 $\lambda$ 的二值掩码。
To recap, we first sample a random complex tensor for which both the real and imaginary part are independent and Gaussian. We then scale each component according to its frequency via the parameter $\delta$ such that higher values of $\delta$ correspond to increased decay of high frequency information. Next, we perform an inverse Fourier transform on the complex tensor and take the real part to obtain a grey-scale image. Finally, we set the top proportion of the image to have value ‘1’ and the rest to have value $\mathrm{{}^{\cdot}0^{\cdot}}$ to obtain our binary mask. Although we have only considered two dimensional data here it is generally possible to create masks with any number of dimensions. We provide some example two dimensional masks and mixed images (with $\delta:=:3$ and $\lambda~=~0.5)$ in Figure 2. We can see that the space of artefacts is significantly increased, furthermore, FMix achieves $I(Z_{A};X)=83.67_{\pm0.89}.$ , $I(Z_{A};\hat{X})=80.28{\scriptstyle\pm0.75}$ , and $\mathrm{MSE}=0.255{\scriptstyle\pm0.003}$ , showing that learning f
