Connecting Low-Loss Subspace for Personalized Federated Learning

连接低损失子空间以实现个性化联邦学习

Minwoo Jeong lloyd.ai@ka kao enterprise.com Kakao Enterprise South Korea

闵宇（Minwoo Jeong） lloyd.ai@kakaoenterprise.com Kakao Enterprise 韩国

ABSTRACT

摘要

Due to the curse of statistical heterogeneity across clients, adopting a personalized federated learning method has become an essential choice for the successful deployment of federated learning-based services. Among diverse branches of personalization techniques, a model mixture-based personalization method is preferred as each client has their own personalized model as a result of federated learning. It usually requires a local model and a federated model, but this approach is either limited to partial parameter exchange or requires additional local updates, each of which is helpless to novel clients and burdensome to the client’s computational capacity. As the existence of a connected subspace containing diverse low-loss solutions between two or more independent deep networks has been discovered, we combined this interesting property with the model mixture-based personalized federated learning method for improved performance of personalization. We proposed SuPerFed, a personalized federated learning method that induces an explicit connection between the optima of the local and the federated model in weight space for boosting each other. Through extensive experiments on several benchmark datasets, we demonstrated that our method achieves consistent gains in both personalization performance and robustness to problematic scenarios possible in realistic services.

由于客户端间统计异质性的诅咒，采用个性化联邦学习方法已成为成功部署基于联邦学习的服务的必然选择。在各类个性化技术分支中，基于模型混合的个性化方法更受青睐，因其能使每个客户端通过联邦学习获得专属个性化模型。该方法通常需要本地模型和联邦模型协同工作，但现有方案要么局限于部分参数交换，要么需要额外本地更新——前者对新型客户端无效，后者则加重客户端的计算负担。随着研究发现两个及以上独立深度网络间存在包含多种低损失解（low-loss solutions）的连通子空间，我们将这一特性与基于模型混合的个性化联邦学习方法结合以提升性能。我们提出SuPerFed方法，通过在权重空间建立本地模型与联邦模型最优解间的显式连接实现相互促进。在多个基准数据集上的实验表明，该方法在个性化性能和现实服务中可能出现的异常场景鲁棒性方面均取得稳定提升。

CCS CONCEPTS

CCS概念

• Computing methodologies $\rightarrow$ Distributed algorithms; Neural networks.

• 计算方法 $\rightarrow$ 分布式算法；神经网络。

KEYWORDS

federated learning, non-IID data, personalization, personalized federated learning, label noise, mode connectivity

联邦学习 (federated learning)、非独立同分布数据 (non-IID data)、个性化 (personalization)、个性化联邦学习 (personalized federated learning)、标签噪声 (label noise)、模式连通性 (mode connectivity)

ACM Reference Format:

ACM 参考文献格式:

Seok-Ju Hahn, Minwoo Jeong, and Junghye Lee. 2022. Connecting Low-Loss Subspace for Personalized Federated Learning. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ’22), August 14–18, 2022, Washington, DC, USA. ACM, New York, NY, USA, 11 pages. https://doi.org/10.1145/3534678.3539254

Seok-Ju Hahn、Minwoo Jeong 和 Junghye Lee。2022。面向个性化联邦学习的低损失子空间连接。载于《第28届ACM SIGKDD知识发现与数据挖掘会议论文集》(KDD '22)，2022年8月14-18日，美国华盛顿特区。ACM，美国纽约州纽约市，11页。https://doi.org/10.1145/3534678.3539254

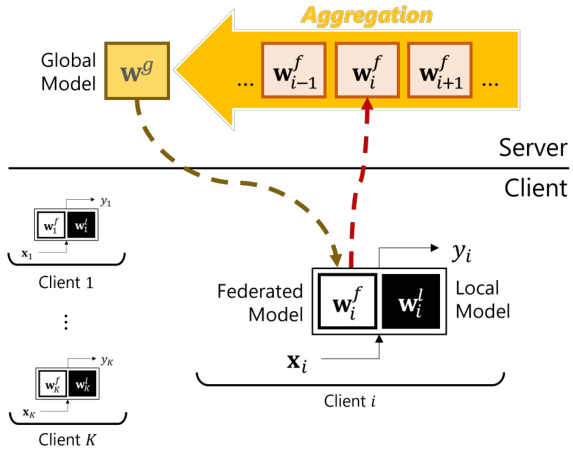
Figure 1: Overview of the model mixture-based personalized federated learning.

图 1: 基于模型混合的个性化联邦学习概览。

1 INTRODUCTION

1 引言

Individuals and institutions are now data producers as well as data keepers, thanks to advanced communication and computation technologies. Therefore, training a machine learning model in a data-centralized setting is sometimes not viable due to many realistic limitations, such as the existence of massive clients generating their own data in real-time or the data privacy issue restricting the collection of data. Federated learning (FL) [46] is a solution to solve this problematic situation as it enables parallel training of a machine learning model across clients or institutions without sharing their private data, usually under the orchestration of the server (e.g., service providers). In the most common FL setting, such as FedAvg [46], when the server prepares and broadcasts a model appropriate for a target task, each participant trains the model with its own data and transmits the resulting model parameters to the server. Then, the server receives the locally updated model parameters to aggregate (i.e., weighted averaging) into a new global model. The new global model is broadcast again to some fraction of participating clients. This collaborative learning process is repeated until convergence. However, obtaining a single global model through FL is not enough to provide satisfiable experiences to all clients, due to the curse of data heterogeneity. Since there exists an inherent difference among clients, the data residing in each client is not statistically identical. That is, a different client has their own different data distribution, or the data is not independent and identically distributed (non-IID). Thus, applying a simple FL method like FedAvg cannot avoid a pitfall of the high generalization error or even the divergence of model training [32]. That is, it is sometimes possible that the performance of the global model is lower than the locally trained model without collaboration. When this occurs, clients barely have the motivation to participate in the collaborative learning process to train a single global model.

得益于先进的通信和计算技术，个人和机构如今既是数据生产者也是数据保管者。因此，在数据集中化的环境中训练机器学习模型常因现实限制而难以实现，例如存在大量实时生成数据的客户端，或数据隐私问题限制数据收集。联邦学习 (FL) [46] 通过允许客户端或机构在不共享私有数据的情况下并行训练机器学习模型（通常由服务器协调，如服务提供商）来解决这一难题。在FedAvg [46]等最常见FL设定中，服务器准备并广播适合目标任务的模型后，各参与者用自身数据训练模型并将所得模型参数传回服务器。服务器汇总本地更新的模型参数（即加权平均）生成新全局模型，再次广播给部分参与客户端。这一协作学习过程重复至收敛。然而，由于数据异构性难题，通过FL获取单一全局模型无法为所有客户端提供满意体验。客户端间存在固有差异，各客户端数据在统计上并非同分布（即非独立同分布non-IID）。因此，采用FedAvg等简单FL方法无法避免高泛化误差甚至模型训练发散的缺陷[32]，可能导致全局模型性能低于未协作的本地训练模型。此时客户端几乎丧失参与协作训练单一全局模型的动机。

Hence, it is natural to rethink the scheme of FL. As a result, personalized FL (PFL) has becomes an essential component of FL, which has yielded many related studies. Many approaches are proposed for PFL, based on multi-task learning [12, 44, 51], regular iz ation technique [11, 23, 38]; meta-learning [14, 31], clustering [20, 43, 49], and a model mixture method [2, 8, 10, 38, 41, 43]. We focus on the model mixture-based PFL method in this paper as it shows promising performance as well as lets each client have their own model, which is a favorable trait in terms of personalization as each participating client eventually has their own model. This method assumes that each client has two distinct parts: a local (sub-)model and a federated (sub-)model (i.e., federated (sub-)model is a global model transferred to a client). In the model mixture-based PFL method, it is expected that the local model captures the information of heterogeneous client data distribution by staying only at the client-side, while the federated model focuses on learning common information across clients by being communicated with the server. Each federated model built at the client is sent to the server, where it is aggregated into a single global model (Figure 1). At the end of each PFL iteration, a participating client ends up having a personalized part (i.e., a local model), which potentially relieves the risks from the non-IIDness as well as benefits from the collaboration of other clients.

因此，重新思考联邦学习 (FL) 的方案是自然而然的。于是，个性化联邦学习 (PFL) 成为 FL 的重要组成部分，并催生了许多相关研究。目前提出的 PFL 方法主要基于多任务学习 [12, 44, 51]、正则化技术 [11, 23, 38]、元学习 [14, 31]、聚类 [20, 43, 49] 以及模型混合方法 [2, 8, 10, 38, 41, 43]。本文聚焦于基于模型混合的 PFL 方法，因其不仅展现出优异性能，还能让每个客户端拥有专属模型——这种特性在个性化方面极具优势，因为最终每个参与客户端都能保有自身模型。该方法假设每个客户端包含两个独立部分：本地（子）模型和联邦（子）模型（即联邦（子）模型是从服务器传输至客户端的全局模型）。在基于模型混合的 PFL 方法中，本地模型通过驻留客户端专门捕捉异构客户端数据分布信息，而联邦模型则通过服务器通信专注于学习跨客户端的共性信息。每个客户端构建的联邦模型会被发送至服务器聚合成单一全局模型（图 1）。每轮 PFL 迭代结束时，参与客户端将保留个性化部分（即本地模型），这既能缓解非独立同分布 (non-IID) 带来的风险，又能从其他客户端的协作中获益。

The model mixture-based PFL method has two sub-branches. One is sharing only a partial set of parameters of one single model as a federated model [2, 8, 41] (e.g., only exchanging weights of a penultimate layer), the other is having two identically structured models as a local and a federated model [10, 11, 23, 38, 43]. However, each of them has some limitations. In the former case, new clients cannot immediately exploit the model trained by FL, as the server only has a partial set of model parameters. In the latter case, all of them require separate (or sequential) updates for the local and the federated model each, which is possibly burdensome to some clients having low computational capacity.

基于模型混合的个性化联邦学习 (PFL) 方法包含两个分支：一是仅共享单一模型的部分参数作为联邦模型 [2, 8, 41] (例如仅交换倒数第二层的权重)，二是采用两个结构相同的模型分别作为本地模型和联邦模型 [10, 11, 23, 38, 43]。但二者均存在局限性：前者因服务器仅保留部分模型参数，新客户端无法直接利用联邦学习训练的模型；后者需对本地模型和联邦模型分别进行独立 (或顺序) 更新，这对计算能力较弱的客户端可能造成负担。

Here comes our main motivation: the development of a model mixture-based PFL method that can jointly train a whole model communicated with the server and another model for personalization. We attempted to achieve this goal through the lens of connectivity. As many studies on the deep network loss landscape have progressed, one intriguing phenomenon is being actively discussed in the field: the connectivity [13, 15, 16, 18, 19, 54] between deep networks. Though deep networks are known to have many local minima, it has been revealed that each of these local minima has a similar performance to each other [7]. Additionally, it has recently been discovered that two different local minima obtained by two independent deep networks can be connected through the linear path [17] or the non-linear path [13, 19] in the weight space, where all weights on the path have a low loss. Note that the two endpoints of the path are two different local minima reached from the two different deep networks. These findings have been extended to a multi-dimensional subspace [4, 54] with only a few gradient steps on two or more independently initialized deep networks. The resulting subspace, including the one-dimensional connected path, contains functionally diverse models having high accuracy. It can also be viewed as an ensemble of deep networks in the weight space, thereby sharing similar properties such as good calibration performance and robustness to the label noise. By introducing the connectivity to a model mixture-based PFL method, such good properties can also be absorbed advantageously.

我们的核心动机由此产生：开发一种基于模型混合的个性化联邦学习 (PFL) 方法，能够联合训练与服务器通信的完整模型和用于个性化的另一模型。我们尝试通过连通性视角实现这一目标。随着深度学习网络损失景观研究的深入，该领域正积极探讨一个有趣现象：深度网络间的连通性 [13, 15, 16, 18, 19, 54]。尽管已知深度网络存在许多局部极小值，但研究表明这些极小值彼此性能相近 [7]。此外，最新发现表明：通过权重空间中的线性路径 [17] 或非线性路径 [13, 19]，可将两个独立深度网络获得的不同局部极小值连通，且路径上所有权重均保持低损失。需注意，该路径的两个端点分别对应两个不同深度网络达到的局部极小值。这些发现已扩展到多维子空间 [4, 54]——仅需对两个及以上独立初始化的深度网络进行少量梯度步骤。由此产生的子空间（包含一维连通路径）涵盖了大量功能多样且高精度的模型，也可视为权重空间中深度网络的集成，因此共享了良好校准性能和标签噪声鲁棒性等特性。将连通性引入基于模型混合的PFL方法后，这些优良特性也能被有效吸收。

Our contributions. Inspired by this observation, we propose SuPerFed, a connected low-loss subspace construction method for the personalized federated learning, adapting the concept of connectivity to the model mixture-based PFL method. This method aims to find a lowloss subspace between a single global model and many different local models at clients in a mutually beneficial way. Accordingly, we aim to achieve better personalization performance while overcoming the aforementioned limitations of model mixture-based PFL methods. Adopting the connectivity to FL is non-trivial as it obviously differs from the setting where the connectivity is first considered: each deep network observes different data distributions and only the global model can be connected to other local models on clients. The main contributions of the work are as follows:

我们的贡献。受此启发，我们提出了SuPerFed——一种面向个性化联邦学习的连通低损失子空间构建方法，将连通性概念适配于基于模型混合的PFL方法。该方法旨在以互利方式，在单一全局模型与客户端多个不同本地模型之间寻找低损失子空间。由此，我们力求在提升个性化性能的同时，克服基于模型混合的PFL方法的上述局限性。将连通性引入联邦学习具有显著挑战性，因其与连通性最初提出的设定存在本质差异：每个深度网络观测不同的数据分布，且仅有全局模型能与客户端的其他本地模型建立连接。本研究的主要贡献如下：

2 RELATED WORKS

2 相关工作

2.1 FL with Non-IID Data

2.1 非独立同分布数据下的联邦学习 (FL with Non-IID Data)

After [46] proposed the basic FL algorithm (FedAvg), handling nonIID data across clients is one of the major points to be resolved in the FL field. While some methods are proposed such as sharing a subset of client’s local data at the server[56], accumulating previous model updates at the server [26]. These are either unrealistic assumptions for FL or not enough to handle a realistic level of statistical heterogeneity. Other branches to aid the stable convergence of a single global model include modifying a model aggregation method at the server [40, 48, 53, 55] and adding a regular iz ation to the optimization [1, 32, 39]. However, a single global model may still not be sufficient to provide a satisfactory experience to clients using FL-driven services in practice.

在[46]提出基础的联邦学习算法(FedAvg)后，处理客户端间的非独立同分布(nonIID)数据成为该领域待解决的核心问题。虽然已有部分解决方案被提出，例如在服务器端共享客户端本地数据子集[56]、在服务器端累积历史模型更新[26]，但这些方法要么违背联邦学习的基本假设，要么难以应对现实场景中的统计异构性。其他促进单一全局模型稳定收敛的研究方向包括：改进服务器端的模型聚合方法[40, 48, 53, 55]，以及在优化过程中添加正则化项[1, 32, 39]。然而实践表明，单一全局模型可能仍无法为使用联邦学习服务的客户提供理想体验。

2.2 PFL Methods

2.2 PFL方法

As an extension of the above, PFL methods shed light on the new perspective of FL. PFL aims to learn a client-specific personalized

作为上述内容的延伸，个性化联邦学习 (Personalized Federated Learning, PFL) 方法为联邦学习提供了新的视角。PFL旨在学习针对特定客户端的个性化

(C) Exploitation of trained models

(C) 训练模型的利用

Case 1) Clients participate in the federated learning → Can utilize any models from the connected low-loss subspace generated by adjusting $\lambda\in[0,1]$

案例1) 客户端参与联邦学习 → 可通过调整 $\lambda\in[0,1]$ 来利用连接的低损失子空间生成的任何模型

Case 2) Novel clients

案例 2) 新客户端

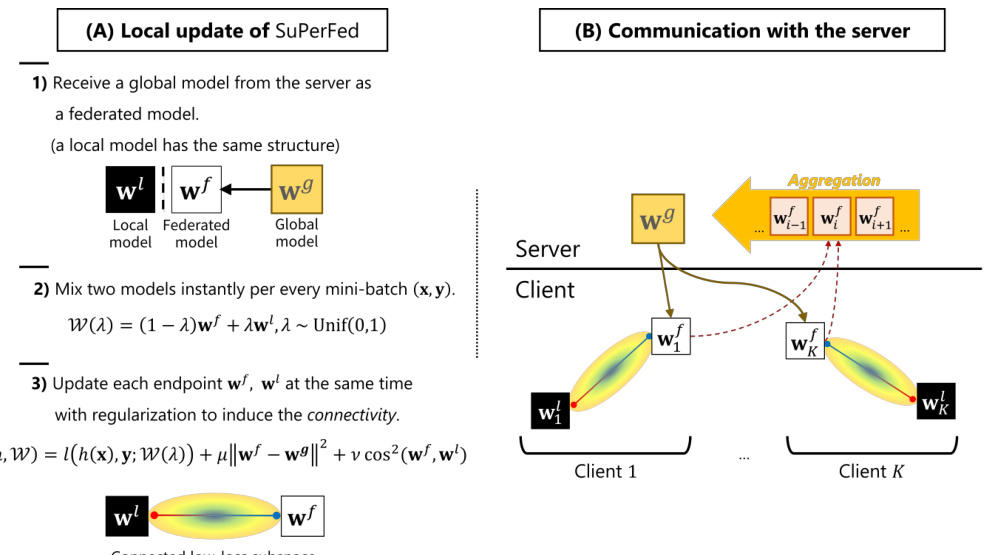
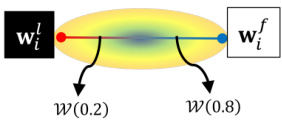
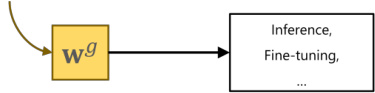
Figure 2: An illustration of the proposed method SuPerFed. (A) Local update of SuPerFed: at every federated learning round, a selected client receives a global model from the server and sets it to be a federated model. After being mixed by a randomly generated $\lambda$ , two models are jointly updated with regular iz ation. (B) Communication with the server: only the updated federated model is uploaded to the server (dotted arrow in crimson) to be aggregated (e.g., weighted averaging) as a new global model, and it is broadcast to clients in the next round (arrow in gray). (C) Exploitation of trained models: (Case 1) FL clients can sample and use any model on the connected subspace (e.g., W(0.2), $\mathcal{W}(0.8))$ because it only contains low-loss solutions. (Case 2) Novel clients can download and use the server’s trained global model $\mathbf{w}_{g}$ .

图 2: 提出的SuPerFed方法示意图。(A) SuPerFed的本地更新：在每轮联邦学习中，选定的客户端从服务器接收全局模型并设为联邦模型。经过随机生成的$\lambda$混合后，两个模型通过正则化联合更新。(B) 与服务器的通信：仅更新后的联邦模型会上传至服务器(深红色虚线箭头)进行聚合(如加权平均)形成新全局模型，并在下一轮广播给客户端(灰色箭头)。(C) 训练模型的利用：(情况1) FL客户端可采样使用连接子空间上的任意模型(如W(0.2), $\mathcal{W}(0.8))$，因其仅包含低损失解。(情况2) 新客户端可下载使用服务器训练好的全局模型$\mathbf{w}_{g}$。

→ Can exploit the global model by downloading from the server.

可以从服务器下载以利用全局模型。

model, and many methodologies for PFL have been proposed. Multitask learning-based PFL [12, 44, 51] treats each client as a different task and learns a personalized model for each client. Local finetuning-based PFL methods [14, 31] adopt a meta-learning approach for a global model to be adapted promptly to a personalized model for each client, and clustering-based PFL methods [20, 43, 49] mainly assume that similar clients may reach a similar optimal global model. Model mixture-based PFL methods [2, 8, 10, 11, 23, 38, 41, 43] divide a model into two parts: one (i.e., a local model) for capturing local knowledge, and the other (i.e., a federated model) for learning common knowledge across clients. In these methods, only the federated model is shared with the server while the local model resides locally on each client. [2] keeps weights of the last layer as a local model (i.e., the personalization layers), and [8] is similar to this except it requires a separate update on a local model before the update of a federated model. In contrast, [41] retains lower layer weights in clients and only exchanges higher layer weights with the server. Due to the partial exchange, new clients in the scheme of [2, 8, 41] should train their models from scratch or need at least some steps of fine-tuning. In [10, 11, 23, 38, 43], each client holds at least two separate models with the same structure: one for a local model and the other for a federated model. In [10, 23, 43], they are explicitly interpolated in the form of a convex combination after the independent update of two models. In [11, 38], the federated model affects the update of the local model in the form of proximity regular iz ation.

模型，并提出了许多个性化联邦学习(PFL)方法。基于多任务学习的PFL [12, 44, 51] 将每个客户端视为不同任务，为其学习个性化模型。基于本地微调的PFL方法 [14, 31] 采用元学习方法，使全局模型能快速适配为各客户端的个性化模型；基于聚类的PFL方法 [20, 43, 49] 主要假设相似客户端可能收敛至相似的全局最优模型。基于模型混合的PFL方法 [2, 8, 10, 11, 23, 38, 41, 43] 将模型分为两部分：一部分(即本地模型)用于捕获本地知识，另一部分(即联邦模型)用于学习跨客户端的共性知识。这些方法中仅联邦模型与服务器共享，本地模型则驻留在各客户端本地。[2] 将最后一层权重保留为本地模型(即个性化层)，[8] 与之类似，但要求在更新联邦模型前对本地模型进行单独更新。[41] 则保留客户端底层权重，仅与服务器交换高层权重。由于这种部分交换机制，[2, 8, 41] 方案中的新客户端需从头训练模型或至少进行若干步微调。在 [10, 11, 23, 38, 43] 中，每个客户端至少持有两个结构相同的独立模型：一个作为本地模型，另一个作为联邦模型。[10, 23, 43] 在两个模型独立更新后以凸组合形式显式插值，而 [11, 38] 通过邻近正则化使联邦模型影响本地模型的更新。

2.3 Connectivity of Deep Networks

2.3 深度网络的连通性

The existence of either linear path [17] or non-linear path [13, 19] between two minima derived by two different deep networks has been recently discovered through extensive studies on the loss landscape of deep networks [13, 15, 16, 18, 19]. That is, there exists a low-loss subspace (e.g., line, simplex) connecting two or more deep networks independently trained on the same data. Though there exist some studies on constructing such a low loss subspace [5, 28– 30, 36, 42], they require multiple updates of deep networks. After it is observed that independently trained deep networks have a low cosine similarity with each other in the weight space [15], a recent study by [54] proposes a straightforward and efficient method for explicitly inducing linear connectivity in a single training run. Our method adopts this technique and adapts it to construct a low-loss subspace between each local model and a federated model (which will later be aggregated into a global model at the server) suited for an effective PFL in heterogeneous ly distributed data.

通过对深度网络损失景观的广泛研究[13, 15, 16, 18, 19]，最近发现由两个不同深度网络产生的极小值之间存在线性路径[17]或非线性路径[13, 19]。也就是说，存在一个低损失子空间（如直线、单纯形）连接两个或多个在同一数据上独立训练的深度网络。尽管已有一些关于构建此类低损失子空间的研究[5, 28–30, 36, 42]，但它们需要对深度网络进行多次更新。在观察到独立训练的深度网络在权重空间中彼此具有较低的余弦相似性后[15]，[54]的最新研究提出了一种简单高效的方法，可在单次训练中显式诱导线性连接。我们的方法采用该技术，并将其适配为构建每个本地模型与联邦模型（后续将在服务器端聚合成全局模型）之间的低损失子空间，以适应异构分布数据中的高效个性化联邦学习(PFL)。

3 PROPOSED METHOD

3 提出的方法

3.1 Overview

3.1 概述

In the standard FL scheme [46], the server orchestrates the whole learning process across participating clients with iterative communication of model parameters. Since our method is essentially a model mixture-based PFL method, we need two models same in structure per client (one for a federated model, the other for a local model), of which initialization is different from each other. As a result, the client’s local models are trained using different random initialization s than its federated model counterpart. Note that different initialization is not common in FL [46]; however, this is intended behavior in our scheme for promoting construction of

在标准联邦学习 (FL) [46] 框架中，服务器通过模型参数的迭代通信协调参与客户端的学习过程。由于我们的方法本质上是基于模型混合的个性化联邦学习 (PFL) 方法，每个客户端需要两个结构相同的模型（一个用于联邦模型，另一个用于本地模型），其初始化方式彼此不同。因此，客户端的本地模型使用与其联邦模型不同的随机初始化进行训练。需注意，不同的初始化在联邦学习 [46] 中并不常见；但这是我们方案中为促进...的预期行为

Algorithm 1 Local Update

算法 1 本地更新

Algorithm 2 SuPerFed

算法 2 SuPerFed

the connected low-loss subspace between a federated model and a local model.

联邦模型与本地模型之间的低损耗连通子空间。

3.2 Notations

3.2 符号说明

We first define arguments required for the federated optimization as follows: a total number of communication rounds (R), a person a lization start round (L) a local batch size (B), a number of local epochs (E), a total number of clients (K), a fraction of clients selected at each round (C), and a local learning rate $(\eta)$ . Following that, three hyper parameters are required for the optimization of our proposed method: a mixing constant $\lambda$ sampled from the uniform distribution ${\mathrm{Unif}}(0,1)$ , a constant $\mu$ for proximity regular iz ation on the federated model $\mathbf{w}^{f}$ so that it is not distant from the global model $\mathbf{w}^{g}$ ; and a constant $\nu$ for inducing connectivity along a subspace between local and federated models $(\mathbf{w}^{l}&\mathbf{w}^{f})$ .

我们首先定义联邦优化所需的参数如下：总通信轮数 (R)、个性化起始轮数 (L)、本地批次大小 (B)、本地训练轮数 (E)、客户端总数 (K)、每轮选中的客户端比例 (C) 以及本地学习率 $(\eta)$。随后，优化我们提出的方法需要三个超参数：从均匀分布 ${\mathrm{Unif}}(0,1)$ 中采样的混合常数 $\lambda$、用于对联邦模型 $\mathbf{w}^{f}$ 施加邻近正则化以使其不远离全局模型 $\mathbf{w}^{g}$ 的常数 $\mu$，以及用于在本地模型与联邦模型 $(\mathbf{w}^{l}&\mathbf{w}^{f})$ 之间诱导子空间连通性的常数 $\nu$。

3.3 Problem Statement

3.3 问题陈述

Consider that each client $c_{i}$ $(i\in[\mathrm{K}])$ has its own dataset $\mathcal{D}{i}={(\mathbf{x}{i},\mathbf{y}{i})}$of size$n{i}$, as well as a model$\mathcal{W}{i}$. We assume that datasets are non-IID across clients in PFL, which means that each dataset$\mathcal{D}{i}$is sampled independently from a corresponding distribution$\mathcal{P}{i}$on both input and label spaces$z=\chi\times y$. A hypothesis$h\in{\mathcal{H}}$can be learned by the objective function$l:\mathcal{H}\times\mathcal{Z}\rightarrow\mathbb{R}^{+}$in the form of$l(h(\mathbf{x};\mathcal{W}),\mathbf{y})$. We denote the expected loss as$\mathcal{L}{\mathcal{P}{i}}(h{i},\mathcal{W}{i})=\mathbb{E}{(\mathbf{x}{i},\mathbf{y}{i})\sim\mathcal{P}{i}}[l(h{i}(\mathbf{x}{i};\mathcal{W}{i}),\mathbf{y}{i})]$, and the empirical loss as$\begin{array}{r}{\hat{\mathcal{L}}{\mathcal{D}{i}}(h{i},\mathcal{W}{i})=\frac{1}{n{i}}\sum_{j=1}^{n_{i}}l_{i}(h_{i}(\mathbf{x}{i}^{j};\mathcal{W}{i}),\mathbf{y}{i}^{j})}\end{array}$; a regular iz ation term$\Omega(\mathcal{W}{i})$ can also be incorporated here. Then, the global objective of PFL is to optimize (1).

假设每个客户端 $c_{i}$ $(i\in[\mathrm{K}])$ 拥有自己的数据集 $\mathcal{D}{i}={(\mathbf{x}{i},\mathbf{y}{i})}$，其大小为$n{i}$，以及一个模型$\mathcal{W}{i}$。我们假设在个性化联邦学习 (PFL) 中，各客户端的数据集是非独立同分布 (non-IID) 的，这意味着每个数据集$\mathcal{D}{i}$是从输入和标签空间$z=\chi\times y$上的对应分布$\mathcal{P}{i}$中独立采样的。假设$h\in{\mathcal{H}}$可以通过目标函数$l:\mathcal{H}\times\mathcal{Z}\rightarrow\mathbb{R}^{+}$以$l(h(\mathbf{x};\mathcal{W}),\mathbf{y})$的形式学习。我们将期望损失表示为$\mathcal{L}{\mathcal{P}{i}}(h{i},\mathcal{W}{i})=\mathbb{E}{(\mathbf{x}{i},\mathbf{y}{i})\sim\mathcal{P}{i}}[l(h{i}(\mathbf{x}{i};\mathcal{W}{i}),\mathbf{y}{i})]$，经验损失表示为$\begin{array}{r}{\hat{\mathcal{L}}{\mathcal{D}{i}}(h{i},\mathcal{W}{i})=\frac{1}{n{i}}\sum_{j=1}^{n_{i}}l_{i}(h_{i}(\mathbf{x}{i}^{j};\mathcal{W}{i}),\mathbf{y}{i}^{j})}\end{array}$；此处还可以加入正则化项$\Omega(\mathcal{W}{i})$ 。因此，PFL 的全局目标是优化 (1)。

We can minimize this global objective through the empirical loss minimization (2).

我们可以通过经验损失最小化 (2) 来最小化这个全局目标。

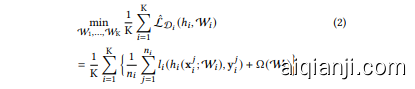
A model mixture-based PFL assumes each client $c_{i}$ has a set of paired parameters $\mathbf{w}{i}^{f},\mathbf{w}{i}^{l}\subseteq\mathcal{W}{i}$. Note that each of which is previously defined as a federated model and a local model. Both of them are grouped as a client model$\mathcal{W}{i}=G(\mathbf{w}{i}^{f},\mathbf{w}{i}^{l})$with the grouping operator$G$. This operator can be a concatenation (e.g., stacking semantically separated layers like feature extractor or classifier [2, 8, 41]):$G(\mathbf{w}{i}^{\bar{f}},\bar{\mathbf{w}{i}^{\bar{l}}})=\mathrm{Concat}(\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l})$, a simple enumeration of parameters having the same structure [11, 38]:$G(\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l}):=:{\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l}},$, or a convex combination [10, 23, 43] given a constant$\lambda\in[0,1]$:$G(\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l};\lambda)=(1-\lambda)\mathbf{w}_{i}^{f}+\lambda\mathbf{w}_{i}^{l}.$ .

基于模型混合的个性化联邦学习 (PFL) 假设每个客户端 $c_{i}$ 拥有一组配对参数 $\mathbf{w}{i}^{f},\mathbf{w}{i}^{l}\subseteq\mathcal{W}{i}$。需注意，其中每个参数先前被定义为联邦模型和本地模型。两者通过分组运算符$G$组合为客户端模型$\mathcal{W}{i}=G(\mathbf{w}{i}^{f},\mathbf{w}{i}^{l})$。该运算符可以是拼接操作 (例如堆叠语义分离层，如特征提取器或分类器 [2, 8, 41]):$G(\mathbf{w}{i}^{\bar{f}},\bar{\mathbf{w}{i}^{\bar{l}}})=\mathrm{Concat}(\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l})$, 对具有相同结构的参数进行简单枚举 [11, 38]:$G(\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l}):=:{\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l}},$, 或给定常数$\lambda\in[0,1]$的凸组合 [10, 23, 43]:$G(\mathbf{w}_{i}^{f},\mathbf{w}_{i}^{l};\lambda)=(1-\lambda)\mathbf{w}_{i}^{f}+\lambda\mathbf{w}_{i}^{l}.$。

3.4 Local Update

3.4 本地更新

In SuPerFed, we suppose both models $\mathbf{w}{i}^{f},\mathbf{w}{i}^{l}$have the same structure and consider$G$to be a function for constructing a convex combination. We will write$\lambda$as an explicit input to the client model with a slight abuse of notation:$\mathbf{\mathcal{W}}{i}(\lambda)\overset{\cdot}{:=}G(\mathbf{\bar{w}}{i}^{f},\mathbf{w}{i}^{l};\lambda)=(1-\lambda)\mathbf{w}{i}^{f}+\lambda\mathbf{w}{i}^{l}.$The main goal of the local update in SuPerFed is to find a flat wide minima between the local model and the federated model. In the initial round, each client receives a global model transmitted from the server, sets it as a federated model, and copies the structure to set a local model. As different initialization is required, clients initialize their local model again with its fresh random seed. During the local update, a client mixes two models using$\lambda\sim\operatorname{Unif}(0,1)$as$\mathcal{W}{i}(\lambda)=(1-\lambda)\mathbf{w}{i}^{f}+\lambda\mathbf{w}{i}^{l},$each time with a fresh mini-batch including$(\mathbf{x},\mathbf{y})$sampled from local dataset$\mathcal{D}$. The local model and the federated model are reduced to be interpolated diversely during local training. Finally, it is optimized with a loss function$l(\cdot)$specific to the task, for example, cross-entropy, with additional regular iz ation$\Omega(\cdot)$ that is critical to induce the connectivity.

在SuPerFed中，我们假设模型$\mathbf{w}{i}^{f},\mathbf{w}{i}^{l}$具有相同结构，并将$G$视为构造凸组合的函数。通过略微简化符号，将$\lambda$显式写入客户端模型输入：$\mathbf{\mathcal{W}}{i}(\lambda)\overset{\cdot}{:=}G(\mathbf{\bar{w}}{i}^{f},\mathbf{w}{i}^{l};\lambda)=(1-\lambda)\mathbf{w}{i}^{f}+\lambda\mathbf{w}{i}^{l}$。SuPerFed本地更新的主要目标是寻找本地模型与联邦模型之间的平坦宽最小值。初始轮次中，每个客户端接收服务器传输的全局模型，将其设为联邦模型，并复制结构建立本地模型。由于需要差异化初始化，客户端使用新随机种子重新初始化本地模型。本地更新时，客户端采用$\lambda\sim\operatorname{Unif}(0,1)$混合两个模型：$\mathcal{W}{i}(\lambda)=(1-\lambda)\mathbf{w}{i}^{f}+\lambda\mathbf{w}{i}^{l}$，每次使用从本地数据集$\mathcal{D}$采样的新小批量数据$(\mathbf{x},\mathbf{y})$。本地训练过程中，本地模型与联邦模型通过多样化插值进行降维。最终通过任务特定损失函数$l(\cdot)$（如交叉熵）及关键连接性正则项$\Omega(\cdot)$进行优化。

Remark 1. Connectivity [17, 54]. There exists a low-loss subspace spanned by $\mathcal{W}(\lambda)$ between two independently trained (i.e., trained from different random initialization s) deep networks ${\bf w}{1}$and$\mathbf{w}{2}$, in the form of a linear combination formed by$\lambda\colon\mathcal{W}(\lambda)=(1-\lambda)\mathbf{w}{1}+\lambda\mathbf{w}{2},\lambda\in[0,1]$ .

备注1. 连通性 [17, 54]。在两个独立训练（即从不同随机初始化开始训练）的深度网络 ${\bf w}{1}$和$\mathbf{w}{2}$之间，存在一个由$\mathcal{W}(\lambda)$张成的低损失子空间，其形式为线性组合$\lambda\colon\mathcal{W}(\lambda)=(1-\lambda)\mathbf{w}{1}+\lambda\mathbf{w}{2},\lambda\in[0,1]$。

The local objective is

本地目标是

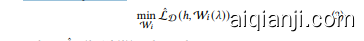
, where $\hat{\mathcal{L}}{\mathcal{D}}(h,\mathcal{W}{i}(\lambda))$ is denoted as:

其中 $\hat{\mathcal{L}}{\mathcal{D}}(h,\mathcal{W}{i}(\lambda))$ 定义为：

Note that the global model $\mathbf{w}^{g}$ is fixed here for the proximity regularization of $\mathbf{w}{i}^{f}$. Denote the local objective (3) simply as$\hat{\mathcal{L}}$. Then, the update of each endpoint$\mathbf{w}{i}^{f}$and$\mathbf{w}{i}^{l}$is done using the following estimates. Note that two endpoints (i.e.,$\mathcal{W}{i}(0)={\bf w}{i}^{f}$and$\mathcal{W}{i}(1)=\mathbf{w}_{i}^{l})$ can be jointly updated at the same time in a single training run.

注意全局模型 $\mathbf{w}^{g}$ 在此处固定，用于 $\mathbf{w}{i}^{f}$的邻近正则化。将局部目标函数 (3) 简记为$\hat{\mathcal{L}}$，则每个端点$\mathbf{w}{i}^{f}$和$\mathbf{w}{i}^{l}$的更新通过以下估计实现。需注意两个端点 (即$\mathcal{W}{i}(0)={\bf w}{i}^{f}$和$\mathcal{W}{i}(1)=\mathbf{w}_{i}^{l})$ 可在单次训练中同步联合更新。

3.5 Regular iz ation

3.5 正则化 (Regularization)

The regular iz ation term $\cos(\cdot,\cdot)$ stands for cosine similarity defined as: $\cos(\mathbf{w}{i}^{f},\mathbf{w}{i}^{l})=\langle\mathbf{w}{i}^{f},\mathbf{w}{i}^{l}\rangle/(\left|\mathbf{w}{i}^{f}\right|\left|\mathbf{w}{i}^{l}\right|)$. This aims to induce connectivity between the local mo del a n d th e federated model, thereby allowing the connected subspace between them to contain weights yielding high accuracy for the given task. Its magnitude is controlled by the constant$\nu$. Since merely applying the mixing strategy between the local and the federated models has little benefit [54], it is required to set$\nu>0$. In [15, 54], it is observed that weights of independently trained deep networks show dissimilarity in terms of cosine similarity, which has functional diversity as a result. Moreover, in [3, 45], inducing orthogonality (i.e., forcing cosine similarity to zero) between weights prevents deep networks from learning redundant features given their learning capacity. In this context, we expect the local model of each client$\mathbf{w}{i}^{l}$to learn client-specific knowledge while the federated model$\mathbf{w}{i}^{f}$learns client-agnostic knowledge in a complementary manner and is harmoniously combined with the local model. The other regular iz ation term adjusted by$\mu$is L2-norm which controls the proximity of the update of the federated model$\mathbf{w}_{i}^{f}$from the global model$\mathbf{w}^{g}$[39]. By doing so, we expect each local update of the federated model not to be derailed from the global model, which prevents divergence of the aggregated global model during the process of FL. Note that an inordinate degree of proximity regular iz ation can hinder the local model’s adaptation and thereby cause the divergence of a global model [11, 39]. Thus, a moderate degree of$\mu$is required. Note that our method is designed to be reduced to the existing$\mathrm{FL}$methods by adjusting hyper parameters, and thus it can be guaranteed to have at least their performance. In detail, when fixing$\lambda=0$,$\nu=0,\mu=0$, the objective of SuPerFed is reduced to FedAvg [46], when$\lambda=0$,$\nu=0,\mu>0$ , it is equivalent to FedProx [39].

正则化项 $\cos(\cdot,\cdot)$ 表示余弦相似度，其定义为：$\cos(\mathbf{w}{i}^{f},\mathbf{w}{i}^{l})=\langle\mathbf{w}{i}^{f},\mathbf{w}{i}^{l}\rangle/(\left|\mathbf{w}{i}^{f}\right|\left|\mathbf{w}{i}^{l}\right|)$。该正则化项旨在建立本地模型与联邦模型之间的连接性，从而使它们之间的连接子空间包含能够为给定任务带来高准确率的权重。其强度由常数$\nu$控制。由于仅应用本地模型与联邦模型之间的混合策略收效甚微 [54]，因此需要设置$\nu>0$。在 [15, 54] 中观察到，独立训练的深度网络权重在余弦相似度方面表现出差异性，从而产生功能多样性。此外，在 [3, 45] 中，通过强制权重之间的正交性（即迫使余弦相似度为零），可以防止深度网络在学习能力范围内学习冗余特征。在此背景下，我们期望每个客户端的本地模型$\mathbf{w}{i}^{l}$学习客户端特定的知识，而联邦模型$\mathbf{w}{i}^{f}$则以互补的方式学习与客户端无关的知识，并与本地模型和谐结合。另一个由$\mu$调整的正则化项是 L2 范数，它控制联邦模型$\mathbf{w}_{i}^{f}$的更新与全局模型$\mathbf{w}^{g}$的接近程度 [39]。通过这种方式，我们期望联邦模型的每次本地更新不会偏离全局模型，从而防止联邦学习 (FL) 过程中聚合的全局模型发散。需要注意的是，过度的接近正则化可能会阻碍本地模型的适应性，从而导致全局模型发散 [11, 39]。因此，需要适度调整$\mu$的值。值得注意的是，我们的方法通过调整超参数可以简化为现有的联邦学习方法，因此可以保证至少达到它们的性能。具体来说，当固定$\lambda=0$、$\nu=0,\mu=0$时，SuPerFed 的目标函数简化为 FedAvg [46]；当$\lambda=0$、$\nu=0,\mu>0$ 时，它等价于 FedProx [39]。

3.6 Communication with the Server

3.6 与服务器通信

At each round, the server samples a fraction of clients at every round (suppose $N$ clients are sampled), and requests a local update to each client. Only the federated model $\mathbf{w}{i}^{f}$and the amounts of consumed training data per client$n{i}$are transferred to the server after the local update is completed in parallel across selected clients. The server then aggregates them to create an updated global model$\mathbf{w}^{g}$as$ $$\begin{array}{r}{\mathbf{w}^{g}\gets\frac{1}{\sum_{i=1}^{N}n_{i}}\sum_{i=1}^{N}n_{i}\mathbf{w}_{i}^{f}}\end{array}$$ $. In the next round, only the updated global model$\mathbf{w}^{g}$is transmitted to another group of selected clients, and it is set to be a new federated model at each client:$\mathbf{w}_{i}^{f}\gets\mathbf{w}^{g}$ It is worth noting that the communication cost remains constant as with the single model-based FL methods [39, 46]. See Algorithm 2 for understanding the whole process of SuPerFed.

在每一轮中，服务器会采样一部分客户端 (假设采样了 $N$ 个客户端)，并请求每个客户端进行本地更新。在选定的客户端并行完成本地更新后，仅联邦模型 $\mathbf{w}{i}^{f}$和每个客户端消耗的训练数据量$n{i}$会被传输到服务器。服务器随后聚合这些信息以创建更新后的全局模型$\mathbf{w}^{g}$，公式为$ $$\begin{array}{r}{\mathbf{w}^{g}\gets\frac{1}{\sum_{i=1}^{N}n_{i}}\sum_{i=1}^{N}n_{i}\mathbf{w}_{i}^{f}\end{array}$$ $。在下一轮中，只有更新后的全局模型$\mathbf{w}^{g}$会被传输到另一组选定的客户端，并在每个客户端设置为新的联邦模型：$\mathbf{w}_{i}^{f}\gets\mathbf{w}^{g}$。值得注意的是，通信成本与基于单一模型的联邦学习方法 [39, 46] 保持一致。完整流程详见算法 2。

3.7 Variation in Mixing Method

3.7 混合方法的变化

Until now, we only considered the setting of applying 𝜆 identically to the whole layers of $\mathbf{w}^{f}$ and $\mathbf{w}^{l}$ . We name this setting Model Mixing, in short, MM. On the one hand, it is also possible to sample different $\lambda$ for weights of different layers, i.e., mixing two models in a layer-wise manner. We also adopt this setting and name it Layer Mixing, in short, LM.

到目前为止，我们仅考虑了将𝜆统一应用于$\mathbf{w}^{f}$和$\mathbf{w}^{l}$所有层的设置。我们将此设置称为模型混合 (Model Mixing)，简称MM。另一方面，也可以为不同层的权重采样不同的$\lambda$，即以分层方式混合两个模型。我们也采用此设置，并将其称为分层混合 (Layer Mixing)，简称LM。

Table 1: Experimental results on the pathological non-IID setting (MNIST and CIFAR10 datasets) compared with other FL and PFL methods. The top-1 accuracy is reported with a standard deviation.

表 1: 病理非独立同分布(non-IID)设置下(MNIST和CIFAR10数据集)与其他联邦学习(FL)和个性化联邦学习(PFL)方法的对比实验结果。报告了top-1准确率及其标准差。

数据集	MNIST	MNIST	MNIST	CIFAR10	CIFAR10	CIFAR10
客户端数量	50	100	500	50	100	500
样本数量	960	480	96	800	400	80
FedAvg	95.69 ± 2.39	89.78 ± 11.30	96.04 ± 4.74	43.09 ± 24.56	36.19 ± 29.54	47.90 ± 25.05
FedProx	95.13 ± 2.67	93.25 ± 6.12	96.50 ± 4.52	49.01 ± 19.87	38.56 ± 28.11	48.60 ± 25.71
SCAFFOLD	95.50 ± 2.71	90.58 ± 10.13	96.60 ± 4.26	43.81 ± 24.30	36.31 ± 29.42	40.27 ± 26.90
LG-FedAvg	98.21 ± 1.28	97.52 ± 2.11	96.05 ± 5.02	89.03 ± 4.53	70.25 ± 35.66	78.52 ± 11.22
FedPer	99.23 ± 0.66	99.14 ± 0.93	98.67 ± 2.61	89.10 ± 5.41	87.99 ± 5.70	82.35 ± 9.85
APFL	99.40 ± 0.58	99.19 ± 0.92	98.98 ± 2.22	92.83 ± 3.47	91.73 ± 4.61	87.38 ± 9.39
pFedMe	81.10 ± 8.52	82.48 ± 7.62	81.96 ± 12.28	92.97 ± 3.07	92.07 ± 5.05	88.30 ± 8.53
Ditto	97.07 ± 1.38	97.13 ± 2.06	97.20 ± 3.72	85.53 ± 6.22	83.01 ± 5.62	84.45 ± 10.67
FedRep	99.11 ± 0.63	99.04 ± 1.02	97.94 ± 3.37	82.00 ± 5.41	81.27 ± 7.90	80.66 ± 11.00
SuPerFed-MM	99.45 ± 0.46	99.38 ± 0.93	99.24 ± 2.12	94.05 ± 3.18	93.25 ± 3.80	90.81 ± 9.35
SuPerFed-LM	99.48 ± 0.54	99.31 ± 1.09	98.83 ± 3.02	93.88 ± 3.55	93.20 ± 4.19	89.63 ± 11.11

4 EXPERIMENTS

4 实验

4.1Setup

4.1 设置

We focus on two points in our experiments: (i) personalization performance in various non-IID scenarios, (ii) robustness to label noise through extensive benchmark datasets. Details of each experiment are provided in Appendix A. Throughout all experiments, if not specified, we set 5 clients to be sampled at every round and used stochastic gradient descent (SGD) optimization with a momentum of 0.9 and a weight decay factor of 0.0001. As SuPerFed is a model mixture-based PFL method, we compare its performance to other model mixture-based PFL methods: FedPer [2], LG-FedAvg [41], APFL [10], pFedMe [11], Ditto [38], FedRep [8], along with basic single-model based FL methods, FedAvg [46] FedProx [39] and SCAFFOLD [32]. We let the client randomly split their data into a training set and a test set with a fraction of 0.2 to estimate the performance of each FL algorithm on each client’s test set with its own personalized model (if possible) with various metrics: top-1 accuracy, top-5 accuracy, expected calibration error (ECE [21]), and maximum calibration error (MCE [34]). Note that we evaluated all participating clients after the whole round of FL is finished. For each variation of the mixing method (i.e., LM & MM) stated in section 3.7, we subdivide our method into two, SuPerFed-MM for Model Mixing, and SuPerFed-LM for Layer Mixing.

我们的实验重点关注两点：(i) 各种非独立同分布(non-IID)场景下的个性化性能，(ii) 通过大量基准数据集验证对标签噪声的鲁棒性。具体实验细节见附录A。所有实验中如未特别说明，默认每轮采样5个客户端，采用动量(momentum)为0.9、权重衰减(weight decay)系数为0.0001的随机梯度下降(SGD)优化器。由于SuPerFed是基于模型混合的个性化联邦学习(PFL)方法，我们将其性能与其他基于模型混合的PFL方法进行比较：FedPer [2]、LG-FedAvg [41]、APFL [10]、pFedMe [11]、Ditto [38]、FedRep [8]，以及基于单一模型的基础联邦学习方法FedAvg [46]、FedProx [39]和SCAFFOLD [32]。我们让客户端随机将其数据按0.2比例划分为训练集和测试集，用各自个性化模型(如适用)通过以下指标评估各联邦学习算法在客户端测试集上的表现：Top-1准确率、Top-5准确率、期望校准误差(ECE [21])和最大校准误差(MCE [34])。需注意，我们是在完整联邦学习轮次结束后评估所有参与客户端。针对3.7节所述的两种混合方法变体(LM和MM)，我们将本方法细分为SuPerFed-MM(模型混合)和SuPerFed-LM(层混合)。

Table 2: Experimental results on the Dirichlet distributionbased non-IID setting (CIFAR100 and Tiny Image Net) compared with other FL and PFL methods. The top-5 accuracy is reported with a standard deviation.

表 2: 基于狄利克雷分布的非独立同分布设置(CIFAR100 和 Tiny Image Net)的实验结果与其他联邦学习(FL)和个性化联邦学习(PFL)方法的对比。报告了 top-5 准确率及标准差。

数据集	CIFAR100	CIFAR100	CIFAR100	TinyImageNet	TinyImageNet	TinyImageNet
客户端数量	100	100	100	200	200	200
集中度(a)	1	10	100	1	10	100
FedAvg	58.12 ± 7.06	59.04 ± 7.19	58.49 ± 5.27	46.61 ± 5.64	48.90 ± 5.50	48.90 ± 5.40
FedProx	57.71 ± 6.79	58.24 ± 5.94	58.75 ± 5.56	47.37 ± 5.94	47.73 ± 5.94	48.97 ± 5.02
SCAFFOLD	51.16 ± 6.79	51.40 ± 5.22	52.90 ± 4.89	46.54 ± 5.49	48.77 ± 5.49	48.27 ± 5.32
LG-FedAvg	28.88 ± 5.64	21.25 ± 4.64	20.05 ± 4.61	14.70 ± 3.84	9.86 ± 3.13	9.25 ± 2.89
FedPer	46.78 ± 7.63	35.73 ± 6.80	35.52 ± 6.58	21.90 ± 4.71	11.10 ± 3.19	9.63 ± 3.12
APFL	61.13 ± 6.86	56.90 ± 7.05	55.43 ± 5.45	41.98 ± 5.94	34.74 ± 5.14	34.23 ± 5.07
pFedMe	19.00 ± 5.37	17.94 ± 4.72	18.28 ± 3.41	6.05 ± 2.84	8.01 ± 2.92	7.69 ± 2.41
Ditto	60.04 ± 6.82	58.55 ± 7.12	58.73 ± 5.39	46.36 ± 5.44	43.84 ± 5.44	43.11 ± 5.35
FedRep	38.49 ± 6.65	26.61 ± 5.20	24.50 ± 4.21	18.67 ± 4.66	9.23 ± 2.84	8.09 ± 2.83
SuPerFed-MM	60.14 ± 6.24	58.32 ± 6.25	59.08 ± 5.12	50.07 ± 5.73	49.86 ± 5.03	49.73 ± 4.84
SuPerFed-LM	62.50 ± 6.34	61.64 ± 6.23	59.05 ± 5.59	47.28 ± 5.19	48.98 ± 4.79	49.29 ± 4.82

Table 3: Experimental results on the realistic non-IID setting (FEMNIST and Shakespeare) compared with other FL and PFL methods. The top-1 accuracy is reported with a standard deviation.

表 3: 现实非独立同分布 (non-IID) 设定下的实验结果 (FEMNIST 和 Shakespeare) 与其他联邦学习 (FL) 和个性化联邦学习 (PFL) 方法的对比。报告了 Top-1 准确率及其标准差。

数据集	FEMNIST	FEMNIST	Shakespeare	Shakespeare
客户端数量	730	730	660	660
准确率	Top-1	Top-5	Top-1	Top-5
FedAvg	80.12 ± 12.01	98.74 ± 2.97	50.90 ± 7.85	80.15 ± 7.87
FedProx	80.23 ± 11.88	98.73 ± 2.94	51.33 ± 7.54	80.31 ± 6.95
SCAFFOLD	80.03 ± 11.78	98.85 ± 2.77	50.76 ± 8.01	80.43 ± 7.09
LG-FedAvg	50.84 ± 20.97	75.11 ± 21.49	33.88 ± 10.28	62.84 ± 13.16
FedPer	73.79 ± 14.10	86.39 ± 14.70	45.82 ± 8.10	75.68 ± 9.25
APFL	84.85 ± 8.83	98.83 ± 2.73	54.08 ± 8.31	83.32 ± 6.22
pFedMe	5.98 ± 4.55	24.64 ± 9.43	32.29 ± 6.64	63.12 ± 8.00
Ditto	64.61 ± 31.49	81.14 ± 28.56	49.04 ± 10.22	78.14 ± 12.61
FedRep	59.27 ± 15.72	70.42 ± 15.82	38.15 ± 9.54	68.65 ± 12.50
SuPerFed-MM	85.20 ± 8.40	99.16 ± 2.13	54.52 ± 7.54	84.27 ± 6.00
SuPerFed-LM	83.36 ± 9.61	98.81 ± 2.58	54.52 ± 7.54	83.97 ± 5.72

4.2 Personalization

4.2 个性化

For the estimation of the performance of SuPerFed as PFL methods, we simulate three different non-IID scenarios. (i) a pathological nonIID setting proposed by [46], which assumes most clients have samples from two classes for a multi-class classification task. (2) Dirichlet distribution-based non-IID setting proposed by [27], in which the Dirichlet distribution with its concentration parameter $\alpha$ determines the label distribution of each client. All clients have samples from only one class when using $\alpha\rightarrow0$ , whereas $\alpha\to\infty$ divides samples into an identical distribution. (3) Realistic non-IID setting proposed in [6], which provides several benchmark datasets for PFL.

为了评估SuPerFed作为个性化联邦学习(PFL)方法的性能，我们模拟了三种不同的非独立同分布场景：(1) [46]提出的极端非独立同分布设置