VGGT: Visual Geometry Grounded Transformer
VGGT: 视觉几何基础 Transformer
Jianyuan Wang1,2 Minghao Chen1,2 Nikita Karaev1,2 Andrea Vedaldi1,2 Christian Rupprecht1 David Novotny2
Jianyuan Wang1,2 Minghao Chen1,2 Nikita Karaev1,2 Andrea Vedaldi1,2 Christian Rupprecht1 David Novotny2
1Visual Geometry Group, University of Oxford 2Meta AI
1牛津大学视觉几何组 2Meta AI

Figure 1. VGGT is a large feed-forward transformer with minimal 3D-inductive biases trained on a trove of 3D-annotated data. It accepts up to hundreds of images and predicts cameras, point maps, depth maps, and point tracks for all images at once in less than a second, which often outperforms optimization-based alternatives without further processing.
图 1: VGGT 是一个大型前馈 Transformer,具有最小的 3D 归纳偏差,并在大量 3D 标注数据上进行训练。它能够接受多达数百张图像,并在不到一秒的时间内一次性预测所有图像的相机、点图、深度图和点轨迹,通常优于基于优化的替代方案,且无需进一步处理。
Abstract
摘要
1. Introduction
1. 引言
We present VGGT, a feed-forward neural network that directly infers all key 3D attributes of a scene, including camera parameters, point maps, depth maps, and 3D point tracks, from one, a few, or hundreds of its views. This approach is a step forward in 3D computer vision, where models have typically been constrained to and specialized for single tasks. It is also simple and efficient, reconstructing images in under one second, and still outperforming alternatives that require post-processing with visual geometry optimization techniques. The network achieves state-of-the-art results in multiple 3D tasks, including camera parameter estimation, multi-view depth estimation, dense point cloud reconstruction, and 3D point tracking. We also show that using pretrained VGGT as a feature backbone significantly enhances downstream tasks, such as non-rigid point tracking and feed-forward novel view synthesis. Code and models are publicly available at https://github.com/facebook research/vggt.
我们提出了 VGGT,这是一种前馈神经网络,能够从一个、几个或数百个场景视图中直接推断出场景的所有关键 3D 属性,包括相机参数、点图、深度图和 3D 点轨迹。这种方法在 3D 计算机视觉领域迈出了一步,因为传统模型通常局限于单一任务并专门针对单一任务。VGGT 简单且高效,能够在一秒内重建图像,并且在不需要视觉几何优化技术后处理的情况下,仍然优于其他替代方案。该网络在多个 3D 任务中取得了最先进的结果,包括相机参数估计、多视图深度估计、密集点云重建和 3D 点跟踪。我们还展示了使用预训练的 VGGT 作为特征骨干可以显著增强下游任务,例如非刚性点跟踪和前馈新视图合成。代码和模型已在 https://github.com/facebookresearch/vggt 公开。
We consider the problem of estimating the 3D attributes of a scene, captured in a set of images, utilizing a feedforward neural network. Traditionally, 3D reconstruction has been approached with visual-geometry methods, utilizing iterative optimization techniques like Bundle Adjustment (BA) [45]. Machine learning has often played an important complementary role, addressing tasks that cannot be solved by geometry alone, such as feature matching and monocular depth prediction. The integration has become increasingly tight, and now state-of-the-art Structure-fromMotion (SfM) methods like VGGSfM [125] combine machine learning and visual geometry end-to-end via differentiable BA. Even so, visual geometry still plays a major role in 3D reconstruction, which increases complexity and computational cost.
我们考虑利用前馈神经网络从一组图像中估计场景的3D属性。传统上,3D重建通常通过视觉几何方法实现,使用诸如捆绑调整 (Bundle Adjustment, BA) [45] 的迭代优化技术。机器学习通常扮演重要的补充角色,解决仅靠几何无法完成的任务,例如特征匹配和单目深度预测。两者的结合越来越紧密,现在最先进的结构从运动 (Structure-from-Motion, SfM) 方法(如 VGGSfM [125])通过可微分的 BA 将机器学习和视觉几何端到端地结合起来。即便如此,视觉几何在3D重建中仍然占据重要地位,这增加了复杂性和计算成本。
As networks become ever more powerful, we ask if, finally, 3D tasks can be solved directly by a neural network, eschewing geometry post-processing almost entirely. Recent contributions like DUSt3R [129] and its evolution
随着网络变得越来越强大,我们不禁要问,是否最终可以通过神经网络直接解决3D任务,几乎完全避免几何后处理。最近的研究成果如DUSt3R [129] 及其演进
MASt3R [62] have shown promising results in this direction, but these networks can only process two images at once and rely on post-processing to reconstruct more images, fusing pairwise reconstructions.
MASt3R [62] 在这方面展示了有前景的结果,但这些网络一次只能处理两张图像,并依赖后处理来重建更多图像,融合成对重建。
In this paper, we take a further step towards removing the need to optimize 3D geometry in post-processing. We do so by introducing Visual Geometry Grounded Transformer (VGGT), a feed-forward neural network that performs 3D reconstruction from one, a few, or even hundreds of input views of a scene. VGGT predicts a full set of 3D attributes, including camera parameters, depth maps, point maps, and 3D point tracks. It does so in a single forward pass, in seconds. Remarkably, it often outperforms optimization-based alternatives even without further processing. This is a substantial departure from DUSt3R, MASt3R, or VGGSfM, which still require costly iterative post-optimization to obtain usable results.
在本文中,我们朝着消除后处理中对3D几何优化的需求迈出了进一步的一步。我们通过引入视觉几何基础Transformer (Visual Geometry Grounded Transformer, VGGT) 来实现这一目标,VGGT是一种前馈神经网络,能够从场景的一个、几个甚至数百个输入视图中执行3D重建。VGGT预测了一整套3D属性,包括相机参数、深度图、点图和3D点轨迹。它只需一次前向传递,耗时仅数秒。值得注意的是,即使不进行进一步处理,它通常也优于基于优化的替代方案。这与DUSt3R、MASt3R或VGGSfM有显著不同,这些方法仍然需要昂贵的迭代后优化才能获得可用的结果。
We also show that it is unnecessary to design a special network for 3D reconstruction. Instead, VGGT is based on a fairly standard large transformer [119], with no particular 3D or other inductive biases (except for alternating between frame-wise and global attention), but trained on a large number of publicly available datasets with 3D annotations. VGGT is thus built in the same mold as large models for natural language processing and computer vision, such as GPTs [1, 29, 148], CLIP [86], DINO [10, 78], and Stable Diffusion [34]. These have emerged as versatile backbones that can be fine-tuned to solve new, specific tasks. Similarly, we show that the features computed by VGGT can significantly enhance downstream tasks like point tracking in dynamic videos, and novel view synthesis.
我们还表明,没有必要为 3D 重建设计专门的网络。相反,VGGT 基于一个相当标准的大 Transformer [119],没有特定的 3D 或其他归纳偏差(除了在帧级注意力和全局注意力之间交替),但在大量带有 3D 标注的公开数据集上进行了训练。因此,VGGT 的构建方式与自然语言处理和计算机视觉领域的大模型(如 GPTs [1, 29, 148]、CLIP [86]、DINO [10, 78] 和 Stable Diffusion [34])相同。这些模型已经成为多功能骨干网络,可以通过微调来解决新的特定任务。同样,我们展示了 VGGT 计算的特征可以显著增强下游任务,如动态视频中的点跟踪和新视角合成。
There are several recent examples of large 3D neural networks, including Depth Anything [142], MoGe [128], and LRM [49]. However, these models only focus on a single 3D task, such as monocular depth estimation or novel view synthesis. In contrast, VGGT uses a shared backbone to predict all 3D quantities of interest together. We demonstrate that learning to predict these interrelated 3D attributes enhances overall accuracy despite potential redundancies. At the same time, we show that, during inference, we can derive the point maps from separately predicted depth and camera parameters, obtaining better accuracy compared to directly using the dedicated point map head.
最近有几个大型 3D 神经网络的例子,包括 Depth Anything [142]、MoGe [128] 和 LRM [49]。然而,这些模型只专注于单一的 3D 任务,例如单目深度估计或新视角合成。相比之下,VGGT 使用共享的主干网络来同时预测所有感兴趣的 3D 量。我们证明了尽管存在潜在的冗余,学习预测这些相互关联的 3D 属性可以提高整体准确性。同时,我们展示了在推理过程中,可以从单独预测的深度和相机参数中导出点云图,与直接使用专用的点云图头相比,可以获得更好的准确性。
To summarize, we make the following contributions: (1) We introduce VGGT, a large feed-forward transformer that, given one, a few, or even hundreds of images of a scene, can predict all its key 3D attributes, including camera intrinsics and extrinsics, point maps, depth maps, and 3D point tracks, in seconds. (2) We demonstrate that VGGT’s predictions are directly usable, being highly competitive and usually better than those of state-of-the-art methods that use slow post-processing optimization techniques. (3) We also show that, when further combined with BA post-processing,
总结来说,我们做出了以下贡献:(1) 我们提出了 VGGT,这是一个大型前馈 Transformer,给定一个场景的一张、几张甚至数百张图像,它可以在几秒钟内预测出所有关键的 3D 属性,包括相机内参和外参、点云图、深度图和 3D 点轨迹。(2) 我们证明了 VGGT 的预测结果可以直接使用,具有高度竞争力,并且通常优于使用缓慢后处理优化技术的最先进方法。(3) 我们还展示了,当进一步结合 BA 后处理时,
VGGT achieves state-of-the-art results across the board, even when compared to methods that specialize in a subset of 3D tasks, often improving quality substantially.
VGGT 在所有任务中都达到了最先进的成果,即使与专门针对 3D 任务子集的方法相比,也常常显著提高了质量。
We make our code and models publicly available at https://github.com/facebook research/vggt. We believe that this will facilitate further research in this direction and benefit the computer vision community by providing a new foundation for fast, reliable, and versatile 3D reconstruction.
我们在 https://github.com/facebook research/vggt 上公开了代码和模型。我们相信,这将为快速、可靠且多功能的 3D 重建提供新的基础,从而促进这一方向的进一步研究,并使计算机视觉社区受益。
2. Related Work
2. 相关工作
Structure from Motion is a classic computer vision problem [45, 77, 80] that involves estimating camera parameters and reconstructing sparse point clouds from a set of images of a static scene captured from different viewpoints. The traditional SfM pipeline [2, 36, 70, 94, 103, 134] consists of multiple stages, including image matching, triangulation, and bundle adjustment. COLMAP [94] is the most popular framework based on the traditional pipeline. In recent years, deep learning has improved many components of the SfM pipeline, with keypoint detection [21, 31, 116, 149] and image matching [11, 67, 92, 99] being two primary areas of focus. Recent methods [5, 102, 109, 112, 113, 118, 122, 125, 131, 160] explored end-to-end differentiable SfM, where VGGSfM [125] started to outperform traditional algorithms on challenging photo tourism scenarios.
运动结构恢复 (Structure from Motion, SfM) 是一个经典的计算机视觉问题 [45, 77, 80],它涉及从不同视角拍摄的一组静态场景图像中估计相机参数并重建稀疏点云。传统的 SfM 流程 [2, 36, 70, 94, 103, 134] 包括多个阶段,如图像匹配、三角测量和捆绑调整。COLMAP [94] 是基于传统流程的最流行框架。近年来,深度学习改进了 SfM 流程的许多组件,其中关键点检测 [21, 31, 116, 149] 和图像匹配 [11, 67, 92, 99] 是两个主要关注领域。最近的方法 [5, 102, 109, 112, 113, 118, 122, 125, 131, 160] 探索了端到端可微分的 SfM,其中 VGGSfM [125] 开始在具有挑战性的照片旅游场景中超越传统算法。
Multi-view Stereo aims to densely reconstruct the geometry of a scene from multiple overlapping images, typically assuming known camera parameters, which are often estimated with SfM. MVS methods can be divided into three categories: traditional handcrafted [38, 39, 96, 130], global optimization [37, 74, 133, 147], and learning-based methods [42, 72, 84, 145, 157]. As in SfM, learning-based MVS approaches have recently seen a lot of progress. Here, DUSt3R [129] and MASt3R [62] directly estimate aligned dense point clouds from a pair of views, similar to MVS but without requiring camera parameters. Some concurrent works [111, 127, 141, 156] explore replacing DUSt3R’s test-time optimization with neural networks, though these attempts achieve only suboptimal or comparable performance to DUSt3R. Instead, VGGT outperforms DUSt3R and MASt3R by a large margin.
多视图立体视觉 (Multi-view Stereo, MVS) 旨在从多个重叠图像中密集重建场景的几何结构,通常假设已知的相机参数,这些参数通常通过 SfM (Structure from Motion) 进行估计。MVS 方法可以分为三类:传统手工方法 [38, 39, 96, 130]、全局优化方法 [37, 74, 133, 147] 和基于学习的方法 [42, 72, 84, 145, 157]。与 SfM 类似,基于学习的 MVS 方法最近取得了很大进展。其中,DUSt3R [129] 和 MASt3R [62] 直接从一对视图中估计对齐的密集点云,类似于 MVS,但不需要相机参数。一些并行工作 [111, 127, 141, 156] 探索用神经网络替代 DUSt3R 的测试时优化,尽管这些尝试仅实现了次优或与 DUSt3R 相当的性能。相比之下,VGGT 大幅优于 DUSt3R 和 MASt3R。
Tracking-Any-Point was first introduced in Particle Video [91] and revived by PIPs [44] during the deep learning era, aiming to track points of interest across video sequences including dynamic motions. Given a video and some 2D query points, the task is to predict 2D correspondences of these points in all other frames. TAP-Vid [23] proposed three benchmarks for this task and a simple baseline method later improved in TAPIR [24]. CoTracker [55, 56] utilized correlations between different points to track through occlusions, while DOT [60] enabled dense tracking through occlusions. Recently, TAPTR [63] proposed an end-to-end transformer for this task, and LocoTrack [13] extended commonly used pointwise features to nearby regions. All of these methods are specialized point trackers. Here, we demonstrate that VGGT’s features yield state-ofthe-art tracking performance when coupled with existing point trackers.
Tracking-Any-Point 最初在 Particle Video [91] 中提出,并在深度学习时代由 PIPs [44] 重新引入,旨在跟踪视频序列中包括动态运动在内的兴趣点。给定一个视频和一些 2D 查询点,任务是在所有其他帧中预测这些点的 2D 对应关系。TAP-Vid [23] 为此任务提出了三个基准,并在 TAPIR [24] 中改进了简单的基线方法。CoTracker [55, 56] 利用不同点之间的相关性来跟踪遮挡,而 DOT [60] 则通过遮挡实现了密集跟踪。最近,TAPTR [63] 提出了一个端到端的 Transformer 来解决此任务,而 LocoTrack [13] 将常用的点特征扩展到附近区域。所有这些方法都是专门的点跟踪器。在这里,我们展示了 VGGT 的特征与现有点跟踪器结合时,能够实现最先进的跟踪性能。
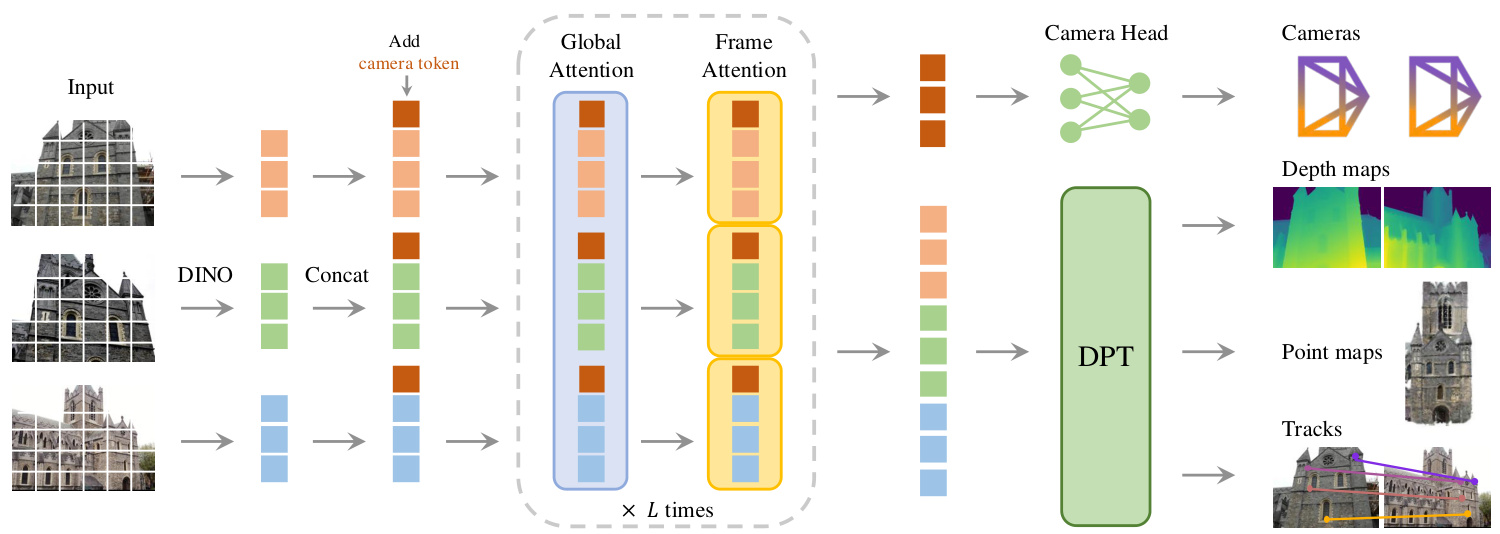
Figure 2. Architecture Overview. Our model first patchifies the input images into tokens by DINO, and appends camera tokens for camera prediction. It then alternates between frame-wise and global self attention layers. A camera head makes the final prediction for camera extrinsics and intrinsics, and a DPT [87] head for any dense output.
图 2: 架构概览。我们的模型首先通过 DINO 将输入图像分割为 Token,并附加相机 Token 用于相机预测。然后,它在帧级和全局自注意力层之间交替。相机头负责最终预测相机外参和内参,而 DPT [87] 头则负责任何密集输出。
3. Method
3. 方法
We introduce VGGT, a large transformer that ingests a set of images as input and produces a variety of 3D quantities as output. We start by introducing the problem in Sec. 3.1, followed by our architecture in Sec. 3.2 and its prediction heads in Sec. 3.3, and finally the training setup in Sec. 3.4.
我们介绍了 VGGT,这是一个大型 Transformer,它接收一组图像作为输入,并生成多种 3D 量作为输出。我们首先在第 3.1 节中介绍了问题,然后在第 3.2 节中介绍了我们的架构,接着在第 3.3 节中介绍了其预测头,最后在第 3.4 节中介绍了训练设置。
3.1. Problem definition and notation
3.1. 问题定义与符号表示
The input is a sequence $(I_{i}){i=1}^{N}$ of $N$ RGB images $I{i}\in\mathbf{\Gamma}$ R3×H×W , observing the same 3D scene. VGGT’s transformer is a function that maps this sequence to a corresponding set of 3D annotations, one per frame:
输入是一个由 $N$ 个 RGB 图像组成的序列 $(I_{i}){i=1}^{N}$,其中 $I{i}\in\mathbf{\Gamma}$ R3×H×W,观察的是同一个 3D 场景。VGGT 的 Transformer 是一个函数,将这个序列映射到一组对应的 3D 标注,每帧一个:

The transformer thus maps each image $I_{i}$ to its camera parameters $\mathbf{g}{i}\in\mathbb{R}^{9}$ (intrinsics and extrinsics), its depth map $D{i}\in\mathbb{R}^{H\times W}$ , its point map $P_{i}\in\mathbb{R}^{3\times H\times W}$ , and a grid $T_{i}\in\mathbb{R}^{C\times H\times W}$ of $C$ -dimensional features for point tracking. We explain next how these are defined.
Transformer 因此将每个图像 $I_{i}$ 映射到其相机参数 $\mathbf{g}{i}\in\mathbb{R}^{9}$(内参和外参)、深度图 $D{i}\in\mathbb{R}^{H\times W}$、点图 $P_{i}\in\mathbb{R}^{3\times H\times W}$,以及用于点跟踪的 $C$ 维特征网格 $T_{i}\in\mathbb{R}^{C\times H\times W}$。接下来我们将解释这些内容的定义。
For the camera parameters $\mathbf{g}{i}$ , we use the para me tri zation from [125] and set $\mathbf{g}=[\mathbf{q},\mathbf{t},\mathbf{f}]$ which is the concatenation of the rotation quaternion $\mathbf{q}\in\mathbb{R}^{4}$ , the translation vec- tor $\mathbf{t}\in\mathbb{R}^{3}$ , and the field of view $\mathbf{f{\alpha}}\in\mathbb{R}^{2}$ . We assume that the camera’s principal point is at the image center, which is common in SfM frameworks [95, 125].
对于相机参数 $\mathbf{g}{i}$,我们使用 [125] 中的参数化方法,并设置 $\mathbf{g}=[\mathbf{q},\mathbf{t},\mathbf{f}]$,这是旋转四元数 $\mathbf{q}\in\mathbb{R}^{4}$、平移向量 $\mathbf{t}\in\mathbb{R}^{3}$ 和视场角 $\mathbf{f{\alpha}}\in\mathbb{R}^{2}$ 的拼接。我们假设相机的主点位于图像中心,这在 SfM 框架中很常见 [95, 125]。
We denote the domain of the image $I_{i}$ with $\begin{array}{r l}{\mathbb{}Z(I_{i})}&{{}=}\end{array}$ ${1,\dots,H}\times{1,\dots,W}$ , i.e., the set of pixel locations. The depth map $D_{i}$ associates each pixel location $\mathbf{y}\in\mathcal{I}(I_{i})$ with its corresponding depth value $D_{i}(\mathbf{y})\in\mathbb{R}^{+}$ , as observed from the $i$ -th camera. Likewise, the point map $P_{i}$ associates each pixel with its corresponding 3D scene point $P_{i}(\mathbf{y})\in\mathbb{R}^{3}$ . Importantly, like in DUSt3R [129], the point maps are viewpoint invariant, meaning that the 3D points $P_{i}(\mathbf{y})$ are defined in the coordinate system of the first camera ${\bf g}_{1}$ , which we take as the world reference frame.
我们将图像 $I_{i}$ 的域表示为 $\begin{array}{r l}{\mathbb{}Z(I_{i})}&{{}=}\end{array}$ ${1,\dots,H}\times{1,\dots,W}$,即像素位置的集合。深度图 $D_{i}$ 将每个像素位置 $\mathbf{y}\in\mathcal{I}(I_{i})$ 与其对应的深度值 $D_{i}(\mathbf{y})\in\mathbb{R}^{+}$ 关联起来,这是从第 $i$ 个相机观察到的。同样,点图 $P_{i}$ 将每个像素与其对应的 3D 场景点 $P_{i}(\mathbf{y})\in\mathbb{R}^{3}$ 关联起来。重要的是,与 DUSt3R [129] 中一样,点图是视角不变的,这意味着 3D 点 $P_{i}(\mathbf{y})$ 是在第一个相机 ${\bf g}_{1}$ 的坐标系中定义的,我们将其作为世界参考系。
Finally, for keypoint tracking, we follow track-anypoint methods such as [25, 57]. Namely, given a fixed query image point ${\bf y}{q}$ in the query image $I{q}$ , the network outputs a track $\begin{array}{r}{\mathcal{T}^{\star}(\mathbf{y}{q})^{\star}=(\mathbf{y}{i}){i=1}^{N}}\end{array}$ formed by the corresponding 2D points $\mathbf{y}{i}\in\mathbb{R}^{2}$ in all images $I_{i}$ .
最后,对于关键点跟踪,我们遵循诸如 [25, 57] 的 track-anypoint 方法。即,给定查询图像 $I_{q}$ 中的一个固定查询图像点 ${\bf y}{q}$,网络输出一个由所有图像 $I{i}$ 中的对应 2D 点 $\mathbf{y}{i}\in\mathbb{R}^{2}$ 组成的轨迹 $\begin{array}{r}{\mathcal{T}^{\star}(\mathbf{y}{q})^{\star}=(\mathbf{y}{i}){i=1}^{N}}\end{array}$。
Note that the transformer $f$ above does not output the tracks directly but instead features $\boldsymbol{T_{i}}\in\mathbb{R}^{C\times H\times W}$ , which are used for tracking. The tracking is delegated to a separate module, described in Sec. 3.3, which implements a function $\mathcal{T}((\mathbf{y}{j}){j=1}^{M},(T_{i})_{i=1}^{N})=((\hat{\mathbf{y}}_{j,i})_{i=1}^{N})_{j=1}^{M}$ . It ingests the query point ${\bf y}_{q}$ and the dense tracking features $T_{i}$ output by the transformer $f$ and then computes the track. The two networks $f$ and $\tau$ are trained jointly end-to-end.
注意,上述的 Transformer $f$ 并不直接输出轨迹,而是输出用于跟踪的特征 $\boldsymbol{T_{i}}\in\mathbb{R}^{C\times H\times W}$。跟踪任务被委托给一个单独的模块,该模块在 3.3 节中描述,它实现了一个函数 $\mathcal{T}((\mathbf{y}{j}){j=1}^{M},(T_{i})_{i=1}^{N})=((\hat{\mathbf{y}}_{j,i})_{i=1}^{N})_{j=1}^{M}$。该模块接收查询点 ${\bf y}_{q}$ 和由 Transformer $f$ 输出的密集跟踪特征 $T_{i}$,然后计算轨迹。两个网络 $f$ 和 $\tau$ 是端到端联合训练的。
Order of Predictions. The order of the images in the input sequence is arbitrary, except that the first image is chosen as the reference frame. The network architecture is designed to be permutation e qui variant for all but the first frame.
预测顺序。输入序列中图像的顺序是任意的,除了第一张图像被选为参考帧。网络架构设计为对除第一帧外的所有帧具有排列等变性。
Over-complete Predictions. Notably, not all quantities predicted by VGGT are independent. For example, as shown by DUSt3R [129], the camera parameters $\mathbf{g}$ can be inferred from the invariant point map $P$ , for instance, by solving the Perspective $^{\cdot n}$ -Point $(\mathrm{{PnP})}$ problem [35, 61].
过度完整的预测。值得注意的是,VGGT 预测的所有量并不都是独立的。例如,如 DUSt3R [129] 所示,相机参数 $\mathbf{g}$ 可以从不变点图 $P$ 中推断出来,例如通过解决 Perspective $^{\cdot n}$ -Point $(\mathrm{{PnP})}$ 问题 [35, 61]。
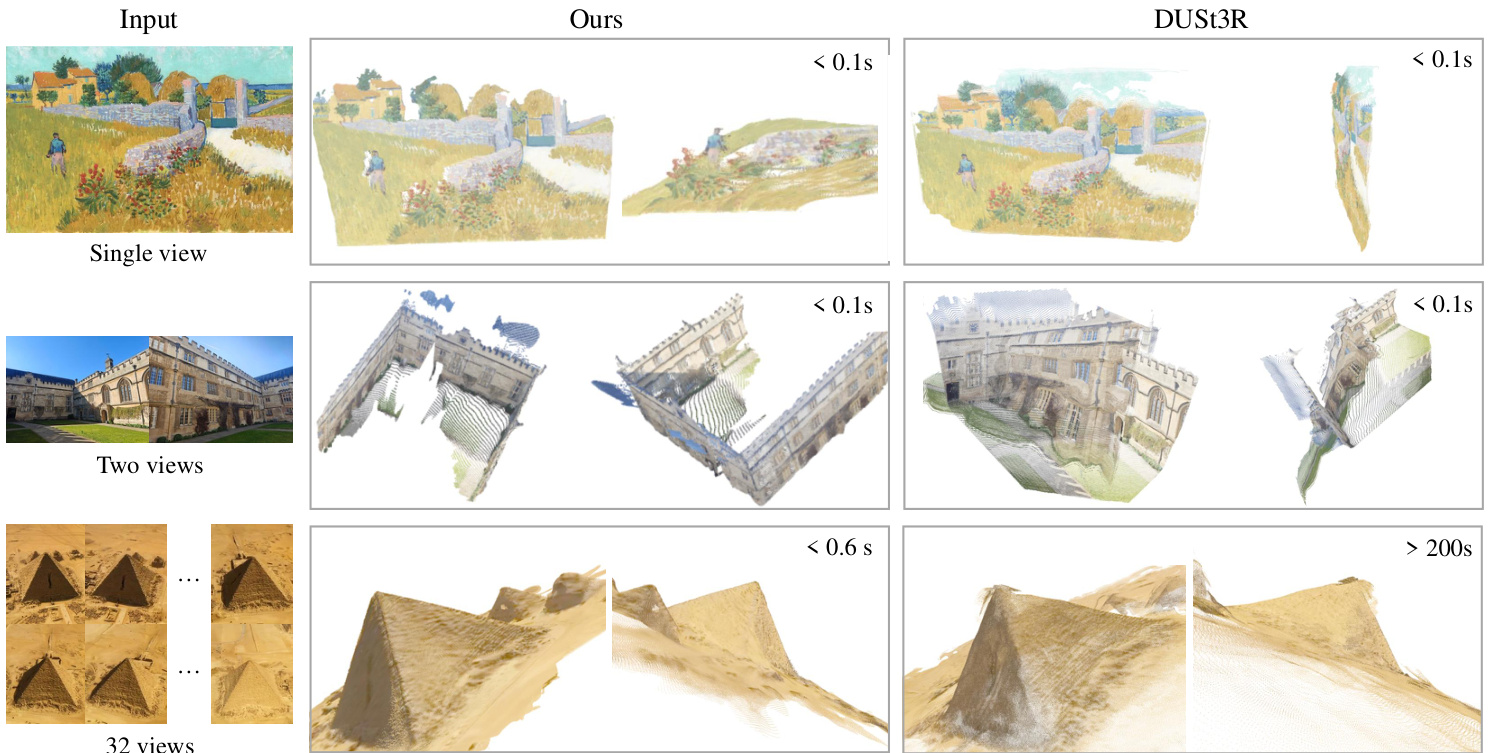
Figure 3. Qualitative comparison of our predicted 3D points to DUSt3R on in-the-wild images. As shown in the top row, our method successfully predicts the geometric structure of an oil painting, while DUSt3R predicts a slightly distorted plane. In the second row, our method correctly recovers a 3D scene from two images with no overlap, while DUSt3R fails. The third row provides a challenging example with repeated textures, while our prediction is still high-quality. We do not include examples with more than 32 frames, as DUSt3R runs out of memory beyond this limit.
图 3: 我们的预测 3D 点与 DUSt3R 在野外图像上的定性对比。如第一行所示,我们的方法成功预测了一幅油画的几何结构,而 DUSt3R 预测了一个略微扭曲的平面。在第二行中,我们的方法从两张没有重叠的图像中正确恢复了 3D 场景,而 DUSt3R 失败了。第三行提供了一个具有重复纹理的挑战性示例,而我们的预测仍然是高质量的。我们没有包含超过 32 帧的示例,因为 DUSt3R 在此限制之外会耗尽内存。
Furthermore, the depth maps can be deduced from the point map and the camera parameters. However, as we show in Sec. 4.5, tasking VGGT with explicitly predicting all aforementioned quantities during training brings substantial performance gains, even when these are related by closed-form relationships. Meanwhile, during inference, it is observed that combining independently estimated depth maps and camera parameters produces more accurate 3D points compared to directly employing a specialized point map branch.
此外,深度图可以从点云图和相机参数中推导出来。然而,正如我们在第4.5节中所示,在训练过程中让VGGT显式预测所有上述量会带来显著的性能提升,即使这些量之间存在闭式关系。同时,在推理过程中,观察到结合独立估计的深度图和相机参数比直接使用专门的点云图分支能产生更准确的3D点。
3.2. Feature Backbone
3.2. 特征骨干网络
Following recent works in 3D deep learning [53, 129, 132], we design a simple architecture with minimal 3D inductive biases, letting the model learn from ample quantities of 3D-annotated data. In particular, we implement the model $f$ as a large transformer [119]. To this end, each input image $I$ is initially patchified into a set of $K$ tokens1 $\mathrm{t}^{I}\in\mathbb{R}^{K\times C}$ through DINO [78]. The combined set of image tokens from all frames, i.e., $\mathrm{t}^{I}=\cup_{i=1}^{N}{\mathrm{t}_{i}^{I}}$ , is subsequently processed through the main network structure, alternating frame-wise and global self-attention layers.
遵循近期3D深度学习的研究 [53, 129, 132],我们设计了一个具有最小3D归纳偏置的简单架构,让模型从大量的3D标注数据中学习。具体来说,我们将模型 $f$ 实现为一个大型Transformer [119]。为此,每个输入图像 $I$ 首先通过DINO [78] 被分割成一组 $K$ 个Token $\mathrm{t}^{I}\in\mathbb{R}^{K\times C}$。所有帧的图像Token组合,即 $\mathrm{t}^{I}=\cup_{i=1}^{N}{\mathrm{t}_{i}^{I}}$,随后通过主网络结构进行处理,交替使用帧内和全局自注意力层。
Alternating-Attention. We slightly adjust the standard transformer design by introducing Alternating-Attention (AA), making the transformer focus within each frame and globally in an alternate fashion. Specifically, frame-wise self-attention attends to the tokens $\mathrm{t}_{k}^{I}$ within each frame separately, and global self-attention attends to the tokens $\mathrm{t}^{I}$ across all frames jointly. This strikes a balance between integrating information across different images and normalizing the activation s for the tokens within each image. By default, we employ $L=24$ layers of global and frame-wise attention. In Sec. 4, we demonstrate that our AA architecture brings significant performance gains. Note that our architecture does not employ any cross-attention layers, only self-attention ones.
交替注意力 (Alternating-Attention)。我们通过引入交替注意力 (AA) 对标准 Transformer 设计进行了轻微调整,使 Transformer 以交替方式在每帧内和全局范围内聚焦。具体来说,帧内自注意力 (frame-wise self-attention) 分别关注每帧内的 Token $\mathrm{t}_{k}^{I}$,而全局自注意力 (global self-attention) 则联合关注所有帧中的 Token $\mathrm{t}^{I}$。这在整合不同图像之间的信息和归一化每张图像内 Token 的激活之间取得了平衡。默认情况下,我们使用 $L=24$ 层全局和帧内注意力。在第 4 节中,我们展示了我们的 AA 架构带来了显著的性能提升。请注意,我们的架构没有使用任何交叉注意力层,仅使用了自注意力层。
3.3. Prediction heads
3.3 预测头
Here, we describe how $f$ predicts the camera parameters, depth maps, point maps, and point tracks. First, for each input image $I_{i}$ , we augment the corresponding image tokens $\mathrm{t}{i}^{I}$ with an additional camera token $\mathbf{t}{i}^{\mathbf{g}}\in\mathbf{\mathbb{R}}^{1\times\check{C^{\prime}}}$ and four register tokens [19] $\mathbf{t}{i}^{R}\in\mathbb{R}^{4\times C^{\prime}}$ . The concatenation of $(\mathbf{t}{i}^{I},\mathbf{t}{i}^{\mathbf{g}},\mathbf{t}{i}^{R}j){i=1}^{N}$ is then passed to the AA transformer, yieldingoutput ensecamek and register tokens of the first frame $(\mathrm{t}{1}^{\mathbf{g}}:=\bar{\mathrm{t}}^{\mathbf{g}}$ , $\mathrm{t}_{1}^{R}:=\bar{\mathrm{t}}^{R})$ are set to a different set of learnable tokens $\bar{\mathrm{t}}^{\mathbf{g}},\bar{\mathrm{t}}^{R}$ than those of all other frames $(\mathbf{t}_{i}^{\mathbf{g}}:=\bar{\mathbf{t}}^{\mathbf{g}},\mathbf{t}_{i}^{R}:=\bar{\mathbf{t}}^{R},i\in[2,\dots,N])$ , which are also learnable. This allows the model to distinguish the first frame from the rest, and to represent the 3D predictions in the coordinate frame of the first camera. Note that the refined camera and register tokens now become frame-specific—–this is because our AA transformer contains frame-wise self-attention layers that allow the transformer to match the camera and register tokens with the corresponding tokens from the same image. Following common practice, the output register tokens $\hat{\mathbf{t}}_{i}^{R}$ are discarded while $\hat{\bf t}_{i}^{I},\hat{\bf t}_{i}^{\bf g}$ are used for prediction.
在这里,我们描述了 $f$ 如何预测相机参数、深度图、点云图和点轨迹。首先,对于每个输入图像 $I_{i}$,我们用额外的相机 token $\mathbf{t}{i}^{\mathbf{g}}\in\mathbf{\mathbb{R}}^{1\times\check{C^{\prime}}}$ 和四个寄存器 token [19] $\mathbf{t}{i}^{R}\in\mathbb{R}^{4\times C^{\prime}}$ 来增强相应的图像 token $\mathrm{t}{i}^{I}$。然后将 $(\mathbf{t}{i}^{I},\mathbf{t}{i}^{\mathbf{g}},\mathbf{t}{i}^{R}j){i=1}^{N}$ 的连接传递给 AA Transformer,生成输出。第一帧的相机 token 和寄存器 token $(\mathrm{t}{1}^{\mathbf{g}}:=\bar{\mathrm{t}}^{\mathbf{g}}$,$\mathrm{t}_{1}^{R}:=\bar{\mathrm{t}}^{R})$ 被设置为与所有其他帧 $(\mathbf{t}_{i}^{\mathbf{g}}:=\bar{\mathbf{t}}^{\mathbf{g}},\mathbf{t}_{i}^{R}:=\bar{\mathbf{t}}^{R},i\in[2,\dots,N])$ 不同的可学习 token $\bar{\mathrm{t}}^{\mathbf{g}},\bar{\mathrm{t}}^{R}$,这些 token 也是可学习的。这使得模型能够区分第一帧与其他帧,并在第一帧相机的坐标系中表示 3D 预测。请注意,优化后的相机 token 和寄存器 token 现在变得特定于帧——这是因为我们的 AA Transformer 包含帧级自注意力层,允许 Transformer 将相机 token 和寄存器 token 与来自同一图像的相应 token 进行匹配。按照常规做法,输出寄存器 token $\hat{\mathbf{t}}_{i}^{R}$ 被丢弃,而 $\hat{\bf t}_{i}^{I},\hat{\bf t}_{i}^{\bf g}$ 用于预测。

Figure 4. Additional Visualization s of Point Map Estimation. Camera frustums illustrate the estimated camera poses. Explore our interactive demo for better visualization quality.
图 4: 点云地图估计的附加可视化。相机视锥体展示了估计的相机姿态。请访问我们的交互式演示以获得更好的可视化效果。
Coordinate Frame. As noted above, we predict cameras, point maps, and depth maps in the coordinate frame of the first camera ${\bf g}{1}$ . As such, the camera extrinsics output for the first camera are set to the identity, i.e., the first rotation quaternion is $\mathbf{q}{1}=[0,0,0,1]$ and the first translation vector is $\mathbf{t}_{1}=[0,0,0]$ . Recall that the special camera and register tokens $\mathbf{t}_{1}^{\mathbf{g}}:=\overline{{\mathbf{t}}}^{\mathbf{g}},\mathbf{t}_{1}^{R}:=\overline{{\mathbf{t}}}^{R}$ allow the transformer to identify the first camera.
坐标系。如上所述,我们在第一个相机 ${\bf g}{1}$ 的坐标系中预测相机、点云图和深度图。因此,第一个相机的外参输出被设置为单位矩阵,即第一个旋转四元数为 $\mathbf{q}{1}=[0,0,0,1]$,第一个平移向量为 $\mathbf{t}_{1}=[0,0,0]$。需要注意的是,特殊的相机和注册 token $\mathbf{t}_{1}^{\mathbf{g}}:=\overline{{\mathbf{t}}}^{\mathbf{g}},\mathbf{t}_{1}^{R}:=\overline{{\mathbf{t}}}^{R}$ 允许 Transformer 识别第一个相机。
Camera Predictions. The camera parameters $(\hat{\mathbf{g}}^{i}){i=1}^{N}$ are predicted from the output camera tokens $(\hat{\mathrm{t}}{i}^{\mathbf{g}})_{i=1}^{N}$ using four additional self-attention layers followed by a linear layer. This forms the camera head that predicts the camera intrin
相机预测。相机参数 $(\hat{\mathbf{g}}^{i}){i=1}^{N}$ 通过四个额外的自注意力层和一个线性层从输出的相机 token $(\hat{\mathrm{t}}{i}^{\mathbf{g}})_{i=1}^{N}$ 中预测得出。这构成了预测相机内参的相机头。
sics and extrinsics.
sics 和 extrinsics。
Dense Predictions. The output image tokens $\hat{\mathrm{t}}{i}^{I}$ are used to predict the dense outputs, $i.e.$ ., the depth maps $D{i}$ , point maps $P_{i}$ , and tracking features $T_{i}$ . More specifically, $\hat{\mathrm{t}}{i}^{I}$ are first converted to dense feature maps $F{i}\in\mathbb{R}^{C^{\prime\prime}\times H\times W}$ with a DPT layer [87]. Each $F_{i}$ is then mapped with a $3\times3$ convolutional layer to the corresponding depth and point maps $D_{i}$ and $P_{i}$ . Additionally, the DPT head also outputs dense features $T_{i}\in\mathbb{R}^{C\times H\times\dot{W}}$ , which serve as input to the tracking head. We also predict the aleatoric uncertainty [58, 76] $\Sigma_{i}^{\breve{D}}\in\mathbb{R}{+}^{H\times W}$ and $\Sigma{i}^{P}\in\mathbb{R}_{+}^{H\times W}$ for each depth and point map, respectively. As described in Sec. 3.4, the uncertainty maps are used in the loss and, after training, are proportional to the model’s confidence in the predictions.
密集预测。输出图像 token $\hat{\mathrm{t}}{i}^{I}$ 用于预测密集输出,即深度图 $D{i}$、点图 $P_{i}$ 和跟踪特征 $T_{i}$。具体来说,$\hat{\mathrm{t}}{i}^{I}$ 首先通过 DPT 层 [87] 转换为密集特征图 $F{i}\in\mathbb{R}^{C^{\prime\prime}\times H\times W}$。然后,每个 $F_{i}$ 通过一个 $3\times3$ 卷积层映射到相应的深度图和点图 $D_{i}$ 和 $P_{i}$。此外,DPT 头还输出密集特征 $T_{i}\in\mathbb{R}^{C\times H\times\dot{W}}$,作为跟踪头的输入。我们还分别预测了每个深度图和点图的随机不确定性 [58, 76] $\Sigma_{i}^{\breve{D}}\in\mathbb{R}{+}^{H\times W}$ 和 $\Sigma{i}^{P}\in\mathbb{R}_{+}^{H\times W}$。如第 3.4 节所述,不确定性图用于损失计算,并且在训练后与模型对预测的置信度成正比。
Tracking. In order to implement the tracking module $\tau$ , we use the CoTracker2 architecture [57], which takes the dense tracking features $T_{i}$ as input. More specifically, given a query point $\mathbf{y}{j}$ in a query image $I{q}$ (during training, we always set $q=1$ , but any other image can be potentially used as a query), the tracking head $\tau$ predicts the set of 2D points $\mathcal{T}((\mathbf{y}{j}){j=1}^{M},(T_{i})_{i=1}^{N})=((\hat{\mathbf{y}}_{j,i})_{i=1}^{N})_{j=1}^{M}$ in all images $I_{i}$ that correspond to the same 3D point as $\mathbf{y}$ . To do so, the feature map $T_{q}$ of the query image is first bilinearly sampled at the query point $\mathbf{y}_{j}$ to obtain its feature. This feature is then correlated with all other feature maps $T_{i},i\neq q$ to obtain a set of correlation maps. These maps are then processed by self-attention layers to predict the final 2D points $\hat{\mathbf{y}}_{i}$ , which are all in correspondence with $\mathbf{y}_{j}$ . Note that, similar to VGGSfM [125], our tracker does not assume any temporal ordering of the input frames and, hence, can be applied to any set of input images, not just videos.
为了实现跟踪模块 $\tau$,我们使用了 CoTracker2 架构 [57],该架构以密集跟踪特征 $T_{i}$ 作为输入。具体来说,给定查询图像 $I_{q}$ 中的查询点 $\mathbf{y}{j}$(在训练过程中,我们始终设置 $q=1$,但任何其他图像也可以作为查询图像),跟踪头 $\tau$ 预测在所有图像 $I{i}$ 中与 $\mathbf{y}$ 对应的 3D 点相同的 2D 点集 $\mathcal{T}((\mathbf{y}{j}){j=1}^{M},(T_{i})_{i=1}^{N})=((\hat{\mathbf{y}}_{j,i})_{i=1}^{N})_{j=1}^{M}$。为此,首先在查询点 $\mathbf{y}_{j}$ 处对查询图像的特征图 $T_{q}$ 进行双线性采样,以获取其特征。然后将该特征与所有其他特征图 $T_{i},i\neq q$ 进行相关,得到一组相关图。这些相关图随后通过自注意力层处理,以预测最终的 2D 点 $\hat{\mathbf{y}}_{i}$,这些点都与 $\mathbf{y}_{j}$ 对应。需要注意的是,与 VGGSfM [125] 类似,我们的跟踪器不假设输入帧的任何时间顺序,因此可以应用于任何输入图像集,而不仅仅是视频。
3.4. Training
3.4. 训练
Training Losses. We train the VGGT model $f$ end-to-end using a multi-task loss:
训练损失。我们使用多任务损失端到端地训练 VGGT 模型 $f$:
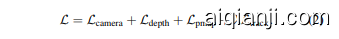
We found that the camera $(\mathcal{L}{\mathrm{camera}})$ , depth $(\mathcal{L}{\mathrm{depth}})$ , and point-map $(\mathcal{L}{\mathrm{pmap}})$ losses have similar ranges and do not need to be weighted against each other. The tracking loss $\mathcal{L}{\mathrm{track}}$ is down-weighted with a factor of $\lambda=0.05$ . We describe each loss term in turn.
我们发现相机损失 $(\mathcal{L}{\mathrm{camera}})$ 、深度损失 $(\mathcal{L}{\mathrm{depth}})$ 和点图损失 $(\mathcal{L}{\mathrm{pmap}})$ 的范围相似,不需要相互加权。跟踪损失 $\mathcal{L}{\mathrm{track}}$ 被下调权重,因子为 $\lambda=0.05$。我们依次描述每个损失项。
The camera loss $\mathcal{L}{\mathrm{camera}}$ supervises the cameras $\hat{\bf g}$ $\begin{array}{r}{\mathcal{L}{\mathrm{camera}}=\sum_{i=1}^{N}\Vert\hat{\mathbf{g}}_{i}-\mathbf{g}_{i}\Vert_{\epsilon}}\end{array}$ , comparing the predicted cameras $\hat{\bf g}_{i}$ wi th the ground truth $\mathbf{g}_{i}$ using the Huber loss $|\cdot|_{\epsilon}$ .
相机损失 $\mathcal{L}{\mathrm{camera}}$ 监督相机 $\hat{\bf g}$ $\begin{array}{r}{\mathcal{L}{\mathrm{camera}}=\sum_{i=1}^{N}\Vert\hat{\mathbf{g}}_{i}-\mathbf{g}_{i}\Vert_{\epsilon}}\end{array}$,通过使用 Huber 损失 $|\cdot|_{\epsilon}$ 将预测的相机 $\hat{\bf g}_{i}$ 与真实值 $\mathbf{g}_{i}$ 进行比较。
The depth loss $\mathcal{L}{\mathrm{depth}}$ follows DUSt3R [129] and implements the aleatoric-uncertainty loss [59, 75] weighing the discrepancy between the predicted depth $\hat{D}{i}$ and the ground-truth depth $D_{i}$ with the predicted uncertainty map $\bar{\hat{\Sigma}}{i}^{D}$ . Differently from DUSt3R, we also apply a gradientbased term, which is widely used in monocular depth estimation. Hence, the depth loss is $\begin{array}{r}{\mathcal{L}{\mathrm{depth}}=\sum_{i=1}^{N}\dot{|}\Sigma_{i}^{D}\odot}\end{array}$ $(\hat{D}_{i}-D_{i})|+|\Sigma_{i}^{D}\odot(\nabla\hat{D}_{i}-\nabla D_{i})|\overset{\cdot}{-}\alpha\log{\Sigma_{i}^{D}}$ , where $\odot$ is the channel-broadcast element-wise product. The point map loss is defined analogously but with the point-map uncertainty $\begin{array}{r}{\Sigma_{i}^{P}\colon\mathcal{L}_{\mathrm{pmap}}=\sum_{i=1}^{N}|\Sigma_{i}^{P}\odot(\hat{P}_{i}-\dot{P}_{i})|+|\dot{\Sigma}_{i}^{P}\odot}\end{array}$ $(\nabla\hat{P}_{i}-\nabla P_{i})|-\alpha\log{\Sigma_{i}^{P}}$ .
深度损失 $\mathcal{L}{\mathrm{depth}}$ 遵循 DUSt3R [129],并实现了基于不确定性的损失 [59, 75],通过预测的不确定性图 $\bar{\hat{\Sigma}}{i}^{D}$ 来加权预测深度 $\hat{D}{i}$ 与真实深度 $D{i}$ 之间的差异。与 DUSt3R 不同的是,我们还应用了基于梯度的项,这在单目深度估计中被广泛使用。因此,深度损失为 $\begin{array}{r}{\mathcal{L}{\mathrm{depth}}=\sum{i=1}^{N}\dot{|}\Sigma_{i}^{D}\odot}\end{array}$ $(\hat{D}{i}-D{i})|+|\Sigma_{i}^{D}\odot(\nabla\hat{D}{i}-\nabla D{i})|\overset{\cdot}{-}\alpha\log{\Sigma_{i}^{D}}$ ,其中 $\odot$ 是通道广播的逐元素乘积。点图损失的定义类似,但使用点图不确定性 $\begin{array}{r}{\Sigma_{i}^{P}\colon\mathcal{L}_{\mathrm{pmap}}=\sum_{i=1}^{N}|\Sigma_{i}^{P}\odot(\hat{P}_{i}-\dot{P}_{i})|+|\dot{\Sigma}_{i}^{P}\odot}\end{array}$ $(\nabla\hat{P}_{i}-\nabla P_{i})|-\alpha\log{\Sigma_{i}^{P}}$ 。
Finally, the tracking loss is given by $\begin{array}{r l}{\mathcal{L}{\mathrm{track}}}&{{}=}\end{array}$ $\begin{array}{r}{\sum{j=1}^{M}\sum_{i=1}^{N}|\mathbf{y}_{j,i}-\hat{\mathbf{y}}_{j,i}|}\end{array}$ . Here, the outer sum runs over all ground-truth query points $\mathbf{y}_{j}$ in the query image $I_{q}$ , $\mathbf{y}_{j,i}$ is $\mathbf{y}_{j}$ ’s ground-truth correspondence in image $I_{i}$ , and $\hat{\mathbf{y}}_{j,i}$ is the corresponding prediction obtained by the application $\mathcal{T}((\mathbf{y}_{j})_{j=1}^{M},\mathbf{\bar{(}}T_{i})_{i=1}^{N}\mathbf{\bar{)}}$ of the tracking module. Additionally, following CoTracker2 [57], we apply a visibility loss (binary cross-entropy) to estimate whether a point is visible in a given frame.
最后,跟踪损失由 $\begin{array}{r l}{\mathcal{L}{\mathrm{track}}}&{{}=}\end{array}$ $\begin{array}{r}{\sum{j=1}^{M}\sum_{i=1}^{N}|\mathbf{y}_{j,i}-\hat{\mathbf{y}}_{j,i}|}\end{array}$ 给出。这里,外部的求和遍历查询图像 $I_{q}$ 中的所有真实查询点 $\mathbf{y}_{j}$,$\mathbf{y}_{j,i}$ 是 $\mathbf{y}_{j}$ 在图像 $I_{i}$ 中的真实对应点,而 $\hat{\mathbf{y}}_{j,i}$ 是通过跟踪模块的应用 $\mathcal{T}((\mathbf{y}_{j})_{j=1}^{M},\mathbf{\bar{(}}T_{i})_{i=1}^{N}\mathbf{\bar{)}}$ 获得的相应预测。此外,遵循 CoTracker2 [57],我们应用可见性损失(二元交叉熵)来估计一个点是否在给定帧中可见。
Ground Truth Coordinate Normalization. If we scale a scene or change its global reference frame, the images of the scene are not affected at all, meaning that any such variant is a legitimate result of 3D reconstruction. We remove this ambiguity by normalizing the data, thus making a canonical choice and task the transformer to output this particular variant. We follow [129] and, first, express all quantities in the coordinate frame of the first camera ${\bf g}_{1}$ . Then, we compute the average Euclidean distance of all 3D points in the point map $P$ to the origin and use this scale to normalize the camera translations $\mathbf{t}$ , the point map $P$ , and the depth map $D$ . Importantly, unlike [129], we do not apply such normalization to the predictions output by the transformer; instead, we force it to learn the normalization we choose from the training data.
真实坐标归一化。如果我们缩放场景或改变其全局参考系,场景的图像不会受到任何影响,这意味着任何此类变体都是3D重建的合法结果。我们通过归一化数据来消除这种歧义,从而做出规范选择,并让Transformer输出这种特定变体。我们遵循[129],首先将所有量表示在第一个相机${\bf g}_{1}$的坐标系中。然后,我们计算点图$P$中所有3D点到原点的平均欧几里得距离,并使用此比例对相机平移$\mathbf{t}$、点图$P$和深度图$D$进行归一化。重要的是,与[129]不同,我们不将这种归一化应用于Transformer输出的预测;相反,我们强制它从训练数据中学习我们选择的归一化。
Implementation Details. By default, we employ $L=24$ layers of global and frame-wise attention, respectively. The model consists of approximately 1.2 billion parameters in total. We train the model by optimizing the training loss (2) with the AdamW optimizer for 160K iterations. We use a cosine learning rate scheduler with a peak learning rate of 0.0002 and a warmup of 8K iterations. For every batch, we randomly sample 2–24 frames from a random training scene. The input frames, depth maps, and point maps are resized to a maximum dimension of 518 pixels. The aspect ratio is randomized between 0.33 and 1.0. We also randomly apply color jittering, Gaussian blur, and grayscale augmentation to the frames. The training runs on 64 A100 GPUs over nine days. We employ gradient norm clipping with a threshold of 1.0 to ensure training stability. We leverage bfloat16 precision and gradient check pointing to improve GPU memory and computational efficiency.
实现细节。默认情况下,我们分别使用 $L=24$ 层的全局注意力和帧级注意力。模型总共包含约 12 亿个参数。我们通过使用 AdamW 优化器优化训练损失 (2) 来训练模型,共进行 160K 次迭代。我们使用余弦学习率调度器,峰值学习率为 0.0002,预热阶段为 8K 次迭代。对于每个批次,我们从随机训练场景中随机采样 2–24 帧。输入帧、深度图和点图被调整为最大尺寸为 518 像素。宽高比在 0.33 到 1.0 之间随机化。我们还对帧随机应用颜色抖动、高斯模糊和灰度增强。训练在 64 个 A100 GPU 上运行了九天。我们采用梯度范数裁剪,阈值为 1.0,以确保训练稳定性。我们利用 bfloat16 精度和梯度检查点来提高 GPU 内存和计算效率。
Training Data. The model was trained using a large and diverse collection of datasets, including: Co3Dv2 [88], BlendMVS [146], DL3DV [69], MegaDepth [64], Kubric [41], WildRGB [135], ScanNet [18], Hyper- Sim [89], Mapillary [71], Habitat [107], Replica [104], MVS-Synth [50], Point Odyssey [159], Virtual KITTI [7], Aria Synthetic Environments [82], Aria Digital Twin [82], and a synthetic dataset of artist-created assets similar to Objaverse [20]. These datasets span various domains, including indoor and outdoor environments, and encompass synthetic and real-world scenarios. The 3D annotations for these datasets are derived from multiple sources, such as direct sensor capture, synthetic engines, or SfM techniques [95]. The combination of our datasets is broadly comparable to those of MASt3R [30] in size and diversity.
训练数据。该模型使用了大量多样化的数据集进行训练,包括:Co3Dv2 [88]、BlendMVS [146]、DL3DV [69]、MegaDepth [64]、Kubric [41]、WildRGB [135]、ScanNet [18]、HyperSim [89]、Mapillary [71]、Habitat [107]、Replica [104]、MVS-Synth [50]、Point Odyssey [159]、Virtual KITTI [7]、Aria Synthetic Environments [82]、Aria Digital Twin [82],以及一个类似于Objaverse [20]的艺术家创建的合成数据集。这些数据集涵盖了室内和室外环境,并包含合成和真实场景。这些数据集的3D标注来自多种来源,如直接传感器捕捉、合成引擎或SfM技术 [95]。我们的数据集组合在规模和多样性上与MASt3R [30]相当。
4. Experiments
4. 实验
This section compares our method to state-of-the-art approaches across multiple tasks to show its effectiveness.
本节将我们的方法与多个任务中的最先进方法进行比较,以展示其有效性。
4.1. Camera Pose Estimation
4.1. 相机姿态估计
We first evaluate our method on the CO3Dv2 [88] and Real Estate 10 K [161] datasets for camera pose estimation, as shown in Tab. 1. Following [124], we randomly select 10 images per scene and evaluate them using the standard metric AUC $\ @30$ , which combines RRA and RTA. RRA (Relative Rotation Accuracy) and RTA (Relative Translation Accuracy) calculate the relative angular errors in rotation and translation, respectively, for each image pair. These angular errors are then threshold ed to determine the accuracy scores. AUC is the area under the accuracy-threshold curve of the minimum values between RRA and RTA across varying thresholds. The (learnable) methods in Tab. 1 have been trained on $\mathrm{Co}3\mathrm{Dv}2$ and not on Real Estate 10 K. Our feedforward model consistently outperforms competing methods across all metrics on both datasets, including those that employ computationally expensive post-optimization steps, such as Global Alignment for DUSt3R/MASt3R and Bundle Adjustment for VGGSfM, typically requiring more than 10 seconds. In contrast, VGGT achieves superior performance while only operating in a feed-forward manner, requiring just 0.2 seconds on the same hardware. Compared to concurrent works [111, 127, 141, 156] (indicated by $^\ddag$ ), our method demonstrates significant performance advantages, with speed similar to the fastest variant Fast3R [141]. Furthermore, our model’s performance advantage is even more pronounced on the Real Estate 10 K dataset, which none of the methods presented in Tab. 1 were trained on. This validates the superior generalization of VGGT.
我们首先在 CO3Dv2 [88] 和 Real Estate 10 K [161] 数据集上评估了我们的相机姿态估计方法,如表 1 所示。遵循 [124],我们随机选择每个场景的 10 张图像,并使用标准指标 AUC $\ @30$ 进行评估,该指标结合了 RRA 和 RTA。RRA(相对旋转精度)和 RTA(相对平移精度)分别计算每对图像的旋转和平移的相对角度误差。然后对这些角度误差进行阈值处理以确定精度分数。AUC 是 RRA 和 RTA 在不同阈值下的最小值精度-阈值曲线下的面积。表 1 中的(可学习)方法已在 $\mathrm{Co}3\mathrm{Dv}2$ 上进行了训练,而未在 Real Estate 10 K 上进行训练。我们的前馈模型在两个数据集的所有指标上均优于竞争方法,包括那些采用计算成本高昂的后优化步骤的方法,例如 DUSt3R/MASt3R 的全局对齐和 VGGSfM 的捆绑调整,通常需要超过 10 秒。相比之下,VGGT 仅以前馈方式运行,在相同硬件上仅需 0.2 秒即可实现卓越性能。与同时期的工作 [111, 127, 141, 156](用 $^\ddag$ 表示)相比,我们的方法展示了显著的性能优势,速度与最快的变体 Fast3R [141] 相似。此外,我们的模型在 Real Estate 10 K 数据集上的性能优势更加明显,表 1 中没有任何方法在该数据集上进行过训练。这验证了 VGGT 的卓越泛化能力。
Table 1. Camera Pose Estimation on Real Estate 10 K [161] and CO3Dv2 [88] with 10 random frames. All metrics the higher the better. None of the methods were trained on the Re10K dataset. Runtime were measured using one $\mathrm{H}100\mathrm{GPU}$ . Methods marked with ‡ represent concurrent work.
表 1. 在 Real Estate 10 K [161] 和 CO3Dv2 [88] 数据集上使用 10 个随机帧进行相机姿态估计的结果。所有指标越高越好。所有方法均未在 Re10K 数据集上进行训练。运行时间使用一个 $\mathrm{H}100\mathrm{GPU}$ 进行测量。标记为 ‡ 的方法表示同期工作。
| 方法 | Re10K (未见) AUC@30↑ | CO3Dv2 AUC@30↑ | 时间 |
|---|---|---|---|
| Colmap+SPSG [92] | 45.2 | 25.3 | ~15s |
| PixSfM [66] | 49.4 | 30.1 | >20s |
| PoseDiff [124] DUSt3R [129] | 48.0 | 66.5 76.7 | ~7s ~7s |
| MASt3R [62] | 67.7 76.4 | 81.8 | ~9s |
| VGGSfMv2 [125] | 78.9 | 83.4 | ~10s |
| MV-DUSt3R [111] | 71.3 | 69.5 | ~0.6s |
| CUT3R [127] | 75.3 | 82.8 | ~0.6s |
| FLARE [156] | 78.8 | 83.3 | ~0.5s |
| Fast3R [141] | 72.7 | 82.5 | ~0.2s |
| 我们的方法 (前馈) | 85.3 | 88.2 | ~0.2s |
| 我们的方法 (带 BA) | 93.5 | 91.8 | ~1.8s |
Table 2. Dense MVS Estimation on the DTU [51] Dataset. Methods operating with known ground-truth camera are in the top part of the table, while the bottom part contains the methods that do not know the ground-truth camera.
表 2: DTU [51] 数据集上的密集多视角立体 (Dense MVS) 估计。使用已知真实相机的方法位于表格的上半部分,而不知道真实相机的方法位于表格的下半部分。
| 已知真实相机 | 方法 | 精度↓ | 完整性↓ | 总体↓ |
|---|---|---|---|---|
| Gipuma [40] | 0.283 | 0.873 | 0.578 | |
| MVSNet [144] | 0.396 | 0.527 | 0.462 | |
| CIDER [139] | 0.417 | 0.437 | 0.427 | |
| PatchmatchNet [121] | 0.427 | 0.377 | 0.417 | |
| MASt3R [62] | 0.403 | 0.344 | 0.374 | |
| GeoMVSNet [157] | 0.331 | 0.259 | 0.295 | |
| DUSt3R [129] | 2.677 | 0.805 | 1.741 | |
| 我们的方法 | 0.389 | 0.374 | 0.382 |
Table 3. Point Map Estimation on ETH3D [97]. DUSt3R and MASt3R use global alignment while ours is feed-forward and, hence, much faster. The row Ours (Point) indicates the results using the point map head directly, while Ours $(D e p t h+C a m)$ denotes constructing point clouds from the depth map head combined with the camera head.
表 3: ETH3D [97] 上的点云地图估计。DUSt3R 和 MASt3R 使用全局对齐,而我们的方法是前馈的,因此速度更快。Ours (Point) 行表示直接使用点云地图头的结果,而 Ours (Depth + Cam) 表示从深度图头与相机头结合构建的点云。
| 方法 | Acc.√ | Comp. | Overall↓ | 时间 |
|---|---|---|---|---|
| DUSt3R | 1.167 | 0.842 | 1.005 | ~7s |
| MASt3R | 0.968 | 0.684 | 0.826 | ~9s |
| Ours (Point) | 0.901 | 0.518 | 0.709 | ~0.2s |
| Ours (Depth + Cam) | 0.873 | 0.482 | 0.677 | ~0.2s |
Table 4. Two-View matching comparison on ScanNet-1500 [18, 92]. Although our tracking head is not specialized for the twoview setting, it outperforms the state-of-the-art two-view matching method Roma. Measured in AUC (higher is better).
表 4: ScanNet-1500 [18, 92] 上的双视图匹配对比。尽管我们的跟踪头并未专门针对双视图设置进行优化,但其性能仍优于当前最先进的双视图匹配方法 Roma。以 AUC 衡量(数值越高越好)。
| 方法 | AUC@5↑ | AUC@10↑ | AUC@20↑ |
|---|---|---|---|
| SuperGlue[92] | 16.2 | 33.8 | 51.8 |
| LoFTR [105] | 22.1 | 40.8 | 57.6 |
| DKM [32] | 29.4 | 50.7 | 68.3 |
| CasMTR [9] | 27.1 | 47.0 | 64.4 |
| Roma [33] | 31.8 | 53.4 | 70.9 |
| Ours | 33.9 | 55.2 | 73.4 |
Our results also show that VGGT can be improved even further by combining it with optimization methods from visual geometry optimization like BA. Specifically, refining the predicted camera poses and tracks with BA further improves accuracy. Note that our method directly predicts close-to-accurate point/depth maps, which can serve as a good initialization for BA. This eliminates the need for triangulation and iterative refinement in BA as done by [125], making our approach significantly faster (only around 2 seconds even with BA). Hence, while the feed-forward mode of VGGT outperforms all previous alternatives (whether they are feed-forward or not), there is still room for improvement since post-optimization still brings benefits.
我们的结果还表明,通过将 VGGT 与视觉几何优化中的优化方法(如 BA)结合,可以进一步提升其性能。具体而言,使用 BA 对预测的相机姿态和轨迹进行细化,可以进一步提高精度。需要注意的是,我们的方法直接预测接近准确的点/深度图,这可以作为 BA 的良好初始化。这消除了 [125] 中所需的三角测量和迭代细化步骤,使得我们的方法显著更快(即使使用 BA,也仅需约 2 秒)。因此,虽然 VGGT 的前馈模式优于所有先前的替代方案(无论它们是否为前馈),但由于后优化仍然带来好处,因此仍有改进空间。
4.2. Multi-view Depth Estimation
4.2. 多视角深度估计
Following MASt3R [62], we further evaluate our multiview depth estimation results on the DTU [51] dataset. We report the standard DTU metrics, including Accuracy (the smallest Euclidean distance from the prediction to ground truth), Completeness (the smallest Euclidean distance from the ground truth to prediction), and their average Overall (i.e., Chamfer distance). In Tab. 2, DUSt3R and our VGGT are the only two methods operating without the knowledge of ground truth cameras. MASt3R derives depth maps by tri angul a ting matches using the ground truth cameras. Meanwhile, deep multi-view stereo methods like GeoMVS
遵循 MASt3R [62],我们进一步在 DTU [51] 数据集上评估了我们的多视角深度估计结果。我们报告了标准的 DTU 指标,包括 Accuracy(预测到真实值的最小欧几里得距离)、Completeness(真实值到预测的最小欧几里得距离)以及它们的平均值 Overall(即 Chamfer 距离)。在表 2 中,DUSt3R 和我们的 VGGT 是仅有的两种在没有真实相机信息的情况下运行的方法。MASt3R 通过使用真实相机信息对匹配进行三角测量来推导深度图。同时,像 GeoMVS 这样的深度多视角立体方法

Figure 5. Visualization of Rigid and Dynamic Point Tracking. Top: VGGT’s tracking module $\tau$ outputs keypoint tracks for an unordered set of input images depicting a static scene. Bottom: We finetune the backbone of VGGT to enhance a dynamic point tracker CoTracker [56], which processes sequential inputs.
图 5: 刚性和动态点跟踪的可视化。顶部:VGGT 的跟踪模块 $\tau$ 为描述静态场景的无序输入图像集输出关键点轨迹。底部:我们对 VGGT 的主干网络进行微调,以增强动态点跟踪器 CoTracker [56],该跟踪器处理顺序输入。
Net use ground truth cameras to construct cost volumes.
Net 使用真实相机来构建成本体积。
Our method substantially outperforms DUSt3R, reducing the Overall score from 1.741 to 0.382. More impor- tantly, it achieves results comparable to methods that know ground-truth cameras at test time. The significant performance gains can likely be attributed to our model’s multiimage training scheme that teaches it to reason about multiview triangulation natively, instead of relying on ad hoc alignment procedures, such as in DUSt3R, which only averages multiple pairwise camera triangulation s.
我们的方法显著优于 DUSt3R,将总体得分从 1.741 降低到 0.382。更重要的是,它在测试时取得了与已知真实相机的方法相当的结果。显著的性能提升可能归因于我们模型的多图像训练方案,该方案教会它自然地推理多视图三角测量,而不是依赖于临时对齐程序,例如在 DUSt3R 中,它仅对多个成对相机三角测量进行平均。
4.3. Point Map Estimation
4.3. 点地图估计
We also compare the accuracy of our predicted point cloud to DUSt3R and MASt3R on the ETH3D [97] dataset. For each scene, we randomly sample 10 frames. The predicted point cloud is aligned to the ground truth using the Umeyama [117] algorithm. The results are reported after filtering out invalid points using the official masks. We report Accuracy, Completeness, and Overall (Chamfer distance) for point map estimation. As shown in Tab. 3, although DUSt3R and MASt3R conduct expensive optimization (global alignment–—around 10 seconds per scene), our method still outperforms them significantly in a simple feed-forward regime at only 0.2 seconds per reconstruction.
我们还将预测点云的准确性与 DUSt3R 和 MASt3R 在 ETH3D [97] 数据集上进行了比较。对于每个场景,我们随机采样 10 帧。使用 Umeyama [117] 算法将预测的点云与真实值对齐。结果在使用官方掩码过滤掉无效点后报告。我们报告了点图估计的准确性、完整性和总体(Chamfer 距离)。如表 3 所示,尽管 DUSt3R 和 MASt3R 进行了昂贵的优化(全局对齐——每个场景大约 10 秒),但我们的方法在简单的前馈机制中仍然显著优于它们,每次重建仅需 0.2 秒。
Meanwhile, compared to directly using our estimated point maps, we found that the predictions from our depth and camera heads (i.e., un projecting the predicted depth maps to 3D using the predicted camera parameters) yield higher accuracy. We attribute this to the benefits of decomposing a complex task (point map estimation) into simpler sub problems (depth map and camera prediction), even though camera, depth maps, and point maps are jointly supervised during training.
与此同时,与直接使用我们估计的点云图相比,我们发现从深度和相机头部(即使用预测的相机参数将预测的深度图反投影到3D)得到的预测结果具有更高的准确性。我们将此归因于将复杂任务(点云图估计)分解为更简单的子问题(深度图和相机预测)所带来的好处,尽管在训练过程中相机、深度图和点云图是联合监督的。
We present a qualitative comparison with DUSt3R on inthe-wild scenes in Fig. 3 and further examples in Fig. 4. VGGT outputs high-quality predictions and generalizes well, excelling on challenging out-of-domain examples, such as oil paintings, non-overlapping frames, and scenes with repeating or homogeneous textures like deserts.
我们在图 3 中展示了与 DUSt3R 在野外场景中的定性对比,并在图 4 中提供了更多示例。VGGT 输出了高质量的预测结果,并且具有良好的泛化能力,在具有挑战性的域外示例(如油画、非重叠帧以及具有重复或均匀纹理的场景(如沙漠))中表现出色。
Table 5. Ablation Study for Transformer Backbone on ETH3D. We compare our alternating-attention architecture against two variants: one using only global self-attention and another employing cross-attention.
表 5. ETH3D 上 Transformer 主干的消融研究。我们将交替注意力架构与两种变体进行比较:一种仅使用全局自注意力,另一种采用交叉注意力。
| ETH3D 数据集 | Acc.√ | Comp.√ | Overall√ |
|---|---|---|---|
| 交叉注意力 | 1.287 | 0.835 | 1.061 |
| 仅全局自注意力 | 1.032 | 0.621 | 0.827 |
| 交替注意力 | 0.901 | 0.518 | 0.709 |
4.4. Image Matching
4.4. 图像匹配
Two-view image matching is a widely-explored topic [68, 93, 105] in computer vision. It represents a specific c
