CONTEXT-AWARE META-LEARNING

上下文感知元学习

ABSTRACT

摘要

Large Language Models like ChatGPT demonstrate a remarkable capacity to learn new concepts during inference without any fine-tuning. However, visual models trained to detect new objects during inference have been unable to replicate this ability, and instead either perform poorly or require meta-training and/or finetuning on similar objects. In this work, we propose a meta-learning algorithm that emulates Large Language Models by learning new visual concepts during inference without fine-tuning. Our approach leverages a frozen pre-trained feature extractor, and analogous to in-context learning, recasts visual meta-learning as sequence modeling over datapoints with known labels and a test datapoint with an unknown label. On 8 out of 11 few-shot image classification benchmarks, our approach—without meta-training or fine-tuning—exceeds or matches the state-ofthe-art algorithm, $\mathrm{>M>F.}$ , which is meta-trained on these benchmarks. Our code is available at https://github.com/cfifty/CAML.

像 ChatGPT 这样的大语言模型展现出无需微调即可在推理过程中学习新概念的卓越能力。然而，经过训练以在推理时检测新物体的视觉模型却无法复制这种能力，要么表现不佳，要么需要对类似物体进行元训练和/或微调。在这项工作中，我们提出一种元学习算法，通过在不进行微调的情况下于推理过程中学习新视觉概念，从而模拟大语言模型。我们的方法利用冻结的预训练特征提取器，类似于上下文学习，将视觉元学习重新定义为对带有已知标签的数据点和带有未知标签的测试数据点进行序列建模。在 11 个少样本图像分类基准测试中的 8 个上，我们的方法——无需元训练或微调——超越或匹配了当前最先进的算法 $\mathrm{>M>F.}$，后者是在这些基准测试上进行元训练的。我们的代码可在 https://github.com/cfifty/CAML 获取。

1 INTRODUCTION

1 引言

Meta-learning refers to a capacity to learn new concepts from a small number of demonstrations (Lake et al., 2015). In a decade of remarkable advances to machine intelligence, it remains an area where human performance continues to surpass that of machines (Brown et al., 2020). To match human capabilities, and towards developing machines that can learn and think like humans, we must develop machine intelligence capable of learning novel concepts from only a few examples (Lake et al., 2017).

元学习 (Meta-learning) 是指从少量演示样本中学习新概念的能力 (Lake et al., 2015) 。在机器智能取得显著进展的十年间，这仍是人类表现持续超越机器的领域 (Brown et al., 2020) 。为了匹配人类能力，并开发能像人类一样学习和思考的机器，我们必须发展能够仅通过少量样本学习新概念的机器智能 (Lake et al., 2017) 。

Many applications of deep learning apply a learning algorithm to a large set of training data; however, learning from a very small number of training examples poses a challenge (Lake et al., 2017; Garnelo et al., 2018). This challenge led to two predominant evaluation settings: in-domain and cross-domain. The in-domain setting evaluates a meta-learner’s ability to quickly adapt to new tasks after training on similar tasks within a specific domain. Models designed for this setting are often extremely fast but exhibit poor generalization to tasks outside the target domain (Chen et al., 2019). Meanwhile, the cross-domain setting evaluates a meta-learner’s ability to adapt to tasks in previously unseen domains. Methods designed for this setting are highly adaptable but slow during inference as they require fine-tuning on the support set (Guo et al., 2020; Oh et al., 2022; Hu et al., 2022). Critically, meta-learners in both settings differ from a human’s capacity to quickly generalize to new tasks.

深度学习的许多应用将学习算法应用于大量训练数据；然而，从极少量训练样本中学习仍是一项挑战 (Lake et al., 2017; Garnelo et al., 2018)。这一挑战催生出两种主流评估场景：域内评估与跨域评估。域内评估检验元学习器在特定领域内经过相似任务训练后快速适应新任务的能力，为此设计的模型通常速度极快，但在目标领域外任务上泛化能力较差 (Chen et al., 2019)。跨域评估则测试元学习器适应全新领域任务的能力，相关方法虽适应性更强，但因需在支持集上进行微调，推理速度较慢 (Guo et al., 2020; Oh et al., 2022; Hu et al., 2022)。关键在于，两种场景下的元学习器都不同于人类快速泛化至新任务的能力。

The problem of simultaneously fast and general meta-learning has recently been addressed in Natural Language by Large Language Models (LLMs). LLMs like ChatGPT can quickly generalize to new tasks through an ability termed in-context learning (Brown et al., 2020). However, it remains an open problem in Computer Vision. Even the best visual meta-learning algorithms cannot be deployed to a ChatGPT-like system because such systems require models that can (1) generalize to a broad set of tasks unknown at training time and (2) do so in real-time, without the time allowance for finetuning the model. LLMs have shown a remarkable ability to do both; however, current visual meta-learners may only satisfy one requirement or the other (Hu et al., 2022).

同时实现快速且通用的元学习问题最近在大语言模型(LLM)处理自然语言领域得到了解决。像ChatGPT这样的大语言模型能够通过上下文学习(context learning)能力快速泛化到新任务(Brown et al., 2020)。然而，这仍是计算机视觉领域悬而未决的难题。即使最优秀的视觉元学习算法也无法部署到类ChatGPT系统中，因为这类系统要求模型能够：(1) 泛化到训练时未知的广泛任务集；(2) 实时完成推理，不给模型微调留出时间余量。大语言模型已展现出同时满足这两点的卓越能力，但当前的视觉元学习器可能仅能满足其中一项要求(Hu et al., 2022)。

To measure progress towards this goal of fast and general visual meta-learners, we develop an evaluation paradigm that we call universal meta-learning. Universal meta-learning measures a model’s capacity to quickly learn new image classes. It evaluates models across a diverse set of meta-learning benchmarks spanning many different image classification tasks without meta-training on any of the benchmarks’ training sets or fine-tuning on the support set during inference. We focus on the application of few-shot image classification—as opposed to dense prediction tasks like in-painting or segmentation—as the universal setting has already been explored for these applications (Bar et al., 2022; Zhang et al., 2023; Wang et al., 2023; Kim et al., 2023; Butoi et al., 2023).

为了衡量快速通用视觉元学习者的进展，我们开发了一种称为通用元学习的评估范式。通用元学习评估模型快速学习新图像类别的能力，它通过跨越多样化元学习基准（涵盖不同图像分类任务）来评估模型，且不依赖任何基准训练集进行元训练，也不在推理时对支持集进行微调。我们专注于少样本图像分类的应用（与修复或分割等密集预测任务不同），因为这些应用已探索过通用设置 (Bar et al., 2022; Zhang et al., 2023; Wang et al., 2023; Kim et al., 2023; Butoi et al., 2023)。

Beyond benchmarking methods in the universal setting, we present a meta-learner that achieves strong universal performance. Drawing inspiration from in-context learning in LLMs, we reformulate $n$ -way $k$ -shot image classification as non-causal sequence modeling over the support set and an unknown query image. Specifically, given $n$ -way classification with $k$ -examples from each class, we train a non-causal model over $\dot{{(x_{i},y_{i})}}{i=1}^{n k}$ (image, label) support set pairs, and an unlabeled query image $x_{n k+1}$ , to predict the label of the query image. This formulation causes the meta-learner to extrapolate to new classes in its parameter space, enabling it to learn new visual concepts during inference without fine-tuning. Due to its capacity to learn visual information “in-context”, we term our approach Context-Aware Meta-Learning (CAML).

除了在通用场景下的基准测试方法外，我们提出了一种实现强大通用性能的元学习器。受大语言模型 (LLM) 上下文学习的启发，我们将 $n$ 类 $k$ 样本图像分类重新定义为支持集和未知查询图像上的非因果序列建模。具体而言，给定每个类别包含 $k$ 个样本的 $n$ 类分类任务，我们在 $\dot{{(x_{i},y_{i})}}{i=1}^{n k}$ (图像, 标签) 支持集对和未标记的查询图像 $x_{n k+1}$ 上训练非因果模型，以预测查询图像的标签。这种表述使得元学习器能够在参数空间中泛化到新类别，从而无需微调即可在推理过程中学习新的视觉概念。由于其"上下文"学习视觉信息的能力，我们将该方法称为上下文感知元学习 (CAML)。

In summary, our contribution is two-fold. First, we develop a meta-learning evaluation paradigm that approximates the performance of visual meta-learners in a ChatGPT-like application. Second, we design a meta-learning algorithm that works well in this setting. Our empirical findings show that CAML outperforms other meta-learners in the universal setting. Remarkably, CAML’s performance in the universal setting often matches—and even exceeds—the in-domain performance of the state-ofthe-art meta-learning algorithm, $\scriptstyle\mathrm{P>M>F}$ (Hu et al., 2022), that is directly trained on each down-stream benchmark.

总之，我们的贡献有两点。首先，我们开发了一种元学习评估范式，能够近似视觉元学习器在类似ChatGPT应用中的表现。其次，我们设计了一种在此场景下表现优异的元学习算法。实验结果表明，CAML在通用场景下优于其他元学习方法。值得注意的是，CAML在通用场景中的表现常常达到甚至超越当前最先进的元学习算法 $\scriptstyle\mathrm{P>M>F}$ (Hu et al., 2022) 在各下游基准测试上直接训练得到的领域内性能。

2 RELATED WORK

2 相关工作

Meta-Learning as Causal Sequence Modeling. Several of the earliest meta-learning algorithms were formulated as causal sequence modeling problems. Hochreiter et al. (2001) leverage a LSTM (Hochreiter & Schmid huber, 1997) to model extensions to semi-linear and quadratic functions, and two decades later, Graves et al. (2014); Santoro et al. (2016); Kaiser et al. (2017) build upon this approach by integrating a form of external memory that the LSTM can read to and write from memory to develop Neural Turing Machines. With the advent of self-attention (Vaswani et al., 2017), Mishra et al. (2017) predict the labels of query images by first composing a sequence of (image, label) pairs and then feeding it through a stack of interleaved causal self-attention and temporal convolution layers. Kirsch et al. (2022) replaces the stack of interleaved causal self-attention and temporal convolution layers with a Transformer encoder; however, their approach is also causal in the input sequence by composing a sequence of (image, label of previous image) pairs. Both Mishra et al. (2017) and Kirsch et al. (2022) are conceptually similar to our work; however, the causal property of both approaches breaks an important symmetry in meta-learning, namely invariance to permutations of the support set (Garnelo et al., 2018; Müller et al., 2021). In Section 5.2, we observe a performance gap between both approaches and CAML and hypothesize the causal approach actually forces a subtly more difficult modeling problem by imposing a causality inductive bias on a fundamentally non-causal prediction task.

元学习作为因果序列建模。最早的元学习算法中有几种被表述为因果序列建模问题。Hochreiter等 (2001) 利用LSTM (Hochreiter & Schmidhuber, 1997) 对半线性和二次函数进行扩展建模，二十年后，Graves等 (2014)、Santoro等 (2016)、Kaiser等 (2017) 在此基础上通过集成一种外部记忆机制，使LSTM能够读写记忆，从而开发出神经图灵机。随着自注意力 (Vaswani等, 2017) 的出现，Mishra等 (2017) 通过首先构建一系列 (图像, 标签) 对序列，然后将其输入交错堆叠的因果自注意力和时间卷积层来预测查询图像的标签。Kirsch等 (2022) 用Transformer编码器替换了交错堆叠的因果自注意力和时间卷积层；然而，他们的方法通过构建一系列 (图像, 前一张图像的标签) 对序列，在输入序列上也是因果的。Mishra等 (2017) 和Kirsch等 (2022) 在概念上与我们的工作相似；然而，这两种方法的因果特性破坏了元学习中的一个重要对称性，即支持集排列的不变性 (Garnelo等, 2018; Müller等, 2021)。在5.2节中，我们观察到这两种方法与CAML之间存在性能差距，并假设因果方法实际上通过在本质上非因果的预测任务上强加因果归纳偏置，迫使建模问题变得更加微妙且困难。

Cross-Domain Meta-Learning. Cross-domain meta-learning refers to a challenging evaluation paradigm where the meta-training and inference-time data distributions are significantly different (Chen et al., 2019). Recent work finds that leveraging self-supervised pre-training—or foundational model feature extractors—can significantly improve cross-domain performance (Hu et al., 2022; Zhang et al., 2021). Moreover, fine-tuning with respect to the support set almost always outperforms meta-learning without fine-tuning in this setting (Guo et al., 2020; Oh et al., 2022; Phoo & Hariharan, 2020; Islam et al., 2021). While effective, fine-tuning is prohibitive to deploying visual meta-learning models in a manner similar to LLMs like ChatGPT as the latency and memory cost to fine-tune a model’s parameters on each user query is untenable. Accordingly, we propose the universal setting to measure a meta-learner’s ability to learn to classify any task seen during inference without fine-tuning.

跨领域元学习。跨领域元学习指的是一种具有挑战性的评估范式，其中元训练和推理时的数据分布存在显著差异 (Chen et al., 2019)。最近的研究发现，利用自监督预训练或基础模型特征提取器可以显著提升跨领域性能 (Hu et al., 2022; Zhang et al., 2021)。此外，在这种设置下，针对支持集进行微调几乎总是优于不进行微调的元学习方法 (Guo et al., 2020; Oh et al., 2022; Phoo & Hariharan, 2020; Islam et al., 2021)。尽管有效，微调方式阻碍了视觉元学习模型像ChatGPT等大语言模型那样部署，因为针对每个用户查询微调模型参数所需的延迟和内存成本过高。因此，我们提出通用设置来衡量元学习器在不进行微调的情况下学习分类推理时遇到的任何任务的能力。

In-Context Learning for Dense Prediction Tasks. Many recent works have explored in-context learning for other applications of computer vision. Bar et al. (2022) casts in-context learning as image in-painting by first concatenating demonstration images with a query image and then using a vision model to fill-in-the-blank within this concatenated image. Building on this work, Zhang et al. (2023) explores what demonstrations lead to strong in-painting performance and Wang et al. (2023) generalizes the approach by formulating other visual applications like segmentation, depth estimation, etc. as in-painting. Other approaches explore in-context learning for applications like scene understanding (Balazevic et al., 2024), medical image segmentation (Butoi et al., 2023), and more generally dense prediction tasks (Kim et al., 2023). Like these approaches, we study visual in-context learning; however, this work focuses on few-shot image classification rather than dense prediction tasks.

密集预测任务中的上下文学习。近期许多研究探索了计算机视觉其他应用中的上下文学习。Bar等人 (2022) 将上下文学习视为图像修复任务，首先将示例图像与查询图像拼接，然后使用视觉模型在这个拼接图像中进行填空。基于这项工作，Zhang等人 (2023) 探究了哪些示例能带来强大的修复性能，而Wang等人 (2023) 通过将分割、深度估计等其他视觉应用形式化为修复问题，对该方法进行了推广。其他方法探索了场景理解 (Balazevic等人, 2024)、医学图像分割 (Butoi等人, 2023) 以及更广泛的密集预测任务 (Kim等人, 2023) 等应用中的上下文学习。与这些方法类似，我们研究了视觉上下文学习；然而，本文关注的是少样本图像分类而非密集预测任务。

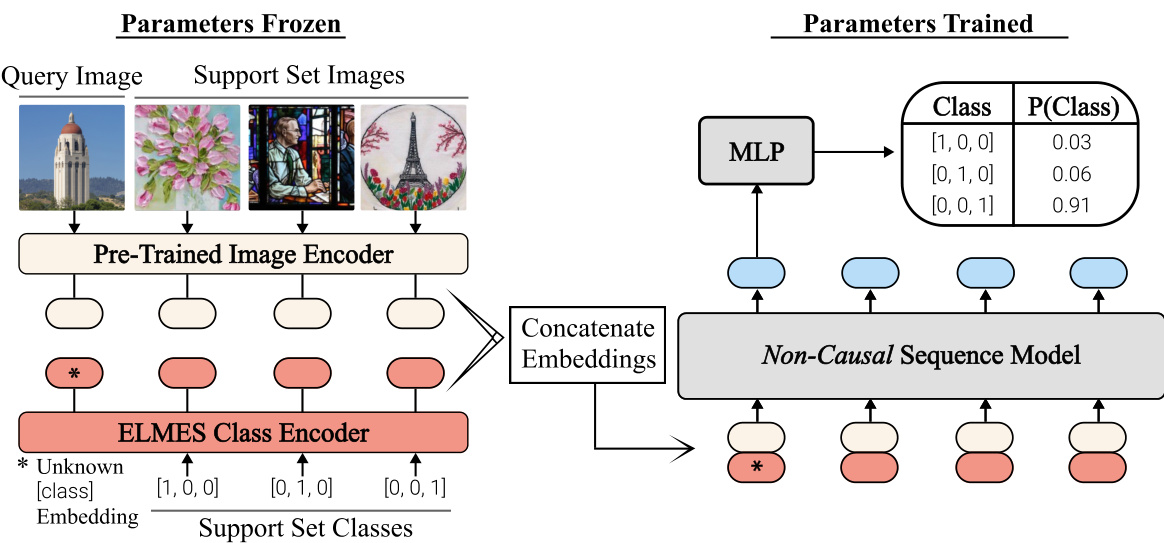
Figure 1: Overview of CAML. Query and support set images are encoded with a pre-trained feature extractor and then concatenated with their corresponding ELMES label embeddings. We feed the resulting sequence of concatenated vectors into a non-casual sequence model and extract the query vector from the output sequence to predict its class.

图 1: CAML 概览。查询图像和支持集图像通过预训练特征提取器编码后，与对应的 ELMES 标签嵌入向量拼接。我们将拼接后的向量序列输入非因果序列模型，并从输出序列中提取查询向量以预测其类别。

3 APPROACH

3 方法

We adapt the ideas underpinning in-context learning in LLMs—namely learning to classify a query from a context of support set demonstrations in a single forward pass—to image classification. However, dissimilar from in-context learning, visual meta-learners should be non-causal: placing one example before another in the support set does not entail a causal relationship (Garnelo et al., 2018; Müller et al., 2021).

我们借鉴了大语言模型中情境学习（in-context learning）的核心思想——即通过单次前向传播，从支持集的示范上下文中学习对查询进行分类——并将其应用于图像分类。然而，与情境学习不同，视觉元学习器应当是非因果性的：在支持集中将一个样本置于另一个样本之前并不意味着存在因果关系 (Garnelo et al., 2018; Müller et al., 2021)。

Architecture. An overview of CAML is shown in Figure 1. It consists of three different components: (1) a frozen pre-trained image encoder, (2) a fixed Equal Length and Maximally Equiangular Set (ELMES) class encoder, and (3) a non-causal sequence model. While pre-trained image encoders and non-causal sequence models are well-known, to encode label information we introduce an ELMES encoder. An ELMES encoder is a bijective mapping between the labels and a set of vectors that are equal length and maximally equiangular. Historically, labels have been encoded with one-hot vectors; however in Section 4, we prove that an ELMES encoding of mutually exclusive classes allows the sequence model to maximally identify classes within the support set.

架构。CAML 的概览如图 1 所示，它包含三个不同组件：(1) 冻结的预训练图像编码器，(2) 固定的等长最大等角集 (ELMES) 类别编码器，(3) 非因果序列模型。虽然预训练图像编码器和非因果序列模型广为人知，但为了编码标签信息，我们引入了 ELMES 编码器。ELMES 编码器是标签与一组等长且最大等角向量之间的双射映射。传统上标签采用独热向量编码，但在第 4 节我们将证明：互斥类别的 ELMES 编码能使序列模型在支持集中实现最大程度的类别识别。

As visualized in Figure 1, CAML first encodes query and support set images using a frozen pre-trained feature extractor. Crucially, the pre-trained image encoder’s embedding space distills images into low-dimensional representations so that images with similar content and visual characteristics have similar embeddings. Classes of the support set are encoded with an ELMES class encoder; however as the class of the query is unknown, we use a special learnable “unknown token” embedding that is learned during large-scale pre-training. CAML then concatenates each image embedding with its corresponding query embedding to form an input sequence.

如图 1 所示，CAML 首先使用冻结的预训练特征提取器对查询集和支持集图像进行编码。关键在于，预训练图像编码器的嵌入空间会将图像提炼为低维表示，从而使内容和视觉特征相似的图像具有相似的嵌入向量。支持集的类别通过 ELMES 类别编码器进行编码；但由于查询样本的类别未知，我们采用了一个在大规模预训练期间习得的特殊可学习"未知 token"嵌入向量。随后，CAML 将每个图像嵌入向量与其对应的查询嵌入向量拼接，形成输入序列。

Progressing through Figure 1, this sequence is fed into a non-causal sequence model, i.e. a Transformer encoder, to condition the output representations on the full context of query and support set points. This enables dynamic and real-time classification; visual characteristics from query and support set images can be compared with each other to determine the specific visual features—such as content, textures, etc.—used to classify the query. From the output sequence of the non-causal sequence model, we select the element at the same position as the query in the input sequence, and pass this vector through a shallow MLP to predict the label of the query.

在图1所示的流程中，该序列被输入到非因果序列模型（即Transformer编码器），使输出表征能够基于查询集和支持集点的完整上下文进行条件化处理。这种设计实现了动态实时分类：通过对比查询图像和支持集图像的视觉特征（如内容、纹理等），系统能动态识别用于分类查询图像的具体视觉特征。我们从非因果序列模型的输出序列中，选取与输入序列里查询位置相对应的元素，并将该向量通过浅层MLP网络来预测查询图像的标签。

Large-Scale Pre-Training. As our focus is universal meta-learning—and CAML may encounter any new visual concept during inference—we pre-train CAML’s non-causal sequence model on few-shot image classification tasks from ImageNet-1k (Deng et al., 2009), Fungi (Schroeder & Cui, 2018), MSCOCO (Lin et al., 2014), and WikiArt (Saleh & Elgammal, 2015). We chose these datasets because they span generic object recognition (ImageNet-1k, MSCOCO), fine-grained image classification (Fungi), and unnatural image classification (WikiArt). To avoid distorting the pre-trained image encoder’s embedding space, we freeze this module and only update the sequence model’s parameters during pre training. Similarly, since an ELMES minimizes the entropy of detecting classes within the support set, the label encoder is also frozen. In the context of pre-training, meta-training, and fine-tuning, CAML only requires pre-training and avoids meta-training on the train/validation splits of meta-learning benchmarks or fine-tuning on the support set during inference.

大规模预训练。由于我们的目标是通用元学习——且CAML在推理过程中可能遇到任何新的视觉概念——我们在ImageNet-1k (Deng et al., 2009)、Fungi (Schroeder & Cui, 2018)、MSCOCO (Lin et al., 2014)和WikiArt (Saleh & Elgammal, 2015)的少样本图像分类任务上对CAML的非因果序列模型进行预训练。选择这些数据集是因为它们覆盖了通用物体识别(ImageNet-1k、MSCOCO)、细粒度图像分类(Fungi)和非自然图像分类(WikiArt)。为避免扭曲预训练图像编码器的嵌入空间，我们冻结该模块并仅在预训练期间更新序列模型的参数。类似地，由于ELMES最小化支持集内检测类别的熵，标签编码器也被冻结。在预训练、元训练和微调的背景下，CAML仅需预训练，避免了在元学习基准的训练/验证分割上进行元训练或在推理期间对支持集进行微调。

4 THEORETICAL ANALYSIS

4 理论分析

In this section, we motivate our choice of the ELMES Class Encoder by considering the symmetries desirable in meta-learning algorithms. Two important symmetries are (1) invariance to the assignment of support set classes to numeric labels and (2) invariance to permutations in the ordering of the input sequence. The first invariance implies the class embeddings must be equiangular and equal norm, with an ELMES configuration minimizing the entropy of learnable model parameters detecting any given class. Later, we show an ELMES also satisfies the second symmetry. Due to space constraints, all proofs and many definitions, properties, lemmas, and theorems are allocated to Appendix A.1. We begin with a formal definition of an ELMES.

在本节中，我们通过考虑元学习算法所需的对称性来阐述选择ELMES类编码器的动机。两个重要的对称性是：(1) 支持集类别与数字标签分配的不变性；(2) 输入序列排列顺序的不变性。第一个不变性意味着类嵌入必须是等角且等范数的，ELMES配置通过最小化可学习模型参数的熵来检测任何给定类别。随后我们将证明ELMES同样满足第二个对称性。由于篇幅限制，所有证明及定义、性质、引理和定理详见附录A.1。我们首先给出ELMES的形式化定义。

4.1 EQUAL LENGTH AND MAXIMALLY EQUIANGULAR SET OF VECTORS

4.1 等长且最大等角向量集

Definition 1. An Equal Length and Maximally Equiangular Set (ELMES) is a set of non-zero vectors ${\phi_{j}}{j=1}^{d}$ , $\hat{\phi_{j}}\in\mathbb{R}^{d+k}$ for some $k\geq0$ and $d>1$ , such that $\forall j\ne j^{\prime}$ , $|\phi_{j}|=|\phi_{j^{\prime}}|$ and $\langle\phi_{j}$ , $\textstyle\phi_{j^{\prime}}\rangle={\frac{-1}{d-1}}$ . Simply, all vectors in this set are equal length and maximally equiangular.

定义 1. 等长最大等角集 (ELMES) 是一组非零向量 ${\phi_{j}}{j=1}^{d}$，$\hat{\phi_{j}}\in\mathbb{R}^{d+k}$ 对于某些 $k\geq0$ 和 $d>1$，使得 $\forall j\ne j^{\prime}$，$|\phi_{j}|=|\phi_{j^{\prime}}|$ 且 $\langle\phi_{j}$，$\textstyle\phi_{j^{\prime}}\rangle={\frac{-1}{d-1}}$。简而言之，该集合中的所有向量都是等长且最大等角的。

An Equal Angle and Maximally Equiangular Set (ELMES) of vectors has connections to both Equiangular Tight Frames in representation theory (Welch, 1974; Fickus et al., 2018) as well as the Simplex Equiangular Tight Frames highlighted in recent neural collapse works exploring softmaxlayer geometry at the terminal phase of training (Papyan et al., 2020; Yang et al., 2022). We offer additional discussion comparing these structures in Appendix A.1 as well as provide an intuitive view of an ELMES as a regular $d$ -simplex immersed in $\mathbb{R}^{\hat{d}+k}$ .

等角最大等角向量集(ELMES)与表示论中的等角紧框架(Welch, 1974; Fickus et al., 2018)以及近期研究训练末期softmax层几何的神经坍缩工作中提出的单纯形等角紧框架(Papyan et al., 2020; Yang et al., 2022)均存在关联。我们在附录A.1中对这些结构进行了比较讨论，并将ELMES直观地视为浸入$\mathbb{R}^{\hat{d}+k}$空间的规则$d$维单纯形。

4.2 LABEL SYMMETRY

4.2 标签对称性

Symmetry in the assignment of support classes to numeric labels is an important property of metalearning algorithms. For example, if we have the support set classes {tower, bear, tree}, the mapping of ${{\mathrm{bear~}}\cdot>1$ , tower $\rightharpoonup$ , tree $\rightarrow3}$ should produce the same prediction for a query point as a different mapping ${{\mathrm{bear}}\rightarrow2$ , tower $\lnot>3$ , tree $\rightarrow1}$ . To explore this symmetry, we examine how class embeddings may be used by the model.

支持类别与数字标签分配的对称性是元学习算法的重要属性。例如，给定支持集类别 {tower, bear, tree}，映射 ${{\mathrm{bear~}}\cdot>1$、tower $\rightharpoonup$、tree $\rightarrow3}$ 应当与另一种映射 ${{\mathrm{bear}}\rightarrow2$、tower $\lnot>3$、tree $\rightarrow1}$ 对查询点产生相同的预测结果。为探究这种对称性，我们分析了模型如何利用类别嵌入。

From our formulation in Section 3, we represent a demonstration vector as a concatenation of an image embedding $\rho$ and a label embedding $\phi$ : $[\rho\mid\phi]$ . This vector is directly fed into the self-attention mechanism, where we matrix multiply with key, query, and value self-attention heads. Taking only one of these matrices for simplicity with head-dimension $k$ :

根据第3节的表述，我们将演示向量表示为图像嵌入 $\rho$ 和标签嵌入 $\phi$ 的拼接：$[\rho\mid\phi]$。该向量直接输入自注意力机制，与键、查询和值的自注意力头进行矩阵乘法运算。为简化起见，仅取其中一个头维度为 $k$ 的矩阵：

$$
[\rho\mid\phi]\left[{\frac{\Gamma_{1}\dots\Gamma_{k}}{\psi_{1}\dots\psi_{k}}}\right]=[\langle\rho,\Gamma_{1}\rangle\dots\langle\rho,\Gamma_{k}\rangle]+[\langle\phi,\psi_{1}\rangle\dots\langle\phi,\psi_{k}\rangle]
$$

$$
[\rho\mid\phi]\left[{\frac{\Gamma_{1}\dots\Gamma_{k}}{\psi_{1}\dots\psi_{k}}}\right]=[\langle\rho,\Gamma_{1}\rangle\dots\langle\rho,\Gamma_{k}\rangle]+[\langle\phi,\psi_{1}\rangle\dots\langle\phi,\psi_{k}\rangle]
$$

The output of this transformation will be the sum of two vectors: one composed of the inner products between the image embedding $\rho$ and the learnable ${\Gamma_{i}}{i=1}^{k}$ and the other composed of the class embedding ϕ and the learnable {ψi}ik=1. Note that Equation (1) implies that CAML is not invariant to the assignment of labels to support set classes due to the addition between $\langle\rho,\Gamma_{i}\rangle$ and $\langle\phi,\psi_{i}\rangle$ ; however, we can constrain the geometry of the class embeddings ${\phi}{j=1}^{d}$ to in principle respect label symmetry. Specifically for $i\neq j\neq k$ , $\langle\phi_{i},\phi_{j}\rangle=\langle\phi_{i},\phi_{k}\rangle$ and $|\boldsymbol{\phi_{i}}|=|\boldsymbol{\phi_{j}}|$ .

该转换的输出将是两个向量的和：一个由图像嵌入 $\rho$ 与可学习的 ${\Gamma_{i}}{i=1}^{k}$ 之间的内积组成，另一个由类别嵌入 $\phi$ 与可学习的 ${\psi_{i}}{i=1}^{k}$ 组成。需要注意的是，方程 (1) 表明 CAML 由于 $\langle\rho,\Gamma_{i}\rangle$ 和 $\langle\phi,\psi_{i}\rangle$ 的相加操作，对支持集类别标签的分配不具备不变性；不过，我们可以约束类别嵌入 ${\phi}{j=1}^{d}$ 的几何结构，使其原则上遵循标签对称性。具体来说，对于 $i\neq j\neq k$，满足 $\langle\phi_{i},\phi_{j}\rangle=\langle\phi_{i},\phi_{k}\rangle$ 且 $|\boldsymbol{\phi_{i}}|=|\boldsymbol{\phi_{j}}|$。

Similar to a convolutional filter learning to match a pattern within an image, our analysis assumes the learnable $\left[\psi_{1}\mathrm{\quad~\ldots~\quad~}\psi_{k}\right]$ will converge to vectors that maximize the inner product with a single $d$ -mclbaesds deinmgb. eTdod ianngss $\bar{{\phi}}{j=1}^{d}$ q alu leo s wt iso an ,l ewaer ndaebflien $\psi_{i}$ v per cot boar btioli tmy omsta ussn a fu m nbc it gi u o on ufsolry edaecteh osivnegrl teh cel assest $\psi_{i}$ of $d-$ classes so that maximizing the probability of the $j^{t h}$ class aligns with maximizing $\langle\phi_{j},\psi_{i}\rangle$ and equally minimizing $\langle\phi_{k},\psi_{i}\rangle$ for $k\neq j$ .

类似于卷积滤波器学习匹配图像中的模式，我们的分析假设可学习的 $\left[\psi_{1}\mathrm{\quad~\ldots~\quad~}\psi_{k}\right]$ 将收敛到与单个 $d$ 维嵌入向量内积最大化的向量。通过定义 $\bar{{\phi}}{j=1}^{d}$ 作为正交基，我们约束 $\psi_{i}$ 为这些基向量的线性组合，使得最大化第 $j^{th}$ 类概率与最大化 $\langle\phi_{j},\psi_{i}\rangle$ 对齐，同时等比例最小化 $k\neq j$ 时的 $\langle\phi_{k},\psi_{i}\rangle$。

Definition 2. Let $X$ be a discrete Random Variable taking on values in ${1,2,...,d}$ . For learnable vector $\psi_{i}$ , define probability mass function $p_{\psi_{i}}(X=j)$ as the softmax over $[\langle\phi_{1},\bar{\psi}{i}\rangle$ ... $\langle\phi_{d},\psi_{i}\rangle]$ so that:

定义 2. 设 $X$ 为在 ${1,2,...,d}$ 中取值的离散随机变量。对于可学习向量 $\psi_{i}$，将概率质量函数 $p_{\psi_{i}}(X=j)$ 定义为 $[\langle\phi_{1},\bar{\psi}{i}\rangle$ ... $\langle\phi_{d},\psi_{i}\rangle]$ 的 softmax，使得：

$$
p_{\psi_{i}}(X=j)=\frac{e^{\parallel\psi_{i}\parallel\parallel\phi_{j}\parallel\cos(\theta_{i,j})}}{\sum_{k=1}^{d}e^{\parallel\psi_{i}\parallel\parallel\phi_{j}\parallel\cos(\theta_{i,k})}}
$$

$$
p_{\psi_{i}}(X=j)=\frac{e^{\parallel\psi_{i}\parallel\parallel\phi_{j}\parallel\cos(\theta_{i,j})}}{\sum_{k=1}^{d}e^{\parallel\psi_{i}\parallel\parallel\phi_{j}\parallel\cos(\theta_{i,k})}}
$$

where $\theta_{i,j}$ is the angle between $\phi_{j}$ and $\psi_{i}$ .

其中 $\theta_{i,j}$ 是 $\phi_{j}$ 与 $\psi_{i}$ 之间的夹角。

We say $\psi_{i}$ learns to detect class $j$ when $p_{\psi_{i}}(X=j)>p_{\psi_{i}}(X=k)$ for $1\leq k\leq d$ with $k\neq j$ . By symmetry in the assignment of class embeddings to support classes, we can assume that the number of $\psi_{i}$ learned to detect class $i$ is similar to the number of $\psi_{j}$ learned to detect class $j$ for all pairs $(i,j)$ . We also leverage symmetry in the assignment of labels to support set classes to make the following assumptions. A justification for each assumption is located in Appendix A.1.

当 $p_{\psi_{i}}(X=j)>p_{\psi_{i}}(X=k)$ 对所有 $1\leq k\leq d$ 且 $k\neq j$ 成立时，我们称 $\psi_{i}$ 学会检测类别 $j$。由于支持类别嵌入分配的对称性，可以假设学会检测类别 $i$ 的 $\psi_{i}$ 数量与学会检测类别 $j$ 的 $\psi_{j}$ 数量对所有 $(i,j)$ 对都相近。我们还利用支持集类别标签分配的对称性作出以下假设，各假设的合理性证明见附录 A.1。

Assumption 1. Suppose ${\psi_{i}}{i=1}^{k}$ are learnable class detectors of unit norm with at least one $\psi_{i}$ detecting each class $1\leq i\leq d$ . The probability $p_{\psi_{j}}(X=j)=p_{\psi_{i}}(X=i)f o r$ $1\leq i,j\leq d$ .

假设1. 假设 ${\psi_{i}}{i=1}^{k}$ 是可学习的单位范数类检测器，其中至少有一个 $\psi_{i}$ 能检测每个类别 $1\leq i\leq d$。概率 $p_{\psi_{j}}(X=j)=p_{\psi_{i}}(X=i)f o r$ $1\leq i,j\leq d$。

Assumption 2. Define $p_{\psi_{i}}(X=i)\backslash{\phi_{l}}{l=(m+1)}^{d}$ as the probability of $\psi_{i}$ detecting $\phi_{i}$ from the set of vectors ${\phi_{j}}{j=1}^{m}$ , $m d$ . Then the probability $p_{\psi_{j}}(X=j)\backslash{\phi_{l}}{l=(m+1)}^{d}=p_{\psi_{i}}(X= $ $i)\backslash{\phi_{l}}_{l=(m+1)}^{d}$ for $1\leq i,j\leq m$ and $m\geq2$ .

假设2. 定义 $p_{\psi_{i}}(X=i)\backslash{\phi_{l}}{l=(m+1)}^{d}$ 为 $\psi_{i}$ 从向量集 ${\phi_{j}}{j=1}^{m}$ ( $m d$ )中检测到 $\phi_{i}$ 的概率。则对于 $1\leq i,j\leq m$ 且 $m\geq2$ 的情况，概率 $p_{\psi_{j}}(X=j)\backslash{\phi_{l}}{l=(m+1)}^{d}=p_{\psi_{i}}(X=i)\backslash{\phi_{l}}_{l=(m+1)}^{d}$ 。

Assumption 3. When $\begin{array}{r}{\psi_{i}=\frac{\phi_{i}}{\parallel\phi_{i}\parallel}}\end{array}$ , $p_{\psi_{i}}(X=i)$ is maximized.

假设3. 当 $\begin{array}{r}{\psi_{i}=\frac{\phi_{i}}{\parallel\phi_{i}\parallel}}\end{array}$ 时， $p_{\psi_{i}}(X=i)$ 达到最大值。

When Assumption 1, Assumption 2, and Assumption 3 hold, the set of class embeddings that maximize the probability of a learnable $\psi_{i}$ detecting class $i$ is necessarily an ELMES.

当假设1、假设2和假设3成立时，最大化可学习$\psi_{i}$检测类别$i$概率的类别嵌入集必然是一个ELMES。

Theorem 1. The set of class embeddings ${\phi_{j}}{j=1}^{d}\forall j$ , $1\leq j\leq d$ that maximizes $p_{\psi_{j}}(X=j)$ is necessarily an ELMES.

定理 1. 最大化 $p_{\psi_{j}}(X=j)$ 的类别嵌入集合 ${\phi_{j}}_{j=1}^{d}\forall j$ , $1\leq j\leq d$ 必然是一个 ELMES。

Alternatively when viewed through the lens of information theory, we can interpret an ELMES as the class embedding that minimizes the entropy of $\psi_{i}$ detecting class $i$ . Informally, ELMES causes $\psi_{i}$ to have the least uncertainty when detecting class $i$ .

从信息论的角度来看，我们可以将ELMES解释为最小化$\psi_{i}$检测类别$i$时熵的类别嵌入。通俗地说，ELMES使得$\psi_{i}$在检测类别$i$时具有最低的不确定性。

Proposition 1. Let $H_{\psi_{i}}(X)$ be the entropy of $p_{\psi_{i}}(X)$ . An ELMES minimizes $H_{\psi_{i}}(X)$ .

命题1. 设$H_{\psi_{i}}(X)$为$p_{\psi_{i}}(X)$的熵。一个ELMES最小化$H_{\psi_{i}}(X)$。

4.3 PERMUTATION INVARIANCE.

4.3 排列不变性

In addition to label symmetry, it is also desirable for the output prediction of CAML to not depend on the order of demonstrations in the sequence. For example, if we have the support set classes $$ {tower, bear, tree}, the sequence ${(\mathrm{bear}\rightarrow1)$ , (tower $->2$ ), (tree $\rightarrow3)}$ should produce the same output as the permuted sequence , (bear $\lnot>1$ ), (tower $\rightharpoonup$ ) . Building on the prior work of Kossen et al. (2021); Fifty et al. (2023), it suffices to show to show that the ELMES label encoder is e qui variant to permutations in the input sequence to show that CAML is invariant to permutations.

除了标签对称性外，CAML的输出预测还应不依赖于演示序列的顺序。例如，若支持集类别为 ${$ {tower, bear, tree}，序列 ${(\mathrm{bear}\rightarrow1)$, (tower $->2$), (tree $\rightarrow3)}$ 应与置换后的序列 (bear $\lnot>1$), (tower $\rightharpoonup$) 产生相同输出。基于Kossen等人(2021)和Fifty等人(2023)的前期工作，只需证明ELMES标签编码器对输入序列置换具有等变性，即可证明CAML对置换具有不变性。

Proposition 2. Consider an $n$ -sequence of one-hot labels stacked into a matrix $S\in\mathbb{R}^{n\times w}$ , and an ELMES label encoder denoted by $W\in\mathbb{R}^{w\times d}$ with w denoting “way” and $d$ the dimension of the label embedding. The label embedding $s W$ is e qui variant to permutations.

命题2. 考虑一个由独热标签堆叠而成的 $n$ 序列矩阵 $S\in\mathbb{R}^{n\times w}$ ，以及由 $W\in\mathbb{R}^{w\times d}$ 表示的ELMES标签编码器，其中 $w$ 表示"类别数"，$d$ 表示标签嵌入的维度。标签嵌入 $s W$ 对排列具有等变性。

5 EXPERIMENTS

5 实验

To quantify universal image classification performance, we evaluate a diverse set of 11 meta-learning benchmarks divided across 4 different categories:

为了量化通用图像分类性能，我们评估了涵盖4个不同类别的11个元学习基准数据集：

1. Generic Object Recognition: mini-ImageNet (Vinyals et al., 2016), tiered-ImageNet (Ren et al., 2018), CIFAR-fs (Bertinetto et a