ABSTRACT

摘要

In accelerated MRI reconstruction, the anatomy of a patient is recovered from a set of undersampled and noisy measurements. Deep learning approaches have been proven to be successful in solving this ill-posed inverse problem and are capable of producing very high quality reconstructions. However, current architectures heavily rely on convolutions, that are content-independent and have difficulties modeling long-range dependencies in images. Recently, Transformers, the workhorse of contemporary natural language processing, have emerged as powerful building blocks for a multitude of vision tasks. These models split input images into non-overlapping patches, embed the patches into lower-dimensional tokens and utilize a self-attention mechanism that does not suffer from the aforementioned weaknesses of convolutional architectures. However, Transformers incur extremely high compute and memory cost when 1) the input image resolution is high and 2) when the image needs to be split into a large number of patches to preserve fine detail information, both of which are typical in low-level vision problems such as MRI reconstruction, having a compounding effect. To tackle these challenges, we propose HUMUS-Net, a hybrid architecture that combines the beneficial implicit bias and efficiency of convolutions with the power of Transformer blocks in an unrolled and multi-scale network. HUMUS-Net extracts high-resolution features via convolutional blocks and refines low-resolution features via a novel Transformer-based multi-scale feature extractor. Features from both levels are then synthesized into a high-resolution output reconstruction. Our network establishes new state of the art on the largest publicly available MRI dataset, the fastMRI dataset. We further demonstrate the performance of HUMUS-Net on two other popular MRI datasets and perform fine-grained ablation studies to validate our design.

在加速MRI重建中，患者解剖结构需从欠采样且含噪声的测量数据中恢复。深度学习方法已被证实能成功解决这一病态逆问题，并可生成极高品质的重建结果。然而，当前架构严重依赖与内容无关的卷积操作，难以建模图像中的长程依赖关系。近年来，作为当代自然语言处理核心的Transformer，已成为众多视觉任务的重要构建模块。这类模型将输入图像分割为不重叠的图块，将其嵌入低维token，并利用自注意力机制克服了卷积架构的上述缺陷。但Transformer在以下场景会引发极高的计算和内存开销：1) 输入图像分辨率较高时；2) 需将图像分割为大量图块以保留精细细节时——这两种情况在MRI重建等底层视觉问题中普遍存在且会产生叠加效应。为应对这些挑战，我们提出HUMUS-Net：一种在展开式多尺度网络中融合卷积有益隐式偏置与高效性、以及Transformer模块强大能力的混合架构。HUMUS-Net通过卷积块提取高分辨率特征，并借助新型基于Transformer的多尺度特征提取器优化低分辨率特征，最终将多层级特征合成为高分辨率输出重建。我们的网络在最大公开MRI数据集fastMRI上创造了新性能标杆，并在另外两个主流MRI数据集上验证了其优越性，同时通过细粒度消融实验证实了设计有效性。

1 Introduction

1 引言

Magnetic resonance imaging (MRI) is a medical imaging technique that uses strong magnetic fields to picture the anatomy and physiological processes of the patient. MRI is one of the most popular imaging modalities as it is noninvasive and doesn’t expose the patient to harmful ionizing radiation. The MRI scanner obtains measurements of the body in the spatial frequency domain also called $k$ -space. The data acquisition process is MR is often time-consuming. Accelerated MRI [Lustig et al., 2008] addresses this challenge by under sampling in the k-space domain, thus reducing the time patients need to spend in the scanner. However, recovering the underlying anatomy from under sampled measurements is an ill-posed problem (less measurements than unknowns) and thus incorporating some form of prior knowledge is crucial in obtaining high quality reconstructions. Classical MRI reconstruction algorithms rely on the assumption that the underlying signal is sparse in some transform domain and attempt to recover a signal that best satisfies this assumption in a technique known as compressed sensing (CS) [Candes et al., 2006, Donoho, 2006]. These classical CS techniques have slow reconstruction speed and typically enforce limited forms of image priors.

磁共振成像 (MRI) 是一种利用强磁场绘制患者解剖结构和生理过程的医学成像技术。由于无创且不会使患者暴露于有害电离辐射，MRI成为最受欢迎的成像方式之一。MRI扫描仪在空间频率域（也称为$k$空间）获取人体测量数据。MR的数据采集过程通常耗时较长。加速MRI [Lustig et al., 2008] 通过在k空间域进行欠采样来应对这一挑战，从而缩短患者在扫描仪内的停留时间。然而，从欠采样测量数据中还原底层解剖结构是一个不适定问题（测量值少于未知量），因此引入某种形式的先验知识对获得高质量重建结果至关重要。传统MRI重建算法基于底层信号在某个变换域具有稀疏性的假设，并尝试通过压缩感知 (CS) 技术 [Candes et al., 2006, Donoho, 2006] 还原最符合该假设的信号。这些传统CS技术重建速度较慢，且通常只能施加有限的图像先验形式。

With the emergence of deep learning (DL), data-driven reconstruction algorithms have far surpassed CS techniques (see Ongie et al. [2020] for an overview). DL models utilize large training datasets to extract flexible, nuanced priors directly from data resulting in excellent reconstruction quality. In recent years, there has been a flurry of activity aimed at designing DL architectures tailored to the MRI reconstruction problem. The most popular models are convolutional neural networks (CNNs) that typically incorporate the physics of the MRI reconstruction problem, and utilize tools from mainstream deep learning (residual learning, data augmentation, self-supervised learning). Comparing the performance of such models has been difficult mainly due to two reasons. First, there has been a large variation in evaluation datasets spanning different scanners, anatomies, acquisition models and under sampling patterns rendering direct comparison challenging. Second, medical imaging datasets are often proprietary due to privacy concerns, hindering reproducibility.

随着深度学习 (DL) 的出现，数据驱动的重建算法已远超压缩感知技术 (CS) (综述见 Ongie 等人 [2020])。深度学习模型利用大规模训练数据集直接从数据中提取灵活、精细的先验信息，从而获得卓越的重建质量。近年来，针对 MRI 重建问题定制深度学习架构的研究呈现爆发式增长。最流行的模型是卷积神经网络 (CNN)，这类网络通常融合了 MRI 重建问题的物理特性，并采用主流深度学习工具 (残差学习、数据增强、自监督学习)。此类模型的性能比较一直存在两大难点：首先，评估数据集存在巨大差异，涉及不同扫描设备、解剖部位、采集模型和欠采样模式，导致直接对比具有挑战性；其次，出于隐私考虑，医学影像数据集通常具有专属性，这阻碍了研究可复现性。

More recently, the fastMRI dataset [Zbontar et al., 2019], the largest publicly available MRI dataset, has been gaining ground as a standard benchmark to evaluate MRI reconstruction methods. An annual competition, the fastMRI Challenge [Muckley et al., 2021], attracts significant attention from the machine learning community and acts a driver of innovation in MRI reconstruction. However, over the past years the public leader board has been dominated by a single architecture, the End-to-End VarNet [Sriram et al., 2020] 1, with most models concentrating very closely around the same performance metrics, hinting at the saturation of current architectural choices.

最近，fastMRI数据集 [Zbontar et al., 2019] 作为最大的公开MRI数据集，正逐渐成为评估MRI重建方法的标准基准。一年一度的fastMRI挑战赛 [Muckley et al., 2021] 吸引了机器学习社区的广泛关注，并推动着MRI重建领域的创新。然而过去几年公开排行榜一直被单一架构End-to-End VarNet [Sriram et al., 2020] 主导，大多数模型的性能指标高度集中，暗示当前架构选择已趋于饱和。

In this work, we propose HUMUS-Net: a Hybrid, Unrolled, MUlti-Scale network architecture for accelerated MRI reconstruction that combines the advantages of well-established architectures in the field with the power of contemporary Transformer-based models. We utilize the strong implicit bias of convolutions, but also address their weaknesses, such as content-independence and inability to model long-range dependencies, by incorporating a novel multi-scale feature extractor that operates over embedded image patches via self-attention. Moreover, we tackle the challenge of high input resolution typical in MRI by performing the computationally most expensive operations on extracted low-resolution features. HUMUS-Net establishes new state of the art in accelerated MRI reconstruction on the largest available MRI knee dataset. At the time of writing this paper, HUMUS-Net is the only Transformer-based architecture on the highly competitive fastMRI Public Leader board. Our results are fully reproducible and the source code is available online 2

在本工作中，我们提出了HUMUS-Net：一种用于加速MRI重建的混合式、展开式、多尺度网络架构，它结合了该领域成熟架构的优势与基于Transformer的现代模型的能力。我们利用了卷积强大的隐式偏置，同时也通过引入一种新颖的多尺度特征提取器（该提取器通过自注意力机制在嵌入的图像块上操作）来解决其弱点，如内容无关性和无法建模长距离依赖关系。此外，我们通过在最耗计算资源的操作中提取低分辨率特征，应对了MRI中典型的高输入分辨率挑战。HUMUS-Net在现有最大的MRI膝关节数据集上建立了加速MRI重建的最新标杆。截至撰写本文时，HUMUS-Net是竞争激烈的fastMRI公共排行榜上唯一基于Transformer的架构。我们的结果完全可复现，源代码已在线公开[2]。

2 Background

2 背景

2.1 Inverse Problem Formulation of Accelerated MRI Reconstruction

2.1 加速MRI重建的逆问题表述

An MR scanner obtains measurements of the patient anatomy in the frequency domain, also referred to as $k$ -space. Data acquisition is performed via various receiver coils positioned around the anatomy being imaged, each with different spatial sensitivity. Given a total number of $N$ receiver coils, the measurements obtained by the ith coil can be written as

磁共振 (MR) 扫描仪获取患者解剖结构的频域测量数据，也称为 $k$ 空间。数据采集通过围绕成像解剖结构布置的多个接收线圈完成，每个线圈具有不同的空间灵敏度。假设共有 $N$ 个接收线圈，第 i 个线圈获取的测量数据可表示为

$$
k_{i}=\mathcal{F}S_{i}x^{*}+z_{i},i=1,..,N,
$$

$$
k_{i}=\mathcal{F}S_{i}x^{*}+z_{i},i=1,..,N,
$$

where $\pmb{x}^{*}\in\mathbb{C}^{n}$ is the underlying patient anatomy of interest, $S_{i}$ is a diagonal matrix that represents the sensitivity map of the $i$ th coil, $\mathcal{F}$ is a multi-dimensional Fourier-transform, and $z_{i}$ denotes the measurement noise corrupting the observations obtained from coil $i$ . We use $\pmb{k}=(\pmb{k}{1},...,\pmb{k}{N})$ as a shorthand for the concatenation of individual coil measurements and ${\pmb x}=({\pmb x}{1},...,{\pmb x}_{N})$ as the corresponding image domain representation after inverse Fourier transformation.

其中 $\pmb{x}^{*}\in\mathbb{C}^{n}$ 是目标患者解剖结构的真实值，$S_{i}$ 是表示第 $i$ 个线圈灵敏度图的对角矩阵，$\mathcal{F}$ 是多维傅里叶变换，$z_{i}$ 表示第 $i$ 个线圈观测数据中的测量噪声。我们用 $\pmb{k}=(\pmb{k}{1},...,\pmb{k}{N})$ 简记各线圈测量数据的拼接结果，用 ${\pmb x}=({\pmb x}{1},...,{\pmb x}_{N})$ 表示经过逆傅里叶变换后对应的图像域表示。

Since MR data acquisition time is proportional to the portion of $\mathrm{k\Omega}$ -space being scanned, obtaining fully-sampled data is time-consuming. Therefore, in accelerated MRI scan times are reduced by under sampling in k-space domain. The under sampled $\mathbf{k}$ -space measurements from coil $i$ take the form

由于MR数据采集时间与扫描的$\mathrm{k\Omega}$空间部分成正比，获取全采样数据非常耗时。因此，在加速MRI中，通过在k空间域进行欠采样来减少扫描时间。来自线圈$i$的欠采样$\mathbf{k}$空间测量形式为

$$
\tilde{k}{i}=M k_{i}i=1,..,N,
$$

$$
\tilde{k}{i}=M k_{i}i=1,..,N,
$$

where $M$ is a diagonal matrix representing the binary under sampling mask, that has 0 values for all missing frequency components that have not been sampled during accelerated acquisition.

其中 $M$ 是一个表示二元欠采样掩码的对角矩阵，其值为0的位置对应加速采集中未采样的缺失频率分量。

The forward model that maps the underlying anatomy to coil measurements can be written concisely as $\tilde{k}=\mathcal{A}\left(x^{}\right)$ , where ${\mathcal{A}}\left(\cdot\right)$ is the linear forward mapping and $\tilde{k}$ is the stacked vector of all under sampled coil measurements. Our target is to reconstruct the ground truth object $\scriptstyle{\pmb{x}}^{*}$ from the noisy, under sampled measurements k. Since we have fewer observations than variables to recover, perfect reconstruction in general is not possible. In order to make the problem solvable, prior knowledge on the underlying object is typically incorporated in the form of sparsity in some transform domain. This formulation, known as compressed sensing [Candes et al., 2006, Donoho, 2006], provides a classical framework for accelerated MRI reconstruction [Lustig et al., 2008]. In particular, the above recovery problem can be formulated as a regularized inverse problem

将底层解剖结构映射到线圈测量的正向模型可以简洁地表示为 $\tilde{k}=\mathcal{A}\left(x^{}\right)$ ，其中 ${\mathcal{A}}\left(\cdot\right)$ 是线性正向映射， $\tilde{k}$ 是所有欠采样线圈测量值的堆叠向量。我们的目标是从噪声干扰的欠采样测量值k中重建真实对象 $\scriptstyle{\pmb{x}}^{*}$ 。由于观测值少于待恢复变量，通常无法实现完美重建。为了使问题可解，通常以某些变换域中的稀疏性形式引入关于底层对象的先验知识。这种称为压缩感知 [Candes et al., 2006, Donoho, 2006] 的公式，为加速MRI重建提供了经典框架 [Lustig et al., 2008]。具体而言，上述恢复问题可表述为带正则化的逆问题

$$
\begin{array}{r}{\pmb{\hat{x}}=\underset{\pmb{x}}{\arg\operatorname*{min}}\left|\pmb{\mathcal{A}}\left(\pmb{x}\right)-\tilde{\pmb{k}}\right|^{2}+\mathcal{R}(\pmb{x}),}\end{array}
$$

$$
\begin{array}{r}{\pmb{\hat{x}}=\underset{\pmb{x}}{\arg\operatorname*{min}}\left|\pmb{\mathcal{A}}\left(\pmb{x}\right)-\tilde{\pmb{k}}\right|^{2}+\mathcal{R}(\pmb{x}),}\end{array}
$$

where $\mathcal{R}(\cdot)$ is a regularize r that encapsulates prior knowledge on the object, such as sparsity in some wavelet domain.

其中 $\mathcal{R}(\cdot)$ 是一个正则化项 (regularizer) ，它封装了关于对象的先验知识，例如在某些小波域中的稀疏性。

2.2 Deep Learning-based Accelerated MRI Reconstruction

2.2 基于深度学习 (Deep Learning) 的加速 MRI 重建

More recently, data-driven deep learning-based algorithms tailored to the accelerated MRI reconstruction problem have surpassed the classical compressed sensing baselines. Convolutional neural networks trained on large datasets have established new state of the art in many medical imaging tasks. The highly popular U-Net [Ronne berger et al., 2015] and other similar encoder-decoder architectures have proven to be successful in a range of medical image reconstruction [Hyun et al., 2018, Han and Ye, 2018] and segmentation [Çiçek et al., 2016, Zhou et al., 2018] problems. In the encoder path, the network learns to extract a set of deep, low-dimensional features from images via a series of convolutional and down sampling operations. These concise feature representations are then gradually upsampled and filtered in the decoder to the original image dimensions. Thus the network learns a hierarchical representation over the input image distribution.

最近，针对加速MRI重建问题量身定制的数据驱动深度学习算法已超越传统压缩感知基线。在大规模数据集上训练的卷积神经网络已在众多医学影像任务中确立了新的技术标杆。广受欢迎的U-Net [Ronneberger et al., 2015] 及其他类似编码器-解码器架构，已被证实在医学图像重建 [Hyun et al., 2018, Han and Ye, 2018] 与分割 [Çiçek et al., 2016, Zhou et al., 2018] 领域具有卓越表现。在编码路径中，网络通过一系列卷积和下采样操作学习从图像中提取深层低维特征，这些精炼的特征表示随后在解码器中逐步上采样并滤波还原至原始图像尺寸，从而实现对输入图像分布的层次化表征学习。

Unrolled networks constitute another line of work that has been inspired by popular optimization algorithms used to solve compressed sensing reconstruction problems. These deep learning models consist of a series of sub-networks, also known as cascades, where each sub-network corresponds to an unrolled iteration of popular algorithms such as gradient descent [Zhang and Ghanem, 2018] or ADMM [Sun et al., 2016]. In the context of MRI reconstruction, one can view network unrolling as solving a sequence of smaller denoising problems, instead of the complete recovery problem in one step. Various convolutional neural networks have been employed in the unrolling framework achieving excellent performance in accelerated MRI reconstruction [Putzky et al., 2019, Hammernik et al., 2018, 2019]. E2E-VarNet [Sriram et al., 2020] is the current state-of-the-art convolutional model on the fastMRI dataset. E2E-VarNet transforms the optimization problem in (2.1) to the $\mathbf{k}$ -space domain and unrolls the gradient descent iterations into $T$ cascades, where the $t$ th cascade represents the computation

展开网络 (unrolled networks) 是另一类受压缩感知重建问题常用优化算法启发的工作。这些深度学习模型由一系列子网络（也称为级联）组成，每个子网络对应梯度下降 [Zhang and Ghanem, 2018] 或 ADMM [Sun et al., 2016] 等流行算法的展开迭代。在 MRI 重建场景中，可将网络展开视为分步求解一系列较小的去噪问题，而非一步完成完整重建。多种卷积神经网络已被应用于展开框架，在加速 MRI 重建中取得优异性能 [Putzky et al., 2019, Hammernik et al., 2018, 2019]。E2E-VarNet [Sriram et al., 2020] 是目前 fastMRI 数据集上最先进的卷积模型，它将式 (2.1) 的优化问题转换到 $\mathbf{k}$ 空间域，并将梯度下降迭代展开为 $T$ 个级联，其中第 $t$ 个级联表示计算

$$
\hat{k}^{t+1}=\hat{k}^{t}-\mu^{t}M(\hat{k}^{t}-\tilde{k})+\mathcal{G}(\hat{k}^{t}),
$$

$$
\hat{k}^{t+1}=\hat{k}^{t}-\mu^{t}M(\hat{k}^{t}-\tilde{k})+\mathcal{G}(\hat{k}^{t}),
$$

where $\hat{k}^{t}$ is the estimated reconstruction in the $\mathbf{k}$ -space domain at cascade $t$ , $\mu^{t}$ is a learnable step size parameter and $\mathcal{G}(\cdot)$ is a learned mapping representing the gradient of the regular iz ation term in (2.1). The first term is also known as data consistency (DC) term as it enforces the consistency of the estimate with the available measurements.

其中 $\hat{k}^{t}$ 是在级联 $t$ 时 $\mathbf{k}$ 空间域的估计重建结果，$\mu^{t}$ 是可学习步长参数，$\mathcal{G}(\cdot)$ 表示 (2.1) 中正则化项梯度的学习映射。第一项也称为数据一致性 (DC) 项，因为它强制估计结果与可用测量值保持一致。

3 Related Work

3 相关工作

Transformers in Vision – Vision Transformer (ViT) [Do sov it ski y et al., 2020], a fully non-convolutional vision architecture, has demonstrated state-of-the-art performance on image classification problems when pre-trained on large-scale image datasets. The key idea of ViT is to split the input image into non-overlapping patches, embed each patch via a learned linear mapping and process the resulting tokens via stacked self-attention and multi-layer perceptron (MLP) blocks. For more details we refer the reader to Appendix G and [Do sov it ski y et al., 2020]. The benefit of Transformers over convolutional architectures in vision lies in their ability to capture long-range dependencies in images via the self-attention mechanism.

视觉领域的Transformer——Vision Transformer (ViT) [Dosovitskiy et al., 2020] 是一种完全非卷积的视觉架构，当在大规模图像数据集上进行预训练时，已在图像分类问题上展现出最先进的性能。ViT的核心思想是将输入图像分割为不重叠的图块，通过学习的线性映射嵌入每个图块，并通过堆叠的自注意力(self-attention)和多层感知机(MLP)块处理生成的token。更多细节请参阅附录G和[Dosovitskiy et al., 2020]。Transformer在视觉领域相比卷积架构的优势在于其能够通过自注意力机制捕捉图像中的长程依赖关系。

Since the introduction of ViT, similar attention-based architectures have been proposed for many other vision tasks such as object detection [Carion et al., 2020], image segmentation [Wang et al., 2021b] and restoration [Cao et al., 2021b, Chen et al., 2021, Liang et al., 2021, Zamir et al., 2021, Wang et al., 2021c]. A key challenge for Transformers in low-level vision problems is the quadratic compute complexity of the global self-attention with respect to the input dimension. In some works, this issue has been mitigated by splitting the input image into fixed size patches and processing the patches independently [Chen et al., 2021]. Others focus on designing hierarchical Transformer architectures [Heo et al., 2021, Wang et al., 2021b] similar to popular ResNets [He et al., 2015]. Authors in Zamir et al. [2021] propose applying self-attention channel-wise rather than across the spatial dimension thus reducing the compute overhead to linear complexity. Another successful architecture, the Swin Transformer [Liu et al., 2021], tackles the quadratic scaling issue by computing self-attention on smaller local windows. To encourage cross-window interaction, windows in subsequent layers are shifted relative to each other.

自ViT问世以来，基于注意力机制的类似架构已被广泛应用于目标检测 [Carion et al., 2020]、图像分割 [Wang et al., 2021b] 和图像修复 [Cao et al., 2021b, Chen et al., 2021, Liang et al., 2021, Zamir et al., 2021, Wang et al., 2021c] 等视觉任务。Transformer在底层视觉任务中的主要挑战在于全局自注意力机制随输入维度呈二次方增长的计算复杂度。部分研究通过将输入图像分割为固定大小的区块并独立处理 [Chen et al., 2021] 来缓解这一问题，另一些则借鉴ResNet [He et al., 2015] 设计分层Transformer架构 [Heo et al., 2021, Wang et al., 2021b]。Zamir等人 [2021] 提出在通道维度而非空间维度应用自注意力，将计算开销降至线性复杂度。Swin Transformer [Liu et al., 2021] 通过局部窗口计算自注意力解决二次方复杂度问题，并通过逐层移动窗口位置促进跨窗口交互。

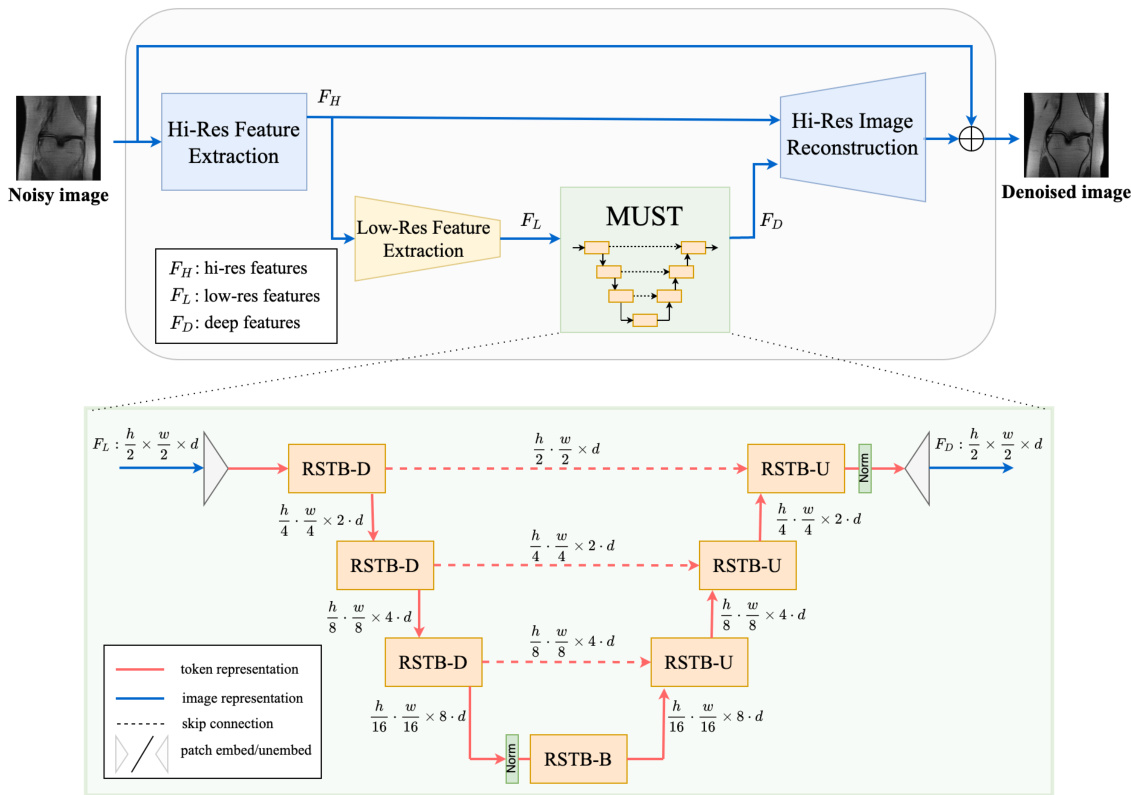
Figure 1: Overview of the HUMUS-Block architecture. First, we extract high-resolution features $F_{H}$ from the input noisy image through a convolution layer $f_{H}$ . Then, we apply a convolutional feature extractor $f_{L}$ to obtain lowresolution features and process them using a Transformer-convolutional hybrid multi-scale feature extractor. The shallow, high-resolution and deep, low-resolution features are then synthesized into the final high-resolution denoised image.

图 1: HUMUS-Block架构概览。首先，我们通过卷积层$f_{H}$从输入噪声图像中提取高分辨率特征$F_{H}$。接着，应用卷积特征提取器$f_{L}$获取低分辨率特征，并使用Transformer-卷积混合多尺度特征提取器进行处理。最终将浅层高分辨率特征与深层低分辨率特征合成为去噪后的高分辨率图像。

Transformers in Medical Imaging – Transformer architectures have been proposed recently to tackle various medical imaging problems. Authors in Cao et al. [2021a] design a U-Net-like architecture for medical image segmentation where the traditional convolutional layers are replaced by Swin Transformer blocks. They report strong results on multi-organ and cardiac image segmentation. In Zhou et al. [2021] a hybrid convolutional and Transformer-based U-Net architecture is proposed tailored to volumetric medical image segmentation with excellent results on benchmark datasets. Similar encoder-decoder architectures for various medical segmentation tasks have been investigated in other works [Huang et al., 2021, Wu et al., 2022]. However, these networks are tailored for image segmentation, a task less sensitive to fine details in the input, and thus larger patch sizes are often used (for instance 4 in Cao et al. [2021a] ). This allows the network to process larger input images, as the number of token embedding is greatly reduced, but as we demonstrate in Section 5.2 embedding individual pixels as $1\times1$ patches is crucial for MRI reconstruction. Thus, compute and memory barriers stemming from large input resolutions are more severe in the MRI reconstruction task and therefore novel approaches are needed.

医学影像中的Transformer架构——近期提出的Transformer架构正被用于解决各类医学影像问题。Cao等人[2021a]设计了一种类似U-Net的医学图像分割架构，用Swin Transformer模块替代了传统卷积层，在多器官和心脏图像分割中取得了优异效果。Zhou等人[2021]则提出了一种结合卷积与Transformer的混合U-Net架构，专门针对三维医学图像分割任务，在基准数据集上表现突出。其他研究[Huang等人，2021；Wu等人，2022]也探索了适用于不同医学分割任务的类似编码器-解码器架构。不过这些网络专为图像分割任务设计（该任务对输入细节的敏感度较低），因此常采用较大分块尺寸（如Cao等人[2021a]中使用的4×4分块）。这种方式通过大幅减少token嵌入数量，使网络能处理更大尺寸的输入图像。但如第5.2节所示，在MRI重建任务中，将单个像素嵌入为$1\times1$分块至关重要。因此，在MRI重建任务中，由高分辨率输入导致的计算与内存压力更为严峻，需要开发新的解决方案。

Promising results have been reported employing Transformers in medical image denoising problems, such as low-dose CT denoising [Wang et al., 2021a, Luthra et al., 2021] and low-count PET/MRI denoising [Zhang et al., 2021]. However, these studies fail to address the challenge of poor scaling to large input resolutions, and only work on small images via either down sampling the original dataset [Luthra et al., 2021] or by slicing the large input images into smaller patches [Wang et al., 2021a]. In contrast, our proposed architecture works directly on the large resolution images that often arise in MRI reconstruction. Even though some work exists on Transformer-based architectures for supervised accelerated MRI reconstruction [Huang et al., 2022, Lin and Heckel, 2022, Feng et al., 2021], and for unsupervised pre-trained reconstruction [Korkmaz et al., 2022], to the best of our knowledge ours is the first work to demonstrate state-of-the-art results on large-scale MRI datasets such as the fastMRI dataset.

在医学图像去噪问题中，Transformer已展现出优异效果，例如低剂量CT去噪 [Wang et al., 2021a, Luthra et al., 2021] 和低计数PET/MRI去噪 [Zhang et al., 2021]。然而这些研究未能解决大输入分辨率下的扩展性难题，仅能通过下采样原始数据集 [Luthra et al., 2021] 或将大图像切割为小块 [Wang et al., 2021a] 来处理小尺寸图像。相比之下，我们提出的架构可直接处理MRI重建中常见的高分辨率图像。尽管已有研究将Transformer架构用于监督式加速MRI重建 [Huang et al., 2022, Lin and Heckel, 2022, Feng et al., 2021] 和无监督预训练重建 [Korkmaz et al., 2022]，但据我们所知，本研究首次在fastMRI等大规模MRI数据集上实现了最先进的性能。

4 Method

4 方法

HUMUS-Net combines the efficiency and beneficial implicit bias of convolutional networks with the powerful general representations of Transformers and their capability to capture long-range pixel dependencies. The resulting hybrid network processes information both in image representation (via convolutions) and in patch-embedded token representation (via Transformer blocks). Our proposed architecture consists of a sequence of sub-networks, also called cascades. Each cascade represents an unrolled iteration of an underlying optimization algorithm in k-space (see (2.2)), with an image-domain denoiser, the HUMUS-Block. First, we describe the architecture of the HUMUS-Block, the core component in the sub-network. Then, we specify the high-level, k-space unrolling architecture of HUMUS-Net in Section 4.3.

HUMUS-Net结合了卷积网络的高效性和有益隐式偏置，以及Transformer的强大通用表征能力及其捕捉长距离像素依赖关系的特性。这种混合网络同时在图像表示（通过卷积）和分块嵌入的token表示（通过Transformer模块）中处理信息。我们提出的架构由一系列子网络（也称为级联）组成，每个级联代表k空间（见(2.2)）中基础优化算法的展开迭代，并包含一个图像域去噪器——HUMUS-Block。首先，我们描述子网络核心组件HUMUS-Block的架构；然后在第4.3节具体说明HUMUS-Net的高层次k空间展开架构。

4.1 HUMUS-Block Architecture

4.1 HUMUS-Block架构

The HUMUS-Block acts as an image-space denoiser that receives an intermediate reconstruction from the previous cascade and performs a single step of denoising to produce an improved reconstruction for the next cascade. It extracts high-resolution, shallow features and low-resolution, deep features through a novel multi-scale transformer-based block, and synthesizes high-resolution features from those. The high-level overview of the HUMUS-Block is depicted in Fig. 1.

HUMUS-Block作为图像空间降噪器，接收来自前一级联的中间重建结果，执行单步降噪以生成供下一级联使用的改进重建。它通过一种新颖的基于多尺度Transformer的模块提取高分辨率浅层特征和低分辨率深层特征，并从中合成高分辨率特征。图1展示了HUMUS-Block的总体架构。

High-resolution Feature Extraction– The input to our network is a noisy complex-valued image $\pmb{x}{i n}\in\mathbb{R}^{h\times w\times c_{i n}}$ derived from under sampled $\mathbf{k}$ -space data, where the real and imaginary parts of the image are concatenated along the channel dimension. First, we extract high-resolution features $\boldsymbol{F_{H}}\in\mathbb{R}^{h\times w\times d_{H}}$ from the input noisy image through a convolution layer $f_{H}$ written as $F_{H}=f_{H}(x_{i n})$ . This initial $3\times3$ convolution layer provides early visual processing at a relatively low cost and maps the input to a higher, $d_{H}$ dimensional feature space. Important to note that the resolution of the extracted features is the same as the spatial resolution of the input image.

高分辨率特征提取——我们的网络输入是一个含噪声的复值图像 $\pmb{x}{i n}\in\mathbb{R}^{h\times w\times c_{i n}}$，该图像源自欠采样的 $\mathbf{k}$ 空间数据，其实部和虚部沿通道维度拼接。首先，我们通过卷积层 $f_{H}$ 从输入噪声图像中提取高分辨率特征 $\boldsymbol{F_{H}}\in\mathbb{R}^{h\times w\times d_{H}}$，记为 $F_{H}=f_{H}(x_{i n})$。这个初始的 $3\times3$ 卷积层以较低成本实现早期视觉处理，并将输入映射到更高的 $d_{H}$ 维特征空间。需注意的是，提取特征的分辨率与输入图像的空间分辨率保持一致。

Low-resolution Feature Extraction– In case of MRI reconstruction, input resolution is typically significantly higher than commonly used image datasets $(32\times32-256\times256)$ , posing a significant challenge to contemporary Transformerbased models. Thus we apply a convolutional feature extractor $f_{L}$ to obtain low-resolution features $\begin{array}{r}{\dot{F}{L}=f_{L}(F_{H})}\end{array}$ , with $F_{L}\in\mathbb{R}^{h_{L}\times w_{L}\times d_{L}}$ where $f_{L}$ consists of a sequence of convolutional blocks and spatial down sampling operations. The specific architecture is depicted in Figure 4. The purpose of this module is to perform deeper visual processing and to provide manageable input size to the subsequent computation and memory heavy hybrid processing module. In this work, we choose $\begin{array}{r}{h_{L}=\frac{h}{2}}\end{array}$ and $\scriptstyle w_{L}={\frac{w}{2}}$ which strikes a balance between preserving spatial information and resource demands. Furthermore, in order to compensate for the reduced resolution we increase the feature dimension to $d_{L}=2\cdot d_{H}:=d$ .

低分辨率特征提取——在MRI重建任务中，输入分辨率通常显著高于常用图像数据集 $(32\times32-256\times256)$ ，这对当前基于Transformer的模型构成重大挑战。为此，我们采用卷积特征提取器 $f_{L}$ 来获取低分辨率特征 $\begin{array}{r}{\dot{F}{L}=f_{L}(F_{H})}\end{array}$ ，其中 $F_{L}\in\mathbb{R}^{h_{L}\times w_{L}\times d_{L}}$ 。该提取器由一系列卷积块和空间下采样操作构成，具体架构如 图 4 所示。该模块旨在进行更深层次的视觉处理，并为后续计算密集、内存占用量大的混合处理模块提供可管理的输入尺寸。本工作中，我们选择 $\begin{array}{r}{h_{L}=\frac{h}{2}}\end{array}$ 和 $\scriptstyle w_{L}={\frac{w}{2}}$ ，以在保留空间信息与资源需求之间取得平衡。此外，为补偿降低的分辨率，我们将特征维度提升至 $d_{L}=2\cdot d_{H}:=d$ 。

Deep Feature Extraction– The most important part of our model is MUST, a MUlti-scale residual Swin Transformer network. MUST is a multi-scale hybrid feature extractor that takes the low-resolution image representations $F_{L}$ and performs hierarchical Transformer-convolutional hybrid processing in an encoder-decoder fashion, producing deep features $F_{D}=f_{D}(F_{L})$ , where the specific architecture behind $f_{D}$ is detailed in Subsection 4.2.

深度特征提取——我们模型中最重要的部分是MUST，一种多尺度残差Swin Transformer网络。MUST是一个多尺度混合特征提取器，它接收低分辨率图像表示$F_{L}$，并以编码器-解码器的方式执行分层Transformer-卷积混合处理，生成深度特征$F_{D}=f_{D}(F_{L})$，其中$f_{D}$背后的具体架构详见第4.2小节。

High-resolution Image Reconstruction– Finally, we combine information from shallow, high-resolution features $F_{H}$ and deep, low-resolution features $F_{D}$ to reconstruct the high-resolution residual image via a convolutional reconstruction module $f_{R}$ . The residual learning paradigm allows us to learn the difference between noisy and clean images and helps information flow within the network [He et al., 2015]. Thus the final denoised image $\pmb{x_{o u t}}\in\mathbb{R}^{h\times w\times c_{i n}}$ is obtained as ${\pmb x}{o u t}={\pmb x}{i n}+f_{R}(F_{H},F_{D})$ . The specific architecture of the reconstruction network is depicted in Figure 4.

高分辨率图像重建——最后，我们结合来自浅层高分辨率特征 $F_{H}$ 和深层低分辨率特征 $F_{D}$ 的信息，通过卷积重建模块 $f_{R}$ 重建高分辨率残差图像。残差学习范式使我们能够学习噪声图像与干净图像之间的差异，并促进信息在网络中的流动 [He et al., 2015]。因此，最终的去噪图像 $\pmb{x_{o u t}}\in\mathbb{R}^{h\times w\times c_{i n}}$ 通过 ${\pmb x}{o u t}={\pmb x}{i n}+f_{R}(F_{H},F_{D})$ 获得。重建网络的具体架构如图 4 所示。

4.2 Multi-scale Hybrid Feature Extraction via MUST

4.2 基于MUST的多尺度混合特征提取

The key component to our architecture is MUST, a multi-scale hybrid encoder-decoder architecture that performs deep feature extraction in both image and token representation (Figure 1, bottom). First, individual pixels of the input representation of shape $\textstyle{\frac{h}{2}}\times{\frac{w}{2}}\times d$ are flattened and passed through a learned linear mapping to yield $ \frac{h}{2}\cdot\frac{w}{2}$ tokens of dimension $d$ . Tokens corresponding to different image patches are subsequently merged in the encoder path, resulting in a concise latent representation. This highly descriptive representation is passed through a bottleneck block and progressively expanded by combining tokens from the encoder path via skip connections. The final output is rearranged to match the exact shape of the input low-resolution features $F_{L}$ , yielding a deep feature representation $F_{D}$ .

我们架构的核心组件是MUST，这是一种多尺度混合编码器-解码器架构，可在图像和token表示中进行深度特征提取 (图1，底部) 。首先，形状为 $\textstyle{\frac{h}{2}}\times{\frac{w}{2}}\times d$ 的输入表示的各个像素会被展平，并通过学习的线性映射生成 $ \frac{h}{2}\cdot\frac{w}{2}$ 个维度为 $d$ 的token。随后，编码器路径中会合并对应于不同图像块的token，从而生成简洁的潜在表示。这一高度描述性的表示会通过瓶颈块，并通过跳跃连接逐步结合编码器路径中的token进行扩展。最终输出会重新排列以匹配输入低分辨率特征 $F_{L}$ 的精确形状，生成深度特征表示 $F_{D}$ 。

Our design is inspired by the success of Residual Swin Transformer Blocks (RSTB) in image denoising and superresolution [Liang et al., 2021]. RSTB features a stack of Swin Transformer layers (STL) that operate on tokens via a windowed self-attention mechanism [Liu et al., 2021], followed by convolution in image representation. However,

我们的设计灵感来源于残差Swin Transformer块 (RSTB) 在图像去噪和超分辨率任务中的成功 [Liang et al., 2021]。RSTB采用堆叠的Swin Transformer层 (STL) 结构，通过窗口自注意力机制 [Liu et al., 2021] 处理token，最后在图像表示层进行卷积操作。然而，

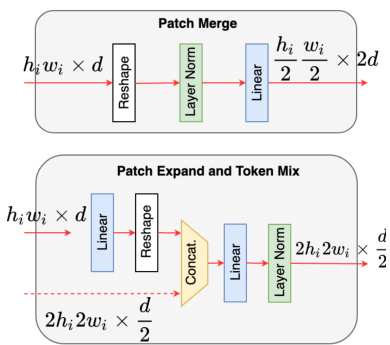
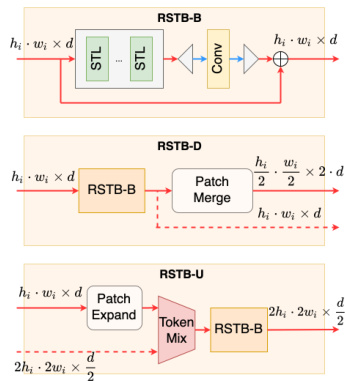
Figure 2: Depiction of differ- Figure 3: Patch merge and expand ent RSTB modules used in the operations used in our multi-scale HUMUS-Block. feature extractor.

图 2: HUMUS-Block 中使用的不同 RSTB 模块示意图
图 3: 我们多尺度特征提取器中使用的补丁合并与扩展操作

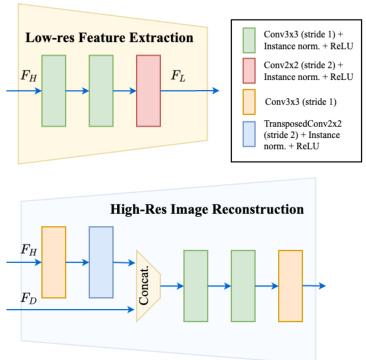
Figure 4: Architecture of convolutional blocks for feature extraction and reconstruction.

图 4: 用于特征提取和重建的卷积块架构。

RSTB blocks operate on a single scale, therefore they cannot be readily applied in a hierarchical encoder-decoder architecture. Therefore, we design three variations of RSTB to facilitate multi-scale processing as depicted in Figure 2.

RSTB模块在单一尺度上运行，因此无法直接应用于分层编码器-解码器架构。为此，我们设计了三种RSTB变体以实现多尺度处理，如图2所示。

RSTB-B is the bottleneck block responsible for processing the encoded latent representation while maintaining feature dimensions. Thus, we keep the default RSTB architecture for our bottleneck block, which already operates on a single scale.

RSTB-B是负责处理编码潜在表示同时保持特征维度的瓶颈块。因此，我们为瓶颈块保留了默认的RSTB架构，该架构已在单一尺度上运行。

RSTB-D has a similar function to convolutional down sampling blocks in U-Nets, but it operates on embedded tokens. Given an input with size $h_{i}\cdot w_{i}\times d$ , we pass it through an RSTB-B block and apply PatchMerge operation. PatchMerge linearly combines tokens corresponding to $2\times2$ non-overlapping image patches, while simultaneously increasing the embedding dimension (see Figure 3, top and Figure 10 in the appendix for more details) resulting in an output of ssiuzbes $\begin{array}{r}{\frac{h_{i}}{2}\cdot\frac{w_{i}}{2}\times2\cdot d}\end{array}$ . n Ftuhret h deer cm odore er , pRatShT vBi-a Ds koiupt cpoutnsn tehceti ohing.her dimensional representation before patch merging to be

RSTB-D的功能类似于U-Net中的卷积下采样块，但它在嵌入的token上进行操作。给定输入尺寸为$h_{i}\cdot w_{i}\times d$，我们将其通过RSTB-B块并应用PatchMerge操作。PatchMerge线性组合对应于$2\times2$非重叠图像块的token，同时增加嵌入维度（详见附录中的图3顶部和图10），输出尺寸为$\begin{array}{r}{\frac{h_{i}}{2}\cdot\frac{w_{i}}{2}\times2\cdot d}\end{array}$。此外，RSTB-D还通过跳跃连接保留了更高维度的表示，以便在块合并前进行特征提取。

RSTB-U used in the decoder path is analogous to convolutional upsampling blocks. An input with size $h_{i}\cdot w_{i}\times d$ is first expanded into a larger number of lower dimensional tokens through a linear mapping via Patch Expand (see Figure 3, bottom and Figure 10 in the appendix for more details). Patch Expand reverses the effect of PatchMerge on feature size, thus resulting in $2h_{i}\cdot2w_{i}$ tokens of dimension $\frac{d}{2}$ . Next, we mix information from the obtained expanded tokens with skip embeddings from higher scales via TokenMix. This operation linearly combines tokens from both paths and normalizes the resulting vectors. Finally, the mixed tokens are processed by an RSTB-B block.

解码路径中使用的RSTB-U类似于卷积上采样块。首先通过Patch Expand的线性映射将尺寸为$h_{i}\cdot w_{i}\times d$的输入扩展为更多低维token（详见附录图10及图3底部）。Patch Expand会逆转PatchMerge对特征尺寸的影响，从而生成$2h_{i}\cdot2w_{i}$个维度为$\frac{d}{2}$的token。接着通过TokenMix将扩展后的token与来自更高尺度的跳跃嵌入(skip embeddings)信息进行混合。该操作会线性组合两条路径的token并对结果向量进行归一化。最后，混合后的token会经过RSTB-B块处理。

4.3 Iterative Unrolling

4.3 迭代展开

Architectures derived from unrolling the iterations of various optimization algorithms have proven to be successful in tackling various inverse problems including MRI reconstruction. These architecture can be interpreted as a cascade of simpler denoisers, each of which progressively refines the estimate from the preceding unrolled iteration (see more details in Appendix F).

源自展开各种优化算法迭代过程的架构已被证明能有效解决包括MRI重建在内的多种逆问题。这类架构可视为由多个简单去噪器组成的级联系统，每个去噪器都会逐步优化前一次展开迭代的估计结果（详见附录F）。

Following Sriram et al. [2020], we unroll t