Regularizing Trajectory Optimization with Denoising Auto encoders

使用降噪自编码器正则化轨迹优化

Rinu Boney∗ Aalto University & Curious AI rinu.boney@aalto.fi

Rinu Boney∗ 阿尔托大学 & Curious AI rinu.boney@aalto.fi

Mathias Berglund Curious AI

Mathias Berglund Curious AI

Norman Di Palo∗ Sapienza University of Rome normand i palo@gmail.com

Norman Di Palo∗ 罗马大学 normand i palo@gmail.com

Alexander Ilin Aalto University & Curious AI

Alexander Ilin 阿尔托大学 & Curious AI

Juho Kannala Aalto University

Juho Kannala 阿尔托大学

Antti Rasmus Curious AI

Antti Rasmus Curious AI

Harri Valpola Curious AI

Harri Valpola Curious AI

Abstract

摘要

Trajectory optimization using a learned model of the environment is one of the core elements of model-based reinforcement learning. This procedure often suffers from exploiting inaccuracies of the learned model. We propose to regularize trajectory optimization by means of a denoising auto encoder that is trained on the same trajectories as the model of the environment. We show that the proposed regular iz ation leads to improved planning with both gradient-based and gradientfree optimizers. We also demonstrate that using regularized trajectory optimization leads to rapid initial learning in a set of popular motor control tasks, which suggests that the proposed approach can be a useful tool for improving sample efficiency.

利用学习到的环境模型进行轨迹优化是基于模型的强化学习的核心要素之一。该方法常因利用学习模型中的不准确性而受到影响。我们提出通过去噪自编码器对轨迹优化进行正则化，该编码器与环境模型在同一轨迹上训练。研究表明，所提出的正则化方法能提升基于梯度和无梯度优化器的规划效果。实验还证明，在多种常见运动控制任务中，使用正则化轨迹优化可加速初期学习进程，这表明该方法有望成为提升样本效率的有效工具。

1 Introduction

1 引言

State-of-the-art reinforcement learning (RL) often requires a large number of interactions with the environment to learn even relatively simple tasks [11]. It is generally believed that model-based RL can provide better sample-efficiency [9, 2, 5] but showing this in practice has been challenging. In this paper, we propose a way to improve planning in model-based RL and show that it can lead to improved performance and better sample efficiency.

最先进的强化学习 (RL) 通常需要与环境进行大量交互才能学习相对简单的任务 [11]。人们普遍认为基于模型的RL能提供更好的样本效率 [9, 2, 5]，但在实践中证明这一点一直具有挑战性。本文提出了一种改进基于模型RL中规划的方法，并证明其能提升性能与样本效率。

In model-based RL, planning is done by computing the expected result of a sequence of future actions using an explicit model of the environment. Model-based planning has been demonstrated to be efficient in many applications where the model (a simulator) can be built using first principles. For example, model-based control is widely used in robotics and has been used to solve challenging tasks such as human locomotion [34, 35] and dexterous in-hand manipulation [21].

在基于模型的强化学习中，规划是通过使用环境的显式模型计算未来动作序列的预期结果来完成的。基于模型的规划已被证明在许多应用中非常高效，这些应用中的模型（模拟器）可以通过基本原理构建。例如，基于模型的控制在机器人技术中广泛应用，并已用于解决具有挑战性的任务，如人体运动 [34, 35] 和灵巧的手内操作 [21]。

In many applications, however, we often do not have the luxury of an accurate simulator of the environment. Firstly, building even an approximate simulator can be very costly even for processes whose dynamics is well understood. Secondly, it can be challenging to align the state of an existing simulator with the state of the observed process in order to plan. Thirdly, the environment is often non-stationary due to, for example, hardware failures in robotics, change of the input feed and deactivation of materials in industrial process control. Thus, learning the model of the environment is the only viable option in many applications and learning needs to be done for a live system. And since many real-world systems are very complex, we are likely to need powerful function ap proxima tors, such as deep neural networks, to learn the dynamics of the environment.

然而在许多应用中，我们往往无法获得精确的环境模拟器。首先，即便对于动力学原理已充分理解的流程，构建近似模拟器的成本也可能极高。其次，将现有模拟器的状态与观测流程的状态对齐以实现规划具有相当挑战性。第三，环境通常具有非平稳性，例如机器人硬件故障、工业流程控制中进料变化和材料失效等情况。因此，学习环境模型成为多数应用中唯一可行的方案，且必须在实际运行系统中完成学习。鉴于许多现实系统极其复杂，我们往往需要深度神经网络等强大的函数逼近器来学习环境动力学。

However, planning using a learned (and therefore inaccurate) model of the environment is very difficult in practice. The process of optimizing the sequence of future actions to maximize the expected return (which we call trajectory optimization) can easily exploit the inaccuracies of the model and suggest a very unreasonable plan which produces highly over-optimistic predicted rewards. This optimization process works similarly to adversarial attacks [1, 13, 33, 7] where the input of a trained model is modified to achieve the desired output. In fact, a more efficient trajectory optimizer is more likely to fall into this trap. This can arguably be the reason why gradient-based optimization (which is very efficient at for example learning the models) has not been widely used for trajectory optimization.

然而，在实践中使用学习到的（因而也是不准确的）环境模型进行规划非常困难。优化未来动作序列以最大化预期回报的过程（我们称之为轨迹优化）很容易利用模型的不准确性，提出极不合理的计划，产生过度乐观的预测奖励。这种优化过程类似于对抗攻击 [1, 13, 33, 7]，即通过修改训练模型的输入来获得期望的输出。事实上，更高效的轨迹优化器更容易陷入这种陷阱。这可以说是基于梯度的优化（例如在学习模型时非常高效）未在轨迹优化中广泛应用的原因。

In this paper, we study this adversarial effect of model-based planning in several environments and show that it poses a problem particularly in high-dimensional control spaces. We also propose to remedy this problem by regularizing trajectory optimization using a denoising auto encoder (DAE) [37]. The DAE is trained to denoise trajectories that appeared in the past experience and in this way the DAE learns the distribution of the collected trajectories. During trajectory optimization, we use the denoising error of the DAE as a regular iz ation term that is subtracted from the maximized objective function. The intuition is that the denoising error will be large for trajectories that are far from the training distribution, signaling that the dynamics model predictions will be less reliable as it has not been trained on such data. Thus, a good trajectory has to give a high predicted return and it can be only moderately novel in the light of past experience.

本文研究了基于模型规划在多种环境中的对抗效应，发现该问题在高维控制空间中尤为突出。我们提出通过去噪自编码器 (denoising auto encoder, DAE) [37] 正则化轨迹优化的解决方案。DAE通过去噪历史经验中的轨迹来学习已收集轨迹的分布特性。在轨迹优化过程中，我们将DAE的去噪误差作为正则化项从最大化目标函数中扣除。其核心思想是：远离训练分布的轨迹会产生较大去噪误差，表明动态模型对此类未经训练数据的预测可靠性较低。因此，优质轨迹需同时满足高预测回报值和基于历史经验的适度新颖性。

In the experiments, we demonstrate that the proposed regular iz ation significantly diminishes the adversarial effect of trajectory optimization with learned models. We show that the proposed regular iz ation works well with both gradient-free and gradient-based optimizers (experiments are done with cross-entropy method [3] and Adam [14]) in both open-loop and closed-loop control. We demonstrate that improved trajectory optimization translates to excellent results in early parts of training in standard motor-control tasks and achieve competitive performance after a handful of interactions with the environment.

实验中，我们证明了所提出的正则化方法能显著降低基于学习模型的轨迹优化的对抗效应。研究表明，该正则化方法在开环和闭环控制中均能良好适配无梯度优化器（采用交叉熵法[3]实验）和基于梯度的优化器（采用Adam[14]实验）。实验显示，改进后的轨迹优化能在标准运动控制任务的训练初期取得优异效果，并在与环境进行少量交互后达到具有竞争力的性能水平。

2 Model-Based Reinforcement Learning

2 基于模型的强化学习

In this section, we explain the basic setup of model-based RL and present the notation used. At every time step $t$ , the environment is in state $s_{t}$ , the agent performs action $a_{t}$ , receives reward $r_{t}=\dot{r}(s_{t},a_{t})$ and the environment transitions to new state $\bar{s_{t+1}}=f(s_{t},a_{t})$ . The agent acts based on the observations $o_{t}=o(s_{t})$ which is a function of the environment state. In a fully observable Markov decision process (MDP), the agent observes full state $o_{t}=s_{t}$ . In a partially observable Markov decision process (POMDP), the observation $o_{t}$ does not completely reveal $s_{t}$ . The goal of the agent is select actions ${a_{0},a_{1},\ldots}$ so as to maximize the return, which is the expected cumulative reward $\mathbb{E}\left[\sum_{t=0}^{\infty}r\left(s_{t},\dot{a_{t}}\right)\right]$ .

在本节中，我们将解释基于模型的强化学习(RL)基本设置，并介绍所使用的符号。在每个时间步$t$，环境处于状态$s_{t}$，智能体执行动作$a_{t}$，获得奖励$r_{t}=\dot{r}(s_{t},a_{t})$，环境转换到新状态$\bar{s_{t+1}}=f(s_{t},a_{t})$。智能体基于观测值$o_{t}=o(s_{t})$采取行动，该观测值是环境状态的函数。在完全可观测的马尔可夫决策过程(MDP)中，智能体观测到完整状态$o_{t}=s_{t}$。在部分可观测的马尔可夫决策过程(POMDP)中，观测值$o_{t}$不能完全揭示$s_{t}$。智能体的目标是选择动作${a_{0},a_{1},\ldots}$以最大化回报，即期望累积奖励$\mathbb{E}\left[\sum_{t=0}^{\infty}r\left(s_{t},\dot{a_{t}}\right)\right]$。

In the model-based approach, the agent builds the dynamics model of the environment (forward model). For a fully observable environment, the forward model can be a fully-connected neural network trained to predict the state transition from time $t$ to $t+1$ :

在基于模型的方法中，智能体构建环境动态模型（前向模型）。对于完全可观测环境，前向模型可以是一个全连接神经网络，训练用于预测从时间$t$到$t+1$的状态转移：

$$
s_{t+1}=f_{\theta}(s_{t},a_{t}).
$$

$$
s_{t+1}=f_{\theta}(s_{t},a_{t}).
$$

In partially observable environments, the forward model can be a recurrent neural network trained to directly predict the future observations based on past observations and actions:

在部分可观测环境中，前向模型可以是一个经过训练的循环神经网络，直接基于过去的观测和动作来预测未来的观测：

$$
o_{t+1}=f_{\boldsymbol\theta}\big(o_{0},a_{0},\ldots,o_{t},a_{t}\big).
$$

$$
o_{t+1}=f_{\boldsymbol\theta}\big(o_{0},a_{0},\ldots,o_{t},a_{t}\big).
$$

In this paper, we assume access to the reward function and that it can be computed from the agent observations, that is $r_{t}=r(o_{t},a_{t})$ .

本文假设可以访问奖励函数，并且该函数可以根据智能体观察结果计算得出，即 $r_{t}=r(o_{t},a_{t})$ 。

At each time step $t$ , the agent uses the learned forward model to plan the sequence of future actions ${a_{t},\dots,a_{t+H}}$ so as to maximize the expected cumulative future reward.

在每个时间步 $t$，智能体使用学习到的前向模型来规划未来动作序列 ${a_{t},\dots,a_{t+H}}$，以最大化预期的累积未来奖励。

This process is called trajectory optimization. The agent uses the learned model of the environment to compute the objective function $G(a_{t},\dots,a_{t+H})$ . The model (1) or (2) is unrolled $H$ steps into the future using the current plan ${a_{t},\dots,a_{t+H}}$ .

这个过程称为轨迹优化。AI智能体利用学习到的环境模型计算目标函数 $G(a_{t},\dots,a_{t+H})$ 。通过当前计划 ${a_{t},\dots,a_{t+H}}$ ，将模型 (1) 或 (2) 向前展开 $H$ 步。

Algorithm 1 End-to-end model-based reinforcement learning

Collect data D by random policy.

for each episode do

Train dynamics model fo using D.

for time t until the episode is over do

Optimize trajectory {at, Ot+1,... , at+H, Ot+ H+1}.

Implement the first action at and get new observation Ot.

endfor

Add data {(s1, a1, ... , aT, or)} from the last episode to D.

算法 1: 端到端基于模型的强化学习
通过随机策略收集数据 D。
对每个回合执行以下操作：
使用 D 训练动态模型 fo。
对时间 t 直到回合结束执行以下操作：
优化轨迹 {at, Ot+1,..., at+H, Ot+H+1}。
执行第一个动作 at 并获取新观测 Ot。
将上一回合的数据 {(s1, a1,..., aT, or)} 添加到 D 中。

The optimized sequence of actions from trajectory optimization can be directly applied to the environment (open-loop control). It can also be provided as suggestions to a human operator with the possibility for the human to change the plan (human-in-the-loop). Open-loop control is challenging because the dynamics model has to be able to make accurate long-range predictions. An approach which works better in practice is to take only the first action of the optimized trajectory and then replan at each step (closed-loop control). Thus, in closed-loop control, we account for possible modeling errors and feedback from the environment. In the control literature, this flavor of model-based RL is called model-predictive control (MPC) [22, 30, 16, 24].

轨迹优化得到的最优动作序列可以直接应用于环境（开环控制），也可以作为建议提供给人类操作员，并允许人类修改计划（人在回路）。开环控制的挑战在于动力学模型必须能够进行精确的长期预测。实践中更有效的方法是仅执行优化轨迹的第一个动作，然后在每一步重新规划（闭环控制）。因此，在闭环控制中，我们会考虑潜在的建模误差和环境反馈。在控制理论文献中，这种基于模型的强化学习方法被称为模型预测控制(MPC) [22, 30, 16, 24]。

The typical sequence of steps performed in model-based RL are: 1) collect data, 2) train the forward model $f_{\theta},3)$ interact with the environment using MPC (this involves trajectory optimization in every time step), 4) store the data collected during the last interaction and continue to step 2. The algorithm is outlined in Algorithm 1.

基于模型的强化学习 (Model-based RL) 典型执行步骤如下：1) 收集数据，2) 训练前向模型 $f_{\theta},3)$ 使用模型预测控制 (MPC) 与环境交互（每个时间步都涉及轨迹优化），4) 存储最近交互期间收集的数据并返回步骤 2。该算法如算法 1 所示。

3 Regularized Trajectory Optimization

3 正则化轨迹优化

3.1 Problem with using learned models for planning

3.1 使用学习模型进行规划的问题

In this paper, we focus on the inner loop of model-based RL which is trajectory optimization using a learned forward model $f_{\theta}$ . Potential inaccuracies of the trained model cause substantial difficulties for the planning process. Rather than optimizing what really happens, planning can easily end up exploiting the weaknesses of the predictive model. Planning is effectively an adversarial attack against the agent’s own forward model. This results in a wide gap between expectations based on the model and what actually happens.

本文聚焦于基于模型的强化学习(RL)内循环——即使用学习得到的前向模型$f_{\theta}$进行轨迹优化。训练模型可能存在的不准确性会给规划过程带来重大困难。规划过程非但无法优化真实发生的情况，反而容易陷入利用预测模型弱点的困境。从本质上说，规划构成了对智能体自身前向模型的对抗性攻击。这导致基于模型的预期与实际发生的情况之间存在巨大差距。

We demonstrate this problem using a simple industrial process control benchmark from [28]. The problem is to control a continuous nonlinear reactor by manipulating three valves which control flows in two feeds and one output stream. Further details of the process and the control problem are given in Appendix A. The task considered in [28] is to change the product rate of the process from 100 to $130\mathrm{kmol/h}$ . Fig. 1a shows how this task can be performed using a set of PI controllers proposed in [28]. We trained a forward model of the process using a recurrent neural network (2) and the data collected by implementing the PI control strategy for a set of randomly generated targets. Then we optimized the trajectory for the considered task using gradient-based optimization, which produced results in Fig. 1b. One can see that the proposed control signals are changed abruptly and the trajectory imagined by the model significantly deviates from reality. For example, the pressure constraint (of max $300\mathrm{kPa},$ is violated. This example demonstrates how planning can easily exploit the weaknesses of the predictive model.

我们以[28]中一个简单的工业过程控制基准为例说明该问题。该问题需通过调节三个阀门来控制两股进料和一股输出流体的流量，从而实现对连续非线性反应器的控制。工艺流程及控制问题的详细说明见附录A。[28]中研究的具体任务是将产品产量从100提升至$130\mathrm{kmol/h}$。图1a展示了采用[28]提出的PI控制器组完成该任务的过程。我们使用循环神经网络(2)和通过实施PI控制策略对随机生成目标采集的数据，训练了该流程的前向模型。随后采用基于梯度的优化方法对目标任务的轨迹进行优化，结果如图1b所示。可见所提出的控制信号存在突变，且模型预测的轨迹与实际情况明显偏离。例如违反了最高$300\mathrm{kPa}$的压力约束。该案例揭示了规划过程如何轻易利用预测模型的缺陷。

3.2 Regularizing Trajectory Optimization with Denoising Auto encoders

3.2 使用去噪自编码器正则化轨迹优化

We propose to regularize the trajectory optimization with denoising auto encoders (DAE). The idea is that we want to reward familiar trajectories and penalize unfamiliar ones because the model is likely to make larger errors for the unfamiliar ones.

我们提出使用去噪自编码器 (DAE) 对轨迹优化进行正则化。其核心思想是通过奖励熟悉轨迹并惩罚陌生轨迹来提升模型性能，因为模型对陌生轨迹可能产生更大误差。

This can be achieved by adding a regular iz ation term to the objective function:

这可以通过在目标函数中添加一个正则化(regularization)项来实现：

$$
G_{\mathrm{reg}}=G+\alpha\log p\bigl(o_{t},a_{t}\ldots,o_{t+H},a_{t+H}\bigr),
$$

$$
G_{\mathrm{reg}}=G+\alpha\log p\bigl(o_{t},a_{t}\ldots,o_{t+H},a_{t+H}\bigr),
$$

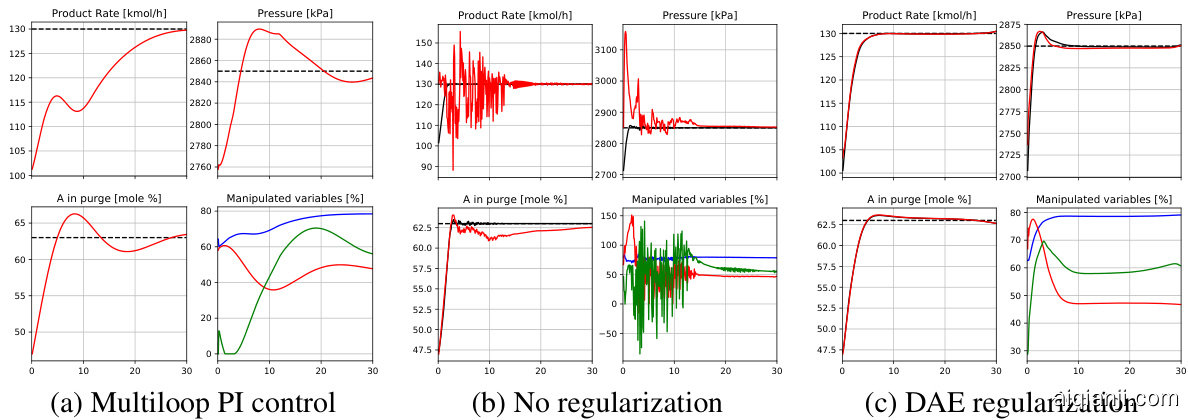
Figure 1: Open-loop planning for a continuous nonlinear two-phase reactor from [28]. Three subplots in every subfigure show three measured variables (solid lines): product rate, pressure and A in the purge. The black curves represent the model’s imagination while the red curves represent the reality if those controls are applied in an open-loop mode. The targets for the variables are shown with dashed lines. The fourth (low right) subplots show the three manipulated variables: valve for feed 1 (blue), valve for feed 2 (red) and valve for stream 3 (green).

图 1: 文献[28]中连续非线性两相反应器的开环规划。每个子图中的三个子图显示三个测量变量(实线): 产物速率、压力和吹扫中的A组分。黑色曲线代表模型预测值，红色曲线表示开环模式下实际应用控制后的真实值。各变量的目标值以虚线显示。右下角第四个子图展示三个操纵变量: 进料1阀门(蓝色)、进料2阀门(红色)和物流3阀门(绿色)。

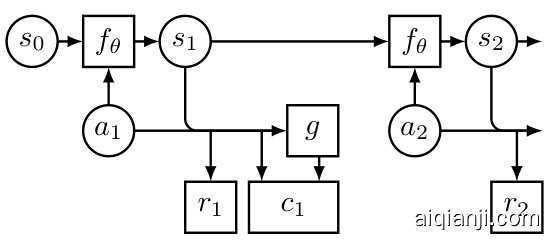
Figure 2: Example: fragment of a computational graph used during trajectory optimization in an MDP. Here, window size $w=1$ , that is the DAE penalty term is $c_{1}\doteq\lVert g([s_{1},\dot{a}_ {1}])^{-}-[s_{1},a_{1}]\rVert^{2}$ .

图 2: 示例：MDP轨迹优化过程中使用的计算图片段。此处窗口大小$w=1$，即DAE惩罚项为$c_{1}\doteq\lVert g([s_{1},\dot{a}_ {1}])^{-}-[s_{1},a_{1}]\rVert^{2}$。

where $p\big(o_{t},a_{t},,\dots,o_{t+H},a_{t+H}\big)$ is the probability of observing a given trajectory in the past experience and $\alpha$ is a tuning hyper parameter. In practice, instead of using the joint probability of the whole trajectory, we use marginal probabilities over short windows of size $w$ :

其中 $p\big(o_{t},a_{t},,\dots,o_{t+H},a_{t+H}\big)$ 表示在过往经验中观察到给定轨迹的概率，$\alpha$ 为调节超参数。实际应用中，我们使用大小为 $w$ 的短窗口边缘概率替代整段轨迹的联合概率:

$$
G_{\mathrm{reg}}=G+\alpha\sum_{\tau=t}^{t+H-w}\log p(x_{\tau})
$$

$$
G_{\mathrm{reg}}=G+\alpha\sum_{\tau=t}^{t+H-w}\log p(x_{\tau})
$$

where $x_{\tau}={o_{\tau},a_{\tau},\dots o_{\tau+w},a_{\tau+w}}$ is a short window of the optimized trajectory.

其中 $x_{\tau}={o_{\tau},a_{\tau},\dots o_{\tau+w},a_{\tau+w}}$ 是优化轨迹的一个短窗口。

Suppose we want to find the optimal sequence of actions by maximizing (4) with a gradient-based optimization procedure. We can compute gradients ∂∂Garieg by back propagation in a computational graph where the trained forward model is unrolled into the future (see Fig. 2). In such back propagationthrough-time procedure, one needs to compute the gradient with respect to actions $a_{i}$ .

假设我们想通过基于梯度的优化程序最大化(4)来寻找最优动作序列。我们可以在计算图中通过反向传播计算梯度∂∂Garieg，其中训练好的前向模型被展开到未来(见图2)。在这种时间反向传播过程中，需要计算关于动作$a_{i}$的梯度。

$$
\frac{\partial G_{\mathrm{reg}}}{\partial a_{i}}=\frac{\partial G}{\partial a_{i}}+\alpha\sum_{\tau=i}^{i+w}\frac{\partial x_{\tau}}{\partial a_{i}}\frac{\partial}{\partial x_{\tau}}\log p(x_{\tau}),
$$

$$
\frac{\partial G_{\mathrm{reg}}}{\partial a_{i}}=\frac{\partial G}{\partial a_{i}}+\alpha\sum_{\tau=i}^{i+w}\frac{\partial x_{\tau}}{\partial a_{i}}\frac{\partial}{\partial x_{\tau}}\log p(x_{\tau}),
$$

where we denote by $x_{\tau}$ a concatenated vector of observations $o_{\tau},\dots o_{\tau+w}$ and actions $a_{\tau},\dots{}a_{\tau+w}$ over a window of size $w$ . Thus to enable a regularized gradient-based optimization procedure, we need means to compute ∂∂x l og p(xτ ).

我们用 $x_{\tau}$ 表示观测值 $o_{\tau},\dots o_{\tau+w}$ 和动作 $a_{\tau},\dots{}a_{\tau+w}$ 在大小为 $w$ 的窗口上的拼接向量。因此，为了实现基于梯度的正则化优化过程，我们需要计算 $\frac{\partial}{\partial x} \log p(x_{\tau})$ 的方法。

In order to evaluate $\log p(x_{\tau})$ (or its derivative), one needs to train a separate model $p(x_{\tau})$ of the past experience, which is the task of unsupervised learning. In principle, any probabilistic model can be used for that. In this paper, we propose to regularize trajectory optimization with a denoising auto encoder (DAE) which does not build an explicit probabilistic model $p(x_{\tau})$ but rather learns to approximate the derivative of the log probability density. The theory of denoising [23, 27] states that the optimal denoising function $g(\tilde{x})$ (for zero-mean Gaussian corruption) is given by:

为了评估 $\log p(x_{\tau})$ (或其导数)，需要针对过往经验训练一个独立的模型 $p(x_{\tau})$ ，这属于无监督学习的任务。理论上，任何概率模型都可用于此目的。本文提出通过去噪自编码器 (DAE) 对轨迹优化进行正则化，该方法无需构建显式概率模型 $p(x_{\tau})$ ，而是学习逼近对数概率密度的导数。去噪理论 [23, 27] 指出，最优去噪函数 $g(\tilde{x})$ (针对零均值高斯噪声) 满足以下关系：

$$
g(\tilde{x})=\tilde{x}+\sigma_{n}^{2}\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x}),
$$

$$
g(\tilde{x})=\tilde{x}+\sigma_{n}^{2}\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x}),
$$

where $p(\tilde{x})$ is the probability density function for data $\tilde{x}$ corrupted with noise and $\sigma_{n}$ is the standard deviation of the Gaussian corruption. Thus, the DAE-denoised signal minus the original gives the gradient of the log-probability of the data distribution convolved with a Gaussian distribution: \begin{array}{r}{\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x})\propto g(x)-\tilde{x}}\end{array} . Assuming $\begin{array}{r}{\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x})\approx\frac{\partial}{\partial x}\log p(x)}\end{array}$ yields

其中 $p(\tilde{x})$ 是加噪数据 $\tilde{x}$ 的概率密度函数，$\sigma_{n}$ 为高斯噪声的标准差。因此，去噪自编码器(DAE)处理后的信号减去原始信号，可得到与高斯分布卷积后的数据分布对数概率梯度：$\begin{array}{r}{\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x})\propto g(x)-\tilde{x}}\end{array}$。假设 $\begin{array}{r}{\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x})\approx\frac{\partial}{\partial x}\log p(x)}\end{array}$ 成立时

$$
\frac{\partial G_{\mathrm{reg}}}{\partial a_{i}}=\frac{\partial G}{\partial a_{i}}+\alpha\sum_{\tau=i}^{i+w}\frac{\partial x_{\tau}}{\partial a_{i}}(g(x_{\tau})-x_{\tau}).
$$

$$
\frac{\partial G_{\mathrm{reg}}}{\partial a_{i}}=\frac{\partial G}{\partial a_{i}}+\alpha\sum_{\tau=i}^{i+w}\frac{\partial x_{\tau}}{\partial a_{i}}(g(x_{\tau})-x_{\tau}).
$$

Using $\begin{array}{r}{\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x})}\end{array}$ instead of $\textstyle{\frac{\partial}{\partial x}}\log p(x)$ can behave better in practice because it is similar to replacing $p(x)$ with its Parzen window estimate [36]. In automatic differentiation software, this gradient can be computed by adding the penalty term $|g(x_{\tau})-x_{\tau}|^{2}$ to $G$ and stopping the gradient propagation through $g$ . In practice, stopping the gradient through $g$ did not yield any benefits in our experiments compared to simply adding the penalty term $|g(\bar{x}_ {\tau})-x_{\tau}|^{2}$ to the cumulative reward, so we used the simple penalty term in our experiments. Also, this kind of regular iz ation can easily be used with gradient-free optimization methods such as cross-entropy method (CEM) [3].

使用 $\begin{array}{r}{\frac{\partial}{\partial\tilde{x}}\log p(\tilde{x})}\end{array}$ 而非 $\textstyle{\frac{\partial}{\partial x}}\log p(x)$ 在实践中表现更优，因为这类似于用 Parzen 窗估计 [36] 替代 $p(x)$。在自动微分软件中，可通过将惩罚项 $|g(x_{\tau})-x_{\tau}|^{2}$ 添加到 $G$ 并阻断梯度通过 $g$ 的传播来计算该梯度。实验中，与简单地将惩罚项 $|g(\bar{x}_ {\tau})-x_{\tau}|^{2}$ 加入累积奖励相比，阻断 $g$ 的梯度并未带来收益，因此我们采用简单惩罚项方案。此外，此类正则化方法可轻松与无梯度优化方法（如交叉熵法 (CEM) [3]）结合使用。

Our goal is to tackle high-dimensional problems and expressive models of dynamics. Neural networks tend to fare better than many other techniques in modeling high-dimensional distributions. However, using a neural network or any other flexible parameterized model to estimate the input distribution poses a dilemma: the regularizing network which is supposed to keep planning from exploiting the inaccuracies of the dynamics model will itself have weaknesses which planning will then exploit. Clearly, DAE will also have inaccuracies but planning will not exploit them because unlike most other density models, DAE develops an explicit model of the gradient of logarithmic probability density.

我们的目标是解决高维问题和动态系统的表达性建模。在建模高维分布时，神经网络通常比其他技术表现更优。然而，使用神经网络或其他灵活的参数化模型来估计输入分布会带来一个两难问题：本应防止规划过程利用动态模型不准确性的正则化网络，其自身存在的缺陷反而会被规划过程利用。显然，去噪自编码器 (DAE) 也存在不准确性，但规划过程不会利用这些缺陷，因为与大多数其他密度模型不同，DAE 会显式建模对数概率密度的梯度。

The effect of adding DAE regular iz ation in the industrial process control benchmark discussed in the previous section is shown in Fig. 1c.

在前文讨论的工业过程控制基准测试中，添加DAE正则化的效果如图1c所示。

3.3 Related work

3.3 相关工作

Several methods have been proposed for planning with learned dynamics models. Locally linear timevarying models [17, 19] and Gaussian processes [8, 15] or mixture of Gaussians [29] are data-efficient but have problems scaling to high-dimensional environments. Recently, deep neural networks have been successfully applied to model-based RL. Nagabandi et al. [24] use deep neural networks as dynamics models in model-predictive control to achieve good performance, and then shows how model-based RL can be fine-tuned with a model-free approach to achieve even better performance. Chua et al. [5] introduce PETS, a method to improve model-based performance by estimating and propagating uncertainty with an ensemble of networks and sampling techniques. They demonstrate how their approach can beat several recent model-based and model-free techniques. Clavera et al. [6] combines model-based RL and meta-learning with MB-MPO, training a policy to quickly adapt to slightly different learned dynamics models, thus enabling faster learning.

针对学习动力学模型的规划问题，已提出多种方法。局部线性时变模型[17, 19]、高斯过程[8, 15]或高斯混合模型[29]具有数据高效性，但难以扩展到高维环境。近年来，深度神经网络在基于模型的强化学习中取得显著成果。Nagabandi等人[24]将深度神经网络作为动力学模型应用于模型预测控制，取得优异性能后，进一步展示了如何通过无模型方法对基于模型的强化学习进行微调以获得更优表现。Chua等人[5]提出的PETS方法，通过集成网络和采样技术来估计和传递不确定性，从而提升基于模型的性能。他们的方法被证明能超越多种近期基于模型和无模型的技术。Clavera等人[6]将基于模型的强化学习与元学习结合，通过MB-MPO训练策略使其快速适应略有差异的学习动力学模型，从而实现更高效的学习。

Levine and Koltun [20] and Kumar et al. [17] use a KL divergence penalty between action distributions to stay close to the training distribution. Similar bounds are also used to stabilize training of policy gradient methods [31, 32]. While such a KL penalty bounds the evolution of action distributions, the proposed method also bounds the familiarity of states, which could be important in high-dimensional state spaces. While penalizing unfamiliar states also penalize exploration, it allows for more controlled and efficient exploration. Exploration is out of the scope of the paper but was studied in [10], where a non-zero optimum of the proposed DAE penalty was used as an intrinsic reward to alternate between familiarity and exploration.

Levine和Koltun [20]以及Kumar等人[17]通过动作分布之间的KL散度惩罚来保持接近训练分布。类似的边界也被用于稳定策略梯度方法的训练[31, 32]。虽然这种KL惩罚限制了动作分布的演变，但所提出的方法还限制了状态的熟悉程度，这在高维状态空间中可能很重要。虽然惩罚不熟悉的状态也会抑制探索，但它允许更可控和高效的探索。探索不在本文讨论范围内，但在[10]中进行了研究，其中将所提出的DAE惩罚的非零最优值用作内在奖励，以在熟悉度和探索之间交替。

4 Experiments on Motor Control

4 电机控制实验

We show the effect of the proposed regular iz ation for control in standard Mujoco environments: Cartpole, Reacher, Pusher, Half-cheetah and Ant available in [4]. See the description of the environments in Appendix B. We use the Probabilistic Ensembles with Trajectory Sampling (PETS) model from [5] as the baseline, which achieves the best reported results on all the considered tasks except for Ant.

我们展示了所提出的正则化方法在标准Mujoco环境中的控制效果：包括[4]中提供的Cartpole、Reacher、Pusher、Half-cheetah和Ant。环境描述详见附录B。我们采用[5]提出的PETS (Probabilistic Ensembles with Trajectory Sampling) 模型作为基线，该模型在所有考虑的任务（除Ant外）上都取得了目前最佳的报告结果。

Figure 3: Visualization of trajectory optimization at timestep $t=50$ . Each row has the same model but 2a0 different optimization method. The models ar1e00 0 o 00 bt a in ed by 5 episodes of end-to-end training. Row above: Cartpole environment. Row below: Half-cheetah environment. Here, the red lines denote the rewards predicted by the model (imagination) and the black lines denote the true rewards obtained when applying the sequence of optimized actions (reality). For a low-dimensional action space (Cartpole), trajectory optimizers do not exploit inaccuracies of the dynamics model and hence DAE regular iz ation does not affect the performance noticeably. For a higher-dimensional action space (Half-cheetah), gradient-based optimization without any regular iz ation easily exploits inaccuracies of the dynamics model but DAE regular iz ation is able to prevent this. The effect is less pronounced with gradient-free optimization but still noticeable.

图 3: 时间步 $t=50$ 的轨迹优化可视化。每行使用相同模型但采用不同优化方法 (2a0)。这些模型通过5轮端到端训练获得。上行: Cartpole环境。下行: Half-cheetah环境。其中红线表示模型预测的奖励 (想象)，黑线表示应用优化动作序列后获得的真实奖励 (现实)。对于低维动作空间 (Cartpole)，轨迹优化器不会利用动态模型的不准确性，因此DAE正则化对性能影响不明显。而在高维动作空间 (Half-cheetah) 中，无正则化的基于梯度优化容易利用动态模型的不准确性，但DAE正则化能有效防止这种情况。无梯度优化的效果虽较不显著但仍可观察到。

The PETS model consists of an ensemble of probabilistic neural networks and uses particle-based trajectory sampling to regularize trajectory optimization. We re-implemented the PETS model using the code provided by the authors as a reference.

PETS模型由一组概率神经网络组成，并采用基于粒子的轨迹采样方法来规范化轨迹优化。我们参考作者提供的代码重新实现了PETS模型。

4.1 Regularized trajectory optimization with models trained with PETS

4.1 基于PETS训练模型的正则化轨迹优化

In MPC, the innermost loop is open-loop control which is then turned to closed-loop control by taking in new observations and replanning after each action. Fig. 3 illustrates the adversarial effect during open-loop trajectory optimization and how DAE regular iz ation mitigates it. In Cartpole environment, the learned model is very good already after a few episodes of data and trajectory optimization stays within the data distribution. As there is no problem to begin with, regular iz ation does not improve the results. In Half-cheetah environment, trajectory optimization manages to exploit the inaccuracies of the model which is particularly apparent in gradient-based Adam. DAE regular iz ation improves both but the effect is much stronger with Adam.

在MPC中，最内层循环是开环控制，随后通过接收新观测值并在每次动作后重新规划转为闭环控制。图3展示了开环轨迹优化过程中的对抗效应，以及DAE正则化如何缓解该效应。在Cartpole环境中，仅需少量数据周期后学习到的模型已表现优异，轨迹优化始终保持在数据分布范围内。由于不存在初始问题，正则化并未带来结果提升。在Half-cheetah环境中，轨迹优化会利用模型的不准确性，这种现象在基于梯度的Adam优化器中尤为明显。DAE正则化对两者均有改善，但对Adam的效果更为显著。

The problem is exacerbated in closed-loop control since it continues optimization from the solution achieved in the previous time step, effectively iterating more per action. We demonstrate how regular iz ation can improve closed-loop trajectory optimization in the Half-cheetah environment. We first train three PETS models for 300 episodes using the best hyper parameters reported in [5]. We then evaluate the performance of the three models on five episodes using four different trajectory optimizers: 1) Cross-entropy method (CEM) which was used during training of the PETS models, 2) Adam, 3) CEM with the DAE regular iz ation and 4) Adam with the DAE regular iz ation. The results averaged across the three models and the five episodes are presented in Table 1.

闭环控制中的问题更为严重，因为它会基于前一步的解决方案持续优化，实际上对每个动作进行了更多迭代。我们展示了正则化(regularization)如何在Half-cheetah环境中改进闭环轨迹优化。首先使用[5]中报告的最佳超参数训练三个PETS模型300个周期，随后用四种轨迹优化器评估这三个模型在五个周期上的表现：1) PETS模型训练时使用的交叉熵方法(CEM)，2) Adam优化器，3) 带DAE正则化的CEM，4) 带DAE正则化的Adam。三个模型在五个周期上的平均结果如 表1 所示。

Table 1: Comparison of PETS with CEM and Adam optimizers in Half-cheetah

Optimizer	CEM	CEM+DAE	Adam	Adam+DAE
Average Return	10955±2865	12967±3216		12796±2716

表 1: Half-cheetah 环境中 PETS 与 CEM 和 Adam 优化器的对比

优化器	CEM	CEM+DAE	Adam	Adam+DAE
平均回报	10955±2865	12967±3216		12796±2716

We first note that planning with Adam fails completely without regular iz ation: the proposed actions lead to unstable states of the simulator. Using Adam with the DAE regular iz ation fixes this problem and the obtained results are better than the CEM method originally used in PETS. CEM appears to regularize trajectory optimization but not as efficiently CEM+DAE. These open-loop results are consistent with the closed-loop results in Fig. 3.

我们首先注意到，在没有正则化的情况下，使用Adam进行规划会完全失败：所提出的动作会导致模拟器进入不稳定状态。使用带有DAE正则化的Adam解决了这一问题，并且获得的结果优于PETS中最初使用的CEM方法。CEM似乎对轨迹优化进行了正则化，但效果不如CEM+DAE。这些开环结果与图3中的闭环结果一致。

4.2 End-to-end training with regularized trajectory optimization

4.2 基于正则化轨迹优化的端到端训练

In the following experiments, we study the performance of end-to-end training with different trajectory optimizers used during training. Our agent learns according to the algorithm presented in Algorithm 1. Since the environments are fully observable, we use a feed forward neural network as in (1) to model the dynamics of the environment. Unlike PETS, we did not use an ensemble of probabilistic networks as the forward model. We use a single probabilistic network which predicts the mean and variance of the next state (assuming a Gaussian distribution) given the current state and action. Although we only use the mean prediction, we found that also training to predict the variance improves the stability of the training.

在以下实验中，我们研究了使用不同轨迹优化器进行端到端训练的性能表现。我们的AI智能体(agent)按照算法1所示流程进行学习。由于环境具备完全可观测性，我们采用如(1)式所示的前馈神经网络来建模环境动态。与PETS不同，我们并未使用概率网络集合作为前向模型，而是采用单一概率网络来预测给定当前状态和动作时下一状态的均值与方差(假设服从高斯分布)。虽然实际仅使用均值预测，但我们发现同时训练方差预测能提升训练稳定性。

For all environments, we use a dynamics model with the same architecture: three hidden layers of size 200 with the Swish non-linearity [26]. Similar to prior works, we train the dynamics model to predict the difference between $s_{t+1}$ and $s_{t}$ instead of predicting $s_{t+1}$ directly. We train the dynamics model for 100 or more epochs (see Appendix C) after every episode. This is a larger number of updates compared to five epochs used in [5]. We found that an increased number of updates has a large effect on the performance for a single probabilistic model and not so large effect for the ensemble of models used in PETS. This effect is shown in Fig. 6.

对于所有环境，我们采用相同架构的动力学模型：三个大小为200的隐藏层，使用Swish非线性激活函数[26]。与先前研究类似，我们训练动力学模型预测$s_{t+1}$与$s_{t}$之间的差值，而非直接预测$s_{t+1}$。每轮训练后，动力学模型会进行100次或更多次迭代训练(详见附录C)，这比文献[5]中采用的5次迭代显著增加。我们发现增加迭代次数对单一概率模型的性能影响较大，而对PETS中使用的模型集成影响相对较小。该效果展示在图6中。

For the denoising auto encoder, we use the same architecture as the dynamics model. The state-action pairs in the past episodes were corrupted with zero-mean Gaussian noise and the DAE was trained to denoise it. Important hyper parameters used in our experiments are reported in the Appendix C. For DAE-regularized trajectory optimization we used either CEM or Adam as optimizers.

对于去噪自动编码器(denoising auto encoder)，我们采用了与动力学模型相同的架构。过去情节中的状态-动作对会被添加零均值高斯噪声进行干扰，然后训练DAE对其进行去噪处理。实验中采用的重要超参数详见附录C。在DAE正则化轨迹优化过程中，我们使用了CEM或Adam作为优化器。

The learning progress of the compared algorithms is presented in Fig. 4. Note that we report the average returns across different seeds, not the maximum return seen so far as was done in [5].2 In Cartpole, all the methods converge to the maximum cumulative reward but the proposed method converges the fastest. In the Cartpole environment, we also compare to a method which uses Gaussian Processes (GP) as the dynamics model (algorithm denoted GP-E in [5], which considers only the expectation of the next state prediction). The implementation of the GP algorithm was obtained from the code provided by [5]. Interestingly, our algorithm also surpasses the Gaussian Process (GP) baseline, which is known to be a sample-efficient method widely used for control of simple systems. In Reacher, the proposed method converges to the same asymptotic performance as PETS, but faster. In Pusher, all algorithms perform similarly.

图 4 展示了各对比算法的学习进度。需要注意的是，我们报告的是不同随机种子的平均回报值，而非[5]中采用的当前最大回报值。在Cartpole环境中，所有方法最终都收敛至最大累积奖励，但本文提出的方法收敛速度最快。该环境中我们还对比了采用高斯过程(GP)作为动力学模型的方法([5]中的GP-E算法，仅考虑下一状态预测的期望值)。GP算法的实现代码来自[5]提供的源码。值得注意的是，我们的算法表现甚至超越了高斯过程(GP)基线——后者作为样本高效的方法，被广泛用于简单系统的控制。在Reacher环境中，本文方法以更快速度达到了与PETS相同的渐近性能。Pusher环境中各算法表现相近。

In Half-cheetah and Ant, the proposed method shows very good sample efficiency and very rapid initial learning. The agent learns an effective running gait in only a couple of episodes.3 The results demonstrate that denoising regular iz ation is effective for both gradient-free and gradient-based planning, with gradient-based planning performing the best. The proposed algorithm learns faster than PETS in the initial phase of training. It also achieves performance that is competitive with popular model-free algorithms such as DDPG, as reported in [5].

在半人马和蚂蚁环境中，所提