Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control 通过整体脉冲控制和模型预测控制实现的高动态四足运动

author

Donghyun Kim1, Jared Di Carlo2, Benjamin Katz1, Gerardo Bledt1, and Sangbae Kim1Authors are with the
1 Department of Mechanical Engineering at the Massachusetts Institute of Technology
2 Department of Electrical Engineering and Computer Science at the Massachusetts Institute of Technology, Cambridge, MA, 02139, USA.

ABSTRACT 摘要

Dynamic legged locomotion is a challenging topic because of the lack of established control schemes which can handle aerial phases, short stance times, and high-speed leg swings. In this paper, we propose a controller combining whole-body control (WBC) and model predictive control (MPC). In our framework, MPC finds an optimal reaction force profile over a longer time horizon with a simple model, and WBC computes joint torque, position, and velocity commands based on the reaction forces computed from MPC. Unlike existing WBCs, which attempt to track commanded body trajectories, our controller is focused more on the reaction force command, which allows it to accomplish high speed dynamic locomotion with aerial phases. The newly devised WBC is integrated with MPC and tested on the Mini-Cheetah quadruped robot. To demonstrate the robustness and versatility, the controller is tested on six different gaits in a number of different environments, including outdoors and on a treadmill, reaching a top speed of 3.7 m/s.

由于没有成熟的控制方案可以处理空中相位，短站姿时间和高速腿部摆动，因此动态腿部移动是一个具有挑战性的主题。在本文中，我们提出了一种结合了全身控制（WBC）和模型预测控制（MPC）的控制器。在我们的框架中，MPC使用简单的模型找到了较长时间范围内的最佳反作用力曲线，而WBC根据从MPC计算出的反作用力来计算关节扭矩，位置和速度指令。与现有的WBC试图跟踪命令的身体轨迹不同，我们的控制器更专注于反作用力命令，这使它可以完成具有空中相位的高速动态运动。新设计的WBC与MPC集成在一起，并在Mini-Cheetah四足机器人上进行了测试。3.7 米/s。

IINTRODUCTION 介绍

To fully exploit the hardware capability of legged systems, we need a controller that can address the challenging issues related to dynamic locomotion, such as body control during short stance periods, aerial phases, and high speed swing leg motion control. Several successful cases for both running bipeds [1, 2] and quadrupeds [3] have been presented, but they are either difficult to scale up to high degree-of-freedom systems [1] or heavily rely on specific system dynamics [2] or are undocumented [3]. Whole-body control (WBC) is a strong candidate as a dynamic motion controller because of its dynamically consistent formulation and general framework, which makes it easy to extend to various systems and tasks. However, existing WBCs focus on how to follow the given trajectory by manipulating contact forces, which makes it nontrivial to address motion involving frequent non-contact phases such as high speed running.

为了充分利用腿式系统的硬件功能，我们需要一种控制器，该控制器可以解决与动态运动相关的挑战性问题，例如，在短时站立期间的身体控制，空中阶段以及高速摆腿运动控制。两种运行的两足动物的几个成功的案例[ 1，2 ]和四足动物 [ 3 ]已经提出，但它们扩展到程度的自由度较高的系统或者困难 [ 1 ]或严重依赖于特定的系统动力学 [ 2 ]或无证件 [ 3 ]。全身控制（WBC）是动态运动控制器的强大候选者，因为它的动态一致配方和通用框架使其易于扩展到各种系统和任务。但是，现有的WBC专注于如何通过控制接触力来遵循给定的轨迹，这使得解决涉及频繁非接触阶段（例如高速行驶）的运动变得不平凡。

Fig. 1: Control Architecture. The proposed control architecture consists of two parts: Model predictive control and whole-body control. The reaction forces computed by MPC are modified by WBC to incorporate body stabilization and swing leg control. The final commands found in WBC are sent to the robot to perform dynamic locomotion.

图1：控制架构。所提出的控制体系结构包括两部分：模型预测控制和全身控制。WPC对MPC计算出的反作用力进行了修改，以纳入车身稳定和摆腿控制。在WBC中找到的最终命令被发送到机器人以执行动态运动。

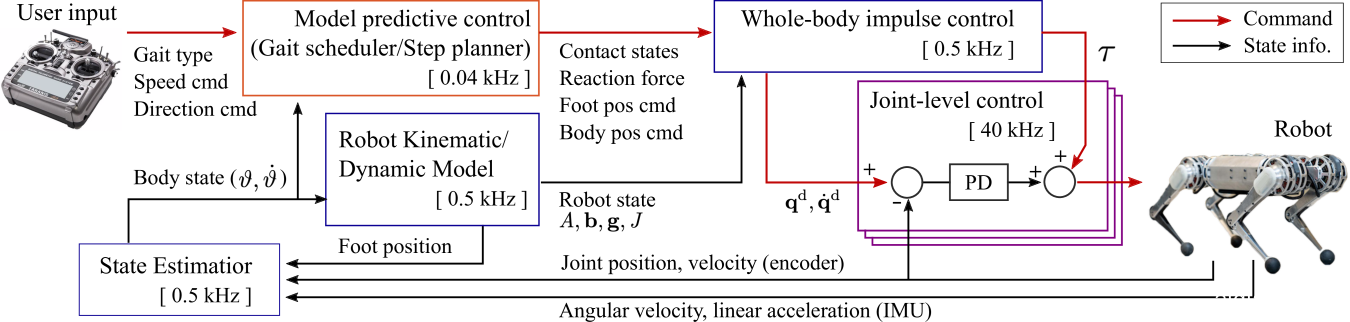
Fig. 2: Overall Control Framework. Using the user commanded gait type, speed, and direction from the RC-controller, the MPC computes desired reaction forces and foot/body position commands. From these, WBC computes joint torque, position, and velocity commands that are delivered to the each joint-level controller. Each component’s update frequency is represented by the color of its box.
图2：总体控制框架。MPC使用来自RC控制器的用户命令的步态类型，速度和方向，计算所需的反作用力和脚/身体位置命令。根据这些信息，WBC计算传递到每个关节级控制器的关节扭矩，位置和速度命令。每个组件的更新频率由其框的颜色表示。

To tackle the issue, we formulate WBC to follow both the reaction force and body trajectory commands. The idea of reaction force tracking originates from the impulse planning used in Cheetah 2 [4], which demonstrates successful dynamic bounding and jumping. The underlying idea of [4] is to plan reaction forces, which are impulses, rather than CoM trajectory, which is not practical to follow when the locomotion is extremely dynamic and has significant periods of under-actuation. In this paper, we embrace the impulse planning idea in WBC and formulate whole-body impulse control (WBIC) that can incorporate both body posture stabilization and reaction force execution. In terms of formulation, WBIC is not significantly different from the existing whole-body controllers [5, 6, 7], but the additional feature, which is an incorporation of pre-computed reaction forces by relaxing the floating base control, plays an important role in dynamic locomotion control. In our formulation, the WBIC is mostly used to track the ground reaction force profile rather than a body trajectory.

为了解决这个问题，我们制定了WBC来遵循反作用力和身体轨迹命令。反作用力跟踪的思想源于Cheetah 2 [ 4 ]中使用的冲动计划，该计划证明了成功的动态边界和跳跃。[ 4 ]的基本思想这是为了计划反作用力，它是脉冲，而不是CoM轨迹，当运动非常动态并且有大量的欠驱动时，要遵循这一点是不切实际的。在本文中，我们在WBC中采用了冲动计划的思想，并制定了可以结合体位稳定和反作用力执行的全身冲动控制（WBIC）。在制剂方面，WBIC不是从现有的全身控制器显著不同[ 5，6，7 ]，但附加功能是通过放松浮动基础控制来合并预先计算的反作用力，在动态运动控制中起着重要作用。在我们的公式中，WBIC主要用于跟踪地面反作用力曲线，而不是身体轨迹。

To find the reaction force command, we utilize model predictive control (MPC). In our previous work, we demonstrated that convex MPC can perform various dynamic gaits at high speed on both Cheetah 3 [8] and Mini-Cheetah [9]. Utilization of MPC enhances the versatility of locomotion, enabling us to switch between various gaits by simply changing the contact sequence. However, using MPC with a simple model has a fundamental limitation in position control because of its low update frequency (40 Hz in our implementations) and model simplifications. WBC provides a solution to the MPC’s limitation by running a high-frequency feedback loop while still accounting for full-body dynamics with contact.

为了找到反作用力命令，我们利用模型预测控制（MPC）。在我们之前的工作中，我们证明了凸面MPC可以在Cheetah 3 [ 8 ]和Mini-Cheetah [ 9 ]上高速执行各种动态步态。MPC的使用增强了运动的多功能性，使我们能够通过简单地更改接触顺序来在各种步态之间进行切换。但是，将MPC与简单模型一起使用会限制位置控制，因为它的更新频率较低（在我们的实现中为40 Hz），并且模型简化。WBC通过运行高频反馈回路，同时仍考虑了接触的全身动力学，为MPC的局限性提供了解决方案。

On the other hand, the prediction horizon of MPC compliments the WBC perfectly to fill in the WBC’s limitation that it cannot consider more than a single time step ahead. This limited time horizon issue has been addressed in [10, 11] which developed an MPC formulation using full-body dynamics. However, even their highly optimized solvers barely fit into a 200 Hz update frequency and the demonstrated results are not very dynamic compared to other controllers presented on the same robots. We believe that effective integration of MPC and WBC has a fundamental benefit over long-time horizon WBC. Moreover, by utilizing convex optimization, our implementation is not only fast, but also reliable because the solver does not get stuck in a strange local minimum.

另一方面，MPC的预测范围很好地补充了WBC，以填补WBC的局限性，即WBC不能考虑仅一步之遥。这种有限的时间范围问题一直在解决[ 10，11 ]其中开发了使用全体动力学的MPC的制剂。但是，即使是高度优化的求解器也几乎无法适应200 Hz的更新频率，并且与同一机器人上提供的其他控制器相比，所展示的结果也不是那么动态。我们认为，MPC和WBC的有效整合相对于长期的WBC具有根本的好处。此外，通过利用凸优化，我们的实现不仅快速，而且可靠，因为求解器不会陷入奇异的局部最小值中。

To integrate the MPC with the WBC, we modified our previous WBC formulation [5] to be compatible with the MPC and to handle dynamic locomotion with aerial phases. However, the novelty of our work does not come from the integration of two methods, MPC and WBC, since the incorporation of WBC with a high-level trajectory generator such as a motion optimizer [12], locomotion planner [13, 14], or MPC [15] is an established control framework. Our contribution lies in the method of how we utilize the results of MPC in the WBC. In our formulation, we use reaction forces computed by MPC as desired reaction forces in our WBC rather than attempting to track body trajectories computed by MPC. This is different from [15] that forces the robot to follow the CoM trajectory found by MPC and uses the reaction forces found by MPC only for regulating internal forces. However, attempting to track a CoM trajectory with a WBC will not be effective for gaits like galloping, where the CoM is never controllable. Our WBIC controls the body posture and swing foot but with a relaxation variable that allows the floating base movement to be different from the commanded trajectory. By doing so, WBC can perform behaviors with uncontrollable center of mass (CoM), movement such as jumping or bounding, by controlling the reaction forces found by MPC.

为了将MPC与WBC集成在一起，我们修改了以前的WBC公式[ 5 ]以与MPC兼容并处理具有空中相位的动态运动。然而，我们的工作的新颖性并非来自两种方法，MPC和WBC的整合，因为WBC的掺入具有高层次的轨迹生成诸如运动优化器[ 12 ]，运动计划器[ 13，14 ]，或MPC [ 15 ]是一个已建立的控制框架。我们的贡献在于如何利用WBC中MPC的结果的方法。在我们的公式中，我们将MPC计算的反作用力用作WBC中的所需反作用力，而不是尝试跟踪MPC计算的身体轨迹。这与[ 15 ]不同迫使机器人遵循MPC找到的CoM轨迹，并使用MPC找到的反作用力仅用于调节内部力。但是，尝试用WBC跟踪CoM轨迹对于像疾驰这样的步态是无效的，因为CoM是无法控制的。我们的WBIC控制身体姿势和摇摆脚，但具有放松变量，使浮动基础运动与命令轨迹不同。这样，WBC可以通过控制MPC发现的反作用力，以无法控制的质心（CoM）进行运动，例如跳跃或跳动。

Integrating WBC and MPC makes our controller versatile and robust. Versatile means that, in our controller, changing behavior or adding more tasks (e.g. manipulation if there are additional limbs) can be done by simply re-configuring the desired motions. For example, selecting different gaits can be done by changing the footstep pattern and timing in our formulation, and the low-level details such as swing foot control and body stabilization are automatically accomplished by our control scheme. Our controller will automatically handle gaits with significant flight periods, such as hopping, pronking, or bounding, without the need for manually planning around periods of flight or underactuation.

WBC和MPC的集成使我们的控制器具有多功能性和鲁棒性。多功能意味着，在我们的控制器中，只需简单地重新配置所需的动作，即可更改行为或添加更多任务（例如，如果有其他肢体，则进行操作）。例如，选择不同的步态可以通过更改我们的配方中的脚步模式和时机来完成，而低级细节（例如，摇摆脚控制和车身稳定性）则可以通过我们的控制方案自动完成。我们的控制器将自动处理具有较大飞行周期的步态，例如跳跃，俯仰或划界，而无需在飞行周期或启动不足时手动进行计划。

“Robust” means that our controller is reliable enough to maintain the robot’s balance while executing a locomotion command, even in the presence of large disturbances. More importantly, the proposed method can be implemented and demonstrates highly dynamic locomotion in a real robot. In our experiments with the Mini-Cheetah robot, we accomplished a 3.7 m/s running speed, corresponding to a Froude number of 4.65. Most documented legged robots’ Froude numbers are smaller than 2 [2, 16], except Cheetah 2 demonstrated 6.4m/s bounding (Froude number 7.1) [4]. To the best of our knowledge, our results demonstrate some of the most agile locomotion of any quadruped robot.

“鲁棒”意味着我们的控制器在执行运动命令时即使在存在较大干扰的情况下也足够可靠，可以保持机器人的平衡。更重要的是，所提出的方法可以实现，并在真实的机器人中演示了高度动态的运动。在Mini-Cheetah机器人的实验中，我们完成了3.7 米/s运行速度，对应于4.65的Froude数。最记录腿式机器人弗劳德数是小于2 [ 2，16 ]，除了猎豹2证明6.4米/s边界（弗劳德数7.1）[ 4 ]。据我们所知，我们的结果证明了四足机器人中一些最敏捷的运动。

Additionally, in order to successfully implement the algorithm on hardware, we developed an efficient dynamics engine including rotor dynamics [17] and linear algebra optimizations through template formatting. These techniques enable the MPC to run at 30 Hz and WBIC to run at 500 Hz on the low power computer installed in the Mini-Cheetah robot. In summary, the major contributions of this paper are two folds: 1) developing a versatile and robust control scheme for highly dynamic locomotion of quadruped robots, and 2) demonstrating high speed running and various gaits in real hardware, on the Mini-Cheetah robot.

另外，为了成功地在硬件上实现该算法，我们开发了一种高效的动力引擎，其中包括转子动力[ 17 ]和通过模板格式化的线性代数优化。这些技术使MPC可以在安装在Mini-Cheetah机器人上的低功耗计算机上以30 Hz的频率运行，而WBIC可以以500 Hz的频率运行。总而言之，本文的主要贡献有两个方面：1）开发用于四足机器人的高动态运动的通用且鲁棒的控制方案，以及2）在小型猎豹机器人上演示高速运行和实际硬件中的各种步态。

IIHYBRID CONTROL ARCHITECTURE 混合控制架构

The key idea of our method is to reduce complexity by separating locomotion control into two simpler controllers. This first controller finds optimal reaction force profiles along a one full gait cycle of locomotion using an MPC with the following simple lumped mass model:
我们方法的关键思想是通过将运动控制分为两个更简单的控制器来降低复杂度。该第一个控制器使用带有以下简单集总质量模型的MPC在一个完整的步态运动周期中找到最佳反作用力曲线：

$$ m \ddot{p} = \sum_{i=1}^{n_c} \mathbf{f}_i - \mathbf{c}_g $$

$$\frac{d}{dt}\left(I{\omega}\right)=\sum_{i=1}^{n_c}\mathbf{r}_i\times \mathbf{f}_i $$

where p, $f_i$, and $c_g$ are three dimensional vectors representing the robot’s position, reaction force, and gravitational acceleration with respect to the global frame. m is the robot’s body mass and $n_c$ is the number of contacts. $I∈R^(3×3) $ is the rotational inertia tensor and ω is the angular velocity of the body. $r_i $is the position of i-th contact point with respect to the CoM of the robot, which is equivalent to the moment arm of the contact force.

p, $f_i$, 和$c_g$ 是三维矢量，表示机器人相对于整体框架的位置，反作用力和重力加速度。m是机器人的体重， $n_c$ 是接触点的数量。 $I∈R^(3×3) $是旋转惯性张量， ω 是身体的角速度。 $r_i $是第i个接触点相对于机器人的位置 ，它等于接触力的力矩臂。

在第二个过程中，我们使用WBIC通过全身动力学和高频反馈控制来实现高带宽控制。与集总质量模型相比，这种更好的动力学模型将确定更准确的扭矩命令。多体动力学可以写成

In the second process, we use WBIC to achieve high bandwidth control through the use of full-body dynamics and high frequency feedback control. This better dynamics model will determine more accurate torque commands than the lumped mass model. The multi-body dynamics can be written as

where A, b, g, τ, fr, and Jc are the generalized mass matrix, Coriolis force, gravitation force, joint torque, augmented reaction force and contact Jacobian, respectively. \ddot{q}_f\in \mathbb{R}^6 is the acceleration of the floating base and \ddot{q}_j\in\mathbb{R}^{n_j} is the vector of joint accelerations, where nj is the number of joints. We use 06 to represent a 6 dimensional zero vector and 0n to represent a n-dimensional zero vector in this paper.

A, b, g, τ, fr, 和Jc 分别是广义质量矩阵，科里奥利力，万有引力，关节扭矩，增强反作用力和接触雅可比行列式。 $\ddot{q}_f\in \mathbb{R}^6$ 是浮基的加速度，并且$\ddot{q}_j\in\mathbb{R}^{n_j}$是关节加速度的向量，其中 $n_j$ 是关节的数量。我们用$\mathbf{0}6$ 代表6维零向量，并且$ \mathbf{0}{n}$ 代表一个 ñ本文中的零维向量。

Our hybrid control scheme combining these two controllers is described in Fig. 2. Beside MPC and WBIC, we use a Kalman Filter-based state estimator to compute global body position and velocity based on kinematics and acceleration data. We also developed a custom dynamics engine that efficiently includes the effects of rotor dynamics on the mass matrix and Coriolis vector. Although the the state estimator and dynamics engine contributed significantly to the locomotion performance, we will not explain them in detail since they are out of the scope of this paper.

我们的混合控制方案结合了这两个控制器，如图2所示 。除了MPC和WBIC，我们还使用基于卡尔曼滤波器的状态估计器，根据运动学和加速度数据来计算全局人体位置和速度。我们还开发了一种自定义动力学引擎，该引擎有效地包括了转子动力学对质量矩阵和科里奥利矢量的影响。尽管状态估计器和动力学引擎对运动性能做出了很大的贡献，但是由于它们不在本文的讨论范围之内，因此我们将不对其进行详细说明。

III MODEL PREDICTIVE CONTROL 模型预测控制

The objective of our MPC to find reaction forces which make the lumped mass follow the given trajectory. In the optimization process of the MPC, a contact sequence is predefined by the gait scheduler and step planner. This keeps the formulation convex, meaining the optimization problem is both fast to solve and can be always solved to a unique global minimum. This is not always obtainable in nonlinear optimization.

我们MPC的目的是寻找使集总质量遵循给定轨迹的反作用力。在MPC的优化过程中，步态计划程序和步骤计划程序会预先定义联系顺序。这样可以使公式保持凸面，这意味着优化问题不仅可以快速解决，而且可以始终解决到唯一的全局最小值。这在非线性优化中并不总是可获得的。

III-A MPC FORMULATION

Even the simple lumped mass model is not completely linear due to the cross product term for the moment arm and the orientation dynamics. To accomplish a convex MPC formulation, we applied three simplifications [8]. The first assumption is that the roll and pitch angles are small. Based on this assumption, we can simplify the coordinate transformation as follows.
由于力矩臂和方向动力学的叉积项，即使是简单的集总模型也不是完全线性的。为了完成凸MPC公式，我们应用了三个简化 [ 8 ]。第一个假设是侧倾角和俯仰角很小。基于此假设，我们可以简化坐标转换，如下所示。
$$ \dot{\Theta} \approx R_z(\psi){\omega} $$
$$ _\mathcal{G}{I} \approx R_z(\psi) _\mathcal{B}{I} {R}_z(\psi)^{\top} $$

where is angular velocity of the body with roll (ϕ), pitch (θ), and yaw (ψ) Euler angle representation. Rz(ψ) is a rotation matrix translating angular velocity in the global frame, ω, to the local (body) coordinate. $ _\mathcal{G}{I}$ and $ _\mathcal{B}{I} $are the inertia tensor seen from the global and local (body) frame, respectively.

$R_z(\psi)$ 是在全局框架中转换角速度的旋转矩阵， ω，以当地（身体）坐标为准。$ _\mathcal{G}{I}$和$ _\mathcal{B}{I} $ 是分别从整体和局部（身体）框架中看到的惯性张量。

The second assumption we made is that states are close to the commanded trajectory. Based on this assumption, we create a time-varying linearization of the dynamics using commanded ψ in a rotational matrix, Rz(ψ), and set the moment arm in Eq. (2) with the predetermined one from the commanded trajectory and step locations. The last assumption is that the pitch and roll velocities are small and off-diagonal terms of the inertia tensor are also small. With the assumption, we approximate Eq. (2) with the following:

我们做出的第二个假设是状态接近命令轨迹。基于此假设，我们使用命令创建动力学的时变线性化ψ 在旋转矩阵中 Rz(ψ)，并在等式中设置力矩臂。（2）从命令的轨迹和步距位置中选择预定的一个。最后一个假设是俯仰和横滚速度很小，惯性张量的非对角项也很小。假设，我们近似方程。（2）具有以下内容：

$$ \frac{d}{dt}\left({I}{\omega} \right) =
{I}\dot{{\omega}} + {\omega}\times\left( {I} {\omega} \right) \approx {I}\dot{{\omega}}. $$

With the above three simplifications, the discrete dynamics of the system can be expressed as
通过以上三个简化，系统的离散动力学可以表示为
$$ \mathbf{x}(k+1) = {A}_k\mathbf{x}(k) + {B}_k\hat{\mathbf{f}} (k)+ \hat{\mathbf{g}} $$

where,

$$ \mathbf{x} = [{\Theta}^{\top} , \mathbf{p}^{\top} , {\omega}^{\top}, \dot{\mathbf{p}}^{\top}] $$

$$ \hat{f} = [ f_1 , \cdots , f_n ] $$

$$ \hat{ g} = [0_{1\times3} , 0_{1\times3} , 0_{1\times3}, g^{\top}] $$

We use the formulation described in [8] to construct a QP which minimizes
我们使用[ 8 ]中描述的公式来构建最小化的QP

$$ \min_{\mathbf{x},\mathbf{f}}\sum_{k=0}^{m}||\mathbf{x}(k+1) - \mathbf{x}^{ ref }(k+1)||q + || \mathbf{f}(k)||_{R} $$

subject to dynamics and initial condition constraints. Additionally, friction cones are approximated by the following ground reaction force constraints
受动力学和初始条件约束。此外，摩擦锥通过以下地面反作用力约束来近似

$$ \mid f_{x}\mid\leq\mu f_{z},\quad\mid f_{y}\mid\leq\mu f_{z},\quad f_{z} $$

To reduce the size of the problem, we eliminate variables which correspond to ground reaction forces for feet which are not touching the ground. This reduces the size of both the cost and constraint matrix, and in practice gives us a speed up of over 10 times. Since all contacts in our problem are point contacts, we do not need to account for the non-flip condition that is described in [18].

为了减小问题的严重性，我们消除了与不接触地面的脚的地面反作用力相对应的变量。这减少了成本和约束矩阵的大小，并且在实践中使我们的速度提高了10倍以上。由于我们问题中的所有接触都是点接触，因此我们不需要考虑[ 18 ]中描述的非翻转条件。

III-BGAIT SCHEDULER 步态调度器

We use a periodic phase-based gait scheduler introduced in [19] that needs only two parameters to specify a gait type; phase offset and stance period for each foot. Since most gaits are basically periodic, proper spacing of swing and stance period in one cycle is enough to define different gaits. We can easily change the gait frequency by changing the cycle duration. Because gaits are defined by a portion of stance/swing period in the cycle, the gait types are maintained even when the gait frequency changes.

我们使用[ 19 ]中介绍的基于周期阶段的步态调度器，该步态调度器仅需要两个参数来指定步态类型。每只脚的相位偏移和站立时间。由于大多数步态基本上都是周期性的，因此在一个周期内适当的摆幅间隔和站姿周期足以定义不同的步态。我们可以通过更改周期持续时间轻松地更改步态频率。因为步态是由周期中的部分站立/摆动周期定义的，所以即使步态频率发生变化，步态类型也可以保持不变。

III-CFOOT STEP PLANNER 脚步计划器

We choose the upcoming foot step location with the following equation:
我们使用以下方程式选择即将到来的脚步位置：

$$ \mathbf{r_i }^{cmd}= p_{shoulder,i }+p_{ symmetry} + p_{ centrifugal} $$
where,

$$ p_{shoulder, i} = p_k + R_z ( \psi_k)I_i, $$
$$ p_{ symmetry} = \frac{t_{ stance}}{2}\mathbf{v} + k \left(\mathbf{v} - v^{ cmd} \right)$$
$$ p_{ centrifugal} = \frac{1}{2}\sqrt{\frac{h}{g}} v\times{\omega}^{ cmd},$$

In Eq. (13), $p_k$is the body position at the k-th timestep and $I_i$ is i-th leg shoulder location with respect to the body’s local frame. Therefore, $p_{shoulder,i} $ is the i-th shoulder location with respect to the global frame. $ p_symmetry$ is a so-called Raibert heuristic [20] that forces the leg’s landing angle and leaving angle be identical if the robot is traveling at the commanded velocity. In our setup, we use 0.03 for the feedback gain, k.

在等式中 （13）， $p_k$ 是身体在 ķ的时间步长和 $I_i$ 是第i个腿部相对于身体局部框架的肩膀位置。所以， $p_{shoulder,i} $ 是个相对于全局框架的第i个肩膀位置。 $ p_symmetry$ 是所谓的Raibert启发式算法[ 20 ]，如果机器人以命令的速度行进，它会迫使腿部的着陆角和离开角相同。在我们的设置中，我们使用0.03作为反馈增益，ķ。

IVWHOLE-BODY IMPULSE CONTROL 整体脉冲控制

Using the reaction forces found by the MPC, the WBIC computes joint position, velocity, and torque commands. For joint position, velocity, and acceleration computation, we utilize an inverse kinematics algorithm that strictly holds task priority. To compute the torque command, we use quadratic programming to find the reaction forces, reducing the both errors in acceleration command tracking and reaction force command tracking while satisfying inequality constraints on the resultant reaction forces.

Joint position and velocity commands are used to stabilize a posture through joint-level position controllers. In addition to the torque command, which is the final output of common WBC, WBIC computes a desired joint position and velocity. Utilizing joint position feedback is beneficial for dynamic locomotion control because of its collocated control input and high frequency update. In the case of Mini-Cheetah, the frequency of joint PD control is 40kHz/, which is 80 times faster than the high-level full body control. The effectiveness of joint position feedback in whole-body control is well demonstrated in the author’s previous work, passive-ankle biped walking [14]. In [14], the robot accomplish the stable body posture control and accurate swing foot control by utilizing joint position control. WBIC uses similar strategy to obtain reliable motion stabilization.

Although we take a similar approach to the author’s previous work [14], we use operational space control instead of configuration impedance control. We made this change based on difference between actuators used in each robot: proprioceptive actuators in Mini-Cheetah and series elastic actuators in Mercury. Since the proprioceptive actuator is highly backdrivable and provides open-loop joint torque control through the motor current control, it is more effective to directly control operational impedance rather than relying on joint impedance control that can delay the operational space control. The following sections explain the formulation of WBIC in detail.
WBIC使用MPC发现的反作用力来计算关节位置，速度和扭矩命令。对于关节位置，速度和加速度的计算，我们利用严格保持任务优先级的逆运动学算法。为了计算转矩指令，我们使用二次编程来找到反作用力，从而在满足合成反作用力的不等式约束的同时，减少了加速度指令跟踪和反作用力指令跟踪中的两个误差。

关节位置和速度命令用于通过关节级位置控制器来稳定姿势。除了扭矩命令（这是普通WBC的最终输出）之外，WBIC还会计算所需的关节位置和速度。利用关节位置反馈，由于其并置的控制输入和高频更新，对于动态运动控制是有益的。对于Mini-Cheetah，联合PD控制的频率为40ķHž/，比高级全身控制快80倍。作者先前的工作，被动脚踝两足动物步行[ 14 ]很好地证明了关节位置反馈在全身控制中的有效性 。在[ 14 ]中，机器人通过利用关节位置控制来实现稳定的身体姿势控制和精确的摆脚控制。WBIC使用类似的策略来获得可靠的运动稳定性。

尽管我们对作者先前的工作采用了类似的方法[ 14 ]，但我们使用操作空间控制代替了配置阻抗控制。我们根据每个机器人中使用的执行器之间的差异进行了此更改：Mini-Cheetah中的本体感觉执行器和Mercury中的系列弹性执行器。由于本体感觉致动器是高度可逆驱动的，并且通过电动机电流控制来提供开环关节转矩控制，因此直接控制操作阻抗比依靠关节阻抗控制来延迟操作空间控制更为有效，因为关节阻抗控制会延迟操作空间。以下各节详细说明了WBIC的制定。

IV-APRIORITIZED TASK EXECUTION 优先执行任务

To execute prioritized tasks, we utilize a null-space projection technique, which enables a strict task hierarchy in a computationally efficient way. When is a vector representing full configuration space, the iteration rules are the following.

为了执行优先任务，我们利用零空间投影技术，该技术以计算有效的方式实现了严格的任务层次。什么时候 是代表完整配置空间的向量，迭代规则如下。

$$ \Delta q_i = \Delta q_{i-1} + {J_{i| pre}}^{\dagger}( e_i -J_i \Delta q_{i-1} ), $$
$$ \dot{q_i}^{cmd}=\dot{q_{i-1}}^{cmd}+{J_{i|pre}}^{\dagger}\left(\dot{x_i}^{des}-J_i \dot{q}_{i-1}^{cmd}\right)$$

$$ \dot{q_i}^{cmd} = \ddot{q_{i-1}^{cmd} + \overline{J_{i|pre}^{dyn}}\left( \dot(x_i}^{cmd} - \dot{J_i}\dot{q} -J_i \ddot{q}_{i-1}^{cmd} \right)$$

where

$$ J_{i|pre} = J_i N_{i-1}, $$
$$N_{i-1} = N_{0} N_{1|0} \cdots N_{i-1|i-2}, $$

$$N_{0} = I - J_c^{\dagger}J_c $$
$$ N_{i|i-1} = I - {J_{i|i-1}}^{\dagger} J_{i|i-1}.$$
Here, i≥1, and

$$ \Delta q_0,\ \dot{q}_0^{ cmd} = \mathbf{0} $$
$$ \ddot{q}_0^{ cmd} = \overline{J_c^{ dyn}}(-J_c\dot{q}).$$
$\mathbf{e}_i$ is the position error defined by $\mathbf{x}_i^{des} - \mathbf{x}_i$ and $\ddot{\mathbf{x}}^{cmd}_i$ is the acceleration command of i-th task defined by

$$\ddot{\mathbf{x}}^{ cmd}_i = \ddot{\mathbf{x}}^{ des} + {K}_p \left(\mathbf{x}^{ des}_i - \mathbf{x}_i\right) + {K}_d\left(\dot{\mathbf{x}}^{ des} - \dot{\mathbf{x}}\right), $$

where ${K}_p$ and ${K}d$ are position and velocity feedback gains, respectively. Note that there is no feedback gain in Eq.\eqref{eq:delta_q}, which can be interpreted as using unity gains. ${J}{i|pre}$is the projection of the i-th task Jacobian into the null space of the prior tasks. ${J}_c$ is a contact Jacobian, which is equivalent to the {J}_c in Eq.\eqref{eq:full_dyn}. We use two types of pseudo-inverses; one is an SVD-based pseudo-inverse denoted by ${\cdot }^{\dagger}$ and the other is dynamically consistent pseudo-inverse defined by

在哪里 {K}_p ，{K}_d分别是位置和速度反馈增益。注意，方程式中没有反馈增益。（16），这可以解释为使用单位增益。 {J}_{i|pre} 是第i个任务Jacobian在先前任务的空间的投影。 {J}_c 是一个联系雅可比，等于 {J}_c 在等式中 （3）。我们使用两种类型的伪逆。一个是基于SVD的伪逆，表示为\{\cdot \}^{\dagger} 另一个是动态一致的伪逆，定义为

$$ \overline{{J}} = {A}^{-1}{J}^{\top}\left( {J} {A}^{-1} {J}^{\top} \right)^{-1}. $$

When computing acceleration (Eq.\eqref{eq:qddot_cmd}), we use the dynamically consistent pseudo-inverse. Therefore, the projected Jacobian, {J}_{i|pre}^{ dyn}, is different from the ones used in kinematics computations. The dynamically consistent Jacobians use \overline{\{\cdot \}} instead of \{\cdot \}^{\dagger} in the null space matrix computation (Eq.~\eqref{eq:null_space_matrix}).

当计算加速度时（式（18）），我们使用动态一致的伪逆。因此，预计的雅可比行列式Ĵdÿñ一世|p[RË，与运动学计算中所使用的不同。动态一致的Jacobian使用¯的¯{⋅} 代替 {⋅}†在零空间矩阵计算中（等式（20））。

Eq. (16) and (17) are used to find desired joint position and velocity for joint PD controller, respectively. We compute the desired joint position by adding the joint position portion of Eq. (16) to the measured joint position,

等式 （16）和（17）分别用于找到关节PD控制器的期望关节位置和速度。我们通过添加方程式的关节位置部分来计算所需的关节位置。（16）到测得的关节位置，

$$ q_j^{ cmd} = q_j + \Delta q_j. $$

The computed joint commands, $q_j^{ cmd}$ and $\dot{q}_j^{ cmd}$, are sent to the joint-level PD controller, and the acceleration commands \ddot{q}^{ cmd} are delivered to the QP optimization to find a torque command.

计算的联合命令， $q_j^{ cmd}$和 $\dot{q}_j^{ cmd}$，被发送到联合级PD控制器，并且加速命令 $\ddot{q}^{ cmd}$ 交付给QP优化以查找扭矩命令。

IV-BQUADRATIC PROGRAMMING

We compute the final reaction force with the acceleration command found in the previous step and the reaction force obtained in MPC. For the optimizatio