Abstract

摘要

We propose a new algorithm, Mean Actor-Critic (MAC), for discrete-action continuous-state reinforcement learning. MAC is a policy gradient algorithm that uses the agent’s explicit representation of all action values to estimate the gradient of the policy, rather than using only the actions that were actually executed. We prove that this approach reduces variance in the policy gradient estimate relative to traditional actor-critic approaches. We show empirical results on two control domains and six Atari games, where MAC is competitive with state-of-the-art policy search methods.

我们提出了一种新算法——均值演员-评论家 (Mean Actor-Critic, MAC) ，用于离散动作连续状态的强化学习。MAC是一种策略梯度算法，它利用智能体对所有动作值的显式表示来估计策略梯度，而非仅使用实际执行的动作。我们证明，相较于传统演员-评论家方法，该方法能降低策略梯度估计的方差。我们在两个控制领域和六款Atari游戏上的实验结果表明，MAC与最先进的策略搜索方法具有竞争力。

Introduction

引言

In reinforcement learning (RL), two important classes of algorithms are value-function-based methods and policy search methods. Value-function-based methods maintain an estimate of the value of performing each action in each state, and choose the actions associated with the most value in their current state (Sutton and Barto 1998). By contrast, policy search algorithms maintain an explicit policy, and agents draw actions directly from that policy to interact with their environment (Sutton et al. 2000). A subset of policy search algorithms, policy gradient methods, represent the policy using a differentiable parameterized function approximator (for example, a neural network) and use stochastic gradient ascent to update its parameters to achieve more reward.

在强化学习(RL)中，两类重要算法是基于价值函数的方法和策略搜索方法。基于价值函数的方法会维护对每个状态下执行每个动作的价值估计，并选择当前状态下最具价值的关联动作 (Sutton和Barto 1998)。相比之下，策略搜索算法会维护一个显式策略，智能体直接从该策略中抽取动作与环境交互 (Sutton等人 2000)。策略搜索算法的一个子集——策略梯度方法，使用可微分的参数化函数逼近器(例如神经网络)来表示策略，并通过随机梯度上升来更新其参数以获得更多奖励。

To facilitate gradient ascent, the agent interacts with its environment according to the current policy and keeps track of the outcomes of its actions. From these (potentially noisy) sampled outcomes, the agent estimates the gradient of the objective function. A critical question here is how to compute an accurate gradient using these samples, which may be costly to acquire, while using as few sample interactions as possible.

为便于梯度上升，智能体根据当前策略与环境交互，并记录其行为结果。通过这些（可能存在噪声的）采样结果，智能体估算目标函数的梯度。此处关键问题在于如何利用这些获取成本较高且样本量尽可能少的交互数据，计算出精确的梯度。

Actor-critic algorithms compute the policy gradient using a learned value function to estimate expected future reward (Sutton et al. 2000; Konda and Tsitsiklis 2000). Since the expected reward is a function of the environment’s dynamics, which the agent does not know, it is typically estimated by executing the policy in the environment. Existing algorithms compute the policy gradient using the value of states the agent visits, and critically, these methods take into account only the actions the agent actually executes during environmental interaction.

行动者-评论家算法 (Actor-critic algorithms) 通过学习的价值函数来估计预期未来奖励，从而计算策略梯度 (Sutton et al. 2000; Konda and Tsitsiklis 2000)。由于预期奖励是环境动态的函数，而智能体并不知晓环境动态，通常通过在环境中执行策略来估计该函数。现有算法利用智能体访问的状态值计算策略梯度，关键在于这些方法仅考虑智能体在环境交互过程中实际执行的动作。

We propose a new policy gradient algorithm, Mean Actor-Critic (or MAC), for the discrete-action continuous-state case. MAC uses the agent’s policy distribution to average the value function over all actions, rather than using the action-values of only the sampled actions. We prove that, under modest assumptions, this approach reduces variance in the policy gradient estimates relative to traditional actor-critic approaches. We implement MAC using deep neural networks, and we show empirical results on two control domains and six Atari games, where MAC is competitive with state-of-the-art policy search methods.

我们提出了一种新的策略梯度算法——均值演员-评论家 (Mean Actor-Critic，简称MAC)，适用于离散动作连续状态场景。该方法利用智能体的策略分布对所有动作的价值函数进行平均，而非仅基于采样动作的动作价值。我们证明，在适度假设下，相较于传统演员-评论家方法，该方案能降低策略梯度估计的方差。基于深度神经网络实现了MAC，并在两个控制域和六款Atari游戏上进行了实验验证，结果表明MAC与最先进的策略搜索方法性能相当。

We note that the core idea behind MAC has also been independently and concurrently explored by Ciosek and Whiteson (2017). However, their results mainly focus on continuous action spaces and are more theoretical. We introduce a simpler proof of variance reduction that makes fewer assumptions, and we also show that the algorithm works well in discreteaction domains.

我们注意到，MAC背后的核心思想也被Ciosek和Whiteson (2017) 独立且同时进行了探索。然而，他们的结果主要集中在连续动作空间，并且更具理论性。我们引入了一个更简单的方差减少证明，该证明做出的假设更少，同时我们还展示了该算法在离散动作领域也能表现良好。

Background

背景

In ${\mathrm{RL}},$ we train an agent to select actions in its environment so that it maximizes some notion of longterm reward. We formalize the problem as a Markov decision process (MDP) (Puterman 1990), which we specify by the tuple $\langle\mathcal{S},\mathcal{s}{0},\mathcal{A},\mathcal{R},\mathcal{T},\gamma\rangle.$ , where $s$ is a set of states, $s_{0}\in~S$ is a fixed initial state, $\mathcal{A}$ is a set of discrete actions, the functions $\mathcal{R}:\mathcal{S}\times\mathcal{A}\rightarrow\mathbb{R}$ and $\mathcal{T}:\mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow[0,1]$ respectively describe the reward and transition dynamics of the environment, and $\gamma\in[0,1)$ is a discount factor representing the relative importance of immediate versus long-term rewards.

在 ${\mathrm{RL}}$ 中，我们训练一个智能体在其环境中选择动作，以最大化某种长期奖励的概念。我们将问题形式化为马尔可夫决策过程 (MDP) (Puterman 1990)，通过元组 $\langle\mathcal{S},\mathcal{s}{0},\mathcal{A},\mathcal{R},\mathcal{T},\gamma\rangle$ 来指定，其中 $s$ 是一组状态，$s_{0}\in~S$ 是固定的初始状态，$\mathcal{A}$ 是一组离散动作，函数 $\mathcal{R}:\mathcal{S}\times\mathcal{A}\rightarrow\mathbb{R}$ 和 $\mathcal{T}:\mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow[0,1]$ 分别描述了环境的奖励和转移动态，$\gamma\in[0,1)$ 是一个折扣因子，表示即时奖励与长期奖励的相对重要性。

More concretely, we denote the expected reward for performing action $a\in{\mathcal{A}}$ in state $s\in S$ as:

具体而言，我们将状态$s\in S$下执行动作$a\in{\mathcal{A}}$的预期奖励表示为：

$$
\begin{array}{r}{\mathcal{R}(s,a)=\mathbb{E}\left[r_{t+1}\middle\vert s_{t}=s,a_{t}=a\right],}\end{array}
$$

$$
\begin{array}{r}{\mathcal{R}(s,a)=\mathbb{E}\left[r_{t+1}\middle\vert s_{t}=s,a_{t}=a\right],}\end{array}
$$

and we denote the probability that performing action $a$ in state s results in state $s^{\prime}\in S$ as:

我们将在状态s执行动作$a$导致状态$s^{\prime}\in S$的概率表示为：

$$
\begin{array}{r}{\mathcal{T}(s,a,s^{\prime})=\operatorname*{Pr}(s_{t+1}=s^{\prime}\vert s_{t}=s,a_{t}=a).}\end{array}
$$

$$
\begin{array}{r}{\mathcal{T}(s,a,s^{\prime})=\operatorname*{Pr}(s_{t+1}=s^{\prime}\vert s_{t}=s,a_{t}=a).}\end{array}
$$

In the context of policy search methods, the agent maintains an explicit policy $\pi(\boldsymbol{a}|\boldsymbol{s};\boldsymbol{\theta})$ denoting the probability of taking action $a$ in state s under the policy $\pi$ parameterized by $\theta$ . Note that for each state, the policy outputs a probability distribution over the discrete set of actions: $\pi:S\overset{\cdot}{\to}\mathcal{P}(A)$ . At each timestep $t,$ the agent takes an action $a_{t}$ drawn from its policy $\pi(\cdot|s_{t};\theta).$ , then the environment provides a reward signal $r_{t}$ and transitions to the next state $s_{t+1}$ .

在策略搜索方法的背景下，智能体维护一个显式策略 $\pi(\boldsymbol{a}|\boldsymbol{s};\boldsymbol{\theta})$ ，表示在参数为 $\theta$ 的策略 $\pi$ 下，于状态 s 采取动作 $a$ 的概率。注意，对于每个状态，策略会输出离散动作集合上的概率分布： $\pi:S\overset{\cdot}{\to}\mathcal{P}(A)$ 。在每个时间步 $t,$ 智能体从其策略 $\pi(\cdot|s_{t};\theta).$ 中抽取动作 $a_{t}$ ，随后环境会提供奖励信号 $r_{t}$ 并转移到下一个状态 $s_{t+1}$ 。

The agent’s goal at every timestep is to maximize the sum of discounted future rewards, or simply return, which we define as:

智能体在每个时间步的目标是最大化未来奖励的折现总和，简称为回报，其定义为：

$$
G_{t}=\sum_{k=1}^{\infty}\gamma^{k-1}r_{t+k}.
$$

$$
G_{t}=\sum_{k=1}^{\infty}\gamma^{k-1}r_{t+k}.
$$

In a slight abuse of notation, we will also denote the total return for a trajectory $\tau$ as $G(\tau)$ , which is equal to $G_{0}$ for that same trajectory.

在不严格遵循符号规范的情况下，我们也将轨迹 $\tau$ 的总回报记为 $G(\tau)$ ，其值等于该轨迹的 $G_{0}$ 。

The agent’s policy induces a value function over the state space. The expression for return allows us to define both a state value function, $V^{\pi}(s)$ , and a stateaction value function, $Q^{\pi}(s,a)$ . Here, $V^{\bar{\pi}}(s)$ represents the expected return starting from state $s,$ and following the policy $\pi$ thereafter, and $Q^{\pi}(s,a)$ represents the expected return starting from s, executing action $a_{.}$ , and then following the policy $\pi$ thereafter:

智能体的策略在状态空间上导出一个价值函数。通过回报的表达式，我们可以定义状态价值函数 $V^{\pi}(s)$ 和状态动作价值函数 $Q^{\pi}(s,a)$ 。其中，$V^{\bar{\pi}}(s)$ 表示从状态 $s$ 开始并遵循策略 $\pi$ 的期望回报，而 $Q^{\pi}(s,a)$ 表示从状态 $s$ 开始执行动作 $a_{.}$ 后遵循策略 $\pi$ 的期望回报：

$$
V^{\pi}(s):=\mathbb{E}\left[G_{t}|s_{t}=s\right],
$$

$$
V^{\pi}(s):=\mathbb{E}\left[G_{t}|s_{t}=s\right],
$$

$$
\begin{array}{r}{Q^{\pi}(s,a):=\mathbb{E}{\pi}\left[G_{t}|s_{t}=s,a_{t}=a\right].}\end{array}
$$

$$
\begin{array}{r}{Q^{\pi}(s,a):=\mathbb{E}{\pi}\left[G_{t}|s_{t}=s,a_{t}=a\right].}\end{array}
$$

Note that:

注意：

$$
V^{\pi}(s)=\sum_{a\in\cal A}[\pi(a\vert s;\theta)Q^{\pi}(s,a)].
$$

$$
V^{\pi}(s)=\sum_{a\in\cal A}[\pi(a\vert s;\theta)Q^{\pi}(s,a)].
$$

The agent’s goal is to find a policy that maximizes the return for every timestep, so we define an objective function $J$ that allows us to score an arbitrary policy parameter $\theta$ :

智能体的目标是找到一个能在每个时间步最大化回报的策略，因此我们定义一个目标函数 $J$ 来评估任意策略参数 $\theta$ 的优劣：

$$
J(\theta)=\underset{\tau\sim P r(\tau\mid\theta)}{\mathbb{E}}\left[G(\tau)\right]=\sum_{\tau}P r(\tau|\theta)G(\tau),
$$

$$
J(\theta)=\underset{\tau\sim P r(\tau\mid\theta)}{\mathbb{E}}\left[G(\tau)\right]=\sum_{\tau}P r(\tau|\theta)G(\tau),
$$

where $\tau$ denotes a trajectory. Note that the probability of a specific trajectory depends on policy parameters as well as the dynamics of the environment. Our goal is to be able to compute the gradient of $J$ with respect

其中 $\tau$ 表示一条轨迹。需要注意的是，特定轨迹的概率取决于策略参数以及环境动态。我们的目标是能够计算 $J$ 关于

to the policy parameters $\theta$ :

策略参数 $\theta$ :

$$
\begin{array}{r l}{\nabla_{\theta}J(\theta)}&{=\phantom{-}\sum_{\eta}\nabla_{\theta}P r(\tau|\theta)G(\tau)}\ {::}&{=\phantom{-}\sum_{\tau}P r(\tau|\theta)\frac{\nabla_{\theta}P r(\tau|\theta)}{P r(\tau|\theta)}G(\tau)}\ {::=::}&{:\sum_{\tau}P r(\tau|\theta)\nabla_{\theta}\log P r(\tau|\theta)G(\tau)}\ {::=::}&{:\times\sim d^{\mathbb{E}}_{\boldsymbol{u},\sim\boldsymbol{u}\sim\boldsymbol{u}}[\nabla_{\theta}\log\pi(a|s;\theta)G_{0}]}\ {::=::}&{:\times\sim d^{\mathbb{E}}_{\boldsymbol{u},\sim\boldsymbol{u}\sim\boldsymbol{u}}[\nabla_{\theta}\log\pi(a|s;\theta)G_{t}]}\ {:::=::}&{:\times\sim d^{\mathbb{E}}_{\boldsymbol{u},\sim\boldsymbol{u}\sim\boldsymbol{u}}[\nabla_{\theta}\log\pi(a|s;\theta)Q^{\pi}(s,a)]}\end{array}
$$

$$
\begin{array}{r l}{\nabla_{\theta}J(\theta)}&{=\phantom{-}\sum_{\eta}\nabla_{\theta}P r(\tau|\theta)G(\tau)}\ {::}&{=\phantom{-}\sum_{\tau}P r(\tau|\theta)\frac{\nabla_{\theta}P r(\tau|\theta)}{P r(\tau|\theta)}G(\tau)}\ {::=::}&{:\sum_{\tau}P r(\tau|\theta)\nabla_{\theta}\log P r(\tau|\theta)G(\tau)}\ {::=::}&{:\times\sim d^{\mathbb{E}}_{\boldsymbol{u},\sim\boldsymbol{u}\sim\boldsymbol{u}}[\nabla_{\theta}\log\pi(a|s;\theta)G_{0}]}\ {::=::}&{:\times\sim d^{\mathbb{E}}_{\boldsymbol{u},\sim\boldsymbol{u}\sim\boldsymbol{u}}[\nabla_{\theta}\log\pi(a|s;\theta)G_{t}]}\ {:::=::}&{:\times\sim d^{\mathbb{E}}_{\boldsymbol{u},\sim\boldsymbol{u}\sim\boldsymbol{u}}[\nabla_{\theta}\log\pi(a|s;\theta)Q^{\pi}(s,a)]}\end{array}
$$

where $\begin{array}{r}{d^{\pi}(s)=\sum_{t=0}^{\infty}\gamma^{t}P r(s_{t}=s|s_{0},\pi)}\end{array}$ is the dis- counted state distribution. In the second and third lines we rewrite the gradient term using a score function. In the fourth line, we convert the summation to an expectation, and use the $G_{0}$ notation in place of $G(\tau)$ . Next, we make use of the fact that $\mathbb{E}[\mathbf{\dot{\boldsymbol{G}}}_{0}]=\mathbb{E}[\mathbf{\dot{\boldsymbol{G}}}_{t}],$ given by Williams (1992). Intuitively this makes sense, since the policy for a given state should depend only on the rewards achieved after that state. Finally, we invoke the definition that $Q^{\pi}(s,a)=\mathbb{E}[G_{t}]$ .

其中 $\begin{array}{r}{d^{\pi}(s)=\sum_{t=0}^{\infty}\gamma^{t}P r(s_{t}=s|s_{0},\pi)}\end{array}$ 表示折扣状态分布。在第二行和第三行中，我们使用评分函数重写了梯度项。第四行将求和转换为期望，并用 $G_{0}$ 替代 $G(\tau)$ 。接着，我们利用 Williams (1992) 提出的 $\mathbb{E}[\mathbf{\dot{\boldsymbol{G}}}_{0}]=\mathbb{E}[\mathbf{\dot{\boldsymbol{G}}}_{t}]$ 这一性质。直观上这是合理的，因为特定状态下的策略应仅取决于该状态后获得的奖励。最后，我们引入 $Q^{\pi}(s,a)=\mathbb{E}[G_{t}]$ 的定义。

A nice property of expectation (1) is that, given access to $Q^{\hat{\pi}}$ , the expectation can be estimated through implementing policy $\pi$ in the environment. Alternatively, we can estimate $Q^{\pi}$ using the return $G_{t}$ , which is an unbiased (and usually a high variance) sample of $Q^{\pi}$ . This is essentially the idea behind the REINFORCE algorithm (Williams 1992), which uses the following gradient estimator:

期望 (1) 的一个良好特性是，在给定访问 $Q^{\hat{\pi}}$ 的情况下，可以通过在环境中实施策略 $\pi$ 来估计期望。或者，我们可以使用回报 $G_{t}$ 来估计 $Q^{\pi}$，这是 $Q^{\pi}$ 的无偏 (但通常高方差) 样本。这本质上是 REINFORCE 算法 (Williams 1992) 背后的思想，该算法使用以下梯度估计器:

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\approx\frac{1}{T}\sum_{t=1}^{T}G_{t}\nabla_{\boldsymbol{\theta}}\log\pi(a_{t}|s_{t};\boldsymbol{\theta}).
$$

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\approx\frac{1}{T}\sum_{t=1}^{T}G_{t}\nabla_{\boldsymbol{\theta}}\log\pi(a_{t}|s_{t};\boldsymbol{\theta}).
$$

Alternatively, we can estimate $Q^{\pi}$ using some sort of function approximation: $\widehat{Q}(s,a;\omega)\approx\bar{Q^{\pi}}(s,a).$ , which results in variants of act obr-critic algorithms. Perhaps the simplest actor-critic algorithm approximates (1) as follows:

或者，我们可以通过某种函数近似来估计 $Q^{\pi}$：$\widehat{Q}(s,a;\omega)\approx\bar{Q^{\pi}}(s,a)$，这会衍生出各类行动者-评论者 (actor-critic) 算法的变体。最简单的行动者-评论者算法对(1)式的近似如下：

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\approx\frac{1}{T}\sum_{t=1}^{T}\widehat{Q}(s_{t},a_{t};w)\nabla_{\boldsymbol{\theta}}\log\pi(a_{t}|s_{t};\boldsymbol{\theta}).
$$

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\approx\frac{1}{T}\sum_{t=1}^{T}\widehat{Q}(s_{t},a_{t};w)\nabla_{\boldsymbol{\theta}}\log\pi(a_{t}|s_{t};\boldsymbol{\theta}).
$$

Note that value function approximation can, in general, bias the gradient estimation (Baxter and Bartlett 2001).

注意，价值函数近似通常会使梯度估计产生偏差 (Baxter and Bartlett 2001)。

One way of reducing variance in both REINFORCE and actor-critic algorithms is to use an additive control variate as a baseline (Williams 1992; Sutton et al. 2000; Greensmith, Bartlett, and Baxter 2004). The baseline function is typically a function that is fixed over actions, and so subtracting it from either the sampled returns or the estimated Q-values does not bias the gradient estimation. We refer to techniques that use such a baseline as advantage variations of the basic algorithms, since they approximate the advantage $A(s,a)$ of choosing action a over some baseline representing “typical”

降低REINFORCE和演员-评论家算法方差的一种方法是使用加法控制变量作为基线 (Williams 1992; Sutton et al. 2000; Greensmith, Bartlett, and Baxter 2004)。基线函数通常是固定于动作的函数，因此从采样回报或估计的Q值中减去它不会使梯度估计产生偏差。我们将使用这种基线的技术称为基本算法的优势变体，因为它们近似于选择动作a相对于代表"典型"行为的基线优势$A(s,a)$。

performance for the policy in state $s$ (Baird 1994). The update performed by advantage REINFORCE is:

状态 $s$ 下策略的性能 (Baird 1994)。advantage REINFORCE 执行的更新为:

$$
\theta\gets\theta+\alpha\sum_{t=1}^{T}(G_{t}-b)\nabla_{\theta}\log\pi(a_{t}|s_{t};\theta),
$$

$$
\theta\gets\theta+\alpha\sum_{t=1}^{T}(G_{t}-b)\nabla_{\theta}\log\pi(a_{t}|s_{t};\theta),
$$

where $b$ is a scalar baseline measuring the performance of the policy, such as a running average of the observed return over the past few episodes of interaction.

其中 $b$ 是一个衡量策略性能的标量基线 (baseline)，例如过去几次交互中观察到的回报的运行平均值。

Advantage actor-critic uses an approximation of the expected value of each state $s_{t}$ as its baseline: $\widehat{V}(s_{t}):=$ $\begin{array}{r}{\sum_{a}\boldsymbol{\pi}(a|s_{t};\theta)\boldsymbol{\widehat{Q}}(s_{t},a;\omega).}\end{array}$ , which leads to the f obllowing update rule:

优势演员-评论家方法使用每个状态 $s_{t}$ 的期望值近似作为基线: $\widehat{V}(s_{t}):=$ $\begin{array}{r}{\sum_{a}\boldsymbol{\pi}(a|s_{t};\theta)\boldsymbol{\widehat{Q}}(s_{t},a;\omega).}\end{array}$ ，从而得到以下更新规则:

$$
\theta\gets\theta+\alpha\sum_{t=1}^{T}\left(\widehat{Q}(s_{t},a_{t};\omega)-\widehat{V}(s_{t})\right)\nabla_{\theta}\log\pi(a_{t}|s_{t};\theta).
$$

$$
\theta\gets\theta+\alpha\sum_{t=1}^{T}\left(\widehat{Q}(s_{t},a_{t};\omega)-\widehat{V}(s_{t})\right)\nabla_{\theta}\log\pi(a_{t}|s_{t};\theta).
$$

Another way of estimating the advantage function is to use the TD-error signal $\delta=r_{t}+\gamma V\widecheck{(}s^{\prime})-V(s)$ . This approach is convenient, because it only requires estimating one set of parameters, namely for $V$ . However, because the TD-error is a sample of the advantage function $A(s,a)=Q^{\pi}(s,a)-V^{\pi}(\dot{s}),$ , this approach has higher variance (due to the environmental dynamics) than methods that explicitly compute $Q(s,a)^{\check{}}-V(s)$ . Moreover, given $Q$ and $\pi,\stackrel{\cdot}{V}$ can easily be computed as $\begin{array}{r}{V=\sum_{a}\pi(a|s)Q(s,a).}\end{array}$ , so in practice, it is still only necessary to estimate one set of parameters (for $Q$ ).

另一种估计优势函数的方法是使用时序差分误差信号 $\delta=r_{t}+\gamma V\widecheck{(}s^{\prime})-V(s)$。这种方法很方便，因为它只需要估计一组参数，即 $V$ 的参数。然而，由于时序差分误差是优势函数 $A(s,a)=Q^{\pi}(s,a)-V^{\pi}(\dot{s})$ 的一个样本，这种方法比显式计算 $Q(s,a)^{\check{}}-V(s)$ 的方法具有更高的方差（由于环境动态性）。此外，给定 $Q$ 和 $\pi$ 时，$\stackrel{\cdot}{V}$ 可以很容易地计算为 $\begin{array}{r}{V=\sum_{a}\pi(a|s)Q(s,a).}\end{array}$，因此在实践中仍然只需要估计一组参数（即 $Q$ 的参数）。

Mean Actor-Critic

Mean Actor-Critic

An overwhelming majority of recent actor-critic papers have computed the policy gradient using an estimate similar to Equation (3) (Degris, White, and Sutton 2012; Mnih et al. 2016; Wang et al. 2016). This estimate samples both states and actions from trajectories executed according to the current policy in order to compute the gradient of the objective function with respect to the policy weights.

绝大多数近期的行动者-评论家论文都采用了类似式(3)的估计来计算策略梯度 (Degris, White, and Sutton 2012; Mnih et al. 2016; Wang et al. 2016)。该估计方法根据当前策略执行的轨迹对状态和动作进行采样，以计算目标函数相对于策略权重的梯度。

Instead of using only the sampled actions, Mean Actor-Critic (MAC) explicitly computes the probability-weighted average over all $\mathrm{Q}.$ -values, for each state sampled from the trajectories. In doing so, MAC is able to produce an estimate of the policy gradient where the variance due to action sampling is reduced to zero. This is exactly the difference between computing the sample mean (whose variance is inversely proportional to the number of samples), and calculating the mean directly (which is simply a scalar with no variance).

均值行动者-评论家 (Mean Actor-Critic, MAC) 并非仅使用采样动作，而是显式计算从轨迹中采样的每个状态下所有 $\mathrm{Q}$ 值的概率加权平均。通过这种方式，MAC 能生成策略梯度的估计值，其中由动作采样引起的方差降为零。这正是计算样本均值 (其方差与样本数成反比) 和直接计算均值 (即无方差的标量) 之间的本质区别。

MAC is based on the observation that expectation (1), which we repeat here, can be rewritten in the following way:

MAC基于以下观察：期望(1) (此处重复)可以改写为如下形式：

$$
\begin{array}{r l}&{\nabla_{\theta}J(\theta)=\underset{s\sim d^{\pi},a\sim\pi}{\mathbb{E}}[\nabla_{\theta}\log\pi(a|s;\theta)Q^{\pi}(s,a)]}\ &{\quad\quad\quad=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\underset{a\in A}{\sum}\pi(a|s;\theta)\nabla_{\theta}\log\pi(a|s;\theta)Q^{\pi}(s,a)\Big]}\ &{\quad\quad\quad=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\underset{a\in A}{\sum}\nabla_{\theta}\pi(a|s;\theta)Q^{\pi}(s,a)\Big].\quad\quad\quad\quad(4)}\end{array}
$$

$$
\begin{array}{r l}&{\nabla_{\theta}J(\theta)=\underset{s\sim d^{\pi},a\sim\pi}{\mathbb{E}}[\nabla_{\theta}\log\pi(a|s;\theta)Q^{\pi}(s,a)]}\ &{\quad\quad\quad=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\underset{a\in A}{\sum}\pi(a|s;\theta)\nabla_{\theta}\log\pi(a|s;\theta)Q^{\pi}(s,a)\Big]}\ &{\quad\quad\quad=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\underset{a\in A}{\sum}\nabla_{\theta}\pi(a|s;\theta)Q^{\pi}(s,a)\Big].\quad\quad\quad\quad(4)}\end{array}
$$

Figure 1: Screenshots of the classic control domains Cart Pole (left) and Lunar Lander (right)

图 1: 经典控制领域任务Cart Pole(左)和Lunar Lander(右)的界面截图

We can estimate (4) by sampling states from a trajectory and using function approximation:

我们可以通过从轨迹中采样状态并使用函数逼近来估计 (4) :

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\approx\frac{1}{T}\sum_{t=0}^{T-1}\sum_{a\in\mathcal{A}}\nabla_{\boldsymbol{\theta}}\pi(a|s_{t};\boldsymbol{\theta})\widehat{Q}(s_{t},a;\omega).
$$

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\approx\frac{1}{T}\sum_{t=0}^{T-1}\sum_{a\in\mathcal{A}}\nabla_{\boldsymbol{\theta}}\pi(a|s_{t};\boldsymbol{\theta})\widehat{Q}(s_{t},a;\omega).
$$

In our implementation, the inner summation is computed by combining two neural networks that represent the policy and state-action value function. The value function can be learned using a variety of methods, such as temporal-difference learning or Monte Carlo sampling. After performing a few updates to the value function, we update the parameters $\theta$ of the policy with the following update rule:

在我们的实现中，内部求和通过结合代表策略和状态-动作值函数的两个神经网络来计算。值函数可以通过多种方法学习，例如时序差分学习或蒙特卡洛采样。在对值函数进行几次更新后，我们使用以下更新规则来更新策略的参数 $\theta$：

$$
\theta\gets\theta+\alpha\sum_{t=0}^{T-1}\sum_{a\in\mathcal{A}}\nabla_{\theta}\pi(a|s_{t};\theta)\widehat{Q}(s_{t},a;\omega).
$$

$$
\theta\gets\theta+\alpha\sum_{t=0}^{T-1}\sum_{a\in\mathcal{A}}\nabla_{\theta}\pi(a|s_{t};\theta)\widehat{Q}(s_{t},a;\omega).
$$

To improve stability, repeated updates to the value and policy networks are interleaved, as in Generalized Policy Iteration (Sutton and Barto 1998).

为提高稳定性，我们对价值网络和策略网络进行交错重复更新，类似于广义策略迭代 (Sutton and Barto 1998) 的做法。

In traditional actor-critic approaches, which we refer to as sampled-action actor-critic, the only actions involved in the computation of the policy gradient estimate are those that were actually executed in the environment. In MAC, computing the policy gradient estimate will frequently involve actions that were not actually executed in the environment. This results in a trade-off between bias and variance. In domains where we can expect accurate Q-value predictions from our function approx im at or, despite not actually executing all of the relevant state-action pairs, MAC results in lower variance gradient updates and increased sample-efficiency. In domains where this assumption is not valid, MAC may perform worse than sampled-action actor-critic due to increased bias.

在传统的行动者-评论家方法（我们称之为采样行动行动者-评论家）中，参与策略梯度估计计算的动作仅限于那些实际在环境中执行的动作。而在MAC中，策略梯度估计的计算经常会涉及未实际执行的动作。这导致了偏差与方差之间的权衡。在我们能够从函数近似器中获得准确Q值预测的领域中，尽管并未实际执行所有相关的状态-动作对，MAC仍能实现更低方差的梯度更新和更高的样本效率。若这一假设不成立，由于偏差增加，MAC的表现可能不如采样行动行动者-评论家。

In some ways, MAC is similar to Expected Sarsa (Van Seijen et al. 2009). Expected Sarsa considers all next-actions $a_{t+1.}$ , then computes the expected TDerror, $\mathbb{E}[\delta]=~\dot{r}{t}+\gamma\mathbb{E}[Q(s_{t+1},a_{t+1})]-Q\dot{(}s_{t},a_{t}),$ and uses the resulting error signal to update the $Q$ function. By contrast, MAC considers all current-actions $^{a_{t},}$ and uses the corresponding $Q(s_{t},a_{t})$ values to update the policy directly.

在某些方面，MAC与Expected Sarsa (Van Seijen等人，2009)类似。Expected Sarsa考虑所有下一个动作$a_{t+1}$，然后计算期望TD误差$\mathbb{E}[\delta]=~\dot{r}{t}+\gamma\mathbb{E}[Q(s_{t+1},a_{t+1})]-Q\dot{(}s_{t},a_{t}),$并使用得到的误差信号更新$Q$函数。相比之下，MAC考虑所有当前动作$a_{t}$，并使用对应的$Q(s_{t},a_{t})$值直接更新策略。

It is natural to consider whether MAC could be improved by subtracting an action-independent baseline, as in sampled-action actor-critic and REINFORCE:

很自然地会考虑是否可以通过减去与动作无关的基线来改进MAC (Mean Actor-Critic) ，就像在采样动作演员-评论家 (sampled-action actor-critic) 和REINFORCE算法中那样：

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\sum_{\boldsymbol{a}\in\mathcal{A}}\nabla_{\boldsymbol{\theta}}\pi(\boldsymbol{a}|s;\boldsymbol{\theta})\Big(Q^{\pi}(s,\boldsymbol{a})-V^{\pi}(s)\Big)\Big].
$$

$$
\nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\sum_{\boldsymbol{a}\in\mathcal{A}}\nabla_{\boldsymbol{\theta}}\pi(\boldsymbol{a}|s;\boldsymbol{\theta})\Big(Q^{\pi}(s,\boldsymbol{a})-V^{\pi}(s)\Big)\Big].
$$

However, we can simplify the expectation as follows:

然而，我们可以将期望简化为如下形式：

$$
\begin{array}{r l}&{\nabla_{\theta}J(\theta)=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\underset{a\in\mathcal{A}}{\sum}\nabla_{\theta}\pi(a|s;\theta)Q^{\pi}(s,a)}\ &{\qquad-V^{\pi}(s)\nabla_{\theta}\underset{a\in\mathcal{A}}{\sum}\pi(a|s;\theta)\Big].}\end{array}
$$

$$
\begin{array}{r l}&{\nabla_{\theta}J(\theta)=\underset{s\sim d^{\pi}}{\mathbb{E}}\Big[\underset{a\in\mathcal{A}}{\sum}\nabla_{\theta}\pi(a|s;\theta)Q^{\pi}(s,a)}\ &{\qquad-V^{\pi}(s)\nabla_{\theta}\underset{a\in\mathcal{A}}{\sum}\pi(a|s;\theta)\Big].}\end{array}
$$

In doing so, we see that both $V^{\pi}(s)$ and the gradient operator can be moved outside of the summation, leaving just the sum of the action probabilities, which is always 1, and hence the gradient of the baseline term is always zero. This is true regardless of the choice of baseline, since the baseline cannot be a function of the actions or else it will bias the expectation. Thus, we see that subtracting a baseline is unnecessary in MAC, since it has no effect on the policy gradient estimate.

这样，我们发现$V^{\pi}(s)$和梯度算子都可以移到求和符号之外，剩下的只是动作概率之和（恒等于1），因此基线项的梯度始终为零。无论选择何种基线，这一结论都成立，因为基线不能是动作的函数，否则会偏置期望值。由此可见，在MAC中减去基线是多余的，因为它对策略梯度估计没有影响。

Analysis of Bias and Variance

偏差与方差分析

In this section we prove that MAC does not increase variance over sampled-action actor-critic (AC), and also, that given a fixed ${\widehat{Q}},$ both algorithms have the same bias. We start with tbhe bias result.

在本节中，我们证明MAC不会增加基于采样动作的演员-评论家(AC)方法的方差，并且给定固定的${\widehat{Q}}$时，两种算法具有相同的偏差。我们从偏差结果开始分析。

Theorem 1

定理 1

If the estimated Q-values, $\widehat{Q}(s,a;\omega)$ , for both MAC and AC are the same in ex pbectation, then the bias of MAC is equal to the bias of AC.

如果 MAC 和 AC 的估计 Q 值 $\widehat{Q}(s,a;\omega)$ 在期望上相同，那么 MAC 的偏差等于 AC 的偏差。

Proof

证明

See Appendix A.

见附录 A。

This result makes sense because in expectation, AC will choose all of the possible actions with some probability according to the policy. MAC simply calculates this expectation over actions explicitly. We now move to the variance result.

这一结果合乎预期，因为AC算法会依据策略以某种概率选择所有可能的动作。MAC则显式地计算了这些动作的期望值。接下来我们讨论方差结果。

Theorem 2

定理 2

If the estimated Q-values, $\widehat{Q}(s,a;\omega)$ , for both MAC and AC are the same in ex pebctation, and if $\widehat{Q}(s,a;\omega)$ is independent of $\widehat{Q}(s^{\prime},a^{\prime};\dot{\omega})$ for $(s,a)\neq(s^{\prime},a^{\prime})$ , then $\mathrm{Var}[\mathrm{M}\hat{\mathrm{A}}C]\leq\mathrm{Var}[\mathrm{AC}]$ . For deterministic policies, there is equality, and for stochastic policies the inequality is strict.

如果MAC和AC的估计Q值 $\widehat{Q}(s,a;\omega)$ 在期望上相同，且对于 $(s,a)\neq(s^{\prime},a^{\prime})$ ， $\widehat{Q}(s,a;\omega)$ 与 $\widehat{Q}(s^{\prime},a^{\prime};\dot{\omega})$ 相互独立，那么 $\mathrm{Var}[\mathrm{M}\hat{\mathrm{A}}C]\leq\mathrm{Var}[\mathrm{AC}]$ 。对于确定性策略，等式成立；对于随机策略，不等式严格成立。

Proof

证明

See Appendix B.

见附录 B。

Intuitively, we can see that for cases where the policy is deterministic, MAC’s formulation of the policy gradient is exactly equivalent to AC, and hence we can do no better than AC. For high-entropy policies, MAC will beat AC in terms of variance.

直观上可以看出，对于确定性策略的情况，MAC的策略梯度公式与AC完全等价，因此我们无法做得比AC更好。而对于高熵策略，MAC在方差方面会优于AC。

Algorithm	CartPole	LunarLander
REINFORCE	109.5±13.3	101.1 ±10.5
Adv.REINFORCE	121.8±11.2	114.7±8.1
Actor-Critic	138.7±13.2	124.6±5.1
Adv.Actor-Critic	157.4±6.4	162.8±14.9
MAC	178.3±7.6	163.5±12.8

算法	CartPole	LunarLander
REINFORCE	109.5±13.3	101.1±10.5
Adv.REINFORCE	121.8±11.2	114.7±8.1
Actor-Critic	138.7±13.2	124.6±5.1
Adv.Actor-Critic	157.4±6.4	162.8±14.9
MAC	178.3±7.6	163.5±12.8

Table 1: Performance summary of MAC vs. sampledaction policy gradient algorithms. Scores denote the mean performance of each algorithm over all trials and episodes.

表 1: MAC与抽样动作策略梯度算法的性能对比。分数表示各算法在所有试验和回合中的平均表现。

Experiments

实验

This section presents an empirical evaluation of MAC across three different problem domains. We first evaluate the performance of MAC versus popular policy gradient benchmarks on two classic control problems. We then evaluate MAC on a subset of Atari 2600 games and investigate its performance compared to state-ofthe-art policy search methods.

本节通过三个不同问题领域对MAC进行实证评估。我们首先在两个经典控制问题上比较MAC与主流策略梯度基准的性能表现。随后在Atari 2600游戏子集上评估MAC，并对比其与最先进策略搜索方法的性能表现。

Classic Control Experiments

经典控制实验

In order to determine whether MAC’s lower variance policy gradient estimate translates to faster learning, we chose two classic control problems, namely Cart Pole and Lunar Lander, and compared MAC’s performance against four standard sampled-action policy gradient algorithms. We used the open-source implementations of Cart Pole and Lunar Lander provided by OpenAI Gym (Brockman et al. 2016), in which both domains have continuous state spaces and discrete action spaces. Screenshots of the two domains are pro- vided in Figure 1.

为了验证MAC的低方差策略梯度估计是否能带来更快的收敛速度，我们选取了倒立摆(Cart Pole)和月球着陆器(Lunar Lander)两个经典控制问题，将MAC与四种标准采样动作策略梯度算法进行对比。实验采用OpenAI Gym (Brockman et al. 2016)提供的开源环境，这两个场景均具有连续状态空间和离散动作空间。图1展示了两个任务的界面截图。

For each problem domain, we implemented MAC using two independent neural networks, representing the policy and Q function. We then performed a hyper parameter search to determine the best network archi tec ture s, optimization method, and learning rates. Specifically, the hyper parameter search considered: 0, 1, 2, or 3 hidden layers; 50, 75, 100, or 300 neurons per layer; ReLU, Leaky ReLU (with leak factor 0.3), or tanh activation; SGD, RMSProp, Adam, or Adadelta as the optimization method; and a learning rate chosen from 0.0001, 0.00025, 0.0005, 0.001, 0.005, 0.01, or 0.05. To find the best setting, we ran 10 independent trials for each combination of hyper parameters and chose the setting with the best asymptotic performance over the 10 trials. We terminated each episode after 200 and 1000 timesteps (in Cart Pole and Lunar Lander, respectively), regardless of the state of the agent.

针对每个问题领域，我们采用两个独立的神经网络分别实现策略函数和Q函数的MAC系统。通过超参数搜索确定了最佳网络架构、优化方法和学习率。具体搜索范围包括：0/1/2/3个隐藏层；每层50/75/100/300个神经元；ReLU/Leaky ReLU(泄漏因子0.3)/tanh激活函数；SGD/RMSProp/Adam/Adadelta优化方法；以及从0.0001/0.00025/0.0005/0.001/0.005/0.01/0.05中选择学习率。每种超参数组合进行10次独立试验，选择10次试验中渐近性能最佳的组合。在Cart Pole和Lunar Lander环境中，分别设置200和1000个时间步长作为单次试验的终止条件，与智能体状态无关。

We compared MAC against four standard benchmarks: REINFORCE, advantage REINFORCE, actorcritic, and advantage actor-critic. We implemented the REINFORCE benchmarks using just a single neural network to represent the policy, and we implemented the actor-critic benchmarks using two networks to represent both the policy and Q function. For each benchmark algorithm, we then performed the same hyperparameter search that we had used for MAC.

我们将MAC与四种标准基准进行了比较：REINFORCE、优势REINFORCE、actor-critic以及优势actor-critic。我们仅使用单个神经网络来表示策略来实现REINFORCE基准，而actor-critic基准则采用两个网络分别表示策略和Q函数。针对每种基准算法，我们执行了与MAC相同的超参数搜索。

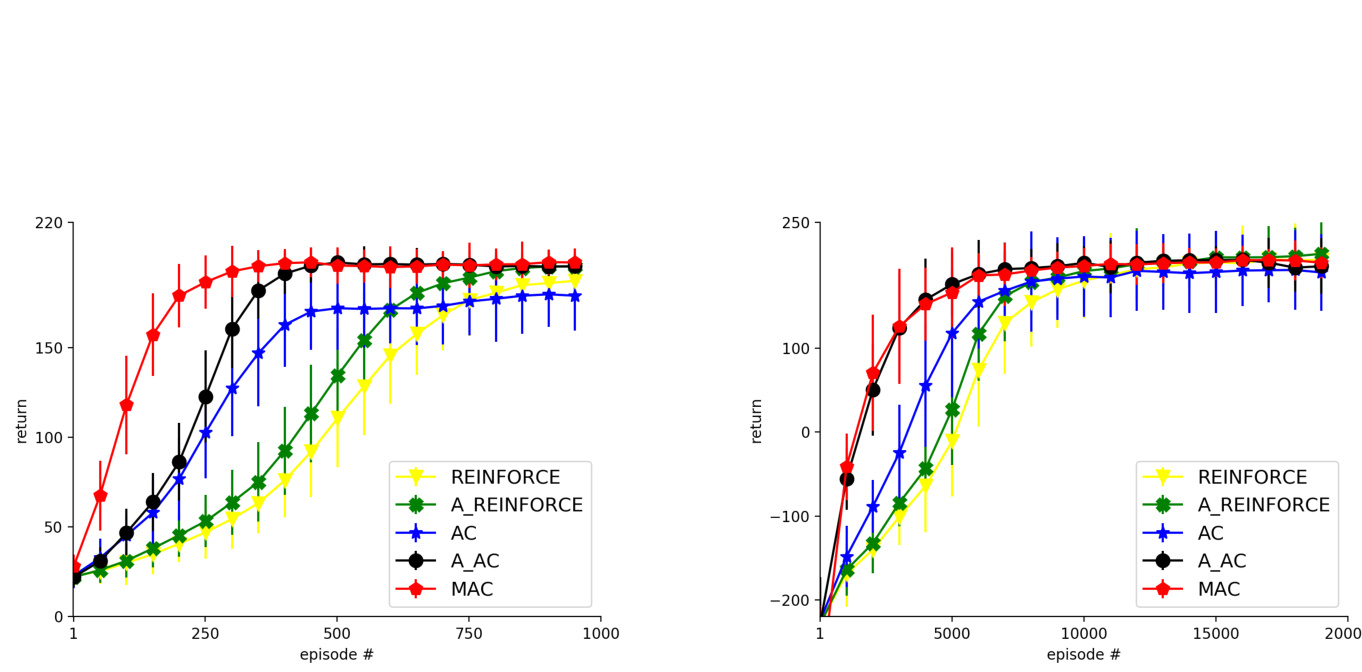
Figure 2: Performance comparison for CartPole (left) and Lunar Lander (right) of MAC vs. sampled-action policy gradient algorithms. Results are averaged over 100 independent trials.

图 2: MAC与采样动作策略梯度算法在CartPole(左)和Lunar Lander(右)任务上的性能对比。结果基于100次独立试验取平均值。

In order to keep the variance as low as possible for the advantage actor-critic benchmark, we explicitly computed the advantage function $A(s,a)=Q\dot{(}s,a)\stackrel{\smile}{-}$ $V(s)$ , where $\begin{array}{r}{V(s)=\sum_{a}\pi(a|s)Q(s,a).}\end{array}$ , rather than sampling it using the TD-error (see Section 2).

为了尽可能降低优势演员-评论家基准的方差，我们显式计算了优势函数 $A(s,a)=Q\dot{(}s,a)\stackrel{\smile}{-}$ $V(s)$ ，其中 $\begin{array}{r}{V(s)=\sum_{a}\pi(a|s)Q(s,a).}\end{array}$ ，而非使用TD误差进行采样(见第2节)。

Once we had determined the best hyper parameter settings for MAC and each of the benchmark algorithms, we then ran each algorithm for 100 independent trials. Figure 2 shows learning curves for the different algorithms, and Table 1 summarizes the results using the mean performance over trials and episodes. On Cart Pole, MAC learns substantially faster than all of the benchmarks, and on Lunar Lander, it performs competitively with the best benchmark algorithm, advantage actor-critic.

在确定MAC及各基准算法的最佳超参数设置后，我们对每个算法进行了100次独立试验。图2展示了不同算法的学习曲线，表1则汇总了各试验轮次和回合的平均性能结果。在Cart Pole任务中，MAC的学习速度显著快于所有基准算法；而在Lunar Lander任务中，其表现与最优基准算法优势行动者-评论家(advantage actor-critic)相当。

Atari Experiments

Atari 实验

To test whether MAC can scale to larger problem domains, we evaluated it on several Atari 2600 games using the Arcade Learning Environment (ALE) (Bellemare et al. 2013) and compared MAC’s performance against that of state-of-the-art policy search methods, namely, Trust Region Policy Optimization (TRPO) (Schulman et al. 2015), Evolutionary Strategies (ES) (Salimans et al. 2017), and Advantage Actor-Critic (A2C) (Wu et al. 2017). Due to the computational load inherent in training deep networks to play Atari games, we limited our experiments to a subset of six Atari games: Beamrider, Breakout, Pong, Q*bert, Seaquest and Space Invaders. These s