Knowledge Editing for Large Language Models: A Survey

大语言模型知识编辑研究综述

SONG WANG, University of Virginia, USA YAOCHEN ZHU, University of Virginia, USA HAOCHEN LIU, University of Virginia, USA ZAIYI ZHENG, University of Virginia, USA CHEN CHEN, University of Virginia, USA JUNDONG LI, University of Virginia, USA

SONG WANG, 美国弗吉尼亚大学
YAOCHEN ZHU, 美国弗吉尼亚大学
HAOCHEN LIU, 美国弗吉尼亚大学
ZAIYI ZHENG, 美国弗吉尼亚大学
CHEN CHEN, 美国弗吉尼亚大学
JUNDONG LI, 美国弗吉尼亚大学

Large Language Models (LLMs) have recently transformed both the academic and industrial landscapes due to their remarkable capacity to understand, analyze, and generate texts based on their vast knowledge and reasoning ability. Nevertheless, one major drawback of LLMs is their substantial computational cost for pre-training due to their unprecedented amounts of parameters. The disadvantage is exacerbated when new knowledge frequently needs to be introduced into the pre-trained model. Therefore, it is imperative to develop effective and efficient techniques to update pre-trained LLMs. Traditional methods encode new knowledge in pre-trained LLMs through direct fine-tuning. However, naively re-training LLMs can be computationally intensive and risks degenerating valuable pre-trained knowledge irrelevant to the update in the model. Recently, Knowledge-based Model Editing (KME), also known as Knowledge Editing or Model Editing, has attracted increasing attention, which aims to precisely modify the LLMs to incorporate specific knowledge, without negatively influencing other irrelevant knowledge. In this survey, we aim to provide a comprehensive and in-depth overview of recent advances in the field of KME. We first introduce a general formulation of KME to encompass different KME strategies. Afterward, we provide an innovative taxonomy of KME techniques based on how the new knowledge is introduced into pre-trained LLMs, and investigate existing KME strategies while analyzing key insights, advantages, and limitations of methods from each category. Moreover, representative metrics, datasets, and applications of KME are introduced accordingly. Finally, we provide an in-depth analysis regarding the practicality and remaining challenges of KME and suggest promising research directions for further advancement in this field.

大语言模型 (LLMs) 凭借其基于海量知识和推理能力的文本理解、分析与生成能力，近期彻底改变了学术界和工业界的格局。然而，LLMs 的一个主要缺点在于其空前庞大的参数量导致预训练计算成本极高。当需要频繁向预训练模型注入新知识时，这一劣势更为突出。因此，开发高效更新预训练 LLMs 的技术势在必行。传统方法通过直接微调将新知识编码到预训练 LLMs 中，但这种简单重训练不仅计算密集，还可能破坏模型中与更新无关的宝贵预训练知识。近年来，基于知识的模型编辑 (Knowledge-based Model Editing, KME) 日益受到关注，其目标是在不影响其他无关知识的前提下，精准修改 LLMs 以融入特定知识。本综述旨在全面深入地概述 KME 领域的最新进展：首先提出涵盖各类 KME 策略的通用框架；随后根据新知识注入预训练 LLMs 的方式建立创新分类体系，系统考察现有 KME 方法并分析各类技术的核心思想、优势与局限；进而介绍代表性评估指标、数据集和应用场景；最后深入探讨 KME 的实用性与现存挑战，并指出该领域未来发展的潜在研究方向。

CCS Concepts: • Computing methodologies $\rightarrow$ Natural language processing.

CCS概念：• 计算方法 $\rightarrow$ 自然语言处理。

Keywords: Model Editing, Knowledge Update, Fine-tuning, Large Language Models

关键词：模型编辑 (Model Editing)、知识更新 (Knowledge Update)、微调 (Fine-tuning)、大语言模型

ACM Reference Format: Song Wang, Yaochen Zhu, Haochen Liu, Zaiyi Zheng, Chen Chen, and Jundong Li. 2024. Knowledge Editing for Large Language Models: A Survey. 1, 1 (September 2024), 35 pages. https://doi.org/10.1145/nnnnnnn.nnnnnnn

ACM参考格式: Song Wang, Yaochen Zhu, Haochen Liu, Zaiyi Zheng, Chen Chen, and Jundong Li. 2024. 大语言模型知识编辑综述. 1, 1 (2024年9月), 35页. https://doi.org/10.1145/nnnnnnn.nnnnnnn

1 INTRODUCTION

1 引言

Recently, large language models (LLMs) have become a heated topic that revolutionizes both academia and industry [10, 109, 144, 173]. With the substantial factual knowledge and reasoning ability gained from pre-training on large corpora, LLMs have exhibited an unprecedented under standing of textual information, which are able to analyze and generate texts akin to human experts [84, 87, 135, 138, 176]. Nevertheless, one main drawback of LLMs is the extremely high computational overhead of the training process due to the large amounts of parameters [59, 64, 179]. This is exacerbated by the continuous evolvement of the world where the requirement of updating pre-trained LLMs to rectify obsolete information or incorporate new knowledge to maintain their relevancy is constantly emerging [85, 92, 128, 134]. For example, as in Fig. 1, the outdated LLM,

近来，大语言模型(LLM)已成为颠覆学术界和工业界的热门话题 [10, 109, 144, 173]。通过在海量语料上进行预训练获得的事实性知识与推理能力，大语言模型展现出对文本信息的空前理解力，能够像人类专家般分析和生成文本 [84, 87, 135, 138, 176]。然而，大语言模型的主要缺陷在于其庞大参数量导致的极高训练计算开销 [59, 64, 179]。随着世界持续演进，为修正过时信息或吸纳新知识以保持相关性，需要不断更新预训练大语言模型，这进一步加剧了计算负担 [85, 92, 128, 134]。例如图1所示，过时的大语言模型...

Fig. 1. An example of KME for efficient update of knowledge in LLMs.

图 1: 大语言模型中知识高效更新的KME示例。

GPT-3.5, cannot precisely describe the latest achievements of the famous soccer player Lionel Messi, which requires an explicit injection of new knowledge to generate the correct answers.

GPT-3.5 无法准确描述著名足球运动员 Lionel Messi 的最新成就，这需要显式注入新知识才能生成正确答案。

One feasible while straightforward strategy for updating pre-trained LLMs is through naive fine-tuning [20, 31, 141, 161], where parameters of pre-trained LLMs are directly optimized to encode new knowledge from new data [6, 99, 111, 173]. For example, various instruction-tuning methods are proposed to fine-tune pre-trained LLMs on newly collected data in a supervised learning manner [100, 112, 157, 159]. Although such fine-tuning techniques are widely used and capable of injecting new knowledge into LLMs, they are known for the following disadvantages: (1) Even with parameter-efficient strategies to improve efficiency [89, 158, 170], fine-tuning LLMs may still require intensive computational resources [97, 102, 174]. (2) Fine-tuning LLMs alters the pre-trained parameters without constraints, which can lead to the over fitting problem, where LLMs face the risk of losing valuable existing knowledge [172].

更新预训练大语言模型的一种可行且直接的策略是通过朴素微调 [20, 31, 141, 161]，即直接优化预训练大语言模型的参数以从新数据中编码新知识 [6, 99, 111, 173]。例如，研究者提出了多种指令微调方法，以监督学习方式在新收集的数据上对预训练大语言模型进行微调 [100, 112, 157, 159]。尽管此类微调技术被广泛使用且能够向大语言模型注入新知识，但它们存在以下缺点：(1) 即使采用参数高效策略提升效率 [89, 158, 170]，微调大语言模型仍可能需要大量计算资源 [97, 102, 174]。(2) 微调会无约束地改变预训练参数，可能导致过拟合问题，使大语言模型面临丢失宝贵已有知识的风险 [172]。

To address the drawbacks of updating LLMs with naive fine-tuning, more attention has been devoted to Knowledge-based Model Editing1 (KME). In general, KME aims to precisely modify the behavior of pre-trained LLMs to update specific knowledge, without negatively influencing other pre-trained knowledge irrelevant to the updates [116, 152, 167]. In KME, the update of a specific piece of knowledge in LLMs is typically formulated as an edit, such as rectifying the answer to “Who is the president of the USA?” from “Trump” to “Biden”. Regarding a specific edit, KME strategies typically modify the model output by either introducing an auxiliary network (or set of parameters) into the pre-trained model [52, 79, 175] or updating the (partial) parameters to store the new knowledge [22, 49, 51, 83]. Through these strategies, KME techniques can store new knowledge in new parameters or locate it in model parameters for updating, thereby precisely injecting the knowledge into the model. In addition, certain methods further introduce optimization constraints to ensure that the edited model maintains consistent behaviors on unmodified knowledge [13, 106, 177]. With these advantages, KME techniques can provide an efficient and effective way to constantly update LLMs with novel knowledge without explicit model re-training [172].

为了解决通过简单微调更新大语言模型(LLM)的缺陷，研究者们将更多注意力转向了基于知识的模型编辑(KME)。总体而言，KME旨在精确修改预训练大语言模型的行为以更新特定知识，同时避免对与更新无关的其他预训练知识产生负面影响[116, 152, 167]。在KME中，对大语言模型中特定知识的更新通常被表述为一个编辑操作，例如将"美国总统是谁？"的答案从"特朗普"修正为"拜登"。针对具体编辑操作，KME策略通常通过两种方式修改模型输出：要么在预训练模型中引入辅助网络（或参数集）[52, 79, 175]，要么更新（部分）参数以存储新知识[22, 49, 51, 83]。通过这些策略，KME技术可以将新知识存储在新参数中，或定位到待更新的模型参数中，从而精确地将知识注入模型。此外，某些方法还引入了优化约束，确保编辑后的模型在未修改知识上保持行为一致[13, 106, 177]。凭借这些优势，KME技术能够提供一种高效且有效的方式，无需显式重新训练模型即可持续更新大语言模型的新知识[172]。

While sharing certain similarities with fine-tuning strategies, KME poses unique advantages in updating LLMs, which are worthy of deeper investigations. Particularly, both KME and model fine-tuning seek to update pre-trained LLMs with new knowledge. However, aside from this shared objective, KME focuses more on two crucial properties that cannot be easily addressed by finetuning. (1) Locality requires that KME does not unintentionally influence the output of other irrelevant inputs with distinct semantics. For example, when the edit regarding the president of the USA is updated, KME should not alter its knowledge about the prime minister of the UK. The practicality of KME methods largely relies on their ability to maintain the outputs for unrelated inputs, which serves as a major difference between KME and fine-tuning [117]. (2) Generality represents whether the edited model can generalize to a broader range of relevant inputs regarding the edited knowledge. Specifically, it indicates the model’s capability to present consistent behavior on inputs that share semantic similarities. For example, when the model is edited regarding the president, the answer to the query about the leader or the head of government should also change accordingly. In practice, it is important for KME methods to ensure that the edited model can adapt well to such related input texts. To summarize, due to these two unique objectives, KME remains a challenging task that requires specific strategies for satisfactory effectiveness.

虽然与微调策略有某些相似之处，但知识模型编辑(KME)在更新大语言模型方面具有独特优势，值得深入研究。具体而言，KME和模型微调都试图用新知识更新预训练的大语言模型。然而，除了这一共同目标外，KME更关注两个无法通过微调轻易解决的关键特性：(1) 局部性要求KME不会无意中影响其他语义无关的输入输出。例如，当更新关于美国总统的编辑时，KME不应改变其对英国首相的知识。KME方法的实用性很大程度上取决于其保持无关输入输出的能力，这是KME与微调的主要区别[117]。(2) 通用性表示编辑后的模型是否能将编辑知识推广到更广泛的相关输入。具体而言，它反映了模型在语义相似输入上表现一致行为的能力。例如，当对总统相关信息进行编辑时，关于领导人或政府首脑的查询答案也应相应改变。实践中，KME方法必须确保编辑后的模型能良好适应此类相关输入文本。总之，由于这两个独特目标，KME仍是一项需要特定策略才能获得满意效果的挑战性任务。

Differences between this survey and existing ones. Several surveys have been conducted to examine various aspects of (large) language models [12, 34, 71, 73, 142, 173]. Nevertheless, there is still a dearth of thorough investigations of existing literature and continuous progress in editing LLMs. For example, recent works [100, 159] have discussed the fine-tuning strategies that inject new knowledge in pre-trained LLMs with more data samples. However, the distinctiveness of KME, i.e., locality and generality, is not adequately discussed, which will be thoroughly analyzed in this survey. Two other surveys [35, 63] review knowledge-enhanced language models. However, they mainly focus on leveraging external knowledge to enhance the performance of the pre-trained LLMs, without addressing the editing task based on specific knowledge. To the best of our knowledge, the most related work [167] to our survey provides a brief overview of KME and concisely discusses the advantages of KME methods and their challenges. Nevertheless, the investigation lacks a thorough examination of more details of KME, e.g., categorizations, datasets, and applications. The following work [172] additionally includes experiments with classic KME methods. Another recent work [152] proposes a framework for KME that unifies several representative methods. This work focuses on the implementation of KME techniques, with less emphasis on the technical details of different strategies. A more recent study [116] discusses the limitations of KME methods regarding the faithfulness of edited models, while it is relatively short and lacks a more comprehensive introduction to all existing methods. Considering the rapid advancement of KME techniques, we believe it is imperative to review the details of all representative KME methods, summarize the common ali ties while discussing the uniqueness of each method, and discuss open challenges and prospective directions in the domain of KME to facilitate further advancement.

本综述与现有研究的差异。已有若干综述研究探讨了(大)语言模型的各个方面[12, 34, 71, 73, 142, 173]。然而，目前仍缺乏对现有文献的系统梳理及对大语言模型编辑技术持续进展的全面考察。例如，近期研究[100, 159]讨论了通过更多数据样本向预训练大语言模型注入新知识的微调策略，但未充分探讨知识模型编辑(KME)的核心特性——局部性与泛化性，这将是本综述的重点分析内容。另有两篇综述[35, 63]回顾了知识增强的语言模型，但其主要关注利用外部知识提升预训练模型性能，未涉及基于特定知识的编辑任务。据我们所知，与本研究最相关的工作[167]简要概述了KME并讨论了其优势与挑战，但缺乏对KME分类体系、数据集和应用场景等细节的深入考察。后续研究[172]补充了经典KME方法的实验验证，近期工作[152]提出了统一多种代表性方法的KME框架，但更侧重技术实现而非不同策略的细节分析。最新研究[116]探讨了KME方法在模型编辑忠实度方面的局限，但篇幅较短且未全面介绍现有方法。鉴于KME技术的快速发展，我们认为亟需：系统梳理所有代表性KME方法的技术细节，在讨论各方法独特性的同时总结共性特征，并探讨该领域的开放挑战与发展方向以推动后续研究。

Contributions of this survey. This survey provides a comprehensive and in-depth analysis of techniques, challenges, and opportunities associated with the editing of pre-trained LLMs. We first provide an overview of KME tasks along with an innovative formulation. Particularly, we formulate the general KME task as a constrained optimization problem, which simultaneously incorporates the goals of accuracy, locality, and generality. We then classify the existing KME strategies into three main categories, i.e., external memorization, global op tim z ation, and local modification. More importantly, we demonstrate that methods in each category can be formulated as a specialized constrained optimization problem, where the characteristics are theoretically summarized based on the general formulation. In addition, we provide valuable insights into the effectiveness and feasibility of methods in each category, which can assist practitioners in selecting the most suitable KME method tailored to a specific task. Our analysis regarding the strengths and weaknesses of KME methods also serves as a catalyst for ongoing progress within the KME research community. In concrete, our key contributions can be summarized into three folds as follows:

本综述的贡献。本综述对预训练大语言模型(LLM)编辑相关的技术、挑战与机遇进行了全面深入的分析。我们首先概述了知识模型编辑(KME)任务并提出创新性形式化框架，特别地将通用KME任务构建为同时兼顾准确性、局部性与通用性目标的约束优化问题。随后将现有KME策略系统归类为外部记忆、全局优化和局部修改三大范式，并论证每类方法均可视为特定约束优化问题的求解方案，基于通用框架从理论层面总结了各类方法的特征。此外，我们针对不同范式方法的有效性与可行性提供了实用洞见，可帮助从业者根据具体任务选择最适合的KME方法。关于KME方法优缺点的分析结论也将推动该研究领域的持续发展。具体而言，我们的核心贡献可归纳为以下三方面：

• Novel Categorization. We introduce a comprehensive and structured categorization framework to systematically summarize the existing works for LLM editing. Specifically, based on how the new knowledge is introduced into pre-trained LLMs, our categorization encompasses three distinct categories: external memorization, global optimization, and local modification, where their common ali ty and differences are thoroughly discussed in this survey. • In-Depth Analysis. We formulate the task of KME as a constrained optimization problem, where methods from each category can be viewed as a special case with refined constraints. Furthermore, we emphasize the primary insights, advantages, and limitations of each category. Within this context, we delve deep into representative methods from each category and systematically analyze their interconnections.

• 新颖分类。我们提出了一个全面且结构化的分类框架，系统性地总结现有的大语言模型编辑方法。具体而言，根据新知识如何被引入预训练大语言模型，我们的分类体系包含三个独立类别：外部记忆 (external memorization)、全局优化 (global optimization) 和局部修改 (local modification)，本综述深入探讨了它们的共性与差异。
• 深度分析。我们将知识模型编辑 (KME) 任务形式化为约束优化问题，其中每个类别的方法都可视为具有特定约束条件的特例。此外，我们重点分析了各类别的主要思路、优势与局限性。在此框架下，我们深入剖析了各类别的代表性方法，并系统性地解析了它们之间的关联。

• Future Directions. We analyze the practicality of existing KME techniques regarding a variety of datasets and applications. We also comprehensively discuss the challenges of the existing KME techniques and suggest promising research directions for future exploration.

• 未来方向。我们分析了现有知识图谱嵌入 (KME) 技术在不同数据集和应用中的实用性，全面探讨了当前技术面临的挑战，并为未来研究提出了潜在探索方向。

The remainder of this paper is organized as follows. Section 2 introduces the background knowledge for KME. Section 3 provides a general formulation of the KME task, which can fit into various application scenarios. Section 4 provides a comprehensive summary of evaluation metrics for KME strategies, which is crucial for a fair comparison across various methods. Before delving into the specific methods, we provide a comprehensive categorization of existing methods into three classes in Section 5.1, where their relationship and differences are thoroughly discussed. Then we introduce the methods from the three categories in detail, where the advantages and limitations of each category are summarized. Section 6 introduces the prevalent ly used public datasets. Section 7 provides a thorough introduction to various realistic tasks that can benefit from KME techniques. Section 8 discusses the potential challenges of KME that have not been addressed by existing techniques. This section also provides several potential directions that can inspire future research. Lastly, we conclude this survey in Section 9.

本文的其余部分组织如下。第2节介绍KME的背景知识。第3节给出KME任务的通用表述，可适配多种应用场景。第4节全面总结KME策略的评估指标，这对各种方法间的公平比较至关重要。在深入具体方法前，我们在第5.1节将现有方法系统划分为三类，并详细讨论其关联与差异。随后详细阐述这三类方法，并总结每类方法的优势与局限。第6节介绍广泛使用的公开数据集。第7节全面介绍可受益于KME技术的各类现实任务。第8节讨论现有技术尚未解决的KME潜在挑战，并提出若干可能启发未来研究的方向。最后，第9节对本次综述进行总结。

2 BACKGROUND

2 背景

In this section, we provide an overview of the editing strategies for machine learning models and the basics of large language models (LLMs) as background knowledge to facilitate the understanding of technical details in KME. In this survey, we use bold uppercase letters (e.g., K and V) to represent matrices, use lowercase bold letters (e.g., k and v) to represent vectors, and use calligraphic uppercase letters (e.g., $\chi$ and $_y$ ) to represent sets. We summarize the primary notations used in this survey in Table 1 for the convenience of understanding.

在本节中，我们概述了机器学习模型的编辑策略和大语言模型(LLM)的基础知识，作为理解KME技术细节的背景知识。本综述使用加粗大写字母(如K和V)表示矩阵，小写加粗字母(如k和v)表示向量，花体大写字母(如$\chi$和$_y$)表示集合。为便于理解，我们在表1中总结了本综述使用的主要符号。

2.1 Editing of Machine Learning Models

2.1 机器学习模型的编辑

Machine learning models [41, 54, 74] pre-trained on large datasets frequently serve as foundation models for various tasks in the real-world [26, 126]. In practical scenarios, there is often a need to modify these pre-trained models to enhance the performance for specific downstream tasks [18, 20, 103, 164, 178], reduce biases or undesirable behaviors [39, 104, 113, 123], tailor models to align more closely with human preferences [44, 72, 88], or incorporate novel information [101, 167, 177].

基于大规模数据集预训练的机器学习模型 [41, 54, 74] 常作为现实任务的基础模型 [26, 126]。实际应用中，通常需要调整这些预训练模型以：提升特定下游任务性能 [18, 20, 103, 164, 178]、减少偏见或不良行为 [39, 104, 113, 123]、使模型更贴合人类偏好 [44, 72, 88]，或融入新信息 [101, 167, 177]。

Model Editing is a special type of model modification strategy where the modification should be as precise as possible. Nevertheless, it should accurately modify the pre-trained model to encode specific knowledge while maximally preserving the existing knowledge, without affecting their behavior on unrelated inputs [68]. First explored in the computer vision field, Bau et al. [8] investigate the potential of editing generative adversarial networks (GAN) [45] by viewing an intermediate layer as a linear memory, which can be manipulated to incorporate novel content. Afterward, Editable Training [133] is proposed to encourage fast editing of the trained model in a model-agnostic manner. The goal is to change the model predictions on a subset of inputs corresponding to mis classified objects, without altering the results for other inputs. In [125], the authors propose a method that allows for the modification of a classifier’s behavior by editing its decision rules, which can be used to correct errors or reduce biases in model predictions. In the field of natural language processing, several works [22, 102] have been proposed to perform editing regarding textual information. Specifically, Zhu et al. [177] propose a constrained fine-tuning loss to explicitly modify specific factual knowledge in transformer-based models [146]. More recent works [42, 43] discover that the MLP layers in transformers actually act as key-value memories, thereby enabling the editing of specific knowledge within the corresponding layers.

模型编辑是一种特殊的模型修改策略，其修改应尽可能精确。它需要准确调整预训练模型以编码特定知识，同时最大限度保留现有知识，且不影响模型在无关输入上的行为 [68]。该技术最早在计算机视觉领域展开探索，Bau等人 [8] 通过将生成对抗网络(GAN) [45] 的中间层视为可线性操作的内存空间，研究了编辑GAN以融入新内容的可能性。随后提出的可编辑训练(Editable Training) [133] 采用模型无关方式，旨在快速修改已训练模型，仅改变模型在误分类对象对应输入子集上的预测结果，同时保持其他输入的输出不变。[125] 中提出的方法通过编辑分类器决策规则来修正预测错误或减少偏差。在自然语言处理领域，多项研究 [22, 102] 实现了文本信息的编辑操作。Zhu等人 [177] 提出约束微调损失函数，专门用于修改基于Transformer [146] 模型中的特定事实知识。最新研究 [42, 43] 发现Transformer中的MLP层实质充当键值存储器，从而实现对特定知识层的精准编辑。

Table 1. Important notations used in this survey.

Notations	Detailed Descriptions
x	Input (prompt) to LLMs
y	Output of LLMs
(x, y)	Input-output pair
t = (s,r,o)	Original knowledge triple (before editing)
s/r/o	Subject/Relation/Object in aknowledgetriple
t* = (s,r,o*)	Target knowledge triple (after editing)
e = (s,r,0 → o*)	Edit descriptor
Xe	In-scope input space
ye	Original output space (before editing)
y*	Target output space (after editing)
8={ei}	Set of edits
Oe	Out-scope input space
	Query/Key/Value vector for the i-th head of the I-th attention module in Transformer
ww	Weights of the fully connected layers of the I-th attention module in Transformer
h(l)	Output from the I-th self-attention module in Transformer
	Vector concatenation

表 1: 本综述使用的重要符号说明

符号	详细描述
x	大语言模型的输入 (prompt)
y	大语言模型的输出
(x, y)	输入-输出对
t = (s,r,o)	原始知识三元组 (编辑前)
s/r/o	知识三元组中的主语/关系/宾语
t* = (s,r,o*)	目标知识三元组 (编辑后)
e = (s,r,0 → o*)	编辑描述符
Xe	范围内输入空间
ye	原始输出空间 (编辑前)
y*	目标输出空间 (编辑后)
8={ei}	编辑集合
Oe	范围外输入空间
	Transformer 中第 I 个注意力模块第 i 个头对应的查询/键/值向量
ww	Transformer 中第 I 个注意力模块全连接层的权重
h(l)	Transformer 中第 I 个自注意力模块的输出
	向量拼接

2.2 Language Models

2.2 语言模型

2.2.1 Transformers. Transformers lie in the core of large language models (LLMs) [27, 121, 146]. The fully-fledged transformer possesses an encoder-decoder architecture initially designed for the neural machine translation (NMT) task [137]. Nowadays, transformers have found wide applications in most fields of the NLP community, beyond their original purpose. Generally, a transformer network is constructed from multiple stacks of the self-attention module with residual connections, which is pivotal for capturing contextual information from textual sequences. The self-attention module is composed of a self-attention layer (SelfAtt) and a point-wise feed-forward neural network layer (FFN) formulated as follows:

2.2.1 Transformer。Transformer 是大语言模型 (LLM) [27, 121, 146] 的核心架构。完整的 Transformer 采用最初为神经机器翻译 (NMT) 任务 [137] 设计的编码器-解码器结构。如今，Transformer 的应用已远超其原始用途，覆盖了自然语言处理领域的大部分方向。通常，Transformer 网络由多个带残差连接的自注意力模块堆叠而成，该结构对捕获文本序列的上下文信息至关重要。自注意力模块由自注意力层 (SelfAtt) 和逐点前馈神经网络层 (FFN) 构成，其公式表示如下：

$$
\begin{array}{r l}&{{\mathbf{h}}{i}^{A,(l-1)}=\mathrm{SelfAtt}{i}\left({\mathbf{h}}{i}^{(l-1)}\right)=\mathrm{Softmax}\left({\mathbf{q}}{i}^{(l)}\left({\mathbf{k}}{i}^{(l)}\right)^{\top}\right){\mathbf{v}}{i}^{(l)},}\ &{{\mathbf{h}}^{F,(l-1)}=\mathrm{FFN}\left({\mathbf{h}}^{(l-1)}\right)=\mathrm{GELU}\left({\mathbf{h}}^{(l-1)}{\mathbf{W}}_{1}^{(l)}\right){\mathbf{W}}_{2}^{(l)},{\mathbf{h}}^{(0)}={\mathbf{x}},}\ &{{\mathbf{h}}^{(l)}={\mathbf{h}}^{A,(l-1)}+{\mathbf{h}}^{F,(l-1)}=\left\Vert_{i}\mathrm{SelfAtt}_{i}\left({\mathbf{h}}_{i}^{(l-1)}\right)+\mathrm{FFN}\left({\mathbf{h}}^{(l-1)}\right),}\end{array}
$$

where $\mathbf{q}{i}^{(l)},\mathbf{k}{i}^{(l)}$ , and $\mathbf{v}{i}^{(l)}$ represent the sequences of query, key, and value vectors for the $i$ -th attention head of the $l$ -th attention module, respectively. GELU is an activation function. They are calculated from $\mathbf{h}{i}^{(l-1)}$ , the $i$ -th slice of the outputs from the $(l-1)$ -th self-attention module (i.e., $\mathbf{h}^{(l-1)})$ , and $\mathbf{x}$ denotes the input sequence of token embeddings. $\parallel$ represents vector concatenation. Normalizing factors in the self-attention layer are omitted for simplicity.

其中 $\mathbf{q}{i}^{(l)}$、$\mathbf{k}{i}^{(l)}$ 和 $\mathbf{v}{i}^{(l)}$ 分别表示第 $l$ 个注意力模块中第 $i$ 个注意力头的查询 (query)、键 (key) 和值 (value) 向量序列。GELU 是一种激活函数。这些向量由第 $(l-1)$ 个自注意力模块输出的第 $i$ 个切片 $\mathbf{h}{i}^{(l-1)}$ (即 $\mathbf{h}^{(l-1)}$ ) 计算得出，$\mathbf{x}$ 表示token嵌入的输入序列。$\parallel$ 表示向量拼接。为简洁起见，省略了自注意力层中的归一化因子。

Generally, multi-head self-attention directs the model to attend to different parts of the sequence to predict the next token. Specifically, the prediction is based on different types of relationships and dependencies within the textual data, where the output $\mathbf{h}{i}^{A,(l-1)}$ is a weighted sum of the value vector of other tokens. In contrast, FFN adds new information h𝑖𝐹,(𝑙 −1) to the weighted sum of the embeddings of the attended tokens based on the information stored in the weights of the fully connected layers, i.e., $\mathbf{W}{1}^{(l)}$ and $\mathbf{W}{2}^{(l)}$ . The final layer outputs of the transformer, i.e., $\mathbf{h}^{(L)}$ , can be used in various downstream NLP tasks. For token-level tasks (e.g., part-of-speech tagging [19]), the entire hidden representation sequence $\mathbf{h}^{(L)}$ can be utilized to predict the target sequence. For the sequence-level tasks (e.g., sentiment analysis [160]), the hidden representation of the last token, i.e., $\mathbf{h}{-1}^{(L)}$ , can be considered as a summary of the sequence and thus used for the predictions.

通常，多头自注意力机制（multi-head self-attention）会引导模型关注序列的不同部分以预测下一个token。具体而言，预测基于文本数据中不同类型的关系和依赖，其中输出$\mathbf{h}{i}^{A,(l-1)}$是其他token值向量的加权和。相比之下，前馈神经网络（FFN）基于全连接层权重（即$\mathbf{W}{1}^{(l)}$和$\mathbf{W}{2}^{(l)}$）中存储的信息，向被关注token嵌入的加权和添加新信息$\mathbf{h}{i}^{F,(l-1)}$。Transformer的最终层输出$\mathbf{h}^{(L)}$可用于各种下游NLP任务：对于token级任务（如词性标注[19]），可利用整个隐藏表示序列$\mathbf{h}^{(L)}$来预测目标序列；对于序列级任务（如情感分析[160]），可将最后一个token的隐藏表示$\mathbf{h}_{-1}^{(L)}$视为序列的摘要并用于预测。

2.2.2 Large Language Models (LLMs). Transformers with billions of parameters trained on large corpora have demonstrated emergent ability, showcasing an unprecedented understanding of factual and commonsense knowledge [173]. Consequently, these models are referred to as large language models (LLMs) to indicate their drastic distinction from traditional small-scale language models [34, 142]. Generally, based on the specific parts of the transformer utilized for language modeling, existing LLMs can be categorized into three classes: encoder-only LLMs, such as BERT [74], encoder-decoder-based LLMs such as T5 [119], and decoder-only models (also the most common structure in LLMs) such as different versions of GPT [118] and LLaMA [144].

2.2.2 大语言模型 (LLMs)
基于数十亿参数并在大规模语料库上训练的Transformer模型展现出涌现能力 (emergent ability) [173]，表现出对事实和常识知识的空前理解。因此，这些模型被称为大语言模型 (LLMs) [34, 142]，以区别于传统小规模语言模型。根据Transformer中用于语言建模的具体模块，现有大语言模型可分为三类：仅编码器架构 (encoder-only) 如BERT [74]，编码器-解码器架构 (encoder-decoder) 如T5 [119]，以及仅解码器架构 (decoder-only) (也是当前大语言模型最常见结构) 如各版本GPT [118] 和LLaMA [144]。

2.3 Relevant Topics

2.3 相关主题

KME intersects with several extensively researched topics, yet these techniques cannot effectively address KME-specific challenges [141, 161]. The most relevant approach is model fine-tuning [6, 20, 99], including parameter-efficient fine-tuning [89, 158, 170], which requires fewer parameter updates. However, fine-tuning remains computationally intensive and is often impractical for blackbox LLMs [172, 173]. Another related area is machine unlearning [105], which aims to remove the influence of individual samples from models. Unlike KME, which focuses on abstract and generalized knowledge updates, machine unlearning targets the elimination of specific training data, making it unsuitable for KME. On the other hand, external memorization KME methods share similarities with RAG (retrieval-augmented generation) [40], where a large repository of documents is stored and retrieved as needed to provide con textually relevant information for generating responses. While RAG can introduce new knowledge into LLMs by retrieving recently added documents, it does not effectively update the inherent knowledge within LLMs. Thus, RAG is not suitable for the fundamental knowledge updates that KME seeks to achieve.

KME 与多个广泛研究领域存在交集，但这些技术无法有效解决 KME 特有的挑战 [141, 161]。最相关的方法是模型微调 (fine-tuning) [6, 20, 99]，包括参数高效微调 (parameter-efficient fine-tuning) [89, 158, 170]，后者所需的参数更新更少。然而微调仍存在计算成本高的问题，且通常不适用于黑盒大语言模型 [172, 173]。另一相关领域是机器遗忘 (machine unlearning) [105]，其目标是消除单个样本对模型的影响。与 KME 专注于抽象化、通用化的知识更新不同，机器遗忘针对的是特定训练数据的删除，因此不适用于 KME。另一方面，外部记忆型 KME 方法与 RAG (检索增强生成) [40] 存在相似性——后者通过存储海量文档库并按需检索，为生成响应提供上下文相关信息。虽然 RAG 能通过检索新增文档向大语言模型引入新知识，但无法有效更新模型内部固有知识。因此 RAG 并不适用于 KME 追求的基础性知识更新。

3 PROBLEM FORMULATION

3 问题描述

In this section, we provide a formal definition for the knowledge-based model editing (KME) task for pre-trained LLMs, where a general formulation of the KME objective is formulated to encompass specific KME strategies. The task of KME for LLMs can be broadly defined as the process of precisely modifying the behavior of pre-trained LLMs, such that new knowledge can be incorporated to maintain the current ness and relevancy of LLMs can be maintained, without negatively influencing other pre-trained knowledge irrelevant to the edits. To provide a clear formulation, we present the definitions of different terms used in KME, where the overall process is illustrated in Fig. 2.

在本节中，我们为预训练大语言模型的知识编辑任务 (KME) 提供了正式定义，其中制定了 KME 目标的通用公式以涵盖特定的 KME 策略。大语言模型的 KME 任务可广义定义为：通过精确修改预训练大语言模型的行为，使其能够融入新知识以保持模型时效性与相关性，同时不影响与编辑无关的其他预训练知识。为明确表述，我们给出了 KME 中使用的各项术语定义，整个过程如图 2 所示。

Editing Target. In this survey, we represent the knowledge required to be injected into LLMs as a knowledge triple $t=\left(s,r,o\right)$ , where $s$ is the subject (e.g., president of the USA), $r$ is the relation (e.g., is), and $o$ is the object (e.g., Biden). From the perspective of knowledge triple, the objective of KME for LLMs is to modify the original knowledge triple $t=\left(s,r,o\right)$ encoded in the pre-trained weights of the model into the target knowledge triple $t^{}=(s,r,o^{})$ , where $o^{}$ is the target object different from 𝑜. In this manner, we can define an edit as a tuple $e=\left(t,t^{}\right)=\left(s,r,o\rightarrow o^{}\right)$ , which denotes the update of the obsolete old knowledge $t$ into the new knowledge $t^{}$ .

编辑目标。在本综述中，我们将需要注入大语言模型的知识表示为知识三元组 $t=\left(s,r,o\right)$ ，其中 $s$ 是主体（如美国总统）， $r$ 是关系（如是）， $o$ 是客体（如Biden）。从知识三元组的角度来看，大语言模型的知识模型编辑（KME）目标是将模型预训练权重中编码的原始知识三元组 $t=\left(s,r,o\right)$ 修改为目标知识三元组 $t^{}=(s,r,o^{})$ ，其中 $o^{}$ 是与𝑜不同的目标客体。通过这种方式，我们可以将编辑定义为一个元组 $e=\left(t,t^{}\right)=\left(s,r,o\rightarrow o^{}\right)$ ，表示将过时的旧知识 $t$ 更新为新知识 $t^{}$ 。

Input and Output Space. Given a pair of subject 𝑠 and relation $r$ , in order to query LLMs to obtain the ob- ject $o$ , $(s,r)$ needs to be transformed into natural language, which we denoted as $x,x$ is also referred to as the prompt in this survey. The LLM output $y$ is also textual and can be converted back to an object 𝑜 as the query result. In this way, $(x,y)$ can

输入与输出空间。给定主体𝑠和关系$r$，为了通过查询大语言模型获取对象$o$，需要将$(s,r)$转换为自然语言，我们将其表示为$x$，在本综述中也称为提示(prompt)。大语言模型的输出$y$同样为文本形式，可转换回对象𝑜作为查询结果。由此，$(x,y)$可

Fig. 2. The formulation of the KME objective.

图 2: KME目标的公式化表达。

be considered as the natural language input-output pair associated with the knowledge triple $t=\left(s,r,o\right)$ . For example, the prompt $x$ transformed from 𝑠 and $r$ can be “The president of the USA is”, and $y$ is the model output “Joe Biden”. Note that due to the diversity of natural language, multiple $(x,y)$ pairs can be associated with the same knowledge triple 𝑡. We denote the set of textual inputs associated with subject 𝑠 and relation $r$ in an edit $e$ as $X_{e}=I(s,r)$ , referred to as in-scope input space. Similarly, we define the set of textual outputs that can be associated with the object $o$ in the same edit $e$ as $y_{e}^{}=O^{}(s,r,o^{})$ (i.e., target output space), and the original textual output space as $y_{e}=O(s,r,o)$ (i.e., original output space). Given an edit $e$ , the aim of KME is to modify the behavior of language models from $y_{e}$ to $y_{e}^{}$ , regarding the input in $X_{e}$ . To accommodate the scenarios where multiple edits are performed, we can define the union of $X_{e}$ over a set of edits ${\mathcal{E}}={e_{1},e_{2},\dots}$ as $\begin{array}{r}{\chi_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}\chi_{e}}\end{array}$ . Similarly, we can define $\begin{array}{r}{\mathfrak{y}_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}\mathfrak{y}_{e}}\end{array}$ and $\begin{array}{r}{\boldsymbol{{y}}_{\mathcal{E}}^{*}=\bigcup_{e\in\mathcal{E}}\boldsymbol{{y}}_{e}^{*}}\end{array}$ .

可视为与知识三元组$t=\left(s,r,o\right)$相关联的自然语言输入-输出对。例如，由𝑠和$r$转换而来的提示$x$可以是"美国总统是"，而$y$则是模型输出"乔·拜登"。需要注意的是，由于自然语言的多样性，同一知识三元组𝑡可能对应多个$(x,y)$对。我们将编辑$e$中与主语𝑠和关系$r$相关联的文本输入集合记为$X_{e}=I(s,r)$，称为输入作用域空间。类似地，定义同一编辑$e$中与宾语$o$相关联的目标文本输出空间为$y_{e}^{}=O^{}(s,r,o^{})$，原始文本输出空间为$y_{e}=O(s,r,o)$。给定编辑$e$，知识模型编辑(KME)的目标是将语言模型在$X_{e}$输入空间中的行为从$y_{e}$修改为$y_{e}^{}$。为适应多编辑场景，可定义编辑集合${\mathcal{E}}={e_{1},e_{2},\dots}$的输入空间并集为$\begin{array}{r}{\chi_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}\chi_{e}}\end{array}$，同理定义$\begin{array}{r}{\mathfrak{y}_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}\mathfrak{y}_{e}}\end{array}$和$\begin{array}{r}{\boldsymbol{{y}}_{\mathcal{E}}^{*}=\bigcup_{e\in\mathcal{E}}\boldsymbol{{y}}_{e}^{*}}\end{array}$。

Formulation. We denote the pre-trained LLM with parameter $\phi$ as $f:X\to y$ and the edited model with updated parameter $\phi^{}$ as $f^{}:X\to y^{}$ . The objective of knowledge-based model editing is to precisely update the pre-trained LLM $f$ into $f^{}$ according to edits in the edit set $\varepsilon$ such that for each edit $e$ and for each $y\in\mathcal{Y}_{e}$ , the changes to the input-output pairs irrelevant to the edits is minimized. The problem of KME can be formulated as follows:

公式化。我们将参数为$\phi$的预训练大语言模型表示为$f:X\to y$，更新参数为$\phi^{}$的编辑后模型表示为$f^{}:X\to y^{}$。基于知识的模型编辑目标是根据编辑集$\varepsilon$中的每个编辑$e$，将预训练大语言模型$f$精确更新为$f^{}$，使得对于每个$y\in\mathcal{Y}_{e}$，与编辑无关的输入输出对变化最小化。该问题可表述为：

Definition 1. The objective for KME on a series of edits $\varepsilon$ is represented as follows:

定义 1. 在编辑序列 $\varepsilon$ 上的 KME 目标表示如下:

$$
.t.f^{*}(x)=f(x),\forall x\in X\backslash\chi_{\mathcal{E}},
$$

where $\mathcal{L}$ is a specific loss function that measures the discrepancy between the model output $f^{}(x)$ and $y^{}$ from the desirable response set $y_{e}^{*}$ $\therefore M(f;{\mathcal{E}})$ denotes the modification applied to $f$ based on the desirable edits $\varepsilon$ .

其中 $\mathcal{L}$ 是衡量模型输出 $f^{}(x)$ 与期望响应集 $y_{e}^{}$ 中 $y^{*}$ 之间差异的特定损失函数，因此 $M(f;{\mathcal{E}})$ 表示基于期望编辑 $\varepsilon$ 对 $f$ 进行的修改。

From the above definition, we can summarize two crucial perspectives regarding the objective of KME: (1) Generality, which requires that the correct answers in the target output space $y_{e}^{}$ can be achieved, provided prompts in the in-scope input space, i.e., $X_{e}$ , where the target knowledge triple $t^{}\in e$ can be updated into the pre-trained model; (2) Locality, which requires the consistency of model output regarding unrelated input, i.e., $\chi\backslash\chi_{\varepsilon}$ , where valuable pre-trained knowledge can be maximally preserved after the editing. Here, we note that locality is especially important for editing LLMs, as the knowledge that needs to be updated often occupies only a small fraction of all knowledge encompassed by the pre-trained model. In other words, the output of an edited model regarding most input prompts should remain consistent with the output before editing.

从上述定义中，我们可以总结出关于KME目标的两个关键视角：(1) 通用性 (Generality) ，要求在目标输出空间 $y_{e}^{}$ 中能获得正确答案，前提是输入提示位于范围内输入空间 $X_{e}$ ，其中目标知识三元组 $t^{}\in e$ 可更新至预训练模型；(2) 局部性 (Locality) ，要求模型对无关输入 $\chi\backslash\chi_{\varepsilon}$ 的输出保持一致性，使得编辑后能最大限度保留有价值的预训练知识。此处需注意，局部性对大语言模型编辑尤为重要，因为需要更新的知识通常仅占预训练模型涵盖知识总量的极小部分。换言之，编辑后模型对大多数输入提示的输出应与编辑前保持一致。

4 EVALUATION METRICS

4 评估指标

Before introducing the taxonomy of KME and the exemplar methods in detail, in this section, we first discuss various metrics commonly used to evaluate the effectiveness of different KME

在详细介绍KME分类法和典型方法之前，本节首先讨论常用于评估不同KME有效性的各类指标

strategies from varied perspectives. We summarize the metrics to facilitate the understanding in terms of the properties and advantages of different methods.

我们从不同视角总结了策略，并通过归纳指标来帮助理解各类方法的特性与优势。

4.1 Accuracy

4.1 准确性

Accuracy is a straightforward metric for evaluating the effectiveness of KME techniques [17, 29, 79, 101, 106, 174, 175], defined as the success rate of editing in terms of a specific set of pre-defined input-output pairs $(x_{e},y_{e}^{})$ associated with all the edited knowledge. Accuracy can be easily defined to evaluate the performance of KME on classification tasks, e.g., fact checking [102, 114], where the answers $y$ are categorical. Defining the prompt and ground truth related to an edit $e$ as $x_{e}$ and $y_{e}^{}$ , respectively, the metric of the accuracy of an edited model $f^{*}$ is formulated as follows:

准确率是评估知识模型编辑(KME)技术有效性的直观指标[17, 29, 79, 101, 106, 174, 175]，其定义为针对所有待编辑知识关联的预定义输入-输出对$(x_{e},y_{e}^{})$的编辑成功率。该指标可轻松用于评估KME在分类任务(如事实核查[102, 114])中的表现，其中答案$y$为分类结果。将编辑$e$相关的提示词和真实值分别定义为$x_{e}$和$y_{e}^{}$，被编辑模型$f^{*}$的准确率指标公式如下：

$$
\begin{array}{r}{\operatorname{Acc}(f^{};\mathcal{E})=\mathbb{E}_{e\in\mathcal{E}}\mathbb{1}{f^{}(x_{e})=y_{e}^{*}}.}\end{array}
$$

Since accuracy is defined on a deterministic set of prompt-answer pairs, it provides a fair comparison between KME methods [22, 97, 98]. Nevertheless, it is non-trivial to evaluate the practicality of KME methods with accuracy, as there is no consensus on how to design the $\varepsilon$ , especially when the task needs to output a long sequence such as question answering or text generation [29, 97, 98].

由于准确率是在一组确定的提示-答案对上定义的，它为不同KME方法提供了公平的比较基准 [22, 97, 98]。然而，用准确率评估KME方法的实用性并非易事，因为对于如何设计$\varepsilon$尚未达成共识，特别是在需要输出长序列的任务（如问答或文本生成）时 [29, 97, 98]。

4.2 Locality

4.2 局部性

One crucial metric for the KME strategies is locality [17, 25, 83, 101], which reflects the capability of the edited model $f^{}$ to preserve the pre-trained knowledge in $f$ irrelevant to the edits in $\varepsilon$ . Note that in most KME applications, the number of required edits makes for an extremely small fraction of the entire knowledge learned and preserved in the pre-trained LLMs [167, 172]. Consequently, the locality measurement is of great importance in assessing the capability of edited models to preserve unrelated knowledge [49, 95, 104]. Given an edit $e$ , the edited model $f^{}$ , and the original pre-trained model $f$ , the locality of $f^{*}$ can be defined as the expectation of matched agreement between the edited model and unedited model for out-scope inputs, which can be defined as follows:

KME策略的一个关键指标是局部性 [17, 25, 83, 101]，它反映了编辑后模型$f^{}$保留预训练模型$f$中与编辑集$\varepsilon$无关知识的能力。需要注意的是，在大多数KME应用中，所需编辑数量仅占预训练大语言模型所学全部知识的极小部分 [167, 172]。因此，局部性度量对于评估编辑模型保留无关知识的能力至关重要 [49, 95, 104]。给定编辑$e$、编辑后模型$f^{}$和原始预训练模型$f$，$f^{*}$的局部性可定义为编辑模型与未编辑模型在非目标输入上预测一致性的期望值，其数学表达如下：

$$
\operatorname{Loc}(f^{},f;e)=\mathbb{E}{x\not\in\chi{e}}\mathbb{1}{f^{}(x)=f(x)}.
$$

We can also consider the locality regarding the entire edit set $\varepsilon$ , which can be defined as follows:

我们还可以考虑整个编辑集 $\varepsilon$ 的局部性，其定义如下：

$$
\operatorname{Loc}(f^{},f;\mathcal{E})=\mathbb{E}{x\notin\chi{\mathcal{E}}}\mathbb{1}{f^{}(x)=f(x)},\mathrm{where}\chi_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}\chi_{e}.
$$

Although the above metric measures the overall locality of $f^{}$ based on all inputs that are not in $\chi_{\varepsilon}$ , it is difficult to compute in realistic scenarios, as the entire input space can be excessively large or even infinite [167]. Therefore, existing methods generally resort to alternative solutions that pre-define the specific range of out-scope inputs to calculate the locality metric [15, 22, 25, 82, 97]. For example, in SERAC [102], the authors generate hard out-scope examples from the dataset zsRE [78] by selectively sampling from training inputs with high semantic similarity with the edit input, based on embeddings obtained from a pre-trained semantic embedding model. Denoting the out-scope input space related to the input $X_{e}$ as $O_{e}$ , we can similarly define the feasible out-scope input space for multiple edits as $\begin{array}{r}{O_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}O_{e}}\end{array}$ . In this manner, we define a specific metric of locality of $f^{}$ regarding $\varepsilon$ as follows:

虽然上述指标基于所有不在 $\chi_{\varepsilon}$ 中的输入来衡量 $f^{}$ 的整体局部性，但在实际场景中难以计算，因为整个输入空间可能过大甚至无限 [167]。因此，现有方法通常采用替代方案，即预定义超出范围输入的具体范围来计算局部性指标 [15, 22, 25, 82, 97]。例如，在 SERAC [102] 中，作者通过从预训练的语义嵌入模型获得的嵌入，选择性地采样与编辑输入具有高语义相似性的训练输入，从数据集 zsRE [78] 生成困难的超出范围示例。将与输入 $X_{e}$ 相关的超出范围输入空间记为 $O_{e}$，我们可以类似地定义多次编辑的可行超出范围输入空间为 $\begin{array}{r}{O_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}O_{e}}\end{array}$。通过这种方式，我们定义了 $f^{}$ 关于 $\varepsilon$ 的特定局部性指标如下：

$$
\begin{array}{r}{\operatorname{Loc}(f^{},f;O_{e})=\mathbb{E}{x\in O{e}}\mathbb{1}{f^{}(x)=f(x)},}\end{array}
$$

$$
\operatorname{Loc}(f^{},f;O_{\mathcal{E}})=\mathbb{E}{x\in O{\mathcal{E}}}\mathbb{1}{f^{}(x)=f(x)},\mathrm{where}O_{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}O_{e}.
$$

4.3 Generality

4.3 通用性

Aside from locality, another crucial metric is generality, which indicates the capability of the edited model $f^{}$ to correctly respond to semantically similar prompts [13, 101, 106, 130, 177]. This requires the generalization of the updated knowledge to other in-scope inputs that do not appear in the training set while conveying similar or related meanings [50, 163]. As such, ensuring the generality of edited models prevents the edited model from over fitting to a particular input [172]. Specifically, in the scenarios of knowledge-based model editing, the inherent diversity of natural language determines that various in-scope inputs $x$ can correspond to a specific knowledge triple $t$ [152]. These semantically equivalent inputs can involve differences in aspects such as syntax, morphology, genre, or even language. Existing works mostly pre-define a specific in-scope input space of each edit via different strategies [61, 86, 136, 166, 168]. For example, in the Counter Fact dataset proposed in ROME [97], the authors utilize prompts that involve distinct yet semantically related subjects as the in-scope input. In general, the generality of an edited model $f^{}$ is defined as the expectation of exact-match agreement between the output of the edited model and true labels for in-scope inputs, which can be defined on either an edit $e$ or the edit set $\varepsilon$ as:

除了局部性，另一个关键指标是泛化性 (generality)，它反映了编辑后模型 $f^{}$ 对语义相近提示词的正确响应能力 [13, 101, 106, 130, 177]。这要求更新后的知识能够泛化至训练集未出现但语义相关的作用域内输入 (in-scope inputs) [50, 163]。因此，确保编辑模型的泛化性可防止模型对特定输入产生过拟合 [172]。具体而言，在基于知识的模型编辑场景中，自然语言固有的多样性决定了多种作用域内输入 $x$ 可能对应同一知识三元组 $t$ [152]。这些语义等价的输入可能涉及句法、词法、文体甚至语言层面的差异。现有研究大多通过不同策略预先定义每个编辑的作用域输入空间 [61, 86, 136, 166, 168]，例如 ROME [97] 提出的 Counter Fact 数据集中，作者采用主语不同但语义相关的提示词作为作用域输入。通常，编辑模型 $f^{}$ 的泛化性定义为编辑模型输出与真实标签在作用域输入上的精确匹配期望值，该指标可针对单个编辑 $e$ 或编辑集 $\varepsilon$ 定义为：

$$
\mathbf{Gen}(f^{};e)=\mathbb{E}{x\in\boldsymbol{\chi}{e}}\mathbb{1}{f^{}(x)\in\boldsymbol{y}_{e}^{*}},
$$

$$
{\bf G e n}(f^{};\mathcal{E})=\mathbb{E}{x\in\chi{\mathcal{E}}}\mathbb{1}{f^{}(x)\in\mathcal{Y}{e}^{*}},\mathrm{where}X{\mathcal{E}}=\bigcup_{e\in\mathcal{E}}\chi_{e}.
$$

4.4 Portability

4.4 可移植性

In addition to generality, another vital metric is portability, which measures the effectiveness of the edited model $f^{}$ in transferring a conducted edit to other logically related edits that can be interpreted via reasoning [172]. For example, if an edit is conducted towards the President of the USA, the edit regarding the query “Which political party does the current President of the USA belong to?” should also be achieved. This ensures that the edited model is not limited to responding to specific input formats. In concrete, the transfer of knowledge is crucial for robust generalization of the edited model. In practice, portability can be assessed with logically related edits obtained in different ways [21, 167]. Denoting an edit as $e=\left(s,r,o\to o^{}\right)$ , hereby we introduce two common types of logically related edits . (1) Reversed Relation: $\tilde{e}=\left(o\rightarrow o^{*},\tilde{r},s\right)$ , where $\tilde{r}$ is the reversed relation of $r$ , and (2) Neighboring Relation: $\tilde{e}=\left(s,r\oplus r_{\epsilon},\epsilon\rightarrow\epsilon^{*}\right)$ , where both $(o,r_{\epsilon},\epsilon)$ and $(o^{*},r_{\epsilon},\epsilon^{*})$ exist in the pre-trained knowledge, and $r\oplus r_{\epsilon}$ is a combined relation from $r$ and $r_{\epsilon}$ . In this manner, we define portability as the edited model performance on one or multiple logically related edits as follows:

除了通用性外，另一个关键指标是可移植性 (portability) ，它衡量编辑后模型 $f^{}$ 将已执行编辑迁移到其他可通过推理解释的逻辑相关编辑中的有效性 [172]。例如，若对美国总统治进行编辑，那么针对查询"美国现任总统属于哪个政党？"的编辑也应同步实现。这确保了编辑后模型不仅能响应特定输入格式。具体而言，知识迁移对编辑后模型的稳健泛化至关重要。实践中，可通过不同方式获取逻辑相关编辑来评估可移植性 [21, 167]。将编辑表示为 $e=\left(s,r,o\to o^{}\right)$ ，此处介绍两种常见逻辑相关编辑类型：(1) 反向关系： $\tilde{e}=\left(o\rightarrow o^{*},\tilde{r},s\right)$ ，其中 $\tilde{r}$ 是 $r$ 的反向关系；(2) 邻近关系： $\tilde{e}=\left(s,r\oplus r_{\epsilon},\epsilon\rightarrow\epsilon^{*}\right)$ ，其中 $(o,r_{\epsilon},\epsilon)$ 和 $(o^{*},r_{\epsilon},\epsilon^{*})$ 均存在于预训练知识中，且 $r\oplus r_{\epsilon}$ 是 $r$ 与 $r_{\epsilon}$ 的组合关系。由此，我们将可移植性定义为编辑后模型在单个或多个逻辑相关编辑上的表现：

$$
\mathbf{Por}(f^{};\tilde{e})=\mathbb{E}{x\in X{\tilde{e}}}\mathbb{1}{f^{}(x)\in{\mathcal{Y}}_{\tilde{e}}^{*}},
$$

$$
\mathbf{Por}(f^{};\widetilde{\mathcal{E}})=\mathbb{E}{x\in X{\widetilde{\mathcal{E}}}}\mathbb{1}{f^{}(x)\in{\mathcal{Y}}{\widetilde{e}}^{*}},\mathrm{where}X{\widetilde{\mathcal{E}}}=\bigcup_{\widetilde{e}\in\widetilde{\mathcal{E}}}X_{\widetilde{e}}.
$$

4.5 Retain ability

4.5 保留能力

Retain ability characterizes the ability of KME techniques to preserve the desired properties of edited models after multiple consecutive edits [47, 69, 169]. In the presence of ever-evolving information, practitioners may need to frequently update a conversational model (i.e., sequential editing). Such a KME setting requires that the model does not forget previous edits after each new modification [81]. It is essential to distinguish retain ability from s cal ability, which evaluates the model’s ability to handle a vast number of edits [15]. In contrast, retain ability assesses the consistent performance of the model after each individual edit, presenting a more challenging objective to achieve. Recently, T-Patcher [66] first explores the sequential setting of KME and observes that many existing approaches significantly fall short in terms of retain ability. In SLAG [53], the authors also discover a significant drop in editing performance when multiple beliefs are updated continuously. To assess the retain ability of an edited language model $f^{*}$ , we define it as follows:

保留能力 (retain ability) 表征了KME技术在多次连续编辑后保持被编辑模型所需属性的能力 [47, 69, 169]。面对不断演进的信息，实践者可能需要频繁更新对话模型(即顺序编辑)。这种KME场景要求模型在每次新修改后不会遗忘先前的编辑 [81]。必须将保留能力与可扩展性 (scalability) 区分开来，后者评估的是模型处理大量编辑的能力 [15]。相比之下，保留能力评估的是模型在每次单独编辑后的一致性能，这是一个更具挑战性的目标。最近，T-Patcher [66] 首次探索了KME的顺序设置，并观察到许多现有方法在保留能力方面存在显著不足。在SLAG [53] 中，作者还发现当连续更新多个信念时，编辑性能会显著下降。为了评估被编辑语言模型 $f^{*}$ 的保留能力，我们定义如下:

$$
\mathbf{Ret}(M;{\mathcal{E}})={\frac{1}{|{\mathcal{E}}|-1}}\sum_{i=1}^{|{\mathcal{E}}|-1}\mathbf{Acc}(M(f;{e_{1},e_{2},\ldots,e_{i+1}}))-\mathbf{Acc}(M(f;{e_{1},e_{2},\ldots,e_{i}}))
$$

where Acc is the accuracy measurement, $|\mathcal{E}|$ is the number of edits in the edit set, and $M$ denotes the editing strategy that modifies the pre-trained model $f$ into $f^{}$ with $i/i+1$ consecutive edits ${e_{1},e_{2},\ldots,e_{i},(e_{i+1})}$ . The retain ability metric aims to quantify the effect of applying consecutive edits to a model and measures how the performance will change the editing strategy $M$ , where a higher retain ability means that after each edit, the less the change in the overall performance of the edited model $f^{}$ is required.

其中 Acc 是准确率度量，$|\mathcal{E}|$ 是编辑集中的编辑数量，$M$ 表示通过连续 $i/i+1$ 次编辑 ${e_{1},e_{2},\ldots,e_{i},(e_{i+1})}$ 将预训练模型 $f$ 修改为 $f^{}$ 的编辑策略。保留能力指标旨在量化对模型应用连续编辑的效果，并衡量编辑策略 $M$ 如何改变性能，其中保留能力越高意味着每次编辑后，对编辑后模型 $f^{}$ 整体性能的改变要求越小。

4.6 S cal ability

4.6 可扩展性

The s cal ability of an editing strategy refers to its capability to incorporate a large number of edits simultaneously [15]. Recently, several works have emerged that can inject multiple new knowledge into specific parameters of pre-trained LLMs [168, 172]. For instance, SERAC [102] can perform a maximum of 75 edits. In addition, MEMIT [98] is proposed to enable thousands of edits without significant influence on editing accuracy. When there is a need to edit a model with a vast number of edits concurrently, simply employing the current knowledge-based model editing techniques in a sequential manner is proven ineffective in achieving such s cal ability [167]. To effectively evaluate the s cal ability of edited language models, we define the s cal ability of an edited model as follows:

编辑策略的可扩展性 (s cal ability) 指的是其同时整合大量编辑的能力 [15]。近期多项研究提出能在预训练大语言模型特定参数中注入多重新知识的方法 [168, 172]。例如 SERAC [102] 最多可执行 75 次编辑，而 MEMIT [98] 则能实现数千次编辑且对编辑准确率影响甚微。当需要同时对模型进行海量编辑时，已证明简单地顺序应用当前基于知识的模型编辑技术无法实现这种可扩展性 [167]。为有效评估编辑后语言模型的可扩展性，我们将其定义如下：

$$
\begin{array}{r}{\mathbf{Sca}(M;\mathcal{E})=\mathbb{E}_{e\in\mathcal{E}}\mathbf{Acc}(M(f;e))-\mathbf{Acc}(M(f;\mathcal{E})),}\end{array}
$$

where $\mathbf{Acc}(M(f;\mathcal{E}))$ denotes the accuracy of the edited model after conducting all edits in $\varepsilon$ , whereas $\mathbf{Acc}(M(f;e))$ is the accuracy of only performing the edit 𝑒. Sca demonstrates the model performance and practicality in the presence of multiple edits. Nevertheless, we note that baseline value $\operatorname{Acc}(M(f;{e}))$ is also important in evaluating the s cal ability of various models. This is because, with higher accuracy for each $e$ , the retainment of such performance after multiple edits is more difficult. Therefore, we further define the relative version of Eq. (13) as follows:

其中 $\mathbf{Acc}(M(f;\mathcal{E}))$ 表示在 $\varepsilon$ 中执行所有编辑后修正模型的准确率，而 $\mathbf{Acc}(M(f;e))$ 是仅执行编辑 𝑒 的准确率。Sca 展示了模型在存在多次编辑时的性能和实用性。然而，我们注意到基线值 $\operatorname{Acc}(M(f;{e}))$ 在评估各种模型的可扩展能力时也很重要。这是因为，对于每个 $e$ 的准确率越高，在多次编辑后保持这种性能就越困难。因此，我们进一步将式 (13) 的相对版本定义如下：

$$
\begin{array}{r}{\mathtt{S c a}{r e l}(M;\mathcal{E})=\left(\mathbb{E}{e\in\mathcal{E}}\mathrm{Acc}(M(f;{e}))-\mathrm{Acc}(M(f;\mathcal{E}))\right)/\mathbb{E}_{e\in\mathcal{E}}\mathrm{Acc}(M(f;{e})).}\end{array}
$$

The introduced s cal ability measurement further considers the magnitude of the original accuracy to provide a fairer evaluation.

引入的可扩展性测量进一步考虑了原始准确率的幅度，以提供更公平的评估。

5 METHODOLOGIES

5 方法论

In this section, we introduce existing knowledge-based model editing (KME) strategies in detail. We first provide an innovative taxonomy of existing KME strategies based on how and where the new knowledge is injected into the pre-trained LLMs, where the advantages and drawbacks are thoroughly discussed. We then introduce various methods from each category, with an emphasis on analyzing the technical details, insights, shortcomings, and their relationships.

在本节中，我们将详细介绍现有的基于知识的模型编辑（KME）策略。首先，我们根据新知识如何及何处注入预训练大语言模型，提出了一种创新的分类方法，并深入探讨了各类策略的优缺点。随后，我们将逐一介绍每个类别中的多种方法，重点分析其技术细节、核心思想、不足之处以及相互关联。

5.1 Categorization of KME Methods

5.1 KME方法分类

Faced with the rapid deprecation of old information and the emergence of new knowledge, various KME methodologies have been proposed to update the pre-trained LLMs to maintain their updatedness and relevancy. KME ensures that new knowledge can be efficiently incorporated into the pre-trained LLMs without negatively influencing the pre-trained knowledge irrelevant to the edit. In this survey, we categorize existing KME methods into three main classes as follows:

面对旧信息快速淘汰和新知识不断涌现的挑战，研究者们提出了多种知识模型编辑（KME）方法，用于更新预训练大语言模型以保持其时效性和相关性。KME能够确保新知识被高效整合到预训练大语言模型中，同时不影响与编辑无关的原有知识。本综述将现有KME方法归纳为以下三大类：

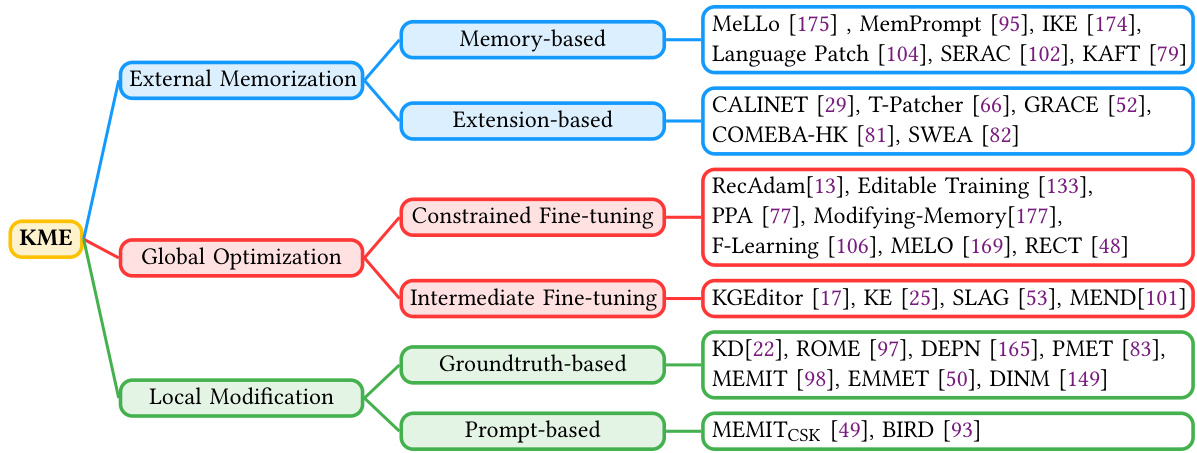
Fig. 3. The categorization of KME techniques for LLMs and the corresponding works.

图 3: 大语言模型的KME技术分类及对应研究成果

• External Memorization-based methods leverage an external memory to store the new knowledge for editing without modifying the pre-trained weights, where the pre-trained knowledge can be fully preserved in the LLM weights. By storing new knowledge with external parameters, the memory-based strategies enable precise representation of new knowledge with good s cal ability, as the memory is easily extensible to incorporate new knowledge. • Global Optimization-based methods seek to achieve general iz able incorporation of the new knowledge into pre-trained LLMs via optimization with the guidance of new knowledge, where tailored strategies are introduced to limit the influence of other pre-trained knowledge, distinguishing it from naive fine-tuning. Nevertheless, these methods may fall short in editing efficiency when applied to LLMs due to the large number of parameters to be optimized. • Local Modification-based methods aim to locate the related parameters of specific knowledge in LLMs and update it accordingly to incorporate the new knowledge relevant to the edit. The main advantage of local modification is the possibility of only updating a small fraction of model parameters, thereby providing considerable memory efficiency compared to memorization-based methods and computational efficiency compared to global optimization.

• 基于外部记忆 (External Memorization) 的方法利用外部存储来保存新知识，无需修改预训练权重，从而完整保留大语言模型权重中的预训练知识。通过外部参数存储新知识，这类策略能精准表征新知识并具备良好可扩展性，因为记忆模块可轻松扩展以纳入新知识。

• 基于全局优化 (Global Optimization) 的方法试图通过新知识指导下的优化，将新知识泛化地融入预训练大语言模型。其采用定制化策略限制其他预训练知识的影响，以此区别于原始微调。然而，由于需要优化大量参数，这些方法在应用于大语言模型时可能面临编辑效率不足的问题。

• 基于局部修改 (Local Modification) 的方法旨在定位大语言模型中特定知识的相关参数，并针对性更新以整合与编辑相关的新知识。该方法的主要优势是仅需更新极小部分模型参数，相比基于记忆的方法具有显著内存效率优势，相比全局优化则具备更高计算效率。

The above categorization is achieved based on where (e.g., external parameters or internal weights) and how (e.g., via optimization or direct incorporation) new knowledge is introduced into the LLM during editing. Methods in each category exhibit different strengths and weaknesses regarding the four crucial evaluation metrics introduced in Sec. 4. For example, external memorization prevails in scenarios that require massive editing while the computational resources are limited, as the size of the memory is controllable to fit into different requirements. On the other hand, global optimization is advantageous when practitioners focus more on the generality of edited knowledge, as the optimization can promote the learning of relevant knowledge [2]. The taxonomy is visually illustrated in Fig. 3, and a more detailed demonstration of each category is presented in Fig. 4.

上述分类是基于新知识在大语言模型编辑过程中被引入的位置（如外部参数或内部权重）和方式（如通过优化或直接整合）而实现的。各类方法在第4节介绍的四个关键评估指标上展现出不同的优缺点。例如，在需要大规模编辑但计算资源有限的场景中，外部记忆法占据优势，因为其记忆大小可根据需求灵活调整。另一方面，当从业者更关注编辑知识的泛化性时，全局优化法更具优势，因为优化过程能促进相关知识的学习 [2]。该分类体系在图3中进行了可视化展示，图4则对每个类别进行了更详细的说明。

5.2 External Memorization

5.2 外部记忆机制

5.2.1 Overview. The editing approaches via external memorization aim to modify the current model $f_{\phi}$ (with parameter $\phi$ ) via introducing external memory represented by additional trainable parameters $\omega$ that encodes the new knowledge, resulting in an edited LLM model $f_{\phi,\omega}^{*}$ . The rationale behind the external memorization strategy is that storing new knowledge in additional parameters is intuitive and straightforward to edit the pre-trained LLMs with good s cal ability, as the parameter size can be expanded to store more knowledge. In addition, the influence on the pre-trained knowledge can be minimized as this strategy does not alter the original parameters $\phi$ . Based on the general formulation of KME in Eq. (2), the objective of external memorization approaches can be formulated as follows:

5.2.1 概述
通过外部记忆的编辑方法旨在通过引入由额外可训练参数 $\omega$ 表示的外部记忆来修改当前模型 $f_{\phi}$ (参数为 $\phi$)，这些参数编码了新知识，从而得到一个经过编辑的大语言模型 $f_{\phi,\omega}^{*}$。外部记忆策略的基本原理是，将新知识存储在额外参数中是直观且直接的方法，可以有效地编辑预训练的大语言模型，因为参数规模可以扩展以存储更多知识。此外，由于该策略不会改变原始参数 $\phi$，因此对预训练知识的影响可以最小化。基于公式(2)中KME的一般形式，外部记忆方法的目标可以表述如下:

Fig. 4. The illustration of three categories of KME methods: External Memorization, Global Optimization, and Local Modification.

图 4: 三类KME方法示意图：外部记忆(External Memorization)、全局优化(Global Optimization)和局部修改(Local Modification)。

$$
\begin{array}{r l}&{\operatorname*{min}\mathbb{E}{e\in\mathcal{E}}\mathbb{E}{x,y^{}\in\mathcal{X}{e},y{e}^{}}\mathcal{L}(f_{\phi,\omega}^{}(x),y^{})\mathrm{,where~}f_{\phi,\omega}^{}=M(f_{\phi},\omega;\mathcal{E})\mathrm{,}}\ &{\mathrm{~~s.t.~~}f_{\phi,\omega}^{}(x)=f_{\phi}(x)\mathrm{,~}\forall x\in\chi\backslash\chi_{\mathcal{E}}\mathrm{,}}\end{array}
$$

where $f_{\phi}$ denotes the LLM before editing with the pre-trained parameter $\phi$ , and $f_{\phi,\omega}^{*}$ denotes the edited LLM with $\phi$ and additional parameter $\omega$ as the external memorization. Moreover, based on whether the introduced parameters are directly incorporated into the model process or not, external memorization strategies can be divided into two categories, i.e., memory-based methods and extension-based methods.

其中 $f_{\phi}$ 表示编辑前使用预训练参数 $\phi$ 的大语言模型，$f_{\phi,\omega}^{*}$ 表示通过 $\phi$ 和额外参数 $\omega$ 作为外部记忆进行编辑后的大语言模型。此外，根据引入参数是否直接融入模型处理流程，外部记忆策略可分为两类：基于记忆的方法和基于扩展的方法。

5.2.2 Memory-based Strategies. In memory-based strategies, the external memory, outside the intrinsic architecture of the pre-trained LLM, functions as a repository to store edited knowledge. Here the edits are generally converted to text via pre-defined templates [154, 174, 175]. The LLM can access and update this memory as required during inference.

5.2.2 基于记忆的策略。在基于记忆的策略中，外部存储器位于预训练大语言模型固有架构之外，充当存储编辑知识的仓库。这些编辑通常通过预定义模板转换为文本 [154, 174, 175]。大语言模型在推理过程中可根据需要访问和更新该存储器。

One exemplar work is SERAC [102], which stores the edited samples $x,y^{}\in\mathcal{X}{e},\mathcal{Y}{e}^{}$ in a cache without performing modifications on the original model. When presented with a new prompt $x^{\prime}$ , SERAC uses a scope classifier to determine whether the prompt falls within the scope of any cached instances. If yes, the desirable output $y^{\prime}$ associated with the new prompt $x^{\prime}$ is predicted via a counter factual model $f_{c}$ which utilizes the most relevant edit example as follows:

一个典型的工作是SERAC [102]，它将编辑过的样本$x,y^{}\in\mathcal{X}{e},\mathcal{Y}{e}^{}$存储在缓存中，而不对原始模型进行修改。当遇到新的提示$x^{\prime}$时，SERAC使用一个范围分类器来判断该提示是否属于任何缓存实例的范围。如果是，则通过一个反事实模型$f_{c}$来预测与新提示$x^{\prime}$相关的期望输出$y^{\prime}$，该模型利用最相关的编辑样本如下：

$$
f_{\phi,\omega}^{*}(x)=\left{\begin{array}{l l}{f_{\phi}(x),}&{\mathrm{if}x\mathrm{is}\mathrm{notinscope}\mathrm{of}\mathrm{any}\mathrm{edit},}\ {f_{c}(x,\mathcal{E}),}&{\mathrm{otherwise}.}\end{array}\right.
$$

SERAC is a gradient-free approach to KME without relying on gradients of the target label $y^{*}$ w.r.t. the pre-trained model parameters. In addition to using memory as an external repository, the desirable edits can also be stored in the form of human feedback. For example, Language Patch [104] performs editing by integrating patches in natural language, and MemPrompt [95] involves human feedback prompts to address the issue of lacking commonsense knowledge regarding a particular task. An integral feature of the Language Patch [104] framework is its ability to empower practitioners with the capability to create, edit, or remove patches without necessitating frequent model re-training. This trait not only streamlines the development process but also enhances the adaptability and versatility of the edited model. To enable the automatic correction in memory, MemPrompt [95] equips the language model with a memory bank containing corrective feedback to rectify misunderstandings. Specifically, MemPrompt leverages question-specific historical feedback to refine responses on novel and un encountered instances through prompt adjustments.

SERAC是一种无需梯度的KME方法，不依赖于目标标签$y^{*}$对预训练模型参数的梯度。除了将记忆用作外部存储库外，理想的编辑还可以以人类反馈的形式存储。例如，Language Patch [104]通过集成自然语言补丁进行编辑，而MemPrompt [95]则利用人类反馈提示来解决特定任务中常识知识缺乏的问题。Language Patch [104]框架的一个核心特性是使从业者能够在不频繁重新训练模型的情况下创建、编辑或删除补丁。这一特性不仅简化了开发流程，还增强了编辑后模型的适应性和多功能性。为实现记忆中的自动校正，MemPrompt [95]为语言模型配备了一个包含校正反馈的记忆库以纠正误解。具体而言，MemPrompt利用特定问题的历史反馈，通过调整提示来优化对未见过新实例的响应。

In KAFT [79], control l ability is achieved through the utilization of counter factual data augmentations. In this approach, the entity representing the answer within the context is substituted with an alternative but still plausible entity. This substitution is intentionally designed to introduce a conflict with the genuine ground truth, thereby enhancing the control l ability and robustness of LLMs with respect to their working memory. The aim is to ensure that LLMs remain responsive to pertinent contextual information while filtering out noisy or irrelevant data.

在KAFT [79]中，可控性通过利用反事实数据增强实现。该方法将上下文中的答案实体替换为另一个合理但不同的实体，这种替换刻意制造与真实基准答案的冲突，从而增强大语言模型在工作记忆方面的可控性和鲁棒性。其目标是确保大语言模型能持续响应相关上下文信息，同时过滤噪声或无关数据。

In addition to relying on parameter-based memory, recent works also leverage prompting techniques of LLMs, e.g., in-context learning [30] and chain-of-thought prompting [162], to promote editing performance of external memorization. Specifically, IKE [174] introduces novel factual information into a pre-trained LLM via in-context learning, where a set of $k$ demonstrations, i.e., $\omega={x_{i},y_{i}^{*}}_{i=1}^{k}$ , is selected as the reference points. These demonstrations will alter the prediction of a target factual detail when the input is influenced by an edit. Particularly, IKE guarantees a balance between generality and locality via storing factual knowledge as prompts. The process can be formulated as follows:

除了依赖基于参数的记忆外，近期研究还利用大语言模型的提示技术（如上下文学习 [30] 和思维链提示 [162]）来提升外部记忆的编辑性能。具体而言，IKE [174] 通过上下文学习向预训练大语言模型引入新事实信息，其中选取一组 $k$ 个示例（即 $\omega={x_{i},y_{i}^{*}}_{i=1}^{k}$）作为参考点。当输入受到编辑影响时，这些示例会改变目标事实细节的预测。特别地，IKE 通过将事实知识存储为提示来保证通用性与局部性的平衡，该过程可表述为：

$$
\begin{array}{r}{f_{\phi,\omega}^{*}(x)=f_{\phi}(\omega|x)\mathrm{,~where}\omega={x_{i},y_{i}^{*}}_{i=1}^{k}.}\end{array}
$$

Here $\parallel$ denotes the concatenation of the reference points in $\omega$ and the input $x$ , which follows an in-context learning manner. Note that in this process, the framework first transforms all new facts into natural language to input them into LLMs. Similar methods of knowledge editing based on prompts [15, 131, 136, 154] can also update and modify knowledge within large language models (LLMs). These approaches allow users to guide the model to generate desired outputs by providing specific prompts, and effectively and dynamically adjusting the model’s knowledge base. By leveraging the flexibility of prompts and the contextual understanding of LLMs, users can correct or update information in real-time. These methods offer immediacy, flexibility, and cost-efficiency, making them powerful tools for maintaining the accuracy and relevance of language models in rapidly evolving knowledge domains. Although the prompt approaches effectively edit factual knowledge via in-context learning, they cannot solve more complex questions that involve multiple relations. To deal with this, MeLLo [175] first explores the evaluation of the editing effectiveness in language models regarding multi-hop knowledge. For example, when editing knowledge about the president of the USA, the query regarding the president’s children should change accordingly. MeLLo proposes to enable multi-hop editing by breaking down each query into sub questions, such that the model generates a provisional answer. Subsequently, each sub question is used to retrieve the most pertinent fact from the memory to assist the model in answering the query.

这里 $\parallel$ 表示 $\omega$ 中的参考点与输入 $x$ 的拼接，遵循上下文学习的方式。需要注意的是，在此过程中，该框架首先将所有新事实转换为自然语言输入到大语言模型 (LLM) 中。类似的基于提示的知识编辑方法 [15, 131, 136, 154] 也可以更新和修改大语言模型中的知识。这些方法允许用户通过提供特定提示来引导模型生成期望的输出，并有效且动态地调整模型的知识库。通过利用提示的灵活性和大语言模型的上下文理解能力，用户可以实时纠正或更新信息。这些方法具有即时性、灵活性和成本效益，是维护语言模型在快速发展的知识领域中准确性和相关性的强大工具。

尽管提示方法通过上下文学习有效地编辑了事实性知识，但它们无法解决涉及多重关系的更复杂问题。为此，MeLLo [175] 首次探索了语言模型在多跳知识方面的编辑效果评估。例如，当编辑关于美国总统的知识时，关于总统子女的查询也应相应改变。MeLLo 提出通过将每个查询分解为子问题来实现多跳编辑，使模型生成临时答案。随后，每个子问题用于从记忆中检索最相关的事实，以帮助模型回答查询。

5.2.3 Extension-based Strategies. Extension-based strategies utilize supplementary parameters to assimilate modified or additional information into the original language model. These supplementary parameters are designed to represent the newly introduced knowledge or necessary adjustments tailored for specific tasks or domains. Different from memory-based methods, by incorporating new parameters into the language model, extension-based approaches can effectively leverage and expand the model’s functionality.

5.2.3 基于扩展的策略。基于扩展的策略利用补充参数将修改或额外信息整合到原始语言模型中。这些补充参数旨在表示针对特定任务或领域新引入的知识或必要调整。与基于记忆的方法不同，通过向语言模型添加新参数，基于扩展的方法能有效利用并扩展模型功能。

Extension-based methods can be implemented through various means, and one representative way is to modify the Feed-forward Neural Network (FFN) output. For example, CALINET [29] uses the output from sub-models fine-tuned specifically on factual texts to refine the original FFN output produced by the base model. Another technique T-Patcher [66] introduces a limited number of trainable neurons, referred to as “patches,” in the final FFN layer to alter the model’s behavior while retaining all original parameters to avoid reducing the model’s overall performance. Generally, these methods that refine the structure of FFN can be formulated as follows:

基于扩展的方法可以通过多种方式实现，其中一种代表性方式是修改前馈神经网络(FFN)的输出。例如，CALINET [29] 使用专门针对事实文本微调的子模型输出来优化基础模型生成的原始FFN输出。另一种技术T-Patcher [66] 在最终FFN层中引入少量可训练神经元（称为"补丁"），在保留所有原始参数的同时改变模型行为，以避免降低模型的整体性能。通常，这些优化FFN结构的方法可以表述为：

$$
\mathrm{FFN}(\mathbf{h})=\mathrm{GELU}\left(\mathbf{h}\mathbf{W}{1}\right)\mathbf{W}{2}+\mathrm{GELU}\left(\mathbf{h}\cdot\mathbf{k}{p}+b{p}\right)\cdot\mathbf{v}_{p},
$$

where $\mathbf{k}{p}$ is the patch key, $\mathbf{v}{p}$ is the patch value, and $b_{p}$ is the patch bias scalar. The introduced patches are flexible in size and can be accurately activated to edit specific knowledge without affecting other model parameters.

其中 $\mathbf{k}{p}$ 是补丁键， $\mathbf{v}{p}$ 是补丁值， $b_{p}$ 是补丁偏置标量。引入的补丁大小灵活，可以精确激活以编辑特定知识，而不影响其他模型参数。

Alternatively, a different technique involves integrating an adapter into a specific layer of a pre-trained model. This adapter consists of a discrete dictionary comprising keys and values, where each key represents a cached activation generated by the preceding layer and each corresponding value decodes into the desired model output. This dictionary is systematically updated over time. In line with this concept, GRACE [52] introduces an adapter that enables judicious decisions regarding the utilization of the dictionary for a given input, accomplished via the implementation of a deferral mechanism. It is crucial to achieve a balance between the advantages of preserving the original model’s integrity and the practical considerations associated with storage space when implementing this approach. COMEBA-HK [81] incorporates hook layers within the neural network architecture. These layers allow for the sequential editing of the model by enabling updates to be applied in batches. This approach facilitates the integration of new knowledge without requiring extensive retraining of the entire model, making it a scalable solution for continuous learning and adaptation. SWEA [82] focuses on altering the embeddings of specific subject words within the model. By directly updating these embeddings, the method can inject new factual knowledge into the LLMs. This approach ensures that the updates are precise and relevant, thereby enhancing the model’s ability to reflect current information accurately.

另一种技术方案是在预训练模型的特定层中集成适配器。该适配器包含由键值对组成的离散字典，其中每个键代表前一层生成的缓存激活值，对应的值则解码为期望的模型输出。该字典会随时间推移进行系统性更新。基于这一理念，GRACE [52] 引入了一种带延迟机制的适配器，可智能判断何时使用字典处理给定输入。实施该方法时，需在保持原始模型完整性的优势与存储空间的实际限制之间取得平衡。COMEBA-HK [81] 在神经网络架构中嵌入了钩子层，通过批量更新实现模型的序列化编辑。这种方法无需全面重训练就能整合新知识，为持续学习和适应提供了可扩展的解决方案。SWEA [82] 则专注于修改模型中特定主题词的嵌入向量，通过直接更新这些嵌入来向大语言模型注入新事实知识，确保更新内容精确相关，从而提升模型准确反映最新信息的能力。

5.2.4 Summary. The eternal memorization methodology operates by preserving the parameters within the original model while modifying specific output results through external interventions via memory or additional model parameters. One notable advantage of this approach is its minimal perturbation of the original model, thereby ensuring the consistency of unedited knowledge. It allows for precise adjustments without necessitating a complete overhaul of the model’s architecture. However, it is imperative to acknowledge a trade-off inherent in this methodology. Its efficacy is contingent upon the storage and invocation of the edited knowledge, a factor that leads to concerns regarding storage capacity. Depending on the scale of knowledge to be edited, this approach may entail substantial storage requisites. Therefore, cautiously seeking a balance between the advantages of preserving the original model’s integrity and the practical considerations of storage capacity becomes a pivotal concern when employing this particular approach.

5.2.4 总结
永恒记忆方法通过保留原始模型中的参数，同时通过内存或额外模型参数的外部干预来修改特定输出结果。这种方法的一个显著优势是对原始模型的扰动极小，从而确保未编辑知识的一致性。它允许进行精确调整，而无需彻底改变模型架构。然而，必须承认这种方法存在固有的权衡。其效果取决于编辑知识的存储和调用，这一因素引发了存储容量的担忧。根据待编辑知识的规模，这种方法可能需要大量的存储需求。因此，在使用这种方法时，谨慎寻求保持原始模型完整性的优势与存储容量的实际考量之间的平衡成为关键问题。

5.3 Global Optimization

5.3 全局优化

5.3.1 Overview. Different from external memorization methods that introduce new parameters to assist the editing of pre-trained LLMs, there also exist branches of works that do not rely on external parameters or memory. Concretely, global optimization strategies aim to inject new knowledge into LLMs by updating all parameters, i.e., $\phi$ in Eq. (15). Through fine-tuning model parameters with specific designs to ensure the preservation of knowledge irrelevant to the target knowledge $t^{*}$ , the LLMs are endowed with the ability to absorb new information without altering unedited knowledge. Generally, the goal of global optimization methods can be formulated as follows:

5.3.1 概述
不同于通过引入新参数辅助预训练大语言模型编辑的外部记忆方法，还存在不依赖外部参数或记忆的研究分支。具体而言，全局优化策略旨在通过更新所有参数（即公式(15)中的$\phi$）将新知识注入大语言模型。通过采用特定设计的微调策略确保与目标知识$t^{*}$无关的知识得以保留，大语言模型被赋予在不改变未编辑知识的前提下吸收新信息的能力。全局优化方法的目标通常可表述为：

$$
\begin{array}{r l}&{\operatorname*{min}\mathbb{E}{e\in\mathcal{E}}\mathbb{E}{x,y^{}\in\mathcal{X}{e},y{e}^{}}\mathcal{L}(f_{\phi^{}}(x),y^{}),\mathrm{where}f_{\phi^{}}=M(f_{\phi};\mathcal{E}),}\ &{\mathrm{s.t.}f_{\phi^{}}(x)=f_{\phi}(x),\forall x\in\chi\backslash\chi_{\mathcal{E}},}\end{array}
$$

where $f_{\phi}$ denotes the LLM before editing with the pre-trained parameter $\phi$ , and $f_{\phi^{}}$ denotes the edited LLM with updated parameter $\phi^{}$ . Generally, these methods focus more on the precision and generality of desirable knowledge, as the fine-tuning process ensures that the LLMs achieve satisfactory results regarding the edits and relevant knowledge. Nevertheless, as fine-tuning affects all parameters, they cannot easily preserve the locality of edited models, i.e., maintaining consistent output for unedited knowledge [167]. In practice, directly applying fine-tuning strategies typically exhibits suboptimal performance on KME due to over fitting concerns [98, 152]. Furthermore, fine-tuning large language models is also time-consuming and lacks s cal ability for multiple edits. Therefore, recently, motivated by these two challenges in fine-tuning, several global optimization works have been proposed and can be categorized as constrained fine-tuning methods and intermediate fine-tuning methods. Note that this section primarily focuses on methods from the model training perspective. Additionally, certain studies [38, 69] address the over fitting challenge by constructing more a comprehensive $X_{\mathcal{E}}^{\prime}$ with the following fine-tuning goal:

其中 $f_{\phi}$ 表示编辑前使用预训练参数 $\phi$ 的大语言模型，$f_{\phi^{}}$ 表示参数更新为 $\phi^{}$ 后的已编辑大语言模型。这类方法通常更关注目标知识的精确性与泛化性，因为微调过程能确保大语言模型在编辑内容及相关知识上达到理想效果。然而由于微调会影响所有参数，这类方法难以保持编辑模型的局部性 (即对未编辑知识维持输出一致性) [167]。实际应用中，直接采用微调策略常因过拟合问题导致知识模型编辑 (KME) 表现欠佳 [98, 152]。此外，大语言模型的微调过程耗时且难以支持多次编辑的规模化扩展。针对微调面临的这两大挑战，近期提出的全局优化方法可分为约束微调法和中间微调法。需注意的是，本节主要从模型训练角度展开论述。另有研究 [38, 69] 通过构建更全面的 $X_{\mathcal{E}}^{\prime}$ 配合以下微调目标来应对过拟合问题：

5.3.2 Constrained Fine-tuning. Constrained fine-tuning strategies generally apply specific constraints to prevent updating on non-target knowledge in ${X\backslash X_{\varepsilon},{\mathfrak{y}}\backslash{\mathfrak{y}}_{\varepsilon}}$ . In this manner, the objective in Eq. (20) is transformed into a constrained optimization problem:

5.3.2 受限微调。受限微调策略通常施加特定约束，以防止对 ${X\backslash X_{\varepsilon},{\mathfrak{y}}\backslash{\mathfrak{y}}_{\varepsilon}}$ 中的非目标知识进行更新。通过这种方式，方程(20)中的目标被转化为一个约束优化问题:

$$
\begin{array}{r l}&{\begin{array}{r l}&{\quad_{1}\mathbb{E}{e\in\mathcal{E}}\mathbb{E}{x,y^{}\in\mathcal{X}{e},y{e}^{}}\mathcal{L}(f_{\phi^{}}(x),y^{}),\mathrm{~~where~~}f_{\phi^{}}=M(f_{\phi};\mathcal{E}),}\ &{\quad|\mathcal{L}(f_{\phi^{}}(x),y)-\mathcal{L}(f_{\phi}(x),y)|\le\delta,\forall x,y\in\chi\backslash\mathcal{X}{\mathcal{E}},y\backslash y{\mathcal{E}},}\end{array}}\end{array}
$$

where $\phi,\phi^{}$ are the parameters before and after updating, respectively. $\delta$ is a scalar hyper-parameter to restrict the difference between losses of $f_{\phi^{}}$ and $f_{\phi}$ . The constraint in Eq. (21) restricts the change of the edited model on unmodified knowledge. Zhu et al. [177] first propose an approximate optimization constraint that is easier for implementation and computation:

其中 $\phi,\phi^{}$ 分别表示更新前后的参数。$\delta$ 是一个标量超参数，用于限制 $f_{\phi^{}}$ 和 $f_{\phi}$ 的损失差异。公式 (21) 中的约束条件限制了编辑模型在未修改知识上的变化。Zhu等人[177]首次提出了一种更易于实现和计算的近似优化约束：

$\operatorname*{min}\mathbb{E}{e\in\mathcal{E}}\mathbb{E}{x,y^{\ast}\in\chi_{e},y_{e}^{\ast}}\mathcal{L}(f_{\phi^{\ast}}(x),y^{\ast})$ , where $f_{\phi^{*}}=M(f_{\phi};\mathcal{E})_{:}$ ,

$\operatorname*{min}\mathbb{E}{e\in\mathcal{E}}\mathbb{E}{x,y^{\ast}\in\chi_{e},y_{e}^{\ast}}\mathcal{L}(f_{\phi^{\ast}}(x),y^{\ast})$ ，其中 $f_{\phi^{*}}=M(f_{\phi};\mathcal{E})_{:}$ ，

The updates are regularized by restricting the norm of parameters before and after updating. RECT [48] adopts a similar yet simpler approach, specifically modifying only the top $\mathbf{\cdotk}%$ of parameters with the largest numerical updates during fine-tuning. Although restricting the norm is helpful in preventing the forgetting of original knowledge, the fine-tuning process can be less effective. To deal with this, RecAdam [13], in addition to the norm constraint, applies an annealing technique to control the ratio between the parameter norm and the fine-tuning loss as follows:

更新过程通过限制参数在更新前后的范数进行正则化。RECT [48] 采用了一种类似但更简单的方法，具体而言仅修改微调过程中数值更新幅度最大的前 $\mathbf{\cdotk}%$ 参数。虽然限制范数有助于防止原始知识遗忘，但微调效果可能减弱。为此，RecAdam [13] 除范数约束外，还采用退火技术控制参数范数与微调损失的比例，具体如下：

$$
\begin{array}{r}{\mathcal{L}{t o t a l}=\lambda(t)\mathcal{L}{F T}+(1-\lambda(t))\lVert\phi^{*}-\phi\rVert,\mathrm{~~where~~}\lambda(t)=\frac{1}{1+\exp(-k\cdot(t-t_{0}))}.}\end{array}
$$

Here $k$ and $t_{0}$ are hyper-parameters. $t$ is the number of fine-tuning steps. Such a design enables a gradual fine-tuning process that prevents massive parameter updates at the beginning. Motivated by the intuition of regular iz ation to preserve original knowledge, PPA [77] employs LoRA [62] in the feed-forward (FFN) layers of the transformer decoder. LoRA is proposed to train the expansion/reduction matrix, instead of the model parameter $\phi$ , to improve training speed by only updating parameters with a low intrinsic rank via dimensionality reduction. PPA leverages plug-in modules trained with constraints via LoRA to keep original knowledge intact. Moreover, the authors assess whether the content of the inputs falls within the scope of $\chi_{\varepsilon}$ using the K-adapter module [153], and redirect such inputs to the new plug-in modules. This information is then used to determine whether to employ LoRA within the FFN layers. Furthermore, MELO [169] clusters the edits and employs multiple non-overlapping LoRA blocks for fine-tuning each cluster separately, thereby mitigating the issue of catastrophic forgetting. F-Learning (Forgetting before Learning) [106] proposes another approach to preserve original knowledge, which learns knowledge parameters $\Delta\phi$ that indicates old knowledge to be forgotten, defined as follows:

这里 $k$ 和 $t_{0}$ 是超参数，$t$ 表示微调步数。这种设计实现了渐进式微调过程，避免初期出现大幅参数更新。基于正则化保留原始知识的直觉，PPA [77] 在Transformer解码器的前馈网络(FFN)层中采用了LoRA [62]技术。LoRA通过训练扩展/缩减矩阵（而非直接调整模型参数 $\phi$），借助降维仅更新低内在秩的参数来提升训练速度。PPA利用LoRA训练的带约束插件模块保持原始知识完整，并通过K-adapter模块 [153] 评估输入内容是否属于 $\chi_{\varepsilon}$ 范畴，将此类输入导向新增插件模块。该信息进一步决定是否在FFN层启用LoRA。此外，MELO [169] 对编辑操作进行聚类，采用多个非重叠LoRA块分别微调每个聚类，从而缓解灾难性遗忘问题。F-Learning（先遗忘后学习）[106] 提出另一种保留原始知识的方法，其学习参数 $\Delta\phi$ 来标识待遗忘的旧知识，定义如下：

$$
\phi^{*}=\phi-\lambda\Delta\phi,\mathrm{where}\Delta\phi=\mathrm{FT}(\phi;\mathcal{K}_{o l d})-\phi.
$$

$$
\phi^{*}=\phi-\lambda\Delta\phi,\mathrm{其中}\Delta\phi=\mathrm{FT}(\phi;\mathcal{K}_{o l d})-\phi.
$$

Here $\mathcal{K}{o l d}$ denotes the dataset composed of old knowledge that we desire to forget, and $\mathrm{FT}(\phi;\mathcal{K}{o l d})$ is the supervised fine-tuning process of parameters $\phi$ on dataset $\mathcal{K}_{o l d}$ . $\lambda$ is a hyper-parameter used to control the rate of forgetting. Based on the assumption that subtracting the parameters $\Delta\phi$ from $\phi$ can help the model forget this part of old knowledge [68], F-Learning defines the forgetting process as a subtraction operation to obtain the updated model parameter $\phi^{*}$ .

这里 $\mathcal{K}{o l d}$ 表示我们希望遗忘的旧知识组成的数据集，$\mathrm{FT}(\phi;\mathcal{K}{o l d})$ 是在数据集 $\mathcal{K}_{o l d}$ 上对参数 $\phi$ 进行监督微调的过程。$\lambda$ 是用于控制遗忘速率的超参数。基于从 $\phi$ 中减去参数 $\Delta\phi$ 可以帮助模型遗忘这部分旧知识的假设 [68]，F-Learning 将遗忘过程定义为减法操作以获得更新后的模型参数 $\phi^{*}$。

On the other hand, other works also resort to meta-learning [36, 145] to apply more flexible constraints. Meta-learning addresses the issue of over fitting by training a model that can quickly adapt to new tasks [60]. By exposing the model to a variety of tasks during training, meta-learning improves the model’s ability to generalize from limited data and reduces the risk of over fitting individual tasks [67]. In the scenario of KME, the optimal model parameters $\phi^{*}$ should minimize the expected loss over a variety of meta-tasks [120]:

另一方面，也有研究采用元学习（meta-learning）[36, 145]来施加更灵活的约束。元学习通过训练能够快速适应新任务的模型来解决过拟合问题 [60]。在训练过程中让模型接触多种任务，元学习提升了模型从有限数据中泛化的能力，并降低了过拟合特定任务的风险 [67]。在知识图谱嵌入（KME）场景中，最优模型参数 $\phi^{*}$ 应当最小化各类元任务的期望损失 [120]:

$$
\phi^{*}=\underset{\phi}{\operatorname{argmin}}\mathbb{E}{D\sim\mathcal{D}}[\mathcal{L}{\phi}(D)],
$$

where $\mathcal{D}$ corresponds to the sample set for each meta-task $D$ . Moreover, each meta task $D$ contains multiple $(x^{},y^{})$ pairs for editing. In practice, such methods often introduce additional objective functions or networks to regulate parameter updates. As a typical meta-learning method for KME, Editable Training [133] focuses on effectively rectifying errors within models while preserving their performance on other irrelevant data instances. Following a model-agnostic training manner, the authors introduce additional constraints to restrict parameter updates in a different way. Specifically, the loss function is separated into $\mathcal{L}{b a s e}$ (task-specific objective function), $\mathcal{L}{e d i t}$ (computed on the edit set $\chi_{\varepsilon}$ ), and $\mathcal{L}{l o c a l}$ (computed on samples in $\boldsymbol{\chi}\setminus\boldsymbol{X}{\mathcal{E}})$ . Moreover, the models are updated in a meta-learning manner, where $k$ steps of gradient descent would be applied for parameters before computing the objective function.

其中 $\mathcal{D}$ 对应于每个元任务 $D$ 的样本集。此外，每个元任务 $D$ 包含多个用于编辑的 $(x^{},y^{})$ 对。在实践中，这类方法通常会引入额外的目标函数或网络来调节参数更新。作为KME的典型元学习方法，可编辑训练 [133] 专注于有效纠正模型内部错误，同时保持其在其他无关数据实例上的性能。采用与模型无关的训练方式，作者通过额外约束以不同方式限制参数更新。具体而言，损失函数被分解为 $\mathcal{L}{base}$ (任务特定目标函数)、$\mathcal{L}{edit}$ (在编辑集 $\chi_{\varepsilon}$ 上计算) 和 $\mathcal{L}{local}$ (在样本集 $\boldsymbol{\chi}\setminus\boldsymbol{X}{\mathcal{E}}$ 上计算)。此外，模型以元学习方式更新，即在计算目标函数前对参数进行 $k$ 步梯度下降。

5.3.3 Intermediate Fine-tuning Strategies. While constrained fine-tuning techniques have demonstrated remarkable efficacy in a variety of NLP tasks [7, 164, 179], they still exhibit instability and high computational cost when applied to KME, primarily due to the necessity of altering all parameters [167]. A potential solution to address this challenge is to utilize an intermediate model to obtain the updated parameters in an efficient manner. Such an intermediate model is required to maintain significantly fewer parameters to ensure efficiency [17]. In general, recent works have widely adopted the Hyper-Network [51] as the intermediate model. Specifically, the Hyper-Network is a small network that generates the weights for a larger network, referred to as the main network. Specifically, the Hyper-Network takes inputs that contain information about the structure of the weights and generates the weights for layers in the main network. With the generated weights, the main network is updated to map input data to desired output targets. The updating process for the main network, denoted as $\phi$ , can be defined as follows:

5.3.3 中间微调策略。虽然约束微调技术已在多种NLP任务中展现出显著成效 [7, 164, 179]，但在应用于KME时仍存在不稳定性和高计算成本的问题，这主要源于需要修改全部参数的特性 [167]。解决这一挑战的潜在方案是采用中间模型来高效获取更新后的参数。此类中间模型需保持远少于主模型的参数量以确保效率 [17]。近期研究普遍采用超网络 (Hyper-Network) [51] 作为中间模型，该小型网络专为生成主网络权重而设计。具体而言，超网络通过接收包含权重结构信息的输入，为主网络各层生成对应权重。主网络（参数记为$\phi$）利用生成的权重进行更新，从而实现输入数据到目标输出的映射，其更新过程可定义为：

where $\mathrm{H}(\cdot)$ denotes the hyper-network. $\Delta\phi$ is the weight deviation calculated by the hyper-network. According to a recent study [147], task-specific Hyper-Networks (i.e., networks that generate target model weights based on task attributes) are effective in mitigating catastrophic forgetting issues. Therefore, such methods are suitable for the setting of KME, which requires the preservation of unedited knowledge.

其中 $\mathrm{H}(\cdot)$ 表示超网络 (hyper-network)。$\Delta\phi$ 是由超网络计算出的权重偏差。根据最新研究 [147]，任务特定超网络 (即基于任务属性生成目标模型权重的网络) 能有效缓解灾难性遗忘问题。因此，这类方法适用于需要保留未编辑知识的KME场景。

Recently, researchers have proposed to adopt hyper-networks in various ways for parameter updates in KME. As a classic example, KE [25] first proposes to edit knowledge and rectify erroneous or unexpected predictions without expensive fine-tuning. Specifically, it trains a hyper-network via constrained optimization to modify facts without affecting pre-trained knowledge irrelevant to the edit. The trained hyper network is then used to predict the weight update at the inference time.

最近，研究人员提出了多种采用超网络(hyper-network)进行知识图谱嵌入(KME)参数更新的方法。以经典工作KE [25]为例，该研究首次提出无需昂贵微调即可编辑知识并修正错误或意外预测。具体而言，该方法通过约束优化训练超网络来修改事实，同时避免影响与编辑无关的预训练知识。训练完成的超网络将在推理阶段用于预测权重更新。

Based on KE, SLAG [53] further appends metrics for two types of input texts: (1) Inputs that are not in the desired edit set $\chi_{\varepsilon}$ but logically related to E; (2) Inputs that share a formal resemblance to edited knowledge, but do not lead to changes in the prediction outcomes.

基于KE，SLAG [53]进一步补充了针对两类输入文本的评估指标：(1) 不属于目标编辑集$\chi_{\varepsilon}$但与E存在逻辑关联的输入；(2) 与编辑知识具有形式相似性但不会导致预测结果变化的输入。

However, hyper-networks are generally not capable of updating large language models due to the massive parameter size. To tackle this challenge, MEND [101] adopts a mechanism referred to as gradient decomposition. In particular, it leverages small auxiliary editing networks to transform the gradients obtained by standard fine-tuning into edits of weights in a pre-trained model. As gradients are generally high-dimensional objects, a low-rank decomposition of the gradients is utilized to achieve the transformation. Particularly, MEND parameter ize s the gradient mapping functions as MLPs with a single hidden layer, such that a significantly small number of parameters are required, compared with the edited models. In this manner, MEND enables fast model editing that can operate on considerably large pre-trained language models. Moreover, KGEditor [17] proposes to combine the benefits of memory-based methods and hyper-networks to ensure flexibility and further reduce computation costs. Particularly, KGEditor introduces an additional layer with the same architecture of FFN layers for storing knowledge. Then it constructs a hyper-network based on a bi-directional LSTM [58] that encodes embeddings of triples. In this manner, KGEditor becomes an efficient way to edit knowledge graph embeddings.

然而，由于参数量庞大，超网络通常无法直接更新大语言模型。为解决这一挑战，MEND [101] 采用了一种称为梯度分解的机制。具体而言，它利用小型辅助编辑网络将标准微调获得的梯度转换为预训练模型中的权重编辑。由于梯度通常是高维对象，该方法通过对梯度进行低秩分解来实现转换。特别地，MEND 将梯度映射函数参数化为单隐藏层的 MLP，相比被编辑模型，所需参数量显著减少。通过这种方式，MEND 实现了对超大规模预训练语言模型的快速编辑。此外，KGEditor [17] 提出结合基于内存的方法和超网络的优势，以确保灵活性并进一步降低计算成本。具体而言，KGEditor 引入了一个与 FFN 层结构相同的附加层用于存储知识，随后构建基于双向 LSTM [58] 的超网络来编码三元组嵌入。这使得 KGEditor 成为编辑知识图谱嵌入的高效方法。

5.3.4 Summary. Global optimization methods typically apply specific fine-tuning restrictions to regularize parameter updates, namely constrained fine-tuning strategies. This is to prevent over fitting and ensure the model’s performance on the unedited knowledge. One crucial advantage of such strategies is its generality regarding the relevant knowledge, i.e., in-scope inputs $X_{e}$ of edit 𝑒. As the global optimization affects all parameters in a language model, the relevant knowledge in it will also be edited, thereby generalizing to such knowledge. On the other hand, the high computation costs of fine-tuning all parameters also motivate researchers to propose intermediate fine-tuning strategies that leverage hyper-networks. Furthermore, global optimization methods are mostly model-agnostic, which means they can be applied to other editing methods. Nevertheless, such possibilities are less explored in the context of KME. In terms of the drawbacks, global optimization methods are suboptimal in maintaining the locality of edited models, as the optimization can easily influence unedited knowledge. Hence, it is crucial to achieve a balance between generality and locality when optimizing language models with specific constraints or intermediate designs.

5.3.4 总结
全局优化方法通常通过特定的微调限制来规范化参数更新，即约束性微调策略。这是为了防止过拟合并确保模型在未编辑知识上的性能。此类策略的一个关键优势在于其对相关知识的普适性，即编辑操作𝑒的范围内输入$X_{e}$。由于全局优化会影响大语言模型中的所有参数，其中的相关知识也会被编辑，从而泛化至此类知识。另一方面，微调全部参数的高计算成本也促使研究者提出利用超网络的中间微调策略。此外，全局优化方法大多与模型无关，这意味着它们可应用于其他编辑方法。然而，这种可能性在知识模型编辑(KME)领域尚未得到充分探索。就缺点而言，全局优化方法在保持编辑模型的局部性方面表现欠佳，因为优化过程容易影响未编辑知识。因此，在通过特定约束或中间设计优化大语言模型时，实现普适性与局部性的平衡至关重要。

5.4 Local Modification

5.4 局部修改

5.4.1 Overview. To tackle the challenge of fine-tuning methods with respect to locality, extensive research has been conducted on the local modification strategy for KME tasks [102, 167]. These techniques originate from the concept of identifying and modifying specific relevant weights in a pre-trained model to achieve desirable outputs. The primary objective is to first locate the weights $\phi_{k}$ that store the knowledge in a pre-trained model $f_{\phi}$ regarding the input $x$ . Afterward, by adjusting these weights, it becomes possible to generate the correct output $y^{*}$ from the same input $x$ without re-training or fine-tuning the whole model. Recently, researchers have generalized the local modification strategy to LLMs, where the efficiency of information updates for pre-trained LLMs can be substantially improved. Generally, the goal of the local modification strategy of KME can be formulated as a constrained optimization problem with refined constraints as follows:

5.4.1 概述
为解决微调方法在局部性方面的挑战，针对KME（知识模型编辑）任务的局部修改策略已开展广泛研究[102, 167]。这些技术源于识别并修改预训练模型中特定相关权重以获得理想输出的理念。其主要目标是首先定位预训练模型$f_{\phi}$中存储输入$x$相关知识的权重$\phi_{k}$，随后通过调整这些权重，无需重新训练或微调整个模型即可从相同输入$x$生成正确输出$y^{*}$。近期，研究者将局部修改策略推广至大语言模型，显著提升了预训练大语言模型的信息更新效率。通常，KME局部修改策略的目标可表述为带精细化约束的优化问题：

$$
\operatorname*{min}{\phi{k}^{\ast}}\mathbb{E}{e\in\mathcal{E}}\mathbb{E}{x,y^{\ast}\in\chi_{e},y_{e}^{\ast}}\mathcal{L}(f_{\bar{\phi}{k},\phi{k}^{\ast}}^{\ast}(x),y^{\ast}),
$$

$$
f_{\bar{\phi}{k},\phi{k}^{}}^{}(x)=f(x),\forall x\in X\backslash X_{\mathcal{E}},
$$

Here $\phi^{}$ denotes the edited weights related to the new knowledge, and $\bar{\phi}{k}$ denotes the unedited weights. Eq. (27) breaks down the local modification strategy for KME into two steps: (1) The locating step, denoted by function $L$ , locates the relevant weights $\phi{k}$ in pre-trained model $f_{\phi}$ that store the obsolete information regarding the query $x$ . (2) The editing step, denoted by function $M$ , edits the located weights $\phi_{k}$ into new weights $\phi_{k}^{}$ such that the correct answer $y^{}$ given the query $x$ can be generated by the model with $\phi_{k}^{}$ . By only updating a small fraction of model weights, the editing step avoids negatively influencing other irrelevant information, (i.e., $x\in X\backslash X_{\mathcal{E}})$ .

这里 $\phi^{}$ 表示与新知识相关的编辑后权重，$\bar{\phi}{k}$ 表示未编辑的权重。公式(27) 将KME的局部修改策略分解为两个步骤：(1) 定位步骤，由函数 $L$ 表示，在预训练模型 $f{\phi}$ 中定位存储与查询 $x$ 相关过时信息的权重 $\phi_{k}$。(2) 编辑步骤，由函数 $M$ 表示，将定位到的权重 $\phi_{k}$ 编辑为新权重 $\phi_{k}^{}$，使得模型使用 $\phi_{k}^{}$ 时能针对查询 $x$ 生成正确答案 $y^{}$。通过仅更新一小部分模型权重，编辑步骤避免了对其他无关信息(即 $x\in X\backslash X_{\mathcal{E}}$) 的负面影响。

In the following subsections, we first introduce the concept of knowledge neuron in LLMs, which are specific neurons that store factual knowledge and can be activated to generate the desirable answer based on a certain query $x$ . Then we dis

[论文翻译]大语言模型知识编辑研究综述

原文地址：https://miner.umaxing.com/miner/v2/analysis/pdf_md?filename=full.md&as_attachment=False&user_id=1027&pdf=77d3c50e6184b5fbe01b2797d4d8fbeb885df049bf2f35e1adf3deee677d80981744797308_2310.16218v4.pdf