使用纯JAX在100行代码中实现LLaMA3

前言

本文将介绍如何从零开始使用纯JAX在仅100行代码内实现LLaMA3模型。为什么选择JAX？因为它的代码风格优美，且它虽然看起来像一个NumPy包装器，但拥有诸如XLA（线性代数加速器）、JIT、vmap和pmap等强大特性，让训练过程更快。

JAX是最早专注于纯函数式编程的库之一，这让它显得更加酷炫！

注意事项

假设前提：本文假定读者熟悉Python和Transformer架构的基础知识。
目的：此实现主要用于教学，涵盖模型的所有组件，但不适合生产环境。
源码链接：如果不想阅读本文，可以直接查看所有代码此处。

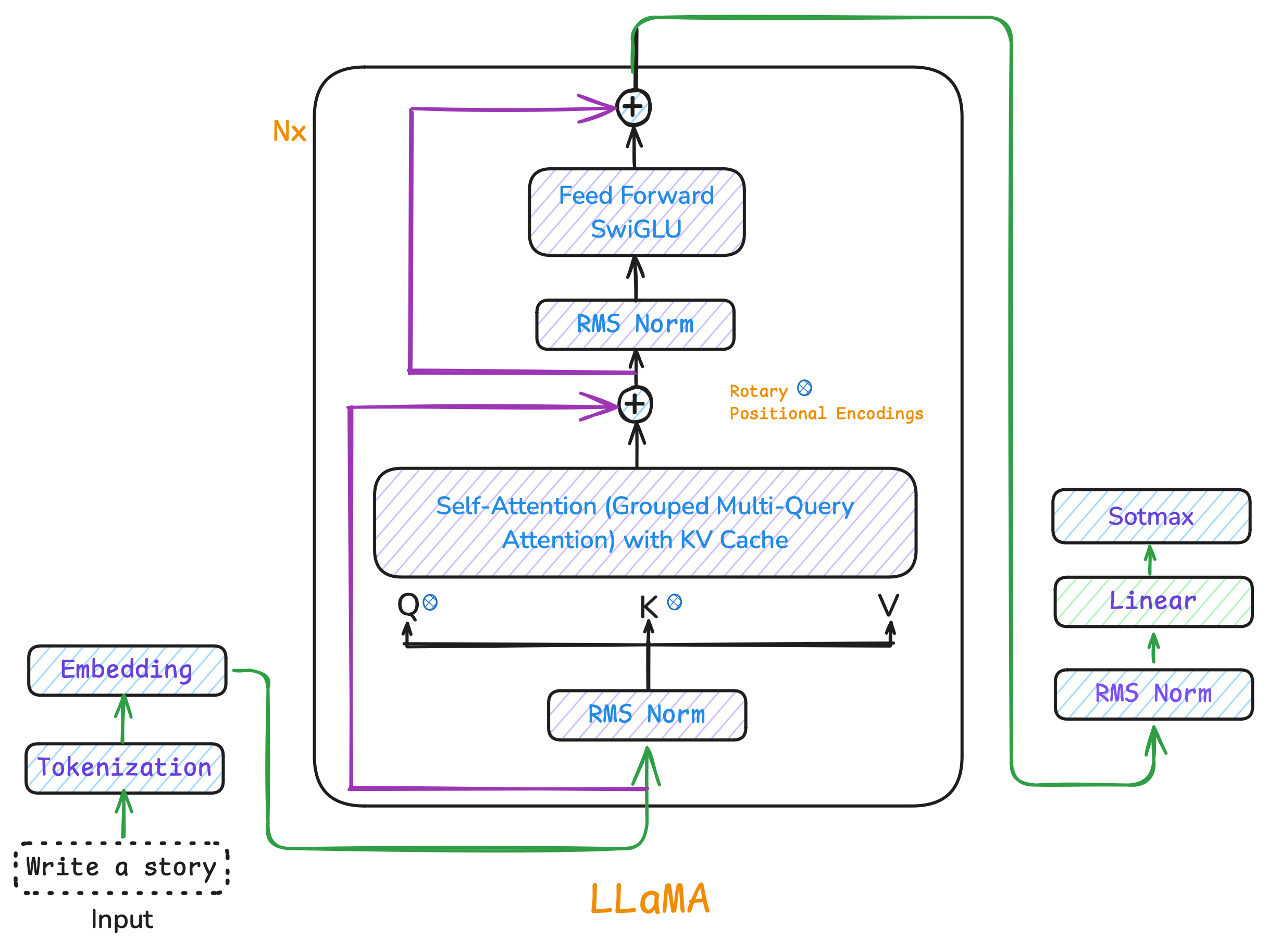
Llama 架构

LLaMA3简介

LLaMA3是一个解码器结构的Transformer语言模型，逐个生成词元，基于先前的词元预测下一个词元，类似于逐词补全句子。

让我们开始吧！首先配置设备并设置模型参数。

os.environ['JAX_PLATFORM_NAME'] = 'gpu'
os.environ['XLA_PYTHON_CLIENT_PREALLOCATE'] = 'false'
print("JAX devices:", jax.devices())

以下是训练大约2百万参数模型所需的超参数：

args = ModelArgs(
  vocab_size=enc.n_vocab,  # 词汇表大小
  dim=256,        # 嵌入维度
  n_layers=6,      # Transformer层数
  n_heads=8,       # 注意力头数
  n_kv_heads=4,     # GQA的键值头数
  max_seq_len=512,    # 最大序列长度
  norm_eps=1e-5     # 归一化参数
)

模型权重初始化

在纯JAX中，我们不使用类（如PyTorch中的nn.Module），而是只用纯函数。这是因为纯函数可以让代码更具可预测性和更易并行化。此外，我们还需要手动初始化和更新权重。

在JAX中处理随机性的方式也有所不同，我们需要显式地管理伪随机数生成器（PRNG）密钥，而不是依赖全局种子。

key = jax.random.PRNGKey(42)
key, subkey = jax.random.split(key)
weights = jax.random.normal(subkey, (784, 512))

接下来定义权重初始化函数：

def init_weight(key, shape, scale=None):
  scale = 1.0 / math.sqrt(shape[0]) if scale is None else scale
  return jax.random.normal(key, shape) * scale

对于多头注意力机制，我们可以这样初始化权重：

def init_attention_weights(key, dim, n_heads, n_kv_heads):
  keys = jax.random.split(key, 4)
  head_dim = dim // n_heads
  return {
    'wq': init_weight(keys[0], (dim, n_heads * head_dim)),
    'wk': init_weight(keys[1], (dim, n_kv_heads * head_dim)),
    'wv': init_weight(keys[2], (dim, n_kv_heads * head_dim)),
    'wo': init_weight(keys[3], (n_heads * head_dim, dim))
  }

随后我们将所有权重组装成完整的模型参数：

def init_model_params(key, vocab_size, dim, n_layers, n_heads, n_kv_heads):
  keys = jax.random.split(key, 4)
  params = {
    'token_embedding': init_weight(keys[0], (vocab_size, dim)),
    'norm_f': init_weight(keys[1], (dim,), scale=1.0),
    'output': init_weight(keys[2], (dim, vocab_size))
  }
  block_keys = jax.random.split(keys[3], n_layers)
  params['blocks'] = [
    init_transformer_block(k, dim, n_heads, n_kv_heads)
    for k in block_keys
  ]
  return params

词元化

词元化是将文本分割为单词或子词（词元）的过程。我们将使用Byte Pair Encoding (BPE)方法来训练模型，而非从头构建BPE，而是使用OpenAI提供的tiktoken库。

enc = tiktoken.get_encoding("gpt2")
with open('../shakespeare.txt', 'r') as f:
  text = f.readlines()[0]
tokens = enc.encode(text)
data = jnp.array(tokens, dtype=jnp.int32)
decoded_text = enc.decode(tokens)
print("Original Text:", text.strip())
print("Encoded Tokens:", tokens)
print("Decoded Text:", decoded_text)

嵌入层

嵌入层用于将离散的词元转换为连续的向量表示，以便进行数学运算，并帮助捕捉词元之间的语义和句法关系。

h = params["token_embedding"][inputs]

根均方层归一化

根均方层归一化有助于保持训练稳定，防止网络中的数值过大或过小。

def rms_norm(x, weight, eps=1e-5):
  variance = jnp.mean(jnp.square(x), axis=-1, keepdims=True)
  return x * weight * jnp.reciprocal(jnp.sqrt(variance + eps))

旋转位置编码

为了给Transformer提供顺序信息，我们使用旋转位置编码（ROPE）。它通过“旋转”查询和键向量来嵌入位置信息。

def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
  freqs = 1.0 / (theta ** (jnp.arange(0, dim // 2, dtype=jnp.float32) / dim))
  t = jnp.arange(end, dtype=jnp.float32)
  freqs = jnp.outer(t, freqs)
  return jnp.complex64(jnp.exp(1j * freqs))

应用旋转操作：

def apply_rotary_emb(xq, xk, freqs_cis):
  xq_r, xk_r = jnp.reshape(xq, (*xq.shape[:-1], -1, 2)), jnp.reshape(xk, (*xk.shape[:-1], -1, 2))
  xq_complex = jnp.complex64(xq_r[..., 0] + 1j * xq_r[..., 1])
  xk_complex = jnp.complex64(xk_r[..., 0] + 1j * xk_r[..., 1])
  freqs_cis = jnp.reshape(freqs_cis, (1, freqs_cis.shape[0], 1, freqs_cis.shape[1]))
  xq_out = xq_complex * freqs_cis
  xk_out = xk_complex * freqs_cis
  xq = jnp.stack([jnp.real(xq_out), jnp.imag(xq_out)], axis=-1).reshape(xq.shape)
  xk = jnp.stack([jnp.real(xk_out), jnp.imag(xk_out)], axis=-1).reshape(xk.shape)
  return xq, xk

分组查询注意力机制

分组查询注意力机制（GQA）是对多头注意力的一种优化，允许共享多个查询头的键值表示，从而减少计算开销和内存占用。

def attention(params, x, mask, freqs_cis, n_heads, n_kv_heads, cache=None, position=0):
  B, T, C = x.shape
  head_dim = C // n_heads
  q = jnp.dot(x, params['wq']).reshape(B, T, n_heads, head_dim)
  k = jnp.dot(x, params['wk']).reshape(B, T, n_kv_heads, head_dim)
  v = jnp.dot(x, params['wv']).reshape(B, T, n_kv_heads, head_dim)
  q, k = apply_rotary_emb(q, k, freqs_cis[position:position + T])
  if cache is not None:
    k = jnp.concatenate([cache[0], k], axis=-1)
    v = jnp.concatenate([cache[1], v], axis=-1)
  new_cache = (k, v)
  k = repeat_kv(k, n_heads // n_kv_heads)
  v = repeat_kv(v, n_heads // n_kv_heads)
  q, k, v = map(lambda x: x.transpose(0

[博客翻译]在100行纯Jax中实现LLaMA3

原文地址：https://saurabhalone.com/blogs/llama3/web