Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach
通过潜在推理扩展测试时计算:一种递归深度方法
Jonas Geiping 1 Sean McLeish 2 Neel Jain 2 John Kirchen bauer 2 Siddharth Singh 2 Brian R. Bartoldson 3 Bhavya Kailkhura 3 Abhinav Bhatele 2 Tom Goldstein 2
Jonas Geiping 1 Sean McLeish 2 Neel Jain 2 John Kirchen bauer 2 Siddharth Singh 2 Brian R. Bartoldson 3 Bhavya Kailkhura 3 Abhinav Bhatele 2 Tom Goldstein 2
Abstract
摘要
We study a novel language model architecture that is capable of scaling test-time computation by implicitly reasoning in latent space. Our model works by iterating a recurrent block, thereby unrolling to arbitrary depth at test-time. This stands in contrast to mainstream reasoning models that scale up compute by producing more tokens. Unlike approaches based on chain-of-thought, our approach does not require any specialized training data, can work with small context windows, and can capture types of reasoning that are not easily represented in words. We scale a proof-ofconcept model to 3.5 billion parameters and 800 billion tokens. We show that the resulting model can improve its performance on reasoning benchmarks, sometimes dramatically, up to a computation load equivalent to 50 billion parameters.
我们研究了一种新颖的大语言模型架构,该架构能够通过在潜在空间中隐式推理来扩展测试时的计算能力。我们的模型通过迭代一个循环块来工作,从而在测试时展开到任意深度。这与主流推理模型形成对比,后者通过生成更多的 Token 来扩展计算。与基于思维链的方法不同,我们的方法不需要任何专门的训练数据,可以在小上下文窗口中工作,并且能够捕捉不易用语言表示的推理类型。我们将一个概念验证模型扩展到 35 亿参数和 8000 亿 Token。我们展示了该模型在推理基准测试中的性能可以提升,有时甚至显著提升,最高可达到相当于 500 亿参数的计算负载。
1. Scaling by Thinking in Continuous Space
1. 通过在连续空间中思考实现扩展
Humans naturally expend more mental effort solving some problems than others. While humans are capable of thinking over long time spans by verbalizing intermediate results and writing them down, a substantial amount of thought happens through complex, recurrent firing patterns in the brain, before the first word of an answer is uttered.
人类在解决某些问题时自然消耗更多的脑力。虽然人类能够通过口头表达中间结果并将其写下来进行长时间的思考,但在回答的第一个词说出之前,大量的思考是通过大脑中复杂、反复的放电模式进行的。
Early attempts at increasing the power of language models focused on scaling model size, a practice that requires extreme amounts of data and computation. More recently, researchers have explored ways to enhance the reasoning capability of models by scaling test time computation. The mainstream approach involves post-training on long chainof-thought examples to develop the model’s ability to verbalize intermediate calculations in its context window and thereby external ize thoughts.
早期提升语言模型能力的尝试主要集中在扩大模型规模上,这种做法需要大量的数据和计算资源。最近,研究人员开始探索通过增加测试时的计算量来增强模型的推理能力。主流方法包括在长链思维示例上进行后训练,以开发模型在其上下文窗口中表达中间计算的能力,从而将思维外化。

Scaling up Test-Time Compute with Recurrent Depth Figure 1: We train a 3.5B parameter language model with depth recurrence. At test time, the model can iterate longer to use more compute and improve its performance. Instead of scaling test-time reasoning by “verbalizing” in long Chains-of-Thought, the model improves entirely by reasoning in latent space. Tasks that require less reasoning like OpenBookQA converge quicker than tasks like GSM8k, which effectively make use of more compute.
图 1: 我们使用深度循环训练了一个 3.5B 参数的语言模型。在测试时,模型可以通过更长时间的迭代来使用更多的计算资源并提升其性能。与通过在长链思维(Chains-of-Thought)中“语言化”来扩展测试时推理不同,该模型完全通过在潜在空间中进行推理来提升性能。像 OpenBookQA 这样需要较少推理的任务比像 GSM8k 这样有效利用更多计算资源的任务收敛得更快。
However, the constraint that expensive internal reasoning must always be projected down to a single verbalized next token appears wasteful; it is plausible that models could be more competent if they were able to natively “think” in their continuous latent space. One way to unlock this untapped dimension of additional compute involves adding a recurrent unit to a model. This unit runs in a loop, iteratively processing and updating its hidden state and enabling computations to be carried on indefinitely. While this is not currently the dominant paradigm, this idea is foundational to machine learning and has been (re-)discovered in every decade, for example as recurrent neural networks, diffusion models, and as universal or looped transformers.
然而,将昂贵的内部推理始终投影到单一的语言化下一个 Token 上的约束似乎是一种浪费;如果模型能够在连续的潜在空间中“思考”,它们可能会更强大。释放这一未开发的额外计算维度的一种方法是在模型中添加一个循环单元。这个单元在循环中运行,迭代地处理并更新其隐藏状态,使得计算可以无限期地进行。虽然目前这不是主流范式,但这一想法是机器学习的基础,并且在每个十年中都被(重新)发现,例如循环神经网络、扩散模型以及通用或循环的 Transformer。
In this work, we show that depth-recurrent language models can learn effectively, be trained in an efficient manner, and demonstrate significant performance improvements under the scaling of test-time compute. Our proposed transformer architecture is built upon a latent depth-recurrent block that is run for a randomly sampled number of iterations during training. We show that this paradigm can scale to several billion parameters and over half a trillion tokens of pre training data. At test-time, the model can improve its performance through recurrent reasoning in latent space, enabling it to compete with other open-source models that benefit from more parameters and training data. Additionally, we show that recurrent depth models naturally support a number of features at inference time that require substantial tuning and research effort in non-recurrent models, such as per-token adaptive compute, (self)-speculative decoding, and KV-cache sharing. We finish out our study by tracking token trajectories in latent space, showing that a number of interesting computation behaviors simply emerge with scale, such as the model rotating shapes in latent space for numerical computations.
在这项工作中,我们展示了深度递归语言模型能够有效学习,以高效的方式进行训练,并在测试时计算资源的扩展下展现出显著的性能提升。我们提出的Transformer架构基于一个潜在深度递归块,该块在训练期间会随机采样多次迭代运行。我们证明,这种范式可以扩展到数十亿参数和超过半万亿Token的预训练数据。在测试时,模型可以通过在潜在空间中的递归推理来提升其性能,使其能够与那些受益于更多参数和训练数据的开源模型竞争。此外,我们还展示了递归深度模型在推理时天然支持一些功能,这些功能在非递归模型中需要大量调优和研究努力才能实现,例如每个Token的自适应计算、(自)推测解码和KV缓存共享。我们通过对潜在空间中的Token轨迹进行跟踪来结束我们的研究,展示了随着规模的扩大,一些有趣的计算行为自然而然地出现,例如模型在潜在空间中旋转形状以进行数值计算。
2. Why Train Models with Recurrent Depth?
2. 为什么要使用递归深度训练模型?
Recurrent layers enable a transformer model to perform arbitrarily many computations before emitting a token. In principle, recurrent mechanisms provide a simple solution for test-time compute scaling. Compared to a more standard approach of long context reasoning (OpenAI, 2024; DeepSeek-AI et al., 2025), latent recurrent thinking has several advantages.
循环层使得 Transformer 模型在生成 Token 之前能够执行任意多的计算。原则上,循环机制为测试时的计算扩展提供了简单的解决方案。与更标准的长上下文推理方法 (OpenAI, 2024; DeepSeek-AI et al., 2025) 相比,潜在循环思维具有几个优势。
On a more philosophical note, we hope that latent reasoning captures facets of human reasoning that defy verbalization, such as spatial thinking, physical intuition or (motor) planning. Over many iterations of the recurrent process, reasoning in a high-dimensional vector space would enable the deep exploration of multiple directions simultaneously, instead of linear thinking, leading to a system capable of exhibiting novel and complex reasoning behavior.
从更哲学的角度来看,我们希望潜在推理能够捕捉到人类推理中难以言述的方面,例如空间思维、物理直觉或(运动)规划。在多次迭代的循环过程中,高维向量空间中的推理将能够同时深入探索多个方向,而不是线性思维,从而形成一个能够展现新颖且复杂推理行为的系统。
Scaling compute in this manner is not at odds with scaling through extended (verbalized) inference scaling (Shao et al., 2024), or scaling parameter counts in pre training (Kaplan et al., 2020), we argue it may build a third axis on which to scale model performance.
通过这种方式扩展计算能力与通过扩展(语言化)推理扩展(Shao et al., 2024)或预训练中扩展参数数量(Kaplan et al., 2020)并不冲突,我们认为这可能会构建第三条扩展模型性能的轴。
Table of Contents —
目录 —
3. A scalable recurrent architecture
3. 可扩展的循环架构
In this section we will describe our proposed architecture for a transformer with latent recurrent depth, discussing design choices and small-scale ablations. A diagram of the architecture can be found in Figure 2. We always refer to the sequence dimension as $n$ , the hidden dimension of the model as $h$ , and its vocabulary as the set $V$ .
在本节中,我们将描述我们提出的具有潜在循环深度 (latent recurrent depth) 的 Transformer 架构,讨论设计选择和小规模消融实验。架构的示意图可以在图 2 中找到。我们始终将序列维度称为 $n$,模型的隐藏维度称为 $h$,其词汇表称为集合 $V$。
3.1. Macroscopic Design
3.1. 宏观设计
The model is primarily structured around decoder-only transformer blocks (Vaswani et al., 2017; Radford et al., 2019). However these blocks are structured into three functional groups, the prelude $P$ , which embeds the input data into a latent space using multiple transformer layers, then the core recurrent block $R$ , which is the central unit of recurrent computation modifying states $\textbf{s}\in,\mathbb{R}^{n\times h}$ , and finally the coda $C$ , which un-embeds from latent space using several layers and also contains the prediction head of the model. The core block is set between the prelude and coda blocks, and by looping the core we can put an indefinite amount of verses in our song.
该模型主要围绕仅解码器 (decoder-only) 的 Transformer 模块构建 (Vaswani et al., 2017; Radford et al., 2019)。然而,这些模块被组织成三个功能组:前奏 $P$,它使用多个 Transformer 层将输入数据嵌入到潜在空间;核心循环模块 $R$,它是修改状态 $\textbf{s}\in,\mathbb{R}^{n\times h}$ 的循环计算中心单元;以及尾声 $C$,它使用多个层从潜在空间中解嵌,并包含模型的预测头。核心模块设置在前奏和尾声模块之间,通过循环核心模块,我们可以在歌曲中放入无限数量的段落。

Figure 2: A visualization of the Architecture, as described in Section 3. Each block consists of a number of sub-layers. The blue prelude block embeds the inputs into latent space, where the green shared recurrent block is a block of layers that is repeated to compute the final latent state, which is decoded by the layers of the red coda block.
图 2: 架构的可视化,如第 3 节所述。每个块由若干子层组成。蓝色的前奏块将输入嵌入到潜在空间中,绿色的共享循环块是由多个层组成的块,重复计算最终的潜在状态,然后由红色的尾声块进行解码。
Given a number of recurrent iterations $r$ , and a sequence of input tokens $\mathbf{x}\in V^{n}$ these groups are used in the following way to produce output probabilities $\mathbf{p}\in\mathbb{R}^{n\times|V|}$
给定一个递归迭代次数 $r$,以及输入 Token 序列 $\mathbf{x}\in V^{n}$,这些组按以下方式用于生成输出概率 $\mathbf{p}\in\mathbb{R}^{n\times|V|}$。

where $\sigma$ is some standard deviation for initializing the random state. This process is shown in Figure 2. Given an init random state $\mathbf{s}{\mathrm{0}}$ , the model repeatedly applies the core block $R$ , which accepts the latent state $\mathbf{s}{i-1}$ and the embedded input e and outputs a new latent state $\mathbf{s}_{i}$ . After finishing all iterations, the coda block processes the last state and produces the probabilities of the next token.
其中 $\sigma$ 是用于初始化随机状态的标准差。该过程如图 2 所示。给定一个初始随机状态 $\mathbf{s}{\mathrm{0}}$,模型反复应用核心块 $R$,它接受潜在状态 $\mathbf{s}{i-1}$ 和嵌入输入 e,并输出一个新的潜在状态 $\mathbf{s}_{i}$。在所有迭代完成后,coda 块处理最后一个状态并生成下一个 token 的概率。
This architecture is based on deep thinking literature, where it is shown that injecting the latent inputs e in every step (Bansal et al., 2022) and initializing the latent vector with a random state stabilizes the recurrence and promotes convergence to a steady state independent of initialization, i.e. path independence (Anil et al., 2022).
该架构基于深度思考文献,文献表明在每个步骤中注入潜在输入 e (Bansal et al., 2022),并用随机状态初始化潜在向量可以稳定递归并促进收敛到与初始化无关的稳态,即路径独立性 (Anil et al., 2022)。
Motivation for this Design. This recurrent design is the minimal setup required to learn stable iterative operators. A good example is gradient descent of a function $E(\mathbf{x},\mathbf{y})$ , where $\mathbf{x}$ may be the variable of interest and y the data. Gradient descent on this function starts from an initial random state, here $\mathbf{x}{\mathrm{0}}$ , and repeatedly applies a simple operation (the gradient of the function it optimizes), that depends on the previous state $\mathbf{x}{k}$ and data y. Note that we need to use $\mathbf{y}$ in every step to actually optimize our function. Similarly we repeatedly inject the data $\mathbf{e}$ in our set-up in every step of the recurrence. If $\mathbf{e}$ was provided only at the start, e.g. via $\mathbf{s}_{0}=\mathbf{e}$ , then the iterative process would not be stable1, as its solution would depend only on its boundary conditions.
该设计的动机。这种循环设计是学习稳定迭代算子的最小设置。一个很好的例子是函数 $E(\mathbf{x},\mathbf{y})$ 的梯度下降,其中 $\mathbf{x}$ 可能是感兴趣的变量,而 y 是数据。该函数的梯度下降从一个初始随机状态 $\mathbf{x}{\mathrm{0}}$ 开始,并反复应用一个简单的操作(它优化的函数的梯度),该操作依赖于前一个状态 $\mathbf{x}{k}$ 和数据 y。注意,我们需要在每一步都使用 $\mathbf{y}$ 来实际优化我们的函数。同样,在我们的设置中,我们在循环的每一步都反复注入数据 $\mathbf{e}$。如果 $\mathbf{e}$ 仅在开始时提供,例如通过 $\mathbf{s}_{0}=\mathbf{e}$,那么迭代过程将不稳定,因为它的解将仅依赖于其边界条件。
The structure of using several layers to embed input tokens into a hidden latent space is based on empirical results analyzing standard fixed-depth transformers (Skean et al., 2024; Sun et al., 2024; Kaplan et al., 2024). This body of research shows that the initial and the end layers of LLMs are noticeably different, whereas middle layers are interchangeable and permutable. For example, Kaplan et al. (2024) show that within a few layers standard models already embed sub-word tokens into single concepts in latent space, on which the model then operates.
使用多层将输入Token嵌入到隐藏潜在空间的结构基于对标准固定深度Transformer的实证分析结果 (Skean et al., 2024; Sun et al., 2024; Kaplan et al., 2024)。这一研究领域表明,大语言模型的初始层和最终层明显不同,而中间层是可互换和可置换的。例如,Kaplan et al. (2024) 表明,在几层之内,标准模型已经将子词Token嵌入到潜在空间中的单一概念中,模型随后在这些概念上操作。
Remark 3.1 (Is this a Diffusion Model?). This iterative architecture will look familiar to the other modern iterative modeling paradigm, diffusion models (Song & Ermon, 2019), especially latent diffusion models (Rombach et al., 2022). We ran several ablations with iterative schemes even more similar to diffusion models, such as $\mathbf{s}{i}=R(\mathbf{e},\mathbf{s}{i-1})+$ $\mathbf{n}$ where $\mathbf{n}\sim\mathcal{N}(\mathbf{0},\sigma_{i}I_{n\cdot h})$ , but find the injection of noise not to help in our preliminary experiments, which is possibly connected to our training objective. We also evaluated and $\mathbf{s}{i}=R{i}(\mathbf{e},\mathbf{s}_{i-1})$ , i.e. a core block that takes the current step as input (Peebles & Xie, 2023), but find that this interacts badly with path independence, leading to models that cannot extrapolate.
备注 3.1 (这是扩散模型吗?). 这种迭代架构会让人联想到另一种现代迭代建模范式,即扩散模型 (Song & Ermon, 2019),尤其是潜在扩散模型 (Rombach et al., 2022)。我们进行了几次与扩散模型更为相似的迭代方案的消融实验,例如 $\mathbf{s}{i}=R(\mathbf{e},\mathbf{s}{i-1})+$ $\mathbf{n}$ ,其中 $\mathbf{n}\sim\mathcal{N}(\mathbf{0},\sigma_{i}I_{n\cdot h})$,但在初步实验中发现噪声的注入并没有帮助,这可能与我们的训练目标有关。我们还评估了 $\mathbf{s}{i}=R{i}(\mathbf{e},\mathbf{s}_{i-1})$,即一个将当前步骤作为输入的核心块 (Peebles & Xie, 2023),但发现这与路径独立性存在严重冲突,导致模型无法外推。
3.2. Microscopic Design
3.2. 微观设计
Within each group, we broadly follow standard transformer layer design. Each block contains multiple layers, and each layer contains a standard, causal self-attention block using RoPE (Su et al., 2021) with a base of 50000, and a gated SiLU MLP (Shazeer, 2020). We use RMSNorm (Zhang & Sennrich, 2019) as our normalization function. The model has learnable biases on queries and keys, and nowhere else. To stabilize the recurrence, we order all layers in the following “sandwich” format, using norm layers $n_{i}$ , which is related, but not identical to similar strategies in (Ding et al., 2021; Team Gemma et al., 2024):
在每个组内,我们大致遵循标准的Transformer层设计。每个块包含多个层,每层包含一个标准的、因果自注意力块,使用基于50000的RoPE (Su et al., 2021),以及一个门控SiLU MLP (Shazeer, 2020)。我们使用RMSNorm (Zhang & Sennrich, 2019)作为归一化函数。模型在查询和键上有可学习的偏置,其他位置则没有。为了稳定递归,我们按照以下“三明治”格式对所有层进行排序,使用与(Ding et al., 2021; Team Gemma et al., 2024)中类似但不同的策略,涉及归一化层$n_{i}$:
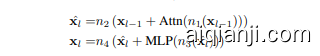
While at small scales, most normalization strategies, e.g. pre-norm, post-norm and others, work almost equally well, we ablate these options and find that this normalization is required to train the recurrence at scale.
在小规模情况下,大多数归一化策略(例如 pre-norm、post-norm 等)效果几乎相同,但我们通过消融实验发现,在大规模训练循环时,这种归一化是必要的。
Given an embedding matrix $E$ and embedding scale $\gamma$ , the prelude block first embeds input tokens $\mathbf{x}$ as $\gamma E(\mathbf{x})$ , and then to applies $l_{P}$ many prelude layers with the layout described above.
给定嵌入矩阵 $E$ 和嵌入尺度 $\gamma$,前导块首先将输入 Token $\mathbf{x}$ 嵌入为 $\gamma E(\mathbf{x})$,然后应用 $l_{P}$ 个前导层,其布局如上所述。
Our core recurrent block $R$ starts with an adapter matrix $A:\mathbb{R}^{2h},\rightarrow,\mathbb{R}^{h}$ mapping the concatenation of $\mathbf{s}{i}$ and $\mathbf{e}$ into the hidden dimension $h$ (Bansal et al., 2022). While re-incorporation of initial embedding features via addition rather than concatenation works equally well for smaller models, we find that concatenation works best at scale. This is then fed into $l{R}$ transformer layers. At the end of the core block the output is again rescaled with an RMSNorm $n_{c}$ .
我们的核心循环块 $R$ 始于一个适配器矩阵 $A:\mathbb{R}^{2h},\rightarrow,\mathbb{R}^{h}$,它将 $\mathbf{s}{i}$ 和 $\mathbf{e}$ 的串联映射到隐藏维度 $h$ (Bansal et al., 2022)。尽管通过加法而非串联重新整合初始嵌入特征在较小的模型上同样有效,但我们发现串联在大规模模型上效果最佳。然后将其输入到 $l{R}$ 层 Transformer 中。在核心块的最后,输出再次通过 RMSNorm $n_{c}$ 进行缩放。
The coda contains $l_{C}$ layers, normalization by $n_{c}$ , and projection into the vocabulary using tied embeddings $E^{T}$ .
Coda 包含 $l_{C}$ 层,通过 $n_{c}$ 进行归一化,并使用绑定嵌入 $E^{T}$ 投影到词汇表中。
In summary, we can summarize the architecture by the triplet $(l_{P},l_{R},l_{C})$ , describing the number of layers in each stage, and by the number of recurrences $r$ , which may vary in each forward pass. We train a number of small-scale models with shape $(1,4,1)$ and hidden size $h=1024$ , in addition to a large model with shape $(2,4,2)$ and $h=5280$ This model has only 8 “real” layers, but when the recurrent block is iterated, e.g. 32 times, it unfolds to an effective depth of $2+4r+2=132$ layers, constructing computation chains that can be deeper than even the largest fixed-depth transformers (Levine et al., 2021; Merrill et al., 2022).
总之,我们可以通过三元组 $(l_{P},l_{R},l_{C})$ 来总结架构,描述每个阶段的层数,以及每次前向传播中可能变化的递归次数 $r$。我们训练了一些小规模模型,其形状为 $(1,4,1)$,隐藏层大小为 $h=1024$,此外还有一个大规模模型,其形状为 $(2,4,2)$,$h=5280$。该模型只有 8 个“真实”层,但当递归块迭代时,例如 32 次,它会展开为有效深度为 $2+4r+2=132$ 层,构建的计算链甚至比最大的固定深度 Transformer 模型还要深 (Levine et al., 2021; Merrill et al., 2022)。
3.3. Training Objective
3.3. 训练目标
Training Recurrent Models through Unrolling. To ensure that the model can function when we scale up recurrent iterations at test-time, we randomly sample iteration counts during training, assigning a random number of iterations $r$ to every input sequence (Schwarz s child et al., 2021b). We optimize the expectation of the loss function $L$ over random samples $x$ from distribution $X$ and random iteration counts $r$ from distribution $\Lambda$ .
通过展开训练循环模型。为了确保模型在测试时扩展循环迭代时能够正常工作,我们在训练期间随机采样迭代次数,为每个输入序列分配一个随机迭代次数 $r$ (Schwarzschild et al., 2021b)。我们优化了从分布 $X$ 中随机采样的样本 $x$ 和从分布 $\Lambda$ 中随机采样的迭代次数 $r$ 的损失函数 $L$ 的期望。

Here, $m$ represents the model output, and $\mathbf{x}^{\prime}$ is the sequence $\mathbf{x}$ shifted left, i.e., the next tokens in the sequence $\mathbf{x}$ . We choose $\Lambda$ to be a log-normal Poisson distribution. Given a targeted mean recurrence $\bar{r}+1$ and a variance that we set to $\begin{array}{r}{\sigma=\frac12}\end{array}$ 12, we can sample from this distribution via
这里,$m$ 表示模型输出,$\mathbf{x}^{\prime}$ 是序列 $\mathbf{x}$ 左移的结果,即序列 $\mathbf{x}$ 中的下一个 Token。我们选择 $\Lambda$ 为对数正态泊松分布。给定目标平均重现 $\bar{r}+1$ 和方差 $\begin{array}{r}{\sigma=\frac12}\end{array}$,我们可以通过以下方式从该分布中采样:

given the normal distribution $\mathcal{N}$ and Poisson distribution $\mathcal{P}$ , see Figure 3. The distribution most often samples values less than $\bar{r}$ , but it contains a heavy tail of occasional events in which significantly more iterations are taken.
给定正态分布 $\mathcal{N}$ 和泊松分布 $\mathcal{P}$,见图 3。该分布最常采样的值小于 $\bar{r}$,但它包含一个显著更多迭代的重尾偶尔事件。

Figure 3: We use a log-normal Poisson Distribution to sample the number of recurrent iterations for each training step.
图 3: 我们使用对数正态泊松分布来采样每个训练步骤的循环迭代次数。
Truncated Back propagation. To keep computation and memory low at train time, we back propagate through only the last $k$ iterations of the recurrent unit. This enables us to train with the heavy-tailed Poisson distribution $\Lambda$ , as maximum activation memory and backward compute is now independent of $r$ . We fix $k,=,8$ in our main experiments. At small scale, this works as well as sampling $k$ uniformly, but with set fixed, the overall memory usage in each step of training is equal. Note that the prelude block still receives gradient updates in every step, as its output $\mathbf{e}$ is injected in every step. This setup resembles truncated back prop agation through time, as commonly done with RNNs, although our setup is recurrent in depth rather than time (Williams & Peng, 1990; Mikolov et al., 2011).
截断反向传播。为了在训练时保持计算和内存的低消耗,我们只通过循环单元的最后 $k$ 次迭代进行反向传播。这使得我们能够使用重尾泊松分布 $\Lambda$ 进行训练,因为最大激活内存和反向计算现在与 $r$ 无关。在我们的主要实验中,我们固定 $k,=,8$。在小规模情况下,这与均匀采样 $k$ 效果相当,但由于固定了 $k$,训练每一步的整体内存使用量是相等的。需要注意的是,前导块在每一步仍然接收梯度更新,因为它的输出 $\mathbf{e}$ 在每一步都被注入。这种设置类似于通过时间截断反向传播 (Williams & Peng, 1990; Mikolov et al., 2011),尽管我们的设置是在深度上循环,而不是在时间上循环。
4. Training a large-scale recurrent-depth Language Model
4. 训练大规模循环深度语言模型
After verifying that we can reliably train small test models up to 10B tokens, we move on to larger-scale runs. Given our limited compute budget, we could either train multiple tiny models too small to show emergent effects or scaling, or train a single medium-scale model. Based on this, we prepared for a single run, which we detail below.
在验证了我们能够可靠地训练高达 100 亿 Token 的小型测试模型后,我们开始进行更大规模的训练。鉴于我们有限的计算预算,我们可以选择训练多个过小以至于无法展现涌现效应或扩展性的微型模型,或者训练一个中等规模的模型。基于此,我们准备了一次单独的运行,具体细节如下。
4.1. Training Setup
4.1. 训练设置
We describe the training setup, separated into architecture, optimization setup and pre training data. We publicly release all training data, pre training code, and a selection of intermediate model checkpoints.
我们描述了训练设置,分为架构、优化设置和预训练数据。我们公开发布了所有训练数据、预训练代码以及部分中间模型检查点。
Pre training Data. Given access to only enough compute for a single large scale model run, we opted for a dataset mixture that maximized the potential for emergent reasoning behaviors, not necessarily for optimal benchmark per- formance. Our final mixture is heavily skewed towards code and mathematical reasoning data with (hopefully) just enough general webtext to allow the model to acquire standard language modeling abilities. All sources are publicly available. We provide an overview in Figure 4. Following Allen-Zhu & Li (2024), we directly mix relevant instruction data into the pre training data. However, due to compute and time constraints, we were not able to ablate this mixture. We expect that a more careful data preparation could further improve the model’s performance. We list all data sources in Appendix C.
预训练数据。鉴于仅能进行一次大规模模型训练的计算资源,我们选择了一个数据集混合方案,以最大化涌现推理行为的潜力,而不一定是为了获得最优的基准性能。我们的最终混合方案严重偏向代码和数学推理数据,同时(希望)包含足够的通用网络文本,以使模型能够获得标准的语言建模能力。所有数据源均为公开可用。我们在图 4 中提供了概述。根据 Allen-Zhu & Li (2024) 的方法,我们直接将相关指令数据混合到预训练数据中。然而,由于计算资源和时间的限制,我们无法对这一混合方案进行消融实验。我们预计更细致的数据准备可以进一步提高模型的性能。我们在附录 C 中列出了所有数据源。

Figure 4: Distribution of data sources that are included during training. The majority of our data is comprised of generic webtext, scientific writing and code.
图 4: 训练中包含的数据源分布。我们的数据主要由通用网页文本、科学写作和代码组成。
Token iz ation and Packing Details. We construct a vocabulary of 65536 tokens via BPE (Sennrich et al., 2016), using the implementation of Dagan (2024). In comparison to conventional tokenizer training, we construct our tokenizer directly on the instruction data split of our pre training corpus, to maximize token iz ation efficiency on the target domain. We also substantially modify the pre-token iz ation regex (e.g. of Dagan et al. (2024)) to better support code, contractions and LaTeX. We include $\mathtt{a}<|\mathtt{b e g i n_t e x t}|>$ token at the start of every document. After tokenizing our pre training corpus, we pack our tokenized documents into sequences of length 4096. When packing, we discard document ends that would otherwise lack previous context, to fix an issue described as the “grounding problem” in Ding et al. (2024), aside from several long-document sources of mathematical content, which we preserve in their entirety.
Token化和打包细节。我们通过 BPE (Sennrich et al., 2016) 构建了一个包含 65536 个 Token 的词汇表,使用了 Dagan (2024) 的实现。与传统 Tokenizer 训练相比,我们直接在预训练语料库的指令数据分割上构建了 Tokenizer,以最大化目标领域的 Token 化效率。我们还大幅修改了预 Token 化的正则表达式 (例如 Dagan et al. (2024)),以更好地支持代码、缩写和 LaTeX。我们在每个文档的开头包含了 $\mathtt{a}<|\mathtt{b e g i n_t e x t}|>$ Token。在 Token 化预训练语料库后,我们将 Token 化的文档打包成长度为 4096 的序列。打包时,我们丢弃了那些缺乏先前上下文的文档结尾,以修复 Ding et al. (2024) 中描述的“基础问题”,除了几个数学内容的长文档来源,我们保留了它们的完整性。
Architecture and Initialization. We scale the architecture described in Section 3, setting the layers to $(2,4,2)$ , and train with a mean recurrence value of $\bar{r},=,32$ . We mainly scale by increasing the hidden size to $h,=,5280$ , which yields 55 heads of size of 96. The MLP inner dimension is 17920 and the RMSNorm $\varepsilon$ is $10^{-6}$ . Overall this model shape has about 1.5B parameters in non-recurrent prelude and head, 1.5B parameters in the core recurrent block, and 0.5B in the tied input embedding.
架构与初始化。我们扩展了第3节中描述的架构,将层数设置为 $(2,4,2)$,并以平均递归值 $\bar{r},=,32$ 进行训练。我们主要通过将隐藏层大小增加到 $h,=,5280$ 来进行扩展,这产生了55个头,每个头的大小为96。MLP内部维度为17920,RMSNorm $\varepsilon$ 为 $10^{-6}$。总体而言,该模型在非递归前导和头部分约有15亿参数,核心递归块中有15亿参数,并在绑定的输入嵌入中有05亿参数。
At small scales, most sensible initialization schemes work. However, at larger scales, we use the initialization of Takase et al. (2024) which prescribes a variance of $\begin{array}{r}{\sigma_{h}^{2}=\frac{2}{5h}}\end{array}$ . We initialize all parameters from a truncated normal distribution (truncated at $3\sigma$ ) with this variance, except all out- projection layers, where the variance is set to $\begin{array}{r}{\sigma_{\mathrm{out}}^{2}=\frac{1}{5h l}}\end{array}$ for $l=l_{P}+\bar{r}l_{R}+l_{C}$ the number of effective layers, which is 132 for this model. As a result, the out-projection layers are initialized with fairly small values (Goyal et al., 2018). The output of the embedding layer is scaled by $\sqrt{h}$ . To match this initialization, the state $s_{0}$ is also sampled from a truncated normal distribution, here with variance $\begin{array}{r}{\sigma_{s}^{2}=\frac{2}{5}}\end{array}$ .
在较小规模下,大多数合理的初始化方案都能奏效。然而,在更大规模时,我们采用了 Takase 等人 (2024) 提出的初始化方法,该方法规定了方差为 $\begin{array}{r}{\sigma_{h}^{2}=\frac{2}{5h}}\end{array}$。所有参数均从截断正态分布(在 $3\sigma$ 处截断)中初始化,方差如此设置,但所有输出投影层除外,其方差设为 $\begin{array}{r}{\sigma_{\mathrm{out}}^{2}=\frac{1}{5h l}}\end{array}$,其中 $l=l_{P}+\bar{r}l_{R}+l_{C}$ 为有效层数,本模型中为 132。因此,输出投影层以相当小的值初始化(Goyal 等人,2018)。嵌入层的输出通过 $\sqrt{h}$ 进行缩放。为了匹配此初始化,状态 $s_{0}$ 同样从截断正态分布中采样,此处方差为 $\begin{array}{r}{\sigma_{s}^{2}=\frac{2}{5}}\end{array}$。
Locked-Step Sampling. To enable synchronization between parallel workers, we sample a single depth $r$ for each micro-batch of training, which we synchronize across workers (otherwise workers would idle while waiting for the model with the largest $r$ to complete its backward pass). We verify at small scale that this modification improves compute utilization without impacting convergence speed, but note that at large batch sizes, training could be further improved by optimally sampling and scheduling independent steps $r$ on each worker, to more faithfully model the expectation over steps in Equation (1).
锁定步长采样。为了实现并行工作器之间的同步,我们为每个微批次的训练采样一个单一的深度 $r$,并在工作器之间进行同步(否则工作器会在等待具有最大 $r$ 的模型完成其反向传播时闲置)。我们通过小规模验证确认这一修改在不影响收敛速度的情况下提高了计算利用率,但需要注意的是,在大批量训练时,可以通过在每个工作器上最优地采样和调度独立的步长 $r$ 来进一步改进训练,从而更准确地模拟方程(1)中步长的期望。
Optimizer and Learning Rate Schedule. We train using the Adam optimizer with decoupled weight regular iz ation $?{1},=,0.9$ , $\beta{2}~=~0.95$ , $\eta,=,5,\times,10^{-4})$ (Kingma & Ba, 2015; Loshchilov & Hutter, 2017), modified to include update clipping (Wortsman et al., 2023) and removal of the $\varepsilon$ constant as in Everett et al. (2024). We clip gradients above 1. We train with warm-up and a constant learning rate (Zhai et al., 2022; Geiping & Goldstein, 2023), warming up to our maximal learning rate within the first 4096 steps of training.
优化器和学习率调度。我们使用 Adam 优化器进行训练,同时采用解耦权重正则化 $?{1},=,0.9$,$\beta{2}~=~0.95$,$\eta,=,5,\times,10^{-4})$(Kingma & Ba, 2015; Loshchilov & Hutter, 2017),并进行了修改以包括更新裁剪(Wortsman et al., 2023)以及移除 $\varepsilon$ 常数(Everett et al., 2024)。我们将梯度裁剪为不超过 1。我们采用预热和恒定学习率的方式进行训练(Zhai et al., 2022; Geiping & Goldstein, 2023),在训练的前 4096 步内逐渐预热至最大学习率。
4.2. Compute Setup and Hardware
4.2. 计算设置与硬件
We train this model using compute time allocated on the Oak Ridge National Lab’s Frontier cluster, a large-scale HPE Cray system containing $^{\mathrm{8}}\mathrm{x}$ AMD MI250X GPU nodes. Nodes are connected via 4xHPE Slingshot NICs. The scheduling system is orchestrated through SLURM. We train in bfloat16 mixed precision using a PyTorch-based imple ment ation (Zamirai et al., 2021).
我们使用在橡树岭国家实验室的 Frontier 集群上分配的计算时间训练该模型,该集群是一个大规模的 HPE Cray 系统,包含 $^{\mathrm{8}}\mathrm{x}$ AMD MI250X GPU 节点。节点通过 4xHPE Slingshot NIC 连接。调度系统通过 SLURM 进行编排。我们使用基于 PyTorch 的实现 (Zamirai et al., 2021) 进行 bfloat16 混合精度训练。
Device Speed and Parallel iz ation Strategy. Nominally, each MI250X chip2 achieves 192 TFLOP per GPU (AMD, 2021). For a single matrix multiplication, we measure a maximum achievable speed on these GPUs of 125 TFLOP/s on our software stack (ROCM 6.2.0, PyTorch 2.6 prerelease 11/02) (Bekman, 2023). Our implementation, using extensive PyTorch compilation and optimization of the hidden dimension to $h=5280$ achieves a single-node training speed of 108.75 TFLOP/s, i.e. $87%$ AFU (“Achievable Flop Utilization”). Due to the weight sharing inherent in our recurrent design, even our largest model is still small enough to be trained using only data (not tensor) parallelism, with only optimizer sharding (Raj bh and ari et al., 2020) and gradient check pointing on a per-iteration granularity. With a batch size of 1 per GPU we end up with a global batch size of 16M tokens per step, minimizing inter-GPU communication bandwidth.
设备速度与并行化策略。名义上,每个 MI250X 芯片在单个 GPU 上实现了 192 TFLOP (AMD, 2021)。对于单次矩阵乘法,我们在我们的软件栈 (ROCM 6.2.0, PyTorch 2.6 预发布版 11/02) 上测量出的这些 GPU 的最大可达到速度为 125 TFLOP/s (Bekman, 2023)。我们的实现通过广泛的 PyTorch 编译和将隐藏维度优化为 $h=5280$,实现了单节点训练速度为 108.75 TFLOP/s,即 $87%$ 的可达到浮点运算利用率 (AFU)。由于我们循环设计中固有的权重共享,即使是我们最大的模型也足够小,可以仅使用数据(而非张量)并行进行训练,仅在每次迭代粒度上使用优化器分片 (Rajbhandari et al., 2020) 和梯度检查点。每个 GPU 的批大小为 1,最终每步的全局批大小为 1600 万 token,最大限度地减少了 GPU 之间的通信带宽。

Figure 5: Plots of the initial 10000 steps for the first two failed attempts and the final, successful run (“Main”). Note the hidden state collapse (middle) and collapse of the recurrence (right) in the first two failed runs, underlining the importance of our architecture and initialization in inducing a recurrent model and explain the under performance of these runs in terms of pre training loss (left).
图 5: 前两次失败尝试和最终成功运行(“Main”)的前 10000 步的图表。注意在前两次失败运行中,隐藏状态的崩溃(中间)和递归的崩溃(右边),这突显了我们的架构和初始化在诱导递归模型中的重要性,并解释了这些运行在预训练损失(左边)方面的表现不佳。
When we run at scale on 4096 GPUs, we achieve 52-64 TFLOP/s per GPU, i.e. $41%{-}51%$ AFU, or 1-1.2M tokens per second. To achieve this, we wrote a hand-crafted distributed data parallel implementation to circumvent a critical AMD interconnect issue, which we describe in more detail in Appendix A.2. Overall, we believe this may be the largest language model training run to completion in terms of number of devices used in parallel on an AMD cluster, as of time of writing.
当我们在 4096 个 GPU 上大规模运行时,每个 GPU 实现了 52-64 TFLOP/s,即 $41%{-}51%$ 的 AFU,或每秒 1-1.2M token。为了实现这一点,我们编写了一个手动的分布式数据并行实现,以规避一个关键的 AMD 互连问题,我们在附录 A.2 中对此进行了更详细的描述。总体而言,我们认为这可能是迄今为止在 AMD 集群上并行使用设备数量最多的语言模型训练任务。
Training Timeline. Training proceeded through 21 segments of up to 12 hours, which scheduled on Frontier mostly in early December 2024. We also ran a baseline comparison, where we train the same architecture but in a feed forward manner with only 1 pass through the core/recurrent block. This trained with the same setup for 180B tokens on 256 nodes with a batch size of 2 per GPU. Ultimately, we were able to schedule 795B tokens of pre training of the main model. Due to our constant learning rate schedule, we were able to add additional segments “on-demand”, when an allocation happened to be available.
训练时间线。训练分21个阶段进行,每个阶段最长12小时,主要安排在2024年12月初的Frontier上。我们还进行了基线比较,训练相同的架构,但仅以前馈方式通过核心/循环块进行1次传递。该训练在256个节点上使用相同的设置,训练了180B个Token,每个GPU的批量大小为2。最终,我们能够为主模型安排795B个Token的预训练。由于我们采用了恒定的学习率计划,当分配可用时,我们能够“按需”添加额外的训练阶段。
4.3. Importance of Norms and Initialization s at Scale
4.3. 大规模下规范和初始化的重要性
At small scales all normalization strategies worked, and we observed only tiny differences between initialization s. The same was not true at scale. The first training run we started was set up with the same block sandwich structure as described above, but parameter-free RMSNorm layers, no embedding scale $\gamma$ , a parameter-free adapter $A(\mathbf{s},\mathbf{e})=\mathbf{s}+\mathbf{e}$ and a peak learning rate of $4\times10^{-4}$ . As shown in Figure 5, this run (“Bad Run 1”, orange), quickly stalled
在小规模情况下,所有归一化策略都有效,我们观察到初始化方法之间只有微小的差异。但在大规模情况下,情况并非如此。我们启动的第一个训练运行采用了与上述相同的块夹层结构,但使用了无参数的 RMSNorm 层,没有嵌入缩放因子 $\gamma$,无参数的适配器 $A(\mathbf{s},\mathbf{e})=\mathbf{s}+\mathbf{e}$,以及峰值学习率为 $4\times10^{-4}$。如图 5 所示,该运行(“Bad Run 1”,橙色)很快陷入了停滞。
While the run obviously stopped improving in training loss (left plot), we find that this stall is due to the model’s represent ation collapsing (Noci et al., 2022). The correlation of hidden states in the token dimension quickly goes to 1.0 (middle plot), meaning the model predicts the same hidden state for every token in the sequence. We find that this is an initialization issue that arises due to the recurrence operation. Every iteration of the recurrence block increases token correlation, mixing the sequence until collapse.
虽然运行显然在训练损失(左图)上停止了改进,但我们发现这种停滞是由于模型的表示崩溃(Noci 等人,2022)所致。Token 维度中隐藏状态的相关性迅速上升到 1.0(中图),这意味着模型为序列中的每个 Token 预测相同的隐藏状态。我们发现这是由于循环操作引起的初始化问题。每次循环块迭代都会增加 Token 的相关性,混合序列直至崩溃。
We attempt to fix this by introducing the embedding scale factor, switching back to a conventional pre-normalization block, and switching to the learned adapter. Initially, these changes appear to remedy the issue. Even though token correlation shoots close to 1.0 at the start (“Bad Run $2^{\circ}$ , green), the model recovers after the first 150 steps. However, we quickly find that this training run is not able to leverage test-time compute effectively (right plot), as validation perplexity is the same whether 1 or 32 recurrences are used. This initialization and norm setup has led to a local minimum as the model has learned early to ignore the incoming state s, preventing further improvements.
我们尝试通过引入嵌入比例因子、切换回传统的预归一化块以及切换到学习到的适配器来解决这个问题。起初,这些更改似乎解决了问题。尽管Token相关性在开始时迅速接近1.0(“坏运行 $2^{\circ}$”,绿色),但模型在前150步后恢复了正常。然而,我们很快发现这个训练运行无法有效利用测试时的计算(右侧图表),因为无论使用1次还是32次递归,验证困惑度都相同。这种初始化和归一化设置导致模型陷入局部最小值,因为模型早期就学会了忽略传入状态s,从而阻止了进一步的改进。
In a third, and final run (“Main”, blue), we fix this issue by reverting back to the sandwich block format, and further dropping the peak learning rate to $4\times10^{-5}$ . This run starts smoothly, never reaches a token correlation close to 1.0, and quickly overtakes the previous run by utilizing the recurrence and improving with more iterations.
在第三次也是最后一次运行(“主运行”,蓝色)中,我们通过恢复到三明治块格式并进一步将峰值学习率降低到 $4\times10^{-5}$ 来解决了这个问题。这次运行开始顺利,从未达到接近 1.0 的 Token 相关性,并通过利用递归和更多迭代迅速超越了之前的运行。
With our successful configuration, training continues smoothly for the next 750B tokens without notable interruptions or loss spikes. We plot training loss and perplexity at different recurrence steps in Figure 6. In our material, we refer to the final checkpoint of this run as our “main model”, which we denote as Huginn $.0I25^{3}$ .
在我们的成功配置下,训练在接下来的750B token中顺利进行,没有出现明显的中断或损失峰值。我们在图6中绘制了不同循环步骤的训练损失和困惑度。在我们的材料中,我们将这次运行的最终检查点称为我们的“主模型”,我们将其表示为Huginn $.0I25^{3}$。

Figure 6: Left: Plot of pretrain loss over the 800B tokens on the main run. Right: Plot of val ppl at recurrent depths 1, 4, 8, 16, 32, 64. During training, the model improves in perplexity on all levels of recurrence.
图 6: 左:主运行中 800B token 的预训练损失图。右:递归深度为 1、4、8、16、32、64 时的验证困惑度图。在训练过程中,模型在所有递归级别上的困惑度都有所改善。
Table 1: Results on lm-eval-harness tasks zero-shot without chat template across various open-source models. We show ARC (Clark et al., 2018), HellaSwag (Zellers et al., 2019), MMLU (Hendrycks et al., 2021b), OpenBookQA (Mihaylov et al., 2018), PiQA (Bisk et al., 2020), SciQ (Johannes Welbl, 2017), and WinoGrande (Sakaguchi et al., 2021). We report normalized accuracy when provided.
表 1: 不同开源模型在 lm-eval-harness 任务上的零样本结果(未使用聊天模板)。我们展示了 ARC (Clark et al., 2018)、HellaSwag (Zellers et al., 2019)、MMLU (Hendrycks et al., 2021b)、OpenBookQA (Mihaylov et al., 2018)、PiQA (Bisk et al., 2020)、SciQ (Johannes Welbl, 2017) 和 WinoGrande (Sakaguchi et al., 2021)。当提供时,我们报告了归一化准确率。
| 模型 | 参数 | Token | ARC-E | ARC-C | HellaSwag | MMLU | OBQA | PiQA | SciQ | WinoGrande |
|---|---|---|---|---|---|---|---|---|---|---|
| random | 25.0 | 25.0 | 25.0 | 25.0 | 25.0 | 50.0 | 25.0 | 50.0 | ||
| Amber | 7B | 1.2T | 65.70 | 37.20 | 72.54 | 26.77 | 41.00 | 78.73 | 88.50 | 63.22 |
| Pythia-2.8b | 2.8B | 0.3T | 58.00 | 32.51 | 59.17 | 25.05 | 35.40 | 73.29 | 83.60 | 57.85 |
| Pythia-6.9b | 6.9B | 0.3T | 60.48 | 34.64 | 63.32 | 25.74 | 37.20 | 75.79 | 82.90 | 61.40 |
| Pythia-12b | 12B | 0.3T | 63.22 | 34.64 | 66.72 | 24.01 | 35.40 | 75.84 | 84.40 | 63.06 |
| OLMo-1B | 1B | 3T | 57.28 | 30.72 | 63.00 | 24.33 | 36.40 | 75.24 | 78.70 | 59.19 |
| OLMo-7B | 7B | 2.5T | 68.81 | 40.27 | 75.52 | 28.39 | 42.20 | 80.03 | 88.50 | 67.09 |
| OLMo-7B-0424 | 7B | 2.05T | 75.13 | 45.05 | 77.24 | 47.46 | 41.60 | 80.09 | 96.00 | 68.19 |
| OLMo-7B-0724 | 7B | 2.75T | 74.28 | 43.43 | 77.76 | 50.18 | 41.60 | 80.69 | 95.70 | 67.17 |
| OLMo-2-1124 | 7B | 4T | 82.79 | 57.42 | 80.50 | 60.56 | 46.20 | 81.18 | 96.40 | 74.74 |
| Ours, (r = 4) | 3.5B | 0.8T | 57.19 | 22.95 | 36.07 | 23.32 | 18.60 | 65.12 | 84.80 | 55.24 |
| Ours, (r = 8) | 3.5B | 0.8T | 66.07 | 32.50 | 45.08 | 24.88 | 22.00 | 70.72 | 91.5 | 55.64 |
| Ours, (r = 16) | 3.5B | 0.8T | 68.43 | 34.38 | 48.65 | 29.21 | 24.00 | 73.99 | 93.60 | 57.77 |
| Ours, (r = 32) | 3.5B | 0.8T | 69.91 | 38.23 | 65.21 | 31.38 | 38.80 | 76.22 | 93.50 | 59.43 |
5. Benchmark Results
5. 基准测试结果
We train our final model for 800B tokens, and a nonrecurrent baseline for 180B tokens. We evaluate these checkpoints against other open-source models trained on fully public datasets (like ours) of a similar size. We compare against Amber (Liu et al., 2023c), Pythia (Biderman et al., 2023) and a number of OLMo 1&2 variants (Groeneveld et al., 2024; AI2, 2024; Team OLMo et al., 2025). We execute all standard benchmarks through the lm-eval harness (Biderman et al., 2024) and code benchmarks via bigcode-bench (Zhuo et al., 2024).
我们训练最终模型使用了 800B 的 token,非循环基线模型使用了 180B 的 token。我们评估了这些检查点与其他在完全公开数据集(与我们的类似)上训练的开源模型。我们与 Amber (Liu et al., 2023c)、Pythia (Biderman et al., 2023) 以及多个 OLMo 1&2 变体 (Groeneveld et al., 2024; AI2, 2024; Team OLMo et al., 2025) 进行了比较。我们通过 lm-eval 工具 (Biderman et al., 2024) 执行所有标准基准测试,并通过 bigcode-bench (Zhuo et al., 2024) 进行代码基准测试。
5.1. Standard Benchmarks
5.1. 标准基准
Overall, it is not straightforward to place our model in direct comparison to other large language models, all of which are small variations of the fixed-depth transformer architecture. While our model has only 3.5B parameters and hence requires only modest interconnect bandwidth during pretraining, it chews through raw FLOPs close to what a 32B parameter transformer would consume during pre training, and can continuously improve in performance with test-time scaling up to FLOP budgets equivalent to a standard 50B parameter fixed-depth transformer. It is also important to note a few caveats of the main training run when interpreting the results. First, our main checkpoint is trained for only 47000 steps on a broadly untested mixture, and the learning rate is never cooled down from its peak. As an academic project, the model is trained only on publicly available data and the 800B token count, while large in comparison to older fully open-source models such as the Pythia series, is small in comparison to modern open-source efforts such as OLMo, and tiny in comparison to the datasets used to train industrial open-weight models.
总体而言,将我们的模型与其他大语言模型直接进行比较并不容易,因为它们都是固定深度Transformer架构的小幅变体。虽然我们的模型只有35亿参数,因此在预训练期间只需要适中的互连带宽,但它在预训练期间消耗的原始FLOPs接近于320亿参数的Transformer,并且可以通过测试时的扩展不断提升性能,达到相当于标准500亿参数固定深度Transformer的FLOP预算。在解释结果时,还需要注意主训练运行中的一些注意事项。首先,我们的主检查点仅在一个广泛未经测试的混合数据上训练了47000步,并且学习率从未从其峰值冷却下来。作为一个学术项目,该模型仅在公开可用的数据上进行训练,8000亿的Token数量虽然与Pythia系列等较旧的完全开源模型相比很大,但与OLMo等现代开源项目相比较小,与训练工业开源模型所使用的数据集相比更是微不足道。
Disclaimers aside, we collect results for established benchmark tasks (Team OLMo et al., 2025) in Table 1 and show all models side-by-side. In direct comparison we see that our model outperforms the older Pythia series and is roughly comparable to the first OLMo generation, OLMo7B in most metrics, but lags behind the later OLMo models trained larger, more carefully curated datasets. For the first recurrent-depth model for language to be trained at this scale, and considering the limitations of the training run, we find these results promising and certainly suggestive that further research into latent recurrence as an approach to test-time scaling is warranted.
表 1: 我们收集了已建立的基准任务 (Team OLMo 等, 2025) 的结果,并将所有模型并列展示。在直接比较中,我们看到我们的模型优于早期的 Pythia 系列,并且在大多数指标上与第一代 OLMo 模型 OLMo7B 大致相当,但在更大的、更精心策划的数据集上训练的后期 OLMo 模型面前稍显落后。作为在这个规模上训练的第一个具有循环深度的语言模型,考虑到训练过程中的限制,我们认为这些结果是有希望的,并且确实表明有必要进一步研究潜在循环作为一种测试时间扩展的方法。
| 模型 | GSM8K | GSM8kCoT | MinervaMATH | MathQA |
|---|---|---|---|---|
| Random | 0.00 | 0.00 | 0.00 | 20.00 |
| Amber | 3.94/4.32 | 3.34/5.16 | 1.94 | 25.26 |
| Pythia-2.8b | 1.59/2.12 | 1.90/2.81 | 1.96 | 24.52 |
| Pythia-6.9b | 2.05/2.43 | 2.81/2.88 | 1.38 | 25.96 |
| Pythia-12b | 3.49/4.62 | 3.34/4.62 | 2.56 | 25.80 |
| OLMo-1B | 1.82/2.27 | 1.59/2.58 | 1.60 | 23.38 |
| OLMo-7B | 4.02/4.09 | 6.07/7.28 | 2.12 | 25.26 |
| OLMo-7B-0424 | 27.07/27.29 | 26.23/26.23 | 5.56 | 28.48 |
| OLMo-7B-0724 | 28.66/28.73 | 28.89/28.89 | 5.62 | 27.84 |
| OLMo-2-1124-7B | 66.72/66.79 | 61.94/66.19 | 19.08 | 37.59 |
| Our w/o sys.prompt (r =32) | 28.05/28.20 | 32.60/34.57 | 12.58 | 26.60 |
| Our w/sys.prompt (r =32) | 24.87/38.13 | 34.80/42.08 | 11.24 | 27.97 |
5.2. Math and Coding Benchmarks
5.2. 数学与编程基准测试
We also evaluate the model on math and coding. For math, we evaluate GSM8k (Cobbe et al., 2021) (as zero-shot and in the 8-way CoT setup), MATH ((Hendrycks et al., 2021a) with the Minerva evaluation rules (Lewkowycz et al., 2022)) and MathQA (Amini et al., 2019). For coding, we check MBPP (Austin et al., 2021) and HumanEval (Chen et al., 2021). Here we find that our model significantly surpasses all models except the latest OLMo-2 model in mathematical reasoning, as measured on GSM8k and MATH. On coding benchmarks the model beats all other general-purpose opensource models, although it does not outperform dedicated code models, such as StarCoder2 (Lozhkov et al., 2024), trained for several trillion tokens. We also note that while further improvements in language modeling are slowing down, as expected at this training scale, both code and mathematical reasoning continue to improve steadily throughout training, see Figure 8.
我们还在数学和编码任务上对模型进行了评估。在数学方面,我们评估了 GSM8k (Cobbe et al., 2021)(作为零样本和在 8 路 CoT 设置下)、MATH (Hendrycks et al., 2021a)(使用 Minerva 评估规则 (Lewkowycz et al., 2022))和 MathQA (Amini et al., 2019)。在编码方面,我们检查了 MBPP (Austin et al., 2021) 和 HumanEval (Chen et al., 2021)。我们发现,在 GSM8k 和 MATH 上,我们的模型在数学推理方面显著超越了除最新的 OLMo-2 模型之外的所有模型。在编码基准测试中,该模型击败了所有其他通用开源模型,尽管它没有优于专门为数千亿 Token 训练的代码模型,例如 StarCoder2 (Lozhkov et al., 2024)。我们还注意到,虽然语言建模的进一步改进正在放缓,这是在此训练规模下预期的,但编码和数学推理在整个训练过程中持续稳步改进,见图 8。
Table 2: Benchmarks of mathematical reasoning and understanding. We report Table 3: Evaluation on code benchmarks, MBPP and flexible and strict extract for GSM8K and GSM8K CoT, extract match for Min- HumanEval. We report pass $@1$ for both datasets. erva Math, and acc norm. for MathQA.
表 2: 数学推理与理解的基准测试。我们报告了 GSM8K 和 GSM8K CoT 的灵活和严格提取匹配,以及 Minerva Math 的提取匹配和 MathQA 的 acc norm。
表 3: 代码基准测试的评估。我们报告了 MBPP 和 HumanEval 的 pass $@1$。
| 模型 | 参数量 | Token 数量 | MBPP | HumanEval |
|---|---|---|---|---|
| Random | 0.00 | 0.00 | ||
| starcoder2-3b | 3B | 3.3T | 43.00 | 31.09 |
| starcoder2-7b | 7B | 3.7T | 43.80 | 31.70 |
| Amber | 7B | 1.2T | 19.60 | 13.41 |
| Pythia-2.8b | 2.8B | 0.3T | 6.70 | 7.92 |
| Pythia-6.9b | 6.9B | 0.3T | 7.92 | 5.60 |
| Pythia-12b | 12B | 0.3T | 5.60 | 9.14 |
| OLMo-1B | 1B | 3T | 0.00 | 4.87 |
| OLMo-7B | 7B | 2.5T | 15.6 | 12.80 |
| OLMo-7B-0424 | 7B | 2.05T | 21.20 | 16.46 |
| OLMo-7B-0724 | 7B | 2.75T | 25.60 | 20.12 |
| OLMo-2-1124-7B | 7B | 4T | 21.80 | 10.36 |
| Ours (r =32) | 3.5B | 0.8T | 24.80 | 23.17 |
5.3. Where does recurrence help most?
5.3. 递归在哪些方面帮助最大?
How much of this performance can we attribute to recurrence, and how much to other factors, such as dataset, tokenization and architectural choices? In Table 4, we compare our recurrent model against its non-recurrent twin, which we trained to 180B tokens in the exact same setting. In direct comparison of both models at 180B tokens, we see that the recurrent model outperforms its baseline with an especially pronounced advantage on harder tasks, such as the ARC challenge set. On other tasks, such as SciQ, which requires straightforward recall of scientific facts, performance of the models is more similar. We observe that gains through reasoning are especially prominent on GSM8k, where the 180B recurrent model is already 5 times better than the baseline at this early snapshot in the pre training process. We also note that the recurrent model, when evaluated with only a single recurrence, effectively stops improving between the early 180B checkpoint and the 800B checkpoint, showing that further improvements are not built into the prelude or coda non-recurrent layers but encoded entirely into the iterations of the recurrent block.
在表 4 中,我们将我们的循环模型与其非循环的双胞胎模型进行了比较,后者在完全相同的设置下训练到了 180B Token。在直接比较这两个模型在 180B Token 时的表现时,我们发现循环模型在较难任务(如 ARC 挑战集)上表现尤为突出。在其他任务(如 SciQ,需要直接回忆科学事实)上,模型的表现更为相似。我们观察到,在 GSM8k 上,通过推理带来的增益尤为明显,180B 循环模型在预训练过程的早期就已经比基线模型高出 5 倍。我们还注意到,当仅使用单次循环进行评估时,循环模型在早期 180B 检查点和 800B 检查点之间实际上停止了改进,这表明进一步的改进并未内置到前奏或尾声的非循环层中,而是完全编码在循环块的迭代中。

Figure 7: Performance on GSM8K CoT (strict match and flexible match), HellaSwag (acc norm.), and HumanEval $(\mathrm{pass}@1)$ . As we increase compute, the performance on these benchmarks increases. HellaSwag only needs 8 recurrences to achieve near peak performance while other benchmarks make use of more compute.
图 7: GSM8K CoT(严格匹配和灵活匹配)、HellaSwag(准确率归一化)和 HumanEval $(\mathrm{pass}@1)$ 的性能表现。随着计算资源的增加,这些基准测试的性能也相应提升。HellaSwag 仅需 8 次递归即可接近峰值性能,而其他基准测试则利用了更多的计算资源。
Further, we chart the improvement as a function of test-time compute on several of these tasks for the main model in Figure 7. We find that saturation is highly task-dependent, on easier tasks the model saturates quicker, whereas it benefits from more compute on others.
此外,我们在图7中绘制了主要模型在这些任务上作为测试时间计算量函数的改进情况。我们发现,饱和高度依赖于任务,在较简单的任务上,模型更快达到饱和,而在其他任务上,模型则能从更多的计算中获益。
Recurrence and Context We evaluate ARC-C performance as a function of recurrence and number of few-shot examples in the context in Figure 9. Interestingly, without few-shot examples to consider, the model saturates in compute around 8-12 iterations. However, when more context is given, the model can reason about more information in context, which it does, saturating around 20 iterations if 1 example is provided, and 32 iterations, if 25-50 examples are provided, mirroring generalization improvements shown for recurrence (Yang et al., 2024a; Fan et al., 2025). Similarly, we see that if we re-evaluate OBQA in Table 5, but do not run the benchmark in "closed-book" format and rather provide a relevant fact, our recurrent model improves significantly almost closing the gap to OLMo-2. Intuitively this makes sense, as the recurrent models has less capacity to memorize facts but more capacity to reason about its context.
循环与上下文
Table 4: Baseline comparison, recurrent versus non-recurrent model trained in the same training setup and data. Comparing the recurrent model with its non-recurrent baseline, we see that even at 180B tokens, the recurrent substantially outperforms on harder tasks.
表 4: 基线对比,相同训练设置和数据下训练的循环模型与非循环模型。将循环模型与其非循环基线进行对比,我们发现即使在 180B Token 的情况下,循环模型在更难的任务上仍然显著优于非循环模型。

Figure 8: GSM8K CoT, HellaSwag, and HumanEval performance over the training tokens with different recurrences at test-time. We evaluate GSM8K CoT with chat template and 8-way few shot as multiturn. HellaSwag and HumanEval are zero-shot with no chat template. Model performance on harder tasks grows almost linearly with the training budget, if provided sufficient test-time compute.
图 8: 不同测试时复发情况下,GSM8K CoT、HellaSwag 和 HumanEval 在训练 token 上的性能表现。我们使用聊天模板和 8-way 少样本评估 GSM8K CoT 作为多轮任务。HellaSwag 和 HumanEval 是零样本任务,没有使用聊天模板。在提供足够的测试时计算资源的情况下,模型在更难任务上的性能几乎随训练预算线性增长。

Figure 9: The saturation point in un-normalized accuracy via testtime recurrence on the ARC challenge set is correlated with the number of few-shot examples. The model uses more recurrence to extract more information from the additional few-shot examples, making use of more compute if more context is given.
图 9: ARC挑战集上通过测试时循环达到的未归一化准确率的饱和点与少样本示例的数量相关。模型使用更多的循环从额外的少样本示例中提取更多信息,如果有更多上下文,则会利用更多的计算资源。
Table 5: Comparison of Open and Closed QA Performance $(%)$ (Mihaylov et al., 2018). In the open exam, a relevant fact is provided before the question is asked. In this setting, our smaller model closes the gap to other open-source models, indicating that the model is capable, but has fewer facts memorized.
表 5: 开放与封闭 QA 性能对比 $(%)$ (Mihaylov et al., 2018). 在开放考试中,问题提出前会提供相关事实。在此设置下,我们的小型模型缩小了与其他开源模型的差距,表明该模型具备能力,但记忆的事实较少。
| 模型 | 封闭 | 开放 | △ |
|---|---|---|---|
| Amber | 41.0 | 46.0 | +5.0 |
| Pythia-2.8b | 35.4 | 44.8 | +9.4 |
| Pythia-6.9b | 37.2 | 44.2 | +7.0 |
| Pythia-12b | 35.4 | 48.0 | +12.6 |
| OLMo-1B | 36.4 | 43.6 | +7.2 |
| OLMo-7B | 42.2 | 49.8 | +7.6 |
| OLMo-7B-0424 | 41.6 | 50.6 | +9.0 |
| OLMo-7B-0724 | 41.6 | 53.2 | +11.6 |
| OLM0-2-1124 | 46.2 | 53.4 | +7.2 |
| Ours (r = 32) | 38.2 | 49.2 | +11.0 |
$\beta,=,0.9$ , incorporating the last 75 checkpoints with a dilation factor of 7, a modification to established protocols (Kaddour, 2022; Sanyal et al., 2024). We provide this EMA model as well, which further improves GMS8k performance to $47.23%$ flexible $(38.59%$ strict), when tested at $r=64$ .
$\beta,=,0.9$,结合了最后 75 个检查点,膨胀因子为 7,这是对现有协议 (Kaddour, 2022; Sanyal et al., 2024) 的修改。我们还提供了这个 EMA 模型,当在 $r=64$ 下测试时,进一步将 GMS8k 性能提升至 $47.23%$ 灵活 $(38.59%$ 严格)。
5.4. Improvements through Weight Averaging
5.4. 通过权重平均提升效果
Due to our constant learning rate, we can materialize further improvements through weight averaging (Izmailov et al., 2018) to simulate the result of a cooldown (Hägele et al., 2024; DeepSeek-AI et al., 2024). We use an exponen- tial moving average starting from our last checkpoint with
由于我们采用恒定的学习率,因此可以通过权重平均 (Izmailov et al., 2018) 来进一步模拟冷却效果 (Hägele et al., 2024; DeepSeek-AI et al., 2024)。我们从最后一个检查点开始使用指数移动平均。
6. Recurrent Depth simplifies LLMs
6. 循环深度简化大语言模型
Aside from encouraging performance in mathematical and code reasoning, recurrent-depth models turn out to be surprisingly natural tools to support a number of methods that require substantial effort with standard transformers. In the next section, we provide a non-exhaustive overview.
除了在数学和代码推理方面提升性能外,递归深度模型(Recurrent-Depth Models)还意外地成为支持多种方法的自然工具,而这些方法在标准 Transformer 中需要大量努力。在下一节中,我们将提供一个非详尽的概述。

Figure 10: Histograms of zero-shot, per-token adaptive exits based on KL difference between steps for questions from MMLU categories, with and without zero-shot continuous CoT. The mean of each distribution is given in the legends. The exit threshold is fixed to $5\times{10}^{-4}$ . We see that the model converges quicker on high school mathematics than tasks such as logical fallacies or moral scenarios. On some tasks, such as philosophy, the model is able to effectively re-use states in its latent CoT and converge quickly on a subset of tokens, leading to fewer steps required overall.
图 10: 基于 MMLU 类别问题的步骤间 KL 差异的零样本、每 Token 自适应退出的直方图,包括有和无零样本连续 CoT 的情况。每个分布的均值在图例中给出。退出阈值固定为 $5\times{10}^{-4}$。我们可以看到,模型在高中数学上比逻辑谬误或道德情景等任务收敛得更快。在某些任务(如哲学)上,模型能够有效地重用其潜在 CoT 中的状态,并在部分 Token 上快速收敛,从而总体上需要更少的步骤。
6.1. Zero-Shot Adaptive Compute at Test-Time
6.1. 零样本自适应计算在测试时
We have shown that the model is capable of varying compute on a per-query level, running the model in different recurrence modes. This is after all also how the model is trained, as in Equation (1). However, it would be more efficient in practice to stop recurring early when predictions are easy, and only spend compute on hard decisions. Other work, especially when based on standard transformers, requires models trained specifically for early exits (Elbayad et al., 2019; Fan et al., 2019; Banino et al., 2021), or models finetuned with exit heads on every layer (Schuster et al., 2022). To test our model’s zero-shot exit abilities, we choose a simple exit criterion to evaluate convergence, the KL-divergence between two successive steps. If this divergence falls below $5\times10^{-4}$ , we stop iterating, sample the output token, and move to generate the next token.
我们展示了该模型能够在每次查询级别上灵活调整计算量,通过不同的递归模式运行模型。毕竟这也是模型的训练方式,如公式(1)所示。然而,在实际应用中,当预测较为简单时,提前停止递归会更加高效,只有在处理复杂决策时才投入更多计算资源。其他工作,尤其是基于标准Transformer的研究,通常需要专门为提前退出训练的模型(Elbayad et al., 2019; Fan et al., 2019; Banino et al., 2021),或者需要在每一层微调退出头(Schuster et al., 2022)。为了测试我们模型的零样本退出能力,我们选择了一个简单的退出标准来评估收敛性,即连续两步之间的KL散度。如果该散度低于$5\times10^{-4}$,我们便停止迭代,采样输出Token,并继续生成下一个Token。
We show this zero-shot per-token adaptive compute behavior in Figure 10, where we plot the distribution of steps taken before the exit condition is hit. We do this for the first 50 questions from different MMLU categories, asked in free-form chat. Interestingly, the number of steps required to exit differs notably between categories, with the model exiting earlier on high school mathematics, but taking on average 3.5 steps more on moral scenarios. As a preliminary demonstration, we verify on MTBench that this adaptivity does not significantly impact performance in a conversational benchmark setting (standard: 5.63, early exits: 5.56 see Appendix Table 6).
我们在图 10 中展示了这种零样本的逐 token 自适应计算行为,其中我们绘制了在满足退出条件之前所采取的步骤的分布。我们对来自不同 MMLU (Massive Multitask Language Understanding) 类别的前 50 个问题进行了这一操作,这些问题以自由形式聊天的方式提出。有趣的是,不同类别所需的退出步骤数量存在显著差异,模型在高中数学问题上退出较早,但在道德场景上平均多出 3.5 个步骤。作为初步验证,我们在 MTBench 上确认这种自适应性在对话基准设置中对性能没有显著影响(标准:5.63,提前退出:5.56,见附录表 6)。
Remark 6.1 (What about missing KV-cache entries?). Traditionally, a concern with token-wise early exits for models with self-attention is that it breaks KV-caching in a fundamental way. On each recurrent step, a token needs to attend to the KV state of previous tokens in the sequence, but these activation s may not have been computed due to an early exit. A naïve fix would be to pause generating and recompute all missing hidden states, but this would remove some of the benefit of early stopping. Instead, as in Elbayad et al. (2019), we attend to the last, deepest available KV states in the cache. Because all recurrent KV cache entries are generated by the same K,V projection matrices from successive hidden states, they “match”, and therefore the model is able to attend to the latest cache entry from every previous token, even if computed at different recurrent depths.
备注 6.1 (缺失的 KV 缓存条目如何处理?)。传统上,对于具有自注意力机制的模型,逐 Token 早退的一个问题是它从根本上破坏了 KV 缓存。在每个递归步骤中,一个 Token 需要关注序列中前一个 Token 的 KV 状态,但由于早退,这些激活可能未被计算出来。一个简单的解决方案是暂停生成并重新计算所有缺失的隐藏状态,但这会削弱早停的部分优势。相反,如 Elbayad 等 (2019) 所述,我们关注缓存中最新的、最深的可用 KV 状态。由于所有递归的 KV 缓存条目都是由相同的 K、V 投影矩阵从连续的隐藏状态生成的,它们“匹配”,因此模型能够关注每个前一个 Token 的最新缓存条目,即使这些条目是在不同的递归深度下计算的。
6.2. Zero-Shot KV-cache Sharing
6.2. 零样本 KV-cache 共享
A different avenue to increase efficiency is to reduce the memory footprint of the KV-cache by sharing the cache between layers (character.ai, 2024; Brandon et al., 2024). Typically, transformers must be trained from scratch with this capability. However, as discussed in the previous section, we find that we can simply share KV-caches in our model with minimal impact to performance. We set a fixed KV-cache budget for the recurrence at every token $k$ , and at iteration $i$ , read and write the cache entry $i$ mod $k$ . For example, we set a maximum KV-cache budget of 16 steps, overwriting the KV-cache of the 1st step when executing the 17th step, and so forth. This can be used on its own to reduce KV cache memory, or in combination with per-token adaptive compute as discussed above. On MTBench, this does not reduce performance (cache budget of 4: 5.86, see Appendix Table 6).
提高效率的另一种方法是通过在层之间共享缓存来减少 KV-cache 的内存占用 (character.ai, 2024; Brandon et al., 2024)。通常,Transformer 必须从头开始训练以实现此功能。然而,正如前一节所讨论的,我们发现可以在我们的模型中简单地共享 KV-caches,而对性能的影响最小。我们为每个 Token $k$ 的循环设置了固定的 KV-cache 预算,并在迭代 $i$ 时读取和写入缓存条目 $i$ mod $k$。例如,我们将最大 KV-cache 预算设置为 16 步,在执行第 17 步时覆盖第 1 步的 KV-cache,依此类推。这可以单独用于减少 KV-cache 内存,也可以与上述的每个 Token 自适应计算结合使用。在 MTBench 上,这不会降低性能(缓存预算为 4: 5.86,见附录表 6)。
6.3. Zero-Shot Continuous Chain-of-Thought
6.3. 零样本连续思维链
Instead of sampling a random initial state $\mathbf{s}{0}$ at every generation step, we can warm-start with the last state ${\bf s}{r}$ from the previous token. As shown in Figure 10, this reduces the average number of steps required to converge by 1-2. Also, on tasks such as philosophy questions, we see that the exit distribution shifts on several tasks, with the model more often exiting early by recycling previous compute. To achieve a similar behavior in fixed-depth transformers, these models need to be trained on reasoning tasks to accept their last hidden state as alternative inputs when computing the next token (Hao et al., 2024).
与其在每一步生成时随机采样初始状态 $\mathbf{s}{0}$,我们可以使用前一个 Token 的最后一个状态 ${\bf s}{r}$ 进行热启动。如图 10 所示,这将收敛所需的平均步数减少了 1-2 步。此外,在哲学问题等任务上,我们看到退出分布在多个任务上发生了变化,模型更倾向于通过重复使用之前的计算来提前退出。为了在固定深度的 Transformer 中实现类似的行为,这些模型需要在推理任务上进行训练,以便在计算下一个 Token 时接受其最后一个隐藏状态作为替代输入 (Hao et al., 2024)。

Figure 11: Convergence of latent states for every token in a sequence (going top to bottom) and latent iterations (going left to right), plotting the distance a final iterate $s^{*}$ , which we set with $r=128$ . Shown is an unsafe question posed to the model. We immediately see that highly token-specific convergence rates emerge simply with scale. This is interesting, as the model is only trained with $r$ fixed for whole sequences seen during training. We see that convergence is especially slow on the key part of the question, really wrong-ed.We further see that the model also learns different behaviors, we see an oscillating pattern in latent space, here most notably for the school token.
图 11: 序列中每个 Token 的潜在状态收敛情况(从上到下)和潜在迭代(从左到右),绘制了最终迭代 $s^{*}$ 的距离,我们设置为 $r=128$。展示的是一个不安全的问题。我们立即看到,随着规模的增加,出现了高度 Token 特定的收敛速度。这很有趣,因为模型在训练期间只看到了固定 $r$ 的整个序列。我们看到,在问题的关键部分收敛速度特别慢,即 really wrong-ed。我们还看到模型学会了不同的行为,在潜在空间中出现了振荡模式,这里最明显的是 school Token。
6.4. Zero-Shot Self-Speculative Decoding
6.4. 零样本自推测解码
Recurrent-depth models can also inherently generate text more efficiently by using speculative decoding (Leviathan et al., 2023) without the need for a separate draft model. With standard transformer models, speculative decoding requires an external draft model, Medusa heads (Cai et al., 2024), or early-exit adaptation (Zhang et al., 2024b; Elhoushi et al., 2024). Zhang et al. (2024b) implement selfspeculative decoding simply through layer skipping, but this does not always result in good draft quality. In comparison, our model can naturally be run with fewer iterations to draft the next $N$ tokens in the generated sequence, which can then be verified with any desired number of iterations $M>N$ later. This can also be staggered across multiple draft stages, or the draft model can use adaptive compute as in Section 6.1. Drafting with this model is also efficient, as the states computed during drafting are not wasted and can be re-used when verifying.
循环深度模型还可以通过使用推测解码 (Leviathan et al., 2023) 更高效地生成文本,而无需单独的草稿模型。对于标准的 Transformer 模型,推测解码需要外部草稿模型、Medusa heads (Cai et al., 2024) 或早期退出适应 (Zhang et al., 2024b; Elhoushi et al., 2024)。Zhang et al. (2024b) 通过层跳过来实现自我推测解码,但这并不总是能产生良好的草稿质量。相比之下,我们的模型可以自然地通过较少的迭代来草拟生成序列中的下一个 $N$ 个 Token,然后在稍后使用任何所需的迭代次数 $M>N$ 进行验证。这也可以分多个草稿阶段进行,或者草稿模型可以像第 6.1 节中那样使用自适应计算。使用此模型进行草拟也很高效,因为在草拟过程中计算的状态不会被浪费,可以在验证时重新使用。
7. What Mechanisms Emerge at Scale in Recurrent-Depth Models
7. 循环深度模型中规模化涌现的机制
Finally, what is the model doing while recurring in latent space? To understand this question better, we analyze the trajectories ${{\bf s}{i}}{i=1}^{r}$ of the model on a few qualitative examples. We are especially interested in understanding what patterns emerge, simply by training this model at scale. In comparison to previous work, such as Bai et al. (2019), where the training objective directly encodes a prior that pushes trajectories to a fixed point, we only train with our truncated unrolling objective.
最后,模型在潜在空间中递归时在做什么?为了更好地理解这个问题,我们分析了模型在一些定性示例上的轨迹 ${{\bf s}{i}}{i=1}^{r}$。我们特别感兴趣的是,通过大规模训练这个模型,会出现哪些模式。与之前的工作相比,例如 Bai 等人 (2019) 的研究,其中训练目标直接编码了一个先验,将轨迹推向固定点,而我们仅使用截断展开目标进行训练。
Figure 11 shows the norm distance $||\mathbf{s}{i}-\mathbf{s}^{*}||$ between each $\mathbf{s}{i}$ in a trajectory and an approximate limit point $\mathbf{s}^{*}$ computed with 128 iterations. We show the sentence top to bottom and iterations from left to right. We clearly see that convergence behavior depends on context. We see that key parts of the question, and the start of the model response, are “deliberated” much more in latent space. The context dependence can also be seen in the different behavior among the three identical tokens representing each of the three dots.
图 11 展示了轨迹中每个 $\mathbf{s}{i}$ 与通过 128 次迭代计算的近似极限点 $\mathbf{s}^{*}$ 之间的范数距离 $||\mathbf{s}{i}-\mathbf{s}^{*}||$。我们从左到右展示迭代过程,从上到下展示句子。可以清楚地看到,收敛行为取决于上下文。问题的关键部分和模型响应的开头在潜在空间中“深思熟虑”得更多。上下文依赖性还可以从三个相同的 Token(每个代表一个点)之间的不同行为中看出。

Figure 12: Latent Space trajectories for select tokens. We show a small part of these high-dimensional trajectories by visualizing the first 6 PCA directions, computing the PCA over all latent state trajectories of all tokens in a sequence. The color gradient going from dark to bright represents steps in the trajectory. The center of mass is marked in red. While on many tokens, the state simply converges (top row), the model also learns to use orbits (middle row), and “sliders” (bottom row, middle) to represent and handle more advanced concepts, such as arithmetic or complicated deliberation.
图 12: 选定 Token 的潜在空间轨迹。我们通过可视化前 6 个 PCA(主成分分析)方向来展示这些高维轨迹的一小部分,PCA 是针对序列中所有 Token 的潜在状态轨迹计算的。从深到浅的颜色渐变代表轨迹中的步骤。质心用红色标记。在许多 Token 上,状态只是简单地收敛(顶部行),模型还学会了使用轨道(中间行)和“滑块”(底部行,中间)来表示和处理更高级的概念,如算术或复杂的推理。
Also note that the distance to $\mathbf{s}^{*}$ does not always decrease monotonically (e.g. for school); the model may also trace out complicated orbits in its latent trajectory while processing information, even though this is not represented explicitly in our training objective.
还需注意,到 $\mathbf{s}^{*}$ 的距离并不总是单调递减的(例如在学校场景中);模型在处理信息时,也可能在其潜在轨迹中描绘出复杂的轨道,尽管这在我们的训练目标中没有明确体现。
We look at trajectories for select tokens in more detail in Figure 12. We compute a PCA decomposition of latent trajectories over all tokens in a sequence, and then show several individual trajectories projected onto the first six PCA directions. See the appendix for more examples. Many tokens simply converge to a fixed point, such as the token in the top row. Yet, for harder questions, such as in the 2nd row4, the state of the token quickly falls into an orbit pattern in all three pairs of PCA directions. The use of multi-dimensional orbits like these could serve a similar purpose to periodic patterns sometimes observed in fixed-depth transformers trained for arithmetic tasks (Nanda et al., 2022), but we find these patterns extend far beyond arithmetic for our model. We often observe use of orbits on tokens such as “makes” (see Figure 16) or “thinks” that determine the structure of the response.
我们在图 12 中更详细地查看了选定 Token 的轨迹。我们计算了序列中所有 Token 的潜在轨迹的 PCA(主成分分析)分解,然后展示了几条投影到前六个 PCA 方向上的单独轨迹。更多示例请参见附录。许多 Token 简单地收敛到一个固定点,例如顶行的 Token。然而,对于更难的问题,例如第二行所示的情况,Token 的状态在所有三对 PCA 方向中迅速陷入轨道模式。这种多维轨道的使用可能类似于在算术任务中训练的固定深度 Transformer 中有时观察到的周期性模式(Nanda et al., 2022),但我们发现这些模式在我们的模型中远远超出了算术范围。我们经常观察到在诸如“makes”(见图 16)或“thinks”等决定响应结构的 Token 上使用轨道。
Aside from orbits, we also observe the model encoding particular key tokens as “sliders”, as seen in the middle of the bottom row in Figure 12 (which is the token “wrong”, from the same message as already shown in Figure 11). In these motions the trajectory noticeably drifts in a single direction, which the model could use to implement a mechanism to count how many iterations have occurred.
除了轨道外,我们还观察到模型将特定的关键 Token 编码为“滑块”,如图 12 底部行中间所示(即 Token “wrong”,来自与图 11 中已显示的相同消息)。在这些运动中,轨迹明显向单一方向漂移,模型可以利用这一机制来计算已发生的迭代次数。
The emergence of structured trajectories in latent space gives us a glimpse into how the model performs its computations. Unlike the discrete sequential chain of reasoning seen in verbalized chain-of-thought approaches, we observe rich geometric patterns including orbits, convergent paths, and drifts - means to organize its computational process spatially. This suggests the model is independently learning to leverage the high-dimensional nature of its latent space to implement reasoning in new ways.
潜在空间中结构化轨迹的出现让我们得以一窥模型是如何执行计算的。与在语言化的思维链方法中看到的离散序列推理不同,我们观察到了丰富的几何模式,包括轨道、收敛路径和漂移——这些都是在空间上组织其计算过程的手段。这表明模型正在独立学习如何利用其潜在空间的高维特性,以新的方式实现推理。
Path Independence. We verify that our models maintain path independence, in the sense of Anil et al. (2022), despite their complex dynamics, which we demonstrate in Figure 22. When re-initializing from multiple starting points $\mathbf{s}_{\mathrm{0}}$ , the model moves in similar trajectories, exhibiting consistent behavior. The same orbital patterns, fixed points, or directional drifts emerge regardless of initialization.
路径独立性。我们验证了模型在复杂动态下仍保持路径独立性(如 Anil 等人 (2022) 所述),如图 22 所示。当从多个起点 $\mathbf{s}_{\mathrm{0}}$ 重新初始化时,模型表现出相似的轨迹,行为一致。无论初始化如何,相同的轨道模式、固定点或方向漂移都会出现。
8. Related Work Overview
8. 相关工作概述
The extent to which recurrence is a foundational concept of machine learning is hard to overstate (Bra it e nberg, 1986; Gers & Schmid huber, 2000; Sutskever et al., 2008). For transformers, recurrence was applied in Dehghani et al. (2019), who highlight the aim of recurrent depth to model universal, i.e. Turing-complete, machines. It was used at scale (but with fixed recurrence) in Lan et al. (2019) and an interesting recent improvement in this line of work are described in Tan et al. (2023); Abnar et al. (2023) and Csordás et al. (2024). Schwarz s child et al. (2021b); Bansal et al. (2022); Bear et al. (2024); McLeish et al. (2024) show that depth recurrence is advantageous when learning generalizable algorithms when training with randomized unrolling and input injections. Recent work has described depthrecurrent, looped, transformers and studied their potential benefits with careful theoretical and small-scale analysis (Giannou et al., 2023; Gatmiry et al., 2024; Yang et al., 2024a; Fan et al., 2025).
递归在机器学习中的基础性地位难以被过分强调 (Bra it enberg, 1986; Gers & Schmid huber, 2000; Sutskever et al., 2008)。对于 Transformer 而言,递归在 Dehghani et al. (2019) 中被应用,强调了递归深度的目标是为了建模通用的、即图灵完备的机器。它在 Lan et al. (2019) 中被大规模使用(但采用了固定的递归),而 Tan et al. (2023); Abnar et al. (2023) 和 Csordás et al. (2024) 描述了这一工作方向的有趣改进。Schwarz s child et al. (2021b); Bansal et al. (2022); Bear et al. (2024); McLeish et al. (2024) 表明,在使用随机展开和输入注入进行训练时,深度递归在学习可泛化算法方面具有优势。最近的研究描述了深度递归、循环的 Transformer,并通过仔细的理论和小规模分析研究了它们的潜在优势 (Giannou et al., 2023; Gatmiry et al., 2024; Yang et al., 2024a; Fan et al., 2025)。
From another angle, these models can be described as neural networks learning a fixed-point iteration, as studied in deep equilibrium models (Bai et al., 2019; 2022). They are further related to diffusion models (Song & Ermon, 2019), especially latent diffusion models (Rombach et al., 2022), but we note that language diffusion models are usually run with a per-sequence, instead of a per-token, iteration count (Lee et al., 2018). A key difference of our approach to both equilibrium models and diffusion models is in the training objective, where equilibrium methods solve the “direct” problem (Geiping & Moeller, 2019), diffusion models solve a surrogate training objective, and our work suggests that truncated unrolling is a scalable alternative.
从另一个角度来看,这些模型可以被描述为学习定点迭代的神经网络,正如深度均衡模型 (Bai et al., 2019; 2022) 中所研究的那样。它们进一步与扩散模型 (Song & Ermon, 2019) 相关,特别是潜在扩散模型 (Rombach et al., 2022),但我们注意到,语言扩散模型通常是以每个序列而非每个 Token 为迭代次数的 (Lee et al., 2018)。我们的方法与均衡模型和扩散模型的一个关键区别在于训练目标,其中均衡方法解决“直接”问题 (Geiping & Moeller, 2019),扩散模型解决替代训练目标,而我们的工作表明,截断展开是一种可扩展的替代方案。
Mor generally, architectures that recur in depth can also be understood as directly learning the analog to the gradient of a latent energy-based model (LeCun & Huang, 2005; LeCun, 2022), or to an implicitly defined intermediate layer (Amos & Kolter, 2017). These analogies to gradient descent at inference time also show the connection to test time adaptation (Sun et al., 2020), especially test-time adaptation of output states (Boudiaf et al., 2022).
更一般地,深度递归的架构也可以理解为直接学习潜在基于能量的模型的梯度的类比 (LeCun & Huang, 2005; LeCun, 2022),或者隐式定义的中间层的类比 (Amos & Kolter, 2017)。这些在推理时与梯度下降的类比也展示了与测试时适应 (Sun et al., 2020),特别是输出状态的测试时适应 (Boudiaf et al., 2022) 的联系。
Aside from full recurrent-depth architectures, there also exist a number of proposals for hybrid architectures, such as models with latent sub networks (Li et al., 2020a), LoRA adapters on top of weight-shared layers (Bae et al., 2024), or (dynamic) weight-tying of trained models (Hay & Wolf, 2023; Liu et al., 2024). As mentioned in Section 6, while we consider the proposed recurrent depth approach to be a very natural way to reason in continuous latent space, the work of Hao et al. (2024) discusses how to finetune existing fixed-depth transformers with this capability.
除了完全递归深度架构外,还存在一些混合架构的提案,例如具有潜在子网络的模型 (Li et al., 2020a),权重共享层之上的LoRA适配器 (Bae et al., 2024),或训练模型的(动态)权重绑定 (Hay & Wolf, 2023; Liu et al., 2024)。如第6节所述,虽然我们认为提出的递归深度方法是在连续潜在空间中进行推理的一种非常自然的方式,但Hao等人 (2024) 的工作讨论了如何微调现有的固定深度Transformer以具备这种能力。
For additional discussions related to the idea of constructing a prior that in centi viz es reasoning and algorithm learning at the expense of memorization of simple patterns, we also refer to Chollet (2019), Schwarz s child (2023), Li et al. (2020b) and Moulton (2023).
有关构建先验以牺牲简单模式记忆为代价来集中推理和算法学习的更多讨论,我们也参考了 Chollet (2019)、Schwarzschild (2023)、Li 等人 (2020b) 和 Moulton (2023)。
9. Future Work
9. 未来工作
Aside from work extending and analyzing the scaling behaviors of recurrent depth models, there are many questions that remain unanswered. For example, to us, there are potentially a large number of novel post-training schemes that further enhance the capabilities of these models, such as fine-tuning to compress the recurrence or reinforcement learning with data with different hardness levels (Zelikman et al., 2024), or to internalize reasoning from CoT data into the recurrence (Deng et al., 2024).
除了扩展和分析循环深度模型的缩放行为之外,还有许多问题尚未解答。例如,对我们而言,可能存在大量新颖的训练后方案,可以进一步增强这些模型的能力,例如通过微调来压缩循环 (Zelikman et al., 2024) ,或通过不同难度级别的数据进行强化学习 (Deng et al., 2024) ,或将 CoT 数据中的推理过程内化到循环中。
Another aspect not covered in this work is the relationship to other modern architecture improvements. Efficient sequence mixing operations, especially those that are linear in sequence dimension, such as linear attention (Katharopoulos et al., 2020; Yang et al., 2024b), are limited in the number of comparisons that can be made. However, with recurrent depth, blocks containing linear operators can repeat until all necessary comparisons between sequence elements are computed (Suzgun et al., 2019). For simplicity, we also focus on a single recurrence, where prior work has considered multiple successive recurrent stages (Takase & Kiyono, 2023; Csordás et al., 2024).
本文未涉及的另一个方面是与其他现代架构改进的关系。高效的序列混合操作,尤其是那些在序列维度上呈线性的操作,如线性注意力 (Katharopoulos et al., 2020; Yang et al., 2024b),在可以进行的比较数量上是有限的。然而,通过递归深度,包含线性算子的块可以重复,直到计算出序列元素之间的所有必要比较 (Suzgun et al., 2019)。为了简化,我们同样专注于单次递归,而先前的工作则考虑了多个连续的递归阶段 (Takase & Kiyono, 2023; Csordás et al., 2024)。
Finally, the proposed architecture is set up to be computeheavy, with more “materialized” parameters than there are actual parameters. This naturally mirrors mixture-of-expert models (MoE), which are parameter-heavy, using fewer active parameters per forward pass than exist within the model (Shazeer et al., 2017; Fedus et al., 2022). We posit that where the recurrent-depth setup excels at learning reasoning patterns, the MoE excels at effectively storing and retrieving complex information. Their complement ari ty supports the hypothesis that a future architecture would contain both modifications. While in a standard MoE model, each expert can only be activated once per forward pass, or skipped entirely, a recurrent MoE model could also refine its latent state over multiple iterations, potentially routing to the same expert multiple times, before switching to a different one (Tan et al., 2023; Csordás et al., 2024). While MoE models are the currently leading solution to implement this type of “memory” in dense transformers, these considerations also hold for other memory mechanisms suggested for LLMs (Sukhbaatar et al., 2019; Fan et al., 2021; Wu et al., 2022; He et al., 2024).
最后,所提出的架构被设置为计算密集型,其“物化”参数多于实际参数。这自然反映了专家混合模型(MoE)的特性,MoE 模型参数密集,每次前向传播使用的活跃参数少于模型中的总参数(Shazeer et al., 2017; Fedus et al., 2022)。我们认为,循环深度结构擅长学习推理模式,而 MoE 则擅长有效地存储和检索复杂信息。它们的互补性支持了未来架构将包含这两种修改的假设。在标准的 MoE 模型中,每个专家在每次前向传播中只能被激活一次,或者完全跳过,而循环 MoE 模型可以在多次迭代中优化其潜在状态,可能多次路由到同一个专家,然后再切换到另一个专家(Tan et al., 2023; Csordás et al., 2024)。虽然 MoE 模型是目前在密集 Transformer 中实现这种“记忆”类型的领先解决方案,但这些考虑也适用于为大语言模型提出的其他记忆机制(Sukhbaatar et al., 2019; Fan et al., 2021; Wu et al., 2022; He et al., 2024)。
10. Conclusions
10. 结论
The models described in this paper are ultimately still a proof-of-concept. We describe how to train a latent recurrent-depth architecture, what parameters we chose,and then trained a single model at scale. Future training runs are likely to train with more optimized learning rate schedules, data mixes and accelerators. Still we observe a number of interesting behaviors emerging naturally from recurrent training. The most important of these is the ability to use latent reasoning to dramatically improve performance on reasoning tasks by expending test-time computation. In addition, we also observe context-dependent convergence speed, path independence, and various zero-shot abilities. This leads us to believe that latent reasoning is a promising research direction to complement existing approaches for test-time compute scaling. The model we realize is surprisingly powerful given its size and amount of training data, and we are excited about the potential impact of imbuing generative models with the ability to reason in continuous latent space without the need for specialized data at train time or verb aliz ation at inference time.
本文描述的模型最终仍是一个概念验证。我们描述了如何训练一个潜在递归深度架构,选择了哪些参数,并大规模训练了一个单一模型。未来的训练可能会使用更优化的学习率调度、数据混合和加速器。尽管如此,我们观察到一些有趣的行为从递归训练中自然涌现。其中最重要的是能够利用潜在推理通过增加测试时计算来显著提高推理任务的性能。此外,我们还观察到上下文相关的收敛速度、路径独立性和各种零样本能力。这使我们相信,潜在推理是一个有前途的研究方向,可以补充现有的测试时计算扩展方法。我们实现的模型在规模和训练数据量上表现出惊人的强大能力,我们对生成式模型在连续潜在空间中推理的潜力感到兴奋,而无需在训练时使用专门数据或在推理时进行明确表达。
Acknowledgements
致谢
This project was made possible by the INCITE program: An award for computer time was provided by the U.S. Department of Energy’s (DOE) Innovative and Novel Computational Impact on Theory and Experiment (INCITE) Program. This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05- 00OR22725. JG further acknowledges the support of the Hector II foundation. A large number of small-scale and preliminary experiments were made possible through the support of the Intelligent Systems compute cluster and funding by the Tübingen AI center. UMD researchers were further supported by the ONR MURI program, DARPA TIAMAT, the National Science Foundation (IIS-2212182), and the NSF TRAILS Institute (2229885). Commercial support was provided by Capital One Bank, the Amazon Research Award program, and Open Philanthropy. Finally, we thank Avi Schwarz s child for helpful comments on the initial draft.
本项目得以实现得益于 INCITE 计划:美国能源部 (DOE) 的创新与新颖计算对理论与实验的影响 (INCITE) 计划提供了计算机时间的奖励。本研究使用了橡树岭国家实验室的橡树岭领导计算设施资源,该设施由美国能源部科学办公室支持,合同编号为 DE-AC05-00OR22725。JG 进一步感谢 Hector II 基金会的支持。大量小规模和初步实验得以进行,得益于智能系统计算集群的支持和图宾根 AI 中心的资助。UMD 研究人员还得到了 ONR MURI 计划、DARPA TIAMAT、国家科学基金会 (IIS-2212182) 和 NSF TRAILS 研究所 (2229885) 的支持。商业支持由 Capital One 银行、Amazon Research Award 计划和 Open Philanthropy 提供。最后,我们感谢 Avi Schwarz 的孩子对初稿的有益评论。
References
参考文献
Bai, Y., Zhang, J., Lv, X., Zheng, L., Zhu, S., Hou, L., Dong, Y., Tang, J., and Li, J. LongWriter: Unleashing $10{,}000+$ Word Generation from Long Context LLMs. arxiv:2408.07055[cs], August 2024. doi: 10.48550/arXiv.2408.07055. URL http://arxiv.org/abs/2408.07055.
Bai, Y., Zhang, J., Lv, X., Zheng, L., Zhu, S., Hou, L., Dong, Y., Tang, J., and Li, J. LongWriter: 释放长上下文大语言模型的 $10{,}000+$ 字生成能力。arxiv:2408.07055[cs], 2024年8月. doi: 10.48550/arXiv.2408.07055. URL http://arxiv.org/abs/2408.07055.
Banino, A., Balaguer, J., and Blundell, C. PonderNet: Learning to Ponder. In 8th ICML Workshop on Automated Machine Learning (AutoML), July 2021. URL https://openrevi ew.net/forum?id $\equiv$ 1EuxRTe0WN.
Banino, A., Balaguer, J., and Blundell, C. PonderNet: Learning to Ponder. 在第八届 ICML 自动化机器学习 (AutoML) 研讨会上,2021 年 7 月。URL https://openreview.net/forum?id $\equiv$ 1EuxRTe0WN.
Bansal, A., Schwarz s child, A., Borgnia, E., Emam, Z., Huang, F., Goldblum, M., and Goldstein, T. End-to-end Algorithm Synthesis with Recurrent Networks: Extrapolation without Overthinking. In Advances in Neural Information Processing Systems, October 2022. URL https://openreview.net/for um?id $\equiv$ PP j SKy 40 XU B.
Bansal, A., Schwarzschild, A., Borgnia, E., Emam, Z., Huang, F., Goldblum, M., and Goldstein, T. 使用循环网络进行端到端算法合成:无需过度思考的外推。In Advances in Neural Information Processing Systems, October 2022. URL https://openreview.net/forum?id $\equiv$ PPjSKy40XUB.
Bauschke, H. H., Moffat, S. M., and Wang, X. Firmly nonexpansive mappings and maximally monotone operators: Correspondence and duality. arXiv:1101.4688 [math], January 2011. URL http://arxiv.org/abs/1101.4688.
Bauschke, H. H., Moffat, S. M., and Wang, X. 严格非扩张映射与极大单调算子:对应性与对偶性. arXiv:1101.4688 [math], January 2011. URL http://arxiv.org/abs/1101.4688.
Bear, J., Prügel-Bennett, A., and Hare, J. Rethinking Deep Thinking: Stable Learning of Algorithms using Lipschitz Constraints. arxiv:2410.23451[cs], October 2024. doi: 10.48550/arXiv.241 0.23451. URL http://arxiv.org/abs/2410.23451.
Bear, J., Prügel-Bennett, A., 和 Hare, J. 重新思考深度思考:使用 Lipschitz 约束的算法稳定学习。arxiv:2410.23451[cs],2024年10月。doi: 10.48550/arXiv.241 0.23451。URL http://arxiv.org/abs/2410.23451。
Bekman, S. Machine Learning Engineering Open Book. Stasosphere Online Inc., 2023. URL https://github.com/s tas00/ml-engineering.
Bekman, S. 机器学习工程开放书籍. Stasosphere Online Inc., 2023. URL https://github.com/s tas00/ml-engineering.
Ben Allal, L., Lozhkov, A., Penedo, G., Wolf, T., and von Werra, L. SmolLM-corpus, July 2024. URL https://huggingfac e.co/datasets/Hugging FaceT B/smollm-corpus.
Ben Allal, L., Lozhkov, A., Penedo, G., Wolf, T., 和 von Werra, L. SmolLM-corpus, 2024年7月. 网址 https://huggingface.co/datasets/HuggingFaceTB/smollm-corpus.
Biderman, S., Schoelkopf, H., Anthony, Q., Bradley, H., O’Brien, K., Hallahan, E., Khan, M. A., Purohit, S., Prashanth, U. S., Raff, E., Skowron, A., Sutawika, L., and van der Wal, O. Pythia: A Suite for Analyzing Large Language Models Across Training and Scaling. arxiv:2304.01373[cs], April 2023. doi: 10.48550 /arXiv.2304.01373. URL http://arxiv.org/abs/23 04.01373.
Biderman, S., Schoelkopf, H., Anthony, Q., Bradley, H., O’Brien, K., Hallahan, E., Khan, M. A., Purohit, S., Prashanth, U. S., Raff, E., Skowron, A., Sutawika, L., 和 van der Wal, O. Pythia: 一套用于分析大语言模型在训练和扩展中的工具。arxiv:2304.01373[cs], 2023年4月。doi: 10.48550/arXiv.2304.01373。URL http://arxiv.org/abs/2304.01373。
Biderman, S., Schoelkopf, H., Sutawika, L., Gao, L., Tow, J., Abbasi, B., Aji, A. F., Amman a man chi, P. S., Black, S., Clive, J., DiPofi, A., Etxaniz, J., Fattori, B., Forde, J. Z., Foster, C., Hsu, J., Jaiswal, M., Lee, W. Y., Li, H., Lovering, C., Mu en nigh off, N., Pavlick, E., Phang, J., Skowron, A., Tan, S., Tang, X., Wang, K. A., Winata, G. I., Yvon, F., and Zou, A. Lessons from the Trenches on Reproducible Evaluation of Language Models. arxiv:2405.14782[cs], May 2024. doi: 10.48550/arXiv.2405. 14782. URL http://arxiv.org/abs/2405.14782.
Biderman, S., Schoelkopf, H., Sutawika, L., Gao, L., Tow, J., Abbasi, B., Aji, A. F., Amman a man chi, P. S., Black, S., Clive, J., DiPofi, A., Etxaniz, J., Fattori, B., Forde, J. Z., Foster, C., Hsu, J., Jaiswal, M., Lee, W. Y., Li, H., Lovering, C., Mu en nigh off, N., Pavlick, E., Phang, J., Skowron, A., Tan, S., Tang, X., Wang, K. A., Winata, G. I., Yvon, F., and Zou, A. 从战壕中获得的语言模型可重复评估的经验教训. arxiv:2405.14782[cs], 2024年5月. doi: 10.48550/arXiv.2405.14782. URL http://arxiv.org/abs/2405.14782.
Bisk, Y., Zellers, R., Bras, R. L., Gao, J., and Choi, Y. Piqa: Reasoning about physical commonsense in natural language. In Thirty-Fourth AAAI Conference on Artificial Intelligence, 2020.
Bisk, Y., Zellers, R., Bras, R. L., Gao, J., and Choi, Y. Piqa: 自然语言中的物理常识推理。在第三十四届AAAI人工智能会议上,2020年。
Boudiaf, M., Mueller, R., Ben Ayed, I., and Bertinetto, L. Parameter-Free Online Test-Time Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8344–8353, 2022. URL https: //openaccess.thecvf.com/content/CVPR2022 /html/Bou dia f Parameter-Free Online Tes t-Time Adaptation CVP R 2022 paper.html.
Boudiaf, M., Mueller, R., Ben Ayed, I., 和 Bertinetto, L. 参数无关的在线测试时间适应。在 IEEE/CVF 计算机视觉与模式识别会议论文集, pp. 8344–8353, 2022. URL https: //openaccess.thecvf.com/content/CVPR2022 /html/Bou dia f Parameter-Free Online Tes t-Time Adaptation CVP R 2022 paper.html.
Bra it e nberg, V. Vehicles: Experiments in Synthetic Psychology. MIT press, 1986.
Braitenberg, V. 《车辆:合成心理学实验》。麻省理工学院出版社,1986年。
Brandon, W., Mishra, M., Nrusimha, A., Panda, R., and Kelly, J. R. Reducing Transformer Key-Value Cache Size with Cross-Layer Attention. arxiv:2405.12981[cs], May 2024. doi: 10.48550/a rXiv.2405.12981. URL http://arxiv.org/abs/2405 .12981.
Brandon, W., Mishra, M., Nrusimha, A., Panda, R., and Kelly, J. R. 利用跨层注意力减少Transformer键值缓存大小。arxiv:2405.12981[cs], 2024年5月. doi: 10.48550/a rXiv.2405.12981. URL http://arxiv.org/abs/2405 .12981.
British Library Labs. Digitised Books. c. 1510 - c. 1900. JSONL (OCR Derived Text $^+$ Metadata). British Library, 2021. URL https://doi.org/10.23636/r7w6-zy15. Cai, T., Li, Y., Geng, Z., Peng, H., Lee, J. D., Chen, D., and Dao, T. Medusa: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads. In Forty-First International Conference on Machine Learning, June 2024. URL https: //openreview.net/forum?id=PEpbUobfJv.
British Library Labs. 数字化图书。约1510年 - 约1900年。JSONL(OCR提取文本 $^+$ 元数据)。British Library, 2021。URL https://doi.org/10.23636/r7w6-zy15。Cai, T., Li, Y., Geng, Z., Peng, H., Lee, J. D., Chen, D., 和 Dao, T. Medusa: 简单的大语言模型推理加速框架,带有多重解码头。发表于第四十一届国际机器学习会议,2024年6月。URL https://openreview.net/forum?id=PEpbUobfJv。
character.ai. Optimizing AI Inference at Character.AI, June 2024. URL https://research.character.ai/optimi zing-inference/.
character.ai。优化Character.AI的AI推理,2024年6月。URL https://research.character.ai/optimizing-inference/.
Chen, M., Tworek, J., Jun, H., Yuan, Q., de Oliveira Pinto, H. P., Kaplan, J., Edwards, H., Burda, Y., Joseph, N., Brockman, G., Ray, A., Puri, R., Krueger, G., Petrov, M., Khlaaf, H., Sastry, G., Mishkin, P., Chan, B., Gray, S., Ryder, N., Pavlov, M., Power, A., Kaiser, L., Bavarian, M., Winter, C., Tillet, P., Such, F. P., Cummings, D., Plappert, M., Chantzis, F., Barnes, E., Herbert- Voss, A., Guss, W. H., Nichol, A., Paino, A., Tezak, N., Tang, J., Babuschkin, I., Balaji, S., Jain, S., Saunders, W., Hesse, C., Carr, A. N., Leike, J., Achiam, J., Misra, V., Morikawa, E., Radford, A., Knight, M., Brundage, M., Murati, M., Mayer, K., Welinder, P., McGrew, B., Amodei, D., McCandlish, S., Sutskever, I., and Zaremba, W. Evaluating large language models trained on code, 2021.
Chen, M., Tworek, J., Jun, H., Yuan, Q., de Oliveira Pinto, H. P., Kaplan, J., Edwards, H., Burda, Y., Joseph, N., Brockman, G., Ray, A., Puri, R., Krueger, G., Petrov, M., Khlaaf, H., Sastry, G., Mishkin, P., Chan, B., Gray, S., Ryder, N., Pavlov, M., Power, A., Kaiser, L., Bavarian, M., Winter, C., Tillet, P., Such, F. P., Cummings, D., Plappert, M., Chantzis, F., Barnes, E., Herbert-Voss, A., Guss, W. H., Nichol, A., Paino, A., Tezak, N., Tang, J., Babuschkin, I., Balaji, S., Jain, S., Saunders, W., Hesse, C., Carr, A. N., Leike, J., Achiam, J., Misra, V., Morikawa, E., Radford, A., Knight, M., Brundage, M., Murati, M., Mayer, K., Welinder, P., McGrew, B., Amodei, D., McCandlish, S., Sutskever, I., and Zaremba, W. 评估训练于代码的大语言模型, 2021.
Choi, E. GoodWiki dataset, September 2023. URL https: //www.github.com/euirim/goodwiki.
Choi, E. GoodWiki数据集, 2023年9月. URL https://www.github.com/euirim/goodwiki.
Chollet, F. On the Measure of Intelligence. arxiv:1911.01547[cs], November 2019. doi: 10.48550/arXiv.1911.01547. URL http://arxiv.org/abs/1911.01547.
Chollet, F. 论智力的衡量。arxiv:1911.01547[cs],2019年11月。doi: 10.48550/arXiv.1911.01547。URL http://arxiv.org/abs/1911.01547。
Chowdhery, A., Narang, S., Devlin, J., Bosma, M., Mishra, G., Roberts, A., Barham, P., Chung, H. W., Sutton, C., Gehrmann, S., Schuh, P., Shi, K., Tsv yash chen ko, S., Maynez, J., Rao, A., Barnes, P., Tay, Y., Shazeer, N., Prabhakaran, V., Reif, E., Du, N., Hutchinson, B., Pope, R., Bradbury, J., Austin, J., Isard, M., Gur-Ari, G., Yin, P., Duke, T., Levskaya, A., Ghemawat, S., Dev, S., Micha lewski, H., Garcia, X., Misra, V., Robinson, K., Fedus, L., Zhou, D., Ippolito, D., Luan, D., Lim, H., Zoph, B., Spiridonov, A., Sepassi, R., Dohan, D., Agrawal, S., Omernick, M., Dai, A. M., Pillai, T. S., Pel- lat, M., Lewkowycz, A., Moreira, E., Child, R., Polozov, O., Lee, K., Zhou, Z., Wang, X., Saeta, B., Diaz, M., Firat, O., Catasta, M., Wei, J., Meier-Hellstern, K., Eck, D., Dean, J., Petrov, S., and Fiedel, N. PaLM: Scaling Language Modeling with Pathways. arXiv:2204.02311 [cs], April 2022. URL http://arxiv.org/abs/2204.02311.
Chowdhery, A., Narang, S., Devlin, J., Bosma, M., Mishra, G., Roberts, A., Barham, P., Chung, H. W., Sutton, C., Gehrmann, S., Schuh, P., Shi, K., Tsvyashchenko, S., Maynez, J., Rao, A., Barnes, P., Tay, Y., Shazeer, N., Prabhakaran, V., Reif, E., Du, N., Hutchinson, B., Pope, R., Bradbury, J., Austin, J., Isard, M., Gur-Ari, G., Yin, P., Duke, T., Levskaya, A., Ghemawat, S., Dev, S., Michalewski, H., Garcia, X., Misra, V., Robinson, K., Fedus, L., Zhou, D., Ippolito, D., Luan, D., Lim, H., Zoph, B., Spiridonov, A., Sepassi, R., Dohan, D., Agrawal, S., Omernick, M., Dai, A. M., Pillai, T. S., Pellat, M., Lewkowycz, A., Moreira, E., Child, R., Polozov, O., Lee, K., Zhou, Z., Wang, X., Saeta, B., Diaz, M., Firat, O., Catasta, M., Wei, J., Meier-Hellstern, K., Eck, D., Dean, J., Petrov, S., and Fiedel, N. PaLM: 用Pathways扩展语言建模。arXiv:2204.02311 [cs], 2022年4月。URL http://arxiv.org/abs/2204.02311.
Clark, P., Cowhey, I., Etzioni, O., Khot, T., Sabharwal, A., Schoenick, C., and Tafjord, O. Think you have solved question answering? try arc, the ai2 reasoning challenge. arXiv:1803.05457v1, 2018.
Clark, P., Cowhey, I., Etzioni, O., Khot, T., Sabharwal, A., Schoenick, C., and Tafjord, O. 你认为你已经解决了问答问题?试试ARC,AI2推理挑战。arXiv:1803.05457v1, 2018.
Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., Plappert, M., Tworek, J., Hilton, J., Nakano, R., Hesse, C., and Schulman, J. Training Verifiers to Solve Math Word Problems. arxiv:2110.14168[cs], November 2021. doi: 10.4
Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., Plappert, M., Tworek, J., Hilton, J., Nakano, R., Hesse, C., and Schulman, J. 训练验证器解决数学应用题. arxiv:2110.14168[cs], 2021年11月. doi: 10.4
Colegrove, O., Paruchuri, V., and OpenPhi-Team. Openphi/textbooks $\cdot$ Datasets at Hugging Face, October 2024. URL https://hugging face.co/datasets/open-phi /textbooks.
Colegrove, O., Paruchuri, V., 以及 OpenPhi-Team. Openphi/textbooks $\cdot$ Hugging Face 上的数据集,2024 年 10 月。URL https://huggingface.co/datasets/open-phi/textbooks.
Csordás, R., Irie, K., Schmid huber, J., Potts, C., and Manning, C. D. MoEUT: Mixture-of-Experts Universal Transformers. In The Thirty-eighth Annual Conference on Neural Information Processing Systems, November 2024. URL https://open review.net/forum?id $\equiv$ ZxVrkm7Bjl¬eId=xzoi2mTLOI.
Csordás, R., Irie, K., Schmidhuber, J., Potts, C., and Manning, C. D. MoEUT: Mixture-of-Experts Universal Transformers. 第38届神经信息处理系统年会, 2024年11月. URL https://openreview.net/forum?id≡ZxVrkm7Bjl¬eId=xzoi2mTLOI.
Dagan, G. Bpeasy, 2024. URL https://github.com/gau tierdag/bpeasy.
Dagan, G. Bpeasy, 2024. URL https://github.com/gautierdag/bpeasy.
Dagan, G., Synnaeve, G., and Rozière, B. Getting the most out of your tokenizer for pre-training and domain adaptation. arxiv:2402.01035[cs], February 2024. URL http://arxi v.org/abs/2402.01035.
Dagan, G., Synnaeve, G., 和 Rozière, B. 在预训练和领域适应中充分利用你的分词器。arxiv:2402.01035[cs], 2024年2月。URL http://arxiv.org/abs/2402.01035.
Dao, T. Flash Attention-2: Faster Attention with Better Parallelism and Work Partitioning. arxiv:2307.08691[cs], July 2023. doi: 10.48550/arXiv.2307.08691. URL http://arxiv.org/ abs/2307.08691.
Dao, T. Flash Attention-2:更快的注意力机制与更好的并行性和工作分区。arxiv:2307.08691[cs],2023年7月。doi: 10.48550/arXiv.2307.08691。URL http://arxiv.org/abs/2307.08691。
Dao, T., Fu, D. Y., Ermon, S., Rudra, A., and Ré, C. FlashAttention: Fast and Memory-Efficient Exact Attention with IOAwareness. arxiv:2205.14135[cs], May 2022. doi: 10.48550/a rXiv.2205.14135. URL http://arxiv.org/abs/2205 .14135.
Dao, T., Fu, D. Y., Ermon, S., Rudra, A., and Ré, C. FlashAttention: 具有IO感知的快速且内存高效的精确实时注意力机制. arxiv:2205.14135[cs], 2022年5月. doi: 10.48550/arXiv.2205.14135. URL http://arxiv.org/abs/2205.14135.
DeepSeek-AI, Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Guo, D., Yang, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Zhang, H., Ding, H., Xin, H., Gao, H., Li, H., Qu, H., Cai, J. L., Liang, J., Guo, J., Ni, J., Li, J., Wang, J., Chen, J., Chen, J., Yuan, J., Qiu, J., Li, J., Song, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Xu, L., Xia, L., Zhao, L., Wang, L., Zhang, L., Li, M., Wang, M., Zhang, M., Zhang, M., Tang, M., Li, M., Tian, N., Huang, P., Wang, P., Zhang, P., Wang, Q., Zhu, Q., Chen, Q., Du, Q., Chen, R. J., Jin, R. L., Ge, R., Zhang, R., Pan, R., Wang, R., Xu, R., Zhang, R., Chen, R., Li, S. S., Lu, S., Zhou, S., Chen, S., Wu, S., Ye, S., Ye, S., Ma, S., Wang, S., Zhou, S., Yu, S., Zhou, S., Pan, S., Wang, T., Yun, T., Pei, T., Sun, T., Xiao, W. L., Zeng, W., Zhao, W., An, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Li, X. Q., Jin, X., Wang, X., Bi, X., Liu, X., Wang, X., Shen, X., Chen, X., Zhang, X., Chen, X., Nie, X., Sun, X., Wang, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yu, X., Song, X., Shan, X., Zhou, X., Yang, X., Li, X., Su, X., Lin, X., Li, Y. K., Wang, Y. Q., Wei, Y. X., Zhu, Y. X., Zhang, Y., Xu, Y., Xu, Y., Huang, Y., Li, Y., Zhao, Y., Sun, Y., Li, Y., Wang, Y., Yu, Y., Zheng, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Tang, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Wu, Y., Ou, Y., Zhu, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Zha, Y., Xiong, Y., Ma, Y., Yan, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Wu, Z. F., Ren, Z. Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Huang, Z., Zhang, Z., Xie, Z., Zhang, Z., Hao, Z., Gou, Z., Ma, Z., Yan, Z., Shao, Z., Xu, Z., Wu, Z., Zhang, Z., Li, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Gao, Z., and Pan, Z. DeepSeek-V3 Technical Report. arxiv:2412.19437[cs], December 2024. doi: 10.48550/arXiv.2412.19437. URL http://arxiv.org/abs/2412.19437.
DeepSeek-AI, Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Guo, D., Yang, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Zhang, H., Ding, H., Xin, H., Gao, H., Li, H., Qu, H., Cai, J. L., Liang, J., Guo, J., Ni, J., Li, J., Wang, J., Chen, J., Chen, J., Yuan, J., Qiu, J., Li, J., Song, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Xu, L., Xia, L., Zhao, L., Wang, L., Zhang, L., Li, M., Wang, M., Zhang, M., Zhang, M., Tang, M., Li, M., Tian, N., Huang, P., Wang, P., Zhang, P., Wang, Q., Zhu, Q., Chen, Q., Du, Q., Chen, R. J., Jin, R. L., Ge, R., Zhang, R., Pan, R., Wang, R., Xu, R., Zhang, R., Chen, R., Li, S. S., Lu, S., Zhou, S., Chen, S., Wu, S., Ye, S., Ye, S., Ma, S., Wang, S., Zhou, S., Yu, S., Zhou, S., Pan, S., Wang, T., Yun, T., Pei, T., Sun, T., Xiao, W. L., Zeng, W., Zhao, W., An, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Li, X. Q., Jin, X., Wang, X., Bi, X., Liu, X., Wang, X., Shen, X., Chen, X., Zhang, X., Chen, X., Nie, X., Sun, X., Wang, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yu, X., Song, X., Shan, X., Zhou, X., Yang, X., Li, X., Su, X., Lin, X., Li, Y. K., Wang, Y. Q., Wei, Y. X., Zhu, Y. X., Zhang, Y., Xu, Y., Xu, Y., Huang, Y., Li, Y., Zhao, Y., Sun, Y., Li, Y., Wang, Y., Yu, Y., Zheng, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Tang, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Wu, Y., Ou, Y., Zhu, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Zha, Y., Xiong, Y., Ma, Y., Yan, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Wu, Z. F., Ren, Z. Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Huang, Z., Zhang, Z., Xie, Z., Zhang, Z., Hao, Z., Gou, Z., Ma, Z., Yan, Z., Shao, Z., Xu, Z., Wu, Z., Zhang, Z., Li, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Gao, Z., and Pan, Z. DeepSeek-V3 技术报告。arxiv:2412.19437[cs], December 2024. doi: 10.48550/arXiv.2412.19437. URL http://arxiv.org/abs/2412.19437.
DeepSeek-AI, Guo, D., Yang, D., Zhang, H., Song, J., Zhang, R., Xu, R., Zhu, Q., Ma, S., Wang, P., Bi, X., Zhang, X., Yu, X., Wu, Y., Wu, Z. F., Gou, Z., Shao, Z., Li, Z., Gao, Z., Liu, A., Xue, B., Wang, B., Wu, B., Feng, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Ding, H., Xin, H., Gao, H., Qu, H., Li, H., Guo, J., Li, J., Wang, J., Chen, J., Yuan, J., Qiu, J., Li, J., Cai, J. L., Ni, J., Liang, J., Chen, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Zhao, L., Wang, L., Zhang, L., Xu, L., Xia, L., Zhang, M., Zhang, M., Tang, M., Li, M., Wang, M., Li, M., Tian, N., Huang, P., Zhang, P., Wang, Q., Chen, Q., Du, Q., Ge, R., Zhang, R., Pan, R., Wang, R., Chen, R. J., Jin, R. L., Chen, R., Lu, S., Zhou, S., Chen, S., Ye, S., Wang, S., Yu, S., Zhou, S., Pan, S., Li, S. S., Zhou, S., Wu, S., Ye, S., Yun, T., Pei, T., Sun, T., Wang, T., Zeng, W., Zhao, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Xiao, W. L., An, W., Liu, X., Wang, X., Chen, X., Nie, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yang, X., Li, X., Su, X., Lin, X., Li, X. Q., Jin, X., Shen, X., Chen, X., Sun, X., Wang, X., Song, X., Zhou, X., Wang, X., Shan, X., Li, Y. K., Wang, Y. Q., Wei, Y. X., Zhang, Y., Xu, Y., Li, Y., Zhao, Y., Sun, Y., Wang, Y., Yu, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Ou, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Xiong, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Zhu, Y. X., Xu, Y., Huang, Y., Li, Y., Zheng, Y., Zhu, Y., Ma, Y., Tang, Y., Zha, Y., Yan, Y., Ren, Z. Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Xie, Z., Zhang, Z., Hao, Z., Ma, Z., Yan, Z., Wu, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Pan, Z., Huang, Z., Xu, Z., Zhang, Z., and Zhang, Z. DeepSeek-R1: In centi viz ing Reasoning Capability in LLMs via Reinforcement Learning. arxiv:2501.12948[cs], January 2025. doi: 10.48550/arXiv.2501.12948. URL http://arxiv.org/abs/2501.12948.
DeepSeek-AI, Guo, D., Yang, D., Zhang, H., Song, J., Zhang, R., Xu, R., Zhu, Q., Ma, S., Wang, P., Bi, X., Zhang, X., Yu, X., Wu, Y., Wu, Z. F., Gou, Z., Shao, Z., Li, Z., Gao, Z., Liu, A., Xue, B., Wang, B., Wu, B., Feng, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Ding, H., Xin, H., Gao, H., Qu, H., Li, H., Guo, J., Li, J., Wang, J., Chen, J., Yuan, J., Qiu, J., Li, J., Cai, J. L., Ni, J., Liang, J., Chen, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Zhao, L., Wang, L., Zhang, L., Xu, L., Xia, L., Zhang, M., Zhang, M., Tang, M., Li, M., Wang, M., Li, M., Tian, N., Huang, P., Zhang, P., Wang, Q., Chen, Q., Du, Q., Ge, R., Zhang, R., Pan, R., Wang, R., Chen, R. J., Jin, R. L., Chen, R., Lu, S., Zhou, S., Chen, S., Ye, S., Wang, S., Yu, S., Zhou, S., Pan, S., Li, S. S., Zhou, S., Wu, S., Ye, S., Yun, T., Pei, T., Sun, T., Wang, T., Zeng, W., Zhao, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Xiao, W. L., An, W., Liu, X., Wang, X., Chen, X., Nie, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yang, X., Li, X., Su, X., Lin, X., Li, X. Q., Jin, X., Shen, X., Chen, X., Sun, X., Wang, X., Song, X., Zhou, X., Wang, X., Shan, X., Li, Y. K., Wang, Y. Q., Wei, Y. X., Zhang, Y., Xu, Y., Li, Y., Zhao, Y., Sun, Y., Wang, Y., Yu, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Ou, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Xiong, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Zhu, Y. X., Xu, Y., Huang, Y., Li, Y., Zheng, Y., Zhu, Y., Ma, Y., Tang, Y., Zha, Y., Yan, Y., Ren, Z. Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Xie, Z., Zhang, Z., Hao, Z., Ma, Z., Yan, Z., Wu, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Pan, Z., Huang, Z., Xu, Z., Zhang, Z., and Zhang, Z. DeepSeek-R1: 通过强化学习增强大语言模型的推理能力. arxiv:2501.12948[cs], January 2025. doi: 10.48550/arXiv.2501.12948. URL http://arxiv.org/abs/2501.12948.
Dehghani, M., Gouws, S., Vinyals, O., Uszkoreit, J., and Kaiser, Ł. Universal Transformers. arxiv:1807.03819[cs, stat], March 2019. doi: 10.48550/arXiv.1807.03819. URL http: //arxiv.org/abs/1807.03819.
Dehghani, M., Gouws, S., Vinyals, O., Uszkoreit, J., and Kaiser, Ł. 通用 Transformer (Universal Transformers). arxiv:1807.03819[cs, stat], March 2019. doi: 10.48550/arXiv.1807.03819. URL http://arxiv.org/abs/1807.03819.
Deng, Y., Choi, Y., and Shieber, S. From Explicit CoT to Implicit CoT: Learning to Internalize CoT Step by Step. arxiv:2405.14838[cs], May 2024. doi: 10.48550/arXiv.2405. 14838. URL http://arxiv.org/abs/2405.14838.
Deng, Y., Choi, Y., 和 Shieber, S. 从显式 CoT 到隐式 CoT:逐步学习内化 CoT。arxiv:2405.14838[cs], 2024 年 5 月。doi: 10.48550/arXiv.2405.14838. URL http://arxiv.org/abs/2405.14838.
Ding, H., Wang, Z., Paolini, G., Kumar, V., Deoras, A., Roth, D., and Soatto, S. Fewer Truncation s Improve Language Modeling. In Forty-First International Conference on Machine Learning, June 2024. URL https://openreview.net/forum?i $\mathrm{\alpha}$ kRxCDDFNpp.
Ding, H., Wang, Z., Paolini, G., Kumar, V., Deoras, A., Roth, D., 和 Soatto, S. 更少的截断提升语言建模能力。发表于第四十一届国际机器学习会议, 2024年6月。URL https://openreview.net/forum?i $\mathrm{\alpha}$ kRxCDDFNpp.
Ding, M., Yang, Z., Hong, W., Zheng, W., Zhou, C., Yin, D., Lin, J., Zou, X., Shao, Z., Yang, H., and Tang, J. CogView: Mastering Text-to-Image Generation via Transformers. In Advances in Neural Information Processing Systems, volume 34, pp. 19822– 19835. Curran Associates, Inc., 2021. URL https://proc eedings.neurips.cc/paper/2021/hash/a4d92 e 2 cd 541 fc a 87 e 4620 aba 658316 d-Abstract.html.
Ding, M., Yang, Z., Hong, W., Zheng, W., Zhou, C., Yin, D., Lin, J., Zou, X., Shao, Z., Yang, H., and Tang, J. 论文标题:CogView: 通过Transformer掌握文本到图像生成。在《神经信息处理系统进展》第34卷中,第19822–19835页。Curran Associates, Inc., 2021。URL https://proceedings.neurips.cc/paper/2021/hash/a4d92e2cd541fca87e4620aba658316d-Abstract.html。
Elbayad, M., Gu, J., Grave, E., and Auli, M. Depth-Adaptive Transformer. In International Conference on Learning Representations, September 2019. URL https://openreview .net/forum?id $\equiv$ SJg7KhVKPH.
Elbayad, M., Gu, J., Grave, E., and Auli, M. 深度自适应Transformer (Depth-Adaptive Transformer). 在国际学习表征会议 (International Conference on Learning Representations) 上, 2019年9月. 网址 https://openreview.net/forum?id $\equiv$ SJg7KhVKPH.
Elhoushi, M., Shri vast ava, A., Liskovich, D., Hosmer, B., Wasti, B., Lai, L., Mahmoud, A., Acun, B., Agarwal, S., Roman,
Elhoushi, M., Shri vast ava, A., Liskovich, D., Hosmer, B., Wasti, B., Lai, L., Mahmoud, A., Acun, B., Agarwal, S., Roman,
A., Aly, A. A., Chen, B., and Wu, C.-J. LayerSkip: Enabling Early Exit Inference and Self-Speculative Decoding. arxiv:2404.16710[cs], April 2024. doi: 10.48550/arXiv.2404. 16710. URL http://arxiv.org/abs/2404.16710.
Aly, A. A., Chen, B., 和 Wu, C.-J. LayerSkip: 实现早期退出推理与自推测解码。arxiv:2404.16710[cs], 2024年4月。doi: 10.48550/arXiv.2404.16710。URL http://arxiv.org/abs/2404.16710。
Everett, K., Xiao, L., Wortsman, M., Alemi, A. A., Novak, R., Liu, P. J., Gur, I., Sohl-Dickstein, J., Kaelbling, L. P., Lee, J., and Pennington, J. Scaling Exponents Across Parameter iz at ions and Optimizers. arxiv:2407.05872[cs], July 2024. doi: 10.4 8550/arXiv.2407.05872. URL http://arxiv.org/abs/ 2407.05872.
Everett, K., Xiao, L., Wortsman, M., Alemi, A. A., Novak, R., Liu, P. J., Gur, I., Sohl-Dickstein, J., Kaelbling, L. P., Lee, J., and Pennington, J. 跨参数化和优化器的缩放指数。arxiv:2407.05872[cs], 2024年7月. doi: 10.48550/arXiv.2407.05872. URL http://arxiv.org/abs/2407.05872.
Fan, A., Grave, E., and Joulin, A. Reducing Transformer Depth on Demand with Structured Dropout. arxiv:1909.11556[cs, stat], September 2019. doi: 10.48550/arXiv.1909.11556. URL http://arxiv.org/abs/1909.11556.
Fan, A., Grave, E., and Joulin, A. 按需减少Transformer深度与结构化丢弃。arxiv:1909.11556[cs, stat], 2019年9月. doi: 10.48550/arXiv.1909.11556. URL http://arxiv.org/abs/1909.11556.
Fan, A., Lavril, T., Grave, E., Joulin, A., and Sukhbaatar, S. Addressing Some Limitations of Transformers with Feedback Memory. arxiv:2002.09402[cs, stat], January 2021. doi: 10.48550/arXiv.2002.09402. URL http://arxiv.or g/abs/2002.09402.
Fan, A., Lavril, T., Grave, E., Joulin, A., 和 Sukhbaatar, S. 通过反馈记忆解决Transformer的一些局限性。arxiv:2002.09402[cs, stat], 2021年1月. doi: 10.48550/arXiv.2002.09402. URL http://arxiv.org/abs/2002.09402.
Fan, Y., Du, Y., Ram chandra n, K., and Lee, K. Looped Transform- ers for Length Generalization. In The Thirteenth International Conference on Learning Representations, 2025. URL https: //openreview.net/forum?id $\equiv$ 2edigk8yoU.
Fan, Y., Du, Y., Ramchandran, K., 和 Lee, K. Looped Transformers for Length Generalization. 在第十三届国际学习表征会议 (The Thirteenth International Conference on Learning Representations) 上, 2025. URL https://openreview.net/forum?id $\equiv$ 2edigk8yoU.
Fedus, W., Zoph, B., and Shazeer, N. Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity. arxiv:2101.03961[cs], April 2022. doi: 10.48550/arXiv.2101.03961. URL http://arxiv.or g/abs/2101.03961.
Fedus, W., Zoph, B., and Shazeer, N. Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity. arxiv:2101.03961[cs], April 2022. doi: 10.48550/arXiv.2101.03961. URL http://arxiv.org/abs/2101.03961.
Feng, X., Luo, Y., Wang, Z., Tang, H., Yang, M., Shao, K., Mguni, D., Du, Y., and Wang, J. ChessGPT: Bridging Policy Learning and Language Modeling. Advances in Neural Information Processing Systems, 36:7216–7262, December 2023. URL https://proceedings.neurips.cc/paper_fil es/paper/2023/hash/16b14e3f288f076e0ca73 b dad 6405 f 77-Abstract-Datasets and Bench m arks.html.
Feng, X., Luo, Y., Wang, Z., Tang, H., Yang, M., Shao, K., Mguni, D., Du, Y., and Wang, J. ChessGPT: 桥接策略学习与语言建模。神经信息处理系统进展,36:7216–7262,2023年12月。URL https://proceedings.neurips.cc/paper_fil es/paper/2023/hash/16b14e3f288f076e0ca73 b dad 6405 f 77-Abstract-Datasets and Bench m arks.html.
Gabarain, S. Locutusque/hercules-v5.0 $\begin{array}{r l}\end{array}.$ Datasets at Hugging Face, December 2024. URL https://hugging face.co /datasets/Locutusque/hercules-v5.0.
Gabarain, S. Locutusque/hercules-v5.0 $\begin{array}{r l}\end{array}$. Hugging Face 数据集,2024年12月。URL https://huggingface.co/datasets/Locutusque/hercules-v5.0。
Gatmiry, K., Saunshi, N., Reddi, S. J., Jegelka, S., and Kumar, S. Can Looped Transformers Learn to Implement Multi-step Gradient Descent for In-context Learning? October 2024. doi: 10.48550/arXiv.2410.08292. URL http://arxiv.org/ abs/2410.08292.
Gatmiry, K., Saunshi, N., Reddi, S. J., Jegelka, S., and Kumar, S. 循环 Transformer 能否学会在上下文中实现多步梯度下降? October 2024. doi: 10.48550/arXiv.2410.08292. URL http://arxiv.org/ abs/2410.08292.
Geiping, J. and Goldstein, T. Cramming: Training a Language Model on a single GPU in one day. In Proceedings of the 40th International Conference on Machine Learning, pp. 11117– 11143. PMLR, July 2023. URL https://proceedings. mlr.press/v202/geiping23a.html.
Geiping, J. 和 Goldstein, T. Cramming: 在一天内用单GPU训练语言模型。在第40届国际机器学习会议论文集上,第11117–11143页。PMLR,2023年7月。URL https://proceedings.mlr.press/v202/geiping23a.html。
Geiping, J. and Moeller, M. Parametric Major iz ation for DataDriven Energy Minimization Methods. In Proceedings of the IEEE International Conference on Computer Vision, pp. 10262– 10273, 2019. URL http://openaccess.thecvf.com/ content ICC V 2019/html/Gei ping Para me tri c Major iz ation for Data-Driven Energy Min i miz ation Methods ICC V 2019 paper.html.
Geiping, J. 和 Moeller, M. 数据驱动能量最小化方法的参数化主要化。在 IEEE 国际计算机视觉会议论文集,第 10262–10273 页,2019。URL http://openaccess.thecvf.com/ content ICC V 2019/html/Gei ping Para me tri c Major iz ation for Data-Driven Energy Min i miz ation Methods ICC V 2019 paper.html。
Gers, F. and Schmid huber, J. Recurrent nets that time and count. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, volume 3, pp. 189–194 vol.3, July 2000. doi: 10.1109/IJCNN.2000.861302. URL https://ieeexplore.ieee.org/document/861302.
Gers, F. 和 Schmidhuber, J. 时序和计数的循环网络。在《IEEE-INNS-ENNS 国际神经网络联合会议论文集》中。IJCNN 2000. 神经计算:新千年的新挑战与展望,第3卷,第189-194页,2000年7月。doi: 10.1109/IJCNN.2000.861302。URL https://ieeexplore.ieee.org/document/861302。
Giannou, A., Rajput, S., Sohn, J.-Y., Lee, K., Lee, J. D., and Papa i lio poul os, D. Looped Transformers as Programmable Computers. In Proceedings of the 40th International Conference on Machine Learning, pp. 11398–11442. PMLR, July 2023. URL https://proceedings.mlr.press/v2 02/giannou23a.html.
Giannou, A., Rajput, S., Sohn, J.-Y., Lee, K., Lee, J. D., 和 Papa i lio poul os, D. Looped Transformers as Programmable Computers. 第40届国际机器学习会议论文集, 第11398–11442页. PMLR, 2023年7月. 网址 https://proceedings.mlr.press/v2 02/giannou23a.html.
Goyal, P., Dollár, P., Girshick, R., Noordhuis, P., Wesolowski, L., Kyrola, A., Tulloch, A., Jia, Y., and He, K. Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour. arxiv:1706.02677[cs], April 2018. URL http://arxiv. org/abs/1706.02677.
Goyal, P., Dollár, P., Girshick, R., Noordhuis, P., Wesolowski, L., Kyrola, A., Tulloch, A., Jia, Y., and He, K. 精确的大批量SGD:在一小时内训练ImageNet。arxiv:1706.02677[cs], 2018年4月。URL http://arxiv.org/abs/1706.02677。
Groeneveld, D., Beltagy, I., Walsh, P., Bhagia, A., Kinney, R., Tafjord, O., Jha, A. H., Ivison, H., Magnusson, I., Wang, Y., Arora, S., Atkinson, D., Authur, R., Chandu, K. R., Cohan, A., Dumas, J., Elazar, Y., Gu, Y., Hessel, J., Khot, T., Merrill, W., Morrison, J., Mu en nigh off, N., Naik, A., Nam, C., Peters, M. E., Pyatkin, V., Ravi chan der, A., Schwenk, D., Shah, S., Smith, W., Strubell, E., Subramani, N., Wortsman, M., Dasigi, P., Lambert, N., Richardson, K., Z ett le moyer, L., Dodge, J., Lo, K., Soldaini, L., Smith, N. A., and Hajishirzi, H. OLMo: Accelerating the Science of Language Models. arxiv:2402.00838[cs], June 2024. doi: 10.48550/arXiv.2402.00838. URL http: //arxiv.org/abs/2402.00838.
Groeneveld, D., Beltagy, I., Walsh, P., Bhagia, A., Kinney, R., Tafjord, O., Jha, A. H., Ivison, H., Magnusson, I., Wang, Y., Arora, S., Atkinson, D., Authur, R., Chandu, K. R., Cohan, A., Dumas, J., Elazar, Y., Gu, Y., Hessel, J., Khot, T., Merrill, W., Morrison, J., Mu en nigh off, N., Naik, A., Nam, C., Peters, M. E., Pyatkin, V., Ravi chan der, A., Schwenk, D., Shah, S., Smith, W., Strubell, E., Subramani, N., Wortsman, M., Dasigi, P., Lambert, N., Richardson, K., Z ett le moyer, L., Dodge, J., Lo, K., Soldaini, L., Smith, N. A., and Hajishirzi, H. OLMo: 加速大语言模型的科学研究. arxiv:2402.00838[cs], June 2024. doi: 10.48550/arXiv.2402.00838. URL http: //arxiv.org/abs/2402.00838.
Hägele, A., Bakouch, E., Kosson, A., Allal, L. B., Werra, L. V., and Jaggi, M. Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations. In Workshop on Efficient Systems for Foundation Models II @ ICML2024, July 2024. URL https://openreview.net/forum?id $=$ ompl 7supoX&referrer $=\frac{0}{0}$ 5Bthe%20profile%20of%20 Martin%20Jaggi%5D(%2Fprofile%3Fid%3D{~}M art in Jag gi 1).
Hägele, A., Bakouch, E., Kosson, A., Allal, L. B., Werra, L. V., and Jaggi, M. 《超越固定训练时长的缩放定律与计算优化训练》。在 ICML2024 的基金会模型高效系统研讨会 II 中,2024 年 7 月。URL https://openreview.net/forum?id $=$ ompl 7supoX&referrer $=\frac{0}{0}$ 5Bthe%20profile%20of%20 Martin%20Jaggi%5D(%2Fprofile%3Fid%3D{~}M art in Jag gi 1).
Hao, S., Sukhbaatar, S., Su, D., Li,
