Assessing Game Balance with AlphaZero: Exploring Alternative Rule Sets in Chess

用AlphaZero评估游戏平衡性：探索国际象棋的替代规则集

Nenad Tomašev*DeepMind

Ulrich Paquet* DeepMind

Demis Hassabis DeepMind

Vladimir Kramnik World Chess Champion 2000–2007§

弗拉基米尔·克拉姆尼克 2000-2007年国际象棋世界冠军§

Abstract

摘要
It is non-trivial to design engaging and balanced sets of game rules. Modern chess has evolved over centuries, but without a similar recourse to history, the consequences of rule changes to game dynamics are difficult to predict. AlphaZero provides an alternative in silico means of game balance assessment. It is a system that can learn near-optimal strategies for any rule set from scratch, without any human supervision, by continually learning from its own experience. In this study we use AlphaZero to creatively explore and design new chess variants. There is growing interest in chess variants like Fischer Random Chess, because of classical chess’s voluminous opening theory, the high percentage of draws in professional play, and the non-negligible number of games that end while both players are still in their home preparation. We compare nine other variants that involve atomic changes to the rules of chess. The changes allow for novel strategic and tactical patterns to emerge, while keeping the games close to the original. By learning near-optimal strategies for each variant with AlphaZero, we determine what games between strong human players might look like if these variants were adopted. Qualitatively, several variants are very dynamic. An analytic comparison show that pieces are valued differently between variants, and that some variants are more decisive than classical chess. Our findings demonstrate the rich possibilities that lie beyond the rules of modern chess.设计引人入胜且平衡的游戏规则并非易事。现代国际象棋历经数百年演变，但若缺乏历史参照，规则改动对游戏动态的影响难以预测。AlphaZero 为游戏平衡评估提供了基于计算机模拟的替代方案——该系统无需人类监督，仅通过持续自我对弈即可从零开始学习任意规则下的近最优策略。本研究利用 AlphaZero 对国际象棋变体进行创造性探索与设计。由于传统国际象棋存在海量开局理论、职业对局高和棋率，以及相当比例对局在双方仍处于预设准备阶段便已结束等问题，类似菲舍尔随机象棋的变体正受到越来越多关注。我们对比了九种对国际象棋规则进行原子级修改的变体：这些改动在保持游戏接近原版的同时，催生了新颖的战略战术模式。通过 AlphaZero 学习各变体的近最优策略，我们推演出人类高手在这些变体下的对局可能形态。定性分析显示，多个变体极具动态性；分析性对比表明不同变体中棋子价值存在差异，且部分变体比传统象棋更具决定性。这些发现揭示了现代国际象棋规则之外蕴藏的丰富可能性。

1. Introduction

1. 引言

Rule design is a critical part of game development, and small alterations to game rules can have a large effect on a game’s overall play ability and the resulting game dynamics. Fine-tuning and balancing rule sets in games is often a laborious and time-consuming process. Automating the balancing process is an open area of research (Jaffe et al., 2012; de Mesentier Silva et al., 2017), and machine learn- ing and evolutionary methods have recently been used to help game designers balance games more efficiently (Andrade et al., 2005; Leigh et al., 2008; Halim et al., 2014; Grau-Moya et al., 2018). Here we examine the potential of AlphaZero (Silver et al., 2018) to be used as an exploration tool for investigating game balance and game dynamics under different rule sets in board games, taking chess as an example use case.

规则设计是游戏开发的关键环节，细微的规则调整可能对游戏整体可玩性和动态体验产生重大影响。游戏规则的微调与平衡通常是一项耗时费力的工作。自动化平衡过程仍是开放研究领域 [20][21]，近年来机器学习与进化方法已被用于帮助设计师更高效地平衡游戏 [22][23][24][25][26]。本文以国际象棋为例，探讨AlphaZero [27]作为探索工具在不同棋盘游戏规则集下研究游戏平衡与动态特性的潜力。

Popular games often evolve over time and modern-day chess is no exception. The original game of chess is thought to have been conceived in India in the 6th century, from where it initially spread to Persia, then the Muslim world and later to Europe and globally. In medieval times, European chess was still largely based on Shatranj, an early variant originating from the Sasanian Empire that was based on the Indian Chaturanga (Murray, 1913). Notably, the queen and the bishop (alfin) moves were much more restricted, and the pieces were not as powerful as those in modern chess. Castling did not exist, but the king’s leap and the queen’s leap existed instead as special first king and queen moves. Apart from checkmate, it was also possible to win by baring the opposite king, leaving the piece isolated with the entirety of its army having been captured. In Shatranj, stalemate was considered a win, whereas these days it is considered a draw. The evolution of chess variants over the centuries can be viewed through the lens of changes in search space complexity and the expected final outcome uncertainty throughout the game, the latter being emphasized by modern rules and seen as important for the overall entertainment value (Cincotti et al., 2007). Modern chess was introduced in the 15th century, and is one of the most popular games to date, captivating the imagination of players around the world.

流行游戏往往随着时间演变，现代国际象棋也不例外。国际象棋最初被认为起源于6世纪的印度，随后传播至波斯，进而传入伊斯兰世界，再后来扩展到欧洲及全球。中世纪时期，欧洲象棋仍主要基于Shatranj（一种源自萨珊王朝的早期变体，其原型为印度恰图兰卡）(Murray, 1913)。值得注意的是，当时皇后和主教(alfin)的走法限制更多，棋子威力远不及现代象棋。王车易位尚未出现，但存在国王跳跃和皇后跳跃作为特殊的首步规则。除了将死对手，通过孤立对方国王（即俘获其全部军队）也能获胜。在Shatranj中，逼和被视为胜利，而现代规则则判定为和棋。数个世纪以来，象棋变体的演变可通过搜索空间复杂度和对局最终结果不确定性的变化来观察，后者被现代规则所强调，并被视为提升娱乐性的关键要素(Cincotti et al., 2007)。现代国际象棋定型于15世纪，至今仍是最受欢迎的棋类游戏之一，持续激发着全球玩家的想象力。

The interest in further development of chess has not subsided, especially considering a decreasing number of decisive games in professional chess and an increasing reliance on theory and home preparation with chess engines. This trend, coupled with curiosity and desire to tinker with such an inspiring game, has given rise to many variants of chess that have been proposed over the years (Gollon, 1968; Pritchard, 1994; Wikipedia, 2019). These variants involve alterations to the board, the piece placement, or the rules, to offer players “something subtle, sparkling, or amusing which cannot be done in ordinary chess” (Beasly, 1998). Probably the most well-known and popular chess variant is the so-called Chess960 or Fischer Random Chess, where pieces on the first rank are placed in one of 960 random permutations, making theoretical preparation infeasible.

对国际象棋进一步发展的兴趣并未减退，尤其考虑到职业棋赛中决定性对局数量减少，以及棋手对棋谱理论和引擎辅助开局准备的依赖日益加深。这一趋势，加上人们渴望改造这款充满魅力的游戏的好奇心，催生了多年来涌现的诸多变体 (Gollon, 1968; Pritchard, 1994; Wikipedia, 2019)。这些变体通过改变棋盘布局、棋子排列或规则，为玩家提供"普通象棋无法实现的精妙、闪耀或趣味体验" (Beasly, 1998)。其中最负盛名的当属Chess960（又称菲舍尔随机象棋），其首排棋子采用960种随机排列之一，使理论开局准备失去意义。

Chess and artificial intelligence are inextricably linked. Turing (1953) asked, “Could one make a machine to play chess, and to improve its play, game by game, profiting from its experience?” While computer chess has progressed steadily since the 1950s, the second part of Alan Turing’s question was realised in full only recently. AlphaZero (Silver et al., 2018) demonstrated state-of-the-art results in playing Go, chess, and shogi. It achieved its skill without any human supervision by continuously improving its play by learning from self-play games. In doing so, it showed a unique playing style, later analysed in Game Changer (Sadler & Regan, 2019). This in turn gave rise to new projects like Leela Chess Zero (Lc0, 2018) and improvements in existing chess engines. CrazyAra (Czech et al., 2019) employs a related approach for playing the Crazyhouse chess variant, although it involved pre-training from existing human games. A model-based extension of the original AlphaZero system was shown to generalise to domains like Atari, while maintaining its performance on chess even without an exact environment simulator (Schr it t wiese r et al., 2019). Alp- haZero has also shown promise beyond game environments, as a recent application of the model to global optimisation of quantum dynamics suggests (Dalgaard et al., 2020).

国际象棋与人工智能密不可分。Turing (1953) 曾提出："能否制造一台会下棋的机器，并通过从经验中学习来逐步提升棋艺？"虽然计算机象棋自1950年代起稳步发展，但艾伦·图灵问题的后半部分直到最近才完全实现。AlphaZero (Silver等人，2018) 在围棋、国际象棋和将棋领域展现了最先进的水平。它完全无需人类监督，仅通过自我对弈学习就能持续提升棋艺。在此过程中，它展现出独特的对弈风格，这一风格后来在《Game Changer》(Sadler & Regan，2019) 中被深入分析。这进而催生了Leela Chess Zero (Lc0，2018) 等新项目，并推动了现有象棋引擎的改进。CrazyAra (Czech等人，2019) 采用类似方法处理Crazyhouse象棋变体，不过它需要基于人类棋局进行预训练。AlphaZero系统的基于模型扩展版本被证明可泛化至Atari等领域，即便没有精确的环境模拟器仍能保持象棋水平 (Schrittweiser等人，2019)。AlphaZero在游戏环境之外也展现出潜力，最近该模型在量子动力学全局优化中的应用就是例证 (Dalgaard等人，2020)。

AlphaZero lends itself naturally to the problem of finding appealing and well-balanced rule sets, as no prior game knowledge is needed when training AlphaZero on any particular game. Therefore, we can rapidly explore different rule sets and characterise the arising style of play through quantitative and qualitative comparisons. Here we examine several hypothetical alterations to the rules of chess through the lens of AlphaZero, highlighting variants of the game that could be of potential interest for the chess community. One such variant that we have examined with AlphaZero, Nocastling chess, has been publicly championed by Vladimir Kramnik (Kramnik, 2019), and has already had its moment in professional play on 19 December 2019, when Luke Mc

AlphaZero 天生适合寻找吸引人且平衡的规则集的问题，因为在任何特定游戏上训练 AlphaZero 时都不需要先验的游戏知识。因此，我们可以快速探索不同的规则集，并通过定量和定性比较来刻画由此产生的游戏风格。在这里，我们通过 AlphaZero 的视角研究了国际象棋规则的几种假设性修改，重点介绍了可能引起国际象棋界潜在兴趣的游戏变体。其中一种我们与 AlphaZero 一起研究过的变体是“无王车易位象棋”(Nocastling chess)，它得到了弗拉基米尔·克拉姆尼克 (Vladimir Kramnik) 的公开支持 (Kramnik, 2019)，并在 2019 年 12 月 19 日的职业比赛中首次亮相，当时卢克·麦克...

Shane and Gawain Jones played the first-ever grandmaster No-castling match during the London Chess Classic. This was followed up by the very first No-castling chess tournament in Chennai in January 2020, which resulted in $89%$ decisive games (Shah, 2020).

Shane和Gawain Jones在伦敦国际象棋经典赛上进行了史上首场无王车易位的特级大师对决。随后于2020年1月在金奈举办了首个无王车易位国际象棋锦标赛，该赛事以89%的决胜局率收官 (Shah, 2020)。

2. Methods

2. 方法

In this section we motivate nine alterations to the modern chess rules, describe the key components of AlphaZero that are used in the analysis in Section 3, and outline how AlphaZero was trained for Classical chess and each of the nine variants.

本节我们提出对现代国际象棋规则的九项改动，描述第3章分析中使用的AlphaZero核心组件，并概述AlphaZero如何针对经典国际象棋及九种变体进行训练。

2.1. Rule Alterations

2.1. 规则变更

There are many ways in which the rules of chess could be altered and in this work we limit ourselves to considering atomic changes that keep the game as close as possible to classical chess. In some cases, secondary changes needed to be made to the 50-move rule to avoid potentially infinite games. The idea was to try to preserve the symmetry and the aesthetic appeal of the original game, while hoping to uncover dynamic variants with new opening, middlegame or endgame patterns and a novel body of opening theory. With that in mind, we did not consider any alterations involving changes to the board itself, the number of pieces, or their arrangement. Such changes were outside of the scope of this initial exploration. Rule alterations that we examine are listed in Table 1. The variants in Table 1 are by no means new to this paper, and many are guised under other names: Self-capture is sometimes referred to as “Reform Chess” or “Free Capture Chess”, while Pawn-back is called “Wren’s Game” by Pritchard (1994). None have yet come under intense scrutiny, and the impact of counting stalemate as a win is a lingering open question in the chess community.

国际象棋规则有多种修改方式，在本研究中我们仅考虑尽可能保持游戏接近经典象棋的原子级改动。某些情况下需对50回合规则进行次要调整以避免潜在无限对局。我们的理念是保留原版游戏的对称性与美学魅力，同时希望发掘具有新开局、中局或残局模式以及全新开局理论体系的动态变体。基于此，我们未考虑涉及棋盘改造、棋子数量或初始布局的改动，这类变更超出了本次探索的范围。表1列出了我们研究的规则改动项。需说明的是，表1中的变体并非本文首创，许多变体以其他名称存在：自吃规则(Self-capture)有时被称为"改革象棋"或"自由吃子象棋"，而兵后退规则(Pawn-back)被Pritchard(1994)称作"雷恩游戏"。这些变体尚未经受严格检验，其中将逼和判胜规则的影响仍是棋界悬而未决的问题。

表1:

Each of the hypothetical rule alterations listed in Table 1 could potentially affect the game either in desired or undesired ways. As an example, consider No-castling chess. One possible outcome of disallowing castling is that it would result in an aggressive playing style and attacking games, given that the kings are more exposed during the game and it takes time to get them to safety. Yet, the inability to easily safeguard one’s own king might make attacking itself a poor choice, due to the counterattacking opportunities that open up for the defending side. In Classical chess, players usually castle prior to launching an attack. Therefore, such a change could alternatively be seen as leading to un enterprising play and a much more restrained approach to the game.

表1中列出的每一项假设性规则改动都可能以预期或非预期的方式影响游戏。以无王车易位(No-castling)象棋为例，禁止王车易位可能导致更具攻击性的对局风格，因为国王在对局中更易受攻击且需要更长时间转移至安全位置。然而，由于防守方可能获得反击机会，无法轻易保护己方国王反而会使进攻策略变得不利。在传统象棋中，棋手通常在发起进攻前完成王车易位，因此这项规则改动也可能导致棋风趋向保守，使对局策略更为克制。

Historically, the only way to assess such ideas would have been for a large number of human players to play the game over a long period of time, until enough experience and understanding has been accumulated. Not only is this a long process, but it also requires the support of a large number of players to begin with. With AlphaZero, we can automate this process and simulate the equivalent of decades of human play within a day, allowing us to test these hypotheses in silico and observe the emerging patterns and theory for each of the considered variations of the game.

历史上，评估这类想法的唯一方法是让大量人类玩家长期进行游戏，直到积累足够的经验和理解。这不仅是一个漫长的过程，还需要大量玩家的支持才能启动。借助 AlphaZero，我们可以自动化这一流程，在一天内模拟相当于人类数十年的游戏对局，从而在计算机环境中测试这些假设，并观察游戏每种变体所呈现的模式和理论。

Table 1. A list of considered alterations to the rules of chess.

Variant	Primary rule change	Secondary rule change
No-castling	Castling is disallowed throughout the game
No-castling (10)	Castling is disallowed for the first 10 moves (20 plies)
Pawn one square	Pawns can only move by one square
Stalemate=win	Forcing stalemate is a win rather than a draw
Torpedo	Pawns can move by 1 or 2 squares anywhere on the board. En passant can consequently happen anywhere on the board.
Semi-torpedo	Pawns can move by two square both from the 2nd and the 3rd rank
Pawn-back	Pawns can move backwards by one square, but only back to the 2nd/7th rank for White/Black	Pawn moves do not count towards the 50 move rule
Pawn-sideways	Pawns can also move laterally by one square. Captures are unchanged, diagonally upwards	Sideway pawn moves do not count towards the 50 move rule
Self-capture	It is possible to capture one's own pieces

表 1: 国际象棋规则修改方案列表

变体名称	主要规则变更	次要规则变更
无王车易位	全局禁止王车易位
无王车易位(10)	前10步(20回合)禁止王车易位
单格兵	兵每次只能前进一格
逼和即胜	制造逼和局面视为胜利而非和棋
鱼雷兵	兵可在棋盘任意位置前进1或2格，因此"吃过路兵"可在任意位置发生
半鱼雷兵	兵在第2和第3横线均可前进两格
后退兵	兵可后退一格，但白/黑兵只能退至第2/7横线	兵移动不计入50回合规则
横向兵	兵可横向移动一格，但保留斜吃规则(仍为斜向前进)	横向移动不计入50回合规则
自吃子	允许吃掉己方棋子

Figure 1 illustrates each of the variants with an example position.

图 1: 通过示例位置展示各变体。

2.2. Key components of AlphaZero

2.2. AlphaZero的关键组件

AlphaZero is an adaptive learning system that improves through many rounds of self-play (Silver et al., 2018). It consists of a deep neural network $f_{\theta}$ with weights $\theta$ that compute

AlphaZero是一个通过多轮自我对弈不断进化的自适应学习系统 (Silver et al., 2018)。该系统包含一个权重为$\theta$的深度神经网络$f_{\theta}$，能够计算

$$
(\mathbf{p},v)=f_{\theta}(s)
$$

for a given position or state $s$ . The network outputs a vector of move probabilities $\mathbf{p}$ with elements $p(s^{\prime}|s)$ as prior probabilities for considering each move and hence each next state $s^{\prime}$ .1 If we denote game outcome numerically by $+1$ , for a win, 0 for a draw and $-1$ for a loss, the network additionally outputs a scalar value $v\in(-1,1)$ which estimates the expected outcome of the game from position $s$ .

对于给定位置或状态$s$，网络输出一个移动概率向量$\mathbf{p}$，其元素$p(s^{\prime}|s)$作为考虑每个移动及对应下一状态$s^{\prime}$的先验概率。若用$+1$表示胜利、0表示平局、$-1$表示失败来量化游戏结果，网络还会输出一个标量值$v\in(-1,1)$，用于评估从位置$s$出发的预期游戏结果。

The two predictions in (1) are used in Monte Carlo tree search (MCTS) to refine the assessment of a board position. The prior network p assigns weights to candidate moves at a “first glance” of the board, yielding an order in which moves are searched with MCTS. The output $v$ can be viewed as a neural network evaluation function for position $s$ . The statistical estimates of the game outcomes after each move are refined through MCTS, which runs repeated simulations of how the game might unfold up to a certain ply depth. In each MCTS simulation, $f_{\theta}$ is recursively applied to a sequence of positions (or nodes) up to a certain ply depth if they have not been processed in an earlier simulation. At maximum ply depth, the position is evaluated with (1), and that evaluation is “backed up” to the root, for each node adjusting its “action selection rule” to alter which moves will be selected and expanded in the next MCTS simulation. After a number of such MCTS simulations, the root move that was visited (or expanded) most is played.

(1) 中的两个预测用于蒙特卡洛树搜索 (MCTS) 以优化棋盘局面的评估。先验网络 p 通过"第一眼"观察为候选走子分配权重，从而确定 MCTS 搜索走子的顺序。输出 $v$ 可视为针对局面 $s$ 的神经网络评估函数。通过 MCTS 反复模拟游戏可能发展到特定步数深度的过程，来优化每个走子后游戏结果的统计估计。在每次 MCTS 模拟中，若某序列位置（或节点）未被先前模拟处理过，则递归应用 $f_{\theta}$ 直至达到指定步数深度。在最大步数深度时，使用 (1) 评估局面，并将该评估值"回传"至根节点，每个节点据此调整其"动作选择规则"以改变下次 MCTS 模拟中将被选择和扩展的走子。经过若干次此类 MCTS 模拟后，选择被访问（或扩展）次数最多的根节点走子。

2.3. Training and evaluation

2.3. 训练与评估

We trained AlphaZero from scratch for each of the rule alterations in Table 1, with the same set of model hyperpa(a) An example from No-castling chess: This is a typical position where both kings haven’t found immediate safety and remain exposed into the middlegame.

我们针对表1中的每条规则改动从头训练了AlphaZero，使用相同的模型超参数集。

(a) 无王车易位象棋示例：这是典型的中局阶段双方王都未找到即时安全位置而持续暴露的局面。

(b) An example from No-castling(10) chess: The play tends to be slower and more strategic, to allow for later castling. Here, on the 11th move, Black castles at the very first opportunity and White castles immediately after as well.

(b) 无王车易位(10) 国际象棋示例: 对局节奏往往更慢且更具策略性, 以便后续进行王车易位。此处在第11步时, 黑方抓住首个机会完成易位, 白方随即也进行了易位。

(d) An example from Stalemate $=$ win chess: An endgame posi- tion that would have been a draw in Classical chess is now a win instead.

图 1:
(d) 僵局变胜局的示例 (Stalemate $=$ win chess) : 在国际象棋残局中,原本是和棋的局面现在变成了胜局。

(c) An example from Pawn-one-square chess: Black just moved the knight to a5. In Classical chess this would seem counterintuitive due to the potential of playing the pawn to b4, forking the knights. Here, however, the pawn cannot move to that square in a single move, justifying the manoeuvre.

Figure 1. Examples of new strategic and tactical themes that arise in the explored chess variants. Figure 1e continues on the following page.

图1: 探索性国际象棋变体中涌现的新战略战术主题示例。图1e续见下页。

(e) An example from Torpedo chess: White needs to generate rapid counter play, and does so with a torpedo move: b4-b6. Black responds with Rh1, to which White promotes to a queen with yet another torpedo move, $_{\mathrm{b}6\mathrm{-}\mathrm{b}8=\mathrm{Q}}$ .

(e) Torpedo象棋示例：白方需要快速展开反击，于是采取鱼雷式走法b4-b6。黑方以Rh1回应，此时白方通过又一记鱼雷走法 $_{\mathrm{b}6\mathrm{-}\mathrm{b}8=\mathrm{Q}}$ 升变为皇后。

(f) An example from Semi-torpedo chess: The ability to rapidly advance pawns from the 3rd/6th rank enables Black the following energetic option: d6-d4, resulting in a forced tactical sequence. See Game AZ-19 in Appendix B.6 for details.

(f) 半鱼雷式象棋示例：黑方能够快速将3/6线的兵推进，从而获得以下有力选择：d6-d4，形成强制战术序列。具体细节参见附录B.6中的对局AZ-19。

图 1:

(g) An example from Pawn-back chess: Here, Black uses this possibility to challenge White’s central pawns, while opening up the diagonal for the b7 bishop, by a pawn-back move d5-d6.

(g) 兵回退国际象棋示例：此处黑方通过d5-d6的兵回退着法，既挑战白方中心兵阵，又为b7象开辟斜线。

(h) An example from Pawn-sideways chess: After sacrificing the knight on f2 the previous move, Black utilises a sideways pawn move f7-e7 for tactical purposes, opening the f-file towards the White king, while attacking the knight on d6.

(h) 兵侧移国际象棋示例：黑方在上一步弃掉f2马后，出于战术目的使用兵侧移f7-e7，既为白王所在的f线打开通路，同时攻击d6马。

(i) An example from Self-capture chess: a self-capture move Rxh4 generates threats against the Black king.

(i) 自吃象棋(Self-capture chess)示例：自吃着法Rxh4对黑王形成威胁。

Figure 1. (Continued from previous page.) Examples of new strategic and tactical themes that arise in the explored chess variants rameters. The models were trained for 1 million training steps, with a batch size of 4096 and allowing for an average 0.12 samples per position from self-play games. In order to encourage exploration during training, a small amount of noise was injected in the prior move probabilities (1) before search, sampled from a Dirichlet Dir(0.3) distribution, followed by a re normalization step (Silver et al., 2018). Further diversity was promoted by stochastic move selection in the first 30 plies of each of the training self-play games, by selecting the final moves proportionally to the softmax of the MCTS visit counts. The remaining game moves from ply 31 onwards were selected as top moves based on MCTS. Training self-play games were generated using 800 MCTS simulations per move.

图 1: (接上页) 所探索的象棋变体参数中产生的新战略和战术主题示例。模型训练了100万步，批量大小为4096，每局自对弈平均采样0.12个棋位。为促进训练探索，在搜索前向先验走子概率(1)注入少量从Dirichlet Dir(0.3)分布采样的噪声，随后进行重归一化步骤(Silver等人，2018)。通过在前30步训练自对弈中按MCTS访问次数的softmax比例随机选择走子，进一步增加多样性。从第31步起，剩余走子均根据MCTS选择最佳着法。训练自对弈每步使用800次MCTS模拟生成。

The absence of baselines makes it hard to formally assess the strength of each model, which is why it was important to couple the quantitative analysis and metrics observed at training and test time with a qualitative assessment in collaboration with Vladimir Kramnik, a renowned chess grandmaster and former world chess champion. As the rule changes that are considered in this study are mostly minor in practical terms, it is reasonable to assume that the trained models are of similar strength, although it is equally reasonable to expect that some of them could be further finetuned to account for the differences in game length and the average number of legal moves that need to be considered at each position. Given the nature of the study, the high level of observed play in trained models, and the number of rule alterations considered, we decided not to pursue such a potentially laborious process, as it would not alter any of the high-level conclusions that we present and discuss.

缺乏基准线使得难以正式评估每个模型的强度，因此有必要将训练和测试阶段观察到的定量分析与指标，与著名国际象棋特级大师、前世界冠军Vladimir Kramnik合作的定性评估相结合。由于本研究中考虑的规则变化在实际应用中大多较为微小，可以合理假设训练出的模型强度相近，尽管同样有理由预期其中某些模型可能需要进一步微调，以适应游戏时长差异及每个位置需考虑合法走法的平均数量差异。鉴于研究性质、训练模型展现的高水平对弈表现以及所考虑的规则修改数量，我们决定不进行这种可能费力的过程，因为这不会改变我们提出和讨论的任何高层结论。

3. Quantitative assessment

3. 定量评估

There are marked differences between the styles of chess that arises from each of the rule alterations Aesthetically, each variant has its own appeal, and we highlight them further in Section 4. Here we provide a quantitative comparison between variants, to complement the qualitative observations. Using a large quantity of self-play games, we infer the expected draw rate and first-move advantage for each variant, expressed as the expected score for White (Section 3.2). We then illustrate how the same opening can lead to vastly different outcomes under different chess variants in Section 3.3, and that these opening-specific differences can differ from the aggregate differences across all openings. An analysis of the util is ation of the newly introduced options made possible by the new rule alterations in Section 3.4 shows that the non-classical moves are used in a large percentage of games, often multiple times per game, in each of the variants. This suggests that the new options are indeed useful, and contribute to the game. We estimate the diversity of opening play by looking at the opening trees which we construct from AlphaZero’s network priors (1) for the first couple of moves and show that the breadth of opening possibilities in each of these chess variants seems to be inversely related to their relative decisiveness (Section 3.5). Sections 3.6 and 3.7 highlight the difference in opening play according to the prior distributions of the variants. Rule adjustments, especially those affecting piece mobility, are also expected to affect the relative material value of the pieces. Finally, Section 3.8 provides approximations for piece values in each of the variants, computed from a sample of 10,000 fast-play AlphaZero games.

每种规则调整所产生的国际象棋风格存在显著差异。从美学角度看，每个变体都有其独特魅力，我们将在第4节进一步阐述。本节通过量化对比来补充定性观察：利用大量自我对弈数据，我们推算出各变体的预期和棋率与先手优势（以白方预期得分表示，见第3.2节）。随后在第3.3节展示相同开局在不同变体下如何导致截然不同的对局结果，且这些开局特异性差异可能与整体差异并不一致。第3.4节对新规则启用率的分析表明，非传统走法在各变体对局中均有高频使用（平均每局多次），证实这些新机制确实具有实战价值。通过基于AlphaZero网络先验(1)构建的开局树（考察前几手），我们估算了开局多样性，发现各变体的开局可能性广度与其相对决断力呈反比关系（第3.5节）。第3.6-3.7节着重分析了不同变体先验分布导致的开局策略差异。规则调整（尤其是影响棋子机动性的改动）预计会改变棋子相对价值，第3.8节基于10,000局AlphaZero快棋样本给出了各变体的棋子价值近似值。

3.1. Self-play games

3.1. 自我对弈游戏

For each chess variant, we generated a diverse set of $N=10{,}000$ AlphaZero self-play games at 1 second per move, and $N=1{,}000$ games at 1 minute per move. The outcomes of the fast self-play games are presented in Figure 2a; the longer games follow in Figure 2b. As AlphaZero is approximately deterministic given the same MCTS depth and number of rollouts, we promote diversity in games by sampling the first 20 plies in each game proportional to the softmax of the MCTS visit counts, followed by playing the top moves for the rest of the game.

对于每种棋类变体，我们生成了多样化的 $N=10{,}000$ 局 AlphaZero 自对弈快棋（每步1秒）和 $N=1{,}000$ 局慢棋（每步1分钟）。快棋对局结果如图 2a 所示，慢棋对局结果如图 2b 所示。由于在相同蒙特卡洛树搜索(MCTS)深度和 rollout 次数下 AlphaZero 近乎确定性，我们通过按 MCTS 访问次数的 softmax 分布采样前20步来增加对局多样性，后续步数则选择最高访问次数的落子。

In addition to that, we generated a set of $N=1{,}000$ fastplay games from fixed starting positions arising from the Dutch Defence, Chigorin Defence, Alekhine Defence and King’s Gambit for each of the variants, as further discussed in Section 3.3.

除此之外，我们还为每个变体从荷兰防御、奇戈林防御、阿廖欣防御和王翼弃兵等固定起始局面生成了一组 $N=1{,}000$ 局快棋对弈数据，具体讨论见第3.3节。

The two sets of diverse self-play games are used in Section 3.2 to compare the decisiveness of each variant, in Section 3.4 to analyse how many special moves are used, and in Section 3.8 to estimate piece values across variants.

两组多样化的自我对弈游戏分别用于：3.2节比较各变体的决定性差异，3.4节分析特殊走法的使用频率，以及3.8节估算不同变体中的棋子价值。

A selection of these games is presented in Appendix B.

这些游戏的精选见附录B。

3.2. Expected scores and draw rates

3.2. 预期得分与平局概率

It is widely hypothesis ed that classical chess is theoretically drawn; that the odds $\pi=(\pi_{\mathrm{win}},\pi_{\mathrm{draw}},\pi_{\mathrm{lose}})$ of white winning, drawing and losing are $(0,1,0)$ at optimal play. We determine how favourable for white or how “drawish” different variants are by estimating the expected scores and draw rates at non-optimal play under the same conditions. We keep the conditions that chess variants are played against themselves with AlphaZero fixed, like the move selection criteria or Monte Carlo Tree Search (MCTS) evaluation time.

普遍假设古典象棋在理论上是和棋；即在最优对弈下，白方胜、和、负的概率 $\pi=(\pi_{\mathrm{赢}},\pi_{\mathrm{和}},\pi_{\mathrm{负}})$ 为 $(0,1,0)$。我们通过评估相同条件下非最优对弈时的预期得分与和棋率，来确定不同变体对白方更有利或更"易和"的程度。保持实验条件一致，例如固定使用AlphaZero自对弈、走子选择标准或蒙特卡洛树搜索(MCTS)评估时长。

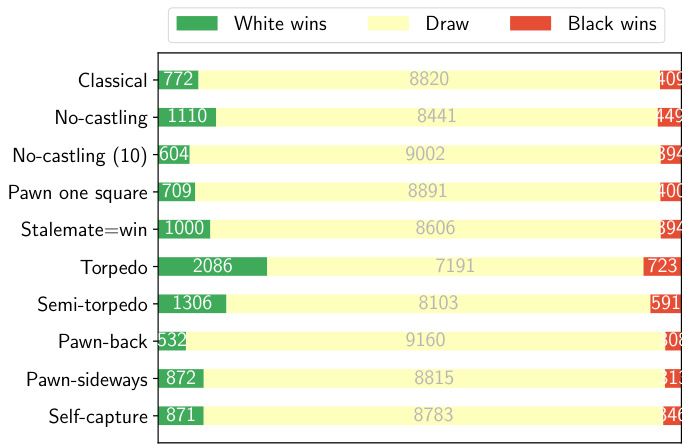
The overall decisiveness in the generated game sets depends on the time controls involved. We see in Figures 2a and 2b that across all variations the percentage of drawn games increases with longer thinking times, and longer thinking times also affect the expected score for White, as shown in Table 2. This suggests that the starting position might be (a) The game outcomes of 10,000 AlphaZero games played at 1 second per move for each different chess variant.

生成游戏集的整体决定性取决于所采用的时间控制。从图2a和图2b可见，在所有变体中，和棋比例随思考时间延长而上升，更长的思考时间也会影响白方预期得分（如表2所示）。这表明初始局面可能是：(a) 每种不同象棋变体以每步1秒时限进行的10,000盘AlphaZero对局结果。

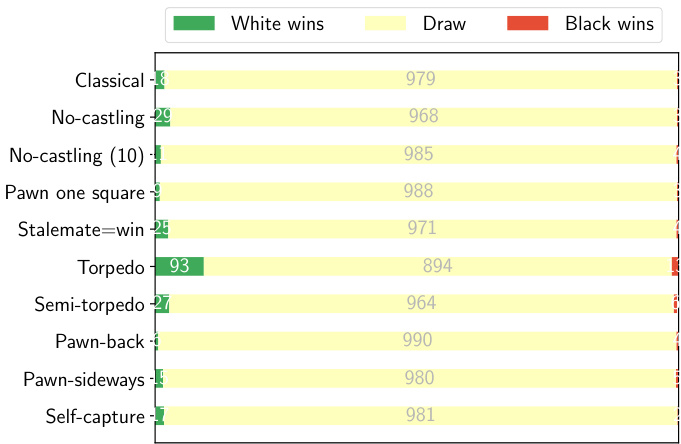
(b) The game outcomes of 1,000 AlphaZero games played at 1 minute per move for each different chess variant.

(b) 每种不同象棋变体在每步1分钟时限下进行的1,000局AlphaZero游戏结果。

Figure 2. AlphaZero self-play game outcomes under different time controls. As moves are determined in a deterministic fashion given the same conditions, diversity was enforced by sampling the first 20 plies in each game proportional to their MCTS visit counts. Across all variations the percentage of drawn games increases with longer thinking times. This seems to suggest that the starting position might be theoretically drawn in these chess variants, like in Classical chess, and that some of the variants are simply harder to play, involving more calculation and richer patterns.

图 2: 不同时间控制下AlphaZero自我对弈的游戏结果。由于在相同条件下走棋以确定性方式决定，我们通过按MCTS访问计数比例采样每局前20步来强制增加多样性。在所有变体中，和棋比例随着思考时间延长而上升。这表明这些象棋变体的起始局面可能像古典象棋一样在理论上是和棋，且某些变体只是更难下，需要更多计算和更丰富的模式。

Variant	Training	1sec	1min
Classical	54.1%	51.8%	50.8%
No castling	55.7%	53.3%	51.3%
No castling (10)	52.5%	51.0%	50.4%
Pawn one square	53.5%	51.6%	50.3%
Stalemate=win	54.9%	53.0%	51.1%
Torpedo	57.0%	56.8%	54.0%
Semi-torpedo	54.7%	53.6%	50.9%
Pawn-back	53.0%	51.1%	50.1%
Pawn-sideways	54.8%	52.8%	50.5%
Self-capture	54.2%	52.6%	50.8%

变体	训练	1秒	1分钟
经典	54.1%	51.8%	50.8%
无王车易位	55.7%	53.3%	51.3%
无王车易位 (10)	52.5%	51.0%	50.4%
兵行一格	53.5%	51.6%	50.3%
逼和=胜	54.9%	53.0%	51.1%
鱼雷	57.0%	56.8%	54.0%
半鱼雷	54.7%	53.6%	50.9%
兵后退	53.0%	51.1%	50.1%
兵侧行	54.8%	52.8%	50.5%
自吃	54.2%	52.6%	50.8%

Table 2. Empirical score for White under different game conditions, for each chess variant: self-play games at the end of model training, 1 second per move games, and 1 minute per move games. Diversity in 1 second per move games and 1 minute per move games was enforced by sampling the first 20 plies in each game proportional to their MCTS visit counts.

表 2: 不同棋类变体下白方的实战得分情况，包括模型训练结束时的自我对弈、每步1秒对局和每步1分钟对局。在每步1秒和每步1分钟对局中，通过按MCTS访问次数比例采样前20步来确保对局多样性。

theoretically drawn in these chess variants, like in Classical chess, and that some of the variants are simply harder to play, involving more calculation and richer patterns. We hypothesis e that the relative differences in AlphaZero’s win rates might translate to differences in human play, although this hypothesis would need to be practically validated in the future. Yet, in absence of any existing human games, we can use these results as a preliminary guess of what those results might be, assuming that what is difficult to calculate for AlphaZero may be difficult for human players as well.

理论上，这些国际象棋变体与古典国际象棋一样存在和棋可能，且某些变体因涉及更多计算和更丰富的模式而更难上手。我们推测AlphaZero胜率差异可能反映人类对弈的难度差异，但这一假设尚需实践验证。在缺乏人类对局数据的情况下，这些结果可作为初步参考——假设AlphaZero难以计算的局面，人类棋手同样可能感到棘手。

3.2.1. INFERENCE FOR GAME ODDS

3.2.1. 比赛赔率推断

To compare variants, we first infer the odds of their outcomes under set playing conditions. For a given variant, let the game outcomes $\mathcal{G}$ be $n_{\mathrm{win}}$ wins and $n_{\mathrm{lose}}$ losses for white, and $n_{\mathrm{draw}}=N-n_{\mathrm{win}}-n_{\mathrm{lose}}$ draws. If we assume a uniform Dirichlet prior on $\pi$ and multi no mi al likelihood for winning, drawing or losing, the posterior distribution is Dirichlet,

为了比较变体，我们首先推断在固定比赛条件下它们的结果概率。对于给定变体，设游戏结果$\mathcal{G}$为白方的$n_{\mathrm{win}}$胜、$n_{\mathrm{lose}}$负以及$n_{\mathrm{draw}}=N-n_{\mathrm{win}}-n_{\mathrm{lose}}$平。若假设$\pi$服从均匀狄利克雷先验，且胜负平结果服从多项分布，则后验分布为狄利克雷分布。

$$
p(\pi|\mathcal{G})=\mathrm{Dir}(n_{\mathrm{win}}+1,n_{\mathrm{draw}}+1,n_{\mathrm{lose}}+1).
$$

3.2.2. DRAW RATES

3.2.2. 绘制速率

To compare the decisiveness of chess variants, we infer the probability that variant A has a lower draw rate than variant B, given the games played $\mathcal{G}^{\mathrm{A}}$ and $\mathcal{G}^{\mathrm{B}}$ under the same conditions:2

为了比较不同象棋变体的决断性，我们在相同条件下根据已进行的对局$\mathcal{G}^{\mathrm{A}}$和$\mathcal{G}^{\mathrm{B}}$推断变体A比变体B和棋率更低的概率：2

$$
\begin{array}{r l}&{p(\pi_{\mathrm{draw}}^{\mathrm{A}}<\pi_{\mathrm{draw}}^{\mathrm{B}})=}\ &{\displaystyle\int\int\mathbb{I}\left[\pi_{\mathrm{draw}}^{\mathrm{A}}<\pi_{\mathrm{draw}}^{\mathrm{B}}\right]p(\pi^{\mathrm{A}}|\mathcal{G}^{\mathrm{A}})p(\pi^{\mathrm{B}}|\mathcal{G}^{\mathrm{B}})\mathrm{d}\pi^{\mathrm{A}}\mathrm{d}\pi^{\mathrm{B}}.}\end{array}
$$

The integral is not available in closed form; we evaluate it with a Monte Carlo estimate by drawing pairs of samples from $p(\pi^{\mathrm{A}}|\mathcal{G}^{\mathrm{A}})$ and $p(\pi^{\mathrm{B}}|\mathcal{G}^{\mathrm{B}})$ – using (2) – and computing the fraction of times that samples satisfy πdAraw $\pi_{\mathrm{draw}}^{\mathrm{A}}<\pi_{\mathrm{draw}}^{\mathrm{B}}$

积分没有闭式解；我们通过蒙特卡洛估计来评估它，从 $p(\pi^{\mathrm{A}}|\mathcal{G}^{\mathrm{A}})$ 和 $p(\pi^{\mathrm{B}}|\mathcal{G}^{\mathrm{B}})$ 中抽取样本对（使用公式 (2)），并计算满足 $\pi_{\mathrm{draw}}^{\mathrm{A}}<\pi_{\mathrm{draw}}^{\mathrm{B}}$ 的样本比例。

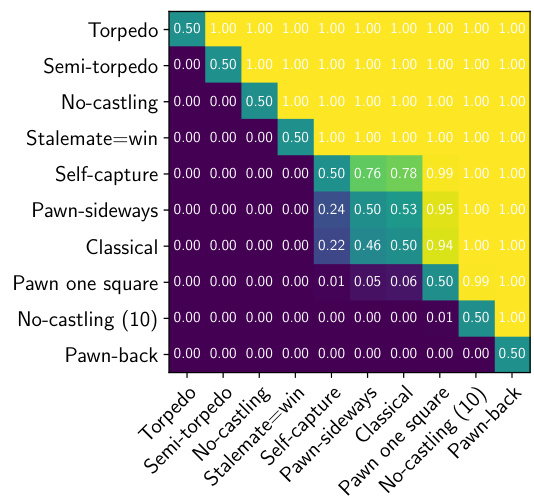
Figure 3a provides an indication of the relative decisiveness of variants, when played by AlphaZero at approximately 1 second per move, and Figure 3b provides the comparison at (a) A draw rate comparison $p(\pi_{\mathrm{draw}}^{\mathrm{row}}<\pi_{\mathrm{draw}}^{\mathrm{column}})$ cd or la uw mn) at approximately 1 seconds per move, on 10,000 AlphaZero games per variation.

图 3a 展示了各变体在 AlphaZero 以每步约 1 秒的思考时间对弈时的相对决策强度，图 3b 则提供了在相同条件下（每步约 1 秒，每个变体进行 10,000 局 AlphaZero 对弈）的和棋率比较 $p(\pi_{\mathrm{draw}}^{\mathrm{row}}<\pi_{\mathrm{draw}}^{\mathrm{column}})$ cd 或 la uw mn)。

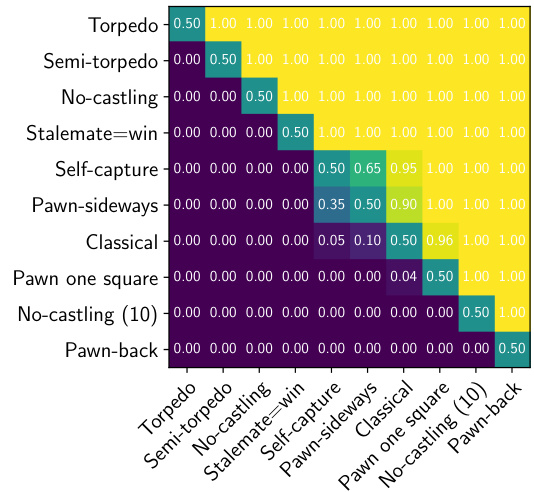
(b) A draw rate comparison p(πrdoraww $p(\pi_{\mathrm{draw}}^{\mathrm{row}}<\pi_{\mathrm{draw}}^{\mathrm{column}})$ πcolumn) at approximately 1 minute per move, on 1,000 AlphaZero games per variation.

(b) 每步约1分钟、每种变体基于1,000局AlphaZero对局的走和率比较 $p(\pi_{\mathrm{draw}}^{\mathrm{row}}<\pi_{\mathrm{draw}}^{\mathrm{column}})$ πcolumn)

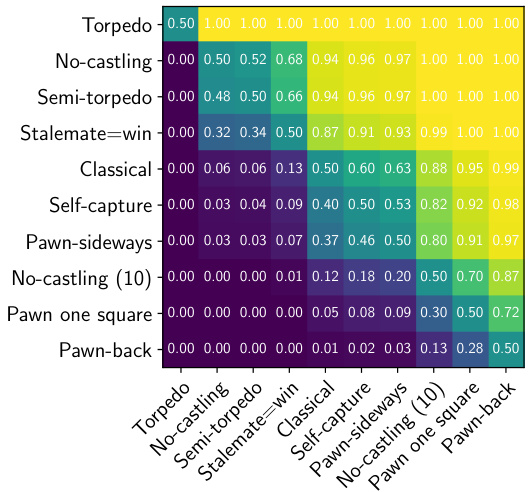
(d) A comparison of expected scores $p(e^{\mathrm{row}}>e^{\mathrm{column}})$ at 1 minute per move, on 1,000 games per variation.

图 1:
(d) 每步1分钟、每种变体进行1,000局游戏时，预期得分 $p(e^{\mathrm{row}}>e^{\mathrm{column}})$ 的对比

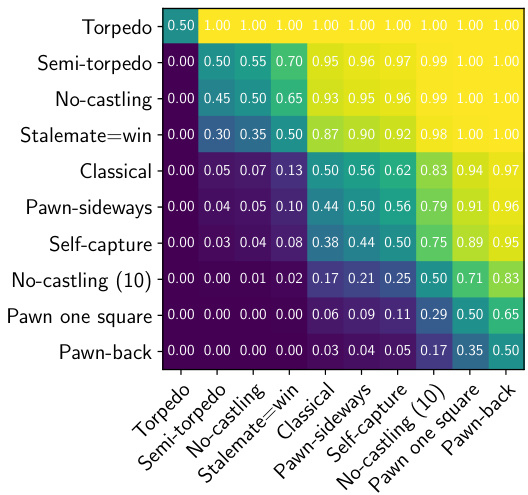
(c) A comparison of expected scores $p(e^{\mathrm{row}}>e^{\mathrm{column}})$ at 1 second per move, on 10,000 games per variation.

Figure 3. A comparison of draw rates. The most decisive chess variants under both time controls are Torpedo, Semi-torpedo, No-castling and Stalemate=win. These four variants also give White the largest first-move advantage.

图 3: 和棋率对比。在两种时限控制下最具决定性的国际象棋变体分别是鱼雷(Torpedo)、半鱼雷(Semi-torpedo)、无王车易位(No-castling)和逼和即胜(Stalemate=win)。这四种变体也赋予白方最大的先手优势。

1 minute per move. Under both time controls, the most decisive chess variants we explored are Torpedo, Semi-torpedo, No-castling and Stalemate $:=$ win. Torpedo and Semi-torpedo have increased pawn mobility, allowing for faster, more dynamic play, leading to more decisive outcomes. There are also more moves to consider at each juncture. No-castling chess makes it harder to evacuate the king to safety, similarly affecting the draw rate. Finally, Stalemate $\leftleftarrows$ win removes one important drawing resource for the weaker side, converting a number of important endgame positions from being drawn to being winning for the stronger side. Under the same conditions of play, the slower Pawn one square chess variant and Pawn-back chess variant are the most drawish. Pawnback chess incorporates additional defensive resources, and the ability to go back to protect the weak squares seems to be more important for defending worse positions than it is for attacking – given that attacking tends to involve moving forward on the board.

每步1分钟。在两种时间控制下，我们探索的最具决定性的国际象棋变体是鱼雷象棋、半鱼雷象棋、无王车易位象棋和逼和判胜象棋。鱼雷和半鱼雷变体提升了兵的移动能力，使对局更快速、更具动态性，从而产生更多决定性结果。这些变体在每个决策点也需要考虑更多着法。无王车易位象棋增加了国王转移至安全区域的难度，同样影响了和棋率。最后，逼和判胜规则移除了弱势方的重要和棋手段，将许多关键残局从和棋转变为优势方必胜局面。在相同对局条件下，速度较慢的一格兵象棋和兵回退象棋变体最容易出现和棋。兵回退象棋引入了额外防御资源，且后退防守弱格的能力对于防守劣势局面比进攻更重要——因为进攻通常需要在棋盘上向前推进。

3.2.3. EXPECTED SCORES

3.2.3. 预期得分

The decisiveness of a chess variant under imperfect play does not necessarily have to correspond to the first-move advantage. In classical chess, White scores higher on average. Top-level chess players tend to press for an advantage with the White pieces and defend with the Black pieces, looking for opportunities to counter-attack. The reason is the first-move advantage; it is an initiative that, with good play, persists throughout the opening phase of the game. This not a universal property that would hold in any game , as playing the first move might also disadvantage a player in some types of games. It is therefore important to estimate the effect of the rule changes on the first-move advantage in each chess variant, expressed as the expected score for White.

棋类变体在不完美对弈下的决定性未必与先手优势相对应。在国际象棋中，执白一方平均得分更高。顶尖棋手倾向于用白棋寻求优势，用黑棋防守并寻找反击机会。其原因在于先手优势——这是一种通过精妙着法能在开局阶段持续保持的主动权。但这一特性并非所有棋类通用，在某些游戏类型中先手反而可能成为劣势。因此，评估规则改动对每个棋类变体中先手优势的影响至关重要，通常以白方预期得分作为量化指标。

The expected score for White is defined as:

白棋的期望得分定义为：

$$
e=\pi_{\mathrm{win}}+{\textstyle\frac{1}{2}}\pi_{\mathrm{draw}}
$$

for a particular set of conditions like time controls, the move selection criteria and the AlphaZero model playing the game. Given the game outcomes $\mathcal{G}^{\mathrm{A}}$ and $\mathcal{G}^{\mathrm{B}}$ of variants A and B, the probability of white having a higher first-move advantage in variant A is

在特定条件下，如时间控制、着法选择标准以及进行游戏的AlphaZero模型。给定变体A和B的游戏结果$\mathcal{G}^{\mathrm{A}}$和$\mathcal{G}^{\mathrm{B}}$，变体A中白方具有更高先手优势的概率为

$$
p(e^{\mathrm{A}}>e^{\mathrm{B}})=\iint\mathbb{I}\left[\pi_{\mathrm{win}}^{\mathrm{A}}+\frac{1}{2}\pi_{\mathrm{draw}}^{\mathrm{A}}>\pi_{\mathrm{win}}^{\mathrm{B}}+\frac{1}{2}\pi_{\mathrm{draw}}^{\mathrm{B}}\right]
$$

which we again evaluate with a Monte Carlo estimate.

我们再次使用蒙特卡洛估计进行评估。

White’s first-move advantage with approximately 1 second and 1 minute per move in AlphaZero games is compared in Figures 3c and 3d respectively. The relative ordering of variations follows the ranking in general decisiveness, suggesting that the new chess variants that are more decisive in AlphaZero games are also more advantageous for White, possibly due to an increase in dynamic attacking options.

白棋先手优势在AlphaZero对局中每步约1秒和1分钟思考时间的对比分别展现在图3c和图3d中。变体排序与总体决定性排名一致，这表明在AlphaZero对局中更具决定性的新国际象棋变体也对白棋更有利，可能是由于动态进攻选择的增加。

3.3. Differences in specific openings

3.3. 具体开局差异

To further illustrate how different alterations of the rule set would require players to adjust their opening repertoires, we provide a comparison of how favourable specific opening positions are for the first player, for each of the variants previously introduced in Table 1. Figure 4 shows the win, draw, and loss percentages for White under 1 second per move, for the Dutch Defence, Chigorin Defence, Alekhine Defence and King’s Gambit, on a sample of 1000 self-play games. The only variant we did not include in these comparisons is Pawn one square, as the lines used in the comparisons involve the double-pawn-moves which are not legal in that variant.

为了进一步说明规则集的不同改动会如何要求玩家调整开局策略，我们针对表1中介绍的各个变体，比较了特定开局对先手方的有利程度。图4展示了在每步1秒的条件下，荷兰防御、奇戈林防御、阿廖欣防御和王翼弃兵这四种开局的白方胜率、和局率和败率（基于1000局自我对弈样本）。这些比较中唯一未包含的变体是"兵行一格"，因为比较所涉及的行棋路线包含双步进兵，而该变体中此着法不合法。

These four opening systems are not considered to be the most principled ways of playing Classical chess. They are therefore particularly interesting for establishing if a certain rule change pushes the evaluation of each of these openings from “slightly inferior” to “unsound” or “unplayable”.

这四种开局体系并非古典国际象棋中最具理论依据的下法。因此，它们特别适合用于验证特定规则修改是否会导致这些开局评估从"稍处下风"恶化为"不合理论"或"无法使用"。

In case of Dutch Defence in Figure 4a, we see that it is more favourable for White in Torpedo and Stalemate $\asymp$ win chess than in Classical chess. This is in line with the overall increase in decisiveness in those variations, but is not more favourable in case of No-castling chess, despite Nocastling chess otherwise being more decisive than Classical chess. We can already see in this one example that the overall differences in decisiveness between variants are not equally distributed across all possible opening lines, and that the evaluation of the difference in the expected score will depend on the style of opening play.

在图 4a 的荷兰防御中，我们可以看到白方在鱼雷变例和僵局变例 $\asymp$ 赢棋中的优势比古典国际象棋更大。这与这些变例中整体决断力的提升一致，但在无王车易位象棋中并未表现出更大优势，尽管无王车易位象棋通常比古典象棋更具决断力。仅从这一例中我们就能看出，不同变体间决断力的整体差异并非均匀分布于所有可能的开局路线，且预期得分差异的评估将取决于开局风格。

In case of Chigorin Defence in Figure 4b, Pawn-sideways chess seems to be refuting the variation, based on our initial findings. In a smaller sample of games played at 1 minute per move, we have seen a $100%$ score being achieved by AlphaZero in this line of Pawn-sideways chess, though these are still preliminary conclusions. To the human eye the line does not appear to be very forcing; it is not a short tactical refutation, but results in a fairly long-term strategic advantage, which AlphaZero converts into a win. This line also seems to be harder to defend in No-castling chess and Torpedo, but not in Stalemate $\because$ win chess, unlike the Dutch Defence.

在图4b所示的奇戈林防御(Chigorin Defence)中，根据我们的初步研究，兵侧行象棋(Pawn-sideways chess)似乎能驳倒该变例。在每步1分钟的较小对局样本中，我们观察到AlphaZero在这条兵侧行象棋变例中取得了100%胜率，尽管这些仍是初步结论。对人类棋手而言，该变例看似并非强制性走法——它并非短促的战术性驳斥，而是会形成相当长期的战略优势，最终被AlphaZero转化为胜势。与荷兰防御(Dutch Defence)不同，该变例在无王车易位象棋(No-castling chess)和鱼雷象棋(Torpedo)中似乎更难防守，但在逼和即胜象棋(Stalemate$\because$win chess)中则不然。

The Alekhine Defence in Figure 4c seems to be less sound in all of the variations considered, compared to Classical chess, with a major increase in decisiveness in Pawn-sideways chess, No-castling chess and Torpedo chess.

图 4c 中的阿廖欣防御 (Alekhine Defence) 在所有变体中似乎都不如古典国际象棋稳固，且在兵横走象棋 (Pawn-sideways chess) 、无王车易位象棋 (No-castling chess) 和鱼雷象棋 (Torpedo chess) 中决定性显著增强。

Finally, King’s Gambit in Figure 4d seems to give a substantial advantage to Black across all chess variants considered, although in No-castling chess and Torpedo chess, White has somewhat better winning chances than in Classical chess. Pawn-sideways chess, again, seems to be the worst of the variants to consider playing this line in. Still, in our preliminary experiments with games at longer thinking times, most games would still ultimately end in a draw. This suggests that it is still likely a playable opening, when played at a very high level with deep calculation.

最后，图4d中的王翼弃兵 (King's Gambit) 在所有考虑的变体棋局中似乎都给黑方带来了显著优势，不过在无王车易位 (No-castling) 象棋和鱼雷 (Torpedo) 象棋中，白方的获胜机会比古典象棋略高。横向走兵 (Pawn-sideways) 象棋再次成为最不适合采用此开局路线的变体。尽管如此，在我们延长思考时间的初步对弈实验中，大多数对局最终仍以和棋告终。这表明在高水平深度计算的情况下，这很可能仍是一个可行的开局。

3.4. Util is ation of special moves

3.4. 特殊移动的利用

Several of the variants that are explored in this study involve additional move options that are not permitted under the rules of Classical chess, like additional pawn moves and self-captures. It is not clear from the outset how often these newly introduced moves would be utilised in each of the variants. Will they make a difference? We use the set of 10,000 games at 1 second per move from Section 3.1 to quantify how often the additional moves are played.

本研究探讨的几种变体规则包含了古典国际象棋规则中不允许的额外走法选项，例如新增的兵步走法和自吃子。这些新引入的走法在各变体中的实际使用频率尚不明确——它们会产生实质影响吗？我们利用第3.1节中10,000盘每步1秒的对局数据，量化统计了这些额外走法的出现频率。

3.4.1. TORPEDO MOVES

In Semi-torpedo chess, $88%$ of all games have at least one torpedo move, and $1.20%$ of all moves played in the game are torpedo moves. In Torpedo chess, these percentages are even higher: $94%$ of games utilise torpedo moves and these represent $2.40%$ of all moves played in the game. Furthermore, $28.7%$ of games featured pawn promotions with a torpedo move, highlighting the speed at which a passed pawn can be promoted to a queen.

在半鱼雷象棋中，88%的对局至少包含一次鱼雷走法，且所有走法中鱼雷走法占比1.20%。鱼雷象棋中这两个比例更高：94%的对局采用鱼雷走法，其占全部走法的2.40%。此外，28.7%的对局通过鱼雷走法实现兵升变，凸显通路兵可快速升变为后的特性。

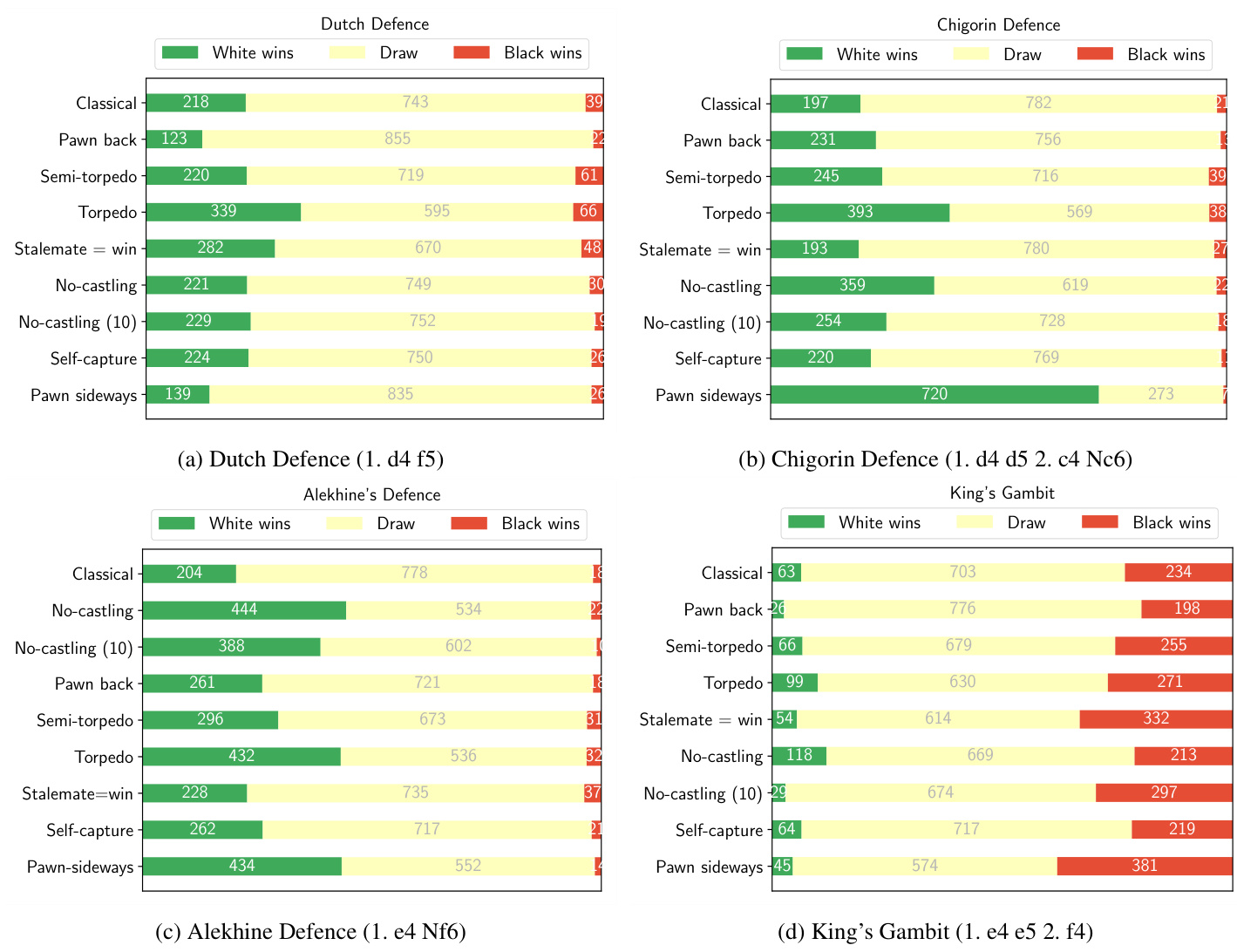
Figure 4. The same opening position can give vastly different degrees of advantage to either play, depending on the variant under consideration, as shown here by the number of games won, drawn and lost for AlphaZero as White when playing at approximately 1 second per move, for a sample of 1000 games, while always playing the best move without any additional noise being added for play diversity. The stochastic it y captured in the results stems from the asynchronous execution of MCTS threads during search. Therefore, these results indicate how favorable the ’main line’ continuation is, for each of the following openings: the Dutch Defence, the Chigorin Defence, Alekhine Defence and the King’s Gambit.

图 4: 相同的开局局面会根据所考虑的变体给任一方带来截然不同的优势程度。如图所示为AlphaZero执白时在每步约1秒的思考时间下，对1000局样本游戏的胜负统计（始终走最佳着法且未添加额外噪声以增加多样性）。结果中的随机性源于搜索过程中MCTS线程的异步执行。因此，这些数据反映了以下开局变体中"主变"延续的有利程度：荷兰防御、奇戈林防御、阿廖欣防御和王翼弃兵。

3.4.2. BACKWARDS AND LATERAL PAWN MOVES

3.4.2. 兵的后退与横向移动

In Pawn-back chess, $96.3%$ of the games involved a backwards pawn move. In Pawn-sideways chess, $99.6%$ of games features lateral pawn moves, and a total of $11.4%$ of all moves in the game were lateral pawn moves, as the reconfiguring of pawn formations was common in AlphaZero’s playing style in this chess variant.

在兵回退象棋(Pawn-back chess)中，96.3%的对局包含兵后退的着法。在兵横移象棋(Pawn-sideways chess)中，99.6%的对局出现了兵横向移动的情况，且所有着法中有11.4%为兵横向移动，因为在这种变体棋中，AlphaZero的行棋风格经常涉及兵形结构的重组。

3.4.3. SELF-CAPTURES

3.4.3. 自我捕获

In Self-capture chess, $52.5%$ of games featured self-capture moves, which represented $0.7%$ of all moves played. The most common self-captures involved sacrificing a pawn $(86.9%)$ , although sacrificing a bishop $(5.3%)$ or a knight $(4.5%)$ was not uncommon. Rook self-capture sacrifices were rare $(2.3%)$ and occasionally AlphaZero would selfcapture a queen $(1%)$ , though these were mostly unnecessary captures in winning positions, given that AlphaZero was not in centi vised to win in the fastest possible way.

在自吃象棋中，52.5%的对局出现了自吃移动，占所有移动的0.7%。最常见的自吃行为是牺牲兵 (86.9%)，尽管牺牲象 (5.3%) 或马 (4.5%) 也并不罕见。车的自吃牺牲较为稀少 (2.3%)，偶尔AlphaZero会自吃后 (1%)，但这些大多是在必胜局面下的非必要行为，因为AlphaZero并未被设定为以最快方式取胜。

3.4.4. WINNING THROUGH STALEMATE

3.4.4. 通过僵局取胜

In Stalemate $=$ win chess the percentage of all decisive games that were won by stalemate rather than mate in AlphaZero games was $37.2%$ , though this number is inflated due to the fact that AlphaZero would often stylistically stalemate rather than mate the opponent in positions where both are possible.

在AlphaZero的对局中，所有决定性胜利里通过逼和(Stalemate)而非将死(Mate)取胜的比例为37.2%。不过该数值存在虚高现象，因为当两种终结方式都可行时，AlphaZero往往会选择更具风格性的逼和方式。

The percentages listed above suggest that the rule changes featured in these chess variants did indeed leave a trace on how the game is being played, and that they are useful additional options that can potentially change the game dynamics. Yet, it is important to note that the resulting games are still of approximately similar length, as shown in Figure 8 in Appendix A, with some changes in the empirical duration of decisive games. This means that playing a game in one of these chess variants is unlikely to prolong or shorten the game by a large amount, meaning that classical time controls should still be appropriate. Note that the numbers in Figure 8 that correspond to the number of plies in AlphaZero games are an upper bound on game length, since AlphaZero was trained without discounting, and would therefore not play the fastest winning sequence in its decisive games.

上述百分比数据表明，这些国际象棋变体中的规则改动确实对游戏方式产生了影响，它们作为附加选项能有效改变游戏动态。但需注意，如附录A中图8所示，对局时长仍保持相近水平，仅决胜局的实际持续时间略有变化。这意味着采用这些变体规则既不会显著延长也不会缩短对局时间，因此传统计时规则依然适用。需特别说明，图8中对应AlphaZero对局步数的数值属于理论上限，因为AlphaZero训练时未采用折扣机制，因此在决胜局中不会选择最快获胜路径。

3.5. Diversity

3.5. 多样性

For a game to be appealing, it has to be rich enough in options that these options do not get quickly exhausted, as play would then become repetitive. We use the average information content (entropy) of the first $T=20$ plies of play from each variant’s prior as a surrogate diversity measure. The trained AlphaZero policy priors model the move probabilities of the positions in self-play training data, and reflects the statistics at which opening lines appear there. An entropy of zero corresponds to there being one and only one forcing sequence of moves to be playable for White and Black, all other moves leading to substantially worse positions for each side. A higher entropy implies a wider and more balanced opening tree of variations, leading to a more diverse set of middlegame positions. The intuition that there would be many more plausible opening lines in slower variants like Pawn one square, holds true experimentally. In simulation, more decisive variants like Torpedo chess typically have fewer plausibly playable opening lines.

要让一款游戏具有吸引力，它必须提供足够丰富的选择，以避免这些选项迅速耗尽，否则游戏会变得重复。我们使用每个变体初始前20步($T=20$)的平均信息量(熵)作为多样性替代指标。经过训练的AlphaZero策略先验模拟了自对弈训练数据中棋局的走子概率，并反映了开局路线出现的统计规律。熵值为零意味着黑白双方只有唯一一条强制走子序列可供选择，其他走法都会导致某一方陷入明显劣势。更高的熵值意味着开局变化树更宽广均衡，从而形成更多样化的中局局面。实验证实了直觉判断：像"兵行一格"这类慢节奏变体确实存在更多合理的开局路线。而在模拟中，像"鱼雷象棋"这类更具决定性的变体通常只有较少可行的开局选择。

The decomposition of the entropy as a statistical expectation can help identify whether there exist defensive lines that equalise the game in an almost forcing way. In Classical chess, one such defensive resource is the Berlin Defence in the Ruy Lopez, taking the sting out of 1. e4. We show in Section 3.5.2 that AlphaZero, when trained on Classical chess, expresses a strong preference for the Berlin Defence, similarly to the human consensus on the solidity of the Berlin endgame. Without the option to castle, this particular line disappears in No-castling chess.

将熵分解作为统计期望有助于识别是否存在以近乎强制方式平衡比赛的防守路线。在国际象棋中，柏林防御( Berlin Defence )就是这样一种防守资源，它能化解1.e4的攻势。我们在3.5.2节中表明，当AlphaZero接受国际象棋训练时，会表现出对柏林防御的强烈偏好，这与人类对柏林残局稳固性的共识相似。在没有王车易位选项的无易位象棋中，这一特定路线便不复存在。

3.5.1. AVERAGE INFORMATION CONTENT

3.5.1. 平均信息量

The prior network from (1) defines the probability of $a$ priori considering move $a_{t}$ in state $s_{t}$ , but as move $a_{t}$ leads to state $s_{t+1}$ deterministic ally, we shall abbreviate the prior with $p(s_{t+1}|s_{t})$ .

来自(1)的先验网络定义了在状态$s_{t}$下先验考虑移动$a_{t}$的概率，但由于移动$a_{t}$确定性地导致状态$s_{t+1}$，我们将先验简写为$p(s_{t+1}|s_{t})$。

The prior is a weighted list of possible moves for state $s_{t}$ that are utilised in AlphaZero’s MCTS search. The weights specify how plausible each move is before MCTS calculation; they specify candidates for consideration. In information

先验概率是状态$s_{t}$下可能走法的加权列表，用于AlphaZero的蒙特卡洛树搜索(MCTS)。这些权重指定了在MCTS计算前每个走法的合理程度，从而确定待考虑的候选走法。

Variant	Entropy	Equivalent 20-ply games
No-castling	27.65	1.02 × 1012
Torpedo	27.89	1.30 × 1012
Self-capture	27.94	1.36 × 1012
No-castling (10)	27.97	1.40 × 1012
Classical	28.58	2.58 × 1012
Stalemate=win	29.01	3.97 x 1012
Semi-torpedo	31.63	5.45 × 1013
Pawn-back	32.30	1.07 × 1014
Pawn-sideways	34.16	6.85 x 1014
Pawn one square	38.95	8.24 × 1016
Uniform random	64.96	1.63 × 1028

变体	熵	等效20回合游戏数
无王车易位	27.65	1.02 × 1012
鱼雷式	27.89	1.30 × 1012
自我捕获	27.94	1.36 × 1012
无王车易位(10)	27.97	1.40 × 1012
经典规则	28.58	2.58 × 1012
逼和即胜	29.01	3.97 × 1012
半鱼雷式	31.63	5.45 × 1013
兵退行	32.30	1.07 × 1014
兵横走	34.16	6.85 × 1014
兵单格行走	38.95	8.24 × 1016
均匀随机	64.96	1.63 × 1028

Table 3. The average information content in nats in the first 20 plies of the AlphaZero prior for each chess variant. The uniform random baseline assumes an equal probability for each move in Classical chess, and provides rough indication of the ratio between “plausible” and “possible” games according to the AlphaZero prior. The uniform random baseline depends on the number of legal moves per position, and is marginally different but of the same magnitude for other variations.

表 3: AlphaZero先验策略在各类象棋变体前20步的平均信息量(单位:nats)。均匀随机基线假设古典象棋中每步棋选择概率均等，据此粗略反映AlphaZero先验中"合理"与"可能"对局的比例。该基线值取决于每步合法移动的数量，在其他变体中数值略有差异但数量级相同。

theoretic terms, the entropy

理论术语中的熵

$$
H(s_{t})=-\sum_{s_{t+1}}p(s_{t+1}|s_{t})\log p(s_{t+1}|s_{t})
$$

is a function of state $s_{t}$ and represents the number of nats (or bits, if $\mathrm{log_{2}}$ is used) that are needed to encode the weighted moves in position $s_{t}$ .

是状态 $s_{t}$ 的函数，表示编码位置 $s_{t}$ 中加权移动所需的信息量（若使用 $\mathrm{log_{2}}$ 则以比特为单位，否则以奈特为单位）。

If there are $M(s_{t})$ legal moves in state $s_{t}$ , then the number of candidate moves $m(s_{t})$ – the number that a top player would realistically consider – is much smaller than $M(s_{t})$ . In de Groot (1946)’s original framing, $M(s_{t})$ is a player’s legal freedom of choice, while $m(s_{t})$ is their objective freedom of choice. Iida et al. (2003) hypothesis e that $m(s_{t})\approx\sqrt{M(s_{t})}$ on average. Because $p(s_{t+1}|s_{t})$ is a distribution on all legal moves, we define the number of candidate moves $m(s_{t})$ by

如果在状态 $s_{t}$ 中有 $M(s_{t})$ 种合法走法，那么候选走法的数量 $m(s_{t})$ ——即顶尖棋手实际会考虑的数量——远小于 $M(s_{t})$。在 de Groot (1946) 最初的框架中，$M(s_{t})$ 是棋手在法律上的选择自由，而 $m(s_{t})$ 是他们客观的选择自由。Iida 等人 (2003) 假设平均而言 $m(s_{t})\approx\sqrt{M(s_{t})}$。由于 $p(s_{t+1}|s_{t})$ 是所有合法走法的分布，我们通过以下方式定义候选走法的数量 $m(s_{t})$：

$$
m(s_{t})=\exp(H(s_{t}));
$$

it is the number of uniformly weighted moves that could be encoded in the same number of nats as $p(s_{t+1}|s_{t})$ .3

这是在相同数量的自然对数单位 (nats) 中可以编码的均匀加权移动次数，即 $p(s_{t+1}|s_{t})$。

We provide insight into the diversity of the prior opening tree through two quantities, the move sequence entropy $\mathcal{H}(t)$ at depth $t$ from the opening position, and the average number of candidate moves at ply $t,\mathcal{M}(t)$ .

我们通过两个量来揭示开局树先验的多样性：从开局位置出发，深度 $t$ 处的着法序列熵 $\mathcal{H}(t)$，以及第 $t$ 步的平均候选着法数 $\mathcal{M}(t)$。

Move sequence entropy Let $\mathbf{s}=\mathbf{s}_ {1:t}=[s_{1},s_{2},...s_{t}]$ be the sequence of states after $t$ plies, starting at $s_{0}$ , the initial position. The prior probability – without search – of move sequence $\mathbf{s}_ {1:t}$ is $\begin{array}{r}{p(\mathbf{\tilde{s}}_ {1:t}^{-}|s_{0})=\prod_{\tau=1}^{t}p(s_{\tau}|s_{\tau-1})}\end{array}$ . The entropy of the move sequence is

移动序列熵

设 $\mathbf{s}=\mathbf{s}_ {1:t}=[s_{1},s_{2},...s_{t}]$ 为从初始位置 $s_{0}$ 开始，经过 $t$ 步后的状态序列。在不进行搜索的情况下，移动序列 $\mathbf{s}_ {1:t}$ 的先验概率为 $\begin{array}{r}{p(\mathbf{\tilde{s}}_ {1:t}^{-}|s_{0})=\prod_{\tau=1}^{t}p(s_{\tau}|s_{\tau-1})}\end{array}$。移动序列的熵为

$$
\begin{array}{r l}{\displaystyle\mathcal{H}(t)=-\sum_{\mathbf{s}_ {1:t}}p(\mathbf{s}_ {1:t})\log p(\mathbf{s}_ {1:t})}&{}\ {\displaystyle=\mathbb{E}_ {\mathbf{s}_ {1:t}\sim p(\mathbf{s}_ {1:t})}\Big[-\log p(\mathbf{s}_{1:t})\Big],}\end{array}
$$

where the starting position $s_{0}$ is dropped from notation for brevity. An entropy $\mathcal{H}(t)=0$ implies that, according to the prior, one and only one reasonable opening line could be considered by White and Black up to depth $t$ , with all deviations form that line leading to substantially worse positions for the deviating side. A higher $\mathcal{H}(t)$ implies that we would a priori expect a wider opening tree of variations, and consequently a more diverse set of middlegame positions.

起始位置 $s_{0}$ 为简洁起见从符号中省略。熵值 $\mathcal{H}(t)=0$ 意味着根据先验条件，白方和黑方在深度 $t$ 之前只能考虑唯一合理的开局路线，任何偏离该路线的走法都会导致偏离方陷入明显劣势局面。较高的 $\mathcal{H}(t)$ 值则意味着我们预期会先验地出现更广泛的开局变体树，从而产生更多样化的中局局面。

Average number of candidate moves The entropy of a chess variant’s prior opening tree is an unwieldy number that doesn’t immediately inform us how many move options we have in each chess variant. A more naturally interpret able number is the expected number of (good) candidate moves at each ply as the game unfolds. The average number of candidate moves at ply $t$ is

候选移动的平均数量

棋类变体的先验开局树熵是一个难以处理的数值，无法直接告诉我们每种棋类变体中可选的移动选项数量。更直观可解释的数值是随着对局进行，每一步预期出现的（优质）候选移动数量。在第$t$步时的候选移动平均数量为

$$
\mathcal{M}(t)=\sum_{\mathbf{s}_ {1:t}}p(\mathbf{s}_ {1:t})m(s_{t})=\mathbb{E}_ {\mathbf{s}_ {1:t}\sim p(\mathbf{s}_ {1:t})}\Big[m(s_{t})\Big].
$$

Both the sums in (8) and (9) are over an exponential number of move sequences. We compute Monte Carlo estimates of $\mathcal{H}(t)$ and $\mathcal{M}(t)$ by sampling $10^{4}$ sequences from $p(\mathbf{s})$ and averaging the negative log probabilities of those sequences to obtain $\mathcal{H}(t)$ , or averaging $m(s_{t})$ over all samples at depth $t$ to obtain $\mathcal{M}(t)$ . We defer a presentation of the breakdown of the average number of candidate moves per variant to Figure 11 in Appendix A, and will encounter $\mathcal{M}(t)$ next in Figure 6 when Classical and No-castling chess are compared side by side.

(8) 和 (9) 中的求和项均涉及指数级移动序列数。我们通过从 $p(\mathbf{s})$ 中采样 $10^{4}$ 条序列来计算 $\mathcal{H}(t)$ 和 $\mathcal{M}(t)$ 的蒙特卡洛估计值：通过平均这些序列的负对数概率获得 $\mathcal{H}(t)$，或通过平均深度 $t$ 处所有样本的 $m(s_{t})$ 获得 $\mathcal{M}(t)$。各变体候选移动平均数的详细分析将延至附录A中的图11展示，而 $\mathcal{M}(t)$ 将在后续图6中用于古典象棋与无王车易位象棋的对比分析。

The entropy of the AlphaZero prior opening tree is given in Table 3 for each variation. Similar to the calculation in (7) we give an estimate of the equivalent number of 20-ply sequences as $\exp(\mathcal{H}(t))$ . As a baseline comparison, we take a prior distribution for Classical chess where all legal moves are equally playable, and estimate the entropy of the “Uniform random” move selection criteria. It affords us a crude estimate of the number of possible classical openings, as opposed to the number of plausibly playable or candidate openings. The estimates in Table 3 for Classical chess and "Uniform random Classical chess” corroborate the claim that the number of playable opening lines – a player’s objective freedom of choice – is roughly the square root of the number of legal opening lines (Iida et al., 2003).

表3给出了AlphaZero先验开局树的每种变体的熵值。类似于(7)中的计算，我们通过$\exp(\mathcal{H}(t))$估算出相当于20步棋序列的数量。作为基线对比，我们采用古典象棋的先验分布（假设所有合法走子概率均等），并估算"均匀随机"走子选择标准的熵值。这为我们提供了古典开局可能数量的粗略估计（与合理可玩或候选开局数量相对）。表3中关于古典象棋和"均匀随机古典象棋"的估算数据验证了以下观点：可玩开局路线的数量（即玩家客观选择自由度）大约是其合法开局路线数量的平方根 (Iida et al., 2003)。

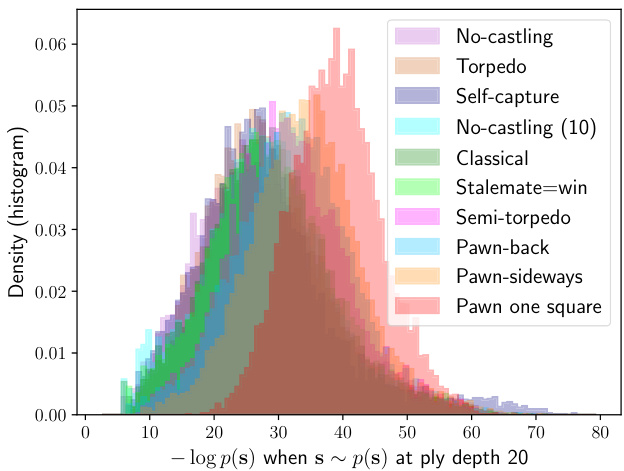
Figure 5. Histograms of $-\log p(\mathbf{s})$ when s $\sim p(\mathbf{s})$ for each vari- ant. Following (8), the means of these distributions give the entropies in Table 3. The individual histograms are separately presented in Figure 9 in Appendix A.

图 5: 各变体在 $\mathbf{s} \sim p(\mathbf{s})$ 时 $-\log p(\mathbf{s})$ 的直方图分布。根据公式(8)，这些分布的均值对应表3中的熵值。各变体的独立直方图详见附录A中的图9。

The two variants that have the largest entropy and hence largest opening tree in Table 3, Pawn-sideways and Pawn one square, also happen to be among the most drawish, according to Figures 3a and 3b. The two variants that have the smallest opening trees under our analysis, No-castling and Torpedo, are also the most decisive and give White some of the largest advantages, according to Figures 3a to 3d. Importantly, we estimate the size of the opening trees of these more decisive versions to still be of the same order of magnitude as that of Classical chess.

表3中熵值最大、开局树最庞大的两个变体——侧行兵(Pawn-sideways)和一步兵(Pawn one square)，根据图3a和图3b显示，恰好也是和棋率最高的变体。而根据图3a至图3d，在我们的分析中开局树规模最小的两个变体——无王车易位(No-castling)和鱼雷兵(Torpedo)，则是胜负最分明且给予白方最大优势的变体。值得注意的是，我们估算这些更具决定性的变体开局树规模仍与古典象棋处于同一数量级。

Figure 5 (a separate figure for each variant appears in Figure 9 in Appendix A) visualises the density of $-\log p(\mathbf{s})$ when state sequences s are drawn from $p(\mathbf{s})$ . The mean of each density is the entropy of (8), and an overlap in the histograms of two variants implies that their opening trees contain a similar number of lines that are considered as candidates with similar odds. In Figure 5, a histogram that is shifted to the left means that fewer move sequences are considered a priori, and each has higher probability. A histogram that is shifted to the right implies that a larger variety of move sequences are a priori considered, and each has to be considered with a smaller probability. “Uniform random” is shown in Figure 9j, and would appear as a tall narrow spike centred around 64 in this figure. In the following section, we shall use log probability histograms as a tool to highlight the differences between Classical and No-castling chess.

图5 (各变体的单独图示见附录A中的图9) 可视化展示了从$p(\mathbf{s})$中抽取状态序列s时$-\log p(\mathbf{s})$的密度分布。每个密度的均值对应公式(8)的熵值，若两个变体的直方图出现重叠，则表明它们的开局树包含数量相近且胜率相似的候选行棋路线。在图5中，左偏的直方图意味着先验考虑的走子序列更少且单个序列概率更高，右偏的直方图则代表先验考虑的走子序列更多且单个序列概率更低。"均匀随机"变体如图9j所示，在本图中会呈现为以64为中心的高窄尖峰。下文将使用对数概率直方图作为工具，突显古典象棋与无王车易位象棋的差异。

3.5.2. CLASSICAL VS. NO-CASTLING CHESS

3.5.2. 传统王车易位与国际象棋无王车易位变体

In Classical chess AlphaZero has a strong preference for playing the Berlin Defence 1. . . e5 2. Nf3 Nc6 3. Bb5 Nf6 in response to 1. e4, and here 4. O-O is White’s main reply, which is not an option in no-castling chess. Yet, castling is also an integral part of most other lines in the Ruy Lopez, affecting each move when considering relative preferences. In the absence of castling, AlphaZero does not have as strong a preference for a particular line for Black after 1. e4, suggesting either that it is not as easy to fully neutralise White’s initiative, or alternatively that there is a larger number of promising defensive options.

在国际象棋经典变体中，AlphaZero对柏林防御(1...e5 2.Nf3 Nc6 3.Bb5 Nf6)应对1.e4开局表现出强烈偏好，而白方的主要回应4.O-O在禁王车易位规则下无法实现。王车易位同样是西班牙开局其他变例的核心组成部分，其存在会影响每一步棋的相对偏好评估。当禁王车易位时，AlphaZero对1.e4后黑棋的特定变例不再表现出强烈倾向性，这表明要么完全抵消白方先手优势更为困难，要么意味着黑方存在更多具有潜力的防御选择。

Table 4. The average information content in nats of the AlphaZero prior for Classical and No-castling chess, estimated on the 20 plies following 1. e4 and 1. Nf3.

Variant	Entropy	Equiv. 21-ply games
Classical (e4)	23.72	2.00 × 1010
Classical (Nf3)	29.54	6.75 × 1012
No-castling (e4)	27.42	8.10 x 1011
No-castling (Nf3)	28.40	2.16 × 1012

表 4: AlphaZero先验在古典象棋和无王车易位象棋中的平均信息量（以纳特为单位），基于1.e4和1.Nf3之后20步的估计。

变体	熵	等效21步对局数
古典象棋(e4)	23.72	2.00 × 10^10
古典象棋(Nf3)	29.54	6.75 × 10^12
无王车易位(e4)	27.42	8.10 × 10^11
无王车易位(Nf3)	28.40	2.16 × 10^12

To indicate the difference between Classical and No-castling chess, we compare the prior’s opening trees after 1. e4 and 1. Nf3 in Figure 6. If we examine the density of $-\log p(\mathbf{s}_ {2:21}|s_{1})$ under $p\big(\mathbf{s}_ {2:21}\big|s_{1}\big)$ , where $s_{1}$ is the board position after either 1. e4 or 1. Nf3, we see a marked shift in the characteristics of the AlphaZero prior opening trees (see Figures 6a and 6b). Statistically, the AlphaZero prior after 1. e4 is much more forcing than after 1. Nf3 in Classical chess. This is also evident from the average information content of the 20 plies after 1. e4 and 1. Nf3 in Table 4. In No-castling chess, 1. e4 seems as flexible as 1. Nf3, with a much wider variety of emerging preferential lines of play in the AlphaZero model.

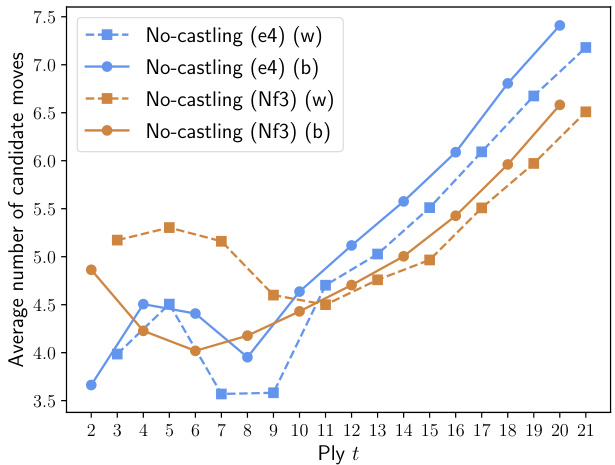
为了展示古典象棋与无王车易位象棋的区别，我们在图6中对比了1. e4和1. Nf3之后的先验开局树。若考察$-\log p(\mathbf{s}_ {2:21}|s_{1})$在$p\big(\mathbf{s}_ {2:21}\big|s_{1}\big)$下的密度（其中$s_{1}$表示1. e4或1. Nf3后的棋盘局面），可观察到AlphaZero先验开局树特征的显著变化（见图6a和6b）。统计数据显示，在古典象棋中，1. e4后的AlphaZero先验比1. Nf3后的更具强制性。这一点从表4中1. e4和1. Nf3之后20步的平均信息量也能明显看出。而在无王车易位象棋中，1. e4与1. Nf3同样灵活，AlphaZero模型中涌现出的优选走法路线更为多样化。

Figure 6 additionally shows the average number of candidate moves at each ply. In Classical chess, White has more options than Black in both lines, the difference slowly diminishing over time as the first-move advantage decreases. 1. Nf3 offers more options, as it is less forcing. In Nocastling chess, there seems to be a higher number of effective available moves for both sides after 1. e4 in the first couple of plies, based on the AlphaZero model.

图 6: 同时展示了每一回合候选着法的平均数量。在国际象棋中，白方在两条线路上的选择都多于黑方，随着先手优势逐渐减弱，这种差异会缓慢缩小。1. Nf3 由于强制性较低，提供了更多选择。根据 AlphaZero 模型，在无王车易位象棋中，前几个回合在 1. e4 之后，双方似乎拥有更多有效可行着法。

The Berlin Defence is a contributing factor to the narrower opening tree footprint we see in Figure 6a. As defensive tool for Black, Vladimir Kramnik successfully used the Berlin Defence in his World Championship Match with Garry Kasparov in 2000. He describes his choice as follows:

柏林防御 (Berlin Defence) 是导致图 6a 中开局树范围较窄的关键因素。作为黑方的防御武器，Vladimir Kramnik 在 2000 年与 Garry Kasparov 的世界冠军赛中成功运用了这一策略。他对此选择的解释如下:

cc Back in the 90s, the engines of the time seemed to think that White had the advantage in the Berlin endgame, giving evaluations around $+l$ in White’s favour. I thought that things weren’t as simple, given that Black’s only real problem was the loss of castling rights, and the difficulty of connecting rooks. The first time that I had $a$ deeper look at it was when I was preparing for the match with Kasparov, and I thought that the opening was a good choice against Kasparov’s playing style. Pursuing it required a belief in instinct and the human assessment of the position. Nowadays, it is considered to be a very solid opening, and modern engines assess most arising positions as being equal.

回到90年代，当时的引擎似乎认为白方在柏林残局中占据优势，给出的评估值约为 $+l$ 对白方有利。我认为事情没那么简单，因为黑方唯一真正的问题是失去了王车易位权，以及难以连接双车。我第一次深入分析这个局面是在准备与Kasparov的比赛时，我认为这个开局很适合对抗Kasparov的棋风。坚持这个选择需要相信直觉和对局面的主观评估。如今，它被认为是非常稳固的开局，现代引擎评估大多数衍生局面均为均势。

3.6. Differences between opening trees

3.6. 开树差异

We compare how similar opening trees are by considering how likely a given sequence of moves is under two variants. To compare, we define one variant $p$ as the reference variant, and generate a move sequence s according to its prior. The Kullback-Leibler divergence is a measure of how likely such sequences of moves are under the opening book of variant $q$ compared to that of $p$ . Given two distributions $p(\mathbf{s})$ and $q(\mathbf{s})$ , the Kullback-Leibler divergence from $q$ to $p$ is the relative entropy of variant $p$ with respect to $q$ ,

我们通过比较两种变体下给定走法序列出现的概率来评估开局树的相似度。设定变体 $p$ 作为参考基准，按其先验分布生成走法序列 s。Kullback-Leibler散度用于衡量该走法序列在变体 $q$ 的开局库中出现的相对概率（相对于变体 $p$）。对于两个分布 $p(\mathbf{s})$ 和 $q(\mathbf{s})$，从 $q$ 到 $p$ 的Kullback-Leibler散度即为变体 $p$ 相对于 $q$ 的相对熵。

$$
\begin{aligned}
\mathcal{D}_ {\mathrm{KL}}[p | q] &= \sum_{\mathbf{s}} p(\mathbf{s}) \log \frac{p(\mathbf{s})}{q(\mathbf{s})} \
&= \mathbb{E}_{\mathbf{s} \sim p(\mathbf{s})} \Big[ \log p(\mathbf{s}) - \log q(\mathbf{s}) \Big].
\end{aligned}
$$

It is the expected number of extra nats (or bits if $\mathrm{log_{2}}$ is used) that is required to compress move sequences from variant $p$ using variant $q$ ’s opening book distribution. The calculation in (10) involves a sum that is exponential in the length of s, and we estimate it with a Monte Carlo average of $\log p(\mathbf{s})/q(\mathbf{s})$ over $10^{4}$ sampled sequences from $p(\mathbf{s})$ .

这是使用变体$q$的开局棋谱分布来压缩变体$p$的走棋序列所需的额外纳特(若使用$\mathrm{log_{2}}$则为比特)的期望数量。(10)中的计算涉及一个随序列s长度呈指数级增长的求和式，我们通过从$p(\mathbf{s})$中采样$10^{4}$个序列，对$\log p(\mathbf{s})/q(\mathbf{s})$进行蒙特卡洛平均来估计该值。

A legal move in variant $p$ may be illegal in variant $q$ , in which case there is no way in which sequences in $p$ can be encoded in $q$ . The Kullback-Leibler divergence in (10) is then infinite. More formally, this happens when $q(s_{t+1}|s_{t})$ puts zero mass on state transitions which are possible in $p$ We therefore need to ensure that the reference variant $p$ is chosen so that its legal moves are a subset of those of $q$ . In Table 5 we show all divergences with respect to Classical chess, and distinguish between two kinds of variants:

变体 $p$ 中的合法走法在变体 $q$ 中可能不合法，此时无法将 $p$ 的走法序列编码到 $q$ 中。此时式 (10) 中的 Kullback-Leibler 散度为无穷大。更形式化地说，当 $q(s_{t+1}|s_{t})$ 对 $p$ 中可能发生的状态转移赋予零概率时就会出现这种情况。因此需要确保参考变体 $p$ 的选择满足其合法走法是 $q$ 合法走法的子集。表 5 展示了所有变体相对于经典国际象棋的散度值，并将变体分为两类：

The legal moves of Stalemate $:=$ win correspond to that of Classical chess, and it is included as both a superset and a subset in Table 5. The density of samples from (10) is given in Figure 10 in Appendix A. The divergence is largest for variants that introduce the largest number of additional pawn moves or the most restrictions. Self-capture chess, despite (c) The average number of candidate moves $\mathcal{M}(t)$ , as computed with (9), for Classical chess.

将死局 (Stalemate) 的合法移动定义为胜利，其规则与古典象棋 (Classical chess) 相同。如表 5 所示，它既作为超集又作为子集被包含其中。来自公式 (10) 的样本密度见附录 A 中的图 10。引入最多额外兵步或最多限制的变体差异最大。自吃象棋 (Self-capture chess) 虽...(c) 古典象棋中根据公式 (9) 计算得出的候选移动平均数量 $\mathcal{M}(t)$。

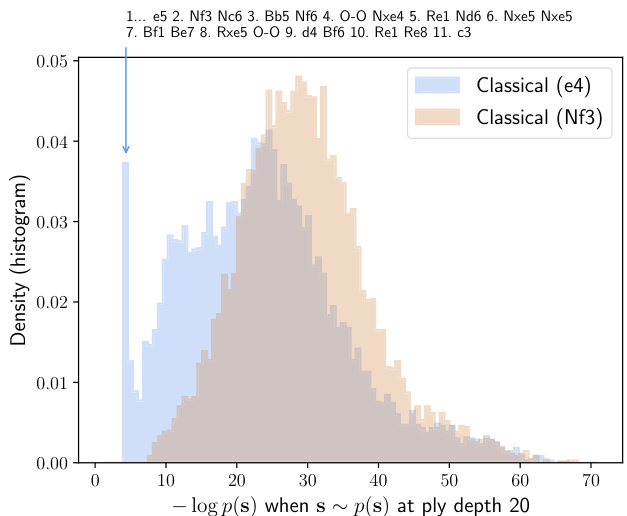
(a) The density of (negative) log likelihoods for opening lines in Classical chess after 1. e4 and 1. Nf3 when move sequences are sampled from the AlphaZero prior. There is a marked difference in overlap between the histograms, suggesting that AlphaZero a priori considers “narrower” opening lines after 1. e4 than after 1. Nf3. We identify the samples s at the high likelihood spike with a particular line in the Berlin Defence.

图 1:
(a) 从AlphaZero先验中采样走法序列时，国际象棋古典开局1.e4和1.Nf3后(负)对数似然密度的分布。直方图重叠区域存在显著差异，表明AlphaZero在1.e4后考虑的"狭窄"开局线比1.Nf3后更集中。我们将高似然峰对应的样本s识别为柏林防御中的特定变例。

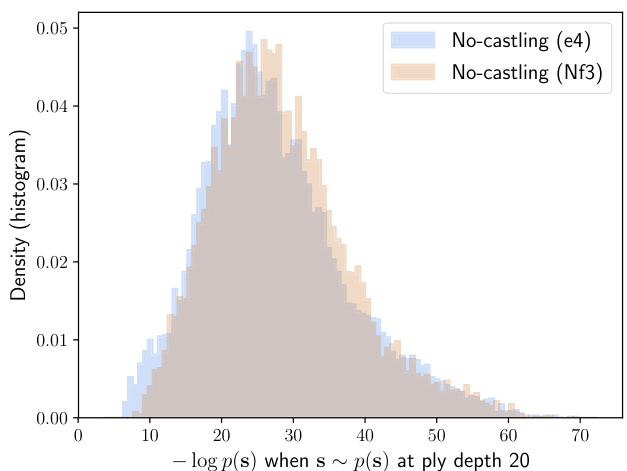
(b) The density of (negative) log likelihoods for opening lines in No-castling chess after 1. e4 and 1. Nf3 when move sequences are sampled from the AlphaZero prior. Without the option of castling a king to safety, the prior opening trees after 1. e4 and 1. Nf3 have more similar “distribution al footprints” compared to Classical chess in Figure 6a.

图 1:
(b) 在无王车易位(No-castling)象棋中，当从AlphaZero先验分布中采样走子序列时，1.e4和1.Nf3开局着法的(负)对数似然密度分布。由于无法通过王车易位将国王转移至安全位置，与图6a中的传统象棋(Classical chess)相比，1.e4和1.Nf3之后的先验开局树具有更相似的"分布足迹"。

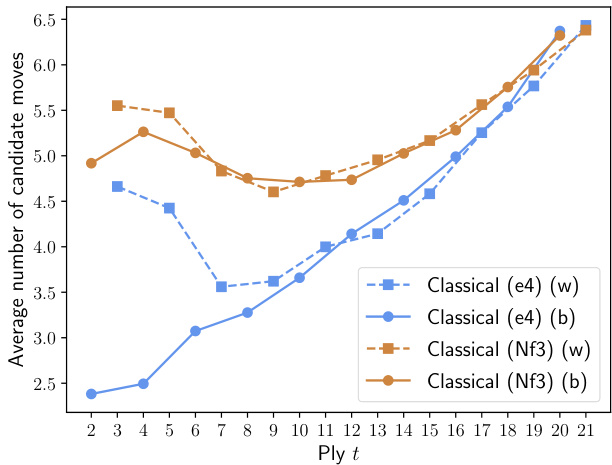
Figure 6. The diversity of responses to 1. e4 and 1. Nf3 in Classical and No-castling chess, as well as the average number of candidate moves available for White and Black at each ply. The spike is in the classical chess 1. e4 response distribution is at 1. . . e5 2. Nf3 Nc6 3. Bb5 Nf6 4. O-O Nxe4 5. Re1 Nd6 6. Nxe5 Nxe5 7. Bf1 Be7 8. Rxe5 O-O 9. d4 Bf6 10. Re1 Re8 11. c3, a known equalising line in the Berlin Defence, leading to drawish positions.

图 6: 古典象棋与无王车易位象棋中对 1. e4 和 1. Nf3 的响应多样性，以及白方与黑方在每个回合可选着法的平均数量。古典象棋 1. e4 响应分布中的峰值出现在 1...e5 2. Nf3 Nc6 3. Bb5 Nf6 4. O-O Nxe4 5. Re1 Nd6 6. Nxe5 Nxe5 7. Bf1 Be7 8. Rxe5 O-O 9. d4 Bf6 10. Re1 Re8 11. c3 这一柏林防御中已知的均势变例，该变例通常导致和棋局面。

(d) The average number of candidate moves $\mathcal{M}(t)$ , as computed with (9), for No-castling chess.

图 1:
(d) 无王车易位象棋中根据公式(9)计算的平均候选移动步数 $\mathcal{M}(t)$。

the plethora of additional opportunities for self-capture, is statistically closer to Classical chess because of the low frequency at which the extra moves are played.

由于额外走棋的低频特性，这种自我捕获的丰富机会在统计上更接近古典象棋。

3.7. How much opening theory should be relearned?

3.7. 需要重新学习多少开局理论？

Although the relative entropy expresses how many more nats are required to encode prior moves of one variant given another, it does not tell us whether one variant’s player is considering the right candidate moves when playing another variant. How many more candidate moves should a player Q, who was trained on one variant of chess, take into consideration when wanting to play at player P’s level in another variation? Let $q(\mathbf{s})$ be the candidate prior for the variation that player Q was trained on, and $p(\mathbf{s})$ the prior for variant P, variant that $\mathsf Q$ wants to play. We define the combination

虽然相对熵能表示在给定另一种变体的情况下编码某变体先手棋步需要多少额外纳特，但它无法说明某变体棋手在对弈另一变体时是否考虑了正确的候选棋步。当接受过某变体训练的棋手Q想在另一变体中达到棋手P的水平时，应当额外考虑多少候选棋步？设 $q(\mathbf{s})$ 表示棋手Q训练所用变体的候选先验概率， $p(\mathbf{s})$ 表示目标变体P的先验概率（即 $\mathsf Q$ 想要对弈的变体）。我们定义组合式

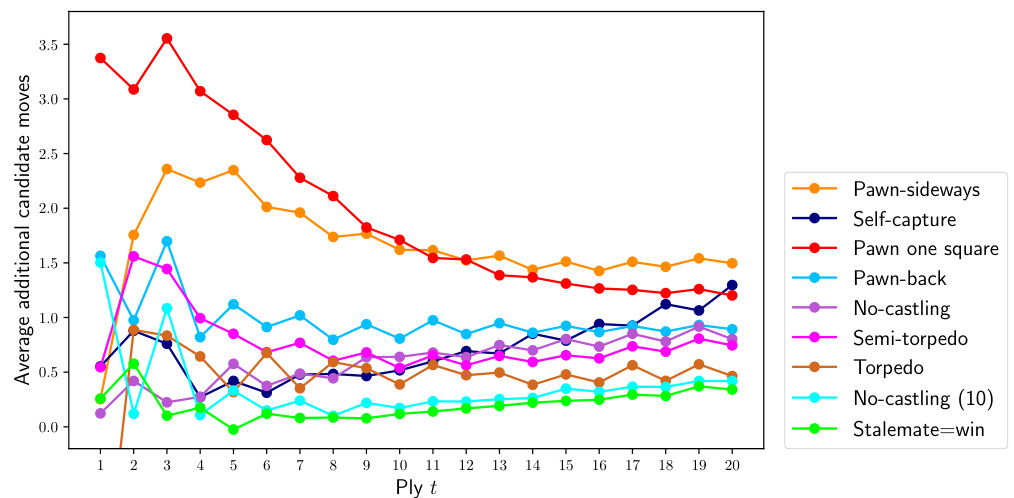
Figure 7. The average number of additional candidate moves $\mathbf{}\mathbf{}{\mathcal{A}}_ {q}(t)$ that a Classical player Q with prior $q(s_{t+1}|s_{t})$ should consider in order to match player P’s candidate moves from prior $p(\mathbf{s})$ for each of the evaluated variants; see (15). (The order of the variants in the legend matches their ordering at ply $t=20.$ .)

图 7: 具有先验 $q(s_{t+1}|s_{t})$ 的经典玩家 Q 为匹配玩家 P 从先验 $p(\mathbf{s})$ 中得出的候选走法，在各评估变体中需额外考虑的平均候选走法数量 $\mathbf{}\mathbf{}{\mathcal{A}}_{q}(t)$ (见公式 (15)) (图例中变体顺序与其在第 20 步时的排序一致)。

Variant p	Variantq	DkL [pllq]
Classical Supersets Classical Classical Classical	Stalemate=win Self-capture Semi-torpedo	2.59 5.24 10.35
	Classical Classical Stalemate=win No-castling (10)	Pawn-back 11.70 Torpedo 11.89 Pawn-sideways
Subsets No-castling Pawn one square	Classical Classical Classical	24.23 2.50 7.17

Variant p	Variantq	DkL [pllq]
Classical Supersets Classical Classical Classical	Stalemate=win Self-capture Semi-torpedo	2.59 5.24 10.35
	Classical Classical Stalemate=win No-castling (10)	Pawn-back 11.70 Torpedo 11.89 Pawn-sideways
Subsets No-castling Pawn one square	Classical Classical Classical	24.23 2.50 7.17

Table 5. Differences in the opening tree of the new chess variants and Classical chess. These are expressed as Kullback-Leibler (KL) divergences, the direction depending on whether a particular variant is a superset or a subset of Classical chess, based on the rule change. In all cases but Stalemate $=$ win the reverse KL divergences are infinite as when there are legal opening lines s in variant $p$ that don’t exist in $q$ , and hence for which $q(\mathbf{s})=0$ when $p(\mathbf{s})$ is not (contributing $\mathrm{-log0}$ to the divergence).

表 5: 新棋类变体与古典象棋开局树差异。这些差异以Kullback-Leibler (KL)散度表示，其方向取决于特定变体基于规则变化是古典象棋的超集还是子集。除"将死=胜利"变体外，所有情况下反向KL散度均为无穷大——当变体p中存在合法开局线路s而变体q中不存在时(即q(s)=0而p(s)≠0时)，会导致散度出现-ln0项。

of the two priors as the normalized supremum

以归一化上确界作为两个先验的

There is a particular reason behind our choice of definition for the combined prior in (11): The number of candidate moves that the combination of players $\mathbf{P}$ and Q would consider, is always smaller than the sum of candidate moves that P and Q would consider individually.

我们选择在(11)中定义组合先验有一个特殊原因：玩家$\mathbf{P}$和Q组合会考虑的候选移动数量，总是小于P和Q单独考虑的候选移动数量之和。

Put more formally, define the number of candidate moves for the combined player as the number of uniformly weighed moves that could be encoded in the same number of nats as $r(s_{t+1}|s_{t})$ ,4

更正式地说，将组合玩家的候选移动次数定义为可以用与$r(s_{t+1}|s_{t})$相同的纳特数编码的均匀加权移动次数。

$$
m_{r}(s_{t})=\exp\left(-\sum_{s_{t+1}}r(s_{t+1}|s_{t})\log r(s_{t+1}|s_{t})\right).
$$

For any choice of priors $p$ and $q$ the number of candidate moves that are considered by the combined player in state $s_{t}$ is lower bounded by

对于任意先验概率 $p$ 和 $q$，组合玩家在状态 $s_{t}$ 中考虑的候选移动数量下界为

$$
m_{r}(s_{t})\leq m_{p}(s_{t})+m_{q}(s_{t}),
$$

which we prove in Appendix A.1.

我们将在附录 A.1 中证明。

We now define the difference

我们现在定义差异

$$
\mathrm{additional}(s_{t})=m_{r}(s_{t})-m_{q}(s_{t})
$$

to represent the number of additional candidate moves that player Q should consider, to play at the level of $\mathbf{P}$ in position $s_{t}$ . The additional number of candidates additional $\left(s_{t}\right)$ is zero when the priors match, $q=p$ , and intuitively Q doesn’t need to consider any further candidate moves. The number of additional moves may be negative; intuitively, Q puts enough weight on all candidates that $\mathbf{P}$ deems important, and doesn’t need to consider any further candidate moves. The number of additional candidate moves and is upper bounded by additional $(s_{t})\leq m_{p}(s_{t})$ according to (13); at the very worst, $\mathsf Q$ would additionally have to consider all of P’s candidates.

代表玩家Q在局面$s_{t}$中为达到$\mathbf{P}$水平所需考虑的额外候选着法数量。当先验概率匹配时$(q=p)$，额外候选数additional$\left(s_{t}\right)$为零，直观上Q无需考虑更多候选着法。该数值可能为负，表示Q已充分覆盖$\mathbf{P}$认为重要的候选着法。根据(13)式，额外候选数存在上限additional$(s_{t})\leq m_{p}(s_{t})$，最坏情况下$\mathsf Q$需额外考虑P的所有候选着法。

We consider positions up to ply $t$ plies sampled from prior for $\mathrm{P},$ , and at ply $t$ evaluate how many additional candidate moves $\mathsf Q$ should consider on average:

我们考虑从先验分布中采样到第 $t$ 步的位置，对于 $\mathrm{P}$，并在第 $t$ 步评估平均需要考虑多少额外候选移动 $\mathsf Q$：

$$
\mathcal{A}_ {q}(t)=\mathbb{E}_ {\mathbf{s}_ {1:t}\sim p(\mathbf{s}_ {1:t})}\left[\mathrm{additional}(s_{t})\right].
$$

The expectation is estimated with a Monte Carlo average over $10^{4}$ samples from $p(\mathbf{s}_{1:t})$ .

期望值通过从 $p(\mathbf{s}_{1:t})$ 中抽取 $10^{4}$ 个样本的蒙特卡洛平均来估计。

Figure 7 shows the average additional number of candidate moves if Q is taken as the Classical chess prior, with P iterating over all other variants. From the outset, Pawn one square places $60%$ of its prior mass on 1. d3, 1. e3, 1. c3 and 1. h3, which together only account for $13%$ of Classical’s prior mass. As pawns are moved from the starting rank and pieces are developed, $\mathbf{}\mathcal{A}_ {q}(t)$ slowly decreases for Pawn one square. As the opening progresses, Stalemate $=$ win slowly drifts from zero, presumably because some board configurations that would lead to drawn endgames under Classical rules might have a different outcome. Torpedo puts $66%$ of its prior mass on one move, 1. d4, whereas the Classical prior is broader (its top move, 1. d4, occupies $38%$ of its prior mass). The truncated plot value for Torpedo is $\mathcal{A}_{q}(1)=-1.8$ , signifying that the first Classical candidate moves effectively already include those of Torpedo chess. There is a slow upward drift in the average number of additional candidates that a Classical player has to consider under Self-capture chess as a game progresses. We hypothesis e that it can, in part, be ascribed to the number of reasonable self-capturing options increasing toward the middle game.

图 7 展示了当 Q 采用古典国际象棋先验时，P 遍历所有其他变体的平均额外候选走法数量。开局阶段，"兵行一格"变体将 60% 的先验概率集中在 1. d3、1. e3、1. c3 和 1. h3 这四步棋上，而这四步在古典变体先验中仅占 13%。随着兵离开起始线且棋子逐步展开，$\mathbf{}\mathcal{A}_ {q}(t)$ 在"兵行一格"变体中缓慢下降。随着开局推进，"将死=胜"变体从零开始缓慢漂移，这可能是因为某些在古典规则下会导致和棋的残局配置在该变体中会产生不同结果。"鱼雷"变体将 66% 的先验概率集中在单步棋 1. d4 上，而古典先验分布更广（其最优着法 1. d4 占先验概率的 38%）。"鱼雷"变体的截断图示值为 $\mathcal{A}_{q}(1)=-1.8$，表明古典变体的首批候选着法已有效涵盖该变体的着法。在"自我吃子"变体中，随着对局进行，古典棋手需考虑的额外候选着法平均数呈现缓慢上升趋势。我们推测这种现象可部分归因于合理的自我吃子选项数量在中局阶段逐渐增加。

3.8. Material

3.8. 材料

Material plays an important role in chess, and is often used to assess whether a particular sequence of piece exchanges and captures is favourable. Material sacrifices in chess are made either for concrete tactical reasons, e.g. mating attacks, or to be traded off for long-term positional strengthening of the position. Understanding the material value of pieces in chess helps players master the game and is one of the very first pieces of chess knowledge taught to beginners. Changes to the rules of chess affect piece mobility, and hence also the relative value of pieces. Without a basic estimate of what the relative piece values in each variant are, it would be harder for human players to start playing these chess variants. As a guide, we provide an experimental approximation to piece values based on outcomes of AlphaZero games under 1 second per move.

棋子在棋局中扮演着重要角色，常被用来评估特定换子与吃子序列是否有利。国际象棋中的弃子行为要么出于具体战术目的（例如杀王进攻），要么是为了换取局面的长期位置强化。理解棋子的子力价值有助于玩家掌握游戏，这也是初学者最早接触的国际象棋基础知识之一。国际象棋规则的变化会影响棋子机动性，进而改变棋子的相对价值。若缺乏对各变体中棋子相对价值的基本估算，人类玩家将更难上手这些国际象棋变体。作为参考，我们基于AlphaZero每步1秒内的对局结果，提供了棋子价值的实验性近似值。

We approximate piece values from the weights of a linear model that predicts the game outcome from the difference in numbers of each piece only. As background, the real AlphaZero evaluation $v$ in $(\mathbf{p},v)=f_{\theta}(s)$ is the output of a deep neural network with weights $\theta$ . The expected game outcome $v$ is the result of a final tanh activation to ensure an output in $(-1,1)$ . If $z\in{-1,0,1}$ indicates the playing side’s game outcome, AlphaZero’s loss function includes the mean squared error $(z-v)^{2}$ (Silver et al., 2018). We create a simplified evaluation function $g_{w}(s)$ that only takes piece counts on the board into consideration. For a position $s$ we construct a feature vector $\begin{array}{r}{d\stackrel{\mathrm{def}}{=}[1,d_{\hat{\Delta}},d_{\hat{\mathcal{Q}}},d_{\hat{\Xi}},d_{\hat{\Xi}},d_{\hat{\Xi}}]}\end{array}$ that contains the integer differences between the playing side and their opponent’s number of pawns, knights, bishops, rooks and queens. We define $g_{w}$ with weights $w\in\mathbb{R}^{6}$ as

我们通过线性模型的权重来近似棋子价值，该模型仅根据各类棋子数量的差异预测游戏结果。作为背景，真实AlphaZero评估值 $v$ 在 $(\mathbf{p},v)=f_{\theta}(s)$ 中是具有权重 $\theta$ 的深度神经网络输出。预期游戏结果 $v$ 经过最终tanh激活确保输出在 $(-1,1)$ 范围内。若 $z\in{-1,0,1}$ 表示当前行棋方的游戏结果，AlphaZero的损失函数包含均方误差 $(z-v)^{2}$ (Silver et al., 2018)。我们创建了一个简化的评估函数 $g_{w}(s)$ ，仅考虑棋盘上的棋子数量。对于某个局面 $s$ ，我们构建特征向量 $\begin{array}{r}{d\stackrel{\mathrm{def}}{=}[1,d_{\hat{\Delta}},d_{\hat{\mathcal{Q}}},d_{\hat{\Xi}},d_{\hat{\Xi}},d_{\hat{\Xi}}]}\end{array}$ ，其中包含行棋方与对手在兵、马、象、车和后数量上的整数差值。我们定义具有权重 $w\in\mathbb{R}^{6}$ 的 $g_{w}$ 为

$$
g_{w}(s)=\operatorname{tanh}(w^{T}d).
$$

When trained on the 10,000 AlphaZero self-play board positions from Section 3.1 for each variant, the piece weights $w$ provide an indication of their relative importance. Let $(s,z)\sim$ games represent a sample of a position and final game outcome from a variant’s self-play games. We minimise

当在3.1节所述的10,000个AlphaZero自对弈棋盘位置上训练每个变体时，棋子权重$w$能够反映它们的相对重要性。设$(s,z)\sim$ games表示某变体自对弈游戏中位置与最终结果的样本，我们最小化

$$
\ell(w)=\mathbb{E}_ {(s,z)\sim\mathrm{games}}\Big[\big(z-g_{w}(s)\big)^{2}\Big]
$$

empirically over $w$ , and normalise weights $w$ by $w_{\hat{\Delta}}$ to yield the relative piece values. The recovered piece values for each of the chess variants are given in Table 6.

通过 $w$ 进行经验性评估，并将权重 $w$ 用 $w_{\hat{\Delta}}$ 归一化，得到相对棋子价值。各象棋变体的恢复棋子价值见表 6。

Variant			鱼
Classical	1	3.05	3.33	5.63	9.5
No castling	1	2.97	3.13	5.02	9.49
No castling (10)	1	3.14	3.40	5.37	9.85
Pawn one square	1	2.95	3.14	5.36	9.62
Stalemate=win	1	2.95	3.13	4.76	8.96
Self-capture	1	3.10	3.22	5.34	9.42
Pawn-back	1	2.65	2.85	4.67	9.39
Semi-torpedo	1	2.72	2.95	4.69	8.3
Torpedo	1	2.25	2.46	3.58	7.12
Pawn-sideways	1	1.8	1.98	2.99	5.92

变体			鱼
古典棋	1	3.05	3.33	5.63	9.5
无王车易位	1	2.97	3.13	5.02	9.49
无王车易位 (10)	1	3.14	3.40	5.37	9.85
兵行一格	1	2.95	3.14	5.36	9.62
逼和即胜	1	2.95	3.13	4.76	8.96
自吃子	1	3.10	3.22	5.34	9.42
兵后退	1	2.65	2.85	4.67	9.39
半鱼雷兵	1	2.72	2.95	4.69	8.3
鱼雷兵	1	2.25	2.46	3.58	7.12
兵横走	1	1.8	1.98	2.99	5.92

Table 6. Estimated piece values from AlphaZero self-play games for each variant.

表 6: 各变体游戏中 AlphaZero 自我对弈的棋子估值

In Classical chess, piece values vary based on positional considerations and game stage. The piece values in Table 6 should not be taken as a gold standard, as the sample of AlphaZero games that they were estimated on does not fully capture the diversity of human play, and the game lengths do not correspond to that of human games, which tend to be shorter. For comparison, we have included the piece value estimates that we obtain by applying the same method to Classical chess, showing that the estimates do not deviate much from the known material values. Over the years, many material systems have been proposed in chess. The most commonly used one (Capablanca & de Firmian, 2006) gives 3–3–5–9 for values of knights, bishops, rooks and queens. Another system (Kaufman, 1999) gives 3.25–3.25– 5–9.75. Yet, bishops are typically considered to be more valuable than the knights, and there is usually an additive adjustment while in possession of a bishop pair. The rook value varies between 4.5 and 5.5 depending on the system and the queen values span from 8.5 to 10. The relative piece values estimated on the AlphaZero game sample for Classical chess, 3.05–3.33–5.63–9.5, do not deviate much from the existing systems. This suggests that the estimates for the new chess variants are likely to be approximately correct as well.

在国际象棋(Classical chess)中，棋子的价值会因位置考量和比赛阶段而变化。表6中的棋子估值不应视为黄金标准，因为其估算所基于的AlphaZero对局样本未能完全涵盖人类对局的多样性，且对局长度也与人类通常更短的对局不符。作为对比，我们展示了通过相同方法对国际象棋进行估值的结果，表明这些估值与传统子力价值并无显著偏差。

多年来，国际象棋领域提出了多种子力价值体系。最常用的体系(Capablanca & de Firmian, 2006)给出马、象、车、后的估值分别为3-3-5-9。另一体系(Kaufman, 1999)则给出3.25-3.25-5-9.75。通常认为象的价值高于马，且拥有双象时会进行额外加分。车的估值根据体系不同在4.5至5.5之间浮动，后的估值则在8.5到10之间。基于AlphaZero对局样本估算的国际象棋相对子力价值(3.05-3.33-5.63-9.5)与现有体系差异不大，这表明对新棋变体的估值可能也基本准确。

We can see similar piece values estimated for No-castling, No-castling(10), Pawn-one-square chess, Self-capture and Stalemate $\asymp$ win. This is not surprising, given that these variants do not involve a major change in piece mobility. Estimated piece values look quite different in the remaining variations, where pawn mobility has been increased: Pawn-back, Semi-torpedo, Torpedo and Pawn-sideways. In Pawn-sideways chess, minor pieces seem to be worth approximately two pawns, which is in line with our anecdotal observations when analysing AlphaZero games, as such exchanges are frequently made. Like Torpedo chess, pawns become much stronger and more valuable than before. Changes in Pawn-back and Semi-torpedo are not as pronounced.

我们可以看到在无王车易位、无王车易位(10)、兵走一格、自吃子和逼和$\asymp$胜利等变体中，棋子的估值相近。这并不令人意外，因为这些变体并未显著改变棋子的机动性。在其余提升兵机动性的变体中（退兵棋、半鱼雷兵、鱼雷兵和横走兵），棋子估值呈现出明显差异。横走兵变体里，轻子价值约等于两个兵，这与我们分析AlphaZero对局时的观察相符——此类兑换频繁发生。与鱼雷兵变体类似，兵的价值和强度都大幅提升。退兵棋和半鱼雷兵变体的数值变化则相对平缓。

4. Qualitative assessment

4. 定性评估

To evaluate the differences in play between the set of chess variations considered in this study, we couple the quantitative assessment of the variations with expert analysis based on a large set of representative games. While the overall decisiveness and opening diversity add to the appeal of any chess variation, the subjective questions of aesthetic value and the types of positions, moves and patterns that arise are not possible to fully capture quantitatively. For providing a deep qualitative assessment of the appeal of these chess variations, we rely on the experience of chess grandmaster Vladimir Kramnik, an ex-world chess champion and an authority on the game. By character ising typical patterns, we hope to provide players with insights to help them judge for themselves if they would find some of these chess variants interesting enough to try out in practice. What we provide here are preliminary findings.

为评估本研究所考察各类国际象棋变体的玩法差异，我们将定量分析与基于大量代表性棋局的专家评估相结合。虽然整体决胜率和开局多样性都能提升棋类变体的吸引力，但关于美学价值以及棋局形态、行棋方式与典型模式的主观评判难以完全量化。为深入定性评估这些象棋变体的魅力，我们依托前世界冠军、国际象棋权威弗拉基米尔·克拉姆尼克的专业经验。通过解析典型模式特征，旨在帮助棋手自主判断哪些变体值得实践尝试。本文呈现的仅为初步研究成果。

The detailed qualitative assessment of the chess variants presented in this article, along with typical motifs and illustrative games, is provided in the Appendix (Section B). For this analysis, we use the 1,000 1-minute per move games of Section 3.1 as well as 200 1-minute per move games from a diverse set of early opening positions that all of the major opening systems. By looking at the former, we were able to assess AlphaZero’s preferred style of play in each chess variant, and by looking at the latter, we could assess how the treatment of different opening lines changes and which of those become more or less promising under each of the rule changes. Figure 1 shows an illustrative example position for each of the considered chess variants.

本文对棋类变体的详细定性评估，连同典型棋局模式和示例对局，均收录在附录(B节)中。为此分析，我们使用了3.1节中的1,000盘每步1分钟的对局，以及200盘来自各类开局体系的早期开局位置、每步1分钟的对局。通过研究前者，我们得以评估AlphaZero在每种棋类变体中的偏好棋风；通过研究后者，我们可以评估不同开局路线的处理方式如何变化，以及哪些路线在规则变更后更具或更不具前景。图1展示了每种考量棋类变体的示例局面。

What follows is a short summary of the main takeaways from the qualitative analysis for each of the variants, provided by GM Vladimir Kramnik.

以下是GM弗拉基米尔·克拉姆尼克对每个变体的定性分析要点总结。

No-castling chess is a potentially exciting variant, given that king safety is often compromised for both players, allowing for simultaneous attacking and counter-attacking and the equality, when reached, tends to be dynamic in nature rather than “dry”. The multitude of approaches to evacuate the king, and their timing, adds complexity to the opening play. No-castling (10), where castling is not permitted for the first 10 moves (20 plies) is a partial restriction, rather than an absolute one – which does not change the game to the same extent. Due to castling being such a powerful option, the lines preferred by AlphaZero all tend to involve castling, only delayed – resulting in a preference for slower, closed positions, and a less attractive style of play. Such partial castling restrictions can be considered if the desire is to sidestep opening theory and preparation, but this may not be of interest for the wider chess audience.

无王车易位(no-castling)国际象棋是一种极具潜力的变体规则——由于双方王的安全都难以保障，对攻与反击往往同时上演，形成的均势局面也更具动态性而非"枯燥"。撤离王位的多种方式及其时机选择，为开局阶段增添了复杂性。部分限制型的"十步无易位(no-castling (10))"(前10回合/20步棋禁止王车易位)相比绝对禁令，对棋局的影响相对有限。鉴于王车易位是极具威慑力的选择，AlphaZero偏好的行棋路线虽会延迟但终将实施易位，这导致其更倾向选择节奏缓慢的封闭局面，降低了棋局观赏性。若旨在规避开局理论研究和准备，此类部分限制规则或可考虑，但可能难以吸引广大棋迷。

Pawn one square chess variant may appeal to players who enjoy slower, strategic play – as well as a training tool for understanding pawn structures, due to the transposition al possibilities when setting up the pawns. The reduced pawn mobility makes it harder to launch fast attacks, making the game overall less decisive.

单兵一格变体棋可能吸引那些喜欢缓慢、战略性对弈的玩家——同时由于布兵时的移调可能性，它也能作为理解兵形结构的训练工具。受限的兵移动力使得快速进攻更难展开，从而整体降低了棋局的决定性。

Stalemate=win chess has little effect on the opening and middlegame play, mostly affecting the evaluation of certain endgames. As such, it does not increase decisiveness of the game by much, as it seems to almost always be possible to defend without relying on stalemate as a drawing resource. Therefore, this chess variant is not likely to be useful for sidestepping known theory or for making the game substantially more decisive at the high level. The overall effect of the change seems to be minor.

和棋即胜规则对开局和中局影响甚微，主要改变特定残局的评估标准。由于棋手几乎总能不依赖和棋规则而守和，该变体对提升棋局决定性作用有限。因此，这种国际象棋变体既难以规避已知理论体系，也无法显著提升高水平对局的决断性。总体而言，规则调整带来的影响较为有限。

Torpedo and Semi-torpedo chess both make the game more dynamic and more decisive, and Torpedo chess in particular leads to new motifs and changes in all stages of the game. Creating passed pawns becomes very important, as they are hard to stop. The attacking possibilities make Torpedo chess quite appealing, and it is likely to be of interest for players that enjoy tactical play.

鱼雷棋和半鱼雷棋都使游戏更具动态性和决定性，特别是鱼雷棋在游戏的各个阶段带来了新的主题和变化。制造通路兵变得非常重要，因为它们难以阻挡。攻击的可能性使鱼雷棋极具吸引力，很可能会吸引喜欢战术玩法的玩家。

Pawn-back chess makes it possible to regain control of the weakened squares in the position and remove some square weaknesses. It also introduces additional possibilities for opening up diagonals and making squares available for the pieces. Counter-intuitively, even though moving the pieces backwards is usually a defensive manoeuvre, this can make more aggressive options possible, given that pawns can now be pushed further earlier on, as there is always an option of moving them back to cover the weakened squares. AlphaZero has a strong preference for playing the French defence with Black, which is particularly interesting.

回兵棋(pawn-back chess)使得棋手能够重新掌控局面中被削弱的格子，并消除部分格子弱点。这种走法还能创造更多可能性：打开斜线通道，为棋子提供可用格子。反直觉的是，尽管退子通常是防御性策略，但由于兵可以更早推进（随时能回退防守薄弱格），这种走法反而能创造更具侵略性的选择。特别值得注意的是，AlphaZero执黑时对法兰西防御(French defence)表现出强烈偏好。

Pawn-sideways chess is incredibly complex, resulting in patterns that are at times quite “alien” when one is used to classical chess. The pawn structures become very fluid and it is impossible to create permanent pawn weaknesses. Given how important this concept is in classical chess, this chess variant requires us to rethink how we approach any given position, making it very concrete and relying on deep calculation. Restructuring the pawn formation takes time, and players need to use that time for creating other types of advantages. Many of AlphaZero games in this variant have been quite tactical, some involving novel tactics that are not possible under classical rules.

兵侧象棋（Pawn-sideways chess）的规则极其复杂，会产生对传统象棋玩家而言颇为"陌生"的局面。兵形结构变得高度流动，无法制造永久性的兵形弱点。鉴于这一概念在传统象棋中的重要性，该变体要求我们彻底重构对局面的评估方式，必须依赖精确计算来应对具体局面。重组兵形结构需要时间，棋手必须利用这段时间创造其他类型的优势。AlphaZero在该变体中的对局多呈现战术性特征，部分战术组合在传统规则下根本无法实现。

Self-capture chess is quite entertaining, as it introduces additional options for sacrificing material – and material sacrifices have a certain aesthetic appeal. Self-capture moves can feature in all stages of the game. Not every game involves self-captures, as giving away material is not always required, but they do feature in a substantial percentage of the games, and in some games they occur multiple times. Self-capture moves can be used to open files and squares for the pieces in the attack; opening up a blockade by sacrificing a pawn in the pawn chain; or in defence, while escaping the mating net.

自吃棋颇具娱乐性，它为弃子引入了更多选择——而弃子本身具有独特的美学吸引力。自吃着法可能出现在棋局的任何阶段。并非每局棋都会出现自吃，因为弃子并非总是必要，但它们在相当比例的棋局中都会出现，有些棋局甚至会出现多次。自吃着法可用于：为进攻子力打开线路和格位；通过牺牲兵链中的兵来突破封锁；或在防守时摆脱杀网。

5. Conclusions

5. 结论

We have demonstrated how AlphaZero can be used for prototyping board games and assessing the consequences of rule changes in the game design process, as demonstrated on chess, where we have trained AlphaZero models to evaluate 9 different chess variants, representing atomic changes to the rules of classical chess. Training an AlphaZero model under these rule changes helped us effectively simulate decades of human play in a matter of hours, and answer the “what if” question: what the play would potentially look like under developed theory in each chess variant. We believe that a similar approach could be used for auto-balancing game mechanics in other types of games, including computer games, in cases when a sufficiently performant reinforcement learning system is available.

我们展示了如何利用AlphaZero进行棋盘游戏原型设计，并在游戏设计过程中评估规则变更的影响。以国际象棋为例，我们训练了多个AlphaZero模型来评估9种不同变体规则，这些变体代表着对经典国际象棋规则的原子级修改。通过在这些修改后的规则下训练AlphaZero模型，我们能在数小时内有效模拟人类数十年的对弈过程，从而回答"假设性"问题：在每种变体规则下，经过理论发展后的对弈可能会呈现何种形态。我们认为，在具备足够高性能的强化学习系统时，类似方法也可用于自动平衡其他类型游戏（包括电子游戏）的机制设计。

To assess the consequences of the rule changes, we coupled the quantitative analysis of the trained model and self-play games with a deep qualitative analysis where we identified many new patterns and ideas that are not possible under the rules of classical chess. We showed that there several chess variants among those considered in this study that are even more decisive than classical chess: Torpedo chess, Semi-torpedo chess, No-castling chess and Stalemate $\asymp$ win chess.

为评估规则变更的影响，我们结合训练模型的定量分析、自我对弈游戏以及深入的定性研究，识别出许多古典象棋规则下无法实现的新模式与策略。研究表明，本论文探讨的若干象棋变体比古典象棋更具决定性：鱼雷象棋 (Torpedo chess) 、半鱼雷象棋 (Semi-torpedo chess) 、无王车易位象棋 (No-castling chess) 以及逼和即胜象棋 (Stalemate $\asymp$ win chess) 。

We additionally quantified the arising diversity of opening play and the intersection of opening trees between chess variations, showing how different the opening theory is for each of the rule changes. There is a negative correlation between the overall opening diversity and decisiveness, as the decisive variants likely require more precise play, with fewer plausible choices per move. For each of the chess variants, we estimated the material value of each of the pieces based on the results of 10,000 AlphaZero games, to provide insight into favourable exchange sequences and make it easier for human players to understand the game.

此外，我们还量化了开局玩法的多样性以及不同象棋变体间开局树的重叠情况，揭示了每种规则改动对开局理论的差异化影响。整体开局多样性与棋局决定性呈负相关，因为更具决定性的变体通常需要更精确的行棋策略，每一步的可选走法更少。针对每种象棋变体，我们基于10,000局AlphaZero对弈结果估算了每个棋子的子力价值，既为优势兑换序列提供参考依据，也帮助人类玩家更易理解游戏机制。

No-castling chess, being the first variant that we analysed (chronologically), has already been tried in an experimental blitz grandmaster tournament in Chennai, as well as a couple of longer grandmaster games. Our assessment suggests that several of the assessed chess variants might be quite appealing to interested players, and we hope that this study will prove to be a valuable resource for the wider chess community.

无王车易位象棋作为我们按时间顺序分析的首个变体，已在金奈举办的超快棋特级大师表演赛及多场慢棋特级大师对局中进行了试验。我们的评估表明，若干被研究的象棋变体可能对感兴趣的棋手颇具吸引力，希望这项研究能为更广泛的国际象棋社群提供有价值的参考。

Acknowledgements

致谢

We would like to thank chess grandmasters Peter Heine Nielsen, and Matthew Sadler for their valuable feedback on our preliminary findings and the early version of the manuscript. Oliver Smith and Kareem Ayoub have been of great help in managing the project. We would also like to thank the team of Chess.com for providing us with a platform to announce and discuss No-castling chess and present annotated games.

我们要感谢国际象棋特级大师Peter Heine Nielsen和Matthew Sadler对我们初步研究结果和手稿早期版本提出的宝贵意见。Oliver Smith和Kareem Ayoub在项目管理方面给予了极大帮助。同时感谢Chess.com团队为我们提供了宣布和讨论无王车易位象棋(No-castling chess)以及展示注释棋局的平台。

References

参考文献

Andrade, G., Ramalho, G., Santana, H., and Corruble, V. Automatic computer game balancing: A reinforcement learning approach. In Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems, pp. 1111–1112, 2005. Beasly, J. What can we expect from a new chess variant? Variant Chess, 4(29):2, 1998. Capablanca, J. and de Firmian, N. Chess Fundamentals: Completely Revised and Updated for the 21st Century. Chess Series. Random House Puzzles & Games, 2006.

Andrade, G., Ramalho, G., Santana, H., and Corruble, V. 自动电脑游戏平衡：一种强化学习方法。第四届自主智能体与多智能体系统国际联合会议论文集，第1111–1112页，2005年。
Beasly, J. 我们能从新国际象棋变体中期待什么？变体国际象棋，4(29):2，1998年。
Capablanca, J. 和 de Firmian, N. 国际象棋基础：21世纪完全修订与更新版。国际象棋系列。 Random House Puzzles & Games出版社，2006年。

\no-castling-chess-kramnik-alphazero (accessed 2 December 2019), 2019.

无王车易位国际象棋-Kramnik与AlphaZero对决（访问于2019年12月2日），2019年。

Lc0. Leela Chess Zero. https://lczero.org/ (accessed November 20, 2019), 2018.

Lc0. Leela Chess Zero. https://lczero.org/ (访问于2019年11月20日), 2018.

A. Quantitative Appendix

A. 量化附录

A.1. Proof of equation (13)

A.1. 方程 (13) 的证明

Let $\mathbf{p}$ and $\mathbf{q}$ be two vectors with non-negative entries that sum to one. Define $\mathbf{r}$ as a vector with elements

设 $\mathbf{p}$ 和 $\mathbf{q}$ 为两个元素非负且总和为一的向量。定义 $\mathbf{r}$ 为一个元素满足以下条件的向量：

$$
r_{i}=\frac{\operatorname*{max}(p_{i},q_{i})}{\sum_{i^{\prime}}\operatorname*{max}(p_{i^{\prime}},q_{i^{\prime}})}~.
$$

We show below that

我们将在下文中证明

$$
\begin{array}{r}{\mathrm{e}^{-\sum_{i}r_{i}\log r_{i}}\le\mathrm{e}^{-\sum_{i}p_{i}\log p_{i}}+\mathrm{e}^{-\sum_{i}q_{i}\log q_{i}}.}\end{array}
$$

Let $\begin{array}{r}{R=\sum_{i}\operatorname*{max}(p_{i},q_{i})}\end{array}$ be the normalizing constant in (18). It is bounded by $1\leq R\leq2$ . We write the entropy as

设 $R=\sum_{i}\operatorname*{max}(p_{i},q_{i})$ 为式 (18) 中的归一化常数，其取值范围为 $1\leq R\leq2$。我们将熵表示为

$$
\begin{array}{r l}&{\displaystyle-\sum_{i}r_{i}\log r_{i}}\ &{\quad=-\displaystyle\frac{1}{R}\sum_{i}\operatorname*{max}(p_{i},q_{i})\log\operatorname*{max}(p_{i},q_{i})+\log R}\ &{\displaystyle=-\frac{1}{R}\sum_{i}\operatorname*{max}(p_{i}\log p_{i},q_{i}\log q_{i})+\log R}\ &{\displaystyle\leq-\sum_{i}\operatorname*{max}(p_{i}\log p_{i},q_{i}\log q_{i})+\log R}\ &{\displaystyle\leq-\frac{1}{2}\sum_{i}p_{i}\log p_{i}-\frac{1}{2}\sum_{i}q_{i}\log q_{i}+\log R}\end{array}
$$

where the last inequality in (20) follows from $\operatorname*{max}(a,b)\geq$ $\textstyle{\frac{a+b}{2}}$ . Exponent i a ting (20) and applying Jensen’s inequality yields

(20) 式中最后一个不等式源于 $\operatorname*{max}(a,b)\geq$ $\textstyle{\frac{a+b}{2}}$。对(20) 式取指数并应用 Jensen 不等式可得

$$
\begin{array}{r l}&{\mathrm{e}^{-\sum_{i}r_{i}\log r_{i}}}\ &{\quad\leq R\mathrm{e}^{\frac{1}{2}(-\sum_{i}-p_{i}\log p_{i})+\frac{1}{2}(-\sum_{i}q_{i}\log q_{i})}}\ &{\quad\leq R\left(\frac{1}{2}\mathrm{e}^{-\sum_{i}p_{i}\log p_{i}}+\frac{1}{2}\mathrm{e}^{-\sum_{i}q_{i}\log q_{i}}\right)}\ &{\quad\leq\mathrm{e}^{-\sum_{i}p_{i}\log p_{i}}+\mathrm{e}^{-\sum_{i}q_{i}\log q_{i}}.}\end{array}
$$

The final line follows from $R/2\leq1$ as $1\leq R\leq2$ . The bound is tight at $R=1$ when $\mathbf{p}$ and $\mathbf{q}$ both put probability mass uniformly on two non-intersecting same-sized subsets of elements.5

当 $1\leq R\leq2$ 时，由 $R/2\leq1$ 可得最后一行。当 $\mathbf{p}$ 和 $\mathbf{q}$ 在不相交的相同大小元素子集上均匀分布概率质量时，该界限在 $R=1$ 处达到紧致。

A.2. Additional figures

A.2. 其他图表

(a) The game length distributions of the total number of plies for all self-play games for each variant.

图 1:
(a) 各变体所有自对弈游戏总步数的对局长度分布。

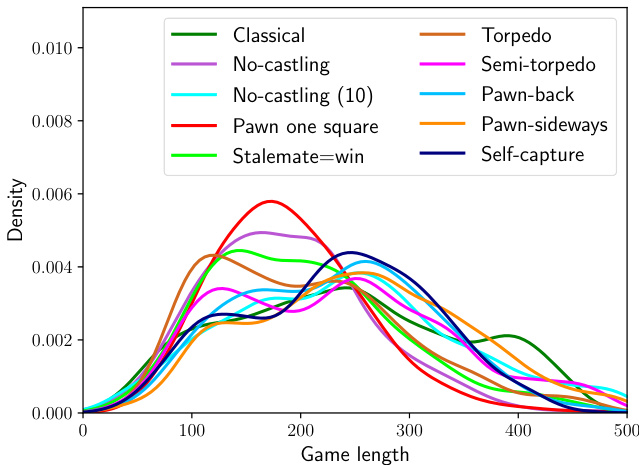
(b) The game length distributions of the total number of plies for the subset of decisive (not drawn) self-games for each variant. Figure 8. The game length distributions of the total number of plies of AlphaZero games in each chess variant, based on a sample of 10,000 games played at 1 second per move. The experimental setup is described in Section 3.1.

(b) 各变体决定性(非和棋)自对弈总步数的对局长度分布。

图 8: 基于每步1秒条件下10,000盘对局样本，各国际象棋变体中AlphaZero对局总步数的长度分布。实验设置详见3.1节。

Figure 9. The density of (negative) log likelihoods for the prior opening lines for Classical chess and each of the variants. The mean of each histogram gives the entropy or average information content for each variant’s prior $p(\mathbf{s})$ , as given in (8). The subfigures are ordered by entropy, following Table 3. Figure $9\mathrm{g}$ continues on the next page.

图 9: 古典象棋及各变体的先手开局行(negative)对数似然密度分布。每个直方图的均值对应(8)式中各变体先验概率$p(\mathbf{s})$的熵或平均信息量。子图按熵值排序(参照表3)。图$9\mathrm{g}$在下一页继续展示。

Figure 9. (Continued from previous page.) The density of (negative) log likelihoods for the prior opening lines for Classical chess and each of the variants. The mean of each histogram gives the entropy or average information content for each variant’s prior $p(\mathbf{s})$ , as given in (8). The subfigures are ordered by entropy, following Table 3.

图 9. (接上页) 古典象棋及各变体的先手开局行棋(负)对数似然密度分布。每个直方图的均值对应(8)式中各变体先验分布 $p(\mathbf{s})$ 的熵或平均信息量。子图按熵值排序，顺序与表 3 一致。

(a) A decomposition of the entropy of subset variants of Classical chess relative to Classical chess.

(a) 古典象棋子集变体相对于古典象棋的熵分解

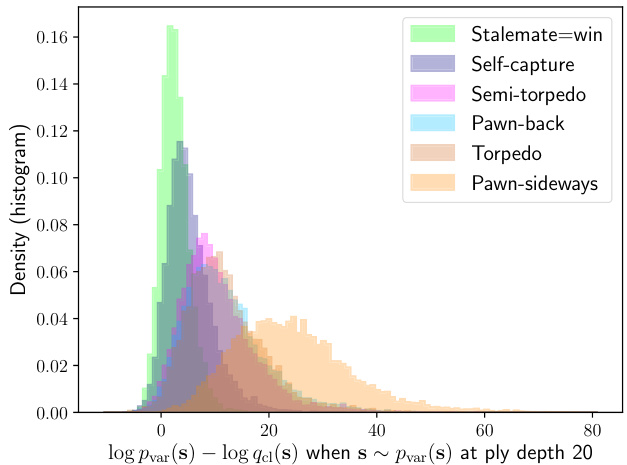
(b) A decomposition of the entropy of Classical chess relative to its superset variants.

图 1:
(b) 古典象棋相对于其超集变体的熵分解。

Figure 10. Histograms of the density of terms $\log p(\mathbf{s})-\log q(\mathbf{s})$ whose mean under $p(\mathbf{s})$ is the Kullback-Leibler divergence in (10).

图 10: 术语密度 $\log p(\mathbf{s})-\log q(\mathbf{s})$ 的直方图，其在 $p(\mathbf{s})$ 下的均值即为式 (10) 中的 Kullback-Leibler 散度。

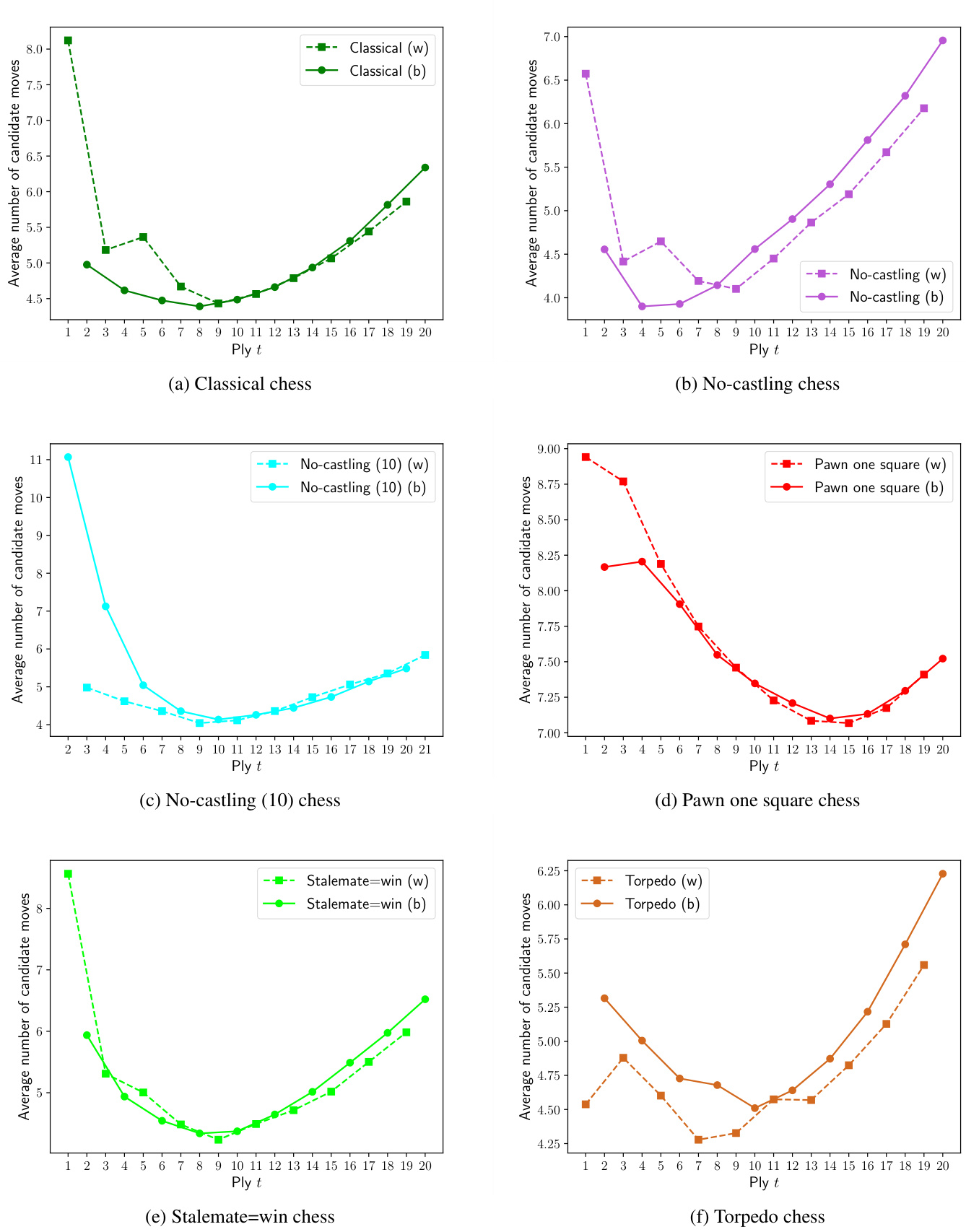
Figure 11. The average number of candidate moves $\mathcal{M}(t)$ from (9) for each of the variants, as computed from their prior distributions $p(\mathbf{s})$ . Figure $11\mathrm{g}$ continues on the next page.

图 11: 各变体根据其先验分布 $p(\mathbf{s})$ 计算得出的候选移动平均数量 $\mathcal{M}(t)$ (来自公式(9))。图 11g 续于次页。

(k) Uniform random moves under classical chess rules Figure 11. (Continued from previous page.) The average number of candidate moves $\mathcal{M}(t)$ from (9) for each of the variants, as computed from their prior distributions $p(\mathbf{s})$ .

图 11: (接上页) 各变体在经典国际象棋规则下均匀随机走法的候选移动平均数量 $\mathcal{M}(t)$ (来自公式9)，根据其先验分布 $p(\mathbf{s})$ 计算得出。

B. Appendix

B. 附录

Here we present a selection of instructive games for each of the chess variations considered in the study, along with a detailed assessment of the variations by Vladimir Kramnik.

在此，我们精选了研究中涉及的每种国际象棋变体的教学对局，并附上弗拉基米尔·克拉姆尼克对这些变体的详细评注。

Given that different rule changes that we examined had led to a different degree of departure from existing chess theory and patterns, we do not present an equal amount of instructive positions and games for each chess variation, and rather focus on those that have either been assessed to be of greater immediate interest or simply employ patterns that are unfamiliar and novel and require more time to introduce and understand.

鉴于我们所考察的不同规则变化导致对现有国际象棋理论和模式的偏离程度各异，我们并未为每种变体提供等量的教学棋局和对局示例，而是重点关注那些被评估为更具即时研究价值、或运用了陌生新颖且需要更多时间介绍理解的棋局模式。

The Appendix is organised into sections corresponding to each of the chess variations and rule alterations examined in this study, in the following order: No-castling chess (Page 25), No-castling (10) chess (Page 31), Pawn one square chess (Page 34), Stalemate $\mathrel{\mathop:}=$ win chess (Page 37), Torpedo (Section 40), Semi-torpedo (Page 54), Pawn-back chess (Page 61), Pawn-sideways chess (Page 70) and Self-capture chess (Page 85).

附录按本研究所考察的各类国际象棋变体及规则修改项分节编排，顺序如下：无王车易位象棋(第25页)、十步无王车易位象棋(第31页)、兵行一格象棋(第34页)、逼和判胜象棋(第37页)、鱼雷象棋(第40页)、半鱼雷象棋(第54页)、回兵象棋(第61页)、横兵象棋(第70页)以及自吃子象棋(第85页)。

Each of the variants-specific sections first introduces the rule change, sets out the motivation for why it seemed of interest to be tried out, gives a qualitative assessment and a high-level conceptual overview of the dynamics of arising play by Vladimir Kramnik and then concludes with several instructive games and positions, selected to illustrate the typical motifs that arise in AlphaZero play in these variations.

每个变体专属章节首先介绍规则变更，阐述尝试该变体的动机，由Vladimir Kramnik对产生的对局动态进行定性评估和高层次概念概述，最后精选若干具有教学意义的对局和局面，用以说明AlphaZero在这些变体中出现的典型模式。

B.1. No-castling

B.1. 无王车易位

In No-castling chess, the adjustment to the original rules involved a full removal of castling as an option.

在无王车易位(No-castling)象棋中，规则调整完全移除了王车易位这一选项。

B.1.1. MOTIVATION

B.1.1. 动机

The motivation for the No-castling chess variant, as provided by Vladimir Kramnik:

弗拉基米尔·克拉姆尼克提出"无王车易位"象棋变体的初衷:

Adjustments to castling rules were chronologically the first type of changes implemented and assessed in this study. Firstly, excluding a single existing rule makes it comparatively easy for human players to adjust, as there is no need to learn an additional rule. Secondly, the right to castle is relatively new in the long history of the game of chess. Arguably, it stands out amongst the rules of chess, by providing the only legal opportunity for a player to move two of their own pieces at the same time.

本研究首先按时间顺序对王车易位规则进行了调整和评估。一方面，仅移除现有规则便于人类棋手适应，无需学习额外规则。其次，王车易位作为国际象棋悠久历史中较新的规则，其特殊性在于：这是棋局中唯一允许玩家同时移动两枚棋子的合法机会。

B.1.2. ASSESSMENT

B.1.2. 评估

The assessment of the no-castling chess variant, as provided by Vladimir Kramnik:

弗拉基米尔·克拉姆尼克对无王车易位国际象棋变体的评估：

I was expecting that abandoning the castling rule would make the game somewhat more favorable for White, increasing the existing opening advantage. Statistics of AlphaZero games confirmed this intuition, though the observed difference was not substantial to the point of un balancing the game. Nevertheless, when considering human practice, and considering that players would find themselves in unknown territory at the very early stage of the game, I would expect White to have a higher expected score in practice than under regular circumstances.

我原本预计，放弃王车易位规则会让棋局对白方更有利，从而扩大现有的开局优势。AlphaZero对局数据证实了这一直觉，但观察到的差异并未达到破坏游戏平衡的程度。不过考虑到人类实战情况，以及棋手们将在开局阶段就踏入未知领域，我预计白方在实际对局中的预期得分会高于常规规则下的表现。

One of the main advantages of no-castling chess is that it eliminates the nowadays overwhelming importance of the opening preparation in professional chess, for years to come, and makes players think creatively from the very beginning of each game. This would inevitably lead to a considerably higher amount of decisive games in chess tournaments until the new theory develops, and more creativity would be required in order to win. These factors could also increase the following of professional chess tournaments among chess enthusiasts.

无王车易位象棋的主要优势之一在于，它消除了多年来职业象棋中开局准备压倒性的重要性，迫使棋手从每局比赛伊始就进行创造性思考。在新理论形成前，这将使象棋赛事中出现更多决定性对局，同时需要更强的创造力才能获胜。这些因素还可能提升象棋爱好者对职业赛事的关注度。

With late middlegame and endgame patterns staying the same as in regular chess, there is a major difference in the opening phase of a no-castling chess game. The main conceptual rules of piece development and king safety are still valid, but most concrete opening variations of regular chess no longer apply, as castling is usually an essential part of existing chess opening variations.

随着中残局模式与常规国际象棋保持一致，无王车易位棋局的开局阶段存在显著差异。棋子展开和国王安全的核心概念规则依然适用，但由于王车易位通常是现有国际象棋开局变例的重要组成部分，常规棋局中的大多数具体开局变例在此均不再适用。

For example, possibly opening a game with 1. f4, which is not a great idea in classical chess, might be one of the better options already, since it might make it easier to evacuate the king after Nf3, g3, Bg2, Kf2, Rf1, Kg1. Some completely new patterns of playing the openings start to make sense, like pushing the side pawns in order to develop the rooks via the “h” file or “a” file, as well as “artificial castling” by means of Ke2, Re1, Kf1 and others. Many new conceptual questions arise in this chess variation.

例如，在古典国际象棋中并不算好棋的1. f4开局，在这种变体中可能已成为较优选择之一，因为能通过Nf3、g3、Bg2、Kf2、Rf1、Kg1等走法更易实现王的安全转移。一些全新的开局模式开始显现价值，比如推进边线兵以通过h线或a线出动车，以及通过Ke2、Re1、Kf1等走法实现"人工王车易位"。这种国际象棋变体衍生出许多新的战略命题。

For instance, one has to think about what ought to be preferable: evacuating the king out of the center of the board as soon as possible or aiming to first develop all the pieces and claim space and central squares. Years of practice are likely required to give a clear answer on the guiding principles of early play and best opening strategies. Even with the help of chess engines, it would likely take decades to develop the opening theory to the same level and to the same depth as we have in regular chess today. The engines can be helpful with providing initial recommendations of plausible opening lines of play, but the right understanding and timing of the implementation of new patterns is crucial in practical play.

例如，必须考虑哪种策略更可取：尽快将国王撤离棋盘中心，还是优先发展所有棋子并占据空间和中心格。要明确早期对局的指导原则和最佳开局策略，可能需要多年的实践。即便借助国际象棋引擎，要将开局理论发展到与传统国际象棋当前水平相当的深度，也可能需要数十年时间。引擎虽能提供可行的开局走法建议，但在实战中，正确理解新模式的运用时机至关重要。

Studying the numerous no-castling games played by AlphaZero, I have noticed one major conceptual change. Since both kings have a harder time finding a safe place, the dynamic positional factors (e.g. initiative, piece activity, attack), seem to have more importance than in regular chess. In other words, a game becomes sharper, with both sides attacking the opponent king at the same time.

在研究AlphaZero进行的众多无王车易位对局时，我注意到一个重大概念变化。由于双方国王更难找到安全位置，动态位置因素（如主动权、子力活跃度、进攻）似乎比常规国际象棋更为重要。换句话说，对局会变得更加尖锐，双方会同时攻击对方的国王。

I am convinced that because of the aforementioned reasons we would see many interesting games, and many more decisive games at the top level chess tournaments in case the organisers decide to give it a try. Due to the simplicity of the adjustment compared to regular chess, it is also easy to implement this variation at any other level, including the online chess playing platforms, as it merely requires an agreement between the t wo players not to play castling in their game.

我确信，基于上述原因，如果赛事组织者愿意尝试，我们将在顶级国际象棋赛事中看到更多精彩且更具决定性的对局。由于这一调整相比常规国际象棋规则更为简单，它也能轻松应用于其他级别的比赛，包括在线对弈平台——只需两位棋手在赛前达成共识，约定本局不使用王车易位规则即可。

B.1.3. MAIN LINES

B.1.3. 主要线路

Here we discuss “main lines” of AlphaZero under Nocastling chess, when playing with roughly one minute per move from a particular fixed first move. Note that these are not purely deterministic, and each of the given lines is merely one of several highly promising and likely options. Here we give the first 20 moves in each of the main lines, regardless of the position.

此处我们探讨AlphaZero在无王车易位(Nocastling)象棋中的"主要变例"，即从特定固定首步起每步约一分钟的走法。需注意这些并非完全确定性路线，每条给定变例仅是若干极具潜力且可能选项之一。以下列出各主要变例的前20步棋着，与具体局面无关。

Main line after d4 The main line of AlphaZero after $\textit{1.}$ d4 in No-castling chess is:

d4后的主要变例
在无王车易位国际象棋中，AlphaZero在$\textit{1.}$ d4后的主要变例为：

Main line after e4 The main line of AlphaZero after $\textit{1.}$ e4 in No-castling chess is:

e4后的主要走法
在无王车易位象棋中，AlphaZero在$\textit{1.}$ e4后的主要走法是：

Main line after c4 The main line of AlphaZero after $\textit{1.}$ c4 in No-castling chess is:

c4后的主变 AlphaZero在无王车易位象棋中$\textit{1.}$ c4后的主变为：

B.1.4. INSTRUCTIVE GAMES

图 1:
B.1.4. 教学游戏

16. . . Ke7 $17.$ Nxc8+ Rxc8 18. a5 Qa7 $I{\boldsymbol{9}}.$ Qb3 Bxf2 20. Bh3 Rb8

图 1:
16... Ke7 $17.$ Nxc8+ Rxc8 18. a5 Qa7 $I{\boldsymbol{9}}.$ Qb3 Bxf2 20. Bh3 Rb8

Game AZ-1: AlphaZero No-castling vs AlphaZero Nocastling The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

对局AZ-1: AlphaZero无王车易位 vs AlphaZero无王车易位
白方与黑方的前十步棋着法均从AlphaZero开局"棋谱库"中随机抽样产生,抽样概率与计算每步棋所耗时间成正比。后续着法遵循最优策略,每步耗时约一分钟。

. . Qg6 $3l.$ . Rg2 Qxf5 32. Rxf5 Ke6 33. Rc5 Kd6 34. Rf5 Ke6 35. $\mathrm{Re5+}$ Kf6 $36.$ h5 Rc8 37. Rg4 Rc1+ 38. $\mathrm{Kg}2\mathrm{Nc}6$
... Qg6 $3l.$ ... Rg2 Qxf5 32. Rxf5 Ke6 33. Rc5 Kd6 34. Rf5 Ke6 35. $\mathrm{Re5+}$ Kf6 $36.$ h5 Rc8 37. Rg4 Rc1+ 38. $\mathrm{Kg}2\mathrm{Nc}6$

Game AZ-2: AlphaZero No-castling vs AlphaZero Nocastling The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-2: AlphaZero 无王车易位对 AlphaZero 无王车易位
白方和黑方的前十步棋着法均从 AlphaZero 的开局"棋谱"中随机抽取，抽样概率与计算每步棋所耗时间成正比。后续着法采用最佳行棋策略，每步棋计算时间约为一分钟。

14. Rc2 Bh6 15. Ng5 Ncb4 16. Rc1 Ke7 17. Rh3 Rhd8 18. a3 Nxc3 19. Bxc3 Rxc3

Game AZ-3: AlphaZero No-castling vs AlphaZero Nocastling The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-3: AlphaZero 无王车易位对战 AlphaZero 无王车易位
白方和黑方的前十步棋着法均从 AlphaZero 的开局"棋谱库"中随机采样，采样概率与计算每步棋所耗时间成正比。后续着法采用最优策略，每步棋计算时长约为一分钟。

The game soon ended in a draw.

游戏很快以平局告终。

1/2–1/2

B.1.5. HUMAN GAMES

B.1.5. 人类游戏

Here we take a brief look at a couple of recently played blitz games between professional chess players from the tournament that took place in Chennai in January 2020 (Shah, 2020). We focus on new motifs in the opening stage of the game, and show how these might be counter-intuitive compared to similar patterns in classical chess.

这里我们简要回顾2020年1月金奈锦标赛中职业棋手间的几场快棋对局(Shah, 2020)。我们重点关注开局阶段出现的新模式，并展示这些模式相较于传统象棋类似局面可能存在的反直觉特性。

Game H-1: Arjun, Kalyan (2477) vs D. Gukesh (2522) (blitz) $\textit{1.}$ d4 d5 2. c4 c6 3. Nc3 Nf6 4. Nf3

图 1: Arjun, Kalyan (2477) 对 D. Gukesh (2522) (快棋) $\textit{1.}$ d4 d5 2. c4 c6 3. Nc3 Nf6 4. Nf3

Interestingly, even at an early stage we can see an example of a difference in patterns that originate in Classical chess and those that arise in No-castling chess. The positioning of the knight on f3 is very natural, but is in fact an imprecision. AlphaZero prefers keeping the option open of playing the pawn to f3 instead, in order to tuck the king away to safety. It gives the following line as its favored continuation: 4. e3 Bf5 $5.$ . Bd3 g6 $\boldsymbol{\delta}.$ h3 e6 7. $\mathrm{Ng}\mathrm{e}2{\mathrm{Be}}7$ 8. f3 Bxd3 9. Qxd3 Kf8 10. Kf2 Bg7 11. Rd1.

有趣的是，即便在开局阶段，我们也能观察到古典象棋与无王车易位象棋在模式上的差异。马走到f3看似自然，实则不够精确。AlphaZero更倾向于保留f3兵推进的选项，以便将王转移到安全位置。它给出的推荐续着如下：4. e3 Bf5 $5.$ . Bd3 g6 $\boldsymbol{\delta}.$ h3 e6 7. $\mathrm{Ng}\mathrm{e}2{\mathrm{Be}}7$ 8. f3 Bxd3 9. Qxd3 Kf8 10. Kf2 Bg7 11. Rd1.

Yet, 4. Nf3 was played in the game, which continued:

然而，对局中实际走的是 4. Nf3，后续着法如下：

. . e6 5. e3 Nbd7 6. Qc2 Bd6 7. b3 b6
. . e6 5. e3 Nbd7 6. Qc2 Bd6 7. b3 b6

Here AlphaZero suggests that it was instead time to move the king to safety. Deciding on when exactly to initiate the evacuation of the king from the centre and choosing the best way of achieving it is one of the key motifs of No-castling chess. This decision is less clear than the decision to castle in Classical chess, due to a larger number of options and the fact that the sequence takes more moves that all need to be staged accordingly. Instead of moving the pawn to b6, AlphaZero suggests the following instead: 7. . . h5 8. Bb2 Kf8 9. Rd1 $\mathrm{Kg}8$ .

AlphaZero 在此建议应将王转移到安全位置。决定何时从中心撤离王以及选择最佳撤离方式，是无王车易位象棋的关键主题之一。由于可选方案更多且整个撤离过程需要多步协调，这一决策比传统象棋中的王车易位更为复杂。AlphaZero 没有选择将兵移到 b6，而是建议如下走法: 7...h5 8.Bb2 Kf8 9.Rd1 $\mathrm{Kg}8$。

Going back to the game continuation, after $7...$ b6 White has the upper hand. The game continued: 8. Bb2 Bb7 $9.$ Bd3 Qe7 10. e4

回到对局后续，在 $7...$ b6 之后，白方占据优势。接下来的走法是：8. Bb2 Bb7 $9.$ Bd3 Qe7 10. e4

This is another example of mistiming the evacuation of the king. Instead of playing 10. e4, it was the right time to move the king to safety instead, retaining a large plus for White after: 10. Kf1 Kf8 $I l.$ h4 h5 12. a4 Ng4 13. Rh3 Rh6

这是另一个错失王车撤离时机的例子。此时不应走10. e4，而应抓住时机将王转移到安全位置，白方在以下变化中仍能保持巨大优势：10. Kf1 Kf8 $I l.$ h4 h5 12. a4 Ng4 13. Rh3 Rh6

Going back to the position after $I{\boldsymbol{O}}.$ . e4, the game continuation goes as follows:

回到 $I{\boldsymbol{O}}$ 后的局面。e4，对局后续如下：

. . dxe4 11. Nxe4 (Giving away the advantage. Recapturing with the bishop was correct, even though it might seem as otherwise counter-intuitive.) $1l...$ Nxe4 12. Bxe4 f5. (This is looking bad for Black; 12. . . Nf6 is the preferred move.) 13. Bd3 c5 (At this point, AlphaZero assesses the position as winning for White.) 14. Kf1 (The advantage could have been kept with ${\mathit{I4}}.$ d5.) 14. . . Bxf3 $I5.$ gxf3 cxd4 (15. . . Rf8 may have been equalizing) 16. Bxd4 (Gives the advantage to Black. White ought to have captured on f5 instead. The right way to respond to the game move would have been 16. . . Qh4.) 16. . . Be5 $17.$ Bxe5 Nxe5 18. Bxf5
. . dxe4 11. Nxe4 (放弃优势。用象吃回才是正确选择，尽管这看似违反直觉。) $1l...$ Nxe4 12. Bxe4 f5. (黑方形势不妙；12. . . Nf6才是首选着法。) 13. Bd3 c5 (此时AlphaZero评估白方胜势。) 14. Kf1 (若走 ${\mathit{I4}}.$ d5可保持优势。) 14. . . Bxf3 $I5.$ gxf3 cxd4 (15. . . Rf8或能扳平局面) 16. Bxd4 (将优势拱手让给黑方。白方应改吃f5兵。应对此着法的正确方式应是16. . . Qh4。) 16. . . Be5 $17.$ Bxe5 Nxe5 18. Bxf5

A brilliant piece sacrifice.

一记精彩的弃子。

. . exf5 19. Re1 Kd8 20. Qxf5 (20. $\mathrm{Qd}2+$ may have been stronger) 20. . . Re8 21. f4 Qb7 22. Rg1 Ng6 (The final mistake, it appears that 22. Nf7 might hold) 23. $\mathrm{Rd}1+\mathrm{Ke}7$ $\mathit{\Omega}_{\mathcal{A}.}\mathrm{Rg}3\mathrm{Qh}1+25\$ . Ke2 $\mathrm{Qe4+}$ 26. R $33{\mathrm{~Qxe3}}+27.$ fxe3 Rad8 28. Rxd8 Rxd8 29. $\mathrm{Qe4+}$ Kf8 30. Qb7 1–0
... exf5 19. Re1 Kd8 20. Qxf5 (20. $\mathrm{Qd}2+$ 可能更强) 20. ... Re8 21. f4 Qb7 22. Rg1 Ng6 (最后的失误，似乎22. Nf7可能守住) 23. $\mathrm{Rd}1+\mathrm{Ke}7$ $\mathit{\Omega}_{\mathcal{A}.}\mathrm{Rg}3\mathrm{Qh}1+25\$ . Ke2 $\mathrm{Qe4+}$ 26. R $33{\mathrm{~Qxe3}}+27.$ fxe3 Rad8 28. Rxd8 Rxd8 29. $\mathrm{Qe4+}$ Kf8 30. Qb7 1–0

Game H-2: Gelfand, Boris vs Kramnik, Vladimir (blitz) $\textit{1.}$ f4 h5 Already Kramnik demonstrates a motif that is quite strong in no-castling chess, pushing one of the side pawns early.

游戏 H-2: Gelfand, Boris 对 Kramnik, Vladimir (快棋) $\textit{1.}$ f4 h5 开局阶段，Kramnik就展示了无王车易位棋局中一个相当有力的主题——早早推进边路兵。

Nf3 e6 3. e3 Nf6 $4.$ b3 (Interestingly, AlphaZero doesn’t like this very normal-looking move, giving Black a slight plus after 4. . . c5 $5.$ Bb2 Be7 $\delta.$ . Be2 d5 7. Rf1 Kf8 8. Kf2 Nc6 9. Kg1 Kg8 10. a4 Bd7.) 4. . . b6 5. Bb2 Bb7 $\smash{6.}$ . Bd3 (5. Be2 might have been better.) 6. . . h4 (Not the most precise, according to AlphaZero, suggesting that 6. . . c5 7. Rf1 Be7 8. Kf2 h4 9. Ng5 Kf8 10. Kg1 Rh6 $I I$ . $\mathrm{Be}2\mathrm{Nc}6$ was still slightly better for Black.) 7. h3 (This turns out to be the wrong reaction, giving the advantage back to Black again.) 7. . . Nh5 8. Kf2 Be7 (Here, there was an opportunity to play 8. . . Bc5 instead:
Nf3 e6 3. e3 Nf6 $4.$ b3 (有趣的是，AlphaZero并不看好这个看似正常的着法，认为在4... c5 $5.$ Bb2 Be7 $\delta.$ Be2 d5 7. Rf1 Kf8 8. Kf2 Nc6 9. Kg1 Kg8 10. a4 Bd7之后黑方稍占优势) 4... b6 5. Bb2 Bb7 $\smash{6.}$ Bd3 (5. Be2或许是更好的选择) 6... h4 (AlphaZero指出这不是最精确的着法，建议6... c5 7. Rf1 Be7 8. Kf2 h4 9. Ng5 Kf8 10. Kg1 Rh6 $I I$. $\mathrm{Be}2\mathrm{Nc}6$ 仍使黑方保持微小优势) 7. h3 (事实证明这是错误的应对，将优势再次让给黑方) 7... Nh5 8. Kf2 Be7 (此时黑方有机会改走8... Bc5：

23. Rf1 (Black gains the upper hand.) 23. . . Re6 24. Nh2 (A mistake, 24. e5 was required.) 24. . . Rae8 25. Rxf4 Nf6 26. e5 dxe5 27. Rf3 (Another mistake, 27. Rxe5 was correct.) 27. . . Qg6 28. d5 (Taking on e5 was still a better continuation.) 28. . . R6e7 29. c4 e4 30. Rc3 Nh5 31. Nf1 Kg8 32. Qe1 Nf4 33. Rd2 e3 34. Rxe3 Rxe3 35. Nxe3 Qe4 0–1

23. Rf1 (黑方占据上风。) 23. . . Re6 24. Nh2 (失误，应走24. e5。) 24. . . Rae8 25. Rxf4 Nf6 26. e5 dxe5 27. Rf3 (再次失误，正确着法是27. Rxe5。) 27. . . Qg6 28. d5 (此时吃e5仍是更优续着。) 28. . . R6e7 29. c4 e4 30. Rc3 Nh5 31. Nf1 Kg8 32. Qe1 Nf4 33. Rd2 e3 34. Rxe3 Rxe3 35. Nxe3 Qe4 0–1

which would have kept a big plus for Black.)

(这原本会是黑方的一大优势。)

B.2. No-castling (10)

B.2. 无王车易位 (10)

In the No-castling (10) variant of chess, castling is only allowed from move 11 onwards, both for the first and the second player.

在国际象棋的无王车易位(10)变体中，双方玩家都只能在第11步之后进行王车易位。

B.2.1. MOTIVATION

B.2.1. 动机

When it comes to limit the impact of castling on the game, it is possible to consider different types of partial limitations, the easiest of which is disallowing it for a fixed number of opening moves. In this variation, we have explored the impact of disallowing castling for the first 10 moves, but any other number could have been used instead. Each choice leads to a slightly different body of opening theory, as particular lines either become viable or stop being viable under different circumstances.

在限制王车易位对棋局影响方面，可以考虑不同类型的局部限制，其中最简单的方式是固定开局步数内禁止使用。本变体中，我们探究了前10步禁止王车易位的影响（但采用其他步数限制亦可）。每种选择都会导致略微不同的开局理论体系，因为特定棋路在不同条件下可能成立或失效。

B.2.2. ASSESSMENT

B.2.2 评估

The assessment of the No-castling (10) chess variant, as provided by Vladimir Kramnik:

弗拉基米尔·克拉姆尼克对"无王车易位(10)"国际象棋变体的评估：

The main purpose of the partial restriction to castling, as a hypothetical adjustment to the rules of chess, would be to sidestep opening theory. As such, it is aimed at professional chess as an option to potentially consider. The game itself does not change in other meaningful ways, and AlphaZero usually aims at playing slower lines where castling does indeed take place after the first 10 moves. This makes sense, given that castling is a fast an powerful move, so aiming to take advantage of it if available makes for a good approach. Yet, the slowing down of the game could as a side-effect lead to an increased number of draws. Another disadvantage is the need to count and keep track of the move number when considering variations.

对王车易位进行部分限制的主要目的，是作为国际象棋规则的假设性调整以规避开局理论。因此，这一调整主要面向职业棋手作为潜在可选项。游戏本身在其他方面并无实质性改变，且AlphaZero通常倾向于采用较慢的行棋节奏——事实上王车易位往往在前10步之后才会发生。这符合逻辑，因为王车易位是快速且强力的着法，若能利用自然是最佳策略。但行棋节奏放缓可能带来和棋率上升的副作用。另一个弊端在于计算变招时需要持续记录着数。

B.2.3. MAIN LINES

B.2.3. 主要线路

Here we discuss “main lines” of AlphaZero under Nocastling (10) chess, when playing with roughly one minute per move from a particular fixed first move. Note that these are not purely deterministic, and each of the given lines is merely one of several highly promising and likely options. Here we give the first 20 moves in each of the main lines, regardless of the position.

此处我们探讨AlphaZero在无王车易位(Nocastling) (10) 国际象棋规则下，从特定固定首步起每步约一分钟思考时间的主要行棋路线。需注意这些路线并非完全确定性，每条给定路线仅是多个极具潜力且可能选项之一。无论棋局形势如何，我们均提供各主要路线的前20步着法。

Main line after d4 The main line of AlphaZero after $\textit{1.}$ d4 in No-castling (10) chess is:

d4后的主要变例
在无王车易位(10)象棋中，AlphaZero在$\textit{1.}$ d4后的主要变例为：

Main line after e4 The main line of AlphaZero after $\textit{1.}$ e4 in No-castling (10) chess is:

e4后的主变 AlphaZero在无王车易位(10)象棋中1.e4后的主变是:

Main line after c4 The main line of AlphaZero after $\textit{1.}$ c4 in No-castling (10) chess is:

c4后的主变
在无王车易位(10)象棋中，AlphaZero在$\textit{1.}$ c4后的主变为：

B.2.4. INSTRUCTIVE GAMES

B.2.4. 教学游戏

Game AZ-4: AlphaZero No-castling (10) vs AlphaZero No-castling (10) The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏AZ-4：AlphaZero无王车易位(10) vs AlphaZero无王车易位(10)
白方与黑方的前十步棋着法均从AlphaZero的开局"棋谱库"中随机抽取，抽样概率与计算每步棋所耗时间成正比。后续着法采用最优策略，每步耗时约一分钟。

c4 e5 2. d4 exd4 3. ${{\mathrm{Qxd4~Nc6}}}$ 4. $\mathrm{Qe}3+\mathrm{Nge}7$ 5. Nf3 d5 6. cxd5 Qxd5 7. Nc3 Qa5 8. Qg5 Bf5 9. Bd2 f6 10. $\mathrm{Qh5+}$ g6 11. Qh4 Nb4 12. Rc1 O-O-O 13. Qxf6 Bh6
c4 e5 2. d4 exd4 3. ${{\mathrm{Qxd4~Nc6}}}$ 4. $\mathrm{Qe}3+\mathrm{Nge}7$ 5. Nf3 d5 6. cxd5 Qxd5 7. Nc3 Qa5 8. Qg5 Bf5 9. Bd2 f6 10. $\mathrm{Qh5+}$ g6 11. Qh4 Nb4 12. Rc1 O-O-O 13. Qxf6 Bh6

A stunning move, offering up a piece on h6. Accepting would be disastrous for White, as Black pieces mobilise quickly via Ned5. The h8 rook can also potentially come to e8, and this justifies the material investment.

一步惊人的棋，在h6献出一子。白方若接受将陷入灾难，因为黑方子力可通过Ned5迅速调动。h8车也可能走到e8，这证明了物质投入的合理性。

e3 Rhe8 15. Qh4 Bg7 16. Nb5 Rxd2
e3 Rhe8 15. Qh4 Bg7 16. Nb5 Rxd2

The fireworks continue. . .

烟火继续绽放...

Rxc7+ Qxc7 18. Nxc7 Rxb2 19. Nxe8 Rb1+
Rxc7+ Qxc7 18. Nxc7 Rxb2 19. Nxe8 Rb1+

Leading to a draw by perpetual check.

通过长将导致和棋。

1/2–1/2

The next game is less tactically rich, but rather interesting from the perspective of showcasing differences in opening play and the overall approach, when castling is not possible in the first ten moves.

下一款游戏在战术上不那么丰富，但从展示开局走法和整体策略差异的角度来看却相当有趣，尤其是在前十步无法进行王车易位的情况下。

Game AZ-5: AlphaZero No-castling (10) vs AlphaZero No-castling (10) The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-5: AlphaZero 无王车易位 (10) 对战 AlphaZero 无王车易位 (10)
白方和黑方的前十步棋着均从AlphaZero的开局"棋谱"中随机采样，采样概率与计算每步棋着所耗时间成正比。后续棋着按最佳走法进行，每步耗时约一分钟。

c4 e5 2. Nc3 Nf6 3. Nf3 Nc6 4. Qa4
c4 e5 2. 马c3 马f6 3. 马f3 马c6 4. 后a4

This is a slightly unusual move, showcasing that the style of play in this variation of chess involves opting for moves that do not necessarily achieve as much immediately and are somewhat less direct, potentially trying to wait for the right time to castle, when possible. In this game, however, castling does not end up being critical.

这是一步略显不寻常的走法，表明这种变体象棋的玩法风格倾向于选择那些不一定会立即获得很大优势、且略显迂回的着法，可能是为了等待合适的时机进行王车易位（如果可行的话）。不过在本局对弈中，王车易位最终并未成为关键因素。

. . e4 5. Ng5 Qe7 6. c5 e3
... e4 5. Ng5 Qe7 6. c5 e3

And the game eventually ended in a draw.

比赛最终以平局告终。

1/2–1/2

B.3. Pawn one square

B.3. 前进一格

B.3.1. MOTIVATION

B.3.1. 动机

Restricting the pawn movement to one square only is interesting to consider, as the double-move from the second (or seventh rank) seems like a “special case” and an exception from the rule that pawns otherwise only move by one square. In addition, slowing down the game could make it more strategic and less forcing.

限制兵(pawn)每次只能移动一格的做法值得探讨，因为第二行(或第七行)的兵允许一次移动两格更像是"特例"，违背了兵通常每次只能移动一格的基本规则。此外，减缓游戏节奏可能增强策略性，降低强制性走法的比重。

B.3.2. ASSESSMENT

B.3.2. 评估

The assessment of the Pawn one square chess variant, as provided by Vladimir Kramnik:

弗拉基米尔·克拉姆尼克对兵进一步变体 (Pawn one square) 的国际象棋变体评估:

CC The basic rules and patterns are still mostly the same as in classical chess, but the opening theory changes and becomes completely different. Intuitively it feels that it ought to be more difficult for White to gain a lasting opening advantage and convert it into a win, but since new opening theory would first need to be developed, this would not pertain to human play at first. In most AlphaZero games one can notice the rather typical middlegame positions arise after the opening phase.

CC的基本规则和模式仍与古典象棋大体相同，但开局理论发生了变化且截然不同。直观上感觉白方更难获得持久的开局优势并将其转化为胜利，但由于需要先发展新的开局理论，这一现象最初不会出现在人类对局中。在大多数AlphaZero对局中，可以观察到开局阶段后出现的相当典型的中局局面。

This variation of chess can be a good pedagogical tool when teaching and practicing slow, strategic play and learning about how to set up and commit to pawn structures. Since the pawns are unable to advance very fast, many attacking ideas that involve rapid pawn advances are no longer relevant, and the play is instead much slower and ultimately more positional. Additionally, this variation of chess could simply be of interest for those wishing for an easy way of side-stepping opening theory.

这种国际象棋变体可以作为一种优秀的教学工具，用于训练和练习缓慢的战略性对弈，并帮助理解如何构建和坚守兵型结构。由于兵的行进速度大幅受限，许多依赖快速推进兵型的进攻策略不再适用，对局节奏因此变得更为缓慢，最终更侧重于局面把控。此外，该变体也能满足那些希望轻松避开开局理论研究的棋手需求。

B.3.3. MAIN LINES

B.3.3. 主要路线

Here we discuss “main lines” of AlphaZero under Pawn one square chess, when playing with roughly one minute per move from a particular fixed first move. Note that these are not purely deterministic, and each of the given lines is merely one of several highly promising and likely options. Here we give the first 20 moves in each of the main lines, regardless of the position.

此处我们探讨在国际象棋兵进一格变体中AlphaZero的"主要行棋路线"，即在每步约一分钟的思考时间下从特定固定首着出发的走法。需注意这些路线并非完全确定性，每条给定路线仅是若干极具潜力且可能性较高的选择之一。无论棋局形势如何，我们在此列出每条主线的首20步着法。

Main line after e3 The main line of AlphaZero after $\textit{1.}$ e3 in Pawn one square chess is:

e3后的主变 AlphaZero在兵前进一步 $\textit{1.}$ e3后的主变路线为：

图 1:

An instructive position, as it looks optically like Black is blundering material. In this variation of chess, however, b2-b4 is not a legal move, because pawns can only move one square. This justifies the move sequence.

一个具有教学意义的位置，因为从视觉上看黑方似乎在失误丢子。然而在这种象棋变体中，b2-b4并非合法着法，因为兵只能前进一格。这解释了该着法序列的合理性。

Nd2 Nc6 15. b3 a6 16. Nf3 Ne6 17. h3 O-O 18. O-O Ncd4 19. Nfxd4 exd4 20. Bd2 c6
Nd2 Nc6 15. b3 a6 16. Nf3 Ne6 17. h3 O-O 18. O-O Ncd4 19. Nfxd4 exd4 20. Bd2 c6

Main line after d3 The main line of AlphaZero after $\textit{1.}$ d3 in Pawn one square chess is:

d3之后的主线 AlphaZero在兵单格象棋中$\textit{1.}$ d3之后的主线是:

Main line after c3 The main line of AlphaZero after $\textit{1.}$ c3 in Pawn one square chess is:

c3后的主变 AlphaZero在兵前进一格国际象棋中$\textit{1.}$ c3后的主变是：

B.3.4. INSTRUCTIVE GAMES

图 1:
B.3.4. 教学游戏

Here we present some examples of AlphaZero play in Pawn one square chess.

这里我们展示一些AlphaZero在兵行一格国际象棋中的对局示例。

Game AZ-6: AlphaZero Pawn One Square vs AlphaZero Pawn One Square The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-6: AlphaZero 单兵一格对 AlphaZero 单兵一格
白方与黑方的前十步棋着法均从 AlphaZero 的开局"棋谱库"中随机抽取，抽样概率与计算每步棋所用时间成正比。后续着法采用最优策略，每步棋计算时长约一分钟。

Here we have a rather normal middlegame position. The game continued:

这里有一个相当正常的中局局面。对局继续：

43. . . Bg4 44. Bg2 Bxf3 45. Bxf3 Qh3 46. dxc4 Qxf3 47. Qd3 Qg4+ 48. Kf2 $\mathrm{Qh4+}$ 49. Ke2 $\mathrm{Qh}2+$ 50. Kf1 ${\mathrm{Qh1+}}$ 51. Kf2 Qh4+ 52. Ke2 $\mathrm{Qh}2+$ 53. Ke1 Bf8 54. Qf3 Bc5 55. Kf1 ${\mathrm{Qg1+}}$ 56. Ke2 $\mathrm{Qh}2+$ 57. Kf1 ${\mathrm{Qg1+}}$ $58.$ . Ke2 $\mathrm{Qh}2+$ 59. Kf1 1/2–1/2

43... Bg4 44. Bg2 Bxf3 45. Bxf3 Qh3 46. dxc4 Qxf3 47. Qd3 Qg4+ 48. Kf2 $\mathrm{Qh4+}$ 49. Ke2 $\mathrm{Qh}2+$ 50. Kf1 ${\mathrm{Qh1+}}$ 51. Kf2 Qh4+ 52. Ke2 $\mathrm{Qh}2+$ 53. Ke1 Bf8 54. Qf3 Bc5 55. Kf1 ${\mathrm{Qg1+}}$ 56. Ke2 $\mathrm{Qh}2+$ 57. Kf1 ${\mathrm{Qg1+}}$ 58. Ke2 $\mathrm{Qh}2+$ 59. Kf1 1/2–1/2

Game AZ-7: AlphaZero Pawn One Square vs AlphaZero Pawn One Square The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-7: AlphaZero 单兵一格对 AlphaZero 单兵一格
白方和黑方的前十步棋着法均从 AlphaZero 开局"棋谱库"中随机抽样得出，抽样概率与计算每步棋所耗时间成正比。后续着法均采用最优下法，每步棋计算时长约一分钟。

This is a very normal-looking position, and one would be hard-pressed to guess that it originated from a different variation of chess, as it looks pretty “classical”.

这是一个看起来非常正常的局面，很难猜出它源自国际象棋的某种变体，因为看起来相当"经典"。

A very instructive position, reminiscent of a famous classical game between Petrosian and Reshevsky from Zurich in 1953, where Petrosian was playing Black. The positional exchange sacrifice allows White easy play on the dark squares.

一个极具启发性的局面，让人想起1953年苏黎世Petrosian与Reshevsky那场著名的经典对局，当时Petrosian执黑。这个局面性弃车让白方轻松掌控黑格。

. . Bxe3 38. fxe3 f6 39. Be2 Rc7 40. Rf1 Rf7 41. Qd2 Ne5 42. Qe1 Bb5 43. Nxb5 axb5 44. a4 Nd3 45. Qh4 bxa4 46. Bxh5 Re5 47. $\mathrm{Be}2+$ Kg7 48. Qg3 Qc7 49. Bxe5 Qxe5 50. Qxe5 fxe5 $5l.$ c6 Rxf1+ 52. Bxf1 a3 53. c7 a2 54. $\scriptstyle{\mathrm{c}}8=Q$ a1=Q 55. $\mathrm{Qb}7+$ Kh6 56. Qxd5 Qe1 57. Qf7 Qxb4 58. Qa2 Qc5 59. Qd2 Nb4 60. Kf2 Nd5 $6l.$ g3 Qf8+ 62. Kg1 Qc5 63. Kf2 Qf8+ 64. Ke1 Nb4 65. Bc4 Kh7 66. Qd7+ Kh6 67. Qd2 Kg7 68. Qf2 Qe7 69. Kf1 Nd3 70. Qe2 Qf6+ 71. Kg2 Qc6 72. Bb3 Qc5 73. h4 Qc1 74. Kh2 Ne1 75. Bd1
. . Bxe3 38. fxe3 f6 39. Be2 Rc7 40. Rf1 Rf7 41. Qd2 Ne5 42. Qe1 Bb5 43. Nxb5 axb5 44. a4 Nd3 45. Qh4 bxa4 46. Bxh5 Re5 47. $\mathrm{Be}2+$ Kg7 48. Qg3 Qc7 49. Bxe5 Qxe5 50. Qxe5 fxe5 $5l.$ c6 Rxf1+ 52. Bxf1 a3 53. c7 a2 54. $\scriptstyle{\mathrm{c}}8=Q$ a1=Q 55. $\mathrm{Qb}7+$ Kh6 56. Qxd5 Qe1 57. Qf7 Qxb4 58. Qa2 Qc5 59. Qd2 Nb4 60. Kf2 Nd5 $6l.$ g3 Qf8+ 62. Kg1 Qc5 63. Kf2 Qf8+ 64. Ke1 Nb4 65. Bc4 Kh7 66. Qd7+ Kh6 67. Qd2 Kg7 68. Qf2 Qe7 69. Kf1 Nd3 70. Qe2 Qf6+ 71. Kg2 Qc6 72. Bb3 Qc5 73. h4 Qc1 74. Kh2 Ne1 75. Bd1

B.4. Stalemate=win

B.4. 僵局即胜

In this variation of chess, achieving a stalemate position is considered a win for the attacking side, rather than a draw.

在这种国际象棋变体中，达成逼和局面被视为进攻方的胜利，而非和局。

B.4.1. MOTIVATION

B.4.1. 动机

The stalemate rule in classical chess allows for additional drawing resources for the defending side, and has been a subject of debate, especially when considering ways of making the game potentially more decisive. Yet, due to its potential effect on endgames, it was unclear whether such a rule would also discourage some attacking ideas that involve material sacrifices, if being down material in endgames ends up being more dangerous and less likely to lead to a draw than in classical chess.

古典国际象棋中的逼和规则为防守方提供了额外的和棋手段，这一规则一直存在争议，尤其是在探讨如何使比赛更具决定性时。然而，由于该规则对残局可能产生的影响，尚不明确的是：若在残局阶段处于子力劣势会比传统象棋更危险且更难达成和棋，此类规则是否会抑制涉及子力牺牲的进攻思路。

B.4.2. ASSESSMENT

B.4.2. 评估

The assessment of the Stalemate $=$ win chess variant, as provided by Vladimir Kramnik:

对僵局 $=$ 赢棋变体的评估，由Vladimir Kramnik提供：

CC I was at first somewhat surprised that the decisive game percentage in this variation was roughly equal to that of classical chess, with similar levels of performance for White and Black. I was personally expecting the change to lead to more decisive games and a higher winning percentage for White.

我最初有些惊讶的是，这一变体的决定性对局比例与古典象棋大致相当，且白方和黑方的表现水平相近。我个人原本预期这一改动会导致更多决定性对局，并提高白方的胜率。

It seems that the openings and the middlegame remain very similar to regular chess, with very few exceptions, but that there is a significant difference in endgame play since some basic endgame like $K{+}P$ vs $K$ are already winning instead of being drawn depending on the position.

开局和中局阶段似乎与常规国际象棋非常相似，只有极少数例外，但在残局阶段存在显著差异，因为一些基本残局如$K{+}P$对$K$原本可能根据局面形成和棋，现在却变为必胜局面。

In the position above, with White to move, in classical chess the position would be a draw due to stalemate after Ke6. Yet, the same move wins in this variation of chess, so the defending side needs to steer away from these types of endgames.

在上述局面中，轮到白方行棋时，传统国际象棋会因Ke6后形成逼和局面而判为和棋。然而，在这种变体规则下，同样的走法却能取胜，因此防守方需避免陷入此类残局。

Similarly, the stalemates that arise in $K{+}N{+}N$ vs K are now wins rather than draws, for example:

同样地，$K{+}N{+}N$ 对 K 的僵局现在变成了胜局而非和局，例如：

Looking at the games of AlphaZero, it seems that there are enough defensive resources in most middlegame positions that certain types of inferior endgame positions, now possible under this rule chance, could be avoided and defended. A strong player can in principle learn to navigate to these positions to take advantage of them, or find ways to escape them.

观察AlphaZero的对局可以发现，大多数中局局面都存在足够的防守资源，使得某些原本可能因这条规则而出现的劣势残局局面得以规避和防守。高水平棋手原则上能够学会引导局势进入这些有利局面加以利用，或是找到摆脱困境的方法。

B.4.3. MAIN LINES

B.4.3. 主要线路

Here we discuss “main lines” of AlphaZero under Stalemate $=$ win chess, when playing with roughly one minute per move from a particular fixed first move. Note that these are not purely deterministic, and each of the given lines is merely one of several highly promising and likely options. Here we give the first 20 moves in each of the main lines, regardless of the position.

在此我们讨论AlphaZero在"将死等于胜利"（Stalemate $=$ win）象棋规则下的主要走法路线，即从特定固定第一步开始、每步约一分钟思考时间的对局。需要注意的是这些路线并非完全确定性，每条给定路线仅是多个极具前景且可能性较高的选择之一。此处我们列出各主要路线的前20步走法，不考虑具体局面。

Main line after e4 The main line of AlphaZero after $\textit{1.}$ e4 in Stalemate=win chess is:

e4后的主变 AlphaZero在Stalemate=win象棋中1.e4后的主变是：

In terms of the anticipated effect on human play, I would still expect this rule change to lead to a higher percentage of wins in endgames where one side has a clear advantage, but probably not as much as one would otherwise have been expecting. This may be a nice variation of chess for chess enthusiasts with an interest in endgame patterns.

就预期对人类对局的影响而言，我仍认为这一规则变化会提高一方有明显优势的残局胜率，但增幅可能不及预期。对于痴迷残局模式的国际象棋爱好者而言，这或许是个有趣的变体。

Main line after d4 The main line of AlphaZero after $\textit{1.}$ d4 in Stalemate=win chess is:

d4后的主要变例
在Stalemate=win象棋中，AlphaZero在$\textit{1.}$ d4后的主要变例为：

图 1:

Main line after c4 The main line of AlphaZero after $\textit{1.}$ c4 in Stalemate $\Leftarrow$ win chess is:

c4后的主变 AlphaZero在Stalemate $\Leftarrow$ win chess中$\textit{1.}$ c4后的主变是：

B.4.4. INSTRUCTIVE GAMES

图 1:
B.4.4. 教学游戏

The games in Stalemate $\mathrel{\mathop:}=$ win chess are at the first glance almost indistinguishable from those of classical chess, as the lines are merely a subset of the lines otherwise playable and plausible under classical rules.

僵局(Stalemate) $\mathrel{\mathop:}=$ 赢棋游戏初看几乎与古典象棋无异，因为其棋路仅是古典规则下可走且合理的走法子集。

Game AZ-8: AlphaZero Stalemate=win vs AlphaZero Stalemate=win6 The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-8: AlphaZero 逼和=胜 vs AlphaZero 逼和=胜6
白方和黑方的前十步棋着法均从AlphaZero的开局"棋谱"中随机采样，采样概率与计算每步棋所花费的时间成正比。后续着法遵循最佳行棋策略，每步棋约耗时一分钟。

h3 Be7 15. Bc4 Ngf4 16. Bf1 g5 17. Ng3 Rg8 18. Bc3 Qc7 19. Nh2 Bg6 20. Ne4 O-O-O
h3 Be7 15. Bc4 Ngf4 16. Bf1 g5 17. Ng3 Rg8 18. Bc3 Qc7 19. Nh2 Bg6 20. Ne4 O-O-O

21. g3 Nxc3 22. bxc3 Nd5 23. Rc1 Qa5 24. Qb3 Qa3 25. Qc2 Kb8 26. Nf3 Bb4

White is clearly winning here, and $\mathrm{Ra}5+$ is good and tempting. AlphaZero is only optimised for achieving an end result. Even though a slower approach achieves the same outcome, a win is a win! This game ultimately finishes with checkmate.

白方在此局面明显占优，$\mathrm{Ra}5+$ 是既有力又诱人的着法。AlphaZero仅以实现最终结果为目标——即便缓慢推进也能达成相同结局，胜利就是胜利！本局最终以将死对手告终。

（注：根据规则要求，已处理以下细节：

保留数学公式 $\mathrm{Ra}5+$ 原样
专有名词 AlphaZero 不翻译
使用中文游戏术语"着法""将死"
破折号改为中文全角格式
保持简洁的棋局解说风格）
Rf5 Kb8 57. g4 Ka8 58. Rf2 b3 59. Qxb3 Qe7 60. $\mathbf{Ra}2+$ Kb8 61. ${\mathrm{Qg}}3+$ Rc7 62. Rf2 Ka7 63. $_{\mathrm{f}8=\mathrm{Q}}$ $\mathrm{Qh}7+$ 64. Qh3 Qb1 65. Qf5 Qa1 66. Qf1 ${\mathrm{Qh8+}}$ 67. Qh5 Qg7 68. Qh4 Rc5 69. Kh1 Ra5 70. Qg3 Ra4 71. Rf3 Ra2 72. ${\mathrm{Qff}}2+$ Rxf2 73. $\mathrm{Qxf2+}$ Ka6 74. Qg3 b5 75. Qf4 Qg8 76. ${\mathrm{Qf}}6+$ Ka5 77. Qf5 Ka4 78. Qf8 Qh7+ 79. Kg2 b4 80. Qe8+ Ka5 81. $\mathrm{Qh5+}$ Qxh5 82. gxh5 Ka4 83. Rf1 Ka3 84. Kf2 Kb2 85. Ke1 b3 86. Kd1 Kc3 87. Kc1 Kd4 88. h6 b2+ 89. Kxb2 Ke5 90. Re1+ Kf6 91. Rd1 Kg6 92. Rc1 Kxh6 93. Rc3 Kg5 94. Rc5+ Kh4 95. Rc7 Kg3 96. Rb7 Kh4 97. Ra7 Kh3 98. Kc3 Kg3 99. Ra1 Kh4 100. Ra3 Kh3 101. Kd4+ Kg4 102. Ra5 Kf4 103. Ra7 Kg5 104. Ra1 Kf5 105. Ra3 Kg4 106. Ke5 Kh5 107. Ra5 Kg5 108. Rd5 Kh6 109. Rd7 Kg5 110. Rc7 Kh6 111. Kf5 Kh5 112. Rh7# 1–0
Rf5 Kb8 57. g4 Ka8 58. Rf2 b3 59. Qxb3 Qe7 60. $\mathbf{Ra}2+$ Kb8 61. ${\mathrm{Qg}}3+$ Rc7 62. Rf2 Ka7 63. $_{\mathrm{f}8=\mathrm{Q}}$ $\mathrm{Qh}7+$ 64. Qh3 Qb1 65. Qf5 Qa1 66. Qf1 ${\mathrm{Qh8+}}$ 67. Qh5 Qg7 68. Qh4 Rc5 69. Kh1 Ra5 70. Qg3 Ra4 71. Rf3 Ra2 72. ${\mathrm{Qff}}2+$ Rxf2 73. $\mathrm{Qxf2+}$ Ka6 74. Qg3 b5 75. Qf4 Qg8 76. ${\mathrm{Qf}}6+$ Ka5 77. Qf5 Ka4 78. Qf8 Qh7+ 79. Kg2 b4 80. Qe8+ Ka5 81. $\mathrm{Qh5+}$ Qxh5 82. gxh5 Ka4 83. Rf1 Ka3 84. Kf2 Kb2 85. Ke1 b3 86. Kd1 Kc3 87. Kc1 Kd4 88. h6 b2+ 89. Kxb2 Ke5 90. Re1+ Kf6 91. Rd1 Kg6 92. Rc1 Kxh6 93. Rc3 Kg5 94. Rc5+ Kh4 95. Rc7 Kg3 96. Rb7 Kh4 97. Ra7 Kh3 98. Kc3 Kg3 99. Ra1 Kh4 100. Ra3 Kh3 101. Kd4+ Kg4 102. Ra5 Kf4 103. Ra7 Kg5 104. Ra1 Kf5 105. Ra3 Kg4 106. Ke5 Kh5 107. Ra5 Kg5 108. Rd5 Kh6 109. Rd7 Kg5 110. Rc7 Kh6 111. Kf5 Kh5 112. Rh7# 1–0

B.5. Torpedo

B.5. 鱼雷

In the variation of chess that we’ve named Torpedo chess, the pawns can move by either one or two squares forward from anywhere on the board rather than just from the initial squares, which is the case in Classical chess. We will refer to the pawn moves that involve advancing them by two squares as “torpedo” moves.

在我们命名为"鱼雷象棋"的变体规则中，兵(pawn)可以从棋盘任意位置向前移动一格或两格，而不像古典象棋那样仅限于初始位置。我们将兵前进两格的走法称为"鱼雷"走法。

We have also looked at a Semi-torpedo variant in our experiments, where we only add a partial extension to the original rule and have the pawns be able to move by two squares from the 2nd/3rd and 6th/7th rank for White and Black respectively. In this section we will focus on the universal motifs of full Torpedo chess, and cover the sub-motifs and sub-patterns that correspond to Semi-torpedo chess in its own dedicated section in Appendix B.6.

在我们的实验中，我们还研究了一种半鱼雷变体 (Semi-torpedo variant)，仅对原始规则进行部分扩展，使得白方和黑方的兵分别能从第2/3横线和第6/7横线移动两格。本节将重点讨论完整鱼雷象棋 (full Torpedo chess) 的通用主题，而半鱼雷象棋特有的子主题和子模式将在附录B.6的专门章节中详述。

B.5.1. MOTIVATION

B.5.1. 动机

In a sense, having the pawns always be able to move by one or two squares makes the pawn movement more consistent, as it removes a “special case” of them only being able to do the “double move” from their initial position. Increasing pawn mobility has the potential of speeding up all stages of the game. It adds additional attacking motifs to the openings and changes opening theory, it makes middle games more complicated, and changes endgame theory in cases where pawns are involved.

从某种意义上说，让兵(pawn)始终能移动一格或两格，使其走法更具一致性，因为这消除了它们只能在初始位置进行"双步移动"的"特殊情况"。增加兵的机动性有可能加速棋局的所有阶段：它为开局增添了新的进攻套路并改变开局理论，使中局更加复杂，并在涉及兵的情况下改变残局理论。

B.5.2. ASSESSMENT

B.5.2. 评估

The assessment of the Torpedo chess variant, as provided by Vladimir Kramnik:

弗拉基米尔·克拉姆尼克对鱼雷象棋变体的评估：

CC The pawns become quite powerful in Torpedo chess. Passed pawns are in particular a very strong asset and the value of pawns changes based on the circumstances and closer to the endgame. All of the attacking opportunities increase and this strongly favours the side with the initiative, which makes taking initiative a crucial part of the game. Pawns are very fast, so less of a strategical asset and much more tactical instead. The game becomes more tactical and calc ul at ive compared to standard chess.

在鱼雷象棋中，兵变得相当强大。通路兵尤其是一项非常有力的资产，且兵的价值会根据局势变化，越接近残局时越高。所有进攻机会都会增加，这极大地有利于掌握主动权的一方，因此夺取主动权成为对局的关键部分。由于兵的行进速度极快，其战略价值降低而战术价值显著提升。与标准国际象棋相比，鱼雷象棋更具战术性和计算性。

There is a lot of prophylactic play, which is why some games don’t feature many “torpedo” moves – “torpedo” moves are simply quite powerful and the play often proceeds in a way where each player positions their pawn structure so as to disin centi vise “torpedo” moves, either by the virtue of directly blocking their advance, or by placing their own pawns on squares that would be able to capture “en passant” if “torpedo” moves were to occur.

对局中存在大量预防性走法，因此某些棋局鲜见"鱼雷式"推进——这种极具威胁的走法往往促使双方调整兵形结构，通过直接阻挡推进路线或将己方兵部署在可"吃过路兵"的格位，从而抑制"鱼雷式"走法的发生。

This seems to favour the “classical” style of play in classical chess, which advocates for strong central control rather than conceding space to later attack the center once established. It seems like it is more difficult to play openings like the Grunfeld or the King’s Indian defence.

这似乎更倾向于国际象棋中的"古典"风格，即主张强有力的中心控制，而非在中心确立后再让出空间进行反击。像格林菲尔德防御或王翼印度防御这类开局似乎更难施展。

In summary, this is an interesting chess variant, leading to lots of decisive games and a potentially high entertainment value, involving lots of tactical play.

总之，这是一个有趣的国际象棋变体，能带来大量决定性对局和潜在的高娱乐价值，包含大量战术玩法。

B.5.3. MAIN LINES

B.5.3. 主要路线

Here we discuss “main lines” of AlphaZero under Torpedo chess, when playing with roughly one minute per move from a particular fixed first move. Note that these are not purely deterministic, and each of the given lines is merely one of several highly promising and likely options. Here we give the first 20 moves in each of the main lines, regardless of the position.

这里我们讨论AlphaZero在鱼雷象棋(Torpedo chess)中的"主要路线"，即在特定固定第一步后每步约一分钟的走法。需要注意的是，这些路线并非完全确定性的，每条给定路线仅是多个极具前景和可能的选择之一。无论局面如何，我们在此提供每条主要路线的前20步走法。

Main line after e4 The main line of AlphaZero after $\textit{1.}$ e4 in Torpedo chess is:

e4后的主要变例
在鱼雷象棋中，AlphaZero在$\textit{1.}$ e4后的主要变例为：

Main line after d4 The main line of AlphaZero after $\textit{1.}$ d4 in Torpedo chess is:

d4后的主要变例
在鱼雷棋中，AlphaZero在$\textit{1.}$ d4后的主要变例为：

Main line after c4 The main line of AlphaZero after $\textit{1.}$ c4 in Torpedo chess is:

c4后的主变 AlphaZero在鱼雷象棋中$\textit{1.}$ c4后的主变为：

B.5.4. INSTRUCTIVE GAMES

B.5.4. 指令性游戏

Here we showcase several instructive games that illustrate the type of play that frequently arises in Torpedo chess, along with some selected extracted game positions in cases where particular (endgame) move sequences are of interest.

这里我们展示几个具有启发性的对局，这些对局体现了鱼雷象棋(Torpedo chess)中常见的棋局类型，并精选了一些特定(残局)着法序列值得关注的棋局局面。

Game AZ-9: AlphaZero Torpedo vs AlphaZero Tor-pedo The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-9: AlphaZero鱼雷对AlphaZero鱼雷
白方与黑方的前十步棋着法均从AlphaZero的开局"棋谱库"中随机抽取，抽样概率与计算每步棋所耗时间成正比。后续着法采用最优策略，每步棋约思考一分钟。

$\textit{1.}$ d4 d5 2. Nf3 Nf6 3. c4 e6 4. Nc3 c6 5. e3 Nbd7 6. g3 Ne4 7. Nxe4 dxe4 8. Nd2 f5 9. c5 Be7 10. h4 O-O

$\textit{1.}$ d4 d5 2. 马f3 马f6 3. c4 e6 4. 马c3 c6 5. e3 马bd7 6. g3 马e4 7. 马xe4 dxe4 8. 马d2 f5 9. c5 象e7 10. h4 O-O

Bc4 Ng4 $I7.$ d6 cxd5 18. h6 Rg8
Bc4 Ng4 $I7.$ d6 cxd5 18. h6 Rg8

19. hxg7+ Rxg7 20. c7 Qd7 21. Bxd5 Qxd5 22. Nc4

22. . . Qg8 23. Ne5 Nxe5 24. Bxe5 Bxg5 25. Qh5

22... Qg8 23. Ne5 Nxe5 24. Bxe5 Bxg5 25. Qh5

25. . . b2 26. axb3 Rxa1+ 27. Bxa1 Be7 28. f4 exf3 29. Rg1 Bf8 30. Qg5

25. ... b2 26. axb3 Rxa1+ 27. Bxa1 Be7 28. f4 exf3 29. Rg1 Bf8 30. Qg5

A normal-looking position arises in the middlegame (this is one of AlphaZero’s main lines in this variation of chess), but the board soon explodes in tactics.

中盘阶段出现了一个看似正常的局面（这是AlphaZero在这种国际象棋变体中的主要走法之一），但棋盘很快在战术交锋中爆发。

Game AZ-10: AlphaZero Torpedo vs AlphaZero Torpedo The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-10: AlphaZero鱼雷对战AlphaZero鱼雷
白方和黑方的前十步棋着法均从AlphaZero的开局"棋谱库"中随机抽取，抽样概率与计算每步棋所耗时间成正比。后续着法遵循最优下法，每步棋耗时约一分钟。

A series of consecutive torpedo moves had given rise to this incredibly sharp position, with multiple passed pawns for White and Black, and the threats are culminating, as demonstrated by the following tactical sequence.

一系列连续的鱼雷式走法形成了这个异常尖锐的局面，白黑双方都拥有多个通路兵，威胁正达到高潮，如下战术序列所示。

Qxe8+ Rxe8 30. a8=Q Nc7
Qxe8+ Rxe8 30. a8=Q Nc7

Here Black utilizes a torpedo move to give back the pawn and protect h5 via d5.

黑方采用鱼雷式走法，通过d5弃还兵并保护h5兵。

And the game soon ends in a draw.

游戏很快以平局告终。

Game AZ-11: AlphaZero Torpedo vs AlphaZero Torpedo The first ten moves for White and Black have been sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-11: AlphaZero鱼雷对AlphaZero鱼雷
白方和黑方的前十步棋着是从AlphaZero的开局"棋谱"中随机采样的，采样概率与计算每步棋着所花费的时间成正比。后续棋着遵循最佳走法，每步棋着耗时约一分钟。

An interesting tactical motif, made possible by torpedo moves. One has to wonder, after $1l...$ Nxd5 12. e4, what happens on 12. . . Nf4? The game would have followed 13. e5 Nxd3 14. exd6 Nxc1 15. dxc7 Qxc7

一个有趣的战术主题，由鱼雷式走法实现。人们不禁要问，在 $1l...$ Nxd5 12. e4 之后，如果走 12... Nf4 会发生什么？对局可能会按以下路线发展：13. e5 Nxd3 14. exd6 Nxc1 15. dxc7 Qxc7

and here, White would have played ${\mathit{I6}}.$ . d6, a torpedo move – gaining an important tempo while weakening the Black king. 16. . . Qc4 17. Rxc1, followed by $\mathrm{Re1+}$ once the queen has moved. AlphaZero evaluates this position as being strongly in White’s favour, despite the material deficit.

此时，白方本应走 ${\mathit{I6}}.$ 着 d6，这是一记鱼雷式招法——在削弱黑王的同时赢得关键步调。16... Qc4 17. Rxc1，待后翼子力调动后接 $\mathrm{Re1+}$。尽管存在子力劣势，AlphaZero仍评估此局面为白方明显优势。

Going back to the game continuation,

回到游戏继续的部分，

Now we see several torpedo moves taking place. First White takes the opportunity to plant a pawn on h6, weakening the Black king, then Black responds by a4 and b4, getting the queenside pawns in motion and creating counter play on the other side of the board.

现在我们看到几个鱼雷式走法接连出现。首先白方抓住机会将兵推进到h6格，削弱黑王阵地；随后黑方应以a4和b4，调动后翼兵群并在棋盘另一侧展开反击。

h6 a4 20. Re1 Qa7 21. Bf5 b4
h6 a4 20. Re1 Qa7 21. Bf5 b4

A critical moment, and a decision which shows just how valuable the advanced pawns are in this chess variation. Normally it would make sense to save the knight, but AlphaZero decides to keep the pawn instead, and rely on promotion threats coupled with checks on d5.

关键时刻，这一决策展现了此变例中通路兵(advanced pawns)的巨大价值。通常救回马是合理选择，但AlphaZero选择保留兵，依靠升变威胁配合d5格的将军展开攻势。

. . d3 40. Bxb6 Qg5 41. Bd1 Qd5+ 42. Kh2 Qe6
... d3 40. Bxb6 Qg5 41. Bd1 Qd5+ 42. Kh2 Qe6

Being a piece down, Black offers an exchange of queens, an unusual sight, but tactically justified – Black is also threatening to capture on a3, and that threat is hard to meet. White can’t passively ignore the capture and defend the b2 pawn with the bishop, because Black could capture on b2, offering the piece for the second time – and then follow up by an immediate a3, knowing that bxa3 would allow for $\mathbf{b}1{=}\mathbf{Q}$ . In addition, Black could retreat the bishop instead of capturing on b2, to make room for a2 bxa3 and again $\mathbf{b}1{=}\mathbf{Q}$ . So, it’s again a torpedo move that makes a difference and justifies the tactical sequence.

少一子的黑方提出后兑换，这一罕见走法在战术上是合理的——黑方还威胁吃掉a3兵，而这一威胁难以化解。白方不能消极地无视吃子并用象防守b2兵，因为黑方可再次弃子吃掉b2兵，随后立即走a3，因为bxa3将允许黑方走 $\mathbf{b}1{=}\mathbf{Q}$ 升变。此外，黑方也可选择退象而非吃b2兵，为a2 bxa3腾出空间，再次实现 $\mathbf{b}1{=}\mathbf{Q}$ 升变。因此，正是鱼雷兵的推进改变了局面，使这一战术序列成立。

Be7 Qc1+ 38. Kg2 Qxh6 39. Bc5
Be7 Qc1+ 38. Kg2 Qxh6 39. Bc5

The position is getting sharp again, with Black having gained a passed pawn, and White making threats around the Black king.

局势再度紧张，黑方获得通路兵，白方则对黑王形成威胁。

White is a piece up for two pawns, and has the bishop pair. Yet, Black is just in time to use a torpedo move to shut the White king out and exchange a pair of pawns on the h-file (by another torpedo move).

白方以一子换两兵，并拥有双象优势。然而黑方及时利用鱼雷招封锁白王，并在h线通过另一记鱼雷招兑换一对兵。

. . g4 49. Bd2 Kg7 50. Kf1 f5 51. Ke1 Be7 52. Bc4 h3
... g4 49. Bd2 Kg7 50. Kf1 f5 51. Ke1 Be7 52. Bc4 h3

Game AZ-12: AlphaZero Torpedo vs AlphaZero Torpedo Playing from a predefined Nimzo-Indian opening position (the first 3 moves for each side). The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-12: AlphaZero鱼雷对AlphaZero鱼雷
从预定义的尼姆佐-印度防御开局位置(双方各走前3步)开始。后续着法按最佳行棋进行,每步约耗时1分钟。

$\textit{1.}$ d4 (book) Nf6 (book) 2. c4 (book) e6 (book) 3. Nc3 (book) Bb4 (book) 4. e3 Bxc3 5. bxc3 d6 6. Nf3 O-O 7. Ba3 Re8 $\delta.$ e5

$\textit{1.}$ d4 (常规走法) Nf6 (常规走法) 2. c4 (常规走法) e6 (常规走法) 3. Nc3 (常规走法) Bb4 (常规走法) 4. e3 Bxc3 5. bxc3 d6 6. Nf3 O-O 7. Ba3 Re8 $\delta.$ e5

Already we see the first torpedo move, keeping the initiative.

我们已经看到第一枚鱼雷开始行动，保持主动权。

Here we see an effect of another torpedo move, after the exchange sacrifice earlier, taking over the initiative and creating a dangerous pawn.

在这里我们看到另一种鱼雷战术的效果，通过之前的弃子交换夺取主动权并制造出一个危险的兵。

The following move shows the power of advanced pawns – 37. e6!, in order to create a threat of 38. $\mathrm{e8=Q}$ , so Black has to block with the knight. If instead 37. e7, Black responds by first giving the knight for the pawn – 37. . . Nxe7, and then after 38. Rxe7 follows it up with 38. . . h4!, similar to the game continuation.

接下来的这步棋展示了高兵(advanced pawns)的威力——37. e6!，旨在制造38. $\mathrm{e8=Q}$的威胁，迫使黑方必须用马阻挡。若改为37. e7，黑方会先弃马换兵——37... Nxe7，接着在38. Rxe7后应以38... h4!，与实战后续类似。

e6 Ne7 38. Bc5 h4 39. Bxe7 hxg3 40. Re3 f4 and Black manages to force a draw, as the pawns are just too threatening.
e6 Ne7 38. Bc5 h4 39. Bxe7 hxg3 40. Re3 f4 黑方成功逼和，因为这些兵实在威胁太大。

Game AZ-13: AlphaZero Torpedo vs AlphaZero Torpedo The game starts from a predefined Ruy Lopez opening position (the first 5 plies). The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-13: AlphaZero鱼雷对战AlphaZero鱼雷
本局从预定的西班牙开局(Ruy Lopez)起始局面开始(前5步)。后续着法均为最佳行棋，每步耗时约一分钟。

Here comes the first torpedo move (b6-b4), gaining space on the queenside.

第一记鱼雷招法 (b6-b4) 出手，在后翼夺取空间。

. . b4 18. a4 h6 19. Qe3 Rad8 20. f3 a5 $2l.$ f5
... b4 18. a4 h6 19. Qe3 Rad8 20. f3 a5 $2l.$ f5

Here we see an effect of another torpedo move, f3-f5, advancing towards the Black king.

这里我们看到另一记鱼雷走法 f3-f5 的效果，向黑方国王推进。

Nxd4 cxd4 28. Qd2 Rd6 29. g5
Nxd4 cxd4 28. Qd2 Rd6 29. g5

White uses a torpedo move to generate play on the kingside.

白方采用鱼雷式推进在王翼展开攻势。

. . hxg5 30. b3 Bd5
... hxg5 30. b3 Bd5

The Black bishop can’t be taken, due to a torpedo threat $\mathrm{e}3+!$

黑象不能被吃掉，因为存在鱼雷威胁 $\mathrm{e}3+!$

Qxg5 Bxe4 32. f7+
Qxg5 Bxe4 32. f7+

And yet another torpedo strike, in order to capture on e5.

又一次鱼雷攻击，为了占领e5格。

White ends up with the queen against the rook and two pawns, but this ends up being a draw, as the pawns are simply too fast and need to remain blocked. Normally the queen on b3 would prevent the c5 pawn from moving, but a c5-c3 torpedo move shows that this is no longer the case!

白方最终以皇后对车和两兵的局面告终，但结果却是和棋，因为兵的行进速度太快且必须被持续阻挡。通常位于b3的皇后会阻止c5兵前进，但c5-c3的"鱼雷式"走法表明这一局面已不复存在！

Game AZ-14: AlphaZero Torpedo vs AlphaZero Torpedo The position below, with Black to move, is taken from a game that was played with roughly one minute per move:

游戏 AZ-14: AlphaZero鱼雷对AlphaZero鱼雷
以下局面轮到黑方行棋，取自每步约1分钟的对局:

A dynamic position from an endgame reached in one of the AlphaZero games. White has an advanced passed pawn, which is quite threatening – and Black tries to respond by creating threats around the White king. To achieve that, Black starts with a torpedo move:

AlphaZero对局中某一残局的动态局面。白方拥有一个极具威胁的通路兵，而黑方试图通过在白王周围制造威胁来应对。为此，黑方先手发动了一记鱼雷式招法：

. . h4 32. e6 hxg3 33. hxg3 Bxe3
... h4 32. e6 hxg3 33. hxg3 Bxe3

White is one torpedo move away from queening, but has to first try to safeguard the king.

白棋只需一步即可升变为后，但必须首先设法保护国王。

Be5 Qd1+ 35. Qf1 Bxf2+
Be5 Qd1+ 35. Qf1 Bxf2+

Black is in time, due to the torpedo threats involving the e-pawn.

黑色方及时应对，由于鱼雷威胁涉及e兵。

Kxf2 e3+ 37. Kxe3 Qxf1
Kxf2 e3+ 37. Kxe3 Qxf1

Black captures White’s queen, but White creates a new one, with a torpedo move.

黑方吃掉白方的皇后，但白方通过一记鱼雷式走法再造新后。

$\mathrm{e8=Q}$ Qe1+ 39. Kd3 Qb1+ 40. Kc3 Qa1+ 41. Kb4 Qxa2
$\mathrm{e8=Q}$ Qe1+ 39. Kd3 Qb1+ 40. Kc3 Qa1+ 41. Kb4 Qxa2

An interesting endgame arises, where White is up a piece, given that Black had to give away its bishop in the tactics earlier, and Black will soon only have a single pawn in return. Yet, after a long struggle, AlphaZero manages to defend as Black and achieve a draw.

一个有趣的残局出现了，白方多一子（因黑方此前战术中被迫弃象），而黑方很快将仅剩一枚兵作为补偿。然而经过漫长缠斗，AlphaZero作为黑方成功守和。

Game AZ-15: AlphaZero Torpedo vs AlphaZero Torpedo The position below, with Black to move, is taken from a game that was played with roughly one minute per move:

游戏 AZ-15: AlphaZero鱼雷对战AlphaZero鱼雷
以下局面为黑方行棋，选自每步约1分钟的对局:

A position from one of the AlphaZero games, illustrating the utilization of pawns in a heavy piece endgame. The b-pawn is fast, and it gets pushed down the board via a torpedo move.

AlphaZero对局中的一个局面，展示了重子残局中兵(pawn)的运用。b线兵速度很快，通过鱼雷式走法(torpedo move)直冲底线。

Unlike in Classical chess, this capture is possible, even though it seemingly hangs the queen. If Black were to capture it with the rook, the c-pawn would queen with check in a single move! The threat of $\mathrm{c}8{=}Q$ forces Black to recapture the pawn instead.

与国际象棋不同，这种吃子是可行的，尽管看似会让皇后陷入险境。如果黑方用车吃掉它，c兵将在一步之内带将升变为皇后！$\mathrm{c}8{=}Q$ 的威胁迫使黑方只能选择回吃这个兵。

Game AZ-16: AlphaZero Torpedo vs AlphaZero Torpedo The first ten moves for White and Black were sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-16: AlphaZero鱼雷对AlphaZero鱼雷
白方与黑方的前十步棋着法均从AlphaZero的开局"棋谱库"中随机抽取，抽样概率与计算每步棋所耗时间成正比。后续着法遵循最优行棋策略，每步耗时约一分钟。

$\boldsymbol{{l}}.$ d4 Nf6 2. c4 e6 3. Nc3 d5 4. Nf3 a6 5. e3 b6 $\boldsymbol{\delta}.$ . g3 dxc4

7. e5 Nd5 8. Bxc4 Be7 9. O-O Bb7 10. Re1 h6 11. a3 b5 12. Bb3 Nxc3 13. bxc3 a4

In the early stage of the game, we see White using a torpedo e3-e5 move to expand in the center and Black responding by an a6-a4 torpedo move to gain space on the queenside.

对局初期，白方采用鱼雷兵e3-e5推进以扩张中心，黑方则以a6-a4鱼雷兵回应争夺后翼空间。

White moves forward with a c3-c5 torpedo move.

白方以c3-c5鱼雷式进招向前推进。

. . Nc4 23. Bc3 Rdf8 24. $\mathrm{Nd}6+$ Bxd6 25. exd6 g5
... Nc4 23. Bc3 Rdf8 24. $\mathrm{Nd}6+$ Bxd6 25. exd6 g5

Black uses two consecutive torpedo moves (b5-b3, a4-a2) on the queenside to create a dangerous passed pawn on a2.

黑方在后翼连续进行两次鱼雷式推进(b5-b3, a4-a2)，在a2格制造出危险的通路兵。

Assessing Game Balance with AlphaZero

使用AlphaZero评估游戏平衡性

Black uses another torpedo move (f5-f3) to advance further on the kingside and create another passed pawn.

黑方采用另一招鱼雷式走法 (f5-f3) ，进一步推进王翼并制造另一只通路兵。

White advances the h-pawn with an h4-h6 torpedo move, seeking counter play.

白方挺进h兵以h4-h6鱼雷式走法寻求反击机会。

The torpedo move g4-g2 forces the White rook away from the h-file.

兵g4-g2的突进迫使白车离开h线。

Re1 Rxh7 70. b6
Re1 Rxh7 70. b6

White needs to generate immediate counter play, and does so via b4-b6, another torpedo move. White then uses a b6- $\mathtt{b8=Q}$ torpedo move to promote to a queen in the next move, demonstrating how fast the pawns are in this variation of chess.

白方需要立即展开反击，于是通过b4-b6这记鱼雷式推进来应对。紧接着白方利用b6-$\mathtt{b8=Q}$的升变鱼雷战术，下一步即可将兵升变为后，充分展示了该变体中兵链的惊人推进速度。

. . Rh1 71. b8=Q Rf1+
. . Rh1 71. b8=Q Rf1+

Rxf1 gxf1 $\mathsf{=}\mathsf{Q}+$ 73. $\mathrm{Kg}3$ and the game eventually ended in a draw due to mutual threats and ensuing checks. 1/2–1/2
Rxf1 gxf1 $\mathsf{=}\mathsf{Q}+$
$\mathrm{Kg}3$ 最终因双方威胁及后续将军导致比赛以和棋告终。1/2–1/2

Game AZ-17: AlphaZero Torpedo No-castling vs AlphaZero Torpedo No-castling This game was an experiment combining the No-castling chess with Torpedo chess, resulting in a highly tactical position. The first ten moves for White and Black were sampled randomly from AlphaZero’s opening “book”, with the probability proportional to the time spent calculating each move. The remaining moves follow best play, at roughly one minute per move.

游戏 AZ-17: AlphaZero 鱼雷无王车易位 vs AlphaZero 鱼雷无王车易位
本局实验结合了无王车易位与国际象棋鱼雷变体，形成了高度战术化的局面。白方与黑方的前十步棋着均从AlphaZero的开局"棋谱库"中随机抽取，抽样概率与计算每步棋所耗时间成正比。后续着法按最佳行棋策略进行，每步耗时约一分钟。

Here White executes a stunning ’double attack’:

白方在此施展了一记精彩的"双重打击":

27. Qc2!! Kg8

Black can’t afford to capture the Queen, due to the powerful attack following 27... Bxc2 28. ${\mathrm{h8}}{=}{\mathrm{Q}}+{\mathrm{\Lambda}}$ . White also had to assess the consequences of 27... gxf4

黑方无法承受吃掉皇后的代价，因为白方在27... Bxc2 28. ${\mathrm{h8}}{=}{\mathrm{Q}}+{\mathrm{\Lambda}}$ 后会发起强力进攻。白方还需评估27... gxf4带来的后续影响。

32... Qg6 33. Rh4 Kh8 34. Rg4 Qe8 35. Qa1 Qf8 36. Qc3 Bf5 37. Rxf4 a6 38. Re1 d3 39. Rxc4 Bxe6 40. Rd4 Bf5 41. Qc7 Ng6 42. Kf2 Qxh6

Qc1 Qxc1 44. Rxc1 Ne7 45. Ne3 Bg6 46. Ra1 Nc6 47. $\mathrm{Rh4+Kg7}48$ . b5 Nb8 49. Rc4 Bf7 50. Rc7 f4 51. Nd1 a4 52. Nc2 a2 53. Nxd3 Kf6 54. Rc8 Ra3 55. Nxf4 Nd7 56. Ne2 Ne5 57. b7 $\mathrm{Rxf}3+58$ . Kg2 Rb3 59. $\scriptstyle{\mathrm{b}}8=Q$ Rxb8 60. Rxb8 and White went on to win the game easily. 1-0
Qc1 Qxc1 44. Rxc1 Ne7 45. Ne3 Bg6 46. Ra1 Nc6 47. Rh4+ Kg7 48. b5 Nb8 49. Rc4 Bf7 50. Rc7 f4 51. Nd1 a4 52. Nc2 a2 53. Nxd3 Kf6 54. Rc8 Ra3 55. Nxf4 Nd7 56. Ne2 Ne5 57. b7 Rxf3+ 58. Kg2 Rb3 59. b8=Q Rxb8 60. Rxb8 白方轻松赢得比赛。1-0

B.6. Semi-torpedo

B.6. 半鱼雷式

In Semi-torpedo chess, we consider a partial extension to the rules of pawn movement, where the pawns are allowed to move by two squares from the 2nd/3rd and 6th/7th rank for White and Black respectively. This is a restricted version of another variant we have considered (Torpedo chess) where the option is extended to cover the entire board. Yet, even this partial extension adds lots of dynamic options and here we independently evaluate its impact on the arising play.

在半鱼雷象棋中，我们对兵的走法规则进行了部分扩展，允许白方和黑方的兵分别从第2/3横排和第6/7横排向前移动两格。这是我们考虑的另一种变体（鱼雷象棋）的限制版本，在该变体中这一选择可覆盖整个棋盘。然而，即便是这种部分扩展也增添了许多动态选择，我们在此独立评估其对棋局产生的影响。

B.6.1. MOTIVATION

B.6.1. 动机

As with Torpedo chess, the motivation in extending the possibilities for rapid pawn movement lies in adding dynamic, attacking options to the middlegame. Yet, given that it is only a partial extension, adding an extra rank for each side from which the pawns can move by two squares, its impact on endgame patterns is much more limited.

与鱼雷象棋类似，扩展兵快速移动可能性的动机在于为中局增添动态进攻选择。然而，由于这仅是部分扩展（为双方各增加一个兵可移动两格的行），其对残局模式的影响要有限得多。

B.6.2. ASSESSMENT

B.6.2. 评估

The assessment of the Semi-torpedo chess variant, as provided by Vladimir Kramnik:

弗拉基米尔·克拉姆尼克对半鱼雷象棋变体的评估：

Compared to Classical chess, the pawns that have been played to the 3rd/6th rank become much more useful, which manifests in several ways. First, prophylactic pawn moves to h3/h6 and a3/a6 now allow for a subsequent torpedo push. Having played h3 for example, it is now possible to play the pawn to h5 in a single move. This also means, if the goal was to push the pawn to h5 in two moves, that there are two ways of achieving it – either via h4 and h5 or via h3 and h5 – and doing the latter does not expose a weakness on the g4 square and can thus be advantageous. Secondly, fianchetto setups now allow for additional dynamic options. The g3 pawn can now be pushed to g5 in a single move, to attack a knight on f6 – and vice versa. Thirdly, openings where one of the central pawns is on the 3rd/6th rank change – consider the Meran for example – the e3 pawn can now go to e5 in a single move.

与传统国际象棋相比，已推进至第3/6横线的兵变得更具战术价值，主要体现在三个方面：首先，预防性推进h3/h6和a3/a6的兵现在可后续实施鱼雷式冲锋。例如走完h3后，现在能直接将兵推进至h5。这也意味着，若计划在两回合内将兵推至h5，存在两种实现路径——通过h4再h5，或通过h3再h5——选择后者不会在g4格留下弱点，因而更具优势。其次，侧翼出象体系现在拥有更多动态选择。g3兵现在能直接推进至g5攻击f6马——反之亦然。第三，中心兵位于第3/6横线的开局（例如梅兰防御）产生变化——e3兵现在能直接跃至e5。

![](https://miner.umaxing.com/miner/v2/analysis/pdf_img?as_attachm

[论文翻译]用AlphaZero评估游戏平衡性：探索国际象棋的替代规则集

原文地址：https://arxiv.org/pdf/2009.04374v2

Assessing Game Balance with AlphaZero: Exploring Alternative Rule Sets in Chess

用AlphaZero评估游戏平衡性：探索国际象棋的替代规则集

Abstract

1. Introduction

1. 引言

2. Methods

2. 方法

2.1. Rule Alterations

2.1. 规则变更

2.2. Key components of AlphaZero

2.2. AlphaZero的关键组件

2.3. Training and evaluation

2.3. 训练与评估

3. Quantitative assessment

3. 定量评估

3.1. Self-play games

3.1. 自我对弈游戏

3.2. Expected scores and draw rates

3.2. 预期得分与平局概率

3.2.1. INFERENCE FOR GAME ODDS

3.2.2. DRAW RATES

3.2.2. 绘制速率

3.2.3. EXPECTED SCORES

3.2.3. 预期得分

3.3. Differences in specific openings

3.3. 具体开局差异

3.4. Util is ation of special moves

3.4. 特殊移动的利用

3.4.1. TORPEDO MOVES

3.4.1. TORPEDO MOVES

3.4.2. BACKWARDS AND LATERAL PAWN MOVES

3.4.2. 兵的后退与横向移动

3.4.3. SELF-CAPTURES

3.4.3. 自我捕获

3.4.4. WINNING THROUGH STALEMATE

3.4.4. 通过僵局取胜

3.5. Diversity

3.5.1. AVERAGE INFORMATION CONTENT

3.5.1. 平均信息量

3.5.2. CLASSICAL VS. NO-CASTLING CHESS

3.5.2. 传统王车易位与国际象棋无王车易位变体

3.6. Differences between opening trees

3.7. How much opening theory should be relearned?

3.7. 需要重新学习多少开局理论？

3.8. Material

4. Qualitative assessment

4. 定性评估

5. Conclusions

5. 结论

Acknowledgements

References

参考文献

A. Quantitative Appendix

A. 量化附录

A.1. Proof of equation (13)

A.1. 方程 (13) 的证明

A.2. Additional figures

A.2. 其他图表

B. Appendix

B. 附录

B.1. No-castling

B.1. 无王车易位

B.1.1. MOTIVATION

B.1.2. ASSESSMENT

B.1.3. MAIN LINES

B.1.5. HUMAN GAMES

B.1.5. 人类游戏

B.2. No-castling (10)

B.2.1. MOTIVATION

B.2.1. 动机

B.2.2. ASSESSMENT

B.2.3. MAIN LINES

B.2.3. 主要线路

B.2.4. INSTRUCTIVE GAMES

B.2.4. 教学游戏

B.3. Pawn one square

B.3. 前进一格

B.3.1. MOTIVATION