
传说中,迈达斯国王触碰的一切都会变成黄金。而数据科学家则把一切都变成了向量。我们这么做是有原因的——正如黄金是商人的语言,向量则是人工智能的语言1。
然而,正如迈达斯发现把一切都变成黄金并不总是好事一样,盲目地使用余弦相似度来比较向量也可能会让我们误入歧途。虽然嵌入(embeddings)确实能捕捉到相似性,但它们往往反映的是错误的相似性——比如把问题与问题匹配,而不是问题与答案匹配,或者被表面的模式(如写作风格和拼写错误)分散注意力,而忽略了真正的语义。这篇文章将告诉你如何更有意识地使用相似性,从而获得更好的结果。
嵌入(Embeddings)
嵌入是如此迷人,以至于我最受欢迎的博客文章仍然是《king - man + woman = queen;但为什么?》。我们有word2vec、node2vec、food2vec、game2vec,如果你能想到什么,可能已经有人把它变成了“vec”。如果还没有,那就是你的机会了!
当我们处理原始ID时,我们无法看到它们之间的关系。比如“brother”和“sister”这两个词——对计算机来说,它们可能和“xkcd42”与“banana”没什么区别。但通过向量,我们可以绘制实体及其之间的关系——既可以为机器学习模型提供结构化的输入,也可以单独用于找到相似的项目。
让我们聚焦于大型语言模型(LLMs)生成的句子嵌入,因为这是嵌入最流行的用例之一。现代LLMs在这方面非常强大,它们可以在没有任何微调的情况下捕捉文本的本质。事实上,最近的研究表明,这些嵌入几乎和原始文本一样具有揭示性——参见Morris等人的论文《文本嵌入揭示(几乎)与文本一样多的信息》,(2023年)。然而,能力越大,责任也越大。
例子
让我们看三个句子:
- A: "Python可以让你致富。"
- B: "Python可以让你发痒。"
- C: "掌握Python可以让你的口袋鼓起来。"
如果你把它们当作原始ID,它们是完全不同的字符串,没有任何相似性。使用字符串相似度(Levenshtein距离),A和B相差2个字符,而A和C相差21个字符。但从语义上讲(除非你对钱过敏),A更接近C而不是B。
我们可以使用OpenAI的text-embedding-3-large,得到以下向量:
- A:
[-0.003738, -0.033263, -0.017596, 0.029024, -0.015251, ...] - B:
[-0.066795, -0.052274, -0.015973, 0.077706, 0.044226, ...] - C:
[-0.011167, 0.017812, -0.018655, 0.006625, 0.018506, ...]
这些向量非常长——text-embedding-3-large的维度高达3072——以至于我们可以在几乎不损失质量的情况下截断它们。当我们计算余弦相似度时,A和C(语义相似的句子)之间的相似度为0.750,而A和B(词汇相似的句子)之间的相似度为0.576。这些数字与我们的预期一致——语义比拼写更重要!
什么是余弦相似度?
在比较向量时,每个数据科学家都会想到一个看似简单的解决方案——余弦相似度:
从几何上讲,它是两个向量之间夹角的余弦值。然而,我避免这样思考——因为我们处理的是几十、几百甚至几千维的空间。在这种高维空间中,我们的几何直觉失效了,我们不应该假装它还能用。
从数值角度看,它是归一化向量的点积。它有一些吸引人的特性:
- 相同的向量得分为1。
- 随机向量得分在0左右(因为维度很多,所以平均值趋近于0)。
- 结果在-1到1之间。
然而,这种简单性是误导性的。仅仅因为值通常在0到1之间,并不意味着它们代表概率或其他有意义的度量。值0.6并不能告诉我们是否真的相似。虽然负值是可能的,但它们很少表示语义上的相反——更多时候,相反的东西是毫无意义的。
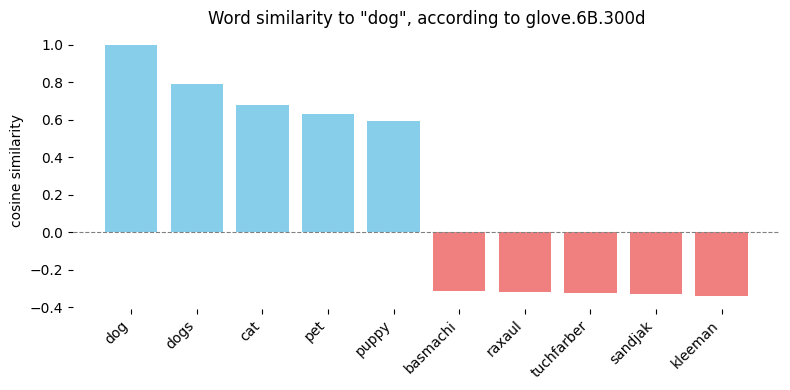
当使用Glove向量(glove.6B.300d)计算余弦相似度时,与“dog”最接近的词是预料之中的,而最远的词则不是。你可以在这里玩一玩。
换句话说,余弦相似度是向量比较的“万能胶”。当然,它能把一切都粘在一起——图像、文本、音频、代码——但就像真正的万能胶一样,它只是一个快速修复,往往掩盖了更深层次的问题,而不是解决它们。正如你不会用万能胶永久修复水管一样,你也不应该盲目信任余弦相似度来满足你所有的向量比较需求。
就像希腊悲剧一样,这种祝福伴随着诅咒:当它奏效时,感觉像是毫不费力的魔法。但当它失败时,我们却毫无头绪,常常陷入即兴修复的困境,每个修复都会带来新的问题。
与相关性的关系
皮尔逊相关系数可以看作是一系列三个操作:
- 减去均值以中心化数据。
- 归一化向量为单位长度。
- 计算它们之间的点积。
当我们处理既中心化又归一化的向量时,皮尔逊相关系数、余弦相似度和点积是相同的。
在实际情况下,我们不想在每次成对比较时都中心化或归一化向量——我们只需做一次,然后直接使用点积。无论如何,当你觉得使用余弦相似度没问题时,你也应该觉得使用皮尔逊相关系数没问题(反之亦然)。
余弦相似度作为相似性度量的问题
使用余弦相似度作为机器学习模型的训练目标是完全有效且数学上合理的。正如我们刚刚看到的,它是深度学习中两个基本操作的组合:点积和归一化。问题出在我们超出其舒适区时,特别是当:
- 模型训练中使用的损失函数不是余弦相似度(通常情况如此!)。
- 训练目标与我们实际关心的东西不同。
模型是否见过余弦相似度?
一个常见的场景是使用未归一化的向量进行训练,当我们处理点积的函数时——例如,使用sigmoid函数预测概率并应用对数损失函数。其他网络的操作方式不同,例如它们使用欧几里得距离,最小化同一类成员之间的距离,最大化不同类成员之间的距离。
归一化给了我们一些很好的数学特性(保持结果在-1到+1之间,无论维度如何),但它最终只是一个技巧。有时它有帮助,有时则没有——参见标题恰当的论文《嵌入的余弦相似度真的与相似性有关吗?》。
当然,在图像检测模型VGG16的时代,我曾经使用分类层的logit向量和皮尔逊相关系数来找到相似的图像。它某种程度上奏效了——但我完全意识到这只是一个技巧,而且仅仅是一个技巧。
只有当模型本身使用余弦相似度或其直接函数时,我们才是安全的——通常实现为保持归一化的向量的点积。否则,我们使用的量是我们无法控制的。它可能在一个实例中奏效,但在另一个实例中则不行。如果某些东西非常相似,当然,许多不同的相似性度量可能会给出相似的结果。但如果它们不相似,我们就会陷入麻烦。
总的来说,这是无监督学习与自监督学习这一更广泛主题的一部分。在无监督学习中,我们使用任意函数并获得一些相似性概念,但无法评估它。而在自监督学习中,它是一个预测模型,我们可以直接评估预测的质量。
这是正确的相似性吗?
这是第二个问题——即使模型明确使用余弦相似度进行训练,我们也会遇到一个更深层次的问题:我们使用的是谁的相似性定义?
以书籍为例。对于文学评论家来说,相似性可能意味着共享主题元素。对于图书管理员来说,它是关于分类的。对于读者来说,它是关于情感的。对于排版师来说,它是页数和格式。每个角度都是有效的,但余弦相似度却把这些细微的观点压缩成一个单一的数字——带着自信和客观性的假象。

在美国,word2vec可能会告诉你espresso和cappuccino几乎相同。但在意大利,你不会这么说。
