Abstract

摘要

We present DeepSeek-V3, a strong Mixture-of-Experts (MoE) language model with 671B total parameters with 37B activated for each token. To achieve efficient inference and cost-effective training, DeepSeek-V3 adopts Multi-head Latent Attention (MLA) and Deep Seek MoE architectures, which were thoroughly validated in DeepSeek-V2. Furthermore, DeepSeek-V3 pioneers an auxiliary-loss-free strategy for load balancing and sets a multi-token prediction training objective for stronger performance. We pre-train DeepSeek-V3 on 14.8 trillion diverse and high-quality tokens, followed by Supervised Fine-Tuning and Reinforcement Learning stages to fully harness its capabilities. Comprehensive evaluations reveal that DeepSeek-V3 outperforms other open-source models and achieves performance comparable to leading closed-source models. Despite its excellent performance, DeepSeek-V3 requires only 2.788M H800 GPU hours for its full training. In addition, its training process is remarkably stable. Throughout the entire training process, we did not experience any irrecoverable loss spikes or perform any rollbacks. The model checkpoints are available at https://github.com/deepseek-ai/DeepSeek-V3.

我们推出了 DeepSeek-V3，这是一个强大的专家混合模型 (Mixture-of-Experts, MoE) 语言模型，总参数量为 671B，每个 Token 激活的参数量为 37B。为了实现高效的推理和成本效益的训练，DeepSeek-V3 采用了多头潜在注意力 (Multi-head Latent Attention, MLA) 和 Deep Seek MoE 架构，这些架构在 DeepSeek-V2 中得到了充分验证。此外，DeepSeek-V3 率先采用了无辅助损失的负载均衡策略，并设定了多 Token 预测训练目标，以实现更强的性能。我们在 14.8 万亿个多样化且高质量的 Token 上对 DeepSeek-V3 进行了预训练，随后进行了监督微调和强化学习阶段，以充分发挥其能力。综合评估表明，DeepSeek-V3 优于其他开源模型，并实现了与领先的闭源模型相当的性能。尽管性能卓越，DeepSeek-V3 的完整训练仅需 2.788M H800 GPU 小时。此外，其训练过程非常稳定。在整个训练过程中，我们没有遇到任何不可恢复的损失峰值或执行任何回滚操作。模型检查点可在 https://github.com/deepseek-ai/DeepSeek-V3 获取。

Figure 1 | Benchmark performance of DeepSeek-V3 and its counterparts.

图 1 | DeepSeek-V3 及其对比模型的基准性能。

1. Introduction

1. 引言

In recent years, Large Language Models (LLMs) have been undergoing rapid iteration and evolution (Anthropic, 2024; Google, 2024; OpenAI, 2024a), progressively diminishing the gap towards Artificial General Intelligence (AGI). Beyond closed-source models, open-source models, including DeepSeek series (DeepSeek-AI, 2024a,b,c; Guo et al., 2024), LLaMA series (AI@Meta, $2024\mathrm{a},\mathrm{b},$ ; Touvron et al., 2023a,b), Qwen series (Qwen, 2023, 2024a,b), and Mistral series (Jiang et al., 2023; Mistral, 2024), are also making significant strides, endeavoring to close the gap with their closed-source counterparts. To further push the boundaries of open-source model capabilities, we scale up our models and introduce DeepSeek-V3, a large Mixture-of-Experts (MoE) model with 671B parameters, of which 37B are activated for each token.

近年来，大语言模型 (LLMs) 经历了快速的迭代和演进 (Anthropic, 2024; Google, 2024; OpenAI, 2024a)，逐步缩小了与通用人工智能 (AGI) 的差距。除了闭源模型外，开源模型，包括 DeepSeek 系列 (DeepSeek-AI, 2024a,b,c; Guo et al., 2024)、LLaMA 系列 (AI@Meta, $2024\mathrm{a},\mathrm{b},$ ; Touvron et al., 2023a,b)、Qwen 系列 (Qwen, 2023, 2024a,b) 和 Mistral 系列 (Jiang et al., 2023; Mistral, 2024)，也在取得显著进展，努力缩小与闭源模型的差距。为了进一步突破开源模型的能力边界，我们扩展了模型规模，并推出了 DeepSeek-V3，这是一个拥有 6710 亿参数的大型专家混合模型 (Mixture-of-Experts, MoE)，每个 token 激活 370 亿参数。

With a forward-looking perspective, we consistently strive for strong model performance and economical costs. Therefore, in terms of architecture, DeepSeek-V3 still adopts Multi-head Latent Attention (MLA) (DeepSeek-AI, 2024c) for efficient inference and Deep Seek MoE (Dai et al., 2024) for cost-effective training. These two architectures have been validated in DeepSeekV2 (DeepSeek-AI, 2024c), demonstrating their capability to maintain robust model performance while achieving efficient training and inference. Beyond the basic architecture, we implement two additional strategies to further enhance the model capabilities. Firstly, DeepSeek-V3 pioneers an auxiliary-loss-free strategy (Wang et al., 2024a) for load balancing, with the aim of minimizing the adverse impact on model performance that arises from the effort to encourage load balancing. Secondly, DeepSeek-V3 employs a multi-token prediction training objective, which we have observed to enhance the overall performance on evaluation benchmarks.

我们始终以长远的眼光追求强大的模型性能和经济成本。因此，在架构方面，DeepSeek-V3 仍然采用多头潜在注意力机制 (Multi-head Latent Attention, MLA) (DeepSeek-AI, 2024c) 以实现高效推理，并采用 Deep Seek MoE (Dai et al., 2024) 以实现经济高效的训练。这两种架构已在 DeepSeekV2 (DeepSeek-AI, 2024c) 中得到验证，证明了它们在保持强大模型性能的同时实现高效训练和推理的能力。除了基础架构外，我们还实施了两种额外策略以进一步提升模型能力。首先，DeepSeek-V3 率先采用无辅助损失的负载均衡策略 (Wang et al., 2024a)，旨在最小化因鼓励负载均衡而对模型性能产生的不利影响。其次，DeepSeek-V3 采用了多 Token 预测的训练目标，我们观察到这能够提升在评估基准上的整体表现。

In order to achieve efficient training, we support the FP8 mixed precision training and implement comprehensive optimization s for the training framework. Low-precision training has emerged as a promising solution for efficient training (Dettmers et al., 2022; Kalamkar et al., 2019; Narang et al., 2017; Peng et al., 2023b), its evolution being closely tied to advancements in hardware capabilities (Luo et al., 2024; Mic ike vici us et al., 2022; Rouhani et al., 2023a). In this work, we introduce an FP8 mixed precision training framework and, for the first time, validate its effectiveness on an extremely large-scale model. Through the support for FP8 computation and storage, we achieve both accelerated training and reduced GPU memory usage. As for the training framework, we design the DualPipe algorithm for efficient pipeline parallelism, which has fewer pipeline bubbles and hides most of the communication during training through computation-communication overlap. This overlap ensures that, as the model further scales up, as long as we maintain a constant computation-to-communication ratio, we can still employ fine-grained experts across nodes while achieving a near-zero all-to-all communication overhead. In addition, we also develop efficient cross-node all-to-all communication kernels to fully utilize InfiniBand (IB) and NVLink bandwidths. Furthermore, we meticulously optimize the memory footprint, making it possible to train DeepSeek-V3 without using costly tensor parallelism. Combining these efforts, we achieve high training efficiency.

为了实现高效的训练，我们支持 FP8 混合精度训练，并对训练框架进行了全面的优化。低精度训练已成为高效训练的一种有前景的解决方案 (Dettmers et al., 2022; Kalamkar et al., 2019; Narang et al., 2017; Peng et al., 2023b)，其发展与硬件能力的进步密切相关 (Luo et al., 2024; Mic ike vici us et al., 2022; Rouhani et al., 2023a)。在这项工作中，我们引入了 FP8 混合精度训练框架，并首次在超大规模模型上验证了其有效性。通过支持 FP8 计算和存储，我们实现了加速训练并减少了 GPU 内存使用。对于训练框架，我们设计了 DualPipe 算法以实现高效的流水线并行，该算法减少了流水线气泡，并通过计算-通信重叠隐藏了大部分训练期间的通信。这种重叠确保了随着模型的进一步扩展，只要我们保持恒定的计算与通信比率，我们仍然可以在节点之间使用细粒度的专家，同时实现接近零的全对全通信开销。此外，我们还开发了高效的跨节点全对全通信内核，以充分利用 InfiniBand (IB) 和 NVLink 的带宽。此外，我们精心优化了内存占用，使得在不使用昂贵的张量并行的情况下训练 DeepSeek-V3 成为可能。结合这些努力，我们实现了高训练效率。

During pre-training, we train DeepSeek-V3 on 14.8T high-quality and diverse tokens. The pre-training process is remarkably stable. Throughout the entire training process, we did not encounter any irrecoverable loss spikes or have to roll back. Next, we conduct a two-stage context length extension for DeepSeek-V3. In the first stage, the maximum context length is extended to 32K, and in the second stage, it is further extended to 128K. Following this, we conduct post-training, including Supervised Fine-Tuning (SFT) and Reinforcement Learning (RL) on the base model of DeepSeek-V3, to align it with human preferences and further unlock its potential. During the post-training stage, we distill the reasoning capability from the DeepSeekR1 series of models, and meanwhile carefully maintain the balance between model accuracy

在预训练阶段，我们在 14.8T 的高质量多样化 Token 上训练 DeepSeek-V3。预训练过程非常稳定。在整个训练过程中，我们没有遇到任何不可恢复的损失峰值，也不需要回滚。接下来，我们对 DeepSeek-V3 进行了两阶段的上下文长度扩展。在第一阶段，最大上下文长度扩展到 32K，在第二阶段进一步扩展到 128K。随后，我们对 DeepSeek-V3 的基础模型进行了后训练，包括监督微调 (SFT) 和强化学习 (RL)，以使其与人类偏好对齐并进一步释放其潜力。在后训练阶段，我们从 DeepSeekR1 系列模型中蒸馏出推理能力，同时精心保持模型准确性的平衡。

Table 1 | Training costs of DeepSeek-V3, assuming the rental price of H800 is $\mathbb{9}2$ per GPU hour.

训练成本	预训练	上下文扩展	后训练	总计
H800 GPU 小时数（美元）	2664K $5.328M	119K $0.238M	5K $0.01M	2788K $5.576M

表 1 | DeepSeek-V3 的训练成本，假设 H800 的租赁价格为每 GPU 小时 $\mathbb{9}2$。

and generation length.

生成长度

We evaluate DeepSeek-V3 on a comprehensive array of benchmarks. Despite its economical training costs, comprehensive evaluations reveal that DeepSeek-V3-Base has emerged as the strongest open-source base model currently available, especially in code and math. Its chat version also outperforms other open-source models and achieves performance comparable to leading closed-source models, including GPT-4o and Claude-3.5-Sonnet, on a series of standard and open-ended benchmarks.

我们在多个基准测试上对 DeepSeek-V3 进行了全面评估。尽管训练成本较低，但综合评估显示，DeepSeek-V3-Base 已成为当前最强的开源基础模型，尤其是在代码和数学领域。其聊天版本也在多个标准和开放式基准测试中超越了其他开源模型，并达到了与 GPT-4o 和 Claude-3.5-Sonnet 等领先闭源模型相当的性能。

Lastly, we emphasize again the economical training costs of DeepSeek-V3, summarized in Table 1, achieved through our optimized co-design of algorithms, frameworks, and hardware. During the pre-training stage, training DeepSeek-V3 on each trillion tokens requires only 180K H800 GPU hours, i.e., 3.7 days on our cluster with 2048 H800 GPUs. Consequently, our pretraining stage is completed in less than two months and costs 2664K GPU hours. Combined with 119K GPU hours for the context length extension and 5K GPU hours for post-training, DeepSeek-V3 costs only 2.788M GPU hours for its full training. Assuming the rental price of the $_{\mathrm{H800}},\mathrm{GPU}$ is $\mathbb{S}2$ per GPU hour, our total training costs amount to only $\mathbb{55.576M}$ . Note that the aforementioned costs include only the official training of DeepSeek-V3, excluding the costs associated with prior research and ablation experiments on architectures, algorithms, or data.

最后，我们再次强调 DeepSeek-V3 的经济训练成本，总结在表 1 中，这是通过我们对算法、框架和硬件的优化协同设计实现的。在预训练阶段，训练 DeepSeek-V3 每万亿 Token 仅需 180K H800 GPU 小时，即在我们拥有 2048 个 H800 GPU 的集群上仅需 3.7 天。因此，我们的预训练阶段在不到两个月内完成，消耗了 2664K GPU 小时。加上上下文长度扩展所需的 119K GPU 小时和后训练所需的 5K GPU 小时，DeepSeek-V3 的完整训练仅消耗 2.788M GPU 小时。假设 $_{\mathrm{H800}},\mathrm{GPU}$ 的租赁价格为每小时 $\mathbb{S}2$，我们的总训练成本仅为 $\mathbb{55.576M}$。需要注意的是，上述成本仅包括 DeepSeek-V3 的正式训练，不包括先前在架构、算法或数据上的研究和消融实验的相关成本。

Our main contribution includes:

我们的主要贡献包括：

Architecture: Innovative Load Balancing Strategy and Training Objective

架构：创新的负载均衡策略与训练目标

• On top of the efficient architecture of DeepSeek-V2, we pioneer an auxiliary-loss-free strategy for load balancing, which minimizes the performance degradation that arises from encouraging load balancing. • We investigate a Multi-Token Prediction (MTP) objective and prove it beneficial to model performance. It can also be used for speculative decoding for inference acceleration.

• 在 DeepSeek-V2 的高效架构基础上，我们率先提出了一种无辅助损失的负载均衡策略，该策略最大限度地减少了因鼓励负载均衡而导致的性能下降。
• 我们研究了多 Token 预测 (Multi-Token Prediction, MTP) 目标，并证明其对模型性能有益。它还可用于推测解码 (speculative decoding) 以加速推理。

Pre-Training: Towards Ultimate Training Efficiency

预训练：追求极致的训练效率

• We design an FP8 mixed precision training framework and, for the first time, validate the feasibility and effectiveness of FP8 training on an extremely large-scale model. • Through the co-design of algorithms, frameworks, and hardware, we overcome the communication bottleneck in cross-node MoE training, achieving near-full computationcommunication overlap. This significantly enhances our training efficiency and reduces the training costs, enabling us to further scale up the model size without additional overhead. • At an economical cost of only 2.664M H800 GPU hours, we complete the pre-training of DeepSeek-V3 on 14.8T tokens, producing the currently strongest open-source base model. The subsequent training stages after pre-training require only 0.1M GPU hours.

• 我们设计了一个FP8混合精度训练框架，并首次在超大规模模型上验证了FP8训练的可行性和有效性。
• 通过算法、框架和硬件的协同设计，我们克服了跨节点MoE训练中的通信瓶颈，实现了近乎完全的计算-通信重叠。这显著提升了我们的训练效率，降低了训练成本，使我们能够在没有额外开销的情况下进一步扩大模型规模。
• 在仅花费2.664M H800 GPU小时的经济成本下，我们完成了DeepSeek-V3在14.8T tokens上的预训练，生成了目前最强的开源基础模型。预训练后的后续训练阶段仅需0.1M GPU小时。

Post-Training: Knowledge Distillation from DeepSeek-R1

后训练：从 DeepSeek-R1 进行知识蒸馏

• We introduce an innovative methodology to distill reasoning capabilities from the longChain-of-Thought (CoT) model, specifically from one of the DeepSeek R1 series models, into standard LLMs, particularly DeepSeek-V3. Our pipeline elegantly incorporates the

• 我们引入了一种创新方法，从长链思维（CoT）模型（特别是DeepSeek R1系列模型之一）中提取推理能力，并将其融入标准大语言模型（LLM），特别是DeepSeek-V3。我们的流程巧妙地结合了...

verification and reflection patterns of R1 into DeepSeek-V3 and notably improves its reasoning performance. Meanwhile, we also maintain control over the output style and length of DeepSeek-V3.

将 R1 的验证和反思模式整合到 DeepSeek-V3 中，显著提升了其推理性能。同时，我们也保持了对 DeepSeek-V3 输出风格和长度的控制。

Summary of Core Evaluation Results

核心评估结果总结

• Knowledge: (1) On educational benchmarks such as MMLU, MMLU-Pro, and GPQA, DeepSeek-V3 outperforms all other open-source models, achieving 88.5 on MMLU, 75.9 on MMLU-Pro, and 59.1 on GPQA. Its performance is comparable to leading closed-source models like GPT-4o and Claude-Sonnet-3.5, narrowing the gap between open-source and closed-source models in this domain. (2) For factuality benchmarks, DeepSeek-V3 demonstrates superior performance among open-source models on both SimpleQA and Chinese SimpleQA. While it trails behind GPT-4o and Claude-Sonnet-3.5 in English factual knowledge (SimpleQA), it surpasses these models in Chinese factual knowledge (Chinese SimpleQA), highlighting its strength in Chinese factual knowledge. • Code, Math, and Reasoning: (1) DeepSeek-V3 achieves state-of-the-art performance on math-related benchmarks among all non-long-CoT open-source and closed-source models. Notably, it even outperforms o1-preview on specific benchmarks, such as MATH-500, demonstrating its robust mathematical reasoning capabilities. (2) On coding-related tasks, DeepSeek-V3 emerges as the top-performing model for coding competition benchmarks, such as Live Code Bench, solidifying its position as the leading model in this domain. For engineering-related tasks, while DeepSeek-V3 performs slightly below Claude-Sonnet-3.5, it still outpaces all other models by a significant margin, demonstrating its competitiveness across diverse technical benchmarks.

• 知识：(1) 在教育基准测试如 MMLU、MMLU-Pro 和 GPQA 上，DeepSeek-V3 超越了所有其他开源模型，在 MMLU 上达到 88.5 分，在 MMLU-Pro 上达到 75.9 分，在 GPQA 上达到 59.1 分。其表现与领先的闭源模型如 GPT-4o 和 Claude-Sonnet-3.5 相当，缩小了开源与闭源模型在这一领域的差距。(2) 在事实性基准测试中，DeepSeek-V3 在 SimpleQA 和中文 SimpleQA 上均表现出色，领先于其他开源模型。虽然在英语事实知识 (SimpleQA) 上略逊于 GPT-4o 和 Claude-Sonnet-3.5，但在中文事实知识 (中文 SimpleQA) 上超越了这些模型，突显了其在中文事实知识方面的优势。

• 代码、数学和推理：(1) DeepSeek-V3 在所有非长链推理的开源和闭源模型中，在数学相关基准测试上达到了最先进的性能。值得注意的是，它在特定基准测试如 MATH-500 上甚至超越了 o1-preview，展示了其强大的数学推理能力。(2) 在编码相关任务中，DeepSeek-V3 成为编码竞赛基准测试（如 Live Code Bench）中表现最佳的模型，巩固了其在这一领域的领先地位。在工程相关任务中，尽管 DeepSeek-V3 的表现略低于 Claude-Sonnet-3.5，但仍以显著优势领先于所有其他模型，展示了其在多样化技术基准测试中的竞争力。

In the remainder of this paper, we first present a detailed exposition of our DeepSeek-V3 model architecture (Section 2). Subsequently, we introduce our infrastructures, encompassing our compute clusters, the training framework, the support for FP8 training, the inference deployment strategy, and our suggestions on future hardware design. Next, we describe our pre-training process, including the construction of training data, hyper-parameter settings, longcontext extension techniques, the associated evaluations, as well as some discussions (Section 4). Thereafter, we discuss our efforts on post-training, which include Supervised Fine-Tuning (SFT), Reinforcement Learning (RL), the corresponding evaluations, and discussions (Section 5). Lastly, we conclude this work, discuss existing limitations of DeepSeek-V3, and propose potential directions for future research (Section 6).

在本文的剩余部分，我们首先详细介绍了我们的 DeepSeek-V3 模型架构（第 2 节）。随后，我们介绍了我们的基础设施，包括计算集群、训练框架、对 FP8 训练的支持、推理部署策略以及我们对未来硬件设计的建议。接下来，我们描述了我们的预训练过程，包括训练数据的构建、超参数设置、长上下文扩展技术、相关评估以及一些讨论（第 4 节）。之后，我们讨论了我们在训练后的努力，包括监督微调（SFT）、强化学习（RL）、相应的评估和讨论（第 5 节）。最后，我们总结了这项工作，讨论了 DeepSeek-V3 的现有局限性，并提出了未来研究的潜在方向（第 6 节）。

2. Architecture

2. 架构

We first introduce the basic architecture of DeepSeek-V3, featured by Multi-head Latent Attention (MLA) (DeepSeek-AI, 2024c) for efficient inference and Deep Seek MoE (Dai et al., 2024) for economical training. Then, we present a Multi-Token Prediction (MTP) training objective, which we have observed to enhance the overall performance on evaluation benchmarks. For other minor details not explicitly mentioned, DeepSeek-V3 adheres to the settings of DeepSeekV2 (DeepSeek-AI, 2024c).

我们首先介绍 DeepSeek-V3 的基本架构，其特点是采用多头潜在注意力机制 (Multi-head Latent Attention, MLA) (DeepSeek-AI, 2024c) 以实现高效推理，以及 Deep Seek MoE (Dai et al., 2024) 以实现经济的训练。接着，我们提出了一种多 Token 预测 (Multi-Token Prediction, MTP) 训练目标，我们观察到该目标能够提升在评估基准上的整体性能。对于未明确提及的其他细节，DeepSeek-V3 遵循 DeepSeekV2 (DeepSeek-AI, 2024c) 的设置。

2.1. Basic Architecture

2.1. 基础架构

The basic architecture of DeepSeek-V3 is still within the Transformer (Vaswani et al., 2017) framework. For efficient inference and economical training, DeepSeek-V3 also adopts MLA and Deep Seek MoE, which have been thoroughly validated by DeepSeek-V2. Compared with DeepSeek-V2, an exception is that we additionally introduce an auxiliary-loss-free load balancing strategy (Wang et al., 2024a) for Deep Seek MoE to mitigate the performance degradation induced by the effort to ensure load balance. Figure 2 illustrates the basic architecture of DeepSeek-V3, and we will briefly review the details of MLA and Deep Seek MoE in this section.

DeepSeek-V3 的基本架构仍然在 Transformer (Vaswani et al., 2017) 框架内。为了实现高效的推理和经济性的训练，DeepSeek-V3 还采用了 MLA 和 Deep Seek MoE，这些已经在 DeepSeek-V2 中得到了充分验证。与 DeepSeek-V2 相比，一个例外是我们额外引入了一种无辅助损失的负载均衡策略 (Wang et al., 2024a) 用于 Deep Seek MoE，以减轻因确保负载均衡而导致的性能下降。图 2 展示了 DeepSeek-V3 的基本架构，我们将在本节简要回顾 MLA 和 Deep Seek MoE 的细节。

Figure 2 | Illustration of the basic architecture of DeepSeek-V3. Following DeepSeek-V2, we adopt MLA and Deep Seek MoE for efficient inference and economical training.

图 2 | DeepSeek-V3 的基本架构示意图。我们延续了 DeepSeek-V2 的设计，采用 MLA 和 Deep Seek MoE 来实现高效的推理和经济性的训练。

2.1.1. Multi-Head Latent Attention

2.1.1. 多头潜在注意力 (Multi-Head Latent Attention)

For attention, DeepSeek-V3 adopts the MLA architecture. Let $d$ denote the embedding dimension, $n_{h}$ denote the number of attention heads, $d_{h}$ denote the dimension per head, and $\mathbf{h}_{t}\in\mathbb{R}^{d}$ denote the attention input for the $t^{\th}$ -th token at a given attention layer. The core of MLA is the low-rank joint compression for attention keys and values to reduce Key-Value (KV) cache during inference:

对于注意力机制，DeepSeek-V3 采用了 MLA 架构。设 $d$ 表示嵌入维度，$n_{h}$ 表示注意力头的数量，$d_{h}$ 表示每个头的维度，$\mathbf{h}_{t}\in\mathbb{R}^{d}$ 表示给定注意力层中第 $t^{\th}$ 个 Token 的注意力输入。MLA 的核心是对注意力键和值进行低秩联合压缩，以减少推理过程中的键值 (KV) 缓存：

where $c_{t}^{K V}\in\mathbb{R}^{d_{c}}$ is the compressed latent vector for keys and values; $d_{c}(\ll d_{h}n_{h})$ indicates the KV compression dimension; $\hat{W}^{D K V}\in\mathbb{R}^{d_{c}\times d}$ denotes the down-projection matrix; $W^{U K}$ , $W^{U V}\in\mathbb{R}^{d_{h}n_{h}\times d_{c}}$ are the up-projection matrices for keys and values, respectively; $W^{K R}\in\mathbb{R}^{d_{h}^{R}\times d}$ is the matrix used to produce the decoupled key that carries Rotary Positional Embedding (RoPE) (Su et al., 2024); RoPE(·) denotes the operation that applies RoPE matrices; and $\left[\cdot;\cdot\right]$ denotes concatenation. Note that for MLA, only the blue-boxed vectors (i.e., $\mathbf{c}{t}^{K V}$ and $\mathbf{k}{t}^{R}$ ) need to be cached during generation, which results in significantly reduced KV cache while maintaining performance comparable to standard Multi-Head Attention (MHA) (Vaswani et al., 2017).

其中 $\mathbf{c}{t}^{K V}\in\mathbb{R}^{d{c}}$ 是键和值的压缩潜在向量；$d_{c}(\ll d_{h}n_{h})$ 表示键值压缩维度；$\hat{W}^{D K V}\in\mathbb{R}^{d_{c}\times d}$ 表示下投影矩阵；$W^{U K}$ 和 $W^{U V}\in\mathbb{R}^{d_{h}n_{h}\times d_{c}}$ 分别是键和值的上投影矩阵；$W^{K R}\in\mathbb{R}^{d_{h}^{R}\times d}$ 是用于生成携带旋转位置嵌入 (RoPE) (Su et al., 2024) 的解耦键的矩阵；RoPE(·) 表示应用 RoPE 矩阵的操作；$\left[\cdot;\cdot\right]$ 表示连接操作。需要注意的是，对于 MLA，在生成过程中只需要缓存蓝色框中的向量（即 $\mathbf{c}{t}^{K V}$ 和 $\mathbf{k}{t}^{R}$），这显著减少了键值缓存，同时保持了与标准多头注意力 (MHA) (Vaswani et al., 2017) 相当的性能。

For the attention queries, we also perform a low-rank compression, which can reduce the activation memory during training:

对于注意力查询，我们还执行了低秩压缩，这可以减少训练期间的激活内存：

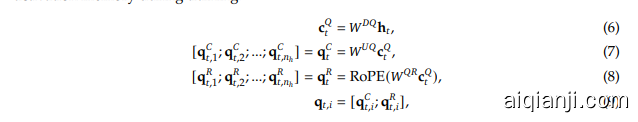
where $\mathbf{c}{t}^{Q};\in;\mathbb{R}^{d{c}^{\prime}}$ is the compressed latent vector for queries; $d_{c}^{\prime}(\ll,d_{h}n_{h})$ denotes the query compression dimension; $W^{D\bar{Q}}\in\mathbb{R}^{d_{c}^{\prime}\times d},W^{U Q}\in\mathbb{R}^{d_{h}n_{h}\times d_{c}^{\prime}}$ are the down-projection and up-projection matrices for queries, respectively; and $W^{Q R}\in\mathbb{R}^{d_{h}^{R}n_{h}\times d_{c}^{\prime}}$ is the matrix to produce the decoupled queries that carry RoPE.

其中 $\mathbf{c}{t}^{Q};\in;\mathbb{R}^{d{c}^{\prime}}$ 是查询的压缩潜在向量；$d_{c}^{\prime}(\ll,d_{h}n_{h})$ 表示查询压缩维度；$W^{D\bar{Q}}\in\mathbb{R}^{d_{c}^{\prime}\times d},W^{U Q}\in\mathbb{R}^{d_{h}n_{h}\times d_{c}^{\prime}}$ 分别是查询的下投影和上投影矩阵；$W^{Q R}\in\mathbb{R}^{d_{h}^{R}n_{h}\times d_{c}^{\prime}}$ 是生成携带 RoPE 的解耦查询的矩阵。

Ultimately, the attention queries $\left(\mathbf{q}{t,i}\right)$ , keys $(\mathbf{k}{j,i})$ , and values $(\mathbf{v}{j,i}^{C})$ are combined to yield the final attention output $\mathbf{u}{t}$ :

最终，注意力查询 $\left(\mathbf{q}{t,i}\right)$、键 $(\mathbf{k}{j,i})$ 和值 $(\mathbf{v}{j,i}^{C})$ 被组合起来，生成最终的注意力输出 $\mathbf{u}{t}$：

where $W^{O}\in\mathbb{R}^{d\times d_{h}n_{h}}$ denotes the output projection matrix.

其中 $W^{O}\in\mathbb{R}^{d\times d_{h}n_{h}}$ 表示输出投影矩阵。

2.1.2. Deep Seek MoE with Auxiliary-Loss-Free Load Balancing

2.1.2. 深度搜索 MoE 与无辅助损失负载均衡

Basic Architecture of Deep Seek MoE. For Feed-Forward Networks (FFNs), DeepSeek-V3 employs the Deep Seek MoE architecture (Dai et al., 2024). Compared with traditional MoE architectures like GShard (Lepikhin et al., 2021), Deep Seek MoE uses finer-grained experts and isolates some experts as shared ones. Let $\mathbf{u}{t}$ denote the FFN input of the $t^{\th}$ -th token, we compute the FFN output $\mathbf{h}{t}^{\prime}$ as follows:

Deep Seek MoE 的基础架构。对于前馈网络 (FFNs)，DeepSeek-V3 采用了 Deep Seek MoE 架构 (Dai et al., 2024)。与传统的 MoE 架构（如 GShard (Lepikhin et al., 2021)）相比，Deep Seek MoE 使用了更细粒度的专家，并将部分专家隔离为共享专家。设 $\mathbf{u}{t}$ 表示第 $t^{\th}$ 个 Token 的 FFN 输入，我们计算 FFN 输出 $\mathbf{h}{t}^{\prime}$ 如下：

where $N_{s}$ and $N_{r}$ denote the numbers of shared experts and routed experts, respectively; $\mathrm{FFN}{i}^{(s)}(\cdot)$ and $\mathrm{FFN}{i}^{(r)}(\cdot)$ denote the 𝑖-th shared expert and the $i\footnote{C o r r e s p o n d i n g a u t h o r.T e l:~+86-1088236095.E-m a i l a d d e n s c o n s t r a d d e n s c o n s t i o n s t i c a l l o r.}$ -th routed expert, respectively; $K_{r}$ denotes the number of activated routed experts; $g_{i,t}$ is the gating value for the $i^{\th}$ -th expert; $s_{i,t}$ is the token-to-expert affinity; $\mathbf{e}_{i}$ is the centroid vector of the $i^{\th}$ -th routed expert; and $\mathrm{Topk}(\cdot,K)$ denotes the set comprising $K$ highest scores among the affinity scores calculated for the $t$ -th token and all routed experts. Slightly different from DeepSeek-V2, DeepSeek-V3 uses the sigmoid function to compute the affinity scores, and applies a normalization among all selected affinity scores to produce the gating values.

其中 $N_{s}$ 和 $N_{r}$ 分别表示共享专家和路由专家的数量；$\mathrm{FFN}{i}^{(s)}(\cdot)$ 和 $\mathrm{FFN}{i}^{(r)}(\cdot)$ 分别表示第 $i$ 个共享专家和第 $i$ 个路由专家；$K_{r}$ 表示激活的路由专家数量；$g_{i,t}$ 是第 $i$ 个专家的门控值；$s_{i,t}$ 是 Token 到专家的亲和度；$\mathbf{e}_{i}$ 是第 $i$ 个路由专家的质心向量；$\mathrm{Topk}(\cdot,K)$ 表示在第 $t$ 个 Token 和所有路由专家之间计算的亲和度得分中，包含 $K$ 个最高得分的集合。与 DeepSeek-V2 略有不同，DeepSeek-V3 使用 sigmoid 函数计算亲和度得分，并在所有选定的亲和度得分之间进行归一化以生成门控值。

Auxiliary-Loss-Free Load Balancing. For MoE models, an unbalanced expert load will lead to routing collapse (Shazeer et al., 2017) and diminish computational efficiency in scenarios with expert parallelism. Conventional solutions usually rely on the auxiliary loss (Fedus et al., 2021; Lepikhin et al., 2021) to avoid unbalanced load. However, too large an auxiliary loss will impair the model performance (Wang et al., 2024a). To achieve a better trade-off between load balance and model performance, we pioneer an auxiliary-loss-free load balancing strategy (Wang et al., 2024a) to ensure load balance. To be specific, we introduce a bias term $b_{i}$ for each expert and add it to the corresponding affinity scores $s_{i,t}$ to determine the top-K routing:

无辅助损失负载均衡。对于 MoE 模型，专家负载不均衡会导致路由崩溃 (Shazeer et al., 2017)，并在专家并行场景中降低计算效率。传统解决方案通常依赖辅助损失 (Fedus et al., 2021; Lepikhin et al., 2021) 来避免负载不均衡。然而，过大的辅助损失会损害模型性能 (Wang et al., 2024a)。为了在负载均衡和模型性能之间取得更好的平衡，我们首创了一种无辅助损失的负载均衡策略 (Wang et al., 2024a) 来确保负载均衡。具体来说，我们为每个专家引入一个偏置项 $b_{i}$，并将其添加到相应的亲和度分数 $s_{i,t}$ 中以确定 top-K 路由：

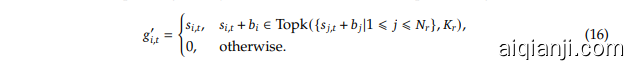
Note that the bias term is only used for routing. The gating value, which will be multiplied with the FFN output, is still derived from the original affinity score $s_{i,t}$ . During training, we keep monitoring the expert load on the whole batch of each training step. At the end of each step, we will decrease the bias term by $\gamma$ if its corresponding expert is overloaded, and increase it by $\gamma$ if its corresponding expert is under loaded, where $\gamma$ is a hyper-parameter called bias update speed. Through the dynamic adjustment, DeepSeek-V3 keeps balanced expert load during training, and achieves better performance than models that encourage load balance through pure auxiliary losses.

需要注意的是，偏置项仅用于路由。与FFN输出相乘的门控值仍然来源于原始的亲和度得分 $s_{i,t}$ 。在训练过程中，我们持续监控每个训练步骤中整个批次的专家负载。在每个步骤结束时，如果对应的专家过载，我们会将偏置项减少 $\gamma$ ；如果对应的专家负载不足，则增加 $\gamma$ ，其中 $\gamma$ 是一个称为偏置更新速度的超参数。通过这种动态调整，DeepSeek-V3 在训练过程中保持了专家负载的平衡，并且比仅通过纯辅助损失来鼓励负载平衡的模型表现更好。

Complementary Sequence-Wise Auxiliary Loss. Although DeepSeek-V3 mainly relies on the auxiliary-loss-free strategy for load balance, to prevent extreme imbalance within any single sequence, we also employ a complementary sequence-wise balance loss:

互补序列辅助损失。尽管 DeepSeek-V3 主要依赖无辅助损失的策略来实现负载均衡，但为了防止任何单个序列内的极端不平衡，我们还采用了互补的序列平衡损失：

where the balance factor $\alpha$ is a hyper-parameter, which will be assigned an extremely small value for DeepSeek-V3; $\mathbb{1}(\cdot)$ denotes the indicator function; and $T$ denotes the number of tokens in a sequence. The sequence-wise balance loss encourages the expert load on each sequence to be balanced.

其中平衡因子 $\alpha$ 是一个超参数，对于 DeepSeek-V3 将被赋予一个极小的值；$\mathbb{1}(\cdot)$ 表示指示函数；$T$ 表示序列中的 Token 数量。序列级别的平衡损失鼓励每个序列上的专家负载保持平衡。

Figure 3 | Illustration of our Multi-Token Prediction (MTP) implementation. We keep the complete causal chain for the prediction of each token at each depth.

图 3 | 我们的多 Token 预测 (MTP) 实现示意图。我们在每个深度保留完整的因果链以预测每个 Token。

Node-Limited Routing. Like the device-limited routing used by DeepSeek-V2, DeepSeek-V3 also uses a restricted routing mechanism to limit communication costs during training. In short, we ensure that each token will be sent to at most 𝑀nodes, which are selected according to the sum of the highest $\frac{K_{r}}{M}$ affinity scores of the experts distributed on each node. Under this constraint, our MoE training framework can nearly achieve full computation-communication overlap.

节点限制路由。与 DeepSeek-V2 使用的设备限制路由类似，DeepSeek-V3 也采用了受限的路由机制来限制训练期间的通信成本。简而言之，我们确保每个 Token 最多只会被发送到 𝑀 个节点，这些节点是根据分布在每个节点上的专家中亲和度得分最高的 $\frac{K_{r}}{M}$ 的总和来选择的。在这种约束下，我们的 MoE 训练框架几乎可以实现计算与通信的完全重叠。

No Token-Dropping. Due to the effective load balancing strategy, DeepSeek-V3 keeps a good load balance during its full training. Therefore, DeepSeek-V3 does not drop any tokens during training. In addition, we also implement specific deployment strategies to ensure inference load balance, so DeepSeek-V3 also does not drop tokens during inference.

无Token丢弃。由于有效的负载均衡策略，DeepSeek-V3在整个训练过程中保持了良好的负载平衡。因此，DeepSeek-V3在训练期间不会丢弃任何Token。此外，我们还实施了特定的部署策略以确保推理负载平衡，因此DeepSeek-V3在推理期间也不会丢弃Token。

2.2. Multi-Token Prediction

2.2. 多Token预测

Inspired by Gloeckle et al. (2024), we investigate and set a Multi-Token Prediction (MTP) objective for DeepSeek-V3, which extends the prediction scope to multiple future tokens at each position. On the one hand, an MTP objective densifies the training signals and may improve data efficiency. On the other hand, MTP may enable the model to pre-plan its representations for better prediction of future tokens. Figure 3 illustrates our implementation of MTP. Different from Gloeckle et al. (2024), which parallelly predicts $D$ additional tokens using independent output heads, we sequentially predict additional tokens and keep the complete causal chain at each prediction depth. We introduce the details of our MTP implementation in this section.

受 Gloeckle 等人 (2024) 的启发，我们为 DeepSeek-V3 研究并设定了多 Token 预测 (MTP) 目标，该目标将预测范围扩展到每个位置的多个未来 Token。一方面，MTP 目标增加了训练信号的密度，可能会提高数据效率。另一方面，MTP 可能使模型能够预先规划其表示，以更好地预测未来的 Token。图 3 展示了我们的 MTP 实现。与 Gloeckle 等人 (2024) 使用独立的输出头并行预测 $D$ 个额外 Token 不同，我们按顺序预测额外的 Token，并在每个预测深度保持完整的因果链。我们在本节中介绍了 MTP 实现的细节。

MTP Modules. To be specific, our MTP implementation uses $D$ sequential modules to predict $D$ additional tokens. The $k$ -th MTP module consists of a shared embedding layer $\operatorname{Emb}(\cdot)$ , a shared output head OutHead $(\cdot)$ , a Transformer block $\mathrm{TRM}{k}(\cdot){\cdot}$ , and a projection matrix $M_{k}\in\mathbb{R}^{d\times2d}$ . For the $i\cdot$ -th input token $t_{i},$ at the $k$ -th prediction depth, we first combine the representation of the $i$ -th token at the $(k-1)$ -th depth $\mathbf{h}{i}^{k-1}\in\mathbb{R}^{d}$ and the embedding of the $(i+k)$ -th token $E m b(t{i+k})\in\mathbb{R}^{d}$

MTP 模块。具体来说，我们的 MTP 实现使用 $D$ 个顺序模块来预测 $D$ 个额外的 Token。第 $k$ 个 MTP 模块由一个共享的嵌入层 $\operatorname{Emb}(\cdot)$、一个共享的输出头 OutHead $(\cdot)$、一个 Transformer 块 $\mathrm{TRM}{k}(\cdot){\cdot}$ 和一个投影矩阵 $M_{k}\in\mathbb{R}^{d\times2d}$ 组成。对于第 $i$ 个输入 Token $t_{i},$ 在第 $k$ 个预测深度，我们首先将第 $(k-1)$ 个深度的第 $i$ 个 Token 的表示 $\mathbf{h}{i}^{k-1}\in\mathbb{R}^{d}$ 和第 $(i+k)$ 个 Token 的嵌入 $E m b(t{i+k})\in\mathbb{R}^{d}$ 结合起来。

where $\left[\cdot;\cdot\right]$ denotes concatenation. Especially, when $k=1,\mathbf{h}{i}^{k-1}$ refers to the representation given by the main model. Note that for each MTP module, its embedding layer is shared with the main model. The combined $\mathbf{h}{i}^{\prime k}$ serves as the input of the Transformer block at the $k$ -th depth to produce the output representation at the current depth $\mathbf{h}_{i}^{k}$ :

其中 $\left[\cdot;\cdot\right]$ 表示拼接。特别地，当 $k=1$ 时，$\mathbf{h}{i}^{k-1}$ 指的是主模型给出的表示。注意，对于每个 MTP 模块，其嵌入层与主模型共享。组合后的 $\mathbf{h}{i}^{\prime k}$ 作为第 $k$ 层深度的 Transformer 块的输入，以生成当前深度的输出表示 $\mathbf{h}_{i}^{k}$：

where $T$ represents the input sequence length and $i{:}j$ denotes the slicing operation (inclusive of both the left and right boundaries). Finally, taking $\mathbf{h}{i}^{k}$ as the input, the shared output head will compute the probability distribution for the $k$ -th additional prediction token $P{i+1+k}^{k}\in\mathbb{R}^{V}.$ , where is the vocabulary size:

其中 $T$ 表示输入序列长度，$i{:}j$ 表示切片操作（包括左右边界）。最后，以 $\mathbf{h}{i}^{k}$ 作为输入，共享的输出头将计算第 $k$ 个额外预测 Token 的概率分布 $P{i+1+k}^{k}\in\mathbb{R}^{V}$，其中 $V$ 是词汇表大小：

The output head OutHead $(\cdot)$ linearly maps the representation to logits and subsequently applies the Softmax(·) function to compute the prediction probabilities of the $k$ -th additional token. Also, for each MTP module, its output head is shared with the main model. Our principle of maintaining the causal chain of predictions is similar to that of EAGLE (Li et al., 2024b), but its primary objective is speculative decoding (Leviathan et al., 2023; Xia et al., 2023), whereas we utilize MTP to improve training.

输出头 OutHead $(\cdot)$ 将表示线性映射到 logits，随后应用 Softmax(·) 函数来计算第 $k$ 个附加 token 的预测概率。此外，对于每个 MTP 模块，其输出头与主模型共享。我们保持预测因果链的原则与 EAGLE (Li et al., 2024b) 类似，但其主要目标是推测解码 (Leviathan et al., 2023; Xia et al., 2023)，而我们利用 MTP 来改进训练。

MTP Training Objective. For each prediction depth, we compute a cross-entropy loss $\mathcal{L}_{\mathrm{MTP}}^{k}$

MTP 训练目标。对于每个预测深度，我们计算交叉熵损失 $\mathcal{L}_{\mathrm{MTP}}^{k}$。

where $T$ denotes the input sequence length, $t_{i}$ denotes the ground-truth token at the $i\cdot$ -th position, and $P_{i}^{k}[t_{i}]$ denotes the corresponding prediction probability of $t_{i},$ given by the $k$ -th MTP module. Finally, we compute the average of the MTP losses across all depths and multiply it by a weighting factor $\lambda$ to obtain the overall MTP loss ${\mathcal{L}}_{\mathrm{MTP}}$ , which serves as an additional training objective for DeepSeek-V3:

其中 $T$ 表示输入序列长度，$t_{i}$ 表示第 $i$ 个位置的真实 Token，$P_{i}^{k}[t_{i}]$ 表示第 $k$ 个 MTP 模块给出的 $t_{i}$ 的对应预测概率。最后，我们计算所有深度的 MTP 损失的平均值，并乘以权重因子 $\lambda$ 以获得整体 MTP 损失 ${\mathcal{L}}_{\mathrm{MTP}}$，作为 DeepSeek-V3 的额外训练目标：

MTP in Inference. Our MTP strategy mainly aims to improve the performance of the main model, so during inference, we can directly discard the MTP modules and the main model can function independently and normally. Additionally, we can also repurpose these MTP modules for speculative decoding to further improve the generation latency.

推理中的 MTP。我们的 MTP 策略主要旨在提高主模型的性能，因此在推理过程中，我们可以直接丢弃 MTP 模块，主模型可以独立且正常地运行。此外，我们还可以将这些 MTP 模块重新用于推测解码，以进一步减少生成延迟。

3. Infrastructures

3. 基础设施

3.1. Compute Clusters

3.1. 计算集群

DeepSeek-V3 is trained on a cluster equipped with 2048 NVIDIA H800 GPUs. Each node in the H800 cluster contains 8 GPUs connected by NVLink and NVSwitch within nodes. Across different nodes, InfiniBand (IB) interconnects are utilized to facilitate communications.

DeepSeek-V3 在配备 2048 个 NVIDIA H800 GPU 的集群上进行训练。H800 集群中的每个节点包含 8 个 GPU，通过节点内的 NVLink 和 NVSwitch 连接。不同节点之间使用 InfiniBand (IB) 互连以促进通信。

3.2. Training Framework

3.2. 训练框架

The training of DeepSeek-V3 is supported by the HAI-LLM framework, an efficient and lightweight training framework crafted by our engineers from the ground up. On the whole, DeepSeek-V3 applies 16-way Pipeline Parallelism (PP) (Qi et al., 2023a), 64-way Expert Parallelism (EP) (Lepikhin et al., 2021) spanning 8 nodes, and ZeRO-1 Data Parallelism (DP) (Rajbhandari et al., 2020).

DeepSeek-V3 的训练由 HAI-LLM 框架支持，这是一个由我们的工程师从头构建的高效且轻量级的训练框架。总体而言，DeepSeek-V3 应用了 16 路流水线并行 (Pipeline Parallelism, PP) (Qi et al., 2023a)、跨 8 个节点的 64 路专家并行 (Expert Parallelism, EP) (Lepikhin et al., 2021)，以及 ZeRO-1 数据并行 (Data Parallelism, DP) (Rajbhandari et al., 2020)。

In order to facilitate efficient training of DeepSeek-V3, we implement meticulous engineering optimization s. Firstly, we design the DualPipe algorithm for efficient pipeline parallelism. Compared with existing PP methods, DualPipe has fewer pipeline bubbles. More importantly, it overlaps the computation and communication phases across forward and backward processes, thereby addressing the challenge of heavy communication overhead introduced by cross-node expert parallelism. Secondly, we develop efficient cross-node all-to-all communication kernels to fully utilize IB and NVLink bandwidths and conserve Streaming Multiprocessors (SMs) dedicated to communication. Finally, we meticulously optimize the memory footprint during training, thereby enabling us to train DeepSeek-V3 without using costly Tensor Parallelism (TP).

为了高效训练 DeepSeek-V3，我们实施了精细的工程优化。首先，我们设计了 DualPipe 算法以实现高效的流水线并行。与现有的流水线并行方法相比，DualPipe 的流水线气泡更少。更重要的是，它在前向和后向过程中重叠了计算和通信阶段，从而解决了跨节点专家并行引入的通信开销大的挑战。其次，我们开发了高效的跨节点全对全通信内核，以充分利用 IB 和 NVLink 带宽，并节省专用于通信的流式多处理器 (SMs)。最后，我们精心优化了训练期间的内存占用，从而使得我们能够在无需使用昂贵的张量并行 (TP) 的情况下训练 DeepSeek-V3。

3.2.1. DualPipe and Computation-Communication Overlap

3.2.1. DualPipe 与计算-通信重叠

For DeepSeek-V3, the communication overhead introduced by cross-node expert parallelism results in an inefficient computation-to-communication ratio of approximately 1:1. To tackle this challenge, we design an innovative pipeline parallelism algorithm called DualPipe, which not only accelerates model training by effectively overlapping forward and backward computationcommunication phases, but also reduces the pipeline bubbles.

对于 DeepSeek-V3，跨节点专家并行引入的通信开销导致计算与通信的比例约为 1:1，效率较低。为了解决这一挑战，我们设计了一种创新的流水线并行算法，称为 DualPipe，该算法不仅通过有效重叠前向和后向计算通信阶段来加速模型训练，还减少了流水线气泡。

The key idea of DualPipe is to overlap the computation and communication within a pair of individual forward and backward chunks. To be specific, we divide each chunk into four components: attention, all-to-all dispatch, MLP, and all-to-all combine. Specially, for a backward chunk, both attention and MLP are further split into two parts, backward for input and backward for weights, like in ZeroBubble (Qi et al., 2023b). In addition, we have a PP communication component. As illustrated in Figure 4, for a pair of forward and backward chunks, we rearrange these components and manually adjust the ratio of GPU SMs dedicated to communication versus computation. In this overlapping strategy, we can ensure that both all-to-all and PP communication can be fully hidden during execution. Given the efficient overlapping strategy, the full DualPipe scheduling is illustrated in Figure 5. It employs a bidirectional pipeline scheduling, which feeds micro-batches from both ends of the pipeline simultaneously and a significant portion of communications can be fully overlapped. This overlap also ensures that, as the model further scales up, as long as we maintain a constant computation-to-communication ratio, we can still employ fine-grained experts across nodes while achieving a near-zero all-to-all communication overhead.

DualPipe 的核心思想是在一对独立的前向和后向块中重叠计算和通信。具体来说，我们将每个块分为四个部分：注意力 (attention)、全对全分发 (all-to-all dispatch)、MLP 和全对全合并 (all-to-all combine)。特别地，对于后向块，注意力和 MLP 都进一步分为两部分，即输入的后向和权重的后向，类似于 ZeroBubble (Qi et al., 2023b)。此外，我们还有一个 PP 通信部分。如图 4 所示，对于一对前向和后向块，我们重新排列这些部分，并手动调整 GPU SMs 用于通信与计算的比例。在这种重叠策略中，我们可以确保全对全和 PP 通信在执行过程中完全隐藏。鉴于这种高效的重叠策略，完整的 DualPipe 调度如图 5 所示。它采用了双向流水线调度，同时从流水线的两端输入微批次，并且大部分通信可以完全重叠。这种重叠还确保了随着模型的进一步扩展，只要我们保持恒定的计算与通信比例，我们仍然可以在节点之间使用细粒度的专家，同时实现接近零的全对全通信开销。

Figure 5 | Example DualPipe scheduling for 8 PP ranks and 20 micro-batches in two directions. The micro-batches in the reverse direction are symmetric to those in the forward direction, so we omit their batch ID for illustration simplicity. Two cells enclosed by a shared black border have mutually overlapped computation and communication.

图 5 | 8 个 PP 等级和 20 个微批次在两个方向上的 DualPipe 调度示例。反向的微批次与正向的微批次对称，因此为了简化说明，我们省略了它们的批次 ID。由共享黑色边框包围的两个单元格具有相互重叠的计算和通信。

方法	Bubble	参数	激活
1F1B	(PP -1)(F + B)	1x	PP
ZB1P	(PP - 1)(F + B - 2W)	1x	PP
DualPipe (Ours)	(P -1)(F&B+ B - 3W)	2x	PP+1

Table 2 | Comparison of pipeline bubbles and memory usage across different pipeline parallel methods. $F$ denotes the execution time of a forward chunk, $B$ denotes the execution time of a full backward chunk, 𝑊denotes the execution time of a "backward for weights" chunk, and $F&B$ denotes the execution time of two mutually overlapped forward and backward chunks.

表 2 | 不同流水线并行方法中的流水线气泡和内存使用情况对比。$F$ 表示前向块 (forward chunk) 的执行时间，$B$ 表示完整反向块 (full backward chunk) 的执行时间，$W$ 表示“权重反向块” (backward for weights chunk) 的执行时间，$F&B$ 表示两个相互重叠的前向和反向块的执行时间。

In addition, even in more general scenarios without a heavy communication burden, DualPipe still exhibits efficiency advantages. In Table 2, we summarize the pipeline bubbles and memory usage across different PP methods. As shown in the table, compared with ZB1P (Qi et al., 2023b) and 1F1B (Harlap et al., 2018), DualPipe significantly reduces the pipeline bubbles while only increasing the peak activation memory by $\frac{1}{P P}$ times. Although DualPipe requires keeping two copies of the model parameters, this does not significantly increase the memory consumption since we use a large EP size during training. Compared with Chimera (Li and Hoefler, 2021), DualPipe only requires that the pipeline stages and micro-batches be divisible by 2, without requiring micro-batches to be divisible by pipeline stages. In addition, for DualPipe, neither the bubbles nor activation memory will increase as the number of micro-batches grows.

此外，即使在通信负担不重的更一般场景中，DualPipe 仍然展现出效率优势。在表 2 中，我们总结了不同流水线并行 (PP) 方法中的流水线气泡和内存使用情况。如表所示，与 ZB1P (Qi et al., 2023b) 和 1F1B (Harlap et al., 2018) 相比，DualPipe 显著减少了流水线气泡，同时仅将峰值激活内存增加了 $\frac{1}{P P}$ 倍。尽管 DualPipe 需要保留两份模型参数副本，但由于我们在训练时使用了较大的 EP 大小，这并不会显著增加内存消耗。与 Chimera (Li and Hoefler, 2021) 相比，DualPipe 仅要求流水线阶段和微批次可被 2 整除，而不要求微批次可被流水线阶段整除。此外，对于 DualPipe 来说，无论是气泡还是激活内存都不会随着微批次数量的增加而增加。

3.2.2. Efficient Implementation of Cross-Node All-to-All Communication

3.2.2. 跨节点全对全通信的高效实现

In order to ensure sufficient computational performance for DualPipe, we customize efficient cross-node all-to-all communication kernels (including dispatching and combining) to conserve the number of SMs dedicated to communication. The implementation of the kernels is codesigned with the MoE gating algorithm and the network topology of our cluster. To be specific, in our cluster, cross-node GPUs are fully interconnected with IB, and intra-node communications are handled via NVLink. NVLink offers a bandwidth of 160 GB/s, roughly 3.2 times that of IB $(50,\mathrm{GB}/\mathrm{s})$ . To effectively leverage the different bandwidths of IB and NVLink, we limit each token to be dispatched to at most 4 nodes, thereby reducing IB traffic. For each token, when its routing decision is made, it will first be transmitted via IB to the GPUs with the same in-node index on its target nodes. Once it reaches the target nodes, we will endeavor to ensure that it is instantaneously forwarded via NVLink to specific GPUs that host their target experts, without being blocked by subsequently arriving tokens. In this way, communications via IB and NVLink are fully overlapped, and each token can efficiently select an average of 3.2 experts per node without incurring additional overhead from NVLink. This implies that, although DeepSeek-V3 selects only 8 routed experts in practice, it can scale up this number to a maximum of 13 experts (4 nodes $\times,3.2$ experts/node) while preserving the same communication cost. Overall, under such a communication strategy, only 20 SMs are sufficient to fully utilize the bandwidths of IB and NVLink.

为了确保 DualPipe 具备足够的计算性能，我们定制了高效的跨节点全对全通信内核（包括分发和合并），以减少专用于通信的 SM 数量。这些内核的实现与 MoE 门控算法和我们集群的网络拓扑共同设计。具体来说，在我们的集群中，跨节点 GPU 通过 IB 完全互连，节点内通信则通过 NVLink 处理。NVLink 提供 160 GB/s 的带宽，大约是 IB $(50,\mathrm{GB}/\mathrm{s})$ 的 3.2 倍。为了有效利用 IB 和 NVLink 的不同带宽，我们将每个 token 分发的节点数限制为最多 4 个，从而减少 IB 流量。对于每个 token，当路由决策完成后，它将首先通过 IB 传输到目标节点上具有相同节点内索引的 GPU。一旦到达目标节点，我们将尽力确保它通过 NVLink 即时转发到托管其目标专家的特定 GPU，而不会被后续到达的 token 阻塞。通过这种方式，IB 和 NVLink 的通信完全重叠，每个 token 可以高效地选择每个节点平均 3.2 个专家，而不会产生额外的 NVLink 开销。这意味着，尽管 DeepSeek-V3 在实践中仅选择 8 个路由专家，但它可以将此数量扩展到最多 13 个专家（4 个节点 $\times,3.2$ 个专家/节点），同时保持相同的通信成本。总体而言，在这种通信策略下，仅需 20 个 SM 即可充分利用 IB 和 NVLink 的带宽。

In detail, we employ the warp specialization technique (Bauer et al., 2014) and partition 20 SMs into 10 communication channels. During the dispatching process, (1) IB sending, (2) IB-to-NVLink forwarding, and (3) NVLink receiving are handled by respective warps. The number of warps allocated to each communication task is dynamically adjusted according to the actual workload across all SMs. Similarly, during the combining process, (1) NVLink sending, (2) NVLink-to-IB forwarding and accumulation, and (3) IB receiving and accumulation are also handled by dynamically adjusted warps. In addition, both dispatching and combining kernels overlap with the computation stream, so we also consider their impact on other SM computation kernels. Specifically, we employ customized PTX (Parallel Thread Execution) instructions and auto-tune the communication chunk size, which significantly reduces the use of the L2 cache and the interference to other SMs.

具体来说，我们采用了 warp specialization 技术 (Bauer et al., 2014)，并将 20 个 SM 划分为 10 个通信通道。在调度过程中，(1) IB 发送、(2) IB 到 NVLink 转发以及 (3) NVLink 接收分别由各自的 warp 处理。分配给每个通信任务的 warp 数量会根据所有 SM 的实际工作负载动态调整。同样，在合并过程中，(1) NVLink 发送、(2) NVLink 到 IB 转发和累加以及 (3) IB 接收和累加也由动态调整的 warp 处理。此外，调度和合并的内核与计算流重叠，因此我们还考虑了它们对其他 SM 计算内核的影响。具体来说，我们采用了定制的 PTX (Parallel Thread Execution) 指令，并自动调整通信块大小，这显著减少了 L2 缓存的使用以及对其他 SM 的干扰。

3.2.3. Extremely Memory Saving with Minimal Overhead

3.2.3. 极低内存占用与最小开销

In order to reduce the memory footprint during training, we employ the following techniques.

为了减少训练期间的内存占用，我们采用了以下技术。

Re computation of RMSNorm and MLA Up-Projection. We recompute all RMSNorm operations and MLA up-projections during back-propagation, thereby eliminating the need to persistently store their output activation s. With a minor overhead, this strategy significantly reduces memory requirements for storing activation s.

重新计算 RMSNorm 和 MLA 上投影。我们在反向传播期间重新计算所有 RMSNorm 操作和 MLA 上投影，从而消除了持久存储其输出激活的需求。通过少量的开销，该策略显著减少了存储激活的内存需求。

Exponential Moving Average in CPU. During training, we preserve the Exponential Moving Average (EMA) of the model parameters for early estimation of the model performance after learning rate decay. The EMA parameters are stored in CPU memory and are updated asynchronously after each training step. This method allows us to maintain EMA parameters without incurring additional memory or time overhead.

CPU 中的指数移动平均。在训练过程中，我们保留模型参数的指数移动平均 (EMA)，以便在学习率衰减后对模型性能进行早期估计。EMA 参数存储在 CPU 内存中，并在每个训练步骤后异步更新。这种方法使我们能够在不增加额外内存或时间开销的情况下维护 EMA 参数。

Shared Embedding and Output Head for Multi-Token Prediction. With the DualPipe strategy, we deploy the shallowest layers (including the embedding layer) and deepest layers (including the output head) of the model on the same PP rank. This arrangement enables the physical sharing of parameters and gradients, of the shared embedding and output head, between the MTP module and the main model. This physical sharing mechanism further enhances our memory efficiency.

共享嵌入和输出头用于多Token预测。通过DualPipe策略，我们将模型的最浅层（包括嵌入层）和最深层（包括输出头）部署在同一个PP rank上。这种安排使得MTP模块和主模型之间能够物理共享共享嵌入和输出头的参数和梯度。这种物理共享机制进一步提高了我们的内存效率。

3.3. FP8 Training

3.3. FP8 训练

Inspired by recent advances in low-precision training (Dettmers et al., 2022; Noune et al., 2022; Peng et al., 2023b), we propose a fine-grained mixed precision framework utilizing the FP8 data format for training DeepSeek-V3. While low-precision training holds great promise, it is often limited by the presence of outliers in activation s, weights, and gradients (Fishman et al., 2024; He et al.; Sun et al., 2024). Although significant progress has been made in inference quantization (Frantar et al., 2022; Xiao et al., 2023), there are relatively few studies demonstrating successful application of low-precision techniques in large-scale language model pre-training (Fishman et al., 2024). To address thi或s ch alI len np ge u at-nd> eAf fc ect it iv veal ty i eoxnte_ndL the dynamic range of the FP8 format, we introduce a fine-grained quantization strategy: tile-wise grouping with $1\times N_{c}$ elements or block-wise grouping with $N_{c}\times N_{c}$ ue tle pm ue tn-t>s. ATchtei a vs s a otc iio at ned {dLeq+u1an}tiza- tion overhead is largely mitigated under our increased-precision accumulation process, a critical aspect for achieving accurate FP8 General Matrix Multiplication (GEMM). Moreover, to further reduce memory and communication overhead in MoE training, we cache and dispatch activations in FP8, while storing low-precision optimizer states in BF16. We validate the proposed FP8 mixed precision framework on two model scales similar to DeepSeek-V2-Lite and DeepSeekV2, training for approximately 1 trillion tokens (see more details in Appendix B.1). Notably, compared with the BF16 baseline, the relative loss error of our FP8-training model remains consistently below $0.25%$ , a level well within the acceptable range of training randomness.

受低精度训练（Dettmers et al., 2022; Noune et al., 2022; Peng et al., 2023b）最新进展的启发，我们提出了一种利用 FP8 数据格式的细粒度混合精度框架，用于训练 DeepSeek-V3。虽然低精度训练具有巨大的潜力，但它通常受到激活值、权重和梯度中异常值的限制（Fishman et al., 2024; He et al.; Sun et al., 2024）。尽管在推理量化方面取得了显著进展（Frantar et al., 2022; Xiao et al., 2023），但在大规模语言模型预训练中成功应用低精度技术的研究相对较少（Fishman et al., 2024）。为了解决这一挑战并有效利用 FP8 格式的动态范围，我们引入了一种细粒度的量化策略：使用 $1\times N_{c}$ 元素的瓦片分组或 $N_{c}\times N_{c}$ 元素的块分组。在我们的增加精度累积过程中，量化开销得到了大幅缓解，这是实现精确 FP8 通用矩阵乘法（GEMM）的关键。此外，为了进一步减少 MoE 训练中的内存和通信开销，我们以 FP8 缓存和分发激活值，同时以 BF16 存储低精度优化器状态。我们在与 DeepSeek-V2-Lite 和 DeepSeekV2 相似的两个模型规模上验证了所提出的 FP8 混合精度框架，训练了大约 1 万亿个 token（更多细节见附录 B.1）。值得注意的是，与 BF16 基线相比，我们的 FP8 训练模型的相对损失误差始终保持在 $0.25%$ 以下，这一水平完全在训练随机性的可接受范围内。

Figure 6 | The overall mixed precision framework with FP8 data format. For clarification, only the Linear operator is illustrated.

图 6 | 使用 FP8 数据格式的整体混合精度框架。为清晰起见，仅展示了线性算子。

3.3.1. Mixed Precision Framework

3.3.1. 混合精度框架

Building upon widely adopted techniques in low-precision training (Kalamkar et al., 2019; Narang et al., 2017), we propose a mixed precision framework for FP8 training. In this framework, most compute-density operations are conducted in FP8, while a few key operations are strategically maintained in their original data formats to balance training efficiency and numerical stability. The overall framework is illustrated in Figure 6.

基于广泛采用的低精度训练技术 (Kalamkar et al., 2019; Narang et al., 2017)，我们提出了一种用于 FP8 训练的混合精度框架。在该框架中，大多数计算密集型操作以 FP8 进行，而少数关键操作则策略性地保持其原始数据格式，以平衡训练效率和数值稳定性。整体框架如图 6 所示。

Firstly, in order to accelerate model training, the majority of core computation kernels, i.e., GEMM operations, are implemented in FP8 precision. These GEMM operations accept FP8 tensors as inputs and produce outputs in BF16 or FP32. As depicted in Figure 6, all three GEMMs associated with the Linear operator, namely Fprop (forward pass), Dgrad (activation backward pass), and Wgrad (weight backward pass), are executed in FP8. This design theoretically doubles the computational speed compared with the original BF16 method. Additionally, the FP8 Wgrad GEMM allows activation s to be stored in FP8 for use in the backward pass. This significantly reduces memory consumption.

首先，为了加速模型训练，大多数核心计算内核（即 GEMM 操作）都以 FP8 精度实现。这些 GEMM 操作接受 FP8 张量作为输入，并生成 BF16 或 FP32 的输出。如图 6 所示，与 Linear 算子相关的三个 GEMM 操作，即 Fprop（前向传播）、Dgrad（激活反向传播）和 Wgrad（权重反向传播），均在 FP8 中执行。理论上，这种设计使计算速度比原始的 BF16 方法提高了一倍。此外，FP8 Wgrad GEMM 允许将激活存储在 FP8 中，以便在反向传播中使用。这显著减少了内存消耗。

Despite the efficiency advantage of the FP8 format, certain operators still require a higher precision due to their sensitivity to low-precision computations. Besides, some low-cost operators can also utilize a higher precision with a negligible overhead to the overall training cost. For this reason, after careful investigations, we maintain the original precision (e.g., BF16 or FP32) for the following components: the embedding module, the output head, MoE gating modules, normalization operators, and attention operators. These targeted retentions of high precision ensure stable training dynamics for DeepSeek-V3. To further guarantee numerical stability, we store the master weights, weight gradients, and optimizer states in higher precision. While these high-precision components incur some memory overheads, their impact can be minimized through efficient sharding across multiple DP ranks in our distributed training system.

尽管 FP8 格式具有效率优势，但某些算子由于对低精度计算敏感，仍需要更高的精度。此外，一些低成本算子也可以利用更高的精度，而对整体训练成本的影响可以忽略不计。因此，经过仔细研究，我们为以下组件保留了原始精度（例如 BF16 或 FP32）：嵌入模块、输出头、MoE 门控模块、归一化算子和注意力算子。这些有针对性的高精度保留确保了 DeepSeek-V3 的训练动态稳定。为了进一步保证数值稳定性，我们将主权重、权重梯度和优化器状态以更高的精度存储。虽然这些高精度组件会带来一些内存开销，但通过在我们的分布式训练系统中跨多个 DP 等级进行高效分片，可以将它们的影响降至最低。

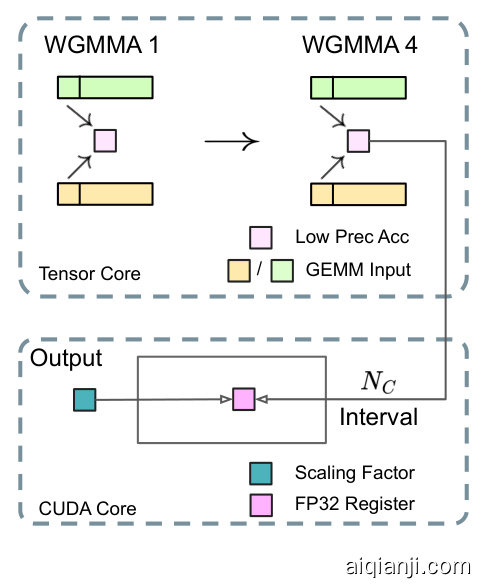
Figure 7 | (a) We propose a fine-grained quantization method to mitigate quantization errors caused by feature outliers; for illustration simplicity, only Fprop is illustrated. (b) In conjunction with our quantization strategy, we improve the FP8 GEMM precision by promoting to CUDA Cores at an interval of $N_{C}=128$ elements MMA for the high-precision accumulation.

图 7 | (a) 我们提出了一种细粒度的量化方法，以减轻由特征异常值引起的量化误差；为了简化说明，仅展示了 Fprop。(b) 结合我们的量化策略，我们通过将 FP8 GEMM 精度提升到 CUDA Cores，以 $N_{C}=128$ 个元素的 MMA 间隔进行高精度累加。

(b) Increasing accumulation precision

(b) 提高累积精度

3.3.2. Improved Precision from Quantization and Multiplication

3.3.2. 量化和乘法带来的精度提升

Based on our mixed precision FP8 framework, we introduce several strategies to enhance lowprecision training accuracy, focusing on both the quantization method and the multiplication process.

基于我们的混合精度 FP8 框架，我们引入了多种策略来提高低精度训练的准确性，重点关注量化方法和乘法过程。

Fine-Grained Quantization. In low-precision training frameworks, overflows and underflows are common challenges due to the limited dynamic range of the FP8 format, which is constrained by its reduced exponent bits. As a standard practice, the input distribution is aligned to the representable range of the FP8 format by scaling the maximum absolute value of the input tensor to the maximum representable value of FP8 (Narang et al., 2017). This method makes lowprecision training highly sensitive to activation outliers, which can heavily degrade quantization accuracy. To solve this, we propose a fine-grained quantization method that applies scaling at a more granular level. As illustrated in Figure 7 (a), (1) for activation s, we group and scale elements on a 1x128 tile basis (i.e., per token per 128 channels); and (2) for weights, we group and scale elements on a 128x128 block basis (i.e., per 128 input channels per 128 output channels). This approach ensures that the quantization process can better accommodate outliers by adapting the scale according to smaller groups of elements. In Appendix B.2, we further discuss the training instability when we group and scale activation s on a block basis in the same way as weights quantization.

细粒度量化。在低精度训练框架中，由于 FP8 格式的动态范围有限，溢出和下溢是常见的挑战，这受到其减少的指数位的限制。作为一种标准做法，输入分布通过将输入张量的最大绝对值缩放到 FP8 的最大可表示值来与 FP8 格式的可表示范围对齐 (Narang et al., 2017)。这种方法使得低精度训练对激活异常值高度敏感，这会严重降低量化精度。为了解决这个问题，我们提出了一种细粒度量化方法，该方法在更细粒度的级别上应用缩放。如图 7 (a) 所示，(1) 对于激活 s，我们在 1x128 的图块基础上对元素进行分组和缩放（即每个 token 每 128 个通道）；(2) 对于权重，我们在 128x128 的块基础上对元素进行分组和缩放（即每 128 个输入通道每 128 个输出通道）。这种方法通过根据较小的元素组调整缩放比例，确保量化过程能够更好地适应异常值。在附录 B.2 中，我们进一步讨论了当我们以与权重量化相同的方式在块基础上对激活 s 进行分组和缩放时的训练不稳定性。

One key modification in our method is the introduction of per-group scaling factors along the inner dimension of GEMM operations. This functionality is not directly supported in the standard FP8 GEMM. However, combined with our precise FP32 accumulation strategy, it can

我们方法的一个关键修改是引入了沿 GEMM 操作内部维度的每组缩放因子。这一功能在标准的 FP8 GEMM 中并不直接支持。然而，结合我们精确的 FP32 累加策略，它可以

be efficiently implemented.

高效实现。

Notably, our fine-grained quantization strategy is highly consistent with the idea of microscaling formats (Rouhani et al., 2023b), while the Tensor Cores of NVIDIA next-generation GPUs (Blackwell series) have announced the support for micro scaling formats with smaller quantization granularity (NVIDIA, 2024a). We hope our design can serve as a reference for future work to keep pace with the latest GPU architectures.

值得注意的是，我们的细粒度量化策略与微缩放格式 (microscaling formats) 的理念高度一致 (Rouhani et al., 2023b)，而 NVIDIA 下一代 GPU (Blackwell 系列) 的 Tensor Cores 已宣布支持具有更小量化粒度的微缩放格式 (NVIDIA, 2024a)。我们希望我们的设计能够为未来的工作提供参考，以跟上最新的 GPU 架构。

Increasing Accumulation Precision. Low-precision GEMM operations often suffer from underflow issues, and their accuracy largely depends on high-precision accumulation, which is commonly performed in an FP32 precision (Kalamkar et al., 2019; Narang et al., 2017). However, we observe that the accumulation precision of FP8 GEMM on NVIDIA H800 GPUs is limited to retaining around 14 bits, which is significantly lower than FP32 accumulation precision. This problem will become more pronounced when the inner dimension K is large (Wortsman et al., 2023), a typical scenario in large-scale model training where the batch size and model width are increased. Taking GEMM operations of two random matrices with $\mathtt{K}=4096$ for example, in our preliminary test, the limited accumulation precision in Tensor Cores results in a maximum relative error of nearly $2%$ . Despite these problems, the limited accumulation precision is still the default option in a few FP8 frameworks (NVIDIA, 2024b), severely constraining the training accuracy.

提高累加精度。低精度 GEMM 操作经常面临下溢问题，其精度很大程度上依赖于高精度累加，通常以 FP32 精度执行 (Kalamkar et al., 2019; Narang et al., 2017)。然而，我们观察到，在 NVIDIA H800 GPU 上，FP8 GEMM 的累加精度仅限于保留约 14 位，这显著低于 FP32 的累加精度。当内维度 K 较大时 (Wortsman et al., 2023)，这一问题将更加明显，这是大规模模型训练中增加批量大小和模型宽度的典型场景。以两个随机矩阵的 GEMM 操作为例，其中 $\mathtt{K}=4096$，在我们的初步测试中，Tensor Cores 中有限的累加精度导致最大相对误差接近 $2%$。尽管存在这些问题，有限的累加精度仍然是少数 FP8 框架 (NVIDIA, 2024b) 中的默认选项，严重限制了训练精度。

In order to address this issue, we adopt the strategy of promotion to CUDA Cores for higher precision (Thakkar et al., 2023). The process is illustrated in Figure 7 (b). To be specific, during MMA (Matrix Multiply-Accumulate) execution on Tensor Cores, intermediate results are accumulated using the limited bit width. Once an interval of $N_{C}$ is reached, these partial results will be copied to FP32 registers on CUDA Cores, where full-precision FP32 accumulation is performed. As mentioned before, our fine-grained quantization applies per-group scaling factors along the inner dimension K. These scaling factors can be efficiently multiplied on the CUDA Cores as the de quantization process with minimal additional computational cost.

为了解决这个问题，我们采用了将计算提升到CUDA Cores以获取更高精度的策略 (Thakkar et al., 2023)。该过程如图7 (b)所示。具体来说，在Tensor Cores上执行MMA（矩阵乘加）时，中间结果使用有限的位宽进行累加。一旦达到$N_{C}$的间隔，这些部分结果将被复制到CUDA Cores上的FP32寄存器中，并在那里执行全精度的FP32累加。如前所述，我们的细粒度量化沿内维度K应用了每组的缩放因子。这些缩放因子可以在CUDA Cores上高效地乘以反量化过程，且额外的计算成本最小。

It is worth noting that this modification reduces the WGMMA (Warpgroup-level Matrix Multiply-Accumulate) instruction issue rate for a single warpgroup. However, on the H800 architecture, it is typical for two WGMMA to persist concurrently: while one warpgroup performs the promotion operation, the other is able to execute the MMA operation. This design enables overlapping of the two operations, maintaining high utilization of Tensor Cores. Based on our experiments, setting $N_{C},=,128$ elements, equivalent to 4 WGMMAs, represents the minimal accumulation interval that can significantly improve precision without introducing substantial overhead.

值得注意的是，这种修改降低了单个 warpgroup 的 WGMMA（Warpgroup-level Matrix Multiply-Accumulate）指令的发出率。然而，在 H800 架构上，通常会有两个 WGMMA 同时存在：当一个 warpgroup 执行提升操作时，另一个 warpgroup 能够执行 MMA 操作。这种设计使得两个操作可以重叠，从而保持 Tensor Core 的高利用率。根据我们的实验，设置 $N_{C},=,128$ 个元素（相当于 4 个 WGMMA）是最小的累加间隔，可以在不引入显著开销的情况下显著提高精度。

Mantissa over Exponents. In contrast to the hybrid FP8 format adopted by prior work (NVIDIA, 2024b; Peng et al., 2023b; Sun et al., 2019b), which uses E4M3 (4-bit exponent and 3-bit mantissa) in Fprop and E5M2 (5-bit exponent and 2-bit mantissa) in Dgrad and Wgrad, we adopt the E4M3 format on all tensors for higher precision. We attribute the feasibility of this approach to our fine-grained quantization strategy, i.e., tile and block-wise scaling. By operating on smaller element groups, our methodology effectively shares exponent bits among these grouped elements, mitigating the impact of the limited dynamic range.

尾数优先于指数。与之前工作采用的混合 FP8 格式（NVIDIA, 2024b; Peng et al., 2023b; Sun et al., 2019b）不同，它们在 Fprop 中使用 E4M3（4 位指数和 3 位尾数），在 Dgrad 和 Wgrad 中使用 E5M2（5 位指数和 2 位尾数），我们在所有张量上采用 E4M3 格式以获得更高的精度。我们将这种方法的可行性归因于我们的细粒度量化策略，即分块和块级缩放。通过在较小的元素组上操作，我们的方法有效地在这些分组元素之间共享指数位，从而减轻了有限动态范围的影响。

Online Quantization. Delayed quantization is employed in tensor-wise quantization frameworks (NVIDIA, 2024b; Peng et al., 2023b), which maintains a history of the maximum absolute values across prior iterations to infer the current value. In order to ensure accurate scales and simplify the framework, we calculate the maximum absolute value online for each 1x128 activation tile or $128\mathtt{x}128$ weight block. Based on it, we derive the scaling factor and then quantize the activation or weight online into the FP8 format.

在线量化。张量级量化框架（NVIDIA, 2024b; Peng et al., 2023b）中采用了延迟量化，该方法通过维护先前迭代中的最大绝对值历史来推断当前值。为了确保准确的缩放比例并简化框架，我们在线计算每个1x128激活块或$128\mathtt{x}128$权重块的最大绝对值。基于此，我们推导出缩放因子，然后在线将激活或权重量化为FP8格式。

3.3.3. Low-Precision Storage and Communication

3.3.3. 低精度存储与通信

In conjunction with our FP8 training framework, we further reduce the memory consumption and communication overhead by compressing cached activation s and optimizer states into lower-precision formats.

结合我们的 FP8 训练框架，我们通过将缓存的激活值和优化器状态压缩为低精度格式，进一步减少了内存消耗和通信开销。

Low-Precision Optimizer States. We adopt the BF16 data format instead of FP32 to track the first and second moments in the AdamW (Loshchilov and Hutter, 2017) optimizer, without incurring observable performance degradation. However, the master weights (stored by the optimizer) and gradients (used for batch size accumulation) are still retained in FP32 to ensure numerical stability throughout training.

低精度优化器状态。我们采用 BF16 数据格式而非 FP32 来跟踪 AdamW (Loshchilov and Hutter, 2017) 优化器中的一阶和二阶矩，而不会导致明显的性能下降。然而，主权重（由优化器存储）和梯度（用于批量大小累积）仍保留在 FP32 中，以确保整个训练过程中的数值稳定性。

Low-Precision Activation. As illustrated in Figure 6, the Wgrad operation is performed in FP8. To reduce the memory consumption, it is a natural choice to cache activation s in FP8 format for the backward pass of the Linear operator. However, special considerations are taken on several operators for low-cost high-precision training:

低精度激活。如图 6 所示，Wgrad 操作在 FP8 中执行。为了减少内存消耗，将激活值以 FP8 格式缓存以用于 Linear 算子的反向传播是一个自然的选择。然而，为了低成本高精度训练，对几个算子进行了特殊考虑：

(1) Inputs of the Linear after the attention operator. These activation s are also used in the backward pass of the attention operator, which makes it sensitive to precision. We adopt a customized E5M6 data format exclusively for these activation s. Additionally, these activation s will be converted from an 1x128 quantization tile to an $128\up x1$ tile in the backward pass. To avoid introducing extra quantization error, all the scaling factors are round scaled, i.e., integral power of 2.

(1) 注意力算子后的线性输入。这些激活值也用于注意力算子的反向传播，这使得它对精度敏感。我们采用定制的 E5M6 数据格式专门用于这些激活值。此外，这些激活值在反向传播过程中将从 1x128 量化块转换为 $128\up x1$ 块。为了避免引入额外的量化误差，所有的缩放因子都是四舍五入的，即 2 的整数幂。

(2) Inputs of the SwiGLU operator in MoE. To further reduce the memory cost, we cache the inputs of the SwiGLU operator and recompute its output in the backward pass. These activation s are also stored in FP8 with our fine-grained quantization method, striking a balance between memory efficiency and computational accuracy.

(2) MoE 中 SwiGLU 算子的输入。为了进一步降低内存成本，我们缓存了 SwiGLU 算子的输入，并在反向传播时重新计算其输出。这些激活值也使用我们的细粒度量化方法以 FP8 格式存储，在内存效率和计算精度之间取得了平衡。

Low-Precision Communication. Communication bandwidth is a critical bottleneck in the training of MoE models. To alleviate this challenge, we quantize the activation before MoE up-projections into FP8 and then apply dispatch components, which is compatible with FP8 Fprop in MoE up-projections. Like the inputs of the Linear after the attention operator, scaling factors for this activation are integral power of 2. A similar strategy is applied to the activation gradient before MoE down-projections. For both the forward and backward combine components, we retain them in BF16 to preserve training precision in critical parts of the training pipeline.

低精度通信。通信带宽是 MoE 模型训练中的一个关键瓶颈。为了缓解这一挑战，我们在 MoE 上投影之前将激活量化为 FP8，然后应用调度组件，这与 MoE 上投影中的 FP8 Fprop 兼容。与注意力算子后的线性输入类似，此激活的缩放因子是 2 的整数幂。类似的策略也应用于 MoE 下投影之前的激活梯度。对于前向和后向组合组件，我们将其保留为 BF16，以保持训练管道关键部分的训练精度。

3.4. Inference and Deployment

3.4. 推理与部署

We deploy DeepSeek-V3 on the H800 cluster, where GPUs within each node are interconnected using NVLink, and all GPUs across the cluster are fully interconnected via IB. To simultaneously ensure both the Service-Level Objective (SLO) for online services and high throughput, we employ the following deployment strategy that separates the prefilling and decoding stages.

我们在 H800 集群上部署了 DeepSeek-V3，其中每个节点内的 GPU 通过 NVLink 互连，集群中的所有 GPU 通过 IB 完全互连。为了同时确保在线服务的服务级别目标 (SLO) 和高吞吐量，我们采用了以下部署策略，将预填充和解码阶段分开。

3.4.1. Prefilling

3.4.1. 预填充

The minimum deployment unit of the prefilling stage consists of 4 nodes with 32 GPUs. The attention part employs 4-way Tensor Parallelism (TP4) with Sequence Parallelism (SP), combined with 8-way Data Parallelism (DP8). Its small TP size of 4 limits the overhead of TP communication. For the MoE part, we use 32-way Expert Parallelism (EP32), which ensures that each expert processes a sufficiently large batch size, thereby enhancing computational efficiency. For the MoE all-to-all communication, we use the same method as in training: first transferring tokens across nodes via IB, and then forwarding among the intra-node GPUs via NVLink. In particular, we use 1-way Tensor Parallelism for the dense MLPs in shallow layers to save TP communication.

预填充阶段的最小部署单元由4个节点和32个GPU组成。注意力部分采用4路张量并行（TP4）与序列并行（SP）结合，同时使用8路数据并行（DP8）。其较小的TP大小为4，限制了TP通信的开销。对于MoE部分，我们使用32路专家并行（EP32），确保每个专家处理足够大的批量大小，从而提高计算效率。对于MoE的全对全通信，我们使用与训练时相同的方法：首先通过IB在节点之间传输Token，然后通过NVLink在节点内的GPU之间转发。特别地，我们在浅层使用1路张量并行来处理密集的MLP，以节省TP通信。

To achieve load balancing among different experts in the MoE part, we need to ensure that each GPU processes approximately the same number of tokens. To this end, we introduce a deployment strategy of redundant experts, which duplicates high-load experts and deploys them redundantly. The high-load experts are detected based on statistics collected during the online deployment and are adjusted periodically (e.g., every 10 minutes). After determining the set of redundant experts, we carefully rearrange experts among GPUs within a node based on the observed loads, striving to balance the load across GPUs as much as possible without increasing the cross-node all-to-all communication overhead. For the deployment of DeepSeek-V3, we set 32 redundant experts for the prefilling stage. For each GPU, besides the original 8 experts it hosts, it will also host one additional redundant expert.

为了实现 MoE 部分中不同专家之间的负载均衡，我们需要确保每个 GPU 处理大致相同数量的 Token。为此，我们引入了一种冗余专家的部署策略，即复制高负载专家并进行冗余部署。高负载专家是基于在线部署期间收集的统计数据检测的，并定期进行调整（例如，每 10 分钟一次）。在确定冗余专家集后，我们根据观察到的负载情况，在节点内的 GPU 之间仔细重新安排专家，力求在不增加跨节点全对全通信开销的情况下，尽可能平衡 GPU 的负载。对于 DeepSeek-V3 的部署，我们为预填充阶段设置了 32 个冗余专家。对于每个 GPU，除了它原本承载的 8 个专家外，还将承载一个额外的冗余专家。

Furthermore, in the prefilling stage, to improve the throughput and hide the overhead of all-to-all and TP communication, we simultaneously process two micro-batches with similar computational workloads, overlapping the attention and MoE of one micro-batch with the dispatch and combine of another.

此外，在预填充阶段，为了提高吞吐量并隐藏 all-to-all 和 TP 通信的开销，我们同时处理两个计算工作量相似的微批次，将一个微批次的注意力机制和 MoE 与另一个微批次的调度和组合重叠。

Finally, we are exploring a dynamic redundancy strategy for experts, where each GPU hosts more experts (e.g., 16 experts), but only 9 will be activated during each inference step. Before the all-to-all operation at each layer begins, we compute the globally optimal routing scheme on the fly. Given the substantial computation involved in the prefilling stage, the overhead of computing this routing scheme is almost negligible.

最后，我们正在探索一种动态冗余策略，即每个 GPU 上托管更多的专家（例如 16 个专家），但在每次推理步骤中只激活 9 个。在每层的 all-to-all 操作开始之前，我们会动态计算全局最优的路由方案。考虑到预填充阶段涉及的大量计算，计算该路由方案的开销几乎可以忽略不计。

3.4.2. Decoding

3.4.2. 解码

During decoding, we treat the shared expert as a routed one. From this perspective, each token will select 9 experts during routing, where the shared expert is regarded as a heavy-load one that will always be selected. The minimum deployment unit of the decoding stage consists of 40 nodes with 320 GPUs. The attention part employs TP4 with SP, combined with DP80, while the MoE part uses EP320. For the MoE part, each GPU hosts only one expert, and 64 GPUs are responsible for hosting redundant experts and shared experts. All-to-all communication of the dispatch and combine parts is performed via direct point-to-point transfers over IB to achieve low latency. Additionally, we leverage the IBGDA (NVIDIA, 2022) technology to further minimize latency and enhance communication efficiency.

在解码过程中，我们将共享专家视为一个路由专家。从这个角度来看，每个 Token 在路由时会选择 9 个专家，其中共享专家被视为一个高负载的专家，始终会被选中。解码阶段的最小部署单元由 40 个节点和 320 个 GPU 组成。注意力部分采用 TP4 和 SP 结合 DP80，而 MoE 部分使用 EP320。对于 MoE 部分，每个 GPU 仅托管一个专家，64 个 GPU 负责托管冗余专家和共享专家。调度和组合部分的全对全通信通过 IB 的直接点对点传输进行，以实现低延迟。此外，我们利用 IBGDA (NVIDIA, 2022) 技术进一步减少延迟并提高通信效率。

Similar to prefilling, we periodically determine the set of redundant experts in a certain interval, based on the statistical expert load from our online service. However, we do not need to rearrange experts since each GPU only hosts one expert. We are also exploring the dynamic redundancy strategy for decoding. However, this requires more careful optimization of the algorithm that computes the globally optimal routing scheme and the fusion with the dispatch kernel to reduce overhead.

与预填充类似，我们根据在线服务的统计专家负载，定期确定某个区间内的冗余专家集。然而，由于每个 GPU 只托管一个专家，我们不需要重新排列专家。我们还在探索解码的动态冗余策略。然而，这需要对计算全局最优路由方案的算法进行更仔细的优化，并与调度内核融合以减少开销。

Additionally, to enhance throughput and hide the overhead of all-to-all communication, we are also exploring processing two micro-batches with similar computational workloads simultaneously in the decoding stage. Unlike prefilling, attention consumes a larger portion of time in the decoding stage. Therefore, we overlap the attention of one micro-batch with the dispatch+MoE $^+$ combine of another. In the decoding stage, the batch size per expert is relatively small (usually within 256 tokens), and the bottleneck is memory access rather than computation. Since the MoE part only needs to load the parameters of one expert, the memory access overhead is minimal, so using fewer SMs will not significantly affect the overall performance. Therefore, to avoid impacting the computation speed of the attention part, we can allocate only a small portion of SMs to dispatch+MoE+combine.

此外，为了提高吞吐量并隐藏全对全通信的开销，我们还在探索在解码阶段同时处理两个计算工作量相似的微批次。与预填充不同，注意力在解码阶段消耗的时间更多。因此，我们将一个微批次的注意力与另一个微批次的调度+MoE$^+$组合重叠。在解码阶段，每个专家的批次大小相对较小（通常在256个Token以内），瓶颈是内存访问而非计算。由于MoE部分只需要加载一个专家的参数，内存访问开销很小，因此使用较少的SM不会显著影响整体性能。因此，为了避免影响注意力部分的计算速度，我们可以只分配一小部分SM给调度+MoE+组合。

3.5. Suggestions on Hardware Design

3.5. 硬件设计建议

Based on our implementation of the all-to-all communication and FP8 training scheme, we propose the following suggestions on chip design to AI hardware vendors.

基于我们对全对全通信和 FP8 训练方案的实现，我们向 AI 硬件供应商提出以下芯片设计建议。

3.5.1. Communication Hardware

3.5.1. 通信硬件

In DeepSeek-V3, we implement the overlap between computation and communication to hide the communication latency during computation. This significantly reduces the dependency on communication bandwidth compared to serial computation and communication. However, the current communication implementation relies on expensive SMs (e.g., we allocate 20 out of the 132 SMs available in the H800 GPU for this purpose), which will limit the computational throughput. Moreover, using SMs for communication results in significant inefficiencies, as tensor cores remain entirely under-utilized.

在 DeepSeek-V3 中，我们实现了计算与通信的重叠，以隐藏计算过程中的通信延迟。与串行计算和通信相比，这显著降低了对通信带宽的依赖。然而，当前的通信实现依赖于昂贵的 SMs（例如，我们在 H800 GPU 的 132 个可用 SMs 中分配了 20 个用于此目的），这将限制计算吞吐量。此外，使用 SMs 进行通信会导致显著的效率低下，因为张量核心（tensor cores）完全未被充分利用。

Currently, the SMs primarily perform the following tasks for all-to-all communication:

目前，SMs 主要执行以下全对全通信任务：

We aspire to see future vendors developing hardware that offloads these communication tasks from the valuable computation unit SM, serving as a GPU co-processor or a network co-processor like NVIDIA SHARP Graham et al. (2016). Furthermore, to reduce application programming complexity, we aim for this hardware to unify the IB (scale-out) and NVLink (scale-up) networks from the perspective of the computation units. With this unified interface, computation units can easily accomplish operations such as read, write, multicast, and reduce across the entire IB-NVLink-unified domain via submitting communication requests based on simple primitives.

我们期望未来的供应商能够开发出将通信任务从宝贵的计算单元 SM 中卸载的硬件，作为 GPU 协处理器或网络协处理器，例如 NVIDIA SHARP Graham 等人 (2016)。此外，为了降低应用程序编程的复杂性，我们希望这种硬件能够从计算单元的角度统一 IB（横向扩展）和 NVLink（纵向扩展）网络。通过这种统一的接口，计算单元可以通过提交基于简单原语的通信请求，轻松完成整个 IB-NVLink 统一域中的读取、写入、多播和归约等操作。

3.5.2. Compute Hardware

3.5.2. 计算硬件

Higher FP8 GEMM Accumulation Precision in Tensor Cores. In the current Tensor Core implementation of the NVIDIA Hopper architecture, FP8 GEMM (General Matrix Multiply) employs fixed-point accumulation, aligning the mantissa products by right-shifting based on the maximum exponent before addition. Our experiments reveal that it only uses the highest 14 bits of each mantissa product after sign-fill right shifting, and truncates bits exceeding this range. However, for example, to achieve precise FP32 results from the accumulation of $32;\mathrm{FP8!\times!FP8}$ multiplications, at least 34-bit precision is required. Thus, we recommend that future chip designs increase accumulation precision in Tensor Cores to support full-precision accumulation, or select an appropriate accumulation bit-width according to the accuracy requirements of training and inference algorithms. This approach ensures that errors remain within acceptable bounds while maintaining computational efficiency.

Tensor Core 中更高的 FP8 GEMM 累加精度。在 NVIDIA Hopper 架构的当前 Tensor Core 实现中，FP8 GEMM（通用矩阵乘法）采用定点累加，通过在加法前根据最大指数右移来对齐尾数乘积。我们的实验表明，它在符号填充右移后仅使用每个尾数乘积的最高 14 位，并截断超出此范围的位。然而，例如，要从 32 个 FP8×FP8 乘法的累加中获得精确的 FP32 结果，至少需要 34 位精度。因此，我们建议未来的芯片设计提高 Tensor Core 中的累加精度，以支持全精度累加，或根据训练和推理算法的精度要求选择合适的累加位宽。这种方法在保持计算效率的同时，确保误差保持在可接受的范围内。

Support for Tile- and Block-Wise Quantization. Current GPUs only support per-tensor quantization, lacking the native support for fine-grained quantization like our tile- and blockwise quantization. In the current implementation, when the $N_{C}$ interval is reached, the partial results will be copied from Tensor Cores to CUDA cores, multiplied by the scaling factors, and added to FP32 registers on CUDA cores. Although the de quantization overhead is significantly mitigated combined with our precise FP32 accumulation strategy, the frequent data movements between Tensor Cores and CUDA cores still limit the computational efficiency. Therefore, we recommend future chips to support fine-grained quantization by enabling Tensor Cores to receive scaling factors and implement MMA with group scaling. In this way, the whole partial sum accumulation and de quantization can be completed directly inside Tensor Cores until the final result is produced, avoiding frequent data movements.

支持分块量化。当前的 GPU 仅支持张量级量化，缺乏对我们分块量化等细粒度量化的原生支持。在当前实现中，当达到 $N_{C}$ 间隔时，部分结果将从 Tensor Core 复制到 CUDA Core，乘以缩放因子，并添加到 CUDA Core 上的 FP32 寄存器中。尽管结合我们精确的 FP32 累加策略，反量化开销得到了显著缓解，但 Tensor Core 和 CUDA Core 之间的频繁数据移动仍然限制了计算效率。因此，我们建议未来的芯片通过使 Tensor Core 能够接收缩放因子并实现分组缩放的 MMA 来支持细粒度量化。这样，整个部分和累加和反量化可以直接在 Tensor Core 内部完成，直到生成最终结果，从而避免频繁的数据移动。

Support for Online Quantization. The current implementations struggle to effectively support online quantization, despite its effectiveness demonstrated in our research. In the existing process, we need to read 128 BF16 activation values (the output of the previous computation) from HBM (High Bandwidth Memory) for quantization, and the quantized FP8 values are then written back to HBM, only to be read again for MMA. To address this inefficiency, we recommend that future chips integrate FP8 cast and TMA (Tensor Memory Accelerator) access into a single fused operation, so quantization can be completed during the transfer of activation s from global memory to shared memory, avoiding frequent memory reads and writes. We also recommend supporting a warp-level cast instruction for speedup, which further facilitates the better fusion of layer normalization and FP8 cast. Alternatively, a near-memory computing approach can be adopted, where compute logic is placed near the HBM. In this case, BF16 elements can be cast to FP8 directly as they are read from HBM into the GPU, reducing off-chip memory access by roughly $50%$ .

支持在线量化。尽管我们的研究证明了在线量化的有效性，但当前的实现难以有效支持这一功能。在现有流程中，我们需要从高带宽内存 (HBM) 中读取 128 个 BF16 激活值（前一次计算的输出）进行量化，然后将量化后的 FP8 值写回 HBM，再重新读取以进行矩阵乘法累加 (MMA)。为了解决这种低效问题，我们建议未来的芯片将 FP8 转换和张量内存加速器 (TMA) 访问集成到一个融合操作中，以便在将激活值从全局内存传输到共享内存的过程中完成量化，从而避免频繁的内存读写。我们还建议支持 warp 级别的转换指令以加速操作，这进一步促进了层归一化和 FP8 转换的更好融合。或者，可以采用近内存计算的方法，将计算逻辑放置在 HBM 附近。在这种情况下，BF16 元素在从 HBM 读取到 GPU 时可以直接转换为 FP8，从而将片外内存访问减少约 $50%$。

Support for Transposed GEMM Operations. The current architecture makes it cumbersome to fuse matrix transposition with GEMM operations. In our workflow, activation s during the forward pass are quantized into 1x128 FP8 tiles and stored. During the backward pass, the matrix needs to be read out, de quantized, transposed, re-quantized into $128\up x1$ tiles, and stored in HBM. To reduce memory operations, we recommend future chips to enable direct transposed reads of matrices from shared memory before MMA operation, for those precisions required in both training and inference. Combined with the fusion of FP8 format conversion and TMA access, this enhancement will significantly streamline the quantization workflow.

支持转置的 GEMM 操作。当前的架构使得将矩阵转置与 GEMM 操作融合变得繁琐。在我们的工作流程中，前向传播中的激活被量化为 1x128 FP8 块并存储。在反向传播期间，矩阵需要被读取、反量化、转置、重新量化为 $128\up x1$ 块，并存储在 HBM 中。为了减少内存操作，我们建议未来的芯片在 MMA 操作之前，能够直接从共享内存中进行矩阵的转置读取，以满足训练和推理中所需的精度。结合 FP8 格式转换和 TMA 访问的融合，这一增强将显著简化量化工作流程。

4. Pre-Training

4. 预训练

4.1. Data Construction

4.1. 数据构建

Compared with DeepSeek-V2, we optimize the pre-training corpus by enhancing the ratio of mathematical and programming samples, while expanding multilingual coverage beyond English and Chinese. Also, our data processing pipeline is refined to minimize redundancy while maintaining corpus diversity. Inspired by Ding et al. (2024), we implement the document packing method for data integrity but do not incorporate cross-sample attention masking during training. Finally, the training corpus for DeepSeek-V3 consists of 14.8T high-quality and diverse tokens in our tokenizer.

与 DeepSeek-V2 相比，我们通过提高数学和编程样本的比例优化了预训练语料库，同时扩展了除英语和中文之外的多语言覆盖范围。此外，我们的数据处理流程经过优化，以在保持语料库多样性的同时最大限度地减少冗余。受 Ding 等人 (2024) 的启发，我们实现了文档打包方法以确保数据完整性，但在训练过程中没有引入跨样本注意力掩码。最终，DeepSeek-V3 的训练语料库在我们的分词器中包含了 14.8T 的高质量和多样化 Token。

In the training process of Deep Seek Code r-V2 (DeepSeek-AI, 2024a), we observe that the Fill-in-Middle (FIM) strategy does not compromise the next-token prediction capability while enabling the model to accurately predict middle text based on contextual cues. In alignment with Deep Seek Code r-V2, we also incorporate the FIM strategy in the pre-training of DeepSeek-V3. To be specific, we employ the Prefix-Suffix-Middle (PSM) framework to structure data as follows:

在 Deep Seek Code r-V2 (DeepSeek-AI, 2024a) 的训练过程中，我们观察到 Fill-in-Middle (FIM) 策略在使模型能够根据上下文线索准确预测中间文本的同时，不会损害下一个 Token 的预测能力。为了与 Deep Seek Code r-V2 保持一致，我们也在 DeepSeek-V3 的预训练中引入了 FIM 策略。具体来说，我们采用 Prefix-Suffix-Middle (PSM) 框架来构建数据，如下所示：

<|fim_begin|> 𝑓pre<|fim_hole|> 𝑓suf<|fim_end|> 𝑓middle<|eos_token|>.

𝑓pre<|fim_hole|> 𝑓suf<|fim_end|> 𝑓middle<|eos_token|>.

This structure is applied at the document level as a part of the pre-packing process. The FIM strategy is applied at a rate of 0.1, consistent with the PSM framework.

此结构在文档级别应用，作为预打包过程的一部分。FIM策略以0.1的比率应用，与PSM框架保持一致。

The tokenizer for DeepSeek-V3 employs Byte-level BPE (Shibata et al., 1999) with an extended vocabulary of 128K tokens. The pre token ize r and training data for our tokenizer are modified to optimize multilingual compression efficiency. In addition, compared with DeepSeek-V2, the new pre token ize r introduces tokens that combine punctuation s and line breaks. However, this trick may introduce the token boundary bias (Lundberg, 2023) when the model processes multi-line prompts without terminal line breaks, particularly for few-shot evaluation prompts. To address this issue, we randomly split a certain proportion of such combined tokens during training, which exposes the model to a wider array of special cases and mitigates this bias.

DeepSeek-V3 的分词器采用了字节级 BPE (Byte-level BPE) (Shibata et al., 1999)，并扩展了词汇表至 128K 个 Token。我们对分词器的预处理和训练数据进行了修改，以优化多语言压缩效率。此外，与 DeepSeek-V2 相比，新的分词器引入了结合标点符号和换行符的 Token。然而，当模型处理没有终止换行符的多行提示时，这种技巧可能会引入 Token 边界偏差 (Lundberg, 2023)，尤其是在少样本评估提示中。为了解决这个问题，我们在训练过程中随机拆分了一定比例的此类组合 Token，从而使模型接触到更多特殊情况，减轻了这种偏差。

4.2. Hyper-Parameters

4.2. 超参数

Model Hyper-Parameters. We set the number of Transformer layers to 61 and the hidden dimension to 7168. All learnable parameters are randomly initialized with a standard deviation of 0.006. In MLA, we set the number of attention heads $n_{h}$ to 128 and the per-head dimension $d_{h}$ to 128. The KV compression dimension $d_{c}$ is set to 512, and the query compression dimension $d_{c}^{\prime}$ is set to 1536. For the decoupled queries and key, we set the per-head dimension $d_{h}^{R}$ to 64. We substitute all FFNs except for the first three layers with MoE layers. Each MoE layer consists of 1 shared expert and 256 routed experts, where the intermediate hidden dimension of each expert is 2048. Among the routed experts, 8 experts will be activated for each token, and each token will be ensured to be sent to at most 4 nodes. The multi-token prediction depth $D$ is set to 1, i.e., besides the exact next token, each token will predict one additional token. As DeepSeek-V2, DeepSeek-V3 also employs additional RMSNorm layers after the compressed latent vectors, and multiplies additional scaling factors at the width bottlenecks. Under this configuration, DeepSeek-V3 comprises 671B total parameters, of which 37B are activated for each token.

模型超参数。我们将 Transformer 层数设置为 61，隐藏维度设置为 7168。所有可学习参数均以标准差为 0.006 进行随机初始化。在 MLA 中，我们将注意力头数 $n_{h}$ 设置为 128，每个头的维度 $d_{h}$ 设置为 128。KV 压缩维度 $d_{c}$ 设置为 512，查询压缩维度 $d_{c}^{\prime}$ 设置为 1536。对于解耦的查询和键，我们将每个头的维度 $d_{h}^{R}$ 设置为 64。我们将除前三层之外的所有 FFN 替换为 MoE 层。每个 MoE 层由 1 个共享专家和 256 个路由专家组成，每个专家的中间隐藏维度为 2048。在路由专家中，每个 token 将激活 8 个专家，并且每个 token 将确保最多发送到 4 个节点。多 token 预测深度 $D$ 设置为 1，即除了精确的下一个 token 外，每个 token 还将预测一个额外的 token。与 DeepSeek-V2 一样，DeepSeek-V3 也在压缩的潜在向量后使用额外的 RMSNorm 层，并在宽度瓶颈处乘以额外的缩放因子。在此配置下，DeepSeek-V3 包含 671B 个总参数，其中每个 token 激活 37B 个参数。

Training Hyper-Parameters. We employ the AdamW optimizer (Loshchilov and Hutter, 2017) with hyper-parameters set to $\beta_{1}=0.9$ , $\beta_{2}=0.95_{\cdot}$ , and weight decay $=0.1$ . We set the maximum sequence length to 4K during pre-training, and pre-train DeepSeek-V3 on $14.8\mathrm{T}$ tokens. As for the learning rate scheduling, we first linearly increase it from 0 to $2.2\times10^{-4}$ during the first 2K steps. Then, we keep a constant learning rate of $2.2\times10^{-4}$ until the model consumes 10T training tokens. Subsequently, we gradually decay the learning rate to $2.2\times10^{-5}$ in $4.3\mathrm{T}$ tokens, following a cosine decay curve. During the training of the final 500B tokens, we keep a constant learning rate of $2.2\times10^{-5}$ in the first 333B tokens, and switch to another constant learning rate of $7.3\times10^{-6}$ in the remaining 167B tokens. The gradient clipping norm is set to 1.0. We employ a batch size scheduling strategy, where the batch size is gradually increased from 3072 to 15360 in the training of the first 469B tokens, and then keeps 15360 in the remaining training. We leverage pipeline parallelism to deploy different layers of a model on different GPUs, and for each layer, the routed experts will be uniformly deployed on 64 GPUs belonging to 8 nodes. As for the node-limited routing, each token will be sent to at most 4 nodes (i.e., $M=4$ ). For auxiliary-loss-free load balancing, we set the bias update speed 𝛾to 0.001 for the first $14.3\mathrm{T}$ tokens, and to 0.0 for the remaining 500B tokens. For the balance loss, we set $\alpha$ to 0.0001, just to avoid extreme imbalance within any single sequence. The MTP loss weight $\lambda$ is set to 0.3 for the first 10T tokens, and to 0.1 for the remaining 4.8T tokens.

训练超参数。我们采用 AdamW 优化器 (Loshchilov and Hutter, 2017)，超参数设置为 $\beta_{1}=0.9$、$\beta_{2}=0.95_{\cdot}$，权重衰减 $=0.1$。在预训练期间，我们将最大序列长度设置为 4K，并在 $14.8\mathrm{T}$ 的 token 上预训练 DeepSeek-V3。对于学习率调度，我们首先在前 2K 步中将其从 0 线性增加到 $2.2\times10^{-4}$。然后，我们保持 $2.2\times10^{-4}$ 的恒定学习率，直到模型消耗了 10T 的训练 token。随后，我们按照余弦衰减曲线在 $4.3\mathrm{T}$ 的 token 中逐渐将学习率衰减到 $2.2\times10^{-5}$。在最后 500B token 的训练中，我们保持 $2.2\times10^{-5}$ 的恒定学习率在前 333B token 中，并在剩余的 167B token 中切换到 $7.3\times10^{-6}$ 的恒定学习率。梯度裁剪范数设置为 1.0。我们采用批量大小调度策略，在前 469B token 的训练中，批量大小从 3072 逐渐增加到 15360，然后在剩余的训练中保持 15360。我们利用流水线并行将模型的不同层部署在不同的 GPU 上，对于每一层，路由的专家将均匀部署在属于 8 个节点的 64 个 GPU 上。对于节点限制的路由，每个 token 最多发送到 4 个节点（即 $M=4$）。对于无辅助损失的负载均衡，我们将偏差更新速度 𝛾 设置为 0.001 在前 $14.3\mathrm{T}$ 的 token 中，并在剩余的 500B token 中设置为 0.0。对于平衡损失，我们将 $\alpha$ 设置为 0.0001，以避免任何单个序列内的极端不平衡。MTP 损失权重 $\lambda$ 在前 10T token 中设置为 0.3，在剩余的 4.8T token 中设置为 0.1。

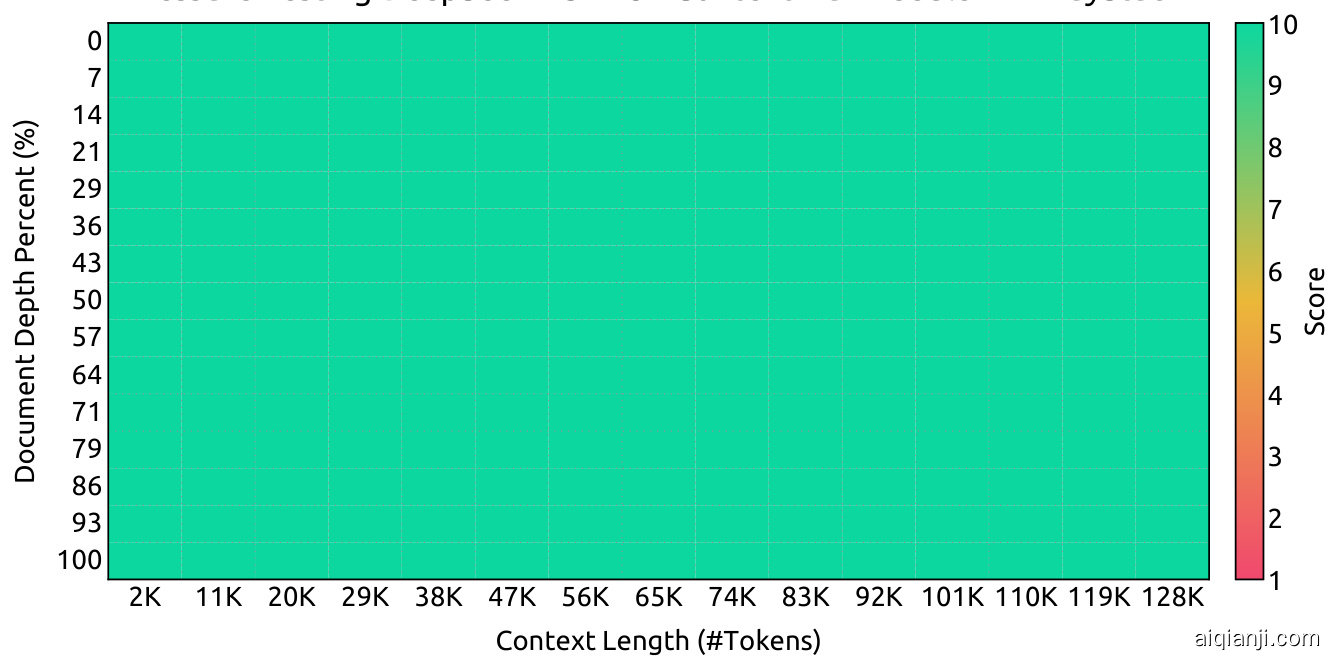
Pressure Testing DeepSeek-V3 128K Context via "Needle In A HayStack" Figure 8 | Evaluation results on the ”Needle In A Haystack” (NIAH) tests. DeepSeek-V3 performs well across all context window lengths up to 128K.

通过“大海捞针”测试 DeepSeek-V3 128K 上下文
图 8 | “大海捞针” (NIAH) 测试的评估结果。DeepSeek-V3 在所有上下文窗口长度（最高达 128K）上表现良好。

4.3. Long Context Extension

4.3. 长上下文扩展

We adopt a similar approach to DeepSeek-V2 (DeepSeek-AI, 2024c) to enable long context capabilities in DeepSeek-V3. After the pre-training stage, we apply YaRN (Peng et al., 2023a) for context extension and perform two additional training phases, each comprising 1000 steps, to progressively expand the context window from 4K to 32K and then to 128K. The YaRN configuration is consistent with that used in DeepSeek-V2, being applied exclusively to the decoupled shared key $\mathbf{k}_{t}^{R}$ . The hyper-parameters remain identical across both phases, with the scale $s=40$ , $\alpha=1$ , $\beta=32.$ , and the scaling factor $\sqrt{t}=0.1\ln s+1.$ . In the first phase, the sequence length is set to $32\mathrm{K},$ and the batch size is 1920. During the second phase, the sequence length is increased to 128K, and the batch size is reduced to 480. The learning rate for both phases is set to $7.3\times10^{-6}$ , matching the final learning rate from the pre-training stage.

我们采用与 DeepSeek-V2 (DeepSeek-AI, 2024c) 类似的方法，在 DeepSeek-V3 中实现长上下文能力。在预训练阶段之后，我们应用 YaRN (Peng et al., 2023a) 进行上下文扩展，并执行两个额外的训练阶段，每个阶段包含 1000 步，逐步将上下文窗口从 4K 扩展到 32K，然后再扩展到 128K。YaRN 配置与 DeepSeek-V2 中使用的配置一致，仅应用于解耦的共享键 $\mathbf{k}_{t}^{R}$。两个阶段的超参数保持一致，其中比例 $s=40$，$\alpha=1$，$\beta=32.$，缩放因子 $\sqrt{t}=0.1\ln s+1.$。在第一阶段，序列长度设置为 $32\mathrm{K},$，批量大小为 1920。在第二阶段，序列长度增加到 128K，批量大小减少到 480。两个阶段的学习率均设置为 $7.3\times10^{-6}$，与预训练阶段的最终学习率一致。

Through this two-phase extension training, DeepSeek-V3 is capable of handling inputs up to 128K in length while maintaining strong performance. Figure 8 illustrates that DeepSeek-V3, following supervised fine-tuning, achieves notable performance on the "Needle In A Haystack" (NIAH) test, demonstrating consistent robustness across context window lengths up to 128K.

通过这种两阶段的扩展训练，DeepSeek-V3 能够处理长达 128K 的输入，同时保持强劲的性能。图 8 展示了 DeepSeek-V3 在经过监督微调后，在 "Needle In A Haystack" (NIAH) 测试中取得了显著的表现，证明了其在长达 128K 的上下文窗口长度上具有一致的鲁棒性。

4.4. Evaluations

4.4. 评估

4.4.1. Evaluation Benchmarks

4.4.1. 评估基准

The base model of DeepSeek-V3 is pretrained on a multilingual corpus with English and Chinese constituting the majority, so we evaluate its performance on a series of benchmarks primarily in English and Chinese, as well as on a multilingual benchmark. Our evaluation is based on our internal evaluation framework integrated in our HAI-LLM framework. Considered benchmarks are categorized and listed as follows, where underlined benchmarks are in Chinese and double-underlined benchmarks are multilingual ones:

DeepSeek-V3 的基础模型是在以英语和中文为主的多语言语料库上进行预训练的，因此我们主要在英语和中文的一系列基准测试中评估其性能，同时也包括一个多语言基准测试。我们的评估基于集成在 HAI-LLM 框架中的内部评估框架。所考虑的基准测试分类如下，其中下划线的基准测试为中文，双下划线的基准测试为多语言：

Multi-subject multiple-choice datasets include MMLU (Hendrycks et al., 2020), MMLURedux (Gema et al., 2024), MMLU-Pro (Wang et al., 2024b), MMMLU (OpenAI, 2024b), C-Eval (Huang et al., 2023), and CMMLU (Li et al., 2023).

多学科多选题数据集包括 MMLU (Hendrycks et al., 2020)、MMLURedux (Gema et al., 2024)、MMLU-Pro (Wang et al., 2024b)、MMMLU (OpenAI, 2024b)、C-Eval (Huang et al., 2023) 和 CMMLU (Li et al., 2023)。

Language understanding and reasoning datasets include HellaSwag (Zellers et al., 2019), PIQA (Bisk et al., 2020), ARC (Clark et al., 2018), and BigBench Hard (BBH) (Suzgun et al., 2022).

语言理解和推理数据集包括 HellaSwag (Zellers et al., 2019)、PIQA (Bisk et al., 2020)、ARC (Clark et al., 2018) 和 BigBench Hard (BBH) (Suzgun et al., 2022)。

Closed-book question answering datasets include TriviaQA (Joshi et al., 2017) and Natural Questions (Kwiatkowski et al., 2019).

闭卷问答数据集包括 TriviaQA (Joshi et al., 2017) 和 Natural Questions (Kwiatkowski et al., 2019)。

Reading comprehension datasets include RACE Lai et al. (2017), DROP (Dua et al., 2019), C3 (Sun et al., 2019a), and CMRC (Cui et al., 2019).

阅读理解数据集包括 RACE (Lai et al., 2017)、DROP (Dua et al., 2019)、C3 (Sun et al., 2019a) 和 CMRC (Cui et al., 2019)。

Reference disambiguation datasets include CLUEWSC (Xu et al., 2020) and WinoGrande Sakaguchi et al. (2019).

参考文献消歧数据集包括 CLUEWSC (Xu et al., 2020) 和 WinoGrande Sakaguchi et al. (2019)。

Language modeling datasets include Pile (Gao et al., 2020).

语言建模数据集包括 Pile (Gao et al., 2020)。

Chinese understanding and culture datasets include CCPM (Li et al., 2021).

中文理解和文化数据集包括 CCPM (Li et al., 2021)。

Math datasets include GSM8K (Cobbe et al., 2021), MATH (Hendrycks et al., 2021), MGSM (Shi et al., 2023), and CMath (Wei et al., 2023).

数学数据集包括 GSM8K (Cobbe et al., 2021)、MATH (Hendrycks et al., 2021)、MGSM (Shi et al., 2023) 和 CMath (Wei et al., 2023)。

Code datasets include HumanEval (Chen et al., 2021), Live Code Bench-Base (0801-1101) (Jain et al., 2024), MBPP (Austin et al., 2021), and CRUXEval (Gu et al., 2024).

代码数据集包括 HumanEval (Chen et al., 2021)、Live Code Bench-Base (0801-1101) (Jain et al., 2024)、MBPP (Austin et al., 2021) 和 CRUXEval (Gu et al., 2024)。

Standardized exams include AGIEval (Zhong et al., 2023). Note that AGIEval includes both English and Chinese subsets.

标准化考试包括AGIEval (Zhong et al., 2023)。需要注意的是，AGIEval包含英文和中文两个子集。

Following our previous work (DeepSeek-AI, $2024\mathrm{b},!\mathrm{c})$ , we adopt perplexity-based evaluation for datasets including HellaSwag, PIQA, WinoGrande, RACE-Middle, RACE-High, MMLU, MMLU-Redux, MMLU-Pro, MMMLU, ARC-Easy, ARC-Challenge, C-Eval, CMMLU,C3, and CCPM, and adopt generation-based evaluation for TriviaQA, Natural Questions, DROP, MATH, GSM8K, MGSM, HumanEval, MBPP, Live Code Bench-Base, CRUXEval, BBH, AGIEval, CLUEWSC, CMRC, and CMath. In addition, we perform language-modeling-based evaluation for Pile-test and use Bits-Per-Byte (BPB) as the metric to guarantee fair comparison among models using different tokenizers.

继我们之前的工作 (DeepSeek-AI, $2024\mathrm{b},!\mathrm{c})$ 之后，我们对包括 HellaSwag、PIQA、WinoGrande、RACE-Middle、RACE-High、MMLU、MMLU-Redux、MMLU-Pro、MMMLU、ARC-Easy、ARC-Challenge、C-Eval、CMMLU、C3 和 CCPM 在内的数据集采用基于困惑度 (perplexity) 的评估方法，并对 TriviaQA、Natural Questions、DROP、MATH、GSM8K、MGSM、HumanEval、MBPP、Live Code Bench-Base、CRUXEval、BBH、AGIEval、CLUEWSC、CMRC 和 CMath 采用基于生成的评估方法。此外，我们对 Pile-test 进行基于语言建模的评估，并使用每字节比特数 (Bits-Per-Byte, BPB) 作为指标，以确保使用不同分词器的模型之间的公平比较。

Table 3 | Comparison among DeepSeek-V3-Base and other representative open-source base models. All models are evaluated in our internal framework and share the same evaluation setting. Scores with a gap not exceeding 0.3 are considered to be at the same level. DeepSeekV3-Base achieves the best performance on most benchmarks, especially on math and code tasks.

	基准 (指标)	#Shots	DeepSeek-V2 Base	Qwen2.5 72B Base	LLaMA-3.1 405B Base	DeepSeek-V3 Base
	架构		MoE	Dense	Dense	MoE
	激活参数量		21B	72B	405B	37B
	总参数量		236B	72B	405B	671B
	Pile-test (BPB)		0.606	0.638	0.542	0.548
	BBH (EM)		78.8	79.8
English		3-shot			82.9	87.5
	MMLU (EM)	5-shot	78.4	85.0	84.4	87.1
	MMLU-Redux (EM)	5-shot	75.6	83.2	81.3	86.2
	MMLU-Pro (EM)	5-shot	51.4	58.3	52.8	64.4
	DROP (F1)	3-shot	80.4	80.6	86.0	89.0
	ARC-Easy (EM)	25-shot	97.6	98.4	98.4	98.9
	ARC-Challenge (EM)	25-shot	92.2	94.5	95.3	95.3
	HellaSwag (EM)	10-shot	87.1	84.8	89.2	88.9
	PIQA (EM)	0-shot	83.9	82.6	85.9	84.7
	WinoGrande (EM)	5-shot	86.3	82.3	85.2	84.9
	RACE-Middle (EM)	5-shot	73.1	68.1	74.2	67.1
	RACE-High (EM)	5-shot	52.6	50.3	56.8	51.3
	TriviaQA (EM)	5-shot	80.0	71.9	82.7	82.9
	NaturalQuestions (EM) AGIEval (EM)	5-shot 0-shot	38.6 57.5	33.2 75.8	41.5	40.0
Code	HumanEval (Pass@1)				60.6	79.6
		0-shot	43.3	53.0	54.9	65.2
	MBPP (Pass@1)	3-shot	65.0	72.6	68.4	75.4
	LiveCodeBench-Base (Pass@1)	3-shot	11.6	12.9	15.5	19.4
	CRUXEval-I (EM) CRUXEval-O (EM)	2-shot 2-shot	52.5 49.8	59.1 59.9	58.5 59.9	67.3
Math						69.8
	GSM8K (EM)	8-shot	81.6	88.3	83.5	89.3
	MATH (EM)	4-shot	43.4	54.4	49.0	61.6
	MGSM (EM) CMath (EM)	8-shot 3-shot	63.6 78.7	76.2 84.5	69.9 77.3	79.8
Chinese	CLUEWSC (EM)					90.7
	C-Eval (EM)	5-shot	82.0 81.4	82.5 89.2	83.0 72.5	82.7
	CMMLU (EM)	5-shot	84.0	89.5		90.1
	CMRC (EM)	5-shot			73.7	88.8
		1-shot	77.4	75.8	76.0	76.3
	C3 (EM) CCPM (EM)	0-shot 0-shot	77.4 93.0	76.7 88.5	79.7 78.6	78.6 92.0
Multilingual	MMMLU-non-English (EM)	5-shot	64.0	74.8	73.8	79.4

表 3 | DeepSeek-V3-Base 与其他代表性开源基础模型的对比。所有模型均在我们的内部框架中评估，并共享相同的评估设置。得分差距不超过 0.3 的模型被视为处于同一水平。DeepSeek-V3-Base 在大多数基准测试中表现最佳，尤其是在数学和代码任务上。

4.4.2. Evaluation Results

4.4.2. 评估结果

In Table 3, we compare the base model of DeepSeek-V3 with the state-of-the-art open-source base models, including DeepSeek-V2-Base (DeepSeek-AI, 2024c) (our previous release), Qwen2.5 72B Base (Qwen, 2024b), and LLaMA-3.1 405B Base (AI@Meta, 2024b). We evaluate all these models with our internal evaluation framework, and ensure that they share the same evaluation setting. Note that due to the changes in our evaluation framework over the past months, the performance of DeepSeek-V2-Base exhibits a slight difference from our previously reported results. Overall, DeepSeek-V3-Base comprehensively outperforms DeepSeek-V2-Base and Qwen2.5 72B Base, and surpasses LLaMA-3.1 405B Base in the majority of benchmarks, essentially becoming the strongest open-source model.

在表 3 中，我们将 DeepSeek-V3 的基础模型与当前最先进的开源基础模型进行了比较，包括 DeepSeek-V2-Base (DeepSeek-AI, 2024c) (我们之前的发布版本)、Qwen2.5 72B Base (Qwen, 2024b) 和 LLaMA-3.1 405B Base (AI@Meta, 2024b)。我们使用内部评估框架对这些模型进行了评估，并确保它们共享相同的评估设置。需要注意的是，由于过去几个月评估框架的变化，DeepSeek-V2-Base 的表现与我们之前报告的结果略有不同。总体而言，DeepSeek-V3-Base 全面超越了 DeepSeek-V2-Base 和 Qwen2.5 72B Base，并在大多数基准测试中超过了 LLaMA-3.1 405B Base，基本上成为了最强大的开源模型。

From a more detailed perspective, we compare DeepSeek-V3-Base with the other open-source base models individually. (1) Compared with DeepSeek-V2-Base, due to the improvements in our model architecture, the scale-up of the model size and training tokens, and the enhancement of data quality, DeepSeek-V3-Base achieves significantly better performance as expected. (2) Compared with Qwen2.5 72B Base, the state-of-the-art Chinese open-source model, with only half of the activated parameters, DeepSeek-V3-Base also demonstrates remarkable advantages, especially on English, multilingual, code, and math benchmarks. As for Chinese benchmarks, except for CMMLU, a Chinese multi-subject multiple-choice task, DeepSeek-V3-Base also shows better performance than Qwen2.5 72B. (3) Compared with LLaMA-3.1 405B Base, the largest open-source model with 11 times the activated parameters, DeepSeek-V3-Base also exhibits much better performance on multilingual, code, and math benchmarks. As for English and Chinese language benchmarks, DeepSeek-V3-Base shows competitive or better performance, and is especially good on BBH, MMLU-series, DROP, C-Eval, CMMLU, and CCPM.

从更详细的角度来看，我们将 DeepSeek-V3-Base 与其他开源基础模型逐一进行比较。(1) 与 DeepSeek-V2-Base 相比，由于我们在模型架构、模型规模和训练 Token 数量上的提升，以及数据质量的增强，DeepSeek-V3-Base 的表现显著优于预期。(2) 与目前最先进的中文开源模型 Qwen2.5 72B Base 相比，DeepSeek-V3-Base 仅使用了其一半的激活参数，但在英语、多语言、代码和数学基准测试中表现出显著优势。在中文基准测试中，除了 CMMLU（一个中文多学科选择题任务）外，DeepSeek-V3-Base 的表现也优于 Qwen2.5 72B。(3) 与最大的开源模型 LLaMA-3.1 405B Base 相比，DeepSeek-V3-Base 的激活参数仅为前者的 1/11，但在多语言、代码和数学基准测试中表现更为出色。在英语和中文语言基准测试中，DeepSeek-V3-Base 表现出竞争性或更好的性能，尤其是在 BBH、MMLU 系列、DROP、C-Eval、CMMLU 和 CCPM 等任务上表现尤为突出。

Due to our efficient architectures and comprehensive engineering optimization s, DeepSeekV3 achieves extremely high training efficiency. Under our training framework and infrastructures, training DeepSeek-V3 on each trillion tokens requires only 180K H800 GPU hours, which is much cheaper than training 72B or 405B dense models.

由于我们高效的架构和全面的工程优化，DeepSeekV3 实现了极高的训练效率。在我们的训练框架和基础设施下，训练 DeepSeek-V3 每万亿 Token 仅需 18 万 H800 GPU 小时，比训练 72B 或 405B 密集模型便宜得多。

Table 4 | Ablation results for the MTP strategy. The MTP strategy consistently enhances the model performance on most of the evaluation benchmarks.

基准 (指标)	# Shots	小型 MoE 基线	小型 MoE w/ MTP	大型 MoE 基线	大型 MoE w/ MTP
#激活参数 (推理)		2.4B	2.4B	20.9B	20.9B
#总参数 (推理)		15.7B	15.7B	228.7B	228.7B
#训练 Token		1.33T	1.33T	540B	540B
Pile-test (BPB)		0.729	0.729	0.658	0.657
BBH (EM)	3-shot	39.0	41.4	70.0	70.7
MMLU (EM)	5-shot	50.0	53.3	67.5	66.6
DROP (F1)	1-shot	39.2	41.3	68.5	70.6
TriviaQA (EM)	5-shot	56.9	57.7	67.0	67.3
NaturalQuestions (EM)	5-shot	22.7	22.3	27.2	28.5
HumanEval (Pass@1)	0-shot	20.7	26.8	44.5	53.7
MBPP (Pass@1)	3-shot	35.8	36.8	61.6	62.2
GSM8K (EM)	8-shot	25.4	31.4	72.3	74.0
MATH (EM)	4-shot	10.7	12.6	38.6	39.8

表 4 | MTP 策略的消融实验结果。MTP 策略在大多数评估基准上持续提升了模型性能。

4.5. Discussion

4.5. 讨论

4.5.1. Ablation Studies for Multi-Token Prediction

4.5.1. 多Token预测的消融研究

In Table 4, we show the ablation results for the MTP strategy. To be specific, we validate the MTP strategy on top of two baseline models across different scales. At the small scale, we train a baseline MoE model comprising 15.7B total parameters on 1.33T tokens. At the large scale, we train a baseline MoE model comprising 228.7B total parameters on 540B tokens. On top of them, keeping the training data and the other architectures the same, we append a 1-depth MTP module onto them and train two models with the MTP strategy for comparison. Note that during inference, we directly discard the MTP module, so the inference costs of the compared models are exactly the same. From the table, we can observe that the MTP strategy consistently enhances the model performance on most of the evaluation benchmarks.

在表 4 中，我们展示了 MTP 策略的消融实验结果。具体来说，我们在两个不同规模的基线模型上验证了 MTP 策略。在小规模情况下，我们训练了一个包含 15.7B 总参数的基线 MoE 模型，使用了 1.33T 的 Token 进行训练。在大规模情况下，我们训练了一个包含 228.7B 总参数的基线 MoE 模型，使用了 540B 的 Token 进行训练。在此基础上，保持训练数据和其他架构不变，我们为它们添加了一个 1 层深度的 MTP 模块，并使用 MTP 策略训练了两个模型进行比较。需要注意的是，在推理过程中，我们直接丢弃了 MTP 模块，因此比较模型的推理成本完全相同。从表中可以看出，MTP 策略在大多数评估基准上持续提升了模型性能。

Table 5 | Ablation results for the auxiliary-loss-free balancing strategy. Compared with the purely auxiliary-loss-based method, the auxiliary-loss-free strategy consistently achieves better model performance on most of the evaluation benchmarks.

基准 (指标)	#Shots	小型 MoE 基于辅助损失	小型 MoE 无辅助损失	大型 MoE 基于辅助损失	大型 MoE 无辅助损失
#激活参数		2.4B	2.4B	20.9B	20.9B
#总参数		15.7B	15.7B	228.7B	228.7B
#训练 Token		1.33T	1.33T	578B	578B
Pile-test (BPB)		0.727	0.724	0.656	0.652
BBH (EM)	3-shot	37.3	39.3	66.7	67.9
MMLU (EM)	5-shot	51.0	51.8	68.3	67.2
DROP (F1)	1-shot	38.1	39.0	67.1	67.1
TriviaQA (EM)	5-shot	58.3	58.5	66.7	67.7
NaturalQuestions (EM)	5-shot	23.2	23.4	27.1	28.1
HumanEval (Pass@1)	O-shot	22.0	22.6	40.2	46.3
MBPP (Pass@1)	3-shot	36.6	35.8	59.2	61.2
GSM8K (EM)	8-shot	27.1	29.6	70.7	74.5
MATH (EM)	4-shot	10.9	11.1	37.2	39.6

表 5 | 无辅助损失平衡策略的消融实验结果。与纯基于辅助损失的方法相比，无辅助损失策略在大多数评估基准上持续实现了更好的模型性能。

4.5.2. Ablation Studies for the Auxiliary-Loss-Free Balancing Strategy

4.5.2. 无辅助损失平衡策略的消融研究

In Table 5, we show the ablation results for the auxiliary-loss-free balancing strategy. We validate this strategy on top of two baseline models across different scales. At the small scale, we train a baseline MoE model comprising 15.7B total parameters on 1.33T tokens. At the large scale, we train a baseline MoE model comprising 228.7B total parameters on 578B tokens. Both of the baseline models purely use auxiliary losses to encourage load balance, and use the sigmoid gating function with top-K affinity normalization. Their hyper-parameters to control the strength of auxiliary losses are the same as DeepSeek-V2-Lite and DeepSeek-V2, respectively. On top of these two baseline models, keeping the training data and the other architectures the same, we remove all auxiliary losses and introduce the auxiliary-loss-free balancing strategy for comparison. From the table, we can observe that the auxiliary-loss-free strategy consistently achieves better model performance on most of the evaluation benchmarks.

在表 5 中，我们展示了无辅助损失平衡策略的消融实验结果。我们在不同规模的两个基线模型上验证了这一策略。在小规模实验中，我们训练了一个包含 15.7B 总参数的基线 MoE 模型，使用了 1.33T 的 token。在大规模实验中，我们训练了一个包含 228.7B 总参数的基线 MoE 模型，使用了 578B 的 token。这两个基线模型都仅使用辅助损失来促进负载平衡，并使用了带有 top-K 亲和度归一化的 sigmoid 门控函数。它们控制辅助损失强度的超参数分别与 DeepSeek-V2-Lite 和 DeepSeek-V2 相同。在这两个基线模型的基础上，保持训练数据和其他架构不变，我们移除了所有辅助损失，并引入了无辅助损失平衡策略进行比较。从表中可以看出，无辅助损失策略在大多数评估基准上始终实现了更好的模型性能。

4.5.3. Batch-Wise Load Balance VS. Sequence-Wise Load Balance

4.5.3. 批次负载均衡 VS. 序列负载均衡

The key distinction between auxiliary-loss-free balancing and sequence-wise auxiliary loss lies in their balancing scope: batch-wise versus sequence-wise. Compared with the sequence-wise auxiliary loss, batch-wise balancing imposes a more flexible constraint, as it does not enforce in-domain balance on each sequence. This flexibility allows experts to better specialize in different domains. To validate this, we record and analyze the expert load of a 16B auxiliaryloss-based baseline and a 16B auxiliary-loss-free model on different domains in the Pile test set. As illustrated in Figure 9, we observe that the auxiliary-loss-free model demonstrates greater expert specialization patterns as expected.

无辅助损失平衡与序列级辅助损失的关键区别在于它们的平衡范围：批次级与序列级。与序列级辅助损失相比，批次级平衡施加了更灵活的约束，因为它不会对每个序列强制实施域内平衡。这种灵活性使得专家能够更好地专注于不同领域。为了验证这一点，我们记录并分析了基于16B辅助损失的基线模型和16B无辅助损失模型在Pile测试集上不同领域的专家负载。如图9所示，我们观察到无辅助损失模型表现出更大的专家专业化模式，符合预期。

To further investigate the correlation between this flexibility and the advantage in model performance, we additionally design and validate a batch-wise auxiliary loss that encourages load balance on each training batch instead of on each sequence. The experimental results show that, when achieving a similar level of batch-wise load balance, the batch-wise auxiliary loss can also achieve similar model performance to the auxiliary-loss-free method. To be specific, in our experiments with 1B MoE models, the validation losses are: 2.258 (using a sequencewise auxiliary loss), 2.253 (using the auxiliary-loss-free method), and 2.253 (using a batch-wise auxiliary loss). We also observe similar results on 3B MoE models: the model using a sequencewise auxiliary loss achieves a validation loss of 2.085, and the models using the auxiliary-loss-free method or a batch-wise auxiliary loss achieve the same validation loss of 2.080.

为了进一步研究这种灵活性与模型性能优势之间的相关性，我们额外设计并验证了一种批量辅助损失 (batch-wise auxiliary loss)，该损失鼓励在每个训练批次上实现负载均衡，而不是在每个序列上。实验结果表明，当达到相似的批次负载均衡水平时，批量辅助损失也能实现与无辅助损失方法相似的模型性能。具体来说，在我们使用 10 亿参数 MoE 模型的实验中，验证损失分别为：2.258（使用序列级辅助损失）、2.253（使用无辅助损失方法）和 2.253（使用批量辅助损失）。我们在 30 亿参数 MoE 模型上也观察到了类似的结果：使用序列级辅助损失的模型验证损失为 2.085，而使用无辅助损失方法或批量辅助损失的模型验证损失均为 2.080。

Figure 9 | Expert load of auxiliary-loss-free and auxiliary-loss-based models on three domains in the Pile test set. The auxiliary-loss-free model shows greater expert specialization patterns than the auxiliary-loss-based one. The relative expert load denotes the ratio between the actual expert load and the theoretically balanced expert load. Due to space constraints, we only present the results of two layers as an example, with the results of all layers provided in Appendix C.

图 9 | 在 Pile 测试集的三个领域中，无辅助损失模型和基于辅助损失模型的专家负载。无辅助损失模型显示出比基于辅助损失模型更强的专家专业化模式。相对专家负载表示实际专家负载与理论平衡专家负载之间的比率。由于篇幅限制，我们仅展示了两层的结果作为示例，所有层的结果见附录 C。

In addition, although the batch-wise load balancing methods show consistent performance advantages, they also face two potential challenges in efficiency: (1) load imbalance within certain sequences or small batches, and (2) domain-shift-induced load imbalance during inference. The first challenge is naturally addressed by our training framework that uses large-scale expert parallelism and data parallelism, which guarantees a large size of each micro-batch. For the second challenge, we also design and implement an efficient inference framework with redundant expert deployment, as described in Section 3.4, to overcome it.

此外，尽管基于批次的负载均衡方法表现出了一致的性能优势，但它们在效率方面也面临两个潜在挑战：(1) 某些序列或小批次内的负载不均衡，(2) 推理过程中由领域转移引起的负载不均衡。第一个挑战通过我们的训练框架自然解决，该框架使用大规模专家并行和数据并行，确保每个微批次的大小足够大。对于第二个挑战，我们还设计并实现了一个高效的推理框架，采用冗余专家部署，如第3.4节所述，以克服这一问题。

5. Post-Training

5. 训练后处理

5.1. Supervised Fine-Tuning

5.1. 监督微调

We curate our instruction-tuning datasets to include 1.5M instances spanning multiple domains, with each domain employing distinct data creation methods tailored to its specific requirements.

我们精心策划了指令微调数据集，包含150万个实例，涵盖多个领域，每个领域都采用针对其特定需求的数据创建方法。

Reasoning Data. For reasoning-related datasets, including those focused on mathematics, code competition problems, and logic puzzles, we generate the data by leveraging an internal DeepSeek-R1 model. Specifically, while the R1-generated data demonstrates strong accuracy, it suffers from issues such as over thinking, poor formatting, and excessive length. Our objective is to balance the high accuracy of R1-generated reasoning data and the clarity and conciseness of regularly formatted reasoning data.

推理数据。对于与推理相关的数据集，包括专注于数学、代码竞赛问题和逻辑谜题的数据集，我们通过利用内部的 DeepSeek-R1 模型生成数据。具体来说，虽然 R1 生成的数据表现出较高的准确性，但它存在过度思考、格式不佳和长度过长等问题。我们的目标是平衡 R1 生成的推理数据的高准确性与常规格式推理数据的清晰性和简洁性。

To establish our methodology, we begin by developing an expert model tailored to a specific domain, such as code, mathematics, or general reasoning, using a combined Supervised FineTuning (SFT) and Reinforcement Learning (RL) training pipeline. This expert model serves as a data generator for the final model. The training process involves generating two distinct types of SFT samples for each instance: the first couples the problem with its original response in the format of <problem, original response>, while the second incorporates a system prompt alongside the problem and the R1 response in the format of <system prompt, problem, R1 response>.

为了建立我们的方法论，我们首先开发一个针对特定领域（如代码、数学或通用推理）的专家模型，使用结合了监督微调（SFT）和强化学习（RL）的训练流程。这个专家模型作为最终模型的数据生成器。训练过程涉及为每个实例生成两种不同类型的SFT样本：第一种将问题与其原始响应配对，格式为<问题，原始响应>；第二种则将系统提示与问题和R1响应结合，格式为<系统提示，问题，R1响应>。

The system prompt is meticulously designed to include instructions that guide the model toward producing responses enriched with mechanisms for reflection and verification. During the RL phase, the model leverages high-temperature sampling to generate responses that integrate patterns from both the R1-generated and original data, even in the absence of explicit system prompts. After hundreds of RL steps, the intermediate RL model learns to incorporate R1 patterns, thereby enhancing overall performance strategically.

系统提示词经过精心设计，包含指导模型生成带有反思和验证机制的响应指令。在强化学习（RL）阶段，即使没有明确的系统提示词，模型也能利用高温采样生成结合了R1生成数据和原始数据模式的响应。经过数百次RL步骤后，中间RL模型学会了融入R1模式，从而策略性地提升整体性能。

Upon completing the RL training phase, we implement rejection sampling to curate highquality SFT data for the final model, where the expert models are used as data generation sources. This method ensures that the final training data retains the strengths of DeepSeek-R1 while producing responses that are concise and effective.

在完成强化学习训练阶段后，我们采用拒绝采样方法来为最终模型筛选高质量的监督微调数据，其中专家模型被用作数据生成源。这种方法确保了最终训练数据保留了 DeepSeek-R1 的优势，同时生成简洁且有效的响应。

Non-Reasoning Data. For non-reasoning data, such as creative writing, role-play, and simple question answering, we utilize DeepSeek-V2.5 to generate responses and enlist human annotators to verify the accuracy and correctness of the data.

非推理数据。对于非推理数据，如创意写作、角色扮演和简单问答，我们使用 DeepSeek-V2.5 生成响应，并聘请人工标注员来验证数据的准确性和正确性。

SFT Settings. We fine-tune DeepSeek-V3-Base for two epochs using the SFT dataset, using the cosine decay learning rate scheduling that starts at $5\times10^{-6}$ and gradually decreases to $1\times10^{-6}$ . During training, each single sequence is packed from multiple samples. However, we adopt a sample masking strategy to ensure that these examples remain isolated and mutually invisible.

SFT 设置。我们使用 SFT 数据集对 DeepSeek-V3-Base 进行两个周期的微调，采用余弦衰减学习率调度，初始学习率为 $5\times10^{-6}$，逐渐降低至 $1\times10^{-6}$。在训练过程中，每个单一序列由多个样本打包而成。然而，我们采用了样本掩码策略，以确保这些样本保持隔离且相互不可见。

5.2. Reinforcement Learning

5.2. 强化学习

5.2.1. Reward Model

5.2.1. 奖励模型

We employ a rule-based Reward Model (RM) and a model-based RM in our RL process.

我们在强化学习 (RL) 过程中采用了基于规则的奖励模型 (Reward Model, RM) 和基于模型的奖励模型。

Rule-Based RM. For questions that can be validated using specific rules, we adopt a rulebased reward system to determine the feedback. For instance, certain math problems have deterministic results, and we require the model to provide the final answer within a designated format (e.g., in a box), allowing us to apply rules to verify the correctness. Similarly, for LeetCode problems, we can utilize a compiler to generate feedback based on test cases. By leveraging rule-based validation wherever possible, we ensure a higher level of reliability, as this approach is resistant to manipulation or exploitation.

基于规则的奖励模型 (Rule-Based RM)。对于可以使用特定规则验证的问题，我们采用基于规则的奖励系统来确定反馈。例如，某些数学问题具有确定性的结果，我们要求模型在指定格式（例如在方框中）提供最终答案，从而允许我们应用规则来验证正确性。同样，对于 LeetCode 问题，我们可以利用编译器根据测试用例生成反馈。通过尽可能利用基于规则的验证，我们确保了更高的可靠性，因为这种方法不易被操纵或利用。

Model-Based RM. For questions with free-form ground-truth answers, we rely on the reward model to determine whether the response matches the expected ground-truth. Conversely, for questions without a definitive ground-truth, such as those involving creative writing, the reward model is tasked with providing feedback based on the question and the corresponding answer as inputs. The reward model is trained from the DeepSeek-V3 SFT checkpoints. To enhance its reliability, we construct preference data that not only provides the final reward but also includes the chain-of-thought leading to the reward. This approach helps mitigate the risk of reward hacking in specific tasks.

基于模型的奖励机制 (Model-Based RM)。对于具有自由形式标准答案的问题，我们依赖奖励模型来判断回答是否符合预期的标准答案。相反，对于没有明确标准答案的问题，例如涉及创意写作的问题，奖励模型的任务是基于问题和相应回答提供反馈。奖励模型是从 DeepSeek-V3 SFT 检查点训练的。为了提高其可靠性，我们构建了偏好数据，这些数据不仅提供最终奖励，还包括导致奖励的思维链。这种方法有助于减轻在特定任务中奖励黑客攻击的风险。

5.2.2. Group Relative Policy Optimization

5.2.2. 群体相对策略优化

Similar to DeepSeek-V2 (DeepSeek-AI, 2024c), we adopt Group Relative Policy Optimiza- tion (GRPO) (Shao et al., 2024), which foregoes the critic model that is typically with the same size as the policy model, and estimates the baseline from group scores instead. Specifically, for each question $q,$ GRPO samples a group of outputs ${o_{1},o_{2},\cdots,,o_{G}}$ from the old policy model $\pi_{\theta_{o l d}}$ and then optimizes the policy model $\pi_{\theta}$ by maximizing the following objective:

与 DeepSeek-V2 (DeepSeek-AI, 2024c) 类似，我们采用了组相对策略优化 (Group Relative Policy Optimization, GRPO) (Shao et al., 2024)，该方法摒弃了通常与策略模型大小相同的评论模型，而是从组分数中估计基线。具体来说，对于每个问题 $q,$ GRPO 从旧策略模型 $\pi_{\theta_{o l d}}$ 中采样一组输出 ${o_{1},o_{2},\cdots,,o_{G}}$，然后通过最大化以下目标来优化策略模型 $\pi_{\theta}$：

where $\varepsilon$ and $\beta$ are hyper-parameters; $\pi_{r e f}$ is the reference model; and $A_{i}$ is the advantage, derived from the rewards $\left{r_{1},r_{2},\dots,r_{G}\right}$ corresponding to the outputs within each group:

其中 $\varepsilon$ 和 $\beta$ 是超参数；$\pi_{ref}$ 是参考模型；$A_{i}$ 是优势，源自每组输出对应的奖励 $\left{r_{1},r_{2},\dots,r_{G}\right}$：

We incorporate prompts from diverse domains, such as coding, math, writing, role-playing, and question answering, during the RL process. This approach not only aligns the model more closely with human preferences but also enhances performance on benchmarks, especially in scenarios where available SFT data are limited.

我们在强化学习（RL）过程中融入了来自不同领域的提示，如编程、数学、写作、角色扮演和问答。这种方法不仅使模型更符合人类偏好，还提高了在基准测试中的表现，尤其是在可用监督微调（SFT）数据有限的场景中。

5.3. Evaluations

5.3. 评估

5.3.1. Evaluation Settings

5.3.1. 评估设置

Evaluation Benchmarks. Apart from the benchmark we used for base model testing, we further evaluate instructed models on IFEval (Zhou et al., 2023), FRAMES (Krishna et al., 2024), LongBench v2 (Bai et al., 2024), GPQA (Rein et al., 2023), SimpleQA (OpenAI, 2024c), C- SimpleQA (He et al., 2024), SWE-Bench Verified (OpenAI, 2024d), Aider 1, Live Code Bench (Jain et al., 2024) (questions from August 2024 to November 2024), Codeforces 2, Chinese National High School Mathematics Olympiad (CNMO 2024)3, and American Invitational Mathematics Examination 2024 (AIME 2024) (MAA, 2024).

评估基准。除了我们用于基础模型测试的基准外，我们还在 IFEval (Zhou et al., 2023)、FRAMES (Krishna et al., 2024)、LongBench v2 (Bai et al., 2024)、GPQA (Rein et al., 2023)、SimpleQA (OpenAI, 2024c)、C-SimpleQA (He et al., 2024)、SWE-Bench Verified (OpenAI, 2024d)、Aider 1、Live Code Bench (Jain et al., 2024)（2024年8月至2024年11月的问题）、Codeforces 2、中国高中数学奥林匹克竞赛 (CNMO 2024) 3 以及美国数学邀请赛 2024 (AIME 2024) (MAA, 2024) 上进一步评估了指令模型。

Compared Baselines. We conduct comprehensive evaluations of our chat model against several strong baselines, including DeepSeek-V2-0506, DeepSeek-V2.5-0905, Qwen2.5 72B Instruct, LLaMA-3.1 405B Instruct, Claude-Sonnet-3.5-1022, and GPT-4o-0513. For the DeepSeek-V2 model series, we select the most representative variants for comparison. For closed-source models, evaluations are performed through their respective APIs.

对比基线。我们对我们的聊天模型进行了全面评估，对比了多个强大的基线模型，包括 DeepSeek-V2-0506、DeepSeek-V2.5-0905、Qwen2.5 72B Instruct、LLaMA-3.1 405B Instruct、Claude-Sonnet-3.5-1022 和 GPT-4o-0513。对于 DeepSeek-V2 模型系列，我们选择了最具代表性的变体进行比较。对于闭源模型，评估通过各自的 API 进行。

Detailed Evaluation Configurations. For standard benchmarks including MMLU, DROP, GPQA, and SimpleQA, we adopt the evaluation prompts from the simple-evals framework4. We utilize the Zero-Eval prompt format (Lin, 2024) for MMLU-Redux in a zero-shot setting. For other datasets, we follow their original evaluation protocols with default prompts as provided by the dataset creators. For code and math benchmarks, the HumanEval-Mul dataset includes 8 mainstream programming languages (Python, Java, Cpp, C#, JavaScript, TypeScript, PHP, and Bash) in total. We use CoT and non-CoT methods to evaluate model performance on Live Code Bench, where the data are collected from August 2024 to November 2024. The Codeforces dataset is measured using the percentage of competitors. SWE-Bench verified is evaluated using the agentless framework (Xia et al., 2024). We use the “diff” format to evaluate the Aider-related benchmarks. For mathematical assessments, AIME and CNMO 2024 are evaluated with a temperature of 0.7, and the results are averaged over 16 runs, while MATH-500 employs greedy decoding. We allow all models to output a maximum of 8192 tokens for each benchmark.

详细评估配置。对于包括 MMLU、DROP、GPQA 和 SimpleQA 在内的标准基准测试，我们采用 simple-evals 框架的评估提示。我们在零样本设置下使用 Zero-Eval 提示格式 (Lin, 2024) 进行 MMLU-Redux 评估。对于其他数据集，我们遵循其原始评估协议，并使用数据集创建者提供的默认提示。对于代码和数学基准测试，HumanEval-Mul 数据集总共包含 8 种主流编程语言 (Python、Java、Cpp、C#、JavaScript、TypeScript、PHP 和 Bash)。我们使用 CoT 和非 CoT 方法评估模型在 Live Code Bench 上的性能，数据收集时间为 2024 年 8 月至 2024 年 11 月。Codeforces 数据集使用参赛者百分比进行衡量。SWE-Bench 验证使用无智能体框架 (Xia et al., 2024) 进行评估。我们使用“diff”格式评估与 Aider 相关的基准测试。对于数学评估，AIME 和 CNMO 2024 在温度为 0.7 的情况下进行评估，结果取 16 次运行的平均值，而 MATH-500 使用贪婪解码。我们允许所有模型在每个基准测试中最多输出 8192 个 Token。

	基准 (指标)	DeepSeek DeepSeek V2-0506 V2.5-0905	72B-Inst.	Qwen2.5 LLaMA-3.1	405B-Inst. Sonnet-1022	1 Claude-3.5-	GPT-40 0513	DeepSeek V3
	架构	MoE	MoE	Dense	Dense			MoE
	激活参数量/总参数量	21B/236B	21B/236B	72B/72B	405B/405B	-	-	37B/671B
英语
	MMLU (EM)	78.2	80.6	85.3	88.6	88.3	87.2	88.5
	MMLU-Redux (EM)	77.9	80.3	85.6	86.2	88.9	88.0	89.1
	MMLU-Pro (EM)	58.5	66.2	71.6	73.3	78.0	72.6	75.9
	DROP (3-shot F1)	83.0	87.8	76.7	88.7	88.3	83.7	91.6
	IF-Eval (Prompt Strict)	57.7	80.6	84.1	86.0	86.5	84.3	86.1
	GPQA-Diamond (Pass@1) SimpleQA (Correct)	35.3	41.3	49.0	51.1	65.0	49.9	59.1
	FRAMES (Acc.)	9.0/66.9	10.2/65.4	9.1/69.8	17.1/70.0	28.4	38.2	24.9
	LongBench v2 (Acc.)	31.6	35.4	39.4	36.1	72.5/41.0	80.5/48.1	73.3/48.7
代码	HumanEval-Mul (Pass@1)	69.3	77.4	77.3	77.2	81.7	80.5	82.6
	LiveCodeBench (Pass@1-COT)	18.8	29.2	31.1	28.4	36.3	33.4	40.5
	LiveCodeBench (Pass@1)	20.3	28.4	28.7	30.1	32.8	34.2	37.6
	Codeforces (Percentile)	17.5	35.6	24.8	25.3	20.3	23.6	51.6
	SWE Verified (Resolved)		22.6	23.8	24.5	50.8	38.8	42.0
	Aider-Edit (Acc.)	60.3	71.6	65.4	63.9	84.2	72.9	79.7
	Aider-Polyglot (Acc)		18.2	7.6	5.8	45.3	16.0	49.6
数学	AIME 2024 (Pass@1)	4.6	16.7	23.3	23.3	16.0	9.3	39.2
	MATH-500 (EM)	56.3	74.7	80.0	73.8	78.3	74.6	90.2
	CNMO 2024 (Pass@1)	2.8	10.8	15.9	6.8	13.1	10.8	43.2
中文	C-Eval (EM)	78.6	79.5	86.1	61.5	76.7	76.0	86.5
	CLUEWSC (EM)	89.9	90.4	91.4	84.7	85.4	87.9	90.9
	C-SimpleQA (Correct)	48.5	54.1	48.4	50.4	51.3	59.3	64.8

Table 6 | Comparison between DeepSeek-V3 and other representative chat models. All models are evaluated in a configuration that limits the output length to 8K. Benchmarks containing fewer than 1000 samples are tested multiple times using varying temperature settings to derive robust final results. DeepSeek-V3 stands as the best-performing open-source model, and also exhibits competitive performance against frontier closed-source models.

表 6 | DeepSeek-V3 与其他代表性聊天模型的比较。所有模型均在限制输出长度为 8K 的配置下进行评估。对于包含少于 1000 个样本的基准测试，使用不同的温度设置进行多次测试，以得出稳健的最终结果。DeepSeek-V3 是性能最佳的开源模型，同时在与前沿闭源模型的竞争中表现出色。

Table 6 presents the evaluation results, showcasing that DeepSeek-V3 stands as the bestperforming open-source model. Additionally, it is competitive against frontier closed-source models like GPT-4o and Claude-3.5-Sonnet.

表 6 展示了评估结果，表明 DeepSeek-V3 是表现最好的开源模型。此外，它与 GPT-4o 和 Claude-3.5-Sonnet 等前沿闭源模型相比也具备竞争力。

English Benchmarks. MMLU is a widely recognized benchmark designed to assess the performance of large language models, across diverse knowledge domains and tasks. DeepSeek-V3 demonstrates competitive performance, standing on par with top-tier models such as LLaMA3.1-405B, GPT-4o, and Claude-Sonnet 3.5, while significantly outperforming Qwen2.5 72B. Moreover, DeepSeek-V3 excels in MMLU-Pro, a more challenging educational knowledge benchmark, where it closely trails Claude-Sonnet 3.5. On MMLU-Redux, a refined version ofMMLU with corrected labels, DeepSeek-V3 surpasses its peers. In addition, on GPQA-Diamond, a PhD-level evaluation testbed, DeepSeek-V3 achieves remarkable results, ranking just behind Claude 3.5 Sonnet and outperforming all other competitors by a substantial margin.

English Benchmarks。MMLU 是一个广泛认可的基准测试，旨在评估大语言模型在不同知识领域和任务中的表现。DeepSeek-V3 展现了极具竞争力的性能，与 LLaMA3.1-405B、GPT-4o 和 Claude-Sonnet 3.5 等顶级模型持平，同时显著优于 Qwen2.5 72B。此外，DeepSeek-V3 在更具挑战性的教育知识基准 MMLU-Pro 中表现出色，紧随 Claude-Sonnet 3.5 之后。在 MMLU-Redux 上，这是一个经过标签修正的 MMLU 改进版本，DeepSeek-V3 超越了其他模型。此外，在 GPQA-Diamond 这一博士级评估测试平台上，DeepSeek-V3 取得了显著成绩，仅次于 Claude 3.5 Sonnet，并大幅领先于其他竞争对手。

In long-context understanding benchmarks such as DROP, LongBench v2, and FRAMES, DeepSeek-V3 continues to demonstrate its position as a top-tier model. It achieves an impressive 91.6 F1 score in the 3-shot setting on DROP, outperforming all other models in this category. On FRAMES, a benchmark requiring question-answering over 100k token contexts, DeepSeekV3 closely trails GPT-4o while outperforming all other models by a significant margin. This demonstrates the strong capability of DeepSeek-V3 in handling extremely long-context tasks. The long-context capability of DeepSeek-V3 is further validated by its best-in-class performance on LongBench v2, a dataset that was released just a few weeks before the launch of DeepSeek V3. On the factual knowledge benchmark, SimpleQA, DeepSeek-V3 falls behind GPT-4o and Claude-Sonnet, primarily due to its design focus and resource allocation. DeepSeek-V3 assigns more training tokens to learn Chinese knowledge, leading to exceptional performance on the C-SimpleQA. On the instruction-following benchmark, DeepSeek-V3 significantly outperforms its predecessor, DeepSeek-V2-series, highlighting its improved ability to understand and adhere to user-defined format constraints.

在 DROP、LongBench v2 和 FRAMES 等长上下文理解基准测试中，DeepSeek-V3 继续展示了其作为顶级模型的地位。在 DROP 的 3-shot 设置中，它取得了令人印象深刻的 91.6 F1 分数，超过了该类别中的所有其他模型。在 FRAMES 上，这是一个需要回答超过 100k Token 上下文问题的基准测试，DeepSeek-V3 紧随 GPT-4o 之后，同时显著优于所有其他模型。这展示了 DeepSeek-V3 在处理极长上下文任务方面的强大能力。DeepSeek-V3 的长上下文能力在 LongBench v2 上的最佳表现得到了进一步验证，LongBench v2 是在 DeepSeek-V3 发布前几周才发布的数据集。在事实知识基准测试 SimpleQA 上，DeepSeek-V3 落后于 GPT-4o 和 Claude-Sonnet，这主要是由于其设计重点和资源分配。DeepSeek-V3 分配了更多的训练 Token 来学习中文知识，从而在 C-SimpleQA 上表现出色。在指令遵循基准测试中，DeepSeek-V3 显著优于其前身 DeepSeek-V2 系列，突显了其在理解和遵守用户定义格式约束方面的改进能力。

Code and Math Benchmarks. Coding is a challenging and practical task for LLMs, encompassing engineering-focused tasks like SWE-Bench-Verified and Aider, as well as algorithmic tasks such as HumanEval and Live Code Bench. In engineering tasks, DeepSeek-V3 trails behind Claude-Sonnet-3.5-1022 but significantly outperforms open-source models. The open-source DeepSeek-V3 is expected to foster advancements in coding-related engineering tasks. By providing access to its robust capabilities, DeepSeek-V3 can drive innovation and improvement in areas such as software engineering and algorithm development, empowering developers and researchers to push the boundaries of what open-source models can achieve in coding tasks. In algorithmic tasks, DeepSeek-V3 demonstrates superior performance, outperforming all baselines on benchmarks like HumanEval-Mul and Live Code Bench. This success can be attributed to its advanced knowledge distillation technique, which effectively enhances its code generation and problem-solving capabilities in algorithm-focused tasks.

代码与数学基准测试。对于大语言模型来说，编码是一项具有挑战性且实用的任务，涵盖了以工程为重点的任务（如 SWE-Bench-Verified 和 Aider）以及算法任务（如 HumanEval 和 Live Code Bench）。在工程任务中，DeepSeek-V3 虽然落后于 Claude-Sonnet-3.5-1022，但显著优于开源模型。开源的 DeepSeek-V3 有望推动编码相关工程任务的进步。通过提供其强大的能力，DeepSeek-V3 可以推动软件工程和算法开发等领域的创新和改进，使开发者和研究人员能够突破开源模型在编码任务中的极限。在算法任务中，DeepSeek-V3 表现出卓越的性能，在 HumanEval-Mul 和 Live Code Bench 等基准测试中优于所有基线模型。这一成功归功于其先进的知识蒸馏技术，有效增强了其在算法任务中的代码生成和问题解决能力。

On math benchmarks, DeepSeek-V3 demonstrates exceptional performance, significantly surpassing baselines and setting a new state-of-the-art for non-o1-like models. Specifically, on AIME, MATH-500, and CNMO 2024, DeepSeek-V3 outperforms the second-best model, Qwen2.5 72B, by approximately $10%$ in absolute scores, which is a substantial margin for such challenging benchmarks. This remarkable capability highlights the effectiveness of the distillation technique from DeepSeek-R1, which has been proven highly beneficial for non-o1-like models.

在数学基准测试中，DeepSeek-V3 表现出卓越的性能，显著超越了基线模型，并为非 o1 类模型设定了新的最先进水平。具体而言，在 AIME、MATH-500 和 CNMO 2024 上，DeepSeek-V3 的绝对分数比第二好的模型 Qwen2.5 72B 高出约 $10%$，这对于如此具有挑战性的基准测试来说是一个显著的差距。这一显著能力凸显了 DeepSeek-R1 蒸馏技术的有效性，该技术已被证明对非 o1 类模型非常有益。

模型	Arena-Hard	AlpacaEval 2.0
DeepSeek-V2.5-0905	76.2	50.5
Qwen2.5-72B-Instruct	81.2	49.1
LLaMA-3.1405B	69.3	40.5
GPT-40-0513	80.4	51.1
Claude-Sonnet-3.5-1022	85.2	52.0
DeepSeek-V3	85.5	70.0

Table 7 | English open-ended conversation evaluations. For AlpacaEval 2.0, we use the lengthcontrolled win rate as the metric.

表 7 | 英文开放式对话评估。对于 AlpacaEval 2.0，我们使用长度控制的胜率作为评估指标。

Chinese Benchmarks. Qwen and DeepSeek are two representative model series with robust support for both Chinese and English. On the factual benchmark Chinese SimpleQA, DeepSeekV3 surpasses Qwen2.5-72B by 16.4 points, despite Qwen2.5 being trained on a larger corpus compromising 18T tokens, which are $20%$ more than the 14.8T tokens that DeepSeek-V3 is pre-trained on.

中文基准测试。Qwen 和 DeepSeek 是两个代表性的模型系列，对中文和英文都有强大的支持。在事实基准测试 Chinese SimpleQA 上，DeepSeekV3 比 Qwen2.5-72B 高出 16.4 分，尽管 Qwen2.5 是在包含 18T token 的更大语料库上训练的，这比 DeepSeek-V3 预训练的 14.8T token 多出 20%。

On C-Eval, a representative benchmark for Chinese educational knowledge evaluation, and CLUEWSC (Chinese Winograd Schema Challenge), DeepSeek-V3 and Qwen2.5-72B exhibit similar performance levels, indicating that both models are well-optimized for challenging Chinese-language reasoning and educational tasks.

在 C-Eval（中文教育知识评估的代表性基准）和 CLUEWSC（中文 Winograd 模式挑战）上，DeepSeek-V3 和 Qwen2.5-72B 表现出相似的性能水平，表明这两个模型在具有挑战性的中文推理和教育任务上都得到了良好的优化。

5.3.3. Open-Ended Evaluation

5.3.3. 开放式评估

In addition to standard benchmarks, we also evaluate our models on open-ended generation tasks using LLMs as judges, with the results shown in Table 7. Specifically, we adhere to the original configurations of AlpacaEval 2.0 (Dubois et al., 2024) and Arena-Hard (Li et al., 2024a), which leverage GPT-4-Turbo-1106 as judges for pairwise comparisons. On Arena-Hard, DeepSeek-V3 achieves an impressive win rate of over $86%$ against the baseline GPT-4-0314, performing on par with top-tier models like Claude-Sonnet-3.5-1022. This underscores the robust capabilities of DeepSeek-V3, especially in dealing with complex prompts, including coding and debugging tasks. Furthermore, DeepSeek-V3 achieves a groundbreaking milestone as the first open-source model to surpass $85%$ on the Arena-Hard benchmark. This achievement significantly bridges the performance gap between open-source and closed-source models, setting a new standard for what open-source models can accomplish in challenging domains.

除了标准基准测试外，我们还使用大语言模型作为评判者，在开放式生成任务上评估我们的模型，结果如表 7 所示。具体而言，我们遵循 AlpacaEval 2.0 (Dubois et al., 2024) 和 Arena-Hard (Li et al., 2024a) 的原始配置，这些配置利用 GPT-4-Turbo-1106 作为成对比较的评判者。在 Arena-Hard 上，DeepSeek-V3 相对于基线 GPT-4-0314 取得了超过 $86%$ 的胜率，与 Claude-Sonnet-3.5-1022 等顶级模型表现相当。这凸显了 DeepSeek-V3 的强大能力，尤其是在处理复杂提示（包括编码和调试任务）方面。此外，DeepSeek-V3 实现了突破性的里程碑，成为首个在 Arena-Hard 基准测试中超过 $85%$ 的开源模型。这一成就显著缩小了开源模型与闭源模型之间的性能差距，为开源模型在挑战性领域中的表现设定了新标准。

Similarly, DeepSeek-V3 showcases exceptional performance on AlpacaEval 2.0, outperforming both closed-source and open-source models. This demonstrates its outstanding proficiency in writing tasks and handling straightforward question-answering scenarios. Notably, it surpasses DeepSeek-V2.5-0905 by a significant margin of $20%$ , highlighting substantial improvements in tackling simple tasks and showcasing the effectiveness of its advancements.

同样，DeepSeek-V3 在 AlpacaEval 2.0 上展示了卓越的性能，超越了闭源和开源模型。这证明了其在写作任务和处理简单问答场景中的出色能力。值得注意的是，它比 DeepSeek-V2.5-0905 显著提升了 $20%$，突显了其在处理简单任务方面的重大改进，并展示了其进步的有效性。

5.3.4. DeepSeek-V3 as a Generative Reward Model

5.3.4 DeepSeek-V3 作为生成式奖励模型

We compare the judgment ability of DeepSeek-V3 with state-of-the-art models, namely GPT-4o and Claude-3.5. Table 8 presents the performance of these models in Reward Bench (Lambert et al., 2024). DeepSeek-V3 achieves performance on par with the best versions of GPT-4o-0806 and Claude-3.5-Sonnet-1022, while surpassing other versions. Additionally, the judgment ability of DeepSeek-V3 can also be enhanced by the voting technique. Therefore, we employ DeepSeekV3 along with voting to offer self-feedback on open-ended questions, thereby improving the effectiveness and robustness of the alignment process.

我们将 DeepSeek-V3 的判断能力与最先进的模型 GPT-4o 和 Claude-3.5 进行了比较。表 8 展示了这些模型在 Reward Bench (Lambert et al., 2024) 中的表现。DeepSeek-V3 的表现与 GPT-4o-0806 和 Claude-3.5-Sonnet-1022 的最佳版本相当，同时超越了其他版本。此外，DeepSeek-V3 的判断能力还可以通过投票技术进一步增强。因此，我们采用 DeepSeek-V3 并结合投票技术来为开放式问题提供自我反馈，从而提高对齐过程的有效性和鲁棒性。

模型	Chat	Chat-Hard	Safety	Reasoning	平均
GPT-40-0513	96.6	70.4	86.7	84.9	84.7
GPT-40-0806	96.1	76.1	88.1	86.6	86.7
GPT-40-1120	95.8	71.3	86.2	85.2	84.6
Claude-3.5-s0nnet-0620	96.4	74.0	81.6	84.7	84.2
Claude-3.5-s0nnet-1022	96.4	79.7	91.1	87.6	88.7
DeepSeek-V3	96.9	79.8	87.0	84.3	87.0
DeepSeek-V3 (maj@6)	96.9	82.6	89.5	89.2	89.6

Table 8 | Performances of GPT-4o, Claude-3.5-sonnet and DeepSeek-V3 on Reward Bench. Table 9 | The contribution of distillation from DeepSeek-R1. The evaluation settings of LiveCodeBench and MATH-500 are the same as in Table 6.

表 8 | GPT-4o、Claude-3.5-sonnet 和 DeepSeek-V3 在 Reward Bench 上的表现
表 9 | DeepSeek-R1 蒸馏的贡献。LiveCodeBench 和 MATH-500 的评估设置与表 6 相同。

模型	LiveCodeBench-CoT		MATH-500
	Pass@1	Length	Pass@1	Length
DeepSeek-V2.5 Baseline	31.1	718	74.6	769
DeepSeek-V2.5 +R1 Distill	37.4	783	83.2	1510

5.4. Discussion

5.4. 讨论

5.4.1. Distillation from DeepSeek-R1

5.4.1. 从 DeepSeek-R1 蒸馏

We ablate the contribution of distillation from DeepSeek-R1 based on DeepSeek-V2.5. The baseline is trained on short CoT data, whereas its competitor uses data generated by the expert checkpoints described above.

我们基于 DeepSeek-V2.5 对 DeepSeek-R1 蒸馏的贡献进行了消融实验。基线模型在短链思维链 (CoT) 数据上进行训练，而其竞争对手则使用上述专家检查点生成的数据。

Table 9 demonstrates the effectiveness of the distillation data, showing significant improvements in both Live Code Bench and MATH-500 benchmarks. Our experiments reveal an interesting trade-off: the distillation leads to better performance but also substantially increases the average response length. To maintain a balance between model accuracy and computational efficiency, we carefully selected optimal settings for DeepSeek-V3 in distillation.

表 9 展示了蒸馏数据的有效性，在 Live Code Bench 和 MATH-500 基准测试中均显示出显著的改进。我们的实验揭示了一个有趣的权衡：蒸馏带来了更好的性能，但也显著增加了平均响应长度。为了在模型准确性和计算效率之间保持平衡，我们为 DeepSeek-V3 在蒸馏过程中精心选择了最优设置。

Our research suggests that knowledge distillation from reasoning models presents a promising direction for post-training optimization. While our current work focuses on distilling data from mathematics and coding domains, this approach shows potential for broader applications across various task domains. The effectiveness demonstrated in these specific areas indicates that long-CoT distillation could be valuable for enhancing model performance in other cognitive tasks requiring complex reasoning. Further exploration of this approach across different domains remains an important direction for future research.

我们的研究表明，从推理模型中进行知识蒸馏为训练后优化提供了一个有前景的方向。虽然我们目前的工作主要集中在数学和编程领域的数据蒸馏上，但这种方法在各种任务领域中都显示出广泛应用的潜力。这些特定领域所展示的有效性表明，长链推理蒸馏 (long-CoT distillation) 对于提升其他需要复杂推理的认知任务中的模型性能可能具有重要价值。在不同领域中进一步探索这种方法仍然是未来研究的重要方向。

5.4.2. Self-Rewarding

5.4.2. 自我奖励

Rewards play a pivotal role in RL, steering the optimization process. In domains where verification through external tools is straightforward, such as some coding or mathematics scenarios, RL demonstrates exceptional efficacy. However, in more general scenarios, constructing a feedback mechanism through hard coding is impractical. During the development of DeepSeek-V3, for these broader contexts, we employ the constitutional AI approach (Bai et al., 2022), leveraging the voting evaluation results of DeepSeek-V3 itself as a feedback source. This method has produced notable alignment effects, significantly enhancing the performance of DeepSeek-V3 in subjective evaluations. By integrating additional constitutional inputs, DeepSeek-V3 can optimize towards the constitutional direction. We believe that this paradigm, which combines supplementary information with LLMs as a feedback source, is of paramount importance. The LLM serves as a versatile processor capable of transforming unstructured information from diverse scenarios into rewards, ultimately facilitating the self-improvement of LLMs. Beyond self-rewarding, we are also dedicated to uncovering other general and scalable rewarding methods to consistently advance the model capabilities in general scenarios.

奖励在强化学习（RL）中扮演着关键角色，引导优化过程。在一些可以通过外部工具轻松验证的领域，如某些编程或数学场景，RL表现出卓越的效果。然而，在更一般的场景中，通过硬编码构建反馈机制是不切实际的。在开发DeepSeek-V3的过程中，针对这些更广泛的场景，我们采用了宪法AI方法（Bai et al., 2022），利用DeepSeek-V3自身的投票评估结果作为反馈来源。这种方法产生了显著的校准效果，显著提升了DeepSeek-V3在主观评估中的表现。通过整合额外的宪法输入，DeepSeek-V3能够朝着宪法方向优化。我们相信，这种将补充信息与大语言模型（LLM）作为反馈来源相结合的范式至关重要。LLM作为一个多功能处理器，能够将来自不同场景的非结构化信息转化为奖励，最终促进LLM的自我改进。除了自我奖励外，我们还致力于发现其他通用且可扩展的奖励方法，以持续提升模型在一般场景中的能力。

5.4.3. Multi-Token Prediction Evaluation

5.4.3. 多Token预测评估

Instead of predicting just the next single token, DeepSeek-V3 predicts the next 2 tokens through the MTP technique. Combined with the framework of speculative decoding (Leviathan et al., 2023; Xia et al., 2023), it can significantly accelerate the decoding speed of the model. A natural question arises concerning the acceptance rate of the additionally predicted token. Based on our evaluation, the acceptance rate of the second token prediction ranges between $85%$ and $90%$ across various generation topics, demonstrating consistent reliability. This high acceptance rate enables DeepSeek-V3 to achieve a significantly improved decoding speed, delivering 1.8 times TPS (Tokens Per Second).

DeepSeek-V3 通过 MTP 技术预测接下来的 2 个 Token，而不仅仅是预测下一个 Token。结合推测解码 (speculative decoding) 框架 (Leviathan et al., 2023; Xia et al., 2023)，它可以显著加速模型的解码速度。一个自然的问题是，额外预测的 Token 的接受率如何。根据我们的评估，在不同生成主题下，第二个 Token 预测的接受率在 $85%$ 到 $90%$ 之间，表现出了一致的可靠性。这种高接受率使 DeepSeek-V3 能够显著提高解码速度，达到 1.8 倍的 TPS (每秒 Token 数)。

6. Conclusion, Limitations, and Future Directions

6. 结论、局限性与未来方向

In this paper, we introduce DeepSeek-V3, a large MoE language model with 671B total parameters and 37B activated parameters, trained on 14.8T tokens. In addition to the MLA and Deep Seek MoE architectures, it also pioneers an auxiliary-loss-free strategy for load balancing and sets a multi-token prediction training objective for stronger performance. The training of DeepSeek-V3 is cost-effective due to the support of FP8 training and meticulous engineering optimi zat ions. The post-training also makes a success in distilling the reasoning capability from the DeepSeek-R1 series of models. Comprehensive evaluations demonstrate that DeepSeek-V3 has emerged as the strongest open-source model currently available, and achieves performance comparable to leading closed-source models like GPT-4o and Claude-3.5-Sonnet. Despite its strong performance, it also maintains economical training costs. It requires only 2.788M H800 GPU hours for its full training, including pre-training, context length extension, and post-training.

本文介绍了 DeepSeek-V3，这是一个拥有 6710 亿总参数和 370 亿激活参数的大型 MoE 语言模型，训练数据量达到 14.8T Token。除了 MLA 和 Deep Seek MoE 架构外，它还首创了无辅助损失的负载均衡策略，并设定了多 Token 预测训练目标以提升性能。得益于 FP8 训练的支持和精细的工程优化，DeepSeek-V3 的训练成本效益显著。训练后阶段还成功从 DeepSeek-R1 系列模型中蒸馏出了推理能力。综合评估表明，DeepSeek-V3 已成为当前最强的开源模型，性能可与 GPT-4o 和 Claude-3.5-Sonnet 等领先的闭源模型相媲美。尽管性能强大，它仍保持了经济的训练成本。其完整训练（包括预训练、上下文长度扩展和训练后阶段）仅需 278.8 万 H800 GPU 小时。

While acknowledging its strong performance and cost-effectiveness, we also recognize that DeepSeek-V3 has some limitations, especially on the deployment. Firstly, to ensure efficient inference, the recommended deployment unit for DeepSeek-V3 is relatively large, which might pose a burden for small-sized teams. Secondly, although our deployment strategy for DeepSeekV3 has achieved an end-to-end generation speed of more than two times that of DeepSeek-V2, there still remains potential for further enhancement. Fortunately, these limitations are expected to be naturally addressed with the development of more advanced hardware.

在承认其强大性能和成本效益的同时，我们也认识到 DeepSeek-V3 存在一些局限性，尤其是在部署方面。首先，为了确保高效的推理，DeepSeek-V3 的推荐部署单元相对较大，这可能会给小型团队带来负担。其次，尽管我们对 DeepSeek-V3 的部署策略已经实现了端到端生成速度比 DeepSeek-V2 快两倍以上，但仍存在进一步优化的潜力。幸运的是，随着更先进硬件的发展，这些局限性有望自然得到解决。

DeepSeek consistently adheres to the route of open-source models with long term is m, aiming to steadily approach the ultimate goal of AGI (Artificial General Intelligence). In the future, we plan to strategically invest in research across the following directions.

DeepSeek 始终坚持开源模型的长期主义路线，旨在稳步接近通用人工智能 (AGI) 的终极目标。未来，我们计划在以下方向进行战略性投资研究。

• We will consistently study and refine our model architectures, aiming to further improve

我们将持续研究和优化模型架构，旨在进一步提升

References

参考文献

AI@Meta. Llama 3 model card, 2024a. URL https://github.com/meta-llama/llama3/bl ob/main/MODEL_CARD.md.

AI@Meta. Llama 3 模型卡片, 2024a. URL https://github.com/meta-llama/llama3/bl ob/main/MODEL_CARD.md.

B. Chan, S. Gray, N. Ryder, M. Pavlov, A. Power, L. Kaiser, M. Bavarian, C. Winter, P. Tillet, F. P. Such, D. Cummings, M. Plappert, F. Chantzis, E. Barnes, A. Herbert-Voss, W. H. Guss, A. Nichol, A. Paino, N. Tezak, J. Tang, I. Babuschkin, S. Balaji, S. Jain, W. Saunders, C. Hesse, A. N. Carr, J. Leike, J. Achiam, V. Misra, E. Morikawa, A. Radford, M. Knight, M. Brundage, M. Murati, K. Mayer, P. Welinder, B. McGrew, D. Amodei, S. McCandlish, I. Sutskever, and W. Zaremba. Evaluating large language models trained on code. CoRR, abs/2107.03374, 2021. URL https://arxiv.org/abs/2107.03374.

B. Chan, S. Gray, N. Ryder, M. Pavlov, A. Power, L. Kaiser, M. Bavarian, C. Winter, P. Tillet, F. P. Such, D. Cummings, M. Plappert, F. Chantzis, E. Barnes, A. Herbert-Voss, W. H. Guss, A. Nichol, A. Paino, N. Tezak, J. Tang, I. Babuschkin, S. Balaji, S. Jain, W. Saunders, C. Hesse, A. N. Carr, J. Leike, J. Achiam, V. Misra, E. Morikawa, A. Radford, M. Knight, M. Brundage, M. Murati, K. Mayer, P. Welinder, B. McGrew, D. Amodei, S. McCandlish, I. Sutskever, 和 W. Zaremba. 评估基于代码训练的大语言模型. CoRR, abs/2107.03374, 2021. URL https://arxiv.org/abs/2107.03374.

P. Clark, I. Cowhey, O. Etzioni, T. Khot, A. Sabharwal, C. Schoenick, and O. Tafjord. Think you have solved question answering? try arc, the AI2 reasoning challenge. CoRR, abs/1803.05457, 2018. URL http://arxiv.org/abs/1803.05457.

P. Clark, I. Cowhey, O. Etzioni, T. Khot, A. Sabharwal, C. Schoenick, 和 O. Tafjord. 你认为你已经解决了问答问题？试试 ARC，AI2 推理挑战。CoRR, abs/1803.05457, 2018. URL http://arxiv.org/abs/1803.05457.

K. Cobbe, V. Kosaraju, M. Bavarian, M. Chen, H. Jun, L. Kaiser, M. Plappert, J. Tworek, J. Hilton, R. Nakano, et al. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168, 2021.

K. Cobbe, V. Kosaraju, M. Bavarian, M. Chen, H. Jun, L. Kaiser, M. Plappert, J. Tworek, J. Hilton, R. Nakano 等. 训练验证器以解决数学文字问题. arXiv 预印本 arXiv:2110.14168, 2021.

Y. Cui, T. Liu, W. Che, L. Xiao, Z. Chen, W. Ma, S. Wang, and G. Hu. A span-extraction dataset for Chinese machine reading comprehension. In K. Inui, J. Jiang, V. $\mathrm{Ng},$ and X. Wan, editors, Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pages 5883–5889, Hong Kong, China, Nov. 2019. Association for Computa- tional Linguistics. doi: 10.18653/v1/D19-1600. URL https://a cl anthology.org/D19-1 600.

Y. Cui, T. Liu, W. Che, L. Xiao, Z. Chen, W. Ma, S. Wang, 和 G. Hu. 一个用于中文机器阅读理解 (Chinese Machine Reading Comprehension) 的片段抽取数据集. 在 K. Inui, J. Jiang, V. $\mathrm{Ng},$ 和 X. Wan 编辑的《2019年自然语言处理经验方法会议暨第九届自然语言处理国际联合会议 (EMNLP-IJCNLP) 论文集》中, 第5883–5889页, 中国香港, 2019年11月. 计算语言学协会. doi: 10.18653/v1/D19-1600. URL https://acl anthology.org/D19-1 600.

D. Dai, C. Deng, C. Zhao, R. X. Xu, H. Gao, D. Chen, J. Li, W. Zeng, X. Yu, Y. Wu, Z. Xie, Y. K. Li, P. Huang, F. Luo, C. Ruan, Z. Sui, and W. Liang. Deep seek moe: Towards ultimate expert specialization in mixture-of-experts language models. CoRR, abs/2401.06066, 2024. URL https://doi.org/10.48550/arXiv.2401.06066.

D. Dai, C. Deng, C. Zhao, R. X. Xu, H. Gao, D. Chen, J. Li, W. Zeng, X. Yu, Y. Wu, Z. Xie, Y. K. Li, P. Huang, F. Luo, C. Ruan, Z. Sui, and W. Liang. Deep seek moe: 面向专家混合语言模型中专家终极专业化的探索。CoRR, abs/2401.06066, 2024. URL https://doi.org/10.48550/arXiv.2401.06066.

DeepSeek-AI. Deepseek-coder-v2: Breaking the barrier of closed-source models in code intelligence. CoRR, abs/2406.11931, 2024a. URL https://doi.org/10.48550/arXiv.2406.11 931.

DeepSeek-AI. Deepseek-coder-v2: 打破闭源模型在代码智能领域的壁垒. CoRR, abs/2406.11931, 2024a. URL https://doi.org/10.48550/arXiv.2406.11931.

DeepSeek-AI. Deepseek LLM: scaling open-source language models with long term is m. CoRR, abs/2401.02954, 2024b. URL https://doi.org/10.48550/arXiv.2401.02954.

DeepSeek-AI. Deepseek LLM: 长期扩展的开源语言模型. CoRR, abs/2401.02954, 2024b. URL https://doi.org/10.48550/arXiv.2401.02954.

DeepSeek-AI. Deepseek-v2: A strong, economical, and efficient mixture-of-experts language model. CoRR, abs/2405.04434, 2024c. URL https://doi.org/10.48550/arXiv.2405. 04434.

DeepSeek-AI. Deepseek-v2: 一个强大、经济且高效的专家混合语言模型。CoRR, abs/2405.04434, 2024c. URL https://doi.org/10.48550/arXiv.2405.04434.

T. Dettmers, M. Lewis, Y. Belkada, and L. Z ett le moyer. Gpt3. int8 (): 8-bit matrix multiplication for transformers at scale. Advances in Neural Information Processing Systems, 35:30318– 30332, 2022.

T. Dettmers, M. Lewis, Y. Belkada, 和 L. Zettlemoyer. GPT3.int8(): 大规模 Transformer 的 8 位矩阵乘法. 神经信息处理系统进展, 35:30318–30332, 2022.

H. Ding, Z. Wang, G. Paolini, V. Kumar, A. Deoras, D. Roth, and S. Soatto. Fewer truncation s improve language modeling. arXiv preprint arXiv:2404.10830, 2024.

H. Ding, Z. Wang, G. Paolini, V. Kumar, A. Deoras, D. Roth, 和 S. Soatto。减少截断改善语言建模。arXiv 预印本 arXiv:2404.10830, 2024。

D. Dua, Y. Wang, P. Dasigi, G. Stanovsky, S. Singh, and M. Gardner. DROP: A reading comprehension benchmark requiring discrete reasoning over paragraphs. In J. Burstein, C. Doran, and T. Solorio, editors, Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 2368– 2378. Association for Computational Linguistics, 2019. doi: 10.18653/V1/N19-1246. URLhttps://doi.org/10.18653/v1/n19-1246.

D. Dua, Y. Wang, P. Dasigi, G. Stanovsky, S. Singh, 和 M. Gardner. DROP: 一个需要段落离散推理的阅读理解基准。在 J. Burstein, C. Doran, 和 T. Solorio 编辑的《2019年北美计算语言学协会会议：人类语言技术论文集》(NAACL-HLT 2019)，美国明尼苏达州明尼阿波利斯，2019年6月2-7日，第1卷（长论文和短论文），第2368–2378页。计算语言学协会，2019年。doi: 10.18653/V1/N19-1246。URLhttps://doi.org/10.18653/v1/n19-1246。

D. Hendrycks, C. Burns, S. Basart, A. Zou, M. Mazeika, D. Song, and J. Steinhardt. Measuring massive multitask language understanding. arXiv preprint arXiv:2009.03300, 2020.

D. Hendrycks, C. Burns, S. Basart, A. Zou, M. Mazeika, D. Song, 和 J. Steinhardt. 测量大规模多任务语言理解. arXiv 预印本 arXiv:2009.03300, 2020.

D. Hendrycks, C. Burns, S. Kadavath, A. Arora, S. Basart, E. Tang, D. Song, and J. Steinhardt. Measuring mathematical problem solving with the math dataset. arXiv preprint arXiv:2103.03874, 2021.

D. Hendrycks, C. Burns, S. Kadavath, A. Arora, S. Basart, E. Tang, D. Song, 和 J. Steinhardt. 使用数学数据集测量数学问题解决能力. arXiv 预印本 arXiv:2103.03874, 2021.

Y. Huang, Y. Bai, Z. Zhu, J. Zhang, J. Zhang, T. Su, J. Liu, C. Lv, Y. Zhang, J. Lei, et al. C-Eval: A multi-level multi-discipline chinese evaluation suite for foundation models. arXiv preprint arXiv:2305.08322, 2023.

Y. Huang, Y. Bai, Z. Zhu, J. Zhang, J. Zhang, T. Su, J. Liu, C. Lv, Y. Zhang, J. Lei, 等. C-Eval: 一个多层次多学科的中文基础模型评估套件. arXiv 预印本 arXiv:2305.08322, 2023.

N. Jain, K. Han, A. Gu, W. Li, F. Yan, T. Zhang, S. Wang, A. Solar-Lezama, K. Sen, and I. Stoica. Live code bench: Holistic and contamination free evaluation of large language models for code. CoRR, abs/2403.07974, 2024. URL https://doi.org/10.48550/arXiv.2403.07974.

N. Jain, K. Han, A. Gu, W. Li, F. Yan, T. Zhang, S. Wang, A. Solar-Lezama, K. Sen, 和 I. Stoica. Live code bench: 大语言模型代码评估的整体且无污染方法. CoRR, abs/2403.07974, 2024. URL https://doi.org/10.48550/arXiv.2403.07974.

A. Q. Jiang, A. S a blay roll es, A. Mensch, C. Bamford, D. S. Chaplot, D. d. l. Casas, F. Bressand, G. Lengyel, G. Lample, L. Saulnier, et al. Mistral 7b. arXiv preprint arXiv:2310.06825, 2023.

A. Q. Jiang, A. S a blay roll es, A. Mensch, C. Bamford, D. S. Chaplot, D. d. l. Casas, F. Bressand, G. Lengyel, G. Lample, L. Saulnier, 等. Mistral 7b. arXiv 预印本 arXiv:2310.06825, 2023.

M. Joshi, E. Choi, D. Weld, and L. Z ett le moyer. TriviaQA: A large scale distantly supervised challenge dataset for reading comprehension. In R. Barzilay and M.-Y. Kan, editors, Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1601–1611, Vancouver, Canada, July 2017. Association for Computational Linguistics. doi: 10.18653/v1/P17-1147. URL https://a cl anthology.org/P17-1147.

M. Joshi, E. Choi, D. Weld, 和 L. Zettlemoyer. TriviaQA: 一个大规模远距离监督的阅读理解挑战数据集. 在 R. Barzilay 和 M.-Y. Kan 编辑的《第55届计算语言学协会年会论文集（第1卷：长论文）》中，第1601–1611页，加拿大温哥华，2017年7月. 计算语言学协会. doi: 10.18653/v1/P17-1147. URL https://acl anthology.org/P17-1147.

D. Kalamkar, D. Mudigere, N. Mellempudi, D. Das, K. Banerjee, S. Avancha, D. T. Vooturi, N. Jam malam ad aka, J. Huang, H. Yuen, et al. A study of bfloat16 for deep learning training. arXiv preprint arXiv:1905.12322, 2019.

D. Kalamkar, D. Mudigere, N. Mellempudi, D. Das, K. Banerjee, S. Avancha, D. T. Vooturi, N. Jammalamadaka, J. Huang, H. Yuen 等. 深度学习训练中的 bfloat16 研究. arXiv 预印本 arXiv:1905.12322, 2019.

S. Krishna, K. Krishna, A. Mohananey, S. Schwarcz, A. Stambler, S. Upadhyay, and M. Faruqui. Fact, fetch, and reason: A unified evaluation of retrieval-augmented generation. CoRR, abs/2409.12941, 2024. doi: 10.48550/ARXIV.2409.12941. URL https://doi.org/10.485 50/arXiv.2409.12941.

S. Krishna, K. Krishna, A. Mohananey, S. Schwarcz, A. Stambler, S. Upadhyay, 和 M. Faruqui. 事实、获取与推理：检索增强生成的统一评估. CoRR, abs/2409.12941, 2024. doi: 10.48550/ARXIV.2409.12941. URL https://doi.org/10.48550/arXiv.2409.12941.

T. Kwiatkowski, J. Palomaki, O. Redfield, M. Collins, A. P. Parikh, C. Alberti, D. Epstein, I. Polosukhin, J. Devlin, K. Lee, K. Toutanova, L. Jones, M. Kelcey, M. Chang, A. M. Dai, J. Uszkoreit, Q. Le, and S. Petrov. Natural questions: a benchmark for question answering research. Trans. Assoc. Comput. Linguistics, 7:452–466, 2019. doi: 10.1162/tacl_a_00276. URL https://doi.org/10.1162/tacl_a_00276.

T. Kwiatkowski, J. Palomaki, O. Redfield, M. Collins, A. P. Parikh, C. Alberti, D. Epstein, I. Polosukhin, J. Devlin, K. Lee, K. Toutanova, L. Jones, M. Kelcey, M. Chang, A. M. Dai, J. Uszkoreit, Q. Le, 和 S. Petrov. Natural questions: 问答研究的基准. Trans. Assoc. Comput. Linguistics, 7:452–466, 2019. doi: 10.1162/tacl_a_00276. URL https://doi.org/10.1162/tacl_a_00276.

G. Lai, Q. Xie, H. Liu, Y. Yang, and E. H. Hovy. RACE: large-scale reading comprehension dataset from examinations. In M. Palmer, R. Hwa, and S. Riedel, editors, Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, EMNLP 2017, Copenhagen, Denmark, September 9-11, 2017, pages 785–794. Association for Computational Linguistics, 2017. doi: 10.18653/V1/D17-1082. URL https://doi.org/10.18653/v1/d17-1082.

G. Lai, Q. Xie, H. Liu, Y. Yang, 和 E. H. Hovy. RACE: 来自考试的大规模阅读理解数据集. 在 M. Palmer, R. Hwa, 和 S. Riedel 编辑的《2017年自然语言处理经验方法会议论文集》(EMNLP 2017) 中, 2017年9月9-11日, 丹麦哥本哈根, 第785-794页. 计算语言学协会, 2017. doi: 10.18653/V1/D17-1082. URL https://doi.org/10.18653/v1/d17-1082.

N. Lambert, V. Pyatkin, J. Morrison, L. Miranda, B. Y. Lin, K. Chandu, N. Dziri, S. Kumar, T. Zick, Y. Choi, et al. Reward bench: Evaluating reward models for language modeling. arXiv preprint arXiv:2403.13787, 2024.

N. Lambert, V. Pyatkin, J. Morrison, L. Miranda, B. Y. Lin, K. Chandu, N. Dziri, S. Kumar, T. Zick, Y. Choi 等. Reward bench: 评估语言建模的奖励模型. arXiv 预印本 arXiv:2403.13787, 2024.

D. Lepikhin, H. Lee, Y. Xu, D. Chen, O. Firat, Y. Huang, M. Krikun, N. Shazeer, and Z. Chen. Gshard: Scaling giant models with conditional computation and automatic sharding. In 9th International Conference on Learning Representations, ICLR 2021. OpenReview.net, 2021. URL https://openreview.net/forum?id=qr we 7 X HTm Yb.

D. Lepikhin, H. Lee, Y. Xu, D. Chen, O. Firat, Y. Huang, M. Krikun, N. Shazeer, 和 Z. Chen. Gshard: 使用条件计算和自动分片扩展巨型模型。在第九届国际学习表征会议 (ICLR 2021) 上。OpenReview.net, 2021. URL https://openreview.net/forum?id=qr we 7 X HTm Yb.

R. Hou, H. Inan, M. Kardas, V. Kerkez, M. Khabsa, I. Kloumann, A. Korenev, P. S. Koura, M. Lachaux, T. Lavril, J. Lee, D. Liskovich, Y. Lu, Y. Mao, X. Martinet, T. Mihaylov, P. Mishra, I. Molybog, Y. Nie, A. Poulton, J. Rei zen stein, R. Rungta, K. Saladi, A. Schelten, R. Silva, E. M. Smith, R. Subramania n, X. E. Tan, B. Tang, R. Taylor, A. Williams, J. X. Kuan, P. Xu, Z. Yan, I. Zarov, Y. Zhang, A. Fan, M. Kambadur, S. Narang, A. Rodriguez, R. Stojnic, S. Edunov, and T. Scialom. Llama 2: Open foundation and fine-tuned chat models. CoRR, abs/2307.09288, 2023b. doi: 10.48550/arXiv.2307.09288. URL https://doi.org/10.48550/arXiv.2307. 09288.

R. Hou, H. Inan, M. Kardas, V. Kerkez, M. Khabsa, I. Kloumann, A. Korenev, P. S. Koura, M. Lachaux, T. Lavril, J. Lee, D. Liskovich, Y. Lu, Y. Mao, X. Martinet, T. Mihaylov, P. Mishra, I. Molybog, Y. Nie, A. Poulton, J. Rei zen stein, R. Rungta, K. Saladi, A. Schelten, R. Silva, E. M. Smith, R. Subramania n, X. E. Tan, B. Tang, R. Taylor, A. Williams, J. X. Kuan, P. Xu, Z. Yan, I. Zarov, Y. Zhang, A. Fan, M. Kambadur, S. Narang, A. Rodriguez, R. Stojnic, S. Edunov, and T. Scialom. Llama 2: 开放基础与微调聊天模型. CoRR, abs/2307.09288, 2023b. doi: 10.48550/arXiv.2307.09288. URL https://doi.org/10.48550/arXiv.2307.09288.

A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin. Attention is all you need. Advances in neural information processing systems, 30, 2017.

A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, 和 I. Polosukhin. Attention is all you need. 神经信息处理系统进展, 30, 2017.

L. Wang, H. Gao, C. Zhao, X. Sun, and D. Dai. Auxiliary-loss-free load balancing strategy for mixture-of-experts. CoRR, abs/2408.15664, 2024a. URL https://doi.org/10.48550/arX iv.2408.15664.

L. Wang, H. Gao, C. Zhao, X. Sun, 和 D. Dai. 无辅助损失的专家混合负载均衡策略. CoRR, abs/2408.15664, 2024a. URL https://doi.org/10.48550/arX iv.2408.15664.

Y. Wang, X. Ma, G. Zhang, Y. Ni, A. Chandra, S. Guo, W. Ren, A. Arulraj, X. He, Z. Jiang, T. Li, M. Ku, K. Wang, A. Zhuang, R. Fan, X. Yue, and W. Chen. Mmlu-pro: A more robust and challenging multi-task language understanding benchmark. CoRR, abs/2406.01574, 2024b. URL https://doi.org/10.48550/arXiv.2406.01574.

Y. Wang, X. Ma, G. Zhang, Y. Ni, A. Chandra, S. Guo, W. Ren, A. Arulraj, X. He, Z. Jiang, T. Li, M. Ku, K. Wang, A. Zhuang, R. Fan, X. Yue, and W. Chen. MMLU-Pro: 一个更稳健且更具挑战性的多任务语言理解基准。CoRR, abs/2406.01574, 2024b. URL https://doi.org/10.48550/arXiv.2406.01574.

T. Wei, J. Luan, W. Liu, S. Dong, and B. Wang. Cmath: Can your language model pass chinese elementary school math test?, 2023.

T. Wei, J. Luan, W. Liu, S. Dong, 和 B. Wang. Cmath: 你的语言模型能通过中国小学数学考试吗？, 2023.

M. Wortsman, T. Dettmers, L. Z ett le moyer, A. Morcos, A. Farhadi, and L. Schmidt. Stable and low-precision training for large-scale vision-language models. Advances in Neural Information Processing Systems, 36:10271–10298, 2023.

M. Wortsman, T. Dettmers, L. Zettlemoyer, A. Morcos, A. Farhadi, 和 L. Schmidt. 大规模视觉-语言模型的稳定低精度训练. 神经信息处理系统进展, 36:10271–10298, 2023.

H. Xi, C. Li, J. Chen, and J. Zhu. Training transformers with 4-bit integers. Advances in Neural Information Processing Systems, 36:49146–49168, 2023.

H. Xi, C. Li, J. Chen, 和 J. Zhu. 使用4位整数训练Transformer. 神经信息处理系统进展, 36:49146–49168, 2023.

C. S. Xia, Y. Deng, S. Dunn, and L. Zhang. Agentless: De mystifying llm-based software engineering agents. arXiv preprint, 2024.

C. S. Xia, Y. Deng, S. Dunn, 和 L. Zhang. Agentless: 揭秘基于大语言模型的软件工程智能体. arXiv 预印本, 2024.

H. Xia, T. Ge, P. Wang, S. Chen, F. Wei, and Z. Sui. Speculative decoding: Exploiting speculative execution for accelerating seq2seq generation. In Findings of the Association for Computational Linguistics: EMNLP 2023, Singapore, December 6-10, 2023, pages 3909–3925. Association for Computational Linguistics, 2023. URL https://doi.org/10.18653/v1/ 2023.findings-emnlp.257.

H. Xia, T. Ge, P. Wang, S. Chen, F. Wei, 和 Z. Sui. 推测解码：利用推测执行加速序列到序列生成。在《计算语言学协会发现：EMNLP 2023》，新加坡，2023年12月6-10日，第3909-3925页。计算语言学协会，2023年。URL https://doi.org/10.18653/v1/2023.findings-emnlp.257。

G. Xiao, J. Lin, M. Seznec, H. Wu, J. Demouth, and S. Han. Smooth quant: Accurate and efficient post-training quantization for large language models. In International Conference on Machine Learning, pages 38087–38099. PMLR, 2023.

G. Xiao, J. Lin, M. Seznec, H. Wu, J. Demouth, 和 S. Han. Smooth quant: 大语言模型的准确高效训练后量化. 在国际机器学习会议上, 页码 38087–38099. PMLR, 2023.

L. Xu, H. Hu, X. Zhang, L. Li, C. Cao, Y. Li, Y. Xu, K. Sun, D. Yu, C. Yu, Y. Tian, Q. Dong, W. Liu, B. Shi, Y. Cui, J. Li, J. Zeng, R. Wang, W. Xie, Y. Li, Y. Patterson, Z. Tian, Y. Zhang, H. Zhou, S. Liu, Z. Zhao, Q. Zhao, C. Yue, X. Zhang, Z. Yang, K. Richardson, and Z. Lan. CLUE: A chinese language understanding evaluation benchmark. In D. Scott, N. Bel, and C. Zong, editors, Proceedings of the 28th International Conference on Computational Linguistics, COLING 2020, Barcelona, Spain (Online), December 8-13, 2020, pages 4762–4772. International Committee on Computational Linguistics, 2020. doi: 10.18653/V1/2020.COLING-MAIN.419. URLhttps://doi.org/10.18653/v1/2020.coling-main.419.

L. Xu, H. Hu, X. Zhang, L. Li, C. Cao, Y. Li, Y. Xu, K. Sun, D. Yu, C. Yu, Y. Tian, Q. Dong, W. Liu, B. Shi, Y. Cui, J. Li, J. Zeng, R. Wang, W. Xie, Y. Li, Y. Patterson, Z. Tian, Y. Zhang, H. Zhou, S. Liu, Z. Zhao, Q. Zhao, C. Yue, X. Zhang, Z. Yang, K. Richardson, and Z. Lan. CLUE: 中文语言理解评估基准。在 D. Scott, N. Bel, 和 C. Zong 编辑的《第28届国际计算语言学会议论文集》(COLING 2020), 2020年12月8-13日, 西班牙巴塞罗那（在线）, 第4762-4772页。国际计算语言学委员会, 2020. doi: 10.18653/V1/2020.COLING-MAIN.419. URLhttps://doi.org/10.18653/v1/2020.coling-main.419.

R. Zellers, A. Holtzman, Y. Bisk, A. Farhadi, and Y. Choi. HellaSwag: Can a machine really finish your sentence? In A. Korhonen, D. R. Traum, and L. Màrquez, editors, Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, July 28- August 2, 2019, Volume 1: Long Papers, pages 4791–4800. Association for Computational Linguistics, 2019. doi: 10.18653/v1/p19-1472. URL https://doi.org/10.18653/v1/p1 9-1472. W. Zhong, R. Cui, Y. Guo, Y. Liang, S. Lu, Y. Wang, A. Saied, W. Chen, and N. Duan. AGIEval: A human-centric benchmark for evaluating foundation models. CoRR, abs/2304.06364, 2023. doi: 10.48550/arXiv.2304.06364. URL https://doi.org/10.48550/arXiv.2304.06364. J. Zhou, T. Lu, S. Mishra, S. Brahma, S. Basu, Y. Luan, D. Zhou, and L. Hou. Instruction-following evaluation for large language models. arXiv preprint arXiv:2311.07911, 2023.

R. Zellers, A. Holtzman, Y. Bisk, A. Farhadi, 和 Y. Choi. HellaSwag: 机器真的能完成你的句子吗？在 A. Korhonen, D. R. Traum, 和 L. Màrquez 编辑的《第57届计算语言学协会会议论文集》，ACL 2019，意大利佛罗伦萨，2019年7月28日-8月2日，第1卷：长论文，第4791–4800页。计算语言学协会，2019年。doi: 10.18653/v1/p19-1472。URL https://doi.org/10.18653/v1/p19-1472。

W. Zhong, R. Cui, Y. Guo, Y. Liang, S. Lu, Y. Wang, A. Saied, W. Chen, 和 N. Duan. AGIEval: 一个以人为中心的基准，用于评估基础模型。CoRR, abs/2304.06364, 2023年。doi: 10.48550/arXiv.2304.06364。URL https://doi.org/10.48550/arXiv.2304.06364。

J. Zhou, T. Lu, S. Mishra, S. Brahma, S. Basu, Y. Luan, D. Zhou, 和 L. Hou. 大语言模型的指令遵循评估。arXiv预印本 arXiv:2311.07911, 2023年。

Appendix

附录

A. Contributions and Acknowledgments

A. 贡献与致谢

Zhigang Yan Zhihong Shao Zhiyu Wu Zhuoshu Li Zihui Gu Zijia Zhu Zijun Liu* Zilin Li Ziwei Xie Ziyang Song Ziyi Gao Zizheng Pan

Zhigang Yan Zhihong Shao Zhiyu Wu Zhuoshu Li Zihui Gu Zijia Zhu Zijun Liu* Zilin Li Ziwei Xie Ziyang Song Ziyi Gao Zizheng Pan

Business & Compliance Dongjie Ji

业务与合规 董杰

W.L. Xiao Wei An Xianzu Wang Xinxia Shan Ying Tang Yukun Zha Yuting Yan Zhen Zhang

W.L. Xiao Wei An Xianzu Wang Xinxia Shan Ying Tang Yukun Zha Yuting Yan Zhen Zhang

Within each role, authors are listed alphabetically by the first name. Names marked with * denote individuals who have departed from our team.

在每个角色中，作者按名字的字母顺序排列。带有 * 标记的名字表示已离开我们团队的成员。

B. Ablation Studies for Low-Precision Training

B. 低精度训练的消融研究

Figure 10 | Loss curves comparison between BF16 and FP8 training. Results are smoothed by Exponential Moving Average (EMA) with a coefficient of 0.9.

图 10 | BF16 和 FP8 训练的损失曲线对比。结果通过指数移动平均 (EMA) 平滑处理，系数为 0.9。

B.1. FP8 v.s. BF16 Training

B.1. FP8 与 BF16 训练

We validate our FP8 mixed precision framework with a comparison to BF16 training on top of two baseline models across different scales. At the small scale, we train a baseline MoE model comprising approximately 16B total parameters on 1.33T tokens. At the large scale, we train a baseline MoE model comprising approximately 230B total parameters on around $0.9\mathrm{T}$ tokens. We show the training curves in Figure 10 and demonstrate that the relative error remains below $0.25%$ with our high-precision accumulation and fine-grained quantization strategies.

我们通过与不同规模的两个基线模型上的 BF16 训练进行比较，验证了我们的 FP8 混合精度框架。在小规模上，我们训练了一个包含约 160 亿总参数的基线 MoE 模型，使用了 1.33T 的 Token。在大规模上，我们训练了一个包含约 2300 亿总参数的基线 MoE 模型，使用了约 $0.9\mathrm{T}$ 的 Token。我们在图 10 中展示了训练曲线，并证明通过我们的高精度累加和细粒度量化策略，相对误差保持在 $0.25%$ 以下。

B.2. Discussion About Block-Wise Quantization

B.2. 关于块级量化 (Block-Wise Quantization) 的讨论

Although our tile-wise fine-grained quantization effectively mitigates the error introduced by feature outliers, it requires different groupings for activation quantization, i.e., $1\mathtt{x128}$ in forward pass and $128\tt x1$ for backward pass. A similar process is also required for the activation gradient. A straightforward strategy is to apply block-wise quantization per $128\mathtt{x}128$ elements like the way we quantize the model weights. In this way, only transposition is required for backward. Therefore, we conduct an experiment where all tensors associated with Dgrad are quantized on a block-wise basis. The results reveal that the Dgrad operation which computes the activation gradients and back-propagates to shallow layers in a chain-like manner, is highly sensitive to precision. Specifically, block-wise quantization of activation gradients leads to model divergence on an MoE model comprising approximately 16B total parameters, trained for around 300B tokens. We hypothesize that this sensitivity arises because activation gradients are highly imbalanced among tokens, resulting in token-correlated outliers (Xi et al., 2023). These outliers cannot be effectively managed by a block-wise quantization approach.

虽然我们的分块细粒度量化有效缓解了特征异常值引入的误差，但它需要对激活量化进行不同的分组，即在前向传播中使用 $1\mathtt{x128}$，在反向传播中使用 $128\mathtt{x1}$。激活梯度也需要类似的处理。一个直接的策略是像量化模型权重那样，对每 $128\mathtt{x}128$ 个元素应用分块量化。这样，反向传播时只需要进行转置操作。因此，我们进行了一项实验，将所有与 Dgrad 相关的张量都进行分块量化。结果表明，Dgrad 操作（计算激活梯度并以链式方式反向传播到浅层）对精度高度敏感。具体来说，激活梯度的分块量化会导致一个包含约 160 亿参数、训练了约 3000 亿 token 的 MoE 模型发散。我们推测这种敏感性源于激活梯度在 token 之间高度不平衡，导致 token 相关的异常值 (Xi et al., 2023)。这些异常值无法通过分块量化方法有效处理。

C. Expert Specialization Patterns of the 16B Aux-Loss-Based and Aux-LossFree Models

C. 基于辅助损失和无辅助损失的 16B 模型的专家专业化模式

We record the expert load of the 16B auxiliary-loss-based baseline and the auxiliary-loss-free model on the Pile test set. The auxiliary-loss-free model tends to have greater expert specialization across all layers, as demonstrated in Figure 10.

我们在 Pile 测试集上记录了基于 16B 辅助损失的基线模型和无辅助损失模型的专家负载。无辅助损失模型在所有层上往往具有更高的专家专业化程度，如图 10 所示。

(b) Layers 7-13

(b) 第 7-13 层

(c) Layers 13-19

(c) 第 13-19 层

(d) Layers 19-25

(d) 第19-25层

Figure 10 | Expert load of auxiliary-loss-free and auxiliary-loss-based models on three domains in the Pile test set. The auxiliary-loss-free model shows greater expert specialization patterns than the auxiliary-loss-based one. The relative expert load denotes the ratio between the actual expert load and the theoretically balanced expert load.

图 10 | 在 Pile 测试集的三个领域中，无辅助损失模型和基于辅助损失模型的专家负载。无辅助损失模型显示出比基于辅助损失模型更强的专家专业化模式。相对专家负载表示实际专家负载与理论上平衡的专家负载之间的比率。