[博客翻译]Nvidia Tensor核心编程

由 发布于 张量核心GEMM矩阵乘法混合精度可编程
 收藏

原文地址：https://leimao.github.io/blog/NVIDIA-Tensor-Core-Programming/


GPT-Academic Report

NVIDIA Tensor Core 编程

简介

自Volta架构以来，NVIDIA Tensor Cores已成为NVIDIA GPU上通用矩阵乘法（GEMM）操作的专用加速器。由于人工智能计算通常以GEMM操作为主，NVIDIA Tensor Core对于加速人工智能应用至关重要。

NVIDIA Tensor Core

NVIDIA Tensor Cores专门用于执行混合精度的GEMM操作，即GEMM输入矩阵采用较低精度，而GEMM输出矩阵则保持高精度。混合精度训练和推理是加速神经网络训练和推理的关键技术。

[NVIDIA Tensor Core GEMM 数学运算NVIDIA Tensor Core GEMM 数学运算

](https://leimao.github.io/images/blog/2023-05-18-NVIDIA-Tensor-Core-Programming/turing-tensor-core-math.png)由于NVIDIA Tensor Cores专为GEMM设计，使用NVIDIA Tensor Core实现的GEMM吞吐量远高于使用更适合通用并行编程的NVIDIA CUDA Cores所能达到的水平。

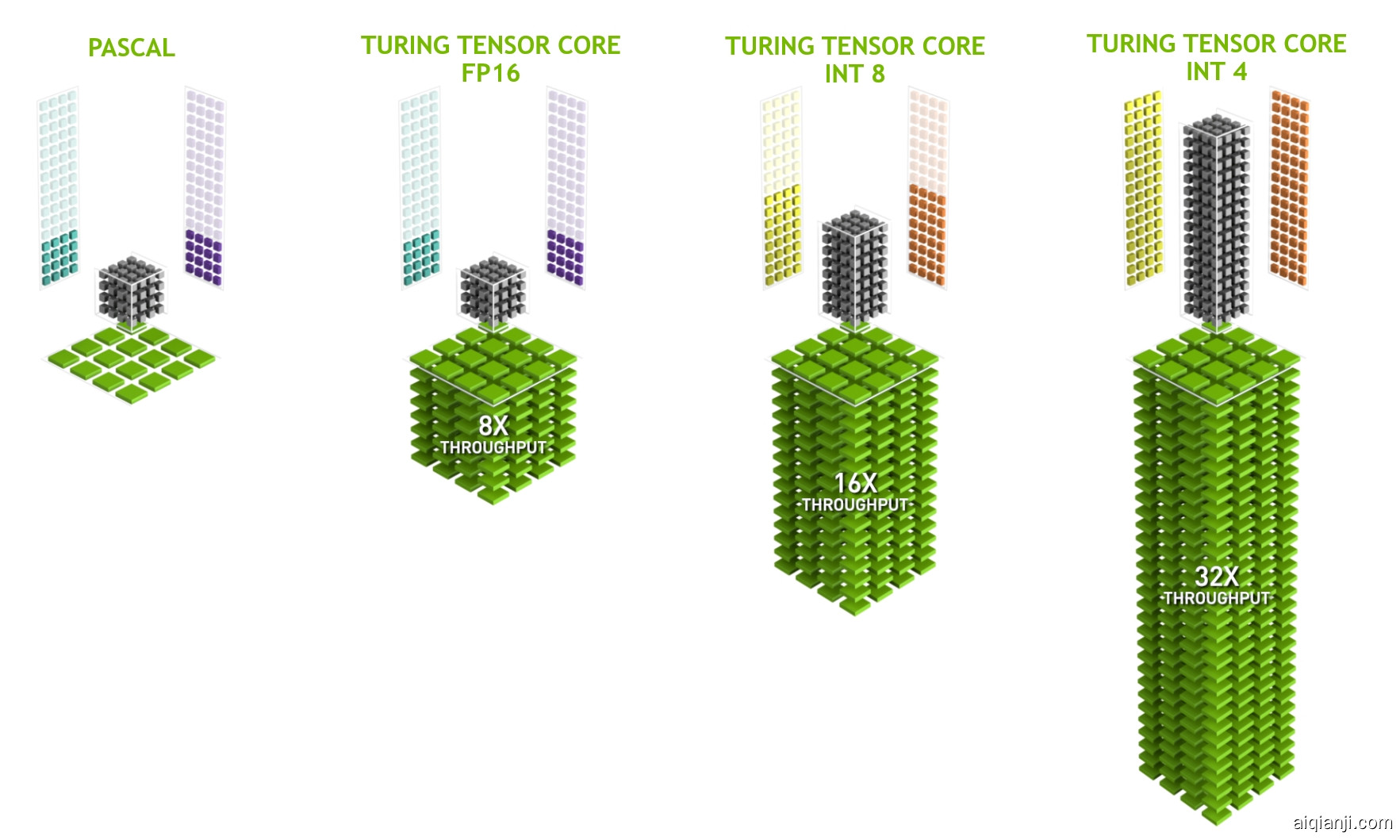[NVIDIA GEMM 吞吐量 Turing Tensor Core 对比 Pascal CUDA CoreNVIDIA GEMM 吞吐量 Turing Tensor Core 对比 Pascal CUDA Core

](https://leimao.github.io/images/blog/2023-05-18-NVIDIA-Tensor-Core-Programming/Turing-Tensor-Core-New-Diag-White-Background.jpg)对于NVIDIA Ampere架构，每个SM（流式多处理器）拥有4个Tensor Cores。特别是，NVIDIA A100 GPU拥有108个流式多处理器（SMs），总计432个Tensor Cores。

[NVIDIA GA100 完整GPU，含128个SMsNVIDIA GA100 完整GPU，含128个SMs

](https://leimao.github.io/images/blog/2023-05-18-NVIDIA-Tensor-Core-Programming/ga100-full-gpu-128-sms.png)[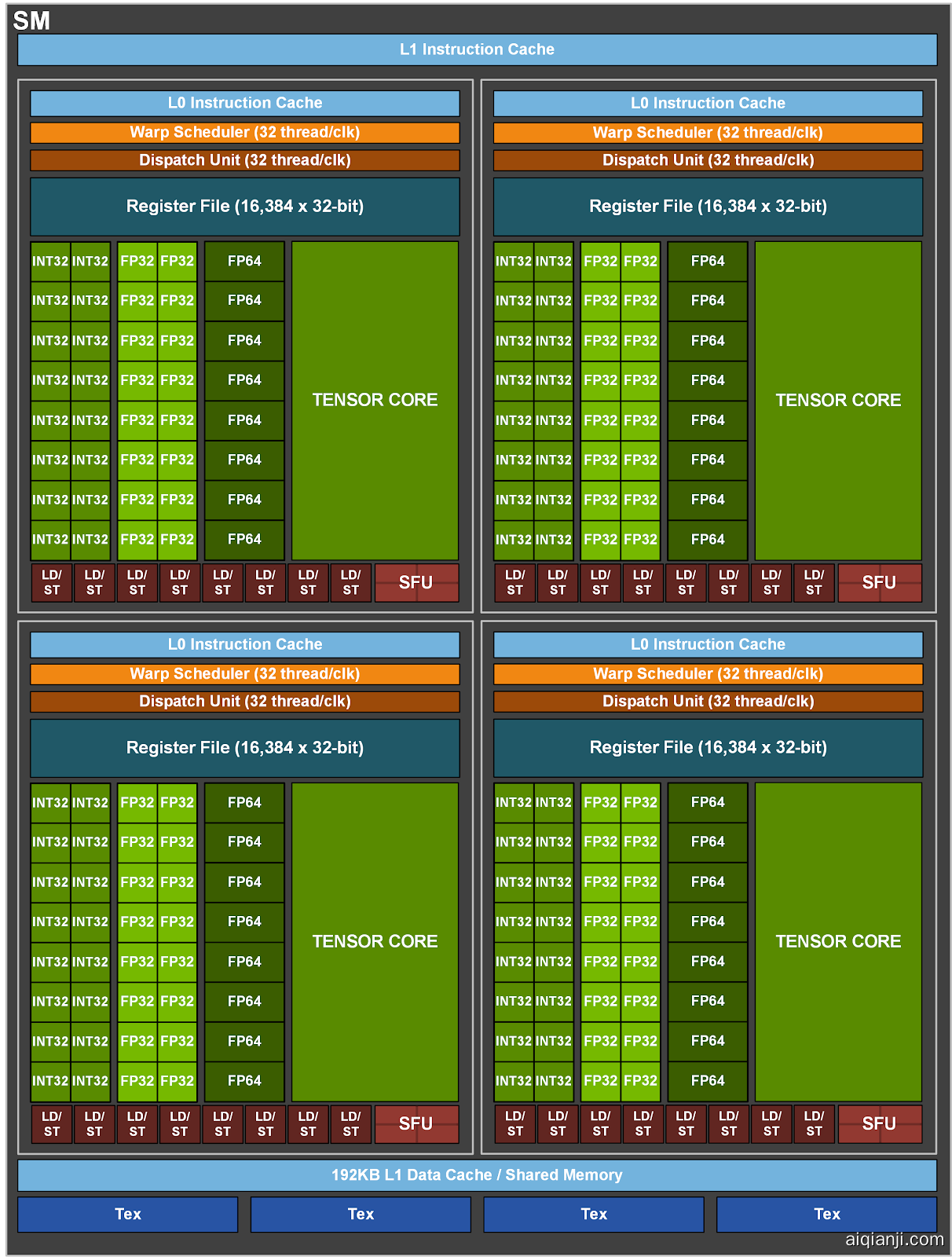每个NVIDIA Ampere SM拥有4个Tensor Cores每个NVIDIA Ampere SM拥有4个Tensor Cores

](https://leimao.github.io/images/blog/2023-05-18-NVIDIA-Tensor-Core-Programming/a100-sm.png)NVIDIA Tensor Cores完全可编程。Tensor Core编程API在warp级别声明，位于nvcuda::wmma命名空间下的mma.h头文件中。

NVIDIA Tensor Core 编程

矩阵乘法分解

NVIDIA CUDA允许用户在warp级别编程Tensor Core的GEMM操作D=AB+C。尽管每个Tensor Core只能执行针对不同数据类型的特定小尺寸矩阵乘法，正如我之前文章“CUDA矩阵乘法”中所讨论的，大型GEMM可以分解为多个小型GEMM并进行累加。

给定一个GEMM操作D=AB+C，其中D∈Rm×n，A∈Rm×k，B∈Rk×n，C∈Rm×n，矩阵可以被划分为更小的矩阵。

A=[A1,1d×dA1,2d×d⋯A1,k/dd×dA2,1d×dA2,2d×d⋯A2,k/dd×d⋮⋮⋱⋮Am/d,1d×dAm/d,2d×d⋯Am/d,k/dd×d]

翻译 private_upload/18682424545/2025-01-13-14-05-25/1.md.part-1.md

B=[B1,1d×dB1,2d×d⋯B1,n/dd×dB2,1d×dB2,2d×d⋯B2,n/dd×d⋮⋮⋱⋮Bk/d,1d×dBk/d,2d×d⋯Bk/d,n/dd×d]

C=[C1,1d×dC1,2d×d⋯C1,n/dd×dC2,1d×dC2,2d×d⋯C2,n/dd×d⋮⋮⋱⋮Cm/d,1d×dCm/d,2d×d⋯Cm/d,n/dd×d]

D=[D1,1d×dD1,2d×d⋯D1,n/dd×dD2,1d×dD2,2d×d⋯D2,n/dd×d⋮⋮⋱⋮Dm/d,1d×dDm/d,2d×d⋯Dm/d,n/dd×d]

D中的每个小矩阵通过多个小型GEMM运算及累加得到。

Dim,ind×d=∑ik=1k/dAim,ikd×dBik,ind×d

在我之前的文章“CUDA矩阵乘法”中，我使用了CUDA核心和CUDA共享内存来执行上述数学运算，每个线程块计算一个Dim,ind×d。这次，我将改用Tensor Core来计算完全相同的数学运算，其中每个warp计算一个Dim,ind×d。更具体地说，每个warp计算一个16×16×16的GEMM，从而在D矩阵中生成一个16×16的区块，即d=16。

使用NVIDIA Tensor Core实现矩阵乘法

在此实现中，我们将利用Tensor Core通过HMMA（半精度矩阵乘法与累加）和IMMA（整数矩阵乘法与累加）指令执行GEMM操作。此外，还实现并验证了涉及转置矩阵乘法的四种不同类型的GEMM。

  • D=AB+C，其中D∈Rm×n，A∈Rm×k，B∈Rk×n，C∈Rm×n
  • D=A⊤B+C，其中D∈Rm×n，A∈Rk×m，B∈Rk×n，C∈Rm×n
  • D=AB⊤+C，其中D∈Rm×n，A∈Rm×k，B∈Rn×k，C∈Rm×n
  • D=A⊤B⊤+C，其中D∈Rm×n，A∈Rk×m，B∈Rn×k，C∈Rm×n

在此实现中，我们主要关注GEMM操作中的矩阵乘法部分，通过设定C=0来简化处理。

|

#include <cassert>
#include <chrono>
#include <functional>
#include <iomanip>
#include <iostream>
#include <random>
#include <utility>
#include <vector>

#include <cuda_runtime.h>
#include <mma.h>

#define CHECK_CUDA_ERROR(val) check((val), #val, __FILE__, __LINE__)
template <typename T>
void check(T err, const char* const func, const char* const file,
int const line)
{
if (err != cudaSuccess)
{
std::cerr << "CUDA 运行时错误位于: " << file << ":" << line
<< std::endl;
std::cerr << cudaGetErrorString(err) << " " << func << std::endl;
std::exit(EXIT_FAILURE);
}
}

#define CHECK_LAST_CUDA_ERROR() checkLast(__FILE__, __LINE__)

void checkLast(const char* const file, int const line)
{
    cudaError_t const err{cudaGetLastError()};
    if (err != cudaSuccess)
    {
        std::cerr << "CUDA 运行时错误位于: " << file << ":" << line
                  << std::endl;
        std::cerr << cudaGetErrorString(err) << std::endl;
        std::exit(EXIT_FAILURE);
    }
}

template <class T>
float measure_performance(std::function<T(cudaStream_t)> bound_function,
                          cudaStream_t stream, int num_repeats = 100,
                          int num_warmups = 100)
{
    cudaEvent_t start, stop;
    float time;

    CHECK_CUDA_ERROR(cudaEventCreate(&start));
    CHECK_CUDA_ERROR(cudaEventCreate(&stop));

    for (int i{0}; i < num_warmups; ++i)
    {
        bound_function(stream);
    }

    CHECK_CUDA_ERROR(cudaStreamSynchronize(stream));

    CHECK_CUDA_ERROR(cudaEventRecord(start, stream));
    for (int i{0}; i < num_repeats; ++i)
    {
        bound_function(stream);
    }
    CHECK_CUDA_ERROR(cudaEventRecord(stop, stream));
    CHECK_CUDA_ERROR(cudaEventSynchronize(stop));
    CHECK_LAST_CUDA_ERROR();
    CHECK_CUDA_ERROR(cudaEventElapsedTime(&time, start, stop));
    CHECK_CUDA_ERROR(cudaEventDestroy(start));
    CHECK_CUDA_ERROR(cudaEventDestroy(stop));

    float const latency{time / num_repeats};

    return latency;
}

// 矩阵中的所有数据均以列主序存储，
// 这与大多数 cuBLAS GEMM API 保持一致。
// 对于形状为 M x N 的矩阵 A，其主维度为 M。
// 对于转置后形状为 N x M 的矩阵 A，
// 其主维度为 N。
// 矩阵 A: M x K，或 K x N（若转置）。
// 矩阵 B: K x M，或 M x K（若转置）。
// 矩阵 C: M x N。
// WMMA_FRAG_LAYOUT_A: 若 A 转置，则为 nvcuda::wmma::row_major，
// 否则为 nvcuda::wmma::col_major。
// WMMA_FRAG_LAYOUT_B: 若 B 转置，则为 nvcuda::wmma::row_major，
// 否则为 nvcuda::wmma::col_major。
template <typename T1, typename T2, int WMMA_M, int WMMA_N, int WMMA_K,
          typename WMMA_FRAG_LAYOUT_A, typename WMMA_FRAG_LAYOUT_B>
__global__ void wmma_gemm_a_col_major_b_col_major(
    T1 const* A, T1 const* B, T2* C, uint32_t m, uint32_t n, uint32_t k,
    uint32_t lda, uint32_t ldb, uint32_t ldc, bool is_A_transpose,
    bool is_B_transpose, float alpha, float beta)
{
    // 使用二维网格进行分块。
    // 确定 warp 的二维索引。
    uint32_t const warpM{(blockIdx.x * blockDim.x + threadIdx.x) / warpSize};
    uint32_t const warpN{blockIdx.y * blockDim.y + threadIdx.y};

    // 声明片段。
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, T1,
                           WMMA_FRAG_LAYOUT_A>
        a_frag{};
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, T1,
                           WMMA_FRAG_LAYOUT_B>
        b_frag{};
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_M, WMMA_N, WMMA_K,
                           T2>
        acc_frag{};
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_M, WMMA_N, WMMA_K,
                           T2>
        c_frag{};

    // 确保累加器从 0 开始。
    nvcuda::wmma::fill_fragment(acc_frag, static_cast<T2>(0));

    // 遍历 K。
    for (uint32_t ki{0}; ki < k; ki += WMMA_K)
    {
        // 确定线性内存上 mma 矩阵的第一个元素。
        // 矩阵 A 的 mma 矩阵
        uint32_t const matrix_mma_a_row_idx{is_A_transpose ? ki
                                                           : warpM * WMMA_M};
        uint32_t const matrix_mma_a_col_idx{is_A_transpose ? warpM * WMMA_M: ki};

// 矩阵B的MMA矩阵
uint32_t const matrix_mma_b_row_idx{is_B_transpose ? warpN * WMMA_N
                                                   : ki};
uint32_t const matrix_mma_b_col_idx{is_B_transpose ? ki
                                                   : warpN * WMMA_N};

// 边界检查
if (matrix_mma_a_row_idx < (is_A_transpose ? k : m) &&
    matrix_mma_a_col_idx < (is_A_transpose ? m : k) &&
    matrix_mma_b_row_idx < (is_B_transpose ? n : k) &&
    matrix_mma_b_col_idx < (is_B_transpose ? k : n))
{
    // 确定MMA矩阵第一个元素的内存地址。注意所有矩阵都假设为列主序。
    // 因此，索引方式与我们常见的行主序索引不同。
    T1 const* matrix_mma_a_mptr{A + matrix_mma_a_row_idx +
                                matrix_mma_a_col_idx * lda};
    T1 const* matrix_mma_b_mptr{B + matrix_mma_b_row_idx +
                                matrix_mma_b_col_idx * ldb};
    // 加载MMA矩阵输入。
    nvcuda::wmma::load_matrix_sync(a_frag, matrix_mma_a_mptr, lda);
    nvcuda::wmma::load_matrix_sync(b_frag, matrix_mma_b_mptr, ldb);

    // 执行矩阵乘法
    nvcuda::wmma::mma_sync(acc_frag, a_frag, b_frag, acc_frag);
}

}

// 加载C的当前值，按beta缩放，并将我们的结果按alpha缩放后相加。
uint32_t const matrix_mma_c_row_idx{warpM * WMMA_M};
uint32_t const matrix_mma_c_col_idx{warpN * WMMA_N};

if (matrix_mma_c_row_idx < m && matrix_mma_c_col_idx < n)
{
T2* matrix_mma_c_mptr{C + matrix_mma_c_row_idx +
matrix_mma_c_col_idx * ldc};
nvcuda::wmma::load_matrix_sync(c_frag, matrix_mma_c_mptr, ldc,
nvcuda::wmma::mem_col_major);
// 让编译器决定如何进行元素级操作。
// 此类元素级操作可以是缩放、累加、量化等。
// https://docs.nvidia.com/cuda/archive/12.0.1/cuda-c-programming-guide/#id40
// 处理整数类型时要小心。
for (uint32_t i = 0; i < c_frag.num_elements; i++)
{
c_frag.x[i] = alpha * acc_frag.x[i] + beta * c_frag.x[i];
}
// 存储输出
nvcuda::wmma::store_matrix_sync(matrix_mma_c_mptr, c_frag, ldc,
nvcuda::wmma::mem_col_major);
}

}

template <typename T1, typename T2>
void launch_wmma_mm(T1 const* A, T1 const* B, T2* C, uint32_t m, uint32_t n,
uint32_t k, bool is_A_transpose, bool is_B_transpose,
cudaStream_t stream)
{
// 假设我们的数据中没有填充。
uint32_t const lda{is_A_transpose ? k : m};
uint32_t const ldb{is_B_transpose ? n : k};
uint32_t const ldc{m};
float const alpha{1.0f};
float const beta{0.0f};

constexpr int WMMA_M{16};
constexpr int WMMA_N{16};
constexpr int WMMA_K{16};

constexpr int WARP_SIZE{32};

dim3 gridDim;
dim3 blockDim;

// blockDim.x必须是warpSize的倍数
// 128x4的块大小意味着我们有16个（4x4）warp，
// 每个warp计算一个16x16的输出块，
// 一个块计算一个64x64的输出块。
// 每个块有4x4个warp，总计4x4x32个线程。
int const num_warps_x = 4;
int const num_warps_y = 4;
blockDim.x = num_warps_x * WARP_SIZE;
blockDim.y = num_warps_y;
// 向上取整。
gridDim.x = (m + (WMMA_M * num_warps_x - 1)) / (WMMA_M * num_warps_x);

```markdown
gridDim.y = (n + WMMA_N * num_warps_y - 1) / (WMMA_N * num_warps_y);

// C = A * B
if ((!is_A_transpose) && (!is_B_transpose))
{
    wmma_gemm_a_col_major_b_col_major<T1, T2, WMMA_M, WMMA_N, WMMA_K,
                                      nvcuda::wmma::col_major,
                                      nvcuda::wmma::col_major>
        <<<gridDim, blockDim, 0, stream>>>(A, B, C, m, n, k, lda, ldb, ldc,
                                           is_A_transpose, is_B_transpose,
                                           alpha, beta);
}
// C = A^T * B
else if ((is_A_transpose) && (!is_B_transpose))
{
    wmma_gemm_a_col_major_b_col_major<T1, T2, WMMA_M, WMMA_N, WMMA_K,
                                      nvcuda::wmma::row_major,
                                      nvcuda::wmma::col_major>
        <<<gridDim, blockDim, 0, stream>>>(A, B, C, m, n, k, lda, ldb, ldc,
                                           is_A_transpose, is_B_transpose,
                                           alpha, beta);
}
// C = A * B^T
else if ((!is_A_transpose) && (is_B_transpose))
{
    wmma_gemm_a_col_major_b_col_major<T1, T2, WMMA_M, WMMA_N, WMMA_K,
                                      nvcuda::wmma::col_major,
                                      nvcuda::wmma::row_major>
        <<<gridDim, blockDim, 0, stream>>>(A, B, C, m, n, k, lda, ldb, ldc,
                                           is_A_transpose, is_B_transpose,
                                           alpha, beta);
}
// C = A^T * B^T
else
{
    wmma_gemm_a_col_major_b_col_major<T1, T2, WMMA_M, WMMA_N, WMMA_K,
                                      nvcuda::wmma::row_major,
                                      nvcuda::wmma::row_major>
        <<<gridDim, blockDim, 0, stream>>>(A, B, C, m, n, k, lda, ldb, ldc,
                                           is_A_transpose, is_B_transpose,
                                           alpha, beta);
}
CHECK_LAST_CUDA_ERROR();
}

// A 和 B 是列主序矩阵。
template <typename T1, typename T2>
void mm_a_col_major_b_col_major(T1 const* A, T1 const* B, T2* C, uint32_t m,
                                uint32_t n, uint32_t k, uint32_t lda,
                                uint32_t ldb, uint32_t ldc, bool is_A_transpose,
                                bool is_B_transpose)
{
    for (uint32_t ni{0}; ni < n; ++ni)
    {
        for (uint32_t mi{0}; mi < m; ++mi)
        {
            // 计算 C[mi, ni]
            T2 accum{0};
            // C = A * B
            if ((!is_A_transpose) && (!is_B_transpose))
            {
                for (uint32_t ki{0}; ki < k; ++ki)
                {
                    // A[mi, ki] * B[ki, ni]
                    accum += A[ki * lda + mi] * B[ni * ldb + ki];
                }
            }
            // C = A^T * B
            else if ((is_A_transpose) && (!is_B_transpose))
            {
                for (uint32_t ki{0}; ki < k; ++ki)
                {
                    // A[ki, mi] * B[ki, ni]
                    accum += A[mi * lda + ki] * B[ni * ldb + ki];
                }
            }
            // C = A * B^T
            else if ((!is_A_transpose) && (is_B_transpose))
            {
                for (uint32_t ki{0}; ki < k; ++ki)
                {
                    // A[mi, ki] * B[ni, ki]
                    accum += A[ki * lda + mi] * B[ki * ldb + ni];
                }
            }
            // C = A^T * B^T
            else
            {
                for (uint32_t ki{0}; ki < k; ++ki)
                {
                    // A[ki, mi] * B[ni, ki]
                    accum += A[mi * lda + ki] * B[ki * ldb + ni];
                }
            }
            C[ni * ldc + mi] = accum;
        }
    }
}

template <typename T1, typename T2>
void launch_mm(T1 const* A, T1 const* B, T2* C, uint32_t m, uint32_t n,
               uint32_t k, bool is_A_transpose, bool is_B_transpose)
{
    // 假设我们的数据没有填充。
    uint32_t const lda{is_A_transpose ? k : m};
    uint32_t const ldb{is_B_transpose ? n : k};
    uint32_t const ldc{m};
    mm_a_col_major_b_col_major(A, B, C, m, n, k, lda, ldb, ldc, is_A_transpose,
                               is_B_transpose);
}

void fill_random_float_values(float* arr, size_t n,
                              std::default_random_engine& e)
{
    std::uniform_real_distribution<float> uniform_dist(-256, 256);
    for (size_t i{0}; i < n; ++i)
    {
        arr[i] = uniform_dist(e);
    }
}

void fill_random_int8_values(int8_t* arr, size_t n,
                             std::default_random_engine& e)
{
    std::uniform_int_distribution<int8_t> uniform_dist(-128, 127);
    for (size_t i{0}; i < n; ++i)
    {
        arr[i] = uniform_dist(e);
    }
}

void fill_random_int32_values(int32_t* arr, size_t n,
                              std::default_random_engine& e)
{
    std::uniform_int_distribution<int32_t> uniform_dist(-128, 127);
    for (size_t i{0}; i < n; ++i)
    {
        arr[i] = uniform_dist(e);
    }
}

void float2half(__half* half_arr, float const* float_arr, size_t n)
{
    for (size_t i{0}; i < n; ++i)