Large Scale GAN Training for High Fidelity Natural Image Synthesis 用于 高保真自然图像合成的大规模GAN训练

Andrew Brock
Heriot-Watt University

&Jeff Donahue
DeepMind

&Karen Simonyan
DeepMind
Work done at DeepMind

ABSTRACT

Despite recent progress in generative image modeling, successfully generating high-resolution, diverse samples from complex datasets such as ImageNet remains an elusive goal. To this end, we train Generative Adversarial Networks at the largest scale yet attempted, and study the instabilities specific to such scale. We find that applying orthogonal regularization to the generator renders it amenable to a simple “truncation trick,” allowing fine control over the trade-off between sample fidelity and variety by truncating the latent space. Our modifications lead to models which set the new state of the art in class-conditional image synthesis. When trained on ImageNet at 128×128 resolution, our models (BigGANs) achieve an Inception Score (IS) of 166.3 and Fréchet Inception Distance (FID) of 9.6, improving over the previous best IS of 52.52 and FID of 18.65.

尽管在生成图像建模方面取得了最新进展，但是从复杂的数据集（例如ImageNet）成功生成高分辨率，多样的样本仍然是一个遥不可及的目标。为此，我们以尚未尝试的最大规模训练了生成对抗网络，并研究了针对这种规模的不稳定性。我们发现，将正交正则化应用于生成器使其适合于简单的“截断技巧”，从而可以通过截断潜在空间来精确控制样本保真度与变化之间的权衡。我们的修改导致建立了模型，该模型在类条件图像合成中设置了新的技术水平。在ImageNet上于128x128分辨率进行训练，我们的模型（BigGAN）的初始得分（IS）为166.3，弗雷谢特初始距离（FID）为9.6，比之前的最佳IS为52.52和FID为18.65有所提高。

1INTRODUCTION

Figure 1: Class-conditional samples generated by our model.
图1：我们的模型生成的类条件样本。

The state of generative image modeling has advanced dramatically in recent years, with Generative Adversarial Networks (GANs, Goodfellow et al. (2014)) at the forefront of efforts to generate high-fidelity, diverse images with models learned directly from data. GAN training is dynamic, and sensitive to nearly every aspect of its setup (from optimization parameters to model architecture), but a torrent of research has yielded empirical and theoretical insights enabling stable training in a variety of settings. Despite this progress, the current state of the art in conditional ImageNet modeling (Zhang et al., 2018) achieves an Inception Score (Salimans et al., 2016) of 52.5, compared to 233 for real data.
近年来，生成图像建模的状态有了显着进步，生成对抗网络（GANs，Goodfellow et al。（2014））致力于通过使用直接从数据中学习的模型来生成高保真，多样化的图像。GAN训练是动态的，并且对设置的几乎每个方面都敏感（从优化参数到模型体系结构），但是大量研究已经获得了经验和理论见解，可以在各种环境中进行稳定的训练。尽管取得了这些进展，但条件ImageNet建模的最新技术（Zhang等人，2018年）仍达到了初始分数（Salimans等人，2016年）。 为52.5，而实际数据为233。

In this work, we set out to close the gap in fidelity and variety between images generated by GANs and real-world images from the ImageNet dataset. We make the following three contributions towards this goal:
在这项工作中，我们着手缩小GAN生成的图像与ImageNet数据集中的真实世界图像之间在保真度和多样性上的差距。我们为实现该目标做出了以下三点贡献：

• We demonstrate that GANs benefit dramatically from scaling, and train models with two to four times as many parameters and eight times the batch size compared to prior art. We introduce two simple, general architectural changes that improve scalability, and modify a regularization scheme to improve conditioning, demonstrably boosting performance.
• As a side effect of our modifications, our models become amenable to the “truncation trick,” a simple sampling technique that allows explicit, fine-grained control of the trade-off between sample variety and fidelity.
• We discover instabilities specific to large scale GANs, and characterize them empirically. Leveraging insights from this analysis, we demonstrate that a combination of novel and existing techniques can reduce these instabilities, but complete training stability can only be achieved at a dramatic cost to performance.
• 我们证明了GAN可以极大地受益于缩放，并且与现有技术相比，可以训练具有两倍至四倍的参数和八倍的批量大小的模型。我们介绍了两个简单的，通用的体系结构更改，这些更改可提高可伸缩性，并修改正则化方案以改善条件，从而明显提高性能。
• 作为我们修改的副作用，我们的模型适合“截断技巧”，这是一种简单的采样技术，可以显式，细粒度地控制样本种类与保真度之间的折衷。
• 我们发现了针对大型GAN的不稳定性，并根据经验对其进行了表征。利用来自此分析的见解，我们证明了将新颖的技术与现有的技术相结合可以减少这些不稳定性，但是要达到完全的训练稳定性，就必须付出巨大的性能代价。

Our modifications substantially improve class-conditional GANs. When trained on ImageNet at 128×128 resolution, our models (BigGANs) improve the state-of-the-art Inception Score (IS) and Fréchet Inception Distance (FID) from 52.52 and 18.65 to 166.3 and 9.6 respectively. We also successfully train BigGANs on ImageNet at 256×256 and 512×512 resolution, and achieve IS and FID of 233.0 and 9.3 at 256×256 and IS and FID of 241.4 and 10.9 at 512×512. Finally, we train our models on an even larger dataset – JFT-300M – and demonstrate that our design choices transfer well from ImageNet.
我们的修改大大改善了类条件GAN。在ImageNet上于128进行培训时×我们的模型（BigGAN）的分辨率为128，将最先进的起始分数（IS）和弗雷谢特起始距离（FID）从52.52和18.65分别提高到166.3和9.6。我们还成功地在256的ImageNet上训练了BigGAN×256和512×512分辨率，并在256时达到233.0和9.3的IS和FID×256，IS和FID为241.4和10.9（512）×512.最后，我们在更大的数据集– JFT-300M上训练模型，并证明我们的设计选择可以很好地从ImageNet转移。

2BACKGROUND

A Generative Adversarial Network (GAN) involves Generator (G) and Discriminator (D) networks whose purpose, respectively, is to map random noise to samples and discriminate real and generated samples. Formally, the GAN objective, in its original form (Goodfellow et al., 2014) involves finding a Nash equilibrium to the following two player min-max problem:
生成对抗网络（GAN）涉及生成器（G）和鉴别器（D）网络，它们的目的分别是将随机噪声映射到样本，并区分真实样本和生成的样本。形式上，GAN目标的正式形式（Goodfellow等，2014）涉及找到以下两个参与者的最小-最大问题的纳什均衡：

$$
\min_{G}\max_{D} E_{x~q_data(x)}[log D(x)]+E_z \sim p(z)}[log(1-D(G(z))) $$

where$z\in\mathbb{R}^{d_z}$ is a latent variable drawn from distribution p(z) such as N(0,I) or U[−1,1]. When applied to images, G and D are usually convolutional neural networks (Radford et al., 2016). Without auxiliary stabilization techniques, this training procedure is notoriously brittle, requiring finely-tuned hyperparameters and architectural choices to work at all.

Much recent research has accordingly focused on modifications to the vanilla GAN procedure to impart stability, drawing on a growing body of empirical and theoretical insights (Nowozin et al., 2016; Sønderby et al., 2017; Fedus et al., 2018). One line of work is focused on changing the objective function (Arjovsky et al., 2017; Mao et al., 2016; Lim & Ye, 2017; Bellemare et al., 2017; Salimans et al., 2018) to encourage convergence. Another line is focused on constraining D through gradient penalties (Gulrajani et al., 2017; Kodali et al., 2017; Mescheder et al., 2018) or normalization (Miyato et al., 2018), both to counteract the use of unbounded loss functions and ensure D provides gradients everywhere to G.
当应用于图像时，G和D通常是卷积神经网络（Radford et al。，2016）。没有辅助稳定技术，该训练过程非常脆弱，需要经过微调的超参数和体系结构选择才能完全起作用。

因此，最近的许多研究都集中在对香草GAN程序的修改上，以赋予稳定性，并利用了越来越多的经验和理论见解（Nowozin等人，2016 ;Sønderby等人，2017 ; Fedus等人，2018）。一项工作重点是改变目标函数（Arjovsky等人，2017 ; Mao等人，2016 ; Lim＆Ye，2017 ; Bellemare等人，2017 ; Salimans等人，2018）以鼓励融合。另一条线着重于通过梯度惩罚来约束D （Gulrajani et al。，2017; Kodali等人，2017年；Mescheder et al。，2018）或归一化（Miyato et al。，2018），既可以抵消无界损失函数的使用，又可以确保D到G各处都提供梯度。

Of particular relevance to our work is Spectral Normalization (Miyato et al., 2018), which enforces Lipschitz continuity on D by normalizing its parameters with running estimates of their first singular values, inducing backwards dynamics that adaptively regularize the top singular direction. Relatedly Odena et al. (2018) analyze the condition number of the Jacobian of G and find that performance is dependent on G’s conditioning. Zhang et al. (2018) find that employing Spectral Normalization in G improves stability, allowing for fewer D steps per iteration. We extend on these analyses to gain further insight into the pathology of GAN training.
与我们的工作特别相关的是光谱归一化（Miyato等人，2018年），该方法通过使用其第一个奇异值的运行估计值对其参数进行归一化来归因于D上的Lipschitz连续性，并引入向后动力学以自适应地对顶部奇异方向进行正则化。有关Odena等。（2018）分析G的雅可比行列的条件数，发现性能取决于G的条件。张等。（2018）发现在G中使用频谱归一化可提高稳定性，从而减少D每次迭代的步骤。我们扩展了这些分析，以进一步了解GAN训练的病理学。

Other works focus on the choice of architecture, such as SA-GAN (Zhang et al., 2018) which adds the self-attention block from (Wang et al., 2018) to improve the ability of both G and D to model global structure. ProGAN (Karras et al., 2018) trains high-resolution GANs in the single-class setting by training a single model across a sequence of increasing resolutions.
其他工作着重于架构的选择，例如SA-GAN （Zhang等人，2018年），它增加了（Wang等人，2018年）的自注意力模块，以提高G和D建模全局的能力结构体。ProGAN （Karras et al。，2018）通过在一系列分辨率提高的情况下训练单个模型来在单班环境中训练高分辨率GAN。

In conditional GANs (Mirza & Osindero, 2014) class information can be fed into the model in various ways. In (Odena et al., 2017) it is provided to G by concatenating a 1-hot class vector to the noise vector, and the objective is modified to encourage conditional samples to maximize the corresponding class probability predicted by an auxiliary classifier. de Vries et al. (2017) and Dumoulin et al. (2017) modify the way class conditioning is passed to G by supplying it with class-conditional gains and biases in BatchNorm (Ioffe & Szegedy, 2015) layers. In Miyato & Koyama (2018), D is conditioned by using the cosine similarity between its features and a set of learned class embeddings as additional evidence for distinguishing real and generated samples, effectively encouraging generation of samples whose features match a learned class prototype.
在有条件的GAN中（Mirza和Osindero，2014年），可以通过多种方式将类信息输入模型。在（Odena et al。，2017）中，它通过将1-hot类向量与噪声向量连接而提供给G，并修改了目标以鼓励条件样本最大化由辅助分类器预测的相应类概率。de Vries等。（2017）和Dumoulin等。（2017）修改类条件传递给G的方式，方法是为它提供BatchNorm中的类条件增益和偏差（Ioffe＆Szegedy，2015）图层。在Miyato＆Koyama（2018）中，D是通过使用其特征和一组学习的类嵌入之间的余弦相似性作为条件来区分D和真实样本和生成的样本的条件，从而有效地鼓励生成其特征与学习的类原型相匹配的样本。

Objectively evaluating implicit generative models is difficult (Theis et al., 2015). A variety of works have proposed heuristics for measuring the sample quality of models without tractable likelihoods (Salimans et al., 2016; Heusel et al., 2017; Bińkowski et al., 2018; Wu et al., 2017). Of these, the Inception Score (IS, Salimans et al. (2016)) and Fréchet Inception Distance (FID, Heusel et al. (2017)) have become popular despite their notable flaws (Barratt & Sharma, 2018). We employ them as approximate measures of sample quality, and to enable comparison against previous work.
客观地评估隐式生成模型是困难的（Theis等，2015）。各种各样的工作提出了启发式方法来测量模型的样本质量而没有难以预测的可能性（Salimans等人，2016 ; Heusel等人，2017 ;Bińkowski等人，2018 ; Wu等人，2017）。其中，Inception Score（IS，Salimans et al。（2016））和FréchetInception Distance（FID，Heusel et al。（2017））尽管存在明显的缺陷（Barratt＆Sharma，2018），但它们仍然很受欢迎。。我们将它们用作样本质量的近似度量，并能够与以前的工作进行比较。

3 SCALING UP GANS

Batch	Ch.	Param (M)	Shared	Hier.	Ortho.	Itr ×103	FID	IS
256	64	81.5	SA-GAN Baseline	1000	18.65	52.52
512	64	81.5	✗	✗	✗	1000	15.30	58.77(±1.18)
1024	64	81.5	✗	✗	✗	1000	14.88	63.03(±1.42)
2048	64	81.5	✗	✗	✗	732	12.39	76.85(±3.83)
2048	96	173.5	✗	✗	✗	295(±18)	9.54(±0.62)	92.98(±4.27)
2048	96	160.6	✓	✗	✗	185(±11)	9.18(±0.13)	94.94(±1.32)
2048	96	158.3	✓	✓	✗	152(±7)	8.73(±0.45)	98.76(±2.84)
2048	96	158.3	✓	✓	✓	165(±13)	8.51(±0.32)	99.31(±2.10)
2048	64	71.3	✓	✓	✓	371(±7)	10.48(±0.10)	86.90(±0.61)

Table 1: Fréchet Inception Distance (FID, lower is better) and Inception Score (IS, higher is better) for ablations of our proposed modifications. Batch is batch size, Param is total number of parameters, Ch. is the channel multiplier representing the number of units in each layer, Shared is using shared embeddings, Hier. is using a hierarchical latent space, Ortho. is Orthogonal Regularization, and Itr either indicates that the setting is stable to 106 iterations, or that it collapses at the given iteration. Other than rows 1-4, results are computed across 8 different random initializations.
表1：我们建议的修改的消融的弗雷谢特起始距离（FID，越低越好）和起始分数（IS，越高越好）。批次是批次大小，参数是参数总数，通道。是表示每个图层中单位数量的渠道乘数，“共享”使用共享嵌入，即“层数”。正在使用分层潜伏空间Ortho。是正交正则化，并且Itr要么表明设置对106迭代，或者它在给定的迭代中崩溃。除了第1-4行，结果是在8种不同的随机初始化中计算得出的。

In this section, we explore methods for scaling up GAN training to reap the performance benefits of larger models and larger batches. As a baseline, we employ the SA-GAN architecture of Zhang et al. (2018), which uses the hinge loss (Lim & Ye, 2017; Tran et al., 2017) GAN objective. We provide class information to G with class-conditional BatchNorm (Dumoulin et al., 2017; de Vries et al., 2017) and to D with projection (Miyato & Koyama, 2018). The optimization settings follow Zhang et al. (2018) (notably employing Spectral Norm in G) with the modification that we halve the learning rates and take two D steps per G step. For evaluation, we employ moving averages of G’s weights following Karras et al. (2018); Mescheder et al. (2018), with a decay of 0.9999. We use Orthogonal Initialization (Saxe et al., 2014), whereas previous works used N(0,0.02I) (Radford et al., 2016) or Xavier initialization (Glorot & Bengio, 2010). Each model is trained on 128 to 512 cores of a Google TPU v3 Pod (Google, 2018), and computes BatchNorm statistics in G across all devices, rather than per-device as in standard implementations. We find progressive growing (Karras et al., 2018) unnecessary even for our largest 512×512 models.
在本节中，我们探索扩大GAN训练规模的方法，以获取更大模型和更大批次的性能收益。作为基准，我们采用了Zhang等人的SA-GAN体系结构。（2018），它使用了铰链损耗（Lim＆Ye，2017 ; Tran等，2017） GAN目标。我们提供的等级信息到ģ与分类条件BatchNorm （等人迪穆兰，。2017 ;德Vries等，2017年）和d与突出部（宫户＆小山，2018）。优化设置遵循Zhang等人的方法。（2018年）（尤其是在G中使用频谱范数），并进行了修改，使我们将学习率减半，并且每G步采取两个D步。为了进行评估，我们采用了Karras等人的G权重的移动平均值。（2018）; Mescheder等。（2018），衰落了。0.9999。我们使用正交初始化（Saxe et al。，2014），而以前的工作使用ñ（0，0.02一世） （Radford等人，2016）或Xavier初始化（Glorot＆Bengio，2010）。每种模型都在Google TPU v3 Pod的128至512核上进行了训练 （Google，2018年），并在所有设备上以G形式计算BatchNorm统计信息，而不是像标准实现那样按设备计算。我们发现即使对于我们最大的512家，也无需进行渐进式增长（Karras等人，2018年）×512个型号。

We begin by increasing the batch size for the baseline model, and immediately find tremendous benefits in doing so. Rows 1-4 of Table 1 show that simply increasing the batch size by a factor of 8 improves the state-of-the-art IS by 46%. We conjecture that this is a result of each batch covering more modes, providing better gradients for both networks. One notable side effect of this scaling is that our models reach better final performance in fewer iterations, but become unstable and undergo complete training collapse. We discuss the causes and ramifications of this in Section 4. For these experiments, we stop training just after collapse, and report scores from checkpoints saved just before.

We then increase the width (number of channels) in every layer by 50%, approximately doubling the number of parameters in both models. This leads to a further IS improvement of 21%, which we posit is due to the increased capacity of the model relative to the complexity of the dataset. Doubling the depth does not appear to have the same effect on ImageNet models, instead degrading performance.
我们首先增加基线模型的批次大小，然后立即发现这样做的巨大好处。表1的第1-4行 显示，仅将批次大小增加8倍就可以将最新的IS提升46％。我们推测这是每批覆盖更多模式的结果，从而为两个网络都提供了更好的渐变。这种缩放的一个显着的副作用是我们的模型在较少的迭代中达到了更好的最终性能，但是变得不稳定并经历了完全的训练崩溃。我们将在第4节中讨论此问题的原因和后果 。对于这些实验，我们会在崩溃后立即停止训练，并报告之前保存的检查点的得分。

然后，我们将每层的宽度（通道数）增加50％，这几乎使两个模型中的参数数增加了一倍。这导致IS进一步提高21％，这是由于相对于数据集的复杂性，模型的容量增加了。深度加倍似乎对ImageNet模型没有相同的影响，反而会降低性能。

We note that class embeddings c used for the conditional BatchNorm layers in G contain a large number of weights. Instead of having a separate layer for each embedding (Miyato et al., 2018; Zhang et al., 2018), we opt to use a shared embedding, which is linearly projected to each layer’s gains and biases (Perez et al., 2018). This reduces computation and memory costs, and improves training speed (in number of iterations required to reach a given performance) by 37%. Next, we employ a variant of hierarchical latent spaces, where the noise vector z is fed into multiple layers of G rather than just the initial layer. The intuition behind this design is to allow G to use the latent space to directly influence features at different resolutions and levels of hierarchy. For our architecture, this is easily accomplished by splitting z into one chunk per resolution, and concatenating each chunk to the conditional vector c which gets projected to the BatchNorm gains and biases. Previous works (Goodfellow et al., 2014; Denton et al., 2015) have considered variants of this concept; our contribution is a minor modification of this design. Hierarchical latents improve memory and compute costs (primarily by reducing the parametric budget of the first linear layer), provide a modest performance improvement of around 4%, and improve training speed by a further 18%.
我们注意到类嵌入 C用于G中的条件BatchNorm层的层包含大量权重。我们没有使用每个嵌入单独的层 （Miyato等人，2018 ; Zhang等人，2018），而是选择使用共享嵌入，将其线性投影到每一层的增益和偏差 （Perez等人，2018））。这样可以减少计算和内存成本，并将训练速度（达到给定性能所需的迭代次数）提高37％。接下来，我们使用分层潜伏空间的一种变体，其中噪声矢量ž被送入G的多个层，而不仅仅是初始层。这种设计的直觉是允许G使用潜在空间直接影响处于不同分辨率和层次级别的要素。对于我们的体系结构，这很容易通过拆分来完成ž 每个分辨率分成一个块，然后将每个块连接到条件向量 C可以预测到BatchNorm的增益和偏差。先前的工作（Goodfellow等，2014； Denton等，2015）已经考虑了该概念的变体。我们的贡献是对该设计的微小修改。分层的潜能改善了内存和计算成本（主要是通过减少第一线性层的参数预算），提供了大约4％的适度性能改进，并进一步提高了18％的训练速度。

3.1TRADING OFF VARIETY AND FIDELITY WITH THE TRUNCATION TRICK 在“截断技巧”中权衡多样性和忠诚度

(a)

(b)

Figure 2: (a) The effects of increasing truncation. From left to right, threshold=2, 1.5, 1, 0.5, 0.04. (b) Saturation artifacts from applying truncation to a poorly conditioned model.Unlike models which need to backpropagate through their latents, GANs can employ an arbitrary prior p(z), yet the vast majority of previous works have chosen to draw z from either N(0,I) or U[−1,1]. We question the optimality of this choice and explore alternatives in Appendix E.
图2：（a）增加截断的影响。从左至右，阈值= 2、1.5、1、0.5、0.04。（b）通过将截断应用于条件较差的模型而产生的饱和伪影。

Remarkably, our best results come from using a different latent distribution for sampling than was used in training. Taking a model trained with z∼N(0,I) and sampling z from a truncated normal (where values which fall outside a range are resampled to fall inside that range) immediately provides a boost to IS and FID. We call this the Truncation Trick: truncating a z vector by resampling the values with magnitude above a chosen threshold leads to improvement in individual sample quality at the cost of reduction in overall sample variety. Figure 2(a) demonstrates this: as the threshold is reduced, and elements of z are truncated towards zero (the mode of the latent distribution), individual samples approach the mode of G’s output distribution.
我们质疑这种选择的最优性，并在附录E中探讨替代方案 。

值得注意的是，我们最好的结果来自于使用与训练中不同的潜在分布进行采样。采取训练有素的模型z∼N(0,I) 和采样 z从截断正常（其中落在外侧的范围的值重采样落在该范围内）立即提供一个升压到IS和FID。我们称其为截断技巧：截断一个ž通过对幅度大于选定阈值的值进行重采样，可以降低单个样本的质量，但会降低总体样本种类。图 2（a）证明了这一点：随着阈值的降低，ž被截断为零（潜在分布的模式），单个样本接近G的输出分布的模式。

This technique allows fine-grained, post-hoc selection of the trade-off between sample quality and variety for a given G. Notably, we can compute FID and IS for a range of thresholds, obtaining the variety-fidelity curve reminiscent of the precision-recall curve (Figure 16). As IS does not penalize lack of variety in class-conditional models, reducing the truncation threshold leads to a direct increase in IS (analogous to precision). FID penalizes lack of variety (analogous to recall) but also rewards precision, so we initially see a moderate improvement in FID, but as truncation approaches zero and variety diminishes, the FID sharply drops. The distribution shift caused by sampling with different latents than those seen in training is problematic for many models. Some of our larger models are not amenable to truncation, producing saturation artifacts (Figure 2(b)) when fed truncated noise. To counteract this, we seek to enforce amenability to truncation by conditioning G to be smooth, so that the full space of z will map to good output samples. For this, we turn to Orthogonal Regularization (Brock et al., 2017), which directly enforces the orthogonality condition:
对于给定的G，该技术允许对样本质量和品种之间的折衷进行细粒度的事后选择。值得注意的是，我们可以针对一定范围的阈值计算FID和IS，从而获得让人联想到精确召回曲线的多样性保真度曲线（图 16）。由于IS不会惩罚类条件模型中的多样性，因此降低截断阈值会导致IS直接增加（类似于精度）。FID会惩罚缺乏多样性的情况（类似于召回），但也会奖励精确度，因此我们最初看到FID有所改善，但随着截断趋近于零且多样性减少，FID急剧下降。对于许多模型来说，由与训练中看到的潜能不同的潜在采样引起的分布偏移是有问题的。我们的某些较大模型不适合截断，在馈入截断噪声时会产生饱和伪像（图 2（b））。为了解决这个问题，我们试图通过将G调整为平滑来增强对截断的适应性，从而使G的整个空间ž将映射到良好的输出样本。为此，我们转向正交正则化（Brock et al。，2017），它直接执行正交条件：

$$
R_{\beta}(W)=\beta|W^{\top}W-I|_{\mathrm{F}}^{2}$$
where W is a weight matrix and β a hyperparameter. This regularization is known to often be too limiting (Miyato et al., 2018), so we explore several variants designed to relax the constraint while still imparting the desired smoothness to our models. The version we find to work best removes the diagonal terms from the regularization, and aims to minimize the pairwise cosine similarity between filters but does not constrain their norm:
W是权重矩阵， β超参数。已知这种正则化通常过于局限（Miyato et al。，2018），因此我们探索了几种旨在放松约束同时仍为模型赋予所需平滑度的变体。我们发现效果最好的版本从正则化中删除了对角项，旨在最大程度地减少滤波器之间的成对余弦相似度，但不限制其范数：

$$
R_{\beta}(W)=\beta|W^{\top}W\odot(\mathbf{1}-I)|_{\mathrm{F}}^{2}$$

where 1 denotes a matrix with all elements set to 1. We sweep β values and select 10−4, finding this small additional regularization sufficient to improve the likelihood that our models will be amenable to truncation. Across runs in Table 1, we observe that without Orthogonal Regularization, only 16% of models are amenable to truncation, compared to 60% when trained with Orthogonal Regularization.
1 表示所有元素均设置为的矩阵 1个。我们遍历β 值并选择 $10^-4$，发现此小的附加正则化足以提高我们的模型可被截断的可能性。在表1的所有运行中 ，我们观察到没有正交正则化的模型只有16％可以被截断，而经过正交正则化训练的模型为60％。

3.2SUMMARY

We find that current GAN techniques are sufficient to enable scaling to large models and distributed, large-batch training. We find that we can dramatically improve the state of the art and train models up to 512×512 resolution without need for explicit multiscale methods like Karras et al. (2018). Despite these improvements, our models undergo training collapse, necessitating early stopping in practice. In the next two sections we investigate why settings which were stable in previous works become unstable when applied at scale.
我们发现，当前的GAN技术足以实现按比例缩放到大型模型和分布式，大批量训练。我们发现我们可以极大地改善现有技术并训练高达512个模型×无需像Karras等人那样的显式多尺度方法即可实现512分辨率。（2018）。尽管有这些改进，但我们的模型仍遭受训练崩溃，因此必须在实践中尽早停止。在接下来的两节中，我们研究了为什么以前的工作中稳定的设置在大规模应用时会变得不稳定。

4 ANALYSIS

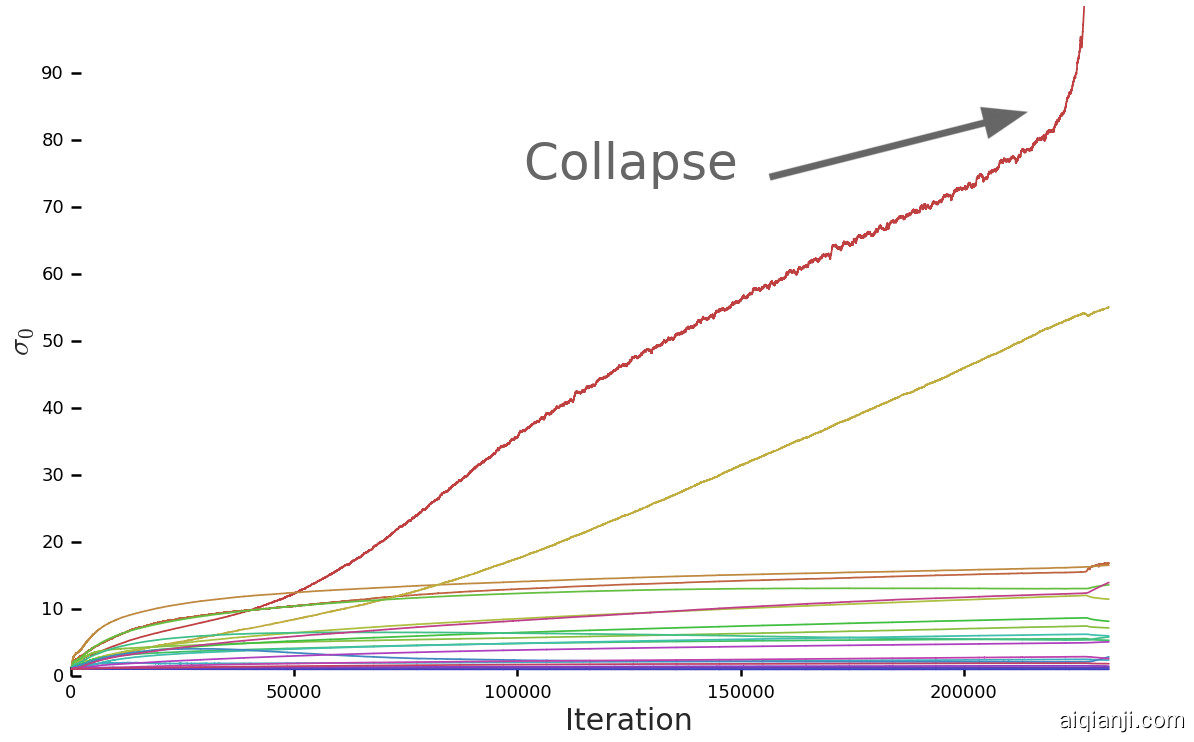(a) G	(b) D

Figure 3: A typical plot of the first singular value σ0 in the layers of G (a) and D (b) before Spectral Normalization. Most layers in G have well-behaved spectra, but without constraints a small subset grow throughout training and explode at collapse. D’s spectra are noisier but otherwise better-behaved. Colors from red to violet indicate increasing depth.
图3：第一个奇异值的典型图σ0在频谱归一化之前的G（a）和D（b）层中。G中的大多数层都具有良好的频谱，但是在没有限制的情况下，一小部分子集会在整个训练过程中增长并在坍塌时爆炸。D的频谱噪声较大，但在其他方面却表现得更好。从红色到紫色的颜色表示深度增加。

4.1CHARACTERIZING INSTABILITY: THE GENERATOR

Much previous work has investigated GAN stability from a variety of analytical angles and on toy problems, but the instabilities we observe occur for settings which are stable at small scale, necessitating direct analysis at large scale. We monitor a range of weight, gradient, and loss statistics during training, in search of a metric which might presage the onset of training collapse, similar to (Odena et al., 2018). We found the top three singular values σ0,σ1,σ2 of each weight matrix to be the most informative. They can be efficiently computed using the Alrnoldi iteration method (Golub & der Vorst, 2000), which extends the power iteration method, used in Miyato et al. (2018), to estimation of additional singular vectors and values. A clear pattern emerges, as can be seen in Figure 3(a) and Appendix F: most G layers have well-behaved spectral norms, but some layers (typically the first layer in G, which is over-complete and not convolutional) are ill-behaved, with spectral norms that grow throughout training and explode at collapse.
以前的许多工作已经从各种分析角度和玩具问题研究了GAN的稳定性，但是我们观察到的不稳定情况发生在小规模稳定的情况下，因此需要大规模直接分析。我们在训练过程中监视一系列重量，梯度和损失统计数据，以寻找可能预示训练崩溃开始的指标，类似于（Odena et al。，2018）。我们找到了前三个奇异值 σ0，σ1个，σ2个每个权重矩阵中的，以提供最多的信息。可以使用Alrnoldi迭代方法（Golub＆der Vorst，2000）有效地计算它们 ，该方法扩展了Miyato等人中使用的幂迭代方法 。（2018），以估计其他奇异向量和值。如图3（a）和附录 F所示，出现了清晰的模式 ：大多数G层具有良好的频谱范数，但有些层（通常是G中的第一层是过度完成的而不是卷积的）表现不佳，频谱规范会在整个训练过程中不断增长，并在崩溃时爆炸。

To ascertain if this pathology is a cause of collapse or merely a symptom, we study the effects of imposing additional conditioning on G to explicitly counteract spectral explosion. First, we directly regularize the top singular values σ0 of each weight, either towards a fixed value σreg or towards some ratio r of the second singular value, r⋅sg(σ1) (with sg the stop-gradient operation to prevent the regularization from increasing σ1). Alternatively, we employ a partial singular value decomposition to instead clamp σ0. Given a weight W, its first singular vectors u0 and v0, and σclamp the value to which the σ0 will be clamped, our weights become:

为了确定这种病理是崩溃的原因还是仅仅是症状，我们研究了在G上施加额外条件以明显抵消光谱爆炸的影响。首先，我们直接对顶部奇异值进行正则化σ0 每个重量的一个，或者朝着固定值的方向移动

$$
W=W-\max(0,\sigma_{0}-\sigma_{clamp})v_{0}u_{0}^{\top}
$$
where σclamp is set to either σreg or r⋅sg(σ1). We observe that both with and without Spectral Normalization these techniques have the effect of preventing the gradual increase and explosion of either σ0 or σ0σ1, but even though in some cases they mildly improve performance, no combination prevents training collapse. This evidence suggests that while conditioning G might improve stability, it is insufficient to ensure stability. We accordingly turn our attention to D.

4.2CHARACTERIZING INSTABILITY: THE DISCRIMINATOR

As with G, we analyze the spectra of D’s weights to gain insight into its behavior, then seek to stabilize training by imposing additional constraints. Figure 3(b) displays a typical plot of σ0 for D (with further plots in Appendix F). Unlike G, we see that the spectra are noisy, σ0σ1 is well-behaved, and the singular values grow throughout training but only jump at collapse, instead of exploding.

The spikes in D’s spectra might suggest that it periodically receives very large gradients, but we observe that the Frobenius norms are smooth (Appendix F), suggesting that this effect is primarily concentrated on the top few singular directions. We posit that this noise is a result of optimization through the adversarial training process, where G periodically produces batches which strongly perturb D . If this spectral noise is causally related to instability, a natural counter is to employ gradient penalties, which explicitly regularize changes in D’s Jacobian. We explore the R1 zero-centered gradient penalty from Mescheder et al. (2018):
D光谱的尖峰可能表明它周期性地接收到很大的梯度，但是我们观察到Frobenius范数是平滑的（附录 F），这表明该效应主要集中在前几个奇异方向上。我们认为，这种噪声是通过对抗训练过程进行优化的结果，其中G周期性地产生强烈干扰D的批次。如果此频谱噪声与不稳定性有因果关系，则自然的对策是采用梯度罚分法，该罚分法明确地规范了D氏雅可比定律的变化。我们探索[R1个Mescheder等人的零中心梯度惩罚。（2018）：
$$
R_{1}:=\frac{\gamma}{2}\E_{p_D(x)}[|\nabla D(x)|_{F% }^{2}]
$$
With the default suggested γ strength of 10, training becomes stable and improves the smoothness and boundedness of spectra in both G and D, but performance severely degrades, resulting in a 45% reduction in IS. Reducing the penalty partially alleviates this degradation, but results in increasingly ill-behaved spectra; even with the penalty strength reduced to 1 (the lowest strength for which sudden collapse does not occur) the IS is reduced by 20%. Repeating this experiment with various strengths of Orthogonal Regularization, DropOut (Srivastava et al., 2014), and L2 (See Appendix H for details), reveals similar behaviors for these regularization strategies: with high enough penalties on D, training stability can be achieved, but at a substantial cost to performance.
默认情况下建议 γ强度为10时，训练变得稳定并改善了G和D光谱的平滑度和有界性，但是性能严重下降，导致IS降低了45％。减少损失可以部分缓解这种退化，但会导致不良行为光谱的增加；即使惩罚强度降低到1个（不会发生突然崩溃的最低强度）IS降低了20％。用正交正则化，DropOut （Srivastava等人，2014）和L2（请参见附录 H的详细信息）的各种强度重复该实验，发现这些正则化策略具有相似的行为：对D施加足够高的惩罚，可以实现训练稳定性，但会大幅降低性能。

We also observe that D’s loss approaches zero during training, but undergoes a sharp upward jump at collapse (Appendix F). One possible explanation for this behavior is that D is overfitting to the training set, memorizing training examples rather than learning some meaningful boundary between real and generated images. As a simple test for D’s memorization (related to Gulrajani et al. (2017)), we evaluate uncollapsed discriminators on the ImageNet