MLP-Mixer: An all-MLP Architecture for Vision 面向视觉的全MLP架构
Ilya Tolstikhin∗, Neil Houlsby∗, Alexander Kolesnikov∗, Lucas Beyer∗,
Xiaohua Zhai, Thomas Unterthiner, Jessica Yung, Daniel Keysers,
Jakob Uszkoreit, Mario Lucic, Alexey Dosovitskiy
∗equal contribution
Google Research, Brain Team
{tolstikhin, neilhoulsby, akolesnikov, lbeyer,
xzhai, unterthiner, jessicayung, keysers,
usz, lucic,
ABSTRACT
Convolutional Neural Networks (CNNs) are the go-to model for computer vision. Recently, attention-based networks, such as the Vision Transformer, have also become popular. In this paper we show that while convolutions and attention are both sufficient for good performance, neither of them are necessary. We present MLP-Mixer, an architecture based exclusively on multi-layer perceptrons (MLPs). MLP-Mixer contains two types of layers: one with MLPs applied independently to image patches (i.e. ‘‘mixing’’ the per-location features), and one with MLPs applied across patches (i.e. ‘‘mixing’’ spatial information). When trained on large datasets, or with modern regularization schemes, MLP-Mixer attains competitive scores on image classification benchmarks, with pre-training and inference cost comparable to state-of-the-art models. We hope that these results spark further research beyond the realms of well established CNNs and Transformers.11MLP-Mixer code will be available at https://github.com/google-research/vision_transformer
卷积神经网络（CNN）是计算机视觉的首选模型。最近，基于注意力的网络（例如Vision Transformer）也变得很流行。在本文中，我们表明，尽管卷积和注意力都足以获得良好的性能，但它们都不是必需的。我们介绍MLP-Mixer，一种仅基于多层感知器（MLP）的体系结构。MLP-Mixer包含两种类型的层：一种将MLP独立应用于图像补丁（即“混合”每个位置特征），另一种将MLP应用到各个补丁（即“混合”空间信息）。在大型数据集上进行训练或采用现代正则化方案进行训练时，MLP-Mixer在图像分类基准上获得竞争性得分，其预训练和推理成本可与最新模型相媲美。我们希望这些结果能引发更多的研究，超越成熟的CNN和transformer的领域。1个
1INTRODUCTION
As the history of computer vision demonstrates, the availability of larger datasets coupled with increased computational capacity often leads to a paradigm shift. While Convolutional Neural Networks (CNNs) have been the de-facto standard for computer vision, recently Vision Transformers (Dosovitskiy et al., 2021) (ViT), an alternative based on self-attention layers, attained state-of-the-art performance. ViT continues the long-lasting trend of removing hand-crafted visual features and inductive biases from models and relies further on learning from raw data.
正如计算机视觉的历史所证明的那样，较大的数据集的可用性以及增加的计算能力通常会导致范式转换。尽管卷积神经网络（CNN）已成为计算机视觉的事实上的标准，但最近基于自注意层的替代方案视觉变形器 （Dosovitskiy等人，2021年）（ViT）达到了最新水平表现。ViT延续了从模型中消除手工制作的视觉特征和归纳偏差的长期趋势，并进一步依赖于从原始数据中学习。
We propose the MLP-Mixer architecture (or “Mixer” for short), a competitive but conceptually and technically simple alternative, that does not use convolutions or self-attention. Instead, Mixer’s architecture is based entirely on multi-layer perceptrons (MLPs) that are repeatedly applied across either spatial locations or feature channels. Mixer relies only on basic matrix multiplication routines, changes to data layout (reshapes and transpositions), and scalar non-linearities.
我们提出了MLP-Mixer体系结构（或简称为“ Mixer”），它是一种竞争性的，但在概念和技术上都很简单的替代方案，它不使用卷积或自我关注。取而代之的是，Mixer的体系结构完全基于多层感知器（MLP），可在空间位置或特征通道上重复应用。Mixer仅依赖于基本矩阵乘法例程，对数据布局的更改（重塑和换位）以及标量非线性。
Figure 1 depicts he macro-structure of Mixer. It accepts a sequence of linearly projected image patches (also referred to as tokens) shaped as a “patches × channels” table as an input, and maintains this dimensionality. Mixer makes use of two types of MLP layers: channel-mixing MLPs and token-mixing MLPs. The channel-mixing MLPs allow communication between different channels; they operate on each token independently and take individual rows of the table as inputs. The token-mixing MLPs allow communication between different spatial locations (tokens); they operate on each channel independently and take individual columns of the table as inputs. These two types of layers are interleaved to enable interaction of both input dimensions.
图 1描绘了混合器的宏观结构。它接受一系列线性投影的图像斑块（也称为令牌），形状为“斑块” × 渠道”表作为输入，并保持此维度。混合器利用两种类型的MLP层：通道混合MLP和令牌混合MLP。通道混合MLP允许在不同通道之间进行通信。它们独立地对每个令牌进行操作，并将表的各个行作为输入。令牌混合MLP允许不同空间位置（令牌）之间的通信；它们在每个通道上独立运行，并以表格的各个列作为输入。这两种类型的层是交错的，以实现两个输入维度的交互。
In the extreme case, our architecture can be seen as a very special CNN, which uses 1×1 convolutions for channel mixing, and single-channel depth-wise convolutions of a full receptive field and parameter sharing for token mixing. However, the converse is not true as typical CNNs are not special cases of Mixer. Furthermore, a convolution is more complex than the plain matrix multiplication in MLPs as it requires an additional costly reduction to matrix multiplication and/or specialized implementation.
Despite its simplicity, Mixer attains competitive results. When pre-trained on large datasets (i.e., ∼100M images), it reaches near state-of-the-art performance, previously claimed by CNNs and Transformers, in terms of the accuracy/cost trade-off. This includes 87.94% top-1 validation accuracy on ILSVRC2012 “ImageNet” (Deng et al., 2009). When pre-trained on data of more modest scale (i.e., ∼1–10M images), coupled with modern regularization techniques Touvron et al. (2020); Wightman (2019), Mixer also achieves strong performance. However, similar to ViT, it falls slightly short of specialized CNN architectures.
在极端情况下，我们的架构可以看作是非常特殊的CNN，它使用1×1个用于通道混合的卷积，以及一个完整接收场的单通道深度卷积和令牌混合的参数共享。但是，相反情况并不正确，因为典型的CNN并不是Mixer的特殊情况。此外，卷积比MLP中的普通矩阵乘法更为复杂，因为卷积需要对矩阵乘法和/或专用实现进行额外的成本降低。
尽管它很简单，但Mixer还是取得了竞争性的成绩。当针对大型数据集进行预训练时（即，〜1亿张图片），就准确性/成本之间的权衡而言，它达到了CNN和Transformers先前声称的最先进的性能。这包括在ILSVRC2012“ ImageNet”上的top-1验证准确性为87.94％ （Deng等，2009）。在以较小规模的数据进行预训练时（即，〜1–10M图像），以及现代正则化技术 Touvron等。（2020）; Wightman（2019），Mixer也取得了出色的表现。但是，类似于ViT，它与专用的CNN架构略有不同。
2MIXER ARCHITECTURE
Figure 1: MLP-Mixer consists of per-patch linear embeddings, Mixer layers, and a classifier head. Mixer layers contain one token-mixing MLP and one channel-mixing MLP, each consisting of two fully-connected layers and a GELU nonlinearity. Other components include: skip-connections, dropout, layer norm on the channels, and linear classifier head.
图1： MLP-Mixer由每个修补程序的线性嵌入，混合器层和一个分类器头组成。混合器层包含一个令牌混合MLP和一个通道混合MLP，每个都包含两个完全连接的层和一个GELU非线性。其他组件包括：跳过连接，丢失，通道上的图层规范以及线性分类器头。
Modern deep vision architectures consist of layers that mix features (i) at a given spatial location, (ii) between different spatial locations, or both at once. In CNNs, (ii) is implemented with N×N convolutions (for N>1) and pooling.Neurons in deeper layers have a larger receptive field (Araujo et al., 2019; Luo et al., 2016). At the same time, 1×1 convolutions also perform (i), and larger kernels perform both (i) and (ii). In Vision Transformers and other attention-based architectures, self-attention layers allow both (i) and (ii) and the MLP-blocks perform (i). The idea behind the Mixer architecture is to clearly separate the per-location (channel-mixing) operations (i) and cross-location (token-mixing) operations (ii). Both operations are implemented with MLPs.
现代深度视觉架构由将特征（i）在给定的空间位置，（ii）在不同的空间位置之间或同时在两者之间混合的层组成。在CNN中，（ii）与N×N 卷积（用于 N>1个）和池化。更深层的神经元具有更大的感受野 （Araujo等，2019； Luo等，2016）。同时1×1个卷积也执行（i），较大的内核同时执行（i）和（ii）。在视觉变形金刚和其他基于关注的体系结构中，自关注层允许（i）和（ii）两者都由MLP块执行（i）。Mixer体系结构背后的思想是清楚地将按位置（通道混合）操作（i）和跨位置（令牌混合）操作（ii）分开。两种操作都通过MLP来实现。
Figure 1 summarizes the architecture. Mixer takes as input a sequence of S non-overlapping image patches, each one projected to a desired hidden dimension C. This results in a two-dimensional real-valued input table, X∈RS×C. If the original input image has resolution (H,W), and each patch has resolution (P,P), then the number of patches is S=HW/P2. All patches are linearly projected with the same projection matrix. Mixer consists of multiple layers of identical size, and each layer consists of two MLP blocks. The first one is the token-mixing MLP block: it acts on columns of X (i.e. it is applied to a transposed input table X⊤), maps RS↦RS, and is shared across all columns. The second one is the channel-mixing MLP block: it acts on rows of X, maps RC↦RC, and is shared across all rows. Each MLP block contains two fully-connected layers and a non-linearity applied independently to each row of its input data tensor. Mixer layers can be written as follows (omitting layer indices):
图 1总结了该体系结构。混音器将以下序列作为输入小号不重叠的图像块，每个块都投影到所需的隐藏尺寸 C。这将产生一个二维实值输入表，$X∈R^(S×C)$。如果原始输入图像具有分辨率 (H,W)，每个补丁都有分辨率 （P，P），则补丁数为 $S=Hw ^/P^2$个。所有面片均使用*相同的*投影矩阵线性投影。混合器由大小相同的多层组成，每层由两个MLP块组成。第一个是*令牌混合*MLP块：它作用于X （即，它应用于转置的输入表 X⊤），地图 RC↦RC，并且在所有列之间共享。第二个是*通道混合*MLP块：它作用于X，地图 [RC↦[RC，并在所有行中共享。每个MLP块包含两个完全连接的层，以及一个非线性，独立地应用于其输入数据张量的每一行。混合器层可以编写如下（省略层索引）：
| U∗,i | =X∗,i+W2σ(W1LayerNorm(X)∗,i),for i=1…C, | (1) | ||
|---|---|---|---|---|
| Yj,∗ | =Uj,∗+W4σ(W3LayerNorm(U)j,∗),for j=1…S. | |||
| - | - | - | - |
Here σ is an element-wise nonlinearity (GELU Hendrycks and Gimpel (2016)). DS and DC are tunable hidden widths in the token-mixing and channel-mixing MLPs, respectively. Note that DS is selected independently of the number of input patches. Therefore, the computational complexity of the network is linear in the number of input patches, unlike ViT whose complexity is quadratic. Since DC is independent of the patch size, the overall complexity is linear in the number of pixels in the image, as for a typical CNN.
这里 σ是逐元素非线性（GELU Hendrycks and Gimpel（2016））。 DS 和 dC分别是令牌混合MLP和通道混合MLP中的可调隐藏宽度。注意DS与输入音色的数量无关地选择。因此，与ViT的复杂度是平方的不同，网络的计算复杂度在输入补丁的数量上是线性的。自从dC 与补丁大小无关，对于典型的CNN，总体复杂度在图像像素数量上呈线性关系。
As mentioned above, the same channel-mixing MLP (token-mixing MLP) is applied to every row (column) of X. Tying the parameters of the channel-mixing MLPs (within each layer) is a natural choice—it provides positional invariance, a prominent feature of convolutions. However, tying parameters across channels is much less common. For example, separable convolutions Chollet (2017); Sifre (2014), used in some CNNs, apply convolutions to each channel independently of the other channels. However, in separable convolutions, a different convolutional kernel is applied to each channel unlike the token-mixing MLPs in Mixer that share the same kernel (of full receptive field) for all of the channels. The parameter tying prevents the architecture from growing too fast when increasing the hidden dimension C or the sequence length S and leads to significant memory savings. Surprisingly, this choice does not affect the empirical performance, see Supplementary A.1.
如上所述，相同的通道混合MLP（令牌混合MLP）应用于行的每行（列） X。将通道混合MLP的参数（在每一层内）捆绑在一起是很自然的选择-它提供位置不变性，这是卷积的显着特征。但是，跨通道绑定参数的情况要少得多。例如，可分离卷积Chollet（2017）; 在某些CNN中使用的Sifre（2014）将卷积应用于每个通道，而与其他通道无关。但是，在可分离的卷积中，将不同的卷积内核应用于每个通道，这与Mixer中的令牌混合MLP不同，后者对于所有通道共享同一内核（具有完整的接收域）。参数绑定可防止架构在增加隐藏维度时增长过快C 或序列长度 小号并节省大量内存。令人惊讶的是，此选择不影响经验性能，请参阅补充 A.1。
Each layer in Mixer (except for the initial patch projection layer) takes an input of the same size. This “isotropic” design is most similar to Transformers, or deep RNNs in other domains, that also use a fixed width. This is unlike most CNNs, which have a pyramidal structure: deeper layers have a lower resolution input, but more channels. Note that while these are the typical designs, other combinations exist, such as isotropic ResNets (Sandler et al., 2019) and pyramidal ViTs (Wang et al., 2021).
Mixer中的每个层（初始面片投影层除外）都采用相同大小的输入。这种“各向同性”的设计与其他使用固定宽度的变压器或其他领域的深层RNN最相似。这与大多数具有金字塔结构的CNN不同：更深的层具有较低的分辨率输入，但具有更多的通道。请注意，虽然这些是典型的设计，但也存在其他组合，例如各向同性ResNet （Sandler等，2019）和金字塔形ViT （Wang等，2021）。
Aside from the MLP layers, Mixer uses other standard architectural components: skip-connections He et al. (2016) and Layer Normalization Ba et al. (2016). Furthermore, unlike ViTs, Mixer does not use position embeddings because the token-mixing MLPs are sensitive to the order of the input tokens, and therefore may learn to represent location. Finally, Mixer uses a standard classification head with the global average pooling layer followed by a linear classifier. Overall, the architecture can be written compactly in JAX/Flax, the code is given in Supplementary E.
除了MLP层，Mixer还使用其他标准架构组件：跳过连接 He等人。（2016）和层归一化 Ba等。（2016）。此外，与ViT不同，Mixer不使用位置嵌入，因为令牌混合MLP对输入令牌的顺序很敏感，因此可以学会表示位置。最后，Mixer使用带有全局平均池化层的标准分类头，然后是线性分类器。总体而言，该体系结构可以用JAX / Flax紧凑地编写，其代码在补充E中给出 。
3EXPERIMENTS
We evaluate the performance of MLP-Mixer models, pre-trained with medium- to large-scale datasets, on a range of small and mid-sized downstream classification tasks. We are interested in three primary quantities: (1) Accuracy on the downstream task. (2) Total computational cost of pre-training, which is important when training the model from scratch on the upstream dataset. (3) Throughput at inference time, which is important to the practitioner. Our goal is not to demonstrate state-of-the-art results, but to show that, remarkably, a simple MLP-based model is competitive with today’s best convolutional and attention-based models.
我们评估了MLP-Mixer模型的性能，这些模型经过中小型规模的数据集的预训练，适用于一系列中小型下游分类任务。我们对三个主要数量感兴趣：（1）下游任务的准确性。（2） 预训练的总计算成本，这对于在上游数据集上从头开始训练模型时非常重要。（3）推理时的吞吐量，这对于从业者很重要。我们的目标不是展示最先进的结果，而是要证明，基于MLP的简单模型与当今最好的卷积和基于注意力的模型相比具有竞争优势。
Downstream tasks
We use multiple popular downstream tasks such as ILSVRC2012 “ImageNet” (1.3M training examples, 1k classes) with the original validation labels (Deng et al., 2009) and cleaned-up ReaL labels (Beyer et al., 2020), CIFAR-10/100 (50k examples, 10/100 classes) (Krizhevsky, 2009), Oxford-IIIT Pets (3.7k examples, 36 classes) (Parkhi et al., 2012), and Oxford Flowers-102 (2k examples, 102 classes) (Nilsback and Zisserman, 2008). We also evaluate on the Visual Task Adaptation Benchmark (VTAB-1k), which consists of 19 diverse datasets, each with 1k training examples (Zhai et al., 2019).
下游任务
我们使用了多个受欢迎的下游任务，例如ILSVRC2012“ ImageNet”（1.3M培训示例，1k类），带有原始验证标签 （Deng等，2009）和清理过的ReaL标签 （Beyer等，2020），CIFAR -10/100（50k例子，10/100类） （Krizhevsky，2009），Oxford-IIIT Pets（3.7k例子，36类） （Parkhi等人，2012）和Oxford Flowers-102（2k例子，102）课） （Nilsback和Zisserman，2008年）。我们还评估了视觉任务适应基准（VTAB-1k），该基准由19个不同的数据集组成，每个数据集都有1000个训练示例 （Zhai等，2019）。
Pre-training data
We follow the standard transfer learning setup: pre-training followed by fine-tuning on the downstream tasks. We pre-train all models on two public datasets: ILSVRC2021 ImageNet, and ImageNet-21k, a superset of ILSVRC2012 that contains 21k classes and 14M images Deng et al. (2009). To assess performance at even larger scale, we also train on JFT-300M, a proprietary dataset with 300M examples and 18k classes (Sun et al., 2017). We de-duplicate all pre-training datasets with respect to the test sets of the downstream tasks as done in Dosovitskiy et al. (2021); Kolesnikov et al. (2020).
训练数据
我们遵循标准的转移学习设置：预训练，然后对下游任务进行微调。我们在两个公共数据集上对所有模型进行了预训练：ILSVRC2021 ImageNet和ImageNet-21k，ILSVRC2012的超集，其中包含21k类和14M图像 Deng等。（2009年）。为了更大规模地评估性能，我们还训练了JFT-300M，这是一个专有数据集，包含300M实例和18k类 （Sun等人，2017年）。我们按照Dosovitskiy等人的方法，对下游任务测试集的所有预训练数据集进行重复数据删除 。（2021）; Kolesnikov等。（2020年）。
Pre-training details 训练细节
We pre-train all models using Adam with β1=0.9, β2=0.999, and batch size 4 096, using weight decay, and gradient clipping at global norm 1. We use a linear learning rate warmup of 10k steps and linear decay. We pre-train all models at resolution 224. For JFT-300M, we pre-process images by applying the cropping technique from Szegedy et al. (2015) in addition to random horizontal flipping. For ImageNet and ImageNet-21k, we employ additional data augmentation and regularization techniques. In particular, we use RandAugment Cubuk et al. (2020), mixup Zhang et al. (2018), dropout Srivastava et al. (2014), and stochastic depth Huang et al. (2016). This set of techniques was inspired by the *timm library* Wightman (2019) and Touvron et al. (2019). More details on these hyperparameters are provided in Supplementary B.
我们使用Adam对所有模型进行预训练 β1个=0.9， β2个=0.999，以及批量大小为4 096（使用权重衰减）和全局标准1的梯度修剪。我们使用的线性学习率预热为10k个步长和线性衰减。我们以224分辨率对所有模型进行预训练。对于JFT-300M，我们通过应用Szegedy等人的裁剪技术对图像进行预处理 。（2015）以及随机水平翻转。对于ImageNet和ImageNet-21k，我们采用了其他数据增强和正则化技术。特别是，我们使用RandAugment Cubuk等。（2020年），张混合 等。（2018），辍学 Srivastava等。（2014年），随机深度 Huang等。（2016）。这套技术的灵感来自*timm库* Wightman（2019）和 Touvron等人。（2019）。在补充提供有关这些超参数的更多细节 乙。
Fine-tuning details
We fine-tune using SGD with momentum, batch size 512, gradient clipping at global norm 1, and a cosine learning rate schedule with a linear warmup. We do not use weight decay when fine-tuning. Following common practice Kolesnikov et al. (2020); Touvron et al. (2019), we also apply fine-tune at higher resolutions with respect to those used during pre-training. Since we keep the patch resolution fixed, this increases the number of input patches (say from S to S′) and thus requires modifying the shape of Mixer’s token-mixing MLP blocks. Formally, the input in Eq. (1) is left-multiplied by a weight matrix W1∈RDS×S and this operation has to be adjusted when changing the input dimension S. For this, we increase the hidden layer width from DS to D′S in proportion to the number of patches and initialize the (now larger) weight matrix W′2∈RD′S×S′ with a block-diagonal matrix containing copies of W2 on its diagonal. See Supplementary C for more details. On the VTAB-1k benchmark we follow the BiT-HyperRule Kolesnikov et al. (2020) and fine-tune Mixer models at resolution 224 and 448 on the datasets with small and large input images respectively.
Metrics
We evaluate the trade-off between the model’s computational cost and quality. For the former we compute two metrics: (1) Total pre-training time on TPU-v3 accelerators, which combines three relevant factors: the theoretical FLOPs for each training setup, the computational efficiency on the relevant training hardware, and the data efficiency. (2) Throughput in images/sec/core on TPU-v3. Since models of different sizes may benefit from different batch sizes, we sweep the batch sizes in {32,64,…,8192} and report the highest throughput for each model. For model quality, we focus on top-1 downstream accuracy after fine-tuning. On one occasion (Figure 3, right), where fine-tuning all of the models would have been too costly, we report the few-shot accuracies obtained by solving the ℓ2-regularized linear regression problem between the frozen learned representations of images and the labels.
我们评估模型的计算成本和质量之间的权衡。对于前者，我们计算两个指标：（1）TPU-v3加速器上的总预训练时间，它综合了三个相关因素：每种训练设置的理论FLOP，相关训练硬件上的计算效率以及数据效率。（2）TPU-v3上的图像/秒/核心的吞吐量。由于不同大小的模型可能会受益于不同的批次大小，因此我们在{32，64，…，8192}并报告每种型号的最高吞吐量。对于模型质量，我们专注于微调后的top-1下游精度。在某些情况下（ 右图3），对所有模型进行微调的成本太高了，我们报告了通过求解ℓ2个冻结的学习图像表示和标签之间的正则化线性回归问题。
| Specification | S/32 | S/16 | B/32 | B/16 | L/32 | L/16 | H/14 |
|---|---|---|---|---|---|---|---|
| Number of layers | 8 | 8 | 12 | 12 | 24 | 24 | 32 |
| Patch resolution P×P | 32×32 | 16×16 | 32×32 | 16×16 | 32×32 | 16×16 | 14×14 |
| Hidden size C | 512 | 512 | 768 | 768 | 1024 | 1024 | 1280 |
| Sequence length S | 49 | 196 | 49 | 196 | 49 | 196 | 256 |
| MLP dimension DC | 2048 | 2048 | 3072 | 3072 | 4096 | 4096 | 5120 |
| MLP dimension DS | 256 | 256 | 384 | 384 | 512 | 512 | 640 |
| Parameters (M) | 10 | 10 | 46 | 46 | 188 | 189 | 409 |
Table 1: Specifications of the Mixer architectures used in this paper. The “B”, “L”, and “H” (base, large, and huge) model scales follow Dosovitskiy et al. (2021). We use a brief notation: “B/16” means the model of base scale with patches of resolution 16×16. “S” refers to a small scale with 8 Mixer layers. The number of parameters is reported for an input resolution of 224 and does not include the weights of the classifier head.
表1：本文使用的混音器架构的规范。“ B”，“ L”和“ H”（基本，大型和大型）模型比例尺遵循 Dosovitskiy等人的观点。（2021年）。我们用一个简短的符号表示：“ B / 16”是指带有分辨率为16的补丁的基本比例模型
Models
We compare various configurations of Mixer, summarized in Table 1, to the most recent, state-of-the-art, CNNs and attention-based models. In all the figures and tables, the MLP-based Mixer models are marked with pink (), convolution-based models with yellow (), and attention-based models with blue (). The Vision Transformers (ViTs) have model scales and patch resolutions similar to Mixer, including ViT-L/16 and ViT-H/14. HaloNets are attention-based models that use a ResNet-like structure with local self-attention layers instead of 3×3 convolutions (Vaswani et al., 2021). We focus on the particularly efficient “HaloNet-H4 (base 128, Conv-12)” model, which is a hybrid variant of the wider HaloNet-H4 architecture with some of the self-attention layers replaced by convolutions. Note, we mark HaloNets with both attention and convolutions with blue (). Big Transfer (BiT) (Kolesnikov et al., 2020) models are ResNets optimized for transfer learning, pre-trained on ImageNet-21k or JFT-300M. NFNets (Brock et al., 2021) are normalizer-free ResNets with several optimizations for ImageNet classification. We consider the NFNet-F4+ model variant. Finally, we consider MPL (Pham et al., 2021) and ALIGN (Jia et al., 2021) for EfficientNet architectures. MPL is pre-trained at very large-scale on JFT-300M images, using meta-pseudo labelling from ImageNet instead of the original labels. We compare to the EfficientNet-B6-Wide model variant. ALIGN pre-train image encoder and language encoder on noisy web image text pairs in a contrastive way. We compare to their best EfficientNet-L2 image encoder.
我们将汇总在表1中的Mixer的各种配置与 最新的CNN和基于注意力的模型进行了比较。在所有图和表中，基于MLP的Mixer模型都标有粉红色（），基于卷积的模型标有黄色（），基于注意力的模型标有蓝色（）。视觉变形器（ViT）具有类似于Mixer的模型比例和面片分辨率，包括ViT-L / 16和ViT-H / 14。HaloNets是基于关注的模型，使用类似于ResNet的结构，具有本地自我注意层，而不是3个×3个卷积 （Vaswani等人，2021年）。我们将重点放在特别有效的“ HaloNet-H4（基本128，Conv-12）”模型上，该模型是更广泛的HaloNet-H4体系结构的混合变体，其中一些自我注意层已被卷积代替。注意，我们用蓝色（）标记了HaloNets的注意力和卷积。大传输（BiT）模型 （Kolesnikov等人，2020年）是针对传输学习而优化的ResNet，已在ImageNet-21k或JFT-300M上进行了预训练。NFNets （Brock等人，2021年）是无规范化的ResNet，针对ImageNet分类进行了多项优化。我们考虑了NFNet-F4 +模型的变体。最后，我们考虑针对EfficientNet架构的MPL （Pham等人，2021）和ALIGN （Jia等人，2021）。MPL在JFT-300M图像上进行了大规模的预训练，使用ImageNet的meta-pseudo标签代替了原始标签。我们将其与EfficientNet-B6-Wide模型变体进行了比较。嘈杂的网络图像文本对上的ALIGN预训练图像编码器和语言编码器采用对比方式。我们将其与最好的EfficientNet-L2图像编码器进行比较。
| ImNet | ReaL | Avg 5 | VTAB-1k | Throughput | TPUv3 | |
|---|---|---|---|---|---|---|
| top-1 | top-1 | top-1 | 19 tasks | img/sec/core | core-days | |
| Pre-trained on ImageNet-21k (public) | ||||||
| HaloNet Vaswani et al. (2021) | 85.8 | — | — | — | 120 | 0.10k |
| Mixer-L/16 | 84.15 | 87.86 | 93.91 | 74.95 | 105 | 0.41k |
| ViT-L/16 Dosovitskiy et al. (2021) | 85.30 | 88.62 | 94.39 | 72.72 | 32 | 0.18k |
| BiT-R152x4 Kolesnikov et al. (2020) | 85.39 | — | 94.04 | 70.64 | 26 | 0.94k |
| Pre-trained on JFT-300M (proprietary) | ||||||
| NFNet-F4+ Brock et al. (2021) | 89.2 | — | — | — | 46 | 1.86k |
| Mixer-H/14 | 87.94 | 90.18 | 95.71 | 75.33 | 40 | 1.01k |
| BiT-R152x4 Kolesnikov et al. (2020) | 87.54 | 90.54 | 95.33 | 76.29 | 26 | 9.90k |
| ViT-H/14 Dosovitskiy et al. (2021) | 88.55 | 90.72 | 95.97 | 77.63 | 15 | 2.30k |
| Pre-trained on unlabelled or weakly labelled data (proprietary) | ||||||
| MPL Pham et al. (2021) | 90.0 | 91.12 | — | — | — | 20.48k |
| ALIGN Jia et al. (2021) | 88.64 | — | — | 79.99 | 15 | 14.82k |
Table 2: Transfer performance, inference throughput, and training cost. The rows are sorted by inference throughput (fifth column). Mixer has comparable transfer accuracy to state-of-the-art models with similar cost. The Mixer models are fine-tuned at resolution 448. Mixer performance numbers are averaged over three fine-tuning runs and standard deviations are smaller than 0.1.
表2： 传输性能，推断吞吐量和培训成本。这些行按推理吞吐量排序（第五列）。Mixer的传输精度可与具有类似成本的最新型号相媲美。在448分辨率下对混音器模型进行了微调。混音器性能数值是在三个微调运行中平均的，标准偏差小于0.1
3.1MAIN RESULTS
Table 2 presents comparison of the largest Mixer models to state-of-the-art models from the literature. “ImNet” and “ReaL” columns refer to the original ImageNet validation labels (Deng et al., 2009) and cleaned-up ReaL labels (Beyer et al., 2020). “Avg. 5” stands for the average performance across all five downstream tasks (ImageNet, CIFAR-10, CIFAR-100, Pets, Flowers). Figure 2 (left) visualizes the accuracy-compute frontier.
表 2列出了最大的混频器模型与文献中最先进的模型的比较。“ ImNet”和“ ReaL”列指的是原始ImageNet验证标签 （Deng等，2009）和清理后的ReaL标签 （Beyer等，2020）。“平均 5英寸代表所有五个下游任务（ImageNet，CIFAR-10，CIFAR-100，宠物，鲜花）的平均性能。图 2 （左）显示了精度计算边界。
When pre-trained on ImageNet-21k with additional regularization, Mixer achieves an overall strong performance (84.15% top-1 on ImageNet), although slightly inferior to other models22In Table 2 we consider the highest accuracy models in each class, that use the largest resolutions (448 and above). However, fine-tuning at smaller resolution leads to substantial improvements in the test-time throughput, with often only a small accuracy penalty. For instance, when pre-training on ImageNet-21k the Mixer-L/16 model fine-tuned at 224 resolution achieves 82.84% ImageNet top-1 accuracy at throughput 420 img/sec/core; the ViT-L/16 model fine-tuned at 384 resolution achieves 85.15% at 80 img/sec/core Dosovitskiy et al. (2021); and HaloNet fine-tuned at 384 resolution achieves 85.5% at 258 img/sec/core Vaswani et al. (2021).. Regularization in this scenario is necessary and Mixer overfits without it, which is consistent with similar observations for ViT Dosovitskiy et al. (2021). We also report the results when training Mixer from scratch on ImageNet in Table 3 and the same conclusion holds. Supplementary B details our regularization settings.
当在ImageNet-21k上进行额外的正则化预训练时，Mixer可以实现整体强大的性能（ImageNet上top-1的84.15％），尽管略逊于其他型号22个在表 2中，我们考虑了使用最大分辨率（448及以上）的每个类别中精度最高的模型。但是，以较小的分辨率进行微调会导致测试时间吞吐量的显着提高，而精度损失通常很小。例如，在ImageNet-21k上进行预训练时，以224分辨率微调的Mixer-L / 16模型在420 img / sec / core的吞吐量下可达到82.84％ImageNet top-1精度；的VIT-L在384分辨率/ 16模型微调在80 IMG /秒/芯达到85.15％Dosovitskiy等。（2021年） ; Vaswani等人以384 img / sec / core的速度对384分辨率进行微调的HaloNet达到了85.5％。（2021年）。。在这种情况下，有必要进行正则化，而没有它的Mixer会过度拟合，这与ViT Dosovitskiy等人的类似观察一致。（2021年）。我们还在表3中报告了在ImageNet上从头开始训练Mixer时的结果， 并且得出相同的结论。附录 B详细介绍了我们的正则化设置。
When the size of the upstream dataset increases, Mixer’s performance improves significantly. In particular, Mixer-H/14 achieves 87.94% top-1 accuracy on ImageNet, which is 0.5% better than BiT-ResNet152x4 and only 0.5% lower than ViT-H/14. Remarkably, Mixer-H/14 runs 2.5 times faster than ViT-H/14 and almost twice as fast as BiT. Overall, Figure 2 (left) supports our main claim that in terms of the accuracy-compute trade-off Mixer is competitive with more conventional neural network architectures. The figure also demonstrates a clear correlation between the total pre-training cost and the downstream accuracy, even across architecture classes.
当上游数据集的大小增加时，Mixer的性能将大大提高。特别是，Mixer-H / 14在ImageNet上的top-1精度达到87.94％，比BiT-ResNet152x4高0.5％，仅比ViT-H / 14低0.5％。值得注意的是，Mixer-H / 14的运行速度是ViT-H / 14的2.5倍，几乎是BiT的两倍。总体而言，图 2 （左）支持我们的主要主张，即就精度计算的权衡而言，混频器与更传统的神经网络体系结构相比具有竞争力。该图还展示了总的预培训成本与下游准确性之间的明显关联，即使在不同的架构类别之间也是如此。
BiT-ResNet152x4 in the table are pre-trained using SGD with momentum and a long schedule. Since Adam tends to converge faster, we complete the picture in Figure 2 (left) with the BiT-R200x3 model from Dosovitskiy et al. (2021) pre-trained on JFT-300M using Adam. This ResNet has a slightly lower accuracy, but considerably lower pre-training compute. Finally, the results of smaller ViT-L/16 and Mixer-L/16 models are also reported in this figure.
表格中的BiT-ResNet152x4已使用SGD进行了预训练，而且动力十足且时间表很长。由于Adam趋于收敛更快，因此我们 使用Dosovitskiy等人的BiT-R200x3模型完成了图2（左）中的图片 。（2021）使用Adam在JFT-300M上进行了预培训。此ResNet的精度略低，但预训练的计算量却低得多。最后，该图中还报告了较小的ViT-L / 16和Mixer-L / 16模型的结果。
Figure 2: Left: ImageNet accuracy/training cost Pareto frontier (dashed line) for the SOTA models presented in Table 2. These model are pre-trained on ImageNet-21k, or JFT (labelled, or pseudo-labelled for MPL), or noisy web image text pairs. In addition, we include ViT-L/16, Mixer-L/16, and BiT-R200x3 (Adam) for context. Mixer is as good as these extremely performant ResNets, ViTs, and hybrid models, and sits on frontier with HaloNet, ViT, NFNet, and MPL. Right: Mixer (solid) catches or exceeds BiT (dotted) and ViT (dashed) as the data size grows. Every point on a curve uses the same pre-training compute; they correspond to pre-training on 3%, 10%, 30%, and 100% of JFT-300M for 233, 70, 23, and 7 epochs, respectively. Mixer improves more rapidly with data than ResNets, or even ViT, and the gap between large scale Mixer and ViT models shrinks until the performance is matched on the entire dataset.
图2：左图： ImageNet准确性/培训成本表2中列出的SOTA模型的帕累托边界（虚线） 。这些模型在ImageNet-21k或JFT（标记为MPL或伪标记为MPL）或嘈杂的Web图像文本对上进行了预训练。另外，我们还包括ViT-L / 16，Mixer-L / 16和BiT-R200x3（Adam）。Mixer与这些性能卓越的ResNet，ViT和混合模型一样出色，并且与HaloNet，ViT，NFNet和MPL一起处于前沿。 正确的： 随着数据大小的增加，混频器（实心）捕获或超过BiT（虚线）和ViT（虚线）。曲线上的每个点都使用相同的预训练计算。它们分别对应于在233、70、23和7个时期分别对JFT-300M进行3％，10％，30％和100％的预训练。与ResNets甚至是ViT相比，Mixer在数据方面的改进速度更快，并且大型Mixer和ViT模型之间的差距不断缩小，直到性能与整个数据集相匹配为止。
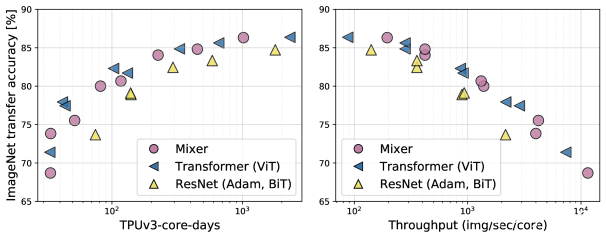Figure 3: The role of the model scale. ImageNet validation top-1 accuracy vs. total pre-training compute (left) and throughput (right) of ViT, BiT, and Mixer models at various scales. All models are pre-trained on JFT-300M and fine-tuned at resolution 224, which is lower than in Figure 2 (left).
图3： 模型规模的作用。ImageNet验证top-1准确性与各种规模的ViT，BiT和Mixer模型的总预训练计算（左）和吞吐量（右）的对比。所有型号均在JFT-300M上进行了预训练，并以224的分辨率进行了微调，该分辨率低于图2 （左）中的分辨率 。
3.2THE ROLE OF THE MODEL SCALE
The results outlined in the previous section focus on (large) models at the upper end of the compute spectrum. We now turn our attention to smaller Mixer models.
We may scale the model in two independent ways: (1) Increasing the model size (number of layers, hidden dimension, MLP widths) when pre-training. (2) Increasing the input image resolution when fine-tuning. While the former affects both pre-training compute and test-time throughput, the latter only affects the throughput. Unless stated otherwise, we fine-tune at resolution 224.
上一节概述的结果集中在计算范围上限的（大型）模型上。现在，我们将注意力转向较小的Mixer模型。
我们可以通过两种独立的方法来缩放模型：（1）在预训练时增加模型的大小（层数，隐藏尺寸，MLP宽度）。（2）微调时增加输入图像的分辨率。前者会影响预训练计算量和测试时间吞吐量，而后者只会影响吞吐量。除非另有说明，否则我们将在224分辨率上进行微调
| Image | Pre-Train | ImNet | ReaL | Avg. 5 | Throughput | TPUv3 | |
|---|---|---|---|---|---|---|---|
| size | Epochs | top-1 | top-1 | top-1 | (img/sec/core) | core-days | |
| Pre-trained on ImageNet (with extra regularization) | |||||||
| Mixer-B/16 | 224 | 300 | 76.44 | 82.36 | 88.33 | 1384 | 0.01k(‡) |
| ViT-B/16 (☎) | 224 | 300 | 79.67 | 84.97 | 90.79 | 861 | 0.02k(‡) |
| Mixer-L/16 | 224 | 300 | 71.76 | 77.08 | 87.25 | 419 | 0.04k(‡) |
| ViT-L/16 (☎) | 224 | 300 | 76.11 | 80.93 | 89.66 | 280 | 0.05k(‡) |
| Pre-trained on ImageNet-21k (with extra regularization) | |||||||
| Mixer-B/16 | 224 | 300 | 80.64 | 85.80 | 92.50 | 1384 | 0.15k(‡) |
| ViT-B/16 (☎) | 224 | 300 | 84.59 | 88.93 | 94.16 | 861 | 0.18k(‡) |
| Mixer-L/16 | 224 | 300 | 82.89 | 87.54 | 93.63 | 419 | 0.41k(‡) |
| ViT-L/16 (☎) | 224 | 300 | 84.46 | 88.35 | 94.49 | 280 | 0.55k(‡) |
| Mixer-L/16 | 448 | 300 | 83.91 | 87.75 | 93.86 | 105 | 0.41k(‡) |
| Pre-trained on JFT-300M | |||||||
| Mixer-S/32 | 224 | 5 | 68.70 | 75.83 | 87.13 | 11489 | 0.01k |
| Mixer-B/32 | 224 | 7 | 75.53 | 81.94 | 90.99 | 4208 | 0.05k |
| Mixer-S/16 | 224 | 5 | 73.83 | 80.60 | 89.50 | 3994 | 0.03k |
| BiT-R50x1 | 224 | 7 | 73.69 | 81.92 | — | 2159 | 0.08k |
| Mixer-B/16 | 224 | 7 | 80.00 | 85.56 | 92.60 | 1384 | 0.08k |
| Mixer-L/32 | 224 | 7 | 80.67 | 85.62 | 93.24 | 1314 | 0.12k |
| BiT-R152x1 | 224 | 7 | 79.12 | 86.12 | — | 932 | 0.14k |
| BiT-R50x2 | 224 | 7 | 78.92 | 86.06 | — | 890 | 0.14k |
| BiT-R152x2 | 224 | 14 | 83.34 | 88.90 | — | 356 | 0.58k |
| Mixer-L/16 | 224 | 7 | 84.05 | 88.14 | 94.51 | 419 | 0.23k |
| Mixer-L/16 | 224 | 14 | 84.82 | 88.48 | 94.77 | 419 | 0.45k |
| ViT-L/16 | 224 | 14 | 85.63 | 89.16 | 95.21 | 280 | 0.65k |
| Mixer-H/14 | 224 | 14 | 86.32 | 89.14 | 95.49 | 194 | 1.01k |
| BiT-R200x3 | 224 | 14 | 84.73 | 89.58 | — | 141 | 1.78k |
| Mixer-L/16 | 448 | 14 | 86.78 | 89.72 | 95.13 | 105 | 0.45k |
| ViT-H/14 | 224 | 14 | 86.65 | 89.56 | 95.57 | 87 | 2.30k |
| Mixer-H/14 | 448 | 14 | 87.78 | 90.08 | 95.62 | 40 | 1.01k |
| ViT-L/16(†) Dosovitskiy et al. (2021) | 512 | 14 | 87.76 | 90.54 | 95.63 | 32 | 0.65k |
| BiT-R152x4 Kolesnikov et al. (2020) | 480 | 40 | 87.54 | 90.54 | 95.33 | 26 | 9.90k |
| ViT-H/14(†) Dosovitskiy et al. (2021) | 518 | 14 | 88.55 | 90.72 | 95.97 | 15 | 2.30k |
Table 3: Performance of Mixer and other models from the literature across various model and pre-training dataset scales. “Avg. 5” denotes the average performance across five downstream tasks and is presented where available. Mixer and ViT models are averaged over three fine-tuning runs and standard deviations are smaller than 0.15. (†) ViT models reported were fine-tuned with Polyak averaging Polyak and Juditsky (1992). (‡) Extrapolated from the numbers reported for the same models pre-trained on JFT-300M without extra regularization. (☎) Numbers provided by authors of Dosovitskiy et al. (2021) through personal communication. Rows are sorted by throughput.
表3： 文献中各种模型和预训练数据集范围内的混频器和其他模型的性能。“平均 5”表示五个下游任务的平均性能，并在可用时显示。混频器和ViT模型在三个微调运行中取平均值，并且标准偏差小于0.15。（†）用Polyak平均Polyak和Juditsky（1992）对报告的ViT模型进行了微调。（‡）从在JFT-300M上预训练的相同模型的报告数量中推算得出，而没有进行额外的正则化处理。（☎）Dosovitskiy等人的作者提供的编号 。（2021）通过个人交流。行按吞吐量排序。
We compare various configurations of Mixer (see Table 1) to ViT models of similar scales and BiT models pre-trained with Adam. The results are summarized in Table 3 and Figure 3. When trained from scratch on ImageNet, Mixer-B/16 achieves a reasonable top-1 accuracy of 76.44%. This is 3% behind the ViT-B/16 model. The training curves (not reported) reveal that both models achieve very similar values of the training loss. In other words, Mixer-B/16 overfits more than ViT-B/16. For the Mixer-L/16 and ViT-L/16 models this difference is even more pronounced.
我们将Mixer的各种配置（请参见表 1）与类似规模的ViT模型和经过Adam预先训练的BiT模型进行了比较。结果总结在表 3和图 3中。在ImageNet上从头开始进行培训时，Mixer-B / 16达到了76.44％的合理的top-1精度。这比ViT-B / 16型号落后3％。训练曲线（未报告）显示，这两个模型均获得非常相似的训练损失值。换句话说，Mixer-B / 16比ViT-B / 16更适合。对于Mixer-L / 16和ViT-L / 16模型，这种差异更加明显。
As the pre-training dataset grows, Mixer’s performance steadily improves. Remarkably, Mixer-H/14 pre-trained on JFT-300M and fine-tuned at 224 resolution is only 0.3% behind ViT-H/14 on ImageNet whilst running 2.2 times faster. Figure 3 clearly demonstrates that although Mixer is slightly below the frontier on the lower end of model scales, it sits confidently on the frontier at the high end.
随着预训练数据集的增长，Mixer的性能稳步提高。值得注意的是，在JFT-300M上进行预训练并以224分辨率进行微调的Mixer-H / 14仅比ImageNet上的ViT-H / 14落后0.3％，而运行速度却快2.2倍。图 3清楚地表明，尽管Mixer在模型比例尺的较低端略低于边界，但它有把握地位于高端的边界。
3.3THE ROLE OF THE PRE-TRAINING DATASET SIZE
The results presented thus far demonstrate that pre-training on larger datasets significantly improves Mixer’s performance. Here, we study this effect in more detail.
迄今为止提供的结果表明，在较大的数据集上进行预训练可以显着提高Mixer的性能。在这里，我们将更详细地研究这种效果。
To study Mixer’s ability to make use of the growing number of training examples we pre-train Mixer-B/32, Mixer-L/32, and Mixer-L/16 models on random subsets of JFT-300M containing 3%, 10%, 30% and 100% of all the training examples for 233, 70, 23, and 7 epochs. Thus, every model is pre-trained for the same number of total steps. We use the linear 5-shot top-1 accuracy on ImageNet as a proxy for transfer quality. For every pre-training run we perform early stopping based on the best upstream validation performance. Results are reported in Figure 2 (right), where we also include ViT-B/32, ViT-L/32, ViT-L/16, and BiT-R152x2 models.
为了研究Mixer利用越来越多的训练示例的能力，我们对JFT-300M的随机子集（包含3％，10％）的Mixer-B / 32，Mixer-L / 32和Mixer-L / 16模型进行了预训练，分别在233、70、23和7个纪元的所有训练示例中占30％和100％。因此，每个模型都针对相同数量的总步骤进行了预训练。我们使用ImageNet上的线性5拍top-1精度作为传输质量的代理。对于每一次预训练，我们都会根据最佳的上游验证性能来尽早停止。结果报告在图 2 （右）中，其中我们还包括ViT-B / 32，ViT-L / 32，ViT-L / 16和BiT-R152x2模型。
When pre-trained on the smallest subset of JFT-300M, all Mixer models strongly overfit. BiT models also overfit, but to a lesser extent, possibly due to the strong inductive biases associated with the convolutions. As the dataset increases, the performance of both Mixer-L/32 and Mixer-L/16 grows faster than BiT; Mixer-L/16 keeps improving, while the BiT model plateaus.
当在JFT-300M的最小子集上进行预训练时，所有Mixer型号都过度适合。BiT模型也过拟合，但程度较小，这可能是由于与卷积相关的强烈归纳偏差。随着数据集的增加，Mixer-L / 32和Mixer-L / 16的性能增长都快于BiT。Mixer-L / 16持续改进，而BiT模型则处于稳定状态。
The same conclusions hold for ViT, consistent with Dosovitskiy et al. (2021). However, the relative improvement of larger Mixer models are even more pronounced. The performance gap between Mixer-L/16 and ViT-L/16 shrinks with data scale. It appears that Mixer models benefit from the growing pre-training dataset size even more than ViT. One could speculate and explain it again with the difference in inductive biases. Perhaps, self-attention layers in ViT lead to certain properties of the learned functions that are less compatible with the true underlying distribution than those discovered with Mixer architecture.
ViT的结论相同，与Dosovitskiy等人一致。（2021年）。但是，较大的Mixer模型的相对改进更加明显。Mixer-L / 16和ViT-L / 16之间的性能差距随着数据规模的缩小而缩小。看来，Mixer模型受益于不断增长的预训练数据集规模，其收益甚至超过了ViT。人们可以通过感应偏置的差异来推测和解释它。也许，ViT中的自我注意层会导致学习功能的某些属性，这些属性与真正的基础分布不兼容，而与Mixer体系结构所发现的功能不兼容。
 |
 |
 |
|---|
Figure 4: A selection of input weights to the hidden units in the first (left), second (center), and third (right) token-mixing MLPs of a Mixer-B/16 model trained on JFT-300M. Each unit has 14×14=196 weights, one for each of the 14×14 incoming patches. We pair units whose inverse is closest, to easily visualize the emergence of kernels of opposing phase. Pairs are sorted approximately by filter frequency. We highlight that in contrast to the kernels of convolutional filters, where each weight corresponds to one pixel in the input image, one weight in any plot from the left column corresponds to a particular 16×16 patch of the input image. Complete plots in Supplementary D.
图4：在JFT-300M上训练的Mixer-B / 16模型 的第一个（左），第二个（中心）和第三个（右）令牌混合MLP中，向隐藏单元的输入权重的选择。每个单元都有14×14=196 砝码，每个 14×14传入补丁。我们将其逆序最接近的单元配对，以轻松可视化反相内核的出现。对大约按滤波器频率排序。我们强调指出，与卷积滤波器的内核不同，卷积滤波器的内核中的每个权重对应于输入图像中的一个像素，而左列中任何图中的一个权重都对应于特定的16×16输入图像的补丁。在补充D中完成情节 。
3.4VISUALIZATION
It is commonly observed that the first layers of CNNs tend to learn Gabor-like detectors that act on pixels in local regions of the image. In contrast, Mixer allows for global information exchange in the token-mixing MLPs, which begs the question whether it processes information in a similar fashion.
Figure 4 shows the weights in the first few token-mixing MLPs of Mixer trained on JFT-300M. Recall that the token-mixing MLPs allow communication between different spatial locations (see Figure 1). Some of the learned features operate on the entire image, while others operate on smaller regions. The first token-mixing MLP contains many local interactions, while the second and third layers contain more mixing across larger regions. Higher layers appear to have no clearly identifiable structure. Similar to CNNs, we observe that many of the low-level feature detectors appear in pairs with opposite phases Shang et al. (2016). In Supplementary D, we show that the structure of learned units depends on the hyperparameters and input augmentations. In the linear projection of the first patch embedding layer we observe a mixture of high and low frequency filters; we provide a visualization in Supplementary Figure 6.
通常观察到，CNN的第一层倾向于学习像Gabor一样的检测器，该检测器作用于图像局部区域中的像素。相反，Mixer允许在令牌混合MLP中进行全局信息交换，这引出了一个问题，即它是否以类似的方式处理信息。
图 4显示了在JFT-300M上训练的Mixer的前几个令牌混合MLP中的权重。回想一下，令牌混合MLP允许不同空间位置之间的通信（请参见图 1）。一些获悉的功能可在整个图像上运行，而其他功能可在较小的区域上运行。第一令牌混合MLP包含许多本地交互，而第二和第三层包含较大区域的更多混合。较高的层似乎没有明显可识别的结构。类似于细胞神经网络，我们观察到，许多低层次特征检测器出现在对具有相反相位 上等。（2016）。在补充 D中，我们证明了学习单元的结构取决于超参数和输入扩充。在第一个贴片嵌入层的线性投影中，我们观察到了高频和低频滤波器的混合。我们在补充图6中提供了可视化效果 。
4RELATED WORK
Mixer is a new architecture for computer vision that differs from previous successful architectures because it uses neither convolutional nor self-attention layers. Nevertheless, the design choices can be traced back to ideas from the literature on CNNs Krizhevsky et al. (2012); LeCun et al. (1989) and Transformers Vaswani et al. (2017).
CNNs have been the de facto standard in computer vision field since the AlexNet model Krizhevsky et al. (2012) surpassed prevailing approaches based on hand-crafted image features, see Pinz (2006) for an overview. An enormous amount of work followed, focusing on improving the design of CNNs. We highlight only the directions most relevant for this work. Simonyan and Zisserman (2015) demonstrated that a series of convolutions with a small 3×3 receptive field is sufficient to train state-of-the-art models. Later, He et al. (2016) introduced skip-connections together with the batch normalization layer Ioffe and Szegedy (2015), which enabled training of very deep neural networks with hundreds of layers and further improved performance. A prominent line of research has investigated the benefits of using sparse convolutions, such as grouped Xie et al. (2016) or depth-wise Chollet (2017); Howard et al. (2017) variants. Finally, Hu et al. (2018) and Wang et al. (2018) propose to augment convolutional networks with non-local operations to partially alleviate the constraint of local processing from CNNs.
Mixer是一种用于计算机视觉的新体系结构，与以前的成功体系结构不同，因为它既不使用卷积层也不使用自我注意层。然而，设计选择可以追溯到有关CNN的文献中的想法 Krizhevsky等。（2012）; LeCun等。（1989）和《变形金刚 Vaswani等》。（2017年）。
自从AlexNet模型Krizhevsky等人提出以来，CNN就已经成为计算机视觉领域的事实上的标准 。（2012年）超越了基于手工图像特征的流行方法，有关概述，请参见 Pinz（2006年）。随后进行了大量工作，重点在于改进CNN的设计。我们仅突出显示与此工作最相关的方向。 Simonyan和Zisserman（2015）证明了一系列的卷积与小3×3接收场足以训练最先进的模型。后来，他等人。（2016）引入了跳过连接以及批处理规范化层 Ioffe和Szegedy（2015），从而可以训练具有数百个层的非常深的神经网络，并进一步提高了性能。一项著名的研究调查了使用稀疏卷积的好处，例如分组 Xie等。（2016）或深度 Chollet（2017）；霍华德等。（2017）变体。最后，胡等人。（2018）和Wang等。（2018）提出用非本地操作来增强卷积网络，以部分缓解来自CNN的本地处理的约束。
Mixer takes the idea of using convolutions with small kernels to the extreme: by reducing the kernel size to 1×1 it effectively turns convolutions into standard dense matrix multiplications applied independently to each spatial location (channel-mixing MLPs). This modification alone does not allow aggregation of spatial information and to compensate we apply dense matrix multiplications that are applied to every feature across all spatial locations (token-mixing MLPs). In Mixer, matrix multiplications are applied row-wise or column-wise on the “patches×features” input table, which is also closely related to the work on sparse convolutions. Finally, Mixer makes use of skip-connections He et al. (2016) and normalization layers Ba et al. (2016); Ioffe and Szegedy (2015).
混合器将使用小内核卷积的想法达到了极致：将内核大小减小到1×如图1所示，它有效地将卷积转换为独立应用于每个空间位置的标准密集矩阵乘法（通道混合MLP）。单独进行此修改不允许聚合空间信息，并且为了进行补偿，我们应用了密集矩阵乘法，该乘法适用于所有空间位置中的每个要素（令牌混合MLP）。在Mixer中，矩阵乘法按行或按列应用于“补丁”×特征”输入表，该表也与稀疏卷积的工作紧密相关。最后，混频器利用了He等人的跳过连接 。（2016）和归一化层 Ba等。（2016）; 艾菲和塞格迪（2015）。
The initial applications of self-attention based Transformer architectures to computer vision were for generative modeling Child et al. (2019); Parmar et al. (2018). Their value for image recognition was demonstrated later, albeit in combination with a convolution-like locality bias Ramachandran et al. (2019), or on very low-resolution images Cordonnier et al. (2020). Recently, Dosovitskiy et al. (2021) introduced ViT, a pure transformer model that has fewer locality biases, but scales well to large data. ViT achieves state-of-the-art performance on popular vision benchmarks while retaining the robustness properties of CNNs Bhojanapalli et al. (2021). Touvron et al. (2020) showed that ViT can be trained effectively on smaller datasets using extensive regularization. Mixer borrows design choices from recent transformer-based architectures; the design of MLP-blocks used in Mixer originates from Vaswani et al. (2017). Further, converting images to a sequence of patches and then directly processing embeddings of these patches originates in Dosovitskiy et al. (2021).
Similar to Mixer, many recent works strive to design more effective architectures for vision. For example, Srinivas et al. (2021) replace 3×3 convolutions in ResNets by self-attention layers. Ramachandran et al. (2019), Li et al. (2021), and Bello ([2021](https://www.arxiv-vanity.com/papers/2105.01601/#S4.p5 "LambdaNetworks: modeling long-range interactio
