STYLEGAN2: Analyzing and Improving the Image Quality of StyleGAN 分析和改善 StyleGAN 的图像质量

Tero Karras
Samuli Laine
Miika Aittala
Janne Hellsten
Jaakko Lehtinen
Timo Aila

校对： 丫丫是只小狐狸

＞　译者语：stylegan改进版

摘要

StyleGAN在数据驱动的无条件生成图像建模中达到了最先进的结果。我们将揭露和分析其出现一些特征伪影的原因，并提出模型架构和训练方法方面的改进以解决这些问题。特别需要注意的是，我们重新设计了生成器归一化方法，重新审视了渐进式增长架构，并对生成器施加了正则化，使得从潜在矢量到图像的映射中得到良好质量的图像。除了改善图像质量外，使用路径长度调节器还带来了额外的好处，即生成器变得非常容易反转。这使得可以可靠地检测图像是否由特定网络生成。我们进一步对生成器是如何充分应用输出分辨率，并如何确定网络容量问题进行了可视化，从而激励我们训练更大的模型，以进一步提高质量。总体而言，我们改进的模型在现有的分布式指标质量和感知的图像质量方面都刷新了无条件图像建模的最先进技术指标。

ABSTRACT

The style-based GAN architecture (StyleGAN) yields state-of-the-art results in data-driven unconditional generative image modeling. We expose and analyze several of its characteristic artifacts, and propose changes in both model architecture and training methods to address them. In particular, we redesign generator normalization, revisit progressive growing, and regularize the generator to encourage good conditioning in the mapping from latent vectors to images. In addition to improving image quality, this path length regularizer yields the additional benefit that the generator becomes significantly easier to invert. This makes it possible to reliably detect if an image is generated by a particular network. We furthermore visualize how well the generator utilizes its output resolution, and identify a capacity problem, motivating us to train larger models for additional quality improvements. Overall, our improved model redefines the state of the art in unconditional image modeling, both in terms of existing distribution quality metrics as well as perceived image quality.

1 介绍 INTRODUCTION

The resolution and quality of images produced by generative methods, especially generative adversarial networks (GAN) [15], are improving rapidly [23, 31, 5]. The current state-of-the-art method for high-resolution image synthesis is StyleGAN [24], which has been shown to work reliably on a variety of datasets. Our work focuses on fixing its characteristic artifacts and improving the result quality further.

The distinguishing feature of StyleGAN [24] is its unconventional generator architecture. Instead of feeding the input latent code z∈Z only to the beginning of a the network, the mapping network f first transforms it to an intermediate latent code w∈W. Affine transforms then produce styles that control the layers of the synthesis network g via adaptive instance normalization (AdaIN) [20, 9, 12, 8]. Additionally, stochastic variation is facilitated by providing additional random noise maps to the synthesis network. It has been demonstrated [24, 38] that this design allows the intermediate latent space W to be much less entangled than the input latent space Z. In this paper, we focus all analysis solely on W, as it is the relevant latent space from the synthesis network’s point of view.

通过生成方法，尤其是生成对抗网络（GAN）[15]生成的图像的分辨率和质量正在迅速提高[23，31，5]。目前，用于高分辨率图像合成的最新方法是 StyleGAN [24]，它已被证明可以在各种数据集上可靠地工作。我们的工作重点是修复其特征伪影，并进一步提高结果质量。StyleGAN [24]的显著特征是其非常规的生成器体系结构。映射网络 f 不再将 输入隐编码 ${\bf z}\in\mathcal{Z}$输入网络，而是将其转换为中间隐编码
${\bf w}\in\mathcal{W}$。然后仿射变换生成控制图层的样式，并通过自适应实例归一化（AdaIN）[20、9、12、8]参与合成网络 g 进行合成。 另外，通过向合成网络提供额外的随机噪声图来促进随机变化.[24，38]研究表明，这种设计能让中间隐空间 W 比输入隐空间 Z 的纠缠少得多。。在本文中，我们所有的分析都只集中在 W 上，因为从合成网络的视角看，它是相关的隐空间。。

Many observers have noticed characteristic artifacts in images generated by StyleGAN [3]. We identify two causes for these artifacts, and describe changes in architecture and training methods that eliminate them. First, we investigate the origin of common blob-like artifacts, and find that the generator creates them to circumvent a design flaw in its architecture. In Section 2, we redesign the normalization used in the generator, which removes the artifacts. Second, we analyze artifacts related to progressive growing [23] that has been highly successful in stabilizing high-resolution GAN training. We propose an alternative design that achieves the same goal — training starts by focusing on low-resolution images and then progressively shifts focus to higher and higher resolutions — without changing the network topology during training. This new design also allows us to reason about the effective resolution of the generated images, which turns out to be lower than expected, motivating a capacity increase (Section 4).

Quantitative analysis of the quality of images produced using generative methods continues to be a challenging topic. Fréchet inception distance (FID) [19] measures differences in the density of two distributions in the high-dimensional feature space of a InceptionV3 classifier [39]. Precision and Recall (P&R) [36, 27] provide additional visibility by explicitly quantifying the percentage of generated images that are similar to training data and the percentage of training data that can be generated, respectively. We use these metrics to quantify the improvements.

Both FID and P&R are based on classifier networks that have recently been shown to focus on textures rather than shapes [11], and consequently, the metrics do not accurately capture all aspects of image quality. We observe that the perceptual path length (PPL) metric [24], introduced as a method for estimating the quality of latent space interpolations, correlates with consistency and stability of shapes. Based on this, we regularize the synthesis network to favor smooth mappings (Section 3) and achieve a clear improvement in quality. To counter its computational expense, we also propose executing all regularizations less frequently, observing that this can be done without compromising effectiveness.

Finally, we find that projection of images to the latent space W works significantly better with the new, path-length regularized generator than with the original StyleGAN. This has practical importance since it allows us to tell reliably whether a given image was generated using a particular generator (Section 5).

Our implementation and trained models are available at https://github.com/NVlabs/stylegan2

许多观察者已经注意到由 StyleGAN [3]生成的图像中的特征伪影。我们确定了造成这些伪影的两个原因，并描述了从结构和训练方法上进行改进来消除这些伪影的方法。
首先，我们研究了常见的斑点状伪影的起源，并发现生成器创建它们是为了规避其体系结构中的设计缺陷。在第 2 节中，我们重新设计了生成器中使用的归一化，该归一化消除了伪影。
其次，我们分析出伪影[23]和高分辨率 GAN 训练中很成功的一个方法 progressive growing渐进式增长相关。 我们提出了一个无需在训练中修改网络拓扑结构就能实现同样目标的设计-即训练从关注低分辨率图像开始，然后逐渐将焦点转移到越来越高的分辨率。这种新设计还能推理所生成图像的有效分辨率，事实证明这个有效分辨率低于预期，说明相关研究还有进一步的提升空间。

使用基于生成方法产生的图像质量的定量分析仍然是一个具有挑战性的话题。Frechet 初始距离（FID）[19]测量了InceptionV3 分类器的高维特征空间中两个分布的密度差异[39]。精确度和召回率（P＆R）[36，27]生成的与训练数据相似的图像的百分比和可以生成的训练数据的百分比，提供了额外的可见性。我们使用这些指标来量化stylegan2的改进。FID 和 P＆R 均基于分类器网络，最近已证明该分类器网络侧重于纹理而不是形状[11]，因此，这些度量不能准确地捕获图像质量的所有方面。我们观察到感知路径长度（PPL）度量[24]被引入作为一种估计潜在空间插值质量的方法，与形状的一致性和稳定性相关。在此基础上，我们对合成网络进行了正则化处理，以支持平滑映射（第 3 节），并明显实现了质量的提高。为了抵消其计算代价，我们建议不要么频繁地执行所有正则化，实验表明，这种做法其实对效果没什么影响。最后，我们发现，使用新的路径长度正则化生成器比使用原始 StyleGAN，将图像投影到潜在空间 W 的效果明显更好。这具有实际意义，因为这让我们可以可靠地辨别给定图像是否是用特定的生成器生成的。（第 5 节）。

我们的实施和经过训练的模型可在下方地址获得：https://github.com/NVlabs/stylegan2

2 消除因归一化导致的伪影 REMOVING NORMALIZATION ARTIFACTS

We begin by observing that most images generated by StyleGAN exhibit characteristic blob-shaped artifacts that resemble water droplets. As shown in Figure 1, even when the droplet may not be obvious in the final image, it is present in the intermediate feature maps of the generator The anomaly starts to appear around 64×64 resolution, is present in all feature maps, and becomes progressively stronger at higher resolutions. The existence of such a consistent artifact is puzzling, as the discriminator should be able to detect it.

We pinpoint the problem to the AdaIN operation that normalizes the mean and variance of each feature map separately, thereby potentially destroying any information found in the magnitudes of the features relative to each other. We hypothesize that the droplet artifact is a result of the generator intentionally sneaking signal strength information past instance normalization: by creating a strong, localized spike that dominates the statistics, the generator can effectively scale the signal as it likes elsewhere. Our hypothesis is supported by the finding that when the normalization step is removed from the generator, as detailed below, the droplet artifacts disappear completely.

我们首先观察到 StyleGAN 生成的大多数图像都呈现出类似于水滴的特征性斑点状伪影。如图 1 所示，即使水滴状伪影在最终图像中可能不明显，它也会出现在生成器的中间特征图中（见底部 1）。异常开始出现在 64×64 分辨率附近，并出现在所有特征图中，并且在更高的分辨率下变得越来越强。这种持续出现的伪影令人困惑，因为判别器应该能够检测到它。

我们将问题精确定位到 AdaIN 运算中，该运算分别归一化每个特征图的均值和方差，潜在地破坏在相关特征这个量级的一些信息。我们假设液滴伪影是生成器故意将信号强度信息偷偷经过实例归一化的结果：通过创建主导统计数据的强的局部尖峰，生成器可以有效地像在其它地方一样扩展该信号。研究者发现，：当从生成器中移除归一化步骤时，如下所述，水滴状伪影会完全消失。

图 1.实例归一化导致 StyleGAN 图像中出现类似水滴的伪影。这些在生成的图像中并不总是很明显，但是如果我们查看生成器网络内部的激活层，则问题始终存在，在所有从 64x64 分辨率开始的特征图中。这是困扰所有 StyleGAN 图像的系统性问题。

2.1. 生成器架构修正 GENERATOR ARCHITECTURE REVISITED

We will first revise several details of the StyleGAN generator to better facilitate our redesigned normalization. These changes have either a neutral or small positive effect on their own in terms of quality metrics.

Figure 2a shows the original StyleGAN synthesis network g [24], and in Figure 2b we expand the diagram to full detail by showing the weights and biases and breaking the AdaIN operation to its two constituent parts: normalization and modulation. This allows us to re-draw the conceptual gray boxes so that each box indicates the part of the network where one style is active (i.e., “style block”). Interestingly, the original StyleGAN applies bias and noise within the style block, causing their relative impact to be inversely proportional to the current style’s magnitudes. We observe that more predictable results are obtained by moving these operations outside the style block, where they operate on normalized data. Furthermore, we notice that after this change it is sufficient for the normalization and modulation to operate on the standard deviation alone (i.e., the mean is not needed). The application of bias, noise, and normalization to the constant input can also be safely removed without observable drawbacks. This variant is shown in Figure 2c, and serves as a starting point for our redesigned normalization.

我们将首先修改 StyleGAN 生成器的几个细节，以更好地促进我们重新设计归一化。就质量指标而言，这些变化本身产生中性或小小的积极影响。

图 2a 显示了原始的 StyleGAN 合成网络 g [24]，在图2b 中，我们将这张结构图的权重和偏差都展示出来，并将 AdaIN 操作分解为其两个组成部分：归一化和调制。这使我们可以重新绘制概念上的灰色框，以便每个框都指示网络中样式激活的部分（即“样式块”style block）。有趣的是，原始的 StyleGAN 在样式块内施加了偏置和噪音，使它们的相对影响与当前样式的大小成反比。
我们观察到，通过将这些操作移到style block之外（它们在未标准化的数据上进行操作），可以获得更可预测的结果。此外，我们注意到，在此更改之后，仅对标准偏差进行标准化和调制就足够了（即不需要均值）。对恒定输入应用的偏置，噪声和归一化也可以安全地消除，而没有明显的缺点。此变体如图 2c 所示，并作为我们重新设计的归一化的起点。

图 2.我们重新设计了 StyleGAN 合成网络的架构。（a）原始 StyleGAN，其中 A 表示从 W 学习的仿射变换，产生样式向量，而 B 表示噪声广播操作。（b）完整细节相同的图。在这里，我们将 AdaIN 分解为显式归一化后再进行调制，然后对每个特征图的均值和标准差进行操作。我们还对学习的权重（w），偏差（b）和常数输入（c）进行了注释，并重新绘制了灰色框，以便每个框都激活一种样式。激活函数（Leaky ReLU）总是在添加偏置后立即应用。（c）我们对原始架构进行了一些改动，这些改动在正文中是有效的。我们从一开始就删除了一些多余的操作，将 b 和 B 的相加移到样式的有效区域之外，并仅调整每个要素图的标准偏差。（d）修改后的体系结构使我们能够用“解调”操作代替实例归一化，该操作适用于与每个卷积层相关的权重。

2.2. 实例归一化修正 ### INSTANCE NORMALIZATION REVISITED

Given that instance normalization appears to be too strong, how can we relax it while retaining the scale-specific effects of the styles? We rule out batch normalization [21] as it is incompatible with the small minibatches required for high-resolution synthesis. Alternatively, we could simply remove the normalization. While actually improving FID slightly [27], this makes the effects of the styles cumulative rather than scale-specific, essentially losing the controllability offered by StyleGAN (see video). We will now propose an alternative that removes the artifacts while retaining controllability. The main idea is to base normalization on the expected statistics of the incoming feature maps, but without explicit forcing.

Recall that a style block in Figure 2c consists of modulation, convolution, and normalization. Let us start by considering the effect of a modulation followed by a convolution. The modulation scales each input feature map of the convolution based on the incoming style, which can alternatively be implemented by scaling the convolution weights:

鉴于实例归一化似乎过于强大，我们如何在保留样式特定比例的效果的同时减弱它呢？我们排除了批量归一化[21]，因为它与高分辨率合成所需的小型minibatch不兼容。或者，我们可以简单地删除归一化。尽管实际上稍微改善了FID [27]，但这使样式的效果得以累积而不是特定于比例，从而实质上失去了 StyleGAN 提供的可控制性（请参见视频）。现在，我们将提出一种替代方法，该方法在保留可控制性的同时删除了伪影。主要思想是基于传入特征图的预期统计量进行归一化，不显式强制。回想一下，图 2c 中的样式块由调制，卷积和归一化组成。让我们开始考虑卷积后的调制效果。调制根据输入样式缩放卷积的每个输入特征图，也可以通过缩放卷积权重来实现：
$$w'{ijk} = s_i \cdot w{ijk}$$

where w and w′ are the original and modulated weights, respectively, si is the scale corresponding to the ith input feature map, and j and k enumerate the output feature maps and spatial footprint of the convolution, respectively.

Now, the purpose of instance normalization is to essentially remove the effect of s from the statistics of the convolution’s output feature maps. We observe that this goal can be achieved more directly. Let us assume that the input activations are i.i.d. random variables with unit standard deviation. After modulation and convolution, the output activations have standard deviation of

其中 w 和 $w^{\prime}$分别是原始权重和调制权重，$s_i$ 是与第i 个输入特征图相对应的比例，而 j 和 k 分别列举输出特征图和卷积的空间下标。现在，实例归一化的目的是从卷积输出特征图的统计信息中实质上消除 s 的影响。我们观察到可以更直接地实现这一目标。让我们假设输入激活是独立同分布,带有单位标准偏差的随机变量。经过调制和卷积后，输出激活的标准偏差为$\sigma_{j}=\sqrt{{\sum{}}{w^{\prime}_{ijk}}^{2}}\tag 2$

i.e., the outputs are scaled by the L2 norm of the corresponding weights. The subsequent normalization aims to restore the outputs back to unit standard deviation. Based on Equation 2, this is achieved if we scale (“demodulate”) each output feature map j by 1/σj. Alternatively, we can again bake this into the convolution weights:

即，通过相应权重的 L2 范数来缩放输出。随后的标准化旨在将输出恢复为单位标准偏差。基于等式 2，如果我们将每个输出特征图 j 缩放（“解调”） ，则可以实现此目的。 或者，我们可以再次将其嵌入到卷积权重中:
$$
\begin{equation}
w''{ijk} = w'{ijk} \bigg/ \sqrt{\raisebox{0mm}[4.0mm][2.5mm]{\underset{i,k}{{}\displaystyle\sum{}}} {w'_{ijk}}^2 + \epsilon},
\label{eq:demodulation}
\end{equation}
$$

is a small constant to avoid numerical issues.

其中ϵ是避免数值问题的小常数。

We have now baked the entire style block to a single convolution layer whose weights are adjusted based on s using Equations 1 and 3 (Figure 2d). Compared to instance normalization, our demodulation technique is weaker because it is based on statistical assumptions about the signal instead of actual contents of the feature maps. Similar statistical analysis has been extensively used in modern network initializers [13, 18], but we are not aware of it being previously used as a replacement for data-dependent normalization. Our demodulation is also related to weight normalization [37] that performs the same calculation as a part of reparameterizing the weight tensor. Prior work has identified weight normalization as beneficial in the context of GAN training [42].

Our new design removes the characteristic artifacts (Figure 3) while retaining full controllability, as demonstrated in the accompanying video. FID remains largely unaffected (Table 1, rows a, b), but there is a notable shift from precision to recall. We argue that this is generally desirable, since recall can be traded into precision via truncation, whereas the opposite is not true [27]. In practice our design can be implemented efficiently using grouped convolutions, as detailed in Appendix B. To avoid having to account for the activation function in Equation 3, we scale our activation functions so that they retain the expected signal variance.

现在，我们已经将整个样式块嵌入到单个卷积层，其权重使用公式 1 和 3 基于 s 进行调整（图 2d）。与实例归一化相比，我们的解调技术较弱，因为它基于信号的统计假设，而不是特征图的实际内容。类似的统计分析已在现代网络初始化程序中广泛使用[13，18]，但我们不知道它先前已被用来代替依赖数据的归一化。我们的解调也与权重归一化[37]有关，权重归一化[37]执行与重新设定权重张量相同的计算。先前的工作已经证明权重归一化在 GAN 训练中是有益的[42]。我们的新设计消除了特征伪影（图 3），同时保持了完全的可控制性，如随附视频所示。FID 基本上不受影响（表1，行 A，B），但是从 Precision 到 Recall 有着明显的转变。我们认为这通常是合乎需要的，因为可以通过截断将召回率转换为精度，但事实并非如此[27]。实际上，我们的设计可以是如附录 B 所述，使用分组卷积有效地实现该功能。为避免必须在公式 3 中考虑激活函数，我们对激活函数进行缩放，以使其保留预期的信号方差。

图 3.用解调代替归一化可从图像和激活中删除特征伪像。

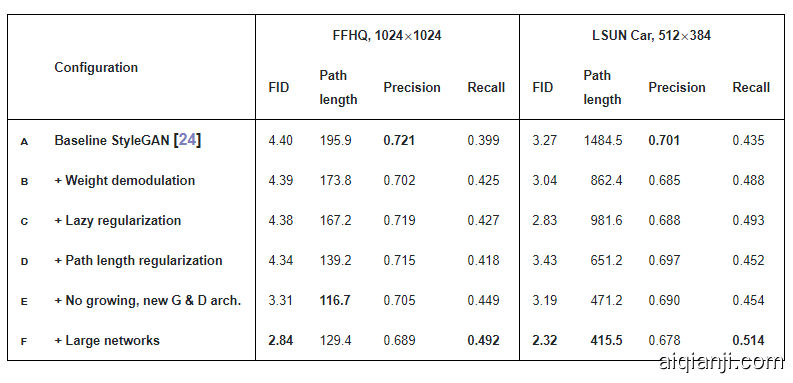
表 1：主要结果。对于每次训练过程，这里选出的都是 FID 最低的训练快照。研究者使用不同的随机种子计算了每个指标 10 次，并报告了平均结果。「path length」一列对应于 PPL 指标，这是基于 W 中的路径端点（path endpoints）而计算得到的。对于 LSUN 数据集，报告的路径长度是原本为 FFHQ 提出的无中心裁剪的结果。FFHQ 数据集包含 7 万张图像，研究者在训练阶段向判别器展示了 2500 万张图像。对于 LSUN CAR 数据集，对应的数字是 89.3 万和 5700 万。

3. 图像质量和生成器平滑度 IMAGE QUALITY AND GENERATOR SMOOTHNESS

While GAN metrics such as FID or Precision and Recall (P&R) successfully capture many aspects of the generator, they continue to have somewhat of a blind spot for image quality. For an example, refer to Figures 13 and 14 that contrast generators with identical FID and P&R scores but markedly different overall quality.

尽管 GAN 度量标准（例如 FID(Frechet inception distance) 或 Precision and Recall（P＆R））成功地捕获了生成器的许多方面，但它们仍然在图像质量上处于盲点。例如，请参考图 13 和图 14，它们对比了具有相同 FID 和 P＆R 分数但整体质量明显不同的生成器。 （我们认为，明显的不一致的关键在于要素空间的特定选择，而不是 FID 或 P＆R 的基础。最近发现，使用 ImageNet [35]训练的分类器倾向于将决策更多地基于纹理而不是形状[11]，而人类则强烈关注形状[28]。这是有意义的，因为 FID 和 P＆R 使用分别来自 InceptionV3 [39]和 VGG-16 [39]的高级特征，这些特征是通过这种方式进行训练的，因此可以预期偏向于纹理检测。这样，具有强烈的猫的纹理的图像可能看起来彼此更相似，比人类观察者所在意的细节还要强，从而部分损害了基于密度的度量（FID）和多方面的覆盖度量（P＆R）。）

We observe an interesting correlation between perceived image quality and perceptual path length (PPL) [24], a metric that was originally introduced for quantifying the smoothness of the mapping from a latent space to the output image by measuring average LPIPS distances [49] between generated images under small perturbations in latent space. Again consulting Figures 13 and 14, a smaller PPL (smoother generator mapping) appears to correlate with higher overall image quality, whereas other metrics are blind to the change. Figure 4 examines this correlation more closely through per-image PPL scores computed by sampling latent space around individual points in W on StyleGAN trained on LSUN Cat: low PPL scores are indeed indicative of high-quality images, and vice versa. Figure 5a shows the corresponding histogram of per-image PPL scores and reveals the long tail of the distribution. The overall PPL for the model is simply the expected value of the per-image PPL scores.

It is not immediately obvious why a low PPL should correlate with image quality. We hypothesize that during training, as the discriminator penalizes broken images, the most direct way for the generator to improve is to effectively stretch the region of latent space that yields good images. This would lead to the low-quality images being squeezed into small latent space regions of rapid change. While this improves the average output quality in the short term, the accumulating distortions impair the training dynamics and consequently the final image quality.

我们观察到了感知的图像质量和感知路径长度（PPL）之间的有趣关系[24]，该指标最初是通过测量在隐空间中的小扰动下生成的图像之间的平均 LPIPS 距离来量化从隐空间到输出图像的映射平滑度的指标[49]。再次参考图 13 和14，较小的PPL（平滑的生成器映射）似乎与较高的整体图像质量相关，而其他指标则看不到该变化。 图 4 证明这种相关性更强，通过在 LSUN CAT 上训练的 StyleGAN 上的 W 上各个点周围的潜在空间采样得出的每幅图像 PPL 分数可以了解到：PPL 分数低实际上表示图像的质量高，反之亦然。

图 4.使用基线 StyleGAN（表 1 中的配置 A）在感知路径长度和图像质量之间建立联系。（a）PPL 低（≤第 10 个百分点）的随机例子。（b）PPL 高（≥第 90 个百分点）的示例。 PPL 分数与图像的语义一致性之间存在明显的相关性。

图 5a 显示了每个图像 PPL 得分的相应直方图，并揭示了分布的长尾。该模型的总体 PPL 只是每个图像 PPL 得分的预期值。为何 PPL 值低与图像质量的关联不太明显？我们假设在训练过程中，由于判别器会对残破的图像进行惩罚，因此生成器改进的最直接方法是有效地拉伸产生良好图像的潜在空间区域，这将导致劣质图像被压缩进快速变化的小型隐藏空间。虽然这可以在短期内提高平均输出质量，但累积的失真会损害训练状态，进而由此影响最终的图像质量。

This empirical correlation suggests that favoring a smooth generator mapping by encouraging low PPL during training may improve image quality, which we show to be the case below. As the resulting regularization term is somewhat expensive to compute, we first describe a general optimization that applies to all regularization techniques.

这种经验相关性表明，在训练过程中通过鼓励低 PPL来支持平滑的生成器映射可能会改善图像质量。实验表明，事实确实如此。由于所得到的正则化项在一定程度上计算成本较高，所以首先描述了一种可应用于所有正则化技术的通用优化方法。

3.1. 延迟正则化（Lazy regularization）

Typically the main loss function (e.g., logistic loss [15]) and regularization terms (e.g., R1 [30]) are written as a single expression and are thus optimized simultaneously. We observe that typically the regularization terms can be computed much less frequently than the main loss function, thus greatly diminishing their computational cost and the overall memory usage. Table 1, row c shows that no harm is caused when R1 regularization is performed only once every 16 minibatches, and we adopt the same strategy for our new regularizer as well. Appendix B gives implementation details.

通常，主要损失函数（例如，逻辑损失[15]）和正则化项（例如， [30]）被写为一个表达式，因此被同时优化。我们观察到，正规化项的计算频率通常比主要损失函数低得多，从而大大降低了它们的计算成本和整体内存使用量。表 1 中的 C 行显示，每 16 个小批量仅执行一次 正则化时，不会造成任何危害，并且我们对新的正则化器也采用了相同的策略。附录 B 给出了实现细节。

3.2. 路径长度正则化 PATH LENGTH REGULARIZATION

Excess path distortion in the generator is evident as poor local conditioning: any small region in W becomes arbitrarily squeezed and stretched as it is mapped by g. In line with earlier work [33], we consider a generator mapping from the latent space to image space to be well-conditioned if, at each point in latent space, small displacements yield changes of equal magnitude in image space regardless of the direction of perturbation.

At a single w∈W, the local metric scaling properties of the generator mapping g(w):W↦Y are captured by the Jacobian matrix Jw=∂g(w)/∂w. Motivated by the desire to preserve the expected lengths of vectors regardless of the direction, we formulate our regularizer as

生成器中的路径失真过大显然是不良的局部条件：W中的任何小区域在被 g 映射时都会被任意挤压和拉伸。与早期工作[33]一致，如果在潜在空间中的每个点处，小的位移都在图像空间中产生相同大小的变化，而与摄动方向无关，则我们认为从潜在空间到图像空间的生成器映射条件良好。在单个${\bf w}\in\mathcal{W}$处，生成器映射g $g({\bf w}):\mathcal{W}\mapsto\mathcal{Y}$ 的局部度量比例缩放属性由雅可比矩阵$\mathbf{J}_{\bf w}={\partial g({\bf w})}/{\partial{\bf w}}$捕获。出于保持向量预期长度（无论方向如何）的动机，我们将正则化定义为：

$$\mathbb{E}{{\bf w},{\bf y}\sim\mathcal{N}(0,\mathbf{I})}\left( \left\lVert\mathbf{J}{\bf w}^{T}{\bf y}\right\rVert_{2}-a \right)^{2} \tag 4$$

where y are random images with normally distributed pixel intensities, and w∼f(z), where z are normally distributed. We show in Appendix C that, in high dimensions, this prior is minimized when Jw is orthogonal (up to a global scale) at any w. An orthogonal matrix preserves lengths and introduces no squeezing along any dimension.

To avoid explicit computation of the Jacobian matrix, we use the identity ${\bf J}^{T}{\bf w}{\bf y}=\nabla{\bf w}(g({\bf w})\cdot{\bf y})$, which is efficiently computable using standard backpropagation [6]. The constant a is set dynamically during optimization as the long-running exponential moving average of the lengths $\lVert{\bf J}^{T}{\bf w}{\bf y}\rVert{2}$, allowing the optimization to find a suitable global scale by itself.

其中 y 是具有正态分布像素强度的随机图像，而${\bf w}\sim f(\mathbf{z})$，其中 z 是正态分布。我们在附录 C 中显示，在高维上，当 $J_w$在任何 w 处都是正交的（最大到全局范围）时，该先验会最小化。正交矩阵会保留长度，并且不会沿任何维度压缩。为了避免对雅可比矩阵的显式计算，我们使用恒等式${\bf J}^{T}{\bf w}{\bf y}=\nabla{\bf w}(g({\bf w})\cdot{\bf y})$，它可以使用标准反向传播有效地计算[6]。
常数 a 在优化过程中动态设置为长度$\lVert{\bf J}^{T}{\bf w}{\bf y}\rVert{2}$ 的长期指数移动平均值，从而使优化本身可以找到合适的全局标度。

Our regularizer is closely related to the Jacobian clamping regularizer presented by Odena et al. [33]. Practical differences include that we compute the products$\mathbf{J}_{\bf w}\boldsymbol{\delta}$analytically whereas they use finite differences for estimating Jwδ with Z∋δ∼N(0,I). It should be noted that spectral normalization [31] of the generator [45] only constrains the largest singular value, posing no constraints on the others and hence not necessarily leading to better conditioning.

In practice, we notice that path length regularization leads to more reliable and consistently behaving models, making architecture exploration easier. Figure 5b shows that path length regularization clearly improves the distribution of per-image PPL scores. Table 1, row d shows that regularization reduces PPL, as expected, but there is a tradeoff between FID and PPL in LSUN Car and other datasets that are less structured than FFHQ. Furthermore, we observe that a smoother generator is easier to invert (Section 5).

我们的正则化器与 Odena 等人提出的 Jacobian“夹紧”正则化器密切相关[33]。实际的差异包括我们通过分析计算出乘积$\mathbf{J}_{\bf w}\boldsymbol{\delta}$，而它们使用有限的差异来估计满足$\mathcal{Z}\ni\boldsymbol{\delta}\sim\mathcal{N}(0,\mathbf{I})$的 。应当指出，生成器[45]的频谱归一化[31]仅约束最大奇异值，对其他奇异值没有约束，因此不一定导致更好的调节。
在实践中，我们注意到路径长度正则化导致更可靠和始终如一的行为模型，从而使架构探索更加容易。图 5b 显示，路径长度正则化明显改善了每个图像 PPL 分数的分布。表 1 的 D 行表明，正则化可以按预期方式降低 PPL，但在 LSUN CAR 和结构比 FFHQ 少的其他数据集中，FID和 PPL 之间需要权衡。此外，我们观察到，更平滑的生成器更易于反转（第 5 节）。

4. 渐进式增长修正 PROGRESSIVE GROWING REVISITED

Progressive growing [23] has been very successful in stabilizing high-resolution image synthesis, but it causes its own characteristic artifacts. The key issue is that the progressively grown generator appears to have a strong location preference for details; the accompanying video shows that when features like teeth or eyes should move smoothly over the image, they may instead remain stuck in place before jumping to the next preferred location. Figure 6 shows a related artifact. We believe the problem is that in progressive growing each resolution serves momentarily as the output resolution, forcing it to generate maximal frequency details, which then leads to the trained network to have excessively high frequencies in the intermediate layers, compromising shift invariance [48]. Appendix A shows an example. These issues prompt us to search for an alternative formulation that would retain the benefits of progressive growing without the drawbacks.

渐进生长[23]在稳定高分辨率图像合成方面已经非常成功，但它会导致其自身的特征失真。关键问题在于，逐渐增长的生成器似乎对细节的位置偏好很高。
随附的视频显示当牙齿或眼睛等特征在图像上平滑移动时，它们可能会停留在原位，然后跳到下一个首选位置。图 6 显示了相关的伪像。我们认为问题在于，在逐步增长的过程中，每个分辨率都会瞬间用作输出分辨率，迫使其生成最大频率细节，然后导致受过训练的网络在中间层具有过高的频率，从而损害了位移不变性[48]。附录 A 显示了一个示例。这些问题促使我们寻找一种替代方法，该方法将保留渐进式增长的好处而消除弊端。

4.1. 可选的网络架构 ALTERNATIVE NETWORK ARCHITECTURES

While StyleGAN uses simple feedforward designs in the generator (synthesis network) and discriminator, there is a vast body of work dedicated to the study of better network architectures. In particular, skip connections [34, 22], residual networks [17, 16, 31], and hierarchical methods [7, 46, 47] have proven highly successful also in the context of generative methods. As such, we decided to re-evaluate the network design of StyleGAN and search for an architecture that produces high-quality images without progressive growing.

Figure 7a shows MSG-GAN [22], which connects the matching resolutions of the generator and discriminator using multiple skip connections. The MSG-GAN generator is modified to output a mipmap [41] instead of an image, and a similar representation is computed for each real image as well. In Figure 7b we simplify this design by upsampling and summing the contributions of RGB outputs corresponding to different resolutions. In the discriminator, we similarly provide the downsampled image to each resolution block of the discriminator. We use bilinear filtering in all up and downsampling operations. In Figure 7c we further modify the design to use residual connections.3 This design is similar to LAPGAN [7] without the per-resolution discriminators employed by Denton et al.

虽然 StyleGAN 在生成器（合成网络）和判别器中使用简单的前馈设计，但仍有大量工作致力于研究更好的网络体系结构。特别地，在生成方法的背景下，跳跃连接[34、22]，残差网络[17、16、31]和分层方法[7、46、47]也被证明是非常成功的。因此，我们决定重新评估 StyleGAN 的网络设计，并寻找一种能够生成高质量图像而不会逐渐增长的体系结构。图 7a 显示了 MSG-GAN [22]，它使用多个跳越连接来连接生成器和判别器的匹配分辨率。修改了 MSG-GAN 生成器以输出多维图像（mipmap） [41]而不是图像，并且还为每个真实图像计算了类似的表示形式。在图 7b 中，我们通过上采样并求和对应于不同分辨率的 RGB 输出的贡献来简化此设计。在判别器中我们类似地将下采样的图像提供给判别器的每个分辨率块。我们在所有上采样和下采样操作中都使用了双线性滤波。在图 7c 中，我们进一步修改了设计以使用残差连接（见底部3）。此设计类似于 LAPGAN [7]，但没有 Denton 等人使用的逐分辨率判别器。

图 7：三种生成器（虚线上面）和判别器架构。Up 和 Down 分别表示双线性的上采样和下采样。在残差网络中，这些也包含用于调整特征图数量的 1×1 卷积。tRGB 和 fRGB 可将每个像素的数据在 RGB 和高维数据之间转换。配置 E 和 F 所用的架构用绿色标注。

Table 2 compares three generator and three discriminator architectures: original feedforward networks as used in StyleGAN, skip connections, and residual networks, all trained without progressive growing. FID and PPL are provided for each of the 9 combinations. We can see two broad trends: skip connections in the generator drastically improve PPL in all configurations, and a residual discriminator network is clearly beneficial for FID. The latter is perhaps not surprising since the structure of discriminator resembles classifiers where residual architectures are known to be helpful. However, a residual architecture was harmful in the generator — the lone exception was FID in LSUN Car when both networks were residual.

For the rest of the paper we use a skip generator and a residual discriminator, and do not use progressive growing. This corresponds to configuration e in Table 1, and as can be seen table, switching to this setup significantly improves FID and PPL.

表 2 比较了三种生成器架构和三种判别器架构：
StyleGAN 中使用的原始前馈网络，跳越连接和残差网络，所有这些网络的训练都没有用渐进式增长(progressive growing)。表中为 9 种组合都计算了 FID 和 PPL。我们可以看到两个趋势：在所有配置中，生成器中的跳越连接会大大改善 PPL，而残差的判别器网络显然对 FID 有利。后者也许不足为奇，因为判别器的结构就是分类器（残差结构会对分类器有利）。但是，残差的体系结构对生成器有害。当两个网络都是残差的时，唯一的例外是 LSUN CAR 中的 FID。在本文的其余部分，我们使用跳越生成器skip generator和残差判别器，而不使用渐进式增长。这对应于表 1 中的配置 E，从表中可以看出，切换到该设置可以显著改善 FID 和 PPL。

4.2. 分辨率的使用 RESOLUTION USAGE

The key aspect of progressive growing, which we would like to preserve, is that the generator will initially focus on low-resolution features and then slowly shift its attention to finer details. The architectures in Figure 7 make it possible for the generator to first output low resolution images that are