HDWallet 原理分析（zz）

AI数据  收藏
0 / 351

HDWallet 原理分析

种子是怎么一步步生成地址的？为何种子能管理那么多地址？为何能在不生成私钥的情况下直接派生出很多公钥？本文为您揭晓。

概述

分层确定性钱包，可以从一个种子派生出一系列密钥对用于生成地址，便于钱包的备份与管理

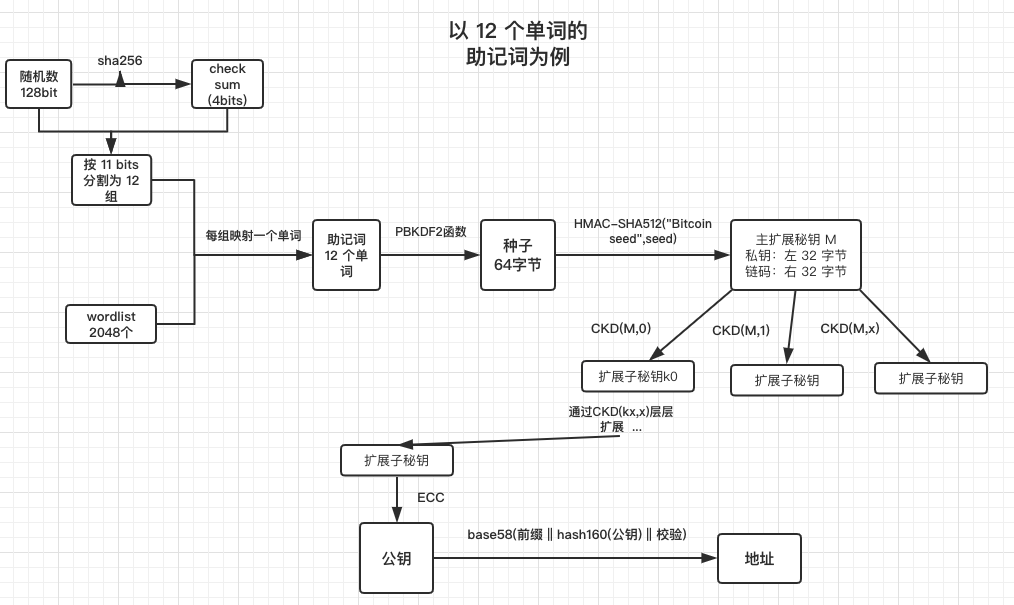
助记词、种子、公钥、地址之间的关系：

助记词与种子公钥与地址之间只能单向推导

hdwallet.png

涉及到的 BIP 协议：

  1. BIP39 定义助记词的生成规则和助记词到种子的推导规则
  2. BIP32 hd 钱包核心提案，定义分层概念和算法
  3. BIP44 定义 5 层路径规则
  4. BIP45 定义多签地址生成规则

本篇文章，我将对上述协议分别展开讨论与分析。

BIP39

此处查看 BIP39 文档

文档概要：

  • 定义了助记词的生成规则
  • 定义了助记词到种子的转换规则
  • 定义了助记词 wordlist，目前包含7种语言，每种 2048个单词
  • 助记词到种子的推导是单向的

助记词的生成：

  1. 产生一个随机数作为熵 entropy，长度为 128-256 bits，必须为 32 bits 的整数倍。
  2. 然后在 entropy 尾部追加校验 checksum，checksum 是取 entropy 的 sha256 哈希值的前 n 位，位数跟 entropy 的长度有关，具体如下：
entropy checksum entropy+checksum mnemonic
128 4 132 12
160 5 165 15
192 6 198 18
224 7 231 21
256 8 264 24
  1. 然后 将 entropy+checksum 进行分组，每组 11 bits，每组的取值范围是 0 ~ 2047，刚好映射 wordlist 里的单词。
  2. 将映射的单词以空格隔开拼接为字符串，即为助记词。

助记词到种子的推导：

通过 PBKDF2 函数生成大小为 64 byte 的种子。

PBKDF2（Password-Based Key Derivation Function 2）是一个基于口令的密钥推导方法，用于增强弱秘钥的安全性。本质上就是基于 hash 函数通过加盐和迭代因子让处理速度变慢，减少爆破风险。具体可参考 wiki

该函数定义如下：

DK = PBKDF2(PRF, Password, Salt, c, dkLen)

其中 ：

  • PRF 为伪随机函数相当于一个 hash 函数
  • Password 是口令，由用户负责安全
  • Salt 是盐，用于增加破解难度
  • c 是迭代次数，越大越安全
  • dkLen 是产生的密钥长度

在 bip39 中，用于产生种子的上述参数分别为：

  • HMAC-SHA512 单向的 hash 算法
  • 助记词字符串
  • “mnemonic"+passphrase（口令是可选的）
  • 2048
  • 512（bits）

由函数 PBKDF2 可知，助记词到种子的推导是单向的不可逆的。

代码参考：https://github.com/tpkeeper/addrtool

func TestGenMnemonic(t *testing.T) {
	//生成熵
	entropyBytes, _ := bip39.NewEntropy(128)
	t.Log("entropyBytes：", entropyBytes)

	//生成助记词
	mnemonic, _ := bip39.NewMnemonic(entropyBytes)
	t.Log("mnemonic：", mnemonic)
}
func TestMnemonicToSeed(t *testing.T) {
	mnemonic := "chef fiction deputy stage pudding pink skirt often decade drift music loop"
	//助记词生成种子 password 为空
	seed := bip39.NewSeed(mnemonic, "")
	t.Log("seed：", hex.EncodeToString(seed))
}

//output:
//entropyBytes： [158 45 139 248 16 245 71 178 223 231 241 118 0 211 244 134]
//mnemonic： owner hobby wrap capable federal sunny legend wreck invite alley wood aspect
//seed： 04ef53d66b17fdfb6538c5d183f0b0569fc1c79d07f044f7670c3038aff411e5abcbe8c457b584d0c1e3504ab94fb311f9097a793c20dfc746a87087ed5dc119

BIP32

查看文档 BIP32

概要：

  • 定义了由种子推导树状扩展密钥对的算法与规则

基本概念：

  • 扩展秘钥有两种，扩展私钥和扩展公钥，扩展私钥可以扩展子私钥，扩展公钥可以扩展子公钥
  • 扩展私钥定义为：(k , c)，其中 k 为私钥，c 为 链码 chaincode
  • 扩展公钥定义为：(K , c)，其中 K 为公钥，c 为 链码 chaincode
  • 子秘钥扩展方法定义为：CKD(extended key , index），其中参数为扩展秘钥和索引。

需要注意：

  • 扩展为非强化子秘钥时 index 范围为: 0~2^{31}-1，扩展为强化子秘钥时 index 范围为: 2^{31} ~ (2^{32}-1)
  • 只有扩展私钥才能扩展强化子扩展秘钥

扩展的具体过程：

  1. 首先计算主扩展秘钥，即树根对应的扩展秘钥。
    计算 HMAC-SHA512("Bitcoin seed" , seed) 得到 512 bits，其中参数 seed 是在 BIP32 中生成的种子。然后将结果分为 L 和 R，各占 32 字节，分别作为主扩展秘钥的私钥和链码，得到主扩展秘钥。
  2. 然后通过 CKD(extended key , index) 方法向下层层扩展子密钥。

CKD()方法扩展子秘钥有如下场景：

  1. 父扩展私钥 -> 强化子扩展私钥
  2. 父扩展私钥 -> 非强化子扩展私钥
  3. 父扩展公钥 -> 非强化子扩展公钥
  4. 父扩展公钥 -> 强化子扩展公钥(不允许)

ckd.png

有上图可知，场景 3，可以在不生成私钥的情况下，通过公钥扩展子公钥。这些公钥对应的私钥正好需要通过场景 2 来额外生成。具体的原理用到了椭圆曲线加密算法 ECC 的运算特性。途中的 || 是字节拼接操作，+ 和 x 都是 ECC 里的运算。在 ECC 中有以下定义：

key x G = pubKey

(key1 + key2) x G = pubKey1 + pubkey2

现在我们来证明 childPrivKey 就是 childPubKey 的私钥：

已知：

上图中场景 2 和场景 3，推导出的 il 是同一个值

il + parentPrivKey = childPrivKey

il x G + parentPubKey = childPubKey

我们可以得出：

il x G + parentPrivKey x G = childPrivKey x G

parentPrivKey x G = parentPubKey

进而得出：

il x G + parentPubkey = childPrivKey x G = childPubKey

所以 childPrivKey 就是 childPubkey 对应的私钥.

由以上过程分析，我们不难发现，ckd 方法的核心思想，就是父私钥加上一个随机数字得到子私钥，而这个随机数字的产生是需要一规则的，这样才能做到子地址可管理。

代码参考: https://github.com/tpkeeper/addrtool/

func TestSeedToPubkey(t *testing.T) {
	seed := "04ef53d66b17fdfb6538c5d183f0b0569fc1c79d07f044f7670c3038aff411e5abcbe8c457b584d0c1e3504ab94fb311f9097a793c20dfc746a87087ed5dc119"
	hexByte, _ := hex.DecodeString(seed)
	//m
	masterExtKey, _ := bip32.NewMasterKey(hexByte)
	//m/purpose'
	purposeExtKey, _ := masterExtKey.NewChildKey(bip32.FirstHardenedChild + 44)
	//m/purpose'/cointype'
	coinTypeExtKey, _ := purposeExtKey.NewChildKey(bip32.FirstHardenedChild + 0)
	//m/purpose'/cointype'/account'
	accountExtKey, _ := coinTypeExtKey.NewChildKey(bip32.FirstHardenedChild + 0)
	//m/purpose'/cointype'/account'/change
	changeExtKey, _ := accountExtKey.NewChildKey(0)
	//m/purpose'/cointype'/account'/change/addrIndex
	addrIndex0ExtKey, _ := changeExtKey.NewChildKey(0)
	//pubkey
	t.Log(hex.EncodeToString(addrIndex0ExtKey.PublicKey().Key))
}

BIP44

查看文档：BIP44

概要：

  • 定义了5层路径规则，可兼容多账号多币种

bip44 协议的 5 层路径规则：

路径：m/purpse’/coin_type’/account’/change/address_index（符号 ‘ 表示强化子秘钥，需要 index >= 2^{31}

  • m：主扩展密钥
  • purpose： bip44/bip45
  • coin_type： 币种
  • account： 钱包账户
  • change： 0 对外 / 1 找零
  • address_index： 地址索引

每一层对应的关系如下：
bip44.png

公钥的推导：

通过场景 1 和 2 扩展的子扩展密钥 (k,c)：

pubKey = k x G

通过场景 3 扩展的子扩展密钥 (K,c):

pubKey = K

地址的最终生成

简单的理解，地址就是 公钥或者脚本 的哈希值的 base58 格式。

常用的地址的格式：

P2PKH (Pay To PubKey Hash) 格式的地址

p2pkh_addr.png

P2SH (Pay To Script Hash) 格式的地址

p2sh_addr.png

前缀占用一个字节，表示地址类型。

hash160(pubkey) 占用 20 字节。

校验位占用 4 个字节，是对 前缀 + hash160(pubkey) 进行两次 sha256 取前四个字节。

使用 base58 便于更友好的显示，增加的校验还可以防止用户输入错误，bip32 中也是这种格式来显示扩展密钥。

代码参考：https://github.com/tpkeeper/addrtool

func PubkeyToAddress(key []byte, netId byte) string {
	hash160Bytes := btcutil.Hash160(key)
	return base58.CheckEncode(hash160Bytes, netId)
}

base58前缀目录一览：

其中 xpub xprv 就是 BIP32 中的扩展公/私密钥的 base58 导出格式

base58pre.png
关于作者更多信息请查看 : https://tpkeep.com

zz来源 https://learnblockchain.cn/article/784